Cuaderno de Cultura Científica

Mireia Martín, Erlantz Lizundia y Estibaliz Saez de Camara

Cuando decidimos cambiar de teléfono móvil valoramos distintos modelos en base a sus características y precios, pero, ¿sabemos el impacto ambiental y social de estos teléfonos? ¿sabemos cuántos móviles se desechan al año en el estado español? ¿por qué desechamos móviles que todavía funcionan? Es difícil saberlo con certeza, pero se estima que ronda los 20 millones de unidades, unas 2.000 toneladas de residuo. Dentro de esas 2.000 toneladas podemos encontrar una gran variedad de materiales, entre ellos el coltán u “oro negro”, un mineral compuesto principalmente por columbita y tantalita. Para conseguirlo, cientos de congoleños se encuentran en condiciones infrahumanas, trabajando de sol a sol entre 12 y 13 horas diarias, bajo la ausencia de prevención de riesgos laborales [1]. Sin embargo, muchos de esos dispositivos que se desechan todavía tienen valor comercial, ya sea porque funcionan o porque tienen en su interior materiales valiosos que se pueden reutilizar o reciclar. Es posible que de aquí a uno o dos años (por no decir meses) nuestros teléfonos móviles actuales parezcan anticuados, eso se debe a la obsolescencia percibida. Sale un nuevo modelo al mercado y ves que han mejorado todavía más la calidad de la cámara y, además, han aumentado la memoria interna. El móvil que hasta hace dos días te parecía como nuevo, ahora ya no te lo parece tanto y no sabes cuánto tardarás en desecharlo para comprar esa nueva versión. Y ahora viene la gran pregunta: ¿qué ocurre con estos residuos?

Foto: John Cameron en Unsplash

Global e-waste Monitor estimó que durante el año 2019 se produjeron alrededor de 53,6 Mt de Residuos de Aparatos Eléctricos y Electrónicos (RAEE) a nivel mundial, pudiendo alcanzar los 74 Mt en el año 2030 debido a la rápida evolución de la tecnología y por consiguiente las altas tasas de eliminación [2]. En el caso de la Unión Europea, sólo se procesa el 35% de los residuos electrónicos, el 65% restante forman parte de las «exportaciones mixtas no documentadas» que acaban en países como Nigeria, Ghana, Brasil, México, China, India, Vietnam, Filipinas y Pakistán. Estos países no cuentan con infraestructuras para llevar a cabo una correcta gestión, ni marcos regulatorios efectivos para tratar las fracciones de los RAEE que están clasificados como residuos peligrosos por contener compuestos tóxicos (tierras raras, mercurio…), halógenos y otros elementos metálicos como el oro y el cobre [3].

Fuente: Mireia Martín. Elaboración propia

La gestión inadecuada de estos residuos peligrosos, al igual que el reciclaje de hidrocarburos, la quema de residuos a cielo abierto o el depósito en vertederos, puede derivar en una acumulación de compuestos tóxicos en el medio terrestre y marino. Además, puede conllevar la liberación de hidrocarburos aromáticos policíclicos, generando un gran impacto en la salud de las personas, flora y fauna y el medio ambiente en general [4].

Clasificando la basura

Los RAEE se clasifican en función de la similitud funcional, la composición de los materiales y las características de obsolescencia. En el Anexo VIII del Real Decreto 27/2021, de 19 de enero, donde se modifica el Real Decreto 110/2015 sobre residuos de aparatos eléctricos y electrónicos se especifica la clasificación en 7 agrupamientos: equipos pequeños, equipos grandes, dispositivos de intercambio de temperatura, dispositivos de pantalla y monitor, equipos de iluminación, dispositivos informáticos y de telecomunicaciones y paneles fotovoltaicos [5]. La categoría con mayor contribución al flujo de residuos proviene de los equipos pequeños, con un total de 17,4 Mt registrados en 2019 [6].

Existe una segunda clasificación de los RAEE en función de los compuestos presentes: férricos, no-férricos (aluminio, cobre, etc.), plástico y otros materiales. Se estima que desechamos un total de 4000 toneladas de basura electrónica cada hora a nivel mundial [4]. En esos desechos podemos encontrar un conjunto de metales básicos, elementos preciosos y tierras raras o Rare-Earth Elements (REE). En este sentido, viendo que los REE son necesarios para una gran cantidad de aplicaciones eléctricas y electrónicas, la gran demanda actual y prevista y que, tras su uso, la tasa de reciclaje mundial es baja (17,4%), puede afirmarse que estos recursos se estén agotando. Un ejemplo es el neodimio (Nd) que se usa tanto en discos duros como en dispositivos de audio, automóviles y turbinas eólicas como imanes permanentes. Además del Nd, se pueden destacar muchos otros elementos del tipo REE en estos imanes: praseodimio (Pr), terbio (Tb), disprosio (Dy), gadolinio (Gd) y holmio (Ho). No obstante, a día de hoy sólo el 1% de los REE son reciclados, y el resto acaba en distintos vertederos eliminándose así el ciclo de los materiales [7].

Reciclar no es fácil

El reciclaje de estos componentes no es tarea fácil debido a la cantidad de elementos distintos que lo componen. Sin embargo, mediante la recuperación de estos elementos se podría mejorar en 3 niveles: ambientalmente, se minimiza el impacto que suponen las actividades de extracción; socialmente, se disminuye la dependencia actual en la cadena de suministro de REE; y económicamente, se estarían recuperando Elementos Tecnológicos Críticos (ETC) que son necesarios para sectores como el sanitario, las tecnologías de información y la comunicación y las tecnologías de energías limpias [4].

En 2019, únicamente se establecía una legislación sobre residuos electrónicos para el 68% de la población mundial (repartida en 78 países). Para 2023 se estima que exista legislación específica en 97 países. Además, en respuesta a la creciente tendencia con los residuos electrónicos, algunos países han aprobado normativa, políticas y están respaldando iniciativas como las de la Asociación para la Acción sobre Equipos de Cómputo (PACE), la Iniciativa Nacional de Administración de Productos Electrónicos (NEPSI) y la iniciativa de la Asociación de Teléfonos Móviles (MPPI) [4]. La UE cada vez está más cerca de introducir un cargador universal para dispositivos electrónicos pequeños, ya que tener distintos cargadores para distintos dispositivos produce una cantidad innecesaria de residuos electrónicos [8].

La extensión de la normativa traccionará avances en la gestión de estos residuos. Para estos avances resulta necesaria la I+D+i en el ámbito de reciclaje de los RAEE y sus componentes. Los RAEE son una mezcla compleja que consta de componentes como REE, otros elementos tecnológicamente críticos (como litio, níquel, platino, etc.), metales y plásticos. La mayoría de los procesos de reciclaje de estos componentes requieren el uso de ácidos fuertes y/o disolventes tóxicos y, además, operan a altas temperaturas, a expensas de la sostenibilidad ambiental. Los subproductos tóxicos resultantes del reciclaje de los REE plantean impactos ambientales negativos, por lo que únicamente se pueden lograr estrategias distintivas mediante la separación selectiva de los RAEE. Otro problema que dificulta el reciclaje de los REE es la falta de métodos rentables para purificar la mezcla de RAEE resultante. A todo lo anterior se suma una normativa ambiental laxa y no aplicada, los problemas de diseño y la negligencia por parte de las empresas mineras. Existe la necesidad de una mayor sensibilización de las personas y organizaciones productoras y consumidoras a todos los niveles a través de publicidad, campañas y otras herramientas [4].

Procesos para reducir el impacto ambiental

Una de las estrategias exitosas y ya implementadas para reducir el impacto ambiental de la extracción de REE son los procesos biológicos de biosorción y biolixiviación. En este sentido, los biomateriales orgánicos, como bacterias, algas, hongos, así como resinas y carbón activado, tienen la capacidad de adsorber REE durante el reciclaje. Los biomateriales, a pesar de ser menos eficientes en comparación con los productos químicos convencionales, tienen un impacto significativamente menor en el medio ambiente. Además, con las mejoras en la utilización de biomateriales aún están en curso, incluida la optimización de procesos, la mejora de cepas microbianas a través de técnicas de mutación, etc. se espera que sustituyan a los productos químicos convencionales a corto plazo [9].

La elección del método de reciclaje depende de la materia prima, el contenido de REE, la composición química de los RAEE, el coste económico y la huella ambiental del método. Para que la recuperación de los materiales sea económicamente viable, los costes operativos deben ser bajos. Asimismo, se requiere un enfoque de economía circular ambiental y socialmente asumible y que cumpla con la normativa actual y en desarrollo. La economía circular persigue la transición de sistemas lineales tradicionales a ciclos circulares, optimizando los ciclos de vida de los productos para avanzar hacia patrones de producción y consumo sostenibles y eficientes [9] en línea con el Objetivo de Desarrollo Sostenible (ODS) 12 de la Agenda 2030. Para ello, los productos deben haber sido diseñados previamente pensando en su fin de vida, se debe buscar la modularidad, el desmontaje, y evitar los elementos multimateriales en la medida de lo posible. Asimismo, la introducción de nuevos modelos de negocio que intensifiquen el uso de los equipos se deberá de mejorar el mantenimiento y la reparabilidad de los mismos, con lo que se alargará la vida útil de los productos y los materiales permanecerán en el ciclo económico el mayor tiempo posible.

Todo ello viene recogido en el marco estatal dentro del Plan de acción de Economía Circular de 2020 [10]. En la Iniciativa sobre la Economía Circular se especifican una serie de acciones para prolongar la vida de los productos. Conforme a la Directiva sobre diseño ecológico, los dispositivos deben estar diseñados bajo unos criterios de eficiencia energética y de durabilidad, reparabilidad, actualizabilidad, mantenimiento, reutilización y reciclado, siendo uno de los sectores prioritarios para la aplicación del«derecho a reparación». Así como medidas reguladoras para los cargadores e incentivos para disociar la compra de cargadores de la compra de nuevos dispositivos. La mejora de la recogida, el tratamiento de las RAEE, la exploración de las distintas opciones para un sistema de restitución que permita la devolución o reventa también queda recogida junto con las restricciones en cuanto a sustancias peligrosas.

Referencias

[1] Villaécija, R. y Rojas, A. (16 de febrero de 2014). Morir por un puñado de arena. EL MUNDO.

[2] Forti, V., Baldé, C. P., Kuehr, R., & Bel, G. (2020). The Global E-waste Monitor 2020. United Nations University (UNU), International Telecommunication Union (ITU) & International Solid Waste Association (ISWA), Bonn/Geneva/Rotterdam, 120.

[3] Huisman, J., Botezatu, I., Herreras, L., Liddane, M., Hintsa, J., Luda di Cortemiglia, V., … & Zan, A. (2015). Countering WEEE illegal trade (CWIT) summary report, market assessment, legal analysis, crime analysis and recommendations roadmap. Lyon, Frankreich, 3(38), 157.

[4] Ramprasad, C., Gwenzi, W., Chaukura, N., Azelee, N. I. W., Rajapaksha, A. U., Naushad, M., & Rangabhashiyam, S. (2022). Strategies and options for the sustainable recovery of rare earth elements from electrical and electronic waste. Chemical Engineering Journal, 135992.

[5] Real Decreto 27/2021, de 19 de enero, por el que se modifican el Real Decreto 106/2008, de 1 de febrero, sobre pilas y acumuladores y la gestión ambiental de sus residuos, y el Real Decreto 110/2015, de 20 de febrero, sobre residuos de aparatos eléctricos y electrónicos. Boletín Oficial del Estado, 17, de 20 de enero de 2021. 

[6] Forti, V., Baldé, C.P., & Kuehr, R. (2018). E-waste statistics: guidelines on classifications, reporting and indicators.

[7] Dang, D. H., Thompson, K. A., Ma, L., Nguyen, H. Q., Luu, S. T., Duong, M. T. N., & Kernaghan, A. (2021). Toward the circular economy of Rare Earth Elements: a review of abundance, extraction, applications, and environmental impacts. Archives of environmental contamination and toxicology, 81(4), 521-530.

[8] La UE está más cerca de introducir un cargador común. (2022, 4 de mayo). Noticias Parlamento Europeo.

[9] de Oliveira, R. P., Benvenuti, J., & Espinosa, D. C. R. (2021). A review of the current progress in recycling technologies for gallium and rare earth elements from light-emitting diodes. Renewable and Sustainable Energy Reviews, 145, 111090.

[10] Comunicación de la comisión al Parlamento Europeo, al Consejo, al Comité Económico y Social Europeo y al Comité de las Regiones. (2020, 11 de marzo). Nuevo Plan de acción para la economía circular por una Europa más limpia y más competitiva.

Para saber más:

Actúa localmente: electrónica de papel
Dando valor a los residuos marinos para cuadrar la economía circular
El verdadero reciclado de los plásticos

Sobre los autores: Mireia Martín es ingeniera y gestiona la actividad del Aula de Transición energética de Fundación Repsol sobre «Economía Circular» de la Escuela de Ingeniería de Bilbao de la UPV/EHU; Erlantz Lizundia es doctor en Ingeniería de Materiales Avanzados y  forma parte del Grupo de Investigación Life Cycle Thinking de la UPV/EHU; Estibaliz Saez de Camara  es doctora en Ingeniería Ambiental y forma  parte del Grupo de Investigación Atmosférica de la UPV/EHU..

El artículo Basura electrónica y economía circular se ha escrito en Cuaderno de Cultura Científica.

¿De qué depende la fama en ciencia? Todo el mundo sabe quiénes fueron Einstein o Curie, sin embargo pocos identifican a Hilleman, que desarrolló más de 40 vacunas, entre ellas, la gran mayoría de las infantiles. Su anonimato, según los expertos, puede deberse a que dedicara su carrera a la industria, pero hay otros factores en la popularidad de una figura científica, como su exposición a la prensa.

Maurice Hilleman en el Centro Médico del Ejército Walter Reed. / Cortesía de Merck, historyofvaccines.org

En marzo de 1963, una niña de cinco años se despertó en mitad de la noche por un dolor de garganta, fue hasta la habitación de su padre y, sin saberlo, inició el proceso que llevaría a conseguir la vacuna más rápida de la historia hasta la llegada de la covid.

El padre no tardó mucho en reconocer que la niña tenía paperas, una enfermedad muy frecuente por entonces y poco grave en general, pero que en algunos casos podía dar lugar a meningitis o sordera. Esa misma noche fue hasta el laboratorio donde trabajaba, recogió el material necesario y, de vuelta a casa, tomó muestras de la garganta de su hija con las que luego cultivaría el virus.

Tres años después, y tras lograr debilitarlo, ensayaba con él una vacuna en voluntarios más o menos forzosos como su hermana mayor, y solo uno más tarde se aprobaba su uso. Con el tiempo pasaría a formar parte de la triple vírica, con la que millones de niños y niñas se vacunan cada año. Como luego escribiría el periodista Alan Dove, “Jeryl [así se llamaba la niña] se recuperó del virus de las paperas, pero el virus nunca se recuperó de haber infectado a Jeryl”.

El padre se llamaba Maurice Hilleman, y la escena de esa noche es algo más que anecdótica, es reveladora. Hilleman participó directamente en el desarrollo de más de 40 vacunas, además de la de las paperas. Hasta nueve de las catorce que conforman los calendarios vacunales tienen que ver con él.

Para el inmunólogo y ahora icónico Anthony Fauci, “sus contribuciones son el secreto mejor guardado para el público lego (…). Maurice fue quizá la figura de la salud pública más influyente del siglo XX, si se tienen en cuenta los millones de vidas salvadas y el sufrimiento evitado gracias a su trabajo”.

Se calcula que sus vacunas evitan ocho millones de muertes al año, pero al revisar la hemeroteca los titulares mezclan conceptos como “la persona que más vidas ha salvado” con apelativos como “el gran desconocido”. Para Luis Ignacio Martínez Alcorta, vocal de la Asociación Española de Vacunología, “Hilleman fue un genio, una figura única y destacada que surge ocasionalmente, y puede ser considerado el vacunólogo más prolífico de la historia de la humanidad”.

¿De qué depende la fama?

Hilleman, una vida de vacunas y conflictos

“Todo lo que tocaba lo convertía en una vacuna”, decía de él Adel Mahmoud, el que fuera presidente de la División de Vacunas de la compañía Merck y donde Hilleman desplegó la mayor parte de su carrera.

Él y su equipo desarrollaron o mejoraron entre muchas otras las vacunas de la hepatitis A y B, del neumococo, la de la bacteria Haemophilus influenzae de tipo B, las de distintos tipos de meningococo, la de la varicela y la triple vírica que incluye la de la parotiditis, la rubeola y el sarampión.

Todas ellas forman parte de los calendarios vacunales infantiles, y solo la del sarampión salvó 20 millones de vidas entre los años 2000 y 2015, según la Organización Mundial de la Salud (OMS).

Un día, seis años antes de que su hija despertara con paperas, leyó una noticia en The New York Times sobre un extraño aumento de contagios por gripe en Hong Kong. “Dios mío, es la pandemia. ¡Está aquí!”, se dice que gritó.

Las autoridades, incluida la OMS, ignoraron en aquel entonces la amenaza. Hilleman consiguió entretanto una muestra del virus y contactó y movilizó a distintos laboratorios y compañías. Lo que luego se conocería como la pandemia de gripe asiática llegó a los Estados Unidos meses después, pero para entonces estos disponían ya de 40 millones de dosis de una vacuna adaptada a la nueva variante. Se calcula que gracias a ella un millón de muertes fueron evitadas.

«Hace poco”, decía Fauci en el año 2005, “pregunté a mis estudiantes posdoctorales si sabían quién había desarrollado las vacunas contra el sarampión, las paperas, la rubeola, la hepatitis B y la varicela. No tenían ni idea. Cuando les dije que fue Maurice Hilleman, dijeron: ‘Oh, ¿te refieres a ese tipo gruñón que viene a todas las reuniones del sida?’».

El trabajo de ese tipo gruñón salva millones de vidas, pero él reconocía “haber tenido conflictos con todo el mundo”.

Si le pedían una definición de sí mismo, reconocía que la mejor la había dado un colega en Merck, que decía que “por fuera parecía un cabrón, pero que si se miraba más a fondo, por dentro, todavía se veía a un cabrón”.

Hilleman fue criado sin apenas recursos por sus tíos, en una granja de Montana. Su hermana gemela murió en el parto, y su madre lo hizo apenas dos días después. Su definición favorita de sí mismo puede traducirse también así: “Malnacido por fuera, malnacido por dentro”.

Reclutaba voluntarios forzosos para los ensayos clínicos —más allá de su propia hija— y se negó a ir a los “cursos de modales” a los que obligaba la compañía.

Obsesionado con el trabajo, que entendía como dedicación exclusiva y total, exigía lo mismo a quienes le rodeaban. Durante una época coleccionó en su despacho réplicas en miniatura de las cabezas de los trabajadores a los que despedía: las hacían sus hijas a partir de manzanas secas.

Su primera esposa murió unos meses antes de la noche de las paperas. Para encontrar a su segunda mujer, pidió a su asistente que hiciera una preselección a su gusto de entre las que habían mandado su currículum para trabajar en la empresa. A la elegida, con la que luego estaría casado durante 42 años, la entrevistó para coordinar ensayos clínicos de parotiditis y sarampión en el Hospital Infantil de Filadelfia.

Apenas un poco antes había dicho: “¡Cristo! Encontrar mujer es una suerte tan aleatoria como el movimiento browniano. Nunca sabes si serán alcohólicas, si gastarán todo tu dinero o si tendrán enfermedades venéreas”.

Robert Weibel vacuna a Kirsten, la hija de Maurice Hilleman contra las paperas, mientras la sostiene su hermana Jeryl Lynn. / Cortesía de Lorraine Hilleman. historyofvaccines.orgRazones para el anonimato

Si se hace pensar en nombres relacionados con las vacunas quizá surjan el de Pasteur o el del iniciador Jenner. Es posible que en Estados Unidos citen a Salk y a Sabin por sus hitos contra la polio; y ahora con la covid pueden no sonar extraños apellidos como los de Sahin o Karikó, los principales promotores de la vacuna de Pfizer-BioNTech. Pero difícilmente se pensará en Maurice Hilleman. ¿Cuál es la razón?

“Demasiadas pocas personas, incluso en la comunidad científica, conocen su alcance y contribución, y a ciencia cierta desconozco el porqué”, reconoce Martínez Alcorta.

Hay varias hipótesis que se han propuesto para explicarlo. Una es su conflictiva y problemática personalidad, aunque la experiencia nos diga que la bondad no parece precisamente condición necesaria para la fama. Otra tiene que ver con el hecho de que nunca reconociera maestros concretos y que, al parecer, le costara citar a otros científicos.

Sin embargo, para el vacunólogo José Tuells, uno de los motivos de su anonimato es paradójicamente su humildad: “A pesar de su estilo irreverente, dominante, sus maneras confrontadoras y provocativas o de su autoconfianza, era un hombre humilde”. A favor de la teoría está que, al contrario que Salk o Sabin con la de la polio, nunca puso su nombre a ninguna vacuna. Incluso varias de ellas contienen guiños o referencias directas al trabajo de otros.

La razón favorita de Tuells y del propio Hilleman es, en cambio, el hecho de haber trabajado casi toda su vida en la industria, y no en la investigación académica.

“Si miras para atrás en la historia”, decía él mismo, “la industria es como un leproso (…). Si yo daba la cara ante la prensa, alguien podría pensar que intentaba venderles algo (…). Debía permanecer en segunda fila”.

Esa explicación no convence a Xavier Roqué, profesor de Historia de la Ciencia en la Universidad Autónoma de Barcelona. “Eso mismo podría aplicarse a los responsables de la vacuna de Pfizer-BioNTech, pero en ese caso sí han llegado a ser más conocidos”, razona.

De hecho, Hilleman ha aparecido con frecuencia en los medios, aunque su figura no ha conseguido cristalizar. En su opinión, “quizás pese más un descubrimiento sensacional en un momento adecuado que un conjunto de ellos, aunque puedan tener más valor en global”. Eso podría explicar que sean más conocidos los inventores de las vacunas contra la polio. No solo les pusieron su nombre, sino que sus efectos eran muy evidentes ante una enfermedad con secuelas visibles y terribles y que llevaba años sembrando el terror.

Para Gema Revuelta, directora del Centro de Estudios de Ciencia, Comunicación y Sociedad y del máster en Comunicación Científica, Médica y Ambiental de la Universidad Pompeu Fabra en Barcelona, “un científico que ha hecho una gran aportación a la ciencia o a la sociedad tiene más probabilidades de ser popular, pero esta es una de tantas variables que le pueden impulsar a la fama. Basta fijarse, sin ir más lejos, en cuántas mujeres quedaron ocultas a lo largo de la historia a pesar de sus importantes contribuciones”.

Hilleman y Anthony Payne en una reunión de la Organización Mundial de la Salud sobre la gripe en Estocolmo, 1958. / Cortesía de Lorraine HillemanAcceso restringido al Salón de la Fama

En el año 2011, los investigadores Adrian Veres y John Bohannon crearon un proyecto llamado “The Science Hall of Fame” (El salón de la fama de la ciencia). Aprovecharon que Google Books había subido ya millones de libros en su plataforma para para hacer un análisis de lo que se había dado en llamar culturómica. En esta ocasión consistía en buscar en ellos cuántas veces aparecían los nombres de miles de personas relacionadas con la ciencia.

La unidad de fama científica la llamaron miliDarwin (mD), y equivalía a la milésima parte de la ostentada por el naturalista inglés. Einstein tenía 878 mD; Marie Curie, 188. De las 100 personas más famosas, solo 11 eran mujeres. Hilleman estaba en el puesto 4504, casi al final de la lista, con apenas 0,89 mD.

Analizando los datos, comprobaron que la fama en la ciencia sigue como muchos otros fenómenos una relación en forma de ley de potencias, donde el 1 % de los científicos más famosos acumula la gran mayoría de las referencias. Como una suerte de milmillonarios capitalistas de la fama.

Dos años después, otro estudio ya más allá de la ciencia, usó las hemerotecas de más de dos mil periódicos para concluir que, una vez superado cierto umbral, la gente realmente famosa se mantiene así durante décadas. El umbral activa el efecto Mateo (“al que tiene, se le dará”), perpetuando las referencias.

Como dijo Eran Shor, uno de los autores del artículo, “la gente que tú y yo consideraríamos famosa, incluso las Kim Kardashians de este mundo, siguen siendo famosas durante mucho tiempo. No es algo que viene y se va”.

Veres y Bohannon analizaron también superficialmente los factores que conducían a esos puestos más altos. Ni las citas en estudios científicos ni siquiera el premio Nobel parecían muy importantes.

Sí lo era la controversia o publicar un libro divulgativo de éxito. “Aún queda mucho por estudiar, pero parece que hay un relativo consenso respecto a qué circunstancias pueden estar detrás de la visibilidad o celebridad de los científicos”, explica Revuelta.

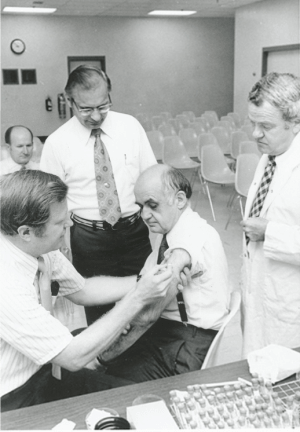Robert E. Weibel vacuna a Maurice Hilleman con la vacuna contra la hepatitis B derivada del suero humano que desarrolló Hilleman. / Cortesía de Lorraine Hilleman

“Podrían citarse más de una docena, pero no todas necesitan estar presentes y los caminos para alcanzar la fama pueden ser distintos”. Entre ellas figuraría “la controversia, pero también el trabajar en temas calientes, una personalidad o apariencia peculiar, la credibilidad entre la comunidad científica o el conocer bien las necesidades de los periodistas y los medios”, resume Revuelta.

Roqué reconoce no identificar un patrón claro, pero apunta particularidades de los casos que más ha estudiado.

En el caso de Einstein, “además de su trabajo y de la capacidad de sugestión del lenguaje relativista, influyó mucho que apareciera en el periodo de entreguerras y que lo hiciera en paralelo al nacimiento del periodismo científico especializado, para el que su figura resultó instrumental”.

La exposición a la prensa de Curie, por su parte, la hizo “consciente de que si no se construía como personaje público alguien lo haría por ella”, de ahí sus textos biográficos y los de su propia hija, que modelaron su personalidad pública y actuaron como “biografías de control”.

La popularidad de Tesla tiene para Roqué “poco que ver con lo que hizo y mucho con el tratamiento que se le dio, realzando la dimensión trágica, focalizándose en el individuo y ocultando las redes a su alrededor”.

La fama interna. De la granja a la cabina

Para el arquitecto y filósofo George Franck, “hay dos motivos que impulsan la decisión de emprender una carrera científica: la curiosidad y la vanidad”. Esta última ligaría con la aspiración a la fama, aunque cada vez más textos abran el debate de la importancia de ser conocido dentro del mundo científico como mera herramienta de supervivencia y progreso.

La ciencia aspira a la objetividad, pero “la hacen personas y todas ellas tienen su subjetividad”, reconoce Revuelta. “A la hora de escoger un proyecto en una convocatoria competitiva, de revisar un artículo para su publicación o de otorgar un premio, nuestros juicios se ven marcados sin duda por la subjetividad, y en esta lo conocido tiene prioridad ante lo desconocido, por lo general”.

Hilleman no acumula apenas miliDarwins, y para los estudiantes jóvenes era un gruñón más o menos anónimo en las reuniones del sida. Pero sí fue reconocido por sus pares más directos.

Hilleman en los 2000. / Lorraine Hilleman

Además de múltiples premios, parte de la flor y nata científica se reunió en Filadelfia para homenajearlo unos meses antes de morir. Esa noche se lo agradeció diciendo: “No hay mayor tributo que se pueda rendir a un científico que recibir el visto bueno de un colega. A todos ustedes los considero pares en el mundo de la ciencia”.

El periodista de la revista Nature escribió: “Dirigida a un grupo de más de cien personas, la declaración era claramente absurda. Desde cualquier punto de vista objetivo, una reunión de pares científicos de Maurice Hilleman no llenaría una cabina telefónica”.

Para Roqué, más allá del anonimato de Hilleman, “lo que me parece sorprendente es casi que alguien sea famoso, particularmente en la ciencia”.

Probablemente la personificación sea siempre algo injusta, y más en el mundo científico, donde el trabajo es cada vez más coral, competitivo en la distancia pero necesariamente colaborativo. Seguramente este artículo también lo sea.

Sobre el autor:

Jesús Méndez es médico y periodista científico.

Este artículo apareció publicado originalmente en SINC el 11 de abril de 2022.

Para saber más:

Vacunas: El arte de salvar vidas
Dudas sobre las vacunas: problemas y soluciones

 

El artículo Si Maurice Hilleman es la persona que más vidas ha salvado, ¿por qué no le conoces? se ha escrito en Cuaderno de Cultura Científica.

¿Estamos realmente diseñados para conectar con los demás? Si es así, ¿por qué siguen existiendo los psicópatas? ¿Se pueden tratar trastornos delirantes como la paranoia desde el punto de vista de la evolución? O ¿cómo ha cambiado la atracción sexual desde la época de nuestros ‘abuelos’ homínidos hasta ahora?

A estas y otras cuestiones relativas a la evolución del comportamiento humano se trató de dar respuesta durante la IV Jornada Nacional de Evolución y Neurociencias, evento organizado por la Cátedra de Cultura Científica de la UPV/EHU y la Red de Salud Mental de Bizkaia, que tuvo lugar los días 28 y 29 de abril en el Bizkaia Aretoa – UPV/EHU de Bilbao.

Desde que en 2017 un grupo de psiquiatras de la Red de Salud Mental de Bizkaia organizara la primera edición de esta jornada, la cita se ha convertido en un punto de encuentro para profesionales de distintos ámbitos científicos como la psiquiatría, la psicología, la biología o la filosofía con un interés común: la conducta humana desde una perspectiva evolucionista y su divulgación científica en un formato accesible y ameno para todos los públicos, a la par que riguroso y actualizado.

La inteligencia artificial es una realidad que está empezando a permearlo todo. Quizás mucho más de lo que nos gustaría reconocer. Es hora a empezar a pensar seriamente en qué es, qué significa y qué implicaciones tiene su diseño y su uso. Es hora de la filosofía. Santiago Sánchez-Migallón es profesor de filosofía y autor de La máquina de von Neumann.



Para saber más:

En el control de la inteligencia artificial nos jugamos el futuro

Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus

El artículo IV Jornada Nacional de Evolución y Neurociencias: Filosofía e inteligencia artificial se ha escrito en Cuaderno de Cultura Científica.

Foto: Umesh Soni / Unsplash

La lágrima tiene una estructura y composición complejas, que mantienen la superficie del ojo húmeda y lubricada, la protege de los patógenos, favorece la cicatrización de las heridas y proporciona una transparencia visual óptima. La película lagrimal contiene una capa lipídica que actúa principalmente como interfaz entre la capa acuosa del ojo y el aire exterior. Dicha capa lipídica está compuesta por una fina capa de lípidos polares que interactúa con la capa mucoacuosa del ojo y sirve de anclaje, y una capa más gruesa de lípidos no polares (que no interactúan con el agua) en la interfaz con el aire.

“El ojo seco tiene una alta prevalencia en la población, sobre todo en mujeres a partir de los 40-50 años. Se trata de una patología que, aunque no es grave, es molesta en el día a día —explica la investigadora Ikerbasque Arantxa Acera—. Los tratamientos habituales para el ojo seco son los sustitutivos de la lágrima, entre los que se encuentran los colirios de hemoderivados como el colirio de plasma enriquecido en factores de crecimiento, que se obtiene de la sangre del propio paciente (los denominados colirios autólogos). Aunque puede ser un proceso un tanto tedioso, realmente no es una terapia cara, sino novedosa y desconocida”.

En ese sentido, el Grupo Oftalmo-Biología Experimental (GOBE) de la UPV/EHU ha realizado un estudio cuyo fin sería conocer mejor la composición de este tipo de colirios “para establecer tratamientos personalizados en función del tipo de ojo seco que tenga el paciente (ojo seco acuodeficiente, evaporativo o mixto)”, añade Acera. Para eso, analizaron qué tipo de lípidos había en el colirio, y los compararon con los lípidos existentes en la lágrima.

El colirio como lágrima personalizada

“Hemos querido saber si este tipo de colirios tiene una composición apropiada para una medicina más personalizada; quizás, si hay algún lípido que falta en el colirio biológico, el objetivo podría ser enriquecerlo con ese lípido”, explica Acera. En el estudio han constatado que “realmente la composición lipídica del colirio autólogo y de la lágrima no es la misma. En el plasma hay gran cantidad de lípidos; sin embargo, en la película lagrimal hay dos lípidos anfipáticos muy importantes, que anclan la parte apolar con la parte acuosa de la lágrima, que no existen en el plasma”.

En este contexto, el grupo de investigación GOBE ha puesto en marcha en colaboración con el Hospital de Basurto, Hospital Donostia, el Instituto Clínico-Quirúrgico de Oftalmología (ICQO) y el Hospital Miguel Servet de Zaragoza “un estudio clínico multicéntrico, para analizar el perfil lipídico de la lágrima de pacientes con diferentes tipos de ojo seco, para conocer qué lípido está alterado en estos pacientes y determinar qué terapia puede ser la más adecuada en cada caso”, explica la investigadora Ikerbasque.

Por otro lado, el Hospital Donostia ha promovido un ensayo clínico con plasma enriquecido en un grupo de pacientes con ojo seco secundario, ya que este tipo de colirios “no están cubiertos por la sanidad pública”, y la investigadora destaca la importancia de “seguir investigando para poder llegar a incorporar este tipo de tratamientos al sistema público” y de “avanzar en el desarrollo de tratamientos personalizados, adaptados al tipo de ojo seco de cada paciente”.

Referencia:

Arantxa Acera, Beatriz Abad, Xandra Pereiro, Francisco David Rodríguez, Noelia Ruzafa, Juan Antonio Duran, Elena Vecino Comparative study of the lipid profile of tears and plasma enriched in growth factors Experimental Eye Research doi: 10.1016/j.exer.2022.109061

Para saber más:

Párkinson en una lágrima

Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa

El artículo El perfil lipídico de la lágrima se ha escrito en Cuaderno de Cultura Científica.

Cada vez se lo ve menos en los conciertos. Desde que tenemos afinadores digitales, su tatarabuelo analógico ha ido cayendo poco a poco en desuso. Pero si tienes un amigo músico un poco friki, o si alguna vez has asistido al ensayo de un coro, por ejemplo, es posible que todavía hayas visto uno. Se trata del diapasón, un curioso objeto metálico en forma de horquilla (o de Y), con dos brazos paralelos y un único pie, rematado por una pequeña bola en la punta inferior. Durante siglos, fue el invento que los músicos profesionales utilizaron para afinar sus instrumentos. Pero además, a finales del siglo XIX, se convirtió en uno de los instrumentos de alta precisión de la física, una especie de láser acústico que nos permitió crear los primeros sonidos sintéticos de la historia y ayudó a medir la velocidad de la luz con una precisión sin precedentes1.

 

Movimiento (exagerado) de un diapasón vibrando a una frecuencia de 440 Hz. Fuente: Wikimedia Commons

¿Pero qué tiene de especial este pequeño resonador? Bien, como sucede a menudo en el mundo de la acústica, la gracia del diapasón está en su forma. Gracias a sus dos brazos alargados, este instrumento es capaz de producir uno de los sonidos más puros de la acústica; una frecuencia fundamental sin apenas armónicos superiores2. Su tono resulta muy reconocible y estable (óptimo para afinar, precisamente), y apenas se desafina con el tiempo. La frecuencia del diapasón depende únicamente de la longitud y la masa de sus brazos, que oscilan en oposición, pero además, su vibración se transmite a la base en dirección longitudinal, de manera que es posible amplificar su sonido apoyándolo contra una superficie o tabla acústica. Se podría comparar el diapasón con un láser de sonido3: un instrumento capaz de producir una onda sinusoidal prácticamente pura, con una frecuencia estable y bien definida.

Pero los orígenes del diapasón no se encuentran en la física. Ni siquiera en la música. Para encontrar la cuna de este instrumento debemos acudir a los otorrinos y a las vibraciones de un humilde tenedor.

Su origen en el tenedor

De acuerdo con Harald Feldmann4, la historia del diapasón comienza con el descubrimiento de que ciertas vibraciones pueden ser transmitidas y escuchadas a través de los huesos de la cabeza, sin que viajen necesariamente a través del aire.

Girolamo Cardano, hoy más conocido como matemático, fue el primero en describir este fenómeno en el siglo XVI. Cardano era médico y astrólogo, y un genio de sorprendentemente multidisciplinar. Entre sus inventos se encuentran el eje cardán (hoy en uso en diversos vehículos) y la suspensión de la brújula de los barcos. También se le asocia con uno de los primeros métodos para resolver ecuaciones de tercer y cuarto grado, si bien parece que se apropió de las ideas de otros contemporáneos (como Targaglia) para publicar su solución. En su libro “De subtilitate” (1550), describe cómo al sujetar una varilla con los dientes, cualquiera puede percibir sonidos, “distinguir voces y oír palabras distantes, que no podría oír de otro modo”5.

Poco más tarde, otro médico de Padua llamado Hieronimus Capivacci pensó en utilizar este fenómeno como método diagnóstico. Si un paciente sordo podía percibir el sonido de una cítara sosteniendo entre los dientes una varilla metálica en contacto con el instrumento, entonces era posible concluir que “la sordera se debe a una enfermedad de la membrana timpánica”. En caso contrario, la causa de su condición debía hallarse en el nervio, en la percepción misma del oído.

Gunther Christoph Schelhammer, también médico, fue el primero en experimentar con la cubertería para realizar este mismo experimento. En 1684 describió cómo el sonido de un tenedor en vibración puede ser escuchado nítidamente a través de los huesos al sostenerlo entre los dientes. Al igual que Capivacci, proponía utilizar este test para diagnosticar distintos tipos de sordera.

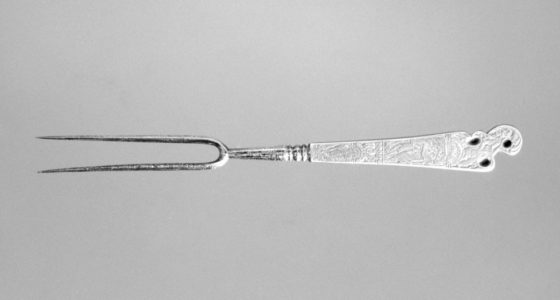Tenedor de la primera mitad del s.XVII. Fuente: Internet Archive

Cabe aclarar que, en aquella época, los tenedores solían ser mucho más parecidos a lo que hoy conocemos como un trinchador. El invento había llegado a Europa a principios del siglo XI de la mano de la princesa Teodora Ana Ducaina, hija del emperador de Bizancio. Teodora se negaba a mancharse las manos para comer y pidió que le fabricasen algún tipo de utensilio para pinchar los alimentos. El invento no se empezó a popularizar hasta mucho después. En el siglo XVI Catalina de Medici lo puso de moda en la corte de Francia, pero aún entonces era considerado una cursilada propia de los aristócratas finolis. Europa no dejó de comer mayoritariamente con las manos hasta el siglo XVIII.

Viajando solo un poco más atrás en el tiempo, encontramos que los tenedores de finales del siglo XVII a menudo tenían únicamente dos puntas alargadas. Esto explica que Schelhammer quisiese aprovechar sus excelentes propiedades acústicas para diagnosticar a sus pacientes. Estas propiedades eran probablemente bien conocidas en su época. Sin embargo, una antigua superstición alemana prohibía hacer sonar estos tenedores de mesa. Se creía que su timbre podía atraer al demonio. No en vano, en la iconografía cristiana, el señor de las tinieblas porta un enorme tridente con el que trinchar las almas pecadoras. Por suerte, Schelhammer no se dejó amedrentar por semejantes creencias. Fue el primero en utilizar el tenedor de dos puntas como un instrumento acústico con finalidades científicas.

En los años siguientes, los esfuerzos de la medicina se centraron en explotar la conducción ósea para mejorar la audición de las personas con problemas en el tímpano. Por otro lado, el tenedor de dos puntas encontró pronto una utilidad inesperada en el mundo de la música.

Notas y referencias:

1Kleppner, D. (2007). Master Michelson’s measurement. Physics Today, 60(8), 8-9. DOI: 10.1063/1.2774115

2Ojo simplificación. En el momento de golpear el diapasón, sí se producen otras frecuencias distintas de la fundamental, pero estas tienden a decaer rápidamente en el tiempo. Cuando la señal se estabiliza, el armónico más prominente tiene una frecuencia que es 6 veces la de la fundamental (mucho más aguda, por tanto, y apenas perceptible).

3Otra simplificación. Un láser de luz, además de producir una frecuencia “pura”, está colimado. No solo tiene coherencia temporal, sino también espacial. En este caso, comparamos el diapasón con un láser por su capacidad de producir una única frecuencia sonora.

4Feldmann, H. (1997). History of the tuning fork. I: Invention of the tuning fork, its course in music and natural sciences. Pictures from the history of otorhinolaryngology, presented by instruments from the collection of the Ingolstadt German Medical History Museum. Laryngorhinootologie, 76(2), 116–122. DOI: 10.1055/s-2007-997398

5Cardano, G. (2013), p. 709. The De Subtilitate of Girolamo Cardano (J. M. Forrester, Ed.; J. Henry & J. M. Forrester, Trans.). ACMRS (Arizona Center for Medieval and Renaissance Studies), Tempe, Arizona. Obra original de 1550.

Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica

El artículo El diapasón: de la cocina al laboratorio, pasando por la orquesta se ha escrito en Cuaderno de Cultura Científica.

En esta entrada del Cuaderno de Cultura Científica vamos a hablar de un concepto sencillo, pero que da mucho juego, los números pandigitales.

Se dice que un número es pandigital si está formado por todas las cifras básicas (incluyendo o no, el número 0), de forma que cada cifra aparece una única vez, como en los números 321.576.984 (sin incluir el 0) o 9.753.102.468 (incluyendo el 0). A estos números en los que cada cifra básica aparece una única vez se les denomina números pandigitales restringidos, en contraposición con los números pandigitales redundantes en los que hay repeticiones de cifras básicas, es decir, cada dígito aparece al menos una vez, como en los números 1.223.445.667.889 o 10.203.040.506.070.809.

Existen 9! = 362.880 números pandigitales restringidos sin cero, desde el número 123.456.789, que es el más pequeño, al número 987.654.321, que es el mayor. Esto se debe a que todos los números pandigitales restringidos sin 0 se obtienen mediante todas las permutaciones de las nueve cifras básicas {1, 2, 3, 4, 5, 6, 7, 8, 9}, de manera que cada permutación da lugar al número pandigital que consiste en las cifras del 1 al 9 colocadas en el orden que determina la permutación (por ejemplo, la permutación {2, 4, 6, 8, 1, 3, 5, 7, 9} tiene asociado el número 246.813.579 o la permutación {2, 1, 4, 3, 6, 5, 8, 7, 9} el número 214.365.879), luego como existen 9! permutaciones de nueve elementos (véase la entrada Buscando lagunas de números no primos), esta es la cantidad de números pandigitales restringidos sin cero que existen.

Por otra parte, cada uno de los números pandigitales restringidos de los anteriores, sin cero, como 123.456.789 da lugar a nueve números pandigitales restringidos con cero, en función de en cuál de las 9 posiciones posibles coloquemos la cifra 0. Así, el número 123.456.789 da lugar a los nueve números que van desde 1.023.456.789 hasta 1.234.567.890. Por lo tanto, en total hay 9 x 9! = 3.265.920 números pandigitales restringidos con cero. Respecto a los números pandigitales redundantes, con o sin cero, claramente existen infinitos.

Ejemplos curiosos de números pandigitales

A. El número pandigital restringuido más pequeño es 123.456.789 (sin cero) y 1.023.456.789 (con cero), mientras que el más grande es 987.654.321 (sin cero) y 9.876.543.210 (con cero).

El número pandigital 123.456.789 es un número curioso ya que si lo multiplicamos por 8 nos da otro número pandigital, que casi (con la excepción del “12” y “21”) es el recíproco del anterior, 123.456.789 x 8 = 987.654.312. Más aún, multiplicando por 2, 4, 5 y 7 seguimos teniendo números pandigitales.

123.456.789 x 2 = 246.913.578,

123.456.789 x 4 = 493.827.156,

123.456.789 x 5 = 617.283.945,

123.456.789 x 7 = 864.197.523,

123.456.789 x 8 = 987.654.312.

Si tomamos números pandigitales restringidos, que incluyan el cero, también nos encontramos ejemplos tales que algunos de sus múltiplos también son pandigitales. Por ejemplo, el número pandigital 1.098.765.432 al multiplicarlo por 2, 4, 5 y 7 da como resultados números pandigitales.

1.098.765.432 x 2 = 2.197.530.864,

1.098.765.432 x 4 = 4.395.061.728,

1.098.765.432 x 5 = 5.493.827.160,

1.098.765.432 x 7 = 7.691.358.024.

O el número pandigital (sin cero) 987.654.321 se transforma en números pandigitales (con cero) al multiplicarlo por 2, 4, 5, 7 y 8.

987.654.321 x 2 = 1.975.308.642,

987.654.321 x 4 = 3.950.617.284,

987.654.321 x 5 = 4.938.271.605,

987.654.321 x 7 = 6.913.580.247,

987.654.321 x 8 = 7.901.234.568.

Más aún, la diferencia entre este, el número pandigital restringido (sin cero) más grande, y 123.456.789, el número pandigital restringido (sin cero) más pequeño, sigue siendo un número pandigital (sin cero).

987.654.321 – 123.456.789 = 864.197.532.

B. No existen números pandigitales restringuidos primos.

Recordemos que los números primos son aquellos números que solamente se pueden dividir por 1 y por ellos mismos, como los números 2, 3, 5, 7, 11, 13 o 19, mientras que números como 6, que también se puede dividir por 2 y 3, o 25, también divisible por 5, no son primos. Sabemos que no existen números pandigitales restringidos primos por el criterio de divisibilidad del número 9, es decir, un número es divisible por 9 si, y sólo si, la suma de sus dígitos es divisible por 9 (véase la entrada Las curiosas reglas de divisibilidad), puesto que la suma de los dígitos de un número pandigital restringido, tenga o no cero, es igual a 45, que es divisible por 9.

Pero sí existen números pandigitales redundantes primos. Los primeros (con cero) son 10.123.457.689, 10.123.465.789, 10.123.465.897, 10.123.485.679, etc., que forman la sucesión denominada A050288 en la Enciclopedia On-line de Sucesiones de Números Enteros (OEIS).

Número pandigital redundante primo más pequeño

 

Si consideramos los números pandigitales redundantes sin cero, entonces el primer primo es 1.123.465.789, seguido de los siguientes 1.123.465.879, 1.123.468.597, 1.123.469.587, 1.123.478.659, etc. que forman la sucesión A050290 de la Enciclopedia On-line de Sucesiones de Números Enteros.

C. El único número pandigital restringido sin cero (respectivamente con cero) que es “polidivisible” es 381.654.729 (resp. 3.816.547.290).

Recordemos, ya que no es un concepto habitual, que un número es polidivisible, también llamado mágico, si verifica las siguientes propiedades: su primer dígito (por la izquierda) es no nulo, sus dos primeros dígitos (por la izquierda) forman un número divisible por 2, el número formado por los tres primeros dígitos es divisible por 3, el formado por los cuatro primeros dígitos es divisible por 4, y así hasta que terminemos con los dígitos del número.

Por lo tanto, el número pandigital con cero 3.816.547.290 es polidivisible ya que 38 es divisible por 2 (38 : 2 = 19), 381 es divisible por 3 (381 : 3 = 127), 3.816 es divisible por 4 (3816 : 4 = 954), 38.165 es divisible por 5 (38.165 : 5 = 7.633), 381.654 es divisible por 6 (381.654 : 6 = 63.609), 3.816.547 es divisible por 7 (3.816.547 : 7 = 545.221), 38.165472 es divisible por 8 (38.165472 : 8 = 4.770.684), 381.654.729 es divisible por 9 (381.654.729 : 9 = 42.406.081) y 3.816.547.290 es divisible por 10 (3.816.547.290 : 10 = 3.816.547.29).

3.816.547.290, único número pandigital restringido con cero polidivisible

 

Por cierto, el número polidivisible más grande que existe tiene 25 dígitos y es el número 3.608.528.850.368.400.786.036.725.

D. El número pandigital restringido sin cero (respectivamente, con cero) más pequeño que es un cuadrado es 139.854.276 = 11.8262 (resp. 1.026.753.849 = 32.0432), mientras que el mayor es 923.187.456 = 30.3842 (resp. 9.814.072.356 = 99.0662), de un total de 30 (resp. 87) números pandigitales restingidos sin cero (resp. con cero) que existen.

La sucesión de los treinta números pandigitales restringidos sin cero que son cuadrados es la sucesión A036744 en la Enciclopedia On-line de Sucesiones de Números Enteros (139.854.276, 152.843.769, 157.326.849, 215.384.976, etc.), mientras que la sucesión A036745 es la formada por los ochenta y siete números pandigitales restringidos con cero que son cuadrados (1.026.753.849, 1.042.385.796, 1.098.524.736, 1.237.069.584, etc.).

E. El número 12.345.678.987.654.321 es un número pandigital redundante sin cero bastante curioso, ya que es capicúa (véase la entrada El secreto de los números que no querían ser simétricos), de hecho, el más pequeño posible entre los pandigitales sin cero, y cuadrado. Este número es igual al cuadrado del número formado únicamente por unos 111.111.111.

F. Potencias de 2 pandigitales.

Busquemos potencias de 2 que sean pandigitales. Si vamos analizando las diferentes potencias de 2, tenemos que hasta la potencia 27 no tenemos un número con nueve cifras (227 = 134.217.728), pero no es pandigital. De hecho, no existen potencias de 2 que sean números pandigitales restringuidos. La primera potencia de 2 que nos da un número pandigital redundante sin cero es 51, ya que 251 = 2.251.799.813.685.248, que claramente es pandigital. La siguiente es 67, que da lugar al número pandigital redundante sin cero 147.573.952.589.676.412.928. Existen cuatro potencias de dos más que nos dan números pandigitales redundantes sin cero, que son 72, 76, 81 y 86. Más aún, 86 es la potencia k más alta conocida para la que 2k no contiene la cifra 0 entre los dígitos de su expresión decimal. Es un problema abierto si existe otra potencia k con esta propiedad.

Por otro lado, la primera potencia de 2 que nos da un número pandigital redundante con cero es 68. En concreto, 268 = 295.147.905.179.352.825.856. Y van apareciendo cada vez más de estas potencias, 70, 79, 82, 84, 87, 88, 89, etc. hasta llegar a 167. Entonces, tenemos 168 que es la última potencia conocida para la que 2168 no es un número pandigital redundante con cero. De hecho, existe la conjetura de que todas las potencias 2k, con k mayor que 168, son pandigitales.

El número 2 elevado a 168 no es un número pandigital, ya que no contiene la cifra 2 entre sus dígitos

 

Rompecabezas numéricos pandigitales

Los números y expresiones numéricas pandigitales han formado parte de las revistas y libros de rompecabezas matemáticos desde hace muchísimo tiempo. A continuación, vamos a mostrar algunos ejemplos clásicos.

A. El siglo digital.

Un problema clásico de este estilo es el que aparece ligado a dos de los más grandes creadores de juegos lógicos y rompecabezas matemáticos, el estadounidense Sam Loyd (1841-1911) y el inglés Henry E. Dudeney (1857-1930), quienes colaboraron por correspondencia durante un tiempo, hasta que el inglés acusó al norteamericano de robarle sus rompecabezas y publicarlos con su nombre. El pasatiempo que vamos a incluir a continuación aparece con el nombre El siglo digital en el libro de Dudeney Diversiones matemáticas (1917) y en el libro de Loyd Cyclopedia de 5000 rompecabezas, trucos y acertijos con respuestas (1914), como El problema centenario.

El siglo digital: Con todas las cifras, del 1 al 9, en orden creciente, intercalar los signos «+» y «–» de forma que el resultado de la operación sea 100. Por ejemplo,

1 + 2 + 3 – 4 + 5 + 6 + 78 + 9 = 100.

Hay diez soluciones, aparte de la mostrada. Si el problema te atrae, intenta encontrar las quince soluciones del mismo problema, pero donde las cifras se colocan en orden decreciente.

Nota: También podrían considerarse otras operaciones como la multiplicación “x” o la división “:” y cualquier orden, no solo los órdenes creciente y decreciente.

Este es un problema muy sencillo que incluimos en las tarjetas de pasatiempos matemáticos del proyecto Marzo, Mes de las Matemáticas, del año 2021. Podéis verlo, con su solución, en la página web del proyecto marzomates.

B. Sumas pandigitales.

En general, este tipo de problemas son de la forma ABC + DEF = GHI, donde las letras corresponden a las nueve cifras básicas no nulas, del 1 al 9, o incluso, a nueve de las 10 cifras básicas, incluyendo el cero. También, puede tenerse la forma ABC + DEF = GHIK, con las diez cifras básicas.

De nuevo, encontramos los primeros ejemplos en los problemas del británico Henry E. Dudeney, en su libro Diversiones matemáticas / Amusements in mathematics (1917). El problema 79 con el título El rompecabezas de las taquillas, que fue originalmente publicado en la revista británica Tits-Bits, en 1897.

El rompecabezas de los casilleros: Un hombre tenía en su oficina tres armarios, cada uno de los cuales contenía nueve casilleros, como se muestra en el diagrama. Le dijo a su empleado que colocara un número de una cifra diferente en cada taquilla del armario A, y que hiciera lo mismo en el caso de B, y de C.

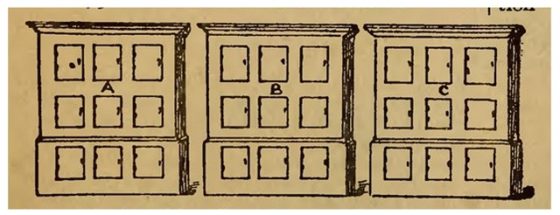
Ahora bien, el empresario no dijo que los armarios debían ser numerados en ningún orden numérico, y se sorprendió al encontrar, cuando el trabajo estaba hecho, que las cifras habían sido aparentemente mezcladas indiscriminadamente. Al pedirle explicaciones a su empleado, el excéntrico muchacho le dijo que se le había ocurrido ordenar las cifras de manera que en cada caso formaran una simple suma, las dos filas superiores de cifras producían la suma de la fila inferior. Pero el punto más sorprendente era éste: que los había dispuesto de tal manera que la suma en A daba la menor suma posible, que la suma en C daba la mayor suma posible, y que los nueve dígitos de los tres resultados totales de las sumas eran diferentes. El acertijo consiste en mostrar cómo se puede hacer esto. No se admiten decimales y el cero no puede aparecer en el lugar de la centena.

Es decir, nos está pidiendo que busquemos tres sumas del tipo ABC + DEF = GHI, como comentábamos al principio. La solución a este problema, aunque os animo a que la encontréis vosotros mismos, es la siguiente. La suma más pequeña de este tipo es 107 + 249 = 356 (que iría en el primer armario), mientras que la suma más grande es 235 + 746 = 981, o también, 324 + 657 = 981 (una de ellas iría en el tercer armario). Como los resultados de esas dos sumas son 356 y 981, entonces el resultado de la suma del armario del centro debe de tener tres de las cifras restantes, es decir, 0, 2, 4, 7. Por lo tanto, las sumas posibles para el armario del centro son 134 + 586 = 720, 134 + 568 = 702 ó 138 + 269 = 407.

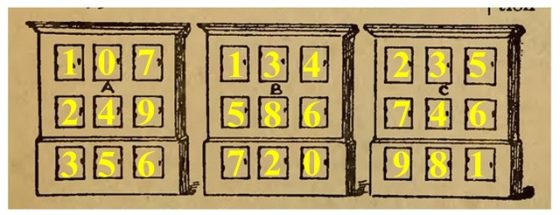Una de las soluciones de El rompecabezas de los casilleros

 

En el mismo libro, Diversiones matemáticas (1917), Dudeney plantea otro interesante problema pandigital, el número 77, llamado dígitos y cuadrados.

Dígitos y cuadrados: Como se muestra en el siguiente diagrama, se han colocado las nueve cifras básicas en un cuadrado de manera que el número de la segunda fila es el doble que el de la primera fila, y el número de la fila inferior sea el triple del de la fila superior. Hay otras tres formas de ordenar los dígitos para obtener el mismo resultado. ¿Puedes encontrarlas?

Antes de comentar la solución a este rompecabezas pandigital, os animo, como siempre, a que os divirtáis buscando vosotras mismas las soluciones. En este problema nos están pidiendo que busquemos tres números, de tres dígitos, de manera que entre los tres tengan las nueve cifras básicas, del 1 al 9, que el segundo sea el doble del primero, que el tercero sea el triple del primero y que la suma de los dos primeros sea el tercero. Como puede verse en la anterior imagen, estas propiedades se cumplen para los tres números incluidos en ella, la terna (192, 384, 596): 192, 384 (= 192 x 2) y 596 (= 192 x 3), que entre los tres tienen las nueve cifras básicas y 192 + 384 = 596. Las otras tres soluciones por las que nos pregunta el rompecabezas son las ternas de números (219, 438, 657), (273, 546, 819) y (327, 654, 981). Una curiosidad más. Las cuatro ternas pueden dividirse en dos grupos de dos ternas, de manera que en cada uno de los dos grupos los tres números de una terna son anagramas (sus dígitos están escritos en otro orden) de los tres números de la otra terna: (192, 384, 596) y (219, 438, 657); (273, 546, 819) y (327, 654, 981).

Otro problema de este tipo aparece propuesto en el libro The Calculator Puzzle Book (1978), de Claude Birtwistle. Este rompecabezas, titulado Tres por tres, segunda parte, aunque con una escritura más literaria que la que proponemos aquí, nos plantea lo siguiente.

Tres por tres, segunda parte: Buscar tres números de tres dígitos ABC, DEF, GHI, que entre los tres tengan las nueve cifras básicas y tales que su suma y su producto sea la menor posible.

La solución sería la siguiente. Para empezar, pensemos en los tres números ABC, DEF y GHI que nos den la menor suma posible. Para ello, los dígitos de las centenas A, B, C deben ser lo más pequeños posibles, luego deberían ser 1, 2 y 3. Y razonando de la misma forma para decenas y unidades, tenemos que la suma más pequeña es 147 + 258 + 369 = 774. Aunque si permutamos el orden de los dígitos de cada posición (centenas, decenas, unidades) se obtiene la misma suma, por ejemplo, 347 + 158 + 269 = 774 ó 368 + 249 + 157 = 774. Como el orden de la suma y del producto no importa, podemos considerar que A = 1, B = 2 y C = 3, luego tendremos 62 = 36 grupos de tres números con tres dígitos cuya suma sea 774 para ver cuánto es su producto. De todos ellos, el menor producto corresponde precisamente a 147 x 258 x 369 = 13.994.694.

Portada del libro The Calculator Puzzle Book (1978), Claude Birtwistle

 

C. Productos pandigitales.

Si miramos la historia de los rompecabezas matemáticos relacionados con los productos pandigitales nos encontramos de nuevo a los dos grandes creadores de juegos lógicos y rompecabezas matemáticos mencionados, Sam Loyd y Henry E. Dudeney. Según el matemático estadounidense David Singmaster la primera aparición de un problema de este tipo fue en la revista Tits-Bits, en 1897. Era el problema Malabares con las cifras de Sam Loyd y se pedía encontrar un producto ABCD x E = FGHIJ, tal que esté formado por las diez cifras básicas, del 0 al 9, y el resultado del producto sea el menor posible. La solución a este problema es 3907 x 4 = 15.628. Además, si nos piden que el resultado sea el mayor posible la solución sería 9.403 x 7 = 65.821.

En el libro Los acertijos de Canterbury (1907) de Henry E. Dudeney nos encontramos también algunos rompecabezas de este tipo, como el siguiente (que había sido publicado en el London Magazine, en 1902).

El acertijo del molinero: El Molinero llevó luego a la compañía hacia un rincón y les mostró nueve sacos de harina, que estaban colocados como se ilustra en la figura.

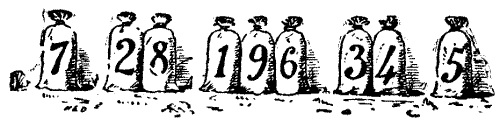
“Ahora escuchad todos — les dijo—, pues os presentaré la adivinanza de los nueve sacos de harina. Y observad, caballeros y señores míos, que hay sólo un saco en cada extremo, cada cual seguido de un par, y tres sacos juntos en medio. Por San Benito, sucede que si multiplicamos el par 28 por su vecino, 7, el producto es 196, que ciertamente es la cifra que muestran los tres sacos del medio. Sin embargo, no es verdad que el otro par, 34, al ser multiplicado por el único saco en ese extremo, 5, resulte también 196. Por tanto, os ruego, gentiles señores, que recoloquéis los sacos con el menor trabajo posible, de tal forma que cada par, al ser multiplicado por su vecino, produzca el número del medio.” Ya que el Molinero ha estipulado, en efecto, que debe moverse la menor cantidad de bolsas posible, hay una sola respuesta a este acertijo, que todos deberían poder hallar.

El problema consiste en buscar el doble producto A x BC = DEF = GH x I formado por las nueve cifras básicas positivas, de 1 al 9, pero de forma que el número de movimientos de los sacos sea el menor posible. Si intentamos solucionar el problema aritmético A x BC = DEF = GH x I, tenemos las siguientes soluciones 2 x 78 = 156 = 39 x 4; 4 x 39 = 156 = 78 x 2; 3 x 58 = 174 = 29 x 6; 6 x 29 = 174 = 58 x 3. La que requiere menos movimientos de sacos es 2 x 78 = 156 = 39 x 4.

Otro rompecabezas en el mismo libro es Los bloques numerados, que dice así.

Los bloques numerados: Los niños de la ilustración han encontrado que se puede inventar una gran cantidad de acertijos muy interesantes e instructivos, a partir de cubos numerados; es decir, cubos que presenten los diez dígitos de las cifras arábigas —1, 2, 3, 4, 5, 6, 7, 8, 9 y 0―. El acertijo en particular con el que se han estado divirtiendo es dividir los bloques en dos grupos de cinco, y luego disponerlos en forma de dos multiplicaciones, en las que un producto sea igual al otro. El número posible de soluciones es muy considerable, pero ellos han dado con la disposición que da el menor producto posible. Así, 3.485 multiplicado por 2 es 6.970, y 6.970 multiplicado por 1 es lo mismo. Les resultará imposible conseguir un resultado menor.

Bien, mi acertijo consiste en hallar el mayor resultado posible. Dividan los cubos en dos grupos de cinco a gusto, y dispónganlos para formar dos multiplicaciones que resulten en el mismo producto y el más alto posible. Eso es todo, y sin embargo es un asunto que requiere bastante trabajo.

Por supuesto, no se permiten fracciones, ni tampoco trucos de ninguna especie. El acertijo es lo bastante interesante en la sencilla forma en que se los he dado. Quizás deba agregarse que los segundos factores pueden tener dos cifras.

En este caso, se busca solucionar el problema aritmético AB x CDE = FG x HIJ, utilizando las diez cifras básicas. La solución es 915 x 64 y 732 x 80, cuyo producto en ambos casos es 58.560

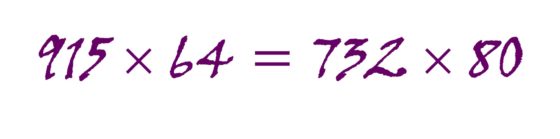
Podríamos contar mucho más sobre los rompecabezas de productos pandigitales y otros tipos de problemas de ingenio relacionados con las expresiones pandigitales, pero eso lo dejamos para otro día, que por hoy ya es suficiente.

Bibliografía:

1.- Raúl Ibáñez, La gran familia de los números, Catarata, 2021.

2.- Wolfram Mathworld: Pandigital number

3.- N. J. A. Sloane, Enciclopedia on-line de sucesiones de números enteros: oeis.org

4.- Wikipedia: Pandigital number

5.- David Wells, The Penguin Dictionary of Curious and Interesting Numbers, Penguin Books, 1986.

6.- Henry E. Dudeney, Amusements in Mathematics, Thomas Nelson and sons,1917 (el original puede verse en la librería Internet Archive).

7.- David Singmaster, Sources in recreational mathematics, an annotated bibliography

8.- Henry E. Dudeney, Los acertijos de Canterbury y otros problemas curiosos, Granica, 1988.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica

El artículo Universo pandigital se ha escrito en Cuaderno de Cultura Científica.

Willem de Sitter fue un respetado astrónomo y físico holandés que contribuyó al nacimiento de la cosmología moderna. Fue uno de los primeros teóricos que interpretó la teoría general de la relatividad desde el punto de vista de su aplicación al conjunto del universo, incorporando la nueva teoría de Einstein a la astronomía y la cosmología.

De izquierda a derecha, de pie, Einstein, Ehrenfest y De Sitter; sentados, Eddington y Lorentz, en la oficina de de Sitter en Leiden el 26 de septiembre de 1923. Fuente: Wikimedia Commons

De Sitter fue astrónomo en Leiden (Holanda), primero en la cátedra de astronomía de la Universidad de Leiden y después como director del Observatorio de Leiden. Estudió el Sistema Solar exhaustivamente y recalculó los movimientos de Júpiter y la Tierra. Sin embargo, se le recuerda más por su trabajo en cosmología, una ciencia que comenzó como tal gracias al trabajo de pioneros como él.

Desde el primer momento que escuchó hablar de las ideas de Einstein, de Sitter quiso aplicarlas a la astronomía. En 1911, después de estudiar la exposición de la teoría especial de la relatividad en el artículo de Einstein de 1905, de Sitter mostró que, si era cierto, el modelo de Einstein modificaría radicalmente todas las interpretaciones astronómicas basadas en el de Newton. En concreto, los movimientos de los planetas en el Sistema Solar no se ajustarían, de hecho, a las predicciones que durante mucho tiempo se consideraron ciertas. Entre 1916 y 1918, Einstein y de Sitter mantuvieron una abundante correspondencia sobre qué modelo de universo se ajusta mejor a las ecuaciones de la relatividad.

De Sitter desarrolló inicialmente un modelo esférico del universo, a diferencia del cilíndrico que Einstein había previsto. De Sitter también intentó trazar la forma de ese universo esférico en ausencia de materia. La reacción de Einstein al modelo de de Sitter fue enérgicamente negativa porque desobedecía algunas premisas importantes para Einstein. Entre ellas la esfera de de Sitter describía un universo que cambiaba de tamaño en vez de permanecer hermosamente constante.

Las objeciones de Einstein iban de lo científico a lo emocional. A nivel científico, ¿qué impedía que el universo se expandiese salvajemente? A nivel emocional, un universo en expansión significaba que yendo hacia atrás en el tiempo, el universo había sido más y más pequeño, comenzando en…nada. Esto significaba que el universo no había existido siempre. En algún punto en el tiempo, el universo había comenzado, lo que olía a superstición y religión.

La ausencia de materia en el universo de de Sitter también le tocaba las narices a Einstein. Einstein veía la materia, y su correspondiente gravitación, como lo que creaba inherentemente la forma del universo. Citó lo que llamaba el “principio de Mach”, una idea del físico austriaco Ernst Mach. El principio afirma que los movimientos de cualquier objeto en el universo están determinados por la distribución de todos los demás cuerpos en el universo. Dado que la manera en el que un cuerpo se mueve en el espacio es equivalente a la forma que tiene el espacio, el concepto de “forma” sin materia, insistía Einstein, no tiene sentido.

Einstein y de Sitter discutieron sus modelos en persona y por carta. Einstein llegó a decir inicialmente que debía haber algún tipo de defecto matemático en el modelo de de Sitter, algo que dijo de viva voz y que también llegó a publicar. Al final, sin embargo, mediante la correspondencia con de Sitter y con otros investigadores, Einstein tuvo que admitir que las matemáticas de de Sitter eran sólidas. No había pues ninguna objeción al modelo salvo que describía un universo no estático, algo metafísicamente imposible para Einstein.

– Pero, Willem, tío, ¿no te das cuenta de que no queda bonito? – Las matemáticas cuadran, ¿qué me estás contando, Albert? Fuente: Wikimedia Commons

Por supuesto, Einstein estaba equivocado, y el hecho de que el universo efectivamente se expande sería demostrado, más allá de toda duda razonable, poco después por Edwin Hubble en 1929. Pero nada de esto se sabía entonces y Einstein se aferró a su creencia de que el universo no podía cambiar de tamaño. Así, aunque Einstein admitiese que no había ningún error matemático con el modelo esférico de de Sitter, ni lo aceptó expresamente, ni publicó una retractación de sus críticas previas.

Más allá del modelo de Sitter

Ni que decir tiene que el modelo de de Sitter siempre fue una versión sobresimplificada del universo. Sabemos positivamente que el universo tiene materia, y los modelos actuales difieren bastante de él. El modelo de de Sitter sí se incorporaría, no obstante, a la teoría del estado estacionario del universo. Mientras que el universo continúa expandiéndose, según esta teoría, se crea nueva materia continuamente de tal manera que la densidad no cambia con el tiempo. El universo no tendría ni principio ni fin.

En las décadas posteriores a la publicación por parte de Einstein de su teoría general de la relatividad en 1915, el aluvión de modelos y teorías sobre los orígenes del universo era inabordable para un cosmólogo que intentase mantenerse al día. En 1931, de Sitter, viendo lo que se había publicado en los últimos veinte años, escribió: “Nunca en toda la historia de la ciencia ha habido un período en el que las nuevas teorías e hipótesis aparezcan, florezcan y se abandonen con tanta rapidez como en los últimos quince o veinte años”. Y, sin embargo, ninguna hipótesis era satisfactoria, siempre había algo que quedaba fuera. En la reunión de enero de 1930 de la Royal Astronomical Society, de Sitter dio una charla sobre precisamente como ningún modelo era capaz de representar completamente el universo.

Seguirían apareciendo modelos incluso más hipotéticos. Después de que Hubble publicase sus descubrimientos sobre la expansión del universo, Otto Heckmann demostró que si un universo se expande y tiene materia no requiere que el espacio sea curvo. Otros modelos interesantes fueron publicados por Georges Lemaître y Alexander Friedmann.

Einstein y de Sitter publicaron un artículo conjuntamente en 1932 en los Proceedings of the National Academy of Sciences, en el que describen el que se conoce como modelo de Sitter-Einstein del universo. Era una solución bastante simple de las ecuaciones de la relatividad general de Einstein, pero el modelo incluía un universo en expansión, materia e, incluso, materia oscura. El modelo describe un espacio euclídeo, es decir, un espacio plano en el que la luz viaja en líneas rectas en vez de en curvas como describían los propios modelos anteriores de de Sitter y Einstein. En este nuevo modelo, el universo tiene un volumen total infinito y comienza en un big bang a partir de un minúsculo punto inicial. El universo también se expande en este modelo, aunque la velocidad de esta expansión disminuye con el tiempo y termina siendo cero.

Al mismo tiempo que se publicaba el artículo de Einstein y de Sitter, Richard Tolman escribió un comentario señalando que no había todavía suficiente información sobre la densidad, velocidad de expansión, o tipos de materia en el universo como para elegir el modelo ganador de todos los propuestos. Ahora décadas más tarde, hay muchos más datos y parece que se converge sobre una respuesta, el modelo Lambda-CDM, que es prácticamente euclídeo, como calcularon Einstein y de Sitter.

Referencia:

Einstein A, & de Sitter W (1932). On the Relation between the Expansion and the Mean Density of the Universe. Proceedings of the National Academy of Sciences of the United States of America, 18 (3), 213-4 doi: 10.1073/pnas.18.3.213

Para saber más:

Teoría de la invariancia (serie). Una introducción sin aparato matemático a los conceptos e ideas de la relatividad.
De la edad y tamaño del universo

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

Una versión anterior de este artículo se publicó en Experientia Docet el 9 de agosto de 2009.

El artículo Einstein y Willem de Sitter se ha escrito en Cuaderno de Cultura Científica.

Uno de los grandes retos de la astrobiología contemporánea es encontrar, entre otras cosas, aquellas causas o “filtros” que impidan el desarrollo o el mantenimiento de la vida en planetas que a priori podrían haber tenido las condiciones adecuadas o haber sido habitables en el sentido amplio de la palabra. Y es que la dinámica de los sistemas planetarios puede ser mucho más diversa y compleja de lo que nos pensamos y que haya numerosos factores intrínsecos, pero también externos, a los planetas capaces de alterar las condiciones ambientales no solo a corto plazo sino a lo largo del tiempo geológico.

Algunos de los factores internos probablemente podamos estudiarlos en el Sistema Solar, ya que en los planetas terrestres como Venus o Marte encontramos situaciones muy diferentes: Venus, un planeta del tamaño de la Tierra y que hoy tiene un efecto invernadero suficiente como para que la temperatura en su superficie llegue a los 480 °C, y Marte, un planeta que sabemos que en los primeros quizás mil o mil quinientos millones de años tuvo una atmósfera sustancial que permitía la existencia de agua líquida en su superficie y, por lo tanto, unas temperaturas templadas.

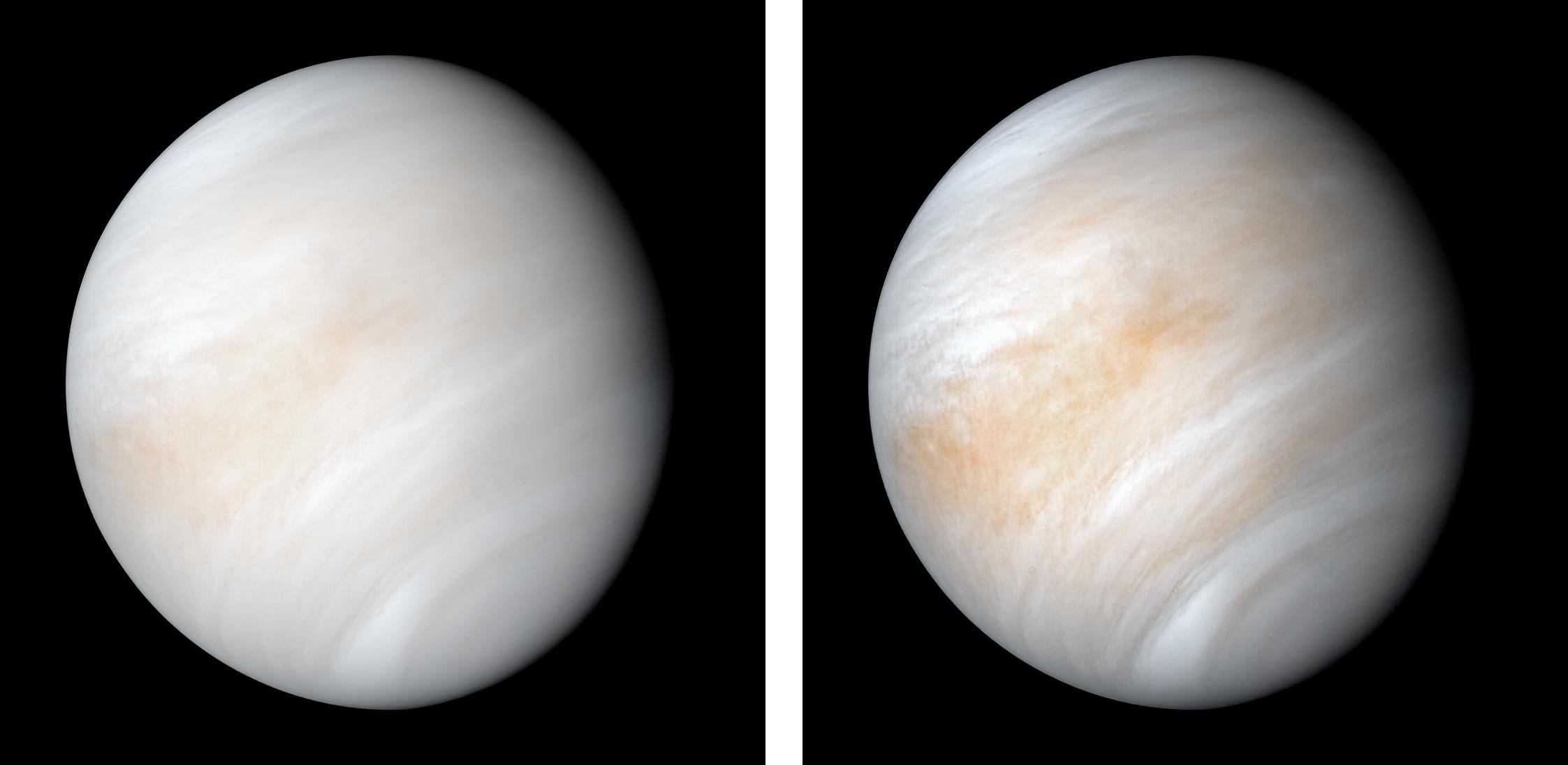Venus a los ojos de la misión Mariner 10. No hay atisbo de su superficie debido a las nubes que la cubren perpetuamente. Fuente: NASA/JPL-Caltech.

Estos cambios nos parecen realmente bruscos si suponemos que nuestro planeta, aunque sus condiciones hayan oscilado entre «bola de nieve» e «invernadero», ha mantenido cierta estabilidad puntuada por algunos momentos ambientales complicados, pero ningún extremo parecido a lo que vemos en nuestro entorno.

Cuando estudiamos fenómenos de extinción en masa en nuestro planeta encontramos que en la mayor parte de los casos estos eventos vienen relacionados en el tiempo con de erupciones volcánicas que forman las denominadas Grandes Provincias Ígneas (LIPs, por sus siglas en inglés), y cuyas dimensiones en cuanto al volumen de lava emitido es realmente grande, del orden de varios cientos de miles a millones de metros cúbicos.

La lava, como es obvio, no viaja en solitario, sino que lo hace acompañada de numerosos gases como el vapor de agua, el dióxido de carbono o el azufre, inyectando a la atmósfera cantidades de gases que antes estaban almacenadas en el interior del planeta y que pueden provocar un cambio climático extremo, especialmente si ocurren varias erupciones de tipo LIPs en periodos cortos de tiempo.

Como decíamos antes, en nuestro planeta tenemos un importante registro de este tipo de erupciones, pero la alteración climática provocada nunca fue permanente, incluso aunque hayan ocurrido algunos eventos en un espacio temporal relativamente corto.

Mismo tipo de eventos, ¿mismos efectos en la habitabilidad?

Un equipo de científicos de la NASA, la Universidad de Princeton y el Massachussets Institute of Technology ha estudiado la posibilidad de que este tipo de eventos fuese el responsable de que Venus tenga estas condiciones hoy día, mediante el análisis de los datos de estas grandes erupciones en la Tierra.

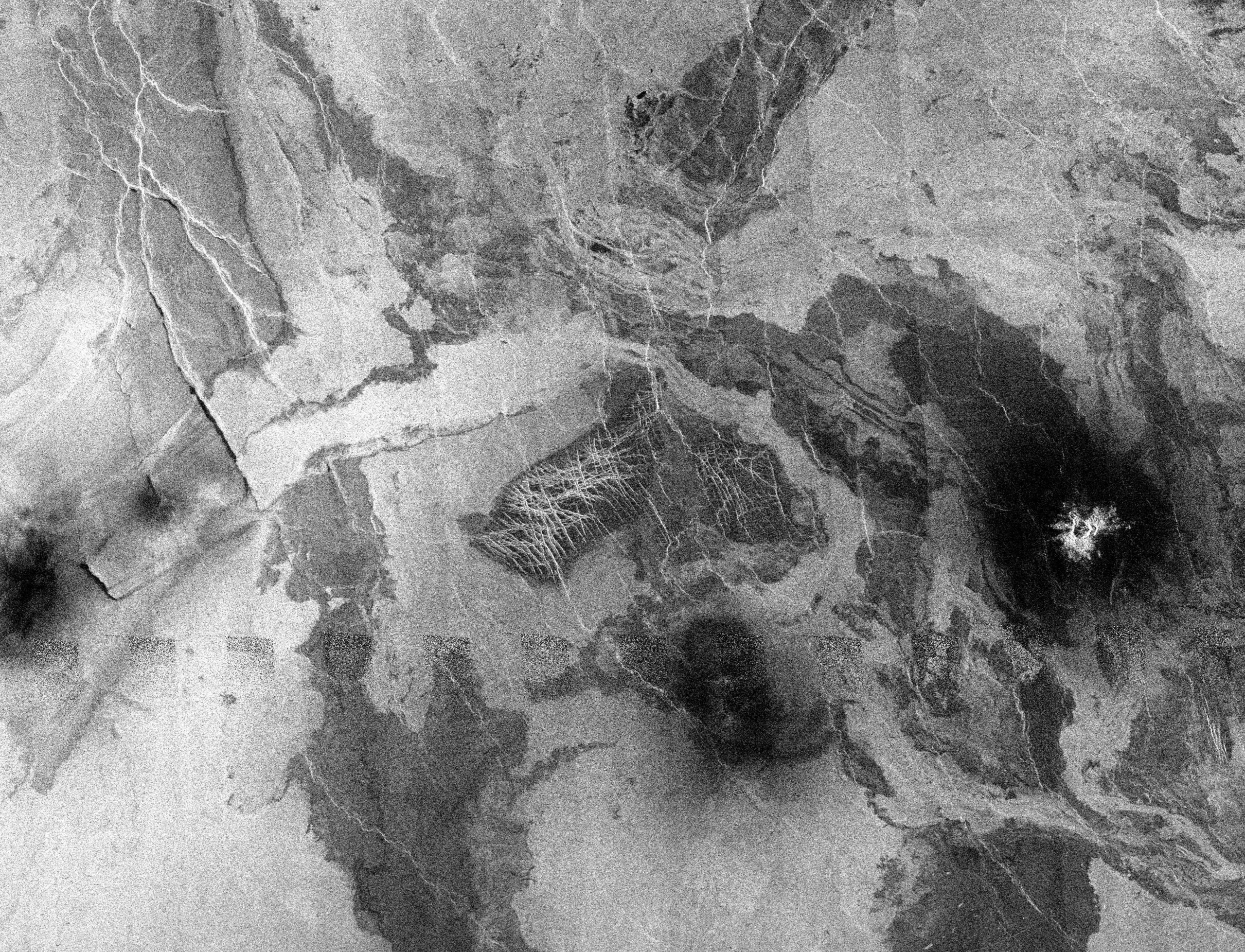Múltiples coladas de lava cubren la región de Lakshimi, en Venus, señal inequívoca de que Venus ha sido (o es) un planeta muy activo. Fuente: NASA/JPL.

Obviamente en el caso de que ocurriesen dos (o más) eventos de gran tamaño de una manera simultánea o casi simultánea el clima podría haber sufrido un importante cambio, quizás permanente, transformando nuestro planeta en un lugar inhabitable de manera permanente.

Han llegado a la conclusión de que en nuestro planeta las LIPs ocurren de manera aleatoria, sin una relación -al menos clara- entre este tipo de eventos, calculando que en los últimos 2800 millones de años, de los que tenemos datos de estas erupciones, podríamos esperar al menos 100 pares de erupciones de tipo LIPs y 10 tripletes con una separación de tan solo un millón de años entre una y otra.

¿Cómo podría haber afectado a Venus? Imaginamos que Venus fue un planeta muy similar a la Tierra al principio, con una atmósfera mucho menos densa, una temperatura mucho menor y una superficie cubierta por océanos, como lo estaría nuestro planeta.

La ocurrencia de varias LIPs aumentaría la concentración de gases de efecto invernadero en la atmósfera, provocando un aumento de las temperaturas que, a su vez, llevaría a una mayor evaporación de agua de los océanos. El vapor de agua liberado del océano también puede atrapar el calor de una manera muy efectiva, haciendo que este ciclo entre en una espiral de calentamiento, finalmente transformando a Venus en el planeta que vemos hoy.

¿Es una explicación plausible con el conocimiento que tenemos hoy de Venus? Lo cierto es que a nivel geológico sería una explicación bastante sencilla: sabemos que Venus ha tenido (y probablemente tenga) vulcanismo activo, y la existencia de LIPs en un planeta de tipo terrestre no es una teoría descabellada, aunque también nos queda por conocer el papel de la radiación solar en los últimos millones de años y como su variación puede también haber contribuido al calentamiento de Venus.

Aun así, todavía nos queda muchísimo por saber sobre Venus. Esperamos que en la próxima década las misiones espaciales planificadas (VERITAS, DAVINCI+ y EnVision) puedan aportarnos una gran cantidad de información que nos permita resolver algunas de las dudas sobre nuestro gemelo planetario.

Referencias:

Way, M., Ernst, R. and Scargle, J. (2022) Large-scale Volcanism and the Heat Death of Terrestrial Worlds The Planetary Science Journal doi: 10.3847/PSJ/ac6033

Para saber más:

Los volcanes de Venus
Lo que Venus, el gemelo infernal de la Tierra, podría enseñarnos sobre lo que hace a un planeta habitable
¿Qué hacemos ahora con Venus?

Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.

El artículo Vulcanismo y habitabilidad planetaria se ha escrito en Cuaderno de Cultura Científica.

Photo: Harli Marten / Unsplash

Las conversaciones rara vez terminan cuando lo desean las dos personas que están hablando; ni siquiera suelen acabar cuando una de ellas lo quiere. Y la diferencia entre el tiempo durante el que hablamos y el que deseamos hacerlo, por exceso o por defecto, representa, aproximadamente, la mitad de la duración de la conversación.

Esa es la conclusión principal que se extrae de dos estudios en los que trataron de indagar acerca de la capacidad para hacer que una conversación concluya cuando lo desean las dos personas que charlan. En uno entrevistaron a personas acerca de alguna conversación que hubiesen mantenido con otra muy próxima a ellas en las horas anteriores. En el otro, que hicieron a continuación, pidieron a otras personas que charlaran por parejas; al acabar, les hicieron las mismas preguntas que a las del primer estudio. En total monitorizaron cerca de mil conversaciones.

A partir de las respuestas, el equipo investigador determinó si las dos personas que conversaban habían querido acabar más o menos al mismo tiempo, si fueron capaces de estimar cuándo querían que acabasen sus contertulios respectivos, y hasta qué punto fueron capaces de utilizar esa estimación para finalizar su conversación cuando ambas -o, al menos, una de ellas- así lo querían.

La mitad de los participantes habrían preferido que la conversación hubiese tenido una duración que difiriese -por más extensa o por más breve- en un tercio o más del tiempo que realmente duró. La otra mitad, lógicamente, habría preferido una desviación inferior a una tercera parte del tiempo durante el que se prolongó. Quienes participaron en el estudio creían que sus contertulios preferían que la conversación hubiese sido, en promedio, algo más larga de lo que fue y, sobre todo, que su duración hubiese diferido sensiblemente. Y aunque sospechaban que sus contertulios preferían que la conversación hubiese sido de duración diferente a la deseada por ellos, minusvaloraron la magnitud de esa diferencia; no fueron capaces de percibir con un mínimo de precisión cuál era la duración deseada por la otra persona ni, por tanto, la desviación o diferencia con respecto a su preferencia.

Como consecuencia de esos desajustes, solo un 1,6% de quienes participaron terminaron su conservación cuando las dos personas lo deseaban. Pero tampoco tuvieron mucho éxito para terminarla cuando, al menos, una de ellas quería: solo un 29% de las conversaciones acabaron así. También fueron pocas las que acabaron en un tiempo intermedio a los deseos de ambos participantes. Y lo más llamativo es que casi la mitad terminaron antes de cuando los dos querían y una décima parte, acabaron después.

Estos desajustes obedecen a dos causas. Por un lado, cuando hablan dos personas, lo más normal es que no quieran prolongar la conversación en la misma medida. Por otro lado, tampoco son capaces de saber, con una mínima precisión, qué desea la otra persona.

Una conversación no es una negociación entre dos personas con diferentes deseos o intereses, sino un problema de coordinación en el que el deseo de cada una por continuar depende en parte de lo que piensa acerca de lo que la otra quiere. El problema es que, cuando de lo que se trata es de terminar conversaciones normales, si una persona manifiesta con claridad que quiere acabar antes que la otra, corre el riesgo de molestarla, de manera que lo normal, sobre todo si se trata de alguien amable, es que enmascare las ganas de acabar la conversación aunque de esa forma se prive al contertulio de la información necesaria para resolver el problema. La amabilidad no siempre resulta beneficiosa.

Fuente: Mastroianni, A. et al. (2021):  Do conversations end when people want them to? PNAS 18 (10)

Para saber más:

Hablando se interrumpe la gente

Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU

El artículo No sabemos cómo acabar una conversación se ha escrito en Cuaderno de Cultura Científica.

¿Estamos realmente diseñados para conectar con los demás? Si es así, ¿por qué siguen existiendo los psicópatas? ¿Se pueden tratar trastornos delirantes como la paranoia desde el punto de vista de la evolución? O ¿cómo ha cambiado la atracción sexual desde la época de nuestros ‘abuelos’ homínidos hasta ahora?

A estas y otras cuestiones relativas a la evolución del comportamiento humano se trató de dar respuesta durante la IV Jornada Nacional de Evolución y Neurociencias, evento organizado por la Cátedra de Cultura Científica de la UPV/EHU y la Red de Salud Mental de Bizkaia, que tuvo lugar los días 28 y 29 de abril en el Bizkaia Aretoa – UPV/EHU de Bilbao.

Desde que en 2017 un grupo de psiquiatras de la Red de Salud Mental de Bizkaia organizara la primera edición de esta jornada, la cita se ha convertido en un punto de encuentro para profesionales de distintos ámbitos científicos como la psiquiatría, la psicología, la biología o la filosofía con un interés común: la conducta humana desde una perspectiva evolucionista y su divulgación científica en un formato accesible y ameno para todos los públicos, a la par que riguroso y actualizado.

La percepción del propio cuerpo, la cognición corporal, es fundamental para la forma en la que un individuo se ubica en el espacio y el tiempo. O, visto de otra manera, el propio cuerpo determina la cognición. Y esto ha tenido su reflejo a lo largo de la evolución humana. Nos lo cuenta Emiliano Bruner, investigador en paleoneurobiología de homínidos en el Centro Nacional de Investigación sobre la Evolución Humana (CENIEH).



Para saber más:

Zurdos prehistóricos

Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus

El artículo IV Jornada Nacional de Evolución y Neurociencias: Emiliano Bruner – Habitar un cuerpo: cognición corporal y evolución humana se ha escrito en Cuaderno de Cultura Científica.

Un estudio realizado por el Grupo de Investigación Bentos Marino UPV/EHU predice que, debido al cambio climático, las especies de macroalgas de la costa cantábrica se parecerán cada vez más a las presentes en la más cálida costa mediterránea. Este tendencia parece que no afectará en principio a la costa gallega.

Toma de datos para el estudio. Foto: UPV/EHU

La distribución de las algas marinas está sufriendo una transformación. El aumento de la temperatura del mar, entre otros factores, está afectando al crecimiento de estos organismos y provocando desequilibrios en los ecosistemas marinos en las últimas décadas.

El efecto del cambio climático sobre la distribución de las especies ha sido objeto de muchas investigaciones recientes, pero a nivel de comunidad local sigue estando poco estudiado. Por ello, “nuestra investigación aplica por primera vez un modelo para predecir los cambios en las comunidades de macroalgas submareales en el norte de la Península Ibérica, desde Galicia hasta el País Vasco, bajo ciertos escenarios climáticos para dentro de cincuenta o cien años”, señala Nahiara Muguerza Latorre primera autora del estudio.

“Hemos observado que la temperatura del agua es el principal factor que determina la distribución de los conjuntos de macroalgas en nuestra área de estudio, mientras que la disponibilidad de nutrientes juega un papel secundario”, comenta la investigadora de la UPV/EHU. “La temperatura del agua tiene una gran influencia en la supervivencia, el crecimiento, la reproducción y el reclutamiento de las macroalgas”, añade.

Meridionalización de las poblaciones de macroalgas Localizaciones de la toma de datos. Fuente: Muguerza et al (2022)

“Los resultados de este trabajo —continúa Nahiara Muguerza— apoyan parcialmente nuestra hipótesis de que podría producirse una meridionalización de las poblaciones del norte de la Península Ibérica en el futuro. […] En el escenario más pesimista, el modelo proyecta que las comunidades del noroeste (Galicia) seguirán siendo distintas del resto, sirviendo de refugio a las especies de aguas más frías, mientras que los conjuntos del centro y el este de la costa norte de la Península Ibérica llegarán a parecerse más a los de la región mediterránea que a los de la costa noroeste. Especies con una afinidad más meridional, es decir, más de aguas cálidas”, explica la investigadora.

El equipo de investigación tiene claro que las algas son muy sensibles a cualquier variación ambiental producida por los efectos del cambio climático. Y, por lo tanto, que podrían ser buenos indicadores de la evolución de este y de sus efectos en el resto de ecosistemas marinos. “Esta investigación puede ayudar a predecir cómo responderá la biodiversidad del ecosistema costero a las nuevas condiciones ambientales. Se trata de una información fundamental para desarrollar políticas de gestión y conservación adecuadas”, apunta Muguerza. “Para otros estudios sería interesante ampliar el área de estudio a la costa occidental de la Península Ibérica y aumentar los lugares de muestreo en el Mediterráneo”, añade.

Referencia:

N. Muguerza, O. Arriaga, I. Díez, M.A. Becerro, E. Quintano y J.M. Gorostiaga (2022) A spatially-modelled snapshot of future marine macroalgal assemblages in southern Europe: Towards a broader Mediterranean region? Marine Environmental Research doi: 10.1016/j.marenvres.2022.105592

Para saber más:

Las algas del Cantábrico: centinelas del cambio climático
El declive de las praderas de algas por el cambio climático
Los invasores: Las algas Caulerpa

Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa

El artículo Las macroalgas cantábricas se volverán mediterráneas se ha escrito en Cuaderno de Cultura Científica.

El pasado 5 de junio se celebró el Día Mundial del Medio Ambiente y, aunque no os lo creáis, es una efeméride muy geológica. Generalmente, cuando hablamos de medio ambiente la primera imagen que nos viene a la cabeza está relacionada con la biodiversidad, es decir, con la diversidad biológica (flora y fauna) que se desarrolla en una zona. Pero rara vez pensamos en la geodiversidad, que es la variedad de procesos, estructuras y materiales geológicos que caracterizan ese territorio. Y, sin embargo, es la geodiversidad la que condiciona la biodiversidad que vamos a encontrarnos.

Panorámica del Valle de Karrantza (Bizkaia) desde el monte Ranero, donde se observan los diferentes parches de vegetación desarrollados de acuerdo a la altitud y el tipo de roca. Imagen: Iranzu Laura Guede.

La geodiversidad de una zona es producto de la historia geológica de ese lugar. Una historia de millones de años de cambios, procesos y acontecimientos naturales que han quedado preservados en las rocas y estructuras que podemos admirar en el paisaje actual. Una historia que nos habla de nuestro pasado, presente y futuro como especie y como sociedad. Y, como he dicho antes, una historia que determina la flora y fauna que se va a desarrollar en esa zona. Como muestra, vamos con algunos ejemplos.

El contexto tectónico sufrido por un territorio controla su topografía, pudiendo encontrarnos con la generación de grandes elevaciones montañosas que afectarán al ciclo atmosférico y provocarán horizontes de distribución de fauna y flora en altitud. O, por el contrario, puede que se produzca el desarrollo de amplias zonas más o menos planas a las que se ha adaptado una biodiversidad completamente diferente.

El tipo de roca que aflora en una zona caracterizará el suelo que se va a generar en la misma. Por ejemplo, en áreas con abundantes afloramientos de rocas calizas se desarrollarán suelos ricos en carbonato cálcico, mientras que en terrenos donde dominan las rocas areniscas, nos encontraremos suelos con un alto contenido en sílice. Esto condicionará el tipo de vegetación que podrá asentarse en estas zonas y, por ende, afectará a toda la cadena trófica.

Geodiversidad acuática Pequeña laguna formada por la acumulación de agua en una pequeña depresión del terreno en Añavieja (Soria). Imagen: Antonio Pérez.

La cantidad de agua disponible en el terreno también depende de las características geológicas del mismo. Por un lado, rocas porosas, como las calizas o los basaltos, permiten que el agua circule y se acumule en ellas, generando reservorios acuáticos tanto en superficie como subterráneos. Por otro lado, la erosión diferencial de los materiales geológicos o los procesos de hundimiento del terreno, generalmente debidos a esfuerzos tectónicos extensivos, favorecerán el desarrollo de zonas deprimidas del terreno en donde puede acumularse el agua, dando lugar a lagos y lagunas con una biodiversidad muy variada.

Playa de Oyambre (Cantabria) formada por arena fina. Imagen: Blanca María Martínez

Los ambientes litorales tampoco se libran de estar condicionados por la geología. El tipo de rocas que afloran en las zonas costeras y la disposición de las capas de esas rocas con respecto a las corrientes de oleaje y las mareas (es decir, si las capas se orientan de manera perpendicular o en paralelo a la línea de costa), determinará su grado de erosión o fragmentación, por lo que podremos encontrarnos con ambientes que varían entre playas de arena muy fina y acantilados rocosos. Mientras que en el primer medio abundarán organismos excavadores que viven enterrados en la arena, en el segundo tendremos una predominancia de los que habitan fijados a las rocas.

Litoral rocoso en Castro Urdiales (Cantabria). Las capas de rocas carbonatadas se disponen inclinadas con una orientación prácticamente perpendicular a la acción del oleaje. Imagen: Blanca María Martínez

Y estos son solo algunos ejemplos muy generales, porque podemos entrar al detalle que nos apetezca y seguiremos encontrando la misma relación geodiversidad – biodiversidad. La composición química y estructura interna de las rocas, así como los procesos y estructuras geológicas que se han producido en una zona a lo largo de millones de años de historia, dan lugar al desarrollo de diversos medios ambientes con características muy diferentes en los que se desarrollan una flora y una fauna adaptada, en muchas ocasiones de manera muy específica, a dichas condiciones. Sin esa historia geológica no tendríamos el paisaje que vemos hoy en día cuando miramos a nuestro alrededor. Y esto debe llevar a plantearnos que, si queremos conservar y proteger nuestra biodiversidad, antes debemos empezar por cuidar, y comprender, nuestra geodiversidad.

Para saber más:

¿De qué está hecha la arena?
Oh, blancos acantilados
Los volcanes submarinos de Bizkaia y Gipuzkoa

Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU

El artículo La geodiversidad que nos rodea se ha escrito en Cuaderno de Cultura Científica.

Eleanor Pairman nació el 8 de junio de 1896 en el pueblo de Lasswade (Escocia). Era la menor de los cuatro hijos de Helen y John Pairman. Su padre, abogado de la Corte Suprema de Escocia, falleció cuando ella aún no había cumplido los 5 años; la familia pasó a partir de ese momento dificultades económicas.

Eleanor Pairman (1914). Imagen: George Watson’s College.

 

Asistió a la escuela local hasta 1908, cuando ingresó en el George Watson’s Ladies’ College. Tras graduarse, en 1914, comenzó a estudiar matemáticas en la Universidad de Edimburgo. En 1917, se graduó con una maestría “con honores de primera clase” en matemáticas y filosofía natural. Gracias a sus excelentes calificaciones obtuvo una beca de tres años que le permitió continuar sus estudios de posgrado en la Universidad de Edimburgo antes de incorporarse, en 1918, al equipo del matemático Karl Pearson (1857-1936) —que impulsó la utilización de métodos estadísticos en biología— en el Departamento de Estadística Aplicada del University College de Londres. Allí trabajó como “computadora” para el matemático, con el que publicó un artículo en la revista Biometrika. En esa época también escribió Tracts for Computers (vol. I. Tables of the digamma and trigamma functions) que fue publicado por Cambridge University Press.

En 1919 viajó a Estados Unidos y comenzó su formación en el Radcliffe College, de Cambridge, una universidad para mujeres muy vinculada al Harvard College en el que solo podían estudiar hombres. Allí investigó bajo la supervisión del prestigioso matemático George David Birkhoff (1884-1944). Defendió su tesis doctoral —Expansion Theorems for Solution of a Fredholm’s Linear Homogeneous Integral Equation of the Second Kind with Kernel of Special Non-Symmetric Type— en 1922, convirtiéndose en la tercera mujer en obtener un doctorado en matemáticas de Radcliffe College.

En ese mismo año se casó con un compañero de estudios de posgrado, Bancroft Huntington Brown (1894-1974), que también había defendido su tesis doctoral en el Harvard College. El matrimonio se trasladó a Hanover donde Bancroft Brown se incorporó como profesor al Dartmouth College, que en ese momento era una universidad exclusivamente masculina. Tuvieron cuatro hijos —John, Barbara, Joanna (que falleció antes de cumplir un año) y Margaret—.

Como ya hemos comentado, Pairman publicó algunos artículos en solitario y en colaboración con Pearson y Rudolph E. Langer (1894-1968) —On a class of integral equations with discontinuous kernels—, otro de los alumnos de Birkhoff.

Entre 1955 y 1959, Eleanor fue contratada como profesora de matemáticas a tiempo parcial en Dartmouth.

La máquina de coser de Pairman

En la década de 1950, Pairman comenzó a interesarse en la enseñanza de las matemáticas a alumnado ciego. Para ello, estudió braille —y más tarde el código Nemeth para matemáticas— y aprendió —fundamentalmente para explicar geometría— a realizar diagramas y símbolos matemáticos usando su máquina de coser y otros utensilios domésticos —como tijeras dentadas o ruedas de pastelería—. Con estas herramientas caseras conseguía realizar diseños sobre delgadas hojas de cartulina, que el alumnado ciego podía “leer” con las yemas de sus dedos. Con su máquina de coser, Eleanor “perforaba” el papel” reproduciendo cada símbolo que deseaba reproducir al pasar la cartulina bajo la aguja de su máquina.

En 1959 el periódico Hanover Gazette publicó un artículo sobre el trabajo de Pairman. En este reportaje, el medio comentaba que Eleanor estaba transcribiendo dos manuales matemáticos, uno para un estudiante de primer curso en el Boston College y otro, un libro de referencia sobre teoría de grupos, destinado a un posgrado en la Universidad de Columbia en Nueva York.

Eleanor, “Nora” para sus personas más allegadas, falleció el 14 de septiembre de 1973. Su hija pequeña, Margaret, comentaba:

A pesar de la satisfacción que obtuvo con estos proyectos [de Braille], la única vez que la vi verdaderamente feliz fue cuando estaba enseñando. Y tuvo muy pocas oportunidades de hacer eso, ya que obviamente estaba adelantada a su tiempo y también atrapada en una comunidad universitaria solo para hombres y en un mundo donde era casi imposible para las mujeres casadas funcionar profesionalmente.

Referencias

• John J. Robertson and F. Edmund, Eleanor Pairman, MacTutor History of Mathematics archive, Universidad de Saint Andrews

• Eleanor Pairman, George Watson’s College

• Eleanor Pairman Brown, Darmouth College, 2016

• Eleanor Pairman, Wikipedia

 

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad

El artículo Eleanor Pairman, la matemática que usó su máquina de coser para enseñar geometría a personas ciegas se ha escrito en Cuaderno de Cultura Científica.

Durante buena parte de su vida Albert Einstein, el físico teórico, se relacionó con inventores y patentó e intentó comercializar sus propios inventos. No solamente trabajó como examinador de patentes en la Oficina Federal de Patentes Suiza en Berna, en una época donde abundaban inventos basados en la electricidad (luz, comunicaciones, generación), sino que durante mucho tiempo fue citado como perito experto en casos de patentes (incluso cuando ya era famoso por su trabajo en física teórica). A lo largo de los años trabajaría en cualquier cosa, desde instrumentos para la medida de precisión del voltaje eléctrico a audífonos.

Esquema de funcionamiento del «Refrigerador Einstein» desarrollado por Einstein y Szilard tal y como aparece en la patente estadounidense de 1930. Fuente: Wikimedia Commons

En 1906 Einstein publicó un artículo sobre cómo estudiar el movimiento browniano bajo los efectos de un campo eléctrico fluctuante. Comenzó a construir una Maschinchen, una “maquinita”, para probar sus ideas. En esa época, los mejores sistemas de medición de electricidad podían detectar solamente unas pocas milésimas de voltio, pero Einstein necesitaba medir menos de una milésima.

El hermano de su amigo de la Academia Olimpia Conrad Habicht, Paul, poseía una pequeña empresa de fabricación de instrumentos. Trabajando con Paul, construyó la máquina. En una carta a su amigo Max von Laue, Einstein decía: “No podrías evitar sonreír […] si pudieras ver mi gloriosa chapucilla casera”. Einstein no patentó este invento; lo intentó pero no tuvo éxito porque no había industriales interesados en fabricarla.

A pesar de ello los hermanos Habicht le siguieron dando vueltas a la máquina y tras unos pocos años obtuvieron una patente para fabricarla. Desafortunadamente, no era muy fiable y la tecnología ya estaba obsoleta. Si bien Einstein no aparecía en la patente, los hermanos le dieron las gracias con una anotación en la que decía que los experimentos se realizaron “conjuntamente con A. Einstein en el laboratorio de la Universidad de Zúrich”. Muchos años después, cuando Paul murió, Einstein escribió a su hermano Conrad una carta de pésame en la que hizo referencia a esta colaboración: “Fue divertido, aunque no obtuviéramos nada útil”.

Tampoco salió nada útil de los intentos de Einstein de desarrollar un nuevo tipo de ala de avión. En el verano de 1915, en medio de sus artículos sobre la relatividad general, Einstein publicó uno breve, “Teoría elemental de ondas en agua y vuelo”, en el que proponía un perfil de ala “con joroba”. Pero nadie continuó el trabajo.

En 1903, un joven millonario llamado Hermann Anschütz-Kaempfe quería explorar el Polo Norte en submarino. Esto era arriesgado porque el submarino no podía emerger para orientarse y el casco metálico hacía inútil la brújula. Anschütz desarrolló un sistema giroscópico que podía ser una alternativa. En 1908 lo patentaba en Europa. Independientemente Elmer Sperry había desarrollado un dispositivo similar que patentó en Estados Unidos. Cuando en 1914 Sperry intentó vender el artefacto, bautizado como girocompás, a la marina de guerra alemana, Anschütz lo denunció por violación de patente. El tribunal nombró perito independiente a Einstein, que tras estudiar los equipos, respaldó la argumentación de Anschütz, que ganó el caso en 1915.

Tras la Primera Guerra Mundial, Anschütz y Einstein colaboraron estrechamente en el desarrollo de una versión mejorada del girocompás, que patentaron. Para 1930, prácticamente todo buque moderno del mundo tenía un girocompás. Einstein recibía por contrato el 3% de las ventas y un 3% de los ingresos por licencias. Irónicamente para un dispositivo que era usado por la marina del III Reich, las ganancias que generaba para Einstein iban a parar a una cuenta en Amsterdam y el dinero empleado en ayudar a científicos judíos a escapar de los nazis.

En 1927 Einstein se puso manos a la obra con otro invento en compañía de su colega Leo Szilard. Diseñaron una bomba frigorífica que no era mecánica sino electromagnética. Un metal líquido se movía en un sentido y el contrario dentro de un tubo cuando se veía afectado por un campo electromagnético alternante. La bomba era elegante conceptualmente hablando y, desde un punto de vista práctico, más silenciosa que los modelos existentes. Los dos hombres patentaron su invento en 1930, y en los siguientes dos años consiguieron siete patentes más. Pero el invento quedó prácticamente en nada comercialmente hablando, porque la competencia, que nunca está quieta, había mejorado considerablemente las bombas basadas en gases por lo que no había necesidad de usar un equipo que usase metales potencialmente tóxicos. Muchos años después, en los inicios de los reactores nucleares de uso civil, se consideró seriamente la posibilidad de usar la bomba Einstein-Szilard pero no llegó a generalizarse su uso industrial.

Otro invento de Einstein fue una cámara de exposición automática desarrollada en 1936 con su amigo Gustav Bucky. Además, Einstein fue el coautor de artículos de contenido experimental sobre audífonos y membranas semipermeables para coloides.

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

Una versión anterior de este artículo se publicó en Experientia Docet el 24 de abril de 2010.

El artículo Einstein y sus inventos se ha escrito en Cuaderno de Cultura Científica.

Un equipo de investigadores liderado por científicos de la UPV/EHU y del BERC POLYMAT analiza de forma crítica las ventajas y retos de los métodos actuales de reciclado de polímeros, y establece una hoja de ruta con el objetivo final de alcanzar una economía de los plásticos sostenible.

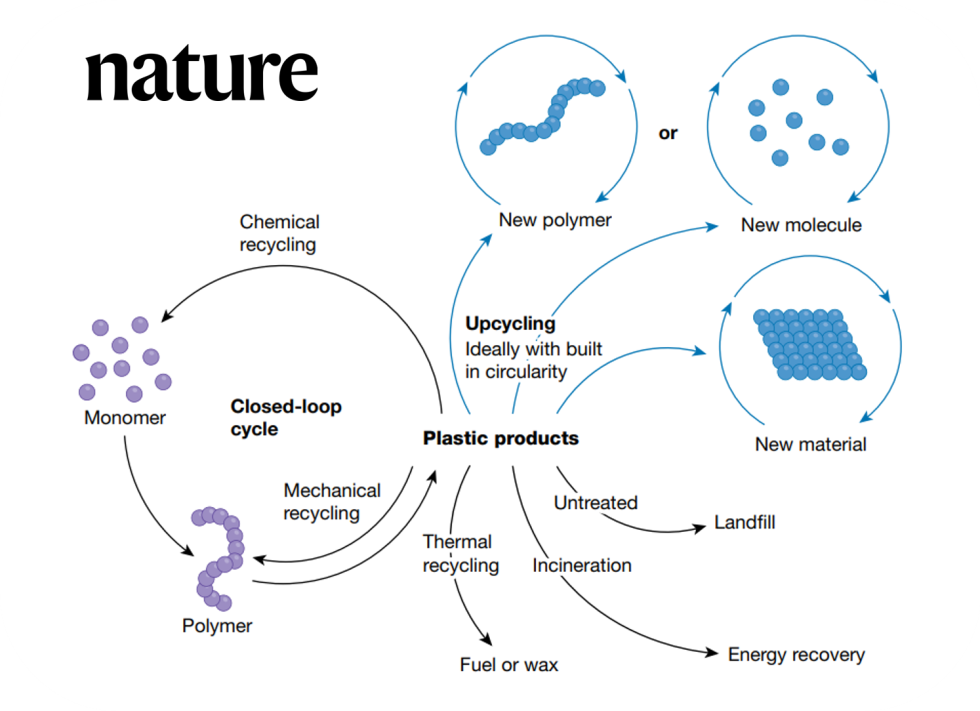Fuente: Nature. Jehanno et al (2022)

Es bien sabido que los plásticos básicos no se degradan y contaminan permanentemente el medio ambiente. También es un hecho conocido, aunque este muy poco publicitado, que el reciclaje químico de los plásticos aun no es viable a escala industrial y aun hay muchas dificultades de toda índole, no solo técnica, que deben resolverse hasta conseguir una economía de plásticos sostenible.

Como resultado, menos del 20% de los residuos plásticos se “reciclan” actualmente en los países desarrollados. Pero quizás no como mucha gente cree: su uso principal es como fuente de energía o su reutilización –que no reciclado- como materiales de menor valor mediante un tratamiento puramente físico, mecánico. Visto de otra forma, actualmente la mayoría de los plásticos desechados se depositan en vertederos o se queman, y los que se reutilizan casi siempre se recombinan mecánicamente.

Las limitaciones de las técnicas de clasificación, algo crítico dada la enorme variedad de plásticos, además de la presencia de aditivos, contaminantes varios, la presencia de polímeros minoritarios o los productos de múltiples capas terminan conduciendo a un deterioro sustancial de las propiedades durante y después del reprocesamiento. Es decir, el reciclaje mecánico de plásticos post-consumo da como resultado con demasiada frecuencia materiales de baja calidad o de baja utilidad.

Para aquellos plásticos de desecho cuyo reciclaje mecánico o químico actualmente es prohibitivo o inviable, ha nacido un nuevo campo de investigación: el upcycling (“superciclaje”) químico, que promete utilizar enfoques químicos o de ingeniería que permitan colocar los plásticos de desecho al comienzo de una nueva cadena de valor.

El verdadero reciclado de los plásticos

El verdadero reciclado de plásticos, a diferencia de la mecanización o su uso como fuente de energía, conlleva transformar un polímero en otro. Esto es upcycling. Para ser precisos, el upcycling de polímero a polímero se traduce en la transformación directa de plásticos desechados en un polímero de una composición diferente que tiene más valor que el material original. Pero “valor” entendido como un concepto más amplio que el puro valor económico, incluyendo también valores ambientales y sociales.

Un nuevo artículo de revisión liderado por Haritz Sardon, profesor adjunto en la UPV/EHU y líder del grupo “Catálisis y Polímeros Sostenibles” en POLYMAT, y la investigadora Coralie Jehanno (POLYMAT, Polykey) analiza los diferentes métodos de última generación para convertir desechos plásticos en materiales de alto rendimiento, productos químicos finos y polímeros especiales de valor añadido. También incluye las últimas innovaciones en conceptos y métodos de upcycling.

La necesidad de desarrollar estrategias para reducir, reutilizar y reciclar los desechos plásticos, es un desafío científico y social apremiante, no solo para reducir la cantidad de plásticos desechados que contaminan el medio ambiente, sino también para reducir las emisiones de gases de efecto invernadero causadas por el fabricación de plásticos vírgenes. Este nuevo artículo, resultado de dos años de trabajo, promete ser una referencia para llegar algún día al verdadero reciclado de los plásticos.

Referencia:

Jehanno C., Alty J. W., Roosen M., De Meester S., Dove A. P., Chen E. Y. X., Leibfarth F. A., Sardon H. (2022) Critical advances and future opportunities in upcycling commodity polymers Nature 603, 803-814, 2022 DOI: 10.1038/s41586-021-04350-0

Para saber más:

Desmitificando: Los plásticos
Bioplásticos, no todos son biodegradables
La pandemia de plástico

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

El artículo El verdadero reciclado de los plásticos se ha escrito en Cuaderno de Cultura Científica.

Se ha descubierto el enterramiento ritual más antiguo de África; el de un niño de aproximadamente 3 años enterrado hace 78.000 años, al que han llamado Mtoto. Este enterramiento se caracteriza por la posición fetal en la que se encontró colocado el cuerpo y por estar arropado con hojas. Ambos elementos son característicos de los entierros humanos realizados por los Homo neanderthalensis y los Homo sapiens durante el Paleolítico (1.000.000-10.000 años antes del presente-AP-). Pero, ¿en qué momento se inicia este comportamiento ritual y cómo va evolucionando a lo largo de las tres etapas en las que se divide este periodo?

Inhumación de Homo sapiens (40.000-10.000 AP). Ilustración: Jon Mikel Tutor Sánchez

Durante el Paleolítico inferior (1.000.000-200.000 años AP), existen pequeñas muestras de cierto comportamiento ritualista del Homo erectus, caracterizado por el canibalismo de los restos humanos. Pero, sólo pueden quedar como elementos para la especulación, porque no constituyen evidencia suficiente para considerar esto como un comportamiento ritual, como tal. Por ello, para responder a la pregunta de cuándo comenzó realmente, debemos situarnos en un contexto posterior, caracterizado por un clima de frío extremo, y protagonizado por el Homo neandertalhensis: el Paleolítico medio (200.000-40.000 años AP). Es esta especie la que comenzará a organizarse en tribus estructuradas, con una división piramidal, en la que se reconocerá un líder de grupo. Con ellos cambia también el asentamiento, comenzarán a establecerse en las cuevas, para protegerse del clima.

Es en estas cuevas donde empezarán a aparecer las primeras muestras de enterramiento ritual de la historia, las inhumaciones. Estos rituales podían ser excavaciones deliberadas de huecos para la colocación de cadáveres en su interior o simplemente el depósito de los cuerpos en el suelo, cubiertos con rocas u otros elementos, con intención de preservarlos. Además, los difuntos se encontraban en unas posiciones concretas. Aparecen con los brazos cruzados sobre el pecho, los brazos y las piernas flexionados o en posición fetal y siempre colocados en una orientación de este-oeste. Las inhumaciones no serían algo generalizado en la población de la época, porque no se daba en todos los casos, pero lo suficiente como para que se aprecie ya una clara intención ritual en ellas.

Así pues, podemos decir que los primeros indicios de enterramiento ritual del periodo Paleolítico comienzan con el Homo neanderthalensis y que una clara muestra de ello es la inhumación del cadáver de Mtoto, del que hablamos con anterioridad. Aunque no es con esta especie con quien evolucionará. Con el tiempo, durante el Paleolítico superior (40.000-10.000 años AP), el Homo neanderthalensis desaparecerá y dejará paso al Homo sapiens. Durante este periodo se producirán una gran cantidad de cambios tecnológicos, económicos, en los métodos de trabajo, en las herramientas y en las creencias esotéricas de la población.

Es entonces cuando se produce la evolución clara de los rituales mortuorios con respecto al Homo neanderthalensis. A pesar de mantener la inhumación como método de enterramiento en común, esta se generalizará entre la población. Además, se comenzará a refinar el ritual, introduciendo elementos novedosos, como las ofrendas acompañando a los cadáveres. El Homo sapiens comenzará durante este periodo a crear también las primeras sepulturas conocidas, más elaboradas que las inhumaciones y algunas de ellas dotadas de un completo ajuar en su interior.

Posteriormente los rituales irán evolucionando hasta llegar a lo que conocemos en la actualidad, pero poco más sabemos de las actividades mortuorias de la época del Paleolítico y los interrogantes más importantes siguen abiertos.; ¿Por qué la posición determinada de los cuerpos?, ¿qué representaban los objetos con los que se enterraban a los cadáveres? Las excavaciones continúan y quizás, algún día, conozcamos las respuestas a estas preguntas.

Referencias consultadas:

Ariana Fernández, A. (2013). Los enterramientos Neandertales en Eurasia; Una comparación con los Homo sapiens arcaicos. Universidad de Cantabria.

Rivera, A. (25 de Febrero de 2011). Los enterramientos del paleolítico medio. Arqueología Cognitiva.

Nuñez, H; Paniagua, A. (2001). Tras las huellas de nuestros orígenes – Las primeras creencias. Olimpiadasquindio.

CENIEH (05 de Mayo de 2021). El enterramiento humano más antiguo de África.

 

 

Autor: Jon Mikel Tutor Sánchez (IG: @JonMikelTutor) es graduado en bellas artes. Postgrado de Ilustración Científica de la UPV/EHU – curso 2020/21

Artículo original: Un niño recostado delicadamente, el primer enterramiento humano de África de María Martinón-Torres. Cuaderno de Cultura Científica, 6 de mayo de 2021

“Ilustrando ciencia” es uno de los proyectos integrados dentro de la asignatura Comunicación Científica del Postgrado de Ilustración Científica de la Universidad del País Vasco. Tomando como referencia un artículo de divulgación, los ilustradores confeccionan una nueva versión centrada en la propia ilustración

El artículo Humanos enterrados en el tiempo se ha escrito en Cuaderno de Cultura Científica.

¿Estamos realmente diseñados para conectar con los demás? Si es así, ¿por qué siguen existiendo los psicópatas? ¿Se pueden tratar trastornos delirantes como la paranoia desde el punto de vista de la evolución? O ¿cómo ha cambiado la atracción sexual desde la época de nuestros ‘abuelos’ homínidos hasta ahora?

A estas y otras cuestiones relativas a la evolución del comportamiento humano se trató de dar respuesta durante la IV Jornada Nacional de Evolución y Neurociencias, evento organizado por la Cátedra de Cultura Científica de la UPV/EHU y la Red de Salud Mental de Bizkaia, que tuvo lugar los días 28 y 29 de abril en el Bizkaia Aretoa – UPV/EHU de Bilbao.

Desde que en 2017 un grupo de psiquiatras de la Red de Salud Mental de Bizkaia organizara la primera edición de esta jornada, la cita se ha convertido en un punto de encuentro para profesionales de distintos ámbitos científicos como la psiquiatría, la psicología, la biología o la filosofía con un interés común: la conducta humana desde una perspectiva evolucionista y su divulgación científica en un formato accesible y ameno para todos los públicos, a la par que riguroso y actualizado.

La evolución no nos ha hecho perfectos del todo. Y puede que si no tenemos cuidado parte de las imperfecciones cognitivas las hereden nuestros futuros amos cibernéticos. Helena Matute, que es catedrática de psicología en la Universidad de Deusto, nos advierte de ello.



Para saber más:

Sesgos cognitivos que aquejan a la ciencia

Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus

El artículo IV Jornada Nacional de Evolución y Neurociencias: Helena Matute – Sesgos cognitivos e Inteligencia Artificial se ha escrito en Cuaderno de Cultura Científica.

Ruth Lazkoz

Foto: Aperture Vintage / Unsplash

Pongamos en la coctelera un título impactante, una pregunta ancestral y unas gotitas de física. Si lo agitamos bien solo nos quedará degustarlo. Pero ¿nos dejará un buen sabor de boca saber qué destino aguarda al universo? Recogemos aquí el testigo de todas las personas que se han preguntado eso mismo desde la antigüedad. No obstante, jugamos con ventaja: por fin podemos dar respuestas usando ciencia puntera y las predicciones sugieren que podríamos dirigirnos a un final violento, un Big Rip o Gran Desgarro.

Los datos experimentales encajan muy bien con el Big Rip, apuntando a que es muy probable que ocurra. La base es que el universo contiene suficiente energía oscura para ir “estirándolo”, expandiéndolo de un modo cada vez más acelerado. Las galaxias se irán separando cada vez más, y la atracción gravitatoria irá poco a poco haciéndose más insignificante hasta que su efecto desaparezca. Los planetas y los satélites perderán sus órbitas y las estrellas se desligarán de las galaxias. Entonces habrá llegado ese Gran Desgarro del universo.

La energía oscura expande aceleradamente el universo

Definitivamente el universo a gran escala se está haciendo cada vez más grande. En concreto, su ritmo de expansión se está acelerando. Las ecuaciones de Einstein indican que la causa es que está compuesto en su mayor parte de energía oscura, la cual produce gravedad repulsiva. Pero ¿podemos afinar más?

Admitamos humildemente antes de ir más allá que nuestros modelos disfrazan nuestra ignorancia haciéndola pasar por sabiduría. En ellos imaginamos la energía oscura como un fluido descrito de forma muy elemental. Usaríamos para ello variables heredadas de la termodinámica.

Por un lado tendríamos la presión de ese fluido y por otro su densidad, es decir, la cantidad de energía por unidad de volumen. Si solo tuviéramos partículas con velocidades pequeñas, esa energía sería esencialmente la de sus masas. Nos bastaría así pensar en la gravitación a la manera de Newton, sin depender de Einstein. Pero eso no es posible porque en nuestro universo también hay partículas muy rápidas, como fotones y neutrinos.

En vista de ello planteamos entonces que el universo es una sopa de distintos fluidos con sus propiedades diversas. Así hacemos que las ecuaciones de Einstein nos hablen de las propiedades que deben tener los distintos fluidos para que se produzca la expansión acelerada. Y no solo eso, nos indican en qué proporciones han de estar esos ingredientes. Aparte de los fotones (neutrinos y otras porquerías) tendremos materia oscura en el sector de componentes que producen gravitación atractiva. Y entran en pugna con la energía oscura.

Científicos del proyecto internacional SDSS-III han elaborado un mapa tridimensional de 1,2 millones de galaxias para comprender las misteriosas propiedades de la energía oscura y sus efectos en la aceleración de la expansión del universo. / Daniel Eisenstein y SDSS-III.

El ritmo de expansión podría hacerse infinito

El tipo de energía oscura más intrigante es la constante cosmológica y representa un barrera muy singular. La hipótesis de trabajo más usual para describir cualquier fluido de los mencionados es que la presión y la densidad de energía son proporcionales entre sí.

¡Pero, cuidado! Si bien la densidad de energía es siempre positiva, la energía oscura tiene presión negativa. De hecho, ha de ser suficientemente negativa. El número que gobierna la proporción de presión frente a densidad de energía juega un papel crucial en las soluciones de las ecuaciones de Einstein. Ese parámetro nos dice en primer lugar si el universo se expande aceleradamente o no. Dicho de otro modo, dicta si la presión es suficientemente negativa como para producir la necesaria repulsión.

Pero una presión aún más negativa podría dar lugar a un comportamiento dramático: el ritmo de expansión podría hacerse infinito de repente. De hecho, lo mismo le ocurriría al propio tamaño del universo (y a su factor de escala). Y eso tendría consecuencias catastróficas, destruyendo todas las estructuras conocidas. De hecho, todo sería un disparate bajo estas condiciones. Y también el cambio del cambio se haría infinito súbitamente.

Hay evidencias

La posibilidad de que ocurra esta situación es bien conocida desde la perspectiva teórica. La sorpresa es que los datos experimentales parecen favorecer esa situación. Dicho de otro modo, hay evidencias de que el universo pueda acabar en un Big Rip.

Bueno, conviene hacer un pequeño matiz para esquivar las protestas de algunos colegas. Dependiendo de las fuentes consultadas, ese escenario no es necesariamente el que la estadística apoya con más fuerza. Pero, curiosamente, el consenso apunta a que el actual rango de incertidumbre sí incluye al Big Rip entre los destinos finales muy probables.

La energía oscura fantasma es la culpable del final violento

El tipo de energía oscura causante de ese fin de fiesta violento se llama energía oscura fantasma. Para ofrecer un poquito más de detalle hay que recurrir a un sistema de unidades escogido al efecto. Usándolo vemos que el Big Rip se producirá si en valor absoluto la presión supera a la densidad de energía. Si son iguales, estamos ante un caso límite, precisamente la famosa constante cosmológica. Este conocido tipo de fluido fue introducido por Einstein. Paradójicamente, su objetivo era conseguir un universo estático, sin expansión. El genio lo abandonó calificándolo del mayor error de su vida al evidenciar Hubble la expansión del universo.

Faltan 130 mil millones de años para el final violento

Pero volvamos a lo que importa. ¿Si el universo va a romperse en mil pedazos, de qué cosas debemos dejar de preocuparnos? ¿Respirarán con alivio quienes aún contemplan seguir pagando hipoteca por 20 años más? Me temo que no soy portadora de buenas noticias. El Gran Desgarro podría tardar en producirse unos 130 mil millones de años. Eso equivale a 10 veces la edad actual del universo.

Esa estimación se basa en seleccionar un par de valores dentro de las ventanas estadísticamente válidas. En primer lugar pondríamos que la energía oscura representase un 70 % del contenido del universo. Y en segundo lugar haríamos la relación entre la presión y la densidad de energía tan solo un 10 % más grande que para la constante cosmológica. Y con eso, ¡listo! Predecimos un Big Rip que tardará muchísimo tiempo en llegar.

El telescopio Nancy Grace Roman, que se lanzará en 2027, podría ayudar a entender si el universo terminará con un Big Rip. @NASA.

Para afinar más todo este panorama necesitamos tener observaciones del universo a gran escala en más cantidad y calidad. Sin duda contribuirán a ello los datos que nos aportarán los telescopios James Webb (en marcha) o Nancy Grace Roman (planificado), combinados con los de otros esfuerzos internacionales. Y quizá lo más interesante no sea resolver el enigma del destino final del universo. Tampoco lo es la oportunidad de resolver otros de los que no hemos hablados. Lo verdaderamente apasionante sería la posibilidad de que emergieran enigmas desconocidos. Porque, como dijo el físico y premio Nobel Kip Thorne, “la respuesta correcta es rara vez tan importante como la pregunta correcta.”

Este artículo fue publicado originalmente en The Conversation. Artículo original.

Para saber más:

La estructura del universo como una interferencia cuántica
Energía oscura
El problema difícil de la materia oscura

Sobre la autora: Ruth Lazkoz es profesora de Física Teórica en la Universidad del País Vasco / Euskal Herriko Unibertsitatea

El artículo Nos dirigimos a un final violento del universo se ha escrito en Cuaderno de Cultura Científica.

Hace 77 años, el 5 de mayo de 1945, el campo de concentración de Mauthausen fue liberado  por la 11ª División Blindada del 3ª Ejército de Estados Unidos.

“Me enteré de que iban a hacer eso, así que fui a su encuentro y les dije: “Escuchadme, muchachos, si vais a liquidar a toda esa gente, al menos sacadles el cerebro, de modo que pueda aprovecharse el material”.

Julius Hallevorden, director del Departamento de Neuropatología del Instituto Kaiser Wilhelm de Investigación del Cerebro. Así respondió al oficial estadounidense que le interrogó al finalizar la guerra.

“Ética y ciencia necesitan darse la mano”.

Richard Clarke Cabot, 1933. El 30 de enero de ese año, Hitler llegó al poder cuando fue nombrado Canciller.

Para mí, y disculpen que empiece este texto con un recuerdo personal, la historia sobre la ciencia de los nazis y su utilidad actual comenzó en 1985 en la Biblioteca Central de la UPV/EHU. Revisaba la bibliografía reciente que aparecía casa semana en una publicación llamada Current Contents, del Instituto para la Información Científica de Philadelphia. En el número del 8 de julio, su director, Eugene Garfield, que publicaba cada semana un texto breve sobre algún asunto científico de actualidad, celebraba el 40 aniversario del final de la Segunda Guerra Mundial y lo hacía desde la perspectiva de un experto en literatura científica. Garfield fue quien propuso el hoy tan utilizado factor de impacto de las revistas científicas. Se preguntaba, junto a otros científicos como Tomas Radil-Weiss, de la Academia de Ciencias de Checoslovaquia y superviviente de Auschwitz, o la periodista Kristine Moe, sobre si se deben utilizar y, en consecuencia, citar, los resultados de los experimentos de los médicos nazis en los campos de concentración.

Gemelos mantenidos con vida en Auschwitz para realizar experimentos. Fotografía realizada el día de la liberación del campo por parte del ejército soviético en enero de 1945. Foto: Alexander Voronzow et al / USHMM / Archivo Estatal Bielorruso de Película Documental y Fotografía / Wikimedia Commons

Esos experimentos eran torturas y, a menudo, muerte para los internados que servían como animales de laboratorio. Es indiscutible que llamar ciencia a lo que hacían los torturadores es un eufemismo odioso. Pero redactaron informes y publicaron los resultados de sus experimentos en revistas científicas, en su gran mayoría alemanas. Y, por tanto, es posible utilizar sus resultados por otros investigadores. Hacerlo o no hacerlo es una cuestión ética que, creo, hay que debatir.

Por ejemplo, hay especialistas en el campo de la hipotermia, dice Garfield, que utilizan y citan en sus publicaciones los resultados de los experimentos que lo habitual es que terminaran con la muerte del que los sufría. Cuando acababa en muerte, los investigadores nazis lo catalogaban como “experimento terminal”. Bernard Dixon, en New Scientist, se pregunta si estas prácticas en científicos del siglo XX “no son sino un insulto gratuito a aquellas patéticas cobayas humanas, y a la memoria de los muertos, desde los libros de texto y las revistas científicas que citan datos obtenidos de esta manera tan odiosa”. Citas de la vergüenza las denomina.

Los científicos que utilizan los datos de los nazis declaran que están obligados a ello, a usar esa información, porque así contribuyen al avance los conocimientos científicos e, incluso, a salvar vidas. Intentan que aquella tragedia sirva, en lo posible, para algo bueno.

Cuando Garfield y su equipo intentaban conocer cuánto se habían citado los artículos de los médicos nazis, se encontraron con el problema de que no sabían con seguridad cómo obtuvieron sus resultados los firmantes de aquellos trabajos. Pero, también, encontraron que algunos de los artículos firmados indiscutiblemente por médicos nazis eran citados con frecuencia.

Por ejemplo, el profesor Kurt Gutzeit, de la Universidad de Breslau, hoy Wroclaw, en Polonia, infectó a prisioneros de Auschwitz con el virus de la hepatitis. Su ayudante, H. Voegt, publicó un artículo en una revista alemana, en 1942, con los resultados de la infección. En 1985, Garfield encontró que este artículo se había citado 50 veces desde 1955.

También se han citado, a veces indirectamente por medio de otros documentos, algunas investigaciones de los campos de concentración. En 1945, Leo Alexander, psiquiatra y médico militar, que intervino como experto en los juicios de Nuremberg, escribió un informe sobre los experimentos de hipotermia en los campos. Este informe se utilizó en los juicios de Nuremberg. El informe fue declarado secreto hasta que se utilizó ante el tribunal y, entonces, se hizo público y Garfield encontró que se había citado 44 veces entre 1955 y 1984 sin citar de donde venían los datos y cómo se habían obtenido. Incluso se cita a Leo Alexander y la ciencia médica nazi en Google Scholar con 544 citas en mayo de este año 2022.

Sin embargo, lo habitual es no citar las fuentes originales y, por tanto, no sabemos si los autores que lo citan lo decidieron después de un debate ético muy personal o, simplemente, lo evitaron o, quizá, no conocían realmente su origen.

¿Y si hay información útil en los datos nazis?

Hay médicos e investigadores actuales para los que la relación con las prácticas nazis parece lejana pero, sin embargo, puede ser esencial para sus propios estudios. Hermann Stieve fue director del Instituto de Anatomía de Berlín entre 1935 y 1952. Especialista en el sistema reproductor femenino, estudiaba al microscopio el ovario y muchas de sus muestras proceden de mujeres ejecutadas en la prisión de Plotzensee, en Berlín (una cárcel que llegó casi a las 1200 ejecuciones en 1943). Cuando iba a celebrarse una ejecución, o una tanda de ejecuciones, a veces hasta 20 en un mismo día, los funcionarios de la prisión avisaban al Instituto de Anatomía, situado a 6 kilómetros del centro, por si necesitaban muestras.

Con este material, Stieve llegó a describir los cambios en el ciclo menstrual provocados por la angustia de estar en la cárcel, o las hemorragias parecidas a la regla provocadas cuando conocían las presas que iban a ser ejecutadas. Todavía ahora, en 2022, los trabajos de Stieve sobrepasan las 120 citas en el Google Scholar. Citas, por supuesto, que no precisan cómo se obtuvieron esos resultados y sin condenar los métodos utilizados.

En entrevistas publicadas entre 2006 y 2011, Sabine Hildebrandt, de la Universidad de Michigan en Ann Arbor, transcribe las respuestas de varios profesores de anatomía que utilizaron cadáveres de mujeres ejecutadas para sus investigaciones y docencia. Walter Krause declaró que “a nadie le importó, y ¿por qué debería importarnos a nosotros?» Su colega Werner Platzer remachó que “a nadie le importó”. Y Michael Arnold explicó que “es estresante saber esto y por lo tanto comprensible si uno no busca una completa información del trasfondo de los cuerpos para anatomía, dado que este trasfondo era irrelevante para el cumplimiento de los deberes educativos”.

En conclusión, fueron los juicios de Nuremberg a los médicos de los campos, con la redacción posterior, en 1947, del Código de Nuremberg sobre la ética en la práctica de la medicina, los que convirtieron, a posteriori, a la ciencia de los campos en ciencia no ética. Y queda la pregunta con la que empezaba este texto: ¿qué hacer con los resultados obtenidos con la práctica de una ciencia no ética? Nosotros debatimos si citar la ciencia de los médicos nazis y, por el contrario, los médicos nazis tenían prohibido citar la ciencia de los médicos y de los científicos judíos.

Kristine Moe propone que solo se deben citar los resultados si son esenciales en la investigación de quien los cita y no existe otra fuente de información. Los expertos de cada campo deben evaluar los datos críticamente antes de utilizarlos. Además, debe quedar claro su origen y cómo se obtuvieron y expresar el agradecimiento más profundo y sentido a los que sufrieron y murieron en esos experimentos. Los conocimientos que suponen y la ayuda que dan para aumentarlos no deben cegar a quien los cita ante la falta de humanidad de quienes los obtuvieron y la crueldad de aquellos experimentos.

Algunas citas califican estos experimentos como lo que son y sin ninguna duda. John Fernandez y su grupo, de la Universidad de Rochester, en su estudio sobre hipotermia, publicado en 1970, dice que “estas sórdidas investigaciones demostraron a satisfacción de los verdugos que el mejor método para resucitar a los prisioneros de la hipotermia fue un recalentamiento rápido e intenso”.

Como escribió Ewald Weibel, de la Universidad de Berna, para los estudios de fisiología, pero que se pueden extender a toda la ciencia y a todos los científicos, “debemos hacer frente a dilemas éticos que no podemos resolver, debemos vivir con ellos. Es importante, sin embargo, que seamos conscientes de los problemas éticos que crea la investigación científica”.

Para Stephen Post, de la Universidad Case Western Reserve en Ohio, los datos obtenidos fuera de la ética nunca deben utilizarse, y los datos ya publicados deben retirarse lo más rápido posible. Los editores de revistas científicas que, en su momento, los publicaron sin añadir una explicación de su origen y una condena moral deben añadirla ahora. En último término, la ciencia debe tener una mínima sensibilidad hacia las emociones de las víctimas. En resumen, después de cometer una atrocidad, se debe seguir la regla de no utilizar los datos obtenidos.

Lynn Gillam, desde la Universidad de Melbourne, mantiene una postura que hemos visto en otros autores. Afirma que la mala conducta no produce, sin más, mala ciencia. No hay una conexión inevitable porque la ciencia no es una conducta moral. Si los datos científicos son pobres o escasos es porque el diseño del estudio o el análisis de los resultados no fueron los adecuados, no por el carácter inmoral del científico. Para Gillam, algunos de los datos de los experimentos nazis todavía son útiles. Pero si se citan debe hacerse con absoluta claridad de su origen y la más enérgica condena de cómo se obtuvieron.

Para terminar, una propuesta diferente y con otros objetivos de las citas de la ciencia nazi. Llega de la Universidad Autónoma de Madrid y la firman Esteban González y Rosa Ríos. Explican que la enseñanza de los aspectos médicos del Holocausto puede ser un modelo nuevo para la educación de médicos y enfermeras sobre su profesión, los Derechos Humanos, la Bioética y el respeto a la diversidad. Unir la enseñanza de la medicina y el Holocausto facilitaría el conocimiento de las violaciones de la Ética médica en el pasado.

Como método proponen un viaje de estudios a campos de concentración y lugares relacionados con el Holocausto y, en especial, con un significado especial de donde se hicieron experimentos médicos. Con todo ello, organizaron un curso optativo titulado “El Holocausto: Lecciones para la Medicina”, dividido en ocho módulos. Lo impartieron durante siete años y, en una escala de 0 a 5, los alumnos lo puntuaron, de media, con 3,74.

Referencias:

Alexander, L. 1945. The treatment of shock from prolonged exposure to cold, especially in water. Combined Intelligence Objectives Sub-committee. Item nº 24. File XXIX-24. 163 pp.

Deichmann, U. 1996. Biologists under Hitler. Harvard University Press. Cambridge & London. 468 pp.

Demarez, J.P. 2005. Recherches cliniques à Dachau. La Lettre du Pharmacologue 19: 23-30.

Dixon, B. 1985. Citations of shame. New Scientist 105: 31.

Fernandez, J.P. et al. 1970. Rapid active external rewarming in accidental hypothermia. Journal of the American Medical Association 212: 153-156.

Garfield, E. 1985. Remembering the Holocaust, Part 1. Current Contents July 8: 3-4.

Garfield, E. 1985. Remembering the Holocaust, Part 2. Current Contents July 15: 3-9.

Gillam, L. 2015. Is it ethical to use data from Nazi medical experiments? The Conversation 10 June.

González-López, E. & R. Ríos-Cortés. 2019. Visiting Holocaust: related sites in Germany with medical students as an aid to teaching medical ethics and human rights. Conatus 4: 303-316.

Hildebrandt, S. 2013. The women on Stieve’s list: Victims of National Socialism whose bodies were used for anatomical research. Clinical Anatomy 26: 3-21.

Moe, K. 1984. Should the Nazi research data be cited? Hastings Center Report 14: 5-7.

Müller-Hill, B. 1985. Ciencia mortífera. La segregación de judíos, gitanos y enfermos mentales (1933-1945). Ed. Labor. Barcelona. 272 pp.

Post, S.G. 1991. The echo of Nuremberg: Nazi data and ethics. Journal of Medical Ethics 17: 42-44.

Radil-Weiss, T. 1983. Men in extreme conditions: Some medical and physiological aspects of the Auschwitz Concentration Camp. Psychiatry 46: 259-269.

Ternon, I. & S. Helman. 1971. Historia de la medicina SS o El mito del racismo biológico. Fomento de la Cultura Eds. Valencia. 408 pp.

Weibel, E.R. 2002. The physiologist’s ethical dilemas. News in Physiological Sciences 17: 43-46.

Winkelmann, A. & U. Schagen. 2009. Stieve’s clinical-anatomical research on executed women during the “Third Reich”. Clinical Anatomy 22: 163-171.

Para saber más:

No todo vale al servicio de la ciencia
Genocidio
Anticiencia (II): nazismo y comunismo

Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.

El artículo Citar la ciencia de los nazis se ha escrito en Cuaderno de Cultura Científica.

En la entrada del Cuaderno de Cultura Científica titulada Las simetrías ocultas de la tabla de multiplicar hablábamos de una idea para crear una pintura basada en las simetrías de la tabla de multiplicar, en concreto, en la del número 30. Esta idea se materializó en la obra Septiembre (2019), realizada, en óleo y papel sobre lienzo, conjuntamente con mi hija Vanessa Ibáñez.

Septiembre (2019), de Vanessa Ibáñez y Raúl Ibáñez

 

Detalles de la obra Septiembre (2019)

 

En esta entrada vamos a analizar una serie de obras de la artista constructivista británica Susan Tebby (1944) inspiradas en la tabla de multiplicar. Se trata de los nueve relieves (recordemos que como se dice en la descripción de los términos de arte de la página web de la Tate Gallery, “un relieve es una escultura montada en la pared en la que los elementos tridimensionales se elevan desde una base plana”) pertenecientes a la serie Nueve por nueve (1977).

Los nueve relieves de la serie Nueve por nueve (1977), de la artista constructivista británica Susan Tebby. Imagen perteneciente a la tesis doctoral Patterns of Organization in Constructed Art (1983)

 

Susan Tebby (1944) es una escultora y profesora británica, cuyo arte se engloba dentro del constructivismo británico. Como puede leerse en la parte biográfica de su página web, Susan Tebby, estudió Bellas Artes en la Escuela de Arte Goldsmiths, entre 1962 y 1966, recibiendo una distinción por su disertación Rhythmic Proportion: a Study of the Relationship Between Art and Mathematics (Proporción rítmica: un estudio sobre la relación entre arte y matemáticas), y un año de posgrado en Bellas Artes en la Escuela de Arte de Chelsea (1966/67). Entre 1976 y 1983 llevó a cabo una investigación para obtener un doctorado en Bellas Artes (interdisciplinario) conjuntamente entre la Escuela de Bellas Artes Slade, de la University College de Londres, y el Politécnico de Leicester (ahora la Universidad de De Montfort), cuya tesis doctoral se titulaba Patterns of Organization in Constructed Art (Patrones de organización en el arte constructivo). En ella investigaba diferentes sistemas matemáticos que podían ser utilizados como estructuras para crear diferentes obras de arte.

Relieve Permutaciones sobre 7 (1973), de la artista británica Susan Tebby, basado en las llamadas permutaciones pendulares. Obra del Arts Council Collection. Imagen de Urban Splash

 

La tabla de multiplicar, o tabla pitagórica

La base de la serie de relieves Nueve por nueve es la tabla de multiplicar básica, del 1 al 9, o tabla pitagórica. La tabla de multiplicar es un retículo numérico cuadrado, que como en el juego de barcos, nos da las tablas de multiplicar de cada una de las cifras básicas, del 1 al 9. Si queremos conocer el resultado de la multiplicación 5 x 9, vamos a la fila del 5 y a la columna del 9 (aunque podría ser la fila 9 y la columna 5, ya que la multiplicación es conmutativa, da igual el orden de los factores, 5 x 9 = 9 x 5), miramos en la intersección de ambas y observamos que el resultado de multiplicar 5 por 9 es 45. O si queremos ver el resultado de multiplicar 3 x 7, vamos a la intersección de la fila 3 y la columna 7, para observar que el producto es 21. Cada fila, respectivamente cada columna, representa la tabla de multiplicar de cada cifra básica, desde el 1 hasta el 9.

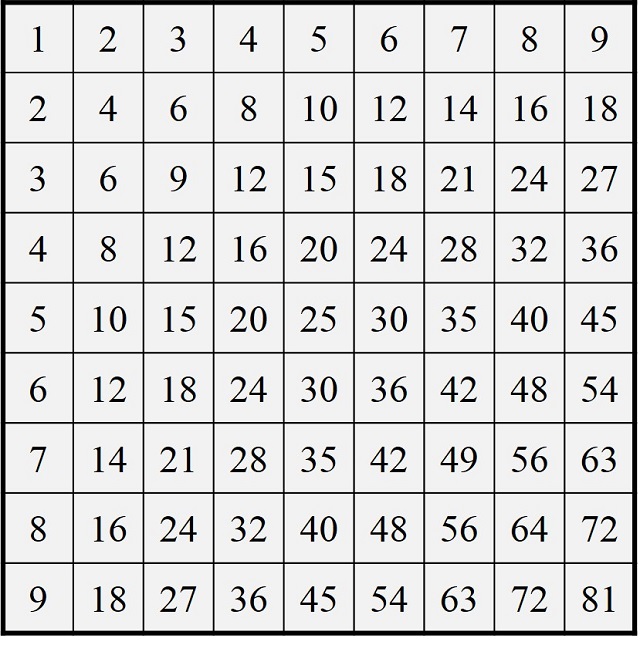Tabla de multiplicar básica, del 1 al 9, en la que cada fila, respectivamente, columna, nos da la tabla de multiplicar de cada cifra básica, del 1 al 9La reducción módulo 9 de la tabla de multiplicar

La siguiente cuestión a tener en cuenta en el sistema desarrollado por Susan Tebby para crear estos relieves es aplicar a la tabla de multiplicar lo se conoce como “reducción cabalística” (por su uso en temas de numerología), que esencialmente es lo que en matemáticas conocemos como trabajar con la aritmética modular y que podríamos denominar “reducción módulo nueve”.

En la entrada del Cuaderno de Cultura Científica titulada Las curiosas reglas de divisibilidad estudiamos la regla de divisibilidad del 9, que dice “un número es divisible por 9 si, y sólo si, la suma de sus dígitos es divisible por 9”. Esta regla puede utilizarse de formar reiterada hasta quedarnos con un número de un dígito, si este es el 9, el número será divisible por 9, y si es otro no lo será. Por ejemplo, si tomamos el número 3.456.394 y queremos saber si es divisible por 9, debemos de sumar los dígitos, en este caso, 3 + 4 + 5 + 6 + 3 + 9 + 4 = 34, que a su vez será divisible por 9 si lo es 3 + 4 = 7, que no lo es. Por lo tanto, el número 3.456.394 no es divisible por 9.

Esto es lo que se conoce como “reducción cabalística”. La reducción de un número, como el 3.456.394, sumando sus dígitos de forma reiterada hasta obtener un número de un solo digito, que en este caso es 7, que sería la reducción del 3.456.394.

Si miramos la explicación de la regla de divisibilidad del nueve que acabamos de comentar, el resultado es realmente más general. En concreto, si tenemos un número N con n + 1 dígitos, N = an an–1 … a2 a1 a0, y le restamos la suma de sus dígitos (an+ an–1+ … + a2+ a1+ a0), es decir, N – (an+ an–1+ … + a2+ a1+ a0), lo que queda es un número que puede demostrarse que es múltiplo de 9 (véase el razonamiento matemático en la entrada Las curiosas reglas de divisibilidad). Por lo tanto, el resto de dividir N por 9 es igual al resto de dividir la suma de sus dígitos por 9.

En conclusión, si se aplica la “reducción cabalística” se obtiene el resto de dividir el número N por 9, salvo en el caso de que sea divisible por 9, que en la reducción cabalística quedará 9. Aunque podemos entender que 9 es divisible por 9 y el resto es 0, coincidiendo también el resto en este caso. Tomemos el ejemplo anterior, 3.456.394, si lo dividimos por 9 se obtiene 384.043 y el resto es 7, que es lo que habíamos obtenido mediante la reducción cabalística. O si tomamos el número 682.227, su reducción cabalística es 9, ya que 6 + 8 + 2 + 2 + 2 + 7 = 27 y 2 + 7 = 9, luego 682.227 es divisible por 9 (o su resto al dividir por 9 es 0).

The Ninth American Dream / El noveno sueño americano (2001), del artista pop norteamericano Robert Indiana. Imagen de WikiArt

 

Desde el punto de vista de la aritmética modular (véase la entrada Un código detector de errores: la letra del DNI) la anterior reducción, ya sea la “reducción cabalística” o más exactamente el proceso de reducir cada número al resto de la división por 9, no es más que trabajar con los “números enteros módulo 9”.

El siguiente paso en el proceso creativo de la artista constructivista británica fue realizar la reducción de la tabla de multiplicar básica, de 1 a 9, módulo nueve, obteniendo la siguiente tabla.

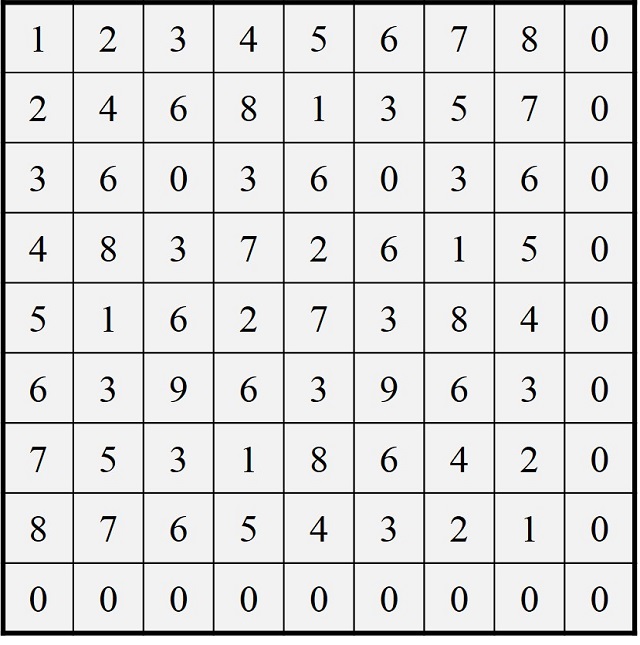
Por ejemplo, en la casilla que se corresponde con 5 x 9, en la que antes había un 45, ahora hay un 0, puesto que 45 es divisible por 9 y el resto es 0 (en la reducción cabalística queda 9). O en la casilla de 3 x 7, en la que antes había un 21, ahora hay un 3 (la reducción cabalística queda 2 + 1 = 3).

La serie de relieves Nueve por nueve

A continuación, como explica la propia artista en su tesis doctoral Patterns of Organization in Constructed Art, cada uno de los nueve relieves de la serie Nueve por nueve, toma como base la cuadrícula 9 x 9 anterior, es decir, la tabla de multiplicar básica, módulo 9.

Para obtener las casillas que se transforman con un agujero y con tablas que sobresalen de la estructura básica, en los nueve relieves, Susan Tebby realiza multiplicaciones de series acumulativas de números con uno, dos, tres, hasta nueve dígitos, 1; 12: 123; 1234; etc, con series acumulativas de números constantes 5; 55; 555; 5555; etc, y aplica la reducción cabalística a los resultados de las mismas. En su proceso de investigación, la artista trabajó con otras series numéricas, pero estas resultaron de mayor interés desde el punto de vista de la simetría, la distribución y la estructura general.

Página de la tesis doctoral Patterns of Organization in Constructed Art (1983), de Susan Tebby, que contiene la imagen de los nueve relieves de la serie Nueve por nueve (1977)

 

A continuación, estudiemos cómo se obtiene la estructura de alguno de los relieves de la serie Nueve por nueve, mediante lo que Susan Tebby denomina proceso de “computación / reducción / secuencia”.

Relieve 1 de la serie Nueve por nueve

El primer par de casillas intervenidas se obtienen mediante el siguiente proceso de “computación / reducción / secuencia”, al tomar las series anteriormente mencionadas, pero para números de un dígito, es decir, se realizan las siguientes multiplicaciones y las reducciones módulo 9 (que denotamos “cbr” siguiendo la notación de la artista para “reducción cabalística”).

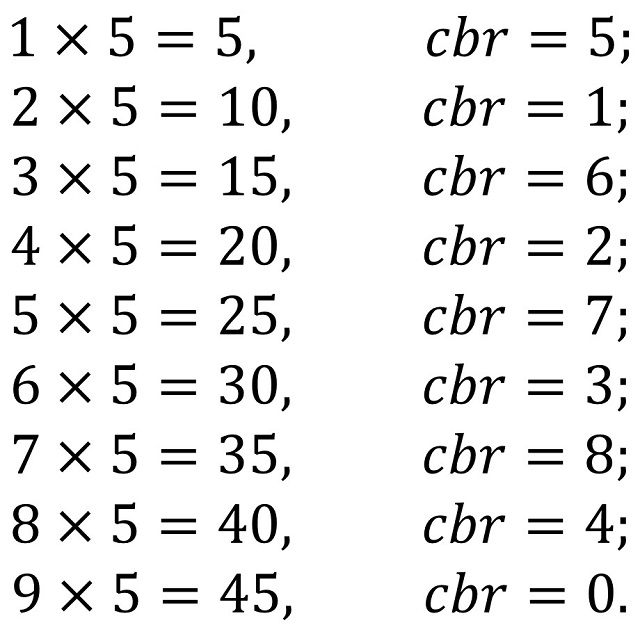
La secuencia obtenida 5, 1, 6, 2, 7, 3, 8, 4, 0 aparece en la quinta fila y la quinta columna de la tabla de multiplicar módulo 9 (ver imagen más arriba). Por lo tanto, se selecciona la casilla de la cifra 5 que inicia la secuencia en la quinta fila –en la cual irá un espacio vacío en el relieve-, y se marca el lado izquierdo de esa casilla indicando que la serie numérica empieza en el 5 y va hacia el otro lado, hacia la derecha –esa marca lateral izquierda en la casilla del 5 se convertirá en un segmento tridimensional en el relieve-. De la misma forma, se selecciona la casilla de la cifra 5 que inicia la secuencia en la quinta columna –que será un espacio vacío en el relieve-, y se marca el lado inferior de esa casilla indicando que la serie numérica empieza en el 5 y va hacia abajo –esa marca lateral inferior en la casilla del 5 se convertirá también en un segmento tridimensional en el relieve-.

Para el segundo par de casillas intervenidas mediante el siguiente proceso de “computación / reducción / secuencia” se considera el producto de las series de dos dígitos 12; 23; 34; 45; etc por 5, como se muestra en la siguiente imagen.

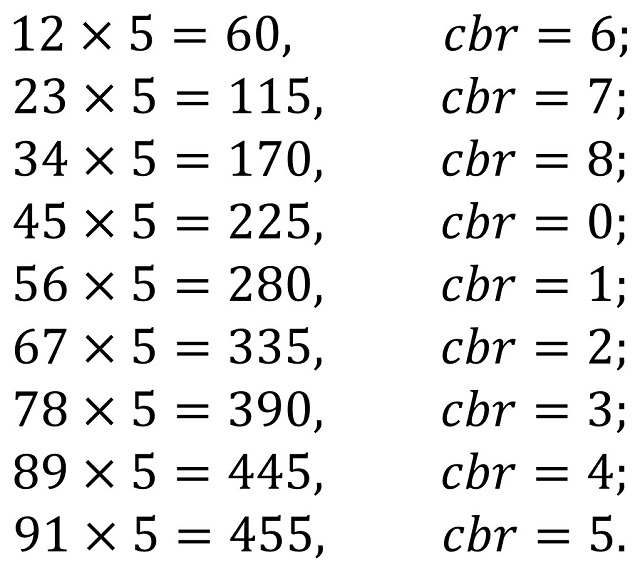
La secuencia obtenida ahora 6, 7, 8, 0, 1, 2, 3, 4, 5 aparece en la primera fila –empezando en la casilla del 6- y la primera columna –empezando en la casilla del 6- de la tabla de multiplicar módulo 9 (ver imagen más arriba). Por lo tanto, las casillas seleccionadas serán las que dan inicio, en la primera fila y columna, a la serie, es decir, las casillas del 6. Como antes, se marcará el lado izquierdo de la casilla del 6 de la primera fila, que inicia la secuencia en esa fila hacia la derecha y se marcará el lado de abajo de la casilla del 6 de la primera columna, que inicia la secuencia en esa columna hacia abajo.

Para el tercer par de casillas intervenidas mediante el siguiente proceso de “computación / reducción / secuencia” se considera el producto de las series de tres dígitos 123; 234; 345; 456; etc por 5, obteniéndose la secuencia 3, 9, 6, 3, 9, 6, 3, 9, 6. Esta aparece en la sexta fila y sexta columna, en las cuales se intervendrá la casilla del 3.

Para el cuarto par de casillas en el proceso de “computación / reducción / secuencia” se toma el producto de la serie 1234; 2345; 3456; etc por 5, dando como resultado la secuencia 5, 7, 0, 2, 4, 6, 8, 1, 3 que aparece en la segunda fila y segunda columna, por lo que se intervienen las casillas del 5 en las mismas.

De esta forma se sigue hasta el noveno par que será fruto de multiplicar por 5 los nueve números con las nueve cifras básicas ordenadas, desde 123456789 hasta 912345678, que como son múltiplos de 9 nos dará, después del proceso de reducción, siempre 0. Así, se obtienen los nueve pares de casillas intervenidas del primer relieve, como queda indicado en la siguiente tabla.

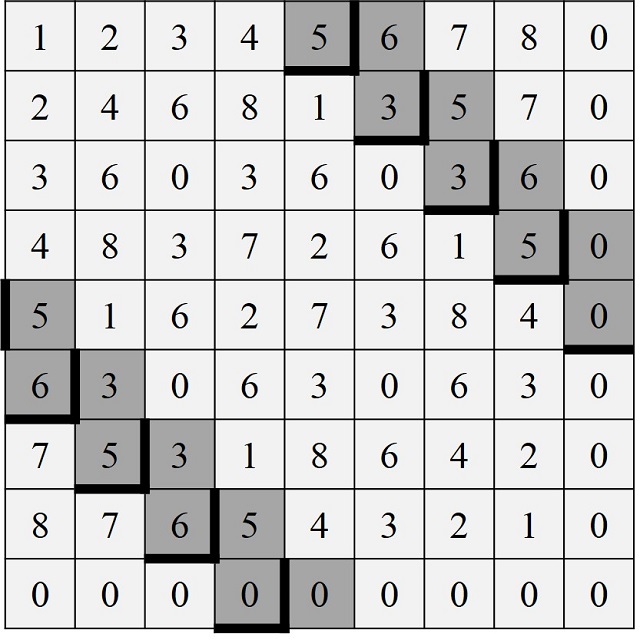
Relieve 2 de la serie Nueve por nueve

En el proceso de “computación / reducción / secuencia” para el segundo relieve se van a multiplicar las series acumulativas anteriores (desde la que tiene un solo dígito 1, 2, 3, 4, 5, 6, 7, 8, 9; hasta la que tiene los nueve dígitos 123456789, 23456789, etc) no por 5, como en el primer relieve, sino por 55. Por ejemplo, para el primer par de casillas intervenidas se obtendrá lo siguiente.

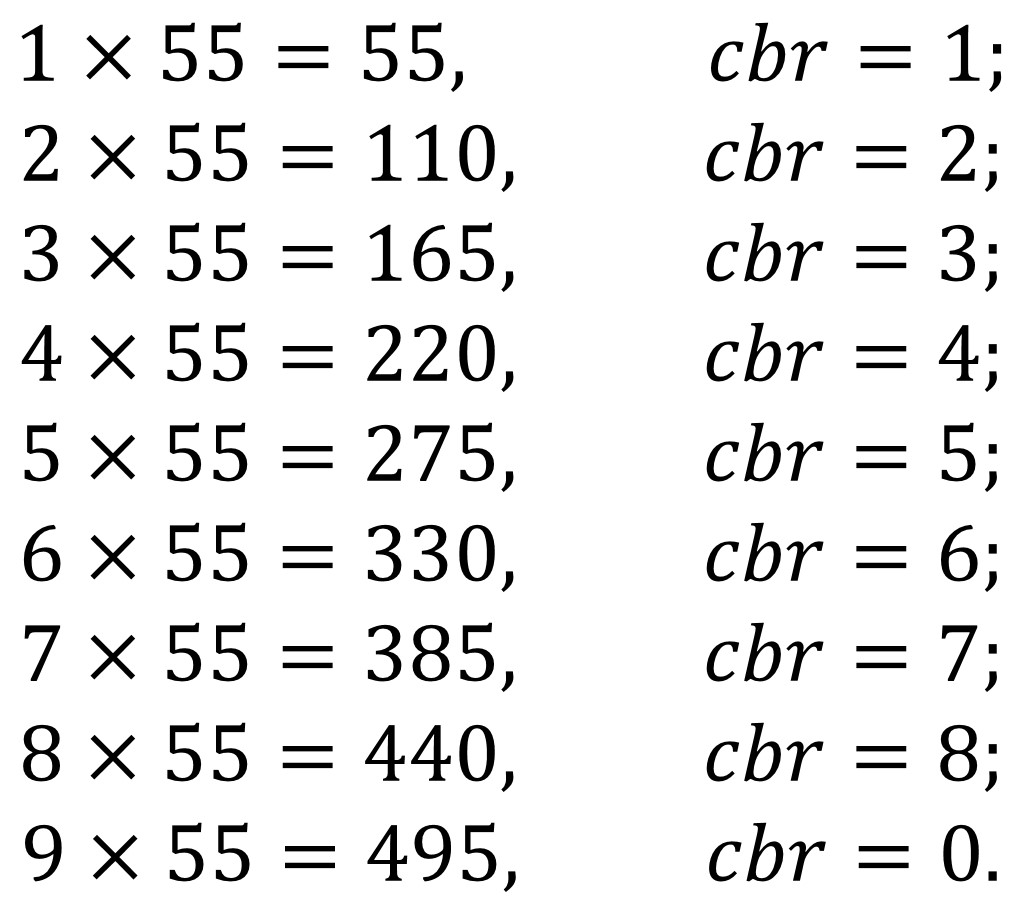
La serie obtenida es 1, 2, 3, 4, 5, 6, 7, 8, 9 que aparece en la primera fila y la primera columna de la tabla de multiplicar módulo 9, por lo que se intervendrán las dos casillas del 1 en esas primera fila y primera columna.

Para obtener el segundo par de casillas intervenidas en este segundo relieve se realizan los productos de 12, 23, 34, 45, 56, 67, 78, 89 y 91 por 55. De esta forma se obtiene la serie 3, 5, 7, 0, 2, 4, 6, 8, 1 que se encuentra en la segunda fila y segunda columna, en las que se intervienen las casillas del 3. Y de esta forma se continúa con los demás pares de casillas intervenidas. El resultado de la intervención sobre la tabla de multiplicar reducida para el segundo relieve es el siguiente.

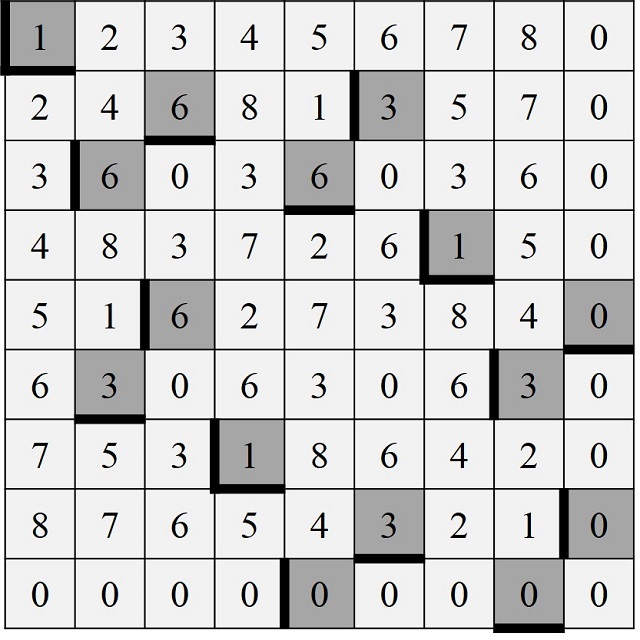
Relieves del 3 al 9 de la serie Nueve por nueve

El tercer relieve toma como punto de partida en el proceso de “computación / reducción / secuencia” las multiplicaciones de las series acumulativas anteriores (desde la que tiene un solo dígito 1, 2, 3, 4, 5, 6, 7, 8, 9; hasta la que tiene los nueve dígitos 123456789, 23456789, etc) con el número 555. El resultado de la intervención para este tercer relieve es el siguiente.

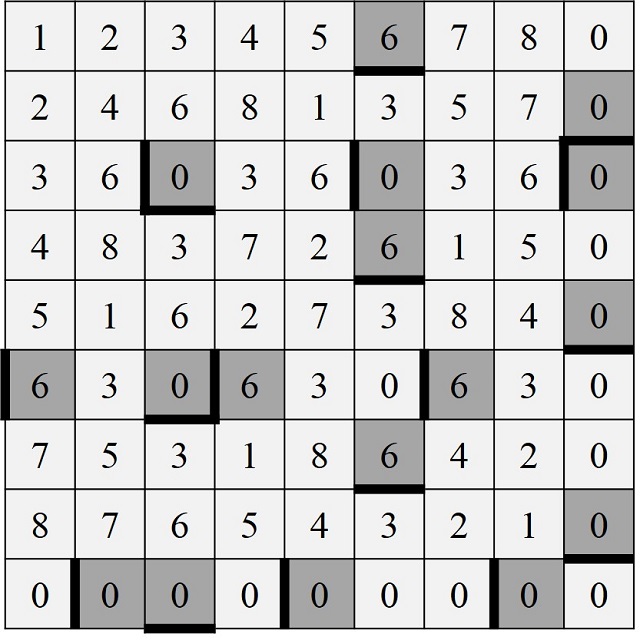
Continuando de esta forma se obtienen las estructuras de los nueve relieves, que podemos ver en la siguiente imagen de la tesis doctoral Patterns of Organization in Constructed Art de Susan Tebby.

Página de la tesis doctoral Patterns of Organization in Constructed Art (1983), de Susan Tebby, en la que aparecen las nueve estructuras realizadas sobre la tabla de multiplicar básica, de 1 al 9, reducida módulo 9, que dan lugar a los relieves de la serie Nueve por nueve (1977)

 

 

La serie de relieves Nueve por nueve es solo un ejemplo de cómo utiliza la artista constructivista británica Susan Tebby las matemáticas para crear estructuras artísticas.

Lattices / Retículos (1984), de Susan Tebby. Imagen de la página web de Susan Tebby

 

Bibliografía:

1.- Raúl Ibáñez, Los secretos de la multiplicación, de los babilonios a los ordenadores, Catarata, 2019.

2.- Susan Tebby, Patterns of Organization in Constructed Art, tesis doctoral de la University College de Londres (Reino Unido), 1983.

 

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica

 

El artículo Sobre cómo crear arte con la tabla de multiplicar se ha escrito en Cuaderno de Cultura Científica.