Sergio Pérez Acebrón – Naukas Bilbao 2019: Conversando con células
 Fuente: Wikimedia Commons
Fuente: Wikimedia Commons¿Cómo decide una célula convertirse en una neurona, una célula epitelial o una célula intestinal si todas tienen el mismo material genético? Una de las formas de responder a esta pregunta es comprendiendo cómo unas células se comunican entre sí diciéndose lo que tienen que hacer. Sergio Pérez Acebrón nos lo explica.
Sergio Pérez Acebrón investiga las rutas de señalización celular involucradas en el desarrollo embrionario y en varios tipos de tumores como líder del grupo en The Centre for Organismal Studies (COS) de la Universidad de Heidelberg (Alemania).
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Sergio Pérez Acebrón – Naukas Bilbao 2019: Conversando con células se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Naukas Bilbao 2017 – Sergio Palacios: Precausión, amigo conduztó
- Adela Torres – Naukas Bilbao 2019: ¿Dónde está la mosca?
- José Ramón Alonso – Naukas Bilbao 2019: Son nuestros amos y nosotros sus esclavos
Detección automatizada de reacciones adversas a medicamentos en las historias clínicas
 Foto: National Cancer Institute / Unsplash
Foto: National Cancer Institute / UnsplashLas historias clínicas en formato electrónico de los pacientes contienen informaciones valiosísimas. La aplicación de técnicas de procesamiento del lenguaje natural a dichas historias puede ser una forma eficaz de extraer información útil en muchos ámbitos: desde el más obvio, mejorar la toma de decisiones clínicas, hasta el más burocrático, la documentación y la facturación clínicas, pasando por la predicción de posibles enfermedades. Todas estas cosas se pueden realizar historia a historia por el personal médico o administrativo. Pero existe una en el que se hace necesario el tratamiento de datos a gran escala: la detección de reacciones adversas a medicamentos. Este tipo de reacciones adversas son un problema importante de salud, ya que pueden provocar ingresos hospitalarios e incluso la muerte de algunos pacientes.
En este contexto, el Hospital Universitario de Basurto y el Hospital de Galdakao “estaban interesados en crear un sistema que, a través de técnicas de procesamiento de lenguaje natural, pudiera analizar los historiales médicos para identificar automáticamente los efectos adversos que hay en ellos”, explica la ingeniera y doctora en informática Sara Santiso. Tras ponerse en contacto con el grupo IXA de la UPV/EHU, varias investigadoras se pusieron a trabajar para encontrar un modelo robusto basado en la minería de textos clínicos con el que extraer los efectos adversos a medicamentos de historias clínicas en formato electrónico escritas en castellano.
Para ello, “hemos utilizado, por un lado, técnicas basadas en algoritmos tradicionales de machine learning, y por otro lado, hemos explorado técnicas de deep learning, llegando a la conclusión de que con estas últimas se detectan mejor los efectos adversos”, explica Santiso, una de las autoras del estudio. Tanto el machine learning como el deep learning imitan la forma de aprender del cerebro humano, y difieren en el tipo de algoritmos que se usan en cada caso.
Santiso remarca la dificultad que han tenido para conseguir un corpus de tamaño adecuado con el que trabajar: “En un principio empezamos con pocos historiales médicos debido a que es difícil conseguirlos por la privacidad, ya que hay que firmar acuerdos de confidencialidad para trabajar con ellos”. Las investigadoras han observado que “contar con un corpus más grande ayuda al sistema a aprender mejor los ejemplos que había en ellos, y por lo tanto el sistema daba mejores resultados”.
Con este estudio llevado a cabo con historias escritas en castellano, “estamos contribuyendo a cerrar la brecha existente entre la minería de textos clínicos realizada en inglés con respecto a la realizada en otros idiomas, que cubre menos del 5 % de los artículos publicados. De hecho, la extracción de información clínica no ha alcanzado aún su pleno desarrollo debido, entre otras cosas, al potencial de extracción de información entre hospitales y entre idiomas”, afirma la investigadora.
Aunque el procesamiento del lenguaje natural ha sido de gran ayuda en la detección asistida por ordenador de las reacciones adversas a medicamentos, todavía hay margen de mejora: “Hasta ahora, los sistemas tienden a centrarse en la detección de pares medicamento-enfermedad situados en la misma frase. Sin embargo, las historias clínicas tienen información implícita que podría revelar relaciones subyacentes (por ejemplo, la información de los antecedentes podría ser relevante para adivinar las causas de un evento adverso). Es decir, la investigación debe esforzarse por detectar las relaciones entre frases, tanto las explícitas como las implícitas”.
Referencia:
Sara Santiso, Alicia Pérez, Arantza Casillas Adverse Drug Reaction extraction: Tolerance to entity recognition errors and sub-domain variants Computer Methods and Programs in Biomedicine DOI: 10.1016/j.cmpb.2020.105891
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Detección automatizada de reacciones adversas a medicamentos en las historias clínicas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Alcanzada la escala atómica en la detección magnética
- Turno para los medicamentos biosimilares
- Detección precoz del cáncer de colon por métodos no invasivos
Guepardos de aguas profundas
 Ilustración: María Lezana
Ilustración: María LezanaMelville escribió en Moby Dick que “el cachalote solo respira la séptima parte, el domingo de su tiempo”. Hacía referencia así a la gran capacidad del gran cetáceo odontoceto de permanecer bajo el agua. Y es que los cachalotes, como el resto de cetáceos son excelentes buceadores. Algunos se sumergen a grandes profundidades, a pesar de que bajo el agua no puedan respirar.
En efecto, los cetáceos son mamíferos, por lo que no pueden hacer uso del oxígeno disuelto en el agua, como hacen los peces y numerosos invertebrados. El oxígeno que respiran ha de ser atmosférico y han de salir fuera del agua a respirar. Los cachalotes, como la gran ballena blanca que obsesionase al capitán Ahab, por ejemplo, llegan a bajar hasta los 1.000 m y más en busca de presas; otros, como los calderones, no llegan tan abajo, pero se sumergen también a grandes profundidades.
El calderón tropical, cuyo nombre científico es Globicephala macrorhynchus, pertenece a la familia Delphinidae. Es, por lo tanto, un delfín, aunque de gran tamaño: pueden llegar a alcanzar 4 m de longitud y más de 4.000 kg de masa. Aunque su nombre vulgar indica que se trata de una especie propia de mares tropicales, su límite de distribución septentrional se halla al norte del Cantábrico, por lo que puede encontrarse en la zona sur del Golfo de Vizcaya.
Hace unos pocos años, en el curso de una investigación realizada en aguas de Tenerife utilizando marcas digitales (DTAG), el equipo de Natacha Aguilar, de la Universidad de La Laguna (Tenerife), registró los movimientos de 23 de estos calderones, así como los “clics” de ecolocación que producían. Gracias a esos registros conocemos algunas características de la estrategia de caza de Globicephala.
De acuerdo con los registros obtenidos se ha podido saber que cuando van de caza, descienden a profundidades de entre 500 y 1.000 m y permanecen, en promedio, unos 20 min bajo el agua. Cuando bajan en busca de una presa emiten largas secuencias de clics (ondas sonoras de ecolocalización), y en ocasiones, entre las secuencias de clics, emiten zumbidos. Los zumbidos, al parecer, están relacionados con los intentos de atrapar a la presa.
Cuando realizan inmersiones profundas, llegan al punto de máxima profundidad tras realizar un rápido esprint, y en ese momento emiten un zumbido. Esa es la secuencia propia de un episodio de caza. Cuando empiezan la inmersión, se mueven con lentitud, pero cuando realizan el esprint llegan a alcanzar una velocidad de 9 m s-1, una velocidad impresionante para un mamífero que se mueve bajo el agua. Los esprints duran entre 20 y 80 s y les salen, en términos energéticos, muy caros a los calderones. De hecho, aunque el esprint representa entre un 2 y un 8% del total del tiempo de inmersión hasta aguas profundas, se estima que supone entre un 10 y un 36% de su gasto energético total.
Es un comportamiento arriesgado. Tan sólo la mitad de los intentos acaban teniendo éxito; en la otra mitad no aciertan. Si tenemos en cuenta que el coste de la caza es muy elevado, las presas han de ser de cierto tamaño, pues de lo contrario no resultaría rentable y no la practicarían de esa forma. Hasta que se realizó la investigación citada, no se conocía esa modalidad de caza de “alto riesgo-alto rendimiento” entre cetáceos, aunque sí era conocida entre depredadores terrestres. Entre los mamíferos terrestres, es quizás el guepardo el que mejor ejemplifica esa táctica.
Otros cetáceos, como los zifios, utilizan estrategias diferentes. Estos pertenecen a la familia Ziphiidae. Su característica más distintiva es el morro largo y delgado; parecen delfines. Los zifios que han sido estudiados en aguas de El Hierro se sumergen durante mucho más tiempo, hasta una hora y media. Por esa razón no se encuentran en condiciones de realizar esprints intensos, puesto que el oxígeno que albergan en sangre y músculos no da para inmersiones que, a la vez, sean prolongadas y acaben con un esprint. Claro que el comportamiento alimenticio de los zifios no es de “alto riesgo-alto rendimiento”, puesto que actúan de un modo mucho más conservador. En cada inmersión se cobran del orden de 30 piezas, aunque se trata de presas pequeñas cada una de las cuales aporta una pequeña cantidad de alimento. Aunque como sus costes de locomoción son reducidos, pueden permanecer largo tiempo bajo el agua en busca de presas y al final, unos y otros obtienen lo que necesitan.
Fuente: N. Aguilar, M. P. Johnson, P. T. Madsen, F. Díaz, I. Domínguez, A. Brito y P. Tyack (2008): “Cheetahs of the deep sea: deep foraging sprints in short-finned pilot whales off Tenerife (Canary Islands)” Journal of Animal Ecology vol. 77 (5): 936-947
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Guepardos de aguas profundas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Un lujo asiático cultivado en aguas del Mediterráneo
- La regulación osmótica e iónica en los teleósteos marinos
- La regulación osmótica de los peces diádromos
Exposiciones matemáticas en el metro de Bilbao (I)
Cuando esta mañana me he sentado frente al ordenador y he empezado a pensar sobre qué iba a escribir en mi entrada del Cuaderno de Cultura Científica, no podía quitarme de la cabeza las diferentes actividades que estamos organizando dentro del proyecto Marzo, mes de las matemáticas.
 Cartel del proyecto Marzo, mes de las matemáticas, diseñado por Carla Garrido
Cartel del proyecto Marzo, mes de las matemáticas, diseñado por Carla Garrido
Finalmente, después de un buen rato dándole vueltas a los diferentes temas matemáticos sobre los que podría escribir, me he rendido a la evidencia, tenía que escribir sobre alguna de las actividades del proyecto Marzo, mes de las matemáticas. Además, lo he tenido claro desde ese momento, el tema de las dos siguientes entradas debería ser la pareja de magníficas exposiciones matemáticas que hemos organizado con Metro Bilbao para colocar en sus estaciones, Geometría Natural y Matemáticas para un mundo mejor.
 Imagen general de la exposición Geometría Natural colocada en la estación de Abando del metro bilbaíno el pasado 1 de marzo de 2021. Fotografía de Metro Bilbao
Imagen general de la exposición Geometría Natural colocada en la estación de Abando del metro bilbaíno el pasado 1 de marzo de 2021. Fotografía de Metro Bilbao
Pero vayamos al principio. El 26 de noviembre de 2019, la UNESCO proclamó el 14 de marzo como el Día Internacional de las Matemáticas a propuesta de la Unión Matemática Internacional (IMU). Cada año se dedicará a una temática especial, tratando de despertar la creatividad y mostrando las conexiones entre las matemáticas y todo tipo de campos, conceptos e ideas. Siguiendo este eje temático tendrán lugar numerosos eventos en todo el mundo. El lema de este año 2021 es “Matemáticas para un mundo mejor”. El motivo de elegir la fecha del 14 de marzo fue que ese día ya contaba con una cierta popularidad, por ser el día conocido como Día de pi y ser un día de celebración de las matemáticas.
El número π (pi) es una de las constantes matemáticas, y científicas, más importantes que existen, pero además es un número fascinante que goza de una gran popularidad entre el público, matemático y no matemático. Por este motivo, el 14 de marzo, es decir, 3/14 en inglés o euskera, se celebra el Día de pi, debido a la sencilla aproximación a π que nos enseñaron en la escuela, 3,14. El día de pi se celebra desde el año 1988 a partir de la idea propuesta por el físico Larry Shaw, y apoyado por el hecho de coincidir con la fecha del cumpleaños de Albert Einstein. Fecha que también era el cumpleaños del matemático polaco Waclaw Sierpinski (1882-1969).
 Etida number pi, de la artista croata Luka Hatvalić. Imagen de Saatchi Art
Etida number pi, de la artista croata Luka Hatvalić. Imagen de Saatchi Art
En el otoño de 2019, la Red de divulgación de las matemáticas DIMA [http://dima.icmat.es/], constituida en mayo de 2018 y cuya presidenta es la profesora de la Universidad de La Laguna Edith Padrón, en colaboración con toda la comunidad matemática española (en particular, la Red Estratégica en Matemáticas (REM), la Real Sociedad Matemática Española (RSME), la Sociedad Española de Matemática Aplicada (SEMA), la Societat Catalana de Matemàtiques (SCM), la Sociedad de Estadística e Investigación Operativa (SEIO), la Federación Española de Profesores de Matemáticas (FEPM), la Federació d’Entitats per a l’Ensenyament de les Matemàtiques a Catalunya (FEEMC), la Conferencia de Decanos de Matemáticas, la Red de Institutos Universitarios de Matemáticas, el Centre de Recerca Matemática (CRM), el Basque Center for Applied Mathematics (BCAM), el Instituto de Ciencias Matemáticas (ICMAT), la Asociación Nacional de Estudiantes de Matemáticas (ANEM), el Museo de Matemàtiques de Catalunya (MMACA), o el Museo de Matemáticas de Aragón y el Comité Español de Matemáticas), diseñaron el proyecto Marzo, mes de las matemáticas, que tiene como objetivo extender la celebración del Día internacional de las matemáticas (14 de marzo), a todo el mes de marzo. El proyecto cuenta con la colaboración de la Fundación Española para la Ciencia y la Tecnología – Ministerio de Ciencia e Innovación (FECYT).
El proyecto Marzo, mes de las matemáticas, cuya web es https://marzomates.webs.ull.es/ , se ha convertido en el mayor evento de divulgación de las matemáticas en España. El proyecto incluye un amplio programa de actividades con diferentes formatos: i) Exposiciones: una exposición temática con paneles interactivos, así como otras exposiciones con formatos y/o temáticas variadas (fotografía matemática, aplicaciones, etc); ii) Conferencias, monólogos y diálogos divulgativos; iii) Tarjetas y carteles matemáticos con contenido diverso y formatos variados (de tres tipos: pasatiempos matemáticos; literatura + matemáticas; sabías que…); iv) Concurso de fotografía escolar “Matemáticas con un clic” a nivel nacional y exposición sobre fotografías matemáticas; v) Escape rooms virtuales, talleres, etc. Además, incluye a diez nodos de trabajo, que son las siguientes autonomías: Andalucía, Aragón, Canarias, Castilla-León, Cataluña, Galicia, La Rioja, Madrid, País Vasco, Valencia.
 Logo del proyecto Marzo, mes de las matemáticas
Logo del proyecto Marzo, mes de las matemáticas
Pero vayamos al tema de esta entrada, las exposiciones que hemos organizado en el metro de Bilbao. En particular, en esta entrada empezaremos con la exposición Geometría Natural, y dejaremos para una próxima entrada la exposición Matemáticas para un mundo mejor.
Desde el principio me vi muy implicado en este proyecto. De hecho, en noviembre de 2019, mientras visitaba la Universidad de La Laguna para impartir algunas conferencias, invitado por mi amiga Edith Padrón, dimos forma al actual proyecto, para presentarlo a la convocatoria de la Fundación Española para la Ciencia y la Tecnología – Ministerio de Ciencia e Innovación (FECYT). Dentro de la estructura organizativa que creamos, mi compañero y amigo Pedro Alegría y yo asumimos la responsabilidad de la organización de las actividades del País Vasco (contando con el apoyo y colaboración de la Universidad del País Vasco/Euskal Herriko Unibertsitatea y el Basque Center for Applied Mathematics-BCAM), así como de la organización de la actividad de las tarjetas matemáticas.
Además, dentro de un proyecto como este no podía faltar la fotografía matemática. Inmediatamente me puse en contacto con la persona idónea para este tema, mi amiga Pilar Moreno, matemática jubilada (ha sido profesora de matemáticas durante 38 años) y fotógrafa valenciana. A quien quiero agradecerle aquí su colaboración, su trabajo y su generosidad.
Pilar Moreno es una de las personas con una mayor trayectoria en España dentro de la fotografía matemática, es la responsable de la sección de fotografía matemática en la página DivulgaMAT con un centenar de pequeñas exposiciones virtuales, ha realizado muchas exposiciones (físicas), tanto individuales (como la que organizamos en 2005 desde la RSME, Anda con ojo, la exposición didáctica Veo, veo … geometría cotidiana, o también las exposiciones Geometría en los puertos y Geometría en la sombra), como colectivas (por ejemplo, las realizadas en los últimos años junto al grupo Enfoque geométrico, como Amor a la línea o Geometría natural). Es autora del libro Anda con ojo, Faktoría K de libros (2006), coautora de los libros Ritmos. Matemáticas e imágenes, Nivola (2002) y de Contemplar, conocer, UPV (2005).
 Catenaria blanca, Paraboloide rojo y Rojo sobre rojo, fotografías incluidas en la exposición Anda con ojo, de Pilar Moreno
Catenaria blanca, Paraboloide rojo y Rojo sobre rojo, fotografías incluidas en la exposición Anda con ojo, de Pilar Moreno
 Portada del libro Anda con ojo, de Pilar Moreno
Portada del libro Anda con ojo, de Pilar Moreno
Pilar Moreno, junto con otros miembros del grupo Enfoque geométrico (como Lucía Morales, Inmaculada Gutierrez, Olga Martín, Leopoldo Martínez, Elia Añón y Amparo Fuentes), aportaron al proyecto Marzo, mes de las matemáticas, dos magníficas colecciones de fotografías para que pudieran organizarse exposiciones en los diferentes nodos del proyecto, una sobre la geometría de la naturaleza (Geometría natural) y otra sobre la geometría de nuestras ciudades (Geometría urbana). A todas ellas quiero agradecerles su colaboración con el proyecto, su generosidad y su arte.
 Líneas de fuga, fotografía de Pilar Moreno dentro de la exposición Geometría Urbana. En esta página de GeoGebra podéis disfrutar de una excelente animación matemática sobre esta fotografía realizada por el matemático Jose Antonio Mora
Líneas de fuga, fotografía de Pilar Moreno dentro de la exposición Geometría Urbana. En esta página de GeoGebra podéis disfrutar de una excelente animación matemática sobre esta fotografía realizada por el matemático Jose Antonio Mora
 Simetría roja, fotografía de Pilar Moreno dentro de la exposición Geometría Urbana. En esta página de GeoGebra podéis disfrutar de una excelente animación matemática sobre esta fotografía realizada por el matemático Jose Antonio Mora
Simetría roja, fotografía de Pilar Moreno dentro de la exposición Geometría Urbana. En esta página de GeoGebra podéis disfrutar de una excelente animación matemática sobre esta fotografía realizada por el matemático Jose Antonio Mora
 Queda curvo el firmamento, fotografía de Amparo Fuentes dentro de la exposición Geometría Urbana
Queda curvo el firmamento, fotografía de Amparo Fuentes dentro de la exposición Geometría Urbana
La siguiente etapa en el proyecto, relacionada con las fotografías matemáticas, era la realización de las exposiciones físicas con el magnífico material aportado por Pilar Moreno y las fotógrafas del grupo Enfoque geométrico. Un lugar ideal para realizar exposiciones dirigidas al público general en Bilbao era el metro de nuestra villa. Ya en 2007 habíamos colaborado con Metro Bilbao para la organización de la exposición Arte fractal, que tuvo lugar en la estación de metro de Sarriko y que fue todo un éxito.
Por este motivo, Pedro Alegría, Marta Macho y yo mismo nos reunimos, en las instalaciones de Metro Bilbao, con Susana Palomino (directora de comunicación y marketing de Metro Bilbao) y Lide Bidaguren (administrativa de comunicación y marketing de Metro Bilbao), quienes desde el primer momento expresaron su interés, y el de Metro Bilbao, por colaborar con nuestro proyecto de divulgación de las matemáticas. En esa reunión acordamos la organización de las dos exposiciones Geometría Natural y Matemáticas para un mundo mejor (sobre las que hablaremos en estas dos entradas de la sección Matemoción del Cuaderno de Cultura Científica) en diferentes estaciones del metro bilbaíno. Quiero expresar aquí mi más sincero agradecimiento a Susana Palomino, a Lide Bidaguren y a Metro Bilbao por su apoyo y colaboración en la organización de estas exposiciones. El metro de Bilbao es un lugar ideal para acercar las matemáticas, a través de elementos visuales, al público general.
 Vista general de la exposición Arte fractal (2007), en la estación de Sarriko de Metro Bilbao. Foto : E. Moreno Esquibel
Vista general de la exposición Arte fractal (2007), en la estación de Sarriko de Metro Bilbao. Foto : E. Moreno Esquibel
Para la primera de las exposiciones, Geometría Natural, seleccionamos doce de las fotografías enviadas por Pilar Moreno y el grupo Enfoque geométrico, cuyos títulos y autoras son: i) Cardioide. Brunnera Macrophylla (Lucía Morales); ii) Arquitectura móvil (Inmaculada Gutierrez); iii) Giros. Dalia (Lucía Morales); iv) Códigos de barras (Pilar Moreno); v) Estrellas pentagonales. Scabiosa Stellata (Lucía Morales); vi) Mosaico poligonal. Fromia Monilis (Leopoldo Martínez); vii) Fractales sobre círculos (Pilar Moreno); viii) Simetría. Asimetría (Pilar Moreno); ix) Ángulos, giros, hélice. Lupinus Nootkatensis (Pilar Moreno); x) Geometría tejida (Pilar Moreno); xi) Lupa natural (Pilar Moreno); xii) Silencio Azul (Pilar Moreno).
El siguiente paso fue escribir unos pequeños textos para acompañar a cada una de las fotografías matemáticas, destacando algún aspecto matemático relacionado con la imagen de la fotografía, labor que realizamos Pedro Alegría, Marta Macho y yo mismo. Además, tuvimos que traducir los textos al euskera y para ello contamos con la colaboración de los matemáticos y amigos Goyo Lekuona y José Ignacio Royo.
Finalmente, el diseño de los paneles de la exposición corrió a cargo de la diseñadora Carla Garrido, que ha realizado un magnífico trabajo.

 Dos fotografías generales de la exposición Geometría Natural, en la estación de Abando de Metro Bilbao. Fotografías de Marian Espinosa
Dos fotografías generales de la exposición Geometría Natural, en la estación de Abando de Metro Bilbao. Fotografías de Marian Espinosa
En lo que resta de entrada daremos un pequeño paseo por la exposición, mostrando algunos de los paneles, con sus fotografías y sus textos.
Empezaremos por el panel de presentación de la exposición, que podéis ver en la siguiente imagen del día que se colocó la exposición para el público (1 de marzo).
 Panel de presentación de la exposición Geometría Natural, en Metro Bilbao. Fotografía de Marian Espinosa
Panel de presentación de la exposición Geometría Natural, en Metro Bilbao. Fotografía de Marian Espinosa
El texto de ese panel de presentación es el siguiente:
“El libro de la naturaleza está escrito en lenguaje matemático”
(Galileo Galilei)
Dirige tu mirada a una flor, una planta, un animal o un paisaje, y sorpréndete con la geometría presente en la naturaleza. Las matemáticas nos ayudan a comprender el mundo en el que vivimos, pero también a crear un mundo mejor. Ojalá esta exposición provoque tu deseo de saber más, de conocer, de investigar y de descubrir las respuestas a los enigmas que la naturaleza nos propone.
Fotografías del grupo Enfoque Geométrico.
Empecemos nuestro recorrido por el panel de la exposición Geometría Natural correspondiente a la hermosa fotografía de Lucía Morales Giros. Dalia.
 Panel de la fotografía Giros. Dahlia, de Lucía Morales, dentro de la exposición Geometría Natural, en Metro Bilbao. Fotografía de Marian Espinosa
Panel de la fotografía Giros. Dahlia, de Lucía Morales, dentro de la exposición Geometría Natural, en Metro Bilbao. Fotografía de Marian Espinosa
El texto que acompaña a dicha fotografía llama la atención sobre el sorprendente hecho de que la belleza de una flor pueda estar relacionada con la sucesión de Fibonacci o el número áureo.
Es sorprendente que detrás de la belleza de esta flor esté la sucesión de Fibonacci (1, 1, 2, 3, 5, 8, 13, …) o el ángulo áureo (137,51º), como explica la filotaxis, la parte de la botánica que se ocupa del estudio de la disposición de hojas, semillas y flores en las plantas.
Otra de las imágenes de la exposición, ahora relacionada con el mundo animal, es la fotografía Arquitectura móvil, de Inmaculada Gutiérrez, que vemos en la siguiente imagen.
 Panel de la fotografía Arquitectura móvil, de Inmaculada Gutiérrez, dentro de la exposición Geometría Natural, en Metro Bilbao. Fotografía de Marian Espinosa
Panel de la fotografía Arquitectura móvil, de Inmaculada Gutiérrez, dentro de la exposición Geometría Natural, en Metro Bilbao. Fotografía de Marian Espinosa
El texto que nos acerca a las matemáticas relacionadas con esta hermosa fotografía es:
Las espirales son curvas geométricas muy frecuentes en la naturaleza. En procesos naturales de crecimiento, como en la concha del caracol, aparece la conocida espiral logarítmica. Es una curva autosemejante, al crecer el caracol cambia de tamaño, pero no de forma.
Otra imagen que llama la atención es la fotografía Lupa natural, de Pilar Moreno, cuyo texto es el siguiente:
La forma esférica que adoptan de manera natural las gotas de lluvia es consecuencia de la tensión superficial y las matemáticas demuestran que esta es la forma óptima, la que tiene menor superficie para un volumen dado.
 Panel de la fotografía Lupa natural, de Pilar Moreno, dentro de la exposición Geometría Natural, en Metro Bilbao. Fotografía de Marian Espinosa
Panel de la fotografía Lupa natural, de Pilar Moreno, dentro de la exposición Geometría Natural, en Metro Bilbao. Fotografía de Marian Espinosa
 Panel de la fotografía Códigos de barras, de Pilar Moreno, dentro de la exposición Geometría Natural, en Metro Bilbao. Fotografía de Marian Espinosa
Panel de la fotografía Códigos de barras, de Pilar Moreno, dentro de la exposición Geometría Natural, en Metro Bilbao. Fotografía de Marian Espinosa
El texto escrito para acompañar a la fotografía Códigos de barras, de Pilar Moreno, que vemos en la anterior imagen, es el siguiente:
¿Por qué algunos animales tienen manchas, como el leopardo y la jirafa, y otros, rayas, como la cebra o el pez cirujano payaso? Las ecuaciones matemáticas llamadas “de reacción-difusión” han sido utilizadas para explicar los patrones de las pieles de los animales.
Otra de las fotografías del mundo vegetal que llama la atención es Cardioide. Brunnera Macrophylla, de Lucía Morales.
 Panel de la fotografía Cardioide. Brunnera Macrophylla, de Lucía Morales, dentro de la exposición Geometría Natural, en Metro Bilbao. Fotografía de Marian Espinosa. En esta página de GeoGebra podéis disfrutar de una excelente animación matemática sobre esta fotografía realizada por la matemática Débora Pereiro
Panel de la fotografía Cardioide. Brunnera Macrophylla, de Lucía Morales, dentro de la exposición Geometría Natural, en Metro Bilbao. Fotografía de Marian Espinosa. En esta página de GeoGebra podéis disfrutar de una excelente animación matemática sobre esta fotografía realizada por la matemática Débora Pereiro
El texto que hemos escrito para la misma es:
Son necesarias fórmulas matemáticas complejas para representar el contorno natural de algunas plantas. La figura en forma de corazón invertido de la Brunnera Macrophylla presenta además una casi perfecta simetría axial.
Aunque realmente todas las fotografías son impactantes, como lo es también la titulada Geometría tejida, de Pilar Moreno, cuyo texto hace referencia a la teoría de grafos, una teoría matemática con muchas aplicaciones.
Las telas de araña recuerdan a una estructura matemática llamada grafo. Están formadas por hilos (aristas) y nudos (vértices) uniendo esas fibras. Las redes sociales se comportan del mismo modo: cada arista envía información entre nodos conectados.
 Panel de la fotografía Geometría tejida, de Pilar Moreno, dentro de la exposición Geometría Natural, en Metro Bilbao. Fotografía de Marian Espinosa
Panel de la fotografía Geometría tejida, de Pilar Moreno, dentro de la exposición Geometría Natural, en Metro Bilbao. Fotografía de Marian Espinosa
Vamos a terminar con una fotografía para la que la matemática Débora Pereiro ha realizado una bella animación con GeoGebra, es Ángulos, giros, hélice. Lupinus Nootkatensis, de Pilar Moreno. Y me gustaría aprovechar para agradecerle a ella y a Juan Antonio Mora su trabajo con GeoGebra animando matemáticamente algunas de las fotografías.
 Panel de la fotografía Ángulos, giros, hélice. Lupinus Nootkatensis, de Pilar Moreno, dentro de la exposición Geometría Natural, en Metro Bilbao. En esta página de GeoGebra podéis disfrutar de una excelente animación matemática sobre esta fotografía realizada por la matemática Débora Pereiro
Panel de la fotografía Ángulos, giros, hélice. Lupinus Nootkatensis, de Pilar Moreno, dentro de la exposición Geometría Natural, en Metro Bilbao. En esta página de GeoGebra podéis disfrutar de una excelente animación matemática sobre esta fotografía realizada por la matemática Débora Pereiro
Estos son algunos de los paneles de la exposición Geometría Natural expuesta en Metro Bilbao, durante el mes de marzo en la estación de Abando y en abril en la estación de Basauri.
Me gustaría terminar expresando mi agradecimiento a todas las instituciones y a todas las personas, que han sido muchas, que han hecho posible la realización de esta exposición, y de todo el proyecto Marzo, mes de las matemáticas.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Exposiciones matemáticas en el metro de Bilbao (I) se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Poesía métrica, ¿de metro?
- Las dos culturas de las matemáticas: construir teorías o resolver problemas
- Fractus, arte y matemáticas
Fusión nuclear en el Sol
 Foto: NASA/JPL-Caltech/GSFC
Foto: NASA/JPL-Caltech/GSFCLas reacciones de fusión nuclear son bastante comunes en la naturaleza, aunque no en la Tierra. Son la fuente de la energía generada por el Sol y los miles de millones de estrellas en todo el Universo. En cierto sentido se puede decir que la energía de fusión es la principal fuente de energía de la naturaleza [1]. En las estrellas el confinamiento del plasma lo logra la atracción gravitacional.
Uno de los aspectos más fascinantes de la física nuclear es el estudio de las reacciones de fusión en los diferentes tipos de estrellas. Estas reacciones son las que terminarán formando muchos de los elementos químicos [2]. El Sol es un buen ejemplo.
En el Sol, el proceso de fusión da como resultado la producción de un núcleo de helio a partir de cuatro protones. El resultado neto de las reacciones que tienen lugar se puede escribir como
![]()
donde +10e es un «anti-electrón», también conocido como positrón. Esta reacción neta no tiene lugar en un solo paso, sino que se puede llegar a ella a través de diferentes conjuntos de reacciones cuyos resultados netos se resumen en esta ecuación. En cualquier caso la cantidad total de energía liberada es siempre la misma: 26 MeV. La fusión de cuatro protones para formar un núcleo de helio es la principal fuente de energía del Sol.
El hidrógeno y el helio juntos constituyen alrededor del 99% de la masa del Sol, con aproximadamente el doble de H que de He. Afortunadamente, hay suficiente hidrógeno como para que el Sol siga suministrando energía durante varios miles de millones de años más.
¿Mediante cuál de los varios conjuntos posibles de reacciones tiene lugar la transformación del hidrógeno en helio? Tenemos que descartar el proceso directo de colisión de cuatro protones para formar un núcleo de helio no porque sea imposible, sino porque la probabilidad de una reacción así en las condiciones del interior del Sol es demasiado baja. Es decir, puede suceder, pero no con la suficiente frecuencia para generar la cantidad de energía liberada que se observa.
Un conjunto de reacciones más probable es el siguiente: cuando la temperatura es de aproximadamente 107 K, las energías cinéticas son lo suficientemente grandes como para superar la repulsión eléctrica entre los protones y se produce la fusión de dos protones. La reacción nuclear da como resultado un deuterón (hidrógeno-2), un positrón y un neutrino. Tan pronto como se forma el deuterón, reacciona con otro protón, dando como resultado helio-3 y un rayo gamma. Los núcleos de helio-3 se fusionan entre sí, formando partículas alfa y dos protones. En cada una de estas reacciones, se libera energía, lo que da como resultado 26 MeV para el ciclo completo de cuatro protones que dan lugar a un núcleo de helio.
La velocidad de la reacción depende del número de núcleos por unidad de volumen y de la temperatura. Cuanto mayor sea la temperatura, más rápido será el movimiento térmico de las partículas y más frecuentes y enérgicas serán las colisiones. A la temperatura del interior del Sol, que se ha estimado que está entre 10 y 20 millones de grados, las energías cinéticas resultantes del movimiento térmico están en entorno de 1 keV.
Notas:
[1] Decimos en cierto sentido porque existen otras formas de energía, como la energía oscura o, incluso, la atracción gravitatoria de los agujeros negros. Pero no las consideramos.
[2] De aquí viene la expresión “somos polvo de estrellas”, porque los elementos que nos componen se crearon en su mayoría por procesos de fusión en las distintas fases de la vida y muerte de diferentes tipos de estrellas.
[3] Quizás convenga comentar que las reacciones químicas no pueden proporcionar energía a velocidades lo suficientemente grandes (o durante un tiempo lo suficientemente largo) como para explicar la producción de energía en el Sol. Las reacciones de fusión nuclear sí lo logran fácilmente.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Fusión nuclear en el Sol se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Fusión nuclear
- Energía de enlace nuclear y estabilidad
- La fusión nuclear como fuente de neutrones eficiente
¿Blanca, beige o marrón? No toda la grasa corporal es mala
Paula Oliver Vara
 Shutterstock / BonNontawat
Shutterstock / BonNontawat
Cuando pensamos en el tejido adiposo, inevitablemente nos vienen a la mente los impopulares “michelines”, que a día de hoy percibimos como un problema. Sin embargo, debemos tener en cuenta que la capacidad de almacenar como depósitos de grasa el excedente de energía ingerida ha permitido la supervivencia de nuestra especie. Osea, que hay mucho que agradecerle.
El principal reservorio de grasa en nuestro cuerpo es el tejido adiposo blanco, pero existe también un tejido adiposo marrón. Este último tiene una función opuesta, ya que nos permite “quemar” la grasa almacenada, disipando la energía como calor. Eso lo convierte en una interesante diana en la lucha contra la obesidad y sus complicaciones.
El tejido adiposo blanco: una reserva de energía para momentos de necesidad
Los alimentos contienen nutrientes que nos proporcionan la energía (calorías) que nuestro cuerpo necesita para funcionar. Si ingerimos más calorías de las que gastamos no las desaprovechamos, sino que las convertimos muy eficientemente en grasa (triacilglicéridos) que almacenamos en unas células, los adipocitos, que forman el tejido adiposo blanco.
Este reservorio de grasa queda disponible para hacer frente a situaciones de escasez de alimentos, en las que podemos movilizar los triacilglicéridos almacenados para obtener la energía que necesitamos. Por eso la grasa aporta una ventaja evolutiva. O más bien la aportaba hasta hace poco. Porque en la época actual, y a diferencia de lo que ha venido ocurriendo a lo largo de miles de años de evolución, nos encontramos frente a una situación bastante diferente.
En estos momentos, la mayoría de individuos de nuestra especie tiene a su disposición una amplia oferta de alimentos, algunos excesivamente calóricos. Si a los frigoríficos y despensas a rebosar le sumamos que nuestro estilo de vida es cada vez más sedentario, la consecuencia inmediata es que acumulamos grasa en exceso y engordamos.
La grasa subcutánea –esto es, la de los michelines– más característica de las mujeres, es la menos problemática. El mayor riesgo para la salud se asocia a la grasa visceral, que es la que se deposita rodeando a órganos como el hígado, corazón o los intestinos.
Es importante resaltar también que el tejido adiposo no solo sirve como reservorio de energía. Los adipocitos blancos son capaces de producir y liberar a la sangre sustancias bioactivas conocidas como adipocitoquinas, con una importante función reguladora del metabolismo. El problema viene cuando acumulamos demasiada grasa en nuestros adipocitos, porque en ese momento la producción de adipocitoquinas se desregula. Como consecuencia, aumentan los procesos inflamatorios y la resistencia a la insulina, que son el detonante de diversas patologías.
Resumiendo, el acúmulo de grasa corporal en forma de sobrepeso u obesidad ha alcanzado a día de hoy dimensiones de pandemia, y van asociado a enfermedades cardiovasculares y a una larga lista de patologías, incluyendo diferentes tipos de cáncer e, incluso, un mayor riesgo de daño cognitivo.
El tejido adiposo marrón: el tejido capaz de quemar la grasa
Si bien el tejido adiposo blanco es el más abundante, existe otro tipo de tejido adiposo, el marrón. Se distingue porque, en respuesta al frío y otros estímulos, moviliza las reservas grasas y libera energía en forma de calor. El proceso se conoce como termogénesis adaptativa, y resulta muy útil para mantener la temperatura corporal en animales, incluidos los hibernantes. Además, en pequeños mamíferos, la termogénesis adaptativa se pone en marcha también frente a la ingesta de dietas ricas en calorías, lo cual les ayuda a mantener el peso corporal.
En el caso de los humanos, durante muchos años se pensó que el tejido adiposo marrón era importante en recién nacidos para regular la temperatura corporal, pero que desaparecía en adultos. La sorpresa surgió hace poco más de una década, cuando se describió que los humanos mantenemos tejido adiposo marrón en edad adulta que es capaz de activarse para generar calor, utilizando ácidos grasos y glucosa.
Este descubrimiento potenció la aparición de proyectos encaminados a identificar diferentes formas de activar la termogénesis en el tejido adiposo marrón para perder peso, mejorar la salud cardiovascular y pararle los pies a la diabetes. Uno de ellos fue el proyecto europeo DIABAT, que se desarrolló entre el 2011 y el 2015, en el que participaron centros de investigación de 12 países europeos, incluido nuestro grupo de Nutrigenómica y Obesidad de la Universidad de las Islas Baleares.
Las investigaciones continúan avanzando, y son múltiples las evidencias que apuntan a los beneficios de la grasa marrón. Por ejemplo, recientemente se ha publicado que la presencia de tejido adiposo marrón está relacionada con un menor riesgo cardiovascular. Y que podría mitigar las complicaciones asociadas a la obesidad, como la diabetes, hipertensión o niveles de lípidos elevados en sangre.
¿Y si pudiéramos convertir la grasa blanca en marrón?
Aunque lo ideal es no acumular grasa en exceso, la buena noticia es que los depósitos de grasa blanca pueden convertirse en lo que ha venido a considerar un tercer tipo de grasa, la grasa beige.
La transformación forma parte de un proceso conocido como marronización. Resulta interesante porque los adipocitos beige son un tipo de células similares a los adipocitos marrones. Como ellos, expresan la proteína UCP1 o termogenina, y por lo tanto pueden realizar termogénesis. Eso sí, están localizados dentro del tejido adiposo blanco.
La marronización del tejido adiposo blanco se puede inducir con estímulos adecuados, como la exposición al frío. Pero también con fármacos, con determinados nutrientes, e incluso con el ejercicio físico. Esta posibilidad es interesante porque con la conversión de grasa blanca en grasa beige se potenciaría la eliminación de los lípidos y glucosa circulantes. Y al incrementar de esta forma el gasto energético contribuiríamos a mantener el peso corporal y la salud metabólica.
Parece indiscutible que estamos ante un arma muy poderosa para combatir la epidemia mundial de obesidad y de diabetes.![]()
Sobre la autora: Paula Oliver Vara es catedrática de bioquímica y biología molecular en la Universitat de les Illes Balears y co-investigadora principal del grupo de “Nutrigenómica y Obesidad” del CIBER de Fisiopatología de la Obesidad y Nutrición (CIBEROBN)
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo ¿Blanca, beige o marrón? No toda la grasa corporal es mala se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Resveratrol y pteroestilbeno en el control epigenético de la acumulación de grasa corporal
- La combinación de dos moléculas marroniza la grasa
- Grasa parda
El día que el arte me ayudó a escribir un artículo de matemáticas
Pablo Rodríguez Sánchez
Este no es mi primer artículo de divulgación. De hecho, si las cuentas no me fallan, es mi centésimo décimo quinto. Sin embargo, es el primer artículo de divulgación en el que hablo de mi propia investigación. Para alguien con una verborrea como la mía, semejante timidez y silencio respecto a mi propio trabajo son, cuanto menos, llamativos. Sospechosos incluso. Pero todo tiene una explicación: he pasado tanto tiempo embarrado ocho horas diarias con estos problemas que para cuando les puse las guinda y fueron publicados… ya hacía meses que habían dejado de divertirme.
Un artículo científico, peor aún si trata sobre matemáticas, se acerca mucho a la antítesis de la diversión. Especialmente para el que lo lee. Hace falta mucha habilidad para hacerlo entretenido, habilidad que yo no tengo. Sin embargo, escribir un artículo científico es una actividad humana llena de altibajos, frustraciones y curiosidades. Ingredientes estos no muy diferentes de los que uno puede encontrar en algunas novelas, películas e incluso chistes.
Permítanme que les cuente aquí la intrahistoria de mi artículo, pues esta, al contrario que el frío y técnico contenido, es completamente inédita.
 Ascendiendo y descendiendo. M.C. Escher (1960). Litografía. Fuente: Wikimedia Commons
Ascendiendo y descendiendo. M.C. Escher (1960). Litografía. Fuente: Wikimedia CommonsEl arte, las matemáticas y yo
Lo reconozco. Hubo un tiempo en el que cada vez que escuchaba juntas las palabras “arte” y “matemáticas” me ponía en guardia. Será que he visto demasiadas películas infumables, demasiadas obras de arte pretenciosas (y a menudo feas), o simplemente que estoy hecho un gruñón.
Digo «hubo un tiempo», en pasado, porque actualmente veo la combinación “arte y matemáticas” con ojos más benévolos. Esto se debe a que este dueto me ha proporcionado muchos buenos momentos en los últimos años. Algunos ejemplos son mi colaboración con el videoartista Johan Rijpma, mis charlas en Naukas, o la historia que hoy les traigo.
Como pez fuera del agua
Permítanme que les ponga en antecedentes. En 2015 comencé un doctorado en matemáticas aplicadas en un departamento de ecología. Esto significaba, entre otras cosas, que tenía que escribir artículos sobre matemáticas que fuesen interesantes para la comunidad ecológica.
La mayoría de ecólogos se pueden clasificar en tres categorías: ecólogos de campo, ecólogos de laboratorio y ecólogos computacionales. O si lo prefieren, ecólogos de bota, de bata y de byte. Los ecólogos suelen tener formación en biología, y cualquier suposición sobre su interés por las matemáticas está abocada al fracaso: este puede ir desde casi nulo a altísimo.
Todo esto plantea una dificultad enorme desde el punto de vista de la comunicación: ¿cómo abordar los problemas matemáticos de la ecología sin perder ni aburrir a nadie? En este otro artículo, publicado en esta misma casa, ofrezco algunos consejos generales. Pero permítanme ir de lo general a lo particular, y explicar cómo el arte me echó una mano en cierta ocasión.
La estabilidad como paisaje
Uno de estos problemas de comunicación interdisciplinar es el siguiente: en ecología aparecen de forma bastante natural conceptos procedentes de la teoría de sistemas dinámicos. Hablo de conceptos como ecuación dinámica, clasificación de equilibrios o teoría de bifurcaciones.
Para los matemáticos, los sistemas dinámicos no son nada más (ni nada menos) que unas reglas, normalmente en forma de ecuaciones, que dictan cómo debe moverse un punto. Ese punto puede representar muchas cosas. Una temperatura a lo largo del año, los ahorros presentes en una cuenta bancaria, la cantidad de peces que viven en un lago, etcétera. En definitiva, cualquier cosa que pueda medirse y cambie en el tiempo. Si las reglas están bien fundadas, podemos usarlas nada menos que para predecir la evolución futura de la variable bajo estudio. Un buen ejemplo son los problemas de mecánica, donde conociendo las fuerzas que actúan sobre un objeto podemos calcular cómo se moverá este.
Estos puntos, según cual sea el problema, pueden moverse por una línea recta, por un plano, por el espacio tridimensional, o por inimaginables hiperespacios de cuatro o más dimensiones. Todo depende del número de variables que estemos estudiando (una temperatura, las poblaciones de dos especies de peces, las tres dimensiones de un objeto en movimiento, etc).
Una manera muy habitual de introducir estos conceptos, que ha demostrado su eficacia en innumerables ocasiones, es usando algo que la comunidad ecológica llama stability landscape o ball-in-a-cup diagram (lo que podríamos traducir libremente como «paisaje de estabilidad» o “diagrama de la bolita en el vaso»; no me miren así, yo no les he puesto esos nombres). La idea consiste en construir una curva sobre la cual una bolita se deja rodar, de modo que la forma de la curva, la forma del «paisaje», nos indica cómo ha de moverse1. Al fin y al cabo la teoría de sistemas dinámicos, recordemos, trata de describir cómo se mueve un punto… y dejar rodar una bolita es, en principio, una manera como otra cualquiera de mover un punto de acá para allá. La idea es muy gráfica y explota nuestra natural intuición respecto al movimiento. Ahí radica su fuerza.
Si, además, permitimos que la forma de los «paisajes» cambie en respuesta a condiciones externas (como temperatura, pH, salinidad, …), estas metáforas gráficas pueden usarse para ilustrar conceptos bastante avanzados, como los de estabilidad, bifurcación, o histéresis (ver ejemplo en la figura, y más aquí).
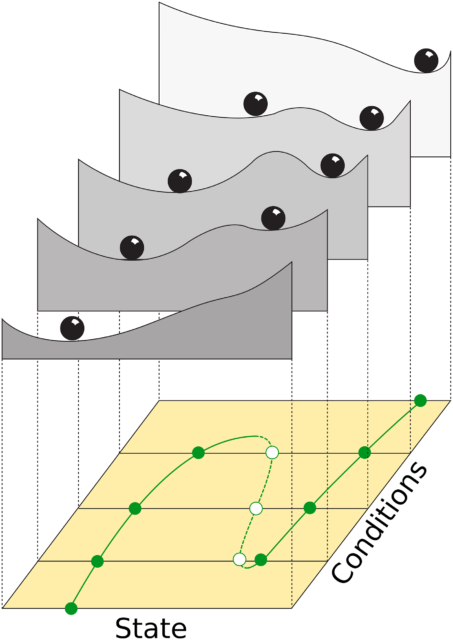
La parte superior de la figura muestra el «paisaje» correspondiente a un sistema dinámico para 5 valores diferentes de las condiciones externas. La parte de abajo muestra, en verde, el diagrama de bifurcación correspondiente, donde los puntos sólidos representan equilibrios estables (correspondientes al fondo de un «valle») y los vacíos equilibrios inestables (correspondientes a una «cresta»). Obsérvese como no sólo la posición, sino también el número de puntos de equilibrio varía con las condiciones externas. Una de las consecuencias de esto es que, para ciertas condiciones externas, el comportamiento del sistema puede cambiar de manera drástica.
Es posible que el lector se haya dado cuenta de que estos «paisajes» se parecen mucho al concepto de potencial en mecánica clásica. De hecho, son casi lo mismo2.
Pedir peras al olmo
Utilizar aproximaciones y analogías gráficas tiene sus ventajas y sus peligros. Algunos, incluso, son ventaja y peligro a la vez. El hecho de que las cosas parezcan más sencillas de lo que realmente son es una de estas ventajas peligrosas.
Muchos biólogos trabajan con sistemas dinámicos de dos variables. Por ejemplo, una coordenada x describiendo una especie de pez, y la coordenada y describiendo a otra. A menudo los peces x se comen a los peces y. ¿Y si usamos estos “paisajes de estabilidad” en modelos con dos (o más) variables? Si una bola rodando sobre curva nos sirve representar la dinámica de una variable, una bola rodando sobre una superficie nos servirá para representar la dinámica de dos variables, ¿no?
En principio no parece mala idea, pero cualquiera que lo intente no tardará en encontrarse en un callejón sin salida. Lo que funciona de maravilla para una variable se convierte en una pesadilla cuando se intenta aplicar a dos o más. En el mejor de los casos, el «paisaje» puede calcularse para algún subcaso muy concreto. En el peor, alguien propondrá un método nuevo, cada cual más complicado y difícil de interpretar que el anterior.
Y es que, aunque en principio usar superficies como “paisajes de estabilidad” puede parecer una buena idea, resulta no serlo. Los motivos últimos son sutiles, y requieren de herramientas con nombres tan poco atractivos como campo irrotacional o teorema del gradiente. Meterme en ese barrizal en un artículo de ecología hubiera sido de un mal gusto intolerable. Pero entonces, ¿cómo abordar el problema?
Aquí es dónde, por fin, el arte vino en mi ayuda. Imaginemos, me dije, un sistema dinámico con estas dos características:
- Tiene dos variables: nuestro punto (x,y) se mueve por un plano.
- Describe una oscilación: el punto describe una trayectoria cerrada, una y otra vez.
Tratemos ahora de imaginar una superficie tal que la bolita, en su constante descenso, dé vueltas y vueltas eternamente en una curva cerrada, sin dejar de rodar hacia abajo. ¿Qué aspecto tendría esa superficie? Intentemos imaginarla. A ojo, sin teoremas ni campos ni derivadas, ¡imaginación al poder! Y hete aquí que, por poder, podemos imaginarla. Y en gran medida, gracias a las extrañas superficies popularizadas por el artista M.C. Escher.
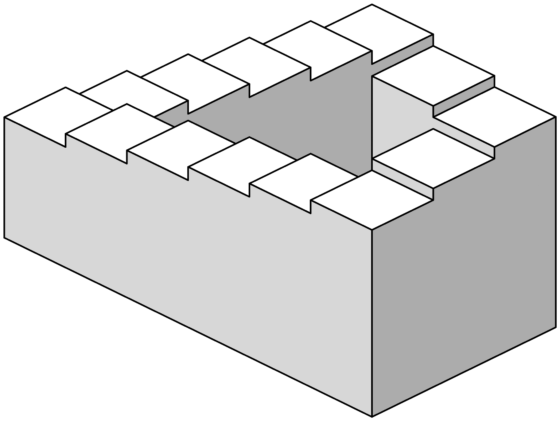
Podemos imaginarla, pero es una superficie que hace saltar todas nuestras alarmas. Algo tiene, algo le pasa, algo no cuadra, es una superficie… imposible. Y lo es, vaya si lo es. Resulta que desde el principio estábamos intentando pedirle peras al olmo. O subir las escaleras de Escher. ¡Con razón la cosa se ponía difícil!
¿Nada más?
Es posible que al lector más acostumbrado a la literatura científica el contenido de este post se le antoje corto para un artículo de investigación. Y llevará razón. El artículo original va más allá de lo que esta pequeña pieza de divulgación pretende (y debe) cubrir. Concretamente, añade un algoritmo para evaluar cuándo y dónde podemos usar estos paisajes de estabilidad en sistemas multidimensionales.
¿Algoritmo has dicho?, o sea, ¡que al final sí que te metiste en berenjenales matemáticos! En efecto… no me quedó más remedio. Diré en mi defensa que, esta parte, la de métodos, intenté hacerla lo más digerible posible. En este caso no fue el arte, sino la ingeniería de software quien vino en mi ayuda. Me explico: además de detallar cómo funciona el algoritmo, lo programé lo mejor que pude, lo empaqueté y lo puse pública y abiertamente a disposición de quien quiera usarlo, mejorarlo o incluso poner a prueba que lo que digo en mi artículo es correcto.
En mi opinión esto es una buena idea por muchos motivos. Además de los obvios (reproducibilidad, comodidad, …) también aporta una ventaja desde el punto de vista de la comunicación: permite a los lectores menos afines a las matemáticas utilizar el algoritmo sin necesidad de bucear demasiado en los detalles.
Para acabar, una reflexión suelta
Escribiendo este artículo tuve el raro honor de citar una publicación antiquísima, concretamente del año 1777. Cuando pensamos en investigación multidisciplinar, tendemos a dar por sentado que los «puentes» que quedan por tender entre disciplinas serán pocos y seguramente muy recientes. Sin embargo, queda claro que aún quedan puentes por tender, incluso, desde los fundamentos.
Y esta es la historia de mi artículo. La parte interesante. Creo. Es, en fin, lo que ningún editor de una revista académica aceptaría. Es también lo que le contaría a un amigo si me insistiese en que hablase del tema durante una cena o tomando unas cervezas.
Notas:
1 En esta otra entrada mostramos algunos ejemplos.
2 ¿Por qué casi?, pues porque el potencial mecánico se relaciona con la derivada segunda del estado, mientras que aquí estamos vinculando los “potenciales” a la derivada primera. Aún así, existe otra analogía mecánica, esta sí, impecable: el movimiento de una bolita en un potencial mecánico al sumergida en un medio viscoso.
Sobre el autor: Pablo Rodríguez Sánchez es doctor en matemáticas aplicadas e ingeniero de software de investigación en el Netherlands eScience Center (Amsterdam, Países Bajos)
El artículo El día que el arte me ayudó a escribir un artículo de matemáticas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Historia de cómo el VIH ayudó a derribar el dogma central de la biología molecular
- Cómo leer un artículo científico
- Cuadrados latinos, matemáticas y arte abstracto
Helena Matute – Naukas Bilbao 2019: Mente humana, mente robótica
 Foto: Alex Knight / Unsplash
Foto: Alex Knight / UnsplashLa mente humana es una gran caja negra. La mente robótica, de hecho, lo es y hasta más oscura. Esta es la tesis que defiende Helena Matute en esta inquietante charla.
Helena Matute es catedrática de psicología experimental de la Universidad de Deusto.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Helena Matute – Naukas Bilbao 2019: Mente humana, mente robótica se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Helena Matute – Naukas P4K 2019: Vulnerable-mente
- Helena Matute: «Los algoritmos nos ganan en cualquier partida que juguemos contra ellos»
- Francisco Villatoro – Naukas Bilbao 2019: El abrazo de la plata
África arde más de lo que se pensaba
 Foto: Tom Eames
Foto: Tom EamesUn equipo de investigadores españoles y holandeses ha estimado que el área afectada por incendios forestales en África es un 80 % máyor de lo que se pensaba. Dado que África representa la mayoría del área quemada a nivel global este nuevo hallazgo modifica sustancialmente las estimaciones de emisiones globales de gases a la atmósfera.
Los incendios forestales suelen aparecer en los medios de comunicación cuando las que se queman son regiones boscosas cercanas a asentamientos humanos, pero la mayor parte de la superficie que arde cada año corresponde a sabanas tropicales donde los incendios son parte integral del ecosistema. El área total que se quema en esos ecosistemas es aproximadamente el equivalente al tamaño de la Unión Europea. Hasta ahora, la evaluación a gran escala del área quemada se ha basado en imágenes de satélites con un tamaño de píxel relativamente grande. Esto es un problema ya que, para que un incendio pueda detectarse de esta manera, es necesario que todo un píxel de la imagen aparezca como incendiado.
Los investigadores Rubén Ramo y Emilio Chuvieco, de la Universidad de Alcalá, y Ekhi Roteta y Aitor Bastarrika de la UPV/EHU han estudiado las imágenes de áreas quemadas aportadas por el satélite europeo Sentinel-2 y han comparado estos datos con los empleados habitualmente, de menor resolución. El Sentinel-2 es capaz de distinguir cuadrados de 20 metros de lado, frente a los 500 m de lado de los cuadrados habituales.
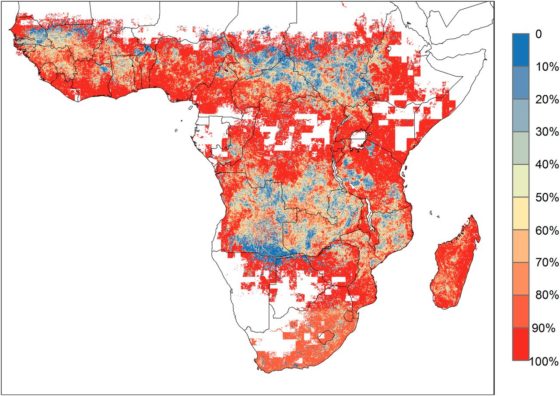 Incendios forestales menores detectados en África. Fuente: PNAS
Incendios forestales menores detectados en África. Fuente: PNASLos investigadores han encontrado que incendios relativamente pequeños, que no pueden ser detectados por los satélites de menor resolución, contribuyen casi tanto al área total quemada como los incendios más grandes. Los incendios pequeños tienen un impacto mucho mayor de lo que se creía.
Por su parte, los investigadores de la Vrije Universiteit Amsterdam, Dave van Wees y Guido van der Werf, han calculado las emisiones de gases correspondientes a dichos incendios menores y encontrado que estas emisiones adicionales son mayores que las emisiones totales producidas por incendios forestales en toda América del Sur.
Se estima que las emisiones totales por incendios forestales en África equivalen al 13 % de las emisiones mundiales por el uso de combustibles fósiles. Sin embargo, dado que las emisiones de dióxido de carbono de esos incendios menores de la sabana africana se compensan con el recrecimiento de la vegetación de la zona afectada, la estimación del aumento del área quemada total no contribuye proporcionalmente a la acumulación de dióxido de carbono en la atmósfera, como lo hacen los combustibles fósiles, pero sí aumenta la contribución de los incendios a las cantidades de otros gases de efecto invernadero como el metano y el óxido nitroso.
Referencia:
Ruben Ramo, Ekhi Roteta, Ioannis Bistinas, Dave van Wees, Aitor Bastarrika, Emilio Chuvieco, and Guido R. van der Werf (2021) African burned area and fire carbon emissions are strongly impacted by small fires undetected by coarse resolution satellite data PNAS March 2, 2021 118 (9) e2011160118 DOI: 10.1073/pnas.2011160118
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo África arde más de lo que se pensaba se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Los ecosistemas acuáticos de África y el cambio climático
- Hubo una migración de vuelta a África en el Paleolítico
- La energía de las olas ha aumentado un 40 % en el último siglo.
El hidrógeno, clave para gestionar las redes eléctricas del futuro
María Retuerto Millán, Miguel Antonio Peña y Sergio Rojas Muñoz
 Petrmalinak/Shutterstock
Petrmalinak/Shutterstock
Es una verdad universalmente admitida que las fuentes energéticas de la humanidad deben ser de carácter renovable. Lo que nos conduce a un uso creciente de las energías eólica y solar fotovoltaica. Estas últimas son actualmente las más desarrolladas y las más competitivas respecto a otras alternativas no sostenibles.
La forma práctica de usar estas fuentes de energía es su transformación en electricidad. Por ello, cualquier país suficientemente avanzado tenderá a la electrificación del sistema energético en los próximos años.
Sin embargo, la gestión de una red eléctrica basada en energías renovables no es sencilla, dado su carácter intermitente. No solo hay que gestionar el ciclo día-noche de la solar fotovoltaica, sino también los ciclos estacionales verano-invierno.
Es necesario almacenar la energía en periodos en los que existan excedentes. De esta forma, se podrán usar en momentos en los que la disponibilidad de energía es menor (menos viento o menos radiación solar en invierno).
Existen diferentes métodos de almacenamiento de energía eléctrica, como las baterías o el bombeo hidráulico. La mayor parte de ellos no permiten cubrir la demanda necesaria o no permiten el almacenamiento a largo plazo de grandes cantidades de energía. Pero existe un vector energético que sí permite ser almacenado y distribuido cumpliendo estos requisitos: el hidrógeno.
Producción y almacenamiento del hidrógeno
El proceso de producción de hidrógeno a partir de la energía eléctrica es conocido como electrolisis. Se realiza aplicando corriente eléctrica al agua, separando así sus elementos: hidrógeno y oxígeno. De esta forma, la electricidad renovable producida se almacena en forma de hidrógeno.
Cuando es necesario disponer de nuevo de electricidad, es posible realizar el proceso inverso: alimentando una pila de combustible con el hidrógeno almacenado se obtiene la electricidad que requerimos, produciéndose también agua.
Existen diversas formas de almacenar hidrógeno, pero la más utilizada actualmente son los depósitos a alta presión. La presión estándar de almacenamiento es 700 bar (unas 700 veces la presión atmosférica). Su uso es seguro gracias a los avances de los últimos años en tecnología de materiales. Podemos almacenar grandes cantidades de energía durante largos periodos de tiempo y, por tanto, gestionar la red eléctrica.
Más allá de la electricidad
Existen otros usos de este hidrógeno renovable diferentes de la electricidad, como los de empresas que requieren calor industrial de calidad. Incluso es posible usar la red de distribución de gas natural inyectando en ella gas de origen renovable.
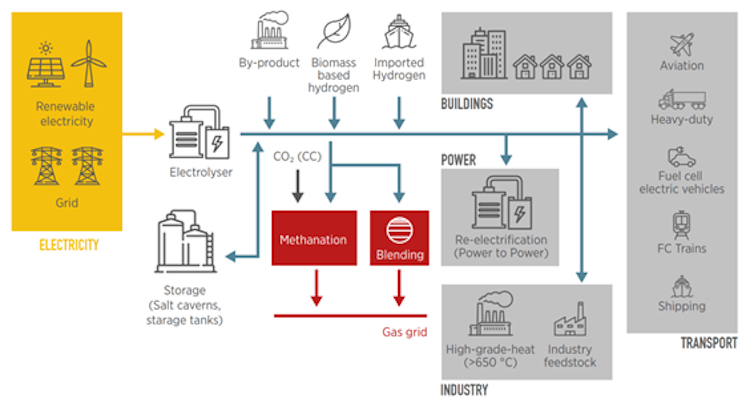 Esquema de almacenaje y distribución directa (línea azul) o a través de la red de gas natural (línea roja) de hidrógeno renovable. Fuente: International Renewable Energy Agency (IRENA)
Esquema de almacenaje y distribución directa (línea azul) o a través de la red de gas natural (línea roja) de hidrógeno renovable. Fuente: International Renewable Energy Agency (IRENA)La eficiencia de los electrolizadores y las pilas de combustible suele ser alta, entre el 70 y 90 %, dependiendo de la tecnología usada. El uso directo de la electricidad renovable no tendría ninguna pérdida. Pero, si es necesario almacenarla, la tecnología del hidrógeno resulta ser la más efectiva.
Aplicaciones en transporte
Las primeras aplicaciones del hidrógeno como vector energético se están produciendo en el sector del transporte. Desde 2015 existen en el mercado vehículos eléctricos, como el Toyota Mirai o el Hyundai Nexo.
En los coches, la electricidad se produce en una pila de combustible alimentada por un depósito de hidrógeno. El repostaje del hidrógeno se realiza en una estación se servicio de forma muy similar a como se realiza con otros combustibles. Un tiempo de repostaje de entre 3 y 5 minutos permite una autonomía cercana a los 700 km.
Países como Japón (con más de 100 estaciones de servicio de hidrógeno) o Alemania (con 50 estaciones de servicio) se encuentran a la vanguardia de la tecnología.
 Recarga del depósito de un Hyundai NEXO. Fuente: Hyundai
Recarga del depósito de un Hyundai NEXO. Fuente: HyundaiAunque en Europa se considera una tecnología prioritaria desde hace unos años, en España no existe aún ninguna estación de servicio de hidrógeno abierta al público de forma similar a como existen en otros países europeos. Desde la Asociación Española del Hidrógeno estamos trabajando para que esta situación cambie.
¿El futuro ya está aquí?
La tecnología ha llegado a su desarrollo comercial en esta última década. Pero los próximos años traerán las mejoras necesarias para que su expansión sea posible.
El precio actual de la producción de hidrógeno se sitúa en unos 8 €/kg y el depósito de los vehículos comerciales contiene unos 6 kg de hidrógeno. Esto supone que el precio de llenar un depósito es similar al de la gasolina o el diésel. Sin embargo, el coste del hidrógeno disminuirá aún más en los próximos años.
En los Juegos Olímpicos de 2020 en Tokyo, la organización ha apostado por un transporte eléctrico basado en el hidrógeno. Será un gran impulso para esta tecnología y un incentivo para que los costes sean aún más bajos.
También se esperan mejoras en la tecnología de la electrolisis del agua y en la aplicación práctica de otros procesos nuevos, como la fotólisis directa del agua con luz solar.
En busca de materiales alternativos
Las nuevas tecnologías suelen generar un problema de aumento de la demanda de materiales estratégicos. Éstos son materiales escasos o que se producen en pocos lugares en el mundo. En el caso de los coches eléctricos de baterías, el litio y el cobalto son los materiales estratégicos. Para los electrolizadores y las pilas de combustible, es el platino. Aun así, la cantidad necesaria de platino no es muy superior a la de metales nobles de los tubos de escape de los vehículos de combustión interna.
Los grupos de investigación que trabajamos en estas tecnologías tenemos en cuenta este problema. Estamos empezando a tener éxito en el desarrollo de materiales alternativos al platino que sean abundantes y sostenibles. Muy probablemente, los sistemas electroquímicos de los vehículos eléctricos del futuro serán muy diferentes a los actuales.
Una última consideración: la mayor parte del hidrógeno producido actualmente se obtiene a partir de combustibles fósiles. Esto no encaja en el esquema de sostenibilidad descrito en este artículo. Pero en los próximos años veremos cómo se usarán cada vez más las fuentes de energía renovables. El hidrógeno tendrá un papel fundamental en esta transición.![]()
Sobre los autores: María Retuerto Millán es investigadora contratada, y Miguel Antonio Peña y Sergio Rojas Muñoz investigadores científicos, en el Instituto de Catálisis y Petroleoquímica (ICP-CSIC)
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo El hidrógeno, clave para gestionar las redes eléctricas del futuro se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Generada en plataformas eólicas marinas, desembarcada como hidrógeno
- Un microrreactor para producir hidrógeno 100 veces más pequeño
- El modelo de Bohr explica las regularidades en el espectro del hidrógeno
Edgardo Mercado: matemáticas en “danza”
La matemática me brinda herramientas, es un camino que tengo más transitado y por lo tanto me sale más naturalmente diseñar espacial y corporalmente en estos términos.
Edgardo Mercado
Edgardo Mercado es coreógrafo, bailarín y docente. Antes de volcarse en el mundo de la danza, estudió ciencias físicas e impartió clases de matemáticas de nivel superior. Esta formación científica es la que, sin duda, le ha llevado a plantear sus coreografías con una especial inspiración matemática y científica: «En mis obras, siempre afloran, desde el diseño y el concepto, temas relacionados a la física o a las matemáticas».

En esta breve reseña destaco cuatro de sus coreografías en las que las matemáticas se incluyen de diferentes maneras.
Tierra de Mandelbrot
Edgardo MercadodescribeTierra de Mandelbrot (2004) de la siguiente manera: «En esta obra no hay narrativa, no hay causa-efecto; solo tres sujetos fractales transformando nuestro modo de mirar, percibir y valorar la realidad dentro del marco del paradigma complejo, regido por el orden-desorden, la recursividad y la autosimilitud».
Tierra de Mandelbrot alude al concepto de conjunto fractal en su contenido y a través del matemático que nombró y estudió este tipo de conjuntos: Benoît Mandelbrot. La obra comienza con dos luces que aparecen en medio de la oscuridad. Apenas se perciben trozos de los cuerpos de dos personas que se dejan ver, reptan, giran y desaparecen. Dos bailarinas, desnudas, se visten con ropas blancas ordenadas de manera geométrica sobre el suelo. Comienzan a proyectarse luces e imágenes: números, códigos de barras y recortes de luz estrían, fraccionan y recomponen los cuerpos de las protagonistas. Aparece un violinista que a veces toca unos acordes que se mezclan con el sonido electrónico grabado, a veces permanece inmóvil en el escenario. Los pequeños cuadrados proyectados sobre los cuerpos provocan un efecto multiplicativo al moverse: las ideas fractales de recursividad y autosimilitud se dejan ver de manera insistente.
Rotonda
Estrenada en 2009, Rotonda se presenta del siguiente modo: «Dos obsesiones que encierran el concepto de infinito se funden en una sola para dar origen a esta obra, la primera de Edgardo Mercado para el Ballet Contemporáneo: la agobiante perfección del círculo y la dificultad a la hora de representar el tiempo.
La imagen del “eterno retorno” habilita un camino tomando esta imagen como un avance infinito, recorriendo la circunferencia finita para volver al estado inicial.
Rotonda intenta reflejar en esta visión la angustia por el envolvente flujo del tiempo, que aniquila o redime. Rotonda es el espacio que habla del tiempo. La música fue compuesta especialmente para la pieza por Gabriel Gendín y tanto ésta como la escenografía de Ariel Vaccaro son de carácter minimalista. El diseño de luces de José Luis Fiorruccio completa la puesta superponiendo otro nivel en el orden geométrico propuesto por el diseño coreográfico».
En Rotonda ocho bailarines y siete bailarinas evolucionan, con diferentes ritmos y velocidades, sobre una rotonda, una figura formada por varias circunferencias concéntricas, donde aparecen además marcadas algunas diagonales. Estas curvas estampadas en el suelo aparecen o desaparecen, dependiendo de la iluminación aplicada en cada momento.
Los movimientos son a veces rápidos y enérgicos, a veces pausados y pronunciados, en ocasiones se observa pura danza, en otras complejas acrobacias. Rotonda analiza la circularidad en veinte minutos de danza.
Topologías para cuerpos infinitamente inconquistables
Estrenada en 2014, esta obra se presenta así: «¿Qué forma tiene el espacio propio hoy? ¿Cómo se extiende, deforma, hincha o repliega nuestra superficie surcada por diferentes flujos de información? Topologías para cuerpos infinitamente inconquistables es una instalación performativa que trae consigo una atención diferente de nuestras percepciones, para sumergirnos en una experiencia que transforma el espacio en un paisaje dinámico a través de los cuerpos del público y de veinte performers. Así nos permite cuestionarnos acerca de la conectividad, ubicuidad, y límites del cuerpo en movimiento hoy».
Realmente, es pura topología.
Apuntes
Augusto Zanela es arquitecto, un verdadero mago de la anamorfosis. Apunte es una de sus propuestas; fue transformada en una video-instalación en el Festival Théâvida 2012. Sin duda esta anamorfosis (que como Rotonda juega con círculos concéntricos) se ha enriquecido con las bellas coreografías de Edgardo Mercado.
Más información:
-
Marta Macho Stadler, Edgardo Mercado: acercando la danza y las matemáticas, DivulgaMAT, mayo 2008
-
Marta Macho Stadler, Rotonda, DivulgaMAT, julio 2011
-
Marta Macho Stadler, Topologías para cuerpos infinitamente inconquistables, DivulgaMAT, febrero 2017
-
Marta Macho Stadler, Anamorfosis danzadas, ZTFNews, abril 2012
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Edgardo Mercado: matemáticas en “danza” se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- FUN WITH MATHS, diversión con matemáticas
- Fractus, arte y matemáticas
- Más FUN WITH MATHS, diversión con matemáticas
Fusión nuclear
 Joint European Torus. Fuente: EUROfusion
Joint European Torus. Fuente: EUROfusionUna reacción de fusión nuclear consiste en la unión de dos núcleos ligeros para formar un núcleo más pesado. La reacción da como resultado energías de enlace por nucleón más altas cuando se combinan núcleos ligeros. Como consecuencia, se libera una gran cantidad de energía.
Las reacciones de fusión se han producido en el laboratorio mediante el bombardeo de dianas de materiales ligeros apropiados con, por ejemplo, deuterones de alta energía de un acelerador de partículas. En estas reacciones resultan núcleos que son más pesados que los núcleos de los «proyectiles» o de la diana; generalmente también se liberan partículas adicionales, así como energía. Algunos ejemplos típicos de estas reacciones de fusión, junto con la energía liberada en cada reacción, son los siguientes:
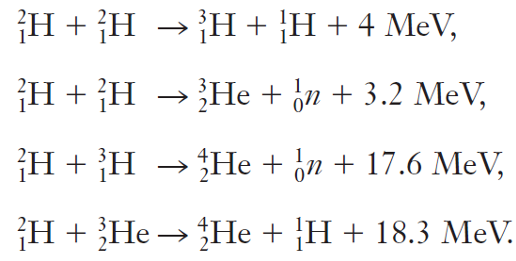
En la primera de las ecuaciones anteriores, el núcleo producto más pesado es un isótopo de hidrógeno, llamado tritio, con número de masa A=3. Se ha encontrado en pequeñas trazas en la naturaleza, es radiactivo, con un periodo de semidesintegración de aproximadamente 12 años, y se desintegra por emisión beta en helio-3, un isótopo de helio. Cuando se bombardea una diana de tritio con deuterones, se puede formar helio-4, como en la tercera ecuación anterior, liberando 17,6 MeV de energía. De esta energía, 14,1 MeV aparecen como energía cinética del neutrón y 3,5 MeV como energía cinética del núcleo producto.
Si bien la energía liberada en una sola fusión es menor que en una sola fisión, la energía liberada por unidad de masa es mucho mayor. Un simple cálculo lo ilustra: la masa de unos 50 átomos de helio es aproximadamente igual a la masa de un átomo de uranio; usando la tercera ecuación tenemos 50 x 17,6 MeV = 1040 MeV, en comparación con los 200 MeV de un fisión típica. De aquí que la fusión de tritio y deuterio ofrece la posibilidad de proporcionar grandes fuentes de energía, por ejemplo, en centrales eléctricas.
El deuterio se encuentra en el agua con una abundancia de aproximadamente una parte en siete mil átomos de hidrógeno y puede separarse del isótopo más ligero. Cuatro litros de agua contienen aproximadamente 0,13 g de deuterio. Si esta pequeña cantidad de deuterio pudiera reaccionar en condiciones apropiadas con tritio la producción de energía sería equivalente a la de aproximadamente 1.140 litros de gasolina. Se estima que la cantidad total de deuterio en los océanos es de aproximadamente 1017 kg, y su contenido energético sería de aproximadamente 1020 kW-año. Si el deuterio y el tritio pudieran usarse para producir energía, proporcionarían una enorme fuente de energía.
Por supuesto, existen algunos problemas no precisamente triviales que deben resolverse antes de que las reacciones de fusión puedan ser útiles como fuentes estables de energía. Los núcleos que reaccionan en los procesos de fusión están cargados positivamente y se repelen entre sí debido a la fuerza eléctrica repulsiva. Por lo tanto, es necesario hacer que los núcleos choquen con una velocidad relativa alta para vencer la fuerza repulsiva que tiende a mantenerlos separados. La interacción nuclear que mantiene unidos a los neutrones y protones en el núcleo es mucho más fuerte que la eléctrica, y a menudo se la llama fuerza nuclear fuerte, pero tiene un alcance muy corto. Su efecto se extiende solo unos 10-14 m, aproximadamente el tamaño de un núcleo. Por lo tanto, los núcleos que se pretende fusionar deben poder situarse a una distancia de ese orden de magnitud para que la fuerza nuclear atractiva supere a la repulsión eléctrica.
Los núcleos también deben estar confinados en una región del espacio donde puedan sufrir muchas colisiones sin que puedan escapar o ser absorbidos por las paredes que limitan la región, o perder energía por colisiones con demasiadas moléculas “más frías” (menos energéticas). Debe haber suficientes colisiones por unidad de tiempo para que la fusión pueda ocurrir a una velocidad que produzca más energía de la necesaria para provocar las colisiones. La combinación de estos requisitos significa que los núcleos deben estar contenidos a una temperatura del orden de 100 millones de grados.
A la temperatura requerida para la fusión, los átomos han perdido sus electrones, este estado de la materia en el que núcleos y los electrones están separados se llama plasma. Un plasma es un gas ionizado en el que las partículas cargadas positiva y negativamente se mueven libremente. Ninguna pared hecha de ningún material conocido puede contener un plasma caliente a 108K (¡la pared se vaporizaría instantáneamente! [1]). Pero la teoría nos dice que las partículas cargadas, y eso es lo que es un plasma, pueden contenerses en un campo magnético diseñado apropiadamente. El primer problema a resolver, por tanto, es contener el plasma de núcleos de deuterio y tritio en un campo magnético, mientras se aceleran los núcleos mediante un campo eléctrico hasta la energía cinética (o temperatura) requerida. El comportamiento de las partículas cargadas en un plasma es, digamos, complicado; hay muchos tipos de inestabilidades que hacen que el plasma sea difícil de contener adecuadamente y durante el tiempo suficiente.
Con todo hay proyectos de fusión muy avanzados. En diciembre de 2020 se iniciaron las pruebas con deuterio y tritio en el Joint European Torus, que es una réplica 1:10 de lo que será el primer reactor de fusión del mundo, el ITER.
Nota:
[1] Para los seguidores de Star Trek: eso es ficción. Por ejemplo, los reactores de fusión de Deep Space 9 usan deuterio como partículas de bombardeo, sí, pero las paredes están hechas de carbono, como que no. No parece ingenierilmente muy trabajado.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Fusión nuclear se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Energía de enlace nuclear y estabilidad
- Control de la reacción nuclear en cadena (2): moderadores
- La energía de enlace nuclear
La improbable vida marciana
Manuel Peinado Lorca
 El astromóvil de la misión Perseverance. Fuente:NASA Science
El astromóvil de la misión Perseverance. Fuente:NASA Science
Cada treinta años, aproximadamente, Marte y la Tierra coinciden en aquellos puntos de sus órbitas respectivas en que estas se acercan más una a la otra. Cuando esto ocurre, como sucedió en 1877, Marte se halla a tan solo unos 56 millones de kilómetros de la Tierra, una magnífica oportunidad para que los astrónomos lo estudien minuciosamente. Es lo que se dispuso a hacer aquel año el italiano Giovanni Schiaparelli, aunque su exceso de celo y el afán de pasar a la posteridad hicieron que se le fuera las manos.
Schiaparelli creyó observar unas líneas finas que corrían desde los polos al ecuador marciano, a las que bautizó como “canali”, porque lo que el astrónomo italiano quería señalar era la apariencia de un sistema irrigador de los canali, que funcionarían a modo de acueductos o acequias extraterrestres.
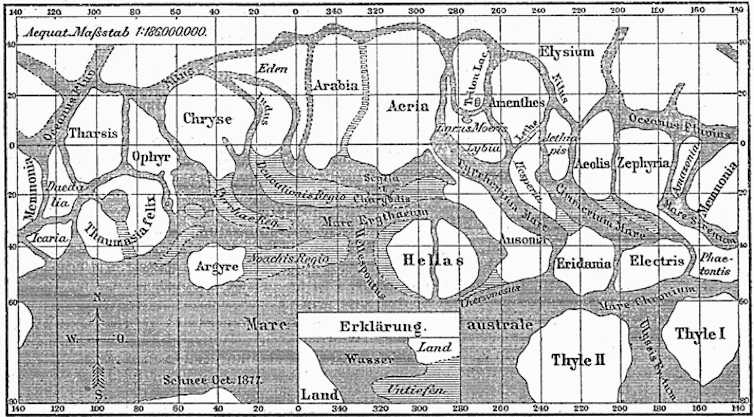 El mapa de Marte publicado por Giovanni Schiaparelli en 1888. Fuente: Meyers Konversations-Lexikon
El mapa de Marte publicado por Giovanni Schiaparelli en 1888. Fuente: Meyers Konversations-LexikonQue se relacionase a los canales de Marte con obras civilizadas fue una predecible consecuencia del momento tecnológico que se vivía, porque por aquel entonces se estaban abriendo gigantescos canales para la navegación en todo el mundo, entre otros los de Suez y Panamá. Su magnitud ciclópea tenía pasmado al personal.
El asunto de los canales despertó la calenturienta imaginación de mucha gente, entre otros del millonario norteamericano Percival Lowell, tan entusiasmado con la idea de una civilización marciana que en 1894 construyó, a sus expensas, su propio, moderno y costosísimo observatorio en Flagstaff, Arizona. Allí sigue hoy, funcionando perfectamente.
 Telescopio Clark del Observatorio Lowell, en Mars Hill, Flagstaff, Arizona, Estados Unidos. Fuente:
Telescopio Clark del Observatorio Lowell, en Mars Hill, Flagstaff, Arizona, Estados Unidos. Fuente:Wikimedia Commons
Dedicado en cuerpo y alma a la astronomía, Lowell gastó gran parte de su tiempo y buena parte de su fortuna persiguiendo la existencia de civilizaciones inteligentes en Marte, una obsesión muy embarazosa para su aristocrática familia bostoniana.
Después de cuatro años de inútiles observaciones astronómicas, la literatura le envió un balón de oxígeno: en 1898 H. G. Wells publicó su memorable novela La guerra de los mundos, inmediatamente convertida en un superventas literario. Cuarenta años después, el 30 de octubre de 1938, Orson Welles lo convertiría en la emisión radiofónica más famosa de todos los tiempos.
Una sabia civilización marciana
Como le sucedió a Alonso Quijano con los libros de caballerías, lecturas como esa y otras relacionadas habían convencido a Lowell no solo de que había vida en Marte, sino que, además, era vida inteligente. Una sabia y antigua civilización había construido esos canales para drenar agua de los helados casquetes polares y abastecer así a las sedientas y desesperadas ciudades edificadas en la zona ecuatorial de un planeta que se estaba desertizando.
La prensa vino en su ayuda. El 27 de agosto de 1911 la sección “Maravillas del cielo” del prestigioso New York Times abrió con un gran titular:
«Los marcianos han construido dos inmensos canales en dos años. Estos vastos trabajos de ingeniería han sido llevados a cabo en un tiempo increíblemente corto por nuestros vecinos planetarios».
La creativa información continuaba:
«[Los canales] son tan grandes que, a su lado, el Cañón del Colorado sería una nimiedad».
Así llegó el gran momento mediático de Lowell y la popularidad de sus tres libros sobre Marte que hasta entonces habían pasado inadvertidos para el gran público.
 Portada del 27 de agosto de 1911 de la sección Maravillas del cielo del New York Times.
Portada del 27 de agosto de 1911 de la sección Maravillas del cielo del New York Times.La ciencia arruina la fiesta
Tras los avances de la Era Espacial en la segunda mitad del siglo XX, y después de que las investigaciones de Kuiper demostraran que la atmósfera de Marte era una mortífera mezcla gaseosa, cualquier posibilidad de vida que fuera más allá de las formas microbianas más simples quedó desvanecida.
A la pregunta de si es posible que ahora mismo haya algún tipo de vida en Marte, la Nasa afirmó hace ya tiempo que no: en 1976, la agencia espacial puso las naves robot conocidas como Viking en el planeta rojo, y tras estudiar durante cuatro y seis años, respectivamente, el suelo marciano en busca de bacterias, los resultados fueron decepcionantes.
El mundo más parecido a la Tierra del que tenemos pruebas no albergaba rastros orgánicos.
Más de treinta años después de las Viking, la sonda Phoenix se posó en las gélidas superficies del norte marciano el 26 de mayo de 2008. Las impresionantes imágenes del amartizaje, televisadas en directo a todo el mundo, quedaron mediáticamente tapadas por la casi simultánea aparición del número de 30 de mayo de la revista Science.
En poco más de dos páginas de esa prestigiosa revista científica, se descartaba la posibilidad de que hubiera existido vida marciana: el líquido imprescindible para sostener la vida, el agua, sobre cuya existencia se habrían centrado las expectativas de vida en Marte hace cientos de millones de años, era una salmuera hipersalina, un caldo absolutamente incapaz de albergar el origen de formas de vida similares a las terrestres.
El exceso de sal es mortal para la vida microbiana, algo que saben los hombres desde muy antiguo: el mismo efecto que conservaba el pescado antes de la invención de los modernos congeladores o que cura los deliciosos jamones conservando los perniles en salmuera, provocando con ello su deshidratación y evitando de paso las infecciones microbianas, habría impedido también que surgieran microbios precursores de formas de vida más evolucionadas y complejas en el planeta rojo. Al menos, tal y como las concebimos por nuestra experiencia terrícola.
En diciembre de 2016, la NASA publicó las imágenes y la información recabada por el astromóvil de exploración marciana transportado por Curiosity, la misión que aterrizó en el cráter Gale el 6 de agosto de 2012. Por primera vez, en la ladera del cráter se encontró boro, un elemento que puede ser un remoto indicio de que en Marte hubo agua con las condiciones necesarias para albergar vida.
Animados por las novedades y para que no perdieran la esperanza los nostálgicos, un estudio publicado en 2019 afirmaba haber hallado indicios de material orgánico en un meteorito marciano encontrado a fines de los años setenta en las colinas Allan, en la Antártida. ¿Indicios de vida marciana en un meteorito? Los antecedentes no ayudaban.
En diciembre de 1984 una expedición del Smithsonian Museum había descubierto en el mismo lugar otro trozo del mismo meteorito. Aunque durante años se especuló con que algunas de las huellas grabadas en ese trozo de diogenita se debían a la acción de seres vivos de origen marciano, un estudio publicado en 2014 descartó que las huellas correspondieran a actividades orgánicas y, además, que la muestra se había contaminado en la Tierra por el hielo antártico en el que permaneció atrapada durante milenios.
 El astromóvil de la Perseverance aterriza en la superficie del cráter Jezero en Marte. Fuente: NASA-Caltech
El astromóvil de la Perseverance aterriza en la superficie del cráter Jezero en Marte. Fuente: NASA-CaltechLa Nasa persevera en su búsqueda de vida
El pasado 18 de febrero, después de un viaje de casi siete meses y 470 millones de km a través del espacio, se posó en Marte el Perseverance, la sonda robótica de la Misión Mars 2020, cuyo primer objetivo es buscar rastros de vida.
Nadie espera encontrar microorganismos vivos. Sería un acontecimiento de proporciones históricas. Tardaremos años en saber los resultados. Parte de las muestras que recoja el Perseverance tendrán que analizarse en la Tierra. Eso ocurrirá, como pronto, hacia 2028 o 2029, cuando otra nave las recoja y regrese con ellas.
El principio de que anuncios extraordinarios requieren pruebas extraordinarias es más válido que nunca. Pero con pruebas o sin ellas, los lectores de Ray Bradbury esperamos ansiosamente poder leer una nueva y definitiva entrega de las descripciones poéticas y melancólicas de Marte y los marcianos que encierran sus Crónicas Marcianas.![]()
Sobre el autor: Manuel Peinado Lorca es catedrático de universidad en el Departamento de Ciencias de la Vida e Investigador del Instituto Franklin de Estudios Norteamericanos, Universidad de Alcalá
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo La improbable vida marciana se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Marte y el enigma de la vida: el gran desembarco robótico de 2021
- Las cartas de Darwin: La vida a bordo de un balandro ataúd
- La evolución nos dice que es probable que seamos la única vida inteligente del universo
Más vale prevenir las demencias, porque no se pueden curar
 Foto: Cristian Newman / Unsplash
Foto: Cristian Newman / UnsplashLa revista The Lancet, publicó en 2017 un informe titulado Dementia prevention, intervention and care (“Prevención, intervención y cuidado de la demencia”). Identificaba los siguientes nueve factores de riesgo para las demencias: escasa educación, pérdida auditiva, consumo de tabaco, obesidad, depresión, inactividad física, diabetes y escasas relaciones sociales.
En el informe, con el mismo título, publicado el año pasado se han añadido tres factores de riesgo adicionales: consumo de alcohol excesivo, lesiones encefálicas traumáticas y contaminación atmosférica. Considerados en conjunto los doce factores de riesgo, dan cuenta de aproximadamente el 40% de las demencias diagnosticadas en el mundo, demencias que, en teoría, podrían prevenirse o retrasarse. Según los autores hay un gran potencial para la prevención, sobre todo en los países de medio y bajo nivel económico, que es en los que más demencias hay.
El informe introduce una dimensión temporal muy interesante para dar cuenta del modo secuencial en el que actúan los factores de riesgo a lo largo de la vida. Y es un aspecto importante porque, dependiendo de la posición de cada factor en esa secuencia, las posibles medidas preventivas han de tomarse en diferentes etapas de la vida.
Contra el déficit educativo, factor al que se atribuye un 7% de las demencias, ha de actuarse en los primeros años, porque afecta a la reserva cognitiva de las personas, que es, por así decir, la inversión en capacidad cognitiva y conocimiento del que pueden hacer uso. Cuanto mayor es esa reserva, más tiempo se puede mantener una persona a salvo de los efectos de las demencias.
En edades intermedias adquieren importancia los factores de riesgo que están en la génesis de patologías neuronales que pueden desembocar en demencia más adelante. Por esa razón debe recomendarse el uso de audífonos para que quienes lo necesiten puedan mantener niveles aceptables de audición; al déficit auditivo se le atribuye un riesgo del 8%. También deben tomarse medidas que minimicen las lesiones encefálicas (3% del riesgo), que ayuden a mantener la presión arterial por debajo de los valores recomendados (2%), que reduzcan el consumo de alcohol (1%) y que prevengan o combatan la obesidad (1%).
Otros factores, aunque de origen anterior, inciden en mayor medida en las etapas últimas de la vida. El tabaquismo (5% del riesgo) no se adquiere a edades avanzadas, pero es entonces cuando más daño causa, por lo que es también cuando se debe evitar su incidencia; a estos efectos, nunca es tarde para dejar de fumar. El 2% de las demencias se asocia a la inactividad física, factor que también suele tener origen en etapas anteriores de la vida, aunque se acentúe con la edad. Por ello, es recomendable promover el ejercicio físico porque tiene efectos protectores, debidos, posiblemente, a que previene la obesidad, la diabetes (1% del riesgo) y la hipertensión. También la contaminación atmosférica (2%) ejerce sus efectos negativos durante etapas anteriores, pero es durante los últimos años cuando son más susceptibles de provocar demencias.
La depresión, vinculada al 4% de las demencias, es un factor problemático, porque no está clara la dirección de la relación causal; en todo caso, dado que sus posibles consecuencias negativas se producen durante la vejez, conviene ser tratada, incluso aunque tenga origen en una etapa anterior. El aislamiento social también es un factor característico de edades avanzadas y a él se atribuye otro 4% del riesgo.
Decimos que más vale prevenir que curar porque no hay mejor remedio que la prevención. Pero dado que ni siquiera pueden ser curadas, para las demencias no hay alternativa a la prevención.
Fuente: Gill Livingston et al (2020): “Dementia prevention, intervention, and care: 2020 report of the Lancet Commission”. The Lancet Commissions| Volume 396, ISSUE 10248, P413-446.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Más vale prevenir las demencias, porque no se pueden curar se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Prevenir y tratar la enfermedad de Alzheimer: Una visión moderna
- Estimada OCU: recuerda que NO se pueden utilizar las cremas solares del año pasado
- No todo vale al servicio de la ciencia
Blanca Martínez García – Naukas Bilbao 2019: Godzilla, king of the geologists
 Shin Godzilla. Fuente: Noger Chen / Wikimedia Commons
Shin Godzilla. Fuente: Noger Chen / Wikimedia CommonsEs muy humano eso de inventarse criaturas fantásticas para explicar cosas reales pero extraordinarias como terremotos o tsunamis. Blanca Martínez nos trae en esta charla una buena colección de cosas que no son dinosaurios radioactivos pero que sí salen en películas y que generan fenómenos naturales perfectamente explicables por la geología.
Blanca Martínez García es licenciada y doctora en Geología por la Universidad del País Vasco, siendo especialista en reconstrucciones paleoambientales, paleoecología y paleoceanografía (varios resultados de sus investigaciones han sido recogidos en el Cuaderno de Cultura Científica: 1, 2) . Actualmente es miembro activo de la Sociedad de Ciencias Aranzadi, vocal de la Sociedad Geológica de España y una de las coordinadoras de la Comisión Mujeres y Geología de la Sociedad Geológica de España.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Blanca Martínez García – Naukas Bilbao 2019: Godzilla, king of the geologists se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Zientziateka: Blanca Mª Martínez García – La geología fantástica de Verne, Poe y H.P. Lovecraft
- Blanca Martínez: “Los geólogos le tenemos mucho cariño a Godzilla”
- Alfredo García – Naukas Bilbao 2019: Derribando mitos sobre la energía nuclear
Gerrymandering: cuando los políticos eligen a sus votantes
Annick Laruelle
 Campaña contra el gerrymandering en el estado Michigan (EE.UU.) en 2018. Fuente: Shutterstock / Susan Montgomery
Campaña contra el gerrymandering en el estado Michigan (EE.UU.) en 2018. Fuente: Shutterstock / Susan Montgomery
Para muchos estados, la representación en el congreso tiene que ser geográfica e igualitaria. El objetivo geográfico se obtiene dividiendo el país en circunscripciones electorales. Tradicionalmente hay dos formas de conseguir el objetivo igualitario. En los sistemas proporcionales cada circunscripción tiene un número de representantes que depende de su población. En los sistemas mayoritarios las circunscripciones tienen poblaciones parecidas y cada una de ellas tiene un único representante.
Cada diez años, se realiza el censo de la población en EEUU. El último fue en 2020. Éste va a determinar el número de escaños que tendrá cada estado en la Cámara de los Representantes hasta 2030. Según las primeras estimaciones unos 17 estados podrían ver su número de escaños afectado, lo que modificará el reparto de poder entre los estados.
Los datos del censo sirven también para garantizar que todas las circunscripciones electorales de un estado tengan poblaciones parecidas. En 2021 las fronteras de las circunscripciones se modificarán para satisfacer este objetivo. El diseño no es neutral, puede determinar el resultado electoral. Sin embargo, el dibujo de las fronteras está generalmente en manos del poder legislativo.
El gerrymandering dibuja las fronteras para favorecer a un grupo de la población o a un partido. El origen del nombre se remonta a 1812 cuando una circunscripción que diseñó el gobernador E. Gerry se caricaturizó como una salamandra (“salamander”).
 Fuente: National Museum of American History / Smithsonian
Fuente: National Museum of American History / SmithsonianLos dos lemas del gerrymandering son “dispersión y concentración” (“CRACK and PACK”). Una técnica consiste en dispersar los votos de la oposición para dejarla en minoría en el mayor número de circunscripciones posible. Otra técnica consiste en concentrar los votos de la oposición en un pequeño número de circunscripciones donde la oposición gana con una amplia mayoría. Si las técnicas son muy antiguas, los métodos informáticos son cada vez más sofisticados y la información sobre los electores más extensa.
En 2010 un comité republicano creó el proyecto REDMAP para ayudar a redibujar las circunscripciones después del censo de 2010. Thomas Hofeller, uno los estrategas del proyecto, afirmó en una conferencia que este proceso era una elección a la inversa, en el sentido que permitía a los políticos elegir a sus votantes.
La efectividad del proyecto se puede ilustrar en el estado de Carolina del Norte.
Las 13 circunscripciones dibujadas después del censo de 2010 son muy poco compactas, en particular las con números 1, 4 y 12. En estas tres circunscripciones los demócratas ganaron las elecciones de 2012 y 2014 con porcentajes de votos superior al 70%. Los republicanos ganaron las elecciones en todos las otras circunscripciones (salvo una en 2012) pero con pequeños márgenes.
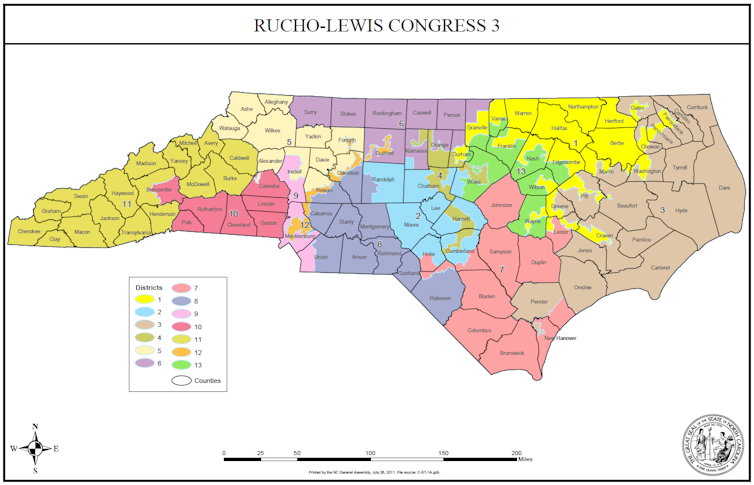 Mapa electoral de Carolina del Norte (elecciones 2012 y 2014). Fuente: North Carolina General Assembly
Mapa electoral de Carolina del Norte (elecciones 2012 y 2014). Fuente: North Carolina General AssemblyAl nivel global del estado, el partido demócrata consiguió menos de 31% de los escaños (4 de 13) en 2012, aunque recibió casi 51% de los votos. En 2014, obtuvo 44% de los votos, que se tradujeron en 23% de los escaños (3 de 13). En 2016, el tribunal supremo federal declaró el mapa anticonstitucional por gerrymandering de tipo racial. El poder legislativo tuvo que modificarlo.
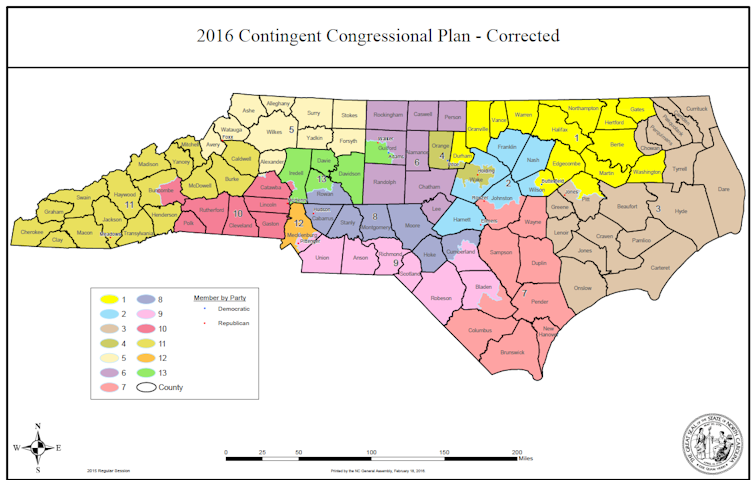 Mapa electoral de Carolina del Norte (elecciones 2016 y 2018). Fuente: North Carolina General Assembly
Mapa electoral de Carolina del Norte (elecciones 2016 y 2018). Fuente: North Carolina General AssemblyEn 2016 y 2018 el partido demócrata obtuvo de nuevo 23% de los escaños a pesar de haber obtenido en ambas elecciones más de 46% de los votos. En 2019 un tribunal estatal reconoció el carácter partidista del mapa electoral modificado. Una vez más el poder legislativo tuvo que redibujar las 13 circunscripciones.
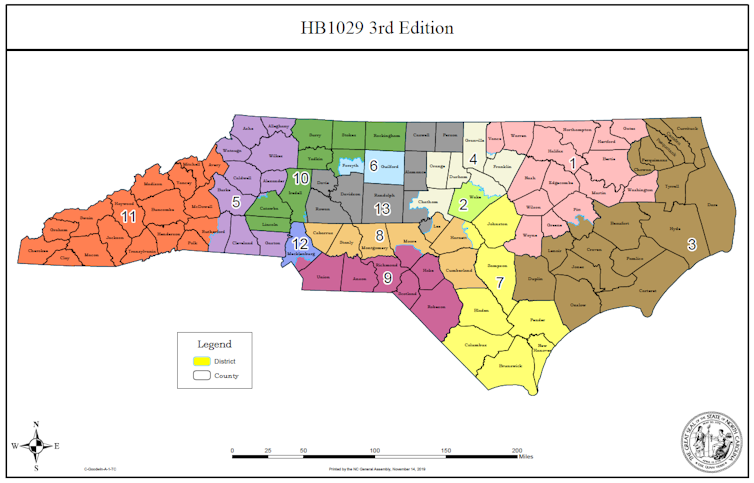 Mapa electoral de Carolina del Norte (eleccion de 2020). Fuente: North Carolina General Assembly
Mapa electoral de Carolina del Norte (eleccion de 2020). Fuente: North Carolina General AssemblyEn 2020 la diferencia entre porcentajes de votos y porcentaje de escaños se redujo: los demócratas obtuvieron casi 50% de los votos y 38% de los escaños (5 de 13). El censo realizado en 2020 modificará de nuevo el mapa, en principio con una circunscripción adicional.
Los republicanos no son los únicos que practican el gerrymandering. En 2019 se intentó conseguir la inconstitucionalidad del mapa electoral de Maryland (dibujado por los demócratas). Hasta la fecha los tribunales federales se han negado a condenar el gerrymandering de tipo partidista.
Demostrar la existencia de gerrymandering no es siempre una tarea fácil. No es suficiente constatar que el porcentaje de votos no coincide con el porcentaje de escaños. A veces es la geografía la que genera diferencias entre votos y escaños.
En un artículo reciente investigadores de la universidad de Duke analizaron los mapas electorales de Carolina del Norte. Dibujaron de manera aleatoria más de 66 000 mapas alternativos. Calcularon las distribuciones de escaños que se habrían obtenido con esos mapas. Las distribuciones de escaños obtenidas en las elecciones de 2012 y 2014 ocurren con una frecuencia inferior a 1% con los mapas alternativos, es decir son muy poco probables.
Además mostraron que pequeños cambios en las fronteras de las circunscripciones demócratas habrían modificado de manera sustancial los resultados. Concluyeron la existencia de gerrymandering. Sin embargo, admitieron que la geografía del estado es más favorable a los republicanos que a los demócratas.
Los objetivos de representación geográfica y representación igualitaria son difícilmente compatibles. Quizás es el momento de replantearse la importancia de la representación geográfica en comparación con el objetivo de tratamiento igual para todos los votantes.![]()
Sobre la autora: Annick Laruelle es profesora IKERBASQUE en el Departamento de Análisis Económico de la Universidad del País Vasco / Euskal Herriko Unibertsitatea
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Gerrymandering: cuando los políticos eligen a sus votantes se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Lo que la búsqueda de inteligencia extraterrestre nos enseña para entender la pandemia
- Políticos y científicos
- Cuando sí es lupus
Los antiguos radicales libres ahora se llaman ROS y no son tan malos
Alfonso Blázquez Castro
 Distintos niveles de ROS (color rojo) en células humanas en cultivo. Fuente: Alfonso Blázquez Castro
Distintos niveles de ROS (color rojo) en células humanas en cultivo. Fuente: Alfonso Blázquez Castro
La virtud fue definida como “el punto medio entre dos vicios” hace más de dos mil años, por Aristóteles. Siglos después, Paracelso establecía que no existían venenos, sino concentraciones dañinas de todas las sustancias.
Estas dos reflexiones son perfectamente aplicables al papel del oxígeno en la biología celular, que ha pasado por distintas etapas en relación a su “bondad” o “maldad”. En un primer momento se observó que el oxígeno es imprescindible para sostener la vida tal y como la conocemos. Sin embargo, en la primera mitad del siglo XX se confirmó que el oxígeno daba lugar a una serie de alteraciones dañinas en las células a largo plazo.
Nacía así el concepto de radicales libres o “teoría de los radicales”, que achacaba a estos compuestos derivados del uso oxígeno el origen de muchos procesos negativos para la vida, como el envejecimiento, el cáncer y otras muchas enfermedades.
En los inicios del siglo XXI se ha empezado a entender mejor el papel de estos “radicales”. Los científicos que nos dedicamos a su estudio estamos encontrando “la virtud entre dos vicios” en relación con ellos. Aunque ahora los llamamos, más correctamente, especies reactivas de oxígeno (ROS, por sus siglas en inglés).
¿Qué son las Especies Reactivas de Oxígeno?
Son un conjunto de compuestos químicos que contienen oxígeno en su fórmula y una mayor o menor reactividad química y capacidad de oxidar. Las más conocidas son el superóxido (O2–), el peróxido de hidrógeno (H2O2, a menudo llamada “agua oxigenada”) y el radical hidroxilo (· OH).
Desde hace muchas décadas se sabe que estas ROS son el resultado inevitable de la respiración en las células. Podría decirse que son como el “humo” del tubo de escape del “motor celular”. A lo largo de los años esta contaminación provoca un daño en nuestras células. Las células pueden anular el daño de las ROS usando compuestos que llamamos reductores, que permiten mantener un equilibrio entre el daño y la salud celular.
Pero lo realmente interesante es que ahora sabemos que las células también producen ROS de manera intencionada. En este caso funcionan como “mensajeros” que llevan mensajes de una parte a otra de la célula, o entre distintas células del cuerpo. Por ejemplo, dependiendo del momento del ciclo celular, más cerca o lejos de dividirse, las células muestran niveles internos de ROS distintos.
Históricamente, la fuente principal de ROS han sido las mitocondrias. Estas estructuras producen la mayor parte de la energía de la célula. Actualmente siguen siendo una fuente muy importante de ROS, pero el giro interesante es que sabemos que muchas de esas ROS se producen a propósito en las mitocondrias y no como resultado de la “mala combustión” que mencionábamos antes.
En paralelo, se ha probado que existen mecanismos alternativos, también bajo un fuerte control celular, para producir ROS cuando son necesarias en otras partes de la célula, como la membrana, el retículo endoplasmático o el medio exterior. Estos mecanismos se basan en proteínas cuya función es la producción de ROS.
Al mismo tiempo, las células producen en todo momento esos compuestos reductores que controlan la acción de las ROS. De esta manera, son capaces de regular de manera muy precisa el dónde y el cuánto de los mensajes que usan ROS como señales.
El mecanismo de señalización de las ROS
Al final, lo que parece indiscutible es que los niveles de ROS no deben ser ni muy altos, ya que provocan daños y “oxidan” la célula, ni muy bajos, ya que no podrían actuar como mensajeros.
En el siguiente esquema se plasma de manera sencilla esta idea. Existe un rango de niveles de ROS que son óptimos para su función celular. Demasiado altos o demasiado bajos, y se echa a perder su utilidad. Existe un punto intermedio adecuado entre dos extremos indeseables.
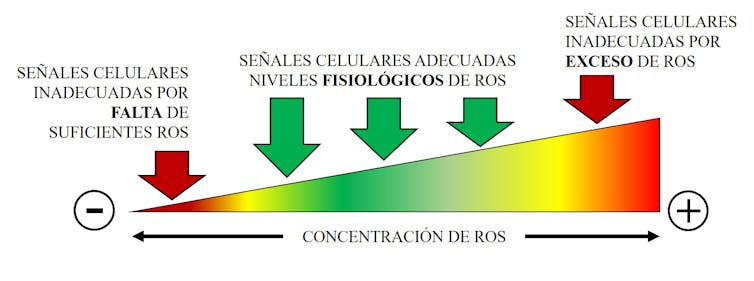 Los niveles de ROS no deben ser ni muy altos, ya que provocan daños a la célula, ni muy bajos, ya que no podrían actuar como mensajeros. Fuente: Alfonso Blázquez Castro
Los niveles de ROS no deben ser ni muy altos, ya que provocan daños a la célula, ni muy bajos, ya que no podrían actuar como mensajeros. Fuente: Alfonso Blázquez CastroPero, ¿cómo pueden las ROS actuar de mensajeros dada su reactividad? La respuesta se encuentra en las proteínas, las máquinas microscópicas que llevan a cabo el metabolismo celular. Algunas proteínas tienen partes que son especialmente sensibles a la oxidación de las ROS. En las concentraciones adecuadas, estas zonas se oxidan y cambian la estructura de la proteína.
Igual que ocurre con un interruptor, la proteína se puede “encender” o “apagar”, dependiendo de su función. Tras un cierto tiempo, la zona oxidada de la proteína se vuelve a reducir y la proteína vuelve a su estado inicial.
Esta es la base del control en las funciones celulares por parte de las ROS: niveles adecuados de ROS y de compuestos reductores permiten que las proteínas se “enciendan” o “apaguen” de manera correcta. Ahora bien, si hay un exceso de ROS, las proteínas se oxidan en demasiados sitios y estos cambios son permanentes: ya no se puede volver al estado inicial y la proteína queda dañada e inservible. Esta es la razón por la cual demasiadas ROS alteran de manera tóxica el metabolismo celular y terminan provocando multitud de trastornos y enfermedades.
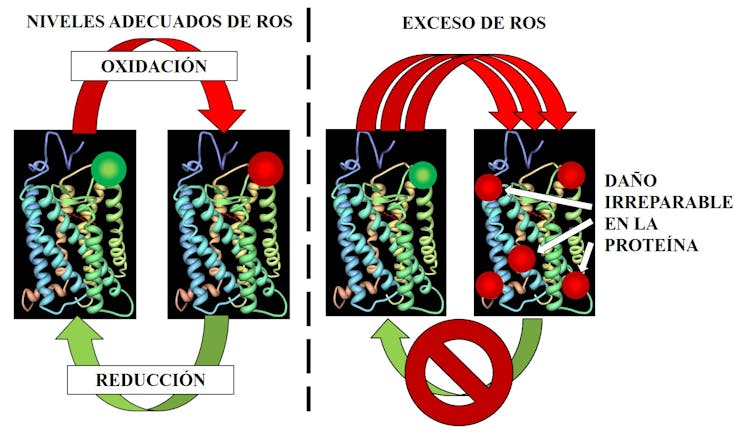 A la izquierda, representación de cómo niveles adecuados de ROS y reductores permiten que las proteínas se enciendan o apaguen de manera correcta. A la derecha, lo que sucede cuando hay exceso de ROS: cambios permanentes que dañan las proteínas de manera irreversible. Fuente: Alfonso Blázquez Castro
A la izquierda, representación de cómo niveles adecuados de ROS y reductores permiten que las proteínas se enciendan o apaguen de manera correcta. A la derecha, lo que sucede cuando hay exceso de ROS: cambios permanentes que dañan las proteínas de manera irreversible. Fuente: Alfonso Blázquez CastroCon este mejor conocimiento de la acción de las ROS se están consiguiendo importantes progresos en el tratamiento de diversas enfermedades. Sabemos, por ejemplo, que se producen demasiadas ROS en el corazón durante los infartos de miocardio, o en el cerebro tras un ictus.
Una forma muy prometedora de abordar estos problemas es disminuir de manera eficaz la producción de ROS en el paciente con nuevos fármacos. Esta es una línea de investigación muy importante en la actualidad.
Y, así, buscando el punto medio entre dos extremos, encontramos no sólo la virtud sino también la salud.![]()
Sobre el autor: Alfonso Blázquez Castro es profesor ayudante doctor en genética en la Universidad Autónoma de Madrid
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Los antiguos radicales libres ahora se llaman ROS y no son tan malos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La ciencia de la cosmética antioxidante contra los radicales libres
- Radicales libres, el libro
- Cuando las algas rojas no pueden gestionar los radicales libres
6.174, un número seductor
Mientras escribía mi último libro Números primos, amigos y demás familia (Catarata, 2021), que estará en las librerías en abril, he descubierto números con propiedades muy curiosas e interesantes, entre ellos, la constante de Kaprekar.
 Número 6.174 realizado con las Tarjetas de Cumpleaños Art Nouveau de la diseñadora estadounidense Laura Beckman. Imágenes de la página de Laura Beckman
Número 6.174 realizado con las Tarjetas de Cumpleaños Art Nouveau de la diseñadora estadounidense Laura Beckman. Imágenes de la página de Laura Beckman
El número 6.174 es aparentemente un número de lo más normal, un número de esos que no llamaría nuestra atención, sin embargo, posee una propiedad matemática que parece pura magia. En 1949 el matemático recreativo indio Dattatreya Ramchandra Kaprekar (1905–1986) publicó el artículo Another Solitaire Game, en la revista Scripta Mathematica, en el que describía las curiosas propiedades que había descubierto sobre el 6.174, aunque fue la publicación en la columna Mathematical Games de Martin Gardner en la revista Scientific American, lo que le daría un mayor reconocimiento.
Consideremos un número de cuatro dígitos cualquiera, tal que estos no sean todos iguales (por ejemplo, 6.282), con sus dígitos escribimos los números mayor y menor que se pueden representar, es decir, 8.622 y 2.268, y los restamos
8.622 – 2.268 = 6.354.
Ahora repetimos este proceso,
6.543 – 3.456 = 3.087.
Seguimos con el mismo proceso,
8.730 – 0378 = 8.352.
Este parece un proceso artificial en el que se irán generando números sin parar. Sin embargo, en el siguiente paso se alcanza el número 6.174, ya que
8.532 – 2.358 = 6.174.
Y nuestro número 6.174 es un número particular respecto a este proceso ya que este se estaciona y siempre queda 6.174.
7.641 – 1.467 = 6.174.
Al proceso descrito se le llama algoritmo de Kaprekar y lo sorprendente es que siempre –salvo para números con los cuatro dígitos iguales– se llega a la denominada constante de Kaprekar, el número 6.174. Veamos otro ejemplo. Si empezamos con el número de cuatro dígitos –recordemos que no todos iguales– 3.631, la sucesión de números que nos da el algoritmo de Kaprekar es
6.331 – 1.336 = 4.995;
9.954 – 4.599 = 5.355;
5.553 – 3.555 = 1.998;
9.981 – 1.899 = 8.082;
8.820 – 0288 = 8.532;
8.532 – 2.358 = 6.174;
donde se estaciona el proceso, ya que hemos llegado a la constante de Kaprekar. Mientras que en el primer ejemplo habíamos necesitado de cuatro pasos, en este han sido necesarios seis pasos.
Si todos los dígitos del número son iguales, como 7.777, entonces el algoritmo de Kaprekar se estaciona en el primer paso, llegando a cero, ya que el mayor y el menor número que se puede formar con esos dígitos es el mismo 7.777, y entonces 7.777 – 7.777 = 0.
 Número 6.174 realizado con la tipografía numérica diseñada por Muokkaa Studio (que es el diseñador madrileño Alejandro López Becerro). Imágenes de la página de Moukkaa en Behance
Número 6.174 realizado con la tipografía numérica diseñada por Muokkaa Studio (que es el diseñador madrileño Alejandro López Becerro). Imágenes de la página de Moukkaa en Behance
Por lo anteriormente visto, sabemos que el número 6.174 es un punto fijo del algoritmo de Kaprekar, es decir, al aplicarlo a él mismo, nos vuelve a dar ese número: 7.641 – 1.467 = 6.174. Una de las cuestiones que nos podríamos haber planteado inicialmente es el cálculo de todos los puntos fijos que existen para ese algoritmo. Veamos, a continuación, una idea de la prueba de que realmente la constante de Kaprekar es el único punto fijo posible.
Sea un número de cuatro dígitos, no todos ellos iguales, entonces podemos expresar al mayor número que se puede representar con sus cuatro dígitos como abcd, donde 0 ≤ a ≤ b ≤ c ≤ d ≤ 9, y al menor como dcba, luego la resta de ambos será un número ABCD tal que
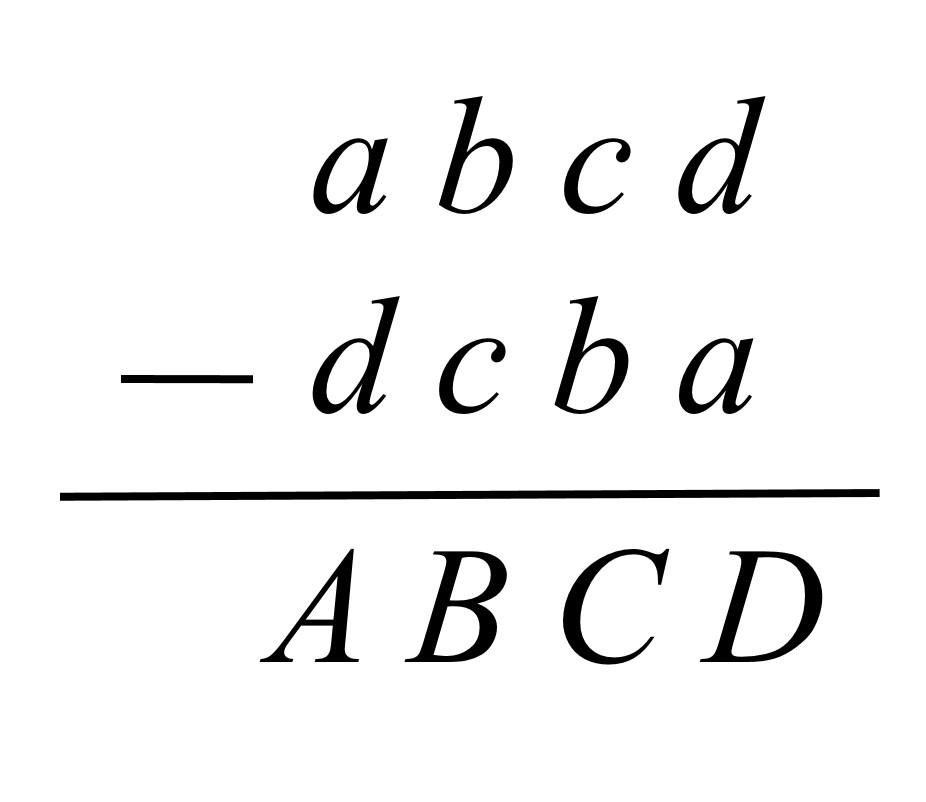
de donde se obtienen las siguientes relaciones:
D = 10 + d − a (a > d)
C = 10 + c − 1 − b = 9 + c − b (b > c − 1)
B = b − 1 − c (b > c)
A = a − d.
Como buscamos un punto fijo, sabemos que {A, B, C, D} = {a, b, c, d}, salvo el orden. Como existen 4! = 24 permutaciones (ordenes) posibles de {a, b, c, d}, si probamos todas ellas veremos que el anterior sistema con cuatro ecuaciones y cuatro incógnitas (a, b, c, d) tiene solución única solo cuando A = b, B = d, C = a, D = c. Además, en ese caso la solución única es precisamente a = 7, b = 6, c = 4 y d = 1.
 Número 6.174 realizado con las dos tipografías de la UPV/EHU, sin y con serif
Número 6.174 realizado con las dos tipografías de la UPV/EHU, sin y con serif
La siguiente cuestión matemática sería demostrar esta propiedad mágica, es decir, que para cualquier número de cuatro dígitos, tal que estos no sean todos iguales, el algoritmo de Kaprekar llega siempre a la contante de Kaprekar, 6.174. Más aún, se puede probar que el número de pasos para llegar a la constante es como mucho siete. Para quien esté interesado en la demostración de esta propiedad puede consultarla en la literatura que existe sobre esta cuestión, por ejemplo, en el artículo The weirdness of number 6174, de Yutaka Nishiyama.
En los ejemplos que se han mostrado en esta entrada del Cuaderno de Cultura Científica, hemos visto que para el número 6.282 se necesitan 4 iteraciones del algoritmo de Kaprekar para llegar a la constante 6.174 y para el número 3.631 se necesitan 6 iteraciones. En el siguiente diagrama vemos la cantidad de números de cuatro dígitos, no todos ellos iguales, que necesitan una cantidad dada de iteraciones para alcanzar el 6.174.
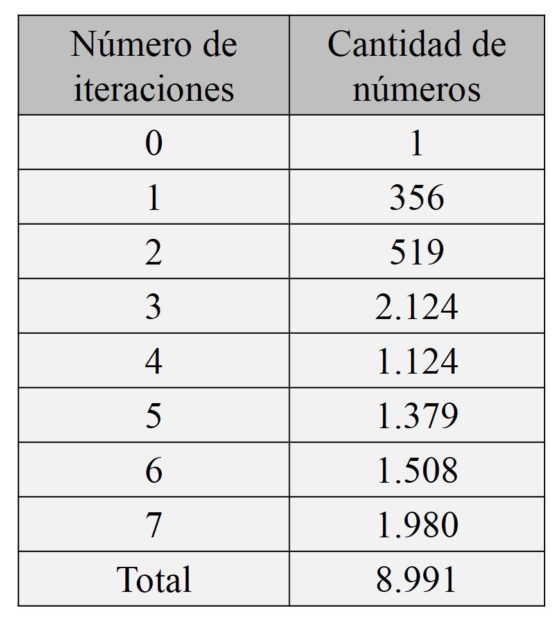
Esta interesante propiedad descubierta por el matemático recreativo indio Dattatreya Ramchandra Kaprekar para números de cuatro dígitos la podríamos pensar para números con otras cantidades de dígitos.
Para números con dos dígitos veamos, para empezar, un ejemplo. Si tomamos el número 53 y realizamos el algoritmo de Kaprekar, la sucesión de números que aparecen es 18, 63, 27, 45, 09, 81 y se repetiría el ciclo 63, 27, 45, 09, 81 todo el tiempo. De hecho, esta situación es la general, para cualquier número de dos dígitos, tal que estos no sean todos iguales, el algoritmo de Kaprekar llega siempre al ciclo 63, 27, 45, 09, 81. Por lo tanto, no existe una contante de Kaprekar de dos dígitos.
Si tomamos un número de tres dígitos, como 184, entonces el algoritmo de Kaprekar da lugar a la sucesión 693, 594 y 495, siendo este último un punto fijo en el que se estaciona la sucesión. De hecho, para números de tres dígitos el número 495 es una constante de Kaprekar, la única para esta cantidad de dígitos.
No existe una constante de Kaprepkar para números de cinco dígitos. Para estos lo que ocurre es que el algoritmo de Kaprekar terminará en alguno de los ciclos siguientes:
Ciclo 1: 53.955, 59.994, 53.955;
Ciclo 2: 61.974, 82.962, 75.933, 63.954, 61.974;
Ciclo 3: 62.964, 71.973, 83.952, 74.943, 62.964.
Mientras que para seis dígitos tenemos una mezcla de las situaciones anteriores. Existen dos constantes de Kaprekar (549.945 y 631.764), es decir, puntos fijos del algoritmo de Kaprekar, a las que convergerán muchas de las sucesiones de números construidas mediante este algoritmo, y un ciclo (420.876, 851.742, 750.843, 840.852, 860.832, 862.632, 642.654, 420.876).
En la Enciclopedia on-line de sucesiones de números enteros (oeis.org [https://oeis.org/]), de N. J. A. Sloane, podéis encontrar la sucesión de constantes de Kaprekar. Es la sucesión etiquetada como A099009, cuyos primeros elementos son:
495, 6.174, 549.945, 631.764, 63.317.664, 97.508.421, 554.999.445, 864.197.532, 6.333.176.664, 9.753.086.421, 9.975.084.201, 86.431.976.532, 555.499.994.445, 633.331.766.664, 975.330.866.421, 997.530.864.201, 999.750.842.001, 8.643.319.766.532, 63.333.317.666.664, etc.
 Crunching Numbers, del artista Dennis Kalow. Imagen de la página del artista en Society of Minnesota Sculptors
Crunching Numbers, del artista Dennis Kalow. Imagen de la página del artista en Society of Minnesota Sculptors
Bibliografía
1.- Raúl Ibáñez, Números primos, amigos y demás familia, Catarata, 2021.
2.- Martin Gardner, Los números mágicos del doctor Matrix, Gedisa, 2019.
3.- David Wells, The Penguin Dictionary of Curious and Interesting Numbers, Penguin Books, 1986.
4.- Yutaka Nishiyama, The weirdness of number 6174, International Journal of Pure and Applied Mathematics, vol. 80, no. 3, pp. 363 – 373, 2012.
5.- Wikipedia: Kaprekar routine
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo 6.174, un número seductor se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Control de la reacción nuclear en cadena (2): moderadores
 Planta de producción de agua pesada en Arak (Irán). Fuente: Wikimedia Commons
Planta de producción de agua pesada en Arak (Irán). Fuente: Wikimedia CommonsLos átomos de hidrógeno del agua son muy efectivos para ralentizar los neutrones por dos motivos: primero porque la masa de un núcleo de hidrógeno (un solo protón) es casi la misma que la de un neutrón y, segundo, porque la cantidad de átomos de hidrógeno por unidad de volumen es alta. Un neutrón, por tanto, puede perder una gran fracción de su energía en una colisión con un núcleo de hidrógeno. Solo se necesitan unas 20 colisiones, en promedio, para ralentizar el neutrón rápido a energías por debajo de 1 eV. Sin embargo, los neutrones también pueden ser capturados por el núcleo de hidrógeno en la colisión, según la reacción
![]()
La probabilidad de que ocurra esta reacción en lugar de una colisión elástica es lo suficientemente alta como para que no se pueda conseguir una reacción en cadena con uranio natural y agua ordinaria. Pero la absorción de un neutrón por un núcleo de deuterio, el isótopo del hidrógeno con un protón y un neutrón (hidrógeno-2), que se encuentra en la llamada agua pesada, tiene una probabilidad extremadamente pequeña.
Los neutrones no pierden tanta energía por colisión con los núcleos hidrógeno-2, pero esta desventaja se ve compensada por la tasa de absorción mucho más baja. Se puede lograr fácilmente una reacción en cadena con uranio natural y agua pesada. Se han construido reactores, con uranio natural como combustible y agua pesada como moderador, en Estados Unidos, Canadá, Francia, Suecia, Noruega y otros países, y científicos alemanes intentaron construirlos durante la Segunda Guerra Mundial [1].
El contraste entre las propiedades nucleares del hidrógeno hidrógeno-1 y el deuterio tiene importantes implicaciones para el desarrollo de los reactores nucleares. El agua pesada es cara de producir, pero cuando se utiliza con uranio natural (en su mayoría uranio-238), se puede lograr, como hemos mencionado, una reacción en cadena de manera eficiente. Aunque el uranio-238 normalmente absorbe neutrones en lugar de fisionarse, el agua pesada consigue ralentizar los neutrones por debajo de la energía a la que serían capturados por los núcleos de uranio-238. Un neutrón lento simplemente rebotará en los núcleos uranio-238 que encuentre hasta que finalmente sea absorbido por un mucho menos abundante núcleo de uranio-235, lo que provocará la fisión de este.
El agua corriente se puede utilizar como moderador en un reactor de uranio si se utiliza uranio enriquecido en el isótopo uranio-235 en lugar de uranio natural. En los Estados Unidos se han construido muchos reactores “alimentados” con uranio enriquecido y moderados con agua corriente. Estos reactores se denominan reactores de agua ligera. De hecho, este tipo de reactor general es el diseño preferido para la producción comercial de energía (electricidad), ya que es menos costoso de construir y menos probable que genere como subproductos materiales fisionables que podrían usarse para armas nucleares.
El carbono en forma de grafito ultrapuro se ha utilizado como moderador en muchos reactores, incluidos los primeros. Al ser más masivos sus átomos, no es tan bueno para ralentizar los neutrones rápidos como el agua ligera y el agua pesada; se necesitan aproximadamente 120 colisiones con átomos de carbono para ralentizar un neutrón rápido con una energía inicial de 2 MeV a la energía deseada de aproximadamente 0.025 eV; en agua pesada sólo se necesitan unas 25 colisiones. Pero aunque el carbono en forma de grafito puro no es el mejor moderador y absorbe algunos neutrones, sí permite que ocurra una reacción en cadena cuando se colocan trozos de uranio natural (barras cilíndricas que contienen gránulos de uranio, por ejemplo) en una gran masa de grafito. Determinar cómo se podría hacer esto realmente fue uno de los principales problemas ingenieriles que tuvo que resolverse antes de que la primera reacción en cadena del mundo se lograra en diciembre de 1942 por un equipo que lideraba Enrico Fermi en la Universidad de Chicago [2]. Muchos reactores moderados por grafito funcionan actualmente en todo el mundo.
El control de un reactor nuclear es relativamente sencillo. Para que no se produzca una fisión con demasiada frecuencia, se insertan algunas barras de control en el reactor. Las barras consisten en un material (como cadmio o boro) capaz de absorber los neutrones lentos, reduciendo así el número de neutrones en el reactor. La eliminación de las barras de control permitirá que aumente la tasa de fisión en el reactor.
Notas:
[1] No podemos dejar de mencionar en este punto la película “Los héroes de Telemark” (Anthony Mann, 1965) que recrea (con muchas licencias artísticas, porque en realidad no se disparó ni un solo tiro) una de las operaciones en la batalla por el agua pesada de la Segunda Guerra Mundial.
[2] Este experimento demostró que una reacción en cadena no era solo una especulación teórica, sino que era algo realizable y controlable en la práctica.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Control de la reacción nuclear en cadena (2): moderadores se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Control de la reacción nuclear en cadena (1): tamaño crítico
- Fisión nuclear (3): más neutrones
- Fisión nuclear (1): los elementos transuránidos
Ramón Picarte, una aproximación a la utopía
Alberto Mercado Saucedo
A mediados del siglo XIX, Ramón Picarte Mujica elaboró tablas de cálculo más precisas que las que se usaban en cualquier parte del mundo. Para publicarlas, viajó a Francia para someter su trabajo a la Academia de Ciencias de París. Regresó a Chile para dedicarse a otra obsesión: aplicar las matemáticas a la búsqueda del bienestar de los trabajadores. Ramón Picarte Mujica, nacido el 9 de junio de 1830, puede considerarse el primer matemático chileno. Esta es su historia.
 Ilustración de Constanza Rojas-Molina. Todos los derechos reservados; cesión en exclusiva para su publicación en el Cuaderno de Cultura Científica.
Ilustración de Constanza Rojas-Molina. Todos los derechos reservados; cesión en exclusiva para su publicación en el Cuaderno de Cultura Científica.Enero de 1857 en Valparaíso. Frente a la principal puerta de entrada y salida de Chile, el mar parece infinito, tanto como los sueños, ambiciones o incertidumbre de las personas que comienzan aquí su personal aventura. Además de grandes embarcaciones que cargan y descargan mercancías de todo tipo, hay diplomáticos, traficantes, estudiantes que parten a estudiar a Europa o inmigrantes que llegan al país. El joven Ramón Picarte, de 26 años, está listo a embarcarse; lleva consigo muy poco equipaje y sus escasos ahorros de cien pesos, además de varios cuadernos y carpetas con hojas manuscritas en las que lleva un gran tesoro, su trabajo de los últimos años. Intenta que sea revisado y publicado, para lo cual necesita apoyo que no ha conseguido por ninguna parte. Apenas unas semanas atrás se entrevistaba con el ministro Antonio Varas, de quien recibió una rotunda respuesta negativa. Convencido de sus logros, no le queda opción que emprender una aventura solitaria, tomar un barco a otras latitudes y mostrar su trabajo a quien sí esté dispuesto a apreciarlo.
Cuando su padre falleció, él apenas tenía cinco años. Ramón Picarte y Castro había sido militar independentista, llegó a ser intendente de Valdivia y sus convicciones liberales le significaron enemistarse con superiores y ser dado de baja del ejército en 1830; murió olvidado y en la pobreza. Carmen Mujica quedó a cargo de sus cinco hijos pequeños y no conseguiría un montepío -pensión estatal- sino muchos años después. Ramón ingresó en 1840 al Instituto Nacional, la primera institución educativa del país independiente, fundada en 1813 a partir de casas de estudio de la época colonial con la misión expresa de formar los ciudadanos que dirigieran a la patria. Se convertiría en el más importante centro de educación media del país y llegaría al siglo XXI con el distintivo de liceo emblemático, siendo todavía un colegio sólo para estudiantes varones, con más de cuatro mil inscritos y manteniendo sin duda una particular mitología propia; del Instituto Nacional han egresado cantidad de jóvenes que se convertirían en deportistas, científicos y artistas -entre ellos premios nacionales de ciencias y artes- además de varios presidentes del país.
Ramón había comenzado sus estudios en humanidades, pero al poco andar cambió el derecho por las ciencias, a pesar de que ello significaba un posible futuro menos oneroso. Se graduó como agrimensor, título al que podía optar tras estudios científicos. Tuvo una valiosa influencia de Andrés Antonio Gorbea, ingeniero vasco que había sido contratado por el gobierno chileno para impartir clases en las instituciones recién creadas: fue profesor en el Instituto Nacional, donde se convirtió en mentor de Picarte, y posteriormente sería el primer decano de la Facultad de Ciencias Físicas y Matemáticas de la Universidad de Chile, fundada en 1843 y que, por cierto, sólo algunas décadas después incorporó en su Estatuto Orgánico a la investigación científica como una labor propia, lo que denota lo incipiente de esta actividad en la época. Gorbea conocía bien los textos matemáticos más modernos, tradujo cursos actualizados que se usaban en Francia y los hizo editar para ser usados en Chile. Sin duda que fue una gran influencia para Ramón Picarte.
Después de abordar una nave en Valparaíso, los pocos ahorros que Picarte había podido reunir no le permiten llegar muy lejos y debe quedarse en el puerto de Callao, en Lima, donde trabaja de cualquier cosa para subsistir durante un par de meses. Intenta conseguir algún editor para publicar sus tablas, sin éxito, y sufre un robo que le obliga a rehacer parte de sus tablas. ¿En qué consiste su trabajo? Simplemente, había mejorado las tablas de cálculo más precisas conocidas hasta entonces en todo el mundo. Diversas actividades requerían operaciones precisas de números con muchas cifras, y las computadoras de la época no eran sino tablas de cálculo: libros con tablas y tablas llenas de números, hojas de cálculo similares a las de Excel o de cualquier otro programa informático, pero no en una pantalla sino impresas en enormes volúmenes. Usadas de manera cuidadosa, el usuario podía realizar operaciones complejas apoyándose en varias operaciones sencillas.
Entre las tablas más usadas en la época estaban las de logaritmos del astrónomo francés Jérôme de Lalande, célebre por haber calculado la distancia de la Tierra a la Luna y la trayectoria de Venus, y sobre todo por haber corregido al astrónomo inglés Edmond Halley sobre el nuevo avistamiento del cometa que llevaría su nombre.Lalande predijo que sería visible en 1759, un año después de la fecha anunciada por Halley, tras calcular la perturbación ocasionada por la fuerza de gravedad de los grandes planetas del sistema solar. Lalande acertó y su logro ayudó al asentamiento de la física newtoniana en la ciencia francesa. Para realizar sus cálculos, Lalande se apoyaba en sus tablas de logaritmos, que se convirtieron en un clásico en todos aquellos campos de la técnica que requerían hacer operaciones con números de gran cantidad de cifras. En Chile estas tablas eran el estándar en el siglo XIX y todo mundo las utilizaba. Por supuesto, no eran perfectas, y ellas mismas eran el resultado de mejorar tablas más antiguas, pero ya llevaban un buen tiempo usándose y aún nadie había logrado mejorarlas. Hasta que llegó Ramón Picarte.
Picarte trabajó como profesor de matemáticas en la Escuela Militar hasta 1856. Como agrimensor, no se conformó con aprender a usar las tablas del astrónomo francés Lalande: después de dominar las propiedades matemáticas que las sustentaban, se propuso nada menos que mejorarlas, lo que consiguió después de mucho trabajo. ¿En qué consistía mejorar una tabla? No se trataba de simplemente añadir más resultados de operaciones matemáticas, hasta eventualmente incluir todas las operaciones posibles. Cada tabla tiene sus reglas de uso: una división u otra operación entre números grandes se obtiene como resultado de varias operaciones parciales más sencillas que dependen de los dígitos de los números en cuestión. El usuario debe conocer estas reglas para utilizar la tabla. Mejorar una tabla consistía en programarla de manera más eficiente. Picarte encontró una mejor manera de separar las operaciones en operaciones auxiliares para que el resultado final fuera más preciso, incluso usando una tabla más pequeña. Separó de ingeniosa manera las operaciones necesarias para hacer una división de una cifra, de manera que bastaba operar con cada dígito y luego sumar los resultados. Además, usó propiedades matemáticas para aumentar el número de dígitos conseguidos en la respuesta. Es decir, Picarte mejoró el algoritmo con el que funcionaban las tablas, fue un programador que dominó las matemáticas que sustentaban las tablas y así fue capaz de crear una tabla más poderosa.
Varado en Lima, sin dinero y sin poder publicar su trabajo, Picarte debe reunir lo suficiente para continuar su viaje. Consigue un préstamo de un compatriota, de apellido Prado, por mil pesos, un gran alivio después de tantas negativas recibidas antes de embarcarse en Valparaíso. Puede ser que en la búsqueda infructuosa de ayuda haya influido el hecho que Andrés Gorbea, su mentor, había fallecido poco antes, en 1852. Es de notar también que Antonio Varas, ministro del Interior y de Relaciones Exteriores, en quien Picarte había cifrado sus últimas esperanzas de obtener ayuda, había sido rector del Instituto Nacional durante los años en que Ramón fue estudiante. De hecho, la historia familiar de Antonio Varas es de cierta forma un reflejo de la trayectoria de la familia Picarte Mujica, desde el lado político opuesto: el padre de Varas había sido partidario de la corona española y después de la independencia, los bienes de la familia fueron incautados, y ésta cayó en la pobreza. Antonio Varas (trece años mayor que Picarte) también había estudiado ciencias en el Instituto Nacional, era agrimensor y abogado; es lógico pensar que comprendía bien el alcance del logro de Ramón Picarte, pero es un hecho que le negó su patrocinio. Quizá no le pareció redituable gastar dinero en ello o quizá simplemente estaba más ocupado en el proceso de colonización del sur del país que llevaba a cabo como ministro: su encargado Vicente Pérez Rosales gestionaba la llegada de ciudadanos europeos, en especial alemanes, para poblar tierras que les eran entregadas bajo condición de trabajarlas. Este proceso, por cierto, con el tiempo llevaría a ocupaciones irregulares de tierras que históricamente pertenecían a las comunidades mapuche y huilliche, originando así conflictos que desgraciadamente perduran hasta nuestros días. Como haya sido, el punto es que Ramón Picarte no había encontrado ningún apoyo del gobierno, y tampoco mucho entusiasmo de la comunidad académica del país.
En Lima, un poco de suerte sonríe a Picarte. Con la ayuda recibida logra proseguir su odisea. Viaja a Panamá y luego hace el largo trayecto hasta Southampton, en el Reino Unido, donde vende su reloj, la única herencia de su padre, para poder sortear el último tramo de su viaje. Picarte casi logra su cometido, está cerca de llegar a Paris y entrevistarse con los matemáticos franceses para mostrarles su trabajo. Irónicamente, sus detractores en Chile solían elogiar a los científicos de estas latitudes, pero lo hacían desde una perspectiva categórica, absolutamente conservadora, más bien una caricatura: “Los grandes descubrimientos de las ciencias están reservadas para los grandes sabios europeos”, había sido la triste declaración al consejo de la facultad de nada menos que el director de la Escuela de Artes y Oficios y que consta en actas de la universidad. Bajo esta óptica, Picarte había perdido su tiempo tratando de equipararse con los matemáticos franceses y debía ubicarse en el papel que esta visión colonial le reservaba. Afortunadamente, no se dejó menospreciar, él creía genuinamente que había conseguido algo importante. Quizá su trabajo tampoco había generado entusiasmo en el medio científico de la época. La astronomía, por ejemplo, desde esos años ya tenía actividad en Chile. En efecto, funcionaba el observatorio del Cerro Santa Lucía, presumiblemente el primero en Latinoamérica (además del pequeño observatorio, considerado más bien como de carácter aficionado, ubicado en el Cerro Cordillera de Valparaíso producto de la iniciativa de Juan Muat, relojero escocés asentado en el puerto chileno, apasionado de la astronomía y cuya historia merecería varias páginas). Hubiese sido natural que la actividad astronómica en Chile propiciara condiciones suficientes para que el trabajo de Picarte fuera reconocido y, por supuesto, utilizado. Después de todo, las tablas usadas hasta entonces eran las del astrónomo Lalande. Pero no fue así, nadie le dio importancia a la mejora de las tablas y todo mundo se conformaba con seguir usando las mismas herramientas conocidas. Los profesionales que observaban astros tan lejanos en el universo poseían una visión mas bien corta, y no fueron capaces de tomar otra decisión que quizá, imposible saberlo, habría propiciado un avance cualitativo en la ciencia chilena.
La miopía de las autoridades y la visión colonial de la comunidad científica era un hecho, y podríamos decir que desgraciadamente sigue siéndolo en alguna medida. Afortunadamente, Ramón Picarte no cejó y decidió emprender esta loca aventura. Después de vender su reloj llega a la capital francesa, su destino final. En Paris, ayudado por conocidos, logra entrevistarse con matemáticos de la Academia de Ciencias, con quienes acuerda los siguientes pasos a realizar: debe redactar un completo informe y pasar en limpio sus tablas, lo que lleva a cabo durante unos cinco meses de constante trabajo. Finalmente, en 1858 presenta sus tablas antes la Academia de Ciencias de Paris y éstas son sometidas a un minucioso examen. Le solicitan una segunda exposición junto con informes con más detalles. Claro, los matemáticos franceses no iban a aprobar tan a la ligera las tablas que pretendían mejorar el trabajo de Lalande. Pero Picarte consigue sortear todos los exámenes: en sesión de febrero de 1859, la Academia evalúa positivamente el trabajo y aprueba la publicación de las tablas con título La división reducida a una suma. Picarte tiene razón y su obstinación rinde frutos.

El logro de Ramón Picarte es una gran noticia, diarios de Francia, España y Chile consignan su proeza. Ahora sí, todos en su país natal reconocen que es un gran matemático, todo mundo lo reconoce y nadie parece recordar los sinsabores y el desprecio que Picarte sufrió por falta de apoyo. En mayo de 1859 el gobierno del país lo nombra adjunto a la Legación de Chile en Francia y en junio el Consejo de la Universidad de Chile lo nombra miembro corresponsal de la Facultad de Ciencias Físicas y Matemáticas. Se encarga a la Academia de Ciencias de París la impresión de trescientos ejemplares de las tablas. Llegan los tiempos de calma y satisfacción para Ramón Picarte, que extiende su estadía en Paris para estudiar directamente de los matemáticos franceses. Al parecer, en esa época se produce un punto de inflexión en sus intereses y motivaciones, pues además de matemáticas y agrimensura, se aboca a otra obsesión: el uso de la ciencia para lograr el bienestar de la sociedad.

En Chile se crea gran expectación, al menos en el medio académico, por tenerlo de regreso, lo cual sucede en 1862. Su primera actividad consiste en dar un discurso ante el Consejo de la universidad, en la sesión en que asume su nombramiento académico. Los académicos esperan ansiosos el mensaje que Picarte les dirigirá, después de haber llegado a la Academia de Ciencias de Paris, donde su trabajo había sido reconocido y publicado. Quizá suponen que les contará noticias sobre los temas científicos de vanguardia que se estudian en Francia en ese momento o sobre proyectos que tiene en mente para los siguientes años. Puede ser que algún antiguo detractor de Picarte tema alguna represalia por parte del ahora académico de la universidad. Pues bien, probablemente el discurso que escuchan extraña a varios de ellos, que no se esperan que la principal preocupación que Ramón Picarte transmite en su discurso sea la del bienestar de los trabajadores.
Como podemos leer en los Anales de la universidad de Chile, disponibles en línea, en su discurso de inauguración Picarte expuso con todo detalle sobre algunas propuestas para asegurar el bienestar de un trabajador, con cálculos precisos incluidos. En particular le preocupaba la ocurrencia de accidentes o enfermedades invalidantes, pues quienes sufrían algo así eran dejados a su suerte. Haciendo uso de las probabilidades, Picarte calculó lo que podía significar que cada trabajador ahorre pequeñas cantidades para usufructo común. Sostiene Picarte que era posible prever y ahorrar recursos para el futuro, organizarse y establecer un sistema de pensiones que permitieran vivir dignamente a quienes debieran dejar de trabajar. Probablemente en Francia se vio atraído por el socialismo utópico de Charles Fourier y otras corrientes de pensamiento similares; también conoció el funcionamiento de compañías de seguro que operaban en Europa. Menciona en su discurso que, para un buen desempeño del sistema de ahorro que propone, se debían evitar las altas cuotas que las compañías de seguros europeas cobraban a sus suscriptores y menciona el ejemplo de compañías británicas, que se estaban haciendo ricas con los altos comisiones cobradas por su servicio. Es inevitable preguntarse qué pensaría Ramón Picarte de los sistemas de capitalización individual para el retiro que rigen en tantos países en nuestros días, como como las AFP chilenas, que actualmente son objeto de importantes discusiones, aunque no es difícil imaginarlo.
Durante los años posteriores a su regreso a Chile, Picarte destinó su tiempo y energía a proyectos sociales, siembre con el objetivo de garantizar el bienestar de los trabajadores por medio del uso racional y equitativo de los recursos generados por el trabajo. Para ello solicitaba ayuda en muchas partes con variados resultados, incluso llegó a instalarse en un puesto permanente en una plaza pública para sumar adeptos a sus proyectos. En 1863 fundó en Santiago una sociedad de zapateros y otra de sastres y en 1864 formó la organización cooperativa “Sociedad trabajo para todos”, proyectos que al parecer tuvieron un modesto alcance y una corta vida. En 1866 se instaló en San Carlos, al sur de Chile, donde intentó crear un falansterio -o comuna-, agrupación de familias cuyo trabajo conjunto la hace autosustentable. Este ambicioso e inédito proyecto en estas latitudes tuvo un buen comienzo según fue comentado en la prensa de la época, pero no se tienen mayores registros sobre su desarrollo. Se casó en 1869 con Clorinda Pardo y se instalaron a vivir en el vecino poblado de Chillán.
Los proyectos sociales absorbieron entonces la energía de Picarte desde su retorno a Chile. De hecho, me parece que es más común encontrar su nombre en fuentes bibliográficas relacionadas con el origen del cooperativismo o del socialismo en Chile que en textos sobre los primeros científicos del país, por lo que su nombre resulta aún muy poco conocido. Una muy valiosa excepción la constituyen los trabajos de Claudio Gutierrez y Flavio Gutierrez, que han rescatado el papel de Ramón Picarte como pionero en la ciencia en Chile.
Sorprendentemente, no conocemos el final de esta historia, ni el de la vida de Ramón Picarte. Se sabe que publicó varias patentes de artefactos tecnológicos diversos y que eventualmente volvió a dedicar tiempo a confeccionar nuevas tablas de cálculo. Consiguió financiamiento para desarrollar y publicar unas “tablas de logaritmos de doce decimales” y emprendió un viaje a Francia en 1884, quizá para quedarse definitivamente allí, pues no se sabe con certeza qué pasó después de tal fecha y tampoco si las tablas fueron publicadas. Un diccionario biográfico en su reedición de 1897 se refiere escuetamente a Picarte con el texto “permanece en París consagrado a estudios científicos” sin proporcionar mayor detalle, y no hay referencias posteriores. Durante el 2019, pude dedicar algunos días de una estadía en Francia a buscar en archivos de Paris alguna pista de las actividades de Picarte. Desgraciadamente, al desconocer la dirección aproximada donde pudo haber fallecido, es difícil encontrar un registro de defunción. Encontré solamente dos pistas certeras: un par de registros de patentes de los años 1884 y 1888. Los artefactos descritos coinciden con actividades anteriores de Picarte, lo que significa una comprobación de su actividad en Paris posterior a su última salida de Chile. Desgraciadamente, la dirección en Paris registrada en la patente no me ayudó a encontrar información adicional.
¿Qué fue de Ramón Picarte? ¿Falleció en Francia? ¿Publicó sus tablas de doce decimales? ¿Se interesó por otros problemas? No lo sabemos aún y sólo podemos imaginar que durante los últimos años del siglo XIX, o quizá incluso durante los primeros del siglo XX, Ramón Picarte estuvo entusiasmado por otros proyectos, siempre con pasión y encarnando la frase del autor italiano Terencio: soy un hombre, nada humano me es ajeno.
Principales referencias
- Gutiérrez Claudio y Gutierrez, Flavio, «Ramón Picarte: la proeza de hacer matemáticas en Chile», Quipu, Revista Latinoamericana de Historia de las Ciencias y la Tecnología, Vol. 13, Num. 3, 2000.
- Gutiérrez Claudio y Gutierrez, Flavio, «Forjadores de la ciencia en Chile», RIL editores, 2008.
- Jaime Massardo, «La formación del imaginario político de Luis Emilio Recabarren», Santiago de Chile, Lom ediciones, 2008.
- Anales de la Universidad de Chile: https://anales.uchile.cl/
- Les procès-verbaux du Bureau des longitudes. http://bdl.ahp-numerique.fr/
- Gallica, Biblothèque Nationale de France https://gallica.bnf.fr/
Sobre el autor: Alberto Mercado Saucedo es profesor de matemáticas en la Universidad Técnica Federico Santa María (Valparaíso, Chile)
Sobre la ilustradora: Constanza Rojas Molina es profesora del departamento de matemáticas de la CY Cergy Paris Université (Cergy-Pontoise, Francia)
El artículo Ramón Picarte, una aproximación a la utopía se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Fraude científico (I). Una primera aproximación
- José Ramón Alonso – Naukas Bilbao 2019: Son nuestros amos y nosotros sus esclavos
- Roberto Frucht, matemático en tránsito

