Más allá del modelo de Bohr
 Foto: Matthew Hicks / Unsplash
Foto: Matthew Hicks / UnsplashAdemás de la incapacidad de predecir ciertas propiedades de los átomos, el modelo de Bohr tenía dos deficiencias adicionales. Primero, predecía algunos resultados que no estaban de acuerdo con el experimento (como espectros incorrectos para elementos con dos o tres electrones en las capas electrónicas más externas). En segundo lugar, predecía resultados que no se podían comprobar de ninguna manera conocida (como los detalles de las órbitas de los electrones). Aunque las órbitas eran fáciles de dibujar en papel, no podían observarse directamente. Tampoco podían relacionarse con ninguna propiedad observable de los átomos [1]. Era evidente pues que el modelo de Bohr planteaba cuestiones que no tenían respuesta experiment [2].
A principios de la década de 1920, los físicos, especialmente el propio Bohr, comenzaron a trabajar seriamente en la revisión de las ideas básicas del modelo. Un hecho que destacaba era, como Rutherford había señalado, que el modelo se basaba en una mezcla de ideas clásicas y cuánticas. Se suponía que un átomo actuaba de acuerdo con las leyes de la física clásica hasta el punto en que estas leyes ya no funcionaban. Más allá de este punto, se introducían ideas cuánticas. La imagen del átomo era el producto de una mezcla inconsistente. Combinaba ideas de la física clásica con conceptos para los que no había lugar en la física clásica.
Las órbitas de los electrones estaban determinadas por las leyes de movimiento clásicas newtonianas, muy parecidas a las órbitas de los planetas alrededor del Sol. Pero de las muchas órbitas teóricas, solo un pequeño número se consideraba posible. Incluso estas pocas órbitas eran seleccionadas por reglas para las que no había lugar en la mecánica clásica. Además, la frecuencia calculada para la revolución orbital de los electrones era bastante diferente de la frecuencia de la luz emitida o absorbida cuando el electrón se movía desde o hacia esta órbita. Por si fuese poco, la decisión de que el número n nunca podía ser cero parecía completamente arbitraria, pero era necesaria evitar que el modelo colapsara dejando que el electrón cayera sobre el núcleo. Se hizo evidente así que un modelo de estructura atómica mejor necesitaría basarse más consistentemente en conceptos cuánticos.
En definitiva, la contribución del modelo de Bohr se puede resumir de la siguiente manera. Proporcionó algunas respuestas excelentes a las preguntas planteadas sobre la estructura atómica. Aunque el modelo resultó ser inadecuado, llamó la atención sobre cómo se pueden usar los conceptos cuánticos. Indicaba el camino que tendría que tomar un nuevo modelo. Un nuevo modelo que tendría que proporcionar las respuestas correctas que daba el modelo de Bohr, pero que también tendría que proporcionar las respuestas correctas para los problemas que el modelo de Bohr no podía resolver.
Uno de los aspectos más fascinantes del trabajo de Bohr fue la prueba de que las propiedades físicas y químicas de la materia ponen de relieve el papel fundamental de los enteros (números cuánticos como n = 1, 2, 3, …). Como dijo Bohr: «La solución de uno de los sueños más audaces de las ciencias naturales es construir una comprensión de las regularidades de la naturaleza sobre la consideración del número puro». Aquí resuenan las ideas de Pitágoras y Platón, de Kepler y Galileo.
Desde la década de 1920, se ha desarrollado un nuevo modelo de éxito de la estructura atómica. Es parte de la mecánica cuántica, llamada así porque es una nueva mecánica construida directamente sobre conceptos cuánticos. La mecánica cuántica va mucho más allá de comprender la estructura atómica. De hecho, es la base de la concepción moderna de los acontecimientos a escala submicroscópica. [3]
Notas:
[1] El modelo planetario tiene un significado muy diferente cuando se aplica a un planeta en una órbita observable que cuando se aplica a un electrón en un átomo. La posición precisa de un planeta es importante, especialmente en experimentos como fotografiar un eclipse o una porción de la superficie de Marte desde un satélite. Pero la posición momento a momento de un electrón en su órbita no tiene ese significado porque no tiene relación con ningún experimento que los físicos hayan podido idear.
[2] En cierto modo pasa una cosa parecida con la teoría de cuerdas hoy día. Otra cuestión es si la solución sigue un camino paralelo al que apuntamos que siguió el modelo atómico.
[3] Algunos aspectos fundamentales de la mecánica cuántica serán objeto de una próxima serie.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Más allá del modelo de Bohr se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El modelo de Bohr explica las regularidades en el espectro del hidrógeno
- Las limitaciones del modelo de Bohr
- El modelo de Bohr explica la fórmula de Balmer
Historia de cómo el VIH ayudó a derribar el dogma central de la biología molecular
![]()
Rosario Sabariegos Jareño y Antonio Mas López
 Imagen de Arek Socha / Pixabay
Imagen de Arek Socha / Pixabay
“El sentido común nos dice que todas las enfermedades han tenido que ser nuevas en algún momento de la historia, pero muchas epidemias que parecen enfermedades nuevas puede que solo sean reconocidas como nuevas por la población que las describe, o puede ser que hayan alcanzado proporciones epidémicas por primera vez”.
Robert Gallo, codescubridor del VIH.
La infección por el virus de la inmunodeficiencia humana (VIH), responsable del síndrome de inmunodeficiencia adquirida (SIDA), cobró importancia en los ochenta, cuando empezaron a aparecer casos en occidente. Todo empezó mucho antes, entre 1910 y 1930, en África.
En función de la secuencia genómica, el VIH se divide en dos grandes grupos: VIH-1 y VIH-2. El VIH-1 (causante de la pandemia) tiene una gran similitud genómica con el virus de inmunodeficiencia en simios (VIS) que afecta a los chimpancés que viven en zonas del sur de Camerún.
Si tenemos en cuenta la biología de estos virus, la transmisión desde los simios a las personas debió ocurrir por la exposición de heridas o mucosas a la sangre o los fluidos contaminados del chimpancé. Esto seguramente ocurrió durante la caza de estos animales. Al principio la enfermedad se limitó a pequeñas zonas de África hasta que llegó, a través del río Congo, a un núcleo urbano grande: Kinshasa (antes, Leopoldville). El río Congo era la ruta principal de viaje y comercio y esta, la ciudad más grande de la época en esa zona.
Kinshasa fue la cuna de la pandemia del sida.
 Kinshasa, República Democrática del Congo.
Kinshasa, República Democrática del Congo.Shutterstock/Valeriya Anufriyeva
Desde ahí el virus se fue extendiendo por el resto del continente sin mayor problema con la garantía que ofrece el contagio sexual. Además, las medidas de higiene sanitaria de la época eran muy deficientes, lo que contribuyó a su diseminación.
También a principios del siglo XX, muy lejos de allí, en Estados Unidos, Peyton Rous y su grupo hicieron un descubrimiento que muchos años después iluminaría los caminos que llevaron al hallazgo del VIH.
Entre 1910 y 1911 demostraron que un tipo de tumor que afecta a los pollos podía ser transmitido mediante la inoculación del tejido afectado a un pollo sano. También vieron que el tumor se transmitía cuando inoculaban en el animal sano tan solo extractos libres de células que habían sido filtrados.
Fue la primera vez que se describió la acción de un retrovirus, familia a la que pertenece el VIH.
¿Qué es un retrovirus?
Hasta 1970 el dogma de la biología molecular decía que la información genética fluía siempre en esta dirección: ADN -> ARN -> proteínas. Así funciona en las células humanas.
En los años sesenta del siglo XX solo un grupo muy reducido de científicos creía que los virus de ARN causantes de tumores hacían algo inaudito: al reproducirse, pasaban su información genética a ADN.
Esto iba contra el dogma central de la biología molecular y llevó un tiempo demoler ese edificio.
Temin y Baltimore, por separado, describieron en 1970 la enzima que sintetiza ADN a partir de ARN en los retrovirus, la retrotranscriptasa o transcriptasa inversa (RT). Esto permitió entender la forma en la que estos virus insertaban su material genético en el genoma humano. La transcriptasa inversa copia el ARN y lo pasa a ADN, que se integra en el genoma humano como si fuera un componente más. Allí queda latente y puede reactivarse en cualquier momento. Reactivarse significa que el virus se replica dentro de las células del sistema inmune (linfocitos T CD4+) a las que destruye, lo que explica que las personas infectadas vean disminuidas sus defensas.
El tratamiento actual contra el sida funciona sobre el virus que se está replicando, no sobre el que está integrado. Las células con genoma de VIH integrado son el reservorio de la enfermedad.
De media, en una infección activa, mueren unos diez millones de linfocitos al día. Estos son reemplazados por otros nuevos, pero hasta la médula ósea tiene sus límites. Cuando los niveles de estas células caen por debajo de un umbral aparece la sintomatología que todos conocemos como sida. El paciente se ha quedado sin defensas y es vulnerable a múltiples infecciones.
Cómo evolucionar para resistir los medicamentos
La transcriptasa inversa tiene otras características que la hacen interesante. Es una polimerasa que comete muchos errores cuando copia el material genético.
Esto tiene un coste evolutivo, ya que se generan variantes que son menos eficaces desde el punto de vista biológico. También es una ventaja indiscutible, pues se crea variabilidad que, en términos de evolución molecular, es lo mismo que decir que se genera flexibilidad.
Los errores son producidos al azar, pero la selección de los mismos no. Cuando el virus está en presencia de un fármaco, se seleccionan aquellas variantes del virus que sobreviven. Dichas variantes pasan a ser mayoritarias en la población viral y la evolución sigue su curso. El medicamento es lo que llamamos una presión selectiva y a las poblaciones virales que aparecen las llamamos resistentes.
Si imaginamos el genoma como un gigantesco puzle de pequeñas piezas, la transcriptasa inversa se equivoca una vez cada 10 000 piezas. El genoma del VIH tiene ese tamaño, lo que significa que cada copia lleva al menos un error. Como se generan mil millones de virus al día, cada día se generan todos los mutantes posibles en cada pieza (posición del genoma) del puzle.
Cuando se comenzó a dar el fármaco 3TC como monoterapia, el virus sensible se había reemplazado totalmente por virus resistente en tan sólo 16 días.
La transcriptasa inversa genera tantas variantes que ha sido necesario el desarrollo de multitud de fármacos que atacan al virus en distintos puntos de su ciclo de replicación. Si apareciera un mutante que escapara a todos los fármacos sería un virus con grandes dificultades para replicar. Por eso funciona la terapia contra el VIH.
La cantidad ingente de dinero invertida en la investigación del VIH nos ha dado un conocimiento igual de grande sobre la biología de los virus. Este ha podido ser extrapolado a otros temas. La terapia combinada se extendió hacia el tratamiento del cáncer (terapia ortogonal), ya que la población de células tumorales es también muy heterogénea. Algunos fármacos anti-VIH han demostrado su eficacia frente a otros virus. El primer fármaco que se diseñó por ordenador fue el saquinavir, un inhibidor de uno de los componentes del VIH. Luego han venido otros.![]()
Rosario Sabariegos Jareño es contratada doctora interina y Antonio Mas López profesor titular de universidad en el laboratorio de virología molecular del área de microbiología del Departamento de Ciencias Médicas de la Universidad de Castilla-La Mancha.
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Historia de cómo el VIH ayudó a derribar el dogma central de la biología molecular se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- «El bacteriófago ø29 como sistema modelo en biología molecular» por Margarita Salas
- Niosomas como vectores de terapia génica del sistema nervioso central
- #Quantum13 De cómo la ciencia ayudó a a ganar una guerra
La tabla periódica en el arte: Oro
Los alquimistas, el rey Midas, y los exploradores norteamericanos tenían un mismo objeto de deseo: el oro. Este metal, además de su intrínseco valor, posee un destacado papel simbólico a nivel religioso: era la carne de los dioses egipcios y el material del que estaban hechos el vellocino que persiguió Jasón, las manzanas que guardaban las Hespérides o la estatua del dios Marduk en Babilonia. La religiones judeocristianas no son una excepción: cuando Moisés se descuidó un momento para recoger las tablas de la Alianza, los israelitas ya estaban idolatrando a un becerro de oro. Siendo un elemento tan arraigado en nuestra tradición y conocido desde hace milenios, es comprensible que sea uno de los materiales más importantes a lo largo de la historia del arte.
De oro macizo
El oro es un elemento químico muy estable, por lo que es raro que forme compuestos con otros elementos y es más frecuente que aparezca en forma nativa, es decir, como metal puro. Esto supone una gran ventaja, ya que, aunque sea escaso, se puede hallar en la naturaleza sin tener que recurrir a complejos métodos de extracción. Pensad por ejemplo en las pepitas de oro de las películas del Lejano Oeste. Eso sí, luego se precisan métodos de purificación para separar el oro de otros metales con los que suele estar aleado.
 Imagen 1. Pepita de oro. Fuente: James St. John.
Imagen 1. Pepita de oro. Fuente: James St. John.
La fascinación que sentimos por el oro se remonta a tiempos prehistóricos como demuestran las piezas de orfebrería más antiguas que conocemos. Se encontraron en la necrópolis de Varna (Bulgaria) y fueron elaboradas en el quinto milenio antes de nuestra era. Sin duda, una de las razones por las que el oro nos atrae es su color: al contrario que todos los elementos metálicos (a excepción del cobre) no es plateado, sino amarillento. Para explicar esta propiedad tendríamos que recurrir a la teoría de la relatividad de Einstein, así que conformémonos con decir que los átomos de oro absorben la luz en la parte azul del espectro y la reflejan en la zona del amarillo-rojo. Pero las propiedades maravillosas del oro no se limitan a su color: tiene una maleabilidad fuera de lo común, lo que permite trabajar con él sin que se rompa y es extremadamente estable, por lo que no se degrada fácilmente como puede suceder con el hierro o el cobre.
En la formidable estabilidad del oro estriba gran parte del simbolismo que se le ha otorgado históricamente. Al ser un elemento prácticamente inmutable se asocia con la eternidad, tal y como hacían los antiguos egipcios, quienes lo vinculaban al faraón y al todopoderoso dios Ra. Pese a que el saqueo y hurto de las tumbas egipcias nos ha privado de un gran número de joyas, han llegado a nuestro días magníficos ejemplares de collares, colgantes, estatuillas, amuletos o pectorales que muestran el buen hacer de los orfebres del país del Nilo.
 Imagen 2. Collar con cabezas de halcón y pectoral que representa a la diosa Nekhbet (1479-1425 a.e.c.). Fuente: Metropolitan Museum.
Imagen 2. Collar con cabezas de halcón y pectoral que representa a la diosa Nekhbet (1479-1425 a.e.c.). Fuente: Metropolitan Museum.Al igual que los egipcios, las grandes civilizaciones hicieron un uso extensivo del oro: fue símbolo de distinción para los persas, dio forma a máscaras mortuorias micénicas, se combinó con el marfil en las estatuas de crisoelefantina griegas, coloreó los mosaicos bizantinos y coronó a reyes y reinas. La conquista de América supuso un flujo constante de oro hacia Europa, pero los pueblos precolombinos también habían desarrollado el arte de trabajar un metal del que disponían en relativa abundancia. Cuando los conquistadores llegaron a aquellos desconocidos territorios quedaron maravillados por las riquezas que ofrecían. Enseguida surgieron todo tipo de leyendas que llevaron a los más intrépidos a la búsqueda de lugares como El Dorado, la legendaria ciudad construida en oro. Aunque tal lugar no existiese, el mito tiene una justificación tal y como refleja una singular balsa dorada de la cultura muisca que se descubrió en Colombia (Imagen 3). Esta pieza representa la ceremonia de coronación del cacique del reino, quien cubierto en polvo de oro arrojaba ofrendas del valioso metal a la laguna de Guatavita. Ante tal maravilloso derroche, normal que se sobreestimasen las riquezas de aquellos pueblos indígenas.
 Imagen 3. Balsa muisca elaborada con una aleación de oro, plata y cobre (Entre 600 y 1600). Fuente: Wikimedia Commons.
Imagen 3. Balsa muisca elaborada con una aleación de oro, plata y cobre (Entre 600 y 1600). Fuente: Wikimedia Commons.
Bañados en oro
A estas alturas ha quedado claro que realizar obras de arte con oro es costoso, especialmente si pensamos en piezas de gran formato. Afortunadamente existe una alternativa mucho más económica que visualmente no afecta al valor de la obra: el dorado. Mediante esta técnica se cubren materiales más pobres con oro, de modo que se abaratan costes y se pueden decorar piezas de un tamaño que sería dificilísimo obtener con el metal macizo: retablos, estatuas, órganos, etc. Por ejemplo, en Quito, el interior de la Iglesia de la Compañía está completamente cubierto en oro. Si este interior hubiese sido realizado en metal macizo sería un tesoro más valioso que las reservas de muchos bancos centrales. Sin embargo, gracias al dorado, este delirio barroco se pudo realizar con poco más de cincuenta kilogramos de oro. No es moco de pavo, pero los jesuitas no se caracterizaban precisamente por su austeridad artística.
 Imagen 4. Iglesia de la Compañía de Jesús de Quito (s. XVI-XVIII). Fuente: Wikimedia Commons
Imagen 4. Iglesia de la Compañía de Jesús de Quito (s. XVI-XVIII). Fuente: Wikimedia CommonsA lo largo de la historia se han desarrollado diferentes métodos para dorar objetos. Uno de los más interesantes desde el punto de vista químico es el que se realiza mediante amalgama de mercurio y que ya explicamos en su momento. Afortunadamente este procedimiento tan perjudicial se pudo abandonar en el s. XIX con la llegada de la galvanoplastia y el dorado por electrólisis. Pero no avancemos tan rápido y quedémonos con una técnica más clásica: el dorado mediante pan de oro. El pan de oro es una finísima lámina de metal que se logra mediante el batido con martillo y que, gracias a la ductilidad del oro, puede alcanzar grosores inferiores a una micra. De este modo, pese a que el material sea caro, se puede lograr mucho pan de oro con una pequeña cantidad de metal (10 000 láminas de 8 x 8 cm pesan unos 130 gramos).
La aplicación del pan de oro depende del material que se vaya a cubrir y, en muchos casos, es una labor costosa. Tradicionalmente se han usado dos técnicas: el dorado al mordiente, en el que se emplea como adhesivo una substancia grasa, y el dorado al agua. En este último, muy habitual para decorar estatuas de madera, la pieza se cubre primero con una cola, luego con una preparación a base de yeso y, finalmente, con una capa de bol. El bol es una arcilla de tonos rojizos que sirve de fondo para el dorado y proporciona una superficie homogénea sobre la que se pegan las láminas del oro para su posterior bruñido. Una vez asentadas las láminas, se pueden lograr decoraciones exquisitas mediante el estofado, técnica que consiste en cubrir el metal con pintura y luego levantarla en las zonas que se quieren dejar el oro al descubierto.
 Imagen 5. Ángel con instrumentos de la Pasión (95×40 cm), de Tydeman Maes (1425-1435). El manto luce un rico paño estofado. Fuente: Museo del Prado.
Imagen 5. Ángel con instrumentos de la Pasión (95×40 cm), de Tydeman Maes (1425-1435). El manto luce un rico paño estofado. Fuente: Museo del Prado.
Oro parece…
Cuando un material es codiciado por el ser humano es inevitable que surjan imitaciones. El oro no es una excepción, pese a que por sus particulares características no resulte fácil de falsificar. Si bien existen compuestos químicos o aleaciones con un brillo dorado que podrían dar el pego, no presentan la misma ductilidad, resistencia a oxidarse o densidad que el áureo elemento. Una de estas substancias es la pirita (FeS2), un mineral de brillo atractivo que la naturaleza suele presentar en forma de cubos. Por su aspecto es conocida con el esclarecedor nombre de oro de los tontos y, aunque se usa en joyería, es fácil de diferenciar del codiciado metal: la pirita es más dura (más difícil de rayar), liviana y menos amarilla, especialmente si se ha oxidado. Otros de los minerales que pueden dar falsas alegrías a quienes juegan a ser geólogos son la calcopirita o algunos tipos de micas.
En todo caso, más allá de los sustitutos naturales, el material más empleado para imitar el oro es el latón, una aleación de cobre y zinc. Este material ya era conocido en época clásica como oricalco, en griego cobre de la montaña, nombre que podría ser un vestigio de cuando el latón se obtenía de menas de cobre ricas en zinc. Los romanos transformaron la etimología de la aleación y la acercaron a la del metal al que se asemejaba con el nombre de aurichalcum. Fue el mismísimo Augusto quien decidió que ese sería el material empleado para elaborar los sestercios del Imperio y en la reforma del año 23 les dio el significativo valor de una centésima de áureo, la valiosa moneda de oro. Claro que, gracias al parecido entre el metal y la aleación, hay estafadores que han conseguido rentabilizar mejor el latón haciendo pasar por piezas de gran valor objetos que no eran más que baratijas.
Otra manera muy efectista de lograr superficies de aspecto dorado es la corladura, técnica en la que se aplica un barniz transparente sobre metales como la plata o el estaño. Allá por el s. VIII este barniz se lograba mezclando algún colorante amarillo como el azafrán con aceites, pero posteriormente se fue avanzando hacia el uso de la goma laca como disolvente. Entre las substancias empleadas para lograr la corla dorada podemos encontrar una gran variedad de productos naturales además del azafrán: la rubia, la cúrcuma, el achiote, la gualda, el ámbar, la gutagamba y hasta la sangre de drago, resina extraída de un árbol tropical. La corla se aplica en capas muy finas conocidas como veladuras, ya que el efecto deseado sólo se logra si se combina el color de esta sustancia con la reflectividad de la plata o el estaño.
 Imagen 6. Los relieves de yeso del frontal del altar de Esterri de Cardós (s. XIII) en el Museo Nacional de Arte de Cataluña estaban recubiertos de estaño y corladura.
Imagen 6. Los relieves de yeso del frontal del altar de Esterri de Cardós (s. XIII) en el Museo Nacional de Arte de Cataluña estaban recubiertos de estaño y corladura.
El artista que pintaba con oro
Como ya hemos visto, el oro se ha empleado para realizar obras de orfebrería, dorar piezas o crear pequeñas esculturas, pero también ha tenido cierta relevancia en la pintura. Aunque aplicar oro con un pincel puede parecer complicado, existe una especie de pintura dorada: el oro en concha. Este curioso nombre es un vestigio de la época en la que el producto se guardaba en conchas de mar. Como el resto de pinturas, ésta consiste en partículas que otorgan color y una substancia que aglutina las partículas. Obviamente, en este caso el color lo otorga el oro metálico, mientras que el aglutinante puede ser goma arábiga, la miel u otras substancias dependiendo de la época y el origen. Aunque esta pintura no ha sido muy empleada para elaborar cuadros, resultaba especialmente útil para cubrir lagunas en dorados o alcanzar zonas a las que no se podía acceder con pan de oro.
En cualquier caso, si hablamos de oro y pintura, hay una figura que destaca por encima de todas las demás: la de Gustav Klimt, hijo de un grabador de oro. El artista austriaco no pintaba con oro en concha, sino que combinaba de forma magistral el óleo con el pan de oro. Klimt fue un creador todoterreno que a finales del s. XIX abanderó la Secesión de Viena, un movimiento de artistas que impulsó la renovación de estilos en Austria. Su primera gran obra con pan de oro fue Palas Atenea (1898), un cuadro donde la diosa griega posa altiva con su casco, égida y vara de noble metal. La blanquecina piel nos recuerda al marfil que Fidias usó para otra Atenea, la virgen (Partenos)que otrora se alzaba imponente en el Partenón.
 Imagen 7. Palas Atenea (75×75 cm), de Gustav Klimt (1898) y recreación de la Atenea Partenos de Fidias en Nashville (Tenessee, Estados Unidos). Fuente: Wikimedia Commons.
Imagen 7. Palas Atenea (75×75 cm), de Gustav Klimt (1898) y recreación de la Atenea Partenos de Fidias en Nashville (Tenessee, Estados Unidos). Fuente: Wikimedia Commons.
Klimt creó sus obras más célebres durante la primera década del siglo XX. En ese momento llega el cenit de su fase dorada, un periodo en el que el artista produce piezas que recuerdan a los antiguos mosaicos bizantinos. Posiblemente la más conocida es El Beso (1908), uno de los grandes iconos del arte mundial, aunque Retrato de Adele Bloch-Bauer I (1907) no le anda a la zaga. Esta última gozó durante unos pocos meses del mérito de haber sido el cuadro más caro de la historia. Pero permítanme que acabemos este artículo con una obra que refleja como pocas la unión entre el valor simbólico y artístico del oro: Dánae.
 Imagen 8. Dánae (77×83 cm), de Gustav Klimt (1907-1908). Fuente: Wikimedia Commons.
Imagen 8. Dánae (77×83 cm), de Gustav Klimt (1907-1908). Fuente: Wikimedia Commons.
Para saber más:
Ainhoa Gómez Pintado. El oro en el arte. Materia y espíritu : contribución a la restauración en el arte contemporáneo. UPV/EHU (2009).
El oro de los faraones. National Geographic.
Sofía Martinez Hurtado. El dorado. Técnicas, procedimientos y materiales. Ars Longa (11) (2002) 137-142.
Sobre el autor: Oskar González es profesor en la facultad de Ciencia y Tecnología y en la facultad de Bellas Artes de la UPV/EHU.
El artículo La tabla periódica en el arte: Oro se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La tabla periódica en el arte: Cobre
- La tabla periódica en el arte: Plata
- La tabla periódica en el arte: Hierro
Un estudio dice que…
Vitoria-Gasteiz acogió por primera vez el pasado 18 de octubre el evento Las pruebas de la educación, una jornada que abordó diversos temas educativos desde la evidencia científica. El acto, organizado por el Consejo Escolar de Euskadi y la Cátedra de Cultura Científica de la UPV/EHU, tuvo lugar en el Salón de Actos del Centro de Investigación Micaela Portilla, ubicado en el Campus de la capital alavesa de la UPV/EHU.

La jornada consta de un total de cinco charlas que tratan temas como el rendimiento académico, los métodos de aprendizaje y la innovación educativa, entre otros. La dirección del seminario corre a cargo de la doctora en psicología Marta Ferrero.
Ante el bombardeo diario que recibimos con resultados de estudios científicos, a veces sorprendentes, cuando no contradictorios, Miguel A. Vadillo, director del Cognition, Attention and Learning Lab en el Departamento de Psicología Básica de la Universidad Autónoma de Madrid, explica en esta charla cómo funciona la ciencia, qué es razonable esperar de ella y en qué plazos.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Un estudio dice que… se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Estudio de eficacia escolar en el País Vasco
- La innovación educativa actual desde la perspectiva histórica
- La letra pequeña de algunos métodos de aprendizaje
Atajos adiabáticos: lo bueno si breve…

En el mundo cuántico, los procesos ‘adiabáticos’ son aquellos en los que los controles del sistema se modifican lentamente. Muy comunes para preparar o cambiar estados sin excitar el sistema que queremos controlar, sufren sin embargo los mismos problemas que hemos mencionado en el párrafo anterior: falta de tiempo y probabilidad muy alta de ser perturbados. Son problemas graves en este contexto, ya que los estados de los sistemas cuánticos tienden a ser muy delicados y a degradarse rápidamente perdiendo precisamente sus valiosas y extrañas propiedades cuánticas como la posibilidad de explorar varios caminos a la vez. Para colmo, en un tiempo demasiado prolongado un átomo puede acabar escapándose de la trampa que lo contiene.
Los ‘atajos a la adiabaticidad’ son técnicas para soslayar las dificultades que acabamos de describir: se trata de conseguir los mismos resultados que los lentos procesos adiabáticos pero en poco tiempo. El término apareció por primera vez en 2010 en un trabajo publicado en Physical Review Letters por investigadores de la UPV/EHU con colaboradores de Alemania y Francia. Desde entonces estas ideas se han desarrollado por los autores del artículo y por muchos otros grupos, y se han puesto en práctica en numerosos experimentos con todo tipo de sistemas cuánticos. Da una idea del crecimiento exponencial de las aplicaciones el que solo en 2018 los atajos se han mencionado o utilizado en más de 1.500 artículos. El concepto de ‘atajo a la adiabaticidad’ se ha extendido también más allá del dominio cuántico hacia campos como la óptica, para fabricar dispositivos más compactos; o la ingeniería, donde, sorprendentemente, permite, por ejemplo, acelerar una grúa mecánica sin poner en riesgo la seguridad.
Un equipo europeo, con Gonzalo Muga (del equipo original) y Sofía Martínez Garaot, como investigadores de la UPV/EHU (Facultad de Ciencia y Tecnología), más otros cuatro coautores, ha compilado los conceptos, métodos y aplicaciones de los ‘atajos’ desarrollados durante estos diez últimos años en un sustancioso artículo –casi un breve libro- que servirá de referencia básica para cualquier avance posterior. El artículo, publicado en Review of Modern Physics, que ocupa el primer lugar entre las revistas de Física según varios criterios como el índice de Scimago o las citas por documento, combina según sus autores el rigor científico con una intención didáctica y tono ameno, como demuestra la Figura 1, que ilustra metafóricamente el espíritu de los atajos mediante una tortuga sobre ruedas.
Referencia:
D. Guéry-Odelin, A. Ruschhaupt, A. Kiely, E. Torrontegui, S. Martínez-Garaot, and J.G. Muga (2019) Shortcuts to adiabaticity: Concepts, methods, and applications Rev. Mod. Phys. doi: 10.1103/RevModPhys.91.045001
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Atajos adiabáticos: lo bueno si breve… se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Sin atajos frente al cáncer
- Breve historia de las ciencias del clima
- El ‘truelo’ de «el bueno», «el feo» y «el malo»
¿Qué es el pH?
 Foto: Kelly Sikkema / Unsplash
Foto: Kelly Sikkema / UnsplashA menudo en cosmética se hace referencia al pH. También en productos de limpieza e higiene, y en alimentación. Incluso hay dietas anticientíficas, como la dieta alcalina, que dicen fundamentarse en el concepto de pH.
Para entender qué es el pH, primero debemos entender qué es un ácido.
A lo largo de la historia hemos dado descripciones cada vez más sofisticadas de qué es un ácido y, en consecuencia, hemos diseñado una variable para medir el nivel de acidez de una sustancia: el pH.
Al principio hablábamos de ácidos como sustancias con una serie de propiedades comunes con respecto al sabor. El sabor ácido del limón o del vinagre, por ejemplo. Ahora sabemos que estos sabores dependen del ácido cítrico y del ácido acético, respectivamente. Además, descubrimos que estas sustancias de “sabor ácido” tiñen de rojo determinados pigmentos, como el tornasol que se extrae de algunos líquenes. Tradicionalmente se extrae de roccellas y dendrographas. También atacan al mármol y reaccionan con algunos metales desprendiendo gas hidrógeno. El químico Robert Boyle fue el primero en llamar ácidos a estas sustancias con propiedades similares. Fue en 1663.
Hay sustancias que son opuestas a los ácidos. Que en contacto con los ácidos amortiguan sus propiedades. Son sustancias de sabor amargo, que producen sensación jabonosa en la piel y tiñen de azul el tornasol. A estas sustancias las denominamos álcalis, del árabe al kali, que significa cenizas vegetales.
Cuando mezclamos una sustancia ácida con otra alcalina se obtiene una sal que pierde las propiedades de ambas. Así los álcalis recibieron más tarde el nombre de bases, del griego basis, que significa fundamento para la obtención de sales. Cuando se mezcla un ácido con una base se forma una sal.
Sabemos que las propiedades de cualquier sustancia dependen de su composición y de su estructura. El químico Lavoisier conjeturó que los ácidos eran sustancias que contenían un elemento químico que en 1777 denominó oxígeno. La palabra oxígeno está formada por dos raíces griegas, oxys, ácido, por el sabor punzante de estas sustancias, y genes, productor o engendrador. De modo que la palabra oxígeno significa engendrador de ácidos.
Sin embargo, años más tarde se descubrieron otras sustancias con propiedades ácidas que no contenían oxígeno en su composición. Como el ácido muriático (hoy llamado ácido clorhídrico, HCl) que sirvió al químico Humphry Davy para conjeturar en 1810 que la acidez de las sustancias depende del hidrógeno, no del oxígeno.
Más adelante, el químico Justus von Liebig quiso completar la idea de Davy. En 1838 propuso la existencia de dos tipos de hidrógeno, siendo el hidrógeno que puede sustituirse por metales el responsable de las propiedades de los ácidos.
El químico Svante August Arrhenius fue más allá. En 1887 propuso que el hidrógeno ácido era hidrógeno que se desprendía de las sustancias ácidas como ion hidrógeno, escrito H+ y coloquialmente denominado protón.
Esto permitió dar una definición más concreta sobre las bases. Arrhenius conjeturó que, si las bases neutralizaban a los ácidos sería porque contienen un ion de carga opuesta que da lugar a la formación de una sustancia que no es ni ácida ni básica, sino neutra. Pensó que ese ion sería el OH–, ya que al unirse al H+ de los ácidos, daría lugar a la formación de agua, H2O.
Las definiciones de Arrhenius para los ácidos y las bases son limitadas, sobre todo para las bases, ya que no todas las sustancias de propiedades básicas contienen OH–, como por ejemplo una conocida base que utilizamos como producto de limpieza: el amoníaco, NH3. Sin embargo, y a pesar de sus inconvenientes, esta teoría estuvo vigente casi cuarenta años, durante los cuales se fueron sucediendo nuevas ideas que darían lugar a teorías más completas.
El químico Johannes Nicolaus Brønsted y el químico Thomas Martin Lowry, simultáneamente, pero siguiendo líneas de trabajo diferentes, propusieron en 1923 una definición más precisa sobre los ácidos y las bases. Esta definición forma parte de la que conocemos como teoría ácido-base de Brönsted-Lowry. Según esta teoría, los ácidos son sustancias capaces de donar un protón (H+), mientras que las bases son capaces de aceptarlos. De esta manera las reacciones entre ácidos y bases pueden interpretarse como reacciones de transferencia de protones. Así por ejemplo el amoníaco (NH3), es una base porque es capaz de captar H+ y formar el ion amonio (NH4+).
 Imagen: Deborah García Bello
Imagen: Deborah García BelloEn la actualidad existen teorías más completas que la de Brönsted-Lowry, siendo la más conocida la teoría de Lewis de 1938, que se basa en un concepto electrónico de mayor complejidad. Aun así, la definición de uso más común de ácidos y bases es la que formularon Brönsted y Lowry.
A partir de la definición de ácido de Brönsted y Lowry, el químico Søren Peter Lauritz Sørensen introdujo por primera vez en 1909 el concepto de pH. El pH está ligado a la cantidad de H+.
Mediante el uso de electrodos podemos medir la cantidad de H+ presente en una disolución, es decir, la concentración de H+.
Para darle una numeración más manejable, Sørensen decidió aplicar la función logaritmo sobre el valor de la concentración de H+. Esa es la definición matemática del pH: el logaritmo en base 10, cambiado de signo, de la concentración de H+, cuando ésta se expresa en moles por decímetro cúbico.
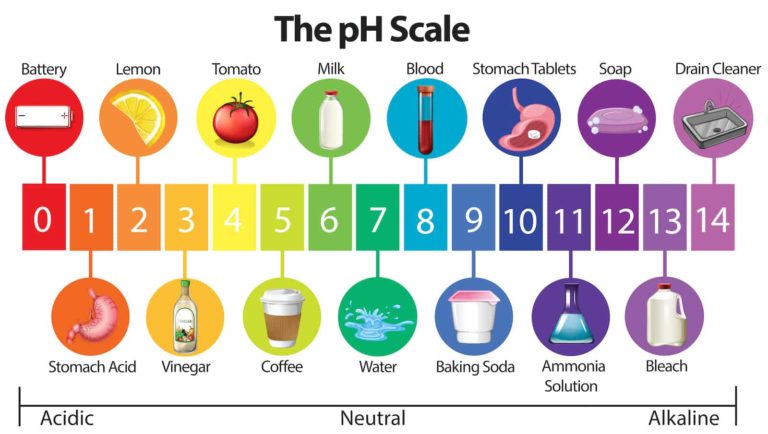 Fuente: Vectores por Vecteezy
Fuente: Vectores por VecteezyDe esa manera obtuvo una escala de pH, que es la que utilizamos en la actualidad, que normalmente oscila entre los valores 0 y 14. Así, el valor de pH 7 se corresponde con las sustancias neutras. El agua pura tiene pH 7. Las sustancias ácidas son las que tienen un pH inferior a 7, y las básicas superior a 7.
En la actualidad, para medir el pH utilizamos un electrodo sensible a los H+. Se conoce como pH-metro (pronunciado peachímetro). Cada vez que se usa hay que calibrarlo usando unas disoluciones de referencia cuyo pH es conocido y sirven de patrón para que el aparato construya la escala de pH.
Hay otras maneras de medir el pH. Una manera no tan precisa, pero útil, es el uso de indicadores colorimétricos de pH. Según el color que adquieren, podemos saber el valor aproximado del pH. El más antiguo y que se sigue usando es el tornasol. En disoluciones ácidas, de pH inferior a 5, el tornasol es rojo, mientras que cuando el pH excede de 8 se vuelve azul.
Los indicadores son ácidos débiles, es decir, aunque tengan preferencia por donar iones H+, también coexisten con otra forma básica que puede aceptarlos, y cada una de estas formas presenta una coloración diferente.
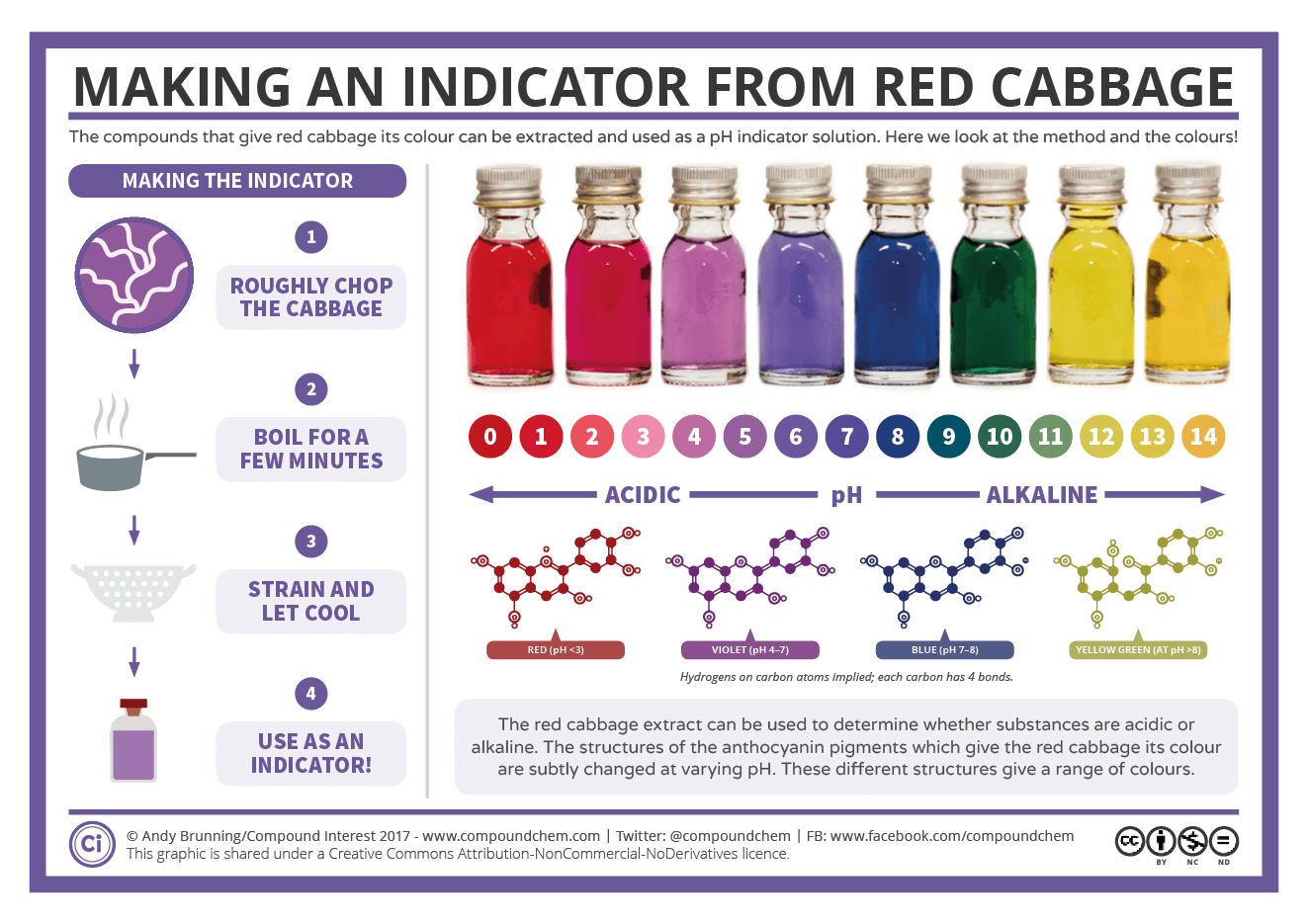
Otro indicador colorimétrico de origen vegetal son las antocianinas. Las antocianinas de la col lombarda se pueden aprovechar para fabricar un papel indicador ácido-base casero. Para eso se empapa un papel de filtro con zumo concentrado de lombarda macerada y hervida. El papel se deja secar y finalmente se corta en tiras para obtener varios indicadores de pH. A pH entre 1 y 2 el color del zumo de lombarda será rojizo, a pH 4 será color ciruela, a pH 5 será púrpura, a pH 6-7 será azul, a pH 8 será azul verdoso, a pH 9-10 será verde esmeralda, a pH 10-11 será verde hierba, a pH 12-13 será verde lima y a pH 14 amarillo.
En el laboratorio utilizamos varios indicadores de pH. Los más habituales son la fenolftaleína, el naranja de metilo o el azul de metileno.
El pH es una variable química que nos permite medir el grado de acidez de una sustancia. Su definición tiene cierta complejidad, y aun así ha calado en el lenguaje coloquial. Sin embargo, la palabra pH no siempre se emplea de manera correcta. De hecho, ignorar el significado del pH, igual que ignorar qué es un ácido o qué es un álcali, hace que las decisiones también sean ignorantes. Como decantarse por la compra de un producto, sin entender si su pH lo hace mejor o peor, o decidir seguir una dieta aberrante porque presuntamente está basada en este concepto científico. Por cierto, el zumo limón no es alcalino, es ácido.
Sobre la autora: Déborah García Bello es química y divulgadora científica
El artículo ¿Qué es el pH? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Por qué se corta la mayonesa y qué relación tiene esto con la cosmética
- Sal de la piscina si te pican los ojos y no mezcles lejía con amoniaco
- El ácido hialurónico no sirve para todo, aunque lo parezca
¿Cuántas bolas contiene el jarrón al mediodía?
Un buen chiste matemático es mejor, y mejor matemática, que una docena de publicaciones mediocres.
John Edensor Littlewood, A Mathematician’s Miscellany, 1953
El matemático británico John Edensor Littlewood (1885-1977) publicó en 1953 su autobiografía, A Mathematician’s Miscellany, que contenía numerosas anécdotas. Se reeditó en 1986, añadiendo más contenidos, bajo el título de Littlewood’s miscellany.

En este último libro, Littlewood utiliza ese sentido del humor al que alude la cita inicial para enunciar la llamada ley de Littlewood que establece que «una persona puede esperar que le suceda un milagro aproximadamente una vez al mes». Pero, ¿qué es un milagro? Littlewood lo define así:
Un evento extraordinario que tiene un significado especial y ocurre con una frecuencia de uno entre un millón.
Y el matemático argumenta entonces de la siguiente manera:
Mientras una persona está despierta puede percibir ‘un evento’ por segundo, evento que puede ser ordinario o extraordinario. Supongamos que una persona es ‘receptiva’ aproximadamente durante ocho horas al día. Así, experimenta 28.800 eventos al día –una hora tiene sesenta minutos y cada minuto sesenta segundos: son 8x60x60–. Así, en 35 días, una persona experimentará 1.008.000 de eventos. Según la definición dada de milagro, una persona puede esperar un acontecimiento milagroso cada 35 días.
Es decir, según Littlewood, los milagros no son tan extraños, ni tienen que ver con poderes sobrenaturales. En efecto, tan solo hay que tener en cuenta la ley de los grandes números…
En A Mathematician’s Miscellany, Littlewood describe un problema conocido actualmente como la paradoja de Ross-Littlewood. Toma su nombre del matemático Sheldon Ross (1943) quien lo detalló en su libro A First Course of Probability (1988). Esta paradoja intenta ilustrar los problemas conceptuales relacionados con la noción de supertarea –sucesión infinita numerable de operaciones que se producen secuencialmente en un intervalo de tiempo finito–.
Planteamiento del problema
Tenemos un jarrón vacío y una cantidad infinita numerable de bolas a nuestra disposición. En cada paso –recordemos que hay un número infinito de ellos– se agregan 10 bolas al jarrón y se retira 1 bola del mismo. Se supone que el jarrón está vacío un minuto antes del mediodía, y que se realizan los infinitos pasos de la manera siguiente:
-
el primer paso se realiza 30 segundos antes del mediodía;
-
el segundo paso se realiza 15 segundos antes del mediodía;
-
así, cada paso siguiente se realiza en la mitad del tiempo del paso anterior, es decir, el paso n se realiza 2−n minutos antes del mediodía.
Continuando de este modo, transcurrido un minuto, se han realizado una cantidad infinita numerable de pasos. La pregunta es: «¿cuántas bolas hay en el jarrón al mediodía?».
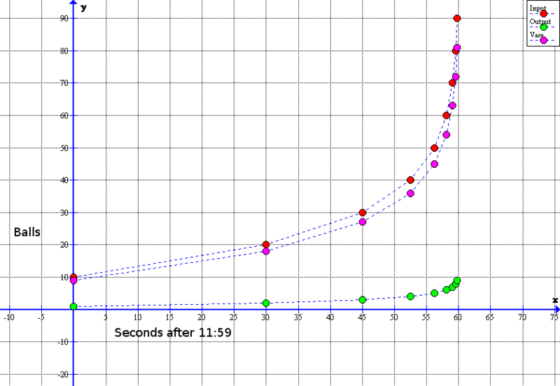 Gráfica que muestra el número de bolas dentro y fuera del jarrón en los diez primeros pasos. Imagen: Wikimedia Commons.
Gráfica que muestra el número de bolas dentro y fuera del jarrón en los diez primeros pasos. Imagen: Wikimedia Commons.
No hay una única respuesta como veremos a continuación, y de allí que hablemos de paradoja… ¿Quizás estemos asistiendo a ese acontecimiento milagroso que es posible que nos ocurra este mes de noviembre?
Algunas respuestas a la pregunta
-
El jarrón contiene infinitas bolas
En efecto, en cada paso se añaden más bolas de las que se eliminan. Es decir, en cada paso habrá un número mayor de bolas que en el paso anterior. Así, si el número de bolas aumenta en cada paso y hay un número infinito de ellos, habrá infinitas de bolas al mediodía.
-
El jarrón está vacío
Supongamos que las bolas están numeradas. Argumentamos del siguiente modo: en el paso 1 se meten en el jarrón las bolas 1 a 10 y se saca la bola número 1. En el paso 2, se introducen las bolas numeradas 11 a 20, y se retira la bola 2. Si se continúa de este modo, al mediodía, la bola número n introducida en el jarrón se elimina en un paso posterior –en el paso n–. Así, si cualquier bola se extrae en alguno de los pasos, el jarrón está obviamente vacío al mediodía.
-
Depende de las condiciones
Esta respuesta afirma que la cantidad de bolas contenidas en el jarrón al mediodía depende del orden en el que se sacan las bolas del jarrón. Antes hemos visto la manera en la que se consigue demostrar que el jarrón está vacío al mediodía. Supongamos ahora que la bola número 10 se retira del jarrón en el paso 1, la bola número 20 en el paso 2, y así sucesivamente. Procediendo de esta manera, es claro que al mediodía quedan infinitas bolas en el jarrón.
Pero, más aún, es posible razonar de manera que, al mediodía, queden cualquier número de bolas –n– en el jarrón. En efecto, si p es el número de paso que se está realizando, se procede del siguiente modo:
-
se ponen las bolas numeradas 10p-9 a 10p en el jarrón,
-
si p≤n, se saca la bola número 2p,
-
si p>n, se saca la bola número n+p del jarrón.
Procediendo de este modo, es claro que las n primeras bolas impares no se sacan del jarrón, mientras que todas las bolas mayores o iguales a 2n sí se eliminan. Así, a mediodía quedan exactamente n bolas en el jarrón.
-
El problema no está bien especificado
Lo que sucede con las bolas y el jarrón está determinado en cada momento antes del mediodía, pero no es posible concluir lo que sucede después del mediodía.
-
El problema está mal planteado
Si deben realizarse infinitos pasos de manera secuencial antes del mediodía, el mediodía es un punto en el tiempo que no se puede alcanzar. Además, preguntar cuántas bolas quedarán en el jarrón al mediodía es asumir que se llegará a ese momento del día. Por lo tanto, hay una contradicción implícita en el planteamiento del problema.
¿Cuál de estas respuestas te convence más?
Referencias
-
John Edensor Littlewood, A Mathematician’s Miscellany, Methuen and Co, 1953
-
Béla Bollobás (ed.),Littlewood’s miscellany, Cambridge University Press, 1986
-
Paradoja de Ross-Littlewood, Wikipedia (consultado el 23 de noviembre de 2019)
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo ¿Cuántas bolas contiene el jarrón al mediodía? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Galileo (V): los experimentos con bolas y planos inclinados
- ¿Cuántas células hay en el cuerpo humano?
- Cuantas menos ecuaciones…. ¿mejor?
Las limitaciones del modelo de Bohr
 Foto: Jeremy Perkins / Unsplash
Foto: Jeremy Perkins / UnsplashEl modelo de Bohr se encontró con críticas fundamentadas graves antes incluso de hacerse público. En marzo de 1913 Bohr escribió a su mentor Rutherford adjuntando un borrador de su primer artículo sobre el modelo cuántico de la constitución atómica. Rutherford respondió en una carta, cuyo comienzo recojemos aquí [1][2]:
Estimado Dr. Bohr:
Recibí su trabajo y lo leí con gran interés, pero quiero volver a revisarlo cuidadosamente cuando tenga más tiempo libre. Sus ideas sobre la forma en la que se originan los espectros en el hidrógeno son muy ingeniosas y parecen funcionar bien; pero la mezcla de las ideas de Planck con la vieja mecánica hace que sea muy difícil formar una idea física de cuál es la base. Me parece una grave dificultad en su hipótesis, de la que no tengo dudas de que se da cuenta plenamente, a saber, ¿cómo decide un electrón a qué frecuencia va a vibrar cuando pasa de un estado estacionario a otro? Me parece que tendría que asumir que el electrón sabe de antemano dónde se detendrá. . . .
Con todo, el modelo de Bohr logró grandes éxitos entre 1913 y 1924. Pero también contenía preguntas sin respuesta y problemas no resueltos, como Rutherford había observado inmediatamente. Con el paso del tiempo surgieron problemas adicionales para los que el modelo resultaba claramente inadecuado. Los tres quizás más significativos eran los siguientes:
1.- El modelo de Bohr explicaba muy bien los espectros de los átomos con un solo electrón en la capa más externa. Sin embargo, aparecieron serias diferencias entre el modelo y el experimento en los espectros de los átomos con dos o más electrones en la capa más externa.
2.- Los experimentos también pusieron de manifiesto que cuando una muestra de un elemento se coloca en un campo eléctrico o magnético su espectro de emisión muestra líneas adicionales. Por ejemplo, en un campo magnético cada línea se divide en varias líneas. El modelo de Bohr no pudo explicar, de manera cuantitativa, algunas de las divisiones observadas.
3.- Además, el modelo no proporcionaba explicación alguna para el brillo relativo (intensidad) de las líneas espectrales. Estas intensidades relativas dependen de las probabilidades con las que los átomos en una muestra experimentan transiciones entre los estados estacionarios; altas probabilidades se traducen en líneas más intensas. Se debería poder calcular la probabilidad de una transición de un estado estacionario a otro, pero el modelo de Bohr no permitía hacerlo.
A principios de años veinte estaba claro que el modelo de Bohr, a pesar de sus notables éxitos, estaba muy limitado. Para crear un modelo que resolviese más problemas el modelo de Bohr tendría que ser o revisado en profundidad o completamente reemplazado [3]. Pero los éxitos de el modelo de Bohr hacían necesario que cualquier nuevo modelo de la estructura atómica aún tendría que explicar la existencia de estados estacionarios. Por lo tanto, un nuevo modelo tendría que basarse en conceptos cuánticos [4].
Notas:
[1] Traducción propia
[2] Original:
Dear Dr. Bohr:
I have received your paper and read it with great interest, but I want to look it over again carefully when I have more leisure. Your ideas as to the mode of origin of spectra in hydrogen are very ingenious and seem to work out well; but the mixture of Planck’s ideas with the old mechanics make it very difficult to form a physical idea of what is the basis of it. There appears to me one grave difficulty in your hypothesis, which I have no doubt you fully realize, namely, how does an electron decide what frequency it is going to vibrate at when it passes from one stationary state to the other? It seems to me that you would have to assume that the electron knows beforehand where it is going to stop. . . .
[3] Un recordatorio de que un objetivo principal de la ciencia hoy es preparar el terreno para una ciencia mejor mañana. Véase Provisional y perfectible.
[4] Un recordatorio de que los nuevas modelos tienden a evolucionar incorporando lo que era bueno en los antiguos. Desde este punto de vista la ciencia es más conservadora que revolucionaria. Esto está íntimamente relacionado con la incapacidad de diseñar experimentos cruciales. Véase a este respecto El experimento crucial que nunca existió o, en general, los artículos de la serie sobre La tesis de Duhem-Quine.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Las limitaciones del modelo de Bohr se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El modelo de Bohr explica las regularidades en el espectro del hidrógeno
- El modelo de Bohr explica la fórmula de Balmer
- El modelo de Bohr-Sommerfeld y las propiedades químicas de los elementos
Concurso: diseña el primer símbolo que represente la resistencia a los antibióticos

Con motivo de la celebración del Día Europeo del Antibiótico en Estocolmo, se ha lanzado un concurso de diseño para encontrar el primer símbolo global de la amenaza de la resistencia a los antibióticos. No se busca un logotipo, sino algo tangible que cualquier persona, en cualquier lugar, pueda hacer en casa y llevar con orgullo; como el lazo del SIDA.
El concurso está abierto a todo el mundo, sin importar su origen o edad. Todo aquel al que le guste la ciencia, tenga una mente creativa o quiera contribuir a concienciar sobre la amenaza global de la resistencia a los antibióticos, puede participar. Se aceptarán candidaturas hasta el 31 de marzo de 2020, y el diseño ganador, que recibirá un premio de 2.000 €, se anunciará el próximo verano. Todas las reglas del concurso están disponibles en eu-jamrai.eu.
Este concurso es una de las actividades desarrolladas por la Acción Conjunta Europea frente a las Resistencias Antimicrobianas y las Infecciones relacionadas con la Asistencia Sanitaria (EU-JAMRAI, por sus siglas en inglés), para promover el uso prudente de antibióticos con el fin de detener el desarrollo de bacterias resistentes y mantener la efectividad de estos medicamentos.
Los antibióticos son medicamentos utilizados para prevenir y tratar infecciones bacterianas. Su uso excesivo tanto en humanos como en animales, está provocando que las bacterias se vuelvan resistentes a los antibióticos. Sin antibióticos que funcionen, cirugías de rutina como el reemplazo de cadera, enfermedades comunes como la diarrea e incluso pequeños cortes, pueden poner en peligro la vida.
A día de hoy, ya hay gente que está muriendo por infecciones resistentes a los antibióticos, y a medida que más antibióticos dejen de funcionar, más vidas se pondrán en peligro.
La resistencia a los antibióticos es una amenaza global y uno de los mayores retos a los que nos enfrentamos, pero muy poca gente lo sabe. ¡Esto hay que cambiarlo! Sé parte del cambio y participa en nuestro concurso para diseñar el primer símbolo que represente la resistencia a los antibióticos a nivel global.
El artículo Concurso: diseña el primer símbolo que represente la resistencia a los antibióticos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Una nueva vía para la lucha contra la resistencia a los antibióticos
- El camino hacia los antibióticos inservibles
- El papel de la agricultura en la transmisión de la resistencia a antibióticos
Cocinar nos hizo humanos
 Foto: Robson Hatsukami Morgan / Unsplash
Foto: Robson Hatsukami Morgan / UnsplashHace una década se publicó un libro sobre evolución humana de mucho impacto y cuya influencia no ha dejado de aumentar desde entonces, al menos entre quienes, sin ser profesionales, nos interesa la evolución de nuestra especie. El libro se titula Catching Fire: How Cooking Made Us Human (traducido este año al español con el título En llamas: Cómo la cocina nos hizo humanos).
Sostiene Richard Wrangham, su autor, que Homo erectus surgió hace dos millones de años en la sabana africana gracias, precisamente, a los efectos que tuvo el control y uso del fuego sobre una serie de rasgos fisiológicos y de comportamiento. Por orden de aparición H. erectus es, probablemente, la segunda especie del género Homo, después de H. habilis, aunque el conocimiento sobre ese periodo de nuestra evolución se está enriqueciendo mucho durante estos años y no cabe descartar que se modifique el estatus de esas especie, así como sus fechas de aparición.
Según Wrangham, aumentó tanto la eficiencia con que digerimos y absorbemos el alimento al cocinarlo, que ello tuvo profundas consecuencias evolutivas. Una misma cantidad de alimento cocinado rinde mucha más energía y nutrientes que si se ingiere crudo. Eso ocurre porque cuando se cocina, moléculas de gran tamaño como proteínas o carbohidratos ven alterada su estructura y se hacen más fácilmente accesibles a la acción digestiva. Como consecuencia, se necesita menos cantidad de alimento para vivir, por lo que debe dedicarse menos tiempo a conseguirlo, masticarlo y digerirlo. Y lo que es tan importante o más: para procesar la comida que necesitamos basta con un sistema digestivo mucho más pequeño que el que tenían nuestros antepasados y el que tienen gorilas y chimpancés.
De esa forma –y aquí está el elemento evolutivo clave-, el sistema digestivo pudo reducir mucho su tamaño y ello hizo que dispusiésemos de mucha más energía con la que nutrir al encéfalo, que pudo así aumentar su tamaño hasta el volumen impresionante que tiene en la actualidad. Para valorar esa transición en sus justos términos debe tenerse en cuenta que el tejido digestivo y el nervioso (junto con el renal) son los que consumen más energía por unidad de masa, por lo que encéfalo y aparato digestivo resultan muy caros de mantener. No tanto los riñones, por su pequeño tamaño.
Además, el control del fuego proporciona calor y una forma de mantener a los depredadores a raya. Eso habría propiciado un modo de vida menos arborícola y con más tiempo y actividad sobre el suelo, lo que habría facilitado el desarrollo o perfeccionamiento de la bipedestación.
El problema de la hipótesis de Wrangham cuando la formuló hace una década era que no había evidencias de control del fuego tan antiguas como dos millones de años. Ahora bien, no es lo mismo ausencia de evidencia que evidencia de ausencia. Diez años después todavía no podemos responder la cuestión de cuándo empezaron los seres humanos a controlar el fuego, pero un trabajo recién publicado ha “documentado la asociación entre combustión y comportamiento humano” en al menos un yacimiento arqueológico de 1,5 millones de años de antigüedad en la Formación de Koobi Fora, en el noroeste de Kenia. Y es muy posible que esa asociación también se produjese en otros dos lugares próximos y de la misma época. Es muy difícil contar con pruebas del uso controlado del fuego tantos miles de años atrás. Pero los hallazgos en Koobi Fora apoyan una hipótesis que, como la de Wrangham, resulta muy atractiva por sus fundamentos fisiológicos y, por qué negarlo, por lo que a muchos nos gusta la buena cocina.
Fuente: Hlubik S, Cutts R, Braun D R, Berna F, Feibel C S & Harris J W K (2019): Hominin fire use in the Okote member at Koobi Fora, Kenya: New evidence for the old debate. Journal of Human Evolution 133: 214-229.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Cocinar nos hizo humanos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¿Qué nos puede decir un elefante del cáncer en humanos?
- Las aves de Prometeo
- Los tipos celulares humanos y su origen embrionario
La innovación educativa actual desde la perspectiva histórica
Vitoria-Gasteiz acogió por primera vez el pasado 18 de octubre el evento Las pruebas de la educación, una jornada que abordó diversos temas educativos desde la evidencia científica. El acto, organizado por el Consejo Escolar de Euskadi y la Cátedra de Cultura Científica de la UPV/EHU, tuvo lugar en el Salón de Actos del Centro de Investigación Micaela Portilla, ubicado en el Campus de la capital alavesa de la UPV/EHU.

La jornada consta de un total de cinco charlas que tratan temas como el rendimiento académico, los métodos de aprendizaje y la innovación educativa, entre otros. La dirección del seminario corre a cargo de la doctora en psicología Marta Ferrero.
Fátima García, diplomada en Magisterio por la USC, licenciada en Filosofía y Ciencias de la Educación por la UNED y doctora en Didáctica e Innovación por la USC, habla en esta charla sobre cómo la perspectiva histórica puede ser un aliado a la hora de tomar decisiones ante el bombardeo de noticias sobre innovaciones educativas.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo La innovación educativa actual desde la perspectiva histórica se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La intervención en la dislexia: de la evidencia científica a la práctica educativa
- Las primeras manifestaciones de las funciones ejecutivas y la acción educativa en el aula 0-1
- La letra pequeña de algunos métodos de aprendizaje
El papel de la agricultura en la transmisión de la resistencia a antibióticos
![]()
Usue Pérez López y Maite Lacuesta Calvo
 Foto: Etienne Girardet / Unsplash
Foto: Etienne Girardet / UnsplashEl aumento de resistencias a antibióticos en bacterias patógenas se ha convertido en un gran problema de salud a nivel mundial, ya que reduce la eficacia terapéutica de los antibióticos.
Aunque este fenómeno ha ocurrido de forma natural desde épocas remotas, se ha hecho mucho más frecuente en las últimas décadas. Las principales causas son el uso excesivo o inadecuado de los antimicrobiales y su mayor presencia y permanencia en el medio ambiente.
La diseminación de antibióticos en el medio natural se asocia principalmente a su aplicación en medicina y veterinaria.
Sin embargo, no se ha considerado adecuadamente el papel que la agricultura, como base de la cadena trófica, puede desempeñar en la transmisión de antibióticos, de bacterias resistentes a antibióticos y de genes de resistencia a antibióticos a través de los alimentos. Podríamos estar infravalorándolo.
¿Cómo llegan los antibióticos al campo?
En el ámbito anglosajón, el término agricultura incluye la producción de cultivos, pero también la ganadería y la acuicultura, que constituyen la principal entrada de antibióticos en el sistema agrario.
Se estima que la cantidad de antibióticos empleados en la protección de cultivos representa menos del 0,5 % del total empleado en producción animal. Esto excluye a Europa, donde su aplicación en cultivos está prohibida.
Sin embargo, cada vez es más frecuente el uso de estiércol animal, residuos orgánicos o lodos de depuradora como material fertilizante. Este material puede contener una alta carga de antibióticos.
Algunos estudios confirman que entre un 30 y un 90 % de los antibióticos usados en animales aparece en los excrementos. El estiércol contaminado expone a los cultivos, incluso a los orgánicos, a la presencia de antibióticos.
Esto, unido al uso de aguas residuales en el riego, provoca que estos agro-ecosistemas estén expuestos repetidamente, y durante largos periodos de tiempo, a la presencia de una considerable y variada carga de antibióticos.
Estos agentes pueden ser tomados por las plantas y causar efectos fitotóxicos que afecten a la germinación y el crecimiento de los distintos cultivos agrícolas. Además, pueden acumularse en los tejidos vegetales y suponer un riesgo potencial para la salud humana, al ser las plantas el primer eslabón de la cadena alimentaria.
Este riesgo se ha tenido en cuenta solo en las dos últimas décadas y, por tanto, la información sobre su impacto es limitada.
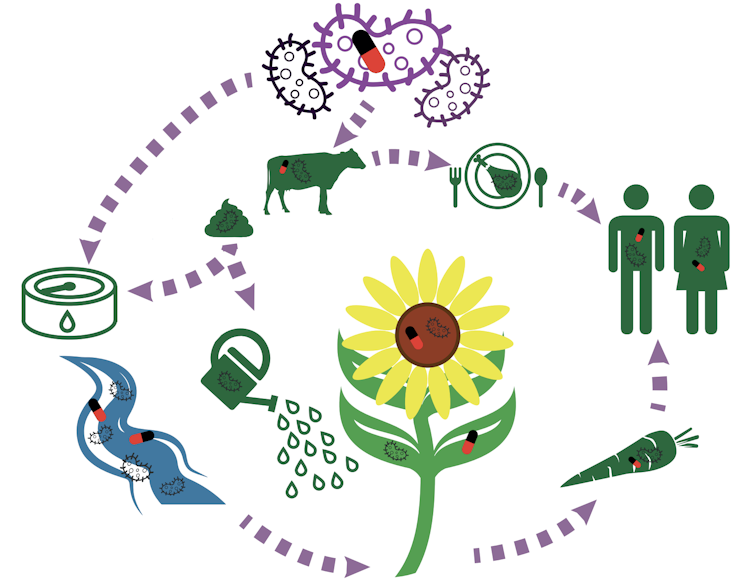 Diseminación de los genes de resistencia y bacterias resistentes a los antibióticos en agricultura.
Diseminación de los genes de resistencia y bacterias resistentes a los antibióticos en agricultura.Asier Cantabrana, Author provided
Efectos de los antibióticos en las plantas
Recientes estudios han demostrado que la fitotoxicidad de los antibióticos en los cultivos depende en gran medida de la especie vegetal y del tipo de antibiótico, así como de su concentración en el suelo.
Sin embargo, la mayoría de los estudios fitotóxicos de los antibióticos se han realizado in vitro. Escasean los estudios en campo. Si bien es cierto que se han observado efectos negativos con altas concentraciones, en bajas concentraciones se ha detectado un efecto estimulador.
Además del impacto directo de los antibióticos en el crecimiento vegetal, indirectamente pueden provocar alteraciones en la microbiota del suelo. Esto afecta a su diversidad y a la presencia de bacterias beneficiosas para el cultivo como las bacterias fijadoras de N₂, lo que también puede afectar al rendimiento del cultivo.
¿Qué hacer a partir de ahora?
Las plantas pueden entrar en contacto con los antibióticos de dos maneras:
- Receptoras directas. Cuando los antibióticos se aplican para el control de enfermedades bacterianas.
- Receptoras indirectas. Por la aplicación de enmiendas orgánicas, lodos de depuradoras o aguas residuales.
Como consecuencia, su crecimiento puede sufrir efectos negativos directos e indirectos, por la modificación de los microorganismos del suelo con los que interaccionan. Además, pueden actuar como transmisoras tanto de antibióticos como de resistencias, puesto que son la base de la cadena alimentaria.
Por ello, resulta necesario monitorizar, cuantificar y minimizar el grado de contaminación por antibióticos de los aportes o enmiendas orgánicas y del agua que se aplica a los cultivos.
Aunque se han utilizado diversos tratamientos como el compostaje o la conversión en biochar (carbón vegetal) para reducir la cantidad de antibióticos y subproductos presentes en el estiércol, no se ha conseguido aún una eliminación del 100 %.
Esto se debe a que la eficiencia del proceso depende de múltiples factores (material de partida, microorganismos presentes, temperatura, tiempo, tipo de antibióticos presentes…). Por ello, se necesitan todavía nuevos estudios y mejoras tecnológicas para poder conseguir una eliminación total de los antibióticos que se aplican mediante enmiendas orgánicas en los cultivos.
Paralelamente, es necesario investigar en profundidad cómo los antibióticos entran en las plantas, su transformación y/o acumulación en los diferentes órganos vegetales y su persistencia en los mismos. Sobre todo, de aquellos que van a destinarse para la alimentación, ya sea animal o humana.
Estos estudios ayudarán a reducir su potencial riesgo para la salud de las personas. Además, teniendo en cuenta que estos sistemas de fertilización y riego se llevan a cabo año a año de manera repetida, es importante realizar análisis sistemáticos a largo plazo.
Sobre las autoras: Usue Pérez López es profesora agregada de fisiología vegetal y Maite Lacuesta Calvo, es profesora titular del Departamento de Biología vegetal y Ecología de la Universidad del País Vasco / Euskal Herriko Unibertsitatea
Este artículo fue publicado originalmente en The Conversation. Artículo original. Es un resumen de la charla impartida en el curso de verano de la UPV/EHU organizada por el JRL Environmental Antibiotic Resistence, al que pertenecen las autoras.![]()
El artículo El papel de la agricultura en la transmisión de la resistencia a antibióticos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Una nueva vía para la lucha contra la resistencia a los antibióticos
- Un nuevo mecanismo de resistencia antifúngico
- El camino hacia los antibióticos inservibles
¿Es la música un lenguaje universal?
 Asentamiento mafa cerca de Maroua, norte de Camerún. ¿Qué opinarán sus habitantes de la música del estonio Arvo Pärt? Fuente: Wikimedia Commons
Asentamiento mafa cerca de Maroua, norte de Camerún. ¿Qué opinarán sus habitantes de la música del estonio Arvo Pärt? Fuente: Wikimedia CommonsEn “Encuentros en la tercera fase”, cuando los alienígenas llegan a la Tierra, parece haber una única manera manera de comunicarse con ellos: a pesar de la separación de millones de galaxias y otros tantos años luz, la música parece ser el punto de encuentro entre la humanidad y la recién llegada civilización extraterrestre.
La famosa película de Spielberg se estrenó en noviembre de 1977, apenas meses después de que Estados Unidos lanzase sus sondas Voyager al espacio. A bordo viajaba (y aún hoy viaja) el famoso disco de oro, un mensaje flotando en medio de la nada; una botella en un océano interminable y sin corrientes; dispuesto para ser leído por cualquiera que lo encuentre, da igual lo pequeña que sea esa probabilidad. Además de saludos en distintos idiomas y ejemplos de sonidos de la Tierra, el disco lleva grabados ejemplos de canciones de todo el mundo.
Probablemente, todos estemos de acuerdo en que estos dos relatos suponen llevar muy al límite la idea de la música como lenguaje universal. Pero, incluso restringiendo lo universal a la superficie de nuestro planeta, la noción de que la música es capaz de comunicar ideas (y, en particular, emociones) más allá de las barreras culturales no está exenta de polémica.
Por un lado, es fácil comprobar que a lo largo y ancho del planeta existen multitud de culturas con una enorme diversidad musical. Las escalas, los ritmos, las formas musicales… la mayoría de los rasgos de la música occidental que solemos dar por supuestos, desaparecen en cuanto nos alejamos un poco de sus fronteras. Incluso dentro de un mismo contexto geográfico, a menudo se nos resisten los estilos musicales que escuchan los demás, o nos resultan directamente desagradables. A mí a veces me cuesta entender el trap, como para meterme con la ópera china…
Desde otro punto de vista, muchos conceptos musicales sí parecen extenderse más allá de las fronteras culturas. Las escalas musicales del mundo difieren de las occidentales, en general, pero allá donde uno vaya, la música utiliza escalas. Los patrones rítmicos cambian, el hecho de que haya siempre algúna forma de ritmo prevalece. Como prevalecen la existencia de formas musicales, de características similares y utilizadas en contextos que se repiten allá donde uno vaya. En 2018 un estudio basado en 750 oyentes procedentes de 60 países y canciones de 86 sociedades minoritarias del mundo entero, mostró que los oyentes podían adivinar para qué se utilizaba cada tipo de música, su función, (si se trataba de una nana, una danza, música para curar enfermedades, una canción de duelo o una canción de amor) tras escuchar apenas 14 segundos de audio1.
Del mismo modo que existen idiomas muy diferentes en el mundo entero, es posible que la música no sea un lenguaje universal. Pero universalmente, encontramos lenguas y encontramos también sistemas musicales que comparten ciertas propiedades. Y, del mismo modo que las lenguas del mundo son el resultado de la capacidad humana para el lenguaje, las músicas del mundo nacen de la pieza verdaderamente universal en toda esta historia: la capacidad para la música o musicalidad humana2. Los humanos, con nuestro sistema perceptivo y cognitivo, nuestras orejas cartilaginosas, nuestras voces, nuestras sociedades… somos el molde que acoge y define lo que se entiende por lenguaje y también lo que se percibe como música.
No obstante, la noción de la música como “lenguaje universal” no alude, probablemente, a este tipo de cuestiones biológicas sino a algo mucho más cotidiano. Cada vez que escuchamos musica, podemos sentir que la entendemos, aunque no haya nada figurativo en ella. Subjetivamente, parece que la música consigue comunicar emociones de manera no mediada, sin referencias, sin símbolos ni convenciones. ¿Es posible que la música nos emocione, más allá de las fronteras?, ¿que recoja algo común a todos, algo innato, no mediado, no aprendido?
De nuevo, la respuesta no es sencilla y como suele pasar en estos casos, apunta a una mezcla de cultura y natura. A menudo, para dirimir la frontera entre una y otra, se realizan estudios interculturales. Sin embargo, con la creciente globalización, la música occidental está perdiendo su valor como estímulo en las investigaciones interculturales 3. La radio y la televisión llegan ya a todas partes y, con ellas, la música tonal a la que aquí estamos tan acostumbrados.
Para investigar los efectos emocionales de este tipo de música, Thomas Fritz y su equipo4 se vieron obligados a buscar una tribu extremadamente aislada en las montañas al norte de Camerún; los mafa. Sus remotos asentamientos ni siquiera tienen suministro eléctrico y están habitados por personas que siguen un estilo de vida tradicional, por lo que en principio no habían estado expuestos a música que no fuese la de su propia cultura. Los investigadores contaron con 20 alemanes y 21 oyentes de Mafa para juzgar las emociones transmitidas en una muestra de música occidental. Si bien, los alemanes realizaron la tarea con mayor acierto en general, los Mafa clasificaron los fragmentos musicales siempre por encima de lo esperable por azar, identificando tres emociones básicas. Una de esas emociones, junto con la alegría y el miedo, era la tristeza.
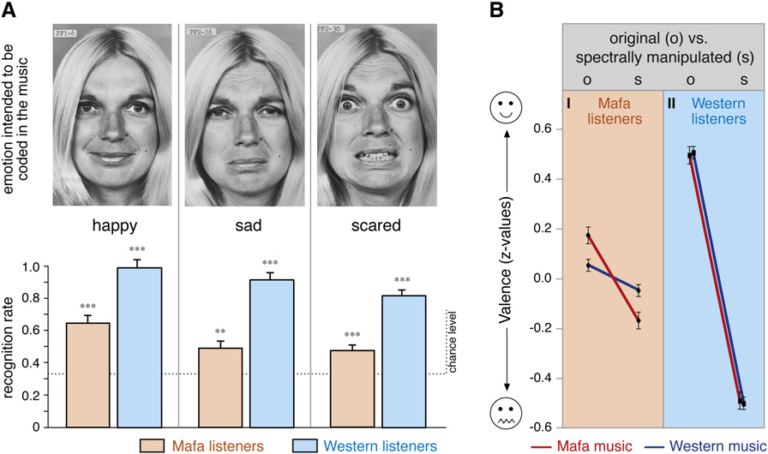 Fuente: Thomas Fritz et al. “Universal Recognition of Three Basic Emotions in Music”. Current Biology, 2009
Fuente: Thomas Fritz et al. “Universal Recognition of Three Basic Emotions in Music”. Current Biology, 2009Referencias:
1Samuel A. Mehr, Manvir Singh, Hunter York, Luke Glowacki, Max M. Krasnow. “Form and Function in Human Song”. Current Biology, 2018.
2The Origins of Musicality. Edited by Henkjan Honing. MIT Press, 2018.
3Laura-Lee Balkwill and William Forde Thomson. “A cross cultural investigation of the perception of emotion”. Music Perception, 1999.
4Thomas Fritz, Sebastian Jentschke, Nathalie Gosselin, Daniela Sammler, Isabelle Peretz, Robert Turner, Angela D. Friederici and Stefan Koelsch. “Universal Recognition of Three Basic Emotions in Music”. Current Biology, 2009.
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
El artículo ¿Es la música un lenguaje universal? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¿Por qué escuchamos música triste?
- #Naukas14 La música de las esferas
- Ciencia, arte y cultura callejera: física y música
La amante cartesiana
No es la primera vez que escribo en la sección Matemoción del Cuaderno de Cultura Científica sobre matemáticas y cómics. He dedicado una serie de entradas a las matemáticas de la novela gráfica Habibi (Astiberri, 2011), de Craig Thompson (véase Habibi y los cuadrados mágicos, parte 1, parte 2 y parte 3), y otra a las matemáticas del cómic Ken Games (Diábolo, 2009-10), de José Robledo (guionista) y Marcial Toledano (dibujante) (véase la entrada Las matemáticas en el cómic Ken Games).
En la entrada de hoy vamos a centrar nuestra atención en la novela gráfica La amante cartesiana (Egales, 2016), escrita por Paloma Ruiz Román y dibujada por Juan Alarcón.
 Portada de la novela gráfica La amante cartesiana, de Paloma Ruiz Román (guión) y Juan Alarcón (dibujo), publicada en 2016 por la editorial Egales
Portada de la novela gráfica La amante cartesiana, de Paloma Ruiz Román (guión) y Juan Alarcón (dibujo), publicada en 2016 por la editorial EgalesLa historia de esta novela gráfica está inspirada en un artículo del matemático José Manuel Rey, de la Universidad Complutense de Madrid, titulado A Mathematical Model of Sentimental Dynamics Accounting for Marital Dissolution (algo así como Un modelo matemático sobre la dinámica sentimental para explicar los divorcios), publicado en 2010, en la revista científica PLOS ONE (esta revista está publicada por la Public Library of Science, que es una organización editorial estadounidense sin ánimo de lucro que tiene como objetivo la publicación de una serie de revistas científicas de contenido abierto).
Este artículo, por su temática, tuvo cierta repercusión en los medios de comunicación. Por ejemplo, en ABC Ciencia se publicó un artículo con el título “El amor para siempre está destinado al fracaso, según una fórmula matemática”. O en el periódico Público apareció otro artículo con un título más destinado a llamar la atención que a describir la realidad de la investigación matemática explicada en el mismo, “El amor no existe, según las matemáticas”, con la volanta más descriptiva, aunque aún un poco exagerada “Un científico español elabora un modelo teórico que sugiere que las relaciones sentimentales duraderas y satisfactorias son prácticamente imposibles”. Y este artículo, con toda probabilidad, fue leído por la autora de La amante cartesiana.
La novela gráfica empieza presentando, en las primeras páginas, la relación sentimental entre la protagonista, una profesora de matemáticas de un instituto de enseñanza secundaria, a la cual se va a ver dando clase en varias páginas de la novela gráfica, y su pareja, una fotógrafa, que más adelante en la historia viajará a Islandia para realizar un reportaje fotográfico durante seis meses.
 Página de la novela gráfica La amante cartesiana, en la que se ve a la protagonista, una profesora de matemáticas de enseñanza secundaria, dando clase de matemáticas. En concreto, explicando algunas propiedades del número dos
Página de la novela gráfica La amante cartesiana, en la que se ve a la protagonista, una profesora de matemáticas de enseñanza secundaria, dando clase de matemáticas. En concreto, explicando algunas propiedades del número dosPresentada la relación sentimental de esta pareja, se muestra un dibujo, de página completa, que ofrece a la persona que lee el cómic la primera pista sobre cuál va a ser el tema de la novela gráfica. En la misma se ve al matemático ruso Lev Poltryagin escribiendo fórmulas matemáticas en una pizarra, además del texto “El matemático ruso Lev Poltryagin elaboró en la década de los cincuenta la teoría de control óptimo, alumbrada para solucionar un contratiempo con un avión de combate soviético. Pero nunca imaginó que unos años más tarde se emplearía para explicar por qué hay un divorcio aproximadamente cada 80 segundos”. Por lo tanto, uno de los puntos de partida de la novela gráfica es el fracaso de las relaciones de pareja.
 Página de la novela gráfica La amante cartesiana, en la que se ve al matemático ruso Lev Poltryagin frente a una pizarra
Página de la novela gráfica La amante cartesiana, en la que se ve al matemático ruso Lev Poltryagin frente a una pizarraLa historia continúa hasta que la fotógrafa debe emprender su viaje a Reikiavik, dejando a la matemática sola, sumida en una cierta tristeza. Y entonces llega la segunda información relevante, relacionada con el artículo del matemático madrileño José Manuel Rey, sobre la historia que nos están contando. Un dibujo a página completa de la protagonista, acompañada de imágenes de su pareja, de un avión, de una ciudad y de fórmulas matemáticas. Todo ello acompañado de dos textos explicativos.
El primero: “En 2010, fue el matemático José Manuel Rey quien, combinando la segunda ley de la termodinámica con las ecuaciones de control óptimo, sacó a la luz una fórmula de conclusiones poco esperanzadoras: el amor no perdura”.
Y el segundo “Las matemáticas, disciplina capaz de explicar cualquier suceso que se repita, toman como punto de partida en la fórmula lo que se puede considerar un hecho común: las relaciones por sí solas, es decir, la sustancia que las mantiene vivas, tienden a extinguirse”.
 Página de la novela gráfica La amante cartesiana, en la que se hace hincapié en el artículo del matemático José Manuel Rey, en el que se modeliza las relaciones de pareja
Página de la novela gráfica La amante cartesiana, en la que se hace hincapié en el artículo del matemático José Manuel Rey, en el que se modeliza las relaciones de parejaEl tema para la novela gráfica está servido, la fragilidad de las relaciones de pareja, y su fuente de inspiración es el artículo A Mathematical Model of Sentimental Dynamics Accounting for Marital Dissolution en el que se obtiene un modelo matemático para describir la dinámica de las relaciones sentimentales.
Como se cita en la introducción del artículo publicado por PLOS ONE, la mayoría de las personas mencionan el amor y las relaciones de pareja cuando se les pregunta por los elementos importantes para tener una vida feliz. Además, cuando las personas inician una relación amorosa a largo plazo, lo hacen bajo la premisa de vivir juntas y felices para siempre. Sin embargo, las altas tasas de divorcios, por ejemplo, en Estados Unidos y Europa, donde prácticamente una de cada dos parejas acaba en divorcio, ponen de manifiesto cierto fracaso de las relaciones sentimentales. Es lo que el matemático de la Universidad Complutense de Madrid llama la “paradoja del fracaso”, es decir, aunque en la base de las relaciones sentimentales está el que duren para siempre, muy probablemente fracasarán.
El sicólogo estadounidense John Gottman, que se ha hecho famoso por su trabajo sobre la predicción del divorcio y la estabilidad en las relaciones sentimentales, fue uno de los primeros en utilizar las matemáticas para estudiar las relaciones de pareja, en concreto, utilizó una ecuación diferencial basada en lo que llama la “segunda ley de la termodinámica para las relaciones sentimentales”, es decir, al igual que un recipiente caliente se enfriará si no se le suministra calor, las relaciones sentimentales se deteriorarán si no reciben un aporte de “energía” que compense esa tendencia al enfriamiento. Aunque, como pone de manifiesto el sociólogo estadounidense, sería interesante poder contar con un modelo matemático que describa la dinámica de las relaciones de pareja y esto es lo que hizo el matemático de la Universidad Complutense de Madrid.
 Parte de una página de la novela gráfica La amante cartesiana, en la que se aparece la protagonista dando clase de matemáticas, en concreto, hablando del número uno
Parte de una página de la novela gráfica La amante cartesiana, en la que se aparece la protagonista dando clase de matemáticas, en concreto, hablando del número unoTodo modelo matemático intenta describir el “objeto de interés”, en este caso la dinámica de las relaciones sentimentales, simplificando el problema, intentando quedarse con las partes esenciales del mismo. Uno de los ejemplos más ilustrativos de esta situación es el grafo del problema de los puentes de Königsberg, que está en el origen de la teoría de grafos (véase el libro Del ajedrez a los grafos (RBA, 2015) o la entrada El problema de los tres caballeros y los tres criados). Cuanto más se simplifique, más manejable será el modelo, más claras y útiles serán las conclusiones, aunque también puede ocurrir que perdamos parte de la información en el proceso de abstracción; pero si no se simplifica lo suficiente el problema, el modelo puede ser demasiado complejo para tratarlo y las conclusiones serán menos útiles. Algo así como ocurre con los mapas. En los mapas siempre se pierde parte de la información, pero son muy útiles. Por ejemplo, entre los mapas más importantes para su uso en la navegación están los que preservan los rumbos, los ángulos, sin embargo, estos no preservan las áreas, los caminos más cortos, ni las distancias; o los que son buenos para la divulgación o la comunicación de información porque preservan las áreas, fallan con los rumbos, los caminos más cortos o las distancias; y lo mismo ocurre con otros mapas (véase El sueño del mapa perfecto (RBA, 2011) o las entradas Imago Mundi, 7 retratos del mundo, Imago Mundi, otros 6 retratos del mundo, Imago Mundi, finalmente 9 retratos más del mundo). Por otra parte, el mapa de escala 1:1 que es (o sobre) la Tierra misma, como en el texto de Borges Del rigor de la ciencia, es el más exacto de todos, pero inútil e inservible.
Del rigor de la ciencia
…En aquel Imperio, el Arte de la Cartografía logró tal Perfección que el mapa de una sola Provincia ocupaba toda una Ciudad, y el mapa del Imperio, toda una Provincia. Con el tiempo, esos Mapas Desmesurados no satisficieron y los Colegios de Cartógrafos levantaron un Mapa del Imperio que tenía el tamaño del Imperio y coincidía puntualmente con él. Menos Adictas al Estudio de la Cartografía, las Generaciones Siguientes entendieron que ese dilatado Mapa era Inútil y no sin Impiedad lo entregaron a las Inclemencias del Sol y de los Inviernos. En los desiertos del Oeste perduran despedazadas Ruinas del Mapa, habitadas por Animales y por Mendigos; en todo el País no hay otra reliquia de las Disciplinas Geográficas.
SUÁREZ MIRANDA: Viajes de varones prudentes, libro cuarto, cap. XLV, Lérida, 1658.
El matemático José Manuel Rey, para realizar su modelo matemático de la dinámica de las relaciones sentimentales, asume que las parejas estarán formadas por individuos más o menos similares, que se da la “segunda ley de la termodinámica para las relaciones sentimentales” y que dos elementos fundamentales en las relaciones de pareja son el sentimiento de bienestar que se siente dentro de la pareja y el esfuerzo que se va realizando desde que empieza la relación. Entonces, utilizando teoría de control óptimo (que es la que desarrolló el matemático ruso Lev Pontryagin), obtuvo la fórmula que describe la dinámica de las relaciones de pareja, que se incluye también en la novela gráfica.
 La fórmula matemática obtenida por el matemático José Manuel Rey para describir la dinámica de las relaciones sentimentales. La imagen pertenece al artículo del periódico Público
La fórmula matemática obtenida por el matemático José Manuel Rey para describir la dinámica de las relaciones sentimentales. La imagen pertenece al artículo del periódico PúblicoEsta fórmula está incluida en el cómic, cuando se está produciendo la separación emocional de la pareja protagonista. De nuevo, en un dibujo de página completa, donde se muestra a la fotógrafa trabajando en Islandia, se incluye y se explica la fórmula, que en el texto se denomina “la fórmula matemática del desamor”.
 Parte de una página de la novela gráfica La amante cartesiana, en la que se aparece la protagonista dando clase de matemáticas, en concreto, hablando del número uno
Parte de una página de la novela gráfica La amante cartesiana, en la que se aparece la protagonista dando clase de matemáticas, en concreto, hablando del número unoLa información que proporciona la fórmula, la variable W, es la “felicidad del matrimonio” (entendiendo matrimonio en un sentido amplio). La fórmula consta de una integral, que como dice el texto “la integral suma las sensaciones cotidianas”. Y dentro de la integral hay dos partes, una positiva, que como dice en el comic “este grupo de variables es el bienestar que se siente dentro de la pareja”, y otra negativa, descrita como “este otro conjunto mide el coste del esfuerzo desde el inicio de la relación”.
Más adelante, cuando la relación entre la protagonista y su pareja ya se ha roto, se incluye otro dibujo con una metáfora sobre el significado del estudio, que seguramente fue fruto de las conversaciones entre la escritora y el matemático. En concreto se añade el texto “Tal y como explica Rey, la manera más sencilla de entender por qué se repite el hecho de que las relaciones no funcionen es a través de la metáfora del jardín”. Y nos la explica: “Para que las plantas se mantengan frondosas durante toda la vida, hay que aportar abono, agua y cuidados. Todo en su justa medida”. Y concluye: “Pero este esfuerzo continuo no es gratuito. Tiene un coste que suele ser excesivo, apocando antes o después a las plantas a un estado marchito”.
 Parte de una página de la novela gráfica La amante cartesiana, en la que la protagonista reflexiona sobre las conclusiones del modelo matemático de la dinámica de las relaciones sentimentales
Parte de una página de la novela gráfica La amante cartesiana, en la que la protagonista reflexiona sobre las conclusiones del modelo matemático de la dinámica de las relaciones sentimentalesEn otra página, que vemos en la anterior imagen, la protagonista reflexiona sobre las conclusiones que nos ofrece el modelo matemático de la dinámica de las relaciones de pareja. Recogiendo las palabras del autor del estudio: “el esfuerzo que es necesario para que una relación funcione siempre será mayor que el esfuerzo que esperamos tener que realizar para ello”.
Y se continúa afirmando en La amante cartesiana “o lo que es lo mismo, hagamos lo que hagamos para que una relación salga bien, siempre será insuficiente, ya que la tendencia natural conduce a la dejadez y, con ella, al fracaso”.
Como reacción a este pensamiento negativo que domina a la protagonista, fruto de su ruptura sentimental, la última parte de la novela es un alegato a favor del amor y las relaciones sentimentales.
Aunque el estudio matemático sobre la dinámica de las relaciones de pareja es la parte matemática central de esa novela gráfica de Paloma Ruiz Román y Juan Alarcón, lo cierto es que la ciencia de Pitágoras impregna toda la historia. Veamos algún ejemplo.
La protagonista de La amante cartesiana, que como hemos comentado es profesora de matemáticas en un instituto de enseñanza secundaria, explicará a sus estudiantes propiedades de ciertos números particulares en paralelo a su historia sentimental. Así, explica en clase algunas propiedades del número 2, cuando se presenta a la pareja en las primeras páginas, como que el 2 es el único número primo par y que es el único número tal que la suma consigo mismo es igual al producto consigo mismo, es decir, 2 + 2 = 2 x 2. Por otra parte, cuando la protagonista se queda sola, por el viaje de su pareja, habla a la clase del número 1, mientras que cuando su relación se rompe lo hace sobre el 0.
Por otra parte, cuando una tercera persona entra en escena, la profesora hablará del número pi, que no es 3, pero está muy cerca (3,14159…), y lo hace en relación con la poesía. En concreto, la bailarina a la que conoce la protagonista le lee una poesía con sabor matemático, el poema Escrito con tiza del poeta chileno Oscar Hahn, que incluimos a continuación.
ESCRITO CON TIZA
Uno le dice a Cero que la nada existe
Cero replica que Uno tampoco existe
porque el amor nos da la misma naturaleza
Cero más Uno somos Dos le dice
y se van por el pizarrón tomados de la mano
Dos se besan debajo de los pupitres
Dos son Uno cerca del borrador agazapado
y Uno es Cero mi vida.
Detrás de todo gran amor la nada acecha.
La protagonista tras escuchar el poema, le contesta que “tiene la estructura de una ecuación, de un problema matemático” y realiza un análisis matemático de la misma. Este es el estudio que realizó el chileno Camilo Herrera y que podéis leer aquí.
 Parte de la página de la novela gráfica La amante cartesiana, en la que la protagonista explica a su clase el poema irracional relacionado con el número pi del ajedrecista Manuel Golmayo
Parte de la página de la novela gráfica La amante cartesiana, en la que la protagonista explica a su clase el poema irracional relacionado con el número pi del ajedrecista Manuel GolmayoTras esa relación entre matemáticas y poesía, en la siguiente escena de la novela gráfica, se ve a la protagonista hablando a sus estudiantes de un poema del ajedrecista español Manuel Golmayo (1883-1973) relacionado con el número pi. En concreto, uno de esos poemas, que en ocasiones son denominados irracionales, en los que cada palabra del poema tiene tantas letras como indican los dígitos del número pi (o también podría ser otro número irracional, como la razón aurea phi o el número e). El poema es el siguiente.
Soy y seré a todos definible, [3,14159]
mi nombre tengo que daros, [26535]
cociente diametral siempre inmedible [8979]
soy de los redondos aros [32384]
Pero en la novela gráfica hay más matemáticas. Descartes, Kepler, la música de las esferas, el azar o la probabilidad son algunas de las cuestiones matemáticas que también encontraréis en esta historia, pero eso lo descubriréis cuando disfrutéis de su lectura. Para terminar, os dejo con el problema de ingenio (relacionado con el problema amoroso de la protagonista) planteado por la profesora de matemáticas en el cómic.
Problema: Supóngase que los dos enunciados siguientes son verdaderos:
(1) Quiero a Elena o quiero a Adriana.
(2) Si quiero a Elena entonces quiero a Adriana.
¿Se sigue necesariamente que quiero a Elena? ¿Se sigue necesariamente que quiero a Adriana?

Bibliografía
1.- Paloma Ruiz Román, Juan Alarcón, La amante cartesiana, Egales, 2016.
2.- José Manuel Rey, A Mathematical Model of Sentimental Dynamics Accounting for Marital Dissolution, PLOS ONE, vol. 5, 2010.
3.- Periódico ABC: El amor para siempre está destinado al fracaso, según una fórmula matemática, Judith de Jorge, 13 de mayo de 2010.
4.- Periódico Público: El amor no existe según las matemáticas, Manuel Ansede, 25 de abril de 2010.
5.- Raúl Ibáñez, Del ajedrez a los grafos, la seriedad matemática de los juegos, El mundo es matemático, RBA, 2015.
6.- Raúl Ibáñez, El sueño del mapa perfecto, cartografía y matemáticas, El mundo es matemático, RBA, 2010.
7.- Camilo Herrera, La solución de la ecuación poética
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo La amante cartesiana se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El diablo y Simon Flagg, una lectura ligera para el verano
- Matemáticas y mundo físico (I): la soberbia cartesiana
- Un kilogramo de novelas y matemáticas
La estructura de la tabla periódica se deduce de la estructura de capas de los átomos
Las consideraciones cualitativas sobre el comportamiento químico de los elementos desde el punto de vista del modelo de Bohr-Sommerfeld llevaron a un cuadro consistente en el que los electrones se distribuían en capas alrededor del núcleo atómico, creando una especie de “núcleo compuesto”. Estos “núcleos compuestos” no eran otra cosa que los gases nobles, que tenían una configuración electrónica especialmente estable.
 Figura 1. Tabla periódica moderna (diseño Werner-Paneth) actualizada con la indicación de los números atómicos y grupos. Fuente: IUPAC
Figura 1. Tabla periódica moderna (diseño Werner-Paneth) actualizada con la indicación de los números atómicos y grupos. Fuente: IUPACAsí, para cada nuevo metal alcalino en el Grupo 1 de la tabla periódica de Werner-Paneth, se inicia una nueva capa. Cada átomo de metal alcalino tiene un solo electrón alrededor de un núcleo compuesto que tiene la estructura del gas noble precedente. Es esperable que este electrón periférico se “pierda” fácilmente por la acción de los átomos vecinos, y esto concuerda con los hechos. Los elementos litio, sodio y potasio son metales alcalinos. Tanto en compuestos como en disolución, están en forma de iones, como Li+, Na+ y K+. Cada ion es un átomo que ha perdido un electrón y, por lo tanto, tiene una carga neta positiva +e. Otra consecuencia es que en los átomos neutros de estos elementos, el electrón externo es relativamente libre de moverse. Esta propiedad se ha utilizado como base de una teoría de la conductividad eléctrica. Según esta teoría, un buen conductor tiene muchos electrones «libres» que pueden formar una corriente en condiciones apropiadas. Un mal conductor pobre tiene relativamente pocos electrones «libres». Los metales alcalinos son todos buenos conductores. Los elementos cuyas capas de electrones están llenas son conductores muy pobres; no tienen electrones «libres».
En el Grupo 2 de la tabla periódica, podemos esperar que los elementos que siguen inmediatamente después de los metales alcalinos tengan átomos con dos electrones periféricos. Por ejemplo, el berilio (Z = 4) debe tener dos electrones en la capa K, llenándola, y dos en la capa L. Si los átomos de todos estos elementos tienen dos electrones periféricos, deberían ser químicamente similares, como lo son realmente. Por lo tanto, el calcio y el magnesio, que pertenecen a este grupo, deberían formar fácilmente iones como Ca++ y Mg++, cada uno con una carga neta positiva de +2e. Esto también se encuentra que es cierto.
Como último ejemplo, consideremos aquellos elementos que preceden inmediatamente a los gases nobles en la tabla periódica, los del grupo 17. Por ejemplo, los átomos de flúor (Z = 9) deberían tener dos electrones llenando la capa K pero solo siete electrones en la capa L, uno menos que de lo necesarioe para llenarla. Si un átomo de flúor captura un electrón adicional, se convertiría en un ion F– con una carga neta negativa. La capa L estaría llena entonces, y sería análoga a la del átomo neutro del gas noble neón (Z = 10), y por este motivo cabe esperar que el ion F sea relativamente estable. Esta predicción concuerda con lo observado. De hecho, todos los elementos que preceden inmediatamente a los gases nobles tienden a formar en disolución iones estables con carga unidad negativa. En estado sólido, es de esperar que estos elementos carezcan de electrones libres. De hecho, todos ellos son malos conductores de electricidad.
 Figura 2. Sistema de periodos de Bohr. Algunos símbolos ya no están en uso o se corresponden a falsas asignaciones en el momento de ser confeccionada la ilustración (1921). Así el elemento 43 masurio, fue una identificación falsa; fue reemplazado por el tecnecio en 1937, primer elemento artificial (de ahí su nombre), aunque sus propiedades las predijo Mendeléyev, que lo llamó ekamanganeso. Fuente: Cassidy Physics Library
Figura 2. Sistema de periodos de Bohr. Algunos símbolos ya no están en uso o se corresponden a falsas asignaciones en el momento de ser confeccionada la ilustración (1921). Así el elemento 43 masurio, fue una identificación falsa; fue reemplazado por el tecnecio en 1937, primer elemento artificial (de ahí su nombre), aunque sus propiedades las predijo Mendeléyev, que lo llamó ekamanganeso. Fuente: Cassidy Physics LibraryTal y como se indica en la figura 2, basada en una ilustración de una publicación de Bohr de 1922, las siete capas principales, K, L, M,. . . , Q, se dividen naturalmente en órbitas o subcapas. Las capas se llenan de electrones para minimizar la energía total del átomo. La periodicidad resulta del llenado de las subcapas.
La tabla de Bohr, aún útil, fue un resultado de física teórica y ofreció una base física fundamental para comprender la química: demostró cómo la estructura de la tabla periódica se deduce de la estructura de capas de los átomos.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo La estructura de la tabla periódica se deduce de la estructura de capas de los átomos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La tabla periódica en el arte: ¿Qué átomos hay en una obra?
- El modelo de Bohr-Sommerfeld y las propiedades químicas de los elementos
- La tabla periódica en el arte: Plata
Cómo la bomba atómica condicionó nuestra comprensión de la ciencia
 Nube producida por la bomba atómica de Hiroshima hecha desde el Enola Gay.
Nube producida por la bomba atómica de Hiroshima hecha desde el Enola Gay.Wikimedia Commons
6 de agosto de 1945. El día se presenta como cualquier otro en la ciudad de Hiroshima, Japón. El cielo está despejado y varios ciudadanos de a pie se dirigen a cubrir sus puestos de trabajo. Hiroshima no es una ciudad grande, viven en ella unas 250 000 personas, pero su interés estratégico, industrial y militar es fundamental para el imperio nipón durante la guerra.
A las 8:15 de la mañana, hora local, el Enola Gay, un bombardero B-29 estadounidense, abre sus compuertas para dejar caer la Little Boy, una bomba de uranio-235 con un potencial explosivo equivalente a 13 000 toneladas de TNT, sobre el centro de la ciudad. 55 segundos después, el estallido de la bomba marcará un antes y un después en el devenir de la historia de las sociedades modernas y de la producción científica.
Aunque ampliamente analizada desde diversas perspectivas políticas, científicas y militares, la historia de la bomba atómica apenas ha recibido atención en lo que se refiere a su papel a la hora de configurar la manera misma en que entendemos la división del conocimiento en el mundo moderno.
La comprensión pública de la ciencia como disciplina de conocimiento especial y superior al resto de saberes, o lo que algunos autores han convenido en concebir como el problema de las Dos Culturas, cambiaría radicalmente tras la detonación de las bombas atómicas de Hiroshima y Nagasaki. Sin saberlo, aquella soleada mañana de verano Paul Tibbets, piloto del Enola Gay, alteraría el curso de la cultura misma.
La historia de un debate histórico
Fue el 7 de mayo de 1959 cuando C. P. Snow subió al palco de la “Senate House” en la Universidad de Cambridge para pronunciar su conferencia “Las Dos Culturas y la Revolución Científica”.
En ella, Snow expuso una preocupación latente en varios círculos académicos de la sociedad británica de su época: la división radical entre las ciencias y las humanidades. Según el reconocido físico y novelista inglés, la sociedad intelectual inglesa estaba irremediablemente dividida entre científicos y humanistas, incluyendo entre estos últimos a historiadores, filósofos y literatos.
Afirmaba que los científicos, progresistas y librepensadores por naturaleza, se encontraban en constante pugna con los literatos, conservadores, individualistas y apartados de toda preocupación moral y social. Snow defendía que, para garantizar el futuro de la nación inglesa, era necesario establecer un sistema educativo en el que primasen los valores de libertad, progreso y comunidad propios de la ciencia, no aquellos valores egoístas y desarraigados de los literatos. En otras palabras, era necesaria una reforma cultural.
Uno puede sentirse un tanto sorprendido por las afirmaciones de Snow. ¿Tan poca cabida tenía la ciencia en la educación de su época? ¿Tan egoístas e individualistas eran los literatos? ¿La separación tajante entre las ciencias y las humanidades es tan clara como lo era para Snow?
Varios estudios históricos del problema han sugerido en los últimos años que la respuesta a estas preguntas es negativa. En primer lugar, hay que entender a Snow en su contexto, un contexto de posguerra y declinismo. Podríamos definir el declinismo como esa tendencia general a pensar que todo tiempo pasado fue mejor.
 Portada del libro
Portada del libroWikimedia Commons
En el periodo concreto en que Snow pronunció su conferencia (que más tarde se convertiría en su aclamada obra Las Dos Culturas), el Reino Unido aún se estaba recuperando de los horrores y las pérdidas de la guerra. No sólo la economía del país se había visto gravemente afectada por los seis años de encarnizada e ininterrumpida lucha contra Alemania, Italia y Japón, sino también su propia capacidad de producción intelectual.
El Reino Unido, bastión de grandes autores como Shakespeare, Dickens o Shelley, y de naturalistas como Darwin, no fue capaz de hacer frente a las grandes innovaciones técnicas, científicas y militares de naciones como Alemania, Estados Unidos o la URSS. Fue en parte esta situación la que provocó ese sentimiento de declinismo en varios de los intelectuales de la época, que consideraron que la hegemonía cultural de la literatura, el arte y la filosofía habían llevado a Gran Bretaña a convertirse en un país muy leído, pero inútil a la hora de enfrentarse a los retos que la nueva ciencia y las nuevas sociedades planteaban.
Al fin y al cabo, ¿cómo podrían enfrentarse a potencias que habían desarrollado la bomba de uranio si seguían recitando sonetos de Shakespeare en la escuela?
El nacimiento de un mito
Esta fue una de las múltiples razones por las que nació el mito de las Dos Culturas: el miedo a no ser capaz de equipararse técnica y científicamente a las grandes potencias protagonistas de la vigente Guerra Fría. El debate generado por Snow, y que ha llegado hasta nuestros días, acerca de la separación cuasi natural entre científicos y literatos, no queda exento de ser comprendido en un contexto ideológico, social y de declinismo más amplio.
Pero, ¿cuál es la importancia de todo esto? Podemos considerar que sólo advirtiendo la contingencia de este contexto, la historicidad de todos los factores que motivaron a Snow a plantear este problema, seremos capaces de desmontar la falsa dicotomía que existe a día de hoy entre las Dos Culturas.
Si somos capaces de ver que fueron la guerra, un cierto complejo de inferioridad y una actitud pesimista hacia la ciencia de su propia nación las que llevaron a Snow a plantear la división necesaria entre las ciencias y las humanidades, podremos ver que dicha división no es tan natural como parece.
Y, así, podremos quitarnos de una vez de la cabeza la ingenua y anticuada idea de que el progreso intelectual, la innovación cultural y el bienestar social sólo pueden darse desde las ciencias.![]()
Urko Gorriñobeaskoa es doctorando en historia y filosofía de la iencia en la Universidad del País Vasco / Euskal Herriko Unibertsitatea. Este texto ha sido revisado por Ekai Txapartegi, profesor de filosofía en la UPV/EHU.
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Cómo la bomba atómica condicionó nuestra comprensión de la ciencia se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Cómo descubrimos tres libros venenosos en la biblioteca de nuestra universidad
- Cómo hacer ciencia en un periódico: la experiencia de ‘Público’
- Cómo nos ayuda la ciencia a tomar decisiones correctas
Hay vida en los extremos
 Río Tinto (Huelva, España). Foto: Alfonso Cerezo / Pixabay
Río Tinto (Huelva, España). Foto: Alfonso Cerezo / PixabayQuizás no se haya buscado en todas partes, pero en los lugares de nuestro planeta en los que se ha buscado, se ha encontrado vida.
Se han hallado bacterias en lagos en la Antártida que se encuentran bajo una capa de hielo de 800 m de espesor, y ahora las buscan, también bajo el hielo, a mayor profundidad aún. A la luz de los antecedentes, lo más probable es que también allí las encuentren. Los llamados organismos psicrofílicos –los que sobreviven, crecen y se reproducen a temperaturas inferiores a 15 ºC bajo cero- viven en suelos congelados, en el interior del hielo de glaciares y en aguas marinas extremadamente frías.
También se han encontrado microorganismos a temperaturas superiores a 100 ºC. Los ejemplos más extremos son, quizás, las arqueas Methanopyrus kandleri, que vive a 110 ºC en fumarolas (surgencias hidrotermales) del Golfo de California (y ha sido cultivada a 122 ºC en el laboratorio) y Geogemma barosii, que crece y se reproduce a 121 ºC. Arqueas del género Pyrococcus no solo abundan en fumarolas, también se han encontrado en la Fosa de las Marianas, el enclave más profundo del planeta, donde soporta presiones superiores a los 1000 bares; a estas las llamamos barófilas o piezófilas. Y no son las únicas; además de esas arqueas también hay bacterias capaces de soportar presiones enormes.
Otras arqueas toleran altísimas concentraciones salinas. Las Halobacteriáceas (una familia de arqueas) se caracterizan, en general, por tolerar condiciones extremas por diferentes motivos, pero la mayor parte de ellas viven en lagos hipersalinos, a concentraciones que van desde 10% de sal hasta la sobresaturación, condiciones bajo las que la sal precipita. Los organismos que se exponen a altas concentraciones de sal pueden desecarse, pues el agua tiende a fluir hacia el exterior por ósmosis. Es lo que ocurre, por ejemplo, cuando se sumerge una pieza de carne o de pescado en salmuera para después conservarla mejor. Algunas cianobacterias del género Chroococcidiopsis toleran la desecación extrema, y son capaces de vivir en zonas tan secas como el desierto de Atacama, al norte de Chile, el lugar más árido del planeta.
Microorganismos como las bacterias Deinococcus radiodurans y Rubrobacter radiotolerans toleran altísimas dosis de radiaciones ionizantes (por encima de 1.500 grays) y, al parecer, su tolerancia a la radiación está relacionada con la resistencia a la desecación. Por su parte, la arquea Thermococcus gammatolerans, el microorganismo conocido que mayores dosis de radiación ionizante tolera, fue aislada en una fumarola submarina al oeste de California.
Uno de los enclaves que, a priori, cabría considerar más hostiles a la vida es el río Tinto. Sus aguas discurren por la denominada Faja pirítica ibérica, una amplia zona en el sudoeste ibérico con una alta concentración de sulfuros polimetálicos. En vez de utilizar la luz como hacen las plantas, en el río Tinto hay unas pocas especies de bacterias y arqueas que obtienen su energía de compuestos inorgánicos. Son lo que se denomina organismos quimiolitotrofos. Gracias a la gran abundancia de sulfuro de hierro (II), las comunidades microbianas oxidan los iones sulfuro y hierro (II), produciendo ácido sulfúrico y hierro (III), lo que da lugar a una gran acidez en el medio. El pH se encuentra entre 2 y 2,5. Lo curioso es que son muy pocas las bacterias y arqueas que toleran esa acidez, pero muchas las especies de algas y hongos unicelulares que viven en esas aguas.
Siempre hemos tratado de buscar y conocer los límites de la vida. Nos interesan, entre otras cosas, porque esas condiciones quizás sean las que albergan la vida en otros mundos.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Hay vida en los extremos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Así se distribuye la biomasa de la Tierra
- Los amiloides y el origen de la vida
- La historia de la vida
Liderazgo escolar y rendimiento académico de los alumnos: estado de la cuestión
Vitoria-Gasteiz acogió por primera vez el pasado 18 de octubre el evento Las pruebas de la educación, una jornada que abordó diversos temas educativos desde la evidencia científica. El acto, organizado por el Consejo Escolar de Euskadi y la Cátedra de Cultura Científica de la UPV/EHU, tuvo lugar en el Salón de Actos del Centro de Investigación Micaela Portilla, ubicado en el Campus de la capital alavesa de la UPV/EHU.

La jornada consta de un total de cinco charlas que tratan temas como el rendimiento académico, los métodos de aprendizaje y la innovación educativa, entre otros. La dirección del seminario corre a cargo de la doctora en psicología Marta Ferrero.
María Gil, doctora en Economía por la Universidad Complutense de Madrid, nos habla en esta charla sobre el liderazgo escolar y el rendimiento académico de los alumnos. Según la experta, incrementar la eficiencia de los recursos al sistema educativo y mejorar los resultados académicos de los alumnos constituyen dos objetivos prioritarios de las autoridades educativas. La ponente hace énfasis en el papel relevante que los líderes de los centros pueden jugar en la consecución de ambos objetivos.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Liderazgo escolar y rendimiento académico de los alumnos: estado de la cuestión se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- A favor de la evaluación escolar objetiva
- Criterios de eficacia escolar y factores asociados a la misma
- Estudio de eficacia escolar en el País Vasco
Un comportamiento pavloviano en amebas
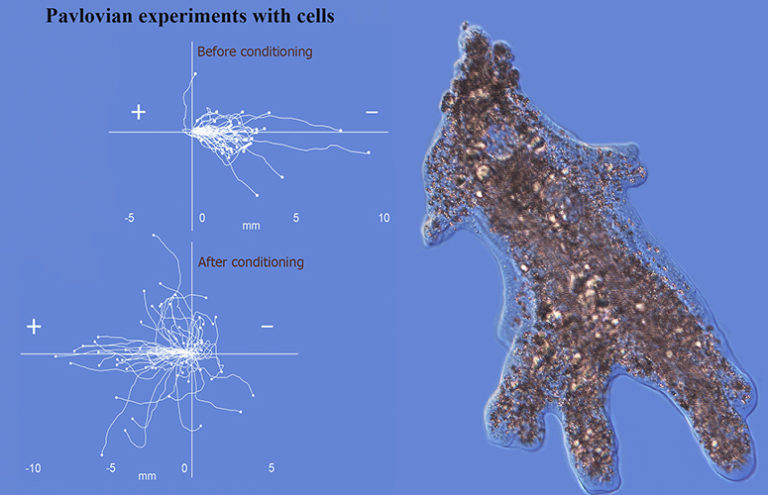
Un grupo científico multidisciplinar formado por investigadores pertenecientes a la UPV/EHU y al Hospital Universitario de Cruces, a la Universidad Ben Gurion de Israel y a tres institutos del CSIC (Instituto de Biofisika de Leioa, el Instituto CEBAS de Murcia e Instituto López-Neyra de Granada) y liderado por el Dr. Ildefonso Martínez de la Fuente (profesor de investigación del CSIC) ha demostrado por primera vez la existencia de un comportamiento condicionado de tipo pavloviano en organismos unicelulares.
Siguiendo el enfoque metodológico experimental que Ivan Pavlov realizó con perros, hace más de un siglo, y por el que fue galardonado con el premio Nobel en 1904, estos investigadores han confirmado en dos especies unicelulares distintas (Amoeba proteus y Metamoeba leningradensis) el aprendizaje asociativo celular.
Hasta ahora, el condicionamiento asociativo, el principal tipo de aprendizaje mediante el cual los organismos dotados de sistema nervioso central responden eficientemente a los estímulos ambientales, se ha constatado en diferentes especies animales, desde cefalópodos hasta humanos, pero nunca había sido observado en células individuales.
Para demostrar la existencia de un comportamiento condicionado de tipo pavloviano en organismos unicelulares, los investigadores utilizaron un campo eléctrico como estímulo condicionado y un péptido quimiotáctico específico como estímulo no condicionado y, a continuación, analizaron las trayectorias migratorias de más de 700 células individuales bajo diferentes condiciones experimentales. Los resultados mostraron inequívocamente que los organismos unicelulares eran capaces de aprender nuevos comportamientos mediante asociación de estímulos.
El grupo de investigación ha puesto de manifiesto en sus experimentos que estas células aprenden nuevos comportamientos migratorios, los recuerdan y memorizan durante largos periodos de tiempo (45 minutos en promedio), respecto de su ciclo celular (24 horas, en condiciones óptimas de laboratorio) y posteriormente los olvidan. Nunca hasta ahora se había observado semejantes comportamientos en organismos unicelulares.
La migración celular es un comportamiento sistémico, esencial en el desarrollo y el mantenimiento funcional tanto de las células libres como las de los organismos pluricelulares. En los humanos, la formación de los órganos durante el desarrollo embrionario, la respuesta inmune o la reparación tisular, por ejemplo, requieren de movimientos celulares migratorios muy precisos y complejos. Los errores en el control de estos procesos migratorios celulares pueden tener consecuencias graves, como el retraso mental, el desarrollo de enfermedades cardiovasculares y el cáncer.
El proceso metastático, por el cual las células cancerígenas abandonan un tumor primario y migran hacia otros órganos para formar tumores secundarios, es la principal causa de muerte en los pacientes con cáncer. Según miembros del equipo de investigación que participan en este estudio, “el conocimiento de los procesos que controlan dicha migración contribuirá a reducir significativamente la mortalidad asociada a esta enfermedad, por lo que esta conexión con la medicina aumenta aún más si cabe la importancia del hallazgo”.
Referencia:
De la Fuente, Ildefonso M.; Bringas, Carlos; Malaina, Iker; Fedetz, María; Carrasco-Pujante, Jose; Morales, Miguel; Knafo, Shira; Martínez, Luis; Pérez-Samartín, Alberto; López, José I.; Pérez-Yarza, Gorka; Boyano, María Dolores «Evidence of conditioned behavior in amoebae» Nature Communications doi: 10.1038/s41467-019-11677-w
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Un comportamiento pavloviano en amebas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Un nuevo mecanismo de resistencia antifúngico
- Cómo ver todas las células en tejido cerebral vivo
- Cómo criopreservar células madre
La ciencia de la cosmética antioxidante contra los radicales libres
 Foto: Christin Hume / Unsplash
Foto: Christin Hume / UnsplashEn 1956 se propuso por primera vez que los radicales libres contribuían al envejecimiento de la piel. En su día esta teoría fue muy criticada, sin embargo, en la actualidad está ampliamente demostrado que los radicales libres que se forman en procesos de oxidación son los principales causantes de los signos de la edad: arrugas, manchas y flaccidez. Hemos caracterizado los radicales libres que se forman, cómo se forman y cuál es su mecanismo de acción. La forma más eficaz de combatirlos es mediante el uso de antioxidantes.
-
¿Qué son los radicales libres y cómo se forman?
Los radicales libres (RL) son moléculas que presentan electrones desparejados. Esto hace que sean moléculas muy inestables y reactivas, por lo que destruyen y alteran los compuestos que tienen a su alrededor en busca de estabilidad, de volver a emparejar sus electrones. Se forman en reacciones químicas de oxidación, que son reacciones que implican pérdida de electrones.
 Imagen: Deborah García Bello
Imagen: Deborah García BelloLos radicales libres más importantes son las denominadas especies reactivas de oxígeno (ROS) y de nitrógeno (RON), principalmente el radical anión superóxido, el peróxido de hidrógeno y el radical óxido nítrico.
Los radicales libres se originan de forma natural como consecuencia del metabolismo celular; también como consecuencia de algunas patologías que producen inflamación e isquemia; y por agentes externos, sobre todo la radiación ultravioleta, la contaminación, el estrés, el alcohol y el tabaco.
-
Los radicales libres tienen un papel fisiológico importante
Aunque los radicales libres estén implicados en procesos de envejecimiento y sean el origen de algunas enfermedades, entre ellas algunos cánceres, también tienen un papel fisiológico importante. Los radicales libres son indispensables en la relajación muscular, la transmisión celular o la defensa microbiana. También regulan la muerte celular activando cascadas de señalización intracelular que pueden terminar por inducir apoptosis; de esta manera se eliminan las células dañinas, con comportamientos nocivos o mutaciones indeseables.
-
Exceso de radicales libres: estrés oxidativo
Hay varios factores que pueden inducir la formación de un exceso de radicales libres. Para neutralizarlos disponemos de defensas antioxidantes como los sistemas enzimáticos (CAT, SOD, GPs) y no enzimáticos (Glutation, Vitaminas: A, C, E).
Cuando se produce un desequilibrio en la formación de radicales libres, el sistema antioxidante del organismo es incapaz de gestionarlo. Cuando esto sucede hablamos de estrés oxidativo. El estrés oxidativo es consecuencia de factores externos, desde una patología que implica inflamación, a la radiación ultravioleta, la contaminación o el estrés.
- Radicales libres y envejecimiento
A nivel cutáneo, los radicales libres pueden provocar acumulación de lesión oxidativa en moléculas como el colágeno y la elastina (glicación), favorecer la acumulación de pigmentos como la lipofucsina y la melanina causando manchas, y provocar fibrosis en los vasos que nutren la dermis, afianzando las arrugas gestuales.
La glicación es una reacción espontánea de la glucosa sanguínea con las fibras dérmicas de colágeno y elastina. La acumulación de los productos resultantes de la glicación (AGEs) es mayor en las proteínas estructurales, como el colágeno y la elastina, pues tienen un tiempo de recambio lento. La formación de puentes moleculares entrelazados y rígidos entre las fibras proteicas con una reorganización de la red conduce a una pérdida de firmeza, elasticidad y movilidad de la piel. Además, los AGEs expuestos a rayos ultravioleta generan radicales libres de oxígeno que constituyen un factor más de envejecimiento. La glicación aumenta exponencialmente con la edad a partir de los 35 años y se incrementa con la exposición al sol.
 Imagen: Deborah García Bello
Imagen: Deborah García BelloAdemás de envejecimiento cutáneo, estos procesos oxidativos alteran el equilibrio celular e inducen procesos cancerosos. Las sustancias proinflamatorias que se producen de manera sostenida provocan daño al ADN y, junto con la producción de especies reactivas de oxígeno y de nitrógeno, generan más daño celular. Si, además, los sistemas de protección como la apoptosis celular no logran eliminar estas células alteradas, se mantendrá un crecimiento celular incontrolado de clones celulares dañados. De esta forma, la producción excesiva de especies reactivas de oxígeno y de nitrógeno induce diferentes tipos de cáncer cutáneo.
También sabemos que la radiación ultravioleta induce daño directo al ADN y activa la producción de especies reactivas de oxígeno que provocan más estrés oxidativo. El daño en el ADN produce mutaciones y genotipos celulares alterados, lo que permite la expansión tumoral.
-
Los antioxidantes estrella: la Vitamina C y la Vitamina E
Los antioxidantes son sustancias que pueden actuar desde tres frentes: inhibir el estrés oxidativo, neutralizar los radicales libres y paliar los efectos de los radicales libres.
 Imagen: Deborah García Bello
Imagen: Deborah García BelloLos antioxidantes convencionales son la vitamina C y la vitamina E. Químicamente ambas sustancias se oxidan con relativa facilidad, por eso suele decirse que son sustancias que se oxidan en lugar de otras, evitando que se formen radicales libres. Esta es la versión corta de su mecanismo de acción. La realidad es que los antioxidantes actúan a más niveles.
—Vitamina C
 Imagen: Deborah García Bello
Imagen: Deborah García BelloLa vitamina C es el ácido L-ascórbico. La nomenclatura INCI, la que se usa en la lista de ingredientes cosméticos, es ascorbic acid, aunque existen derivados. Es hidrosoluble y es el antioxidante predominante. Neutraliza los radicales libres en los compartimentos acuosos de la piel.
La única manera de obtener grandes cantidades es aplicándola tópicamente, ya que por vía oral los mecanismos de control biológico restringen su absorción y posterior transporte a la piel. Para optimizar su absorción percutánea, la formulación del vehículo de la vitamina C debe tener un pH menor de 3.5, logrando máximas concentraciones en piel al 15%.
Por vía tópica protege a la piel contra eritema e inmunosupresión producida por UVB y UVA, mediante un mecanismo no relacionado con la absorción de radiación ultravioleta. Y reduce la hiperpigmentación al inhibir la tirosinasa implicada en la síntesis de melanina, por lo que previene las manchas.
La vitamina C es un cofactor de enzimas críticas en la síntesis de colágeno. A partir del 3% de concentración es capaz de restaurar las fibras de colágeno en pieles jóvenes e incrementa el número de vasos capilares que nutren la dermis en mujeres postmenopaúsicas.
—Vitamina E
 Imagen: Deborah García Bello
Imagen: Deborah García BelloLa vitamina E, también conocida como alfatocoferol. La nomenclatura INCI, la que se usa en la lista de ingredientes cosméticos, es tocopherol, aunque existen derivados. Es liposoluble. Su principal función es proteger las membranas celulares del estrés oxidativo. Múltiples estudios han demostrado una reducción del estrés oxidativo, del fotoenvejecimiento, la inmunosupresión y la carcinogénesis.
También inhibe la síntesis de melanina por acción contra la tirosinasa y la tirosina, y posee una modesta absorción de la radiación ultravioleta cerca de los 290 nm, lo que, junto con su efecto antioxidante, podría explicar su acción fotoprotectora.
—Sinergias de la vitamina C y E
 Imagen: Deborah García Bello
Imagen: Deborah García BelloLas vitaminas C y E actúan de forma sinérgica, por eso es frecuente encontrarlas juntas en cosméticos antioxidantes. El origen de esta sinergia está en que cuando la vitamina E se oxida es regenerada en la membrana celular por la vitamina C a partir del radical tocoferilo. Es decir, cuando la vitamina E se oxida, la vitamina C revierte ese proceso devolviendo a la vitamina E su forma antioxidante.
Agentes estabilizadores como el ácido ferúlico al 1,5% y la floretina, dos potentes antioxidantes de origen vegetal, aumentan la absorción de las fórmulas combinadas.
Como la vitamina C es hidrosoluble y la E es liposoluble, las encontramos combinadas en productos con fase acuosa y fase grasa que suelen presentarse en forma de emulsión.
Las vitaminas C y E actúan en conjunto para evitar el estrés oxidativo. En comparación con la vitamina C sola, la combinación de ácido L-ascórbico en un 15% con un 1% de alfatocoferol duplica la protección contra la formación de eritema y minimiza el daño al ADN de la radiación ultravioleta. En pieles con daño solar, la cantidad de vitaminas C y E se reduce en un 70%.
-
Conclusión
Los antioxidantes tópicos sirven para suplementar la protección antioxidante innata de la piel y reponer las reservas que se agotan por estrés oxidativo.
En cosmética se utilizan diferentes antioxidantes, siendo los más comunes la vitamina C y la E. En combinación con la protección solar, forman un gran equipo contra el envejecimiento de la piel.
Referencias:
Harman D. Aging. A theory base don free radical and radiation chemistry. J Gerontol. 1956; 11:298-300
M. Florez-White. Antioxidantes tópicos: su papel en el manejo del fotoenvejecimiento. Más Dermatol. 2013; 19:3-4
J. Honorato. Glication’s processes and oxidation in the aging of the skin. Med Cutan Iber Lat Am 2010;38(2):101-104
Sander ChS, Chang H, Salzmann S et al. Photoaging is associated with protein oxidation in human skin in vivo. J Invest Dermatol 2002; 118: 618-25
Halliwell B, Whiteman M. Measuring reactive species and oxidative damage in vivo and cell culture. How should you do it and what does it mean? Br J Pharmacol. 2004;142:231-55
Willcox J, Ash S, Catignani G. Antioxidants and prevention of chronic disease. Crit Rev Food Sci Nutr. 2004;44:275-95
Ghersetich I, Troiano M, De Giorgi V, Lotti T. Receptors in skin ageing and antiageing agents. Dermatol Clin. 2007;25:655-62
Franco R, Schoneveld O, Georgakilas A, Panayiotidis M. Oxidative stress, DNA methylation and carcinogenesis. Cancer Lett. 2008;266:6-11
Sara María Lozada, Lucy García. Oxidative stress and antioxidants: how to keep the balance.Rev Asoc Colomb Dermatol. 2009;17:172-9.
Gissel Ivonne Castellanos Ramos , Daniel Alcalá Pérez. Antioxidants in Dermatology. DermatologiaCMQ2010;8(4):272-277
Sobre la autora: Déborah García Bello es química y divulgadora científica
El artículo La ciencia de la cosmética antioxidante contra los radicales libres se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Radicales libres, el libro
- Cuando las algas rojas no pueden gestionar los radicales libres
- Así es la mejor crema antiedad según la ciencia

