Materiales inteligentes y multifuncionales para impulsar el desarrollo tecnológico

Los materiales inteligentes, también denominados activos o multifuncionales, son estructuras capaces de modificar sus propiedades como respuesta a estímulos físicos o químicos externos, como la presión, la temperatura o la humedad del entorno.
Por sus características, estos componentes ofrecen un elevado potencial de aplicación en sectores como el transporte, la energía o la biomedicina. Combinados con técnicas de fabricación avanzada como la fabricación aditiva o las nuevas tecnologías de impresión, estos materiales resultan particularmente relevantes en ámbitos como la Industria 4.0 o el denominado “Internet de las cosas”, con importantes implicaciones sociales, económicas y laborales, entre otras.
El físico Senentxu Lanceros-Mendez, actual director científico del BCMaterials (Basque Center for Materials, Applications and Nanostructures), analizó la relevancia de estos elementos en la conferencia titulada “Importancia de los materiales inteligentes y multifuncionales en el desarrollo tecnológico actual”, que se celebró el pasado 27 de febrero en la Biblioteca Bidebarrieta de Bilbao. El investigador Ikerbasque explica en ella no solo los aspectos más destacados de los nuevos materiales inteligentes, sino también las aplicaciones hasta hace poco inimaginables que estos permiten y sus implicaciones económicas y sociales.
Senentxu Lanceros-Mendez es licenciado en Física por la UPV/EHU y doctorado por la Universidad Julius-Maximilians-Universität Würzburg (Alemania). Su investigación está centrada en el desarrollo de nuevos materiales inteligentes y multifuncionales para su aplicación en sensores, actuadores, energía y biomedicina.
La charla se enmarca dentro del ciclo “Bidebarrieta Científica” una iniciativa que organiza todos los meses la Cátedra de Cultura Científica de la UPV/EHU y la Biblioteca Bidebarrieta para divulgar asuntos científicos de actualidad.
Edición realizada por César Tomé López
El artículo Materiales inteligentes y multifuncionales para impulsar el desarrollo tecnológico se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Un atlas para materiales 2D
- Ciencia, arte y cultura callejera: materiales y obra artística
- Un algoritmo genético para buscar materiales 2D
¿Son evitables los ataques con drones?
La respuesta corta a la pregunta del título es: ahora mismo, no.
Si algún lector quiere seguir leyendo, desarrollaré un poco más la explicación. Al hilo de los ataques sufridos en las instalaciones de Saudi Aramco, muchas personas se preguntan si el ataque se pudo evitar. O incluso, pensando en el futuro, si se podrá evitar cuando vuelva a pasar. La respuesta es que no será nada fácil. No hay un sistema de contramedidas 100 % fiable.
¿Se acuerdan los lectores de que el año pasado unos drones obligaron a cerrar el aeropuerto de Gatwick? Fíjense en el caos y en la dificultad para tratar estas emergencias, que incluso las autoridades llegaron a pensar que quizás esos drones nunca habían existido. Había tal confusión que, meses más tarde, la policía en uno de sus informes finales recogió más de 100 visiones de estos multirrotores.
 Unos drones domésticos paralizaron el aeropuerto de Gatwick.
Unos drones domésticos paralizaron el aeropuerto de Gatwick.El caso de Gatwick es diferente del de Aramco, ya que no se emplearon los drones para el ataque. Estas máquinas se llevan usando para hacer daño al enemigo desde hace bastante tiempo. Ya en el siglo XIII a.C. la dinastia china Song usaba cometas para sobrevolar por encima de sus enemigos, a las que entonces prendía fuego. Ese episodio representa el primer vestigio de la guerra con drones.
Si viajamos a tiempos más recientes, en 2003 la OTAN lanzó un programa que duraría 10 años para el estudio de contramedidas contra esta tecnología. Este informe no ha sido abierto al público. En 2008, el think tank RAND Corporation publicó un informe sobre la amenaza que los robots voladores suponían para la seguridad de Estados Unidos. El ISIS usó con gran éxito estos aparatos en sus ataques. Una de las maniobras más sonadas fue la de enero de 2018, cuando este grupo terrorista coordinó una docena de estos ingenios contra dos instalaciones militares en Rusia.
Además, a los responsables de seguridad les pone los pelos como escarpias la aparente naturalidad con la que los vehículos aéreos no tripulados se acercan a objetivos muy sensibles. Como Pedro por su casa, que dirían. En 2013, por ejemplo, el Partido Pirata alemán voló un drone muy cerca de Angela Merkel, sin ningún peligro, pero dejando muchas dudas sobre la preparación de la seguridad ante estas eventualidades. Incluso en 2015, un hombre estrelló su juguete en los terrenos de la Casa Blanca.
Medidas de defensa
Conviene aclarar que las medidas antiaéreas tradicionales no sirven de nada contra estos aparatos. En 2016, un sencillo drone que sobrevoló el cielo de Israel procedente de Siria no sucumbió ante el ataque de dos misiles Patriot ni de un misil aire-aire lanzado desde un avión israelí. Las medidas antidrones son más sutiles.
Actualmente, los sistemas para combatir a los vehículos aéreos no tripulados los podemos clasificar en los siguientes tipos:
Detección
Los drones son tan pequeños que no son fáciles de detectar con un radar. Se emplean otras tecnologías como sensores de radiofrecuencia, acústicos y ópticos. Estas medidas tienen la desventaja de que necesitan tener línea directa de visión con la máquina voladora. Para solventarlo, existen sensores acústicos, que se valen de grandes librerías que intentan detectar el sonido característico de estos aparatos. Pero la incorporación al mercado de estos drones es muy rápida, y la librería no siempre es fácil de mantener actualizada. Todas estas imprecisiones llevan a que haya un gran número de falsos positivos, lo cual no es nada deseable.
Interceptación
Estas medidas consisten en interrumpir las comunicaciones del drone. Ya sea con el operador que lo maneje, con una estación o con un satélite. Esto tampoco es 100 % efectivo, ya que muchos están programados para navegar de manera autónoma.
Por otro lado, también se contempla la idea de lanzar redes para atascar los rotores del drone. Hay espectaculares vídeos comerciales sobre estas iniciativas de derribo de UAVs con unas armas bastante aparatosas que normalmente requieren un espacio aéreo totalmente despejado.
Vídeo promocional de SkyWall 100, una bazuca anti drones.En esta línea encontramos también el famoso caso de las águilas usadas por la policía holandesa, aunque esta idea se rechazó finalmente.
Algunos fabricantes de drones tienen la opción de configurar en qué área geográfica pueden operar sus productos, tal y como lo demostró la empresa DJI en el conflicto de Siria. Esta medida parece fácilmente salvable por unos terroristas.
Aunque el mayor problema de atacar un drone que transporta una bomba es: ¿qué hacer cuando caiga? Por lo tanto, vuelve a quedar claro que no existen medidas 100 % efectivas de interceptación.
Conclusión
El número y el mercado de contramedidas se ha multiplicado en los últimos años y la amenaza hace tiempo que está detectada. Muchas medidas que he presentado aquí no se pueden usar directamente en un aeropuerto, ya que podría interferir en la comunicación con los aviones, así que un caso como el de Gatwick podría repetirse.
Sin embargo, tanto pero no significa que evitar este tipo de ataques sea imposible. Aunque no sean tan mediáticos, ya existen casos de interceptación de drones, como en el aeropuerto de Londres hace unos pocos días. El interés de las fuerzas de seguridad y los ejércitos en este ámbito va en aumento.![]()
Sobre el autor: Julián Estévez Sanz es profesor ayudante de Robótica e Inteligencia Artificial en el Departamento de Ingeniería Mecánica de la Universidad del País Vasco / Euskal Herriko Unibertsitatea
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo ¿Son evitables los ataques con drones? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Adulterar los cigarrillos electrónicos te puede matar
 Foto de Austin Lawrence
Foto de Austin Lawrence
-
805 afectados y 12 muertos
El New York Times alertaba a principios de septiembre de una nueva muerte consecuencia del vapeo en el estado de Oregón. Es la segunda muerte registrada después de la acontecida en Illinois hace casi dos meses.
Cuando el número de afectados ingresados llegó a 53, el Departamento de Salud Pública de Illinois elaboró un informe acerca de las similitudes de estos pacientes. Todos ellos presentaban infiltraciones pulmonares, es decir, tenían sustancias adheridas a los pulmones que dificultaban su normal funcionamiento, provocando inflamación e impidiendo la respiración. Fueron tratados con esteroides para frenar la inflamación, coma inducido, lavado broncoalveolar, antibióticos para tratar las neumonías y con respiración asistida. Los expertos se enfrentan a un nuevo síndrome cuyas causas, aseguran en el informe, requieren un estudio urgente.
Según los CDC (Centros para el Control y la Prevención de Enfermedades de Estados Unidos) los casos de enfermedad pulmonar asociados al mal uso de cigarrillos electrónicos aumentaron un 52% en la última semana. Hay 805 afectados y 12 muertos. En su mayoría adolescentes. En todos los casos parece que los consumidores manipularon los vapeadores para fumar otro tipo de sustancias, diferentes a las que contienen los cigarrillos electrónicos convencionales, y utilizaron cartuchos del mercado negro. La inhalación de sustancias tóxicas es el origen del misterioso síndrome pulmonar.
-
La “epidemia” no es por vapear. Hay algo más.
Lo más importante de este suceso es que los afectados no fumaban con vapeadores normales, sino que los manipularon y usaron cargas irregulares.
Mas del 90% de los afectados reconoció haber utilizado vapeadores cargados con aceites que contenían cannabinoides, como el THC (tetrahidrocannabinol) y el CBD (cannabidiol). Es decir, alteraron las cargas originales de estos dispositivos.
Se están estudiando otros posibles contaminantes como hidrocarburos aromáticos policíclicos, compuestos liposolubles como la vitamina E, nitrosaminas, productos químicos orgánicos volátiles como el formaldehído y productos químicos inorgánicos como metales. También se han detectado endotoxinas y compuestos aromatizantes como el diacetilo y la 2,3-pentanodiona.
En busca de respuestas, NBC News encargó a CannaSafe, un laboratorio experto en análisis de cartuchos de vapeadores, el análisis de 18 cartuchos, 3 comprados en dispensadores legales de California y 15 del mercado ilegal. De los tres comprados en dispensarios legales, la compañía de pruebas CannaSafe no encontró metales pesados, pesticidas o disolventes residuales como la vitamina E. Pero 13 de las otras 15 muestras de cartuchos de THC del mercado negro sí contenían vitamina E.
La vitamina E es una sustancia liposoluble, es decir, en los pulmones puede comportarse como un aceite que se va adhiriendo al árbol respiratorio. El organismo se defiende intentando eliminar ese cuerpo extraño y para ello utiliza las células expertas en ello: los eosinófilos. El resultado de esto puede derivar en neumonía eosinófila aguda.
CannaSafe también probó pesticidas en 10 de los cartuchos no regulados. Los 10 dieron positivo. Todos los productos contenían el fungicida myclobutanil, una sustancia que puede transformarse en cianuro de hidrógeno cuando se quema. El cianuro es tóxico por inhalación, ya que inhibe la respiración celular. Es mortal a partir de 300 ppm de concentración.
Los jóvenes afectados por esta “epidemia” no habían utilizado cápsulas comerciales, sino que las habían adulterado para poder fumar otras drogas o ahorrar dinero.
La razón por la que llevamos meses preguntándonos si el origen de este misterioso síndrome pulmonar está en los cigarrillos electrónicos, es que muchos de los jóvenes afectados ocultaron la información. Los médicos no sabían qué estaban fumando. Esto obstaculiza el tratamiento y el diagnóstico.
-
Composición de los cigarrillos electrónicos convencionales
Los principales componentes de los cigarrillos electrónicos convencionales a base de nicotina incluyen propilenglicol y glicerina, además de la nicotina. También algún aromatizante. En ningún caso contienen aceites.
A excepción de la nicotina, inhalar estas sustancias no supone ningún peligro. Sin embargo, aunque en estos dispositivos no se producen reacciones de combustión, tal y como ocurre con el tabaco convencional, sí se produce calentamiento. El calentamiento sí puede dar lugar a la formación de otras sustancias que están en el punto de mira. Se sigue estudiando la formación de sustancias peligrosas como el formaldehído y las acroleínas como subproducto de reacción en algunos de estos dispositivos. Sea como fuere, los niveles de estas sustancias potencialmente tóxicas que se pueden formar en los cigarrillos electrónicos estarán muy por debajo de las que se forman en el tabaco. Desde el punto de vista exclusivamente bioquímico, atendiendo a las sustancias presentes en el humo y su impacto en la salud, los cigarrillos electrónicos no son totalmente inocuos, pero sí son más seguros que fumar tabaco convencional.
-
Pros de los cigarrillos electrónicos
Durante la combustión del tabaco convencional se producen sustancias relacionadas con el cáncer, como bencenos, alquitrán y amoniaco. Sustancias que no se producen en los vapeadores.
Un estudio de Sigma Dos asegura que el 96,3% de los españoles recurren al cigarrillo electrónico como sustituto del tabaco. De ellos, el 69,8% ha logrado cambiar el humo por el vapor; reemplazar por completo el tabaco por los nuevos dispositivos electrónicos de liberación controlada de nicotina consiguiendo así no volver a fumar tabaco convencional.
Sin embargo, los estudios realizados hasta la fecha no son muy prometedores con respecto al abandono del tabaquismo. Aunque fumar es significativamente más insalubre que vapear, no hay evidencias sobre que el vapeo sea una estrategia útil para dejar de fumar. Al menos no parece ofrecer una tasa de éxito mayor que otras estrategias.
No obstante, en 2015 el Gobierno del Reino Unido decidió autorizar a los médicos de su sistema público de salud a prescribir los vaporizadores como tratamiento alternativo para dejar de fumar, igual que ocurre en España con las terapias de reemplazo de nicotina, como los parches o chicles de nicotina. Una decisión avalada por un informe del Real Colegio de Médicos británicos que asegura que el uso de vaporizadores es «un 95% menos dañino» que el tabaco.
Aunque los autores del trabajo en el que se citaba este dato fueron acusados de conflicto de interés, la evidencia científica nos dice que los cigarrillos electrónicos ofrecen niveles mucho más bajos de carcinógenos que los cigarrillos convencionales. No son inocuos, pero sí suponen una mejora significativa.
Con respecto a la salud cardiovascular, el cigarrillo electrónico no parece ofrecer ventajas frente al tabaco convencional. El riesgo de infarto de miocardio e ictus es prácticamente el mismo.
-
Contras de los cigarrillos electrónicos
Aunque la evidencia científica es escasa, con respecto a enfermedades pulmonares, todo apunta a que el cigarrillo electrónico podría aumentar el riesgo de bronquitis y asma. Pero este no es el contra más importante.
 Austin Lawrence retratado por Matt Martin para GQ
Austin Lawrence retratado por Matt Martin para GQEste tipo de dispositivos se han introducido en el mercado como sustitutos del tabaco, como una transición plácida hasta dejar definitivamente de fumar. Aparentemente es un win-win. Los consumidores van dejando de fumar y esto sigue reportando beneficios a la industria del tabaco. British American Tobacco (BAT), Philip Morris, Japan Tobacco International (JTI) y Altadis, las cuatro grandes del sector, comercializan distintas modalidades de cigarrillos electrónicos.
Pero a su vez, estos dispositivos que se presentaban como una alternativa para dejar de fumar, se han colado en el mercado como un caballo de Troya capaz de persuadir a nuevos clientes. Vapear se ha convertido en una moda que arrasa en las redes sociales. Uno de los más famosos es Austin Lawrence, que cuenta con más de 3 millones de seguidores en Intagram y en Youtube.
Los adolescentes son atraídos mediante técnicas de marketing que van desde el «esto que fumas no hace daño» hasta el «te ofrezco sabores como el de pepino«, claramente dirigidas a los más jóvenes. Las campañas publicitarias son del tipo “glamur y libertad”. Nos recuerdan a las que en su día se hacían con el tabaco convencional. Quienes comienzan a fumar utilizando cigarrillos electrónicos con nicotina no deberían olvidarse de que la nicotina es una sustancia adictiva, y la adicción es contraria a la libertad.

-
Los jóvenes fuman menos y empiezan más tarde, pero vapean más
En la encuesta Estudes sobre consumo de drogas entre estudiantes se muestra que el 20,1% de los alumnos ha utilizado cigarrillos electrónicos alguna vez en su vida, observándose una mayor extensión entre los chicos. Entre los que admiten haber vapeado en alguna ocasión, el 52,6% utilizó cartuchos sin nicotina, el 22,4% con nicotina y el 24,9% admitieron haber utilizado ambos tipos. La proporción de usuarios de cigarrillos electrónicos es considerablemente más alta ente los que fuman tabaco a diario que entre los que no lo hacen.
El 34,7% (31,4 en 2014) de los alumnos ha fumado tabaco en el último año. El consumo diario se sitúa en el 8,8% (8,9% en 2014), cifra mínima de la serie histórica de Estudes. En 2004, el 21,5% de este sector de la población fumaba a diario. Por término medio, el primer consumo de tabaco se produce a los 14,1 años; por primera vez a lo largo de toda la serie histórica de Estudes se supera la frontera de los 14 años. La adquisición del hábito de fumar diariamente, igual que ocurría en 2014, comienza a los 14,6 años de media, apenas medio año después de haberlo probado por primera vez. Parece que la irrupción del cigarrillo electrónico no ha aumentado el número de fumadores adolescentes ni la edad a la que empiezan a fumar. Parece que un hábito ha reemplazado en parte al otro.
 Meme creado por Adam Padilla
Meme creado por Adam Padilla
Aunque el juguete mi primer vapeador no existe, fue un meme creado por Adam Padilla, sí se comercializaron cigarrillos de chocolate, que vienen a ser lo mismo. Los cigarrillos de chocolate fueron creados por Milton Snavely Hershey en 1906 y se popularizaron en España en la década de los 80, cuando un tercio de la población era fumadora. En 2005 fueron retirados del mercado español debido a la aprobación de la Ley Antitabaco, que especifica: «En particular, se prohíbe la venta de dulces, refrigerios, juguetes y otros objetos que tengan forma de productos del tabaco y puedan resultar atractivos para los menores».
La prohibición de los cigarrillos de chocolate pretendía lanzar el mensaje de que el tabaquismo no es un juego. El meme de Adam Padilla pretende lo mismo con respecto al vapeo. Del mismo modo, decenas de sociedades médicas han firmado la llamada Declaración de Madrid, promovida por el Comité Nacional de Prevención del Tabaquismo, que insta a aplicar la actual regulación sobre espacios sin humo a los cigarrillos electrónicos. El objetivo es doble. Por un lado, evitar la toxicidad pasiva que estos ocasionan, y por otro, conseguir la desnormalización del vapeo en lugares públicos.
-
Reflexión final
La manipulación de cigarrillos electrónicos ha causado la muerte de 12 personas y ya hay 805 afectados por un síndrome pulmonar grave. Los afectados adulteraron deliberadamente estos dispositivos, por lo que no podemos culpar a los cigarrillos electrónicos de esta “epidemia”. Lo responsable desde los medios de comunicación es alertar del peligro que supone adulterar estos dispositivos.
La evidencia científica apunta a que es mucho peor para la salud fumar que vapear. No está tan claro que sea una buena estrategia para dejar de fumar, pero al menos vapear en lugar de fumar sí es un cambio a mejor siempre y cuando se utilice tal y como indica el fabricante y con las recargas oficiales.
Aunque vapear no es totalmente inocuo, el principal contra no está tanto en las sustancias que se inhalan, sino en el hábito al que inducen.
Los cigarrillos electrónicos irrumpieron en el mercado como una estrategia más para dejar de fumar. La intuición nos dice que es una estrategia ganadora, ya que imita el hábito de fumar, cosa que no ocurre con los chicles o los parches de nicotina. El cigarrillo electrónico era un objeto tosco y caro, así que en principio era difícil imaginarse que el vapeo se convertiría en una actividad lúdica. Pero el glamur es muy importante. Los cigarrillos electrónicos son dispositivos cada vez más sofisticados. Además, la nube de vapor que crean al exhalar es muy estética. Permite hacer trucos visuales, como aros y otras formas, muy atractivos para la fotografía. El vapeo es instagrameable. La publicidad ha hecho el resto.
Que los jóvenes vapeen con cigarrillos electrónicos en lugar de fumar tabaco convencional no es el escenario ideal, pero siempre y cuando no manipulen los dispositivos, desde el punto de vista de la salud pública puede verse como una mejora. No obstante, las restricciones legales del tabaco convencional deberían extenderse al cigarrillo electrónico, a fin desincentivar su uso. La situación ideal sería que los jóvenes no fumasen si lo uno ni lo otro. Pero no vivimos en un mundo ideal.
La realidad es que si los cigarrillos electrónicos e Instagram hubiesen existido cuando yo tenía 15 años, en lugar de dar una primera calada a un pitillo, se la habría dado a un cigarrillo electrónico. Porque cuando tienes 15 años, molar es lo más importante. Habría sido mejor, pero no lo mejor. Ojalá hubiese sabido que para molar no hacía falta inhalar mierdas.
Sobre la autora: Déborah García Bello es química y divulgadora científica
El artículo Adulterar los cigarrillos electrónicos te puede matar se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Polímeros biocompatibles para integrar dispositivos electrónicos en nuestro cuerpo
- Todo lo que se puede medir en un río
- Lo que la tensión puede hacer en dos capas de grafeno
Dos teoremas de la amistad
Entre los individuos, la amistad nunca viene dada, sino que debe conquistarse indefinidamente.
Simone de Beauvoir
Decir amistad es decir entendimiento cabal, confianza rápida y larga memoria; es decir, fidelidad.
Gabriela Mistral
Recordemos que, en matemáticas, un grafo está definido por un conjunto de vértices y un conjunto de aristas uniendo algunos de estos vértices. Un grafo se llama plano cuando puede dibujarse en el plano sin que ninguna arista se cruce. Los ejemplos más sencillos de grafos no planos son los conocidos como K5 y K3,3.
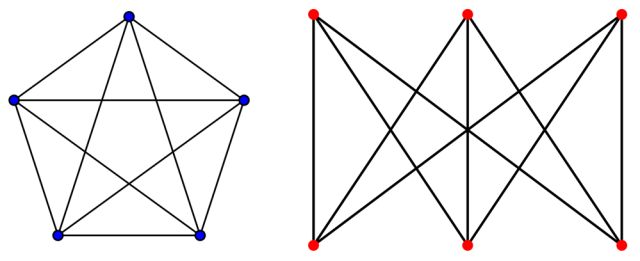 Grafos K5 y K3,3.
Grafos K5 y K3,3.
De hecho, en 1930, el matemático y lógico Kazimierz Kuratowski (1896-1980) demostró este bello teorema que caracteriza la ‘planitud’ de cualquier grafo:
Un grafo es plano si y solo si no contiene ningún subgrafo homeomorfo a K5 o K3,3.
El grafo de la amistad Fnse construye uniendo n copias del grafo cíclo C3 a través de un vértice común.
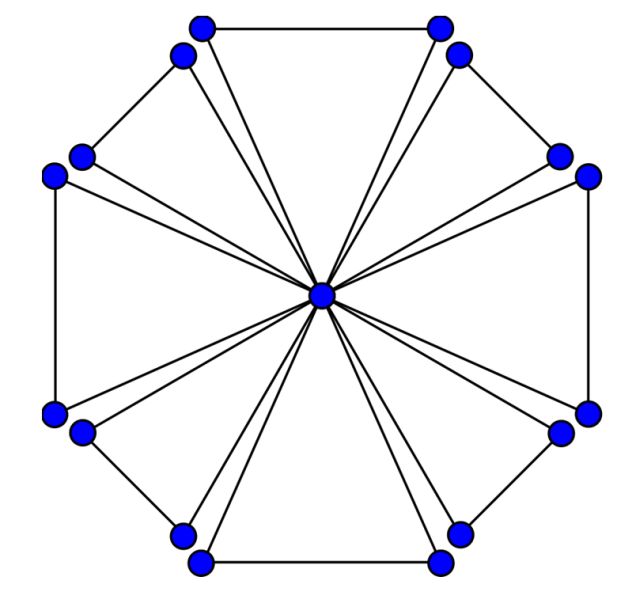 El grafo de la amistad F8 como unión a través de un vértice de 8 copias de C3.
El grafo de la amistad F8 como unión a través de un vértice de 8 copias de C3.Se trata de un grafo plano que posee 2n+1 vértices y 3n aristas.
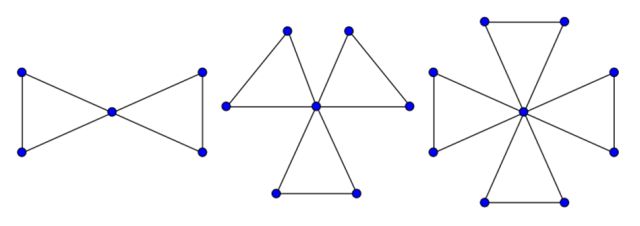 Grafos de la amistad F2, F3 y F4
Grafos de la amistad F2, F3 y F4
En 1966 Paul Erdős, Alfréd Rényi y Vera T. Sós demostraron el que llamaremos el primer teorema de la amistad, que dice lo siguiente (ver [2]):
Los grafos finitos con la propiedad de que dos vértices cualesquiera tienen exactamente un vértice vecino en común son precisamente los grafos de la amistad.
Una manera de pensar en este teorema –y de allí su nombre– es el siguiente: si un grupo de personas posee la característica de que cada par de ellas tiene exactamente un amigo en común, entonces debe de haber una persona que sea amiga de todas las demás.
El primer teorema de la amistad no funciona para grafos infinitos, es decir, pueden existir grafos infinitos diferentes, con la propiedad de que ‘dos vértices cualesquiera tienen exactamente un vértice vecino en común’ y con el mismo cardinal (ver [3]).
Por cierto, Vera T. Sós (1930) es una especialista en combinatoria. Esa “T.” corresponde al apellido de su marido, Pál Turán (1910-1976). Ambos fueron estudiantes de Lipót Fejér… y ambos poseen número de Erdős igual a 1.
Para establecer el segundo teorema de la amistad, supongamos que en una fiesta hay 6 personas. Si tomamos dos de ellas al azar, o bien se encuentran por primera vez –les llamaremos mutuamente extraños– o bien se conocían previamente –los llamaremos mutuamente conocidos–. El teorema dice entonces lo siguiente:
En cualquier grupo de seis personas, existen tres personas que son mutuamente conocidas o mutuamente desconocidas.
Este problema puede reformularse en términos de teoría de grafos. Recordemos que un grafo se llama completo si es un grafo simple –sin aristas múltiples entre vértices, en particular, sin bucles– donde cada par de vértices está conectado por una arista. Un grafo completo de n vértices se denota Kn –antes hemos hablado de K5–.
K6 contiene 15 aristas.
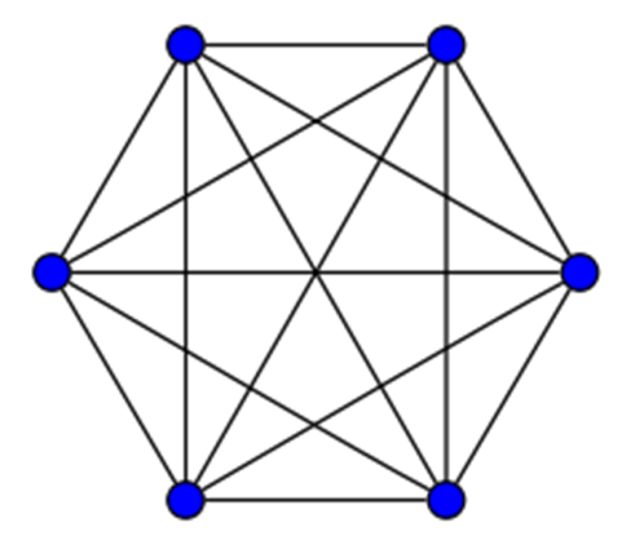 Grafo K6.
Grafo K6.
Cada persona asistente a esa fiesta se puede representar por uno de los vértices. Coloreemos la arista uniendo dos vértices de rojo si las personas correspondientes son mutuamente conocidas y de azul si son mutuamente extrañas.
El segundo teorema de la amistad se reformula entonces en términos de coloreado de grafos:
Si coloreamos con rojo o azul las 15 aristas de K6 siempre habrá un triángulo rojo o un triángulo azul.
La prueba es muy sencilla. Elegimos un vértice cualquiera V. Cinco aristas inciden con V, y serán de color rojo o azul. El principio del palomar garantiza que al menos tres aristas deben ser del mismo color; supongamos que es rojo. Llamemos A, B y C los vértices correspondientes a estas tres aristas. Si alguna de las aristas AB, BC, CA es roja, entonces esta arista junto con las dos aristas incidentes a V forman los lados de un triángulo rojo. Si ninguna de las aristas AB, BC, CA es roja, entonces las tres aristas son de color azul y se tiene el triángulo azul ABC.
El matemático Frank P. Ramsey (1903-1930) demostró un teorema general de combinatoria en su artículo On a problem of formal logic, este fue el origen de la llamada teoría de Ramsey. El segundo teorema de la amistad es un caso particular de este resultado.
Por cierto, el segundo teorema de la amistad no funciona para grupos de menos de 6 personas…
Referencias
[1] Dutch Windmill Graph, Wolfram MathWorld
[2] Paul Erdős, Alfréd Rényi and Vera T. Sós, On a problema of graph theory, Studia Scientiarum Mathematicarum Hungarica 1 (1966) 215-235
[3] Václav Chvátal, Anton Kotzig, Ivo G Rosenberg and Roy O. Davies, Roy O., There are 2ℵα friendship graphs of cardinal ℵα, Canadian Mathematical Bulletin 19 (4) (1976) 431-433
[4] Teorema de la amistad, Wikipedia (consultado el 18 septiembre 2019)
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo Dos teoremas de la amistad se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El juego del Sim
- Shizuo Kakutani y sus teoremas
- El teorema de los cuatro colores (3): Tras más de un siglo de aventura… ¿un ordenador resuelve el problema?
Los postulados de Bohr
 Imagen: Gerd Altmann / Pixabay
Imagen: Gerd Altmann / PixabaySi suponemos, como hizo Rutherford, que un átomo consiste en un núcleo cargado positivamente rodeado de varios electrones cargados negativamente, ¿qué impide que los electrones y el núcleo se unan debido a la atracción eléctrica? Una posible respuesta es que un átomo podría ser como un sistema planetario, con los electrones girando en órbitas alrededor del núcleo [1]. Podemos pensar en un planeta que orbita alrededor del Sol como sujeto a una fuerza atractiva hacia el centro [2]. Si no fuese así el planeta seguiría en línea recta, de acuerdo con la primera ley del movimiento de Newton. Esta fuerza hacia el centro a menudo se llama fuerza centrípeta. Para los planetas, esta fuerza surge de la atracción gravitacional del Sol sobre el planeta [2]. Para el caso de los electrones en los átomos Rutherford sugirió que, haciendo el papel de fuerza gravitacional, la fuerza de atracción eléctrica entre el núcleo y el electrón suministraría una fuerza centrípeta. Esta fuerza centrípeta mantendría en órbita al electrón en movimiento.
La idea parece ser una buena base para un modelo útil de la estructura atómica. Pero surge un grave problema con respecto a la estabilidad de un átomo «planetario». Según la teoría del electromagnetismo de Maxwell, una partícula cargada pierde energía cuando se acelera. Un electrón que se mueve en una órbita alrededor de un núcleo cambia continuamente su dirección, por lo tanto, también su vector de velocidad. En otras palabras, siempre está siendo acelerado por la fuerza eléctrica centrípeta.
El electrón, por lo tanto, debería perder energía emitiendo radiación y, por lo tanto, acercándose constantemente al núcleo. En muy poco tiempo, el electrón que pierde energía se termina precipitando en el núcleo. [1] Según la física clásica, la mecánica y el electromagnetismo, un átomo planetario no sería estable durante más de una fracción muy pequeña de un segundo. Con todo, y a sabiendas de esta dificultad insalvable desde el punto de vista clásico, la idea de un átomo planetario era muy atractiva.
La comunidad física continuó buscando un modelo que incluyese una estructura planetaria estable y que, entre otras cosas, pudiese explicar los espectros de emisión de los elementos. Niels Bohr, entonces un físico danés desconocido que acababa de recibir su doctorado, logró construir un modelo muy interesante en 1912-1913. Este modelo se conoce como modelo de Bohr o modelo cuántico del átomo [4], porque incorporó con éxito la idea cuántica de Einstein y Planck. Fue ampliamente reconocido como una gran victoria. Aunque tuvo que modificarse más tarde para tener en cuenta muchos más fenómenos, mostró cómo atacar problemas atómicos mediante el uso de la teoría cuántica. Dado que Bohr incorporó la idea de átomo nuclear de Rutherford, algo crucial para el modelo, el nombre más apropiado para éste quizás sería modelo de Rutherford-Bohr.
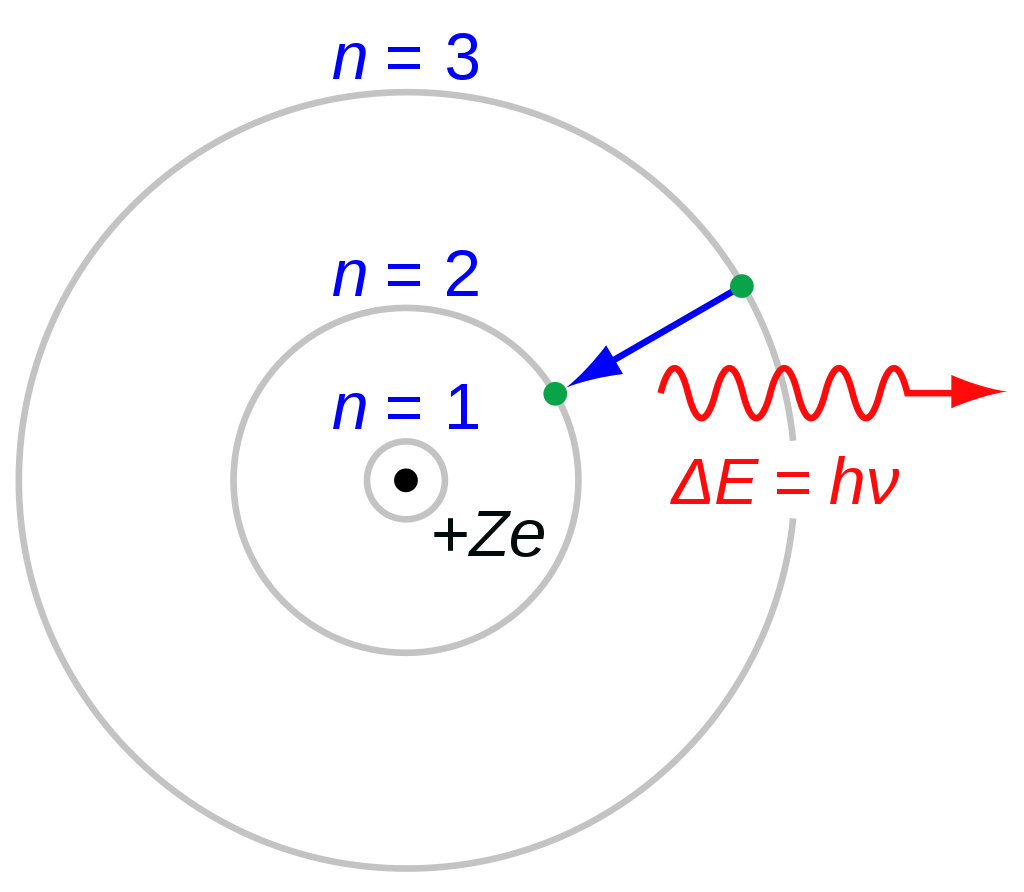 El modelo de Rutherford-Bohr en una imagen. La expresión en rojo es otra forma de escribir hf = Ei – Ef. Imagen: Wikimedia Commons
El modelo de Rutherford-Bohr en una imagen. La expresión en rojo es otra forma de escribir hf = Ei – Ef. Imagen: Wikimedia CommonsBohr introdujo dos nuevos postulados [5] específicamente para explicar la existencia de órbitas de electrones estables y espectros de emisión diferentes para cada elemento. Estos postulados pueden expresarse de la siguiente manera:
1. Contrariamente a las predicciones de la física clásica, que después de todo había sido probada solo para circunstancias relativamente a gran escala, existen estados para un sistema atómico en el que no se emite radiación electromagnética a pesar de la aceleración de las partículas cargadas (electrones) . Estos estados se denominan estados estacionarios del átomo.
2. Cualquier emisión o absorción de radiación, ya sea como luz visible u otra radiación electromagnética, corresponde a una transición repentina de la carga entre dos de estos estados estacionarios. La radiación emitida o absorbida tiene una frecuencia f determinada por la relación hf = Ei – Ef (en esta ecuación h es la constante de Planck, y Ei y Ef son las energías del átomo en los estados estacionarios inicial y final, respectivamente.
La teoría cuántica había comenzado con la idea de Planck de que los átomos emiten luz solo en cantidades definidas de energía. Este concepto fue ampliado por la idea de Einstein de que la luz viaja solo como paquetes definidos, cuantos, de energía. Ahora se extendía aún más por lel postulado de Bohr de que los átomos existen en un estado estable solo en estados de energía definidos y «cuantizados». Pero Bohr también usó el concepto cuántico para decidir cuál de todos los estados estacionarios concebibles son realmente posibles. Veremos un ejemplo en la siguiente entrega de la serie.
Notas:
[1] La imagen del sistema planetario atómico es parte del desarrollo histórico del modelo. Debemos recordar que los átomos NO son sistemas planetarios de la misma forma que no son pudin de pasas.
[2] Este es el modelo newtoniano. Sabemos desde la aparición de la relatividad general que esto es solo una aproximación válida matemáticamente.
[3] Parecido a lo que le ocurre a un satélite artificial, que pierde energía debido a la fricción en la atmósfera superior, y gradualmente se mueve en espiral hacia la Tierra. Caería si no se corrigiese su trayectoria con propulsores.
[4] Se lo conoce así pero, en realidad, el modelo de Bohr es el quinto modelo cuántico construido. Más sobre ello en este vídeo.
[5] Son postulados porque se postulan, es decir, al asumir que son ciertos el modelo arroja resultados coherentes con los datos experimentales. No hay otro razonamiento más que este.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Los postulados de Bohr se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- #Quantum13 Bohr no fue el primero
- 1913-2013: del modelo atómico de Bohr al Higgs
- Bohr y la veneración de la autoridad
Lo prudente es hablar de emergencia climática
 Río Segura a su paso por Murcia tras las intensas lluvias provocadas por el fenómeno DANA a principios de septiembre.
Río Segura a su paso por Murcia tras las intensas lluvias provocadas por el fenómeno DANA a principios de septiembre.Jose y yo Estudio/Shutterstock
No podíamos seguir permitiéndonos en España una falta de atención mediática al cambio climático. Y menos tras haber sufrido una gota fría sin precedentes en diversos puntos de la costa mediterránea.
Se dijo que “era demasiado pronto” para relacionar las lluvias torrenciales con el cambio climático. Y mucha gente nos preguntamos hasta cuándo iba a seguir siendo demasiado pronto y si no era contraproducente guardar cautela a la hora de informar acerca de uno de los mayores retos de nuestro tiempo.
Frente a esa prudencia de no querer atribuir un evento regular como la gota fría al cambio climático, existe el consenso científico de que el aumento de la temperatura está detrás de la intensificación y la recurrencia de estos fenómenos.
 Imágenes del municipio de Los Alcázares (Murcia) y el mar Menor del 19 de agosto de 2019 (izquierda) y del 13 de septiembre (derecha), tras el episodio de lluvias torrenciales.
Imágenes del municipio de Los Alcázares (Murcia) y el mar Menor del 19 de agosto de 2019 (izquierda) y del 13 de septiembre (derecha), tras el episodio de lluvias torrenciales.Satélites Sentinel del programa europeo Copernicus/SnapPlanet
Dada la inacción política frente a la crisis climática, no querer precipitarse en mencionar el cambio climático solo ha retrasado el momento de poner sobre la mesa medidas urgentes tanto para mitigar emisiones como para adaptarnos a fenómenos extremos. Quizás, lo “prudente” sea informar con frecuencia sobre la emergencia climática.
Signos de una crisis sin precedentes
Si repasamos la actualidad climática, los últimos cinco años han sido los más cálidos jamás registrados. Así lo indica el reciente informe de la Organización Meteorológica Mundial encargado para la cumbre de la ONU sobre Acción Climática que se celebra estos días en Nueva York.
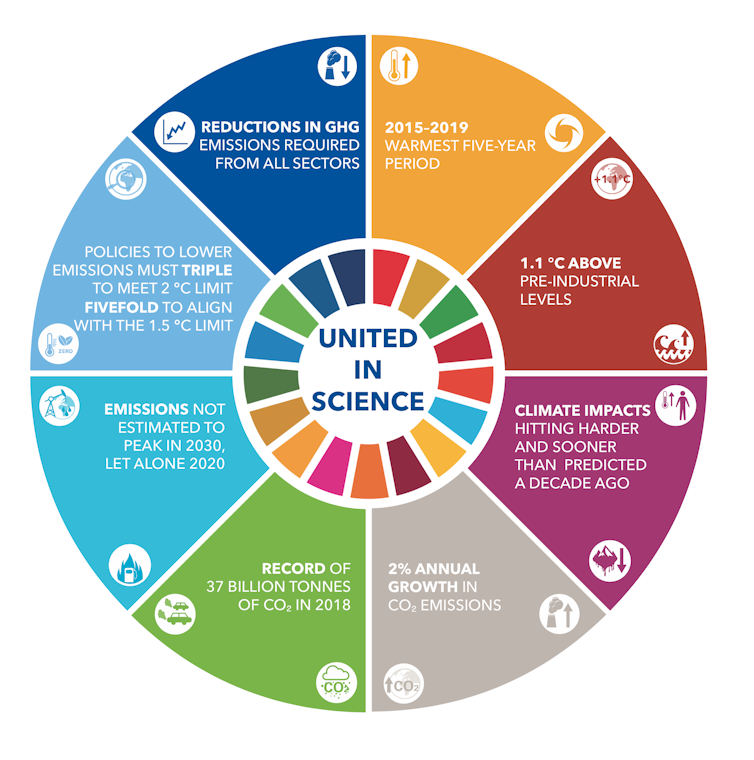 Mensajes clave del informe ‘Unidos en la ciencia’ producido por el Grupo Asesor de Ciencias Climáticas de la Cumbre de Acción Climática de la ONU 2019, Nueva York.
Mensajes clave del informe ‘Unidos en la ciencia’ producido por el Grupo Asesor de Ciencias Climáticas de la Cumbre de Acción Climática de la ONU 2019, Nueva York.Organización Meteorológica Mundial
El hemisferio norte acaba de experimentar el verano más caluroso desde que se tienen registros. La proporción de ciclones tropicales intensos (categorías 4 y 5) se ha incrementado en el Atlántico Norte desde 1970.
Dorian ha sido el huracán más potente jamás registrado en azotar Las Bahamas. Ha dejado el archipiélago devastado a su paso. En su deriva hacia el norte, Dorian irrumpió en la circulación atmosférica de latitudes medias, generando perturbaciones en la corriente en chorro (chorro polar o jet stream).
Como si fuera el meandro abandonado de un río, de las ondulaciones generadas se descolgó una bolsa de aire frío –una depresión aislada en niveles altos (DANA) o gota fría– que llegó a alcanzar la franja mediterránea.
 Mapa animado de isobaras donde se aprecian las perturbaciones generadas por Dorian y la formación de una DANA o gota fría. Alicia M. Bentley, Ph.D.
Mapa animado de isobaras donde se aprecian las perturbaciones generadas por Dorian y la formación de una DANA o gota fría. Alicia M. Bentley, Ph.D.Sabemos desde hace tiempo que la temperatura superficial del Mediterráneo ha subido 1,27 °C de media en los últimos 35 años. Es una media aritmética, lo que significa que existe una mayor amplitud en eventos puntuales.
Un mar caliente junto con bolsas de aire frío en altura son dos de los ingredientes principales para el desarrollo de fenómenos convectivos adversos, como las intensas tormentas de las pasadas semanas.
Incertidumbre no significa inacción
Pese a la incertidumbre que pueda existir al relacionar los puntos arriba mencionados, no podemos permitirnos el lujo de continuar desperdiciando ocasiones para informar sobre la necesidad de actuar frente al cambio climático. Lo prudente es hablar de soluciones a la emergencia climática.
Si alguien todavía considera que la evidencia científica no es suficiente, las compañías aseguradoras también manejan una gran cantidad de indicadores al respecto.
Dado el grado de inacción, los peores escenarios pueden pasar a ser probables. Y recordemos que la comunidad científica tiende a ser conservadora en sus predicciones.
Hoy sabemos que, lejos de ser alarmistas, los científicos han subestimado la velocidad, la magnitud y la recurrencia de algunos de los impactos que estamos viviendo como consecuencia del cambio climático.
Más allá de la dimensión biofísica, los modelos económicos también han subestimado, o directamente omitido, muchas de las graves consecuencias del fenómeno en los medios de vida de las personas. Así lo pone de manifiesto el reciente informe de perspectiva política publicado por The Earth Institute, The Grantham Research Institute on Climate Change and the Environment y The Postdam Institute for Climate Impact Research.
Un punto de inflexión
La crisis climática no nos va a afectar menos por dejar de mentarla. Sin embargo, aumentar la cobertura mediática es fundamental para el llamamiento a la acción.
Iniciativas recientes como Covering Climate Now (The Nation y Columbia Journalism Review) y la Declaración de los Medios de Comunicación Frente al Cambio Climático (ECODES, MDCS y periodistas especializados) están logrando un punto de inflexión a la hora de informar sobre la emergencia climática.
Se trata del mayor esfuerzo hasta ahora realizado por los medios de comunicación para dar cobertura a la crisis climática. Y se refieren a crisis climática o emergencia climática porque el término cambio climático no reflejaba la urgencia del momento.
“Covering Climate Now es inusual, ambicioso, oportuno y bienvenido, sobre todo porque es raro ver medios de comunicación a menudo altamente competitivos colaborando por un propósito compartido”.
Editorial de Nature (15 de septiembre, 2019).
Llamamiento a la acción política
La atención mediática se suma al poderoso altavoz de la movilización mundial por el clima, que protagonizan los más jóvenes en todos los rincones del planeta. Desde que el año pasado Greta Thunberg comenzara las huelgas escolares Fridays for Future, millones de personas inspiradas por Greta, conscientes de la urgencia climática, se han sumado al llamamiento a la acción en más de 163 países.
¿Ha existido alguna vez una movilización tan extendida en todo el planeta? Probablemente no. Es, sin duda, un movimiento histórico, desde la base de la sociedad y sustentado en la ciencia, que está transformando el mundo a través de la equidad y la justicia intergeneracional.
Las movilizaciones por el clima, el apoyo de los medios de comunicación y la nueva convocatoria de elecciones en España suponen una oportunidad histórica para trasladar, de una vez por todas, la necesidad de acción climática a los responsables políticos.
No permitamos de nuevo que la crisis climática quede omitida o silenciada durante la campaña ni en los debates políticos. Solo así podremos elegir, de manera informada, líderes del lado de la ciencia para hacer frente a los retos del siglo XXI.![]()
Daniel Ortiz Gonzalo es p ofesor e investigador postdoctoral en la Facultad de Ciencias, Departamento de Geociencias y Gestión de los Recursos Naturales, University of Copenhagen
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Lo prudente es hablar de emergencia climática se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Naukas Bilbao 2017 – José Miguel Viñas: Me río yo del cambio climático
- Los ecosistemas acuáticos de África y el cambio climático
- Hablar de lo que pasa y de lo que pasó
La tabla periódica en el arte: Plata
La plata es un metal de propiedades fascinantes: conduce la electricidad y el calor como ningún otro, es muy maleable y hasta posee propiedades desinfectantes. Sin embargo, quedémonos con un detalle que podría pasar inadvertido: es el único elemento “femenino” de la tabla periódica. A ninguno de los otros 117 elementos le acompaña el artículo la. Precisamente la plata está vinculada a divinidades femeninas en muchísimas culturas, casi siempre asociadas a la luna. Quizás la unión más hermosa sea la de civilización incaica que considera que la plata proviene de las lágrimas de la Mama Killa (Madre Luna), hermana y esposa de Inti, divinidad solar asociada al oro. Vemos, por tanto, que para este pueblo los metales preciosos tenían también valor religioso y no es de extrañar que elaborasen con ellos una gran cantidad de objetos ceremoniales. En la Imagen 1 podemos ver la representación de una llama trabajada en una aleación de plata, aunque en este caso de femenino tiene poco.
 Imagen 1. Efigie inca de una llama (1450-1550), aleación de plata (4,5 x 4,5 x 1 cm). Fuente: Museum of Fine Arts Boston
Imagen 1. Efigie inca de una llama (1450-1550), aleación de plata (4,5 x 4,5 x 1 cm). Fuente: Museum of Fine Arts BostonRecordemos que una aleación es una mezcla de metales como, por ejemplo, cobre y estaño para formar bronce o cobre y zinc para crear latón. La mayoría de los objetos de plata están elaborados realmente con aleaciones, ya que en su forma pura es excesivamente maleable. Así que si tu collar o brazalete no es cien por cien plata, no te preocupes, se le ha añadido algún otro metal (generalmente cobre) para mejorar sus propiedades mecánicas. Así, cuando leas: realizado en plata de ley 925 (plata esterlina), significa que el 92,5 % de esa aleación es plata. En las joyerías podréis encontrar diferentes aleaciones que indican la proporción de ese metal: 800, 900, 958, etc. Claro que no todas las aleaciones tienen tanta plata. El vellón, por ejemplo, es una aleación que supera el 50 % de cobre. Se empleó mucho para acuñar monedas y, en ausencia de mejores materiales, para elaborar alhajas. Pese al bajo contenido en plata de esta aleación, puede haber casos peores: la plata que no es plata. Nos referimos a la alpaca, una aleación de cobre, zinc y níquel que en apariencia se asemeja al metal precioso que nos ocupa (no en vano también se conoce como plata alemana). Lo podéis juzgar en la Imagen 2.
 Imagen 2. Boys Toys, de Willem Lenssinck (2014). Fuente: Willem Lenssinck
Imagen 2. Boys Toys, de Willem Lenssinck (2014). Fuente: Willem LenssinckPosiblemente, al relacionar la plata con el arte, lo primero que nos venga a la cabeza sean objetos como los que acabamos de ver o delicadas piezas de orfebrería (platería, mejor dicho). Sin embargo, el papel de la plata en la Historia del Arte va mucho más allá y abarca ámbitos tan dispares como la fotografía, las vidrieras o el dibujo. Pasen y vean.
Una calle de París
El 19 de agosto de 1839 Louis Daguerre presentaba en la Academia de Ciencias de París una técnica que permitía capturar la realidad en una placa. En un alarde de imaginación la llamó daguerrotipia. Ya desde el siglo anterior se sabía que las sales de plata eran fotosensibles, así que sólo era necesario lograr un método para, valiéndose de esa propiedad, plasmar imágenes en un soporte sólido. Daguerre lo consiguió suspendiendo una placa de plata (o cobre plateado) sobre vapores de yoduro caliente, de modo que en la superficie se crease una capa de yoduro de plata (AgI). A continuación la placa se introducía dentro de una cámara oscura y se exponía a la luz durante varios minutos. Así, la luz provocaba que los iones de plata de la sal se convirtiesen en plata metálica, dando lugar a una imagen latente (con más plata donde más luz incidía). Posteriormente esa imagen latente se hacía visible gracias a la formación de amalgamas de mercurio y plata, para lo que era necesario exponer la placa a vapores del tan tóxico elemento. Finalmente, para que la imagen se fijase, se empleaba una disolución de sal común (que luego se sustituyó por tiosulfato de sodio por sugerencia de John Herschel). Mediante esta proceso fotográfico Daguerre capturó el Boulevard du Temple(Imagen 3), la primera fotografía que se conserva en la que aparecen humanos. Curiosamente sólo podemos ver a dos (en la parte inferior izquierda): un limpiabotas y su cliente, los únicos que permanecieron relativamente estáticos durante los más de diez minutos de exposición.
 Imagen 3. Vista del Boulevard du Temple, de Louis Daguerre (1838 ó 1839): Fuente: Wikimedia Commons.
Imagen 3. Vista del Boulevard du Temple, de Louis Daguerre (1838 ó 1839): Fuente: Wikimedia Commons.
Nótese que la de Daguerre es la primera fotografía en la que aparecen personas, pero no es la primera fotografía que se conserva. Sería injusto quitarle ese mérito a Nicéphore Niépce con quien Daguerre colaboró hasta la muerte del primero en 1833. Niépce ya había conseguido realizar fotografías hacia 1816, aunque la más antigua que se conserva data de 1826 (Imagen 4). Para ello empleó betún de Judea, un material fotosensible que necesita varias horas de exposición. Sin embargo, tampoco fue Niépce el primero en realizar una fotografía. En 1802, Thomas Wedgwood publicó, nada más y nada menos que junto a Humphry Davy, un artículo en el que describía el uso de nitrato de plata para capturar fotogramas, pero, como no consiguió que la imagen se fijase, no ha tenido tanta transcendencia.
 Imagen 4. Placa original de Vista desde la ventana en Le Gras, de Nicéphore Niépce (1826) en el Harry Ransom Center.
Imagen 4. Placa original de Vista desde la ventana en Le Gras, de Nicéphore Niépce (1826) en el Harry Ransom Center.
Los daguerrotipos tuvieron un gran éxito en Europa continental hasta 1860 y eclipsaron provisionalmente el trabajo presentado por William Fox Talbot en Inglaterra durante los años 30. El británico había seguido explorando las posibilidades que ofrecía el nitrato de plata y había logrado el primer papel fotográfico. Bajo la exposición a la luz y el posterior fijado, se conseguía una imagen en negativo (Imagen 5) que luego se podía pasar a positivo de una forma relativamente sencilla todas las veces que se desease. A partir de ahí se fue mejorando el método con el desarrollo de papeles fotográficos (colodión, baritado…) y emulsiones fotográficas, por lo que podemos considerar el proceso de Talbot como la base de la fotografía del s. XIX y el s. XX
 Imagen 5. La ventana de Oriel en la Abadía de Lacock fotografíada por William Fox Talbot hacia 1835. Nótese que las zonas con más luz están más oscuras (lo que conocemos como negativo). Fuente: The Met.
Imagen 5. La ventana de Oriel en la Abadía de Lacock fotografíada por William Fox Talbot hacia 1835. Nótese que las zonas con más luz están más oscuras (lo que conocemos como negativo). Fuente: The Met.
Y se hizo la luz
Durante el siglo XIII el estilo gótico se extendió por gran parte de Europa. Así, las otrora sólidas paredes se poblaron de ventanales y rosetones decorados con vidrieras en las que se narraban historias de Cristo, la Virgen y los santos. Los artesanos lograron auténticas maravillas pese a una enorme limitación técnica: tenían vidrios de diferentes colores, pero no podían “pintar” otro color sobre ellos. Cada vez que querían cambiar de color tenían que usar un trozo de vidrio diferente, como si de un puzle se tratase. Todo lo que podían hacer era emplear una pasta negra o marrón que servía para realizar dibujos o cambiar las tonalidades y que se fijaba al vidrio tras un proceso de horneado (es decir, trabajaban con grisalla). Entonces llegó el amarillo de plata y lo cambió todo. Con este amarillo se podían colorear las vidrieras sin tener que añadir nuevas piezas al puzle. Puede parecer intranscendente, pero las posibilidades se multiplicaron. Ya no había que recurrir a otros trozos de vidrio para representar coronas, cabellos, nimbos o detalles dorados. Curiosamente las vidrieras se llenaron de oro gracias a la plata. Es más, combinando el amarillo de plata con vidrios azules se lograba verde, por lo que se podía obtener este color sin tener que usar trozos de vidrio verdes. Así se simplificó el arduo trabajo de plomado y el arte de la vidriera se acercó al de la pintura.
 Imagen 6. Vidriera del s. XV de la iglesia de San Pedro de Mancfrot en Glasgow Museums.
Imagen 6. Vidriera del s. XV de la iglesia de San Pedro de Mancfrot en Glasgow Museums.
Todo esto fue posible gracias al modo en el que el amarillo de plata interacciona con el vidrio. Al contrario de lo que pasa con muchas otras substancias, no se queda en la superficie de la vidriera, sino que penetra al interior hasta formar parte del vidrio. Se trata de un fenómeno fisicoquímico de gran interés que trataremos de resumir. Cuando se deposita una sal de plata (nitrato, normalmente) en la parte trasera del vidrio y se mete al horno (a unos 500 ó 600 ⁰C) los iones de plata viajan al interior reemplazando a iones de potasio o sodio. Poco a poco los iones siguen penetrando por difusión hasta zonas más profundas, por lo que no estamos hablando de un fenómeno superficial. Estos iones tomarán parte en reacciones de oxidación-reducción en las que los iones de plata se transformarán en plata metálica. Finalmente, los átomos de plata que se han creado formarán agregados hasta crear partículas microscópicas entre uno y cien nanómetros (cualquier bacteria es más grande que eso). Estas partículas interaccionan con la luz de diferente forma creando tonalidades que varían del amarillo al naranja. La nanotecnología al servicio del arte en pleno s. XIV.
 Imagen 7. El Arcángel Miguel derrotando al demonio (27cm), copia de una xilografía de Jacob Cornelisz van Oossanen en vidrio incoloro con amarillo de plata (ca. 1530). Fuente: Getty Museum.
Imagen 7. El Arcángel Miguel derrotando al demonio (27cm), copia de una xilografía de Jacob Cornelisz van Oossanen en vidrio incoloro con amarillo de plata (ca. 1530). Fuente: Getty Museum.
Cuestión de óxidos
Si tienes un anillo de plata o te regalaron una cubertería de este brillante metal el día de tu boda, sabrás que se oscurece con el tiempo. La formación de esta pátina oscura se debe a un proceso de oxidación (entendido como la pérdida de electrones) en el que se crea una capa oscura de sulfuro de plata (Ag2S) sobre la superficie del metal. Por cierto, existen remedios caseros para devolver el brillo al objeto que se basan en revertir ese proceso empleando algo que todos tenemos en casa: papel de aluminio. El aluminio es un reductor excelente (concede electrones) y en una disolución acuosa junto con bicarbonato o sal permite que la plata recupere los electrones que había perdido volviendo a su estado original.
 Imagen 8. Un cáliz de plata de época bizantina (s. VI) Fuente: The Walters Art Museum
Imagen 8. Un cáliz de plata de época bizantina (s. VI) Fuente: The Walters Art MuseumEn cualquier caso, la capa de sulfuro no siempre es algo indeseable. El lustre que otorga a los objetos puede resultar atractivo, por lo que se buscan métodos para provocar el oscurecimiento. Eso es lo que se logra mediante el “hígado de azufre”, un producto rico en sulfuros (normalmente sulfuro de potasio) que se emplea en joyería. También hay una opción más casera: usar huevos cocidos, una excelente fuente de azufre. De hecho, el mal olor de los huevos podridos se debe al ácido sulfhídrico (H2S).
 Imagen 9. Un anillo de plata oscurecido mediante hígado de azufre. Fuente: Mauro Cateb.
Imagen 9. Un anillo de plata oscurecido mediante hígado de azufre. Fuente: Mauro Cateb.La oxidación de la plata es también un proceso trascendental en una técnica de dibujo antiquísima: la punta de plata. En esta técnica se emplea una varilla del noble metal para realizar trazos sobre un papel previamente preparado para tal uso (de lo contrario la plata no dibuja bien sobre papel). Una vez finalizado, el dibujo será tenue y tendrá el característico brillo grisáceo de la plata, pero, según pase el tiempo, la plata irá oscureciéndose y el dibujo cobrará tonalidades marrones más perceptibles. La punta de plata ya se empleaba en época medieval sobre pergamino y fue muy popular entre grandes artistas del Renacimiento como Leonardo o Durero (Imagen). Quítense el sombrero ante el autorretrato del alemán con tan solo trece añitos.
 Imagen 10. Izquierda: Busto de un guerrero (29×21 cm), de Leonardo da Vinci (ca. 1475). Derecha: Autorretrato a la edad de 13 años (28×20 cm), de Alberto Durero (1484) Fuente: British Museum y Wikimedia Commons.
Imagen 10. Izquierda: Busto de un guerrero (29×21 cm), de Leonardo da Vinci (ca. 1475). Derecha: Autorretrato a la edad de 13 años (28×20 cm), de Alberto Durero (1484) Fuente: British Museum y Wikimedia Commons.
Para saber más:
D. Stulik y A. Kaplan, Salt Print en The Atlas of Analytical Signatures of Photographic Processes (2013) The Paul Getty Trust, Los Angeles. LINK
J. Delgado et al. Characterisation of medieval yellow silver stained glass from Convento de Cristo in Tomar, Portugal. Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms 269 (20) (2011) 2383-2388. DOI.
JCE Staff. Silver to black and back. Journal of Chemical Education. 77 (3) (2000) 328A-328B. DOI.
Sobre el autor: Oskar González es profesor en la facultad de Ciencia y Tecnología y en la facultad de Bellas Artes de la UPV/EHU.
El artículo La tabla periódica en el arte: Plata se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La tabla periódica en el arte: Titanio
- La tabla periódica en el arte: Cobre
- La tabla periódica en el arte: Arsénico
José Ramón Alonso – Naukas Bilbao 2019: Son nuestros amos y nosotros sus esclavos
 Foto: Ian Espinosa / Unsplash
Foto: Ian Espinosa / UnsplashHay charlas que te impactan. Y hay charlas que van más allá del impacto, como las de José Ramón Alonso. Seguro que esta no te deja indiferente. Te adelanto que no va de la alienación de los trabajadores que explicaba Marx precisamente. Va de suicidios.
José Ramón Alonso: 'Son nuestros amos y nosotros sus esclavos'Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo José Ramón Alonso – Naukas Bilbao 2019: Son nuestros amos y nosotros sus esclavos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Curso de verano “La ciencia de nuestras vidas”: Neurobiología del amor. ¿Una locura transitoria?, por José Ramón Alonso
- Naukas Bilbao 2017 – José Miguel Viñas: Me río yo del cambio climático
- Naukas Bilbao 2017 – María José Calderón y Belén Valenzuela: Esta física es la leche
El Universo en un supercomputador

La Biblioteca Bidebarrieta de Bilbao acogió los pasados febrero y marzo dos conferencias organizadas en el marco de la segunda edición del ciclo sobre cine y ciencia “Lo Desconocido”, un evento impulsado por el Donostia International Physics Center (DIPC) de San Sebastián y la Filmoteca Vasca.
La segunda conferencia del ciclo (la primera, en euskara, puede verse aquí) titulada “El Universo en un supercomputador”, se celebró el día 6 de marzo a partir de las 19:00 horas, y corrió a cargo del astrofísico e investigador Ikerbasque del Donostia International Physics Center (DIPC) Raúl Angulo.
El investigador, especializado en cosmología computacional, comenta en esta charla los últimos avances realizados en esta rama de la astrofísica moderna. Los estudios en este ámbito han permitido en los últimos años realizar grandes descubrimientos en torno a la formación y evolución del Universo.
En su ponencia, Angulo nos cuenta cómo los astrónomos usan los ordenadores más grandes del mundo para simular las leyes de la física durante el equivalente a miles de millones de años. Gracias a estas simulaciones, hoy en día los científicos pueden empezar a explicar el mundo astronómico que nos rodea, pero también abrir nuevos y apasionantes interrogantes acerca de la naturaleza de nuestro Universo.
Edición realizada por César Tomé López
El artículo El Universo en un supercomputador se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El Universo en un día: El final del Universo, por Aitor Bergara
- Un universo inesperado, por Ana Achúcarro
- El mito de Arquímedes, mención especial del jurado “On zientzia”
Nunca es tarde para volver a empezar, lo dice el cerebro
Cada vez que alguien plantee como único argumento para resistirse al cambio que así se ha hecho toda la vida habría que pedirle que preguntara a su cerebro qué opina de esa respuesta, porque resulta que el órgano que rige la actividad del sistema nervioso no solo no es refractario a las transformaciones, sino que tiene la capacidad de reprogramarse y reconfigurarse para seguir aprendiendo y volver a empezar.
Esta capacidad, denominada plasticidad cerebral, es el pilar en el que el equipo del doctor Juan Antonio Barcia, del Hospital Clínico San Carlos de Madrid, se ha apoyado para lograr operar tumores cerebrales que hasta ese momento eran inoperables y lo ha conseguido mediante una técnica revolucionaria que ha permitido trasladar funciones esenciales, como el habla o la movilidad, a zonas del cerebro no afectadas por la enfermedad.
 Imagen: El periodista Antonio Martínez Ron en las calles de Bilbao antes del inicio de su conferencia en la Biblioteca Bidebarrieta, «Plasticidad a la carta, un plan B para salvar cerebros«. (Fotografía: Iñigo Sierra)
Imagen: El periodista Antonio Martínez Ron en las calles de Bilbao antes del inicio de su conferencia en la Biblioteca Bidebarrieta, «Plasticidad a la carta, un plan B para salvar cerebros«. (Fotografía: Iñigo Sierra)Con la intención de narrar este hito, el divulgador científico Antonio Martínez Ron ha invertido cinco años en recoger las historias de las personas a las que el doctor Barcia y su equipo han intervenido con éxito y crear el documental “Vida Extra”, un trabajo realizado con la productora 93 Metros que relata la vida de esas personas a las que la pericia de los médicos, el esfuerzo personal y la capacidad de reinventarse de su propio cerebro han dado una segunda oportunidad.
Este 25 de septiembre, como cierre a la programación del evento de divulgación científica Bizkaia Zientzia Plaza, el periodista compartió con la audiencia el fruto de ese esfuerzo en la charla “Plasticidad a la carta, un plan B para salvar cerebros”, en la Biblioteca Bidebarrieta de Bilbao.
Martínez Ron acercó al público los casos de algunos pacientes de Barcia para ilustrar el concepto de plasticidad cerebral, pero también se valió de otros ejemplos reales no vinculados a la terapia del neurocirujano para demostrar cómo el cerebro es capaz de reiniciarse.
“El documental se estrenará pronto y con él buscamos explicar lo increíble que es la plasticidad cerebral”, aseguró Martínez Ron.
 Imagen: Antonio Martínez Ron explicó en su conferencia que en algunos casos de tumores malignos no se puede operar porque el precio a pagar por el paciente es demasiado alto. (Fotografía: Iñigo Sierra)
Imagen: Antonio Martínez Ron explicó en su conferencia que en algunos casos de tumores malignos no se puede operar porque el precio a pagar por el paciente es demasiado alto. (Fotografía: Iñigo Sierra)Durante la charla, el periodista explicó que “cuando un tumor se encuentra en un área funcional que afecta al habla o a la capacidad de movimiento, los cirujanos solo pueden retirar tejido hasta el punto límite que no afecte a esas funciones”.
Esa limitación fue el detonante que hizo al doctor Barcia desarrollar una técnica que consiste en forzar al cerebro, mediante estimulación eléctrica, a mover las funciones de lugar para poder extirpar el tumor. “Es como mover los muebles de sitio para poder pintar una habitación”, precisó el divulgador.
En concreto el método se centra en retirar el tejido canceroso hasta donde sea posible y, en esa intervención, introducir una manta de electrodos. En las siguientes semanas se inhibe la actividad de esas áreas mediante descargas eléctricas, al tiempo que se activa una rehabilitación intensiva de las funciones que podrían deteriorarse para que el cerebro las comience a trasladar a zonas adyacentes. Una vez que el paciente ha desplazado la función crítica a una zona sana del cerebro, se le vuelve a operar para eliminarle la totalidad del tumor.
 Imagen: Tras finalizar la conferencia Antonio Martínez Ron respondió las muchas preguntas de los asistentes a Bidebarrieta Científica. (Fotografía: Iñigo Sierra)
Imagen: Tras finalizar la conferencia Antonio Martínez Ron respondió las muchas preguntas de los asistentes a Bidebarrieta Científica. (Fotografía: Iñigo Sierra)Durante la charla, Martínez Ron contó el caso de un paciente de epilepsia al que se le trasladó la función del lenguaje de un hemisferio a otro para poder retirarle el foco epiléptico y que hoy hace una vida completamente normal. También relató la historia del canadiense Stephen Sumner, amputado de una pierna tras un accidente de tráfico, que recorre Asia para ayudar a personas que han perdido alguna extremidad y sufren dolores en la parte del cuerpo desaparecida, un fenómeno conocido como “dolor de miembro fantasma”.
Sin otro transporte que su bicicleta, Sumner visita a los pacientes cargado de espejos para enseñarles a mitigar su dolor mediante la técnica desarrollada por el neurocientífico indio V.S. Ramachandran, que consiste en reeducar al cerebro gracias a un espejo que permite ver el miembro amputado en el lugar en el que ya no se encuentra y paliar de esta forma el dolor. Este sencillísimo método se apoya también en el concepto de plasticidad cerebral.
Parece arte de magia, pero en realidad es una capacidad humana y natural. Así que la próxima vez que parezca que es demasiado tarde, tal vez valga la pena preguntarle al cerebro ¿tú, qué opinas?
Sobre la autora: Marta Berard, es periodista, responsable de contenidos de la agencia de comunicación GUK y colaboradora de la Cátedra de Cultura Científica de la UPV/EHU.
El artículo Nunca es tarde para volver a empezar, lo dice el cerebro se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Nunca es tarde
- Los escultores del cerebro, charla de Mara Diersen
- Lo mejor de dos mundos para avanzar en el tratamiento del cáncer
¿Por qué escuchamos música triste?
“En cuanto la música empezó a sonar, el hermoso mundo que había dejado en casa y que había olvidado […] lo inundó de golpe. Fue entonces cuando las lágrimas empezaron a brotar […] —dijo que lloró y lloró hasta que su almohada se empapó— dijo que nunca había sentido semejante “feliz infelicidad” —esas fueron sus palabras. Le gustaba la música pero no sabía que le apasionaba —no sabía lo que podía hacerle— dijo que durante la siguiente semana, cuando miraba a las cosas que siempre había mirado —el cielo azul, el verde de la selva, la claridad del agua corriente, incluso los ojos cansados de sus compañeros— lloró otra vez —podía llorar cuando alguien le daba un cigarrillo— cuando alguien le preguntaba por su mujer y sus hijos —al recordar que era el cumplaños de su niño— al recordar el sabor del pastel de cumpleaños o de una mazorca de maíz, o el olor a palomitas en una sala de cine, o la cara de su hijo mientras dormía. Lloró —y lloró también al contarme esta historia— dijo que era todo por culpa de la música […] sabía que quizás no la volvería a escuchar —porque le devolvería a ese momento—el momento de “feliz infelicidad”.
Thomas Larson (2012) «The Saddest Music Ever Written: The Story of Samuel Barber’s Adagio for Strings». Traducción de Almudena M. Castro.
 Foto: Benjamin Wagner / Unsplash
Foto: Benjamin Wagner / UnsplashEn 2004, la BBC Radio lanzó una encuesta a sus oyentes para elegir la música más triste jamás escrita. Tras recibir más de 400 propuestas, sometieron las 5 más populares a votación. El resultado fue concluyente: el Adagio para cuerdas, de Samuel Barber quedó en primer lugar, con un 52.1% de los votos. En el podio le seguían:
- El Lamento de Dido, en segundo lugar con un 20,6 % de los votos; la maravillosa aria de la ópera Dido y Eneas de Henry Purcell.
- En tercera posición, el Adaggieto de la 5ª Sinfonía de Mahler, con un 12,3 % de los votos.
- “Gloomy Sunday” de Rezsô Seress, interpretada por Billie Holiday (9.8 % de los votos)
- Y finalmente, Metamorphosen, de Richard Strauss (5.1% de los votos).
El sondeo en sí es puramente anecdótico, por supuesto; el palmarés de la tristeza bien afinada se encuentra mucho más reñido. Si uno le pregunta a Google por “la música más triste”, lo que encuentra son cientos de antologías en tono menor compitiendo, a su vez, entre los resultados. Aún así, el famoso Adagio de Barber acumula muchos méritos para encontrarse entre las vencedoras. Desde su estreno en 1938, el Adagio ha acompañado los funerales de personalidades como Einstein (1953), Grace Kelly (1982) o el Príncipe Rainier de Mónaco (2005), entre otros personajes famosos y tantos más desconocidos. Fue la música que acompañó el anuncio televisado del asesinato de Kennedy en 1963, el relato en la BBC Radio de la muerte de Roosevelt (1945) y de la Princesa Diana (1997). Se ha utilizado para homenajear a las víctimas del 11S (2011), a las víctimas del tiroteo contra Charlie Hebdo (2015), a las víctimas del atentado de Manchester (2017)…
El adagio para cuerdas de Barber es lo que técnicamente se conoce como un dramón. Y dada su histórica trayectoria de infligir tristeza allá donde suena, cabe preguntarse por qué nadie querría escucharlo. A fin de cuentas, la tristeza no es una emoción que, a priori, parezca deseable sentir. ¿Por qué nadie querría provocársela a sí mismo?, ¿por qué diseñar melodías que nos asedian, nos roban el pulso, nos bloquean los párpados y la garganta?
Decía Oscar Wilde que “después de tocar Chopin, me siento como si hubiese estado llorando por pecados que yo nunca cometí, lamentando tragedias que no son mías1”. Lo raro es que este afán por llenarse de “tragedias ajenas” sea tan habitual, tanto que un 10% de la población afirma preferir la música triste a cualquier otro tipo de música y apenas un 1% dice odiarla2 . Entre estos dos extremos, la mayoría de la gente (entre el 66 y el 80 %) dice disfrutar de este tipo de música en general y son bastantes menos los que parecen no apreciarla (entre un 10 y un 33%).
Las variaciones entre unos grupos y otros podrían tener que ver con diversos factores personales y sociológicos. Como por ejemplo, la edad: los niños, en concreto, muestran una clara preferencia por la música alegre frente a la triste y tienden a evitar esta última. También, la personalidad de cada cual: la apertura experiencias nuevas, la empatía3 y también cierta tendencia a la introversión y la inestabilidad emocional, correlan bastante bien con el gusto por la música triste. Pero también, y de manera significativa, la cultura: no en todos los contextos se tolera la tristeza por igual, ni se valora estéticamente. En un estudio de 2011 en el que 116 participantes debían evaluar distintos fragmentos de bandas sonoras, las valoraciones de “belleza” parecían relacionarse con la música triste mucho antes que con la alegre, lo cual parece indicar que la apreciación estética podría jugar un papel importante en nuestro disfrute de la tristeza4 (valga como ejemplo el Adaggieto de Mahler, que mencionábamos antes: medalla de bronce en la encuesta de la BBC… y mucho más hermoso que triste, diría yo).
El investigador David Huron, de la Universidad de Ohio (EEUU), sostiene una hipótesis alternativa. Su idea es que, al escuchar música triste nuestro cuerpo responde al dolor liberando una hormona llamada prolactina5 cuyo efecto es el de calmarnos y consolarnos. En último término, sin embargo, la causa de esa tristeza es puramente ficticia: como dice Wilde, nos sentimos como si lamentásemos tragedias, pero en realidad estas nunca fueron nuestras. Y, a pesar de ello, logramos obtener consuelo, bienestar… nuestro cuerpo entero cantando “eaea” para que podamos regodearnos en nuestra “feliz infelicidad”.
Coda: Música para llorar a gusto
Hace unos meses pregunté a Twitter por su música triste preferida. En apenas unas horas, recibí tantas respuestas que me resulta sencillamente imposible recopilarlas aquí. Pero podéis verlas todas todas pinchando en el tuit. Por cierto, el Adagio de Barber sale hasta 4 veces:
(Hoy es un lunes como para preguntar esto…
Blanca Martínez: “Los geólogos le tenemos mucho cariño a Godzilla”
“Godzilla no es un dinosaurio, es un anfibio radioactivo y Rodan es un reptil volador. En realidad estos monstruos son un reflejo de cómo los humanos recurrimos a la mitología para dar una explicación a los fenómenos de la naturaleza”, asegura la doctora en Geología Blanca Martínez García, que ha aprovechado los conflictos que enfrentan a estas criaturas de ficción en las calles de Tokio para explicar las causas de los movimientos sísmicos al público de Naukas Bilbao, el evento de divulgación científica que se ha desarrollado los días 20 y 21 de septiembre en el Palacio Euskalduna de la capital vizcaína.
 Imagen: Blanca Martínez García, doctora en Geología, durante el desarrollo de su conferencia «Godzilla, king of the geologists» en Naukas Bilbao 2019. (Fotografía: Iñigo Sierra)
Imagen: Blanca Martínez García, doctora en Geología, durante el desarrollo de su conferencia «Godzilla, king of the geologists» en Naukas Bilbao 2019. (Fotografía: Iñigo Sierra)Resulta que cuando Godzilla es despertado por unas pruebas nucleares llevadas a cabo en el Pacífico, sale del agua y provoca un tsunami. Mientras que Rodan está relacionado con la entrada en erupción de un volcán. Pero es que, además, cuando ambos animalitos “se zurran entre ellos” se producen terremotos y se caen los edificios.
Cada vez que el ser humano tiene dificultades para encontrar la causa de temas complejos pide auxilio a la mitología, vamos, que se cuenta un cuento, y este ha sido el hilo conductor de la charla “Godzilla, king of the geologists”, una intervención con la que la experta, además de rendir homenaje al célebre monstruo japonés, ha conseguido explicar cómo funciona la tectónica de placas y cuál es el origen de terremotos, volcanes y tsunamis.
El planeta Tierra tiene diferentes capas. La que está en el exterior, denominada corteza, es rígida, pero se trata de una superficie discontinua, está fragmentada, dividida en pedazos que reposan sobre el manto terrestre. A diferencia de la corteza, el manto no es rígido, es más bien una masa cremosa. Para explicarlo, Martínez García ha recurrido a una analogía de lo más golosa: “es como un bol con natillas con una galleta encima. Si rompes en pedazos esa galleta tendrías la corteza terrestre sobre el manto”.
Esos fragmentos de galleta flotando sobre las natillas son las placas tectónicas que, al desplazarse, pueden causar terremotos. Japón se encuentra situado en el límite entre tres placas tectónicas y, por ese motivo, su actividad sísimica es tan potente. Parece natural que, de entre todos los pueblos del planeta, sea precisamente el nipón el que más necesidad haya tenido de alumbrar criaturas mitológicas para explicar por qué la tierra se mueve bajo sus pies con tanta asiduidad.
 Imagen: La geólogao Blanca Martínez explicó en su charla porqué los geólogos le tienen tanto cariño a Godzilla. (Imagen: Iñigo Sierra)
Imagen: La geólogao Blanca Martínez explicó en su charla porqué los geólogos le tienen tanto cariño a Godzilla. (Imagen: Iñigo Sierra)Para contrarrestar los efectos negativos de estos fenómenos, los japoneses son toda una referencia en la construcción de edificios sismorresistentes. Es decir, construcciones que se apoyan en cimientos que oscilan con las ondas sísmicas como si fueran muelles y no se desploman aunque los bichos hagan de las suyas.
La idea de que los responsables de los movimientos de las placas sean unos enormes y tremendos monstruos es bastante seductora, pero en realidad las causas de este tipo de fenómenos tienen su perfecta explicación en la ciencia, en concreto en la geología, una disciplina rigurosa que, sin embargo, siente una gran inclinación por el relato de ficción.
“Los geólogos le tenemos mucho cariño a Godzilla”, dice Martínez García, quien, para ilustrar su afirmación, explica que el paleontólogo estadounidense Kenneth Carpenter bautizó a un dinosaurio como Gojirasaurus en su honor (Gojira es Godzilla en japonés).
Los científicos buscan en la ciencia las respuestas a sus preguntas, pero, a veces, también ellos distraen la vista de las fórmulas matemáticas y las demostraciones empíricas para que les cuenten un buen cuento.
Sobre la autora: Marta Berard, es periodista, responsable de contenidos de la agencia de comunicación GUK y colaboradora de la Cátedra de Cultura Científica de la UPV/EHU.
El artículo Blanca Martínez: “Los geólogos le tenemos mucho cariño a Godzilla” se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Zientziateka: Blanca Mª Martínez García – La geología fantástica de Verne, Poe y H.P. Lovecraft
- Ciencia en primera persona: Icíar Martínez
- De robots geólogos y rayos X
Lo mejor de dos mundos para avanzar en el tratamiento del cáncer
El tratamiento del cáncer avanza hacia fórmulas menos agresivas para el organismo como la inmunoterapia, que consiste en desarrollar estrategias que hagan posible estimular la respuesta del sistema inmunitario contra las células tumorales.
Desde la perspectiva funcional, el sistema inmunitario en realidad no es uno, sino varios. Por un lado está el sistema inmunitario innato, que constituye la primera línea de defensa frente a agentes infecciosos. En segundo lugar está el sistema adaptativo, que elabora una respuesta específica para cada agente patógeno y se activa cuando la inmunidad innata no ha funcionado.
 Imagen: Antonio Pérez-Martínez, jefe del servicio de Hemato-Oncología Infantil del Hospital Universitario de la Paz en su intervención en Naukas Bilbao 2019. (Fotografía: Iñigo Sierra)
Imagen: Antonio Pérez-Martínez, jefe del servicio de Hemato-Oncología Infantil del Hospital Universitario de la Paz en su intervención en Naukas Bilbao 2019. (Fotografía: Iñigo Sierra)Partiendo de este conocimiento, el jefe del Servicio de Hemato-Oncología Infantil del Hospital Universitario de La Paz (Madrid), Antonio Pérez Martínez, ha explicado como la combinación “de lo mejor del sistema inmune innato con lo mejor del sistema inmune adaptativo” abre nuevas vías para avanzar en el tratamiento de algunos tipos de cáncer durante el evento de divulgación científica Naukas Bilbao, que se ha desarrollado los días 20 y 21 de septiembre en el Palacio Euskalduna de la capital vizcaína. Su intervención se titulaba “Lo mejor de dos mundos” por una buena razón.
El especialista ha condensado en sus diez minutos de charla el funcionamiento terapéutico de la célula CAR-T, un medicamento generado en el laboratorio que combina las funciones de un anticuerpo y de un linfocito T. Este medicamento está cambiando la historia natural de los pacientes con leucemia aguda linfoblástica B, una dolencia que afecta especialmente a los niños, pero también tiene aplicación en pacientes con linfoma difuso de célula grande B y, en este segundo caso, se trata mayoritariamente de adultos.
Para ilustrar su exposición, Pérez Martínez ha empleado vídeos en los que se ha podido ver el propio funcionamiento del sistema inmunitario y cómo éste reconoce las células tumorales, pero también imágenes que reflejan los trabajos que él y su equipo de investigadores realizan en el laboratorio para desarrollar nuevas terapias basadas en células quiméricas que no solo incluyen anticuerpos y linfocitos T, sino también receptores y otras células del sistema inmune innato como las células NK.
 Imagen: Antonio Pérez-Martínez, oncólogo infantil explicó en su conferecia «Lo mejor de dos mundos» el funcionamiento terapéutico de la célula CAR-T. (Fotografía: Iñigo Sierra)
Imagen: Antonio Pérez-Martínez, oncólogo infantil explicó en su conferecia «Lo mejor de dos mundos» el funcionamiento terapéutico de la célula CAR-T. (Fotografía: Iñigo Sierra)El objetivo ha sido mostrar a la audiencia que la suma de fuerzas entre las capacidades de cada uno de los sistemas inmunitarios puede ser una fórmula para el tratamiento de enfermedades complejas, de la misma forma que la suma del conocimiento acumulado a través de siglos de estudio en medicina, con los trabajos de investigación actuales -realizados con tecnologías punteras que hace apenas unos años no existían- conquistan avances de calado.
“Por separado cada sistema inmune tiene una función. La célula híbrida CAR-T es un medicamento nuevo, un constructo, que une lo mejor de cada sistema inmunológico para eliminar de forma específica células tumorales, intentado hacerlo con menos efectos adversos que los tratamientos convencionales”, precisa el doctor.
Todavía es pronto para determinar si este tipo de terapias serán eficaces contra otros tumores hematológicos o tumores sólidos. De momento, esta célula híbrida “está curando a niños con leucemia, que antes no se curaban”.
Cada día se da un pasito más y es de esta forma como se recorren las rutas de larga distancia.
Sobre la autora: Marta Berard, es periodista, responsable de contenidos de la agencia de comunicación GUK y colaboradora de la Cátedra de Cultura Científica de la UPV/EHU.
El artículo Lo mejor de dos mundos para avanzar en el tratamiento del cáncer se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Nanopartículas para reducir la metástasis hepática del cáncer de colon
- Seguridad diagnóstica en el cáncer de colon y tratamiento del de páncreas
- Medicina regenerativa: utilización de células madre para el tratamiento de enfermedades humanas
La ciencia de la incertidumbre
“Son once contra once”, “No hay rival pequeño” o “Un partido no termina hasta que el árbitro pita el final” son solo algunos de los tópicos asociados al fútbol que oímos incansablemente a jugadores, entrenadores, analistas y portavoces de clubes deportivos. Pero detrás de estas declaraciones enlatadas y reutilizadas hasta la extenuación se esconde una reflexión de cierto calado: el fútbol es un juego en el que intervienen variables muy diversas y, por este motivo, disponer de los mejores jugadores, del mejor equipo técnico o de los mejores servicios médicos no garantiza la victoria. Por más que se prepare un partido siempre hay elementos que escapan del control de los protagonistas. Una lesión fortuita de la estrella del equipo, un arbitraje desafortunado o un espontáneo que salta al terreno de juego y obliga a suspender el encuentro. En definitiva, la incertidumbre también juega. Los profesionales del fútbol lo saben y por eso se dedican a dibujar esquemas de juego en la pizarra, a estudiar concienzudamente a los rivales, a ensayar disparos desde el punto de penalti o a preparar jugadas con el objetivo de intentar sustituir el azar por el conocimiento. Pero ¿de verdad son la incertidumbre y la ciencia rivales tan irreconciliables?
 Imagen: Eva Ferreira, catedrática de Economía Aplicada de la UPV/EHU, durante el desarrollo de su conferencia «Hacer predicciones es muy difícil, sobre todo las del futuro» en Naukas Bilbao 2019 (Fotografía: Iñigo Sierra)
Imagen: Eva Ferreira, catedrática de Economía Aplicada de la UPV/EHU, durante el desarrollo de su conferencia «Hacer predicciones es muy difícil, sobre todo las del futuro» en Naukas Bilbao 2019 (Fotografía: Iñigo Sierra)El antagonismo secular entre el devenir de la fortuna y la sabiduría, entre la ciencia y la incertidumbre, ha sido el punto de partida de la charla “Hacer predicciones es muy difícil, sobre todo las del futuro” con la que la catedrática de Economía Aplicada de la UPV/EHU, Eva Ferreira, ha repasado la evolución de los vínculos entre lo que sabemos y lo que predecimos desde los tiempos de los faraones hasta el momento presente. La intervención se ha desarrollado en el marco del evento de divulgación científica Naukas Bilbao, que ha tenido lugar los días 20 y 21 de septiembre en el Palacio Euskalduna de la capital vizcaína.
“El desarrollo del conocimiento científico no ha tenido en cuenta la gestión de la incertidumbre hasta hace bien poco. El cálculo de probabilidades comienza en el siglo XVII y la extensión a todas las ramas del conocimiento no llega hasta el siglo XX”, ha asegurado Ferreira, quien ha detallado que fue en el pasado siglo cuando se introdujo la “consideración de que la mayoría de las medidas son inciertas” a un paradigma hasta ese momento centrado en “un desarrollo científico casi totalmente determinista”.
De acuerdo con el relato de Ferreira, “el uso de la inferencia estadística” ha hecho posible establecer patrones usando muestras seleccionadas y controlar las probabilidades de error, un modelo que se basa en la existencia de datos y en la habilitación de métodos efectivos para su sistematización. Los datos y su gestión como antídoto a la incertidumbre.
En la actualidad existe abundante y sofisticada tecnología para gestionar cantidades ingentes de información, procesarlas, jerarquizarlas, analizarlas, extraer conclusiones y optimizar los procesos de toma de decisiones.
“Oír los términos Big data, inteligencia artificial, revolución digital, machine learning es muy común cuando se habla del modelo de negocio de una empresa, de la selección de personal, de inversiones financieras, de estrategias políticas, de marketing… La publicidad de quienes diseñan algoritmos para estos fines nos habla de dejar atrás la improvisación y el caos para disfrutar del marketing predictivo”, ha apostillado la experta, que, sin embargo, advierte de los riesgos de asignar a las herramientas -por avanzadas y precisas que estas sean- capacidades de las que carecen: “La gestión sistemática de datos tiene una importancia enorme, pero corremos el riesgo de atribuirle a los instrumentos propiedades que no tienen”.
 Imagen: Eva Ferreira, experta en estadística, señaló que los comportamientos cambian a tenor de los datos que se tienen entre manos. (Fotografía: Iñigo Sierra)
Imagen: Eva Ferreira, experta en estadística, señaló que los comportamientos cambian a tenor de los datos que se tienen entre manos. (Fotografía: Iñigo Sierra)Para abundar en este tema, Ferreira ha explicado que conferir propiedades predictivas a los datos y a su sistematización es osado porque para que esto fuera cierto no se deberían producir transformaciones sociales o cambios de conducta.
“Nuestro comportamiento puede cambiar según los datos que tenemos a disposición. De hecho, no hace falta decir que nuestras preferencias, nuestro comportamiento y las decisiones que tomamos pueden cambiar en función de la información que recibimos”, agrega.
En su opinión es imprescindible, por tanto, construir modelos dinámicos, que incluyan información tanto cuantitativa como cualitativa, procedente de fuentes diversificadas y pasada por el tamiz de las distintas ramas del conocimiento.
“Hay multitud de ejemplos que nos ilustran cómo el tratamiento de datos debe ir de la mano de la reflexión previa. La debacle de Nokia, el algoritmo de Amazon que no reclutaba mujeres, las burbujas financieras… nos recuerdan una máxima muy sencilla: que ningún algoritmo que se base únicamente en el pasado, predecirá por sí mismo algo que nunca antes haya sucedido”, concluye Ferreira.
El fútbol y las predicciones son así: una apasionante mezcla de ciencia, técnica e incertidumbre.
Sobre la autora: Marta Berard, es periodista, responsable de contenidos de la agencia de comunicación GUK y colaboradora de la Cátedra de Cultura Científica de la UPV/EHU.
El artículo La ciencia de la incertidumbre se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La certeza de la incertidumbre en los informes del IPCC
- El legado de Fisher y la crisis de la ciencia
- Ciencia Clip: un concurso de vídeos de ciencia para jóvenes estudiantes
La geología y sus superpoderes
Vamos a comenzar con un arranque provocador. Partamos de la premisa de que la ficción es la única forma de realidad que existe. Vale, tal vez esta afirmación pueda resultar excesiva. ¿Qué tal si decimos que Dostoievski puede dar tantas claves para comprender el mundo como un informativo? ¿Y qué pasaría si seguimos avanzando por esta senda y al relato de ficción, que tantas veces nos ayuda a entender la complejidad de la vida, le añadimos el rigor empírico de la ciencia? ¿Y si no fuera cualquier ciencia, sino una que está tan vinculada a los cambios que suceden en el planeta que parece que tenga superpoderes?
Los terremotos, los tsunamis, la formación de los recursos hídricos, los yacimientos minerales, la meteorología, la mismísima historia de la vida se explica gracias a la geología, una disciplina tan apasionante como desconocida.
Del potencial de esta rama del conocimiento se han dado cuenta destacados creadores de ficción, que se nutren de sus principios básicos para dar vida a superhéroes y supervillanos. Tanto los responsables del universo de cómics Marvel, como los de la serie de animación Steven Universe están explotando este filón (aquí el término casi deja de ser una metáfora) para hilvanar sus guiones.
El fenómeno no ha pasado inadvertido al divulgador y profesor de Biología y Geología de secundaria Carlos Lobato. Valiéndose de los personajes y elementos protagonistas de sagas como Vengadores o los Cuatro Fantásticos ha mostrado los misterios de la geología al público de la novena edición del evento de divulgación científica Naukas Bilbao 2019, celebrado los días 20 y 21 de septiembre en la capital vizcaína.
“No es la primera vez que relaciono la ciencia con el cine o los dibujos animados, pero casi siempre lo he hecho desde el punto de vista de la biología y creo que es de recibo darle su sitio a la geología, que suele ser una de las grandes olvidadas a pesar de ser muy atractiva tanto para el alumnado, como para el público en general”, asegura Lobato.
La charla del profesor concentró en 10 minutos esenciales las características de minerales, rocas y otros materiales a través de superhéroes como Iron Man, ese tipo duro, muy duro, que basa sus poderes en las propiedades del hierro. También hubo espacio para la Cosa, uno de los protagonistas de los Cuatro Fantásticos, que tiene tantísima fuerza y resistencia porque en realidad es una roca metamórfica.
Como la intervención se titulaba «Las Gemas de Cristal del Infinito» se prestó especial atención a las piedras preciosas: las del Infinito (Vengadores) y las de Cristal (Steven Universe).
Resulta que la gama cromática de las Gemas del Infinito por las que tanto se afana el villano Thanos no son casuales sino que se trata de los colores reales que tienen los minerales y las rocas de la naturaleza.
Y luego están las Gemas de Cristal de Steven, que en la ficción de Cartoon Network se encargan de la protección del planeta y pueden adaptarse a diferentes campos gravitacionales, cambiar de forma, regenerarse y unirse entre sí para crear otras piedras más poderosas, como es el caso de Granate, surgida de la fusión de un rubí y un zafiro.
“Los rubíes y los zafiros presentan la misma composición química: Al2O3, por lo que pertenecen a la misma familia de minerales. El color azul del zafiro se debe al titanio, mientras que el color rojo del rubí se debe al cromo y al hierro. Es una genialidad de la serie que hayan creado personajes basados en dos gemas con la misma composición química, porque de esta manera se puede entender mejor su deseo de pasar su vida juntos formando a Granate”, reflexiona un entusiasta Lobato.
Después de esto no hay duda: la geología está llena de superpoderes y la ficción puede que no sea la única forma de realidad que existe, pero casi, casi.
Sobre la autora: Marta Berard, es periodista, responsable de contenidos de la agencia de comunicación GUK y colaboradora de la Cátedra de Cultura Científica de la UPV/EHU.
El artículo La geología y sus superpoderes se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Otra mirada al planeta: arte y geología
- Geología, ver más allá de lo que pisamos
- Arquitectura y geología: materialidad y emplazamiento
Más allá de las neuronas
Al hablar de las células del sistema nervioso todo el mundo piensa inmediatamente en las neuronas, unidades de importancia capital porque están especializadas en recibir, procesar y transmitir información a través de señales químicas y eléctricas y sirven, entre otras funciones, para pensar y recordar. Pero las neuronas no están solas en el cerebro, sino que hay otras células que las acompañan y se encargan de tareas tan relevantes como la respuesta inmune o la eliminación de los residuos que se generan en el sistema nervioso central. Estas últimas células han sido las protagonistas de la charla que la doctora en Neurobiología Amanda Sierra ha ofrecido en el programa de conferencias Naukas Pro, que tienen lugar en el marco del evento de divulgación científica Bizkaia Zientzia Plaza, que se celebra en Bilbao del 18 al 25 de septiembre.
 Imagen: Amanda Sierra, neurocientífica y profesora investigadora Ikerbasque en la Universidad del País Vasco y el Centro Vasco de Neurociencia Achucarro durante su charla en Naukas PRO 2019. (Fotografía: Iñigo Sierra)
Imagen: Amanda Sierra, neurocientífica y profesora investigadora Ikerbasque en la Universidad del País Vasco y el Centro Vasco de Neurociencia Achucarro durante su charla en Naukas PRO 2019. (Fotografía: Iñigo Sierra)En concreto la investigadora Ikerbasque se ha centrado en la microglía, un tipo de célula “muy pequeña que está constantemente escaneando el cerebro” en busca de estructuras dañadas, células muertas o residuos con la intención de eliminarlos.
Según la experta, el cerebro es como una sabana en la que habitan diferentes especies. Si un ejemplar muere, los animales carroñeros eliminan los residuos que se generan, llevando a cabo una función esencial para el equilibrio de ese ecosistema.
En el sistema nervioso ocurre algo parecido. Cuando las células mueren la microglía se encarga de encontrar y fagocitar esos residuos. Pero ¿cómo lo hacen? Lo cierto es que las células muertas emiten señales para llamar la atención de la microglía, se trata de “señales encuéntrame, como la galleta de Alicia en el País de las Maravillas que decía: cómeme”. Esta señal es la que permite que la microglía localice el tejido dañado y lance sus prolongaciones alrededor de la célula muerta formando un bolsillo tridimensional que la envuelve completamente y la atrae hacia sí para poder fagocitarla.
“Una de las preguntas que nos hacemos es qué le ocurre a la microglía después de llevar a cabo ese proceso. Estamos intentando responderla, ya que comerse una célula muerta implica una serie de cambios metabólicos en la microglía, modifica su función”, asegura la experta.
Este tipo de trabajos, que Sierra desarrolla en el laboratorio del Achucarro Basque Center for Neuroscience en el que trabaja, tienen relevancia para descubrir, por ejemplo, cómo se desenvuelven estas células en las situaciones en las que aparecen enfermedades neurodegenerativas. Lamentablemente, en algunos casos como el infarto cerebral o la epilepsia ya se ha detectado que no cumplen correctamente su función, por lo que los residuos se acumulan en el cerebro y se aumenta el daño todavía más.
 Imagen: La investigadora Amanda Sierra explicó las líneas de investigación que desarrolla en Achucarro Center for Neuroscience, que se centra en las células microgliales y la interacción entre la fagocitosis y la inflamación en el cerebro enfermo. (Imagen: Iñigo Sierra)
Imagen: La investigadora Amanda Sierra explicó las líneas de investigación que desarrolla en Achucarro Center for Neuroscience, que se centra en las células microgliales y la interacción entre la fagocitosis y la inflamación en el cerebro enfermo. (Imagen: Iñigo Sierra)Las investigaciones de Sierra buscan generar conocimiento para abrir nuevas vías que permitan influir en el proceso de fagocitosis de la microglía, mejorar su eficiencia y acelerar las tareas de limpieza.
La experta aprovechó asimismo la cita para rendir homenaje al investigador Pío del Río Hortega, discípulo del científico vasco Nicolás Achúcarro, que murió en el exilio y fue una figura clave en el descubrimiento y estudio de la microglía hace aproximadamente 100 años. Aunque no lo logró, Río Hortega estuvo nominado al premio Nobel de Medicina en dos ocasiones por su contribución a la ciencia. Sus restos mortales descansan desde 1986 en el Panteón de Hombres Ilustres del cementerio de Valladolid, de donde era oriundo.
Sobre la autora: Marta Berard, es periodista, responsable de contenidos de la agencia de comunicación GUK y colaboradora de la Cátedra de Cultura Científica de la UPV/EHU.
El artículo Más allá de las neuronas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La hiperactividad neuronal impide que las microglías realicen su trabajo
- El citoesqueleto de las neuronas y el alzhéimer
- Las dos culturas y más allá: Ciencia, Sociedad y Desarrollo (curso de verano)
¿Y si el futuro de la refrigeración estuviera en Galicia? Caliente, caliente
Si jugáramos a asociar un concepto a un topónimo y para empezar la partida escogiéramos el término frío, seguramente mucha gente contestaría Siberia. Lo cierto es que es una muy buena respuesta, porque el clima siberiano se caracteriza por unas temperaturas extraordinariamente bajas. Pero cuando hablamos del frío generado artificialmente hay otro territorio geográfico que está emergiendo con fuerza: se trata de Galicia, y muy particularmente del Centro de Investigaciones Científicas Avanzadas (CICA) de la Universidad de A Coruña, porque es allí donde un equipo de investigadores ha descubierto las perovskiñas, una nueva familia de materiales sólidos con potencial para revolucionar el futuro de la refrigeración.
 Imagen: Juan M Manuel Bermúdez, doctor en Química Ambiental y Fundamental por la Universidade da Coruña e investigador que desarrolla su labor en el ámbito de la química del estado sólido y ciencia de materiales, durante su charla en Naukas PRO 2019. (Fotografía: Iñigo Sierra) (Fotografía: Iñigo Sierra)
Imagen: Juan M Manuel Bermúdez, doctor en Química Ambiental y Fundamental por la Universidade da Coruña e investigador que desarrolla su labor en el ámbito de la química del estado sólido y ciencia de materiales, durante su charla en Naukas PRO 2019. (Fotografía: Iñigo Sierra) (Fotografía: Iñigo Sierra)“Es una investigación realizada por un equipo formado íntegramente por miembros de la Universidad de A Coruña”, asegura uno de los padres de las perovskiñas, el doctor en Química Ambiental y Fundamental Juan Manuel Bermúdez. El científico ha presentado los resultados de su estudio y sus posibles aplicaciones dentro del programa de conferencias Naukas Pro, que tienen lugar en el marco del evento de divulgación científica Bizkaia Zientzia Plaza, que se celebra en Bilbao del 18 al 25 de septiembre.
Pero para entender el hallazgo un poco mejor hay que volver al punto de partida. Según los datos que maneja Bermúdez, el 10% del consumo eléctrico mundial se destina a dispositivos de aire acondicionado. Si a este dato le sumamos el consumo de neveras domésticas, frigoríficos y cámaras industriales el porcentaje se sitúa en el 20% del total. Generar frío de forma artificial es necesario para conservar los alimentos, garantizar el buen estado de muchos medicamentos y mejorar la calidad de vida de las personas, pero, para conseguirlo, se emplean diversos tipos de fluidos refrigerantes que tienen impacto en el medioambiente. Por este motivo resulta imperativo investigar en el descubrimiento de nuevas fórmulas de enfriar más respetuosas con el medio natural. Eso es exactamente lo que Bermúdez ha compartido en una charla en la que se ha valido de imágenes térmicas de objetos cotidianos tomadas con cámaras de infrarrojos, que se pueden consultar en el perfil de Instagram @thermogramer.
El experto ha hecho un repaso por los principales inconvenientes que presentan para el medio ambiente los actuales sistemas de refrigeración y ha presentado a la audiencia las ventajas de las perovskiñas, una familia de materiales barocáloricos muy flexibles que tienen la capacidad de producir efectos de refrigeración si se les aplica presión.
 Imagen: Juan Manuel Bermúdez presentó un nuevo material en Naukas PRO 2019, la perovskiña. La perovskiña es un nuevo material sólido que responde a aplicación de bajas presiones enfriándose con facilidad. (Fotografía: Iñigo Sierra)
Imagen: Juan Manuel Bermúdez presentó un nuevo material en Naukas PRO 2019, la perovskiña. La perovskiña es un nuevo material sólido que responde a aplicación de bajas presiones enfriándose con facilidad. (Fotografía: Iñigo Sierra) Pero ¿por qué se llaman perovskiñas? El término constituye la versión gallega del sustantivo perovskita, que abarca los compuestos que presentan una estructura reticular en forma de cubos que alojan iones en su interior. De hecho la perovskita es un mineral poco frecuente que fue descubierto a inicios del siglo XIX en los Montes Urales. ¡Tachán! Al hablar de frío tarde o temprano tenía que aparecer Rusia.
Además de servir para enfriar neveras y aparatos de aire acondicionado, las perovskiñas presentan, según Bermúdez, un enorme potencial de aplicación. Por ejemplo, como plantillas de calzado para que los deportistas puedan evitar el sobrecalentamiento del pie y autorrefrigerarse a través de sus propias pisadas (hay que recordar que las perovskiñas despliegan sus efectos refrigerantes mediante presión).
También podrían ser útiles para concebir colchones que dieran fresquito en verano, evitar el sobrecalentamiento de teléfonos móviles e incluso contribuir a la refrigeración de un gran equipamiento como un aeropuerto o una estación si se aplican al suelo y se aprovecha la presión ejercida por las personas que lo recorren. Nada de esto existe en este momento, pero hay un universo de posibilidades por explorar. Seguramente por eso la investigación ha sido publicada en Nature Communications y ha recibido reconocimientos como el Premio de Investigación Ernesto Viéitez de la Real Academia Galega de Ciencias.
Sobre la autora: Marta Berard, es periodista, responsable de contenidos de la agencia de comunicación GUK y colaboradora de la Cátedra de Cultura Científica de la UPV/EHU.
El artículo ¿Y si el futuro de la refrigeración estuviera en Galicia? Caliente, caliente se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Recomiendan el antibiótico Eridosis para el acné en sus redes sociales, pero no son médicos
 Foto: Deborah García Bello
Foto: Deborah García BelloEn las redes sociales hay personas con miles de seguidores que enseñan cuáles son sus remedios para luchar contra el acné. Personas sin formación científica ni vínculo alguno con la profesión sanitaria recomiendan mascarillas de yogur, miel, bicarbonato o limón. Estas mascarillas, además de ser ineficaces contra el acné, pueden causar graves daños en la piel. Desde hace poco nos enfrentamos a una nueva recomendación por parte de algunos influencers cuyo daño es de mayor envergadura. Se trata de las toallitas Eridosis. Las toallitas Eridosis son un medicamento sujeto a prescripción médica cuyo principio activo es un antibiótico. En las redes hay quien recomienda este medicamento con ligereza, como si se tratase de una simple toallita desmaquillante. Este es el origen del problema, pero no termina ahí. Hay farmacias que dispensan este medicamento sin pedir la receta médica y sin dar ningún tipo de información.
-
Las toallitas Eridosis son un medicamento, no un cosmético.
La diferencia entre un medicamento de uso tópico y un cosmético es la actividad farmacológica. Mientras que en un cosmético ningún principio activo puede penetrar más allá de la dermis, en un medicamento de uso tópico el principio activo sí puede penetrar y tener actividad farmacológica más allá de la barrera cutánea. Las bases reguladoras para su fabricación y distribución también son diferentes. Los medicamentos solo se venden en farmacia; mientras que los cosméticos son de venta libre. El laboratorio cosmético es quien decide en qué canal vende sus productos.
Las toallitas Eridosis son un medicamento. Pertenecen a los laboratorios Reig Jofre y son un preparado anti-acné para uso tópico. Es uno de los tratamientos más prescritos por médicos ante casos de acné leve y moderado.
El principio activo que contiene es la eritromicina. Cada toallita está impregnada con un mililitro de una disolución de eritromicina al 2% de concentración (20 mg de eritromicina por cada ml de preparado).
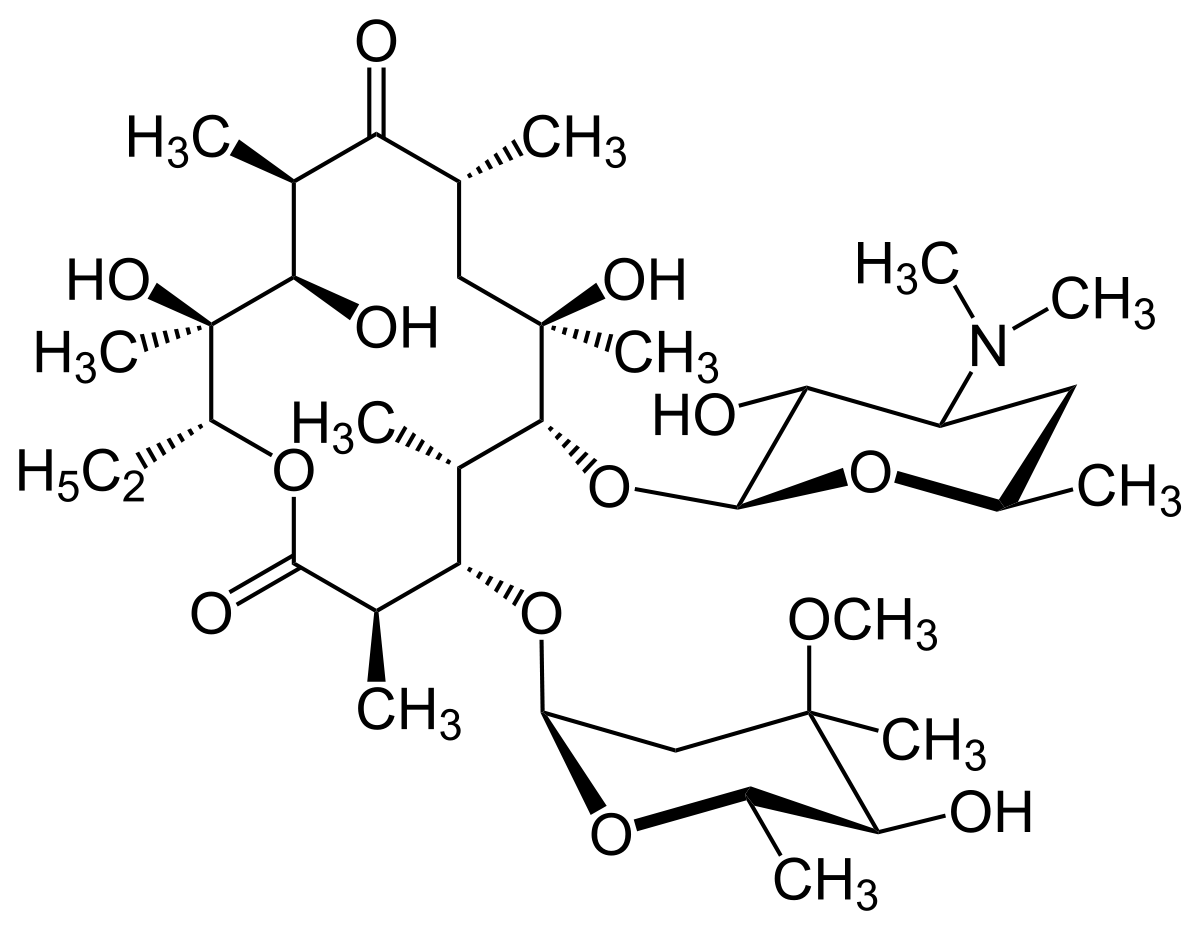 Eritromicina. Fuente: Wikimedia Commons
Eritromicina. Fuente: Wikimedia Commons
La eritromicina es un antibiótico del grupo de los macrólidos, con acción bacteriostática. Aunque es un antibiótico de espectro antibacteriano moderadamente amplio, es especialmente activo frente al Propionibacterium acnes, la bacteria responsable del acné.
El mecanismo exacto por el cual la eritromicina reduce el acné vulgar no es bien conocido. Sin embargo, se sabe que la eritromicina actúa por inhibición de la síntesis de proteínas en microorganismos sensibles y de esa forma se explica su actividad antibacteriana.
-
Contraindicaciones y advertencias de Eridosis.
Como en cualquier otro medicamento, en el prospecto de Eridosis figuran una serie de contraindicaciones, precauciones, advertencias y reacciones adversas. Es un medicamento y, como tal, puede producir ciertos efectos secundarios.
Hay que tener especial precaución durante el embarazo y la lactancia con el uso de eritromicina tópica. La razón es que la eritromicina atraviesa la placenta, alcanzando concentraciones bajas en el feto, pero no despreciables. La seguridad de su uso durante el embarazo no ha sido establecida, por eso se aconseja que este medicamento se utilice solo cuando se estime imprescindible y siempre que el beneficio supere el posible riesgo.
Con respecto a la lactancia se desconoce si la eritromicina se excreta con la leche materna tras la administración tópica. Sin embargo, es sabido que la eritromicina administrada por vía sistémica se excreta con la leche materna, por ese motivo se aconseja administrar este medicamento con precaución a madres lactantes.
No obstante, en el prospecto de Eridosis se indica que «los resultados de los estudios realizados con Eridosis al 2% demostraron que no aparecen niveles detectables de eritromicina en el suero sanguíneo de los pacientes acneicos tratados».
Los efectos adversos de este medicamento son, en general, leves y transitorios. Los efectos secundarios que se manifiestan más frecuentemente son alteraciones dermatológicas como eritema, sequedad de la piel, piel escamosa, prurito, irritación, sensación de quemazón cutánea y ampollas (pustulosis exantemática). El uso tópico de este medicamento, concomitante con otras terapias contra el acné, deben realizarse con precaución y bajo supervisión médica debido a la posibilidad de acumulación de efectos irritantes.
En el prospecto de Eridosis también se advierte que «la utilización de agentes antimicrobianos (especialmente en terapias prolongadas) puede estar asociada con la proliferación de gérmenes resistentes a los antibióticos». La resistencia a los antibióticos es la pandemia más grave que se nos viene encima en este siglo.
-
Los influencers recomiendan y las farmacias dispensan
Para documentarme para este artículo visité seis farmacias españolas. En todas ellas pedí “las toallitas Eridosis”. Solo en una de las seis farmacias me indicaron que se trataba de un medicamento sujeto a prescripción médica y que no lo dispensarían sin receta. Allí me explicaron que se trata de un antibiótico, me hablaron del problema de la resistencia a los antibióticos y de los posibles efectos adversos y contraindicaciones. En las otras cinco farmacias no habría tenido ningún problema en llevarme el medicamento. No me hicieron ninguna pregunta. Son tres euros veinte. Nada más. Compré el medicamento en una de ellas para ver el prospecto actual y escribir este artículo.
 Foto: Deborah García Bello
Foto: Deborah García BelloEn el lateral de la caja de Eridosis aparece escrito en negrita «Con receta médica». En el frontal, al lado del código nacional del medicamento, aparece un círculo. También aparece en cada sobre. Ese círculo es el símbolo que indica «dispensación sujeta a prescripción médica».
-
A modo de cierre
Las redes sociales son muy útiles a la hora de difundir información, también desinformación. Y aunque las recomendaciones sanitarias de un influencer sin formación científica tendrían que parecer un chiste para cualquiera, la realidad es que no es así, y hay personas que siguen sus consejos. Unos y otros por ignorancia.
Compañías como Google han empezado a tomar medidas relacionadas con esto, como prohibir los anuncios de tratamientos médicos especulativos y sin evidencia científica suficiente. Sería conveniente que las redes sociales filtrasen los contenidos con implicaciones sanitarias. Se censuran los pezones femeninos, pero no se controlan los anuncios de antibióticos. Al teclear “eridosis” en el buscador de cualquier red social aparecen decenas de publicaciones en las que personas sin formación recomiendan su uso.
No obstante, la responsabilidad final recae en el personal sanitario. Las farmacias no deberían dispensar medicamentos sujetos a prescripción médica sin solicitar receta y sin orientar al paciente.
A modo de cierre. Si tienes la sospecha de padecer acné, no busques el remedio en las redes sociales. Pide consejo en la farmacia y acude al médico.
Para saber más:
Ni mitos ni remedios caseros: así me libré del acné.
Sobre la autora: Déborah García Bello es química y divulgadora científica
Nota de la autora: Deliberadamente en este artículo no se ha enlazado ninguna publicación de influencers que hayan recomendado el uso de Eridosis. Una de las razones es no fomentar más su difusión. Otra de las razones es no inducir linchamientos en las redes sociales. Por educación y por elegancia, elijo criticar el hecho y no la persona. Y porque para brillar es mejor echarse purpurina.
El artículo Recomiendan el antibiótico Eridosis para el acné en sus redes sociales, pero no son médicos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La confianza en las redes sociales y el uso de electrodomésticos inteligentes
- Ni mitos ni remedios caseros: así me libré del acné
- Las redes 5G no afectan a la salud… pero podrían hacer que el hombre del tiempo acierte menos
Números primos gemelos, parientes y sexis (2)
En mi anterior entrada de la sección Matemoción de Cuaderno de Cultura Científica, titulada Números primos gemelos, parientes y sexis (1), estuvimos hablando de los números primos gemelos, que son aquellas parejas de números primos que están lo más cerca que pueden estar dos números primos, excepto el 2 y el 3, con solo un número par entre ellos, (p, p + 2), así como de algunas familias de números primos relacionadas con los gemelos, como son los trillizos, cuatrillizos, quintillizos, etc.
En esta entrada, vamos a considerar otras familias de números primos, que también generalizan, en otro sentido, a los números primos gemelos, como son los números primos parientes y sexis.
 Escena de la primera cita entre el profesor de matemáticas de la Universidad de Columbia (Jeff Bridges) y la profesora de literatura inglesa de la misma universidad (Barbra Streisand), en la película El amor tiene dos caras (1996), dirigida por Barbra Streisand. El profesor de matemáticas explica en la misma qué son los números primos gemelos
Escena de la primera cita entre el profesor de matemáticas de la Universidad de Columbia (Jeff Bridges) y la profesora de literatura inglesa de la misma universidad (Barbra Streisand), en la película El amor tiene dos caras (1996), dirigida por Barbra Streisand. El profesor de matemáticas explica en la misma qué son los números primos gemelosPero primero vayamos con un poquito de historia. Como puede leerse en el artículo A note on the Origin of the Twin Prime Conjecture (Nota sobre el origen de la conjetura de los números primos gemelos), del historiador de las matemáticas estadounidense William Dunham, en 1849 el matemático francés y oficial de artillería Alphonse de Polignac (1826–1863), un personaje prácticamente desconocido, publicó el artículo Recherches Nouvelles sur les Nombres Premiers ( Nuevas investigaciones sobre números primos), en la revista Comptes rendus de la Academia de Ciencia Francesa, en la que afirmaba lo siguiente (aunque lo presentó como un teorema, era más bien una conjetura).
Conjetura de Polignac: para cada número natural k, existen infinitos números primos p, tales que (p + 2k) también es primo.
Observemos que para k = 1, es la conjetura de los números primos gemelos.
El siguiente protagonista de esta historia es el matemático inglés James Whitbread Lee Glaisher (1848 – 1928), profesor del Trinity College de Cambridge y que tuvo una reconocida carrera dentro de la matemática y la ciencia británicas. En 1879, publicó en la revista Messenger of Mathematics, de la que fue editor durante 56 años, el artículo An Enumeration of Prime-Pairs (Enumeración de pares primos), en la que estudiaba lo que llamó “pares primos”, que eran números primos “separados por un solo número” (lo que conocemos como números primos gemelos). Contó la cantidad de “pares primos” que había hasta un millón, dos millones, etcétera, con el objetivo de analizar la distribución de estos. Y afirmó “Hay poca o ninguna duda de que el número de pares primos es ilimitado; pero sería interesante, aunque probablemente no sencillo, demostrarlo”. Es decir, la conjetura de los números primos gemelos.
Aunque fue el matemático alemán Paul Stäckel (1862 – 1919), quien acuñó el término “números primos gemelos”, en alemán Primzahl-Zwillinge, en un artículo de 1916. Poco después el matemático francés Viggo Brun, utilizaría ese mismo término en francés, en su artículo de 1919 (véase a entrada Números primos gemelos, parientes y sexis (1)), y acabó convirtiéndose en el término utilizado para ese concepto.
 Fotografía de 1908 del matemático de Trinity College, Cambridge, James Whitbread Lee Glaisher (1848-1928)
Fotografía de 1908 del matemático de Trinity College, Cambridge, James Whitbread Lee Glaisher (1848-1928)
Sobre la conjetura de los números primos gemelos ya estuvimos hablando en la primera parte de esta serie, Números primos gemelos, parientes y sexis (primera parte) [https://culturacientifica.com/2019/09/04/numeros-primos-gemelos-parientes-y-sexis-1/]. En esta entrada vamos a analizar las otras parejas de números primos que aborda la conjetura de Polignac, en particular, los números primos parientes (k = 2) y sexis (k = 3).
Si los números primos gemelos son aquellas parejas de números primos tales que la diferencia entre ellos es 2 (k = 1), es decir, parejas de primos (p, p + 2), se van a llamar números primos parientes (“cousin” en inglés) a las parejas de números primos con una diferencia entre ellos de 4 (k = 2), luego de la forma (p, p + 4), como (3, 7), (7, 11) o (13, 17).
Las parejas de números primos parientes menores de 500 son (véase la sucesión A023200 de la enciclopedia online de números enteros):
(3, 7), (7, 11), (13, 17), (19, 23), (37, 41), (43, 47), (67, 71), (79, 83), (97, 101), (103, 107), (109, 113), (127, 131), (163, 167), (193, 197), (223, 227), (229, 233), (277, 281), (307, 311), (313, 317), (349, 353), (379, 383), (397, 401), (439, 443), (457, 461), (463, 467), (487, 491), (499, 503).
La pareja de números primos parientes más grande conocida, a día de hoy, fue obtenida en 2009, y está formada por los números (p, p + 4), tal que
p = [311.778.476 x N x (N + 1) + 210] x [N – 1] / 35 + 1,
para N = 587.502 x 9.001#, donde 9.001# denota el primorial de 9.001, que definiremos a continuación, que tiene 11.594 dígitos.
El primorial de un número n, que se denota n#, es una especie de factorial del número (véase Buscando lagunas de números no primos) que se define como el producto de todos los números primos menores, o iguales, que ese número n. Así, si tomamos el número primo 23, entonces 23# = 2 x 3 x 5 x 7 x 11 x 13 x 17 x 19 x 23 = 223.092.870 o para el número 39 se tiene que 39# = 2 x 3 x 5 x 7 x 11 x 13 x 17 x 19 x 23 x 29 x 31 x 37 = 7.420.738.134.810.
Para los números primos parientes existe un resultado análogo al teorema de Brun para números primos gemelos, es decir, la suma de los recíprocos de los números primos parientes (salvo la pareja 3 y 7)
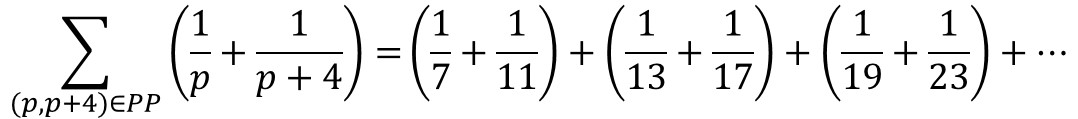
también es convergente, y su límite es el número B4, conocido como constante de Brun para números primos parientes, que tiene un valor aproximado de 1,1970449 (véase el artículo On the Twin and Cousin Primes, de Marek Wolf).
Nos podemos interesar ahora por las ternas de números primos parientes, como (3, 7, 11). Pero resulta que esa es la única terna de números primos parientes que existe, puesto que si tenemos una terna de números primos de la forma (p, p + 4, p + 8), necesariamente uno de ellos es divisible por 3. Esto es fácil de probar. Si escribimos p de la forma p = 3 n + r, donde r = 0, 1 ó 2, entonces la terna anterior es de la forma (p = 3 n + r, p + 4 = 3 (n + 1) + r + 1, p + 8 = 3 (n + 2) + r + 2), luego si r = 0, el primer número de la terna es divisible por 3, si r = 1, lo es el tercero y si r = 2, lo es el segundo.
 La investigación de los matemáticos Yitang Zhang, Terence Tao y James Maynard sobre la conjetura de los números primos gemelos, ha conseguido grandes avances en los últimos años. Véase la entrada Números primos gemelos, parientes y sexis (1)
La investigación de los matemáticos Yitang Zhang, Terence Tao y James Maynard sobre la conjetura de los números primos gemelos, ha conseguido grandes avances en los últimos años. Véase la entrada Números primos gemelos, parientes y sexis (1)La siguiente familia de números primos, relacionada con la conjetura de Polignac, que nos interesa, son los números primos sexis. Estos son parejas de números primos de la forma (p, p + 6), es decir, la diferencia entre ellos es 6 (k = 3), como (5, 11), (7, 13) o (11, 17). Su nombre se debe a que la palabra en latín para el número “seis” es “sex” (de hecho, los diez primeros números, en latín, son unus, duo, tres, quattuor, quinque, sex, septem, octo, novem, decem).
Las parejas de números primos sexis menores de 500 son (véase la sucesión A023201):
(5, 11), (7, 13), (11, 17), (13, 19), (17, 23), (23, 29), (31, 37), (37, 43), (41, 47), (47, 53), (53, 59), (61, 67), (67, 73), (73, 79), (83, 89), (97, 103), (101, 107), (103, 109), (107, 113), (131, 137), (151, 157), (157, 163), (167, 173), (173, 179), (191, 197), (193, 199), (223, 229), (227, 233), (233, 239), (251, 257), (257, 263), (263, 269), (271, 277), (277, 283), (307, 313), (311, 317), (331, 337), (347, 353), (353, 359), (367, 373), (373, 379), (383, 389), (433, 439), (443, 449), (457, 463) y (461, 467).
Además, la pareja de números primos sexis más grande conocida, a día de hoy, es la pareja (p, p + 6), tal que
p = (187.983.281 x 251.478 + 4) x (5 x 251.478 – 1) – 1,
con 31.002 dígitos, que fue encontrada por S. Batalov, en abril de 2019.
Algunas parejas de números primos sexis forman parte de grupos de tres primos muy próximos, como (5, 7, 11) o (7, 11, 13), lo que en la anterior entrada denominados números primos trillizos, los cuales son de la forma (p, p + 2, p + 6) o (p, p + 4, p + 6). Por lo tanto, en cada terna de números primos trillizos, hay una pareja de números primos gemelos, (p, p + 2) o (p + 4, p + 6), una pareja de números primos parientes, (p +2, p + 6) o (p, p + 4), y una pareja de números primos sexis, (p, p + 6). Por ejemplo, en la terna de números primos trillizos (67, 71, 73), 71 y 73 son gemelos, 67 y 71 parientes, y 67 y 73 sexis.
 El número 283.281.277 es el número primo más pequeño formado por los tres miembros, en sentido inverso, de una terna de números primos trillizos (277, 281, 283). Visto en The Prime pages
El número 283.281.277 es el número primo más pequeño formado por los tres miembros, en sentido inverso, de una terna de números primos trillizos (277, 281, 283). Visto en The Prime pages
A diferencia de lo que ocurría con los números primos parientes, que no pueden ir en grupos de tres, ahora se pueden considerar ternas de números primos sexis como (7, 13, 19), (17, 23, 29) o (31, 37, 43), formadas por tres números primos sexis consecutivos, (p, p + 6, p + 12), tal que el siguiente p + 18 no es primo, pero podría serlo el anterior p – 6, y que llamaremos tripletes, o tríos, de números primos sexis.
Más aún, se pueden considerar cuartetos de números primos sexis, formados por cuatro números primos sexis consecutivos, de la forma (p, p + 6, p + 12, p + 18), como (5, 11, 17, 23), (11, 17, 23, 29) o (41, 47, 53, 59). Curiosamente, salvo para el primer cuarteto, el primer número primo de cualquier cuarteto de números primos sexis termina en 1, como podemos observar en los primeros términos de la sucesión A023271, que está formada por los primeros primos de los cuartetos de números primos sexis: 5, 11, 41, 61, 251, 601, 641, 1091, 1481, 1601, 1741, 1861, 2371, 2671, 3301, 3911, 4001, 5101, …
Sin embargo, no existen quintetos de números primos sexis, salvo (5, 11, 17, 23, 29), puesto que dados cinco números con una deferencia de seis entre ellos (p, p + 6, p + 12, p + 18, p + 24), entonces uno de ellos debe ser divisible por 5, para lo cual basta escribir p de la forma p = 5 n + r, para r = 0, 1, 2, 3 ó 4.
 Curiosa pareja de números primos sexis, formada por los nueves dígitos, del 1 al 9, pero duplicados, pero terminados luego en 1 y 7. Visto en The Prime pages
Curiosa pareja de números primos sexis, formada por los nueves dígitos, del 1 al 9, pero duplicados, pero terminados luego en 1 y 7. Visto en The Prime pagesAdemás de las parejas de números primos gemelos, parientes y sexis, se pueden estudiar otras parejas de números primos (p, p + 2k), para k mayor que 3, relacionadas con la conjetura de Polignac. Parejas de números primos cuya distancia entre ellos sea 8 (k = 4), como (3, 11), (5, 13), (11, 17), (23, 31) o (29, 37), cuya distancia sea 10 (k = 5), como (3, 13), (7, 17), (13, 23), (19, 29) o (31, 41), cuya distancia sea 12 (k = 6), como (5, 17), (7, 19), (11, 23), (17, 29) o (19, 31), o mayores distancias aún.
 Die Droguen /Las drogas –Novalis– (2011), 150 × 110 cm, de la artista alemana Rune Mields. Los números que aparecen en esta obra son números primos. Imagen de ART SY
Die Droguen /Las drogas –Novalis– (2011), 150 × 110 cm, de la artista alemana Rune Mields. Los números que aparecen en esta obra son números primos. Imagen de ART SY
Bibliografía
1.- William Dunham, A Note on the Origin of the Twin Prime Conjecture, Notices of the ICCM, vol. 1, n. 1, pp. 63-65, 2013.
2.- Wolfram Mathworld: Cousin Primes
3.- Wikipedia: Cousin prime
4.- The Prime pages
5.- Wolfram Mathworld: Sexy Primes
6.- Wikipedia: Sexy prime
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Números primos gemelos, parientes y sexis (2) se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Números primos gemelos, parientes y sexis (1)
- Buscando lagunas de números no primos
- Los ritmos primos de Anthony Hill
La carga del núcleo y el sistema de periodos
 Foto: vubp / Pixabay
Foto: vubp / PixabayA pesar del éxito del modelo atómico de Rutherford a la hora de explicar los resultados de los experimentos de dispersión de partículas α, seguía habiendo un problema sin resolver. Todavía no había forma de medir la carga Q en el núcleo de forma independiente. Sin embargo, los experimentos de dispersión habían confirmado las predicciones de Rutherford sobre el efecto de la velocidad de la partícula y el grosor de la lámina sobre el ángulo de dispersión. Como sucede a menudo cuando se confirma parte de una hipótesis, es razonable proceder temporalmente como si toda la hipótesis estuviera justificada; es decir, hasta que no hubiese más resultados, se podría suponer que el valor de Q necesario para explicar los datos de dispersión observados fuese el valor correcto de Q para el núcleo real, determinado por la ley de Coulomb y el movimiento de las partículas α.
Sobre esta base, el laboratorio de Rutherford compiló datos de dispersión para varios elementos diferentes, entre ellos carbono, aluminio y oro. De estos experimetos resultaba que las siguientes cargas positivas para el núcleo eran las que cuadraban mejor: para el carbono, Q = 6e ; para el aluminio dos valores parecían funcionar, Q = 13e o 14e; y para el oro, Q = 78e o 79e [1]. Del mismo modo, se encontraron valores para el resto de elementos.
La magnitud de la carga positiva del núcleo fue un dato de trascendental importancia para entender cómo era un átomo. Como el átomo en su conjunto es eléctricamente neutro, se sigue que, si el núcleo tiene una carga positiva de 6e, 13e, 14e, etc., el número de electrones cargados negativamente que rodean el núcleo debe ser 6 para el carbono, 13 o 14 para el aluminio, etc. Por lo tanto, por primera vez, la comunidad científica tenía idea de cuántos electrones puede tener un átomo.
Pero un hecho más importante si cabe resultó rápidamente evidente. Para cada elemento, el valor de la carga nuclear, en múltiplos de e, estaba cerca del número atómico Z, ¡el número de lugar de ese elemento en la tabla periódica! Los resultados de los experimentos de dispersión con partículas α aún no eran lo suficientemente precisos como para llegar afirmarlo con certeza, pero todo apuntaba a que cada núcleo tiene una carga positiva Q numéricamente igual a Ze.
Esta posibilidad hacía la imagen del átomo nuclear mucho más clara y simple. Sobre esta base, el átomo de hidrógeno (Z = 1) tiene un electrón en algún lugar que no es el núcleo. Un átomo de helio (Z = 2) tiene en su estado neutro dos electrones en algún lugar que no es el núcleo. Un átomo de uranio (Z = 92) tiene 92 electrones en algún lugar que no es el núcleo. Experimentos adicionales respaldaron aún más este sencillo esquema. Los experimentos demostraban que era posible producir átomos de hidrógeno ionizados con una carga, H+, y átomos de helio ionizados con dos cargas, He2+, pero no había forma de conseguir H2+ ni He3+. Evidentemente, un átomo de hidrógeno tiene solo un electrón que perder, y un átomo de helio solo dos. Inesperadamente, el concepto de átomo nuclear proporcionaba una nueva visión completamente nueva de la tabla periódica de los elementos. El átomo nuclear sugiere que la tabla periódica es realmente una lista de los elementos de acuerdo con el número de electrones alrededor del núcleo, o lo que es lo mismo, con el número de unidades de carga positiva en el núcleo.
Estos resultados aclaraban algunas de las problemas en el sistema de periodos de Mendeléyev. Por ejemplo, a los elementos teluro y yodo se les habían asignado las posiciones Z = 52 y Z = 53 en función de sus propiedades químicas. Este posicionamiento contradecía el orden de sus pesos atómicos. Pero ahora se veía que Z correspondía a un hecho fundamental sobre el núcleo. Por lo tanto, lo que se pensaba que era una carencia del sistema de Mendeléyev en realidad no lo era. [2]
Notas:
[1] Donde e es la magnitud de la carga de un electrón (e = −1,602·10−19 C ). Para una explicación de cómo se determina e véase La carga más pequeña.
[2] Esto es algo a lo que no se le da tanta importancia como a las predicciones de nuevos elementos que hizo Mendeléyev, pero es algo del mismo calibre. A toro pasado parece obvio, pero cuando Mendeléyev presenta el sistema de periodos es toda una expresión de rigor químico.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo La carga del núcleo y el sistema de periodos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:

 Foto:
Foto: