Adiós a las grasas trans
Querido lector, si estás comiendo algo mientras lees este artículo, lamento informarte que probablemente estés ingiriendo grasas trans. ¿Que no sabes qué son? Para empezar, estas grasas no tienen nada de transgénico. Su nombre y el porqué se consideran “malas” radica en su estructura molecular, en cómo están orientados los átomos de carbono al interaccionar entre sí mediante un doble enlace químico.

Estas grasas pueden perjudicar tu salud favoreciendo el desarrollo de enfermedades cardiovasculares. Están presentes en alimentos como la leche y la carne de rumiantes, pero sobretodo se obtienen como productos no deseados durante procesos industriales como la hidrogenación de aceites vegetales. Están por todas partes, hasta en la sopa (¡y no es broma!).
Como si todo esto fuera poco, en numerosos países europeos, entre ellos España, no existe una legislación que regule la cantidad permitida de grasas trans en los alimentos. Pero que no cunda el pánico. Lo cierto es que en realidad consumimos mucha menos grasas trans de lo que creemos. Los procesos industriales por los cuales se obtienen han mejorado tanto que la ingesta de este tipo de grasas suele ser inferior al límite aconsejado por la OMS.
Así que tranquilo/a, sigue disfrutando sin culpa de lo que estés comiendo, porque las grasas trans son cosa del pasado.
Referencias consultadas:- Riobó, Pilar y Breton, Irene (2014). Ingesta de grasas trans; situación en España. Nutrición Hospitalaria, 29(4), 704-711. DOI:10.3305/nh.2014.29.4.7337.
———————————-
Autora: Agustina Taglialegna (@AgustinaTaglia), alumna del Postgrado de Ilustración Científica de la UPV/EHU – curso 2018/19
Artículo original: A nadie le preocupan las grasas trans. Déborah García Bello, Cuaderno de Cultura Científica, 4 de octubre de 2018.
———————————-
“Ilustrando ciencia” es uno de los proyectos integrados dentro de la asignatura Comunicación Científica del Postgrado de Ilustración Científica de la Universidad del País Vasco. Tomando como referencia un artículo de divulgación, los ilustradores confeccionan una nueva versión con un eje central, la ilustración.
El artículo Adiós a las grasas trans se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- A nadie le preocupan las grasas trans
- Adiós a las microesferas de plástico en los cosméticos
- ¿Azúcar moreno o azúcar milagro?
¿El escudo del Capitán América? A mí tráeme un casco de obra
Imagina que estás en una obra y se suelta un pedrolo bien gordo que comienza a caer y va directo a tu cabeza, ¿qué eliges para cubrirte? ¿El escudo del Capitán América…
 Imagen: Wikimedia Commons
Imagen: Wikimedia Commons
… o el típico casco de obra?
 Imagen: Wikimedia Commons
Imagen: Wikimedia Commons
Unos millones de obreros y yo nos decantamos por el casco, te explicaré por qué.
El primer motivo es que el escudo no existe, pero no es el principal.
Para entenderlo bien tenemos que precisar qué es la fuerza.
No es infrecuente definir las magnitudes físicas según alguna fórmula en las que participan. Por ejemplo, la fuerza es aquello capaz de cambiar el estado de movimiento de un sistema. Simplificando podría decirse que bien aumentando/disminuyendo su velocidad o bien cambiándola de dirección, lo que implica generar una aceleración. Recuerda la segunda ley de Newton: F = m·a
Aquí se suele obviar que hay otro fenómeno en el que se manifiestan las fuerzas, cuando se producen deformaciones.
(En realidad es trabajo hecho contra las fuerzas que mantenían las partes del sistema en sus posiciones relativas)
Pero, para verlo bien claro, nos quedamos con que las fuerzas producen cambios en el estado de movimiento o deformaciones.
Y volvamos a nuestros superhéroes, esos que se ponen cotas de mithril y escudos de vibranium, materiales tremendamente resistentes y que no se romperán cuando se les aplique una fuerza, por intensa que sea.
Muy bien, te lo compro, pero tú estás detrás, querido amigo… Y para mostrarte lo que te pasará si confías ciegamente en los Vengadores o en tu tío Bilbo, recordemos un conocido juguete, el péndulo de Newton (Newton’s cradle).
 Imagen: Wikimedia Commons
Imagen: Wikimedia Commons
Si piensas en que la bola de la izquierda es el objeto que te golpea; las del centro, tu cobertura, y la de la derecha, tu cabeza… creo que verás que te llevas el impacto completo, con toda su energía.
Eso es lo que pasará si te cubres con un elemento rígido en contacto contigo. El impacto te llegará con toda su fuerza. La única ventaja que puedes obtener sería que si el objeto es puntiagudo, su fuerza se repartirá por todo el “protector” que uses y la presión será menor (se clavará menos), pero la energía del golpe será la misma.
Por lo tanto, si te tiras de un edificio con la mejor armadura de vibranium el golpe va a ser equivalente al que te darías si fueras desnudo, sólo que, en lugar de chocar contra el suelo, chocarás contra la armadura.
Puedes comprobarlo por ti mismo con monedas sobre una mesa. Mira este vídeo.
Estarás pensando: “Vale, quizá el truco sea, no estar en contacto con la armadura, dejar hueco. Así no me llegará el impacto.” Si es así, es que has olvidado la primera ley Newton, la ley de la inercia.
Si sobre un cuerpo la fuerza neta es cero, este seguirá con su estado de movimiento constante. Bien parado o con movimiento rectilíneo y uniforme.
Ponte la armadura de nuevo, ahora usaremos una de una talla más, y saltemos desde lo alto de un edificio. Cuando la armadura toque el suelo no te pasará la fuerza (¡Bien!), pero la armadura se parará… y tú seguirás cayendo el trocito que te faltaba y te darás el tortazo que te mereces por no estudiar física (¡MAL!).
Esto es justo lo que les pasa al cerebros cuando la cabeza sufre un movimiento brusco en un accidente de coche o al recibir un puñetazo. El cráneo se mueve, pero el cerebro que está suspendido en medio no, al final es el propio cráneo el que le golpea en su movimiento.
Y, entonces, ¿por qué es mejor el caso frente al escudo? Si cuando el objeto golpee el casco me pasará toda la fuerza y energía, ¿qué ventaja me ofrece?
El secreto, claro, está en el interior.
 Imagen: Wikimedia Commons
Imagen: Wikimedia Commons
El casco de seguridad no va apoyado sobre el cráneo, va sujeto a la cabeza con una estructura de plástico que, por un lado nos separa del casco y por otro… es FLEXIBLE.
Recuerda que dijimos que las fuerzas también podían producir una deformación, como cuando espachurramos una lata de refresco. En este caso, el entramado de plástico hace de amortiguador, deformádose un poco, sin que el casco toque la cabeza), absorbiendo la energía del golpe y salvándonos esta mollera que tantos años ha costado educar. Por supuesto, después vuelve a estirarse y en ese proceso disipa la energía en forma de calor y todos contentos.
Ya sólo me queda pedirte perdón por estropearte el 90% de las películas de ciencia ficción y fantasía, pero es que el universo de verdad es más fascinante aún.
Sobre el autor: Javier Fernández Panadero es físico y profesor de secundaria además de escritor de libros de divulgación.
El artículo ¿El escudo del Capitán América? A mí tráeme un casco de obra se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Las cartas de Darwin: El capitán y el filósofo
- #Naukas14: Con casco a la ducha
- Una brecha en nuestro escudo
Placer y geometría
Cuando pensamos en chocolate nuestro cerebro activa las sensaciones y recuerdos de placer, pero ¿y si nos abre las puertas a degustar algo tan en principio alejado como las matemáticas?
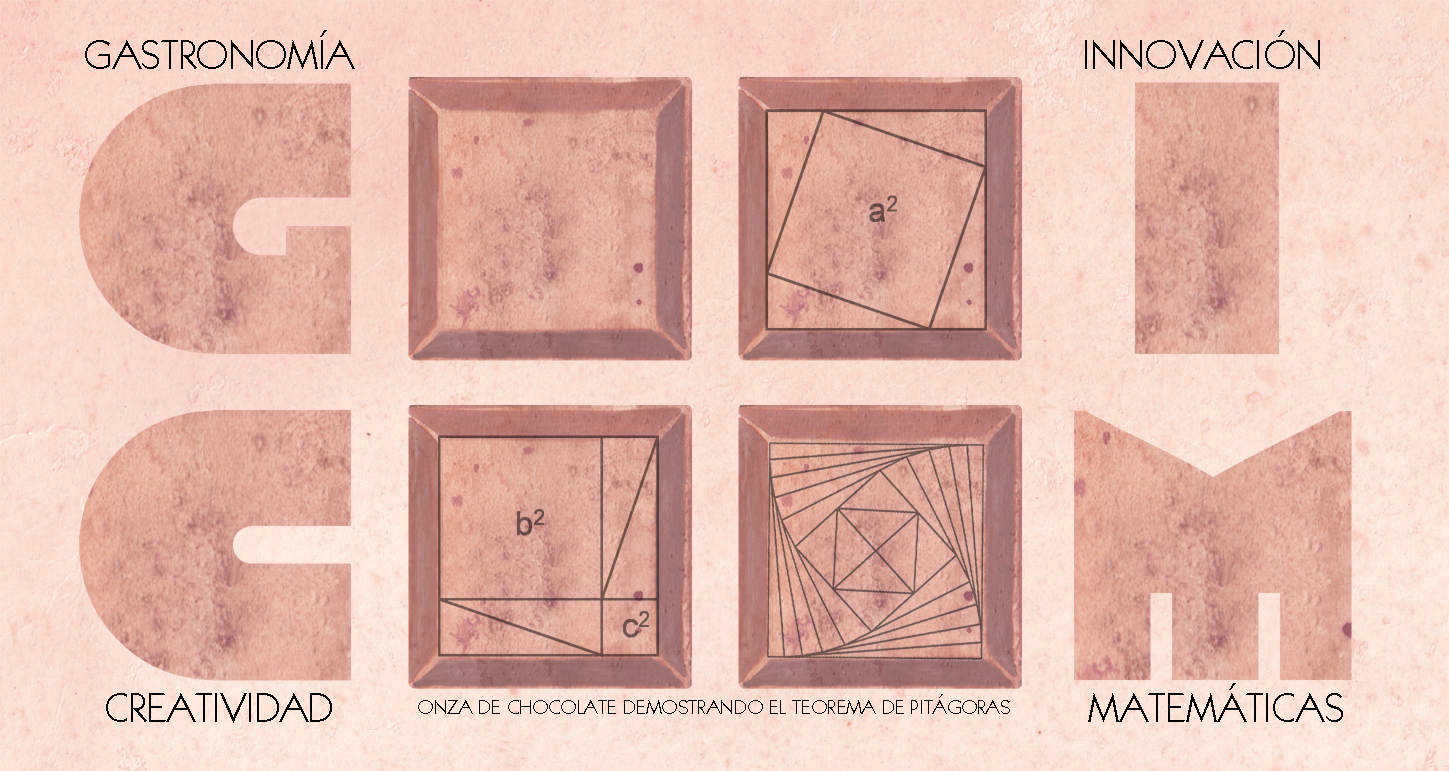 Imagen: Diseño de tableta que demuestra visualmente el teorema de Pitágoras: girando el cuadrado típico de la onza de chocolate hacia el interior crea triángulos de diferentes medidas, pero que mantienen la misma superficie. (Ilustración: Olga Carmona Peral)
Imagen: Diseño de tableta que demuestra visualmente el teorema de Pitágoras: girando el cuadrado típico de la onza de chocolate hacia el interior crea triángulos de diferentes medidas, pero que mantienen la misma superficie. (Ilustración: Olga Carmona Peral)
La gastronomía va mucho más allá de cubrir una necesidad primaria, y se considera un arte con relaciones íntimas con nuestro mundo, nuestra cultura e incluso la ciencia. El gourmet busca en la alta cocina dar un valor añadido a sus platos y que actúen como elemento de distinción y atractivo.
Un buen ejemplo es el maestro chocolatero barcelonés Enric Rovira que viene desarrollando desde hace 25 años propuestas rompedoras que unen lógica con placer, sensaciones con geometría. Parecen mundos muy distantes pero, ¿y si no lo son tanto?
Ya la tradicional tableta de chocolate es un ejemplo maestro de geometría de gran sencillez y sentido práctico, pero él va un paso más allá. Mediante la innovación y la creatividad nos propone diseños de tabletas que nos remiten a la arquitectura modernista o a medidas armónicas y orgánicas más propias de Le Corbusier, incluso una tableta realizada junto al diseñador Santos Bregaña y el matemático Enrique Zuazua, que demuestra visualmente el teorema de Pitágoras.
Son propuestas que unen lógica con placer, sensaciones con geometría, matemáticas con gastronomía, así ambos mundos nos enriquecen cuando damos un delicioso bocado a ese chocolate.
———————————-
Autora: Olga Carmona Peral (@olga_CPeral), alumna del Postgrado de Ilustración Científica de la UPV/EHU – curso 2018/19
Artículo original: Diseños geométricos de chocolate. Raúl Ibáñez, Cuaderno de Cultura Científica, 8 de octubre de 2014.
———————————-
“Ilustrando ciencia” es uno de los proyectos integrados dentro de la asignatura Comunicación Científica del Postgrado de Ilustración Científica de la Universidad del País Vasco. Tomando como referencia un artículo de divulgación, los ilustradores confeccionan una nueva versión con un eje central, la ilustración.
El artículo Placer y geometría se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Cálculo y geometría analítica, de George F. Simmons
- La geometría de la obsesión
- Arte y geometría del triángulo rectángulo: Broken Lights
Matemáticas modernas

Las matemáticas son el lenguaje en el que está escrito el univero y eso hace que el grado en matemáticas sirva para muchas más cosas que para dar clases. Lo ilustra Paz Morillo de la Universitat Politècnica de Catalunya con 6 casos de chicas que aplican las matemáticas en ámbitos muy distintos.
Quizás sea el número más famoso de la historia. Lo cierto es que el número Pi, representado por la letra griega π, es una de las constantes matemáticas más importantes que existen en el mundo, estudiada por el ser humano desde hace más de 4.000 años. La fascinación que ha suscitado durante siglos es tal que el popular número cuenta con su propio día en el calendario, así el mes de marzo se celebra el Día de Pi en todo el planeta.
Este evento internacional vino de la mano del físico estadounidense Larry Shaw, quien lanzó en 1988 la propuesta de celebrar esta efeméride. La forma en la que se escribe el 14 de marzo en inglés y euskera coincide con los tres primeros dígitos de la famosa constante matemática. (3-14 martxoaren 14 en euskara / 3-14 march, 14th en inglés) y además, la celebración coincide con la fecha del nacimiento de Albert Einstein. En 2009, el congreso de EEUU declaró oficialmente el 14 de marzo como el Día Nacional de Pi.
Actualmente, el Día de Pi es una celebración mundialmente conocida que sobrepasa el ámbito de las matemáticas. Este número irracional, que determina la relación entre la longitud de una circunferencia y su diámetro, concierne a múltiples disciplinas científicas como la física, la ingeniería y la geología, y tiene aplicaciones prácticas sorprendentes en nuestro día a día.
Este 2019 nos unimos de nuevo al festejo con el evento BCAM–NAUKAS, que se desarrolló a lo largo del 13 de marzo en el Bizkaia Aretoa de UPV/EHU. BCAM-NAUKAS contó durante la mañana con talleres matemáticos para estudiantes de primaria y secundaria y durante la tarde con una serie de conferencias cortas dirigidas al público en general.
Este evento es una iniciativa del Basque Center for Applied Mathematics -BCAM, enmarcada en la celebración de su décimo aniversario, y de la Cátedra de Cultura Científica de la Universidad el País Vasco.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Matemáticas modernas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Historia y peligros del cultivo de arroz
En la actualidad, muchas regiones del mundo consumen alimentos que no se producen en el propio país. Este es el caso del arroz (Oryza sativa). Se calcula que en el sur-sudeste de Asia se produce entorno al 90% del arroz consumido en el mundo.
Análisis arqueológicos y genéticos indican que el arroz se domesticó hace 14.000-10.000 años en China. Tardó alrededor de 10.000-8.000 años en llegar a India y otros 2.000 en expandirse por Japón, Oriente Medio, Egipto, Grecia y Roma. Hace 1.300 años se introdujo en la Península Ibérica, gracias a los árabes. 500 años después se consumía en el norte de Europa y fue hace 300 años cuando se introdujo en Norteamérica, mediante esclavos africanos.
No hay que olvidar que el cultivo del arroz es complicado y peligroso ya que se necesita mucha agua y los lodazales de siembra son lugares idóneos para la cría de mosquitos Anopheles, puesto que sus huevos y el crecimiento de la larva y pupa se desarrolla en un medio acuático. En su etapa adulta, mediante sus picaduras, transmiten enfermedades como el paludismo o malaria.
En un estudio psicológico se comparó el comportamiento de los cultivadores de arroz con los de trigo. Los resultados mostraron que los primeros eran más interdependientes y holistas que los segundos. Esto ocurre porque la siembra del arroz, a diferencia del trigo, requiere cooperación.
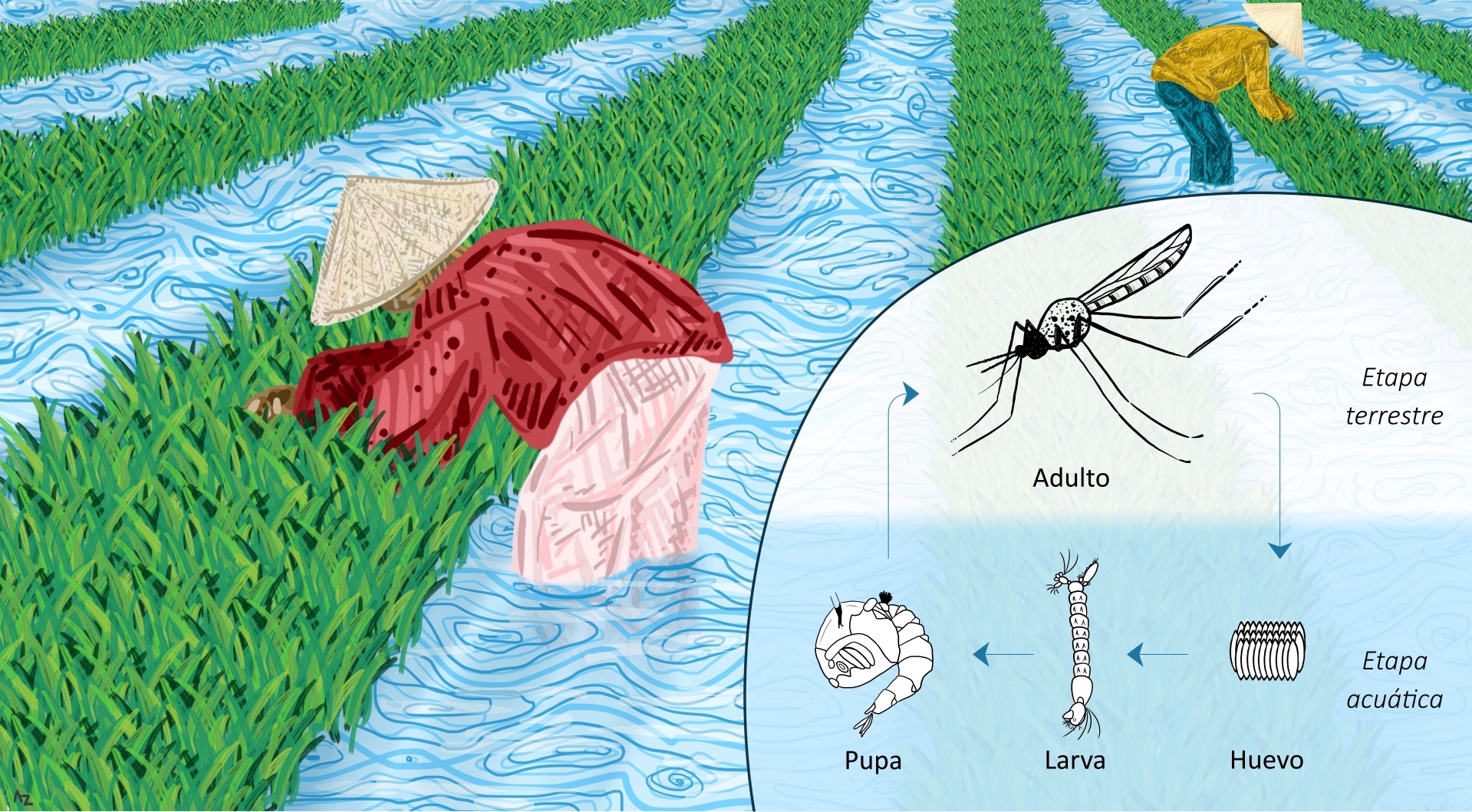 Imagen: Ilustración del cultivo del arroz en un lodazal de siembra y la relación que muestra con el ciclo de vida del mosquito Anopheles. (Ilustración: Aida Zuriñe Campos Vivanco)
Imagen: Ilustración del cultivo del arroz en un lodazal de siembra y la relación que muestra con el ciclo de vida del mosquito Anopheles. (Ilustración: Aida Zuriñe Campos Vivanco)
En conclusión, el cultivo del arroz es una actividad que puede ser complicada y peligrosa, que lleva tras de sí miles de años de historia y expansión.
———————————-
Autora: Aida Zuriñe Campos Vivanco (@az_ciencia), alumna del Postgrado de Ilustración Científica de la UPV/EHU – curso 2018/19
Artículo original: Ingredientes para la receta: El arroz. Eduardo Angulo, Cuaderno de Cultura Científica, 5 de diciembre de 2018.
———————————-
“Ilustrando ciencia” es uno de los proyectos integrados dentro de la asignatura Comunicación Científica del Postgrado de Ilustración Científica de la Universidad del País Vasco. Tomando como referencia un artículo de divulgación, los ilustradores confeccionan una nueva versión con un eje central, la ilustración.
El artículo Historia y peligros del cultivo de arroz se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¿Desde cuándo nos repite el ajo?
- Ingredientes para la receta: El arroz
- En el mar, allí donde todo comienza
Parque cretácico
La Facultad de Ciencias de Bilbao comenzó su andadura en el curso 1968/69. 50 años después la Facultad de Ciencia y Tecnología de la UPV/EHU celebra dicho acontecimiento dando a conocer el impacto que la Facultad ha tenido en nuestra sociedad. Publicamos en el Cuaderno de Cultura Científica y en Zientzia Kaiera una serie de artículos que narran algunas de las contribuciones más significativas realizadas a lo largo de estas cinco décadas.

Algunas producciones cinematográficas y su despliegue mediático han permitido que nuestra sociedad esté familiarizada con el Jurásico, ese periodo de la historia de la Tierra de hace entre 201 y 145 millones de años (ma a partir de aquí). Y yo, como geólogo, agradezco esta difusión, pero nuestro planeta presenta una gran historia de 4500 ma que podríamos considerar plenamente fascinante. La Geología, con la ayuda de las otras ciencias básicas, ha permitido conocer esta dilatada historia. Y de ella, voy a destacar la del periodo Cretácico (145-100 ma)… y os preguntaréis por qué…
Las montañas y valles de nuestro entorno, que tan acostumbrados estamos a pisar fruto de nuestra fusión ancestral con el territorio, están formadas principalmente por rocas sedimentarias que se originaron en el mar, y precisamente, las del Cretácico son las que mayor extensión presentan en el paisaje… ¡Las que más pisamos!
Geológicamente, nuestro entorno forma la región que denominamos vasco-cantábrica, donde localizamos Euskal Herria y zonas aledañas (Cantabria, Burgos,…). Este territorio se formó por el plegamiento de sedimentos y rocas que dio origen a los Pirineos; de hecho, también podemos denominarla Pirineo Occidental. Entre los periodos Triásico (hace aproximadamente 200 ma) y Paleógeno (hace aprox. 35 ma) esta región no era como la conocemos sino una amplia zona de sedimentación continental y marina comprendida entre el Macizo de Asturias al Oeste, la Sierra de la Demanda al Sur, y el Macizo de Bortziri-Aldude, al Este: la conocida por los geólogos como Cuenca (de sedimentación) Vasco-Cantábrica. Podemos imaginarla como un mar alimentado por ríos que nacían en las áreas continentales mencionadas (imagen 1).
 Imagen 1. La región Vasco-Cantábrica hace 100 millones de años (edad Albiense). La imagen se presenta como si estuviera tomada desde el aire mirando hacia el sureste. Modificada de una imagen del mapa geológico del País Vasco (EVE. Ente Vasco de la Energia / Energiaren Euskal Erakundea).
Imagen 1. La región Vasco-Cantábrica hace 100 millones de años (edad Albiense). La imagen se presenta como si estuviera tomada desde el aire mirando hacia el sureste. Modificada de una imagen del mapa geológico del País Vasco (EVE. Ente Vasco de la Energia / Energiaren Euskal Erakundea).
Pero esta imagen no era estática sino que iba cambiando a lo largo del tiempo: conforme se movía la placa de Iberia respecto de la de Europa y se iba abriendo el Golfo de Bizkaia (imagen 2), el mar iba ganando extensión y profundidad progresivamente hasta el momento en el que comienza la formación de los Pirineos, elevándose la topografía y pasando a ser una zona montañosa en erosión (imagen 3).
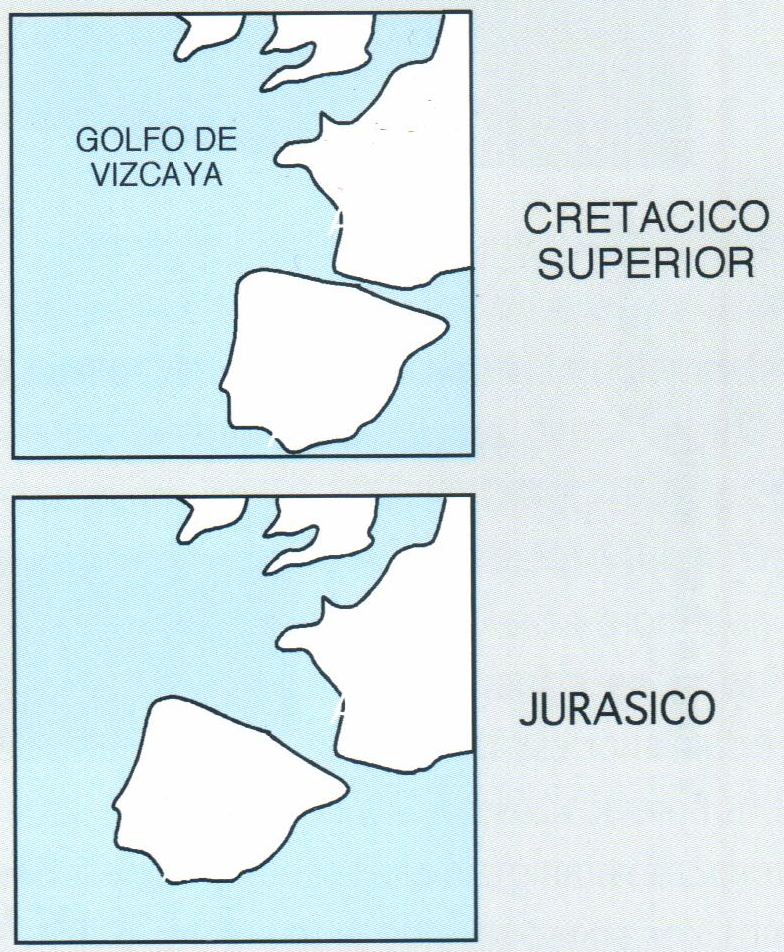 Imagen 2. Posición relativa de las placas de Iberia y de Europa en el Jurásico y en el Cretácico superior, donde se observa la apertura del Golfo de Bizkaia como consecuencia del movimiento relativo de ambas placas. Tomada del libro de Bodego et al. Eds. (ISBN 978-84-9860-991-2).
Imagen 2. Posición relativa de las placas de Iberia y de Europa en el Jurásico y en el Cretácico superior, donde se observa la apertura del Golfo de Bizkaia como consecuencia del movimiento relativo de ambas placas. Tomada del libro de Bodego et al. Eds. (ISBN 978-84-9860-991-2).
Así, durante el Cretácico, en nuestra región, además de mares y ríos que llevaban sus sedimentos hacia zonas costeras, había deltas, playas, estuarios…, los cuales son ejemplos de lo que denominamos medios sedimentarios. En ellos vivían comunidades de seres vivos que florecieron y se extinguieron, pero que dejaron su carácter en los sedimentos y rocas. El estudio de los organismos fósiles nos ayuda a entender mejor cómo era el medio sedimentario y viceversa, ya que los condicionantes físicos (p. ej. el oleaje) y químicos (p. ej. la salinidad del agua) influyen en el desarrollo de los seres vivos y en la distribución y depósito de sedimento.
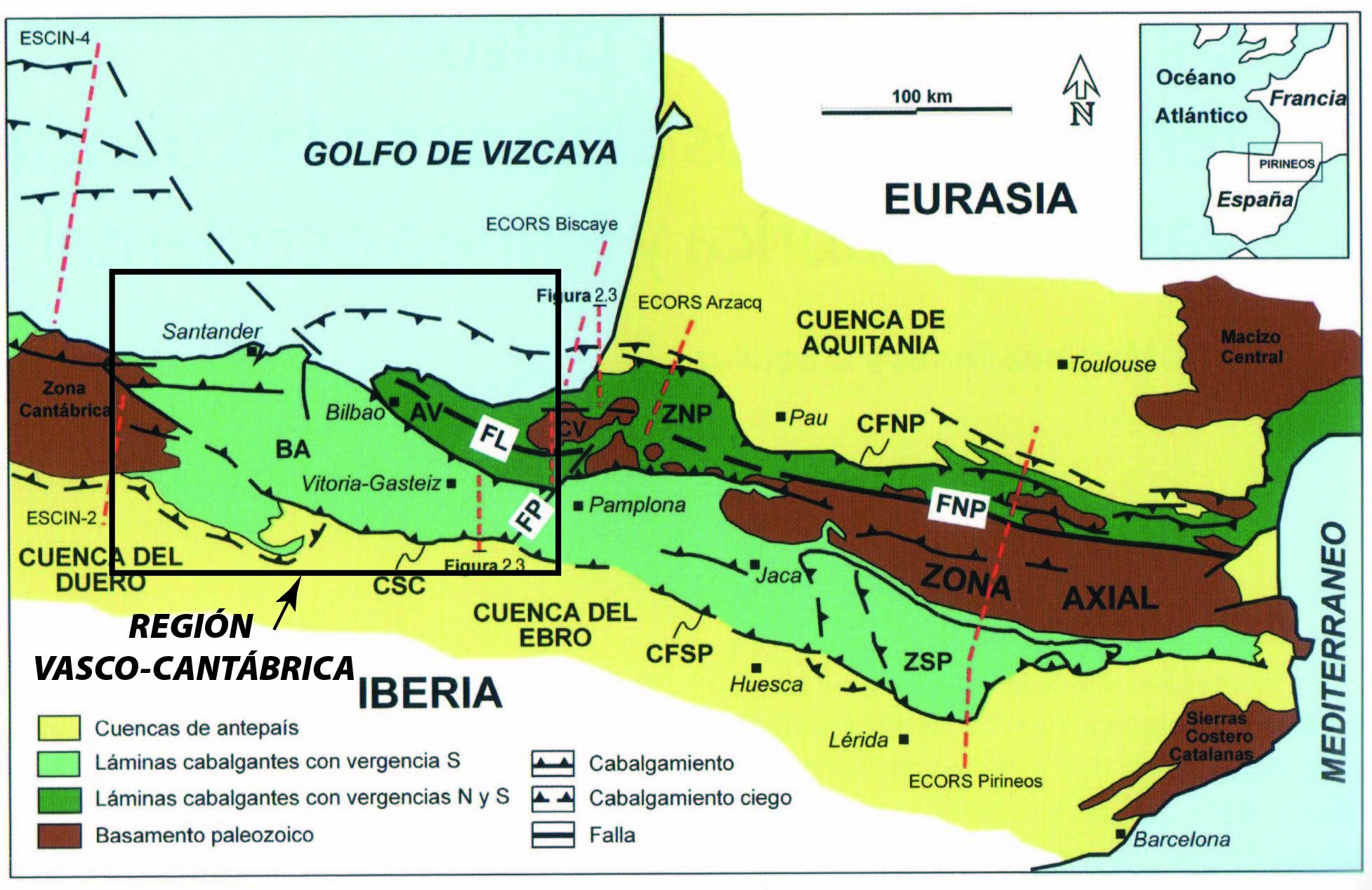 Imagen 3. Mapa geológico actual de los Pirineos. La Región Vasco-Cantábrica es la parte occidental de esta cadena montañosa. Los colores verdes indican rocas sedimentarias plegadas. Con color amarillo se representan las zonas actuales con sedimentación continental. Tomada del libro de Bodego et al. Eds. (ISBN 978-84-9860-991-2).
Imagen 3. Mapa geológico actual de los Pirineos. La Región Vasco-Cantábrica es la parte occidental de esta cadena montañosa. Los colores verdes indican rocas sedimentarias plegadas. Con color amarillo se representan las zonas actuales con sedimentación continental. Tomada del libro de Bodego et al. Eds. (ISBN 978-84-9860-991-2).
La Cuenca Vasco-Cantábrica estuvo influenciada por procesos geológicos tales como actividad de fallas, vulcanismo, expansión de las áreas marinas, entre otros. El estudio de las rocas cretácicas de nuestra región ha permitido y permite conocer como han actuado estos procesos en un periodo con muchos cambios ambientales e influenciado por una climatología subtropical.
El Cretácico se divide en intervalos de tiempo Inferior y Superior y a su vez, en intervalos menores llamados edades, los cuales usaremos para ilustrar los principales ambientes y fósiles de nuestra región.
Así, al comienzo del Cretácico Inferior (edad Berriasiense a Barremiense; hace 145-125 ma) los ríos principales drenaban las zonas de Asturias y llevaban sus sedimentos arenoso-arcillosos a un mar de poca profundidad. En las zonas costeras se desarrollaron comunidades piscícolas de teleósteos primitivos, los antepasados directos de la mayoría de las especies actuales de peces (imagen 4).
 Imagen 4. Pez fósil llamado Ezkutuberezi carmeni. Es un teleósteo primitivo que tiene el honor de ser el primer vertebrado fósil en conexión anatómica encontrado y descrito en nuestra Región. Longitud aproximada: 10 cm. Cretácico inferior. Foto: Mikel A. López-Horgue.
Imagen 4. Pez fósil llamado Ezkutuberezi carmeni. Es un teleósteo primitivo que tiene el honor de ser el primer vertebrado fósil en conexión anatómica encontrado y descrito en nuestra Región. Longitud aproximada: 10 cm. Cretácico inferior. Foto: Mikel A. López-Horgue.
Poco después, geológicamente hablando (Aptiense y Albiense; hace 125-100 ma), el mar ocupó mayor superficie y ganó en profundidad. La actividad de las fallas aumentó de tal manera, que sobre los bloques de falla hundidos el mar presentó profundidades mayores (>200m) mientras que sobre los bloques elevados no se pasaron de 40-50 m de columna de agua. En estas zonas de menor profundidad y con menor aporte de arenas y arcillas, las asociaciones de corales, bivalvos rudistas, algas y bacterias, entre otros, indujeron una sedimentación de carbonato cálcico que hoy día forman las calizas (arrecifales y de plataforma) tan abundantes y que configuran los principales relieves en nuestra geografía: Karrantza, Anboto, Aitzgorri, Aralar, entre otros. En las zonas con mayor profundidad proliferaban los ammonites, cefalópodos de concha tabicada, que ocupaban distintos hábitats pelágicos. El vulcanismo submarino del Albiense es un fenómeno que influyó en el medio marino, con procesos tales como la introducción de metales (p. ej. hierro) y la variación de la temperatura del entorno. La abundancia de calizas con microbios (bacterias, algas,…) y la diversificación de ciertos grupos (p. ej. crustáceos decápodos-cangrejos, langostas- y ammonites; imagen 5) son hitos evolutivos que suceden en el Albiense vasco-cantábrico, aunque no se ha demostrado todavía si hubo relación con el vulcanismo.
 Imagen 5. A la izquierda una langosta fósil de edad Albiense. Habitaba en las zonas alejadas de la costa de un mar somero. Longitud aproximada: 10 cm. (Foto: Patxi Rosales Espizua). A la derecha un ammonite de gran tamaño. Edad Albiense. Habitaba un medio marino de mayor profundidad y alejado de la costa. Diámetro del fósil: 45 cm. Foto: Mikel A. López-Horgue.
Imagen 5. A la izquierda una langosta fósil de edad Albiense. Habitaba en las zonas alejadas de la costa de un mar somero. Longitud aproximada: 10 cm. (Foto: Patxi Rosales Espizua). A la derecha un ammonite de gran tamaño. Edad Albiense. Habitaba un medio marino de mayor profundidad y alejado de la costa. Diámetro del fósil: 45 cm. Foto: Mikel A. López-Horgue.
Un gran cambio ambiental ocurre al comienzo del Cretácico Superior (Cenomaniense; hace 100-93 ma): una subida del nivel del mar permitió que éste ocupara progresivamente amplias zonas continentales en toda la región (este fenómeno se conoce como transgresión marina), llegando la línea de costa hasta más al sur de la actual Soria, y desarrollándose una sedimentación de carbonato cálcico aportado principalmente por organismos unicelulares planctónicos (algas calcáreas, foraminíferos). En las zona de Bilbao-Plencia se llegó a un máximo de profundidad del mar, que según autores, alcanzaría los 1500-2000 m durante el Coniaciense (hace 86 ma). Esta transgresión es un proceso rápido geológicamente (aprox. 15 ma) que dificultó que los seres vivos respondieran a unas nuevas condiciones con áreas marinas más extensas, cambio en las corrientes oceánicas y en la profundidad, entre otros efectos, aunque también supuso oportunidades para nuevos grupos emergentes. Como ejemplo, la mayoría de los grupos de ammonites del Cretácico inferior desparecieron al final del Albiense (99 ma), diversificándose rápidamente a partir de pocos grupos con las nuevas condiciones. Asimismo, los peces teleósteos primitivos dejaron paso a los nuevos peces óseos. Los “constructores” de arrecifes y plataformas carbonatadas (corales, rudistas) se redujeron a algunas zonas de menor profundidad hacia el sur de la región. Una nueva fase de vulcanismo tuvo lugar durante el Santoniense (86-83 ma) en las zonas de mayor profundidad.
En el Campaniense-Maastrichtiense (83-66 ma), los ríos avanzaron sustancialmente hacia el norte, posibilitando un nuevo cambio en los ambientes. En estuarios y zonas costeras con sedimentación de arenas y arcillas proliferaron los tiburones y rayas, presentando una alta biodiversidad en la región. Asimismo, en sedimentos fluviales de este tiempo se ha encontrado una diversa asociación con más de 40 especies de vertebrados continentales, entre dinosaurios, pterosaurios, cocodrilos, tortugas, serpientes, lagartos, anfibios, mamíferos y peces, constituyendo uno de los yacimientos de vertebrados del Cretácico superior más importante de Europa.
El impacto de un meteorito en Yucatán marca el final del Cretácico (66 ma) y con ello se produce una de las llamadas extinciones masivas (en la historia de la Tierra se han diferenciado al menos 7), donde desaparecieron un 76% de las especies. Este fenómeno quedó registrado en los sedimentos arcillosos de mar profundo de Sopela, Zumaia y Bidart como una fina capa de entre 1 y 7 cm de espesor con un alto contenido en Iridio que supera cien veces la concentración de la corteza terrestre; este hecho se toma como evidencia directa del impacto de un meteorito, ya que éstos presentan igualmente concentraciones muy altas.
La vida volvió a abrirse camino después del Cretácico, y también volvió a sufrir cambios. La geología nos enseña una Tierra dinámica con procesos geológicos que controlan los cambios ambientales y el desarrollo de los seres vivos. El Cretácico es una pequeño pero apasionante capítulo de la historia de la Tierra, y su registro es especialmente importante en nuestra región vasco-cantábrica. ¿A que ahora podemos “pisar” nuestro paisaje de otra manera?
Para saber más:
- Bodego, A., López-Horgue, M. A., (2018). “Geología de los Pirineos occidentales: evolución ambiental a través de sus rocas y fósiles”. Registro fósil de los Pirineos occidentales, Eds.: Badiola et al., p.35-52. Vitoria-Gasteiz. Eusko Jaurlaritza.
- López-Horgue, M. A., Agirrezabala, L. M., Burgos, J., (2018). “Los ammonoideos de Mutriku: patrimonio único a preservar”. Registro fósil de los Pirineos occidentales, Eds.: Badiola et al., p.269-271. Vitoria-Gasteiz. Eusko Jaurlaritza.
- Bodego, A., López-Horgue, M. A., (2018). “Grandes desconocidos del registro fósil: los crustáceos decápodos del Mesozoico y Cenozoico de los Pirineos occidentales”. Registro fósil de los Pirineos occidentales, Eds.: Badiola et al., p.109-116. Vitoria-Gasteiz. Eusko Jaurlaritza.
Sobre el autor: Mikel López-Horgue es profesor en el Departamento de Estatigrafía y Paleontología de la Facultad de Ciencia y Tecnología de la UPV/EHU.
El artículo Parque cretácico se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Arrecifes fósiles, una paradoja geológica
- Geología, Antropoceno y cambio climático
- La regla de los números intermedios y el parque automovilístico de Bilbao
¿Azúcar moreno o azúcar milagro?
Seguro que alguna vez habéis observado a gente echar azúcar moreno al café alegando que es más sano y contiene menos calorías que el blanco. No obstante, esto no es cierto.
 Imagen: Proceso de obtención del azúcar blanco y moreno. Este comienza con la recolección de la caña o la remolacha azucarera, las cuales son troceadas y mezcladas con agua para poder extraer el jugo. Posteriormente se realiza un proceso de decantación química para eliminar las sustancias no deseadas, así como la evaporación del agua, de forma que parte de la sacarosa cristaliza y otra parte carameliza formando la melaza. Finalmente, la sacarosa se mezcla con la melaza en cantidades controladas para obtener el azúcar moreno. (Ilustración: Ledicia Prieto Vázquez)
Imagen: Proceso de obtención del azúcar blanco y moreno. Este comienza con la recolección de la caña o la remolacha azucarera, las cuales son troceadas y mezcladas con agua para poder extraer el jugo. Posteriormente se realiza un proceso de decantación química para eliminar las sustancias no deseadas, así como la evaporación del agua, de forma que parte de la sacarosa cristaliza y otra parte carameliza formando la melaza. Finalmente, la sacarosa se mezcla con la melaza en cantidades controladas para obtener el azúcar moreno. (Ilustración: Ledicia Prieto Vázquez)
Partimos de que estos dos tipos de azúcar salen de la caña o remolacha y al principio sufren un proceso de transformación idéntico. ¿Entonces, dónde difieren? Básicamente lo hacen en que el azúcar moreno lleva la propia sacarosa cristalizada junto con la melaza (sacarosa caramelizada, de color parduzco), mientras que el azúcar blanco solo lleva la primera. Es decir, el azúcar moreno, al igual que el blanco, está compuesto por sacarosa y por lo tanto no hay diferencia a nivel de calorías; aunque sí en la cantidad de minerales (ínfima) y en el sabor.
El azúcar moreno, debido a la melaza, es más amargo que el blanco. Así que si sumamos las creencias de que el azúcar moreno es más sano y más amargo, ¿qué se obtiene? Que se echará mayor cantidad de azúcar en la comida o bebida y se consumirán más calorías aún.
———————————-
Autora: Ledicia Prieto Vázquez (@araliart_l), alumna del Postgrado de Ilustración Científica de la UPV/EHU – curso 2018/19
Artículo original: Azúcar moreno, ¿mejor que el azúcar blanco? Déborah García Bello, Cuaderno de Cultura Científica, 3 de diciembre de 2018.
———————————-
“Ilustrando ciencia” es uno de los proyectos integrados dentro de la asignatura Comunicación Científica del Postgrado de Ilustración Científica de la Universidad del País Vasco. Tomando como referencia un artículo de divulgación, los ilustradores confeccionan una nueva versión con un eje central, la ilustración.
El artículo ¿Azúcar moreno o azúcar milagro? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Azúcar moreno, ¿mejor que el azúcar blanco?
- Miel y siropes, ¿son mejores que el azúcar?
- El azúcar oculto en los alimentos
Puedes llamarlo responsabilidad, pero es censura
Hay hechos que pueden hacer que ciertas ideologías se tambaleen. Hay hechos cuya difusión puede causar una importante repercusión social, sanitaria, incluso moral. Podemos optar por negarlos, por divulgarlos, o por ocultarlos. La oscuridad (en contraposición etimológica a ilustración) acostumbra a presentarse como un acto de responsabilidad. La posmodernidad y su disfraz lingüístico. En ocasiones llamamos responsabilidad a lo que realmente es censura.
Para ponernos en situación imaginemos que un hecho disparatado es cierto. Por ejemplo, se ha comprobado científicamente que las personas de color son intelectualmente inferiores a las blancas. (Obviamente esto no es así, pero sirve de ejemplo). ¿Qué hacemos con este hecho? ¿Es posible divulgar este hecho de forma responsable? ¿Lo responsable sería ocultarlo? Si optásemos por censurarlo, la razón a la que se apelaría es la responsabilidad social. Se ocultaría para prevenir un mal mayor, como dotar de argumentos a los movimientos xenófobos. No obstante, si un hecho así fuese cierto, no tendría porqué hacer peligrar la igualdad de derechos y oportunidades. Un estado de derecho debería garantizarlos igualmente, sean cuales sean las capacidades intelectuales de los individuos de esa sociedad. De la misma manera, el estado procura que las personas con algún tipo de discapacidad intelectual no sean discriminadas por ello. Sí, pero. Vaya dilema. ¿Lo divulgamos o lo censuramos?
Cuando un hecho contradice aquello en lo que se sustentan nuestras ideologías y nuestros valores, nos coloca ante el espejo. Siguiendo con el ejemplo. Si el hecho probado fuese el contrario, que las personas de color son intelectualmente superiores a las blancas, con toda seguridad este hecho se divulgaría sin problemas y sin tanto dilema moral de por medio. Esto nos lleva a una reflexión que esconde una realidad todavía más incómoda: la condescendencia y el paternalismo por el que decidimos qué hechos científicos divulgamos. También revela algo peor.
La realidad es que este tipo de situaciones se dan con cierta frecuencia, sobre todo en la actualidad y, sobre todo en ciencias. Hay hechos científicos que generan acalorados debates sobre la idoneidad de su divulgación. No hay debate sobre su veracidad, sino sobre la conveniencia de sacarlos a la luz.
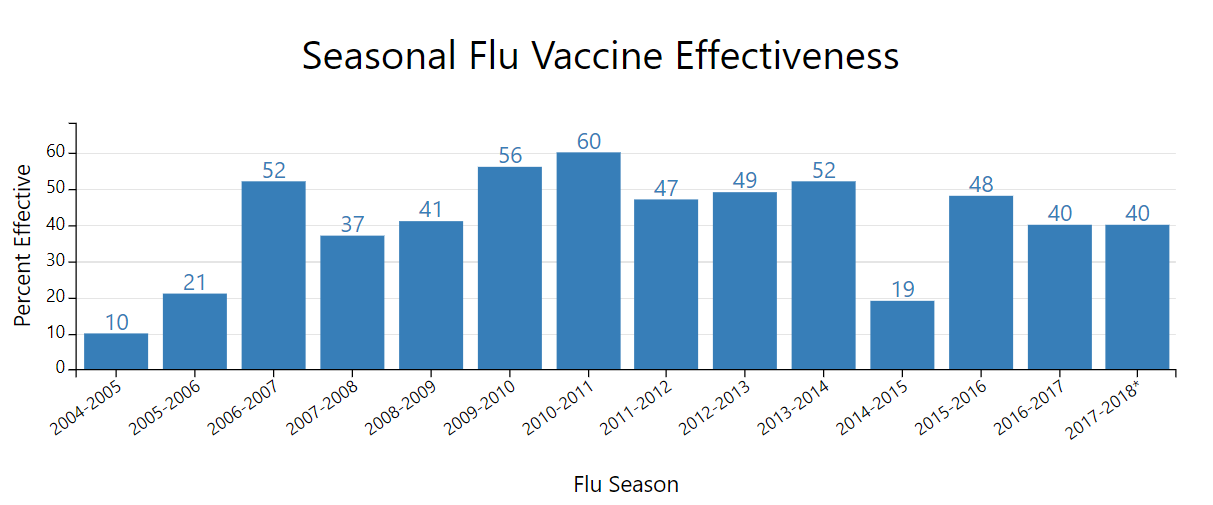 Fuente: CDC
Fuente: CDC
Por ejemplo, es un hecho conocido por la comunidad científica que la eficacia de la vacuna de la gripe es baja. Algunos años fue solo del 10%, y otros alcanzó máximos del 60%. Para una vacuna, es una efectividad baja. La divulgación de este hecho es controvertida porque hay quien opina que puede disuadir a grupos de riesgo de vacunarse, puede poner en entredicho la efectividad de las vacunas en su conjunto o puede usarse como argumento antivacunas. Quien defiende su divulgación argumenta que la información debe estar a disposición de todos y que ocultar estos datos es una forma de censura. También se puede llamar responsabilidad social. O condescendencia. Al fin y al cabo, ocultar esta información nos da la medida de lo poco preparada que pensamos que está la sociedad para asumir este hecho y actuar igualmente de forma responsable. También nos da la medida de cómo creemos que algunos medios de comunicación podrían informar de este hecho o alarmar sobre él.
Con respecto a temas sanitarios hay otros muchos hechos cuya divulgación está sujeta a controversia, como la insuficiente efectividad del cribado o diagnóstico precoz en algunos tipos de cáncer, o el uso deliberado de placebos como método terapéutico efectivo. Hechos cuya divulgación podría hacerse de forma tendenciosa e irresponsable a fin de desprestigiar el sistema sanitario.
 Ilustración: César Mejías para El Definido
Ilustración: César Mejías para El Definido
La divulgación de hechos biológicos también suscita apasionadas discusiones. Las diferencias halladas entre los cerebros de hombres y mujeres resultan inconvenientes para los creyentes en ciertas ideologías, que consideran estos hechos como un ataque que podría hacer peligrar la igualdad de género. También hay quien los niega tildándolos de neurosexismo, es decir, negando que sean hechos y defendiendo que solo se trata de la lectura estereotipada de los datos.
La realidad es que las diferencias entre los cerebros masculino y femenino tienen interés científico. De igual manera que ha resultado muy esclarecedor el estudio de las diferencias metabólicas, hormonales o de las de cualquier órgano entre hombres y mujeres, incluido el cerebro. Tanto es así, que la inclusión de las mujeres en estudios clínicos supuso un gran adelanto en medicina, pudiendo ofrecer tratamientos más adaptados a las necesidades de unos y otros.
El miedo a la divulgación de estos hechos de nuevo nos coloca ante el espejo. ¿Qué es lo que genera tanta preocupación? ¿Qué es lo que está en juego, la credibilidad del sistema científico, o la del estado de derecho? La igualdad de derechos y oportunidades en ningún caso debe depender de la igualdad biológica entre individuos. Si esto es lo que algunos pretenden, tienen asegurado el fracaso, desde el punto de vista social y moral. La igualdad de derechos y oportunidades debe garantizarse por encima de cualquier diferencia biológica, esté localizada en el cerebro, en el páncreas o en los genitales.
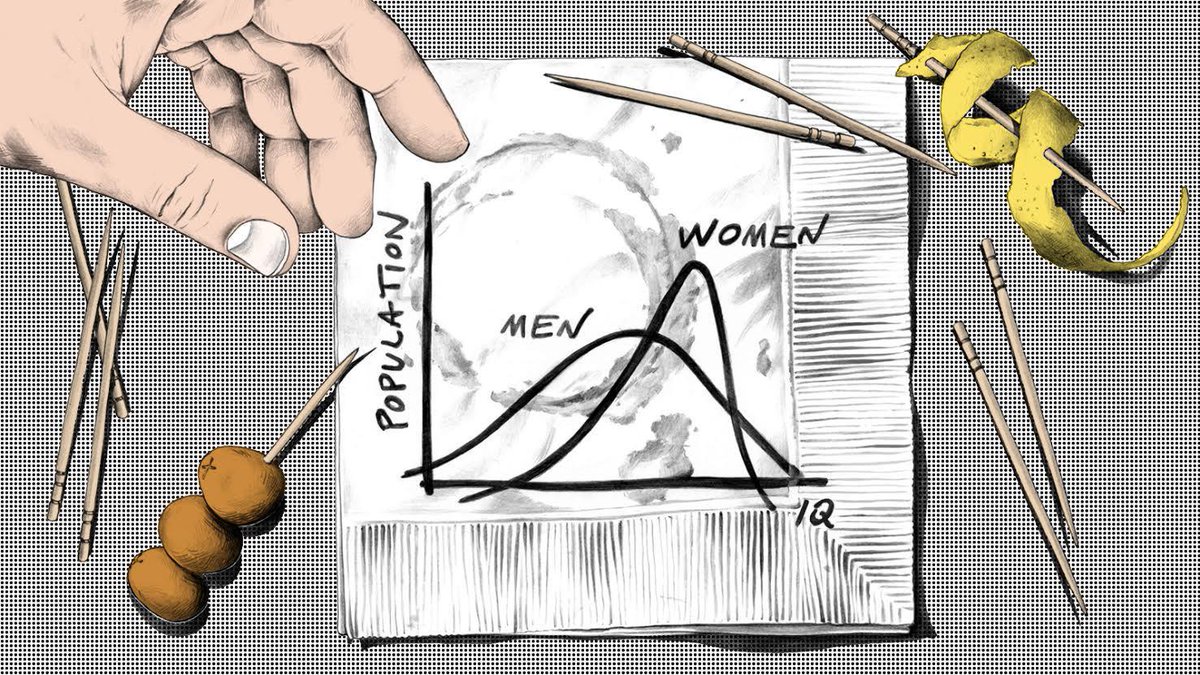 Ilustración: Giada Fiorindi para Quartz
Ilustración: Giada Fiorindi para Quartz
Debates de naturaleza similar llegaron a causar fisuras en el sistema científico. El caso más sonado aconteció en 2017, cuando la revista Mathematical Intelligencer retiró un artículo científico por presión de la asociación Women in Mathematics de la Universidad Estatal de Pensilvania, entre otros. El estudio en cuestión concluía que la inteligencia de los hombres presenta mayor variabilidad que la de las mujeres. Es decir, que entre los hombres hay más genios, pero también más inútiles. Y que las mujeres presentan un nivel de inteligencia más homogéneo.
No había ningún error científico, ni de método, ni fraude académico, que es la razón por la que un estudio se retiraría de una revista científica. El artículo fue revisado y aceptado y, aun así, decidieron retirarlo por cuestiones ideológicas, no científicas.
Los hechos que promueven el pensamiento, cambios en las acciones acometidas, cambios en los cimientos ideológicos en temas tan sensibles como por ejemplo el movimiento feminista, a menudo suscitan más ataques que reflexiones. Si un movimiento es suficientemente fuerte y necesario (y el feminismo lo es) no necesita negar los hechos, sino servirse de ellos. Esa es una de las mayores diferencias entre un movimiento posmoderno y un movimiento ilustrado.
Sobre la autora: Déborah García Bello es química y divulgadora científica
El artículo Puedes llamarlo responsabilidad, pero es censura se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Puedes presumir de tener la mejor piel del mundo.
- El aguacate debería haberse extinguido, pero él no lo sabe todavía
- Sobre igualdad, excelencia, ejemplaridad y responsabilidad en los premios Nobel
Guía para un consumo de cafeína
Cada vez más productos incluyen cafeína en su composición, y muchos emplean la publicidad engañosa, haciendo referencia a sus supuestas propiedades funcionales. Pero ¿sabemos qué beneficios nos aporta realmente?, ¿a partir de qué cantidades? y ¿a partir de cuáles se vuelve perjudicial?
 Imagen: Guía para un consumo de cafeína funcional y seguro. Efectos de la cafeína en función de la dosis y niveles promedio de cafeína que contienen distintas bebidas. (Ilustración: Mikel Rodríguez Hidalgo)
Imagen: Guía para un consumo de cafeína funcional y seguro. Efectos de la cafeína en función de la dosis y niveles promedio de cafeína que contienen distintas bebidas. (Ilustración: Mikel Rodríguez Hidalgo)
Según el Panel de Expertos en Nutrición, Alergias y Dietéticos de la Autoridad Europea de Seguridad Alimentaria (EFSA), la cafeína que contiene 1 expreso, 75 mg, es la cantidad mínima a partir de la cual se favorecen los procesos cognitivos, como la memoria, el aprendizaje, la concentración, la resistencia ante el estrés o el tiempo de reacción.
Para emplearla como sustancia ergogénica en el ejercicio, es necesaria ingerir una dosis de entre 200- 300 mg, equivalente a 3 tazas de café, una hora antes de la actividad física, de este modo se consigue un aumento del rendimiento en el ejercicio de resistencia aeróbica y retardar la sensación de fatiga.
Sin embargo una vez superados los 300- 400 mg o 4 tazas de café, se alcanza el umbral de la sobre dosis, a partir de la cual se producen efectos negativos como taquicardia, arritmia, aumento de la tensión, insomnio, irritabilidad o problemas gastrointestinales.
Para alcanzar la dosis letal se deben superar los 5-10 g, que equivaldrían a 70 expresos, aunque ciertos parámetros pueden reducir esta cantidad, como la edad, el peso, la genética o la tolerancia de cada persona, a si como él mezclarlo con otras sustancias como el alcohol o ciertos medicamentos.
Por lo que la cafeína que contiene 1 expreso es la dosis mínima efectiva para sentir ciertos beneficios y es a partir de los 3 cafés, cuando podríamos comenzar a padecer efectos no deseados.
Referencias consultadas:- Picjering, C., Kiely, J. (2017). Are the Current Guidelines on Caffeine Use in Sport Optimal for Everyone? Inter-individual Variation in Caffeine Ergogenicity, and a Move Towards Personalised Sports Nutrition. Sports Medicine, 48(1), 7–16. DOI: 10.1007/s40279-017-0776-1.
- Ramírez-Montes, C.A., Osorio J.H. (2013). Uso de la cafeína en el ejercicio físico: ventajas y riesgos. Revista de la Facultad de Medicina, 61(4), 459-468.
———————————-
Autor: Mikel Rodríguez Hidalgo (@mikelgraphicscience), alumno del Postgrado de Ilustración Científica de la UPV/EHU – curso 2018/19
Artículo original: La cafeína y su renacimiento como ingrediente estrella de los productos funcionales. José Manuel López Nicolás, Cuaderno de Cultura Científica, 25 de abril de 2014.
———————————-
“Ilustrando ciencia” es uno de los proyectos integrados dentro de la asignatura Comunicación Científica del Postgrado de Ilustración Científica de la Universidad del País Vasco. Tomando como referencia un artículo de divulgación, los ilustradores confeccionan una nueva versión con un eje central, la ilustración.
El artículo Guía para un consumo de cafeína se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La cafeína y su renacimiento como ingrediente estrella de los productos funcionales
- Variantes genéticas exóticas, claves para nuestra salud
- Genética molecular para el rastreo de la caza furtiva
FUN WITH MATHS, diversión con matemáticas
Antes de iniciar esta entrada del Cuaderno de Cultura Científica, me gustaría justificar brevemente el título de la misma. Es un pequeño homenaje a la serie de televisión The Big Bang Theory que, tomando como punto de partida la ciencia, nos ha hecho reír estos años. Como pequeño homenaje he realizado, en el título de esta entrada, un paralelismo con el nombre de la serie de programas emitidos vía streaming, dentro de la ficción de la serie, por los personajes del físico teórico Sheldon Lee Cooper y la neurobióloga Amy Farraw Fowler, en concreto, Sheldon Cooper Presents: Fun with Flags (Sheldon Cooper presenta: diversión con banderas), sobre vexilología (siempre es bueno aprender nuevas palabras), es decir, el estudio de las banderas.
 Imagen del primer episodio de la serie The Big Bang Theory en el que aparece Sheldon Cooper Presents: Fun with Flags (Sheldon Cooper presenta: diversión con banderas), el capítulo de la quinta temporada titulado The Beta Test Initiation
Imagen del primer episodio de la serie The Big Bang Theory en el que aparece Sheldon Cooper Presents: Fun with Flags (Sheldon Cooper presenta: diversión con banderas), el capítulo de la quinta temporada titulado The Beta Test Initiation
El otro motivo para titular esta entrada como “diversión con matemáticas”, es que vamos a explicar algunos sencillos trucos de magia relacionados con las matemáticas. Más concretamente, con los números. He de confesar que lo mío no es la magia, aunque sí tengo en mi entorno de amistades algunas personas expertas en lo que se ha dado en llamar “matemagia”, personas que son matemáticas y también magas.
Una de ellas es mi compañero y amigo Pedro Alegría (UPV/EHU), uno de los decanos en España en magia matemática, responsable, desde marzo de 2004, de la sección El rincón matemágico de DivulgaMAT, Centro virtual de divulgación de las matemáticas de la Real Sociedad Matemática Española, autor del libro Magia por principios (2008) y que fue quien me enseñó el truco que expliqué en el video de la sección Una de mates, de la Cátedra de Cultura Científica, y que fue emitido en el programa de humor y ciencia de televisión, dirigido por José A. Pérez Ledo, Orbita Laika (segunda temporada) de La2, de Televisión Española: Una de mates, magia matemática (temporada 2).
Otro mago matemático amigo es Fernando Blasco (UPM), autor de libros como Matemagia (2007), que fue quien me enseñó el truco del video para la sección Una de mates, del programa de humor y ciencia de televisión, dirigido por José A. Pérez Ledo, Orbita Laika (primera temporada) de La2, de Televisión Española: Una de mates, magia matemática (temporada 1).
O también el matemático y mago Nelo Maestre (Divermates), que es el responsable, junto a Tania Giraldo, de la sección Objetos matemáticos con materiales cotidianos de DivulgaMAT.
Pero vayamos a lo que quería contar en esta entrada del Cuaderno de Cultura Científica. Justo estos días estaba yo revisando algunas multiplicaciones curiosas, como

de la que hablamos en la entrada del Cuaderno de Cultura Científica, El secreto de los números que no querían ser simétricos o esta otra

cuando me vino a la cabeza un truco de magia que aprendí en un libro clásico de matemagia, Mathemagic, magic-puzzles-games with numbers (1953), en el cual la base en la que se apoyaba el truco era precisamente este segundo grupo de multiplicaciones curiosas.
El truco consistiría en lo siguiente. Se le pide a la persona a la que se le va a realizar el truco, o a una de las personas del público, que escriba el número “doce millones, trescientos cuarenta y cinco mil, seiscientos setenta y nueve”, es decir, 12.345.679, sobre una pizarra o una hoja de papel que se le haya suministrado previamente (si son grandes mejor).
A continuación, se le pide a esa persona que elija una de las cifras que componen ese número y que escriba una x encima de ella, o que dibuje una circunferencia alrededor de la misma, y que se lo enseñe a todo el público, incluida la persona que realiza el truco. Supongamos que hubiese elegido el 6.
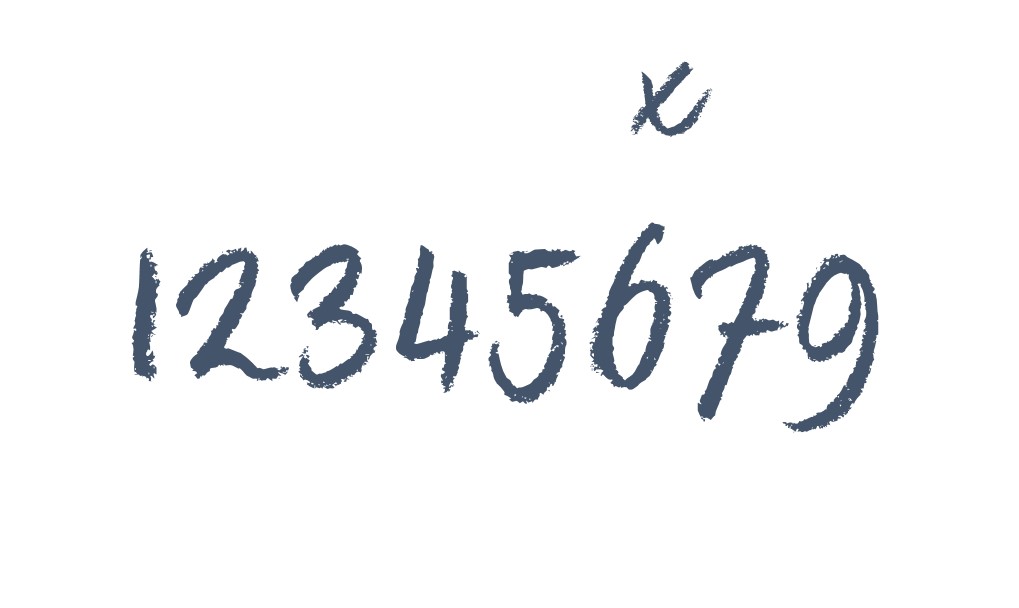
Entonces, se le pide que multiplique el número inicial, 12.345.679, por un número que tú le vas a indicar, por ejemplo, si el 6 fuese la cifra elegida por ella, le pedirías que lo multiplicase por 54, que no es otro (esto no se lo dirás al público, claro) que multiplicar la cifra elegida por 9, es decir, 6 x 9 = 54. Cuando la persona realice la anterior multiplicación se llevará una sorpresa, ya que el resultado será el número 666.666.666, es decir, todos sus dígitos son la cifra elegida por ella.

La explicación del truco es sencilla y tiene que ver con la curiosa torre de multiplicaciones anteriormente vista. Para explicar un poco más el truco, si no estuviese del todo claro, podemos mencionar que la anterior torre se puede expresar de la siguiente forma

para c tomando los valores de las cifras básicas, salvo el cero, es decir, c = 1, 2, 3, 4, 5, 6, 7, 8 y 9. Luego, por este motivo le pedimos a la persona que multiplique por c x 9, es decir, la cifra elegida c multiplicada por 9.
Obsérvese que la igualdad también valdría para el 8, luego se podría plantear que eligiera una de las cifras básicas no nulas, del 1 al 9, aunque es más teatral pedirle que elija una de las cifras del número escrito.
El autor del libro, el bróker y mago estadounidense Royal Vale Heath (1883-1960), menciona también que ese número, 12.345.679, tiene otras interesantes propiedades. Por ejemplo, pueden considerarse las siguientes multiplicaciones

Puede observarse que, en los resultados de cada grupo de tres multiplicaciones, aparecen solamente tres cifras repetidas. En cada resultado la disposición de las tres cifras se repite tres veces y de un resultado al siguiente las cifras se desplazan una posición a la izquierda, o a la derecha. Por ejemplo, en el primer grupo de multiplicaciones las cifras de los resultados son 0, 3, 7, y los resultados verifican las dos propiedades comentadas, 037.037.037 (añadimos el cero de la derecha, que no es necesario, para ver que realmente se produce el efecto), 370.370.370 y 703.703.703.
Más aún, en cada grupo de tres multiplicaciones, la suma de los dígitos de los resultados de las tres multiplicaciones es igual a la suma de los números por los que se ha multiplicado el número 12.345.679. Así, en el primer grupo, las cifras de cada resultado suman 30, luego entre los tres resultados, 90, y si miramos la suma de los números multiplicadores se obtiene la misma cantidad, 3 + 30 + 57 = 90. Lo mismo en los demás grupos.
 Portada del libro de Royal Vale Heath, Mathemagic, magic-puzzles-games with numbers, publicado en la editorial Dover en 1953
Portada del libro de Royal Vale Heath, Mathemagic, magic-puzzles-games with numbers, publicado en la editorial Dover en 1953
Sigamos con otro truco de magia relacionado con los números, que aparece en este texto clásico de matemagia de Royal Vale Heath, Mathemagic, magic-puzzles-games with numbers.
El truco consiste en adivinar tres números del 1 al 9, elegidos por alguien del público o mejor aún, que sean las respuestas a tres preguntas realizadas por la persona que realiza el truco. Por ejemplo, si el truco se realiza en una clase se les podría preguntar por la nota que han sacado en la anterior evaluación en tres asignaturas, por ejemplo, Lengua, Matemáticas e Historia, entendiendo que las respuestas deben ser números enteros, 1, 2, 3, 4, 5, 6, 7, 8 o 9. Otra opción podría ser preguntarle a la persona del público ¿cuántos hermanos y hermanas son (incluido él o ella)? ¿cuántos hermanos y hermanas tiene su padre (incluido el padre)? y ¿cuántos hermanos y hermanas tiene su madre (incluida la madre)? O cualquier otra pregunta que se le ocurra a quien realiza el truco adaptada al público concreto.
Supongamos que hemos preguntado por el número de hermanos y hermanas a una persona elegida al azar del público. Esta persona deberá escribir las respuestas a las tres preguntas en una hoja de papel que se le habrá proporcionado previamente, pero no deberá decirlo en alto, para que la persona que hace el truco no lo sepa. Imaginemos que las respuestas a esas tres preguntas son 2, 9 y 5.

Entonces se le va a pedir que realice una serie de operaciones (las mostramos todas juntas en la siguiente imagen):
1.- que multiplique el número de hermanos y hermanas que tiene, incluido él o ella, por 2 [en este caso, 2 x 2 = 4];
2.- que le sume 3 [en este caso, 4 + 3 = 7];
3.- que multiplique el resultado por 5 [en este ejemplo, 7 x 5 = 35];
4.- a continuación, que sume a ese número, el número de hermanos y hermanas de su padre [en este ejemplo, 35 + 9 = 44];
5.- que multiplique el resultado por 10 [es decir, 44 x 10 = 440];
6.- y finalmente, que sume el número de hermanos y hermanas de la madre (incluida ella) [440 + 5 = 445]
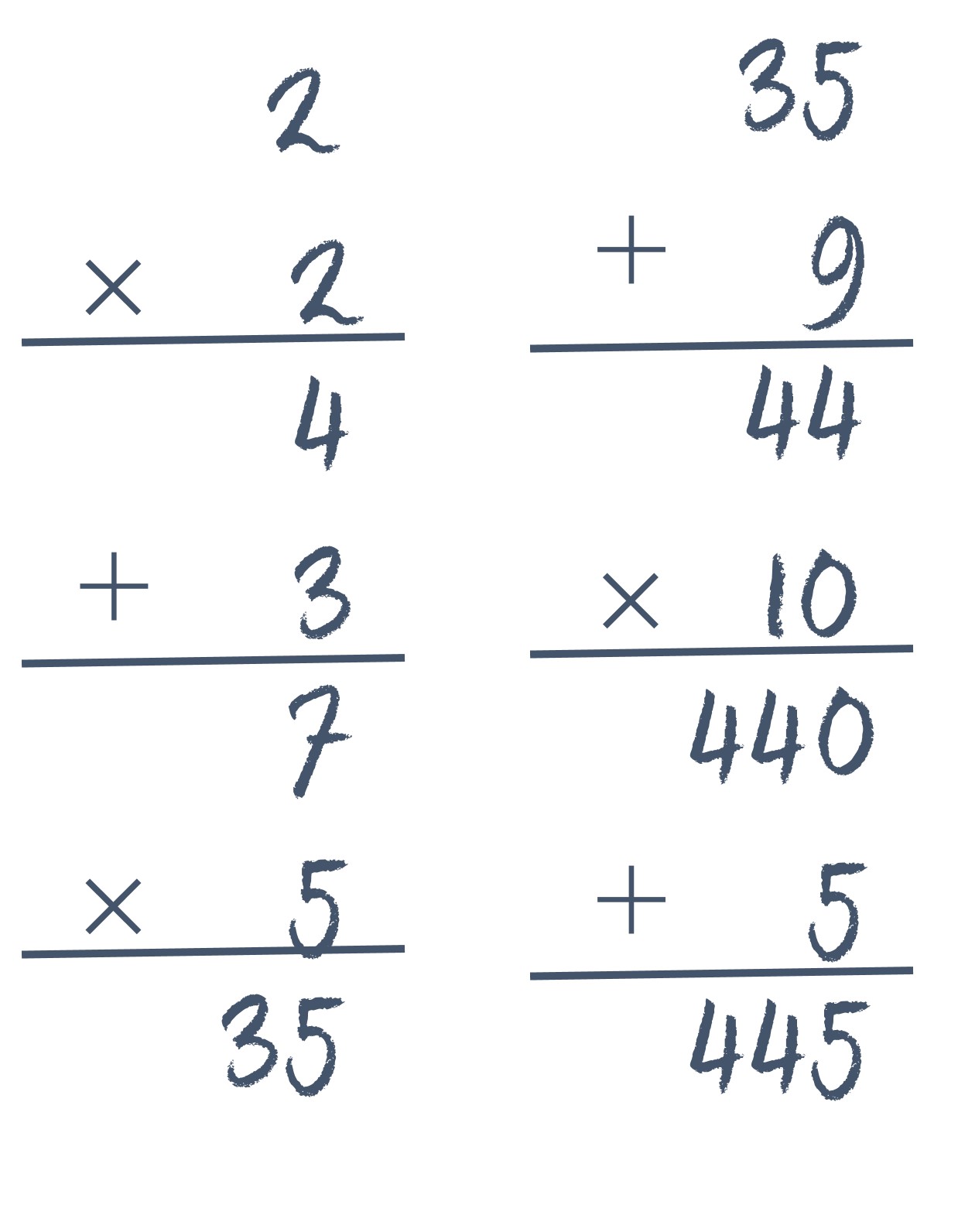
Una vez realizadas estas operaciones se le pide que diga en alto el resultado de las mismas, que es 445, y mientras se le da un poco de teatralidad a la situación, se resta mentalmente 150 al número que nos han proporcionado, en este ejemplo, 445 – 150 = 295.

La persona que realiza el truco tendrá, por tanto, en su cabeza el número 295 y, de nuevo con mucha teatralidad, dirá en alto, dándole la emoción de que está adivinando las respuestas que desconoce,
1.- que esa persona tiene 2 hermanos y hermanas (incluida ella);
2.- que su padre tiene 9 hermanos y hermanas (incluido él);
3.- y que su madre tiene 5 hermanos y hermanas (incluida ella).
Espero haberos proporcionado un poco de diversión con matemáticas. Hasta la siguiente entrada.
 Natural numbers / Números naturales (2015), del artista británico Andrew Crane. Imagen de la página web de Axisweb.
Natural numbers / Números naturales (2015), del artista británico Andrew Crane. Imagen de la página web de Axisweb.
Bibliografía
1.- Pedro Alegría, Magia por principios, Publidisa, 2008.
2.- Fernando Blasco, Matemagia, Temas de Hoy, 2007.
3.- Royal Vale Heath, Mathemagic, magic-puzzles-games with numbers, Dover, 1953.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo FUN WITH MATHS, diversión con matemáticas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Un kilogramo de novelas y matemáticas
- Personas famosas que estudiaron matemáticas: música y deporte
- Artistas que miran a las matemáticas
Esas tipografías que viven entre nosotros
Las fuentes tipográficas que vemos a nuestro alrededor, y que nos acompañan día a día, no solo son formas –las que unidas entre sí- develan un lenguaje- sino que también nos muestran algo más allá de su arquitectura, la cual contiene en sí el origen de su creación.
Las tipografías que nos rodean, son parte fundamental en nuestra comunicación, sus formas y usos responden a diversos contextos y estas nos develan informacion relevante que al momento de su creación, el diseñador tuvo en mente. Desde su etimología, podríamos definirla como la huella que queda al escribir, esto derivado de los tipos móviles que se utilizaban para grabar los textos en las imprentas. Curiosamente antes del siglo XX los números –también parte del diseño tipográfico- eran diseñados de manera separada al igual que otros signos. Algunas formas tipográficas las llevamos grabadas en nuestro imaginario colectivo.

Para entender de manera sencilla a que corresponde cada tipografía, debemos clasificarlas según sus formas, en cuatro grandes grupos:
- Aquellas que poseen serifa; formas que poseen un apéndice o remate en sus terminaciones.
- Las que no poseen serifa, también llamadas “palo seco”.
- Las caligráficas que emulan a la letra manuscrita o elaborada a mano.
- Las decorativas, que tienen como función llamar la atención del observador y se pueden construír a partir de diversos elementos.
Cada una de las tipografías demuestran en su estructura constructiva formas diversas que tienen como eje de inspiración la observación de lo que nos rodea y los objetos de uso cotidiano.
———————————-
Autora: Francisca Veas Carvacho (@franveasiluciencia), alumna del Postgrado de Ilustración Científica de la UPV/EHU – curso 2018/19
Artículo original: La tipografía de los números (1 y 2). Raúl Ibáñez, Cuaderno de Cultura Científica, 30 de diciembre de 2015 y de 13 de enero de 2016.
———————————-
“Ilustrando ciencia” es uno de los proyectos integrados dentro de la asignatura Comunicación Científica del Postgrado de Ilustración Científica de la Universidad del País Vasco. Tomando como referencia un artículo de divulgación, los ilustradores confeccionan una nueva versión con un eje central, la ilustración.
El artículo Esas tipografías que viven entre nosotros se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Asociación evolutiva entre la higuera común y las avispas
- #Naukas14: Knockouts entre nosotros
- La historia del bolígrafo más famoso del mundo
La incompatibilidad del efecto fotoeléctrico con la física clásica
 The Walt Disney Concert Hall en Los Ángeles (EE.UU.) está recubierto de paneles de acero inoxidable. ¿De qué modo depende el que emita electrones durante el día de que esté nublado? Fuente: Reza Rostampisheh / Unsplash
The Walt Disney Concert Hall en Los Ángeles (EE.UU.) está recubierto de paneles de acero inoxidable. ¿De qué modo depende el que emita electrones durante el día de que esté nublado? Fuente: Reza Rostampisheh / Unsplash
Los resultados experimentales del estudio del efecto fotoeléctrico se pueden resumir en las siguientes afirmaciones.
1. Un metal muestra un efecto fotoeléctrico si, y solo si, la luz incidente tiene una frecuencia superior a una determinada frecuencia umbral característica de ese metal, que simbolizaremos como f0.
2. Si la luz de una frecuencia dada f produce un efecto fotoeléctrico (por tanto, f > f0), la corriente fotoeléctrica desde la superficie es proporcional a la intensidad de la luz que incide sobre ella.
3. Si la luz de una frecuencia f dada libera fotoelectrones (f > f0) , la emisión de estos electrones es inmediata.
4. Las energías cinéticas de los electrones emitidos muestran un valor máximo, que es proporcional a la frecuencia f de la luz incidente (f > f0).
5. La energía cinética máxima de los fotoelectrones aumenta en proporción directa a la frecuencia de la luz que causa su emisión. La forma en que la energía cinética máxima de los electrones varía con la frecuencia de la luz incidente se muestra en la Figura 1 para distintos elementos. Para cada elemento los puntos de los datos experimentales caen en una línea recta. Cada recta comienza en una frecuencia distinta que se corresponde a las distintas frecuencias umbral. Todas las rectas tienen la misma pendiente.
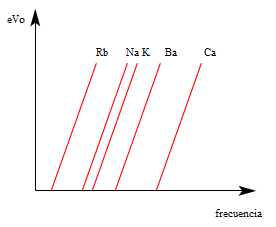 Figura 1. En esta figura eV0 se corresponde a la energía cinética máxima. Explicamos como se encuentra experimentalmente aquí, aunque nosotros la llamamos Vp (voltaje de parada) a lo que en esta figura llaman V0.
Figura 1. En esta figura eV0 se corresponde a la energía cinética máxima. Explicamos como se encuentra experimentalmente aquí, aunque nosotros la llamamos Vp (voltaje de parada) a lo que en esta figura llaman V0.
Salvo la 2, todas las afirmaciones son inexplicables usando la teoría electromagnética clásica de la luz. Veamos.
Empecemos por la 3: la emisión es inmediata. El intervalo de tiempo medido entre el instante en que la luz incide en la superficie metálica y la aparición de los electrones es como mucho 3·10-9 s y probablemente mucho menos. En algunos experimentos, la intensidad de luz utilizada fue extremadamente baja. En estos casos y de acuerdo con la teoría ondulatoria clásica de la luz, se deberían necesitar varios minutos para que un electrón acumulase la suficiente energía de esa luz para ser emitido. Pero incluso en estos casos de baja intensidad de la luz los electrones se emiten en cuanto la la luz incide en la superficie.
Sin duda la afirmación más sorprendente es la 1: hay una frecuencia umbral. Los fotoelectrones se emiten si la frecuencia de la luz incidente está por encima de esa frecuencia de umbral, sin importar lo débil que sea el haz de luz. Pero si la frecuencias de la luz está justo por debajo de la frecuencia umbral, no se emiten electrones, no importa lo grande que sea la intensidad del haz de luz. La teoría ondulatoria clásica de la luz no puede explicar la existencia de una frecuencia umbral. No parece haber ninguna razón desde el punto de vista clásico por la cual un haz de alta intensidad de baja frecuencia no debería producir fotoelectricidad si la radiación de baja intensidad de mayor frecuencia puede producirla.
La energía cinética máxima no depende de la intensidad de la luz incidente, como requeriría la teoría ondulatoria clásica de la luz, sino de la frecuencia (afirmación 4). La teoría clásica tampoco podría explicar por qué la energía cinética máxima de los fotoelectrones aumenta directamente con la frecuencia de la luz (afirmación 5), pero es independiente de la intensidad.
En definitiva, los científicos estaban desconcertados. La teoría ondulatoria clásica de la luz funcionaba perfectamente bien en todas las circunstancias conocidas en la época, pero no en el efecto fotoeléctrico. ¿Cómo era posible que un tren de baja intensidad de ondas de luz, que incide sobre una enorme cantidad de átomos en la superficie de un metal, pudiese concentrar, en un intervalo de tiempo muy corto, suficiente energía en un electrón como para que el electrón abandonase el metal?
Era necesario un nuevo concepto revolucionario sobre la estructura de los átomos y cómo interactuaban con la luz. Tan revolucionaria era la idea necesaria que la tenía que proponer alguien que no tuviese mucho que perder si decía un disparate…como un ingeniero de tercera de una oficina de patentes suiza. Ese ingeniero se llamaba Albert Einstein.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo La incompatibilidad del efecto fotoeléctrico con la física clásica se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El desconcertante efecto fotoeléctrico
- Física clásica
- Física de las ondas estacionarias: frecuencia fundamental y sobretonos
La historia del bolígrafo más famoso del mundo
Si nos paramos a pensar cuál es el bolígrafo que más hemos visto o utilizado a lo largo de nuestras vidas, muy probablemente la respuesta sea común a todos. Pensamos en uno de los más baratos del mercado, fácil de usar y, como solíamos pensar de pequeños, de tinta casi inagotable: el bolígrafo BIC. Este bolígrafo es el más venido del mundo y está presente en 160 países.
 Imagen: Línea de tiempo indicando las principales fechas en la historia del bolígrafo. (Ilustración: Paula Martín)
Imagen: Línea de tiempo indicando las principales fechas en la historia del bolígrafo. (Ilustración: Paula Martín)
Para llegar hasta el bolígrafo que conocemos hoy en día hicieron falta una numerosa serie de patentes a lo largo de los siglos XIX y XX que desarrollaron bolígrafos de similar funcionamiento. La característica común a todos es la pequeña bola en la punta que permite distribuir la tinta a lo largo del papel. Fue el diseño del inventor húngaro László Bíró el que ha llegado a nuestros días a través del del francés Marcel Bich y su fábrica de objetos de escritura en Clichy (Francia).
El bolígrafo BIC tiene una gran historia tras de sí, sin embargo, aquello que prevalece en nuestra memoria cada vez que pensamos en él es un simple eslogan, un eslogan capaz de retrotraernos al pupitre de nuestra escuela: “BIC Naranja escribe fino, BIC Cristal escribe normal”.
———————————-
Autora: Paula Martín Rodríguez (@paulailustra), alumna del Postgrado de Ilustración Científica de la UPV/EHU – curso 2018/19
Artículo original: Historia del bolígrafo. Eduardo Angulo, Cuaderno de Cultura Científica, 14 de mayo de 2018.
———————————-
“Ilustrando ciencia” es uno de los proyectos integrados dentro de la asignatura Comunicación Científica del Postgrado de Ilustración Científica de la Universidad del País Vasco. Tomando como referencia un artículo de divulgación, los ilustradores confeccionan una nueva versión con un eje central, la ilustración.
El artículo La historia del bolígrafo más famoso del mundo se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Los científicos que miraban fijamente a las cabras
¿Por qué las cabras?, se preguntarán. ¿Y por qué no?, les respondo yo. ¿Acaso no son las cabras un animal interesante, simpático e importante en nuestras vidas, lo suficiente como para que les dediquemos un ratito de nuestras ajetreadas vidas y así aprendamos algo más sobre ellas? Reconozco que mi interés por las cabras viene de lejos, de una visita escolar a una granja escuela en la que uno de estos animales se zampó de dos masticadas la etiqueta de cartulina en la que ponía mi nombre y un dibujito identificativo (una zanahoria, siempre me caía una zanahoria, por aquello del pelirrojismo).
El caso es que aquella cabra o cabrito, no recuerdo, se comió mi etiqueta y me metió un susto considerable pero sobre todo me dejó muy preocupada por su salud. Comiesen las cabras lo que comiesen, la cartulina no me parecía una opción saludable para el animal. El responsable de los animales al que se lo conté muy preocupada me respondió, divertido, que no me preocupase, que las cabras comían cualquier cosa y nunca les pasaba nada. Recuerdo que me lo creí tirando a poco, pero si aquel adulto que cuidaba de las cabras no parecía inquietarse, qué podía hacer yo.
 Imagen: Wikimedia Commons
Imagen: Wikimedia Commons
Cómo se las apañan para comer así y no morir en el intento
Les cuento esto porque hace pocos días la revista Mammalian Biology publicaba un pequeño estudio que ha analizado cómo la estructura digestiva de las cabras les ayuda, al menos en parte, a procesar todas las cosas extrañas que les da por comer, principalmente tierra y gravilla (aunque mi cartulina también andará por ahí) sin que eso les destroce la boca y los dientes.
El estudio es modesto: participaron 28 cabras a las que durante 6 meses se les alimentó con una dieta consistente en parte en distintas cantidades de arena. A los 3 meses de empezar se sometió a los animales a un TAC y al final fueron sacrificadas para analizar el contenido de sus tractos digestivos. Esto reveló que la arena que habían ido tragando no estaba distribuida de forma homogénea por sus tripas, sino que se había ido acumulando en las cavidades inferiores de sus estómagos.
Las cabras, como las vacas y otros rumiantes, tienen un estómago con cuatro cavidades que tienen diferentes funciones. Las cavidades superiores acogen grandes cantidades de comida que van regurgitando poco a poco para volver a ser masticadas (de ahí lo de rumiantes…), mientras que las cavidades inferiores reciben pequeñas cantidades de alimento que son digeridas directamente.
Según los autores, debido a que la arena va principalmente directa a la zona inferior del estómago se expulsa con las heces y no es regurgitada de vuelta a la boca para ser masticada después, lo cual ayuda a los animales a evitar un impacto sobre sus dientes y su salud. Es decir, que los estómagos superiores son a las cabras lo que los barreños y escurridores son para nosotros: un sistema de lavado de verduras y alimentos que nos evita muchos problemas.
Me pregunto cómo procesarían mi cartulina los estómagos de aquella cabra…
 Imagen: Wikimedia Commons
Imagen: Wikimedia Commons
Las cabras aprenden, pero no con el ejemplo
Llegados a este punto, sigamos hablando de cabras, un animal asociado a la locura en los dichos populares y que sin embargo ha demostrado en varias investigaciones y experimentos una inteligencia asombrosa, al nivel de los perros en algunos aspectos.
Hay algunas señales obvias para quienes las observan de que su inteligencia está por encima de la de otros animales con los que suelen compartir granjas: viven en grandes grupos sociales lo que supone entablar relaciones de colaboración y asociación, son capaces de alcanzar alimentos que se encuentran en lugares intrincados, viven muchos años y se sirven de recuerdos y, a pesar de que, como ya hemos dicho, son capaces de comer cualquier cosa, también son muy selectivas en lo que a sus alimentos se refiere, comiendo solo las hojas más verdes y tiernas de arbustos llenos de espinas.
Para poner a prueba esta inteligencia que intuían, en 2014 científicos de la Universidad Queen Mary de Londres y del Instituto de Ciencias de la Agricultura de Suiza decidieron poner a las cabras a prueba con el desafío de la fruta artificial, un test desarrollado en principio para realizarlo en primates. Para llevarlo a cabo, los investigadores colocaron unas piezas de fruta dentro de una caja que solo se podía abrir resolviendo un puzzle. En este caso, las cabras tenían que utilizar los dientes para tirar de una cuerda para activar una palanca y después levantar la palanca. Cuando realizaban las tareas correctamente y en orden, una pieza de fruta caía de la caja a modo de recompensa.
Los resultados fueron interesantes y, además, tienen cierta gracia. Trataron de enseñar a 12 cabras a llevar a cabo la prueba, de las cuales 9 lo consiguieron en solo cuatro intentos. De las otras tres, dos trataron de pasarse de listas y utilizaron los cuernos para intentar abrir la caja sin tanto lío, por lo que fueron eliminadas de la prueba. La otra no había mostrado señales de ir pillando la dinámica después de 22 intentos, así que la descartaron por considerarla un caso perdido.
Una vez que las nueve brillantes alumnas habían descansado durante 10 meses, se les pusieron delante las mismas cajas con el mismo mecanismo para comprobar cuánto tardaban en recordar los movimientos necesarios para abrirlas. Todas ellas consiguieron hacerlo en menos de un minuto, algo que se puede considerar una prueba de su excelente memoria a largo plazo.
Sin embargo lo que consideramos inteligencia es algo muy difícil de definir y medir, y ser sobresaliente en un aspecto no quiere decir serlo igual en todos. En otro experimento, los investigadores permitieron a cabras no entrenadas observar a sus congéneres ya aprendidas mientras estas accedían a sus sabrosos premios, pero eso no les supuso ninguna ventaja a la hora de llevar a cabo las tareas ellas mismas respecto a otras cabras que no habían observado previamente el proceso.
Esto sería una señal de que las cabras necesitan aprender los trucos y procesos por sí mismas, ya que han perdido, o nunca han tenido, esa habilidad social en concreto, la de aprender observando a sus iguales, que sí tienen otros animales como los delfines o los primates.
 Imagen: Wikimedia Commons
Imagen: Wikimedia Commons
Sonríe, hay cabras mirando
Pero que no se entienda esto como que no son buenas observadoras, sagaces e incluso empáticas, ya que algunos estudios han demostrado también que son capaces de distinguir las emociones en las caras de los seres humanos y que de hecho prefieren interaccionar con personas felices antes que con personas enfadadas, según publicaron en 2018 de nuevo científicos de la Universidad Queen Mery de Londres.
Para analizar esta cuestión, los autores mostraron a 20 animales distintas imágenes de caras humanas no familiares con emociones que mostraban alegría o enfado y observaron que las imágenes de caras felices obtenían de forma consistente una mayor interacción por parte de las cabras que las miraban, se acercaban a ellas y las olisqueaban.
Que una cabra sepa cuando un humano está contento o cabreado puede parecer una anécdota chistosa pero de hecho tiene varias implicaciones interesantes y sorprendentes. Por un lado, puede tener importancia a la hora de manejar el ganado de forma menos estresante para los animales. Por otro, sugiere que no solamente los animales que han sido entrenados individualmente, como perros o caballos, son capaces de relacionarse emocionalmente con los humanos, sino que otros también pueden desarrollar esas capacidades.
Referencias:
Goats prefer positive human emotional facial expressions – Royan Society Open Science
Goats excel at learning and remembering a highly novel cognitive task – Frontiers in sociology
The rumen washes off abrasives before heavy-duty chewing in ruminants – Mammalian Biology
Sobre la autora: Rocío Pérez Benavente (@galatea128) es periodista
El artículo Los científicos que miraban fijamente a las cabras se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Científicos, animalistas y el uso de animales para investigación
- ¿Son arrogantes los científicos?
- Artistas científicos
¿Desde cuándo nos repite el ajo?
El ajo es hoy día un producto esencial de la cocina cotidiana. ¿Pero de dónde viene? ¿Y desde cuándo nos acompaña?
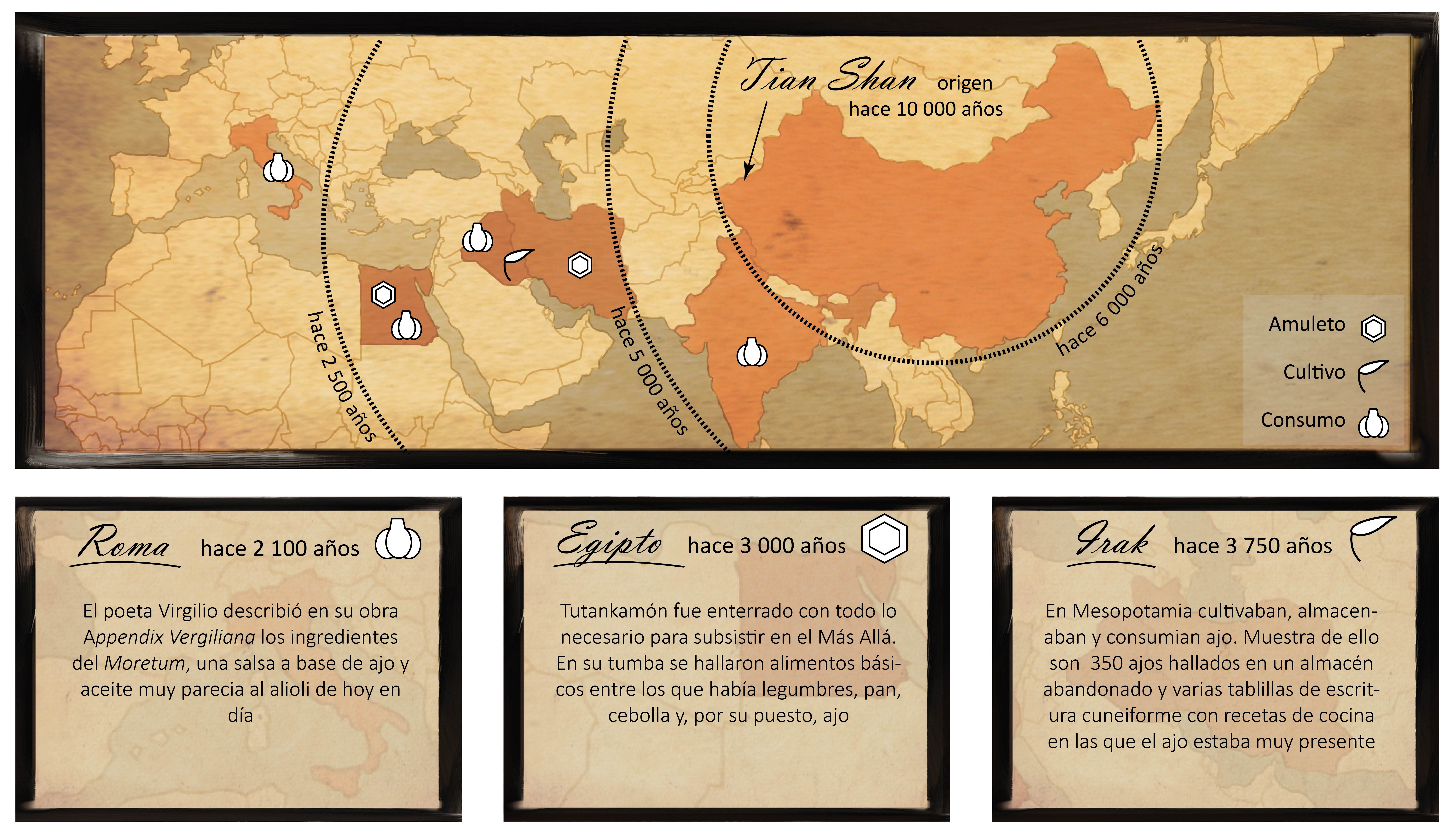 Imagen: Tras las huellas del ajo. Mapa de la expansión de la domesticación del ajo y clasificación de los diferentes hallazgos según el uso. (Ilustración: Iratxe Rojo)
Imagen: Tras las huellas del ajo. Mapa de la expansión de la domesticación del ajo y clasificación de los diferentes hallazgos según el uso. (Ilustración: Iratxe Rojo)
La domesticación del ajo se remonta a hace 10.000 años con el comienzo de la agricultura en el Neolito. Entonces se usaban especies silvestres, entre ellas nuestro ajo, del que hoy solo quedan variedades cultivadas. Se cree que la domesticación comenzó en las montañas de Tian en el Turkestán. De ahí se extendió hasta la costa del Pacífico hace 6.000 años y a la India hace 5.000, llegando a Europa hace 2.500 años por Grecia y Roma.
Algunas muestras de su expansión son los dientes de ajo hallados en tumbas de 5.000 años de antigüedad en Irán y en la tumba de Tutankamón (Egipto), las semillas incrustadas en herramientas y dentaduras de hace 5.000 años descubiertas en India, los registros de cultivo de las antiguas civilizaciones y numerosas recetas, como la del Moretum antecesor del alioli descrita hace 2.000 años en Roma.
Es innegable pues que el repetitivo ajo es apreciado; tanto que ha viajado con nosotros en el tiempo y el espacio desde hace 10.000 años hasta hoy, extendiéndose desde Asia Central por casi todo el Mundo.
Referencias consultadas:- Mascort, Maite (2018). El tesoro de Tutankamón: la vida del rey en el Más Allá. National Geographic España. (Fecha de consulta: 3/2019)
- Wikipedia: Moretum. (Fecha de consulta: 3/2019)
———————————-
Autora: Iratxe Rojo Bartolomé, alumna del Postgrado de Ilustración Científica de la UPV/EHU – curso 2018/19
Artículo original: Ingredientes para la receta: el ajo. Eduardo Angulo, Cuaderno de Cultura Científica, 10 de abril de 2017.
———————————-
“Ilustrando ciencia” es uno de los proyectos integrados dentro de la asignatura Comunicación Científica del Postgrado de Ilustración Científica de la Universidad del País Vasco. Tomando como referencia un artículo de divulgación, los ilustradores confeccionan una nueva versión con un eje central, la ilustración.
El artículo ¿Desde cuándo nos repite el ajo? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- En el mar, allí donde todo comienza
- Metamorfosis criogénica de la rana del bosque
- Un ornitisquio emplumado
La civilización ha transformado la especie humana
 Foto: Thomas Tucker / Unsplash
Foto: Thomas Tucker / Unsplash
La selección natural opera a través del éxito reproductor de los individuos. Los rasgos hereditarios de quienes dejan más descendencia son los que, andando el tiempo, serán más abundantes. Y las razones para ello no son en absoluto evidentes. Las transformaciones que se produjeron tras la adopción de la agricultura y la ganadería, entre las que cabe incluir el cambio de la alimentación y la vida en núcleos estables de población de tamaño creciente, por ejemplo, ha tenido efectos evolutivos en nuestra especie. O sea, la frecuencia de determinadas variantes genéticas en las poblaciones humanas ha aumentado, mientras que la de otras ha disminuido. Por otro lado, ciertas funciones biológicas se han enriquecido genéticamente -en la población hay más variantes implicadas en ellas-, mientras que otras se han empobrecido.
En una investigación reciente se han comparado los genomas de individuos que vivieron en Europa hace entre 5.500 y 3.000 años con los de europeos actuales. En el estudio han identificado las funciones cuyo sustrato genético ha sufrido más cambios (mutaciones), dando lugar, por lo tanto, a más variantes, y también aquellos en los que ha ocurrido lo contrario. Ha aumentado el número de variantes genéticas implicadas en el metabolismo de carbohidratos, los mecanismos de desintoxicación, el transporte de sustancias a través de membranas, el sistema de defensa inmunitaria, la señalización celular, la actividad física y la percepción olfativa. Y han disminuido las relacionadas con la generación de óvulos -y por lo tanto, en ese aspecto, con la fisiología reproductiva femenina-, y con un mecanismo neurológico denominado potenciación a largo plazo. Veamos, a modo de ejemplo, algunas de estas funciones en su contexto.
Que se hayan enriquecido genéticamente las relacionadas con el metabolismo de carbohidratos tiene que ver, seguramente, con la expansión de la agricultura y la ganadería. La producción de cereales provocó un aumento de la proporción de carbohidratos en la dieta y la ganadería propició el consumo de leche por adultos, gracias a la mutación que les permite retener la capacidad para digerir lactosa, que es un azúcar, al fin y al cabo.
Algo similar ha ocurrido con las variantes implicadas en el funcionamiento del sistema inmunitario. Las altas densidades de población y, en especial, la convivencia próxima con animales domésticos generó condiciones propicias para la proliferación de parásitos patógenos. No es de extrañar, pues, que el sistema inmunitario de los pueblos agricultores y ganaderos haya adquirido capacidades de las que carecía el de cazadores-recolectores, o haya reforzado ciertos aspectos de su funcionamiento como consecuencia de esas condiciones.
La potenciación a largo plazo es un mecanismo que intensifica la transmisión de señales entre neuronas, por lo que está implicado en el aprendizaje y la memoria. Que ese mecanismo haya experimentado una reducción de variantes en su sustrato genético quizás esté relacionado con la importancia creciente del aprendizaje y la transmisión cultural a partir del asentamiento en poblaciones y la emergencia de lo que conocemos como civilización. Aunque ignoramos cómo es esa relación.
Antes se pensaba –y todavía hay quien lo cree- que la civilización, con sus comodidades y su capacidad para amortiguar los efectos de la intemperie sobre nuestro organismo, ha detenido la evolución del linaje humano e, incluso, que al desaparecer las presiones selectivas que actuaron en la prehistoria, nos hemos ido convirtiendo en seres cada vez más defectuosos, pues los menos aptos cada vez sobreviven en mayor medida; y pueden además dejar descendencia. Pero las cosas no son así, sino, como suele ocurrir, más complejas. Porque las presiones selectivas no desaparecen; cambian. Y con ellas, también nuestra naturaleza se transforma.
Fuente: Evgeny Chekalin et al (2019): Changes in Biological Pathways During 6,000 Years of Civilization in Europe. Molecular Biology and Evolution, Vol 36 (1): 127–140
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo La civilización ha transformado la especie humana se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Apocalipsis alienígena: ¿puede alguna civilización sobrevivir a un cambio climático?
- Una proteína humana para potabilizar agua
- Activa Tu Neurona – Evolución Humana
Palo seco

Deborah García Bello, las tipografías y pi. A palo seco.
Quizás sea el número más famoso de la historia. Lo cierto es que el número Pi, representado por la letra griega π, es una de las constantes matemáticas más importantes que existen en el mundo, estudiada por el ser humano desde hace más de 4.000 años. La fascinación que ha suscitado durante siglos es tal que el popular número cuenta con su propio día en el calendario, así el mes de marzo se celebra el Día de Pi en todo el planeta.
Este evento internacional vino de la mano del físico estadounidense Larry Shaw, quien lanzó en 1988 la propuesta de celebrar esta efeméride. La forma en la que se escribe el 14 de marzo en inglés y euskera coincide con los tres primeros dígitos de la famosa constante matemática. (3-14 martxoaren 14 en euskara / 3-14 march, 14th en inglés) y además, la celebración coincide con la fecha del nacimiento de Albert Einstein. En 2009, el congreso de EEUU declaró oficialmente el 14 de marzo como el Día Nacional de Pi.
Actualmente, el Día de Pi es una celebración mundialmente conocida que sobrepasa el ámbito de las matemáticas. Este número irracional, que determina la relación entre la longitud de una circunferencia y su diámetro, concierne a múltiples disciplinas científicas como la física, la ingeniería y la geología, y tiene aplicaciones prácticas sorprendentes en nuestro día a día.
Este 2019 nos unimos de nuevo al festejo con el evento BCAM–NAUKAS, que se desarrolló a lo largo del 13 de marzo en el Bizkaia Aretoa de UPV/EHU. BCAM-NAUKAS contó durante la mañana con talleres matemáticos para estudiantes de primaria y secundaria y durante la tarde con una serie de conferencias cortas dirigidas al público en general.
Este evento es una iniciativa del Basque Center for Applied Mathematics -BCAM, enmarcada en la celebración de su décimo aniversario, y de la Cátedra de Cultura Científica de la Universidad el País Vasco.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Palo seco se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- E-pi-logo (después de esto, mi carrera ha muerto)
- El efecto Talbot: tejiendo alfombras con luz
- Sigue al conejo blanco
Dietas de adelgazamiento
La Facultad de Ciencias de Bilbao comenzó su andadura en el curso 1968/69. 50 años después la Facultad de Ciencia y Tecnología de la UPV/EHU celebra dicho acontecimiento dando a conocer el impacto que la Facultad ha tenido en nuestra sociedad. Publicamos en el Cuaderno de Cultura Científica y en Zientzia Kaiera una serie de artículos que narran algunas de las contribuciones más significativas realizadas a lo largo de estas cinco décadas.

Todos hemos oído hablar de ellas. La del Dr. X, la del Dr. Y, la del pomelo, la del pepino… La lista sería interminable. Todas garantizan una rápida pérdida de peso sin ningún sacrificio. Por supuesto, el que haya tantas “dietas milagro” tiene una explicación sencilla: son todas falsas.
 Foto: Jan Sedivy / Unsplash
Foto: Jan Sedivy / Unsplash
¿Por qué fallan? Hay dos motivos por los cuales las “dietas milagro” no funcionan nunca. Uno es que, muchas veces, las dietas no tienen ningún fundamento racional: es como si quisiéramos curarnos el dolor de muelas subiendo en el ascensor tres veces al tercer piso, en jueves. El segundo es que, otras tantas veces, aun cuando a largo plazo pudieran funcionar, son tan poco apetecibles que nadie es capaz de mantenerlas por mucho tiempo.
El negocio del sobrepeso. El abandono de las dietas estrafalarias me lleva a otro tema muy relacionado: el negocio (fraudulento) del adelgazamiento. Vivimos en una sociedad en la que uno puede ser cualquier cosa… menos gordo. La publicidad, dirigida sobre todo a adolescentes, se encarga de recordárselo a todas horas. Se forma así un círculo diabólico en el que: (a) con razón o sin ella, uno se ve gordo, (b) comienza una dieta que no la soportaría Robinson Crusoe aunque no tuviera otra comida en su isla, (c) la abandona, por razones obvias, y (d) se culpabiliza por su “falta de voluntad”. Hemos pasado de tener un supuesto sobrepeso a tener una bonita combinación de sobrepeso y falta de autoestima: gran éxito. Pero, claro está, ésta es la base, más bien el círculo vicioso, en el que se apoya el mercado multimillonario derivado de supuestas obesidades y muy humanas debilidades.
¿Es malo estar gordo? Desgraciadamente, el negocio fraudulento del adelgazamiento tiene bastante razón en una cosa: la obesidad es una enfermedad, y es un agente que causa o empeora otras enfermedades. Ahora bien, todo es cuestión de grados, no es lo mismo un sobrepeso ligero que una obesidad mórbida, y cuál sea nuestro problema concreto lo podemos averiguar fácilmente midiéndonos en casa y pesándonos en una farmacia. Y el principal problema de la obesidad no es que nos vaya a quedar mal el traje de baño en la playa.
¿Por qué hay tantos gordos? Los biólogos suelen decir que en biología nada se entiende si no es a la luz de la teoría de la evolución. La obesidad no es una excepción. Desde que la vida existe sobre la tierra (unos 4.000 millones de años) el alimento ha sido la principal limitación para el crecimiento de las especies. En otras palabras, de toda la vida, lo normal ha sido pasar hambre. Sólo hace unas pocas generaciones (¿100 años?) en una región privilegiada del planeta, el llamado primer mundo, se da el fenómeno inaudito de una población que, en el caso de los humanos, tiene asegurada una comida caliente tres veces al día. Hasta ahora, se comía cuando había, que eran pocas veces. En esas condiciones sobrevivían los que, por azar, llevaban los genes que les permitían almacenar energía en forma de grasa cuando comían. Hoy, la inmensa mayoría de los miembros de nuestra sociedad actual son herederos de aquéllos supervivientes, y mantienen intactos sus genes almacenadores de grasa. Ésta es la sencilla verdad, no hay que darle más vueltas al asunto y, sobre todo, no hay que culpabilizarse.
Cambiar de vida. Si, primero, objetivamente necesitamos adelgazar, y, segundo, queremos hacerlo, no nos basta con seguir una u otra dieta. Nuestra tarea es mucho más difícil: tenemos que luchar contra nuestros genes. Tenemos que corregir una deriva de millones y millones de años de evolución. ¿Es imposible? No, pero hay que acertar con la dieta. Para los antiguos griegos, la dieta no era sólo un régimen de comidas, sino todo un sistema de vida. Eso es lo que tenemos que hacer para adelgazar, seguir la dieta adecuada, y no solo la de comidas. Y así, no esperaremos adelgazar en un mes, ni en tres. Todo esto es un proceso a largo plazo. Un objetivo razonable es perder un kilo al mes. Al cabo de un año, serán doce kilos, que no está mal.
Adelgazamiento y termodinámica. La termodinámica es una parte importante de la física, pero la verdad es que se puede entender bastante bien si uno se la imagina como una especie de contabilidad, solo que, en vez de ser una contabilidad de euros, es una contabilidad de calorías. Para entender esta analogía, hay que imaginar nuestro cuerpo como una libreta de ahorros, solo que la cuenta no está en euros, sino en calorías. Y, cosa rara, queremos tener cada vez más euros, pero cada vez menos calorías. Salvando esto, el mecanismo es el mismo. Para tener muchos euros, debemos ingresar mucho, y/o sacar poco. Para tener pocas calorías, debemos sacar muchas, y/o meter pocas. Es igual que metamos cien euros por la mañana o por la noche. En billetes de veinte, o de diez. Es igual que los saquemos en día par o impar. A fin de mes, el estado de nuestra cuenta dependerá de la suma de los ingresos menos la suma de los gastos. Y de nada más. En física, esto se llama el “primer principio de la termodinámica”, y es una ley que no conoce excepción alguna. Así pues, olvídese el lector de desayunar mucho o poco, comer más que cenar o viceversa, una comida o cinco, etc. Solo cuenta el saldo de la libreta a fin de mes.
La dieta. No digo “una dieta”, ni “las dietas”, digo “la dieta”. Con pequeños ajustes, como es natural, pero “la dieta”. Y, ¿en qué consiste esa dieta tan universal? Pues, en comer menos. Bastante menos, e incluso mucho menos. Ojo: aquí no se engaña a nadie, ya hemos dicho que para adelgazar (permanentemente, aquí no estamos hablando de la Operación Bikini), hay que CAMBIAR DE VIDA. Y lo esencial en esa nueva vida es comer significativamente menos. Por poner una cifra, variable según los casos, un 40% menos. No menos de unas cosas, o de otras, sino menos de todo. Bueno, dirá el lector, también podré seguir empapuzándome si de una vez me pongo a hacer ejercicio. Pues, no señor. No tenemos hueco aquí para explicar los detalles, o más bien para hacer las cuentas de la termodinámica del ejercicio, pero algo así como una hora diaria de ejercicio moderado (que es el objetivo realista cuando es para toda la vida) no va a aumentar significativamente el número de calorías que salen de la hucha. Paradójicamente, los buenos dietistas saben que el ejercicio es esencial en el adelgazamiento, pero no tanto por la energía que consume sino por los efectos relajantes sobre el organismo, que compensan el stress de la restricción calórica. En fin, por si no quedaba claro, comer menos y hacer más ejercicio. No queda otra.
A mí no me funciona. Pues algo falla con Vd., y ese algo no es el primer principio de la termodinámica. A ver si lo hemos entendido. Si Vd. come menos (no un poco menos) y hace ejercicio (nada del otro jueves), va a adelgazar. Y si no adelgaza, tendrá que comer aún menos. Tenga la completa seguridad de que su sobrepeso, no digamos obesidad, se debe exclusivamente a que come mucho más de lo que necesita.
Por supuesto que el procedimiento es costoso. Pero piense en dos cosas. La primera, es el ÚNICO modo de adelgazar. Y la segunda, mucho antes de lo que se piensa, quizá en unas pocas semanas, Vd. se habrá habituado a su nueva vida, y no le costará nada mantenerla. Y al cabo de seis meses, o de un año, comprobará que el esfuerzo ha valido la pena. ¡ÁNIMO!
Pues Fulanito come como una lima, y no engorda. La vida es injusta, a veces. El pobre Fulanito carece de los genes de almacenamiento de grasas. Si se embarcan Fulanito y Vd., y su balsa se extravía en el océano, y se pasan dos meses a la deriva, lo probable es que sólo sobreviva uno de los dos, y, créame, salvo antropofagia, el superviviente no será Fulanito, sino Vd., y sin sus lorcitas.
Sobre el autor: Félix M. Goñi es catedrático en el Departamento de Bioquímica y Biología Molecular de la Facultad de Ciencia y Tecnología de la UPV/EHU.
El artículo Dietas de adelgazamiento se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La adherencia, clave en el seguimiento de las dietas
- Las dietas detox ni desintoxican ni adelgazan
- 50 años de secretos: la era de la criptografía moderna
Cómo nos ayuda la ciencia a tomar decisiones correctas
![]()
Jose Luis Arroyo Barrigüete y Francisco Borrás Palá
 Unsplash, CC BY-SA
Unsplash, CC BY-SAImaginemos que, tras diez años trabajando en una empresa, otra compañía nos llama y nos hace una oferta de trabajo. Esta tiene ventajas respecto a nuestras condiciones actuales pero, como en toda decisión, hay riesgos asociados a la incertidumbre. ¿Me llevaré bien con los compañeros? ¿Tendré una buena relación con mi nuevo jefe? ¿Encajaré en la cultura corporativa de esta compañía?
Ahora supongamos que alguien nos dijera cuál es la probabilidad que tenemos de equivocarnos. Por ejemplo que, en caso de aceptar la oferta, tenemos una probabilidad del 0,7 % de estar tomando la decisión incorrecta. Dicho de otra forma: tenemos un 99,3 % de probabilidad de tomar la decisión adecuada. En estadística, a esto lo llamamos p-valor.
En ciencia es muy frecuente utilizar el contraste de hipótesis. La idea es partir de una hipótesis nula (H₀), que no es sino el statu quo, la situación actual. En nuestro ejemplo, permanecer en la empresa en la que estamos. Frente a ella se contrasta la hipótesis alternativa (H₁), es decir, una idea contraria a la anterior. En nuestro caso, cambiar de trabajo.
Si encontramos una fuerte evidencia empírica en contra de la hipótesis nula, decimos que la rechazamos y, por tanto, aceptamos la alternativa. Siguiendo con nuestro ejemplo, esta evidencia sería lo que yo pudiera llegar a saber, después de investigarlo, sobre las mejores condiciones de trabajo que nos ofrecen.
Pero, ¿qué significa “fuerte evidencia empírica”? Para responder a esa pregunta, tenemos un concepto muy útil llamado p-valor. Este es la probabilidad que tenemos de equivocarnos si rechazamos la hipótesis nula con la información (evidencia empírica) de la que disponemos.
Cuanto más pequeño sea el p-valor, más improbable es que nos estemos equivocando al rechazar la hipótesis nula. Dicho de otro modo, más probable es que estemos acertando. En nuestro ejemplo, cuanto más pequeño sea el p-valor, más probable es que cambiar de trabajo sea una decisión adecuada.
Entonces, ¿qué p-valor necesitaría yo para cambiar de trabajo? ¿Cuánto riesgo estaría dispuesto a asumir? ¿Un 10 %? ¿Quizá un 5 %? ¿O se sentiría más cómodo con un 1 %? Estos son, de hecho, valores típicos usados en ciencia. Usaremos uno u otro en función del riesgo que estemos dispuestos a asumir.
Estos porcentajes son valores subjetivos que dependen del individuo que toma la decisión y de las consecuencias de la misma. En cambio, el p-valor es un dato objetivo que calculan todos los programas informáticos de estadística a partir de los datos de una muestra. Aparece de forma mágica como un resultado, aunque detrás hay un proceso de cálculo.
Si el p-valor se encuentra por debajo del nivel de riesgo, rechazaremos H₁. De hecho, los ordenadores habitualmente facilitan todavía más la decisión poniendo un asterisco al lado del p-valor si es menor que el 10 %, dos si es menor que el 5 % y tres si es menor que el 1 %.
En nuestro ejemplo de la oferta de trabajo, con un p-valor del 0,7 % los tres asteriscos nos dejarían bastante tranquilos respecto a aceptar la propuesta, salvo que seamos de esas personas que no se arriesgan nunca.
En el año 2314…
Ana sale de casa con sus gafas cuantrónicas de realidad aumentada, y tras llegar a la oficina en su aerodeportivo, se plantea si tomar un segundo café antes de entrar, o bien subir directamente a su despacho para comenzar la jornada. Sus gafas captan el pensamiento, y tras apenas unos microsegundos de cálculo, proyectan en el visor tridimensional el siguiente mensaje:
H₀ : subir directamente al despacho, como es habitual.
H₁ : tomar un segundo café.
P-valor: 0.841
Ana, sorprendida por un p-valor tan alto, decide subir directamente y olvidar la idea del café, pero se pregunta a qué se deberá tal cifra. Solo mientras asciende hasta la planta 159 en el ascensor gravítico cae en la cuenta de que, apenas en media hora, tiene una importante reunión que debe preparar. De haber tomado ese café, probablemente no habría tenido el tiempo suficiente para hacerlo. Esa es la información de que disponían sus gafas cuantrónicas, que no se olvidan de nada.
 Shutterstock
ShutterstockTras una intensa jornada, Ana recibe una holo-llamada de Bernardo, que la invita a cenar esta noche. Ana, tras haber terminado una relación previa hace varios meses, tiene dudas sobre si está interesada en la proposición. Las gafas, captando sus pensamientos, proyectan un nuevo mensaje:
H₀ : cenar sola en casa, como es habitual.
H₁ : aceptar la proposición de Bernardo y cenar con él.
P-valor: 0.053
Por segunda vez en el día, Ana queda sorprendida por la información que le proporcionan sus gafas. ¿A qué se debe un p-valor tan bajo? ¿Tan seguro está su micro-ordenador de que debe aceptar la propuesta de Bernardo? ¿Solo una probabilidad del 5,3 % de equivocarse si la acepta? Ana reflexiona unos segundos y recuerda que las gafas han sido capaces de buscar todo el rastro que ha ido dejando Bernardo en las redes sociales en un instante, muchísimo menos tiempo que el que hubiera empleado ella. Entonces le responde…
Volviendo al presente
¿Qué sucedería si dispusiésemos de las gafas cuantrónicas de Ana? Ante cualquier pequeña decisión, estas procesarían toda la información disponible y nos facilitarían de inmediato la probabilidad de equivocarnos. No cabe duda de que, por una parte, nos equivocaríamos mucho menos. Por otra, ¡la vida sería mucho más aburrida!
Como, afortunadamente, aún estamos muy lejos de que tales gafas existan, de momento el p-valor queda restringido a la experimentación científica, donde nos dará una idea de cuán probable es que estemos equivocados. En el resto de casos, deberemos seguir utilizando un análisis DAFO.
La próxima vez que lea algún estudio en el que se menciona el p-valor, ya sabe a qué se refieren los autores: al riesgo que tienen de equivocarse en sus afirmaciones con la evidencia empírica de los datos de una muestra. Como la muestra es solo una parte de la población, es una información imperfecta. Por ello el p-valor no podrá ser nunca 100 % o 0 %, que supondría una seguridad absoluta a la hora decidir.![]()
Sobre los autores: Jose Luis Arroyo Barrigüete y Francisco Borrás Palá son profesores de métodos cuantitativos en ICADE – Universidad Pontificia Comillas
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Cómo nos ayuda la ciencia a tomar decisiones correctas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Fórmulas matemáticas y números: cómo ayuda la economía al fútbol
- Cómo hacer ciencia en un periódico: la experiencia de ‘Público’
- Cómo descubrimos tres libros venenosos en la biblioteca de nuestra universidad
La eterna promesa del ‘blockchain’
Este año se cumple una década de la aparición del famoso paper que planteó el sistema Bitcoin, dando así pistoletazo de salida a la proliferación del “dinero electrónico”. Esta y otras criptomonedas se sustentan en una tecnología denominada blockchain que, de acuerdo con muchos analistas, está llamada a ser una revolución en el ámbito de la llamada Industria 4.0. Pero ¿qué es el blockchain y qué capacidad transformadora tiene?
 Foto: Hitesh Choudhary / Unsplash
Foto: Hitesh Choudhary / Unsplash
El blockchain surge en 2009 como solución a un problema clásico de sistemas de moneda virtual descentralizados: el problema del doble gasto. Las divisas tradicionales funcionan porque hay una entidad central que se encarga de su buen funcionamiento, y por ende donde el sistema económico y financiero deposita la confianza (e.g., el Banco Central Europeo). Con la adopción de Internet y los sistemas distribuidos, surge un interés en el desarrollo de divisas digitales que no dependan de un mediador de confianza, pero todos los planteamientos chocan frontalmente con el problema del doble gasto: que una misma moneda (en el sentido de “unidad básica” de la divisa) pueda ser falsificada y gastada más de una vez. Hasta 2009, cuando el creador del Bitcoin (bajo el pseudónimo Satoshi Nakamoto) propone una solución basada en un triple enfoque: todas las transacciones se comparten públicamente; las transacciones válidas se determinan por un sistema de prueba de trabajo (proof of work); y se incentiva económicamente la contribución a este sistema (por los llamados mineros).
Estos tres pilares se integran en la tecnología blockchain, que no es más que la unión de dos técnicas bien conocidas y desarrolladas: los árboles Merkle y la criptografía (en forma de firma digital de clave pública y funciones hash). El árbol Merkle es una estructura de datos ideada y patentada en 1979 por Ralph Merkle, diseñada para concatenar información de forma que un nodo dado permite verificar de forma segura y eficiente toda la información que cuelga de él. Tiene muchas aplicaciones, como en el intercambio de archivos en redes P2P o en software de control de versiones como Git. Blockchain es básicamente una cadena de bloques (tipo Merkle, pero, en principio, sin ramificaciones) a la que se añade la firma digital para verificar los participantes en las transacciones.
Bitcoin funciona como una red distribuida de forma que las transacciones se propagan por todos los nodos de la red. Estas transacciones se validan y, en un primer momento, se encuentran sin confirmar. Los mineros recolectan transacciones y tratan de añadirlas en forma de nuevo bloque al blockchain en un proceso que requiere gran capacidad de computación. El incentivo principal por conseguirlo es una fracción de Bitcoin (proporcional a la dificultad en términos de cómputo, que es variable, en ese momento), que no es otra cosa que crear dinero de la nada (de ahí lo de minero…), aunque también se puede llevar un impuesto sobre las transacciones que agrega el bloque. Por supuesto, puede suceder que varios bloques diferentes sean añadidos al blockchain más o menos simultáneamente por diferentes mineros. Lo que sucede es que, al no haber una autoridad central, la propia red “decide” qué rama es la válida, y es simplemente la que la mayoría acepta y sigue utilizando para poner nuevos bloques con transacciones. Los bloques de las ramas que no se continúan quedan huérfanos y dejan de tener validez.
Como consecuencia, este sistema ha dado lugar a una carrera “armamentística” para acumular capacidad de cómputo hasta un límite en el que el gasto energético para minar un bloque es mayor en muchas partes del mundo que el rédito que se obtiene. El Bitcoin, la gran promesa de las monedas libres, ha sido básicamente absorbido por el mercado y se ha convertido en un instrumento financiero más de especulación (recordemos la gran burbuja de finales de 2017), y es susceptible de quedar controlado por las grandes granjas de minado que se han establecido en países donde la energía es barata. El llamado “ataque del 51%” es una sombra que planea sobre este tipo de divisas, y que se hace más fácil a medida que la capacidad para minar se centraliza.
En definitiva, el Bitcoin (y demás criptodivisas) no ha triunfado ni triunfará en los términos que sus proponentes imaginaban. Los problemas no son meramente técnicos, sino fundamentales a la tecnología: es un sistema donde las transacciones son costosas, irreversibles y lentas; es un sistema que solo merece la pena para personas que operan fuera de la ley, o bien, como decíamos, como producto de especulación. Una criptomoneda puede ser 1) descentralizada, 2) barata, 3) segura; y solo podemos elegir dos. Para evitar la necesidad de una autoridad central, se necesitan mecanismos que son computacionalmente costosos de falsificar; para que sea segura, el coste económico del minado tiene que ser alto para que se desincentiven los ataques al sistema. Cualquier intento de arreglar un aspecto compromete el resto.
What are some industries where #blockchain would be useful?
✔️ #voting#CyberSecurity #HealthIT #education #Insurtech #Retail #SupplyChain #WEFLIVE pic.twitter.com/aEtz1J23Q2
— Michael Fisher (@Fisher85M) January 22, 2018
A partir del surgimiento de las criptomonedas, se ha propuesto a lo largo de esta década una infinidad de aplicaciones del blockchain, donde es usado como contenedor genérico de otros tipos de dato, en lugar de transacciones monetarias. Aquí, cabe destacar que poner información en un blockchain simplemente asegura que no se puede cambiar sin mucho esfuerzo y dinero, pero no dice nada de la validez de esa información. A pesar de ello, año tras año, hemos venido asistiendo a un desfile interminable de analistas y gurús de toda índole donde se nos promete que el blockchain es la nueva revolución en todo tipo de campos, pero esa revolución sigue sin llegar, ni siquiera en su aplicación original. En efecto, ¿cómo podría una base de datos lenta y costosa transformar nuestra industria?
Sobre el autor: Iñaki Úcar es doctor en telemática por la Universidad Carlos III de Madrid e investigador postdoctoral del UC3M-Santander Big Data Institute.
El artículo La eterna promesa del ‘blockchain’ se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:
