Ignacio López Goñi – Naukas Bilbao 2018: La pandemia del siglo XXI
 Imagen de Ally White / Pixabay
Imagen de Ally White / PixabayIgnacio López Goñi es un divulgador de la microbiología siempre excelente pero de alguna manera proporcional: crece con el tamaño del escenario. En esta charla ante 2000 personas reunidas en el Euskalduna explica como nadie la pandemia que se nos viene encima en este siglo, la resistencia bacteriana a los antibióticos. López Goñi consigue que en la explicación intervengan todas y cada una de las personas presentes en el auditorio.
Ignacio López Goñi: ''La pandemia del siglo XXI''Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Ignacio López Goñi – Naukas Bilbao 2018: La pandemia del siglo XXI se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Naukas Bilbao 2017 – Ignacio López-Goñi: Las bacterias también se vacunan
- Ignacio López-Goñi: «El sistema de defensa de las bacterias es el mejor editor de genomas que existe»
- Ana Aguirre – Naukas Bilbao 2018: Somos binarios…. ¿o no?
¿Cómo llegan bacterias resistentes y residuos de antibióticos a los alimentos?
 Foto: Brian Chan / Unsplash
Foto: Brian Chan / UnsplashHoy en día, prácticamente todas las personas constituimos un eslabón en la cadena de transmisión de antibióticos y de bacterias resistentes a antibióticos en el medio ambiente.
Esto es así porque prácticamente todo lo que ingerimos, empezando por el agua que bebemos y pasando por los alimentos de origen animal y vegetal, puede contener residuos de antibióticos o bacterias resistentes a antibióticos o sus genes. Los adquieren bien por contaminación, bien porque se encuentran naturalmente en los alimentos o bien porque se les ha añadido en el proceso de elaboración.
Residuos de antibióticos en alimentos
Las normativas europeas y estadounidenses definen los residuos de antibióticos como sustancias farmacológicamente activas (ya sea el principio activo, sus productos de degradación o sus metabolitos) que permanecen en el alimento obtenido a partir de animales a los que se les ha administrado el fármaco.
En principio, los productos de origen animal no deben ser consumidos hasta que el animal haya metabolizado el fármaco. Hay un tiempo establecido entre la administración y el sacrificio del animal para su consumo. Pero, aun así, es posible encontrar residuos en carnes, huevos y leche. También se han encontrado residuos de antibióticos en alimentos de origen vegetal e incluso en el agua de grifo.
 Los huevos pueden contener residuos de antibióticos.
Los huevos pueden contener residuos de antibióticos.Tookapic/Visualhunt
La presencia de residuos de antibióticos utilizados en veterinaria en alimentos está limitada por normativas establecidas por las autoridades competentes en cada caso. En Europa, la EFSA (European Food Safety Authority) establece las directrices a aplicar y cada país miembro debe adecuar su normativa ajustada a esas directrices.
En general, cada vez que se aprueba un nuevo antibiótico (u otro tipo de medicamento) de uso veterinario para animales de consumo humano, debe de pasar una serie de análisis y evaluación de riesgos. Teniendo en cuenta los datos obtenidos de estos análisis, se establecen los límites aceptables de ingesta diaria (ADI). A partir de estos, se determinan los niveles máximos de residuos (LMR) permitidos en alimentos.
Es muy difícil determinar la ingesta real de residuos de antibióticos de cada individuo. Puede variar mucho dependiendo del país, de la dieta, etc. Por ello, los trabajos científicos publicados se refieren a lugares concretos y los resultados son difíciles de extrapolar.
En un estudio realizado en Hong Kong con niños, se analizaron los residuos de antibióticos en leche, agua potable y alimentos ingeridos y en orina. Se detectaron residuos de quinolinas, sulfamidas, macrólidos y penicilina. Pero tanto la ingesta estimada como los niveles detectados en orina estaban por debajo de los límites establecidos por las normativas vigentes.
Efectos para la salud
Sin embargo, aunque los niveles estén dentro de la normativa vigente y sean incluso indetectables, lo cierto es que las personas estamos continuamente expuestas a residuos de antibióticos. Esta exposición crónica a cantidades muy pequeñas de numerosos compuestos diferentes puede ser más perjudicial para la salud que las dosis terapéuticas durante periodos cortos, como cuando se trata una infección.
Los residuos de antibióticos en los alimentos pueden causar problemas graves de salud en las personas, como alergias, efectos inmunopatológicos y citotóxicos y aumentar el riesgo de desarrollar cáncer. Además, pueden alterar la composición del microbioma humano, especialmente del microbioma intestinal.
Comparada con la exposición por uso terapéutico, la exposición crónica a muchos antibióticos diferentes, aunque sea a niveles muy bajos, puede ejercer una mayor presión de selección sobre bacterias resistentes y no resistentes a antibióticos.
La exposición crónica a antibióticos es especialmente importante en niños después de la lactancia, cuando empiezan a ingerir otro tipo de productos. Los residuos de antibióticos en los alimentos pueden determinar el desarrollo de su microbioma. Estudios epidemiológicos y experimentales sugieren que tienen un efecto acumulativo, por lo que su efecto puede ir sumándose incluso de generación en generación.
Por otra parte, en 1976 se demostró por primera vez que el uso de antibióticos en veterinaria provocaba la colonización de bacterias resistentes en los pollos de una granja. También la adquisición de esa resistencia en el microbioma del tracto intestinal de los trabajadores de la granja.
En muchos estudios posteriores se ha demostrado que bacterias resistentes en animales pueden transmitir los genes de resistencia a bacterias presentes en el intestino humano. Esto ocurre, muy presumiblemente, vía alimentos.
Bacterias resistentes a antibióticos en alimentos
La presencia de bacterias en los alimentos puede ser intencionada, como, por ejemplo, en productos fermentados, como probióticos o incluso como bioconservantes. Los órganos competentes en cada caso (EFSA, en Europa) publican periódicamente listas de bacterias reconocidas como seguras para su uso en alimentación. Entre otras condiciones, estos microrganismos no deben producir antibióticos ni tener genes de resistencia.
No obstante, la presencia de bacterias resistentes puede ocurrir en alimentos preparados a partir de materia prima cruda, como, por ejemplo, alimentos fermentados tradicionales. O puede ser accidental, por contaminación de diferentes fuentes. Además, la matriz de los alimentos y las condiciones de conservación y procesado pueden favorecer la transmisión de genes de resistencia entre bacterias.
 ‘Staphylococcus aureus’, principal causa de mastitis en vacas.
‘Staphylococcus aureus’, principal causa de mastitis en vacas.Wikimedia Commons / Eric Erbe, Christopher Pooley
Preocupa especialmente la presencia de bacterias resistentes que provocan enfermedades transmitidas por los alimentos, como Salmonella o Campylobacter o bacterias responsables de zoonosis, como cepas resistentes de Staphylococcus aureus.
Además, bacterias comensales resistentes, no patógenas, pueden transferir los genes de resistencia a bacterias patógenas tanto en el procesado de los alimentos como tras la ingestión. Dado que algunas de las bacterias presentes en los alimentos tienen capacidad de aguantar las condiciones del tracto digestivo, colonizar el intestino y permanecer en él largos periodos de tiempo, pueden aumentar el riesgo de transmitir genes de resistencia tanto en el microbioma humano como en el medio ambiente.
Por todo ello, es importante monitorizar y reducir la presencia de todo tipo de bacterias resistentes (tanto comensales como patógenas) en los alimentos. Así mismo, es importante estudiar los elementos genéticos móviles presentes en los alimentos para entender su epidemiología e implementar métodos para reducir su presencia.
Todo ello, unido al cumplimiento de las buenas prácticas en los procesos de elaboración y buenas prácticas de higiene en todas las fases de la cadena alimentaria, “desde la granja a la mesa”.
Nota: Este artículo constituye un resumen de la charla impartida en el curso de verano de la UPV/EHU organizada por el JRL Environmental Antibiotic Resistence.![]()
Sobre la autora: Mailo Virto Lekuona es profesora titular de Biquímica y Biología Molecular en la Universidad del País Vasco / Euskal Herriko Unibertsitatea
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo ¿Cómo llegan bacterias resistentes y residuos de antibióticos a los alimentos? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El camino hacia los antibióticos inservibles
- Bacterias hospitalarias: resistentes e indetectables
- Una nueva vía para la lucha contra la resistencia a los antibióticos
No todo es ciencia en ‘El club de la lucha’
 Copyright © 1999 by 20th Century Fox. All Rights Reserved. Fair use.
Copyright © 1999 by 20th Century Fox. All Rights Reserved. Fair use.
«Tyler se lame los labios, húmedos y brillantes, y me besa el dorso de la mano».
La película que más veces he visto en mi vida es El club de la lucha. Dirigida por David Fincher, está basada en la novela homónima de Chuck Palahniuk, un escritor discípulo de la generación beat, héroe de muchas adolescencias rebeldes.
«Tyler inclina unos centímetros el bote que contiene el polvo de hipoclorito sobre el beso húmedo y brillante del dorso de mi mano. —Es una quemadura química—dice Tyler—y te dolerá más que cualquier otra quemadura. Peor que cien cigarrillos.
El beso brilla en el dorso de mi mano. —Te quedará una cicatriz—dice Tyler».
La primera regla del club de la lucha es no hablar del club de la lucha. Así que no voy a hablar del club de la lucha, sino de la ciencia de El club de la lucha. En esta novela hay descripciones científicas veraces mezcladas con licencias fantásticas. Desde cómo fabricar una bomba casera, cómo hacer una quemadura química con hipoclorito, a cómo fabricar jabón utilizando la grasa que se desecha tras las liposucciones.
Las descripciones son exquisitas. La ciencia se utiliza como recurso literario para tratar cuestiones de calado como el individuo, la libertad y la propiedad.
«Un explosivo interesante es el permanganato potásico mezclado con azúcar en polvo. La idea consiste en mezclar un ingrediente que se queme con rapidez con un segundo ingrediente que aporte oxígeno suficiente para la combustión. Al arder tan rápido se produce la explosión.
Peróxido de bario y polvo de zinc.
Nitrato de amoníaco y aluminio en polvo.
La nouvelle cuisine de la anarquía.
Nitrato de bario con salsa de azufre y guarnición de carbón vegetal. Ya tienes un compuesto de pólvora básica.
Bon appétit».
 Copyright © 1999 by 20th Century Fox. All Rights Reserved. Fair use.
Copyright © 1999 by 20th Century Fox. All Rights Reserved. Fair use.El club de la lucha es un ejemplo de que la cultura científica puede refinar el argumento de una novela o de una película. Se puede utilizar como metáfora, igual que cualquier otro recurso. Para plumas adecuadas, las descripciones científicas pueden ser tan hermosas como las de cualquier otro paisaje. No todo van a ser profundos ojos azules.
«Con jabón suficiente —dice Tyler— podrás volar el mundo entero».
En el octavo capítulo de la novela comienzan a fabricar jabón a partir de grasa humana.
«Esta grasa —me explica Tyler— tiene mucha sal, así que, cuanta más agua, mejor».
Vierte toda la grasa en ollas con agua hirviendo. Cuando la grasa se derrite, el sebo sube a la superficie, mientras que la sal se irá disolviendo en el agua. Esto se hace porque la grasa humana contiene mucha sal y con tanta sal el jabón no solidifica. El sebo de calidad es el que se forma en superficie.
«Hierve y espuma. Hierve y espuma».
La pastilla de jabón de color rosa se convirtió en el emblema de la película.
El sebo espumado lo van colocando en briks abiertos para que enfríe. Luego los meten en la nevera para que no se enrancie.
«Una capa de algo espeso y claro comienza a cubrir la superficie del sebo del frigorífico. —El sebo —le advierto—se está separando. —No importa —dice Tyler—. La capa más clara es de glicerina. O la agregas de nuevo cuando hagas el jabón o bien la espumas y la quitas».
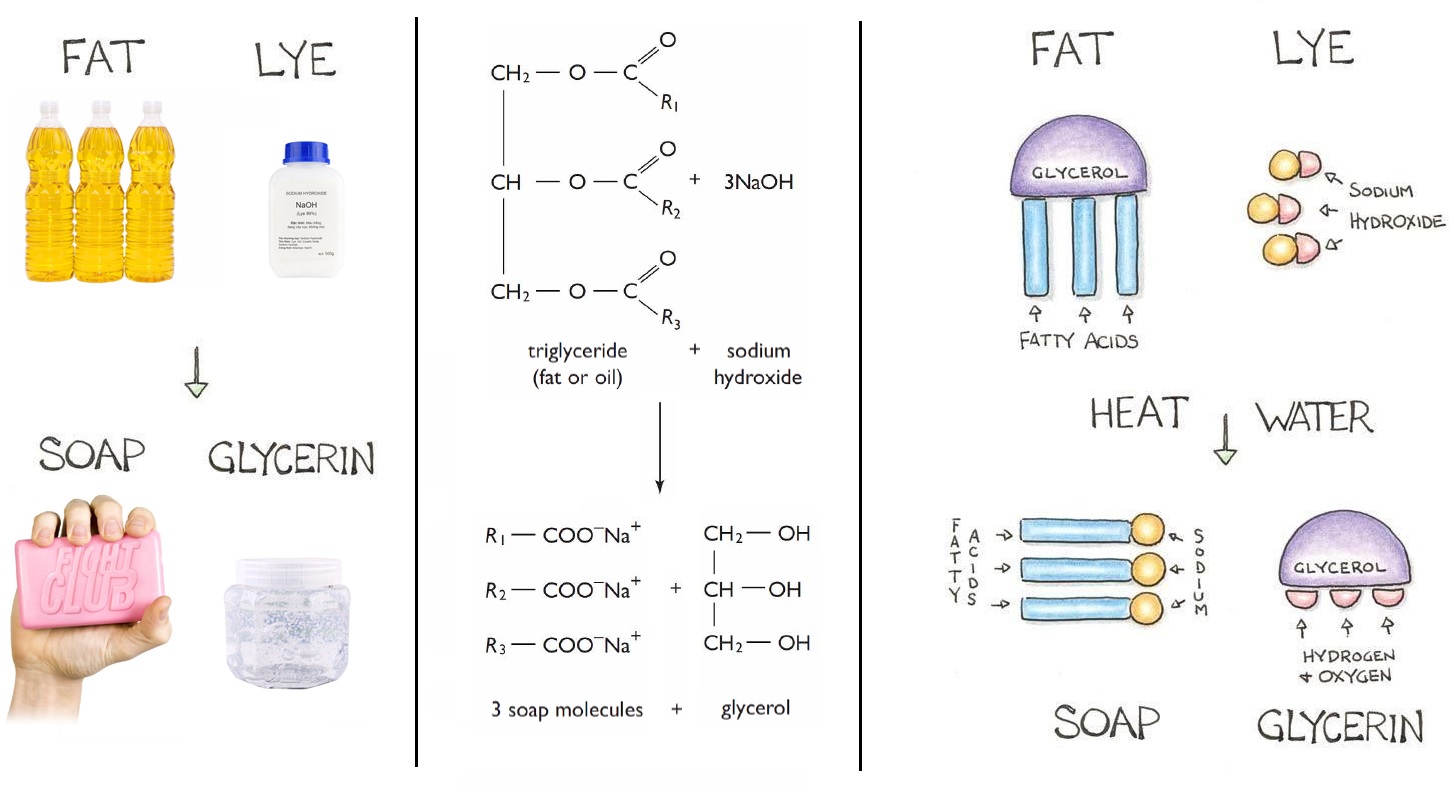
Las grasas son químicamente triglicéridos. Esto es glicerina unida con enlace tipo éster a ácidos grasos. Durante la reacción de saponificación en la que las grasas se transforman en jabón, estos enlaces tipo éster se rompen y dan lugar a la formación de sales, dejando libre la glicerina. Para formar sales, lo que se hace en esta reacción es mezclar la grasa con una base como el NaOH o el KOH, así se forman las sales de sodio y de potasio respectivamente. Esas sales son lo que conocemos como jabón.
«Tyler vendía el jabón en los grandes almacenes a 20 dólares la pastilla. Dios sabe a cuánto lo venderían ellos. Era maravilloso. Le revendíamos a las mujeres ricas sus propios culos celulíticos».
En El club de la lucha fabrican jabón no solo por lo lucrativo del negocio del jabón. Lo que les interesaba realmente es la glicerina. La glicerina es uno de los reactivos necesarios para fabricar explosivos como nitroglicerina, dinamita o gelignita.
Chuck Palahniuk escribió sobre química en El club de la lucha. Años más tarde, David Fincher, incluyó en la película las descripciones completas de los procesos químicos más relevantes. Pero El club de la lucha no me gusta por eso, sino por lo importante. De todos modos, es interesante saber cuándo Tyler dice la verdad y cuándo no, porque no toda la ciencia que aparece en El club de la lucha es completamente veraz. Como otras muchas cosas que suceden en la historia. Sirven de migas de pan en el camino, manteniendo el suspense a medida que nos acercan a la verdad.
«La saliva de Tyler tenía dos funciones. El beso húmedo en la palma de mi mano retuvo el polvo de hipoclorito mientras me achicharraba. Esa fue la primera función. La segunda fue convertir el hipoclorito en cáustico. El polvo de hipoclorito solo es cáustico cuando lo mezclas con agua. O saliva.
Cierra los ojos».
 Copyright © 1999 by 20th Century Fox. All Rights Reserved. Fair use.
Copyright © 1999 by 20th Century Fox. All Rights Reserved. Fair use.La historia de El club de la lucha no va de ciencia, ni mucho menos. Pero se sirve de la ciencia para crear una atmósfera y, sobre todo, para hablar de asuntos trascendentes.
«Una mezcla de hipoclorito y agua llega a perforar una cacerola de aluminio. Una disolución de hipoclorito en agua disolverá una cuchara de madera. Combinado con agua, supera los cien grados de temperatura y al calentarse me quema el dorso de la mano. Tyler posa sus dedos sobre los míos; tenemos las manos extendidas sobre mis pantalones manchados de sangre, y Tyler me pide que preste atención».
En la escena en la que uno de los protagonistas padece la agonía de una quemadura química, se describe con detalle todo el proceso, el que le sucede a la carne y el importante, el que sucede en la mente.
«Regresa al dolor y presta atención. Es el momento más importante de tu vida».
Sobre la autora: Déborah García Bello es química y divulgadora científica
El artículo No todo es ciencia en ‘El club de la lucha’ se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Con los edulcorantes artificiales (casi) todo son ventajas
- El ácido hialurónico no sirve para todo, aunque lo parezca
- No todo ha sido malo este año: la ciencia nos dejó algunas buenas noticias
Números primos gemelos, parientes y sexis (1)
Hace unos meses, mientras buscaba información para mis entradas del Cuaderno de Cultura Científica Los números enamorados y ¿Pueden los números enamorarse de su propia imagen?, descubrí dos familias de números primos especiales, los números primos “parientes” (llamados cousin en inglés) y los sexis, ambas relacionadas con los números primos gemelos. Entonces me las guardé en el baúl de los temas pendientes, que acabo de abrir para poder hablar en esta entrada y en la próxima sobre estas familias de números primos.
 1.2.3.5.7.11.13 (2018), del artista estadounidense Tim McKay, 332,7 x 152,4 cm, una de las obras de la exposición Primes, celebrada en 2019 en el espacio artístico Pirate: Contemporary Art, de Lakewood (Colorado). Imagen de la página web del artista
1.2.3.5.7.11.13 (2018), del artista estadounidense Tim McKay, 332,7 x 152,4 cm, una de las obras de la exposición Primes, celebrada en 2019 en el espacio artístico Pirate: Contemporary Art, de Lakewood (Colorado). Imagen de la página web del artistaPero empecemos por el principio, por los números primos gemelos. Como es bien conocido, los números primos son aquellos números naturales que solamente se pueden dividir por 1 y por ellos mismos, como el 2, el 3, el 5 o el 7, pero no el 9 (que se puede dividir por 3) o el 12 (que se puede dividir por 2, 3, 4 o 6). Puede leerse más sobre ellos en la entrada Buscando lagunas de números primos, como que existen infinitos números primos, que cada número natural puede expresarse, de forma única, como producto de números primos, qué es la criba de Eratóstenes o sobre el problema de la distribución de los números primos.
Como todos los números pares, a excepción del 2, son números compuestos, no primos, entonces lo más cerca que pueden estar dos números primos, salvo el 2 y el 3 que están pegados, es con solo un número par entre ellos. Y precisamente, a las parejas de números primos que están tan cerca, es decir, con solo un número par entre ellos, o dicho de otra forma, que la diferencia entre ellos es 2, se les llama números primos gemelos, como las parejas 11 y 13, 17 y 19, o 59 y 61. Las parejas de números primos gemelos menores de 500 son (véase la sucesión A0077800 de la enciclopedia online de números enteros):
(3, 5), (5, 7), (11, 13), (17, 19), (29, 31), (41, 43), (59, 61), (71, 73), (101, 103), (107, 109), (137, 139), (149, 151), (179, 181), (191, 193), (197, 199), (227, 229), (239, 241), (269, 271), (281, 283), (311, 313), (347, 349), (419, 421), (431, 433) y (461, 463).
Por eso en la novela La soledad de los números primos (Salamandra, 2009), del escritor italiano Paolo Giordano, se dice de los protagonistas, Mattia, que es matemático, y Alice: “Mattia pensaba que él y Alice eran eso, dos primos gemelos solos y perdidos, próximos, pero nunca juntos”.
 Prime Rhythms / Ritmos primos (1959 -1962), de Anthony Hill, realizada en plástico laminado y de unas dimensiones de 91.5 x 91.5 x 1.9 cm. Imagen del artículo del artista A View of Non-Figurative Art and Mathematics and an Analysis of a Structural Relief. Obra relacionada con los números primos gemelos, como se explica en la entrada Los ritmos primos de Anthony Hill
Prime Rhythms / Ritmos primos (1959 -1962), de Anthony Hill, realizada en plástico laminado y de unas dimensiones de 91.5 x 91.5 x 1.9 cm. Imagen del artículo del artista A View of Non-Figurative Art and Mathematics and an Analysis of a Structural Relief. Obra relacionada con los números primos gemelos, como se explica en la entrada Los ritmos primos de Anthony HillUn primer resultado sobre las parejas de números primos gemelos es que, salvo la pareja (3, 5), son de la forma (6 n – 1, 6 n + 1). Veamos una justificación de este hecho. Un número cualquiera puede escribirse de la forma 6 n + d, para d = 0, 1, 2, 3, 4 o 5. Entonces:
i) si d = 0, 2 o 4, el número 6 n + d no es primo, ya que es divisible por 2;
ii) si d = 3, se puede dividir 6 n + d por 3;
iii) si d = 1, el número es de la forma 6 n + 1;
iv) si d = 5, la forma del número es 6 n + 5 = 6 (n + 1) – 1 = 6 m – 1, si tomamos m = n +1.
De hecho, hemos probado más. Hemos demostrado que todos los números primos, en particular, todos los números no divisibles por 2 y 3, son de una de estas dos formas: 6 n – 1 y 6 n + 1. Por lo tanto, la suma de dos números primos gemelos es divisible por 12 (5 + 7 = 12, 11 + 13 = 24, 17 + 19 = 36, etc).
Más aún, si tenemos una pareja de números primos (6 n – 1, 6 n + 1), entonces el dígito de las unidades del número n debe ser 0, 2, 3, 5, 7 u 8, ya que en otro caso – 1, 4, 6 o 9 – uno de los dos números de esa pareja sería múltiplo de 5.
Lo siguiente que podríamos plantearnos es cuántos números primos gemelos existen. Mientras que la existencia de infinitos números primos es un hecho conocido desde la matemática griega y que posee una sencilla demostración (véase Buscando lagunas de números primos), el problema de si existen infinitas parejas de números primos gemelos sigue estando abierto a día de hoy. Es la conocida como conjetura de los números primos gemelos.
Existen números primos gemelos muy grandes, por ejemplo, la pareja de números primos 1.000.000.000.061 y 1.000.000.000.063, que menciona Keith J. Devlin en su libro El lenguaje de las matemáticas (Ma Non Troppo, 2002), y mucho más grandes aún, como se verá más adelante, pero se desconoce si existen infinitos números primos gemelos. Sin embargo, en los últimos años se ha realizado un importante avance en esta conjetura.
En 2013 nos sorprendió la noticia de que el matemático chino, residente en Estados Unidos, Yitang Zhang, había probado una versión débil de la conjetura de los números primos (el correspondiente artículo fue publicado en 2014 en la prestigiosa revista de investigación matemática, Annals of Mathematics). En concreto, había demostrado que existen infinitas parejas de números primos cuya diferencia entre ellos es menor que 70 millones (70.000.000). No era la conjetura de los números primos gemelos, pero era un gran paso, ya que se había fijado una cota finita que, aunque no era 2 (que establece la conjetura para los números primos gemelos), al menos era finita, para la existencia de infinitas parejas de números primos cuya diferencia entre ellos fuera menor que esa cota.
A partir del resultado de Yitang Zhang, el matemático australiano-americano Terence Tao, propuso un proyecto polymath (que son proyectos colaborativos masivos para resolver problemas matemáticos) para reducir la cota de Zhang. Esta ha conseguido reducirse hasta 246. Es decir, existen infinitas parejas de números primos, cuya diferencia entre ellos es menor que 246. Dentro de ese conjunto infinito de parejas de números primos está el conjunto de los números primos gemelos (cuya diferencia es 2), el conjunto de las parejas de números primos cuya diferencia es 4, que son los llamados primos parientes, o el de aquellas cuya diferencia es 6, los primos sexis, que aún no sabemos si ellos solos son conjuntos infinitos o no, pero también todas las demás parejas de números primos con una diferencia menor que 246, como 29 y 41 (cuya diferencia es 12) o 47 y 269 (cuya diferencia es 222).
Más aún, asumiendo la conjetura de Elliot-Halberstam, sobre la distribución de números primos en progresión aritmética, y una generalización de la misma, se ha demostrado que la cota puede reducirse a 12 y 6.
 Poema de los números primos (años 1980), rotulador e hilo sobre lienzo, 97,5 x 130 cm. Archivo Esther Ferrer y perteneciente al catálogo Esther Ferrer, todas las variaciones son válidas, incluida esta. Obra en la que aparecen los números primos gemelos más grandes conocidos en 1980, con 703 dígitos
Poema de los números primos (años 1980), rotulador e hilo sobre lienzo, 97,5 x 130 cm. Archivo Esther Ferrer y perteneciente al catálogo Esther Ferrer, todas las variaciones son válidas, incluida esta. Obra en la que aparecen los números primos gemelos más grandes conocidos en 1980, con 703 dígitosComo puede verse en la página web dedicada a los números primos y sus records, The Prime pages, los números primos gemelos más grandes conocidos, a día de hoy, fueron obtenidos en septiembre de 2016, y son los números
2.996.863.034.895 · 21.290.000 – 1 y 2.996.863.034.895 · 21.290.000 + 1,
que tienen nada más y nada menos que 388.342 dígitos.
Otra cuestión interesante que nos podríamos plantear, es cuál es el porcentaje de parejas de números primos gemelos dentro del conjunto de todos los números primos, entendiendo que estamos contando solo el primer primo de la pareja, es decir, el primo p tal que p + 2 es también primo. Si miramos los listados existentes de ambos conjuntos, veremos que, entre los 100 primeros números, hay 25 números primos (2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97) y 8 números primos p tales que p + 2 es también primo (3, 5, 11, 17, 29, 41, 59, 71), es decir, parejas de números primos gemelos, luego hay un 32% de parejas de números primos gemelos. Si tomamos ahora los 1000 primeros números, hay 168 números primos y 35 parejas de números primos gemelos, luego un 20,8%. Y va disminuyendo el porcentaje, de manera que cuando tomamos los primeros un millardo de números (1.000.000.000), hay 50.847.534 números primos, pero solo un 6,7% son primos p tales que p + 2 es primo, 3.424.506.
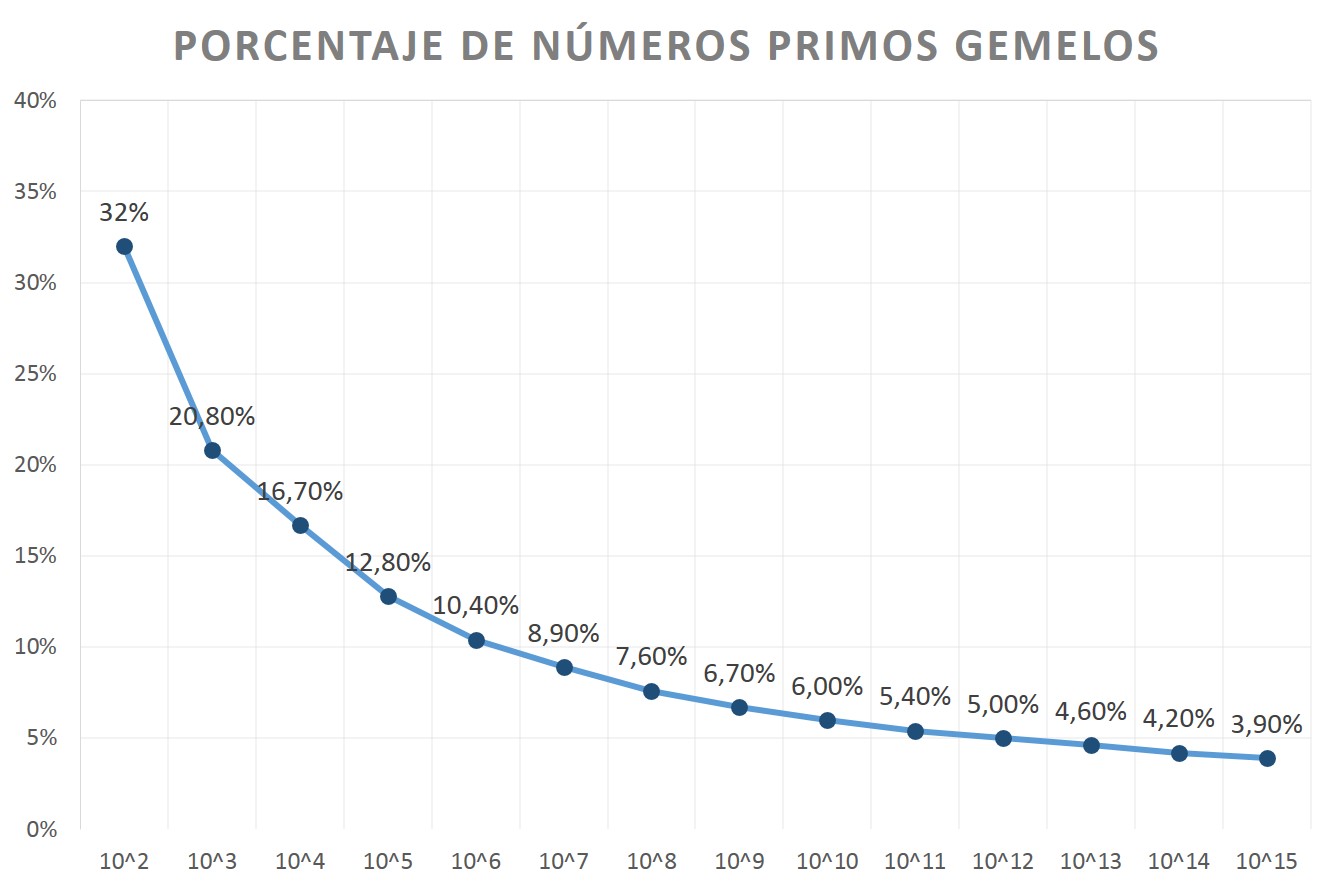
Como puede observarse, cada vez hay menos números primos gemelos (en realidad, primos p tales que p + 2 es primo), dentro del conjunto de números primos.
Un resultado curioso relacionado con los números primos gemelos es el conocido como teorema de Brun, demostrado por el matemático noruego M. Viggo Brun (1885-1978) en 1919.
Teorema de Brun (1919): La suma de los recíprocos de los números primos gemelos

es convergente, y converge al número B2, la conocida como constante de Brun, que tiene un valor aproximado de 1,902160583104 (esta aproximación fue obtenida en 2002, por Pascal Sebah y Xavier Gourdon).
Si la anterior serie, la suma de los recíprocos de los números primos gemelos, fuese divergente, es decir, que la secuencia infinita de sumas parciales de la serie no tuviese límite, entonces podríamos afirmar que existen infinitos números primos gemelos. Esto se debe a que si fuesen finitos la serie sería convergente, ya que la suma tendría un número finito de sumandos, luego sería finita, tendría límite. Sin embargo, la serie es convergente, por lo que no podemos deducir de ahí que sea una familia finita o infinita.
Por otra parte, si la constante de Brun B2 fuese un número irracional, es decir, que no se puede escribir como cociente de dos números enteros, podríamos afirmar que entonces existen infinitos números primos gemelos. Esto se debe a que, si fuesen finitos, la serie anterior sería una suma finita de números racionales, luego racional. Pero se desconoce si B2 es racional o irracional.
 The First Ten Prime Numbers, Suite I (2004), de la artista estadounidense Nancy Macko, litografía, 76,2 x 55,9 cm. La imagen pertenece a la instalación de la obra en Commissary Arts (Venecia, California), en 2008, obtenida de la página web de Nancy Macko
The First Ten Prime Numbers, Suite I (2004), de la artista estadounidense Nancy Macko, litografía, 76,2 x 55,9 cm. La imagen pertenece a la instalación de la obra en Commissary Arts (Venecia, California), en 2008, obtenida de la página web de Nancy MackoContinuando con nuestro interés por los números primos gemelos, podríamos plantearnos si existen ternas de números primos gemelos. La respuesta es negativa, salvo para la terna (3, 5, 7), ya que cada tres números impares consecutivos, uno de ellos necesariamente es múltiplo de 3. Es fácil observar esto. Todo número puede escribirse como 3 n + r, con r = 0, 1 o 2, entonces tres números impares consecutivos pueden escribirse de la forma 3 n + r, 3 n + r + 2 y 3 n + r + 4 = 3 (n + 1) + r + 1. Si r = 0, el primer número es múltiplo de 3, si r = 1, lo es el segundo, y si r = 2, el múltiplo de 3 es el tercero.
En conclusión, no hay ternas de números primos gemelos. Lo más cerca que pueden estar tres números primos entre sí es cuando son de la forma (p, p + 2, p + 6), como (5, 7, 11) o (11, 13, 17), y de la forma (p, p + 4, p + 6), como (7, 11, 13) o (13, 17, 19), a los cuales se les llama números primos trillizos.
Los números primos trillizos de la forma (p, p + 2, p + 6), menores de 500, son (véase la sucesión A022004 de la enciclopedia online de números enteros):
(5, 7, 11), (11, 13, 17), (17, 19, 23), (41, 43, 47), (101, 103, 107), (107, 109, 113), (191, 193, 197), (227, 229, 233), (311, 313, 317), (347, 349, 353), (461, 463, 467).
Mientras que los números primos trillizos de la forma (p, p + 4, p + 6), menores de 500, son (véase la sucesión A022005):
(7, 11, 13), (13, 17, 19), (37, 41, 43), (67, 71, 73), (97, 101, 103), (103, 107, 109), (193, 197, 199), (223, 227, 229), (277, 281, 283), (307, 311, 313), (457, 461, 463).
Además, la terna de números trillizos, de la forma (p, p + 2, p + 6), más grande que se conoce en la actualidad, obtenida en abril de 2019 (véase The Prime pages), es
4.111.286.921.397 x 266.420 – 1,
4.111.286.921.397 x 266.420 + 1,
4.111.286.921.397 x 266.420 + 5,
que tienen 20.008 dígitos. Mientras que para la forma (p, p + 4, p + 6), los números primos trillizos más grandes, obtenidos en abril de 2013 (véase The Prime pages), son
6.521.953.289.619 x 255.555 – 5
6.521.953.289.619 x 255.555 – 1
6.521.953.289.619 x 255.555 + 1,
con 16.717 dígitos cada uno. Además, de forma similar a la conjetura de los números primos gemelos, existe una conjetura sobre la existencia de infinitos números primos trillizos.
En general, nos podemos plantear el estudio de las familias de los grupos de k números primos más próximos posibles, que podemos llamar, para k = 4, cuatrillizos, para k = 5, quintillizos, luego sextillizos, septillizos, octillizos, nonillizos, etcétera y, en general, para cualquier k, números primos k-tillizos.
 Dos fotografías, con 6 años de diferencia (2010-2016), de la familia McGee, con sus seis hijos sextillizos, Elijah, Issac, Josiah, Madison, Olivia and Rozonno Jr., que han sido las estrellas de un programa de televisión llamado “Growing Up McGee”. Imagen e información de la página de TODAY, fotografías de Janine and Brian Killian, de Peters Photography
Dos fotografías, con 6 años de diferencia (2010-2016), de la familia McGee, con sus seis hijos sextillizos, Elijah, Issac, Josiah, Madison, Olivia and Rozonno Jr., que han sido las estrellas de un programa de televisión llamado “Growing Up McGee”. Imagen e información de la página de TODAY, fotografías de Janine and Brian Killian, de Peters PhotographyLos números primos cuatrillizos son de la forma (p, p + 2, p + 6, p + 8). Las primeras cuaternas de números primos cuatrillizos (véase la sucesión A007530) son
(5, 7, 11, 13), (11, 13, 17, 19), (101, 103, 107, 109), (191, 193, 197, 199), (821, 823, 827, 829), (1481, 1483, 1487, 1489), (1871, 1873, 1877, 1879), (2081, 2083, 2087, 2089).
Además, puede demostrarse que los números primos cuatrillizos son de la forma
(30 n + 11, 30 n + 13, 30 n + 17, 30 n + 19),
salvo la cuaterna inicial (5, 7, 11, 13). Este resultado, y otros similares, ayudan a la hora de encontrar números primos cuatrillizos (véase, por ejemplo, el artículo Two Algorithms to Find Primes in Patterns, de Jonathan Sorenson).
Si tenemos una cuaterna de números primos cuatrillizos (p, p + 2, p + 6, p + 8) tal que uno de los números, p – 4 o p + 12, es primo, entonces se tiene una quinterna de números primos lo más próximos posibles entre ellos, es decir, una quinterna de números primos quintillizos. Por lo tanto, los números primos quintillizos son de la forma (p, p + 2, p + 6, p + 8, p + 12), como las quinternas (5, 7, 11, 13, 17) y (11, 13, 17, 19, 23), o de la forma (p, p + 4, p + 6, p + 10, p + 12), como (7, 11, 13, 17, 19) y (97, 101, 103, 107, 109).
Mientras que los números primos sextillizos son de la forma (p, p + 4, p + 6, p + 10, p + 12, p + 16), como (7, 11, 13, 17, 19, 23) y (97, 101, 103, 107, 109, 113), y así podríamos seguir con más agrupaciones próximas de números primos.
Despidamos la primera parte de esta miniserie de entradas sobre los números primos gemelos, parientes y sexis, y otras familias relacionadas, con otra obra relacionada con los números primos de la artista donostiarra Esther Ferrer.
 Poema de los números primos (2016), de Esther Ferrer, dibujo para suelo, realizado en tinta sobre papel cuadriculado, 104,5 cm x 83,5 cm, del Archivo de Esther Ferrer. Imagen de la exposición Esther Ferrer 2, 3, 5, 7, 11, 13, 17, 19, 23,… en Tabakalera. Fotografía de Raúl Ibáñez
Poema de los números primos (2016), de Esther Ferrer, dibujo para suelo, realizado en tinta sobre papel cuadriculado, 104,5 cm x 83,5 cm, del Archivo de Esther Ferrer. Imagen de la exposición Esther Ferrer 2, 3, 5, 7, 11, 13, 17, 19, 23,… en Tabakalera. Fotografía de Raúl Ibáñez
Bibliografía
1.- Wolfram Mathworld: Twin Primes
2.- Wikipedia: Twin prime
3.- Yitang Zhang, Bounded gaps between primes, Annals of Mathematics 179 (3), pp. 1121–1174, 2014.
4.- The Prime pages
5.- Chris, Di and Matthew Stevenson, Hugin Home Page: Prime numbers
6.- X. Gourdon, P. Sebah: Introduction to Twin Primes and Brun’s Constant Computation
7.- Wolfram Mathworld: Prime Triplet
8.- Wikipedia: Prime triplet
9.- Wikipedia: Prime quadruplet
10.- Jonathan Sorenson, Two Algorithms to Find Primes in Patterns
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Números primos gemelos, parientes y sexis (1) se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El poema de los números primos (2)
- Buscando lagunas de números no primos
- El poema de los números primos
Un átomo con un centro masivo diminuto
 Artilleros británicos preparándose para disparar un obús con proyectiles de 15 pulgadas en 1917. Esto tenía en mente Rutherford al hacer el comentario que leerás en el texto. Fuente: Wikimedia Commons
Artilleros británicos preparándose para disparar un obús con proyectiles de 15 pulgadas en 1917. Esto tenía en mente Rutherford al hacer el comentario que leerás en el texto. Fuente: Wikimedia CommonsComo ocurre a menudo, el siguiente avance hacia la comprensión de la estructura atómica surgió de una investigación completamente sin ninguna relación con los espectros atómicos. La visión y el liderazgo de Ernest Rutherford hicieron que el equipo del Laboratorio Cavendish de la Universidad de Cambridge proporcionase durante el período 1909-1911 una nueva base sobre la que construir los modelos atómicos. Una base revolucionaria: los átomos son fundamentalmente espacio vacío.
Rutherford estaba interesado en los rayos emitidos por las sustancias radiactivas, especialmente los llamados rayos α (alfa). Estos rayos α consisten en partículas cargadas positivamente [1]. Algunas sustancias radiactivas emiten partículas α a velocidades y energías muy altas que pueden emplearse como proyectiles para bombardear muestras. Los experimentos que Rutherford y sus colegas hicieron con estas partículas son ejemplos de un tipo muy importante de experimento en física atómica y nuclear: el experimento de dispersión.
En un experimento de dispersión, un haz estrecho y paralelo de «proyectiles» (por ejemplo, partículas α, electrones o rayos X) se apunta a un objetivo. El objetivo suele ser una lámina delgada o una película de algún material. Cuando el rayo golpea el objetivo algunos de los proyectiles se desvían de su dirección original, dispersándose. La dispersión es el resultado de la interacción entre las partículas en el haz y los átomos del material. Un estudio cuidadoso de los proyectiles después de la dispersión puede generar información sobre los propios proyectiles, los átomos de la muestra y la interacción entre unos y otros. Así, si conocemos la masa, la energía y la dirección de los proyectiles y vemos como se dispersan podemos deducir las propiedades de los átomos que ocasionaron que los proyectiles se dispersasen de esa manera.
Rutherford notó que cuando un haz de partículas pasaba a través de una delgada lámina de metal, el haz se esparcía. Se puede pensar que esta dispersión está causada por interacciones electrostáticas entre las partículas α cargadas positivamente y las cargas que forman los átomos. Sabemos que los átomos contienen cargas positivas y negativas. Por lo tanto, una partícula α debería sufrir tanto fuerzas repelentes como atrayentes a medida que pasa a través de la materia. La magnitud y la dirección de estas fuerzas dependen de la distribución de las cargas en los átomos que constituyen la muestra y de la proximidad en cada momento de cada partícula a esas cargas. Cuando se propone un modelo atómico concreto, la extensión de la dispersión esperada se puede calcular y comparar con el experimento. Así, el modelo del átomo de Thomson predice una probabilidad casi nula de que una partícula se desvíe de su trayectoria inicial en un ángulo de más de unos pocos grados.
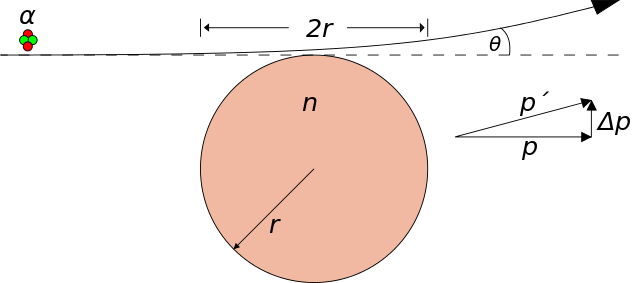 Previsión de la dispersión según el modelo atómico de Thomson. Fuente: Wikimedia Commons
Previsión de la dispersión según el modelo atómico de Thomson. Fuente: Wikimedia CommonsEl avance que condujo al modelo moderno del átomo siguió al descubrimiento de uno de los ayudantes de Rutherford, Hans Geiger. Geiger descubrió que el número de partículas dispersadas en ángulos de 10 ° o más era mucho mayor que el número predicho por el modelo de Thomson. De hecho, increíblemente un número significativo de partículas α se dispersaba en un ángulo superior a 90 °, es decir, muchas partículas prácticamente rebotaban directamente desde la lámina. Según el modelo de Thomson, el átomo debería haber actuado solo ligeramente sobre el proyectil. Algunos años después, Rutherford escribiría [2]:
[. . .] Había observado la dispersión de partículas α, y el Dr. Geiger en mi laboratorio la había examinado en detalle. Descubrió, en piezas delgadas de metal pesado, que la dispersión era generalmente pequeña, del orden de un grado. Un día, Geiger vino a mí y me dijo: «¿No crees que el joven Marsden, a quien estoy enseñando métodos radiactivos, debería comenzar una pequeña investigación?» Resulta que yo también lo había pensado, así que dije: «¿Por qué no le dejas ver si alguna partícula α se dispersa con un ángulo grande? ”. Puedo decirle con confianza que no creía que ninguna lo hiciese, ya que sabíamos que la partícula α era una partícula masiva muy rápida, con una gran cantidad de energía [cinética], y se podía demostrar que si la dispersión se debía al efecto acumulado de varias dispersiones pequeñas, la posibilidad de que una partícula se dispersara hacia atrás era muy pequeña. Entonces recuerdo que dos o tres días después Geiger se acercó a mí muy excitado y me dijo: “Hemos podido hacer que algunas de las partículas vuelvan atrás. . . »
Fue lo más increíble que me ha sucedido en mi vida. Fue casi tan increíble como si dispararas un proyectil de 15 pulgadas [3] contra un trozo de papel de seda y volviera y te golpeara. Reflexionando, me di cuenta de que esta dispersión hacia atrás debía ser el resultado de una sola colisión, y cuando hice los cálculos vi que era imposible obtener algo de ese orden de magnitud a menos que tomaras un sistema en el que la mayor parte de la masa del átomo se concentraba en un núcleo diminuto. Fue entonces cuando tuve la idea de un átomo con un centro masivo diminuto, con una carga.
Estos experimentos y la interpretación de Rutherford marcaron el origen del concepto moderno del átomo nuclear. Pero, pensemos un momento. A la vista de lo que hemos visto, ¿por qué el átomo debería tener su masa y carga positiva concentradas en un pequeño núcleo en el centro alrededor del cual se agrupan los electrones? Necesitamos más datos para poder llegar nosotros a esa conclusión también.
Notas:
[1] Estas partículas α son iones de helio cargados positivamente o, si se prefiere, núcleos de helio, con masas aproximadamente 7500 veces la masa del electrón.
[2] Rutherford, E. (1936) “The Development of the Theory of Atomic Structure”, publicado en “Background to Modern Science” McMillan, New York, 1940. Traducción propia.
[3] Un señor obús de 38,1 cm de diámetro. Véase la imagen que encabeza el texto.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Un átomo con un centro masivo diminuto se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Un método para determinar la estructura átomo a átomo en un cristal
- La ley del gas ideal a partir del modelo cinético
- Las partículas de los rayos catódicos
Sobre gustos……¿no hay nada escrito?
Juan Felipe Castro
 Foto: Natema Drummond / Unsplash
Foto: Natema Drummond / UnsplashDesde hace mucho tiempo y en diversas culturas se acuñó la expresión “sobre gustos no hay nada escrito”. Parece ser que desde un punto de vista genético, fisiológico y cultural, ésta frase ya ha pasado de moda.
Según Nicholas Archer de la Organización de Investigación Científica e Industrial de la Commonwealth (CSIRO), nuestras preferencias a la hora de los gustos por las comidas varía según la persona y se crean a partir de una combinación de 3 factores: el entorno (la salud de cada uno en particular, dieta e influencias culturales), las experiencias previas y los genes.
Actualmente reconocemos los siguientes sabores en nuestra lengua y parte superior del esófago: amargo, dulce, salado, ácido, umami y también hay una nueva tendencia a reconocer el sabor “graso” como un sabor diferente de los otros.
El sabor como tal es en sí un concepto diferente del gusto, ya que implica una experiencia sensorial, donde se incluyen los olores, texturas y experiencias previas de los alimentos. Siempre decimos que cada alimento tiene su sello de olor propio. De hecho una misma comida preparada por dos personas distintas puede llegar a tener un sabor diferente, -“nadie hace la sopa de gallina como mi abuela”.
 Fuente: elgourmet.com
Fuente: elgourmet.comCon respecto a los factores de la salud que influencian los gustos, tenemos que tener en cuenta que los sabores que percibimos en la lengua y los olores que registramos en la mucosa pituitaria de la nariz, están regidos por receptores específicos. Esos receptores se conocen a nivel genético como lo demuestran Keller et al (2002). Variaciones en esos genes hacen que tengamos preferencias por determinadas comidas, como también que tengamos aprehensión por otras. Si por ejemplo no nos gustan los vegetales y no los integramos en nuestra dieta, es probable que tengamos alguna deficiencia en algunas de las vitaminas o fibras que aportan esos vegetales. Hay una tendencia a padecer enfermedades relacionadas a la alimentación cuando dejamos de tener una dieta variada y sólo ingerimos alimentos que son exclusivamente de nuestro agrado. De hecho se conoce desde hace mucho tiempo que los sabores dulces evolutivamente se relacionan con los alimentos y por eso disfrutamos de frutas dulces que nos aportan energía en forma de azúcares. Por otro lado, los sabores amargos se relacionan con la presencia de algunas sustancias tóxicas en vegetales, por eso somos reticentes a algunas verduras que persisten en sabores amargos, ¿acaso el café sin azúcar o la cerveza son bien recibidos en nuestra dieta desde un primer instante?.
Según el portal “Nutrición personalizada” la percepción del gusto amargo es un rasgo variable y su base genética fue identificada hace más de 70 años mediante una serie de estudios en respuestas individuales a la feniltiocarbamida (PTC). PTC y el compuesto relacionado 6-n-propiltiouracilo (PROP) son miembros de las tioureas y contienen una fracción tiocianato (N-C=S).
De acuerdo a la presencia de estos genes se puede decir que algunas personas son catadores, semi catadores y no catadores de los sabores amargos. Eso explicaría cómo habemos personas que odiamos profundamente la rúcula y cómo hay otras que les gusta, porque no perciben con fuerza el sabor amargo, incluso poniéndose de moda como un ingrediente gourmet.
Sin lugar a duda un componente fundamental en nuestra elección de diferentes gustos es la experiencia previa. En cada una de nuestras culturas (incluso algunas no muy distintas) desde pequeños probamos y nos amigamos con sabores ancestrales, a tal punto que en nuestra memora emotiva esos sabores nunca dejan de conmovernos. Recordamos lugares, paisajes, fiestas familiares o fiestas populares. Existen comidas especiales en algunas regiones (cada lector puede recordar en su caso particular) que mantienen sus recetas originales centenarias que han sufrido muy pocas modificaciones.
¿O sea que conociendo los antecedentes genéticos y culturales de una zona determinada podemos llegar a predecir cuáles serán los gustos de las personas de esa región? Esto es muy cierto. Muchas empresas de marketing se encargan de predecir los gustos de una población determinada para poder instalar productos de comercio. Esta realidad excede a los gustos culinarios y se hace extensible a todos los gustos para cualquier bien de consumo.
Volviendo a nuestra frase inicial, cuando hablamos de los gustos tendemos a pensar que los gustos son algo muy subjetivo, que es propio de cada persona en particular. No caemos en cuenta que sobre ese tema de verdad ya hay mucho escrito y a diario se usa para bombardearnos con publicidades para que compremos tal o cual producto, o que accedamos a promociones de “el producto que estamos buscando”. En fin, como vimos, sobre gustos ya hay mucho escrito.
Referencias:
Keller KL et al. (2002) Genetic taste sensitivity to 6-n-propylthiouracil influences food preference and reported intake in preschool children. Appetite 2002;38:3-12.
Variación genética en la percepción del gusto (2012) Nutrición personalizada
Archer, N. (2017) Curious Kids: why do some people find some foods yummy but others find the same foods yucky? The Conversation
Sobre el autor: Juan Felipe Castro es licenciado en ciencias biológicas y trabaja en el Instituto de Fisiología animal de la Fundación Miguel Lillo (Argentina) donde investiga en productos vegetales para el control de la glucemia.
El artículo Sobre gustos……¿no hay nada escrito? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Dudas sobre las vacunas: problemas y soluciones
- Sobre la predisposición genética a padecer enfermedades
- Sobre el origen del uso de herramientas en aves
El legado de Carlomagno
 Si visitas la catedral de Aquisgrán (Alemania) y tienes ascendencia europea puedes señalar a quien quiera oirte que aquí yacen los restos de un abuelo tuyo. Karlsschrein / Wikimedia Commons
Si visitas la catedral de Aquisgrán (Alemania) y tienes ascendencia europea puedes señalar a quien quiera oirte que aquí yacen los restos de un abuelo tuyo. Karlsschrein / Wikimedia CommonsTodos hemos tenido un padre y una madre biológicos. Ellos, a su vez, tuvieron los suyos, de manera que todos hemos tenido dos abuelos y dos abuelas; si seguimos la secuencia hacia atrás, ocho bisabuelos, dieciséis tatarabuelos, etc. Si cada generación está separada de la anterior por 30 años, podríamos haber llegado a tener unos 16 000 ascendientes al comienzo del siglo XVII, unos 16 millones a principios del XIV y unos 16 000 millones en los albores del XI, hace unos mil años. A estas alturas ya se ha dado usted cuenta de que eso, sencillamente, es imposible.
En efecto, sin tener que retrotraernos tanto, el número real de nuestros ascendientes es muy inferior al que se calcula haciendo esas operaciones. La razón es clara: muchos de nuestros ancestros lo son por varias líneas genealógicas. Esa eventualidad es más improbable cuanto más cercanos en el tiempo son los ascendientes, pero aumenta conforme vamos hacia atrás.
A comienzos del siglo XIV había unas 450 millones de personas en el Mundo (alrededor de 70 en Europa), por lo que bien pudieron haber vivido unos 16 millones de ancestros de cada uno de nosotros entonces. Pero hace mil años sólo vivían 400 millones (unos 50 en Europa). Por lo tanto, es matemáticamente imposible que viviesen 16 000 millones de antepasados nuestros en aquella época.
Hablamos con naturalidad de “árbol genealógico” porque visualizamos nuestros ancestros como un árbol que se ramifica poco a poco hacia atrás. Pero la realidad es muy diferente. Ya desde generaciones no tan lejanas algunas de las ramas confluyen, y si nos retrotraemos a tiempos remotos, ni siquiera cabe hablar de ramas. Las líneas genealógicas configuran una especie de maraña o, si se quiere, de malla con múltiples cruzamientos. Por otro lado, muchas líneas no dejan descendencia ninguna en cada generación. Conforme retrocedemos en el tiempo, la red va haciéndose más y más estrecha: se calcula que en los albores del Neolítico, hace unos 12 000 años, vivían en el mundo menos de 4 millones de personas, unos 60 millones en la época homérica, y mil millones al comienzo del siglo XIX.
Adam Rutherford cuenta, en su “Breve historia de todos los que han vivido”, que todos los que tenemos ascendencia europea procedemos, por una vía u otra, de Carlomagno. Todos pertenecemos, por lo tanto, a un linaje real. No es broma, aunque sea del todo irrelevante. Quienes tenemos algún ancestro europeo no solo descendemos de Carlomagno, también procedemos de todos los europeos de su época –alrededor del año 800– que dejaron descendencia y ha llegado hasta el siglo XXI. Se estima que la de un 20% no ha llegado.
No hace falta ir tan atrás en el tiempo para localizar el momento en que confluyen nuestras líneas genealógicas. Todos los europeos compartimos un antepasado común que vivió hace, aproximadamente, unos 600 años. Y si los mismos cálculos que han permitido obtener esa cifra se hacen para toda la humanidad, se estima que todos los seres humanos compartimos un antepasado común que vivió hace unos 3 400 años. Porque aunque cueste creerlo, no se sabe de ninguna población que haya permanecido completamente aislada durante los últimos siglos.
Estas cosas resultan desconcertantes. Piénselo si ha depositado una muestra de saliva en un tubito y le han dicho que en su linaje confluyen ascendientes de las tribus guerreras de las estepas rusas, de los bravos vikingos que sembraron el caos y la destrucción en Europa, y de los egipcios que levantaron las pirámides. Lo más probable es que usted tenga esa ascendencia. También la tengo yo.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo El legado de Carlomagno se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Ana Aguirre – Naukas Bilbao 2018: Somos binarios…. ¿o no?
 Foto: Mario Purisic / Unsplash
Foto: Mario Purisic / Unsplash¿Cuántos sexos, géneros, si así lo prefieres, diferentes tiene nuestra especie?¿Dos o más de dos? Tanto si tienes clara la respuesta como si no esta charla de Ana Aguirre te resultará extremadamente útil y esclarecedora… salvo si estás en el grupo de los negacionistas de la ciencia, claro. La charla solo tiene un problema: el volumen del sonido; aun así la publicamos debido a su excepcional calidad de fondo y forma.
Ana Aguirre es profesora titular de Genética en el departamento de Genética, Antropología Física y Fisiología Animal de la UPV/EHU. Su trayectoria profesional incluye la participación en investigaciones sobre la caracterización genética de poblaciones humanas, la detección de productos genotóxicos o la identificación de factores genéticos en la enfermedad de Huntington, entre otros temas.
Ana Aguirre: ''Somos binarios, ¿o no?''Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Ana Aguirre – Naukas Bilbao 2018: Somos binarios…. ¿o no? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Francisco R. Villatoro – Naukas Bilbao 2018: El ángulo mágico del grafeno
- Carlos Briones – Naukas Bilbao 2018: Os voy a contar una historia (en imágenes)
- Naukas Bilbao 2017 – Guillermo Peris: Los trapecistas del genoma
Detección e identificación de residuos de disparos a contrarreloj
Servicio Central de Análisis de Araba (SGIker – UPV/EHU)
 Foto: Sofia Sforza / Unsplash
Foto: Sofia Sforza / UnsplashHoy en día, la detección e identificación de residuos de disparos con arma de fuego (GSR, por sus siglas en inglés) proporciona información forense valiosa que generalmente se utiliza para determinar si una persona ha disparado un arma de fuego, confirmar una coartada, determinar orificios de entrada y salida de la bala, estimar de la distancia de disparo, establecer el tipo de munición utilizada, diferenciar entre suicidio u homicidio y en general, para relacionar a un individuo con una situación en la que se vea implicada el uso de un arma de fuego.
En el Servicio Central de Análisis de Álava (SGIker) se ha desarrollado un método basado en la ablación láser de barrido y espectrometría de masas con plasma de acoplamiento inductivo (SLA-ICPMS), cuya combinación instrumental ha sido aplicada para la caracterización de partículas GSR [1].
Este método ha permitido desarrollar un enfoque alternativo para la identificación inequívoca de GSR, lo que proporciona información precisa sobre la composición química de partículas GSR individuales de diferentes tipos de municiones.
El procedimiento más frecuentemente usado para el muestreo de residuos inorgánicos de la mano es una superficie de adhesivo de carbono como la que se muestra en la figura (muestreo de tape-lifting).
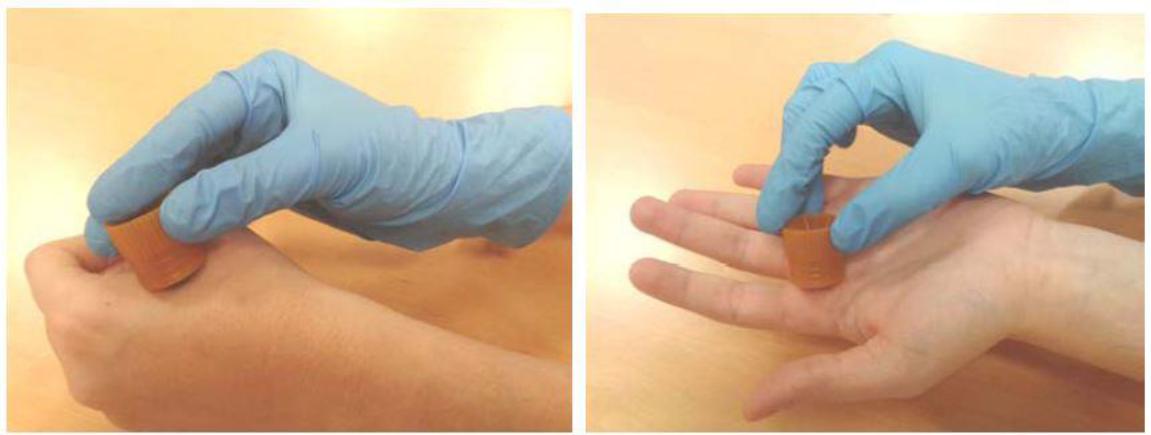 Imagen 1. Muestreo de GSR en manos con tape lifts comerciales. Fuente: Zuriñe Abrego, Characterization of gunshot residues by surface analysis techniques, UPV/EHU (2014) 1-313.
Imagen 1. Muestreo de GSR en manos con tape lifts comerciales. Fuente: Zuriñe Abrego, Characterization of gunshot residues by surface analysis techniques, UPV/EHU (2014) 1-313.La mayor parte de los residuos químicos que se producen en el disparo de un arma de fuego se depositan sobre las manos del tirador en forma de partículas metálicas de 0.5 a 5 µm de diámetro, que se deben recogen en un tiempo limitado ya que desaparecen por el contacto de las manos con diversas superficies o mediante su lavado.
El patrón de ablación láser y las condiciones de ICPMS se optimizaron para la identificación del perfil elemental de partículas GSR. Se seleccionaron 15 isótopos 121Sb, 137Ba, 208Pb,27Al, 29Si, 31P, 33S, 35Cl, 39K, 44Ca, 57Fe, 60Ni, 63Cu, 66Zn y 118Sn, que fueron monitoreados para obtener información sobre la composición de las partículas GSR y para clasificarlas como características de GSR o consistente con GSR.
Una vez que se verificó la validez del método, se realizó un estudio sobre muestras reales, muestreadas en campo de tiro (Academia de Policía de la Ertzainta, Arkaute, Álava). Se realizaron más de 1400 disparos, utilizando diferentes armas de fuego, calibres y municiones, que permitieron validar el estudio.
En posteriores trabajos se extendió esta metodología para la determinación de GSR de munición libre de plomo, en la que se monitorizaron otros metales característicos de este tipo de munición (Gd-Ti-Zn y Ga-Cu-Sn). Se desarrolló además un método de muestreo conjunto de GRS orgánicos e inorgánicos, que permitió determinar en la misma muestra ambos tipos de residuos: los primeros determinados mediante espectrometría de masas de tiempo de vuelo (LC-QTOF) y los segundos mediante SLA-ICPMS [2,3].
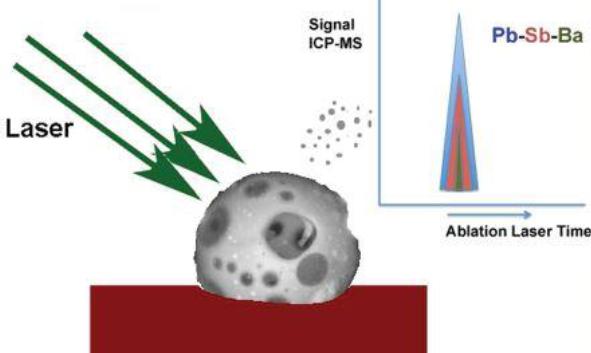 Figura 2. Esquema del proceso de ablación para la identificación de GSR por LA-ICP-MS. Fuente: Analytical Chemistry . 84 (2012) 2402–2409.
Figura 2. Esquema del proceso de ablación para la identificación de GSR por LA-ICP-MS. Fuente: Analytical Chemistry . 84 (2012) 2402–2409.Pero sin lugar a dudas, la principal ventaja de la metodología desarrollada, es que se puede usar como una alternativa a la técnica estándar de microscopía electrónica de barrido – espectroscopia de energía dispersiva (SEM-EDS), reduciendo drásticamente el tiempo de análisis a menos de 60 min. El hecho de que se tarde aproximadamente 1 hora en obtener resultados, frente a las 6-8 h de las técnicas habituales, aumenta la fiabilidad los procedimientos de cadena de custodia de las muestras, fundamentales en análisis forense.
Estos trabajos de investigación forman parte de la Tesis Doctoral de Zuriñe Abrego, “Characterization of gunshot residues by surface analysis techniques”, que mereció el premio extraordinario de doctorado.
Referencias:
[1] Z. Abrego, A. Ugarte, N. Unceta, A. Fernández-Isla, M. A. Goicolea, and R. J. Barrio*. Unambiguous Characterization of Gunshot Residue Particles Using Scanning Laser Ablation and Inductively Coupled Plasma-MassSpectrometry. Analytical Chemistry, 84 (2012) 2402–2409.
[2]. S. Benito, Z. Abrego, A.Sanchez, N. Unceta, M. A. Goicolea, R.J. Barrio. Characterization of organic gunshot residues in lead-free ammunition using a new sample collection device for liquid chromatography–quadrupole time-of-flight mass spectrometry Forensic Science International 246 (2015) 79–85
[3] Z. Abrego, N. Grijalba, N. Unceta, M. Maguregui, A. Sanchez, A. Fernandez-Isla, M. A. Goicolea and .R J. Barrio*A novel method for the identification of inorganic and organic gunshot residue particles of lead-free ammunitions from the hands of shooters using scanning laser ablation-ICPMS and Raman microspectroscopy. Analyst, 2014, 139, 6232
El artículo Detección e identificación de residuos de disparos a contrarreloj se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Bioóleo a partir de residuos cítricos
- Los residuos nucleares y la memoria de las arcillas
- La variedad de residuos madereros y la riqueza ecológica de los hayedos
Hay que ser más extenso y menos intenso…
 Foto: Lautaro Andreani / Unsplash
Foto: Lautaro Andreani / UnsplashSeguro que todos habéis tenido en vuestras manos alguna bengala encendida. Son una cosa casi mágica: fuego, chispas… follón. Lo que le gusta a cualquier crío.
Es posible que también hayáis dado un salto al ver que una chispa caía en vuestra piel o en vuestra ropa… con el consiguiente alivio y sorpresa al ver que no pasaba nada (a no se que, en lugar de una chispa, fuera un “trocito” de la bengala”).
¿Cómo es esto posible si la chispa de la bengala está a más de mil grados y ya chillamos si el agua de la ducha sale un poco caliente?
Quizá la culpa la tengamos los propios profesores, solemos decir que la temperatura de una idea de la energía térmica que hay en un sistema, y quizá dimos a entender que la temperatura y la energía térmica eran la misma cosa. Y no lo son.
Usemos un símil. Si te digo que tengo un conjunto de personas que con bastante dinero en sus bolsillos, ¿qué puedes decirme sobre la cantidad de dinero total de ese conjunto? Espera, otra pregunta, y si te digo que también tengo otro conjunto de personas con no demasiado dinero en sus bolsillos, ¿puedes saber si la cantidad de dinero total del primer conjunto es superior a la del segundo?
Efectivamente, no se puede afirmar absolutamente nada. Si el segundo conjunto es mucho más numeroso que el primero, podría tener un montante total muy superior. La medida “dinero por persona” no es suficiente para saber la “energía total” del conjunto. Bien, pues la temperatura se parece un poco a eso, a una variable que puede estimar la energía “promedio” de las partículas elementales que vibran o se mueven en un sistema.
Volviendo a nuestra bengala, podríamos decir que hay mucha “densidad de energía” en esa chispa tan pequeña, lo que no implica que la cantidad total de energía sea mucha, precisamente por lo pequeña que es. De esta forma, la chispa no tiene energía suficiente para quemarme.
En física llamamos variables intensivas a aquellas que no dependen del tamaño del sistema, como la temperatura o la densidad. Ya sabéis que la densidad del agua es, aproximadamente un kilogramo por litro, ya tengas un vaso o una piscina. La densidad nos da “cuánta masa hay en un volumen dado” no la cantidad global (como si habláramos de personas por metro cuadrado en una manifestación). Por eso bromas como “mira, estamos a dos grados centígrados, no tocamos ni a uno cada uno”, no tienen ningún sentido. Cada punto de la estancia estará a dos grados.
Hay otras variables que llamamos extensivas que sí que aumentan o disminuyen al cambiar el tamaño del sistema, como la masa, el volumen o la energía térmica. Una curiosidad, a veces al operar con variables extensivas nos da una variable intensiva. Por ejemplo, el volumen o la masa de un objeto son variables extensivas, si hago el objeto el objeto el doble de grande, tendrá dos veces el volumen, claro, y dos veces la masa. Pero si pienso en la densidad, que es la masa dividida por el volumen, esos dos factores “2” se simplifican y la densidad seguirá siendo la misma, sin variar por el tamaño del sistema, por lo tanto una variable intensiva.
Pero hablemos con un poco más de detalle de cómo se da la transferencia de energía entre los cuerpos calientes y los fríos (si no hay cambio de estado).
Primero, aclarar que la temperatura es una variable macroscópica, no tiene sentido decir que una molécula está a tantos grados centígrados, diremos que los sistemas macroscópicos están a cierta temperatura, y podremos relacionar esta magnitud con asuntos microscópicos como la velocidad a la que se mueven las partículas.
Digamos entonces que tenemos dos sistemas de distinta masa y de distinto material que están a distinta temperatura.
De nuestro símil de antes, sabemos que estos dos sistemas difieren tanto en la temperatura, como en la energía total que tienen, pudiendo suceder que tenga más energía térmica global aquel que tiene menor temperatura.
¿Qué pasa cuando los ponemos en contacto térmico?
Pues, antes de que empecéis a soltar hipótesis, os diré que pasa exactamente lo que le da la gana a la naturaleza. Nunca está de más recordar que la ciencia se basa en el empirísmo, en ver qué sucede y dar cuenta de ello intentando buscar patrones y regularidades.
Podría ser que la energía pasase del que tiene más energía al que tiene menos hasta igualarse las energías globales en ambos sistemas. Podría ser. Pero no es. Lo que ocurre es que la energía pasa de uno a otro hasta que las temperaturas se equilibran, quedando ambos sistemas con energías distintas, y a este “estado de vibración similar” es lo que llamamos equilibrio térmico y es de lo que habla la Ley Cero de la Termodinámica.
De esta forma, si el cuerpo frío tiene menos materia, con una fracción pequeña de energía proveniente del cuerpo grande, sería suficiente para agitar sus “pocas partículas” hasta tener “un estado de vibración similar” entre ambos sistemas, una misma temperatura.
Pero aún falta otro factor a tener en cuenta. La distinta naturaleza de los materiales entre ambos sistemas. Si un kilo de material absorbe una unidad de energía, ¿elevará su temperatura los mismos grados, sea cual sea el material? Podría ser, ya sabéis, no depende de lo que os apetezca u os parezca razonable. Podría ser… pero no.
Algunos materiales necesitan absorber mucha energía para que un kilo de sustancia incremente su temperatura un grado y otros, bastante menos. A esta característica le llamamos calor específico.
Así, hay sustancias que cuesta mucho calentar. Tú aportas y aportas energía, y aquello no sube la temperatura. Fíjate que también hay otra manera de ver este efecto: estos materiales funcionan como una “reserva de energía” porque al enfriarse, cederán un montón de energía cada grado que vayan bajando su temperatura.
Una sustancia común con una capacidad calorífica bastante relevante es el agua líquida y, por esa razón, funciona como un regulador de temperatura en la costa. Absorbiendo el calor cuando la temperatura es alta y cediéndolo cuando baja.
Esto se resume en una fórmula que quizá ahora os parezca muy sencilla de entender.
Q = m C (T2-T1)
La pondríamos en palabras así: El calor que un material absorbe o cede* al cambiar su temperatura de T1 a T2 es proporcional a cuánta materia hay y a cual es su calor específico.
Si volvemos a pensar en nuestra chispa, aunque la diferencia de temperatura con nuestra piel es elevada, debido a la poca masa, cuando iguale su temperatura con nosotros, el calor que nos cederá será una cantidad muy pequeña.
La idea de este artículo nace al ver un tuit en el que se hablaba de la influencia en el calentamiento global de las pruebas nucleares y detonaciones que se llevaron a cabo en la segunda mitad del siglo XX y argumentaban la enorme temperatura de esas explosiones.
Ya estáis en condiciones de buscar vuestra propia información (o hacer vuestros propios cálculos), lo que está claro es que esa afirmación no puede sostenerse exclusivamente argumentado la temperatura de las explosiones, hay que estimar qué energía total se disipó y cuánto aumento de temperatura sería capaz de producir en la atmósfera como conjunto.
Aquí tenéis un interesante hilo de Pedro J. Hernandez (@ecosdelfuturo) donde hace las cuentas… los números os sorprenderán. Agradecemos a Pedro, como siempre, su incansable labor en la información y el detalle.
Como suelo decir: El que mide, sabe. El que no, sólo opina.
Sobre el autor: Javier Fernández Panadero es físico y profesor de secundaria además de escritor de libros de divulgación.
[*] Nota del editor: Esto es una forma coloquial de hablar. En puridad lo que se absorbe o cede es energía y la forma en la que se transfiere es calor. El calor, recordemos, es una forma de transferencia de energía, no un fluido o cosa similar. Más aquí.
El artículo Hay que ser más extenso y menos intenso… se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Menos felices y menos insatisfechos a medida que envejecemos
- Una fórmula para dominarlos a todos: La conservación de la energía y la ley de la palanca
- No era tan fácil: wifi y cáncer
Shizuo Kakutani y sus teoremas
El matemático Shizuo Kakutani (1911-2004) nació tal día como hoy, hace 108i años.
 Shizuo Kakutani. Imagen: Wikimedia Commons.
Shizuo Kakutani. Imagen: Wikimedia Commons.
Es sobre todo conocido por haber demostrado el teorema del punto fijo que lleva su nombre y que generaliza el teorema del punto fijo de Brouwer:
Consideremos S un subconjunto no vacío, compacto y convexo del espacio euclidiano de dimensión n. Sea φ una función de S en el conjunto potencia de S, semicontinua superiormente, convexa y tal que φ(x) es un conjunto cerrado y no vacío para todo x en S. Entonces φ tiene un punto fijo.
Este teorema posee aplicaciones en economía y teoría de juegos. Por ejemplo John Nash lo utilizó para demostrar la existencia de equilibrios de Nash en estrategias mixtas.
Otras de sus contribuciones matemáticas son el teorema de Kakutani (todo cuerpo convexo en un espacio tridimensional tiene un cubo circunscrito, es decir, un cubo tal que todas sus caras tocan al cuerpo), el concepto de descomposición en rascacielos de Kakutani en teoría ergódica o su solución de la ecuación de Poisson usando métodos de análisis estocástico.
Kakutani ayudó a difundir la conjetura de Collatz, que a veces se nombra también “conjetura de Kakutani”. ¿Y qué dice la conjetura de Collatz? Lo vamos a recordar a través de un fragmento de la obra de teatro Incendios del dramaturgo Wajdi Mouawad. La siguiente es una conversación entre Jeanne, matemática, y su hermano gemelo Simon:
Jeanne (J): ¡De acuerdo! Hay una conjetura muy extraña en matemáticas. Una conjetura que nunca se ha demostrado. Me vas a dar un número, cualquiera. Si el número es par, se divide por dos. Si es impar, se multiplica por tres y se suma uno. Haremos lo mismo con el número que se obtiene. Esta conjetura afirma que cualquiera que sea el número de partida, por este procedimiento se llega siempre a uno. Di un número.
Simon (S): Siete.
J: Bueno siete es impar. Lo multiplicamos por tres y le añadimos uno, da…
S: Veintidós.
J: Veintidós es par, se divide por dos.
S: Once.
J: Once es impar, se multiplica por tres, y se añade uno:
S: Treinta y cuatro.
J: Treinta y cuatro es par. Se divide por dos, diecisiete. Diecisiete es impar, se multiplica por tres, y se suma uno, cincuenta y dos. Cincuenta y dos es par, se divide por dos, veintiséis. Veintiséis es par, se divide por dos, trece. Trece es impar. Se multiplica por tres y se suma uno cuarenta. Cuarenta es par, se divide por dos, veinte. Veinte es par, se divide por dos, diez, diez es par, se divide por dos, cinco. Cinco es impar, se multiplica por tres y se suma uno. Dieciséis. Dieciséis es par, se divide por dos, ocho, ocho es par, se divide por dos, cuatro, cuatro es par, se divide por dos, dos, dos es par, se divide por dos, uno. Independientemente de la cifra inicial, se llega a… ¡No!
¿A qué se llega? Al número 1.
En este enlace, puedes introducir el número que quieras y comprobar que, efectivamente, realizando las operaciones indicadas se llega a 1…
Por si acaso, he hecho una prueba con el famoso número 241543903 y, siguiendo la regla antes explicada, este calculador ha ido obteniendo los siguientes números:
241543903, 724631710, 362315855, 1086947566, 543473783, 1630421350, 815210675, 2445632026, 1222816013, 3668448040, 1834224020, 917112010, 458556005, 1375668016, 687834008, 343917004, 171958502, 85979251, 257937754, 128968877, 386906632, 193453316, 96726658, 48363329, 145089988, 72544994, 36272497, 108817492, 54408746, 27204373, 81613120, 40806560, 20403280, 10201640, 5100820, 2550410, 1275205, 3825616, 1912808, 956404, 478202, 239101, 717304, 358652, 179326, 89663, 268990, 134495, 403486, 201743, 605230, 302615, 907846, 453923, 1361770, 680885, 2042656, 1021328, 510664, 255332, 127666, 63833, 191500, 95750, 47875, 143626, 71813, 215440, 107720, 53860, 26930, 13465, 40396, 20198, 10099, 30298, 15149, 45448, 22724, 11362, 5681, 17044, 8522, 4261, 12784, 6392, 3196, 1598, 799, 2398, 1199, 3598, 1799, 5398, 2699, 8098, 4049, 12148, 6074, 3037, 9112, 4556, 2278, 1139, 3418, 1709, 5128, 2564, 1282, 641, 1924, 962, 481, 1444, 722, 361, 1084, 542, 271, 814, 407, 1222, 611, 1834, 917, 2752, 1376, 688, 344, 172, 86, 43, 130, 65, 196, 98, 49, 148, 74, 37, 112, 56, 28, 14, 7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2 y 1.
¡Bien! Pasando por 109 números pares y 51 impares, hemos verificado lo que dice la conjetura de Kakutani con el número 241543903, un número cualquiera. ¿Será cierta la conjetura de Collatz? ¿O quizás alguien consiga encontrar un contraejemplo? El tiempo lo dirá…
Más información
-
In Memoriam: Shizuo Kakutani, noted mathematician and inventor, Yale Bulletin & Calendar 33 (1), 27 agosto 2004
-
John J. O’Connor y Edmund F. Robertson, Shizuo Kakutani, MacTutor History of Mathematics archive, Universidad de Saint Andrews
BONUS: Entre otras propiedades matemáticas, 108 es un número abundante (hablamos de este tipo de números en Sumas y sucesiones alícuotas), semiperfecto, tetranacci, hiperfactorial, refactorable o de Devlali. Además, es el número atómico del elemento hasio y la medida (en grados) de los ángulos internos de un pentágono regular. Y, por cierto, con una temperatura interna de 108 grados Fahrenheit (algo más de 42 grados centígrados), los órganos vitales del cuerpo humano comienzan a fallar por sobrecalentamiento…
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo Shizuo Kakutani y sus teoremas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Una conjetura sobre ciertos números en el ‘sistema Shadok’
- Incendios, los grafos de visibilidad y la conjetura de Collatz
- El teorema de Ducci
Las regularidades en el espectro del hidrógeno
 Foto: Adam Kring / Unsplash
Foto: Adam Kring / UnsplashLas ideas de Balmer sobre el espectro del hidrógeno tuvieron un éxito enorme. Veámoslo.
Para usar la notación moderna, reescribimos la fórmula de Balmer λ = b [n2/(n2-22)] en una forma que nos será más útil:
1/λ = RH (1/22 – 1/n2)
En esta ecuación que, como decimos, puede derivarse de la anterior, RH es una constante, igual a 4 / b. Se llama constante de Rydberg para el hidrógeno, en honor del espectroscopista J.R. Rydberg. Continuando el trabajo de Balmer, Rydberg hizo un gran progreso en la búsqueda de varias series espectrales. La serie de líneas descritas por la fórmula de Balmer se llama la serie de Balmer. Balmer construyó su fórmula a partir de las longitudes de onda conocidas de solo cuatro líneas en la parte visible del espectro. Esta fórmula de Balmer predice correctamente cada una de estas cuatro líneas con una precisión considerable. La fórmula, sin embargo, parecía indicar que podrían existir muchas más líneas en la misma serie [1]. Además,
La sugerencia especulativa [2] de Balmer de reemplazar 22 por otros números ofrece las siguientes posibilidades:
1/λ = RH (1/12 – 1/n2)
1/λ = RH (1/32 – 1/n2)
1/λ = RH (1/42 – 1/n2)
…
Cada una de estas ecuaciones describe una posible serie de líneas de emisión. Todas estas series hipotéticas de líneas pueden resumirse en una fórmula general
1/λ = RH (1/nf2 – 1/ni2)
donde nf sería un número entero que es fijo para cada serie para la que se encuentren longitudes de onda (por ejemplo, nf = 2 para todas las líneas de la serie Balmer). Por otro lado ni representa enteros que toman los valores nf + 1, nf + 2, nf + 3,. . . para las sucesivas líneas individuales en una serie dada (las cuatro primeras líneas de la serie de Balmer, ni toma por tanto los valores 3, 4, 5, y 6) La constante RH debe tener el mismo valor para todas las series del hidrógeno.
Reiteremos que todo esto es pura especulación [2]. No hay nada que indique que deba existir ninguna otra serie, ninguna línea que se ajuste a la fórmula general, excepto la serie de Balmer observada experimentalmente, donde nf = 2. Pero resultó que, cuando la comunidad científica se puso a buscar estas líneas hipotéticas con buenos espectrómetros descubrió que, de hecho, ¡existen!
En 1908, F. Paschen encontró dos líneas del hidrógeno en el infrarrojo. Sus longitudes de onda se correspondían con notable precisión a la fórmula general estableciendo nf = 3 y ni = 4 y 5. Desde entonces, se han identificado muchas otras líneas en esta «serie de Paschen». Con técnicas y aparatos experimentales mejorados, se pudieron explorar nuevas regiones del espectro. Así, se fueron agregando gradualmente otras series a las series de Balmer y de Paschen. Las series del espectro del hidrógeno descubiertas son las siguientes (entre paréntesis año de descubrimiento):
Lyman (1906–1914) nf =1, ni = 2, 3, 4, . . . en el ultravioleta;
Balmer (1885) nf = 2, ni = 3, 4, 5, . . . en el ultravioleta-visible;
Paschen (1908) nf = 3, ni = 4, 5, 6, . . . en el infrarrojo;
Brackett (1922) nf = 4, ni = 5, 6, 7, . . . en el infrarrojo;
Pfund (1924) nf = 5, ni = 6, 7, 8, . . . en el infrarrojo;
Humphreys (1953) nf = 6, ni = 7, 8, 9, . . .en el infrarrojo.
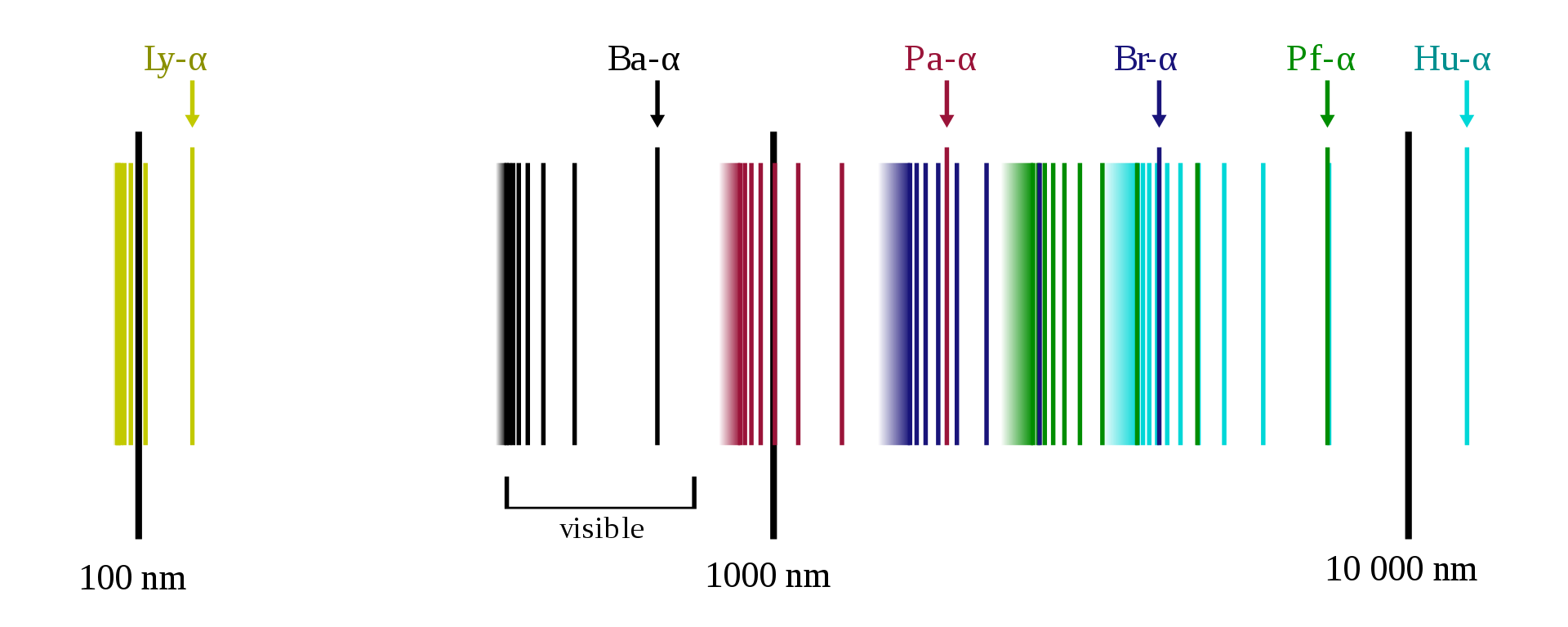 Líneas espectrales del hidrógeno en escala logarítmica. Se señala la primera línea (α) de cada una de las series. Imagen: Wikimedia Commons
Líneas espectrales del hidrógeno en escala logarítmica. Se señala la primera línea (α) de cada una de las series. Imagen: Wikimedia CommonsBalmer también especuló con la idea de que su fórmula para el espectro del hidrógeno pudiera ser un patrón para encontrar relaciones en los espectros de otros gases. Esta sugerencia también dio fruto. La fórmula de Balmer en sí misma no funcionó directamente para describir espectros de gases distintos al hidrógeno. Pero sí inspiró fórmulas de forma matemática similar que describieron con éxito el orden en porciones de muchos espectros complejos [3].
Para sorpresa de muchos y desesperación de otros no se podía construir ningún modelo basado en la mecánica clásica y el electromagnetismo que explicara los espectros descritos por estas fórmulas.
Lo que ya hemos visto sobre la teoría cuántica sugería una línea de ataque. Obviamente, la emisión y absorción de luz de un átomo debe corresponder a una disminución y un aumento de la energía del átomo. Si los átomos de un elemento emiten luz de solo ciertas frecuencias, entonces la energía de los átomos debe poder cambiar solo en ciertas cantidades. Estos cambios de energía deben implicar la reorganización de las partes del átomo. Se hacía imprescindible cambiar radicalmente el enfoque a la hora de construir un modelo de átomo viable. Pero era necesario un ingrediente fundamental adicional antes de que se construyese un modelo atómico que pudiese tener éxito: el descubrimiento de que el átomo es, básicamente, espacio vacío.
Notas:
[1] De hecho, infinitas, ya que n = 3, 4, 5, 6, 7, 8,… ∞
[2] Y numerológica. Es por pura simetría matemática. Funciona porque funciona, pero recordemos que tras la sugerencia de Balmer no hay ninguna base física a priori.
[3] La constante de Rydberg RH también reapareció en estas fórmulas empíricas.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Las regularidades en el espectro del hidrógeno se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Las líneas de Balmer
- El hidrógeno en el Universo (I): La emisión del hidrógeno neutro a 21 cm.
- La ley del gas ideal y la tercera ley de la termodinámica
Los límites del ferrocarril
Iván Rivera
 Foto:Konstantin Planinski / Unsplash
Foto:Konstantin Planinski / UnsplashYa han pasado doce años desde que se logró el récord del mundo de velocidad en ferrocarril. La que se dio en llamar «Operación V150» por la velocidad objetivo, 150 metros por segundo o 540 kilómetros por hora, ocupó desde enero de 2007 hasta abril del mismo año a un equipo formado por la operadora SNCF, el gestor de infraestructuras Réseau Ferré de France y el fabricante de material móvil Alstom. El 3 de abril, a las 13 horas, 13 minutos y 40 segundos, el TGV V150 construido para la ocasión por esta última empresa alcanzó los 574,8 km/h en el punto kilométrico 194 de la línea TGV-Est entre las estaciones de Prény y Champagne-Ardennes, cerca de la localidad de Éclaires —quizá en un giro involuntariamente poético para los ingenieros a cargo: éclaires significa en español «(tú) iluminas».
Con un gasto de 30 millones de euros, la Operación V150 no fue solo un ardid publicitario para cementar el prestigio nacional de una industria ante la dura competencia alemana y, cada vez más, china. Durante los múltiples recorridos de prueba en los que el anterior récord de 1990 (515,3 km/h) fue superado extraoficialmente en varias ocasiones, los ingenieros del proyecto monitorizaron en detalle el comportamiento del vehículo, la vía y la catenaria para determinar en cada caso sus límites operativos.
Más de una década después, ¿qué conclusiones pueden extraerse de este experimento para el ferrocarril? ¿Por qué la velocidad máxima de los trenes ha parecido estancarse en los 350 kilómetros por hora desde hace décadas? Para entenderlo, hagamos un repaso por el sistema ferroviario prestando especial atención a los factores susceptibles de limitar su rendimiento.
El contacto rueda-carril
El tren es un medio de transporte terrestre guiado, lo que significa que solo puede moverse a lo largo de una estructura —la vía— formada por raíles paralelos entre sí, mantenidos en su sitio mediante sujeciones a unas piezas usualmente de hormigón denominadas traviesas. La vía no está anclada a su plataforma: solo descansa sobre ella. Su estabilidad está asegurada por su propio peso. Las ruedas del tren, de acero como los raíles, tienen un perfil ligeramente cónico rematado por una pestaña por el lado interior que asegura que los ejes se mantengan centrados sobre la vía sin descarrilamientos [Casanueva, 2014]. El perfil de las ruedas garantiza el centrado durante la mayor parte de los trayectos apoyándose sobre la cabeza del raíl, mientras que las pestañas sujetan al tren en caso de desplazamientos laterales excesivos.
 Imagen1. Rueda y carril. Foto: CAF.
Imagen1. Rueda y carril. Foto: CAF.
Cuando la vía no se bifurca, presenta una estructura geométrica formada por secuencias de rectas y arcos de circunferencia unidos entre sí mediante curvas de acuerdo para evitar discontinuidades en el radio de curvatura —infinito en una recta, finito en plena curva— y, por tanto, eliminando así posibles saltos en la aceleración radial experimentada por los trenes a lo largo de su trayecto. Para limitar aún más esta aceleración y tolerar radios de curvatura más pequeños, las vías van peraltadas: el plano de rodadura se inclina hacia el lado interior de la curva con un ángulo que depende de la velocidad esperada de los trenes y su peso por eje.
Sin duda, el contacto rueda-carril es uno de los grandes inventos de la humanidad a la hora de reducir la energía necesaria para transportar grandes cantidades de pasajeros y carga. La superficie de contacto por rueda sobre la cabeza del carril apenas es de 250 mm², garantizando unas fuerzas de rozamiento mínimas —el coeficiente de resistencia a la rodadura del acero sobre acero es, en el peor de los casos, 30 veces menor que el del caucho sobre asfalto.
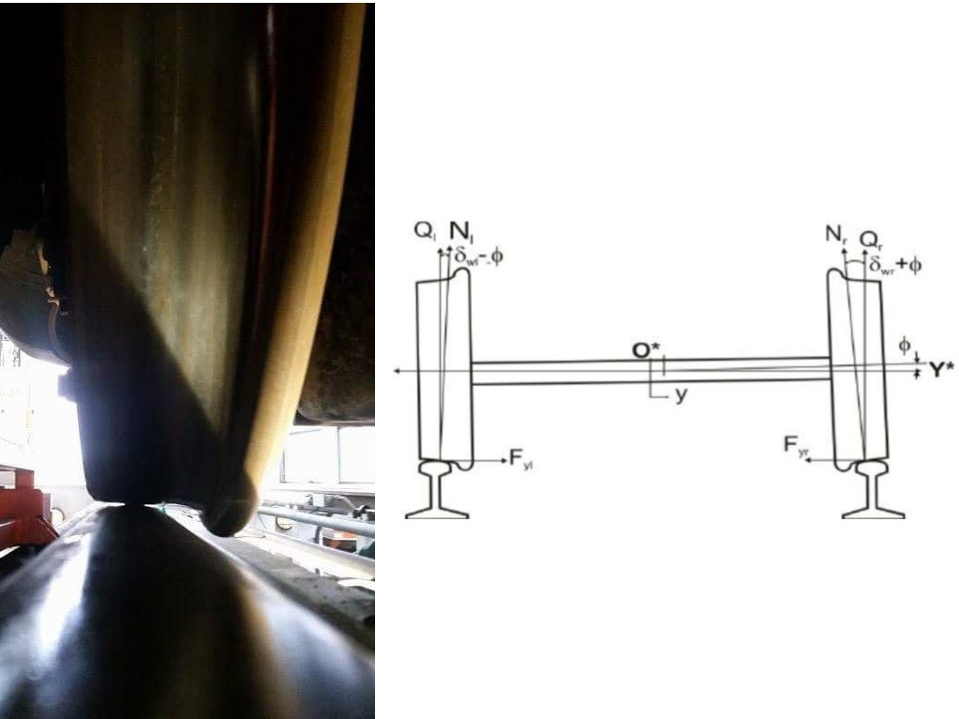 Imagen 2. Contacto rueda-carril: detalle y diagrama. Fuente: TER Pays de la Loire / Anyakwo, Pislaru, Ball, & Gu, 2011.
Imagen 2. Contacto rueda-carril: detalle y diagrama. Fuente: TER Pays de la Loire / Anyakwo, Pislaru, Ball, & Gu, 2011.Sin embargo, en Física nunca se obtiene nada sin sacrificar otra cosa a cambio: la capacidad de mover centenares de toneladas con una fuerza de tracción moderada solo se obtiene a cambio de perder la capacidad de frenar en espacios cortos o de superar pendientes pronunciadas. Es totalmente intuitivo si pensamos en cómo se comporta un automóvil sobre asfalto frente a su respuesta sobre hielo. Si, además, reducimos la anchura de las ruedas y las fabricamos en un material de menor coeficiente de rozamiento («más liso»), no debería resultar extraño que un tren ligero de viajeros requiera algún centenar de metros para detenerse, mientras que un mercante pesado necesite uno o dos kilómetros de vías.
La aerodinámica
Tiempo atrás los trenes tenían testeros —la denominación en jerga ferroviaria del frontal— completamente rectangulares. La velocidad que alcanzaban no era suficiente para que los ingenieros debieran preocuparse por la resistencia que opusiera el aire al avance de un vehículo tan pesado. Sin embargo, el advenimiento de plantas motrices más capaces trajo consigo la preocupación por encontrar formas que permitieran «penetrar» el aire más fácilmente. Hay que buscar el origen de todo ello en la relativamente sencilla ecuación de la fuerza de arrastre aerodinámico, que establece que la resistencia al avance debida al aire es directamente proporcional al cuadrado de la velocidad [1].
 Imagen 3. Locomotora de vapor Mallard en el National Railway Museum, York. Foto: PTG Dudva.
Imagen 3. Locomotora de vapor Mallard en el National Railway Museum, York. Foto: PTG Dudva.La lucha por reducir al mínimo el coeficiente de arrastre aerodinámico, en principio empírica y realizada en túneles de viento, y más adelante numérica y ejecutada mediante simulaciones llevadas a cabo en ordenadores de gran potencia de cálculo, tiene límites. Un carenado con un buen coeficiente puede mejorarse mediante faldones específicos para los pantógrafos, sistemas de enganche escamoteables o reduciendo la separación entre coches (vagones, una vez más en jerga ferroviaria). Sin embargo, es fácil ver que rápidamente es necesario llegar a compromisos con la mantenibilidad del sistema o su propia durabilidad. En particular, la separación entre coches debe ser la suficiente como para acomodar sus conexiones flexibles durante la inscripción del tren en las curvas. Cómo un tren formado por elementos fundamentalmente rígidos toma curvas con facilidad es materia para otro artículo.
El contacto pantógrafo-catenaria
La interfaz rueda-carril es la más evidente para quien no haya prestado demasiada atención a la disposición física del sistema ferroviario. Es, además, la única interfaz mecánica que presentan los trenes de propulsión diésel. Sin embargo, las plantas motrices diésel tienen limitaciones intrínsecas que no afectan a los trenes eléctricos y que se resumen en que el rendimiento de los motores de combustión interna tiene un límite impuesto por el segundo teorema de Carnot y la temperatura (fija) de la combustión de la mezcla diésel-aire. Ningún motor diésel presenta rendimientos superiores al 48%, por lo que disponer de más potencia —y a la postre más velocidad— es cuestión, únicamente, de aumentar el número de cilindros. Aumenta así también el consumo de combustible, que debe ser además transportado en depósitos específicos.
El conjunto de compromisos de ingeniería en los que se incurre deriva en que el récord mundial de velocidad de un tren con planta motriz diésel está fijado desde 1987 en 238 km/h, aunque no sin cierta polémica: el prototipo Talgo XXI (actualmente al servicio del gestor de infraestructuras Adif como tren laboratorio) alcanzó los 256,38 km/h entre Olmedo y Medina del Campo en 2002, aunque no se aceptó oficialmente el registro por la falta de una verificación independiente.
 Imagen 4. Talgo XXI «Virgen del Pilar» en 2002. Foto: Photocapy
Imagen 4. Talgo XXI «Virgen del Pilar» en 2002. Foto: PhotocapyLos trenes eléctricos presentan una segunda interfaz mecánica. Al no transportar su propia fuente de energía, un tren eléctrico debe avanzar gracias a la corriente eléctrica que toma gracias a un contacto móvil con una estructura conductora ubicada sobre las vías. El contacto móvil se efectúa mediante el pantógrafo: un brazo articulado que mantiene una mesilla con una banda frotadora presionando contra el hilo de contacto, un hilo en aleación de cobre con plata con una resistencia muy baja al paso de la corriente, un coeficiente de rozamiento por fricción muy bajo y una alta resistencia al desgaste.
El hilo de contacto está sujeto —abusando un poco de la terminología— a dos tensiones. Por un lado, la tensión eléctrica que establece (dada la resistencia constante del metal empleado) la máxima corriente que puede solicitar el motor del tren. Por otro, la tensión mecánica que lo mantiene lo más horizontal posible, ya que la mejor calidad del contacto se obtendrá cuanto más regular sea. Naturalmente, el peso propio del hilo provoca una flecha: una diferencia de alturas entre los apoyos del sistema y el centro del vano. La flecha se reduce aumentando la tensión mecánica, que se consigue gracias a sistemas denominados de compensación automática: equipos compuestos por polipastos y contrapesos que mantienen constante la tensión mecánica del hilo de contacto ante los cambios de temperatura diarios y estacionales.
 Imagen 5. Poleas del sistema de compensación automática de tensión en
Imagen 5. Poleas del sistema de compensación automática de tensión encatenaria de alta velocidad. Foto: Electrén, S.A.
Las fuerzas involucradas en el contacto pantógrafo-catenaria son despreciables a la hora de calcular la resistencia al avance de un tren, pero deben ser tenidas en cuenta para determinar la durabilidad de la propia catenaria. Al tratarse de una estructura ligera mantenida en tensión mecánica y atravesada por un flujo de corriente eléctrica, la catenaria puede resultar dañada tanto por causas mecánicas como eléctricas. Estos daños pueden ser nominales, provocando desgastes esperables en la estructura, o catastróficos, provocando cortes del hilo o enganchones en el pantógrafo.
La Operación V150
Los trabajos de la Operación V150 se desarrollaron en un doble sentido. Por un lado, se procedió a la construcción de una unidad laboratorio capaz de superar la velocidad de 150 m/s (540 km/h) —de ahí el nombre del proyecto, TGV V150 (Train à Grande Vitesse, tren de alta velocidad). Por el otro, se acondicionó un tramo de 94 kilómetros especialmente escogido de la línea TGV Est con una ligera pendiente descendiente uniforme y radios de curvatura suficientemente amplios para acomodar sin problemas el conjunto de pruebas a realizar. Las circulaciones del proyecto comenzaron en enero de 2007 y terminaron en abril, aumentando paulatinamente la velocidad. Se registraron un total de casi 1000 kilómetros a velocidades superiores a los 500 km/h.
La unidad V150 estaba formada por una inusual composición de dos cabezas motrices situadas entre tres coches remolque: dos unidades de doble cubierta y un coche cafetería central, especialmente construido para la ocasión y habilitado como laboratorio. Además, disponía de una serie de modificaciones especialmente concebidas para el intento de récord.
 Imagen 6. Cabeza tractora y coche de la composición, expuestas en París tras la campaña del récord. Foto: Gonioul.
Imagen 6. Cabeza tractora y coche de la composición, expuestas en París tras la campaña del récord. Foto: Gonioul.La propulsión estaba garantizada por las dos cabezas motrices («locomotoras», traduciendo una vez más de la jerga profesional) y por dos bogies motores [2] articulados AGV montados en los extremos del coche cafetería. Los motores asíncronos de las cabezas habían sido potenciados un 56% por encima del valor habitual en su clase, hasta llegar a los 1950 kW. Los motores síncronos de imanes permanentes de los bogies fueron ajustados igualmente hasta alcanzar los 1000 kW (un 39% por encima de su potencia nominal). El conjunto podía desarrollar así una potencia total de 19,6 MW.
Se recurrió a un «viejo truco» empleado en las locomotoras de vapor para mejorar la velocidad a expensas del par motor —lo que afecta, fundamentalmente, a la capacidad de arranque: usar ruedas de un diámetro mayor. Se montaron ruedas de 1092 mm frente a las habituales de 920 mm. El ligero incremento de la altura del conjunto fue compensado, para mejorar sus prestaciones aerodinámicas, con mayores faldones en todo su contorno.
Además de éste, las modificaciones destinadas a enfrentar el flujo de aire a velocidades superiores a los 150 m/s fueron muy numerosas. Se sustituyó el carenado retráctil de dos piezas que protege el sistema de enganche automático de los testeros con una sola pieza continua. Se montó un parabrisas especial enrasado con la carrocería, y se desmontó el limpiaparabrisas. Toda la superficie inferior del conjunto fue panelada para reducir la resistencia aerodinámica y proteger los componentes expuestos al fenómeno de vuelo de balasto que producen las turbulencias propias de la circulación a altas velocidades.
Además, los pantógrafos de corriente continua que permiten la operación de las cabezas motrices en vías alimentadas de esta forma fueron retirados, y sus huecos panelados y enrasados. Las separaciones entre coches fueron protegidas con juntas flexibles superficiales. Incluso llegaron a diseñarse faldones específicos para los bogies, que finalmente no fueron utilizados durante la prueba del récord.
Las modificaciones de la infraestructura
El ferrocarril es un sistema de transporte en el que los vehículos y su infraestructura correspondiente están fuertemente acoplados. Por este motivo, era de esperar que la vía y la catenaria del programa V150 también sufrieran una serie de ajustes y modificaciones destinadas a garantizar un resultado final exitoso.
Los acuerdos entre rectas y arcos de circunferencia del trayecto fueron exhaustivamente revisados y ajustados para garantizar una transición completamente suave en la aceleración normal. Los peraltes de todas las curvas, así como sus correspondientes acuerdos de peralte, fueron aumentados hasta en 130 mm para evitar que el tren pudiera rodar bajo la condición conocida como «insuficiencia de peralte», que provoca que las pestañas de las ruedas del lado exterior de la curva rocen la cabeza del carril, provocando el desgaste prematuro tanto de éste como de las ruedas.
Se utilizó un balasto especialmente perfilado para reducir el impacto del ya citado efecto de vuelo. Finalmente en lo que respecta a la vía, todas las agujas existentes en el trayecto de prueba (del tipo conocido como corazón móvil) fueron enclavadas manualmente en la posición de vía directa, reduciendo así al mínimo toda posible discontinuidad física en los carriles.
 Imagen 7. Tramo de ensayos de aerotraviesas —resultado de un desarrollo de Adif y SENER para minimizar el vuelo de balasto. Foto: Adif.
Imagen 7. Tramo de ensayos de aerotraviesas —resultado de un desarrollo de Adif y SENER para minimizar el vuelo de balasto. Foto: Adif.Por lo que respecta a la catenaria, se realizaron cambios tanto de la alimentación eléctrica como mecánicos. Los grupos de subestaciones y autotransformadores destinados a mantener un voltaje constante sin carga de 25 kV de corriente alterna en todo el trayecto fueron alterados para suministrar voltajes máximos de 31,7 kV. Se añadieron bancos de condensadores especialmente diseñados para apoyar a los autotransformadores y absorber la potencia reactiva extra generada por las mayores cargas inductivas de los motores de la unidad V150.
El factor clave para la circulación a muy alta velocidad, sin embargo, es la respuesta mecánica de la catenaria. Su comportamiento es sencillo de entender si imaginamos un dedo pulsando una cuerda de guitarra. El «dedo» representa el pantógrafo de un tren. Al desplazarse longitudinalmente por la catenaria aplicando una fuerza vertical para garantizar la continuidad del contacto eléctrico, el pantógrafo crea una onda que se desplaza en ambos sentidos a lo largo de cada cantón (tramo) de compensación automática de la tensión mecánica de la catenaria.
La frecuencia de la onda generada aumenta con la tensión mecánica —y por ese motivo las cuerdas más tensas de una guitarra suenan más agudas. Pero si el dedo se desplaza presionando la cuerda en vez de pulsarla, la onda deja de ser estática para pasar a desplazarse con una velocidad proporcional a la tensión mecánica e inversamente proporcional a la masa por unidad de longitud del material [3].
Esta situación ideal se ve modificada por la existencia de masas fijas en la catenaria, necesarias para su sujeción mecánica. Las péndolas y los brazos de atirantado, que permiten mantener la forma del hilo de contacto anclándolo al hilo sustentador y a los postes respectivamente, provocan ondas reflejadas que alteran el comportamiento del conjunto. A velocidades elevadas la interacción dinámica entre el pantógrafo y la catenaria se complica aún más debido al efecto Doppler que acorta las ondas en el sentido de avance (y las alarga en el sentido contrario).
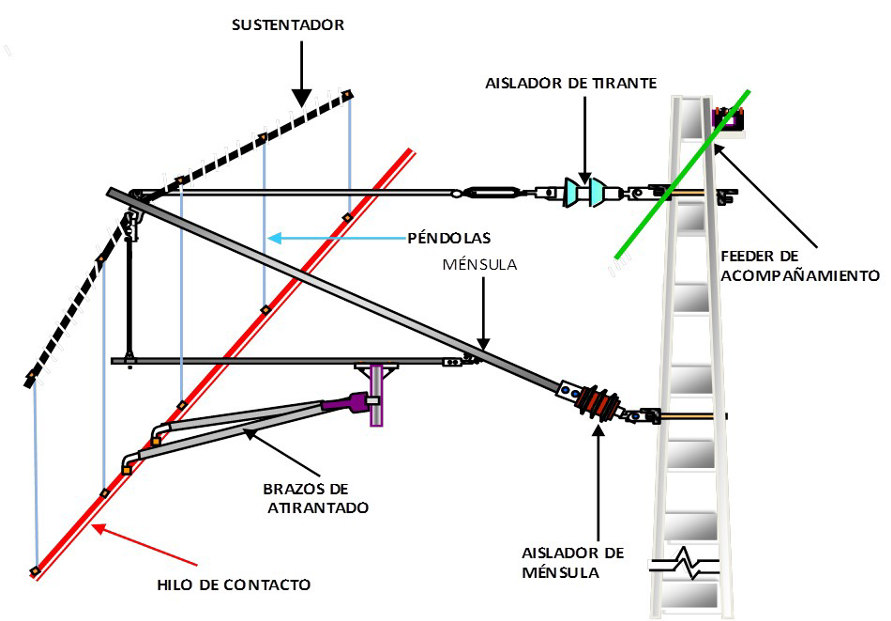 Imagen 8. Diagrama descriptivo de una catenaria de alta velocidad.
Imagen 8. Diagrama descriptivo de una catenaria de alta velocidad.Fuente: Adif.
Dado que el hilo de contacto usado durante las pruebas del récord es el mismo que se utiliza en producción, el único parámetro que podía alterarse era su tensión mecánica: de los 25 kN nominales se aumentó hasta 40 kN —la tensión equivalente a colgar del hilo una masa de 4 toneladas, aproximadamente. La velocidad estimada para la perturbación ondulatoria resultante sería de 610 km/h, dejando suficiente margen de seguridad respecto de la velocidad finalmente alcanzada por el tren.
El récord
A las 13 horas exactas del día 3 de abril, Daniel Beylot, jefe de la Operación V150, dio la orden de arranque. Reconoce la orden Eric Pieczak, el maquinista designado para conducir el tren durante el intento de récord. En la cabina le acompañan Georges Pinquié, inspector de tracción y Claude Maro, director del departamento correspondiente. A bordo del tren, y mostrando la confianza absoluta de los ingenieros en la seguridad de la prueba, se encuentran 105 personas, incluyendo a la presidenta de la SNCF, Anne-Marie Idrac, su director general, Guillaume Pépy, el presidente de RFF, Hubert du Mesnil y el comisario europeo de Transportes, Jacques Barrot, junto con un nutrido complemento de invitados y periodistas.
Tres cámaras de televisión de gran formato y diez minicámaras adicionales montadas en diferentes puntos del tren transmitían imágenes en directo a los informativos nacionales. Junto a la vía, siete cámaras adicionales capturarían imágenes del tren —una en el lugar de partida y otra en el de llegada, con cinco más dispuestas en la zona en la que se esperaba conseguir el récord de velocidad. Una cámara adicional a bordo de un avión reactor Aérospatiale Corvette seguiría la totalidad del trayecto. Los alrededores de la vía, y muy en particular todos los pasos superiores y la estación de Meuse, a mitad del trayecto, están abarrotados de espectadores.
El tren sale de Prény y rápidamente alcanza la zona neutra de la catenaria que separa la alimentación convencional de 25 kV de alta velocidad de la especial a 31 kV, proporcionada desde la subestación especialmente preparada de Trois Domaines. Siguiendo el protocolo habitual en el cambio de alimentación, Pieczak baja el pantógrafo al entrar en la zona neutra, y vuelve a elevarlo a la salida. Son las 13 horas y cinco minutos.
Al alcanzar los 500 km/h la cámara que muestra la situación del pantógrafo muestra ya un arco continuo. Los arcos, provocados por pequeños despegues del pantógrafo y el hilo de contacto, son uno de los factores fundamentales que reduce la durabilidad de ambos elementos. A las 13 horas y 10 la estación de Meuse pasa ante los ojos de los pasajeros como una exhalación. El tren levanta a su paso una nube de polvo proveniente del balasto sobre el que descansa la vía. La velocidad es de 535 km/h.
 Imagen 9. El TGV V150 en el momento del récord. Foto: Alain Stoll.
Imagen 9. El TGV V150 en el momento del récord. Foto: Alain Stoll.El objetivo oficial del intento de récord son los 540 km/h, que se superan entre aplausos. También se superan en breve los 550. Finalmente, el tren supera los 574 km/h antes de comenzar su deceleración. A las 13:30 ya está deteniéndose en el andén de la estación de Champagne-Ardenne. El tour de force publicitario se ha conseguido.
¿El cielo es el límite?
Los ingenieros de Alstom parecieron confiados en que la prueba no sujetó a su tren a ninguna condición límite. Creían posible superar los 600 km/h, aunque esa velocidad hubiera puesto al pantógrafo peligrosamente cerca de la de la perturbación ondulatoria de la catenaria. De superarla, el tren adelantaría a su propia onda generada en un efecto similar al que sufre un avión al rebasar la velocidad del sonido. El régimen de contacto entre el pantógrafo y la catenaria cambiaría abruptamente, pudiendo provocar incluso la destrucción de la catenaria por enganchón en el pantógrafo.
Existía, además, un límite «diplomático»: cinco años antes, un maglev japonés había establecido un récord de velocidad a 581 km/h. Los gestores franceses consideraron poco útil, a la vez que prudente, forzar el experimento para rebasar esa velocidad, ya que podrían haber entrado en una especie de «carrera internacional» que no tenían demasiadas probabilidades de ganar. El tiempo les daría la razón: en 2015, otro maglev de la serie L0 alcanzó los 603 km/h en la línea de pruebas de Yamanashi. Toda la comunicación relacionada con la Operación V150 hizo hincapié en que los resultados obtenidos solo tendrían relevancia para la tecnología de contacto rueda-carril y alimentación eléctrica mediante hilo de contacto.
 Imagen 10. Maglev Serie L0 de Mitsubishi Heavy Industries en la línea de pruebas de Yamanashi. Foto: Saruno Hirobano.
Imagen 10. Maglev Serie L0 de Mitsubishi Heavy Industries en la línea de pruebas de Yamanashi. Foto: Saruno Hirobano.Parece claro que el límite práctico con la tecnología ferroviaria actual se alcanzaría antes de llegar a los 600 km/h. Resolver los problemas técnicos del contacto pantógrafo-catenaria a tales velocidades implica aumentar la tensión mecánica del hilo, lo que comprometería su resistencia y obligaría a usar mayores secciones. Esto, a su vez, tendría efectos en cascada en todo el sistema, aumentando los valores de las masas fijas y complicando la integridad del contacto.
Un pie en la tierra
La tecnología actual parece marcar el entorno de los 600 km/h como una cota superior de velocidad para el ferrocarril. Sin embargo, las condiciones de explotación habituales, en las que las composiciones de material rodante realizan rutinariamente millones de kilómetros, son necesariamente más conservadoras que las de un proyecto como la Operación V150. Tanto desde el punto de vista de la seguridad como del consumo energético y de las necesidades de un mantenimiento controlado en costes, es preciso poner un pie (al menos) en la tierra y volver a examinar la situación de la tecnología comercialmente disponible para comprender por qué la velocidad punta no evoluciona por encima de los 350 km/h, así como cuáles son sus posibilidades en el largo plazo.
Las condiciones de la operación de un trayecto de alta velocidad se revelan rápidamente como factores limitantes. La Operación V150 reveló que los fenómenos aerodinámicos son dominantes en el comportamiento del tren por encima de los 500 km/h, pero por motivos evidentes las pruebas no incluyeron algunos de los efectos de este tipo con más peso en la explotación comercial: la interacción con la infraestructura en túneles, la afectación debida al cruce de circulaciones y el efecto del viento cruzado en zonas vulnerables como viaductos. Solo por esto es razonable suponer que ningún tren actual podría alcanzar comercialmente los 500 km/h sin modificaciones extensivas. Además, la señalización más avanzada en uso en las líneas de alta velocidad (ETCS/ERTMS) llega a su límite precisamente en esa cota.
Esta suposición encaja a la perfección con los récords de velocidad registrados por trenes comerciales. El CRH380BL chino, una variante de 16 coches y gálibo ampliado del Velaro de Siemens (conocido en España como S-103, en servicio en la línea Madrid-Barcelona-frontera francesa), alcanzó los 487,3 km/h en enero de 2011 en un tramo de la línea Beijing-Shanghai. Más cerca y sin preparación especial, Renfe alcanzó en julio de 2006 los 403,7 km/h entre Guadalajara y Calatayud con una unidad S-103 —durante un breve tiempo estableció el récord del mundo de velocidad para trenes comerciales.
Los límites prácticos
En Feng, Sun, Liu, & Li (2014) se propone un modelo para la estimación del consumo energético de un tren de alta velocidad en función de la velocidad punta en un determinado trayecto. Un ejemplo numérico para la línea Shanghai-Hangzhou arroja el siguiente resultado:
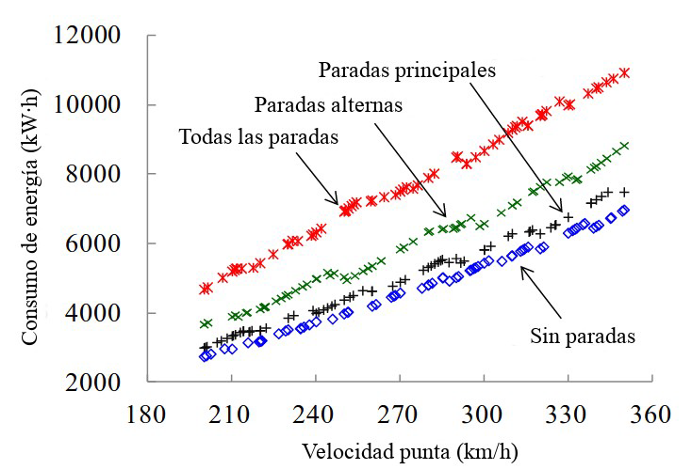 Imagen 11. Consumo de energía estimado frente a velocidad punta. Ejemplo numérico. Adaptado de Feng, Sun, Liu, & Li (2014).
Imagen 11. Consumo de energía estimado frente a velocidad punta. Ejemplo numérico. Adaptado de Feng, Sun, Liu, & Li (2014).La línea del ejemplo tiene 169 km de longitud y nueve posibles paradas incluyendo las estaciones inicial y final, que se usan para establecer cuatro estrategias de explotación: con todas las paradas, con paradas alternas, con una parada intermedia y sin paradas. Debido a la alta concentración de la población en España, ninguna de las líneas de tren existentes dispone de semejante concentración de estaciones intermedias. Aun así, es interesante observar cómo un tren sin paradas con velocidad punta objetivo de 300 km/h arroja un consumo de energía total idéntico al de otro con tres paradas intermedias (estrategia de paradas alternas) y velocidad punta de 250 km/h. Al contrario: si fijamos la velocidad punta en 300 km/h, el tren con la estrategia de paradas alternas consume casi un 30% más de energía que el que realiza la circulación directa.
Este resultado nos sirve para darnos cuenta de que el modo de operación es crítico para determinar la viabilidad de un sistema de alta velocidad, ya que es el número de paradas intermedias y no tanto la velocidad punta objetivo, en los rangos estudiados, lo que determina el consumo final de energía. Al mismo tiempo, es posible realizar una extrapolación razonable por encima del rango de velocidades cubiertas por el modelo para ver cómo a 400 km/h de velocidad punta los consumos para la estrategia directa son equivalentes a los de paradas alternas con punta de 350 km/h.
La cuestión a resolver queda así mucho más clara. La explotación comercial del ferrocarril de alta velocidad debe buscar tanto una rentabilidad económica como un control de la huella medioambiental. Lo segundo es teóricamente posible gracias a la flexibilidad ofrecida por la fuente energética utilizada, y depende del mix de generación eléctrica particular del entorno de la línea, algo que queda fuera del ámbito de este artículo. Por su parte, la rentabilidad económica depende de si somos capaces de compensar el consumo energético realizado con la productividad de transporte del tren, medido en pasajeros-kilómetro [4].
 Imagen 12. Interior de un coche de clase turista del futuro Talgo AVRIL, con
Imagen 12. Interior de un coche de clase turista del futuro Talgo AVRIL, conasientos en disposición 3+2. Foto: Talgo.
Es posible entonces que, simplemente aumentando la capacidad bruta de transporte de un tren (y manteniendo su ocupación alta, naturalmente), un aumento de la velocidad punta pueda ser compensado, tanto desde el punto de vista de consumo energético como del de gasto de mantenimiento —más complejo de modelar— con una productividad mayor. Las estrategias ferroviarias para conseguir esto sin aumentar el número de trenes circulando son conocidas: desde aumentar ligeramente los gálibos para admitir coches con disposición de asientos por fila de 3+2 (como en el caso de China), pasando por una reducción del espacio disponible por pasajero con este mismo objeto (como ocurrirá en el tren Talgo Avril), utilizar trenes de doble cubierta (Alstom es líder en este tipo de coches, muy frecuentes en la red de alta velocidad francesa con sus TGV Duplex), prescindir de coches-cafetería o primeras clases (como se plantea en el futuro servicio «EVA» de Renfe Operadora) o, directamente, operar los trenes en doble composición —dos trenes unidos—, opción que se caracteriza por doblar el número de pasajeros sin consumir el doble de energía.
El tren de alta velocidad del futuro puede alcanzar los 400 kilómetros por hora si realiza pocas paradas y transporta a un gran número de personas a la vez. Ahora es nuestro turno, no solo como ingenieros, sino también como gestores y creadores de políticas de transporte, decidir si esto es deseable, cuáles son las alternativas y cómo es el sistema de transporte con el que queremos enfrentarnos a los retos que nos plantea el futuro.
Notas:
1. La fuerza de arrastre aerodinámico puede expresarse de este modo: D = 1/2 Cd ρ A V2 , donde D es la fuerza que se opone al avance, Cd el coeficiente de arrastre aerodinámico (viene dado por la forma del objeto en movimiento), ρ la densidad del aire (a nivel del mar, en condiciones normales, es de alrededor de 1,2 kg/m²), A el área de la sección transversal del tren (en el caso del ferrocarril es prácticamente constante para todos los vehículos y corresponde con el área del gálibo cinemático, es decir, el hueco más pequeño por el que pasa un tren sin chocar con elementos de la infraestructura) y V la velocidad en la dirección de avance.
2. Un bogie (normalmente pronunciado como se escribe) es un conjunto rígido habitualmente formado por dos ejes —y por tanto cuatro ruedas— que contiene los elementos fundamentales para asegurar la inscripción en curva de los coches, el frenado, la suspensión y, en algunos casos, también la propulsión del tren. Los bogies se montan en los extremos de los coches o, si son articulados, entre dos coches. No todos los trenes los llevan: el ejemplo más característico de composición con ejes sencillos es la del sistema Talgo.
3. La velocidad de propagación de la onda inducida por el pantógrafo es: Cp = √ (T/m)
4. El pasajero-kilómetro (y no «pasajeros partido por kilómetro»), o p·km, es una unidad de medida de la capacidad de transporte que permite comparar trenes individuales o líneas completas con varios trenes entre sí sin necesidad de tener en cuenta diferencias de capacidad bruta o distancias recorridas.
Bibliografía:
Anyakwo, A., Pislaru, C., Ball, A., & Gu, F. (2011). Modeling the dynamic behaviour of the wheel rail interface using a novel 3D wheel-rail contact model. 5th IET Conference on Railway Condition Monitoring and Non-Destructive Testing (RCM 2011). doi:10.1049/cp.2011.0616
Casanueva, C. (29/10/2014). Los trenes no se van por la tangente. Visitado el 18 de agosto de 2019, en https://ccasanueva.wordpress.com/2014/10/26/los-trenes-no-se-van-por-la-tangente/.
DVV Media International Ltd. (01/05/2007). V150: Power-packed train proves AGV technology in record sprint. Visitado el 18 de agosto de 2019, en https://www.railwaygazette.com/news/single-view/view/v150-power-packed-train-proves-agv-technology-in-record-sprint.html.
DVV Media International Ltd. (01/05/2007). V150: 574·8 km/h eclipses the 1990 world record. Visitado el 18 de agosto 2019, en https://www.railwaygazette.com/news/single-view/view/v150-5748-kmh-eclipses-the-1990-world-record.html.
Feng, X., Sun, Q., Liu, L., & Li, M. (2014). Assessing Energy Consumption of High-speed Trains based on Mechanical Energy. Procedia – Social and Behavioral Sciences, 138, 783-790. doi:10.1016/j.sbspro.2014.07.260.
Liu, Z. (2017). Measures to Enhance the Dynamic Performance of Raiway Catenaries. Stockholm: KTH Royal Institute of Technology.
Researching the train of the future. Colonia: Deutsches Zentrum für Luft- und Raumfahrt, Institute of Vehicle Concepts. Visitado el 18 de agosto de 2019, en https://www.dlr.de/dlr/en/desktopdefault.aspx/tabid-10467/740_read-916/#/gallery/2043.
Wu, J. (2018). Dynamic Interaction Between Pantograph and Contact Line. In Chapter 4: Pantograph and contact line system (pp. 130-131). London: Academic Press.
Sobre el autor: Iván Rivera (@brucknerite) es ingeniero especializado en proyectos de innovación de productos y servicios para ferrocarriles.
El artículo Los límites del ferrocarril se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:La tabla periódica en el arte: Titanio
El titanio es el noveno elemento químico más abundante en la corteza terrestre y está presente en decenas y decenas de minerales. Sin embargo, no se tuvo constancia de su existencia hasta finales del s. XVIII. En 1795 Martin Heinrich Klaproth lo bautizó inspirándose en los titanes, antiguos dioses de la mitología griega e hijos de Gea (Tierra). Pese a no ser un metal de uso histórico, el titanio cobró gran importancia en las diferentes artes plásticas a lo largo del s. XX hasta convertirse en un elemento de gran transcendencia.
 Imagen 1. El museo Guggenheim de Bilbao. Fuente: Mariordo / Wikimedia Commons
Imagen 1. El museo Guggenheim de Bilbao. Fuente: Mariordo / Wikimedia CommonsUna nueva arquitectura
Cualquier persona que viva en Bilbao o alrededores asociará automáticamente el titanio con el museo Guggenheim. Para que luego se diga que los materiales artísticos no tienen importancia. Cuando Frank Gehry diseñó un gigantesco barco metálico junto a la ría del Nervión inició una pequeña revolución arquitectónica. Es cierto que desde los años 70 ya se venía empleando el titanio con ese fin, pero su uso en un edificio tan singular y de dimensiones colosales supuso un antes y un después.
La decisión de emplear titanio para forrar el museo no fue sencilla. Uno de los grandes inconvenientes era su precio: más del doble que el del acero de uso tradicional. Si tenemos en cuenta que se emplearon 42 875 paneles (o 33 000 según otras fuentes), estamos hablando de un auténtico dineral. Eso sí, con el titanio se pueden hacer planchas de la mitad de grosor, así que tampoco fue un drama. A partir de ahí todo fueron ventajas: es un material ligero, pero con una elevadísima resistencia mecánica, aguanta bien frente a la corrosión gracias a la capa de óxido que lo cubre y ofrece una estética insuperable en la que el color varía en función de las condiciones ambientales.
Así el Guggenheim se convirtió en el primer gran icono arquitectónico de titanio, lo que no quiere decir que sea el único. Por citar algunos casos repartidos por todo el orbe, tenemos: el Museo de la Ciencia de Glasgow, el Gran Teatro Nacional de Pekín, la Biblioteca Cerritos Millenium de California o la sede de Fuji en Japón. En la mayoría de los casos el titanio se combina con el vidrio, en lo que resulta una de las parejas de materiales más exitosas de este siglo.
 Imagen 2. Sede de Fuji en Odaiba (Japón) y Cerritos Millenium Library en California. Fuente: Mark J. Nelson y Cerritos disaster / Wikimedia Commons
Imagen 2. Sede de Fuji en Odaiba (Japón) y Cerritos Millenium Library en California. Fuente: Mark J. Nelson y Cerritos disaster / Wikimedia CommonsArcoíris metálico
Pese a los edificios que acabamos de mencionar y el nombre del elemento que nos ocupa, no siempre se ha usado el titanio para obras de grandes dimensiones. El titanio en forma metálica también se puede emplear en esculturas y en joyería. En estos casos resulta de gran interés una propiedad bastante peculiar del metal: puede ofrecer diferente color en función del grosor de la capa de óxido que lo cubre.
 Imagen 3. A Parliament of some things, de Mark Hagen (2014) hecho con titanio anodizado. Fuente: Wall Street International
Imagen 3. A Parliament of some things, de Mark Hagen (2014) hecho con titanio anodizado. Fuente: Wall Street InternationalSobre la superficie del titanio se crea una delgadísima capa de óxido (de menos de una micra) que interactuará con la luz y provocará que veamos un color u otro. Seguro que en alguna ocasión has visto una especie de arcoíris en un charco con restos de aceite o en una pompa de jabón. Pues este mecanismo es similar: la luz blanca se dispersa al entrar en contacto con la superficie del óxido y se generan interferencias que varían con el grosor, permitiendo que sólo se observen ciertas longitudes de onda, es decir, ciertos colores. Para lograr diferentes colores se puede alterar el grosor del óxido mediante un proceso que se conoce como anodización en el que el titanio se conecta a una fuente de alimentación. Jugando con el voltaje que se aplica se provocan reacciones de oxidación-reducción y se logra una capa más o menos delgada en función del color que deseemos lograr (Imagen 4).
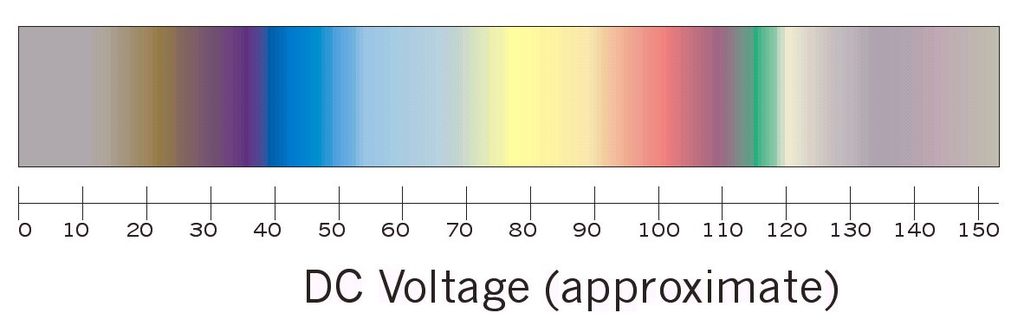 Imagen 4. Color obtenido en el titanio anodizado en función del voltaje aplicado. Fuente: Instructables
Imagen 4. Color obtenido en el titanio anodizado en función del voltaje aplicado. Fuente: InstructablesEl blanco de nuestros tiempos
La pintura blanca no puede faltar en la paleta del artista. No sólo para pintar con ese color, sino para variar las tonalidades del resto de los colores. Históricamente el pigmento blanco más importante ha sido el albayalde o blanco de plomo, pero tiene algunos inconvenientes, entre ellos que te puede matar debido a la toxicidad del plomo. Ante esa perspectiva era necesaria la aparición de otros blancos. Así, en el s. XIX se comercializó el blanco de zinc, pero en el siglo siguiente fue desbancado por el blanco más empleado hoy en día: el blanco de titanio (TiO2).
 Imagen 5. Number 1A, 1948 (173×264 cm), de Jackson Pollock (1948) contiene blanco de titanio. Fuente: MOMA
Imagen 5. Number 1A, 1948 (173×264 cm), de Jackson Pollock (1948) contiene blanco de titanio. Fuente: MOMAPara que os hagáis una idea de la importancia del blanco de titanio, tened en cuenta que la industria de los pigmentos y los colorantes mueve alrededor de 30 billones (americanos) de dólares al año y unos 13,2 corresponden a este blanco. Claro que no sólo se usa en pintura de caballete, sino en pintura industrial, esmaltes, plásticos, opacificador de papel, etc. Todo ello gracias a que es un blanco con un excelente poder cubriente, relativamente barato y no tóxico (aunque recientemente la Unión Europea ha alertado sobre su posible efecto cancerígeno).
El óxido de titanio (IV) se puede encontrar en la naturaleza formando tres minerales: rutilo, anatasa y brookita. Se sabe que durante el s. XIX se empleó rutilo natural en pintura, pero su calidad es mucho menor que el sintético, por lo que no llegó a ser un pigmento trascendental como este último. Pese a que en 1821 ya se había sintetizado blanco de titanio, no fue hasta 1916 cuando se empezó a comercializar, casi simultáneamente en Noruega y Estados Unidos.
 Imagen 6. Primera fábrica de blanco de titanio. Fredrikstad (Noruega). Fuente: Painter’s Palettes
Imagen 6. Primera fábrica de blanco de titanio. Fredrikstad (Noruega). Fuente: Painter’s PalettesLa síntesis del blanco de titanio ha ido evolucionando desde aquel momento. Al principio se partía del mineral ilmenita (FeTiO3) para lograr anatasa sobre un substrato de sulfato de bario o de calcio, pero ya en los años 30 se descubrió cómo lograr rutilo sintético, forma que hoy en día sigue siendo la más popular. El siguiente gran hito fue el desarrollo de un método de síntesis, empleando cloro, que resultó ser mucho más eficiente que el empleado hasta la fecha y que se basaba en el uso de sulfatos.
Como os podéis imaginar, el blanco de titanio sólo aparece en obras de arte a partir del s. XX, algo que resulta muy útil para detectar falsificaciones. Ya contamos en su momento que en un estudio realizado en la Universidad Politécnica de Catalunya se detectó rutilo y azul de ftalocianina en una obra inicialmente atribuida al pintor valenciano Cecilio Pla y Gallardo, fallecido antes de que esos productos se comercializasen. Mucho más espectacular es sin duda el caso de Wolfgang y Helene Beltracchi, una pareja de falsificadores que la lio parda, como podéis aprender en este hilo de Luis Pastor. Tras vender obras por varios millones de euros se descubrió su estafa porque en un supuesto Campendonk de 1914 había blanco de titanio (Imagen 7). Como ya os habréis dado cuenta, dicho pigmento no estaba disponible en el mercado. No penséis que Wolfgang no era consciente de ello (o por lo menos, eso declaró en el Spiegel). Él empleó un tubo de blanco de zinc, pero no se dio cuenta de que también contenía blanco de titanio. Maldita química.
 Imagen 7. Pintura roja con caballos. El supuesto Campendonk por el que atraparon a los Beltracchi. Fuente: The Times
Imagen 7. Pintura roja con caballos. El supuesto Campendonk por el que atraparon a los Beltracchi. Fuente: The TimesPara saber más:
Nippon Steel Corporation. Features of Titanium Building Materials (2019).
A. Mendelsohn How Analog and Digital Came Together in the 1990s Creation of the Guggenheim Museum Bilbao en Guggenheim.org (2017).
E. West FitzHugh. Artist’s Pigments: A Handbook of Their History and Characteristics. (Volume 3). National Gallery of Art (1998).
B.A. van Driel et al. The white of the 20th century: an explorative survey into Dutch modern art collections. Heritage Science 6(16) (2018).
Sobre el autor: Oskar González es profesor en la facultad de Ciencia y Tecnología y en la facultad de Bellas Artes de la UPV/EHU.
El artículo La tabla periódica en el arte: Titanio se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La tabla periódica en el arte: Cobre
- La tabla periódica en el arte: Arsénico
- La tabla periódica en el arte: Cobalto
Francisco R. Villatoro – Naukas Bilbao 2018: El ángulo mágico del grafeno
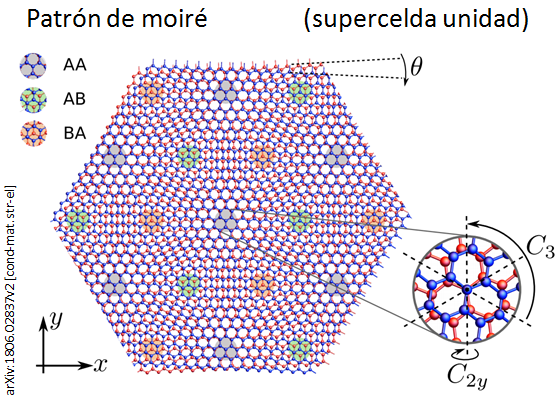
La gran noticia científica de 2018 fue que el grafeno bicapa rotado con ángulo mágico es un superconductor no convencional (y un aislante Mott cuando deja de serlo). Este material “mágico” promete revolucionar nuestro conocimiento sobre la superconductividad de alta temperatura. Francisco R. Villatoro presentó el descubrimiento durante Naukas Bilbao 2018 en una charla impecable, con una densidad de conocimientos difícilmente superable. No es una charla fácil de seguir sin fundamentos de física del estado sólido, pero merece muy mucho la pena el esfuerzo. Francis publicó una transcripción de la misma para que se pueda estudiar con mayor profundidad aquí.
Francis Villatoro: ''El ángulo mágico del grafeno''Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Francisco R. Villatoro – Naukas Bilbao 2018: El ángulo mágico del grafeno se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Naukas Bilbao 2017 – Francisco R. Villatoro: El espín para irreductibles
- Carlos Briones – Naukas Bilbao 2018: Os voy a contar una historia (en imágenes)
- Lo que la tensión puede hacer en dos capas de grafeno
La química analítica como base para el estudio de las prácticas pastoriles prehistóricas
Servicio Central de Análisis de Araba (SGIker – UPV/EHU)
La arqueología actual pretende reconstruir eventos del pasado desde sus restos y determinar la experiencia humana del pasado, es decir, cómo se organizaban socialmente y por qué cambiaban sus sociedades, cómo explotaban sus recursos, qué comían, qué creían, cómo se comunicaban… [1]. El desarrollo de nuevas técnicas analíticas permite al arqueólogo pasar de preguntarse de qué material están hechos los utensilios encontrados en las excavaciones a preguntarse sobre la procedencia, origen de lo encontrado y costumbres/actividades humanas [2].
Hace unos 10.500-10.000 años, en el oeste de Euroasia, fueron domesticadas las cabras Capra aegagrus, ovejas Ovis orietalis y vacas Bos primisgenius. Con la domesticación, el ser humano logró ampliar los recursos obtenidos de de los animales y pasar de ser una fuente exclusiva de aporte proteico a través de su carne, a ser también fuente de leche y lana [3].
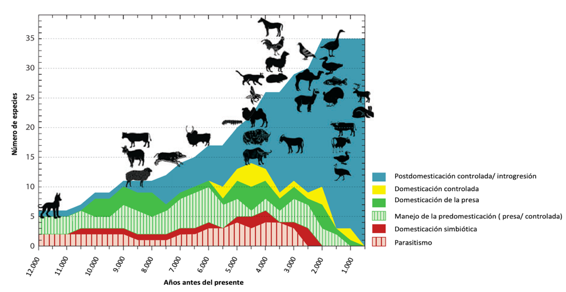 Figura 1. Cronología de la domesticación animal. Fuente: [3]
Figura 1. Cronología de la domesticación animal. Fuente: [3]
El desarrollo y proliferación de la domesticación obligó a los pastores a buscar refugio para sus reses y mantenerlas a salvo. El uso de cuevas o abrigos refugio como establos fue una práctica habitual a lo largo y ancho del mediterráneo desde el Neolítico a la Edad de Hierro [4]. El principal rasgo común de los yacimientos encontrados en dichos refugios son sus sedimentos, que se presentan como espacios con depósitos de apariencia arcillosa originados por grandes cantidades de estiércol generado por presencia continuada de ganado, principalmente ovicaprino [5]. Los animales estabulados provocan el incremento de los residuos del establo, constituidos por la acumulación del estiércol junto con productos aportados por ellos mismos, hierbas, tierra y piedras.
Con el objeto de mantener limpio y libre de parásitos el establo, frecuentemente se reducía el volumen de estiércol mediante su quema, siendo una práctica que se estima que duró hasta la Edad de Bronce, ya que a partir de entonces se generaliza el uso del estiércol generado en las estabulaciones como abono para los campos [6].
La quema continuada de este estiércol a lo largo de los años genera unos depósitos que están constituidos por diferentes capas de sedimentos, generadas por la sucesión de unidades de combustión, que son denominadas de forma genérica como fumier (estiércol en francés) [7], que en general están formadas por una capa blanca o gris (combustión total), otra negra (combustión parcial) y finalmente una marrón (sin combustión). Estas capas, sobre todo las negras y las marrones, poseen una buena conservación, lo que permite la caracterización de compuestos orgánicos que nos pueden ayudar a identificar especies de animales estabulados y costumbres pastoriles.
Uno de los yacimientos más destacados donde se utilizó esta estrategia de eliminación de excremento animal es el de San Cristóbal, situado en la Sierra de Cantabria (Araba/Álava)
 Figura 2. Excavación de San Cristobal.
Figura 2. Excavación de San Cristobal.
Los estudios comenzaron por el interés del Prof. Fernández Eraso del Dpto. de Geografía, Prehistoria y Arqueología de la UPV/EHU y su grupo High Yield Research Group of Prehistory (IT 622-13), que abrió la posibilidad de establecer una línea de investigación que permitiera relacionar la naturaleza de los animales estabulados con la presencia de ciertas sustancias orgánicas en los estratos excavados de los abrigos de la Sierra Cantabria.
En este yacimiento no se encuentran restos óseos de los animales allí estabulados y es necesario realizar análisis de biomarcadores de especie para determinar que tipo de animal ha sido estabulado. Este estudio, llevado a cabo en el Servicio Central de Análisis de Álava, se focalizó en el análisis cuantitativo de ácidos biliares, esteroles y fitoesteroles en los residuos/sedimentos orgánicos (capas blancas, negras y marrones) del yacimento de San Crístobal usando como técnica de medida la cromatografía de gases acoplada a espectrometría de masas (GC-MS) .
 Figura 3. Yacimiento San Cristobal, Sierra de Cantabria (Araba/Álava). Estructura del fumier. Fotografía: Javier Fernández Eraso
Figura 3. Yacimiento San Cristobal, Sierra de Cantabria (Araba/Álava). Estructura del fumier. Fotografía: Javier Fernández Eraso
Los compuestos orgánicos de los sedimentos seleccionados como biomarcadores para este estudio, fueron sometidos a una etapa de extracción asistida por microondas, a una etapa de limpieza y finalmente el extracto fue derivatizado y analizado por GC-MS. Los resultados del análisis de los biomarcados fueron procesados utilizando herramientas quimométricas (ver figura 2), que facilitan la clasificación de los residuos/sedimentos orgánicos prehistóricos, permitiendo diferenciar el origen de los restos y la actividad pastoril.
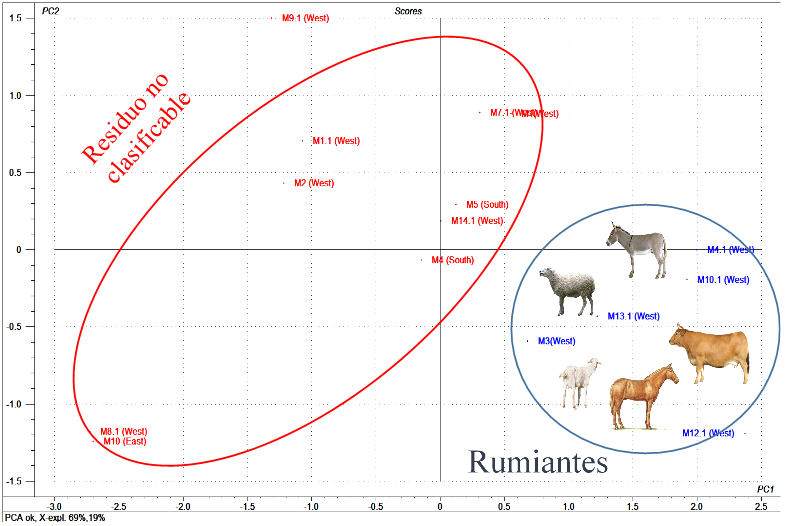 Figura 2. Análisis de componentes principales para muestras de rumiantes y residuos no clasificables. Fuente: Journal of separation Science (2017, 40, 4549-4562)
Figura 2. Análisis de componentes principales para muestras de rumiantes y residuos no clasificables. Fuente: Journal of separation Science (2017, 40, 4549-4562)
La capas marrones y negras clasifican los restos como restos de animales rumiantes mientras que el resto no se pueden usar para la clasificar el tipo de animal estabulado debido a que no se conservan los compuestos de interés. Además, se observan actividad pastoril en desde 6010±30 BP (Neolítico temprano) hasta 4030±30 BP (Calcolítico) lo que corrobora estudios anteriores y además no hay indicios de estabulación de otros animales no rumiantes.
Este estudio forma parte del trabajo de la tesis doctoral de Jaime Gea del Río del grupo METABOLOMIPs de la Facultad de Farmacia de la UPV/EHU.
Referencias bibliográficas:
[1] .M. Pollard, C. Batt, B. Stern, S. Young, Analytical Chemistry in Archaeology, 2006.
[2] .B.T. Nigra, K.F. Faull, H. Barnard, Analytical Chemistry in Archaeological Research, Anal. Chem. 87 (2014) 3–18
[3].Larson, G. & Fuller, D. Q. The Evolution of Animal Domestication. Annual Review of Ecology, Evolution, and Systematics 45, 115–136 (2014).
[4]. Fernández-Eraso, J. et al. Beginnings, settlement and consolidation of the production economy in the Basque region. Quaternary International 364, 162–171 (2015).
[5]. Angelucci. Shepherds and karst: the use of caves and rock- shelters in the Mediterranean region during the Neolithic Diego. 191–214 (1999).
[6]. Boschian, G. and Miracle, P. T. 2008. Shepherds and caves in the Karst of Istria (Croatia). In Proceedings of the 2nd International Conference on Soils and Archaeology (ed. G. Boschian). Atti Società toscana Scienze naturali, Mem., Serie A, 112(2007), pp. 173–80. (2008)
[7]. Fernández Eraso, J. U. D. P. V. (España) & Polo Díaz, A. U. D. P. V. (España). Establos en abrigos bajo roca de la Prehistoria Reciente: su formación, caracterización y proceso de estudio. Los casos de Los Husos y de San Cristóbal. 2008.pp39-51. Krei 10, 39–51 (2008).
El artículo La química analítica como base para el estudio de las prácticas pastoriles prehistóricas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El metanol es clave para entender cómo se forman las estrellas
- Técnicas «low cost» para el estudio de obras de arte
- Por qué España es un modelo para el estudio de la economía
Por qué la langosta es el emoji del lujo
 Lobster Telephone 1936 Salvador Dal? 1904-1989 Purchased 1981 http://www.tate.org.uk/art/work/T03257
Lobster Telephone 1936 Salvador Dal? 1904-1989 Purchased 1981 http://www.tate.org.uk/art/work/T03257La langosta ha sido objeto de representación artística por sus cualidades simbólicas como alimento de lujo y signo de opulencia. También por sus cualidades plásticas, sobre todo en los estudios de color y formas de los bodegones. La langosta está presente en obras de Albrecht Dürer, Antonio Viladomat, Zacarias González Velázquez, Adriaen van Utrecht, José María Corchón, José Serra y Porson, Eugene Delacroix, Utagawa Kuniyoshi, Pablo Picasso, Salvador Dalí y Jeff Koons, entre muchos otros.
No obstante, la langosta no siempre ha sido un alimento de ricos. El lujo está sujeto a la abundancia relativa y a los vaivenes de la moda, a veces caprichosos. Hasta mediados del siglo XIX la langosta era considerada una especie de cucaracha marina. En las costas atlánticas de Canadá y Nueva Inglaterra eran tan abundantes que los colonos las consideraban un estorbo para la pesca. En las playas de Massachusetts Bay las langostas se acumulaban a montones. Tanto es así que las utilizaban para fertilizar suelos, para dar de comer a cerdos y vacas, y también para alimentar a los sirvientes.
A finales del siglo XIX el ferrocarril y la incipiente industria conservera cambiaron el estatus de la langosta. Una de las primeras conserveras estadounidense fue la de Maine, fundada en 1841. Uno de sus productos estrella era la langosta enlatada. Este producto se servía a los turistas que viajaban en tren como si se tratase de un alimento exótico y exquisito. La ceremonia tenía la suficiente pompa como para que les pareciese un alimento de lujo. De hecho, la llegada de los ferrocarriles refrigerados permitió la exportación de la langosta a Inglaterra, donde se vendía por diez veces su precio original. Una estrategia de marketing muy efectiva. En los años 20 la langosta alcanzó su precio máximo, convirtiéndose en el alimento más caro del momento.

La cantidad de langosta ha ido variando a lo largo del tiempo, sobre todo en función de la temperatura de las aguas. En los mares de Maine se recogieron 56 millones de kilos de carne de langosta en 2013, seis veces más que en 1986. El calentamiento de las aguas hace que las langostas sean más grandes y produzcan más descendencia. Además, el calentamiento también ha afectado a su depredador natural, el bacalao.
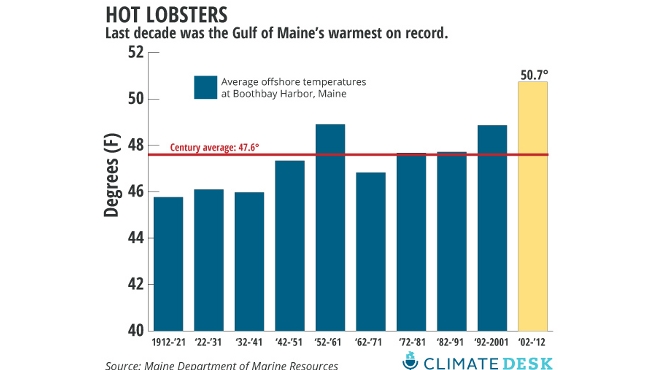
En Estados Unidos se está viviendo tal bonanza de langosta que su precio ha caído lo suficiente como para que el consumo se esté volviendo masivo. Tanto es así que McDonald’s ofrece menús con langosta en algunas regiones durante la temporada de verano. Eso sí, el McDonald’s lobster roll es el menú más caro de la cadena. El lujo se paga, incluso el que se sirve en plato de cartón.

Para Dalí la langosta era uno de sus animales preferidos «porque además de ser inteligente por llevar el esqueleto por fuera y no por dentro como los cretinos». En su Autorretrato anecdótico Dalí escribió: «Me gusta sólo comer cosas de forma bien definida, detesto la espinaca por su carácter absolutamente amorfo. Lo directamente opuesto a la espinaca es la armadura, he aquí porqué me gusta tanto comer armadura y especialmente las pequeñas variedades, esto es los mariscos, estos son una organización material de la originalísima e inteligente idea de llevar los propios huesos fuera más bien que dentro. El crustáceo puede con las armas de su anatomía proteger el blando y nutritivo delirio de su interior cobijado contra toda profanación y encerrado como un hermético y virginal vaso que lo deja vulnerable sólo a la más alta forma de conquista imperial en la noble guerra del descortezamiento: la del paladar».
En varias de sus obras, Dalí asocia las langostas con el deseo carnal, con lo sexual. Frecuentemente muestra a la langosta adherida a la mujer, como si ambos compartiesen la cualidad de ser eróticamente apetecibles, «pues tienen ambos el interior exquisito y se enrojecen cuando se las quiere hacer comestibles».
La langosta se enrojece al cocinarse a causa de la astaxantina, que es un pigmento soluble que en su forma libre es de color bermellón. Cuando este crustáceo está vivo, el carotenoide permanece oculto porque está ligado a una proteína, la crustacianina, causante del color pardo azulado. Esta coloración resulta muy útil para pasar desapercibidos ante los depredadores. Cuando la langosta se cocina, la proteína se desnaturaliza perdiendo su estructura y liberando la astaxantina de color bermellón. En la astaxantina ocurre un cambio químico durante este proceso en el que el compuesto pasa de ser un enolato a una hidroxicetona neutra.

Tanto la langosta como el teléfono tenían para Dalí una fuerte connotación sexual. En su autobiografía, La vida secreta de Salvador Dalí, aparece un dibujo de un teléfono langosta con la siguiente anotación: «No entiendo por qué, cuando pido una langosta asada en un restaurante, nunca se me sirve un teléfono asado; no entiendo por qué el champán siempre se sirve frío mientras que, sin embargo, los teléfonos, que son a menudo excepcionalmente cálidos y desagradablemente pegajosos al tacto, no son servidos en cubos plateados con hielo triturado».
El teléfono langosta de Dalí es completamente funcional y cuatro de ellos fueron utilizados por su mecenas Edward James en su vivienda vacacional. Dalí realizó un total de once Teléfonos langosta, cuatro de color rojo y siete en blanco. Como parte del discurso artístico daliniano, resulta interesante que estos teléfonos fuesen funcionales, ya que el propio sistema del arte se encargaría de convertirlos en objetos inútiles. Los teléfonos langosta fueron concebidos como futuros readymades, objetos cotidianos reconvertidos en objetos artísticos y por tanto inútiles, o bien a través del contexto en el que se exponen (un museo, una vitrina, una peana…) o bien a través de una manipulación que los inutiliza o los transforma en otra cosa. Hacer una llamada con el teléfono langosta, además de ser una extravagancia, sería una performance. La seducción comienza en la llamada con la que conciertas la cita.
Los materiales del teléfono langosta son materiales innobles. La langosta es de yeso y el teléfono es un teléfono de rueda de baquelita. El yeso es un sulfato de calcio, uno de los materiales más empleados en construcción. Y la baquelita es un polímero sintético del tipo plástico termoestable: al solidificarse y darle forma no puede volver a ablandarse con calor. Por su resistencia térmica se empleaba para fabricar las carcasas de aparatos ordinarios como teléfonos y radios.
En los años 30 tanto la langosta como el teléfono representaban el lujo. Esa idea de lujo cambiante, reconocible y suficientemente accesible. Solo las clases acomodadas tenían teléfono en sus viviendas, y la langosta era un alimento reservado para las celebraciones. Para Dalí, el placer del lujo, por lo exclusivo, era un placer semejante al de la conquista y el sexo.
 Wallis Simpson posando para Vogue con un vestido de Elsa Schiaparelli y Salvador Dalí. Fotografía de Cecil Beaton, 1937.
Wallis Simpson posando para Vogue con un vestido de Elsa Schiaparelli y Salvador Dalí. Fotografía de Cecil Beaton, 1937.
En 1937, Salvador Dalí y la legendaria diseñadora de moda italiana, Elsa Schiaparelli, se unieron para crear un vestido de noche de verano de seda. El vestido tenía impresa una langosta creada por Dalí localizada sobre la zona genital. Este vestido fue el que lució Wallis Simpson en un reportaje para Vogue cuando había anunciado su compromiso con el príncipe Eduardo. Wallis Simpson fue una socialite estadounidense que, después de haberse divorciado dos veces, se casó con el príncipe Eduardo, duque de Windsor, quien antes de su matrimonio había sido Eduardo VIII, rey del Reino Unido de Gran Bretaña e Irlanda del Norte y emperador de la India. Al comprometerse con Wallis Simpson, Eduardo fue obligado a renunciar a su título. En aquellos años, casarse con una mujer divorciada era algo moralmente inadmisible, así que no tuvo más remedio que abdicar. Por este motivo, que Wallis Simpson decidiese posar para la prensa con el vestido langosta fue toda una provocación.

En 1989, la firma de moda Moschino, sacó varias prendas en las que empleaba la langosta como símbolo de opulencia. Entre ellas destacó una icónica chaqueta cuya botonadura estaba decorada con langostas bordadas con hilo de oro.
Por aquel entonces, el diseñador y director de arte de Moschino era Franco Moschino, quien definió las bases de lo que siempre sería Moschino. Hoy en día, la dirección de arte corre a cargo del extraordinario diseñador Jeremy Scott, que con maestría continúa reavivando la fricción entre lo lujoso y lo hortera.
 A la izquierda Gigi Hadid camina en el show Moschino de febrero de 2015 en Milán. A la derecha Katy Perry luce el mismo vestido en la Gala Met de 2015 con el bolso de la colección inspirado en los espráis Krylon de los 80.
A la izquierda Gigi Hadid camina en el show Moschino de febrero de 2015 en Milán. A la derecha Katy Perry luce el mismo vestido en la Gala Met de 2015 con el bolso de la colección inspirado en los espráis Krylon de los 80.
Esto lo logra poniendo en cuestión el propio sistema de la moda, la elección a veces arbitraria del valor de las cosas y elevando lo ordinario a categoría de moda. Así, hay colecciones de Moschino inspiradas en el graffiti, en los útiles de limpieza, en la construcción o en la comida basura. Como colecciones que rinden tributo a iconos pop contemporáneos como Barbie o McDonald’s. Prendas y accesorios de lujo ejecutados con exquisitez que representan lo que comúnmente llamamos baja cultura. Por este motivo Moschino es a la moda lo que Jeff Koons es al arte.
 Langosta. Jeff Koons, 2003
Langosta. Jeff Koons, 2003
La langosta es una de las esculturas más icónicas del artista Jeff Koons. Se trata de una langosta colchoneta de aluminio policromado colgada del techo con una cadena de acero. La langosta además de ser una obra de arte mayúscula es una virguería técnica. Si uno no se fija en la ficha técnica, estaría convencido de que se trata de una colchoneta auténtica.
La escultura Langosta pertenece a la serie Popeye. Este personaje es un icono popular y símbolo proletario del triunfo sobre la adversidad. Con la escultura Langosta, Koons reflexiona acerca del concepto del triunfo proletario y acerca de la noción de readymade. La colchoneta langosta es un objeto ordinario al que cualquiera puede acceder. Además, en sí mismo es una representación de un símbolo de lujo, la langosta, reconvertido en un objeto de plástico hortera y divertido. Puede entenderse como una suerte de readymade porque se trata de un objeto transformado en arte a través de un cambio de contexto (de la piscina a estar colgado en un museo) y de una manipulación. En lugar de ser de plástico, la colchoneta langosta de Koons es de aluminio policromado. Tanto el material como el objeto que representa, la colchoneta, son innobles. Además, existen tres copias y la prueba de artista, con lo cual la exclusividad se comparte, aunque de forma limitada, se comparte. Con todo esto Koons logra interpelar acerca de la noción de lujo y por supuesto, de mercado. La langosta simboliza ambas cosas.
La obra de Koons es en apariencia frívola, pero esconde un profundo recorrido intelectual. Igual que el provocador título de este trabajo, «Por qué la langosta es el emoji del lujo», es un disfraz frívolo e insultantemente contemporáneo. Como una escultura de bronce que parece de plástico.
Sobre la autora: Déborah García Bello es química y divulgadora científica
El artículo Por qué la langosta es el emoji del lujo se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Un lujo asiático cultivado en aguas del Mediterráneo
- Si hacer fármacos fuese como jugar a Lego, la pieza más guay se llamaría carbino
- En The Big Bang Theory no hay químicos, sin embargo…
Las simetrías ocultas de la tabla de multiplicar
Hace unos meses, buscando material para mi libro Los secretos de la multiplicación (Catarata, 2019), que estará en las librerías el 2 de septiembre, encontré un interesante artículo del profesor de francés argelino Zoheir Barka, que es un apasionado de las matemáticas, titulado The Hidden Symmetries of the Multiplication Table (Las simetrías ocultas de la tabla de multiplicar). En esta entrada veraniega de la sección Matemoción del Cuaderno de Cultura Científica vamos a iniciar un pequeño paseo por algunas de esas simetrías ocultas en las tablas de multplicar.
 Portada del libro Los secretos de la multiplicación, de los babilonios a los ordenadores, colección Miradas Matemáticas, Catarata, 2019
Portada del libro Los secretos de la multiplicación, de los babilonios a los ordenadores, colección Miradas Matemáticas, Catarata, 2019
La idea de Zoheir Barka es crear diferentes patrones geométricos planos de color sobre la tabla de multiplicar, de tamaños variables, asociando colores a los múltiplos de algunos números. Por lo tanto, el punto de partida es una tabla de multiplicar cuadrada o rectangular, con un cierto número de filas y columnas, en función de las necesidades estéticas del patrón que se quiere realizar.
La siguiente imagen es una tabla de multiplicar normal, con los productos de los diez primeros números, del 1 al 10, a la que se ha añadido además los productos por cero, es decir, todo ceros, por lo que resulta una retícula cuadrada con 11 filas y 11 columnas.
Una vez que disponemos de la tabla de multiplicar, del tamaño que se considere oportuno, se trata de colorear cada celda de la misma en función de si el número de la celda es, o no, múltiplo de un número o de alguno de los números seleccionados. El caso más sencillo sería dar color a los múltiplos de un número, por ejemplo, el 2 y dejar sin color, o utilizar otro distinto, para los que no son múltiplos de 2, obteniendo así el siguiente patrón, que es muy sencillo.
Es evidente que, si tomamos los múltiplos de un número primo, como el 2, pero también el 3, el 5 o el 7, por ejemplo, los patrones serán sencillos enrejados, como el anterior, pero con zonas cuadradas blancas, o sin colorear, más grandes aún. Para el 2 las zonas blancas eran sencillas celdas, para el 3 serían cuadrados de 2 x 2 celdas, para el 5 cuadrados de 4 x 4 celdas, y así para el resto de los números primos. Es decir, se crea un patrón simétrico en el que se están repitiendo, en horizontal y vertical, bloques básicos de tamaño igual al número cuyos múltiplos se están considerando. A continuación, vemos los bloques básicos para 2, 3 y 5.

Pero si consideramos los múltiplos de números no primos, como el número 4, cuyo divisor no trivial es 2 (4 = 2 x 2), o el número 6, cuyos divisores no triviales son el 2 y el 3 (6 = 2 x 3), la estructura se complica un poco más, como vemos a continuación.

Por motivos estéticos, podríamos llamar la “zona básica” de cada ejemplo a la cuadrícula de tamaño (n + 1) x (n + 1), si estamos considerando los múltiplos del número n, que consiste en añadir al bloque básico la siguientes fila y columna, cuyas celdas tienen color (ya que son los primeros múltiplos del número n) y que cierran los bloques básicos.
Así las zonas básicas de los casos en los que se consideran los múltiplos de los números 4, 6 y 10, que son producto de dos primos (iguales o distintos), son las siguientes.

Y si el número considerado es múltiplo de más números primos (iguales o distintos), como el 12, que es igual al producto 2 x 2 x 3, se complica un poco más el entramado. Veámoslo.

Otro ejemplo es el siguiente, en el que se muestra la zona básica del número 30, que es igual al producto 2 x 3 x 5.

Como vemos la estructura se enriquece en función de la cantidad de números primos que generan el número cuyos múltiplos se están coloreando.
El siguiente paso natural, que es el que considera también Zoheir Barka en su artículo, es considerar los múltiplos de dos o más números, utilizando tantos colores como números. Empecemos con los múltiplos de 2 y de 3, los números más pequeños posibles para los que esto tiene sentido, y coloreemos los múltiplos de 2 en verde y los múltiplos de 3 en azul. Aquí se nos plantea una duda, qué hacer con los números que son múltiplos de los dos, luego múltiplos de 6. Tendríamos tres opciones, que se mantenga el color del múltiplo mayor, que en este caso es el 3 (azul),

que se mantenga el color del múltiplo menor, que en este ejemplo es el 2 (verde),

o incluso, utilizar otro color para los múltiplos de 6 = 2 x 3, que en la siguiente imagen utilizamos el amarillo.
Y veamos ahora un ejemplo en el que uno de los dos números no es primo, por ejemplo, 4 = 2 x 2, pero los números primos que lo componen, 2 (dos veces), no son el otro número primo, 3. En este caso, las zonas básicas que se repiten en las tres opciones son las de las siguientes imágenes. En cada uno de los casos hemos añadido a la versión con números, una sin números, que nos permite apreciar mejor el patrón geométrico que se genera.
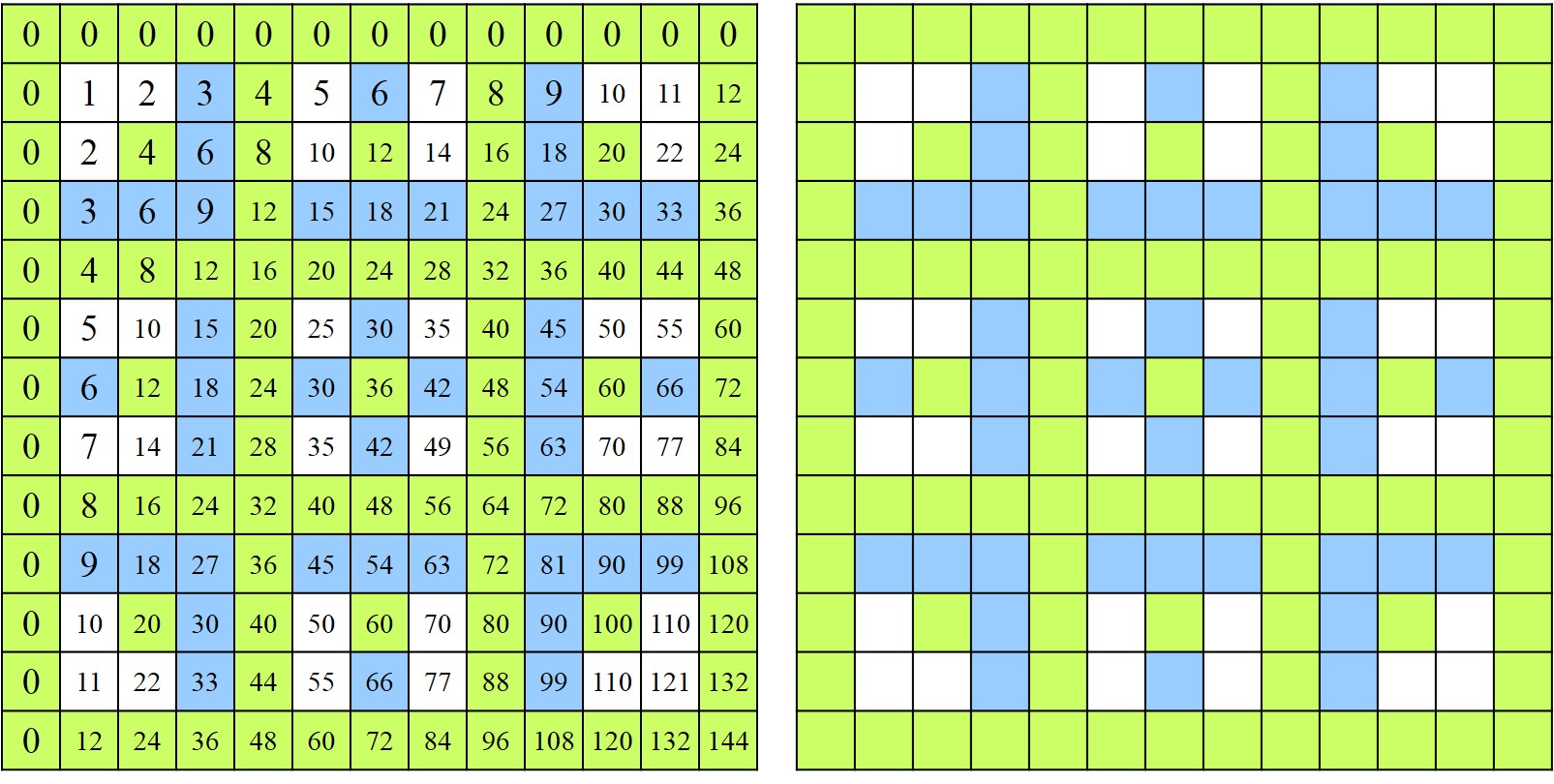
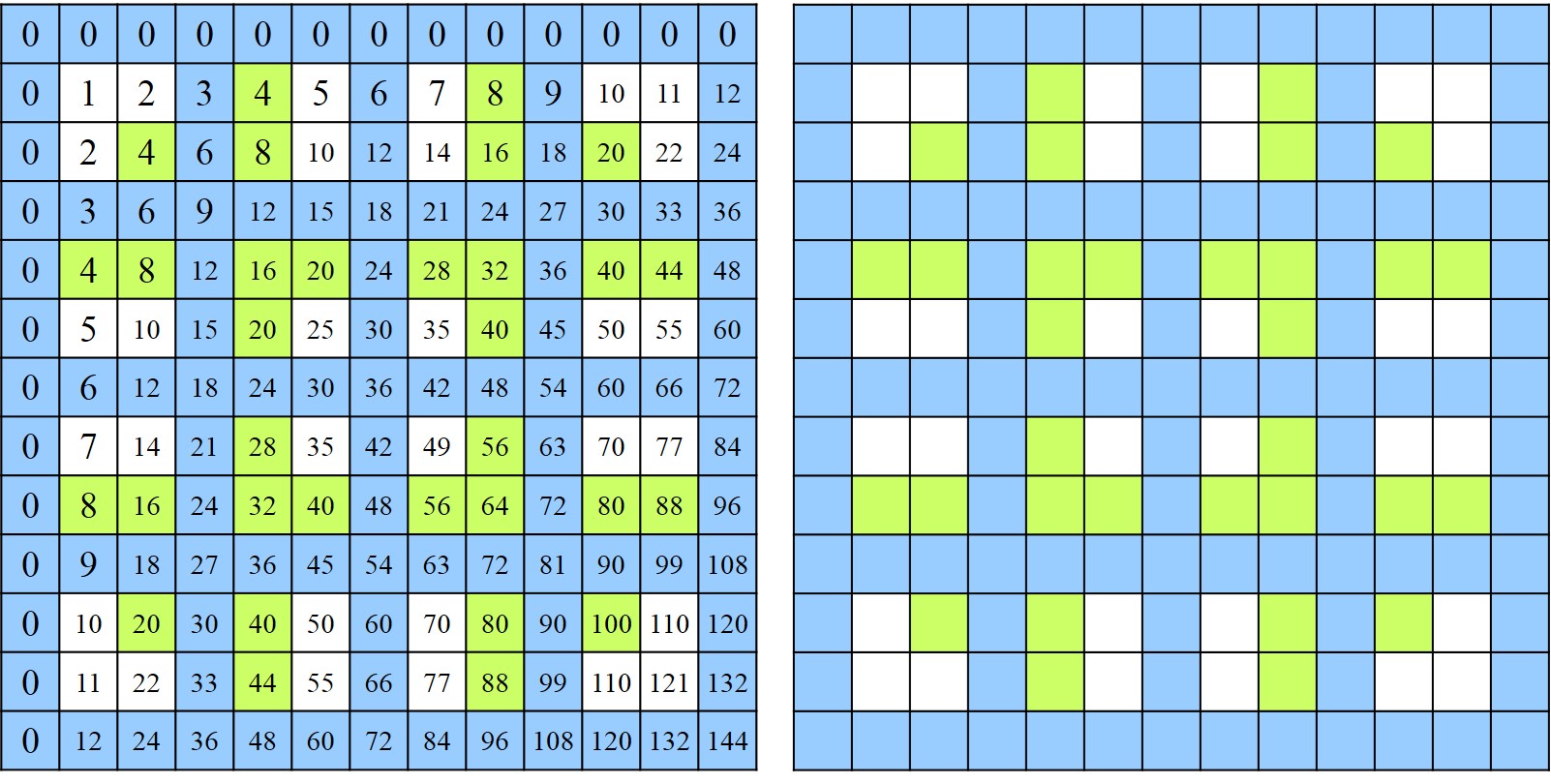
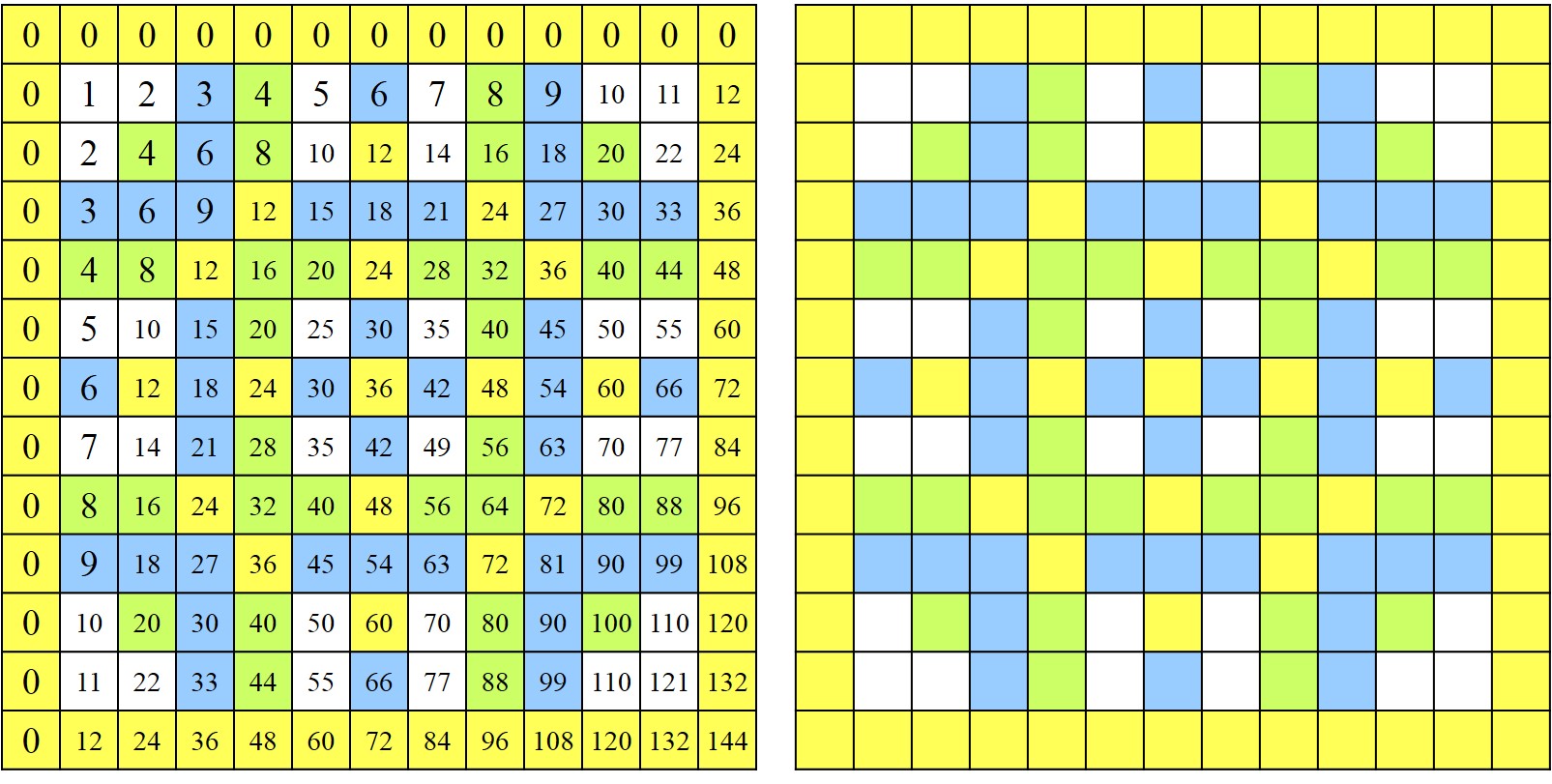
El siguiente es un ejemplo de dos números que comparten un número primo, como los números 6 y 9, para los que el 3 es divisor de ambos. Mostramos las zonas básicas en los casos en los que prima, en el primero, el color del número 9 y, en el segundo, el color del número 6.

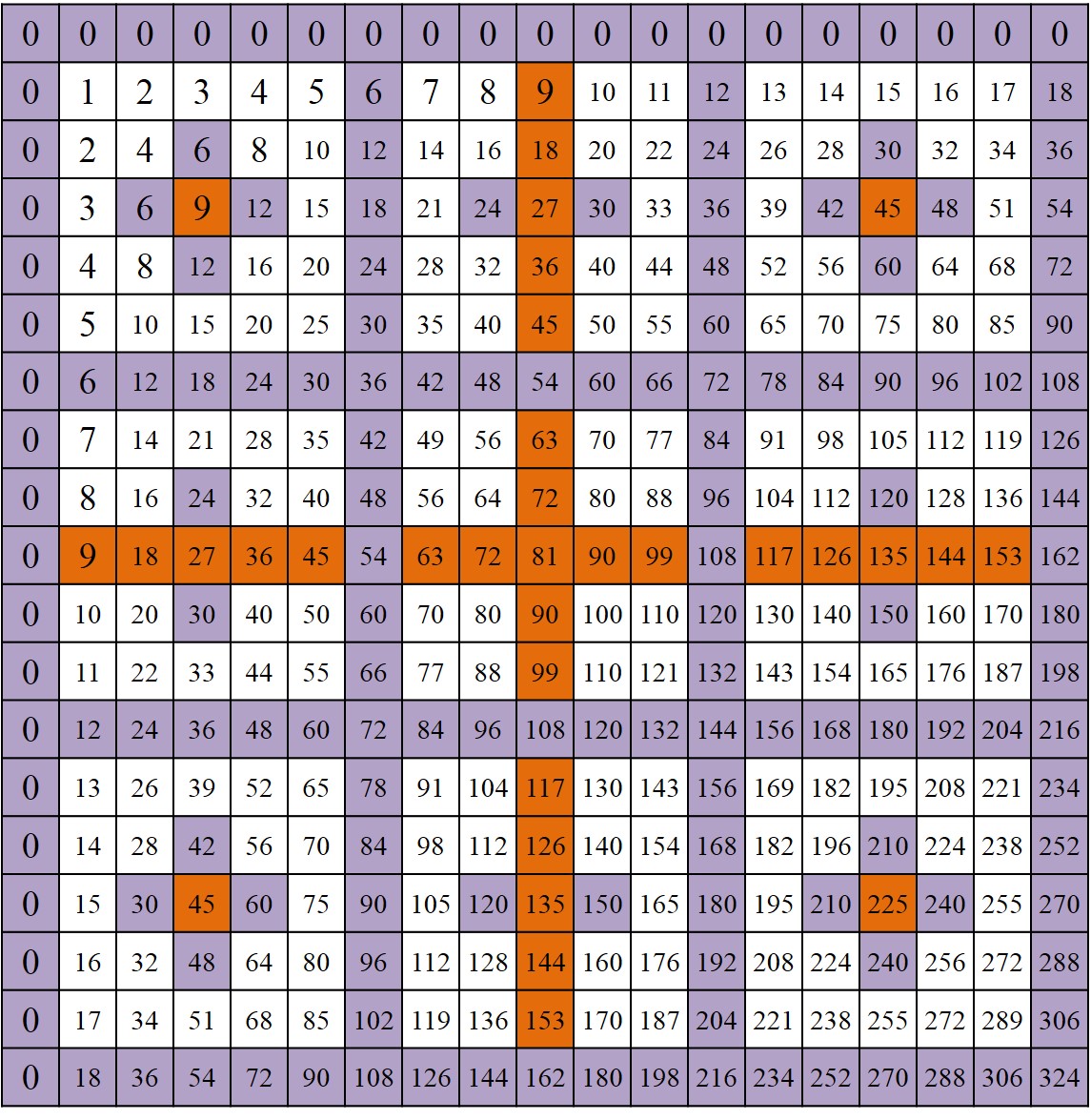
Y, para terminar, tomamos un ejemplo en el que uno de los números es múltiplo del otro, por ejemplo, los números 6 y 12.

En la segunda parte de esta entrada del Cuaderno de Cultura Científica continuaremos con más patrones geométricos planos sobre la tabla de multiplicar.
 Maqueta para una futura pintura, Raúl Ibáñez
Maqueta para una futura pintura, Raúl Ibáñez
Bibliografía
1.- Raúl Ibáñez, Los secretos de la multiplicación, de los babilonios a los ordenadores, colección Miradas Matemáticas, Catarata, 2019.
2.- Zoheir Barka, The Hidden Symmetries of the Multiplication Table, Journal of Humanistic Mathematics, vol. 6, n. 1, pp. 189-203, 2016.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Las simetrías ocultas de la tabla de multiplicar se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Multiplicar con las manos
- Multiplicar no es difícil: de los egipcios a los campesinos rusos
- Uno, dos, muchos
Las líneas de Balmer

De todos los espectros, el espectro de emisión del hidrógeno es especialmente interesante por razones históricas y teóricas. En las regiones visible y casi ultravioleta, el espectro de emisión consiste en una serie de líneas en las que aparentemente hay cierto orden.
En 1885, Johann Jakob Balmer (1825-1898), un profesor de una escuela femenina Suiza, interesado en los acertijos numéricos y la numerología, encontró una fórmula simple [1] que daba las longitudes de onda de las líneas conocidas en el hora. La formula es λ = b [n2/(n2-22)].

En esta fórmula b es una constante que Balmer determinó empíricamente y encontró que era igual a 364,56·10-9 m; n es un número entero, diferente para cada línea. Específicamente, para que la ecuación produzca el valor observado para las longitudes de onda respectivas, n debe ser 3 para la primera línea visible (roja) del espectro de emisión de hidrógeno (denominada Hα); n = 4 para la segunda línea (verde) (Hβ); n = 5 para la tercera línea (azul) (Hγ); y n = 6 para la cuarta (violeta) (Hδ). [2]
Fueron necesarios 30 años más para comprender cómo era posible que la fórmula de Balmer funcionase tan bien, el por qué el hidrógeno emitía en longitudes de onda con esa regularidad tan simple.
Balmer fue un paso más allá. Se planteó si no sería posible que existiesen otras series de líneas hasta ese momento desconocidas en el espectro del hidrógeno. Sus longitudes de onda, en la mejor lógica numerológica, podrían obtenerse simplemente cambiando el 22 de su fórmula por 12, 32, 42… Esta idea llevó a muchos científicos a buscar estas líneas. Con éxito, como veremos.
Notas:
[1] Se trata de una relación puramente empírica sin ninguna base teórica física. En otras palabras, la ecuación se ajusta a los datos, sin ninguna explicación de por qué.
[2] En esta tabla podemos apreciar el nivel de precisión de la fórmula al compararla con las mediciones efectuadas por Ångström:
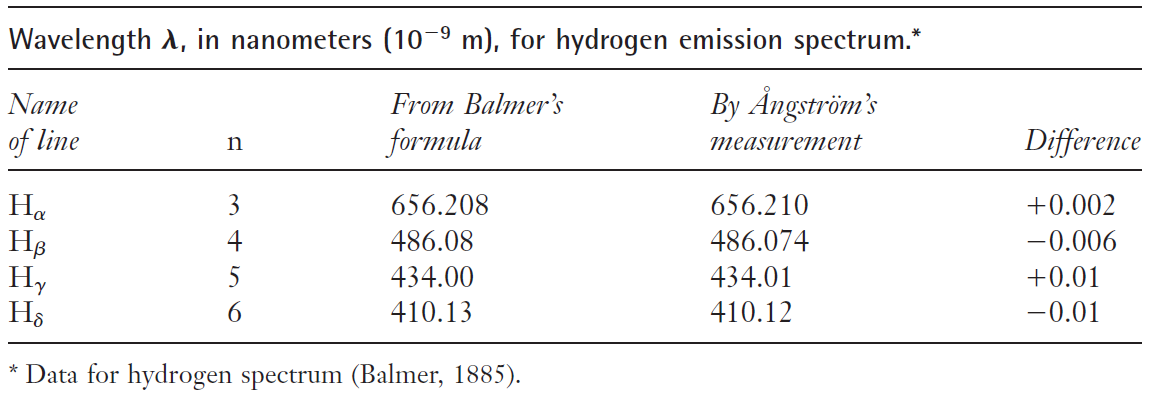
Más detalles, aquí.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Las líneas de Balmer se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La mágica fórmula de Balmer
- Los espectros de absorción de los gases
- Los espectros de emisión de los gases
Una historia de mosquitos, escoceses, esclavos y nazis
 Foto: Wikimedia Commons
Foto: Wikimedia CommonsPara la mayoría de nosotros, pensar en mosquitos es pensar en picores y picaduras, pero no más. Son una anécdota molesta asociada al verano. Pero en la mayoría del mundo y durante la mayor parte de la historia, los mosquitos han sido más que eso, forman una de las grandes amenazas para la población humana a causa de su efecto transmisor de enfermedades contagiosas como la malaria, el dengue o el zika. Se considera, de hecho, el animal más peligroso para el ser humano, por encima de grandes depredadores terrestres o marinos.
Eso significa que su impacto va más allá de una incomodidad veraniega semejante al sudor o la música de chiringuito. Los mosquitos han influido en los movimientos de población y en los resultados bélicos durante siglos. Así lo explica el libro The Mosquito: A Human History of Our Deadliest Predator del historiador Timothy Winegard, que retrata a estos insectos como una fuerza de la naturaleza modeladora de la historia humana.
Los mosquitos panameños y la independencia escocesa
 Foto: Wikimedia Commons
Foto: Wikimedia CommonsCuenta Winegard, por ejemplo, la siguiente historia que recoge este artículo en The New Yorker. En 1968, cinco barcos partieron de Escocia hacia el Nuevo Mundo con un cargamento comercial de lo más suculento: pelucas, calcetines y mantas de lana, peines hecho de madre perla, biblias y zapatos de piel. Llevaban también a bordo una imprenta con la que los colonos planeaban imprimir todo tipo de contratos, tratados y acuerdos al llegar a su destino. Para hacer sitio al cargamento las raciones de comida se redujeron a la mitad.
El destino era la región panameña de Darien, donde la Compañía Escocesa esperaba crear un centro de comercio que hiciese de vía de contacto a través del istmo y así conectar Pacífico y Atlántico. Con esto esperaban también lograr un impulso económico para su país, que llevaba ya años en guerra contra Inglaterra para defender su independencia, que peligraba a causa de una larga hambruna. No era una iniciativa aislada: se calcula que por entonces entre un cuarto y la mitad del dinero en circulación en Escocia estuvo relacionado con el comercio en Panamá.
La expedición fue un desastre. Los colonos enfermaron de fiebre amarilla y malaria, enfermedades para las que no tenían defensas, y llegaron a morir hasta una decena al día. Las referencias a los mosquitos en sus diarios son constantes. Tras seis meses, los supervivientes partieron y se fueron hacia el norte, aunque siguieron muriendo durante la travesía y sus cuerpos lanzados al mar.
Los resultados comerciales de aquel empeño fueron decepcionantes como poco. De todos aquellos peines y zapatos y demás solo terminó llegando a su destino la imprenta. Pero el fracaso de la misión tuvo un resultado inesperado, cuenta Winegard en su libro: la enorme deuda que generó el viaje fue uno de los motivos que terminó obligando a los escoceses a aceptar la oferta de unificación de Inglaterra. Así fue como los mosquitos panameños favorecieron el nacimiento de Gran Bretaña.
Claro que mosquitos (con sus infecciones) y humanos llevan tanto tiempo viviendo en una relación tan estrecha que lo que para unos fue un desastre, para otros, mucho antes, fue una ayuda. Quince siglos antes de que los escoceses tratasen de conquistar Panamá sin éxito, fueron los ejércitos de Roma los que trataron de conquistarles a ellos. Se calcula que entonces aproximadamente la mitad de los ochenta mil soldados romanos enviados con este objetivo perecieron a causa de una cepa endémica de la malaria. Otras cepas locales diezmaron a las tropas de Aníbal a su paso por Italia, detuvieron a las fuerzas de Gengis Khan antes de que avanzasen por el sur de Europea o impidieron a los cruzados europeos conquistar Tierra Santa entre otros momentos clave de la historia.
Enfermedades viejas, continentes nuevos
 Imagen: Wikimedia Commons
Imagen: Wikimedia CommonsLos mosquitos jugaron papeles especialmente importantes en aquellos escenarios históricos en los que viejas enfermedades llegaban a nuevos continentes. Cuando Colón desembarcó en América, los mosquitos que los colonos trajeron consigo trajeron a su vez nuevas enfermedades. Junto con la viruela y la gripe, las enfermedades causadas por este insecto provocaron la muerte de 95 millones de indígenas, más de un 90% de la población que vivía allí antes de que llegasen los europeos, lo cual tuvo un impacto directo en la conquista del territorio y en las relaciones que los distintos grupos de población tendrían desde entonces y durante siglos. Principalmente sirvió para modelar la idea de una tierra vasta y fértil prácticamente despoblada que esperaba pacientemente la llegada de los colonos para aprovecharla, casi como una cuestión de designación divina.
Como al ser humano parecen sobrarle excusas para ser inhumano con sus semejantes, la influencia de los mosquitos, sus picaduras y sus enfermedades influyeron también en el desarrollo y evolución del comercio de esclavos a través del Atlántico. Con la llegada a América de los primeros esclavos de origen africano, llegó también una versión especialmente virulenta de la malaria causada por un parásito llamado Plasmodium falciparum, transmitido por mosquitos.
En aquel momento, siglos XVII y XVIII, la vulnerabilidad de un esclavo a las enfermedades importadas se reflejaba en sus precios: un indígena, con alto riesgo de morir por esta causa costaba menos que un europeo que ya había demostrado ser resistente a ella, y éste menos que un africano traído directamente de su continente original. Los más caros eran los africanos que habían pasado suficiente tiempo en el Nuevo Mundo como para haber probado ser capaces de aguantar las enfermedades de una y otra tierra.
Los mosquitos como arma biológica nazi
 Visita de Himmler a Dachau. Foto: Wikimedia Commons
Visita de Himmler a Dachau. Foto: Wikimedia CommonsEn otros momentos, el ser humano ha intentado dominar y aprovechar este letal insecto a su favor. Fue el caso de la Alemania nazi de Hitler. En 1942, Heinrich Himmler, comandante de las SS, creó un Instituto Entomológico en el campo de concentración de Dachau con el objetivo de experimentar con el uso de mosquitos como elementos de una guerra química y bacteriológica contra los enemigos de guerra del II Reich. La idea no fue espontánea: meses antes, en la navidad de 1941, Himmler había visitado a las tropas alemanas en el frente oriental y se había encontrado a los soldados comidos por los piojos. Conocía de primera mano cómo en la I Guerra Mundial el tifus transmitido por los piojos había diezmado a las tropa germanas y el mismo jerarca nazi tenía fobia a las moscas. La idea de utilizar insectos a su favor ya estaba plantada.
Durante mucho tiempo, los historiadores pensaron que las actividades del Instituto Entomológico de Himmler estaban orientadas aprender más sobre los insectos, sus ciclos de vida, las enfermedades que transmitían y cómo inmunizarse para proteger a las tropas alemanas de sus efectos. Pero en 2014, el entomólogo Klaus Reindhart revisó la documentación disponible y llegó a otra conclusión: parecía haber otro motivo, o al menos otro motivo más, detrás del interés de Himmler por los bichos, y éste sería el utilizarlos a su favor como arma de guerra contra el enemigo.
El hecho de que la experimentación se llevase a cabo en Dachau, que estaba bajo completo control de las SS y donde ya se estaban realizando los experimentos más inhumanos sobre sus prisioneros, algunos de ellos precisamente sobre la malaria, o que eligiese para dirigirla a Eduard May, un entomólogo mediocre pero abiertamente antisemita, en vez de a otros expertos alemanes en entomología hicieron a Reindhart sospechar que la ciencia básica tras el ciclo de vida de los mosquitos no era lo único que interesaba a Himmler. En un informe de May de 1944 que comenta Reindhart se puede leer: “para aclarar la cuestión de si era posible una infección masiva artificial del parásito de la malaria”.
La historia de la humanidad ha estado siempre condicionada por muchos factores distintos, algunos de ellos fuera de control de nuestra especie. Uno de ellos, esta otra especie a la que solo recientemente estamos aprendiendo a combatir y solo un poco. Después de todo, siguen sacándonos de nuestras casillas cuando les oímos zumbar junto a nuestra oreja en las noches de verano. Piense que una picadura sin mayores consecuencias es de lo menos que nos puede ocurrir al entrar en contacto con los mosquitos. Que se lo pregunten a los colonos escoceses…
Referencias
The Mosquito: A Human History of Our Deadliest Predator – Timothy Winegard
How Mosquitoes Helped Shape the Course of Human History – The Smithsonian Magazine
How mosquitos changed everything – The New Yorker
Los nazis investigaron con mosquitos infectados de malaria como armas biológicas – Materia
The Entomological Institute of the Waffen-SS: evidence for offensive biological warfare research in the third Reich – Endeavour
Sobre la autora: Rocío Pérez Benavente (@galatea128) es periodista
El artículo Una historia de mosquitos, escoceses, esclavos y nazis se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Mosquitos transgénicos
- Si no puedes con tu enemigo, modifícalo para que te ayude en la lucha contra enfermedades infecciosas
- Historia y peligros del cultivo de arroz

