¿Qué pasa en tu cerebro cuando duermes?
De la misma forma que el hígado, el corazón, los pulmones o los riñones no dejan de funcionar cuando duermes, el encéfalo tampoco lo hace. Si alguno de estos órganos lo hiciese el resultado es el mismo: la muerte. Pero, si la consciencia no está operativa, ¿a qué se dedica el cerebro mientras dormimos?
Los vídeos de ¿Preguntas frecuentes? presentan de forma breve y amena cuestiones que, probablemente, nos hayamos planteado en alguna ocasión. Los vídeos, realizados para la Cátedra de Cultura Científica de la UPV/EHU, se estrenan en el programa de ciencia Órbita Laika (@orbitalaika_tve), los lunes a las 22:00 en la 2 de RTVE.
Edición realizada por César Tomé López
El artículo ¿Qué pasa en tu cerebro cuando duermes? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¿Hemos intentando contactar con extraterrestres?
- ¿Cómo demonios funcionan las copas musicales?
- #Naukas16 Qué pasa cuando le das un péndulo a una máquina
Geología, Antropoceno y cambio climático
La Facultad de Ciencias de Bilbao comenzó su andadura en el curso 1968/69. 50 años después la Facultad de Ciencia y Tecnología de la UPV/EHU celebra dicho acontecimiento dando a conocer el impacto que la Facultad ha tenido en nuestra sociedad. Publicamos en el Cuaderno de Cultura Científica y en Zientzia Kaiera una serie de artículos que narran algunas de las contribuciones más significativas realizadas a lo largo de estas cinco décadas.

 Nauru. Fuente: Wikimedia Commons
Nauru. Fuente: Wikimedia CommonsTras su lanzamiento por Paul Crutzen en el año 2000, el alcance social y académico del Antropoceno ha crecido de una manera sorprendente. Este concepto se acuñó para materializar nuestra percepción de que las actividades humanas han cambiado el Sistema Tierra. El comportamiento de los océanos, la atmósfera, la superficie terrestre, la criosfera, la biosfera y el clima ya no es el mismo que ha caracterizado durante más de 11.000 años la época geológica en la que formalmente aún vivimos, el Holoceno.
El hecho de que los humanos podamos afectar de modo tan significativo el curso de la evolución geológica de nuestro planeta dio pie en 2009 a la creación del Grupo de Trabajo sobre Antropoceno que está examinando la posibilidad de la formalización e inclusión del término en la Tabla Cronoestratigráfica Internacional (conocida como la Escala del Tiempo Geológico). Ya que la historia de la Tierra anterior a la documentación humana sólo se puede reconstruir a partir de su registro en las rocas, este enfoque centrado en el análisis de las evidencias contenidas en los sedimentos recientes es fundamental para comparar adecuadamente las historias moderna y antigua de nuestro planeta y, por lo tanto, para medir la magnitud y la velocidad de la perturbación planetaria provocada por los humanos.
El Antropoceno se caracteriza por un conjunto de señales de naturaleza sedimentaria, biológica y química que se pueden encontrar en la mayor parte de la superficie terrestre. Algunas de estas evidencias tienen equivalentes en unidades geológicas más antiguas (por ejemplo, el enriquecimiento en metales), pero otras señales son completamente novedosas (como los radioisótopos artificiales o los plásticos dentro de los sedimentos). Estas evidencias reflejan una fase distinta en la historia de la Tierra, que se alejó de su estabilidad general holocena a partir de la Revolución Industrial y, en particular, desde la “Gran Aceleración” en el crecimiento de la población humana, la industrialización y la globalización a mediados del siglo XX, momento que se considera como el límite más adecuado para marcar su inicio.
Desde el punto de vista climático, el rápido aumento de los gases de efecto invernadero desde el siglo XIX (Figura 1) ha provocado un creciente ascenso de la temperatura y del nivel del mar, acompañados por una pérdida de hielo en los continentes. Este calentamiento ha alcanzado ya niveles más altos que los detectados durante el Holoceno y se acerca a los de otras etapas interglaciares del periodo Cuaternario.
 Figura 1. Tasas de cambio en las concentraciones de gases de efecto invernadero desde el inicio de la Revolución Industrial. La década de 1950 marca una aceleración de su crecimiento (gráficos originales en W. Steffen, W. Broadgate, L. Deutsch, O. Gaffney y C. Ludwig (2015) “The trajectory of the Anthropocene: The Great Acceleration” The Anthropocene Review 2, 81-98). Imagen tomada de WWF (2018) “Informe Planeta Vivo-2018: Apuntando más alto”. M. Grooten y R.E.A. Almond (Eds.), Suiza.
Figura 1. Tasas de cambio en las concentraciones de gases de efecto invernadero desde el inicio de la Revolución Industrial. La década de 1950 marca una aceleración de su crecimiento (gráficos originales en W. Steffen, W. Broadgate, L. Deutsch, O. Gaffney y C. Ludwig (2015) “The trajectory of the Anthropocene: The Great Acceleration” The Anthropocene Review 2, 81-98). Imagen tomada de WWF (2018) “Informe Planeta Vivo-2018: Apuntando más alto”. M. Grooten y R.E.A. Almond (Eds.), Suiza.La asociación de los humanos con las regiones costeras se remonta a las primeras civilizaciones, cuando nos concentramos en las desembocaduras de los ríos, deltas y estuarios, debido a la disponibilidad de alimentos abundantes y accesibles. Durante el siglo XX, la zona costera ha cambiado profundamente a medida que las poblaciones humanas iban creciendo y los ambientes costeros se ocupaban para la agricultura, la urbanización y la industria. Gran parte de la población mundial vive hoy en las áreas costeras con una densidad 3 veces superior al promedio mundial y la mayoría de las megaciudades planetarias también se encuentran en la costa. Sin embargo, los registros instrumentales y geológicos muestran que la velocidad de aumento reciente del nivel marino es anómala con respecto a los últimos miles de años y muchas zonas costeras se encuentran ahora amenazadas. Se ha observado globalmente una transición en el ascenso marino desde valores relativamente bajos durante el Holoceno superior (3 mm/año.
El estudio del nivel marino es un campo muy interdisciplinar y de creciente importancia. En el 1º informe de evaluación del IPCC (1990) no había referencia alguna a los cambios en el nivel del mar anteriores al siglo XX. Ya en el 3º informe de evaluación (2001) se incorporó el cambio del nivel marino a escalas de tiempo más largas, pero sólo en el 4º informe (2007) se agrupó la información geológica sobre el paleoclima en un solo capítulo, como asimismo se ha hecho en el 5º y último informe de evaluación (2013). Los registros instrumentales del nivel del mar comenzaron con el mareógrafo de Ámsterdam en 1682 y la altimetría de precisión por satélite se inició tras el lanzamiento del TOPEX/Poseidon a finales de 1992. Estos datos han demostrado que las velocidades de cambio del nivel del mar varían regionalmente y a escalas temporales de décadas debido a cambios en la densidad del océano. Es ahí donde los datos geológicos se hacen necesarios para poder situar estas estimaciones instrumentales en un contexto temporal a más largo plazo (Figura 2).
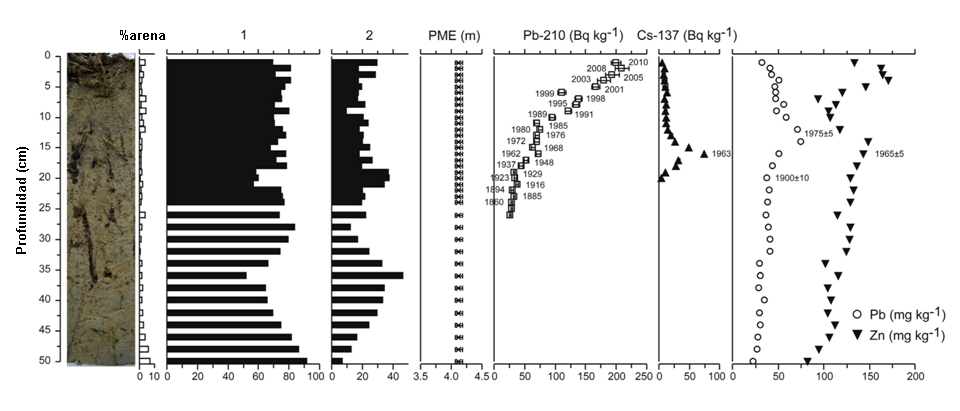 Figura 2. Fotografía del testigo, contenido en arena, principales especies de microfósiles (1: Entzia macrescens; 2: Trochammina inflata), elevación de la paleomarisma (PME), actividad de los radioisótopos Pb-210 y Cs-137 y distribución del Pb y Zn durante los últimos 300 años en un sondeo perforado en la marisma de Murueta (Reserva de la Biosfera de Urdaibai). Imagen modificada de A. García-Artola, A. Cearreta y E. Leorri (2015) “Relative sea-level changes in the Basque coast (northern Spain, Bay of Biscay) during the Holocene and Anthropocene: The Urdaibai estuary case” Quaternary International 364, 172-180. DOI: 10.1016/j.quaint.2014.06.040
Figura 2. Fotografía del testigo, contenido en arena, principales especies de microfósiles (1: Entzia macrescens; 2: Trochammina inflata), elevación de la paleomarisma (PME), actividad de los radioisótopos Pb-210 y Cs-137 y distribución del Pb y Zn durante los últimos 300 años en un sondeo perforado en la marisma de Murueta (Reserva de la Biosfera de Urdaibai). Imagen modificada de A. García-Artola, A. Cearreta y E. Leorri (2015) “Relative sea-level changes in the Basque coast (northern Spain, Bay of Biscay) during the Holocene and Anthropocene: The Urdaibai estuary case” Quaternary International 364, 172-180. DOI: 10.1016/j.quaint.2014.06.040Durante el siglo XX, el nivel del mar ha aumentado globalmente unos 30 cm y la magnitud del ascenso del nivel marino previsto para este siglo es un tema muy controvertido. Las últimas proyecciones del IPCC (2019) auguran un aumento medio del nivel del mar a finales del siglo XXI de 28–57 cm para un escenario con reducción drástica de las emisiones de efecto invernadero, y de 55–140 cm si hubiese un crecimiento de estas emisiones. Otras estimaciones recientes sugieren que el ascenso medio global del nivel del mar podría incluso superar los 150-200 cm en el año 2100 (Figura 3). Esta diferencia en las previsiones refleja las grandes incertidumbres que existen sobre el comportamiento futuro de los casquetes glaciares de Groenlandia y Antártida.
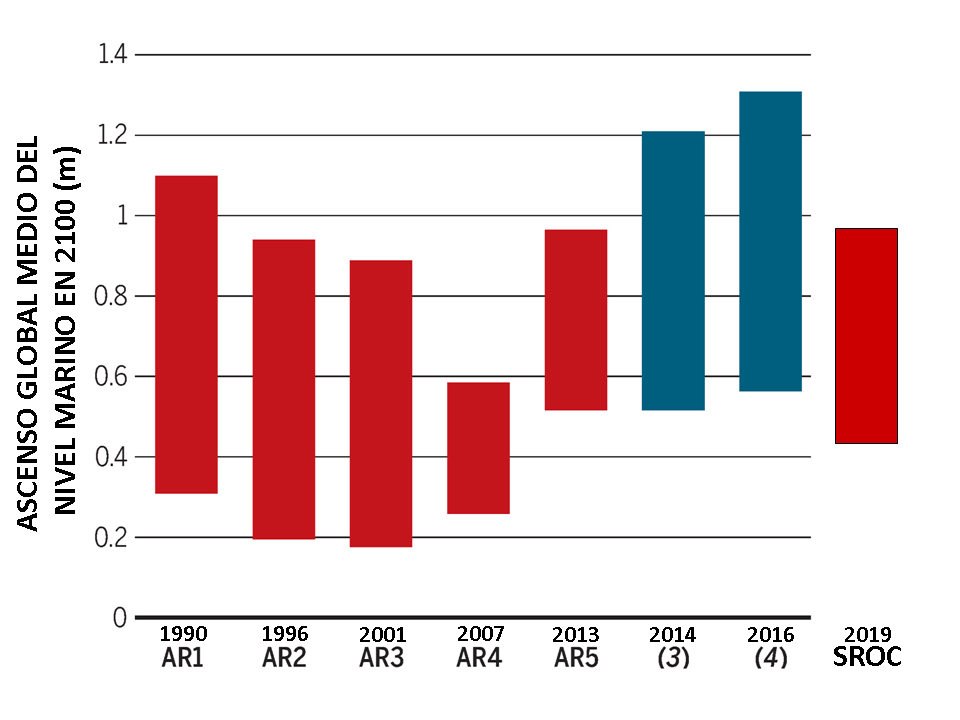 Figura 3. Las distintas proyecciones del nivel marino para el año 2010 realizadas a partir de modelos han variado mucho a lo largo del tiempo desde la publicación del Primer Informe de Evaluación del IPCC (AR1) en 1990 hasta el último Informe Especial sobre el Océano y la Criosfera (SROC) de 2019. Imagen modificada de M. Oppenheimer y R.B. Alley (2016) “How high will the seas rise?” Science 354, 1375-1377. DOI: 10.1126/science.aak9460
Figura 3. Las distintas proyecciones del nivel marino para el año 2010 realizadas a partir de modelos han variado mucho a lo largo del tiempo desde la publicación del Primer Informe de Evaluación del IPCC (AR1) en 1990 hasta el último Informe Especial sobre el Océano y la Criosfera (SROC) de 2019. Imagen modificada de M. Oppenheimer y R.B. Alley (2016) “How high will the seas rise?” Science 354, 1375-1377. DOI: 10.1126/science.aak9460El aumento del nivel del mar tiene una amplia gama de efectos sobre las zonas costeras que incluyen la inundación y pérdida de marismas, la erosión de playas, dunas y acantilados, la incursión de agua salada en acuíferos y centros urbanos, y el desplazamiento general de los ecosistemas costeros hacia tierra. La magnitud de estos impactos y sus consecuencias estarán asociadas, además, con los efectos de otros procesos humanos que han estado operando en el litoral durante décadas, como la disminución del aporte fluvial de sedimentos, la extracción de aguas subterráneas o la ocupación de las tierras costeras.
La duración del Antropoceno hasta ahora ha sido geológicamente muy breve, equivalente a una vida humana, pero sus impactos ya han cambiado de manera irrevocable el curso futuro de la historia de nuestro planeta. Algunos de estos cambios son irreversibles, incluso si la humanidad y sus efectos ambientales desaparecieran mañana mismo, y sus consecuencias persistirán durante siglos, milenios y millones de años.
Para saber más:
C.N. Waters, J. Zalasiewicz, C. Summerhayes, A.D. Barnosky, C. Poirier, A. Gałuszka, A. Cearreta, M. Edgeworth, E. Ellis, M.A. Ellis, C. Jeandel, R. Leinfelder, J.R. McNeill, D. deB. Richter, W. Steffen, J. Syvitski, D. Vidas, M. Wagreich, M. Williams, A. Zhisheng, J. Grinevald, E. Odada, N. Oreskes, y A.P. Wolfe (2016) “The Anthropocene is functionally and stratigraphically distinct from the Holocene” Science 351, 137 (aad2622.1-aad2622.10). DOI: 10.1126/science.aad2622
C. Summerhayes y A. Cearreta (2019) “Chapter 6. Climate Change and the Anthropocene” En: J. Zalasiewicz, C.N. Waters, M. Williams y C.P. Summerhayes (Eds.), The Anthropocene as a geological time unit: A guide to the scientific evidence and current debate. Cambridge University Press, 200-241. DOI: 10.1017/9781108621359
Sobre los autores: Alejandro Cearreta y Ane García Artola pertenecen al Departamento de Estratigrafía y Paleontología de la Facultad de Ciencia y Tecnología de la UPV/EHU.
El artículo Geología, Antropoceno y cambio climático se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Verdín, eucaliptos y cambio climático
- Los ecosistemas acuáticos de África y el cambio climático
- Naukas Bilbao 2017 – José Miguel Viñas: Me río yo del cambio climático
Por qué nos fascinan los neandertales
![]()
 Réplica de un cráneo neandertal en la cueva de San Miguel (St. Michael’s Cave), Gibraltar. Boaski / Flikr
Réplica de un cráneo neandertal en la cueva de San Miguel (St. Michael’s Cave), Gibraltar. Boaski / FlikrEntre los muchos enigmas de la ciencia prehistórica que provocan fascinación, tanto a científicos como al público interesado, la desaparición de los neandertales ocupa un lugar privilegiado.
Los neandertales poblaron Europa y Asia occidental desde hace unos 300.000 años y desaparecieron hace poco más de 40.000, coincidiendo con la llegada a Europa de los Humanos modernos –nuestra especie– tras su salida de África. Este último es uno de los períodos más críticos en la Prehistoria humana, pues no sólo incluyó un cambio de poblaciones definitivo, sino también una importante transformación cultural.
Dicha transformación supuso el asentamiento en todo el viejo mundo de los comportamientos complejos que caracterizarían el posterior desarrollo de las formas de vida asociadas a nuestra especie. Los prehistoriadores llevamos más de un siglo discutiendo sobre los factores y características de estos procesos de cambio, sin haber consensuado aún interpretaciones plenamente satisfactorias.
Las implicaciones ideológicas que supone el estudio de un pariente evolutivo tan cercano a la humanidad actual, y por tanto vital para entendernos a nosotros mismos, han provocado que la investigación de los neandertales haya estado históricamente cargada de prejuicios y mitos diversos. Sin embargo, los avances teóricos y metodológicos de las últimas décadas han permitido que actualmente el problema sobre su desaparición se plantee como una de las controversias científicas de mayor complejidad en el campo de la Prehistoria.
“El mito”, o la historia de la investigación sobre los neandertales
La investigación de Homo neanderthalensis, como se denominó la especie definida a partir de los restos humanos encontrados en 1856 en el valle de Neander (Alemania), es uno de los mejores ejemplos de cómo en ocasiones la ciencia puede verse influida por el contexto histórico en el que se desarrolla.
Las implicaciones ideológicas y sociales que conllevó el reconocimiento de una humanidad remota, distinta pero emparentada con la actual, inauguraron una tradición investigadora sobre los Neandertales en la que éstos, de forma más o menos directa, han sido objeto de prejuicios e ideologías de distinto pelaje.
 Valle de Neander. Cordula / Wikimedia Commons
Valle de Neander. Cordula / Wikimedia CommonsLas primeras interpretaciones que acusaron estas influencias externas a la ciencia se dieron ya desde finales del siglo XIX y principios del XX, en un contexto de fuerte oposición a la teoría de la evolución formulada por Darwin solo tres años después del descubrimiento de los restos de Neander. Entonces, una compleja mezcla de ideas racistas, colonialistas y religiosas contribuyeron a dibujar un neandertal troglodítico y animalizado, esencialmente distinto a nosotros, para el que en todo caso se tenían aún muy pocas evidencias arqueológicas y paleontológicas.
Tras la Segunda Guerra Mundial, las ideologías dominantes viraron para fomentar la imagen de un neandertal más humanizado y capaz. Sin embargo, durante los años 80 el péndulo volvió a oscilar y la visión del neandertal basculó hacia interpretaciones que le volvían a alejar de la humanidad moderna, tanto en capacidades culturales como en naturaleza biológica.
Es esta última visión, y en cierto modo las reminiscencias de las imágenes animalizadas de principios de siglo, la que cuestionan la mayoría de los investigadores desde hace tres décadas, y a la cual suelen enfrentar sus investigaciones.
Podemos situar en la última década del siglo XX el comienzo de una etapa historiográfica, la actual, en la que la investigación sobre los neandertales ha alcanzado una verdadera madurez científica. Aunque las implicaciones ideológicas que supone el estudio de este tipo humano siguen flotando en el ambiente, el asentamiento de la Prehistoria como una ciencia interdisciplinar, con métodos y técnicas avanzados, ha hecho que nuestro conocimiento actual de esta especie humana se encuentre fundamentalmente basado en evidencias y pruebas empíricas. Algunas de ellas presentan una solidez científica que apenas podía ser imaginada pocos años atrás.
Por ello, el enigma de la desaparición de los neandertales, históricamente cargado de tópicos y prejuicios, es hoy investigado como un complejo problema científico de primera magnitud. Arqueólogos, paleoantropólogos, geólogos, ecólogos o físicos, entre otros, aúnan esfuerzos para recomponer un puzle poliédrico y, como siempre en Prehistoria, parcial e incompleto.
Por tanto, puede concluirse sin ambages que, en los últimos años, las influencias externas a la investigación meramente científica han perdido fuerza para dejar paso a marcos de trabajo cada vez más objetivos. Hemos pasado del mito al logos.
“El logos”, o la investigación interdisciplinar de un problema científico
El planteamiento tradicional del problema de la desaparición neandertal se hacía en términos simples y dicotómicos. O bien nuestra especie, superior en biología y tecnología, protagonizó un proceso de suplantación poblacional, más o menos violento y a escala continental, o bien los neandertales evolucionaron cultural y anatómicamente hacia las formas modernas de Homo sapiens.
Hoy en día se da la situación paradójica (en realidad bastante habitual en ciencia) de que, sabiendo bastante más sobre el problema, somos incapaces de defender teorías tan definidas. Las nuevas evidencias arqueológicas, paleontológicas, geológicas, paleoecológicas y paleogenéticas nos han empujado progresivamente a abandonar la idea de un proceso de cambio único y monolítico, y valorar, por el contrario, marcos interpretativos basados en la variabilidad regional y cronológica.
Hoy sabemos que neandertales y Humanos modernos tuvieron descendencia fértil en varios momentos y regiones geográficas, pero aún desconocemos si esos procesos de hibridación fueron responsables de la desaparición (en este caso asimilación) de los neandertales en toda su extensión geográfica. Sabemos también que los neandertales fueron capaces de desarrollar tecnologías y estrategias de subsistencia complejas durante el Paleolítico medio, pero no tenemos aún la seguridad de que dichas estrategias contribuyeran directamente al posterior desarrollo cultural del Paleolítico superior.
Sabemos que los neandertales tuvieron la inteligencia e inquietudes necesarias para desarrollar comportamientos simbólicos, incluyendo probablemente la creación de las primeras grafías pintadas en cuevas, pero se discute si dichos comportamientos fueron recurrentes, o incluso si los métodos utilizados para su verificación son fiables.
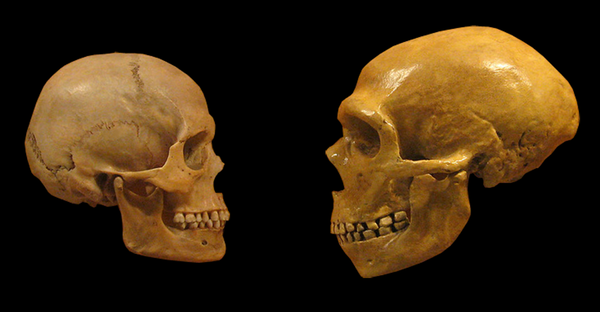 Comparación de un cráneo de Homo sapiens y de un neandertal. Wikimedia Commons
Comparación de un cráneo de Homo sapiens y de un neandertal. Wikimedia CommonsHasta hace poco creíamos saber que neandertales y Humanos modernos convivieron durante milenios en distintas regiones europeas, pero el refinamiento de los métodos de datación nos ha obligado a cuestionar fuertemente esa idea. Igualmente, creíamos saber que los neandertales estaban especialmente adaptados a climas fríos, pero hoy se baraja la hipótesis de que la variabilidad climática fuera un factor relevante para su desaparición.
Nos encontramos en un momento de grandes cambios teóricos e interpretativos, en el que el final de los neandertales se estudia desde un marco interdisciplinar alejado de los mitos y prejuicios del pasado, por más que en ocasiones estos traten de volverse a incluir en escena. Al obtener evidencias cada vez más certeras en distintos ámbitos, el problema se hace aún más complejo, y evitamos las respuestas simplistas y viciadas que se han propuesto en el pasado.
Son especialmente relevantes los proyectos de investigación a escala regional realizados con metodologías modernas e interdisciplinares, cada vez más numerosos y relevantes en la península ibérica. Precisamente, esta macro región geográfica se ha revelado clave para estudiar el final de los neandertales y el primer poblamiento europeo de Humanos modernos, pues es probable que aquí se produjeran los últimos episodios de este complejo proceso de cambio biocultural.
Y aunque nuestras respuestas probablemente nunca serán definitivas, si mantenemos el pensamiento crítico y el método científico como guías, sin duda se acercarán cada vez más a la realidad prehistórica.![]()
Sobre el autor: Manuel Alcaraz Castaño es investigador en arqueología del Paleolítico en la Universidad de Alcalá
This article is republished from The Conversation under a Creative Commons license. Original article.
El artículo Por qué nos fascinan los neandertales se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Neandertales ¿crónica de una muerte anunciada?, por María Martinón-Torres
- La cronología de la desaparición de los neandertales
- Los neandertales respiraban de otra manera
Datos que entran por los ojos
Si uno le pregunta a Google Images qué es un una gráfica, puede encontrarse con un esperpento como el siguiente:
Más allá de la fealdad generalizada y los colores estridentes, la web y los medios de comunicación están plagados de ejemplos de malas representaciones de datos. Ejemplos donde el artificio y la ornamentación pervierten la función de estas poderosas herramientas.
¿Qué es una gráfica entonces? Dado que Google no parece ser de gran ayuda en este caso, yo os propongo la siguiente definición: una gráfica es una representación de datos numéricos mediante recursos visuales que permite interpretarlos y extraer información de ellos. Las gráficas son herramientas de comunicación para un tipo de mensaje muy determinado (los datos) y un tipo de receptor muy determinado (monos con buenos ojos), y como tal, utilizan un código muy especializado.
Los ojos son nuestra principal fuente de información. Se estima que nuestras retinas reciben unos 10 Gbps de información, de los cuales, pasan por el nervio óptico unos 100 Mbps hasta nuestro córtex visual. De hecho, según calculan los neurocientíficos, al menos un tercio de nuestro cerebro está ocupado procesando información visual. Por eso, a veces, cerramos los ojos cuando intentamos concentrarnos: para ser capaces de destinar más recursos a pensar o recordar mejor. En realidad, no es que tengamos una vista muy buena en comparación con otras especies. En lo que realmente somos buenos es en el análisis de la imagen, en extraer información útil a partir de lo que vemos… como caras de otros monos o un león camuflado en las hierbas.
En cambio, nuestra memoria de trabajo es bastante más modesta. Quizás resulte familiar la conocida como ley de Miller: “the magic number seven, plus or minus two1”. Es uno de los artículos más citados en psicología y, aunque ha sido revisada y matizada posteriormente, viene a decir que, en general, los humanos no podemos retener más de 7 elementos o grupos en nuestra memoria a corto plazo. Es decir, que si nos dan un listado de, pongamos, 10 cosas, nos va a resultar difícil retenerlas todas a la vez en nuestra cabeza y hacer comparaciones entre ellas mentalmente.
Por tanto, la magia de la visualización de datos consiste en convertir “cifras” (números abstractos que requerirían nuestra pobre memoria para ser comparados) en estímulos visuales, de esos que somos tan buenos en analizar.
Por poner un ejemplo, os proponemos encontrar el número más alto en tres tipos de representaciones distintas:
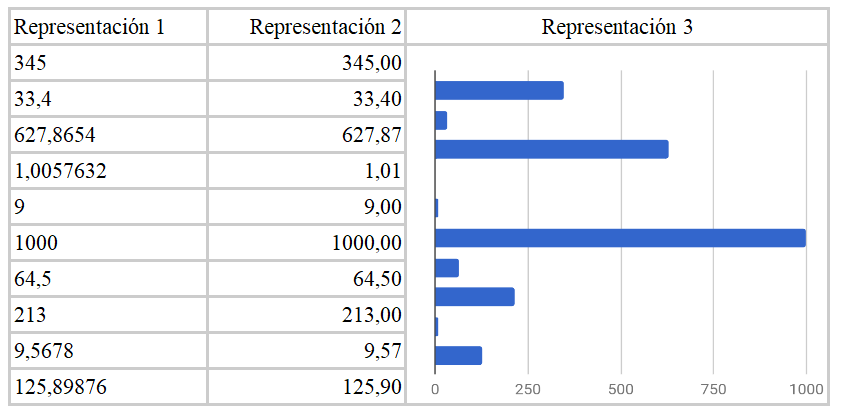
En la primera representación, habréis tenido algunos problemas para encontrarlo, y probablemente hayáis escaneado varias veces la lista, hacia arriba y hacia abajo, para recordar un número o comprobar otra vez dónde estaba la coma de los decimales. En la segunda representación, las cifras están estandarizadas para mostrar dos posiciones decimales. Una vez visto este detalle, la alineación a la derecha hace que encontrar el número más grande sea prácticamente inmediato, dado que “sobresale” hacia la izquierda más que los demás. Pero fijaos que ya hemos recurrido a un truco visual, tomando un atajo que nos permite evitar la memorización, y esto se hace especialmente evidente en la representación final en forma de gráfica.
Existe otro ejemplo muy representativo del poder de nuestros ojos procedente, en este caso, del mundo de los juegos. El juego es como sigue:
- Hay 2 jugadores.
- Cada jugador escoge un número del 1 al 9 en su turno.
- Una vez un número es escogido, nadie puede volver a usarlo.
- Gana el jugador que primero sume 15 usando 3 números.
Planteado de esta manera, es posible que al lector le cueste hacerse a una idea de en qué consiste el juego o qué estrategia elegir. Parece ciertamente complejo. Jugar requiere retener en la memoria una lista de los números escogidos, las posibles sumas que se forman con ellos y los números eliminados por el otro jugador. Todo un dolor de cabeza. Sin embargo, este mismo juego puede presentarse de manera visual, simplificándose enormemente: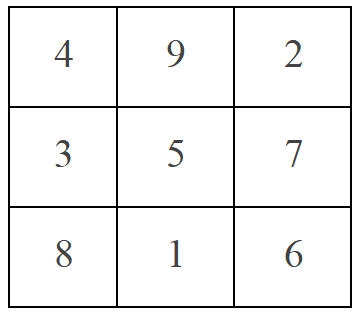 Esta representación visual resume todas las posibles combinaciones, ya que cualquier fila, columna o diagonal suma 15; nos revela, además, algunas propiedades interesantes de estos números. Por ejemplo, el 5 participa en más sumas cuyo resultado es 15 que ningún otro número (ya que se encuentra en el centro de la distribución). Los números pares participan, cada uno, en 3 sumas. Los números impares sólo pueden formar 2 sumas. Son propiedades matemáticas que podríamos haber deducido de haber analizado en detalle el problema inicial. Pero la representación visual nos permite pensar de manera visual, sin abstracciones previas.
Esta representación visual resume todas las posibles combinaciones, ya que cualquier fila, columna o diagonal suma 15; nos revela, además, algunas propiedades interesantes de estos números. Por ejemplo, el 5 participa en más sumas cuyo resultado es 15 que ningún otro número (ya que se encuentra en el centro de la distribución). Los números pares participan, cada uno, en 3 sumas. Los números impares sólo pueden formar 2 sumas. Son propiedades matemáticas que podríamos haber deducido de haber analizado en detalle el problema inicial. Pero la representación visual nos permite pensar de manera visual, sin abstracciones previas.
En definitiva, la gracia de las gráficas y de las representaciones visuales de cualquier tipo de problema es que convierten datos abstractos, que nuestra memoria de trabajo no puede retener, en estímulos perceptivos, que entran en nuestra cabeza sin necesidad de mediación, sin necesidad de que comprendamos y retengamos cada uno de esos numeritos. Esto las convierte, a su vez, en un arma enormemente peligrosa. Precisamente porque las gráficas hacen innecesario el proceso de lectura (de interpretación mediada y meditada de los datos), es muy fácil engañar y distorsionar los datos recurriendo a su poder.
Referencia:
1Miller, G. A. (1956). “The magical number seven, plus or minus two: Some limits on our capacity for processing information”. Psychological Review. 63(2): 81–97
Sobre los autores: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica. Iñaki Úcar es doctor en telemática por la Universidad Carlos III de Madrid e investigador postdoctoral del UC3M-Santander Big Data Institute.
El artículo Datos que entran por los ojos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Sal de la piscina si te pican los ojos y no mezcles lejía con amoniaco
- #Naukas14 Arqueología de datos
- Colonialismo científico: los investigadores africanos se rebelan contra el expolio de datos genéticos
Cuatro leyes consumadas siguiendo una banda de Möbius
La escritora danesa Solvej Balle (1962) publicó en 1983 Ifølge loven Fire beretninger om mennesket,novelatraducida al castellano como Según la ley. Cuatro relatos sobre el ser humano (Seix Barral, 1995).

Como indica el título, cuatro historias componen este libro. Son cuatro metáforas sobre la búsqueda de la verdad. Son cuatro relatos sobre las obsesiones de otras tantas personas que realizan su peculiar búsqueda para llegar a entender la naturaleza del ser humano.
La banda de Möbius estructura la novela que, a priori, podría parecer formada por relatos independientes. Pero cada historia lleva a la siguiente, y la cuarta conduce inevitablemente a la primera, que reanuda el ciclo interminable del libro. La habitual metáfora de la banda de Möbius, pensada como la cinta del eterno retorno, se muestra de este modo en la novela.
Cuatro son también las leyes que actúan como hilo conductor de esta singular narración, algunas de ellas conocidas leyes científicas. Describimos brevemente cada relato.
1. Ley sobre examen forense y autopsia
De acuerdo con la ley, el cuerpo que después del óbito ofrece dudas sobre la causa de la muerte deberá ser sometido a autopsia.
Ley sobre examen forense y autopsia (Dinamarca)
El bioquímico canadiense Nicholas S. investiga sobre el misterio de la verticalidad del cuerpo humano. Presencia la autopsia de una joven que ha fallecido de hipotermia –se ha suicidado– y que ha donado su cuerpo a la ciencia. Estudia con minuciosidad el cerebro del cadáver en cuya corteza busca ‘un determinado color verde’ que probaría la existencia de una sustancia denominada filodoxa-tri-fosfato que –según una teoría muy controvertida– desempeñaría un papel fundamental en el movimiento bípedo del ser humano…
Si esta sustancia era un error, éste era de la evolución, no suyo. Si la naturaleza había cometido un error, su misión no era ocultarlo.
2. Ley del talión
El que maltrate a su prójimo será tratado de la misma manera; fractura por fractura, ojo por ojo y diente por diente, es decir, recibirá lo mismo que él ha hecho al prójimo.
Levítico, 24:19-21
Tanja L., estudiante de Derecho en Suiza, posee poderes paranormales y sospecha que provoca –en contra de su voluntad– caídas y accidentes, causando de este modo dolor y sufrimientos a otras personas. Desea descubrir la naturaleza del dolor, y para ello viaja a Barcelona, Madrid y París, buscando señales que le ayuden a descifrarlo.
Su búsqueda había sido un malentendido. Había aprendido bastante sobre la fragilidad y la fuerza destructora del ser humano, pero no podía lastimarse con tanta facilidad a una persona.
3. Ley de la gravedad
Dos cuerpos de diferente peso se moverán a la misma velocidad de caída en el vacío.
Ley de la caída de los cuerpos de Galileo
René G. es un matemático danés con un único deseo: no ser nadie.
Deseaba saber hasta qué punto podía acercarse un ser humano a la transparencia del no ser y estaba seguro de que, una vez hubiese alcanzado ese punto cero, podría hacer lo que se esperaba de él, proseguir sus estudios, realizar su trabajo sobre las relaciones entre los teoremas de incompletitud de Gödel y los postulados paralelos no euclidianos, y después pasar el resto de su vida describiendo sosegados círculos alrededor del punto cero humano.
Pero, no es tan fácil…
4. Ley de la termodinámica
En un sistema aislado, los procesos en los que interviene el calor suceden sólo en una dirección
Segunda ley de la termodinámica
Alette V. es una escultora canadiense que se dedica a realizar bustos a los transeúntes. Adora la materia inanimada y sueña con fundirse con ella. En ese afán por desprenderse de su parte humana, decide suicidarse dejándose morir de hipotermia. Así, su cadáver pasará a ser un objeto más en su habitación.
Trasladaba las personas al mundo de los objetos. […] Ella pertenecía a los objetos, pero ¿qué era?
Alette ha donado su cuerpo-objeto a la ciencia… un bioquímico canadiense llamado Nicholas S. conseguirá el cerebro de la fallecida para avanzar en sus investigaciones sobre el misterio de la verticalidad del cuerpo humano…
Nota: Adaptado de “Según la ley. Cuatro relatos sobre el ser humano”, de Solvej Balle, en DivulgaMAT, 2013
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo Cuatro leyes consumadas siguiendo una banda de Möbius se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Poesía retorcida sobre banda de Möbius
- La Formación Jaizkibel y sus singulares geoformas “de Möbius”
- El teorema de los cuatro colores (1): una historia que comienza en 1852
Descomposición de la luz
 Vidriera modernista del Museo Art Nouveau y Art Déco Casa Lis (Salamanca). Fuente: Museo Casa Lis
Vidriera modernista del Museo Art Nouveau y Art Déco Casa Lis (Salamanca). Fuente: Museo Casa LisLos agentes colorantes encontrados en la pintura y la cerámica prehistóricas muestran que los humanos han apreciado el color desde los tiempos más antiguos. Pero, increiblemente, no existió ninguna hipótesis científica sobre el hasta Newton. Hasta entonces, la mayoría de las ideas aceptadas sobre el color procedían de artistas y técnicos como da Vinci, que basaban sus ideas en su experiencia con la mezcla de pigmentos.
Desafortunadamente, las lecciones aprendidas con la mezcla de pigmentos rara vez se aplican a la mezcla de haces de luz de diferentes colores. En la antigüedad, se pensaba que la luz del Sol era “pura”. El color resultaba de la adición de impurezas, como los casos en los que un rayo de “luz pura” se refracta en una pieza de vidrio y emerge con bordes de colores.
 Fuente: Smithsonian Libraries
Fuente: Smithsonian LibrariesNewton se interesó por los colores cuando todavía era estudiante en la Universidad de Cambridge. En 1672, a la edad de 29 años, Newton publicó un modelo del color en las Philosophical Transactions de la Royal Society de Londres. Este fue su primer artículo científico publicado. En él escribió:
In the beginning of the Year 1666, at which time I applyed myself to the grinding of Optick glasses of other figures than Spherical, I procured me a Triangular glass-Prisme, to try therewith the celebrated Phaenomena of Colours. And in order thereto haveing darkened my chamber, and made a small hole in my window-shuts, to let in a convenient quantity of the Suns light, I placed my Prisme at his entrance, that it might be thereby refracted to the opposite wall. It was at first a very pleasing divertisement, to view the vivid and intense colours produced thereby. . . .
[A comienzos del año 1666, momento en el que me apliqué al pulimiento de lentes ópticas de formas diferentes a la esférica, me hice de un prisma triangular de vidrio para comprobar el famoso fenómeno de los colores. Para ello, tras oscurecer mi habitación y hacer un pequeño agujero en mis contraventanas para dejar entrar una cantidad conveniente de la luz del Sol, coloqué mi prisma en su entrada, para que así pudiera ser refractada hacia la pared opuesta. Al principio fue un divertimento muy agradable ver los colores vívidos e intensos producidos así. . . .] (Traducción propia)
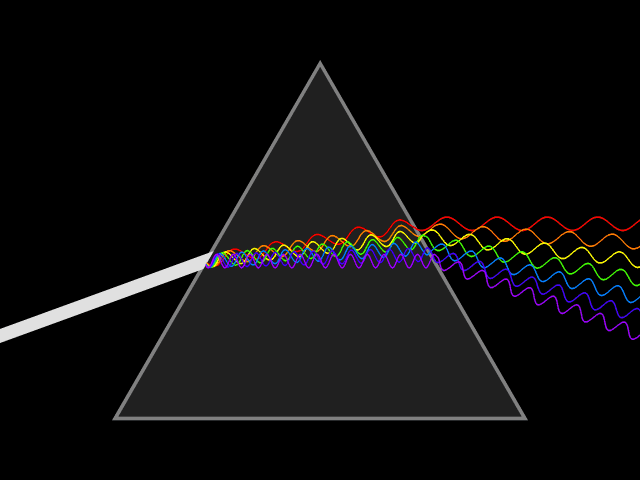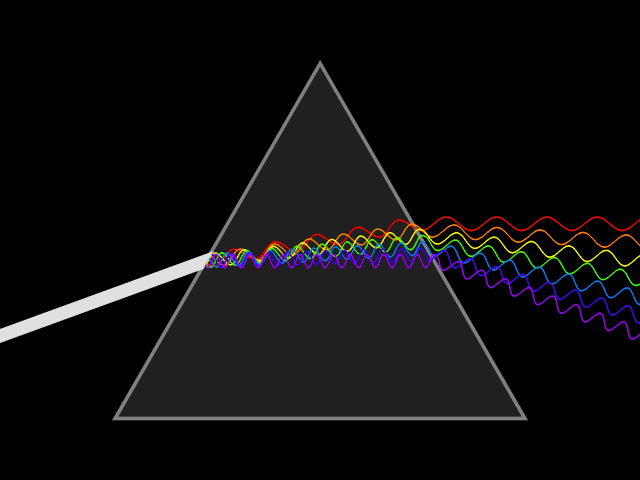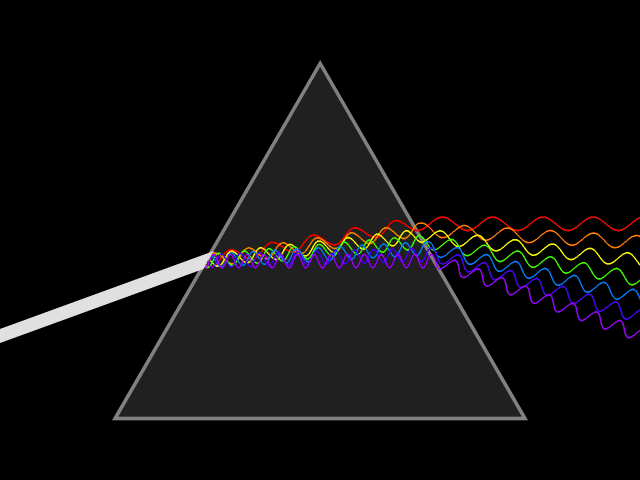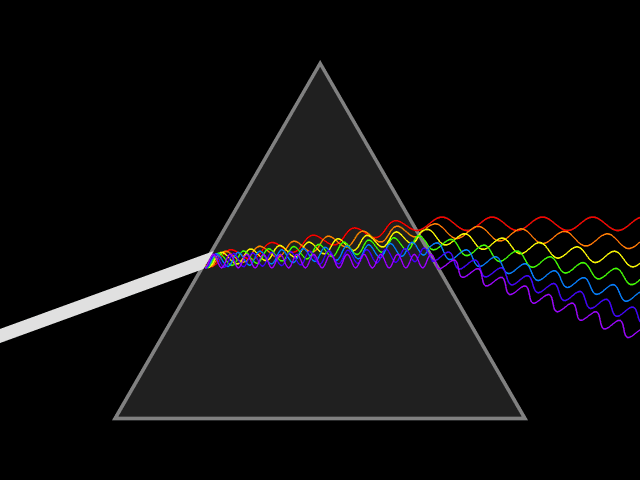
El haz cilíndrico de luz solar “incolora” de la abertura circular pasaba a través del prisma y producía una mancha alargada de luz coloreada en la pared opuesta. Esta mancha era violeta en un extremo, rojo en el otro y mostraba una gradación continua de colores en el medio. Para este patrón de colores Newton inventó un nombre: espectro.
Pero, ¿de dónde vienen los colores? ¿Y por qué la imagen se extiende en una mancha alargada en len vez de ser un círculo? Newton pasó la luz a través de diferentes espesores de vidrio, cambió el tamaño del agujero en la contraventana e incluso colocó el prisma fuera de la ventana.
 Fuente: Wikimedia Commons
Fuente: Wikimedia CommonsNinguno de estos cambios tuvo ningún efecto en el espectro. Tal vez alguna rugosidad o irregularidad en el vidrio era lo que producía el espectro, pensó Newton. Para probar esta posibilidad pasó los rayos de colores de un prisma a través de un segundo prisma similar puesto del revés. Si alguna irregularidad en el vidrio causaba que el haz de luz se extendiera, entonces pasar este haz a través del segundo prisma debería extenderlo aún más. En cambio, el segundo prisma, cuando se colocaba en determinada posición, volvía a juntar los colores bastante bien. Ahora se formaba un punto de luz blanca, como si la luz no hubiera pasado a través de ninguno de los prismas.
 Fuente: Wikimedia Commons
Fuente: Wikimedia CommonsSiguiendo un proceso de eliminación, Newton se convenció a sí mismo de lo que probalmente creía desde el principio era cierto: la luz incolora (blanca) está compuesta de colores. El prisma no fabrica ni añade los colores; estaban allí todo el tiempo, pero mezclados no se podían distinguir. Cuando la luz incolora pasa a través de un prisma, cada uno de los colores componentes se refracta en un ángulo diferente. Como consecuencia el haz se despliega en un espectro.
Como prueba adicional de esta hipótesis, Newton cortó un pequeño agujero en una pantalla en la que proyectó un espectro. De esta manera, la luz de un solo color podría separarse y pasar a través de un segundo prisma. Encontró que el segundo prisma no tenía ningún efecto adicional en el color de este haz, tan solo cambiaba su dirección, lo refractaba, aún más. Es decir, una vez que el primer prisma había hecho su trabajo de separar los componentes de color de la luz incolora, el segundo prisma no podía cambiar el color de los componentes. Resumiendo sus conclusiones, Newton escribió:
Colors are not Qualifications of Light derived from Refraction or Reflection of natural Bodies (as ’tis generally believed) but Original and Connate Properties, which in divers Rays are divers. Some Rays are disposed to exhibit a Red Colour and no other; some a Yellow and no other, some a Green and no other, and so of the rest. Nor are there only Rays proper and particular to the more Eminent Colours, but even to all their intermediate gradations.
[Los colores no son calidades de la luz producidas por la refracción o reflexión de los cuerpos (como se cree en general), sino propiedades originales inherentes, que en los diferentes rayos son distintas. Algunos rayos exhiben un color rojo y ningún otro; algunos uno amarillo y ningún otro; otros uno verde y ningún otro, e igualmente el resto. Tampoco hay rayos propios y concretos de los colores primarios, sino iguales para todas sus gradaciones intermedias.] (Traducción propia)
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Descomposición de la luz se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Estructura y motilidad del intestino delgado
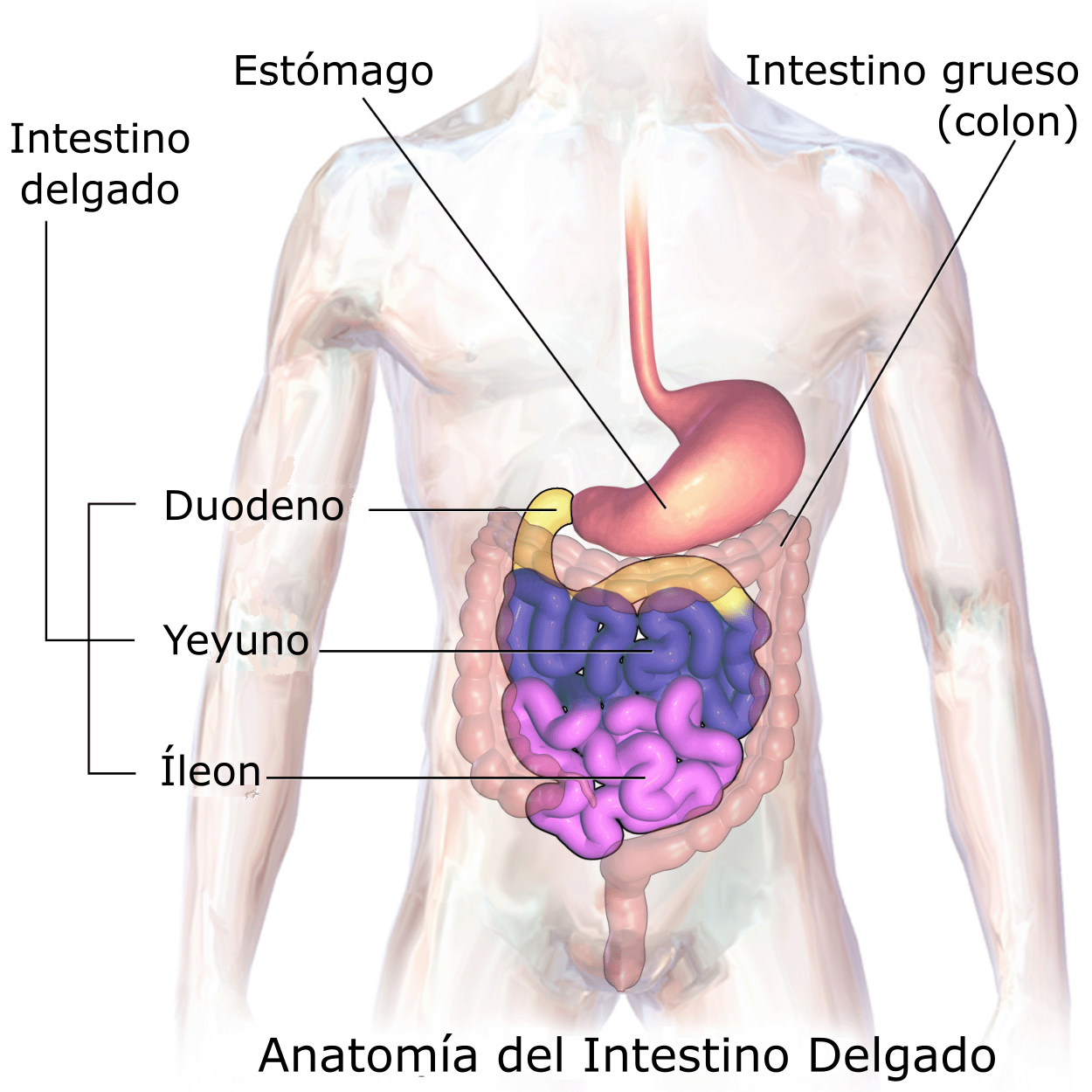 Imagen: Wikimedia Commons
Imagen: Wikimedia CommonsEstructura
El intestino delgado es un tubo que se extiende desde el estómago hasta el intestino grueso. Se encuentra alojado en la cavidad abdominal, y recibe secreciones del páncreas y del sistema biliar. En la mayor parte de los vertebrados el intestino delgado es el principal órgano de digestión y absorción del alimento. En los terrestres se subdivide en tres áreas: duodeno, yeyuno e íleon.
Una sección transversal del tubo digestivo a la altura del intestino delgado revela la existencia de cuatro capas principales: mucosa, submucosa, muscular (muscularis externa) y serosa.
La mucosa se subdivide en tres láminas. La primera es el epitelio, denominado también membrana mucosa1, una lámina epitelial interior que contiene células exocrinas (secretan jugos digestivos), endocrinas (secretan hormonas) y epiteliales (especializadas en la absorción de nutrientes). La segunda es la lámina propia, una capa un tanto difusa de tejido conjuntivo en el que se insertan las células epiteliales de la membrana mucosa. La lámina propia se encuentra atravesada por finos vasos sanguíneos, conductos linfáticos y fibras nerviosas. Alberga además el tejido linfoide asociado al intestino, que es la barrera de defensa inmunitaria frente a los patógenos del intestino. La mucosa muscular es una fina capa de músculo liso que se encuentra entre la lámina propia y la submucosa.
La submucosa es una gruesa capa de tejido conjuntivo, al que debe la pared del intestino delgado su elasticidad. Contiene vasos sanguíneos y linfáticos cuyas ramificaciones se proyectan hacia la mucosa y hacia la capa muscular más externa. La submucosa también alberga una red nerviosa, llamada plexo submucoso o plexo de Meissner.
Por el exterior de la submucosa se encuentra la capa muscular. En la mayor parte del intestino delgado esta capa tiene dos subcapas, una interna, circular, y otra externa, longitudinal. La contracción de la subcapa interna provoca la constricción del tubo allí donde se produce, mientras que la contracción de la exterior provoca el acortamiento del tubo. La contracción combinada y coordinada de ambas subcapas es lo que produce la mezcla de los contenidos intestinales y su propulsión a lo largo del tubo. Entre ambas subcapas se encuentra otra red nerviosa, el plexo mientérico que junto al plexo submucoso ayuda a regular la actividad intestinal local.
La serosa es la capa de tejido conjuntivo que cubre el tubo digestivo. Secreta un fluido seroso de efecto lubricante que previene la fricción entre el aparato digestivo y los órganos adyacentes. No hay discontinuidad entre la serosa y el mesenterio que ancla el tubo digestivo a la pared de la cavidad abdominal.
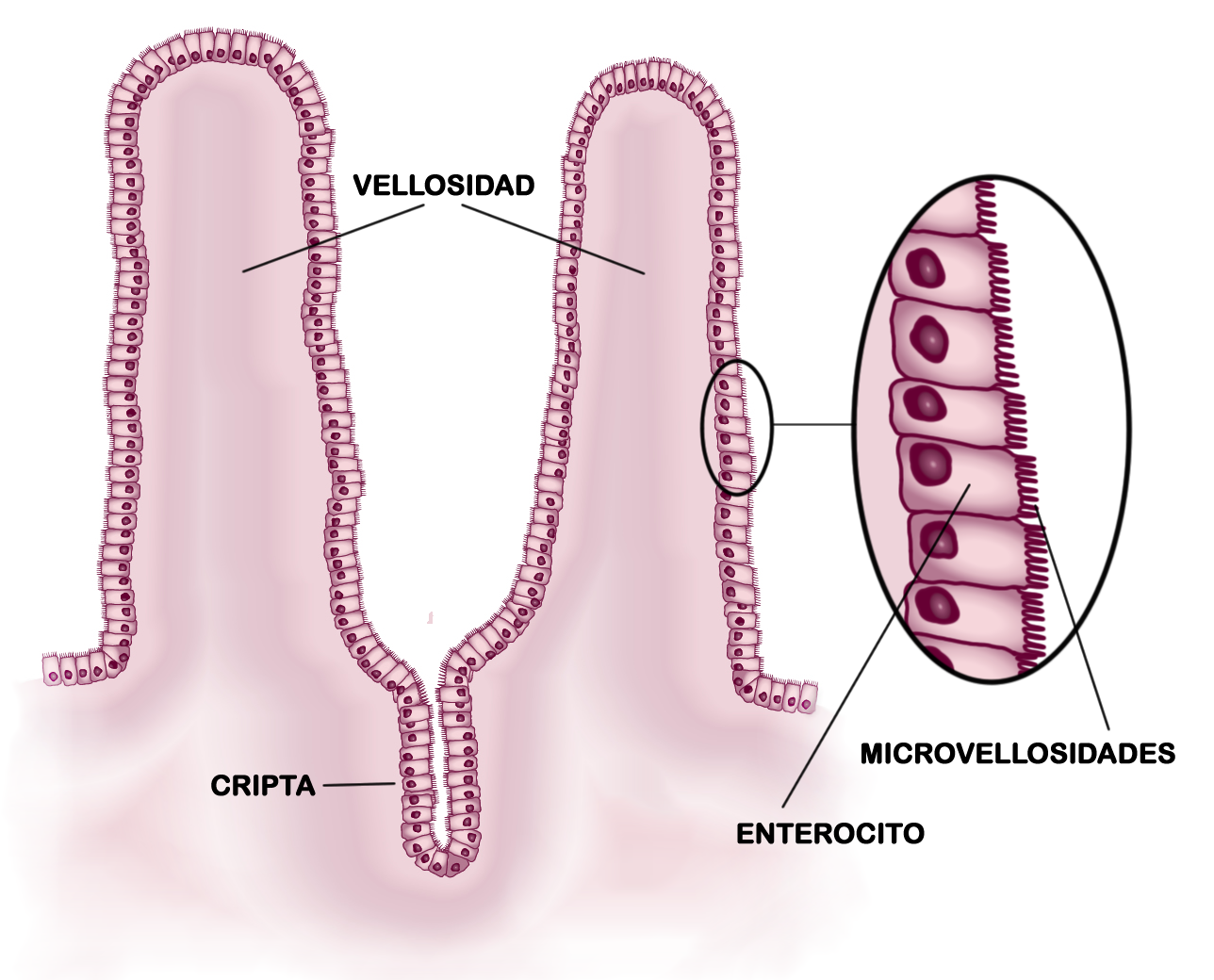 Imagen: Wikimedia Commons
Imagen: Wikimedia CommonsLa estructura del intestino delgado es tal que da lugar a un área superficial de gran extensión, muy superior a la que tendría un simple tubo de la misma longitud y diámetro luminal. La existencia en la mucosa de pliegues, vellosidades y microvellosidades es lo que permite que la superficie interior sea muy superior a lo que cabría esperar de un tubo sin esas particularidades, y gracias a ello el área disponible para la absorción alcanza una gran magnitud.
La superficie interior de la mucosa se dispone en pliegues circulares que multiplican por tres la superficie interna del tubo. De los pliegues salen proyecciones similares a dedos microscópicos; son los villi (villus en singular) o vellosidades, y dan una apariencia aterciopelada a la superficie interna del intestino. Multiplican por diez el área superficial. La superficie de cada villus se halla cubierta por células epiteliales, de las que salen las microvellosidades (o microvilli); estas forman lo que se denomina borde en cepillo (brush border). Cada célula epitelial puede contener en su parte apical entre 3000 y 6000 microvillosidades, y permiten multiplicar por veinte el área superficial de las células. El borde en cepillo alberga enzimas que participan en la digestión y la absorción simultánea de sus productos. En total, la superficie efectiva para la absorción es seiscientas veces mayor de lo que sería en un tubo cuya pared interna fuese lisa.
Las uniones estrechas (o zonulae occludentes) entre las células epiteliales de los villi mantienen herméticamente aislados la luz intestinal y el medio intersticial. La absorción se produce gracias al concurso de transportadores específicos de cada nutriente o electrolito en el borde en cepillo, y a la acción de las enzimas allí insertas que completan la digestión de carbohidratos y proteínas.
Por otro lado, cada villus recibe una arteriola que se ramifica en una red de capilares en su interior. Además, el centro de cada vellosidad está ocupada por un vaso linfático ciego que denominado vaso quilífero. La absorción consiste en la transferencia de los nutrientes digeridos a los capilares y al vaso linfático terminal, para lo que han de atravesar las células epiteliales de la mucosa, difundir a través del fluido intersticial que baña el tejido conjuntivo del núcleo de las vellosidades y atravesar el endotelio de algún capilar o del vaso quilífero.
Motilidad
Al llegar el quimo al duodeno, las contracciones de la musculatura lisa provocan su mezcla con las secreciones procedentes de páncreas e hígado, y lo impulsan a lo largo del tubo. La forma primaria de motilidad es la segmentación, proceso que consiste en contracciones anulares de la muscula lisa circular a lo largo del intestino delgado. Las contracciones obliteran el tracto intestinal, de manera que entre cada dos zonas contraídas, las relajadas albergan porciones discretas de quimo. Esas contracciones no se desplazan de la forma en que lo hacen las peristálticas, sino que se alternan con momentos de relajación. Contracciones y relajaciones se suceden en cada zona, lo que provoca que el quimo que se hallaba entre dos zonas contraídas se divida en dos partes y se mezcle con el de las zonas adyacentes. La reiteración de esa secuencia de contracciones y relajaciones sucesivas da lugar a una mezcla completa del contenido intestinal. Además, de esa forma se expone todo ese contenido a la superficie interna de la mucosa, lo que permite la absorción homogénea de todos los nutrientes.
Las contracciones de la segmentación empiezan debido a la acción de las células marcapasos del intestino delgado, células que generan un ritmo eléctrico básico similar al del estómago. Si el potencial eléctrico que produce esas células supera un determinado umbral, provoca la contracción de la capa de musculatura lisa circular a la frecuencia propia de las células marcapasos.
La intensidad de la respuesta de la musculatura no es constante, por lo que la intensidad de las contracciones de segmentación depende del grado de distensión de la pared intestinal, de la acción de la gastrina y de la acción nerviosa extrínseca. Entre comidas, la segmentación es mínima o, sencillamente, no se produce. Pero cuando llega la comida al tracto digestivo se producen fuertes contracciones de segmentación. Las contracciones duodenales empiezan en respuesta a la distensión producida por la presencia de quimo procedente del estómago. Pero las que se producen más adelante, en el íleon, son estimuladas por la gastrina, que se libera en respuesta a la presencia de quimo en el estómago. Además, la estimulación parasimpática (y por lo tanto, extrínseca), refuerza la segmentación, mientras que la simpática provoca el efecto contrario.
La progresión del quimo a lo largo del intestino delgado no se produce mediante peristaltismo, como ya se ha señalado. El quimo avanza porque la frecuencia de la segmentación se reduce a lo largo de su recorrido. De lo contrario no ocurriría, dado que las contracciones provocan el desplazamiento del quimo tanto hacia delante como hacia atrás. Las células marcapasos del duodeno se despolarizan espontáneamente con una frecuencia mayor que las más alejadas, siendo las del íleon terminal las que lo hacen a menor frecuencia. Las segmentaciones del intestino delgado humano pasan así de ser 12 por minuto en el duodeno a solo 9 por minuto en el íleon terminal. Esa diferencia hace que se desplace algo más quimo hacia delante que hacia atrás, dando lugar a un lento avance. De ese modo se va produciendo la mezcla a la vez que los nutrientes son absorbidos, habiendo tiempo suficiente para ello. Normalmente, el quimo tarda entre 3 y 5 horas en recorrer el intestino delgado humano.
Cuando ya se ha absorbido la mayor parte del alimento la segmentación cesa y es sustituida por lo que se denomina complejos mioeléctricos migratorios (o complejo motor migrante, CMM), también denominados “amo de casa intestinal”. Consiste este complejo en ondas de actividad eléctrica que se desplazan a lo largo del intestino delgado entre comidas. Las ondas eléctricas generan contracciones peristálticas. Y de esa forma, los restos de alimento no digerido, junto con bacterias, sustancias difíciles de digerir y restos de mucosa son transportadas hasta la válvula ileocecal y el interior del colon para su expulsión final como restos fecales. Un complejo motor migrante se desarrolla a lo largo de unas dos horas, y una vez finalizado vuelve a producirse hasta que vuelve a llegar quimo al estómago.
La válvula ileocecal permanece abierta mientras los contenidos del intestino delgado son impulsados a su través hacia el intestino grueso. Pero se cierra ante la mínima señal que amenace con retrotraer los restos de la digestión al intestino delgado. Por otro lado, la musculatura lisa del último tramo del íleon se encuentra engrosada y, por lo tanto, en condiciones, al contraerse, de formar un esfínter que se encuentra bajo control hormonal y nervioso. Normalmente ese esfínter se encuentra prácticamente cerrado, y se cierra con más intensidad si hay alguna presión en el lado del intestino grueso; por el contrario, si el lado del íleon se encuentra distendida, entonces ese esfínter se mantiene abierto. Mediante esos dos mecanismos (válvula ileocecal y musculatura lisa engrosada) permiten controlar el posible retroceso de los restos de alimento no digerido y, lo que es más importante, la invasión de patógenos procedentes del intestino grueso.
Nota:
1 Aunque esa denominación se presta a confusión porque a la mucosa también se la suele denominar así.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Estructura y motilidad del intestino delgado se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La motilidad estomacal
- El intestino no es nuestro segundo cerebro
- Sistemas nerviosos: evolución de la estructura encefálica
La tabla periódica en el arte: Cobre
El cobre debe su nombre a la isla de Chipre de donde en la Antigüedad se extraían abundantes cantidades del metal que los romanos llamaron aes cyprium yque posteriormente derivó en cuprum. De ahí proviene también el símbolo químico de este metal que ocupa el número 29 en la tabla periódica (Cu). Por ser fácil de obtener y por su maleabilidad, su relativa estabilidad y su atractivo color se ha empleado desde tiempos inmemoriales para realizar ornamentos. El vestigio más antiguo que se conoce es un pendiente encontrado en el norte del actual Iraq y se estima que fue elaborado hace la friolera de 10 700 años. La cantidad de objetos elaborados con cobre es inmensa e incluye desde brazaletes y collares a obras escultóricas como el friso que decoraba el templo de Tell al-`Ubaid hacia 2500 AEC. (también en la actual Iraq, Imagen 1). Y más inmensa hubiese sido si el ser humano no hubiese descubierto que añadiendo estaño al cobre se lograba un material mucho más resistente: el bronce. El dominio de la metalurgia de esta aleación nos permitió un entrar en una nueva edad en la que se produjo un cambio social como no se había visto desde que dejásemos de perseguir animales y recoger bayas para desarrollar la ganadería y la agricultura.
 Imagen 1. El relieve de Imdugud del templo de Tell al-`Ubaid (2500 AEC) (260 x 107 cm). Fuente: British Museum (CC BY-NC-SA 4.0)
Imagen 1. El relieve de Imdugud del templo de Tell al-`Ubaid (2500 AEC) (260 x 107 cm). Fuente: British Museum (CC BY-NC-SA 4.0)
Esculturas de bronce
El bronce se empleó en muchos ámbitos del arte, pero su uso más conocido es el de material escultórico, que se sigue manteniendo en nuestros días. Como profundizar en el uso del bronce en escultura daría para varias entradas, conformémonos con un somero repaso a algunas obras célebres. Una de las piezas más fascinantes es el Carro solar del Trundholm (Imagen 2), un caballo sobre ruedas que arrastra un disco solar dorado y pertenece a la Edad del Bronce Nórdica (hacia 1400 a.e.c.). Pero eso no lo sabía el granjero danés que lo encontró en 1902 y se lo llevó a sus hijos ¿Quién no ha tenido un juguete de más de 3000 años de antigüedad? Claro que para los escandinavos que lo realizaron tuvo un papel diferente, ya fuera ceremonial, ya fuese una especie de calendario.
 Imagen 2. El Carro Solar de Trundholm (1050 AEC) (54 cm × 35 cm × 29 cm). Fuente: National Museum of Denmark
Imagen 2. El Carro Solar de Trundholm (1050 AEC) (54 cm × 35 cm × 29 cm). Fuente: National Museum of DenmarkSi hay una cultura que ha destacado por el uso del bronce en la escultura, esa es la griega. En el imaginario colectivo todas las estatuas griegas son de níveo mármol, pero eso se debe a que en la época helenística se empleó ese material para realizar una gran cantidad de copias de originales de bronce. El problema es que como la propia materia prima era muy apreciada, muchas esculturas fueron fundidas y se perdieron para siempre. Afortunadamente obras como el Auriga de Delfos y el Poseidón de Artemisón (o Zeus de Artemisón) sobrevivieron para dar fe de la maestría alcanzada.En el Renacimiento quisieron recuperar la gloria clásica y también retomaron el uso del bronce, dejando para la posteridad obras de la talla del David y la Judith de Donatello o el Perseo con la cabeza de Medusa de Cellini. De época más cercana es el Pensador de Rodin o las célebres obras de Giacometti o Botero.
 Imagen 3. El Auriga de Delfos (ca. 475 AEC) y David de Donatello (ca. 1440). Fuente: Wikimedia Commons.
Imagen 3. El Auriga de Delfos (ca. 475 AEC) y David de Donatello (ca. 1440). Fuente: Wikimedia Commons.
Verdes y azules. Los pigmentos con cobre
El cobre metálico tiene un color rojizo tan característico que hasta lo adjetivamos para definir un tipo de tonalidad. Pero este omnipresente metal también se encuentra en numerosos pigmentos, entre otros en dos de los más trascendentales de la historia del arte: la azurita (2CuCO3·Cu(OH)2) y la malaquita (CuCO3·Cu(OH)2). Ambos se obtenían moliendo minerales formados por carbonatos básicos de cobre. Si reparamos en su forma química observaremos que son muy similares y, de hecho, la azurita puede transformarse en malaquita con el paso del tiempo. De ahí que estos minerales suelan aparecer conjuntamente, como si la naturaleza jugase a ser una artista que combina colores (Imagen 4).
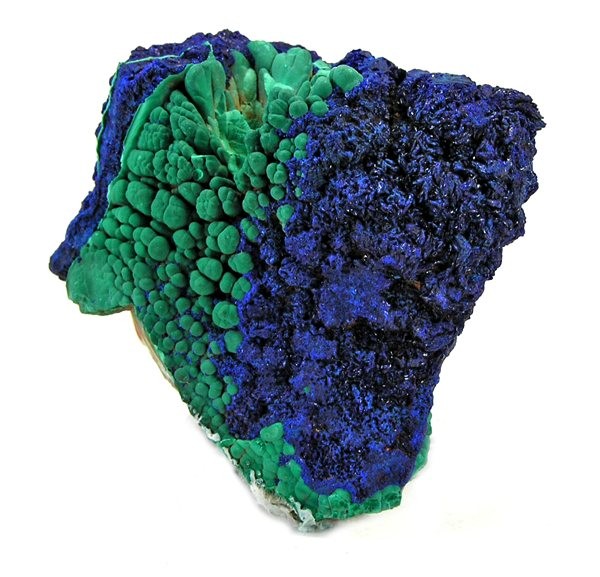 Imagen 4. Una mezcla de azurita y malaquita hallada en Arizona. Fuente: Wikimedia Commons.
Imagen 4. Una mezcla de azurita y malaquita hallada en Arizona. Fuente: Wikimedia Commons.
La azurita era abundante en las montañas germanas, por lo que también se conoce como azul de Alemania o azul de las montañas. Es cierto que existía un pigmento azul mucho más deseado conocido como azul ultramar, pero su altísimo coste impedía que se usase habitualmente y de ahí que la azurita fuese tan popular durante la Edad Media y el Renacimiento.
La malaquita es posiblemente el primer pigmento verde jamás empleado. Quizás por eso los griegos le pusieron ese nombre que significa “del color de las hojas de la malva”. Resulta curioso que las flores y hojas de una misma planta den nombre a colores tan diferentes. Antes que los griegos, los egipcios habían dado buen uso del mineral, tanto en maquillajes del periodo predinástico como en la decoración de sarcófagos y papiros. Debido al escaso número de pigmentos verdes naturales que existen, la malaquita se ha empleado desde Japón a Occidente con todo tipo de técnicas pictóricas. En Europa se usó abundantemente en frescos y temples, aunque no tuvo el mismo éxito en óleos, quizás porque su color podía resultar demasiado pálido. Eso explicaría que se usase en veladuras y que otros pigmentos verdes tuviesen mayor aceptación para ser usados al óleo.
Entre estos pigmentos verdes se encontraba otro en el que el cobre juega un papel predominante: el verdigrís. Este pigmento está estrechamente relacionado con la pátina que se forma sobre los objetos de cobre y bronce conocida como cardenillo. Si dibujas en tu mente obras como La Estatua de la Libertad o El Pensador, seguramente las pintes de color verde. Pero ese tono sólo lo adquieren con el paso de los años por la degradación del cobre para formar ciertas sales (sulfatos, cloruros, etc.) Históricamente se han empleado procesos de degradación similares para lograr el verdigrís. Las recetas antiguas cuentan que se exponían planchas de cobre a una fuente de ácido acético como vinagre o heces de uvas. El contacto del cobre con el ácido acético hace que se forme una costra verdiazulada compuesta por diferentes acetatos de cobre que pueden tener naturaleza neutra (Cu(CH3COO)2·H2O) o básica (Cu(CH3COO)2·Cu(OH)2·5H2O).
 Imagen 5. Verdigrís producido por el contacto entre vinagre y cobre. Fuente: Por gentileza de Yaiza Lascorz (CC-BY-SA-4.0).
Imagen 5. Verdigrís producido por el contacto entre vinagre y cobre. Fuente: Por gentileza de Yaiza Lascorz (CC-BY-SA-4.0).
Un pigmento estrechamente ligado al verdigrís fue el resinato de cobre, con cuyo nombre se engloban a las sales que forma el metal con las resinas de ciertos árboles. Esa combinación que une lo inorgánico y lo orgánico, lo vegetal y lo metal, la explicó mejor que nadie Théodore de Mayerne, médico genovés que vivió a caballo entre los siglos XVI y XVII. Al parecer esa profesión se le quedaba corta, ya que también desarrolló varias recetas para la síntesis de pigmentos. Cuenta de Mayerne en un célebre manuscrito que hay que mezclar dos onzas de verdigrís (fuente de cobre), dos de trementina de Venecia y media de trementina y llevar a ebullición. Luego se va probando el color que se obtiene sobre un trozo de vidrio hasta lograr el tono deseado, se filtra la mezcla con un paño de lino y se deja secar antes de moler. Como vemos, llamarlo receta está más que justificado. En este caso la resina es la trementina que exudan ciertas pináceas y que son fuente de ácido abiético (C20H30O2), uno de los principales componentes del resinato de cobre.
 Imagen 6. Detalle del Políptico de Gante de Jan van Eyck (1432) que conserva veladuras de resinato de cobre. Fuente: Wikimedia Commons.
Imagen 6. Detalle del Políptico de Gante de Jan van Eyck (1432) que conserva veladuras de resinato de cobre. Fuente: Wikimedia Commons.
El cobre como soporte pictórico
Acrílico sobre lienzo, óleo sobre tabla o acuarela sobre papel son combinaciones de palabras que estamos acostumbrados a encontrar en los museos. Sin embargo, es posible que el uso de metales como superficie donde realizar una pintura sea menos conocido. Pese a lo que se pueda pensar, el cobre ofrece ciertas ventajas, ya que está menos expuesto al deterioro biológico y a las tensiones provocadas por los cambios de humedad y temperatura que los tejidos. Otra gran ventaja desde el punto de vista de ejecución es la posibilidad de trabajar directamente sobre la superficie, que se trataba con abrasivos para lograr cierta rugosidad y que la pintura se adhiriese mejor. La correcta adhesión al cobre es precisamente el factor más importante para la conservación de este tipo de obras y explica que en algunas ocasiones la pintura se descascarille. Aunque estas pérdidas vengan provocadas normalmente por factores mecánicos, la pintura sobre cobre no es ajena a los ataques químicos. Acabamos de ver que el cobre reacciona con la atmósfera y se forma la pátina verde que conocemos como cardenillo. Obviamente esto también sucederá en las láminas de cobre, aunque la pintura protegerá al soporte de esta degradación que sólo se observará en las partes no cubiertas. Por último, si hablamos del cobre como soporte, es imposible no acordarse de la serie Oxidation de Andy Warhol, creada a base de mear sobre planchas de cobre. ¿Quién necesita vinagre teniendo orina?
 Imagen 7. Autorretrato (15 x 12 cm) de Rembrandt (1630). Óleo sobre cobre. Fuente: Wikimedia Commons.
Imagen 7. Autorretrato (15 x 12 cm) de Rembrandt (1630). Óleo sobre cobre. Fuente: Wikimedia Commons.
Grabando al aguafuerte
Para realizar un grabado es necesaria una plancha en la que se realiza un dibujo que luego se estampará en un soporte, normalmente papel. Esa plancha (también llamada matriz) puede ser de madera (xilografía), de piedra (litografía) o de metal, en cuyo caso el cobre es el más empleado. En este último tipo de grabados el dibujo se realiza sobre la plancha de forma incisa. Al aplicar tinta sobre la matriz, la tinta entrará en los huecos y al presionar sobre el papel pasará a éste para producir la imagen. Pero, ¿cómo se realiza el dibujo inciso en una plancha de cobre? La manera más sencilla es grabar sobre el metal empleando un instrumento afilado de acero como el buril o la punta seca. Ahora bien, existe una manera de realizar ese grabado muchísimo más interesante desde el punto de vista químico: el aguafuerte. En este procedimiento se emplea la capacidad del ácido nítrico (HNO3) para oxidar el cobre. Para conseguir el grabado se tiene que proteger la plancha de cobre con un barniz que sea resistente al ácido. Después de realizar el dibujo arañando el barniz con una punta, se introduce la plancha en un baño que contiene ácido nítrico en la concentración deseada. El ácido corroerá solo las partes que no están cubiertas con barniz de modo que se formará el dibujo inciso en la plancha. Este procedimiento facilita la labor de realizar el dibujo, ya que trabajar con el buril sobre el metal es mucho más complicado. En cambio, se necesita controlar adecuadamente la concentración del ácido nítrico para lograr la penetración deseada. Artistas de la talla de Rembrandt o Canaletto emplearon el aguafuerte, pero puede que sea Piranesi el que mejor refleje el éxito de la técnica. Él solito grabó cerca de 2000 planchas de la ciudad de Roma.
 Imagen 8. Grabado de Piranesi (1773). Fuente: Wikimedia Commons.
Imagen 8. Grabado de Piranesi (1773). Fuente: Wikimedia Commons.Para saber más:
Natalia Sancho Cubino “Verdigrís, pigmento histórico de cobre: estudio de su composición y color a partir de reproducciones de antiguas recetas” Universidad Complutense Madrid (2016).
Antonio J. Sánchez Fernández y Beatriz Prado-Campos “Pintura sobre cobre: estudio técnico-material, indicadores de alteración y conservación” Cuadernos de los Amigos de los Museos de Osuna (2014) 16, 139-145).
Sobre el autor: Oskar González es profesor en la facultad de Ciencia y Tecnología y en la facultad de Bellas Artes de la UPV/EHU.
El artículo La tabla periódica en el arte: Cobre se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La tabla periódica en el arte: ¿Qué átomos hay en una obra?
- Deconstruyendo la tabla periódica
- Cómo mecanizar una pieza de cobre usando bacterias
¿Cómo demonios funcionan las copas musicales?
Mozart y Beethoven compusieron para las copas musicales, pero ¿cuál es el fundamento físico de su funcionamiento? Aquí te lo explicamos en poco más de un minuto, pero si quieres saber algo más quizás esto te ayude.
Los vídeos de ¿Preguntas frecuentes? presentan de forma breve y amena cuestiones que, probablemente, nos hayamos planteado en alguna ocasión. Los vídeos, realizados para la Cátedra de Cultura Científica de la UPV/EHU, se estrenan en el programa de ciencia Órbita Laika (@orbitalaika_tve), los lunes a las 22:00 en la 2 de RTVE.
Edición realizada por César Tomé López
El artículo ¿Cómo demonios funcionan las copas musicales? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¿Hemos intentando contactar con extraterrestres?
- Ciencia express: Cómo funcionan las vacunas
- Ciencia express: Cómo se formó la luna
La FCT viaja a Marte
La Facultad de Ciencias de Bilbao comenzó su andadura en el curso 1968/69. 50 años después la Facultad de Ciencia y Tecnología de la UPV/EHU celebra dicho acontecimiento dando a conocer el impacto que la Facultad ha tenido en nuestra sociedad. Publicamos en el Cuaderno de Cultura Científica y en Zientzia Kaiera una serie de artículos que narran algunas de las contribuciones más significativas realizadas a lo largo de estas cinco décadas.

 Oxia Planum, lugar de aterrizaje de Exomars 2020. Fuente: NASA
Oxia Planum, lugar de aterrizaje de Exomars 2020. Fuente: NASAEl próximo año 2020 se lanzarán dos misiones a Marte en la que participan investigadores del Departamento de Química Analítica de la Facultad de Ciencia y Tecnología (FCT) de la UPV/EHU, la misión Exomars2020 de la Agencia Espacial Europea (ESA) y la misión Mars2020 de la NASA. Ambas misiones comparten objetivos similares ya que van a estudiar la geoquímica de las zonas de aterrizaje, para entender cómo han sido los procesos de transformación de minerales volcánicos en filosilicatos debido a la acción del agua, cómo han sido los procesos de sedimentación y compactación de materiales alterados y cómo se han podido conservar moléculas orgánicas sean o no precursoras de formas de vida microbiana. Pero son misiones complementarias, no son misiones competidoras, ya que van a aterrizar en dos sitios geológicamente muy diferentes y los experimentos que van a realizar son distintos, aunque ambas pretender avanzar en el conocimiento de los tres aspectos mencionados.
Nosotros nos incorporamos al equipo de ciencia del instrumento Raman Laser Spectrometer (RLS), de la misión Exomars2020 en 2014, por invitación del Profesor Fernando Rull Pérez, de la Universidad de Valladolid, Investigador Principal del instrumento RLS. Este instrumento va en un Laboratorio Analítico Limpio, junto con un espectrómetro infrarrojo (micrOmega) y un cromatógrafo de gases con detección por espectrometría de masas (MOMA), instalado en el interior del rover al que llegarán las muestras que van a ser tomadas en superficie y en profundidad (desde 0 a 2 metros) mediante un taladro de perforación.
 Exomars 2020 rover. Fuente: ESA/ATG medialab
Exomars 2020 rover. Fuente: ESA/ATG medialabCuando la muestra llega al Laboratorio Analítico, se tritura hasta tener un tamaño de grano de 50 micras o menor. Antes de hacer la medida de espectroscopia Raman, el funcionamiento del RLS se optimiza con la muestra de calibrado. La definición y construcción de esa muestra de calibrado fue una de las primeras tareas que tuvimos en la Misión Exomars2020.
El instrumento de vuelo ya ha sido entregado a la ESA y ahora el equipo de ciencia del RLS estamos preparando las bases de datos espectroscópicas para poder interpretar la información que llegue desde Marte a partir de 2021. También estamos trabajando en un análogo de Marte que tenemos en Meñakoz y en Armintza. Son los restos de un volcán submarino que emergió a través de sedimentos marinos hace 100 millones de años y que tras la erupción continuaron los procesos de deposición de nuevos sedimentos. De modo que ahora tenemos estratos sedimentarios en la parte inferior, con capas volcánicas en la parte intermedia, y con otras capas sedimentarias en la parte superior, alcanzando una distancia vertical de unos 25 metros. Esa distribución es muy similar a la observada para Oxia Planum, el sitio de aterrizaje de la misión Exomars2020.
En ese análogo estamos estudiando en qué condiciones ambientales las fases minerales originales del volcán se han transformado a otros compuestos de alteración, en concreto a filosilicatos. Los filosilicatos, junto con fases minerales de origen volcánico, son los componentes principales de lo observado por los orbitadores al analizar espectroscópicamente la superficie de Oxia Planum. Pretendemos que los procesos que estudiemos en nuestros análogos sirvan para interpretar las observaciones experimentales que en su día nos envíe el rover desde Marte. Este trabajo se realizará dentro de un equipo multidisciplinar compuesto por grupos de investigación de España, Francia, Alemania, Inglaterra y Estados Unidos.
La otra misión en la que participamos es Mars2020, donde formamos parte desde 2015 del equipo de ciencia del instrumento SuperCam, un instrumento que integra cinco técnicas espectroscópicas: Visible, Infrarrojo Cercano, Raman, Fluorescencia Resuelta en el Tiempo (TRLS) y LIBS (Laser Induced Breakdown Spectroscopy). Los análisis con estas técnicas se van a hacer a distancia (entre 1 y 7 metros) mediante un conjunto de rayos láser que se envían desde el cabezal del rover a las zonas de interés. La interacción producida en la superficie es captada por detectores telescópicos, obteniéndose los espectros propios de cada técnica espectroscópica.
 Mars 2020 rover. Fuente: NASA
Mars 2020 rover. Fuente: NASAPara el correcto funcionamiento de este instrumento multianalítico es necesario usar una tarjeta de calibrado compuesta por 27 muestras minerales (para calibrar las medidas LIBS, Raman y TRLS) más 8 muestras metálicas (para calibrar los espectrómetros, la cámara visible y el NIR). La construcción de esa tarjeta fue una labor encomendada por NASA al Profesor Fernando Rull para lo que se creó un equipo multidisciplinar en el que nos integramos. En los últimos dos años hemos estado estudiando diferentes candidatos a las muestras de calibrado. Nuestra misión ha sido verificar que las muestras candidatas cumplían los criterios de homogeneidad química establecidos, de modo que aquellas muestras candidatas que no eran homogéneas se descartaron.
Como todo el hardware de vuelo, se deben construir tres modelos hasta tener el elemento físico final que se integrará en el rover. Cada modelo debe superar una serie de tests físicos (resistencia a choques de 4000 G, resistencia termo-mecánica y ausencia de emisión de gases al pasar de 120ºC) y químicos (mantenimiento de las características químicas tras los tests físicos y ausencia de contaminación durante los mismos). El tercer diseño fue el que superó todos los tests físicos y químicos y ha sido la tarjeta de calibrado que se ha enviado en enero de 2019 a NASA.
En el mes de febrero hemos participado en un ejercicio de operaciones, simulando cómo se trabajaría con el rover y los distintos instrumentos durante seis días marcianos (unos doce días terrestres). En nuestro caso, hemos ayudado a tomar decisiones de dónde dirigir el rover y qué muestras analizar para el día siguiente en función de las respuestas espectroscópicas que “llegaban de Marte” del día anterior y de la interpretación que hacíamos en el día de hoy en cuanto a composición de fases minerales y compuestos orgánicos.
En estos meses, estamos concluyendo los test de calibrado del instrumento SuperCam. Dos de nuestros investigadores van a desplazarse al Laboratorio Nacional de Los Alamos para realizar las medidas de optimización de las distintas técnicas espectroscópicas a -10oC, temperatura promedio de Marte durante el día. Para validar el correcto funcionamiento de los espectrómetros de las cinco técnicas analíticas, se procesarán muestras reales que deberán de ser confirmadas con el conjunto de los resultados proporcionados por SuperCam.
A partir del segundo semestre de 2019 se iniciarán los trabajos de caracterización de análogos marcianos y de Meteoritos de Marte para tener los sistemas de interpretación a punto, de modo que, cuando llegue la información espectroscópica real a partir de 2021, seamos capaces de hacer unas correctas interpretaciones diarias y pasar las mejores ordenes de trabajo al rover para el día siguiente. Y todo ello, dentro de un amplio equipo multidisciplinar de Estados Unidos, Francia, Inglaterra, Canadá, Dinamarca y España.
Sobre el autor: Juan Manuel Madariaga es catedrático en el Departamento de Química Analítica de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo La FCT viaja a Marte se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Activa tu neurona – 560 soles en busca de ambientes habitables en Marte
- Los ojos que explorarán la superficie de Marte (Mars2020)
- El sorprendente penacho de Marte
Así es la química de una buena pizza

La pizza puede ser una comida rica y saludable. El secreto de ambas cosas está en una buena elección de ingredientes. La parte más complicada de encontrar son las bases de pizza precocinadas o masas extendidas elaboradas con 100% harina integral. Sin embargo, en poco más de media hora podemos hacer nosotros mismos una base para pizza excepcional. El secreto de una buena masa de pizza está en la química.
Necesitamos los siguientes ingredientes para 2-4 personas: 250 g de harina integral, 3 cucharadas soperas de aceite de oliva virgen extra, 25 g de levadura de pan, 125 ml de agua (medio vaso) y una cucharadita de sal.

-
¿Por qué es mejor usar harina integral?
Por sabor y por salud.
La harina puede ser refinada o integral. La diferencia entre una y otra es la parte del grano que se usa para su elaboración. En la harina refinada se utiliza sólo el endospermo del grano, mientras que la integral incluye el cereal completo.
Los cereales tienen tres partes: la cáscara del cereal es el salvado, donde está la mayor parte de la fibra; la parte central es el endospermo, compuesto mayoritariamente por almidón; y el núcleo es el germen, donde se concentra la fracción grasa del cereal. Por eso el sabor de las harinas integrales es más intenso y complejo que el de las refinadas.
Las harinas integrales contienen todas la vitaminas y nutrientes del cereal completo, siendo especialmente interesante para nuestra salud su alto contenido en fibra. La fibra favorece el tránsito intestinal y además hace que el pan sea más saciante. No es que el integral tenga menos calorías, de hecho tiene las mismas, pero al resultar más saciante necesitaremos comer menos cantidad.
La fibra hace que el pan integral tenga menor índice glucémico, es decir, hace que metabolicemos los carbohidratos lentamente y que no aumenten repentinamente los niveles de glucosa en sangre. Por el contrario, los panes blancos tienen alto índice glucémico, lo que significa que se metabolizan muy rápido dando elevados y repentinos picos de glucosa en sangre y, en consecuencia, picos de insulina. Este es el motivo por el que el pan blanco es poco saciante y por el que las personas con diabetes limitan su consumo.
Además de la tradicional harina de trigo, se puede obtener harina de distintos cereales ricos en almidón como la espelta, el centeno, la cebada, la avena, el maíz, e incluso de leguminosas como los garbanzos o las judías, o del arroz. La harina está formada básicamente por hidratos de carbono, y en menor proporción proteínas, dependiendo del tipo de harina. El hidrato de carbono de las harinas vegetales es el almidón.
Para elaborar pan y masas de pizza se suele utilizar la harina de trigo porque ésta contiene gluten, un conjunto de proteínas, esencialmente gliadina y glutenina, que le otorgan elasticidad y consistencia a la masa. Las harinas sin gluten como las de trigo sarraceno, maíz o garbanzo, son muy difíciles de manejar. Extenderlas en forma de base de pizza es una tarea muy compleja, precisamente porque no producen masas elásticas.
-
La química del amasado y del fermentado
Cuando hacemos la masa de una pizza tienen lugar varias reacciones químicas que serán las responsables de su textura, color y sabor.
Lo primero que hacemos es poner en un bol los 250 g de harina integral. A continuación desmenuzamos la levadura, añadimos la sal, el medio vaso de agua y las tres cucharadas de aceite de oliva virgen extra. Mezclamos inicialmente todos los ingredientes con ayuda de una cuchara, y a continuación amasamos a mano sobre una encimera durante 5-10 minutos. Después dejamos reposar la masa unos 30 minutos en el bol cubierto por un trapo.

Durante este proceso estarán ocurriendo una serie de reacciones químicas y bioquímicas que determinarán la textura y el sabor de la masa.
El protagonista del amasado es el gluten. La gliadina y la glutenina que componen el gluten se hidratan, captan el agua e interactúan entre sí dando lugar a la formación de un entramado reticular de gluten, que dota a la masa de elasticidad. El agua también hidrata el almidón, provoca la apertura de su estructura y la deja expuesta al ataque de las enzimas. Las enzimas también se activan al hidratarse, entre ellas las amilasas, que actúan rompiendo el almidón en hidratos de carbono simples.
La levadura (saccharomyces cerevisiae) la podemos comprar en el supermercado o en la panadería. La levadura se alimenta de los hidratos de carbono simples liberados y desprende dióxido de carbono y alcohol, responsables de la formación de burbujas. Para acelerar el proceso o crear más burbujas hay quien añade azúcar. La razón es que así la levadura tendrá más alimento con el que generar burbujas de dióxido de carbono. Aunque la textura puede mejorar en tiempo récord, nutricionalmente no es aconsejable añadir azúcar.
En el caso de no tener levadura, podemos hacer la masa con una cerveza, ya que la levadura de la cerveza es la misma que la del pan.
Hay que tener en cuenta que la sal inhibe el crecimiento de la levadura, así que añadir sal hace que el fermentado sea más lento, sin embargo, la fermentación lenta repercute positivamente en la textura final de la masa.
En el mercado tenemos otro tipo de productos que llamamos levaduras químicas que, aunque no son levaduras propiamente dichas, producen un efecto parecido sobre la masa. Se usan más en repostería para no tener que dejar fermentar la masa y poder hornearla inmediatamente. Estas levaduras químicas están compuestas esencialmente por bicarbonato sódico que en contacto con la masa y durante el horneado desprenden dióxido de carbono, responsable de las burbujas.
El aceite protege la masa de la pérdida progresiva de agua, lo que evita que se endurezca demasiado durante el horneado y una vez se enfríe.
Todas estas reacciones se producen durante el amasado y el reposo. Una vez transcurrido el tiempo de reposo, la masa habrá duplicado su volumen.

-
La química del horneado.
Una vez tenemos la masa fermentada, el siguiente paso será extenderla. Si la harina tiene gluten, este proceso será bastante sencillo porque la masa será muy elástica. Podemos extenderla con las manos o con ayuda de un rodillo.
Extendemos la masa sobre una bandeja de horno cubierta con papel de horno. Este papel es un papel vegetal sulfurizado. Se ha tratado químicamente con un baño de ácido sulfúrico -de ahí el nombre- para tapar los poros de la celulosa y hacerlo impermeable y antiadherente. Este proceso también lo hace resistente a las temperaturas que manejamos en los hornos domésticos.
Sobre la masa podemos añadir los ingredientes que nos apetezcan. En este caso he utilizado tomate triturado, orégano, queso mozzarella rallado, champiñones frescos, aceitunas negras, jamón cocido extra y pimientos rojos asados.

Metemos la pizza en el horno y la dejamos a 240oC con calor arriba y abajo entre 20 y 25 minutos.
La levadura de la masa muere como consecuencia de las altas temperaturas, y el alcohol se evapora. El almidón de la harina comienza a gelatinizar, es decir, a formar una estructura diferente a la original en la que es capaz de atrapar el agua de la masa. En este proceso también interviene el gluten, que se pega al almidón creando una red que evita que las burbujas se escapen de la masa. A medida que la temperatura aumenta y la pizza continúa en el horno, empieza a dorarse. Este cambio paulatino de color es debido a la reacción química más famosa de la cocina: la reacción de Maillard entre los hidratos de carbono y las proteínas.

Todas las formas de conocimiento guardan relación entre sí, en mayor o menor medida. Preparar una pizza tiene su fundamento químico detrás. Desde el punto de vista de la salud y desde el punto de vista gastronómico. Conocerlo nos permite disfrutar más de todo el proceso. Esto es así porque el conocimiento es una forma de placer.
Sobre la autora: Déborah García Bello es química y divulgadora científica
El artículo Así es la química de una buena pizza se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Los números enamorados
El artista futurista italiano Giacomo Balla (1871-1958) pintó una obra titulada Los números enamorados en 1924, asociando una cualidad humana, como es el enamoramiento, a los números. También en el ámbito de las matemáticas nos gusta asociar a los números, en particular, a los números naturales, cualidades humanas. Existen números amigos, sociables, novios, narcisistas, felices, tristes, hambrientos, intocables, ambiciosos, afortunados, poderosos, malvados, odiosos, prácticos o raros, pero también, con otras denominaciones curiosas, como números vampiros, parásitos, perniciosos, apocalípticos, perfectos, poligonales, cíclicos, automorfos, sublimes, abundantes, escasos o intocables.
 Números enamorados (1924), del artista futurista italiano Giacomo Balla, MART, Museo d’arte moderna e contemponanea di Trento e Rovereto, Italia. Fotografía de MART
Números enamorados (1924), del artista futurista italiano Giacomo Balla, MART, Museo d’arte moderna e contemponanea di Trento e Rovereto, Italia. Fotografía de MARTAlgunas de estas familias de números deben su propiedad definitoria al comportamiento de sus divisores propios, es decir, entre los divisores no se considera al propio número. Son a estas familias de números naturales a las que vamos a dedicar la entrada de hoy de la sección Matemoción del Cuaderno de Cultura Científica.
Empecemos con unas familias de números con un origen muy antiguo. Un número se dice que es perfecto si es igual a la suma de sus divisores (propios), como ocurre con los números 6 = 1 + 2 + 3 y 28 = 1 + 2 + 4 + 7 + 14. Se los denominó perfectos porque en tiempos antiguos se dio a esta propiedad una interpretación divina. Por ejemplo, San Agustín relaciona el hecho de que Dios crease el mundo en 6 días, con la perfección de este número.
Los siguientes números perfectos, después de 6 y 28, conocidos ya desde la antigüedad, son
496 = 1 + 2 + 4 + 8 + 16 + 31 + 62 + 248
8.128 = 1 + 2 + 4 + 8 + 16 + 32 + 64 + 127 + 254 + 508 + 1.016 + 2.032 + 4.084
Se desconoce el origen exacto de los números perfectos, aunque ya eran conocidos por los matemáticos griegos. Euclides de Alejandría (aprox. 325 – 265 a.n.e.) los estudia en su obra Los Elementos, aunque antes los había estudiado Pitágoras (aprox. 570 – 495 a.n.e.), e incluso podrían haber sido conocidos por los egipcios.
Euclides demostró que para algunos números primos p, los números de la forma 2p–1 (2p – 1) son perfectos, por ejemplo, para p = 2, 3, 5, y 7, se obtienen los perfectos anteriores. Dos milenios después, el matemático suizo Leonhard Euler (1707 – 1783) demostraría que todos los números perfectos pares son de esta forma, con (2p – 1) un número primo.
El quinto número primo encontrado fue 33.550.336, para p = 13, que aparece en un manuscrito del siglo XV. El sexto y séptimo –para p = 17 y 19– fueron descubiertos por el matemático italiano Pietro Cataldi (1548 – 1626) en 1588, en concreto, 8.589.869.056 y 137.438.691.328. Y Euler, en 1772, descubrió el octavo, que es 230 (231 – 1) = 2.305.843.008.139.952.128.
Obtener números perfectos es una tarea muy difícil, luego podemos decir que “la perfección es difícil de conseguir”. Antes del siglo XX solo se conocían 9 números perfectos. El noveno fue obtenido, para p = 61, por el matemático ruso Iván Pervushin (1827 – 1900), en 1883. De hecho, en la fórmula de Euclides-Euler no basta con que p sea primo, ya que para p = 11, 211 – 1 = 2.047 = 23 x 89, no es primo, con lo cual 210 (211 – 1) no es perfecto.
Con la ayuda de los ordenadores ha sido posible calcular muchos más, pero no demasiados. Solo se conocen, hasta la fecha, 51 números perfectos. El último descubierto, en 2018, fue el correspondiente al primo p = 82.589.933.
Se desconoce si existe un número infinito o finito de números perfectos. Además, todos los números perfectos conocidos son pares, y no se sabe si existen impares. Lo que se ha conseguido demostrar es que de existir tendrían que cumplir una serie de propiedades, como tener al menos 9 divisores primos distintos o ser mayores que 101.500, entre muchas otras.
 Veintiocho (modelo para una escultura pública), 1992, del artista estadounidense Jonathan Borofsky. Imagen de su página web
Veintiocho (modelo para una escultura pública), 1992, del artista estadounidense Jonathan Borofsky. Imagen de su página webYa los griegos dividieron a los números naturales que no son perfectos en dos categorías, los abundantes y los deficientes. Los números que no son perfectos pueden ser abundantes, cuando el número es menor que la suma se los divisores, como el 12 deficientes en el caso contrario, como el 14 > 1 + 2 + 7 = 10 o todos los números primos, cuyo único divisor propio es el 1. Estos conceptos, como la perfección, formaron parte de la numerología griega.
El religioso, teólogo y matemático anglosajón Alcuino de York (735 – 804) relacionaba la “segunda creación” de Dios, el diluvio universal y el Arca de Noé, con el número 8, ya que la humanidad desciende de las 8 almas que se salvaron del diluvio refugiándose en el Arca de Noé. Por lo tanto, esta es una creación imperfecta, puesto que el número 8 es deficiente, 8 > 1 + 2 + 4.
Los números llamados abundantes no son, sin embargo, tan abundantes como su nombre indica. Existen 245 números abundantes menores que 1.000, aunque solo uno de ellos impar, el número 945 = 33 x 5 x 7, los demás son pares, y solo 3 números perfectos (por supuesto, pares), el resto son deficientes. Entre los primeros 50.000 números hay 37.602 deficientes, 4 perfectos y 12.394 abundantes. Entre estos 12.394 números abundantes, solo 114 son impares.
Así como lo bello y lo excelente es raro de encontrar y se cuenta pronto, pero lo feo y lo malo siempre es prolífico, así también los números abundantes y deficientes resultan ser muchos y en desorden, y su descubrimiento no obedece a sistema alguno. Pero los perfectos, son a un tiempo escasos en número y se hallan dispuestos en un orden apropiado.
Nicómaco de Gerasa (aprox. 60 – 120 n.e.), Introducción a la Aritmética
Imagen 3 (Pie de imagen: You know my name (look up the number), acrílico sobre papel, 63 x 90 cm, del artista suizo Eugen Jost. Entre las sucesiones de números que aparecen, están los primeros números perfectos. Imagen de Plus Magazine [https://plus.maths.org/content/postcard-italy])
Entre los números abundantes, es decir, aquellos que son menores que la suma de sus divisores, se considera que son números casi perfectos aquellos tales que la suma de sus divisores es uno menos que el número. Así, el 16 es un número casi perfecto ya que 1 + 2 + 4 + 8 = 15. De hecho, todas las potencias de 2 son casi perfectas:

Los únicos números casi perfectos que se conocen son las potencias de 2, y es un problema abierto demostrar que estos son los únicos que existen.
Otra familia de números relacionada con la perfección, son los números múltiplo-perfectos o multi-perfectos, aquellos tal que la suma de sus divisores (recordemos que todo el tiempo estamos refiriéndonos a los divisores propios) no es el número, sino un múltiplo del mismo. Por ejemplo, los divisores del número 120 = 23 x 3 x 5 son 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40 y 60, cuya suma es 240 = 2 x 120. Solo se conocen 6 números multi-perfectos cuya suma sea el doble del número, 120, 672, 523.776, 459.818.240, 1.476.304.896, 51.001.180.160, y todos son pares. O, se conocen 36 cuya suma es el triple, de nuevo todos pares, de los cuales el más pequeño es 30.240.
 Hardy’s Taxi, acrílico sobre lienzo, 60 x 60 cm, del artista suizo Eugen Jost. Obra perteneciente a la exposición Everything is number
Hardy’s Taxi, acrílico sobre lienzo, 60 x 60 cm, del artista suizo Eugen Jost. Obra perteneciente a la exposición Everything is numberMás aún, un número se dice que es ambicioso si puede llegar a ser perfecto de la siguiente forma. Dado el número se toma la suma de sus divisores, con este nuevo número se vuelve a considerar la suma de sus divisores, y se continúa así, de forma que el número es ambicioso si llega un momento que se alcanza un número perfecto, como en el caso del número 95, cuyos divisores suman 1 + 5 + 19 = 25, y los divisores de este suman 1 + 5 = 6, que es perfecto. Números no ambiciosos son el 24 o los números primos (cuyo único divisor es el 1).
Veamos que el 24 = 23 x 3 no es ambicioso. Sus divisores son 1, 2, 3, 4, 6, 8 y 12, cuya suma es 1 + 2 + 3 + 4 + 6 + 8 + 12 = 36. Ahora, los divisores de 36 = 22 x 32 son 1, 2, 3, 4, 6, 9, 12 y 18, cuya suma es 55. Ahora este número, 55 = 5 x 11, tiene solo tres divisores 1, 5 y 11, cuya suma es 17, que es primo, luego su único divisor es 1 y se estaciona la sucesión. En consecuencia, el 24 no es ambicioso. Solo se conocen 16 números ambiciosos, 25, 95, 119, 143, 417, 445, 565, 608, 650, 652, 675, 685, 783, 790, 909, 913, e incluso un número tan bajo como 276 se desconoce si es, o no, ambicioso (aunque seguramente no).
Y también relacionados con la perfección están los números sublimes, aquellos tales que tanto el número de sus divisores (incluido ahora el propio número), como la suma de los mismos son perfectos, como el 12, que tiene 6 divisores y su suma es 1 + 2 + 3 + 4 + 6 + 12 = 28, aunque solo se conoce otro número sublime más, que es el siguiente
6.086.555.670.238.378.989.670.371.734.243.169.622.657.830.773.351.885.970.528.324.860.512.791.691.264.
 Números amigos (2010), del artista británico Andrew Crane
Números amigos (2010), del artista británico Andrew CraneA continuación, vamos a introducir parejas de números con una fuerte conexión entre ellos, desde la perspectiva que estamos analizando en esta entrada. Empecemos por el número 284, que se puede escribir como la multiplicación de los números primos 71 y 2 de la siguiente forma 284 = 71 x 22. Por lo tanto, los divisores propios del 284 son 1, 2, 4, 71 y 142, cuya suma es
1 + 2 + 4 + 71 + 142 = 220.
Si ahora consideramos el número que nos ha salido, 220, y buscamos sus divisores, como 220 = 11 x 5 x 22, entonces estos son 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 y 110, y la suma de ellos es
1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 + 110 = 284,
precisamente el primer número. Por este motivo, se dice que los números 220 y 284 son números amigos. Es decir, dos números son amigos si la suma de los divisores (propios) del primero es igual al segundo, y viceversa.
Este par de números amigos (220, 284) ya era conocido por los pitagóricos, quienes les atribuían propiedades místicas. En general, en la antigüedad se pensaba que estos números tenían poderes místicos, y eran utilizados en textos religiosos y de magia, en particular, en relación al amor y la amistad. Los astrónomos griegos los incorporaron en sus horóscopos, talismanes y amuletos.
“Las personas expertas en los talismanes afirman que los números amigos 220 y 284 ejercen una fuerte influencia para establecer una unión o una amistad muy fuerte entre dos personas”
Ibn Jaldún (1332-1406), Muqaddima (prolegómenos), 1377
Cuenta una leyenda que había un sultán aficionado a los puzzles, que al descubrir que tenía a un matemático como prisionero, decidió plantearle la siguiente cuestión. El sultán le dijo al matemático que le planteara un reto, un problema, y que estaría libre durante el tiempo que él necesitara para resolverlo, pero una vez resuelto por el sultán, el matemático sería ejecutado.
El matemático le explicó que los números 220 y 284 son números amigos, y le planteó que buscara otro par de números amigos. El sultán no lo consiguió y el matemático murió de viejo y siendo un hombre libre.
De hecho, calcular más pares de números amigos no es una tarea sencilla. Muchos matemáticos árabes estudiaron los números amigos, entre los siglos IX y XIV, como el iraquí Thabit ibn Qurra (826 – 901) quien dio una fórmula para obtener números amigos. En particular, se obtuvieron dos nuevos pares de números amigos
(17.296, 18.416) y (9.363.584, 9.437.056).
En el siglo XVII los grandes matemáticos franceses Pierre de Fermat (1601 – 1665) y René Descartes (1596 – 1650) redescubrieron la fórmula del matemático árabe, así como los dos anteriores pares de números amigos, que es ocasiones son atribuidos a ellos. Otro gran matemático ya mencionado, Leonhard Euler, extendió la fórmula de Qurra y obtuvo 64 nuevos pares de números amigos.
Curiosamente, a todos ellos se les pasó el siguiente par de números amigos más pequeño, después de (220, 284), el par (1.184, 1.210), descubierto por el adolescente Nicolo Paganini, de 16 años, en 1866.
La tarea siguió siendo compleja y hasta 1946 solo se consiguieron descubrir 390 pares de números amigos, hasta que llegó la era de los ordenadores, y su potencia de cálculo, que, junto a nuevos algoritmos, ha permitido calcular (según la wikipedia) hasta marzo de 2019 exactamente 1.223.386.359 parejas de números amigos. Sin embargo, a día de hoy no se sabe aún si existen infinitos pares de números amigos.
 Anillos hexagonales, con oro amarillo y oro rosa, con la pareja de números amigos 220 y 284, de la tienda londinense Comford Station, y la caja con la explicación de la pareja de números amigos
Anillos hexagonales, con oro amarillo y oro rosa, con la pareja de números amigos 220 y 284, de la tienda londinense Comford Station, y la caja con la explicación de la pareja de números amigosOtro nexo de unión entre números. Se dice que dos números son novios o casi-amigos si cada uno de ellos es igual a la suma de sus divisores menos 1, como el 48 = 1 + 3 + 5 + 15 + 25 – 1 y el 75 = 1 + 2 + 3 + 4 + 6 + 8 + 12 + 16 + 24 – 1. Las primeras parejas de números novios son (48, 75), (140, 195), (1.050, 1.925), (1.575, 1.648), (2.024, 2.295) y (5.775, 6.128). Los números de todas las parejas de novios conocidas tienen paridad opuesta, es decir, uno es par y el otro impar.
La propiedad de amistad puede generalizarse a un grupo de números, de forma que la suma de los divisores de cada uno es igual al siguiente, y la del último igual al primero, entonces se habla de números sociables. El grupo de números más pequeños que son sociables son 12.496, 14.288, 15.472, 14.536 y 14.264. Comprobémoslo:
1) 12.496 = 24 x 11 x 71, divisores: 1, 2, 4, 8, 11, 16, 22, 44, 71, 88, 142, 176, 284, 568, 781, 1.136, 1.562, 3.124 y 6.248, cuya suma es 14.288;
2) 14.288 = 24 x 19 x 47, divisores: 1, 2, 4, 8, 16, 19, 38, 47, 76, 94, 152, 188, 304, 376, 752, 893, 1.786, 3.572 y 7.144, cuya suma es 15.472;
3) 15.472 = 24 x 967, divisores: 1, 2, 4, 8, 16, 967, 1.934, 3.868 y 7.736, cuya suma es 14.536;
4) 14.536 = 23 x 23 x 79, divisores: 1, 2, 4, 8, 23, 46, 79, 92, 158, 184, 316, 632, 1.817, 3.634 y 7268, cuya suma es 14.264;
5) 14.264 = 23 x 1.783, divisores: 1, 2, 4, 8, 1.783, 3.566 y 7.132, cuya suma es 12.496.
Se conocen 5.410 grupos de números sociables (véase la lista de números sociables de David Moews), la mayoría formados por 4 números, aunque existe un grupo formado por 28 números.

También existen intocables dentro de la familia de los números naturales, son aquellos que no se pueden expresar como suma de los divisores de ningún número. El número 2 es intocable, el 3 no lo es (3 = 1 + 2, divisores del 4), el 4 tampoco (4 = 1 + 3, divisores del 9) y el 5 sí, ya que solo puede expresarse como 1 + 4, pero si el 4 es divisor del número, también lo es el 2 y la suma sería al menos 7. El siguiente intocable es el 52.
Los números intocables menores de 500 son:
2, 5, 52, 88, 96, 120, 124, 146, 162, 188, 206, 210, 216, 238, 246, 248, 262, 268, 276, 288, 290, 292, 304, 306, 322, 324, 326, 336, 342, 372, 406, 408, 426, 430, 448, 472, 474, 498.
El matemático húngaro Paul Erdös (1913-1996) demostró que existen infinitos números intocables.
“Dice Trece [la protagonista se refiere con números a los hombres que han pasado por su vida] que le ha hecho esos dos regalos –el libro [de Murakami] y lo del segundo cajón [un consolador]– para que se acuerde de él. Sin embargo, por la esencia oriental de uno y las dimensiones del otro, lo que Trece ha conseguido es que Pi, en lugar de acordarse de él, se acuerde de Dos. Por ambas razones.
Dos se ha convertido en una medida (de hecho, es un número intocable, pues no es la suma de los divisores de ningún número). No tiene tanta importancia como persona real en el presente […] sino como recuerdo y, sobre todo, como convención, como medida. Dos es la medida del sistema métrico sentimental”
Juan Pardo Vidal, La luz de la mesita de noche, Sloper, 2012
Por otra parte, un número se dice que es práctico si todos los números naturales más pequeños que él pueden ser expresados como suma de distintos divisores del número. Así, el número 12 es un número práctico ya que todos los números menores que él, desde el 1 al 11, pueden ser expresados como suma de algunos de los divisores de 12. Veámoslo: los divisores de 12 son 1, 2, 3, 4 y 6, luego 1 = 1, 2 = 2, 3 = 3, 4 = 4, 5 = 1 + 4, 6 = 2 + 4, 7 = 1 + 2 + 4, 8 = 2 + 6, 9 = 3 + 6, 10 = 4 + 6 y 11 = 1 + 4 + 6.
Los números prácticos menores que 100 son: 1, 2, 4, 6, 8, 12, 16, 18, 20, 24, 28, 30, 32, 36, 40, 42, 48, 54, 56, 60, 64, 66, 72, 78, 80, 84, 88, 90 y 96.
El concepto fue definido en 1948 por el matemático indio A. K. Srinivasan, números que en su opinión eran interesantes de estudiar por su relación con las subdivisiones del dinero, los pesos y las medidas. Aunque estos números ya fueron utilizados por el matemático italiano Fibonacci (Leonardo de Pisa, 1170 – 1240), en su obra Liber Abaci (Libro del Ábaco, 1202), en relación a las fracciones egipcias (véase la entrada de Marta Macho, Sobre fracciones egipcias).
Claramente, todas las potencias de 2 son prácticas, ya que dado 2n, se puede expresar cualquier número entre 1 y 2n – 1 como suma de potencias de 2, menores que 2n, que son sus divisores. Es solamente una cuestión de divisibilidad y el fundamento del sistema binario. Se conocen muchas propiedades de los números prácticos, como que existen infinitos, el producto de dos números prácticos es un número práctico, los números perfectos pares, luego de la forma 2p–1 (2p – 1), son prácticos, o que, salvo el 1 y el 2, todos los números prácticos son divisibles por 4 o 6, entre otras.
 Instalación Forest of numbers – Bosque de números (2017), de la artista francesa Emmanuelle Moureaux. Imagen de su página web
Instalación Forest of numbers – Bosque de números (2017), de la artista francesa Emmanuelle Moureaux. Imagen de su página webY no podían faltar los números raros, o extraños, que son aquellos que son abundantes, es decir, la suma de los divisores es mayor que el número, pero no se puede obtener el número exacto quitando algunos de los divisores, es decir, como suma de un subconjunto de divisores propios. Por ejemplo, el 12 es abundante, pero como 12 = 2 + 4 + 6, no es raro, y el número raro más pequeño es 70 (cuyos divisores son 1, 2, 5, 7, 10, 14, 35).
Aunque se sabe que existen infinitos números raros, estos son relativamente escasos, por ejemplo, solamente hay 7 números raros menores que 10.000, que son 70, 836, 4.030, 5.830, 7.192, 7.912 y 9.272. Todos los números raros conocidos son pares y si existe alguno impar deberá ser, por lo menos, mayor que 1021.
Cerramos este repaso a algunas tribus numéricas con los números poderosos, que son aquellos tales que, si un número primo p es divisor suyo, también lo es su cuadrado p2, como el 36, cuyos divisores primos son 2 y 3, y sus cuadrados también son divisores de 36. Curiosamente, un número m es poderoso si, y sólo si, se puede expresar como m = a2b3, para algún par de números a y b. Claramente, si un número es de la forma a2b3 es poderoso (ya que los cuadrados de los primos de la descomposición en primos de a y b claramente dividen a a2b3), pero, además, todos los números poderosos son de esta forma. Veámoslo:

Por ejemplo, para el número m = 21.600 = 25 x 33 x 52, tendríamos que b = 2 x 3 = 6 y a = 2 x 5 = 10.
Existen algunos problemas interesantes sobre los números poderosos. Como se observa fácilmente, todo número impar es resta de dos cuadrados, luego de dos números poderosos, 2 k + 1 = (k + 1)2 – k2. Lo mismo ocurre con los múltiplos de 4, ya que 4 k + 4 = (k + 2)2 – k2.
Pero, ¿qué pasaba con los números pares no divisibles por 4, podían expresarse como resta de números poderosos? El matemático e ingeniero estadounidense Solomon W. Golomb (1932 – 2016), conocido por sus trabajos sobre juegos matemáticos, observó que algunos sí podían expresarse, como 2 = 33 – 52, 10 = 133 – 37 o 18 = 192 – 73 = 35 – 152, y conjeturó que el número 6 no podía expresarse como resta de números poderosos, así como infinitos otros números pares. El matemático polaco Władysław Narkiewicz demostró que el 6 no solo podía representarse de esta forma, 6 = 5473 – 4632, sino que existían infinitas formas de hacerlo. Más aún, en 1982, el matemático estadounidense Wayne L McDaniel extendió el resultado para todos los números pares, no divisibles por 4.
Por otra parte, Paul Erdös conjeturó, y fue demostrado por el matemático británico Roger Heath-Brown, que todo número natural suficientemente grande puede expresarse como suma de tres números poderosos.
 Instalación “SOHO” (2008), del artista japonés Tatsuo Miyajima. Imagen de su página web
Instalación “SOHO” (2008), del artista japonés Tatsuo Miyajima. Imagen de su página web Bibliografía
1.- Clifford A. Pickover, El prodigio de los números. Desafíos, paradojas y curiosidades matemáticas, Ma Non Troppo (ediciones Robinbook), 2002.
2.- Clifford A. Pickover, La maravilla de los números. Un viaje por los secretos de las matemáticas, sus desafíos y caprichos, Ma Non Troppo (ediciones Robinbook), 2002.
3.- Lamberto García del Cid, Números notables. El 0, el 666 y otras bestias numéricas, El mundo es matemático, RBA, 2010.
4.- Howard H. Eves, Mathematical Circles, The Mathematical Association of America (MAA), 2003.
5.- Wikipedia: Perfect number
6.- David G. Kendall, The Scale of Perfection, Journal of Applied Probability, Vol. 19, Essays in Statistical Science, pp. 125-138, 1982.
7.- Eugen Jost, A postcard from Italy, Plus Magazine, 1999
8.- Wolfram Mathworld: Multiperfect number
9.- Wolfram Mathworld: Aspiring number
10.- Wikipedia: Amicable numbers
11.- Wikipedia: Betrothed or quasi amicable numbers
12.- Wikipedia: Untouchable number
13.- Wikipedia: Practical number
14.- Página web de la artista Emmanuelle Moureaux
15.- Wikipedia: Weird number
16.- Wikipedia: Powerful number
17.- Página web del artista japonés Tatsuo Miyajima
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Los números enamorados se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Una conjetura sobre ciertos números en el ‘sistema Shadok’
- El origen poético de los números de Fibonacci
- Buscando lagunas de números no primos
Interferencia y difracción de la luz
 Imagen: Wikimedia Commons
Imagen: Wikimedia CommonsA principios del siglo XIX, cuando el prestigio de Newton era en gran medida el sostén de la hipótesis corpuscular de la luz, Thomas Young resucitó la hipótesis ondulatoria. En experimentos realizados entre 1802 y 1804 Young descubrió que la luz muestra el fenómeno de interferencia. La hipótesis corpuscular de la luz no puede explicar fácilmente los patrones de interferencia producidos por la luz. El famoso “experimento de doble rendija” de Young proporcionó la prueba convincente de que la luz tiene propiedades que solo se pueden explicar en términos de ondas.
El experimento de Young se puede realizar muy fácilmente. Consiste, básicamente, en dividir un solo haz de luz en dos haces para garantizar que estén en fase. Luego se permite que los haces resultantes de la división se superpongan, y los dos trenes de ondas interfieren, constructivamente en algunos lugares y destructivamente en otros. Para simplificar la interpretación del experimento, podemos suponer que se realiza con luz que tiene una única longitud de onda definida λ.
Young usó una pantalla negra con un pequeño agujero perforado para producir un haz de luz estrecho en una habitación a oscuras. En la trayectoria del haz colocó una segunda pantalla negra en la que había cortado dos rendijas estrechas, muy juntas. Tras esta pantalla colocó otra pantalla más, pero blanca. La luz que entraba por cada rendija se difractó y se extendió por el espacio más allá de la pantalla. La luz de cada rendija interfirió con la luz de la otra, y el patrón de interferencia se mostró en la pantalla blanca. Donde la interferencia era constructiva había una banda brillante en la pantalla. Donde la interferencia era destructiva, la pantalla permanecía oscura.
 Reproducción del diagrama de Thomas Young (1807) para explicar el resultado del experimento de la doble rendija (situadas en A y B) que produce mínimos en C,D,E y F, tal y como aparece en T. Young (ed. G. Peacock), 1855, Miscellaneous Works of the late Thomas Young, London: J. Murray, vol. 1. Imagen: Wikimedia Commons
Reproducción del diagrama de Thomas Young (1807) para explicar el resultado del experimento de la doble rendija (situadas en A y B) que produce mínimos en C,D,E y F, tal y como aparece en T. Young (ed. G. Peacock), 1855, Miscellaneous Works of the late Thomas Young, London: J. Murray, vol. 1. Imagen: Wikimedia CommonsEs una medida del genio de Young el que pudiese encontrar, por experimento, valores numéricos para algo tan pequeño como la longitud de onda de la luz. Él lo expresó así:
From a comparison of various experiments, it appears that the breadth of the undulations constituting the extreme red light must be supposed to be, in air, about one 36 thousandth of an inch, and those of the extreme violet about one 60 thousandth.
A partir de una comparación de varios experimentos, parece que la amplitud de las ondulaciones que constituyen la luz roja extrema debe suponerse que sea, en el aire, aproximadamente una 36-milésima de pulgada. [7·10-7 m], y las del violeta extremo alrededor de una 60-milésima [4·10-7 m].
Al anunciar su resultado, Young hizo un especial esfuerzo por evitar las críticas de los seguidores de Newton, a quien se consideraba un partidario de la hipótesis corpuscular de la luz. Señaló que el propio Newton había hecho varias afirmaciones a favor de una teoría de la luz que tenía algunos aspectos de la hipótesis ondulatoria.
Sin embargo, Young no fue tomado en serio. No fue hasta 1818, cuando el físico francés Augustin-Jean Fresnel propuso su propia hipótesis ondulatoria de base matemática, que la investigación de Young comenzó a ser reconocida como merecía.
Fresnel también tuvo que enviar su trabajo para su aprobación a un grupo de físicos comprometidos con la hipótesis corpuscular de la luz. Uno de ellos, el matemático Simeón Poisson, trató de refutar la hipótesis ondulatoria de Fresnel. Si realmente describía el comportamiento de la luz, argumentaba Poisson, debería suceder algo muy peculiar cuando se coloca un pequeño disco macizo en un haz de luz. La difracción de algunas de las ondas de luz alrededor del borde del disco redondo debería conducir a una interferencia constructiva, produciendo un punto brillante en el centro de la sombra del disco en una pantalla blanca colocada detrás del disco. La hipótesis corpuscular de la luz no permitía ideas como la difracción y la interferencia constructiva. Además, nunca se había informado de la observación de un punto brillante; incluso la idea de un punto brillante en el centro de una sombra parecía absurda. Con estos razonamientos Poisson anunció que había refutado la hipótesis ondulatoria.
Sin embargo, Dominique-François Arago, presidente del comité de la Académie des sciences que entendía del asunto, era un empirist e inmediatamente dispuso que la prueba aparentemente ridícula de Poisson se probara mediante un experimento. ¡El resultado fue que apareció un punto brillante en el centro de la sombra!
 Sombra proyectada por un obstáculo de 5,8 mm de diámetro en una pantalla colocada a 183 cm detrás, cuando es iluminado por la luz del sol que pasa a través de un agujero colocado 153 cm por delante. Los colores tenues de las franjas muestran la dependencia de la longitud de onda del patrón de difracción. En el centro está el punto brillante de Poisson / Arago. Imagen: Wikimedia Commons
Sombra proyectada por un obstáculo de 5,8 mm de diámetro en una pantalla colocada a 183 cm detrás, cuando es iluminado por la luz del sol que pasa a través de un agujero colocado 153 cm por delante. Los colores tenues de las franjas muestran la dependencia de la longitud de onda del patrón de difracción. En el centro está el punto brillante de Poisson / Arago. Imagen: Wikimedia CommonsA partir de entonces, un número cada vez mayor de personas de ciencia valoró como importantísimos los resultados del experimento de Young de la doble rendija y el “punto brillante de Poisson”. Para 1850, con los experimentos de Foucault-Fizeau, la hipótesis ondulatoria de la luz era el consenso científico; los físicos ya habían comenzado a concentrarse en resolver las consecuencias matemáticas de este modelo y aplicarlo a las diferentes propiedades de la luz.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Interferencia y difracción de la luz se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Patrón de interferencia en pulsos de ondas
- Patrón de interferencia en ondas periódicas
- Patrones de difracción
“Fuego, foca, foto…” ¿Podemos decir estas palabras gracias a la dieta de nuestros antepasados?
 Alineación dental antes y después (derecha) de los cambios en la dieta. Imagen: Scott Moisik a partir de D. E. Blasi et al (2019) Human sound systems are shaped by post-Neolithic changes in bite configuration Science doi: 10.1126/science.aav3218
Alineación dental antes y después (derecha) de los cambios en la dieta. Imagen: Scott Moisik a partir de D. E. Blasi et al (2019) Human sound systems are shaped by post-Neolithic changes in bite configuration Science doi: 10.1126/science.aav3218 Fuego, foca, foto, fofo, fumar, fieltro, feminista… Es gustoso pronunciar el sonido de la efe, ¿verdad? Quizá por eso la palabra malsonante por excelencia en inglés sea “fuck” (disculpen el exabrupto), porque a los anglosajones se les da mejor que a nadie el convertir un sonido u onomatopeya en el centro de sus palabras (“crack” es más sonoro que “crujir”, aunque tampoco está mal, y “ring” es mejor que “llamar al timbre”, ahí sí que no hay discusión).
Pero volvamos al hilo, que me pierdo. Hablábamos del sonido de la efe, y la reflexión viene a cuento de un estudio recientemente publicado en la revista Science que sugiere que si somos capaces de pronunciarlo, así como otras consonantes labiodentales (en el castellano, solo le acompañaría la pronunciación tradicional de la uve, que solo se conserva en algunas regiones), es porque hace miles de años nuestros antepasados cambiaron su alimentación, eso cambió sus mandíbulas y con eso, los sonidos que eran capaces de pronunciar, abriendo la puerta a una variedad lingüística y comunicativa no disponible anteriormente.
 Imagen: D. E. Blasi et al (2019) Human sound systems are shaped by post-Neolithic changes in bite configuration Science doi: 10.1126/science.aav3218
Imagen: D. E. Blasi et al (2019) Human sound systems are shaped by post-Neolithic changes in bite configuration Science doi: 10.1126/science.aav3218Comida dura, mandíbulas potentes
Vamos por partes. El estudio ha sido realizado por Balthasar Bickel, Damián Blasi y Steven Moran, del laboratorio de Lingüística de la Universidad de Zúrich, en Suiza. Su intención era poner a prueba una idea propuesta por otro lingüista, el americano Charles Hockett en 1985. Hocket escribió entonces que las lenguas habladas por los cazadores-recolectores carecían de estas consonantes labiodentales y que, al menos en parte, su dieta podía ser responsable.
Según su teoría, consumir y masticar alimentos fibrosos y duros requería de una mayor fuerza en la mandíbula y suponía un mayor desgaste de los molares, y como tal, sus mandíbulas inferiores eran mayores y los molares ocupaban más espacio en ella, empujando las demás piezas dentales hacia delante y causando una alineación entre los dientes delanteros de la mandíbula inferior y la mandíbula superior.
Esto dificultaba, dijo Hockett entonces, que los dientes de arriba tocasen el labio inferior, contacto necesario para pronunciar la gustosa efe. Para hacerse una idea, pruebe a colocar hacia delante su mandíbula inferior hasta que dientes de arriba y abajo coincidan. ¿Verdad que le resulta una postura incómoda? Eso es por la llamada sobremordida, ese espacio que la mayoría tenemos entre los dientes superiores y los inferiores cuando cerramos la mandíbula. Al introducirse la agricultura y técnicas como el molido de los cereales, la fabricación de derivados lácteos y más formas de cocinado para la carne, la postura anterior habría sido menos necesaria y esta sobremordida habría ido haciéndose cada vez más común, hasta el día de hoy.
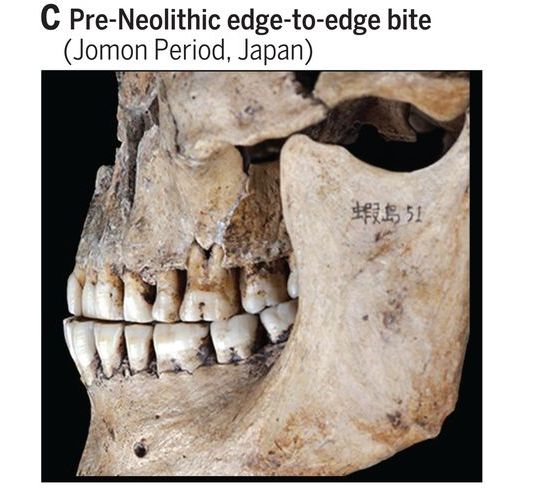 Imagen: D. E. Blasi et al (2019) Human sound systems are shaped by post-Neolithic changes in bite configuration Science doi: 10.1126/science.aav3218
Imagen: D. E. Blasi et al (2019) Human sound systems are shaped by post-Neolithic changes in bite configuration Science doi: 10.1126/science.aav3218Un 29% menos de energía para pronunciar la F
Blasi y compañía querían poner a prueba esta idea y, esperaban a priori, demostrar que Hockett se había equivocado.
Para empezar, los investigadores utilizaron un modelo informático para calcular que con una sobremordida, producir esas consonantes labiodentales cuesta un esfuerzo un 29% inferior. Después, analizaron las lenguas del mundo y descubrieron que en las civilizaciones de cazadores y recolectores hay un 75% menos de consonantes labiodentales que en las lenguas habladas en sociedades agrícolas. Por último, estudiaron las relaciones y evoluciones lingüísticas y determinaron que las consonantes labiodentales se difunden con rapidez, de forma que esos sonidos podrían haber pasado de ser raros a ser comunes en los 8.000 años que han pasado desde la adopción de la agricultura y otros métodos de manipulación de los alimentos.
Teniendo en cuenta estas averiguaciones. Bickel sugiere que a medida que la comida más blanda se fue haciendo más habitual, más adultos fueron desarrollando sobremordidas y fueron utilizando consonantes labiodentales de forma accidental, y que por ejemplo en la antigua India, el uso de esos sonidos pudo haber sido una señal de estatus al significar un acceso a una dieta más delicada y costosa. A día de hoy hay consonantes labiodentales en el 76% de los idiomas provenientes de lenguas indoeuropeas.
“Una de las conclusiones principales es que el panorama de sonidos que tenemos hoy en día está fundamentalmente afectado por la biología de nuestro aparato fonador. No es solamente una cuestión de evolución cultural”, explicaba Bickel en una rueda de prensa.
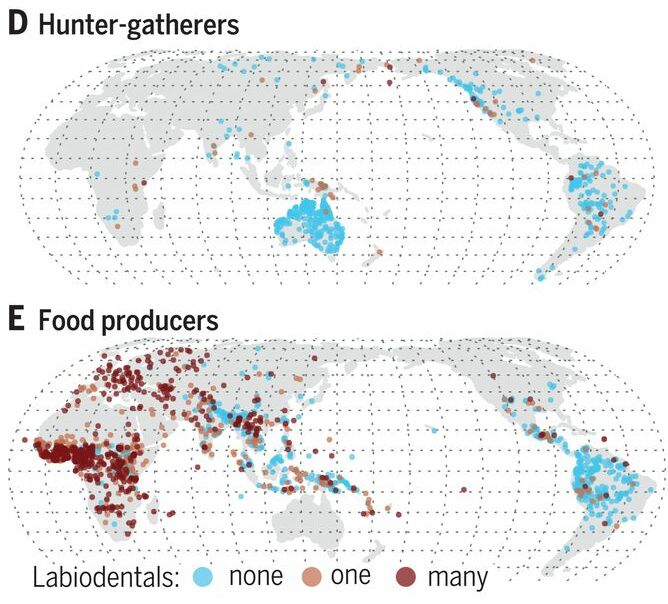 Imagen: D. E. Blasi et al (2019) Human sound systems are shaped by post-Neolithic changes in bite configuration Science doi: 10.1126/science.aav3218
Imagen: D. E. Blasi et al (2019) Human sound systems are shaped by post-Neolithic changes in bite configuration Science doi: 10.1126/science.aav3218Si ocurrió así, no ocurrió en todas partes
Aun así, no todo el mundo ve clara la relación que Bickel y su equipo proponen entre dieta, forma de la mandíbula y sonidos del idioma. Inevitablemente, su hipótesis está basada en algunas ideas difíciles de comprobar y también en algunas contradicciones. Por ejemplo, que en la Antigua China también se comenzó a cultivar y procesar arroz de forma que fuese más sencillo de masticar y comer y en las lenguas de esa región los sonidos labiodentales son mucho menos comunes que en las lenguas europeas.
Claro que los autores no defienden que la evolución hacia la sobremordida signifique necesariamente la aparición de las consonantes labiodentales, sino que “la probabilidad de producción de esos sonidos aumenta ligeramente con el tiempo, y eso significaría que es probable que algunas lenguas los adquieran, pero no todas”, explica otro de los autores, Steven Moran, en este artículo de Smithsonian Magazine.
“¿Dónde está la causalidad, que yo la vea?”
Algunos críticos, como el paleoantropólogo Rick Potts, no terminan de aceptar la conclusión del estudio: “En mi opinión, no dan suficientes razones para aceptar que la dieta fue el motivo por el que se hicieron más comunes estos sonidos, porque no tienen en cuenta en ningún momento los componentes anatómicos de producir estos sonidos”, explica en el artículo mencionado.
Potts explica que para hacer el sonido de la efe cuando no hay sobremordida simplemente hay que retraer un poco los músculos de los lados de la mandíbula, que la hacen retroceder ligeramente. “¿Cómo podría una dieta más dura y áspera limitar esa retracción? Esa es la base para hacer esos sonidos. El estudio no demuestra de ninguna forma que una mordida en la que los dientes coinciden impida o haga energéticamente más costoso pronunciar estos sonidos”, señala.
Así que en su opinión, el estudio señala algunas correlaciones que resultan interesantes pero no llega a demostrar una causalidad probable. Es, dice, como si una investigación descubriese que culturas que habiten en el ecuador tienen preferencia por el color rojo y también que esas personas tienen en sus ojos una densidad de receptores de color menor que las personas que habitan en el Ártico, por ejemplo, y concluyesen que la falta de receptores de color es lo que las hace preferir el color rojo.
“Pero ¿cómo íbamos con eso a descartar que fuese una cuestión cultural e histórica lo que hace que los habitantes de una cultura ecuatorial tiendan a elegir el rojo, y los habitantes de culturas del polo no lo hagan?”, argumenta, señalando que el estudio no ha tenido suficientemente en cuenta la acción de la historia, la cultura y la identidad de cada grupo y cada lengua a la hora de favorecer o no los sonidos labiodentales.
Referencias:
Human sound systems are shaped by post-Neolithic changes in bite configuration – Science
Ancient switch to soft food gave us an overbite—and the ability to pronounce ‘f’s and ‘v’s – Science
The Ability to Pronounce ‘F’ and ‘V’ Sounds Might Have Evolved Along With Diet – Smithsonian Magazine
Sobre la autora: Rocío Pérez Benavente (@galatea128) es periodista
El artículo “Fuego, foca, foto…” ¿Podemos decir estas palabras gracias a la dieta de nuestros antepasados? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¿Qué nos puede decir un elefante del cáncer en humanos?
- Los vegetales de la dieta neandertal
- Nuestros ancestros asesinos
Actos por el 50 aniversario de la Facultad de Ciencia y Tecnología de la UPV/EHU

50 años de ciencia viva
Los actos de conmemoración del 50 aniversario de la Facultad de Ciencia y Tecnología de la UPV/EHU comenzaron el 28 de enero de este año con la plantación de un tilo de hoja pequeña (Tila cordeta Mill.), que representa el Árbol de la Ciencia como símbolo de su unidad fundamental. El acto simbolizó la siembra de la semilla plantada en mayo de 1968, cuando se creó la Facultad de Ciencias de la Universidad de Bilbao, hoy en día Facultad de Ciencia y Tecnología.
Los primeros pasos de la Facultad de Ciencias en el curso 1968/69 se dieron junto al puente de Deusto, en “Botica Vieja, 1”. No fue hasta finales de 1971 cuando se trasladó a su emplazamiento actual en Leioa.
La Facultad de Ciencia y Tecnología ha sido una facultad viva en su oferta de titulaciones. Comenzó ofertando las cinco ramas clásicas de las Ciencias Naturales: Biología, Física, Geología, Matemáticas y Química. Entre los cursos 1994/95 y 2000/01, su oferta se amplía a las licenciaturas de segundo ciclo en Bioquímica, Ingeniería Electrónica, Ingeniería Química y Ciencias Ambientales, pasando a llamarse en el curso 2004/2005 Facultad de Ciencia y Tecnología. Hoy, oferta nueve grados, dos en la rama de Ingeniería (Ingeniería Electrónica e Ingeniería Química), y siete en la de Ciencias (Biología, Bioquímica y Biología Molecular, Biotecnología, Física, Geología, Matemáticas y Química). Se oferta también el doble grado en Física e Ingeniería Electrónica y tres dobles titulaciones internacionales de grado. Esta oferta hace de la Facultad de Ciencia y Tecnología uno de los referentes más importantes del País Vasco en la formación de profesionales capaces de jugar un papel crucial en los retos de nuestra sociedad, desde el desarrollo en nuevas tecnologías, el desarrollo sostenible, la conservación del medio ambiente o la investigación en biociencias.
Los inicios fueron precarios, como se podría esperar ante la difícil situación política de aquellos años. Hoy la facultad es un centro con gran experiencia en docencia, investigación y desarrollo tecnológico, como queda acreditado por las muy buenas posiciones en el ranking de Shanghái de distintas áreas de investigación que se desarrollan en nuestro centro.
La calidad de una facultad no se mide sólo por la excelencia del profesorado, sino también por la calidad de su alumnado: hoy cuenta con estudiantes de primer nivel. Las notas de acceso más elevadas para acceder a las titulaciones universitarias se encuentran en varias de las titulaciones de esta facultad. Un claro ejemplo es la nota de acceso superior a 13, sobre 14, para acceder al doble grado, la más alta de la UPV/EHU.
Tras 50 años de intenso trabajo, 17.500 personas han egresado en licenciatura, ingeniería o grado, y 2.000 se han doctorado. Estas cifras suponen una gran aportación de personal cualificado, profesionales que están trabajando en distintos ámbitos sociales, fundamentalmente en el tejido productivo, pero también en el institucional y el educativo, ocupando muchos de ellos puestos de responsabilidad.
Queremos compartir con la sociedad vasca el trabajo que la Facultad de Ciencia y Tecnología ha desarrollado a lo largo de medio siglo, mediante una investigación de excelencia y una formación rigurosa de profesionales en distintas áreas, mostrando así nuestro orgullo por haber colaborado en el crecimiento económico y social del País Vasco.
Biba Zientzia!, Ciencia Viva.
Todas las actividades programadas las encontrará aquí.
Las actividades programadas en el Bizkaia Aretoa de Bilbao durante los próximos 4 meses son:
Semana de la física
- 20 de marzo
18:30 Conferencia: A. Sanchez-Lavega: “¿Hay mas vida en el universo?
19:00 Mesa redonda: “Ciencia y Tecnología en el siglo XXI”
-Cristina Oyon (Responsable de Iniciativas Estratégicas del Grupo SPRI),
-Jose Maria Pitarke (Director General del CIC-Nanogune),
-Javier García-Abajo (Prof. Investigación CSIC y Research Prof. ICREA)
-Agustin Sanchez Lavega (Catedrático UPV/EHU)
Moderadora: Eva Caballero (Periodista de radio Euskadi)
- 21 de marzo
18:00 Conferencia: Roberto Emparan (Research Prof. ICREA y autor del libro de divulgación reciente “Iluminando el lado oscuro del Universo”): “Stephen Hawking: de los agujeros negros a la Teoría del Todo”
Semana de las matemáticas
- 25 de marzo
18:00 Mesa redonda: “Experiencias Matemáticas en empresa”
Dirigido a: Estudiantes de Bachillerato y de Matemáticas, Orientadores
- 2 de abril
19:00 Evento: Judith Rivas (UPV/EHU); Nagore de las Cuevas y Arkaitz Pascuas; Andoni Aresti Dantza Eskola y Mungiako Udal Dantza Eskola : “Pasos de baile a ritmo de matemáticas”
Dirigido a: Público general
Semana de la geología
- 1 de abril
18:00 Conferencia: Irantzu Guede, doctora de la UPV/EHU en Geología, en Mineralogía Petrología: “Geología en Mitos y Leyendas”.
- 2 de abril
18:00 Conferencia: Humberto Astibia, catedrático de la UPV/EHU: “Los fósiles, documentos de la historia de la Vida archivados en las rocas”.
16:00-20:00 Taller de Geología para familias. Aintzane Goffard (Geologa de la UPV/EHU, ayudante en Estratigrafía-Paleontología) e Irantzu Guede (Doctora de la UPV/EHU en Geología, Mineralogía-Petrología).
- 3 de abril
18:00 Conferencia: Blanca Martínez, doctora de la UPV/EHU en Geología, en Estratigrafía-Paleontología: “Geología y música”.
- 4 de abril
18:00 Conferencia: Ihintza Urain Alberdi, geóloga: “Geologia eta ingurugiroa: Geologoaren papera energia aldaketan eta Lurraren inguruko kultura berri baten aurrean”.
- 8 de abril
18:00 Conferencia: Jose María Tubía, catedrático de Geodinámica de la UPV/EHU: “Riesgo geológico de los tsunamis”.
Acto central
- 11 de abril
18:30 Conferencia: Prado Martín Moruno, 2017 L’Oreal-Unesco awarded Women for Science: “La energía oscura y el destino del Universo”.
Estreno de la obra de baile “GARGANTUA” (basada en el agujero negro GARGANTUA de la película “Interstellar”). Martxel Rodriguez, físico y bailarín profesional. Miembro de “KUKAI dantza taldea”.
Semana de la química
- 29 de abril
18:00 Conferencia: Oskar González. Profesor del Departamento de Química Analítica:“Artelanetan aurkitu diren gauzarik bitxienak”
- 30 de abril
18:00 Conferencia: Pascual Román, profesor emérito. Catedrático de Química Inorgánica: “El sesquicentenario de la tabla periódica de los elementos químicos”
- 2 de mayo
18:00 Conferencia: Jose Luis Vilas, director del Grupo de Química Macromolecular. Departamento de Química Física FCT-EHU: “Hidrogeles: imprimiendo salud”
Semana de la biociencia
- 6 de mayo
18:00 Mesa redonda: “Zientzia, jainkoaren esistentzia, zergatik du gizakiak sinisteko beharra”
Otros actos
- 27 de Junio
19:00 “ZTF/FCTren ekarpena Euskararen Normalizazioan” Conferenciantes: Pedro Miguel Etxenike, Jacinto Iturbe y Jesusmari Txurruka
Acto de clausura. 12 de julio
Bilbao Bizkaia AretoaSe comunicará
Sobre el autor: Fernando Plazaola Muguruza es el decano de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo Actos por el 50 aniversario de la Facultad de Ciencia y Tecnología de la UPV/EHU se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Presentación del estudio “Percepción social de la ciencia y la tecnología en el País Vasco”
- Geología, ver más allá de lo que pisamos
- Geología: la clave para saber de dónde venimos y hacia dónde vamos
El cerebro humano tarda en madurar
 Imagen: Gordon Johnson / Pixabay
Imagen: Gordon Johnson / PixabayUna característica peculiar de los seres humanos es que, aunque nacemos con una cabeza de gran tamaño, tardamos en completar el crecimiento y desarrollo del encéfalo. A los dos años de edad alcanza el 85% de su volumen máximo, por lo que ha de seguir creciendo. Por otro lado, no todas sus áreas se desarrollan y maduran a la vez. La corteza cerebral, que es la parte más exterior, madura en último lugar. Y en ese proceso la proporción entre las denominadas materia gris y materia blanca cambia.
La materia gris corresponde a diferentes elementos: cuerpos neuronales y sus dendritas, que son prolongaciones ramificadas a través de las cuales una neurona recibe señales de otras; células de la glía, que dan soporte y protección a las anteriores; capilares sanguíneos, que proporcionan a neuronas y células gliales el oxígeno y los nutrientes que necesitan; y las conexiones entre neuronas, denominadas sinapsis. La materia gris se distribuye en la corteza del cerebro y del cerebelo, así como en numerosas estructuras de ubicación más profunda en el interior del encéfalo.
La materia blanca corresponde a los axones de las neuronas que se encuentran recubiertos por una sustancia lipídica denominada mielina. Un axón es una proyección de forma tubular que conducen señales nerviosas desde el cuerpo de una neurona hasta otras que pueden encontrarse a cierta distancia o hasta células musculares, principalmente. La vaina de mielina que recubre el axón lo aísla, y ayuda, de esa forma, a que los impulsos nerviosos se transmitan más rápida y eficazmente.
El volumen de materia gris de varias regiones de la corteza cerebral alcanza su máximo desarrollo alrededor de los 10 años de edad. Ese incremento refleja un aumento de las conexiones entre neuronas que se producen como consecuencia de la experiencia, el adiestramiento y el aprendizaje. Durante esos años, la actividad encefálica es tan intensa que llega a gastar un 60% de la energía que consume el organismo en reposo, y casi la mitad de las necesidades diarias totales de energía. Hay quienes atribuyen a ese gran consumo de energía el hecho de que el crecimiento del cuerpo durante la niñez sea lento y se prolongue en el tiempo.
A partir de los once o doce años las cosas cambian. El grosor de la materia gris de la corteza cerebral empieza a reducirse, y lo hace de forma sustancial durante la adolescencia. En algunas zonas esa reducción llega a ser del 17% hacia el final del proceso, unos 15 años después. Lo que ocurre, en parte, es que una cierta proporción de las conexiones sinápticas se “podan”, como se dice en la jerga neurocientífica. Esa poda elimina conexiones que no se usan o se usan poco y se mantienen las que más tráfico registran. A la vez aumenta la proporción de materia blanca. Eso es indicio de que los axones que conducen las señales se hacen más gruesos y que aumenta su grado de cobertura por la capa lipídica de mielina. El engrosamiento de los axones y el mayor grado de mielinización promueven una más rápida y eficaz transmisión de impulsos nerviosos y , por lo tanto, una comunicación más eficiente entre la corteza cerebral y el resto de áreas encefálicas. En definitiva: el cerebro funciona mejor.
La maduración de la corteza cerebral requiere tiempo y hace que la adolescencia sea un periodo difícil. Pero durante ese periodo la mente humana aprende a navegar en el complejo entorno social en que se desenvolverá en la edad adulta. La adolescencia puede entenderse así como el precio que paga por ese aprendizaje.
Nota:
Esta anotación es parte de una colección de tres artículos dedicados a la neuropsicología de la adolescencia. Los artículos son El desajuste adolescente, En busca de la identidad personal y este, El cerebro humano tarda en madurar.
——————-
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo El cerebro humano tarda en madurar se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Sistemas nerviosos: el cerebro de vertebrados
- Daños estructurales por consumo de alcohol en el cerebro humano
- ¿Cuántas células hay en el cuerpo humano?
¿Hemos intentando contactar con extraterrestres?
¿Hemos intentando contactar con extraterrestres? Y si es así, ¿cómo y cuándo se ha hecho? ¿Quién lo ha hecho? Y sobre todo, ¿qué se les ha dicho en los mensajes que se han enviado? Todas las respuestas en minuto y medio.
Los vídeos de ¿Preguntas frecuentes? presentan de forma breve y amena cuestiones que, probablemente, nos hayamos planteado en alguna ocasión. Los vídeos, realizados para la Cátedra de Cultura Científica de la UPV/EHU, se estrenarán en el programa de ciencia Órbita Laika (@orbitalaika_tve), a partir del próximo 18 de marzo todos los lunes a las 22:00 en la 2 de RTVE.
Edición realizada por César Tomé López
El artículo ¿Hemos intentando contactar con extraterrestres? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Ciencia express: los transgénicos
- Ciencia express: el carbono-14 y los rayos cósmicos
- Ciencia express: Cómo se formó la luna
Los biólogos de la UPV/EHU y la conservación de la naturaleza
La Facultad de Ciencias de Bilbao comenzó su andadura en el curso 1968/69. 50 años después la Facultad de Ciencia y Tecnología de la UPV/EHU celebra dicho acontecimiento dando a conocer el impacto que la Facultad ha tenido en nuestra sociedad. Publicamos en el Cuaderno de Cultura Científica y en Zientzia Kaiera una serie de artículos que narran algunas de las contribuciones más significativas realizadas a lo largo de estas cinco décadas.

 Toma de muestras de bivalvos en los manglares nicaragüenses. Foto: Ionan Marigomez / UPV/EHU
Toma de muestras de bivalvos en los manglares nicaragüenses. Foto: Ionan Marigomez / UPV/EHUA menudo se critica a la universidad por falta de conexión con la sociedad. Se afirma que la universidad enseña conocimientos arcanos y que la investigación apenas tiene implicaciones prácticas. Este punto de vista es compartido por bastantes universitarios, por lo que algo habrá detrás del mismo. Sin embargo, un poco de perspectiva histórica muestra que hay numerosas interacciones entre la universidad y la sociedad. A título de ejemplo, vamos a analizar cuál ha sido el impacto de la Sección de Biología en la conservación de la naturaleza.
La Sección de Biología comenzó su andadura muy modestamente en la por entonces denominada Facultad de Ciencias de la Universidad de Bilbao. Esta Sección carecía de catedráticos hasta 1975 y, de los tres profesores agregados de aquel momento, ninguno pertenecía a alguna de las áreas de la biología más naturalistas, es decir, la botánica, la zoología o la ecología. Tampoco llegaban fondos para apoyar proyectos de investigación en estos ámbitos. El bum llegó en la segunda mitad de los años 80, cuando se multiplicó el número de profesores, se potenció la formación de doctores y los grupos de investigación comenzaron a recibir financiación pública para el desarrollo de sus proyectos. Los años 90 vieron la aparición de cursos de postgrado tipo máster, como por ejemplo el de “Evaluación y Recuperación Ambiental”, y el afianzamiento de colaboraciones externas de los equipos de investigación. El siglo XXI ha supuesto la puesta de largo de la investigación en muchos de esos grupos, que participan en proyectos multinacionales de indudable repercusión sobre la conservación y el manejo de los recursos naturales, llegando a alcanzar niveles de excelencia y prestigio internacionales.
En estos años, la Facultad de Ciencia y Tecnología ha formado un gran número de personas en Biología, Ciencias Ambientales y otras disciplinas ligadas con la conservación de la naturaleza. Según las estadísticas oficiales, los egresados de la la FCT incluyen más de 3850 licenciados y más de 450 graduados en Biología, a lo que se suman centenares de estudiantes de master y 475 doctores. De ellos, muchos trabajan en ámbitos relacionados con la conservación de la naturaleza. Algunos lo hacen para la administración como técnicos de medio ambiente municipales, en consorcios y mancomunidades, en las diputaciones forales, departamentos del Gobierno Vasco, parques naturales, etc. Otros muchos trabajan en empresas relacionadas con la conservación de la naturaleza, como consultoras (por ejemplo, Anbiotek o Ekolur) o en centros de I+D+I como Neiker o Azti. Otros muchos se han dedicado a la enseñanza, tanto la reglada en institutos, ikastolas, colegios y universidades, como no reglada en aulas de naturaleza, CEIDAs, etc. Finalmente, muchos egresados colaboran en asociaciones y otras entidades en pro de la conservación de la naturaleza, como grupos ecologistas, asociaciones conservacionistas o entidades de estudio e interpretación del medio ambiente como la Sociedad de Ciencias Aranzadi. Aunque es imposible de cuantificar, podemos afirmar que esta masa de gente con una formación en biología y actitudes conservacionistas ha tenido mucho que ver con la transformación que se ha registrado en la forma de entender la relación de la especie humana con el medio ambiente en el País Vasco.
 Miembros de la FCT discutiendo un proyecto de restauración en el Parque Natural de Aiako Harria con técnicos de la Diputación Foral de Gipuzkoa, de Aguas del Añarbe de URA y de la Confederación Hidrográfica del Cantábrico. Fuente: Arturo Elosegi.
Miembros de la FCT discutiendo un proyecto de restauración en el Parque Natural de Aiako Harria con técnicos de la Diputación Foral de Gipuzkoa, de Aguas del Añarbe de URA y de la Confederación Hidrográfica del Cantábrico. Fuente: Arturo Elosegi.Por otro lado, algunos equipos de la FCT han sido muy activos en el inventariado y seguimiento de la biodiversidad de nuestro entorno. Por citar sólo algunos de ellos, el laboratorio de zoología abrió varias líneas de investigación sobre fauna fluvial y marina, sobre artrópodos del suelo o sobre moluscos terrestres. A esas líneas posteriormente se han incorporado otros grupos como el de murciélagos. Por su parte, el laboratorio de botánica abrió líneas de investigación sobre algas, musgos, plantas superiores y hongos, así como otra sobre geobotánica, que caracterizó y cartografió las principales comunidades vegetales de nuestro entorno. La información acumulada durante décadas ha sido esencial para caracterizar los lugares más biodiversos del País Vasco, para identificar sus principales factores de riesgo y, entre otras, para diseñar y optimizar la red Natura 2000.
Además de los inventarios de biodiversidad, algunos grupos han trabajado activamente en evaluar el estado de salud del medio ambiente, colaborando en poner las bases del sistema de información medioambiental del País Vasco. Por ejemplo, en los años 80, los entonces laboratorios de zoología y ecología se embarcaron en el primer gran estudio hidrobiológico de los ríos de Bizkaia, así como en la evaluación del estado medioambiental de la ría de Bilbao. El primer trabajo fue la semilla de la que derivó la red de seguimiento de los ríos del País Vasco, actualmente en manos de URA, la Agencia Vasca del Agua, mientras que el segundo comenzó una serie de estudios sobre la salud de nuestra costa. También hay que citar en este apartado al laboratorio de microbiología, que durante muchos años ha colaborado en la determinación de la calidad de las aguas de baño de la Comunidad Autónoma.
Otros grupos han centrado sus estudios en la detección y evaluación de los impactos que causa la actividad humana en la estructura y el funcionamiento de los ecosistemas. El grupo de ecología fluvial ha estudiado el impacto de las prácticas forestales, de la contaminación agrícola y urbana, de las detracciones de agua o del cambio climático en ríos vascos y de otras regiones. Lo que comenzó siendo el laboratorio de citología, por su parte, ha ido convirtiéndose en un grupo de investigación sobre ecotoxicología, que es hoy la base de la Estación Marina de Plentzia, mientras que el grupo de ecotoxicología animal y biodiversidad utiliza especies como centinelas del estado de salud de las aguas continentales. Otras líneas aplicadas han sido el estudio de suelos contaminados, que se ha abordado desde los laboratorios de zoología y fisiología vegetal, o los trabajos más agronómicos realizados en este último. Toda la información obtenida por estos grupos es utilizada por la Diputaciones Forales, por el Gobierno Vasco y por otras entidades en la planificación y gestión del territorio.
 Miembros de la FCT revisando trabajos de restauración ecológica en el río Araxes (Gipuzkoa), junto con técnicos de la Diputación Foral de Gipuzkoa, de las empresas Ekolur y Basoinsa, y un científico del IGB de Berlín. Fuente: Arturo Elosegi.
Miembros de la FCT revisando trabajos de restauración ecológica en el río Araxes (Gipuzkoa), junto con técnicos de la Diputación Foral de Gipuzkoa, de las empresas Ekolur y Basoinsa, y un científico del IGB de Berlín. Fuente: Arturo Elosegi.Más allá de la obtención de información, algunos grupos de la Sección han colaborado estrechamente con la administración en trabajos de gestión de poblaciones, comunidades o ecosistemas. Por ejemplo, el grupo de ecología y evolución del comportamiento ha trabajado en la gestión de mamíferos amenazados, como el visón, el desmán ibérico o los murciélagos, el de ecología y gestión del pastoreo en la gestión de la ganadería en pastos de montaña, el grupo de ecofisiología vegetal en la, entre otras, recuperación de suelos degradados o contaminados, y el de ecología fluvial en proyectos de restauración de ríos. Estos trabajos no se han limitado a evaluar el efecto de prácticas de conservación realizadas por la administración, sino que han implicado a la universidad en el diseño, ejecución y seguimiento de estas prácticas, muchas de las cuales han sido pioneras a nivel estatal.
Finalmente, no podemos olvidar el papel de asesoría realizado por muchos miembros de la Sección, en su participación en los patronatos de parques naturales o de la Reserva de la Biosfera de Urdaibai, o en Naturzaintza, el consejo asesor de conservación de la naturaleza del Gobierno Vasco. Además de estas colaboraciones, es habitual que miembros de la Sección participen en reuniones para definir estrategias y planes de la administración, como la Estrategia Española de Restauración de Ríos o la Estrategia Vasca de Biodiversidad.
La Sección de Biología continúa aportando conocimiento sobre los ecosistemas de nuestro entorno, lo cual facilita la gestión de nuestros recursos naturales. Si bien hasta hace bien poco esta aportación de conocimiento residía básicamente en las áreas más naturalistas referidas arriba, hoy en día las herramientas de la biología molecular son esenciales en el estudio de la biodiversidad, lo que aumenta el número de grupos que trabajan en este campo. Por todo ello, es de esperar que la Sección de Biología de la FCT siga teniendo un papel importante en la conservación de la naturaleza en el País Vasco y en el mundo en general.
Sobre los autores: Arturo Elosegi es profesor de ecología en el Departamento de Biología Vegetal y Ecología de la Facultad de Ciencia Tecnología de la UPV/EHU. Jesús Pozo se retiró recientemente del mismo departamento.
El artículo Los biólogos de la UPV/EHU y la conservación de la naturaleza se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Una fórmula para dominarlos a todos: La conservación de la energía y la ley de la palanca
- De las leyes de conservación (I)
- Naturaleza, ciencia y cultura en el bicentenario de Henry David Thoreau
Aprendiendo de las máquinas
 Imagen: Pixabay
Imagen: PixabayLa segunda mitad del siglo XX vio nacer la computación y el sueño de la inteligencia artificial —“la ciencia de conseguir que las máquinas hagan cosas que requerirían inteligencia si las hiciesen humanos”, en palabras de Marvin Minsky—, que hoy en día está despertando un renovado interés gracias a la rama del aprendizaje automático. Se trata de un conjunto de técnicas que se benefician de los avances tecnológicos en materia de computación de las últimas dos décadas, y se caracterizan por su capacidad de engullir enormes cantidades de datos para enfrentarse a problemas de gran complejidad. Las aplicaciones son vastas, y ya forman parte de nuestro día a día: se utilizan para detección de fraude, navegación en vehículos autónomos, sistemas de recomendación (de productos, música…), diagnóstico médico, optimización de procesos, juegos… y un largo etcétera.
En todos estos casos, decimos que la máquina aprende. Y sabemos perfectamente cómo aprende (la lógica matemática y computacional subyacente), pero ¿qué aprende exactamente? Esta pregunta, aparentemente sencilla, nos persigue en todas sus aplicaciones. Por ejemplo, ¿qué lleva a AlphaZero a considerar ventajosos los movimientos que hace y que epatan por igual a aficionados y expertos ajedrecistas? Lo cierto es que no lo sabemos. La importancia de la cuestión puede parecer relativa en decisiones no críticas como la recomendación de una película, pero resulta esencial, e incluso abre derivadas éticas, cuando hablamos de cosas como conceder o no conceder un crédito, o la reacción de un coche autónomo ante un accidente.
En realidad, el tipo de problema al que se enfrentan las técnicas de aprendizaje automático es el mismo al que se viene enfrentando la ciencia, estadística mediante, desde su nacimiento: la inferencia de patrones, de generalizaciones, a partir de datos observacionales con el objetivo de obtener predicciones. En otras palabras, dada una entrada X, ¿qué modelo o función “f” genera la salida Y=f(X)? La gran diferencia se encuentra en que tradicionalmente nos hemos enfrentado a problemas para los cuales hay una teoría matemática previa que establece la estructura de “f”. La estadística clásica es la ciencia que estudia los diferentes tipos de modelos “f” y genera las técnicas para obtener y evaluar el mejor ajuste a partir de las observaciones (x, y). Por otro lado, las técnicas de aprendizaje automático de la nueva ciencia de datos son capaces de aprender la función “f” a partir de los datos sin ningún modelo previo, sin ningún conocimiento a priori del problema. La función “f” inferida se encuentra de alguna forma codificada tras el proceso de aprendizaje, pero nos es completamente desconocida y no hay forma de extraerla: es por eso que suelen llamarse “algoritmos de caja negra”.
Así pues, la estadística clásica define modelos matemáticos en los que las relaciones entre variables son explícitas y, por tanto, son directamente interpretables. Pensemos en una simple relación lineal: cuando crece X, crece Y; por tanto, obtenemos un valor grande de Y porque X es grande. En cambio, estos algoritmos de caja negra son capaces de capturar relaciones arbitrariamente complejas y predecir con gran precisión, pero su desventaja a día de hoy es que nos las ocultan, matemáticamente hablando: no somos capaces de interpretar qué propiedades de X influyen en Y.
Por tanto, uno de los grandes retos que la inteligencia artificial tiene por delante es el de intentar obtener conocimiento a partir de la estructura que las máquinas son capaces de extraer de grandes volúmenes de datos. Quizás se logre mediante una formalización matemática de las técnicas actuales, o quizás se desarrolle una nueva estadística ahora desconocida. Sea como sea, aprender de las máquinas puede ser uno de los principales hitos del presente siglo.
Sobre el autor: Iñaki Úcar es doctor en telemática por la Universidad Carlos III de Madrid e investigador postdoctoral del UC3M-Santander Big Data Institute
El artículo Aprendiendo de las máquinas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Máquinas inteligentes (y III): Deep blue, HAL 9000 y más allá
- Seminario Famelab: aprendiendo a hacer monólogos
- Máquinas inteligentes (II): Inteligencia artificial y robótica
Paradojas: contando peces, pesando patatas y… detectando agujeros
Tengo un acuario en casa. Contiene doscientos peces, de los cuales el 99% son rojos. Quiero conseguir que sólo el 98% de los peces de mi pecera sean colorados, eliminando sólo algunos de este color, pero sin tener que comprar más de otras tonalidades. ¿Cuántos peces rojos debo sacar del acuario?
 Imagen: Pixabay
Imagen: PixabaySeguro que son pocos los que debo extraer de mi pecera. Veamos: los peces rojos representan el 99%. Por lo tanto, el 1% no son colorados, es decir, solo hay dos peces que no son rojos en el acuario. Necesito extraer algunos peces rojos para conseguir que estos dos peces lleguen a ser el 2% de los peces del acuario. Así, si dos peces no colorados deben ser el 2% del total, una sencilla regla de tres dice que deben quedar en el acuario ¡solo 98 peces rojos! Es decir, deben sacarse 100 peces rojos para que el porcentaje de peces colorados pase del 99%al 98%. Sorprendente, ¿no?
¿Y qué hago ahora con los cien peces que me sobran? Decido cambiarlos a un colega por cien kilos de patatas. Es justo, ¿no? Un pez por un kilo de patatas… Y se me plantea un nuevo problema.
Tengo 100 kilos de patatas. El 99% de su peso corresponde al agua que contienen. Quiero deshidratarlas para conseguir que contengan solo un 98% de agua. Tras hacerlo, ¿cuánto pesan las patatas? ¡Si sólo pesan 50 kilos! ¿Por qué?
 Imagen: Wikimedia Commons.
Imagen: Wikimedia Commons.Veamos: si de esos 100 kilos, 99 kilos son de agua, 1 kilo corresponde a sólido seco. Vaya, parece que estoy teniendo un “déjà vu”… esto me recuerda mucho al caso de los peces rojos. Pero centrémonos, volvamos a los tubérculos. Si tras deshidratar las patatas la parte sólida pasa a ser del 2% del total –que sigue pesando 1 kilo, porque no se ve afectada por la deshidratación– de nuevo puedo hacer una sencilla regla de tres que me dice que debe de haber solo 49 kilos de agua. Así que, efectivamente, las patatas pasan a pesar 50 kilos. Bueno, así me costará menos transportarlas.
Creo que compraré algo de queso para elaborar alguna receta y acompañar a parte de esas patatas. Me gusta el Emmental porque tiene agujeros, y –como todo el mundo sabe– a las personas que nos dedicamos a la topología nos encanta contar agujeros. Para eso se inventó la teoría de homología, ¿no? Para eso, para contar agujeros de diferentes dimensiones y así distinguir espacios no homeomorfos.
Y me ha dado por pensar en los agujeros del queso, que parece que proceden de la fermentación producida por partículas microscópicas de heno presentes en la leche. A ver:
Cuanto más queso Emmental compre, más agujeros habrá. Pero, cuantos más agujeros haya, tendré menos queso. Es decir, cuanto más queso compre… ¡tendré menos queso!
 Imagen: Wikimedia Commons.
Imagen: Wikimedia Commons.¡No me lo puedo creer! Y todo esto por culpa de cien peces rojos…
Referencias
-
Marta Macho Stadler, La paradoja de los peces colorados, ZTFNews, 4 octubre 2013
-
Weisstein, Eric W., Potato Paradox, MathWorld
-
Paradoxe du fromage à trous, Wikipédia (consultado el 10 de marzo de 2019)
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo Paradojas: contando peces, pesando patatas y… detectando agujeros se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Patatas ‘perfectas’ con el método ‘Edge Hotel School’
- La topología modifica la trayectoria de los peces
- Los peces en el río

