Historia de la bombilla
Las bombillas incandescentes nos alumbraron en el siglo XX. Sin duda, la bombilla ha sido uno de los avances más importantes de la historia y junto a ella, probablemente, nos vendrá a la mente el nombre de Thomas Edison. Sin embargo, la invención de la lámpara incandescente tiene una extensa lista de aportaciones. Los historiadores Robert Friedel y Paul Israel han llegado a contabilizar hasta 22 inventores de lámparas incandescentes. Lo que sí señalan ambos es que la versión de Edison fue capaz de superar a las demás debido a las mejoras realizadas lo que convirtieron su bombilla es más eficaz, resistente y económicamente viable.
Edison, cuyo mérito no discute nadie, fue lo que hoy llamamos un emprendedor, lo que de toda la vida ha sido un empresario. Eso no le desmerece en absoluto, pero sí es necesario tenerlo en cuenta para entender su forma de actuar, siempre con ánimo de lucro y en términos de competencia en un mercado limitado. Edison creaba, mejoraba lo que hacían otros y sobre todo, ponía en el mercado magistralmente productos revolucionarios. Todo lo anterior es para mencionar que la primera bombilla de filamento de carbono la creó el físico, químico e inventor Joseph Swan en febrero de 1879, quien también fue el primero en suministrarlas para un uso comercial, en concreto para iluminar el Hotel Savoy de Londres en 1881.
Los vídeos de Historias de la Ciencia presentan de forma breve y amena pasajes de la nuestra historia científica y tecnológica. Los vídeos, realizados para la Cátedra de Cultura Científica de la UPV/EHU, se estrenan en el programa de ciencia Órbita Laika (@orbitalaika_tve), los lunes a las 22:00 en la 2 de RTVE.
El artículo Historia de la bombilla se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La bombilla de colores (y el método científico)
- Historia del cura rompecristales
- Historia de Nicolas Bourbaki
El descubrimiento de la desintegración artificial
 Foto: Naufal Ardi Santoso / Unsplash
Foto: Naufal Ardi Santoso / UnsplashLa serendipia que condujo a una mejor comprensión de la composición nuclear ocurrió en 1919. Ese año Rutherford se dio cuenta de que, cuando bombardeaba gas nitrógeno con partículas alfa procedentes de bismuto-214, se producían partículas rápidas que podían viajar más lejos en el gas que las propias partículas alfa. Cuando estas partículas golpeaban una pantalla de centelleo producían destellos de luz más débiles que los producidos por las partículas alfa. Unos cálculos rápidos indicaban que esa intensidad era aproximadamente la intensidad que se esperaría que produjesen los iones positivos de hidrógeno [1].
Las mediciones del efecto que un campo magnético tenía en las trayectorias de estas partículas apuntaban a que, en efecto, eran protones. Con el escepticismo que caracteriza a toda buena investigación científica, Rutherford descartó, mediante cuidadosos experimentos, la posibilidad de que los protones procedieran del hidrógeno presente como impureza en el nitrógeno.
Dado que los átomos de nitrógeno del gas eran la única fuente posible de protones, Rutherford llegó a la conclusión de que una partícula alfa, al chocar con un núcleo de nitrógeno, ocasionalmente puede expulsar una partícula más pequeña (un protón) del núcleo de nitrógeno. En otras palabras, Rutherford dedujo que una partícula puede provocar la desintegración artificial de un núcleo de nitrógeno, siendo el protón uno de los productos de esta desintegración. Pero este proceso no ocurre fácilmente. Los resultados experimentales mostraban que solo se producía un protón por aproximadamente cada millón de partículas alfa que atraviesan el gas.
Entre 1921 y 1924 Rutherford y su colega James Chadwick ampliaron el trabajo sobre el nitrógeno a otros elementos y encontraron pruebas de que era posible producir la desintegración artificial de todos los elementos ligeros, desde el boro al potasio, con la excepción del carbono y el oxígeno [2].
El siguiente paso era determinar la naturaleza del proceso nuclear que conduce a la emisión del protón. Se sugirieron dos hipótesis para este proceso:
(a) El núcleo del átomo bombardeado pierde un protón, que se “desprende” como resultado de una colisión con una partícula alfa especialmente rápida.
(b) La partícula alfa es “capturada” por el núcleo del átomo al que ha golpeado, formando un nuevo núcleo que, inmediatamente después, emite un protón.
¿Cómo distinguir experimentalmente entre ambas hipótesis? Un nuevo instrumento marcaría toda la investigación nuclear desde entonces hasta nuestros días: la cámara de niebla.
Notas:
[1] El nombre protón para el ion positivo del hidrógeno se adoptaría al año siguiente, en 1920, a sugerencia del propio Rutherford.
[2] Años más tarde y con mejor tecnología se demostró que estos elementos también se podían desintegrar artificialmente.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo El descubrimiento de la desintegración artificial se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Las series de desintegración radiactiva
- El problema de la estructura nuclear
- La transformación radiactiva
Ríos atmosféricos, las autopistas aéreas que regulan el clima
Jorge Eiras Barca y Iago Algarra Cajide
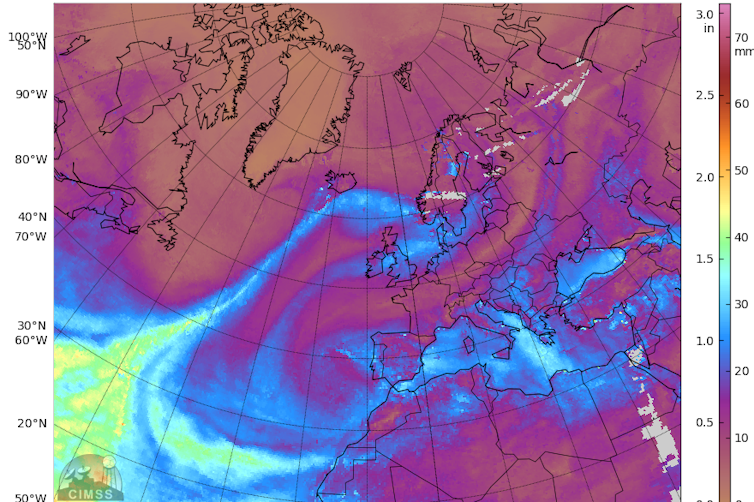 Imagen de satélite donde se observa un río atmosférico que atraviesa el Atlántico en dirección a Islandia.
Imagen de satélite donde se observa un río atmosférico que atraviesa el Atlántico en dirección a Islandia.Fuente: MIMIC-TPW v2
Si existe un campo de estudio dentro de la dinámica atmosférica cuya notoriedad haya experimentado un crecimiento exponencial en las últimas décadas es, sin duda, el de los ríos atmosféricos (AR, por sus siglas en inglés).
El motivo quizás sea que los ríos atmosféricos juegan un papel destacado en un gran número de factores del clima, como el balance radiativo (energético) del planeta o su ciclo hidrológico. O quizás sea su creciente tendencia a ser nombrado en los boletines meteorológicos cuando, en compañía de una tormenta tropical o una ciclogénesis explosiva, traen en ocasiones más de 70 l/m² de precipitación en unas pocas horas.
¿Qué son los ríos atmosféricos?
Los ríos atmosféricos son regiones de la atmósfera cuyo contenido de humedad es muy superior al de las regiones colindantes. Suelen ser regiones muy alargadas y (relativamente) estrechas –miles de km de largo frente a unos cientos de km de ancho– y acompañan normalmente a los frentes fríos tan característicos de las latitudes medias.
Su naturaleza les permite funcionar como grandes autopistas que distribuyen la humedad –y con ello, energía en forma de calor latente– desde las húmedas y cálidas regiones subtropicales y tropicales hacia el resto del planeta.
Estas formaciones son, por tanto, esenciales para el mantenimiento de la buena salud de nuestro ciclo hidrológico, y un mecanismo indispensable del balance radiativo del planeta. Su forma alargada y la enorme cantidad de agua que transportan (superior al caudal del río Mississippi) han inspirado el característico y atrayente nombre de “ríos atmosféricos”.
Su papel en las precipitaciones
Los ríos atmosféricos presentan una enorme variabiliad entre ellos. No hay dos iguales. La mayor parte son eventos de intensidad moderada, y son por tanto considerados como beneficiosos. Entre otras cosas, aportan una cantidad indispensable de humedad a la atmósfera de latitudes medias y continentales, que no podría recibirse de otra manera.
Otros ríos atmosféricos, sin embargo, son fenómenos extremos que pueden llevar asociadas precipitaciones superiores a los 100 l/m² en un solo día, teniendo un impacto económico y social negativo en las regiones que se ven afectadas por ellos.
A nivel global, se trata de fenómenos comunes. Suelen existir unos tres o cuatro simultáneamente por cada hemisferio, situados habitualmente sobre los grandes corredores oceánicos. Su temporada alta es el invierno correspondiente a cada hemisferio, cuando la atmósfera es menos húmeda, pero mucho más dinámica que la de la temporada estival.
Las costas occidentales de los grandes continentes, incluida la costa atlántica ibérica, son las regiones calientes de llegada de ríos atmosféricos. Los que llegan a España transportan un elevado porcentaje de lluvia desde el golfo de México. En invierno la península ibérica acostumbra a recibir 3 o 4 al mes.
Otra región activa del mundo hispanoparlante es la costa de Chile, donde los ríos atmosféricos del Pacífico suelen generar importantes precipitaciones en su interacción con la cordillera de los Andes.
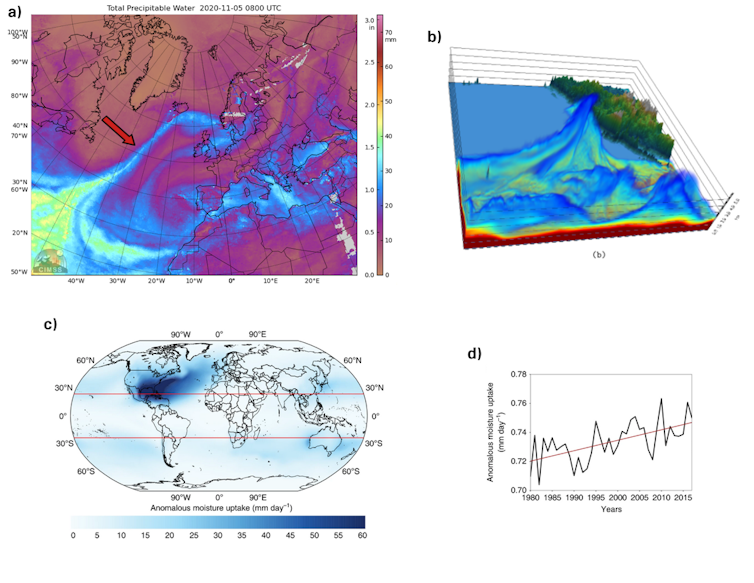 a) Composición satelital (05 de noviembre de 2020) de agua precipitable en mm donde se observa un AR atravesando el océano Atlántico hasta llegar a las costas de Islandia. b) Vista tridimensional de un AR simulado con el modelo meteorológico WRF. c) y d) Regiones anómalas de humedad asociada a AR y su progresión creciente en el período 1979-2016.
a) Composición satelital (05 de noviembre de 2020) de agua precipitable en mm donde se observa un AR atravesando el océano Atlántico hasta llegar a las costas de Islandia. b) Vista tridimensional de un AR simulado con el modelo meteorológico WRF. c) y d) Regiones anómalas de humedad asociada a AR y su progresión creciente en el período 1979-2016.Fuentes: CIMSS / Eiras-Barca et al. (2016) / Algarra et al., (2020)
¿Cómo serán los ríos atmosféricos del mañana?
La respuesta a la pregunta de como serán los ríos atmosféricos del mañana depende, como es lógico, de cómo sea la atmósfera en la que residan.
La mayor parte de los análisis prospectivos predicen una atmósfera más cálida, y con una dinámica diferente. En este contexto, se considera que los ríos atmosféricos irán tendiendo a ser más frecuentes, y también más intensos, aunque con grandes diferencias entre las diferentes regiones del planeta.
En un reciente estudio liderado por los profesores Luis Gimeno y Raquel Nieto de la Universidad de Vigo, y realizado en colaboración con la Universidad de Lisboa y la Universidad de Illinois, hemos analizado la variación el contenido de humedad durante las últimas décadas en las regiones estratégicas para el fenómeno. Esto nos sirve para realizar una proyección robusta y determinar como serán el día de mañana en un contexto de calentamiento global.
En el artículo, publicado en Nature Communications, se muestra que el contenido de humedad se ha incrementado –y por tanto, con mucha probabilidad, se incrementará– aproximadamente en un 7 % por cada grado centígrado de humedad que se calienta la parte inferior de la atmósfera.
Esta es una proporción bien conocida para los estudiosos de la termodinámica, pues es predicha por la ecuación de Clausius-Clapeyron, que determina la cantidad máxima de humedad que puede contener una celda de aire antes de llegar a la saturación.
Además, hemos demostrado que, de todas las regiones del planeta, la señal más clara a este respecto se observa precisamente en la región donde se origina la mayor parte de la humedad que llega a Europa en forma de ríos atmosféricos: el golfo de México.
Una atmósfera más cálida será una atmósfera más húmeda, y tenemos ahora motivos de peso para asumir que ese incremento de humedad se trasladará en una proporción similar a los ríos atmosféricos.
La cantidad de humedad que recibiremos en el futuro desde las regiones subtropicales será mayor, y también la probabilidad de precipitaciones extremas, poco convenientes para el correcto aprovechamiento del agua como recurso, y peligrosas.
El esfuerzo de la comunidad científica para procurar entender, predecir y adelantarse al clima del futuro es grande, y no sin motivo, pues del clima dependen una buena parte de los recursos que nos proporciona el planeta.
Entre ese complejo collage de fenómenos que constituirán el clima del mañana, parecen jugar un papel destacado los ríos atmosféricos a los que podemos atribuir, sin miedo a equivocarnos, una buena parte del agua que llega a nuestras casas, cultivos, embalses y ríos.
Sobre los autores: Jorge Eiras Barca y Iago Algarra Cajide son investigadores postdoctorales en física de la atmósfera en la Universidade de Vigo
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Ríos atmosféricos, las autopistas aéreas que regulan el clima se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Breve historia de las ciencias del clima
- La contribución global de los ríos intermitentes al ciclo del carbono
- Planeta océano: el corazón líquido que nos mantiene vivos
Lo que funciona, y lo que no, contra la Covid-19
 Foto: Camila Pérez / Unsplash
Foto: Camila Pérez / UnsplashEstá en marcha un experimento a escala planetaria. Nunca antes tantos países habían sido, a la vez, sujetos y objetos de experimentación de forma simultánea. La primera gran pandemia del siglo XXI ha obligado a adoptar una batería de medidas no farmacológicas para limitar los expansión del virus SARS-Cov2 y reducir así las hospitalizaciones y muertes debidas a la Covid-19. En el experimento cada país o cada región está aplicando un conjunto de medidas, las que considera más efectivas. Y un equipo de investigación, combinando cuatro metodologías diferentes, ha estimado el grado de efectividad de cada medida en virtud de su capacidad para reducir la multiplicación del virus.
Las que de forma más eficaz contribuyen a reducir la expansión del SARS-Cov2 son las que evitan que las personas se junten y las que limitan sus movimientos. A esos propósitos obedecen la suspensión de reuniones de no demasiada gente (menos de 50 personas) durante mucho tiempo (en tiendas, restaurantes, bares, centros de trabajo), el cierre de centros docentes (principalmente de estudiantes de entre 10 y 19 años), los toques de queda, las limitaciones a viajar entre países, los confinamientos, y la suspensión de actos multitudinarios.
Algunas de esas medidas tienen efectos muy negativos sobre la salud. El cierre de centros escolares acarrea, potencialmente, una peor alimentación, estrés y aislamiento social de los afectados. El confinamiento domiciliario provoca una mayor violencia familiar contra las mujeres y los menores de edad. Además, reduce el acceso a la atención sanitaria, lo que eleva, incluso, la mortalidad. Por si eso era poco, no está clara la efectividad real de esa medida, porque suele implantarse a la vez que se adoptan otras muy efectivas. Por esa razón, los autores de la investigación no la consideran recomendable salvo, quizás, si se implanta en fases muy tempranas de la expansión de la pandemia.
Dados los efectos adversos -también sobre los derechos y libertades- de las medidas anteriores, los gobiernos han considerado y aplicado opciones alternativas. Y resulta que, curiosamente, medidas no intrusivas han mostrado gran efectividad, mayor incluso que la de algunas restrictivas. Es el caso de la disponibilidad de mascarillas para todos; las campañas para informar a la ciudadanía, específicas de cada tipología de destinatario; o las ayudas económicas a personas con pocos recursos o en situación vulnerable para que no sufran económicamente en caso de no poder acudir al trabajo o mantener su actividad económica. También resulta sorprendente que la implantación, con carácter obligatorio, de ciertas medidas apenas resulte más efectiva que las campañas de comunicación que promueven la adopción de esas mismas medidas de forma voluntaria.
Por el contrario, actuaciones a las que se ha dado mucha importancia no cuentan con suficiente respaldo. Por ejemplo, no parece estar justificada la limpieza y desinfección sistemática de superficies; las limitaciones al transporte público, pues los vehículos no parecen ser enclaves que propicien la expansión del virus; o el cierre de parques o museos. El estudio no ha podido contrastar la efectividad de las campañas de detección de personas contagiadas, y trazado y aislamiento de sus contactos, seguramente porque la mayor parte de los datos se obtuvieron en marzo y abril, cuando la mayoría de los países experimentaron la mayor incidencia de la epidemia y carecían aún de buenos sistemas de trazado.
El experimento planetario ha puesto de manifiesto que lo que creemos saber hoy quizás no sea válido mañana, porque el conocimiento es contingente y siempre provisional. La ciencia se corrige a sí misma. Esa es la razón por la que avanzamos y tomamos cada vez mejor decisiones.
Fuente: Haug, N., Geyrhofer, L., Londei, A. et al. (2020) Ranking the effectiveness of worldwide COVID-19 government interventions. Nat Hum Behav doi: 10.1038/s41562-020-01009-0
Nota: Para quien interese, Elhuyar ha publicado una reseña de este mismo trabajo en lengua vasca.
Adenda (sobre la importancia de la ventilación de locales): Los resultados y conclusiones del estudio de Haung et al (2020) se basan, como se indica en el texto, en datos procedentes de los meses de marzo y abril. En esos meses existía el convencimiento de que las principales vías de contagio eran, por un lado, el contacto con superficies (de ahí la importancia que se daba a la limpieza de manos y a no tocarse la cara, por ejemplo); y por el otro, las gotículas que se expelen al toser o estornudar (por lo que se empezó a recomendar el mantenimiento de una distancia de 2 m entre personas y, más adelante, el uso de mascarillas e espacios cerrados o, en general, muy concurridos). Pero en aquellos meses no se recomendó la ventilación de los locales porque no había evidencias suficientes de que los aerosoles pudiesen ser una vía importante de contagio. Los primeros datos que avalaban esa posibilidad se empezaron a publicar en la prensa científica a finales de abril. A partir de mayo se empezó a recomendar la ventilación de lugares cerrados. En junio, ya había evidencias suficientes al respecto. Y a partir de julio ya eran muchos los investigadores que pensaban que el riesgo de transmisión aérea del coronavirus se estaba infravalorando. En definitiva, el trabajo reseñado aquí no considera la ventilación de los locales como una medida potencialmente eficaz por la sencilla razón de que en los meses de marzo y abril, por carecer de evidencias firmes en ese sentido, no se promovió. Durante la segunda ola, sin embargo, dadas las evidencias abrumadoras al respecto, se recomienda mantener los locales bien ventilados con carácter general.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Lo que funciona, y lo que no, contra la Covid-19 se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¿De qué se muere la gente en el mundo?
- Mascarilla y COVID-19: ¿dilema del prisionero o juego de coordinación?
- No habrá solución sin más conocimiento
Catástrofe Ultravioleta #31 SIBERIA
 Catástrofe Ultravioleta #31 SIBERIA
Catástrofe Ultravioleta #31 SIBERIA“Yo no debería seguir en este mundo”. Así empieza nuestra nueva aventura: al borde de la muerte.
Viajamos a Siberia para pasar frío y conocer un proyecto de etnografía que se ha desarrollado durante más de una década. Y lo hacemos de la mano del físico Miguel Ángel Julián, un enamorado de las regiones polares.
Agradecimientos: Miguel Ángel Julián y Agustín Amaro.
https://www.ivoox.com/t03e07-siberia_md_60527063_wp_1.mp3Puedes escucharnos en:
– Podium Podcast
– iVoox
– Spotify
– Apple Podcasts
** Catástrofe Ultravioleta es un proyecto realizado por Javier Peláez (@Irreductible) y Antonio Martínez Ron (@aberron) para PODIUM PODCAST con el patrocinio parcial de la Cátedra de Cultura Científica de la Universidad del País Vasco y la Fundación Euskampus. La edición, música y ambientación obra de Javi Álvarez y han sido compuestas expresamente para cada capítulo.
El artículo Catástrofe Ultravioleta #31 SIBERIA se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Catástrofe Ultravioleta #29 ALHAMBRA
- Catástrofe Ultravioleta #30 INMERSIÓN
- Catástrofe Ultravioleta #27 VOZ 2
Koskobilo, un mundo perdido en la Burunda
Asier Gómez Olivencia, Joseba Rios-Garaizar, Mikel Arlegi
El valle de la Burunda forma parte del corredor de la Sakana, un paso natural que conecta la llanada alavesa con Pamplona/Iruña y se encuentra delimitado por el final del macizo de Aizkorri y la Sierra de Aralar al norte, y por Urbasa-Andia al sur. De hecho, por esta vía natural transcurría la calzada romana que iba desde Asturica Augusta (Astorga) a Burdigala (Burdeos) pasando por Iruña-Veleia y Pompaelo (Pamplona-Iruña) entre otras poblaciones. En este entorno, la explotación de las calizas albienses de la colina de Koskobilo (Olazti, Navarra) durante el siglo XX puso al descubierto el yacimiento cuaternario más antiguo de Navarra.
 La Sakana (barranca en castellano) desde la sierra de Aralar. Foto: Theklan / Wikimedia Commons
La Sakana (barranca en castellano) desde la sierra de Aralar. Foto: Theklan / Wikimedia CommonsEn 1940 los trabajos de la cantera descubrieron una sima vertical en Koskobilo. Entre los sedimentos de esa sima, aparecieron diversos restos fósiles y el capataz de la cantera le hizo llegar un canino de gran tamaño a Máximo Ruiz de Gaona. Además de docente y micropaleontólogo, Máximo Ruiz de Gaona fue un naturalista polifacético, y contribuyó a los campos de la paleontología de vertebrados y de la arqueología. Este hallazgo le interesó mucho y como él mismo relata, además de recuperar fósiles de los sedimentos de dicha sima, ya casi completamente destruida, recuperó otros muchos en las dos escombreras situadas en las laderas de Koskobilo (Figura 1). Ruiz de Gaona envió estos fósiles a Federico Gómez Llueca, paleontólogo del Museo de Ciencias Naturales (Madrid) para su clasificación, proporcionando una lista de al menos 26 especies de vertebrados, entre los que se destacaban los primeros restos de castor descubiertos en la península ibérica, así como la presencia de restos de rinoceronte e hipopótamo.
 Figura 1. Arriba, aspecto de la cantera de Koskobilo en 1945-46 (pseudo-ortofoto, fuente: Gobierno de Navarra). En moteado gris la extensión de la cantera, en moteado blanco la posición de las escombreras (letras “a” y “b”). Abajo, vista de la cantera, posición hipotética de la cueva de la que procedían los sedimentos con industrias líticas (línea m-n) y posición de las escombreras (letras “a” y “b”) según foto de Ruiz de Gaona (1952). Figura publicada originalmente en Arlegi et al. (2018). Licencia Creative Commons BY-NC-ND.
Figura 1. Arriba, aspecto de la cantera de Koskobilo en 1945-46 (pseudo-ortofoto, fuente: Gobierno de Navarra). En moteado gris la extensión de la cantera, en moteado blanco la posición de las escombreras (letras “a” y “b”). Abajo, vista de la cantera, posición hipotética de la cueva de la que procedían los sedimentos con industrias líticas (línea m-n) y posición de las escombreras (letras “a” y “b”) según foto de Ruiz de Gaona (1952). Figura publicada originalmente en Arlegi et al. (2018). Licencia Creative Commons BY-NC-ND.Diez años más tarde, en abril de 1950, con la intención de recuperar más fósiles, Ruiz de Gaona volvió a visitar las escombreras de la cantera, pero su hallazgo principal fue un importante conjunto de industria lítica en sílex de más de 5.000 piezas. Su estudio indicaba la presencia de piezas de distintos momentos del Paleolítico, entre las que destacaban las industrias del Solutrense, y además sugería que el sílex procedía de afloramientos cercanos en la Sierra de Urbasa, a unos 5 km de Koskobilo. Este hallazgo interesó al prestigioso prehistoriador J.M. de Barandiarán, que en 1955 recuperó de las escombreras un pequeño conjunto de restos paleontológicos y 1.146 restos de industria lítica (Figura 2). Estos últimos restos fueron estudiados por María Amor Beguiristáin en 1974, quien indicó el aspecto paleolítico de este conjunto con varias culturas representadas. Durante los años 70, Ruiz de Gaona publicó también material inédito de Koskobilo de su colección particular y de indudable origen paleolítico, incluyendo cinco puntas foliáceas claramente solutrenses, así como tres bifaces cuya tipología indicaría una industria anterior al Paleolítico Superior. El interés de Ruiz de Gaona por entender el origen de estas piezas líticas hace que hable con el personal de la cantera, y en base a estos testimonios, intenta “reconstruir imaginativamente” el destruido yacimiento: una caverna de unos 40 m de longitud, aproximadamente horizontal y no muy ancha. En base a la fragmentación de los huesos, Ruiz de Gaona relaciona el yacimiento del que él extrajo personalmente restos en 1940 con la caverna, donde los humanos dejaron sus restos de industria lítica, que descubriría 10 años más tarde. Los humanos usarían la caverna, fracturarían los huesos de los animales para extraer la médula y los arrojarían por la sima, que estaría situada cerca de la boca de la cueva. A pesar de cierto debate historiográfico, la visión de este “yacimiento” se queda fijada por Barandiarán y Vallespí en 1984 quienes destacan la presencia de tres culturas: Musteriense de Tradición Achelense (MTA), Perigordiense (actualmente denominado Gravetiense) y Solutrense. Posteriormente en la década de los 90 Jesús García Gazólaz atribuye una serie de cuatro bifaces de Koskobilo al final del Achelense, en lo que actualmente se considera Paleolítico Medio Antiguo y situado cronológicamente a finales del Pleistoceno Medio (300-100 mil años antes del presente).
 Figura 2. Puntas recuperadas en Koskobilo por J.M. de Barandiarán en 1955. A la izquierda, preforma de pieza foliácea solutrense y a la derecha punta foliácea solutrense terminada (aunque posiblemente rota al final de la fabricación). Fotografía: Asier Gómez-Olivencia. Licencia Creative Commons 4.0.
Figura 2. Puntas recuperadas en Koskobilo por J.M. de Barandiarán en 1955. A la izquierda, preforma de pieza foliácea solutrense y a la derecha punta foliácea solutrense terminada (aunque posiblemente rota al final de la fabricación). Fotografía: Asier Gómez-Olivencia. Licencia Creative Commons 4.0.
Desde hace 15 años una de nuestras líneas de investigación está relacionada con el estudio de las ocupaciones humanas más antiguas de Pirineos Occidentales, así como sus condiciones paleoecológicas, excavando yacimientos como Arlanpe (Lemoa, Bizkaia) y revisando diversas colecciones paleontológicas como la de Punta Lucero (Zierbena, Bizkaia). Los estudios paleontológicos indican que los hipopótamos desaparecieron de Europa occidental después del último interglacial, hace unos 117 mil años. Por ello, la presencia de esta especie en Koskobilo resultaba especialmente interesante porque podría indicar que nos encontrábamos (al menos en parte) ante un yacimiento del Pleistoceno Medio. Por ello, con esta hipótesis de trabajo en mente, nos propusimos volver a estudiar las colecciones que se conservaban de este yacimiento, ya que éste había sido destruido por la cantera. Establecimos tres líneas de trabajo complementarias: la revisión de la colección paleontológica, la prospección del entorno del yacimiento y sus escombreras, y el estudio de la bibliografía existente hasta ese momento.
En 2016 realizamos varias prospecciones en la zona de la antigua cantera donde recuperamos nuevas evidencias de industria lítica, pero también algunos restos óseos. La revisión de las publicaciones sobre de la industria lítica y el estudio de los restos recuperados en estas últimas prospecciones indicaba que había varias cronologías representadas en la colección de Koskobilo depositada en el Museo de Navarra. Asimismo, el estudio preliminar de la colección paleontológica también indicaba la presencia de fauna del Pleistoceno Medio (la presencia de macaco y de oso tibetano, de los que hablaremos más adelante) y del Pleistoceno Superior (como el oso de las cavernas; Figura 3). Además de conocer las especies que estaban representadas por los restos fósiles, también nos interesaba el proceso por el cual esos restos se habían acumulado en los yacimientos: ¿eran tal y como propuso Ruiz de Gaona, el resultado de actividades humanas? El estudio de las superficies de los huesos indicaba que había dos grandes grupos. Por un lado, la pequeña colección paleontológica recuperada por Barandiarán en 1955 junto a los restos que habíamos recuperado nosotros en 2016 estaban formados en su mayor parte por fragmentos no identificables de diáfisis de huesos largos, y presentaban marcas de corte, y manipulación antrópica. En cambio, la colección paleontológica recuperada por Ruiz de Gaona en 1941estaba compuesta mayoritariamente por restos fósiles que se podían clasificar taxonómicamente, no presentaban (salvo una excepción) marcas de corte, y presentaban evidencias de haber sido alterados por actividad de carnívoros. Con las evidencias que disponíamos propusimos que en realidad en Koskobilo se habían recuperado restos arqueo-paleontológicos de al menos dos yacimientos distintos que podrían pertenecer (o no) al mismo sistema de galerías. Por un lado estaría la sima descubierta en 1940 de la que Ruiz de Gaona recuperó la mayor parte de la colección paleontológica, cuyos fósiles representarían distintos momentos del Pleistoceno Medio y Superior, y en cuya acumulación habían participado carnívoros. Por otro lado, la mayor parte de los restos líticos del Paleolítico Superior, que fueron arrojados a la escombrera en algún momento indeterminado entre 1940 y su descubrimiento en 1950, así como la mayor parte de los restos de fauna con marcas de corte seguramente corresponderían a un segundo yacimiento, que fue destruido completamente por los trabajos de la cantera y cuyos restos se recuperaron directamente de las escombreras.
 Figura 3. Vista labial (fila superior) y vista oclusal de segundos molares superiores junto con la reconstrucción (fila inferior) de oso negro asiático (izquierda) y oso de las cavernas (derecha). Ilustración: Amaia Torres Piñeiro (@amaiatorresart)
Figura 3. Vista labial (fila superior) y vista oclusal de segundos molares superiores junto con la reconstrucción (fila inferior) de oso negro asiático (izquierda) y oso de las cavernas (derecha). Ilustración: Amaia Torres Piñeiro (@amaiatorresart)
Nótese que el molar de oso de las cavernas, además de presentar un mayor tamaño, en consonancia con su mayor tamaño corporal, también tiene un patrón de cúspides más complicado. Los restos de oso negro asiático han sido atribuidos al Pleistoceno Medio mientras que los restos de oso de las cavernas han sido atribuidos al Pleistoceno Superior. Dibujos realizados por Amaia Torres Piñeiro.
 Figura 4. Vista oclusal del molar inferior de rinoceronte recubierto de espeleotema, datado mediante series de Uranio. Fotografía: Virginia Martínez-Pillado.
Figura 4. Vista oclusal del molar inferior de rinoceronte recubierto de espeleotema, datado mediante series de Uranio. Fotografía: Virginia Martínez-Pillado.Para el trabajo en detalle de los restos de fauna contamos con un nutrido grupo de investigadores: paleontólogos de distintas especialidades, geólogos y arqueólogos, con la intención de sacar la máxima cantidad de información a la colección. Los resultados merecieron la pena. Curiosamente, los supuestos restos de hipopótamo que habían despertado inicialmente nuestro interés por el yacimiento resultaron ser restos de un canino (colmillo) de jabalí de grandes dimensiones. Por otro lado, pudimos datar un espeleotema que cubría un diente de la especie de rinoceronte Stephanorhinus hemitoechus, que proporcionó una edad mínima de 220 mil años para este diente (Figura 4) y por extensión para parte de la colección paleontológica. Esta colección estaba compuesta por 38 taxones de mamíferos, desde rinocerontes hasta murciélagos (incluyendo 4 especies de oso), 6 taxones de aves, incluyendo una especie que ya no habita la península ibérica (el gallo lira, Lyrurus tetrix), y tres vértebras de peces (Figura 5). El estudio en detalle confirmaba nuestros resultados preliminares: la existencia entre los restos recuperados en 1940 de fósiles tanto del Pleistoceno Superior como del Pleistoceno Medio, aunque en muchos casos, debido a que ciertas especies presentaban amplias cronologías no era posible adscribir estos restos a ninguno de esos periodos. Entre los restos fósiles, destacaban los restos de dos de las especies de oso: el antepasado de los osos de las cavernas (el oso de Deninger Ursus cf. deningeri) y el oso negro asiático (u oso tibetano, Ursus thibetanus; Figura 3). También cabe destacar la presencia de restos de otras especies, de cuon (Cuon cf. priscus), de macaco de Berbería (Macaca sylvanus; Figura 6) y de ciervo gigante que atribuimos al género Megaceroides. Por los datos biocronógicos de los que disponemos, estas especies podrían haber sido contemporáneas con los restos del rinoceronte datados en el Pleistoceno Medio (en el MIS 7d o antes) proporcionando datos de unas cronologías muy poco representadas en el registro fósil de los Pirineos occidentales. La importancia del estudio de estas especies para el estudio de la evolución humana es su contemporaneidad con los últimos preneandertales, lo que nos ayuda a entender mejor el ecosistema en el que habitaron y explotaron estos homininos. Estos restos fósiles probablemente se acumularon en un momento interglacial, similar al actual, en que las faunas eran muy diversas, y donde los caballos, ciervos, bisontes, ciervos gigantes y rinocerontes eran cazados por leones, leopardos, cuones, lobos y hienas. Asimismo, a las orillas del Arakil, desbordadas por las presas de los castores, bajarían dos especies de oso a beber agua, y por las laderas calizas de Koskobilo se podrían ver grupos de macacos. Los yacimientos (o niveles) de estas cronologías son muy escasos en los Pirineos occidentales, entre los que podemos citar básicamente los niveles inferiores de Arlanpe (Dima, Bizkaia), los niveles inferiores de los yacimientos Lezetxiki I y Lezetxiki II (Arrasate, Gipuzkoa), y los restos de león y oso de Deninger de Santa Isabel de Ranero (Karrantza, Bizkaia).
 Figura 5. Selección de restos de fauna de Koskobilo. De izquierda a derecha y de arriba a abajo: distintas vistas de un canino de jabalí (Sus scrofa) inicialmente descrito como perteneciente a un hipopótamo de pequeño tamaño; vista oclusal de dos molares de rinoceronte de estepa (Stephanorhinus hemitoechus); distintas vistas de un tercer molar inferior de ciervo gigante atribuido al género Megaceroides; distintas vistas de un canino superior de leopardo (Panthera pardus); fragmento de muela carnicera superior de león de las cavernas (Panthera spelaea), fragmento de mandíbula de cuón (Cuon cf. alpinus europaeus); mandíbula izquierda de comadreja (Mustela nivalis).
Figura 5. Selección de restos de fauna de Koskobilo. De izquierda a derecha y de arriba a abajo: distintas vistas de un canino de jabalí (Sus scrofa) inicialmente descrito como perteneciente a un hipopótamo de pequeño tamaño; vista oclusal de dos molares de rinoceronte de estepa (Stephanorhinus hemitoechus); distintas vistas de un tercer molar inferior de ciervo gigante atribuido al género Megaceroides; distintas vistas de un canino superior de leopardo (Panthera pardus); fragmento de muela carnicera superior de león de las cavernas (Panthera spelaea), fragmento de mandíbula de cuón (Cuon cf. alpinus europaeus); mandíbula izquierda de comadreja (Mustela nivalis).
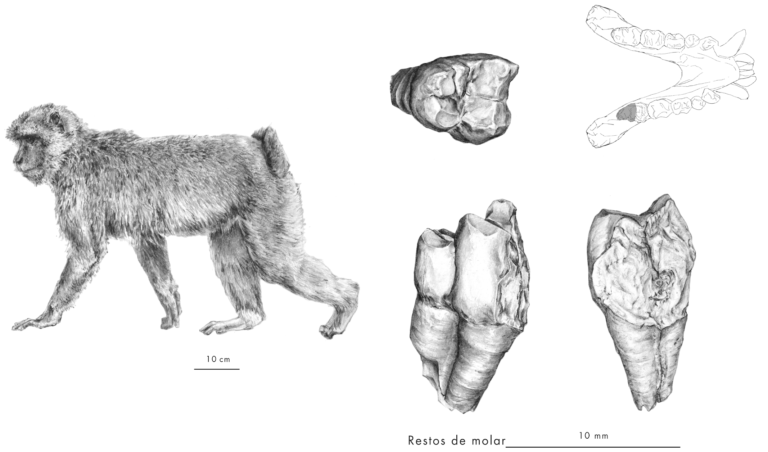 Figura 6. Reconstrucción (izquierda) y dibujo en distintas vistas del fragmento de tercer molar inferior derecho de macaco de Berbería (Macaca sylvanus) de Koskobilo. Ilustración: Amaia Torres Piñeiro (@amaiatorresart).
Figura 6. Reconstrucción (izquierda) y dibujo en distintas vistas del fragmento de tercer molar inferior derecho de macaco de Berbería (Macaca sylvanus) de Koskobilo. Ilustración: Amaia Torres Piñeiro (@amaiatorresart).
Hace 80 años Ruiz de Gaona salvó de su destrucción una importante colección paleontológica de lo que fue el yacimiento cuaternario más antiguo de Navarra, Koskobilo. Actualmente la cantera que destruyó los yacimientos está abandonada, pero nuevos trabajos arqueológicos en la zona promovidos por la Sociedad de Ciencias Aranzadi y dirigidos por Daniel Ruiz González aportarán más información sobre la Prehistoria en la Burunda.
Para saber más:
Arlegi, M., Rios-Garaizar, J., Rodríguez-Hidalgo, A., López-Horgue, M.A., Gómez-Olivencia, A. 2018. Koskobilo (Olazti, Nafarroa): nuevos hallazgos y revisión de las colecciones. Munibe Antropologia-Arkeologia 69, 21-41. doi: 10.21630/maa.2018.69.07
Arlegi, M., Rios-Garaizar, J., Rodríguez-Hidalgo, A., Gómez-Olivencia, A. 2018. Nuevos datos sobre la colección arqueo-paleontológica de Koskobilo. En: Badiola, A., Gómez-Olivencia, A., Pereda Suberbiola, X. (Editores). Registro fósil de los Pirineos occidentales. Bienes de interés paleontológico y geológico. Proyección social. Vitoria-Gasteiz, Servicio Central de Publicaciones del Gobierno Vasco-Eusko Jaurlaritzaren Argitalpen Zerbitzu Nagusia, pp. 209-212. ISBN: 978-84-457-3437-7
Astibia, H., Murelaga, X., Pereda-Suberbiola, X., 1996. Máximo Ruiz de Gaona como prehistoriador y paleontólogo de vertebrados. Príncipe de Viana. Suplemento de Ciencias XVI- Núm 14/15, 65-76.
Barandiarán, I., Vallespí, E., 1984. Prehistoria de Navarra, Trabajos de Arqueología Navarra. Gobierno de Navarra, Pamplona.
Gómez-Olivencia, A., Arlegi, M., Arceredillo, D., Delson, E., Sanchis, A., Núñez-Lahuerta, C., Fernández-García, M., Villalba de Alvarado, M., Galán, J., Pablos, A., Rodríguez-Hidalgo, A., López-Horgue, M.A., Rodríguez-Almagro, M., Martínez-Pillado, V., Rios-Garaizar, J., van der Made, J. The Koskobilo (Olazti, Navarre, Northern Iberian Peninsula) paleontological collection: new insights for the Middle and Late Pleistocene in Western Pyrenees. Quaternary International. doi: 10.1016/j.quaint.2020.06.005
Ruiz de Gaona, M., 1941. Un yacimiento de mamíferos pleistocénicos en Olazagutía (Navarra). Boletín de la Real Sociedad Española de Historia Natural 39, 155-160.
Príncipe de Viana. Suplemento de Ciencias Año 1996, Número 14-15. Dedicado a: Homenaje a Máximo Ruiz de Gaona: Naturalista y Paleontólogo (1902-1971)
Sobre los autores: Asier Gómez Olivencia (@AsierGOlivencia) es investigador Ramón y Cajal en el Departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU y miembro activo del Departamento de Prehistoria de la Sociedad de Ciencias Aranzadi. Joseba Rios-Garaizar (@jorios) es investigador y gestor de colecciones líticas en el Centro Nacional de Investigación sobre Evolución Humana (CENIEH). Mikel Arlegi (@ArlegiMikel) es investigador postdoctoral de la UPV/EHU y de la Université de Bordeaux.
El artículo Koskobilo, un mundo perdido en la Burunda se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Todo lo que se puede medir en un río
- Verdín, eucaliptos y cambio climático
- Los umbrales ecológicos en la bioacumulación de metales
Así enseñamos a los ordenadores a identificar especies de peces
José Luis Lisani Roca e Ignacio Catalán Alemany
 La inteligencia artificial permite identificar peces en imágenes de forma automática. Imagen: IMEDEA-UIB
La inteligencia artificial permite identificar peces en imágenes de forma automática. Imagen: IMEDEA-UIB
Para planificar estrategias de gestión sostenible de los recursos marinos, es necesario entender su funcionamiento. En el caso de las poblaciones de peces, necesitamos saber, entre otras variables, su localización, abundancia y fluctuaciones.
En la actualidad la adquisición de datos sobre estos recursos se lleva a cabo de diferentes formas. Una de ellas es el análisis de imágenes submarinas, que suele basarse en la identificación y el conteo manual de las especies en miles de imágenes por parte de personal especializado, lo que implica la inversión de una enorme cantidad de tiempo y esfuerzo.
La automatización del proceso de recogida de datos permitiría la extracción masiva de información con un considerable ahorro de recursos humanos, permitiendo a los investigadores dedicar más tiempo al análisis de los resultados. Además, el aumento del volumen de datos disponibles propiciaría un análisis más preciso y estadísticamente relevante. Esta automatización pasa por enseñar a los ordenadores a ver los peces en las imágenes.
Inteligencia artificial para reconocer objetos
Cuentan que Marvin Minsky (MIT), uno de los padres de la inteligencia artificial, propuso en 1966 a uno de sus alumnos un proyecto de verano consistente en conectar un ordenador a una cámara y conseguir que describiera lo que veía. Ese proyecto, previsto para 3 meses, se ha alargado más de 50 años. Solo en los últimos 8 se han obtenido progresos significativos.
Hasta 2012, el hecho de que los ordenadores pudieran reconocer los objetos presentes en una escena era más ciencia ficción que una posibilidad real. Aunque se habían conseguido algunos progresos, estaban limitados a casos muy particulares (por ejemplo, el reconocimiento de caras) y para imágenes sencillas. A partir de ese año, con la aparición de técnicas de aprendizaje automático basadas en redes neuronales convolucionales profundas, la realidad superó a la ficción.
Una red neuronal artificial es un algoritmo compuesto por varias etapas interconectadas entre sí y llamadas neuronas. Este modelo de conexión se inspira en la forma en que se relacionan las neuronas del cerebro, de ahí su nombre.
Cada neurona artificial implementa una función matemática que combina una serie de operaciones sencillas (sumas y productos de los valores de entrada por unos factores o pesos asociados a la neurona) y una operación más compleja que se aplica a la señal de salida.
En una red neuronal, las neuronas se organizan formando capas, de manera que las salidas de las neuronas de una capa se utilizan como entrada de las neuronas de la capa siguiente.
La concatenación de muchas de estas capas permite crear funciones muy complejas que relacionan los valores de entrada de la red con el valor (o valores) a la salida. Mediante técnicas de optimización, los pesos de la red se pueden ajustar (el algoritmo aprende) para obtener a la salida un resultado adaptado a cada entrada.
Aunque la base teórica de las redes neuronales se estableció a mediados del siglo pasado, no fue hasta principios del presente siglo cuando la potencia de computación permitió procesar la gran cantidad de datos necesaria para la resolución de problemas complejos con este tipo de algoritmos.
Cómo se entrenan las neuronas artificiales
El modelo más habitual de red aplicado al procesamiento de imágenes recibe el nombre de red neural convolucional (o CNN, por sus siglas en inglés). En este caso, cada neurona de la primera capa de la red está conectada a un pequeño grupo de píxeles de la imagen de entrada.
Una de las primeras aplicaciones de las CNN fue la clasificación de imágenes según su contenido. Dada una imagen de entrada, la red debe decidir, por ejemplo, si se trata de la imagen de una persona, de un coche, etc. Para ajustar los pesos de la red (entrenarla) de manera que se cumpla este objetivo son necesarios los siguientes ingredientes:
- Una gran cantidad de imágenes, llamadas de entrenamiento, que contienen los objetos a reconocer y etiquetadas por un humano (imágenes de personas con la etiqueta “persona”, de coches con la etiqueta “coche”, etc.).
- Una red que toma como entrada una imagen y proporciona a la salida una etiqueta (“persona”, “coche”, etc.).
- Una función (función de coste) que compara las etiquetas proporcionadas por la red con las etiquetas asignadas por el humano y que toma un valor mínimo cuando ambas coinciden.
Los pesos de la red se van modificando en el proceso. Si el número de imágenes de entrenamiento y el número de capas de la red son suficientemente grandes, tras un número suficiente de iteraciones la red es capaz de simular la manera que tienen los humanos de etiquetar las imágenes.
En 2012, una CNN profunda (formada por una gran número de capas)
llamada AlexNet fue capaz de clasificar 1 000 objetos diferentes con un error muy inferior al de cualquier técnica anterior. Este hecho impulsó definitivamente la utilización de este tipo de algoritmos en el campo de la visión por computador. Desde 2015, las CNN son capaces de clasificar esos 1 000 objetos con un error inferior al cometido por los humanos.
Basados en los principios enunciados más arriba, redes cada vez más complejas se aplicaron desde 2012 al reconocimiento de objetos en imágenes: la red no solo debía distinguir un objeto de otro, sino también indicar en qué parte de la imagen se encontraba. El modelo de red más popular en la actualidad para la resolución de este tipo de problemas fue propuesto en 2018 y recibe el nombre de Mask R-CNN.
Inteligencia artificial para identificar peces
Mask R-CNN se ha utilizado para detectar multitud de objetos de la vida cotidiana, desde coches y personas a corbatas, sillas o cepillos de dientes. Nosotros lo empleamos en el proyecto DEEP-ECOMAR con el objetivo de reconocer diferentes especies de peces en imágenes submarinas.
Para conseguirlo, entrenaremos la red con miles de imágenes previamente etiquetadas por expertos en las que aparecen las especies de interés. Una vez
entrenada, la red será capaz de identificar estas especies de manera automática.
 La inteligencia artificial puede identificar peces en las imágenes. Fuente: IMEDEA
La inteligencia artificial puede identificar peces en las imágenes. Fuente: IMEDEAUna parte importante del proyecto se dedicará al etiquetado manual de las imágenes, para lo que se desarrollarán herramientas de software que permitirán agilizar la tarea. Asimismo, se investigará el efecto de la aplicación de técnicas de mejora del color y el contraste de las imágenes en los resultados del aprendizaje. Finalmente, se ajustarán los parámetros de la función de coste de la red para obtener resultados óptimos y aplicables a imágenes obtenidas en entornos marinos diferentes al utilizado para el entrenamiento.
El proyecto DEEP-ECOMAR lo realizamos de manera conjunta investigadores del IMEDEA (Instituto Mediterráneo de Estudios Avanzados, CSIC-UIB) y de la Universitat de les Illes Balears (UIB). Utilizaremos el vídeo submarino y el banco de imágenes del observatorio submarino Sub-Eye, situado en Andratx (Mallorca).
Sobre los autores: José Luis Lisani Roca es profesor titular de universidad en el área de matemática aplicada en la Universitat de les Illes Balears e Ignacio Catalán Alemany es investigador en oceanografía pesquera en el Instituto Mediterráneo de Estudios Avanzados (IMEDEA – CSIC – UIB)
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Así enseñamos a los ordenadores a identificar especies de peces se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Especies exóticas invasoras
- Juan Ignacio Cirac – P4K 2019: ¿Cómo serán los ordenadores cuánticos?
- Animales en equilibrio osmótico: invertebrados marinos y peces bruja
¿Cuántas estructuras rítmicas existen en poesía?
En la sección Matemoción del Cuaderno de Cultura Científica somos unos apasionados de la poesía, así como de la relación de esta con las matemáticas. Si miramos en el histórico de la misma podremos encontrar muchas entradas vinculando ambas, desde la serie Los números poéticos (primera parte, segunda parte y tercera parte) en la que se hablaba de poemas con temática matemática, como el poema sobre el número pi de la premio nobel de literatura polaca Wisława Szymborska o Los números oscuros de la poeta barcelonesa Clara Janés, hasta poemas en cuya estructura hay matemáticas, como poemas sobre una banda de Moebius (véase la entrada Poesía retorcida sobre la banda de Moebius), la combinatoria de la obra poética Cien mil millardos de poemas del escritor francés Raymond Queneau (véase 100 000 000 000 000 poemas) o el uso de la sucesión de Fibonacci, tanto en la obra Alfabeto de la poeta danesa Inger Christensen (véase ¡Nos encanta Fibonacci! ), como en los llamados poemas Fibonacci (véase Poemas Fibonacci).
 Cartel de la exposición Matematicopoemes (2018), en la Universitat de Barcelona, del artista visual catalán Toni Prat, con uno de sus poemas visuales matemáticos. Imagen de su blog Poesía visual
Cartel de la exposición Matematicopoemes (2018), en la Universitat de Barcelona, del artista visual catalán Toni Prat, con uno de sus poemas visuales matemáticos. Imagen de su blog Poesía visual
Pero también hemos abordado el análisis matemático de algunas cuestiones relacionadas con la poesía, como en la entrada El origen poético de los números de Fibonacci, en la cual se muestra que la cantidad de estructuras posibles para versos con m moras (la mora es la “la unidad que mide el peso silábico, es decir, la duración de los segmentos fonológicos que componen la sílaba” y hay dos tipos de sílabas, unas cortas de una mora o instante silábico y otras largas de dos moras) es igual al número de Fibonacci Fm + 1.
 Pisa Fibonacci II (2009), realizada en neón, tubos de luz y formica, de la artista conceptual argentina Margarita Paksa (1932-2020). Imagen de ARTSY
Pisa Fibonacci II (2009), realizada en neón, tubos de luz y formica, de la artista conceptual argentina Margarita Paksa (1932-2020). Imagen de ARTSYEn esta entrada del Cuaderno de Cultura Científica vamos a continuar con el análisis matemático de la poesía, en concreto, vamos a interesarnos por la cuestión de la métrica y a responder a la siguiente pregunta:
¿cuántas posibles estructuras de rimas existen para estrofas o poemas con un número fijo de versos?
Aunque sea una cuestión conocida, vamos a empezar por el principio. ¿Qué es la rima? Según el diccionario de la RAE es la “identidad de sonidos vocálicos y consonánticos, o solo vocálicos, a partir de la última vocal acentuada en dos o más versos”. Así, en el pareado final del poema Frases de la poeta argentina Alfonsina Storni (1892-1938),
Bravo león, mi corazón,
tiene apetitos, no razón
la rima es “ón”, luego rima consonante, mientras que en el pareado final del poema Lunes, miércoles y viernes del poeta andaluz Federico García Lorca (1898-1936)
Ante una vidriera rota
coso mi lírica ropa
la rima es “ota” y “opa”, luego rima asonante, ya que se repiten las vocales o-a.
Aunque la cuestión que nos interesa en esta entrada no es tanto si la rima es asonante o consonante, como analizar la cantidad de estructuras de rimas posibles para una estrofa, o poema, con un número fijo de versos. Por ejemplo, en una estrofa de dos versos hay dos posibilidades, que los dos rimen, como en el caso del pareado, que sería la estructura AA, o que no rimen, que sería la estructura libre AB, como en el haiku del poeta japonés Taneda Santoka (1882-1940)
Mi cuenco de mendigar
acepta hojas caídas
Por lo tanto, para estrofas o poemas con dos versos solo hay dos tipos de rima, AA y AB (en esta entrada vamos a escribir siempre la rima con letras mayúsculas, independientemente de que el verso sea de arte menor –de entre dos y ocho sílabas– o arte mayor –más de ocho sílabas–). Evidentemente, en el caso trivial de un solo verso solo hay una posibilidad trivial.
Pensemos ahora en la cantidad de estructuras rítmicas que son posibles en tercetos, es decir, en estrofas o poemas con tres versos. Por ejemplo, los haikus, que son pequeños poemas de origen japonés que habitualmente cuentan con tres versos, no suelen tener rima, luego ABC, como este poema del poeta donostiarra Karmelo C. Iribarren, titulado Domingo tarde.
Qué hago
mirando la lluvia
si no llueve
Por otra parte, la rima de la soleá andaluza es ABA, como en la siguiente soleá del poeta sevillano Antonio Machado (1875-1939).
Tengo un querer y una pena:
la pena quiere que viva;
el querer quiere que muera.
Se llama terceto monorrimo a aquellos tercetos que tienen la misma rima, ya sea asonante o consonante, en los tres versos, AAA, como en los tercetos del poema A Goya del poeta nicaragüense Rubén Darío (1867-1916), dentro de los Cantos de vida y esperanza. Así empieza el poema.
Poderoso visionario,
raro ingenio temerario,
por ti enciendo mi incensario.
Por ti, cuya gran paleta,
caprichosa, brusca, inquieta,
debe amar todo poeta;
por tus lóbregas visiones,
tus blancas irradiaciones,
tus negros y bermellones;
por tus colores dantescos,
por tus majos pintorescos,
y las glorias de tus frescos.
Otra rima posible para los tercetos es AAB, como en el poema La muerte de Melisanda del poeta chileno Pablo Neruda (1904-1973), cuyas estrofas son de dos versos (empieza así … A la sombra de los laureles / Melisanda se está muriendo.), salvo la anteúltima estrofa que es un terceto con rima AAB.
Por ella pisará las rosas,
perseguirá las mariposas
y dormirá en los cementerios.
Mientras que la rima ABB la encontramos por ejemplo en el siguiente poema de la poeta madrileña Gloria Fuertes (1917-1998).
En las noches claras,
resuelvo el problema de la soledad del ser.
Invito a la luna y con mi sombra somos tres.
Por lo tanto, hemos puesto ejemplos de todas las posibles rimas para estrofas o poemas con tres versos, AAA, AAB, ABB, ABA y ABC. Es decir, para tres versos son cinco las estructuras rítmicas posibles.
 Matematicopoema n. 26, del poeta visual catalán Toni Prat. Imagen de su blog Poesía visual
Matematicopoema n. 26, del poeta visual catalán Toni Prat. Imagen de su blog Poesía visualA continuación, analicemos cuántas son las estructuras posibles de rimas en las estrofas o poemas con cuatro versos. Empecemos con una composición poética clásica, el soneto, que consta de catorce versos separados en dos cuartetos y dos tercetos. Veamos un ejemplo clásico y jocoso de soneto del poeta y dramaturgo madrileño Lope de Vega (1562-1635).
Un soneto me manda hacer Violante,
que en mi vida me he visto en tanto aprieto;
catorce versos dicen que es soneto;
burla burlando van los tres delante.
Yo pensé que no hallara consonante,
y estoy a la mitad de otro cuarteto;
mas si me veo en el primer terceto,
no hay cosa en los cuartetos que me espante.
Por el primer terceto voy entrando,
y parece que entré con pie derecho,
pues fin con este verso le voy dando.
Ya estoy en el segundo, y aun sospecho
que voy los trece versos acabando;
contad si son catorce, y está hecho.
Como se ve en este ejemplo, los cuartetos de un soneto tienen rima ABBA, a la cual se la conoce como rima abrazada. A la estructura rítmica en la cual riman los cuatro versos AAAA se la conoce como continua o cuarteto monorrimo. Un ejemplo lo encontramos en el Libro del buen amor del Arcipreste de Hita (aprox. 1283-1350), en el capítulo Enxiemplo del garçón que quería casar con tres mujeres.
Era un garçón loco, mançebo bien valiente:
Non quería cassarse con una solamente;
Synon con tres mugeres: tal era su talente.
Porfiaron en cabo con él toda la gente.
Su padre é su madre é su hermano mayor
Afyncáronle mucho que ya por su amor
Con dos que se cassase, primero con la menor,
Dende á un mes conplido, casase con la mayor.
A la rima ABAB se la conoce como rima cruzada. Nos podemos encontrar ejemplos de esta rima en muchos poemas, por ejemplo, en el poema del poeta valenciano Miguel Hernández (1910-1942), titulado Niño yuntero, del que mostramos las primeras estrofas.
Carne de yugo, ha nacido
más humillado que bello,
con el cuello perseguido
por el yugo para el cuello.
Nace, como la herramienta,
a los golpes destinado,
de una tierra descontenta
y un insatisfecho arado.
Entre estiércol puro y vivo
de vacas, trae a la vida
un alma color de olivo
vieja ya y encallecida.
Releyendo algunos poemas del poeta portugués Fernando Pessoa (1888-1935), también he encontrado muchos cuartetos con rima ABAB, como el siguiente poema.
El poeta es un fingidor.
Finge tan completamente
que hasta finge que es dolor
el dolor que de veras siente.
Y quienes leen lo que escribe,
sienten, en el dolor leído,
no los dos que el poeta vive
sino aquél que no han tenido.
Y así va por su camino,
distrayendo a la razón,
ese tren sin real destino
que se llama corazón.
Pero también encontramos cuartetos con otras rimas, como AABA, en el poema que empieza así.
Siervo impasible de un fin desolado,
No creas o descreas demasiado.
Lo mismo da que pienses o no pienses.
Todo es irreal, anónimo, impensado.
Pero existen más estructuras rítmicas posibles para un cuarteto, AAAB, AABB, ABAA, ABBB, AABC, ABAC, ABCA, ABBC, ABCB, ABCC e incluso sin rima ABCD. En total, hay quince estructuras rítmicas para cuatro versos.
 Matematicopoema n. 20, del poeta visual catalán Toni Prat. Imagen de su blog Poesía visual
Matematicopoema n. 20, del poeta visual catalán Toni Prat. Imagen de su blog Poesía visualLo siguiente sería obtener cuántas estructuras de rimas posibles hay para estrofas o poemas de cinco versos. Podéis listar vosotras mismas todas las posibilidades que existen y descubriréis que son 52, aunque nosotros vamos a aprovechar para utilizar unos diagramas muy especiales para mostrarlas.
En la novela clásica de la literatura japonesa El romance de Genji, de la escritora Murasaki Shikibu (aprox. 978-1014), aparecen representados con bonitos diagramas las 52 estructuras rítmicas posibles. Las líneas verticales con los versos de la estrofa o poema, y las líneas horizontales unen las líneas que riman. Cada capítulo, en total son 54, empieza con la imagen de uno de esos diagramas, aunque hay uno que se repite y otro extra. Los símbolos utilizados en El romance de Genji son los que aparecen en esta imagen.

Por ejemplo, el primer signo se correspondería con la rima ABACC, el número 37 con ABCAA o el número 52 con ABABA. Un ejemplo de rima ABABB, que es el diagrama 29 de la imagen anterior, es el poema Noche oscura del fraile y poeta castellano Juan de la Cruz (1542-1591), que empieza así:
En una noche oscura
con ansias, en amores inflamada,
¡oh dichosa ventura!
salí sin ser notada,
estando ya mi casa sosegada.
A oscuras, y segura,
por la secreta escala disfrazada,
¡Oh dichosa ventura!
a oscuras, y en celada,
estando ya mi casa sosegada.
 La demostración (2008), del poeta colombiano Rafael García Z., que aparece en el libro El mago natural y otros abracadabras
La demostración (2008), del poeta colombiano Rafael García Z., que aparece en el libro El mago natural y otros abracadabras
Y podríamos seguir estudiando cuantas estructuras de rimas son posibles para estrofas o poemas de seis o más versos.
Si hacemos un balance de los resultados que hemos obtenido sobre cuántas posibles estructuras de rimas existen para estrofas o poemas con un número fijo n de versos, hemos visto que para los valores n = 1, 2, 3, 4 y 5, desde uno a cinco versos, la cantidad de posibles estructuras rítmicas son: 1, 2, 5, 15 y 52.
Estos son los cinco primeros términos de una sucesión importante de la combinatoria, los números de Bell (la sucesión A000110 en la Enciclopedia online de sucesiones de números enteros), que reciben su nombre del matemático y novelista estadounidense Eric Temple Bell (1883-1960), conocido por ser el autor del libro Los grandes matemáticos, de Zenón a Poincaré.
En combinatoria se define el número de Bell Bn como el número de posibles particiones de un conjunto de n elementos, es decir, la cantidad de formas distintas de distribuir los n elementos de un conjunto en grupos.
Si para todo número natural n se toma como conjunto de referencia el conjunto de los números naturales hasta n, {1, 2, …, n – 1, n}, calculemos las particiones posibles de ese conjunto y, por tanto, los números de Bell.
Para n = 1, solo hay una partición posible del conjunto {1}, la trivial, luego B1 = 1;
para n = 2, las particiones del conjunto {1, 2}, es decir, las formas de distribuir los elementos de ese conjunto en grupos son {1}{2} y {1, 2}, por lo tanto, B2 = 2;
para n = 3, las particiones de {1, 2, 3} son {1}{2}{3}, {1, 2}{3}, {1, 3}{2}, {2, 3}{1} y {1, 2, 3}, por eso B3 = 5;
para n = 4, son {1}{2}{3}{4}, {1, 2}{3}{4}, {1, 3}{2}{4}, {1, 4}{2}{3}, {2, 3}{1}{4}, {2, 4}{1}{3}, {3, 4}{1}{2}, {1, 2}{3, 4}, {1, 3}{2, 4}, {1, 4}{2, 3}, {1, 2, 3}{4}, {1, 2, 4}{3}, {1, 3, 4}{2}, {2, 3, 4}{1} y {1, 2, 3, 4}, es decir, B4 = 15;
de la misma forma podéis calcular las particiones de {1, 2, 3, 4, 5} y obtener que B5 = 52. En general, los primeros miembros de la sucesión de números de Bell son
1, 2, 5, 15, 52, 203, 877, 4.140, 21.147, 115.975, …
Como el conjunto sobre el que consideremos las particiones puede ser cualquiera, esto permite hacer diferentes diagramas e interpretaciones de los números de Bell. Por ejemplo, si se consideran puntos en el plano se pueden representar las particiones de estos como aparece en las siguientes imágenes, para B3 y B4.
 Las 5 particiones del conjunto de tres puntos
Las 5 particiones del conjunto de tres puntos
 Las 15 particiones del conjunto de cuatro puntos
Las 15 particiones del conjunto de cuatro puntos
Aunque si le metemos color a las particiones queda más bonito el diagrama, como la siguiente imagen para el cálculo de B5.
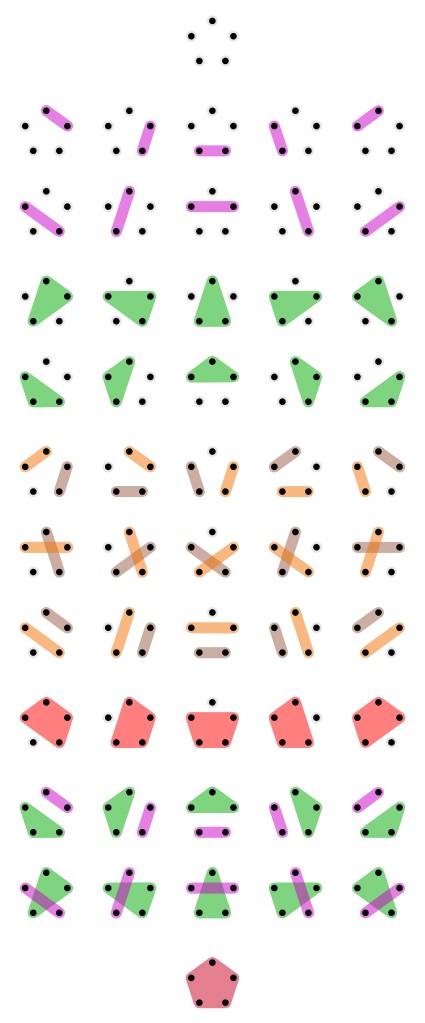 Las 52 particiones del conjunto de cinco puntos. Imagen: Wikimedia Commons
Las 52 particiones del conjunto de cinco puntos. Imagen: Wikimedia Commons
Por otra parte, si un número N es producto de n números primos distintos, lo que se suele denominar un número libre de cuadrados, entonces Bn es igual al número de formas de expresar N como producto de divisores suyos, salvo el 1. Así, el número 105 puede expresarse como 105 = 3 · 5 · 7 = 15 · 7 = 21 · 5 = 35 · 3 (b3 = 5). Notemos que el conjunto que se considera es el formado por los divisores primos del número N, en el caso de 105 sería {3, 5, 7}, y cada partición da lugar a una forma de expresar el número N como producto de divisores suyos, así la partición {3, 7}{5} da lugar a 105 = 21 · 5 , ya que 21 = 3 · 7.
 La espera eterna, de la poeta catalana Ariadna Torres
La espera eterna, de la poeta catalana Ariadna Torres
Pero volviendo al tema central de esta entrada si ahora se toma el conjunto de los versos de una estrofa o poema con n versos para calcular el número de Bell Bn, entonces la cantidad de estructuras para las rimas de una estrofa o un poema de n versos es igual al número de Bell Bn, ya que se considera que los versos que están en un mismo grupo tienen la misma rima.
Si miramos a la sucesión de los números de Bell, B7 = 877, es decir, existen 877 estructuras rítmicas para estrofas o poemas de 8 versos, entre las que están las rimas ABCBDAD, ABCBADA de las primeras estrofas del poema Nanas de la cebolla del poeta Miguel Hernández.
La cebolla es escarcha
cerrada y pobre:
escarcha de tus días
y de mis noches.
Hambre y cebolla:
hielo negro y escarcha
grande y redonda.
En la cuna del hambre
mi niño estaba.
Con sangre de cebolla
se amamantaba.
Pero tu sangre
escarchaba de azúcar,
cebolla y hambre.
 An Inkblack, Triangled, Sequential Letterwork, del artista visual holandés Pixie Pravda
An Inkblack, Triangled, Sequential Letterwork, del artista visual holandés Pixie Pravda
Bibliografía
1.- Toni Prat, Poesía visual (blog)
2.- Raúl Ibáñez, La gran familia de los números (título provisional), Catarata, 2020.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo ¿Cuántas estructuras rítmicas existen en poesía? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Historia de Nicolas Bourbaki
En 1923 Raoul Husson (1901-1967), en aquel momento alumno de la Escuela Superior Normal de París (École Normale Supérieure), inventó el nombre de un supuesto matemático llamado Nicolas Bourbaki. Husson se disfrazó de matemático barbudo e impartió una falsa conferencia científica, que fue intencionadamente incomprensible y con razonamientos sutilmente falsos.
El objetivo de esta conferencia era dar a conocer el supuesto teorema de Bourbaki, una invención, para poner de manifiesto el cinismo de algunos intelectuales, que daban por buena cualquier explicación siempre que sonase lo suficientemente complicada.
Los vídeos de Historias de la Ciencia presentan de forma breve y amena pasajes de la nuestra historia científica y tecnológica. Los vídeos, realizados para la Cátedra de Cultura Científica de la UPV/EHU, se estrenan en el programa de ciencia Órbita Laika (@orbitalaika_tve), los lunes a las 22:00 en la 2 de RTVE.
El artículo Historia de Nicolas Bourbaki se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:La hipótesis protón-electrón de la composición nuclear
 Foto: Tanja Cotoaga / Unsplash
Foto: Tanja Cotoaga / UnsplashAl describir el problema de la estructura nuclear, terminamos planteándonos una pregunta: ¿Podría un núcleo de masa A consistir en un número A de protones? La respuesta corta es no.
Si este fuera el caso, la carga del núcleo sería de A unidades, pero, a excepción del hidrógeno, sabemos que la carga nuclear Z es siempre menor que A, generalmente menor que A/2. Para sortear esta dificultad, se asumió desde el principio que, además de los protones, los núcleos atómicos contenían los electrones suficientes para cancelar la carga positiva de los protones adicionales; es decir, se suponía que contenían (A-Z) electrones. Después de todo, los núcleos emiten electrones al desintegrarse, por lo que, aparentemente, los electrones deben existir dentro del núcleo. Estos electrones contribuirían con solo una pequeña cantidad a la masa del núcleo, pero junto con los protones harían que la carga neta fuera igual a Z unidades, como era necesario.
Parecía plausible, entonces, considerar que el átomo consistía en un núcleo formado por A protones y (A-Z) electrones, con Z electrones adicionales fuera del núcleo para obtener como resultado un átomo eléctricamente neutro. Por ejemplo, un átomo de oxígeno-16 tendría un núcleo con 16 protones y 8 electrones, con 8 electrones adicionales fuera del núcleo. Este modelo del núcleo se conoce como la hipótesis protón-electrón de la composición nuclear. [1]
La hipótesis protón-electrón parecía ser coherente con la emisión de partículas alfa y beta por los átomos de las sustancias radiactivas. Al incluir electrones en el núcleo la explicación de la desintegración beta no era un problema: cuando el núcleo alcanza un estado determinado simplemente expulsa uno de sus electrones. También parecía razonable que se pudiera formar una partícula alfa en el núcleo mediante la combinación de cuatro protones y dos electrones; una partícula alfa podría existir ya preformada en el núcleo, o formarse en el instante de la emisión.
Aunque la hipótesis protón-electrón era satisfactoria en algunos aspectos, el desarrollo de la mecánica cuántica, entre otros problemas, obligó a descartarla. Una de las dificultades más serias surge del principio de incertidumbre de Heisenberg y de la teoría de la relatividad de Einstein: el confinamiento de un electrón en un espacio tan pequeño como el núcleo daría lugar a la circunstancia de que a veces la velocidad del electrón sería mayor que la velocidad de la luz, lo que no es posible según la teoría de la relatividad especial.
¿Cómo podría explicarse el hecho de que los electrones no puedan estar confinados en el núcleo, pero emerjan del núcleo en la desintegración? Heisenberg contaba la siguiente anécdota:
Estaban un día él y sus asistentes discutiendo este problema mientras tomaban un café enfrente del edificio que albergaba la piscina cubierta de la ciudad. El movimiento de gente que entraba y salía del mismo sugirió a Heisenberg un posible nuevo enfoque del problema. “Ves a la gente entrando en el edificio completamente vestida, y la ves salir completamente vestida. ¿Pero significa eso que también nada completamente vestida?” O sea, ves electrones que salen del núcleo y, en otras ocasiones, ves electrones que son capturados por el núcleo, pero eso no significa que permanezcan como electrones mientras están en el núcleo. Quizás los electrones se creasen en el proceso de emisión desde el núcleo. Era necesario un modelo completamente nuevo.
Notas:
[1] La hipótesis protón-electrón es similar a una idea anterior sugerida por el médico inglés William Prout en 1815. Sobre la base del pequeño número de masas atómicas conocidas entonces, Prout propuso que todas las masas atómicas son múltiplos de la masa atómica del hidrógeno y que por tanto, todos los elementos podrían estar formados por hidrógeno. La hipótesis de Prout fue descartada cuando, a finales del siglo XIX, se encontró que las masas atómicas de algunos elementos eran, sin ningún género de dudas, fraccionarias, en concreto, las de cloro (35,46 unidades) y cobre (63,54 unidades). Sin embargo, con el descubrimiento de los isótopos, se descubrió que las masas atómicas fraccionarias de cloro y cobre, como la del neón, surgen porque estos elementos son mezclas de isótopos, y cada isótopo sí tiene una masa atómica cercana a un número entero.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo La hipótesis protón-electrón de la composición nuclear se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Pigmentos y fotones: la ciencia detrás de los colores otoñales del bosque
Manuel Peinado Lorca y Luis Monje
 Foto: Luis Monje
Foto: Luis Monje
A medida que los días se vuelven más fríos y aparecen las primeras escarchas, árboles y arbustos de hoja caduca comienzan el despliegue otoñal de tonos rojos, amarillos, púrpuras y marrones que caracterizan a los bosques templados de ambos hemisferios. Para comprender el proceso de diseño del fantástico espectáculo otoñal de los caducifolios es importante entender qué son y para qué sirven los pigmentos.
La magia química y lumínica de los pigmentos
Las plantas son expertas en capturar la energía de la luz y utilizarla para crear azúcares mediante la fotosíntesis. Este proceso comienza con la absorción de luz mediante moléculas orgánicas especializadas, los pigmentos, que se encuentran en los cloroplastos y en las vacuolas celulares (Figura 1).
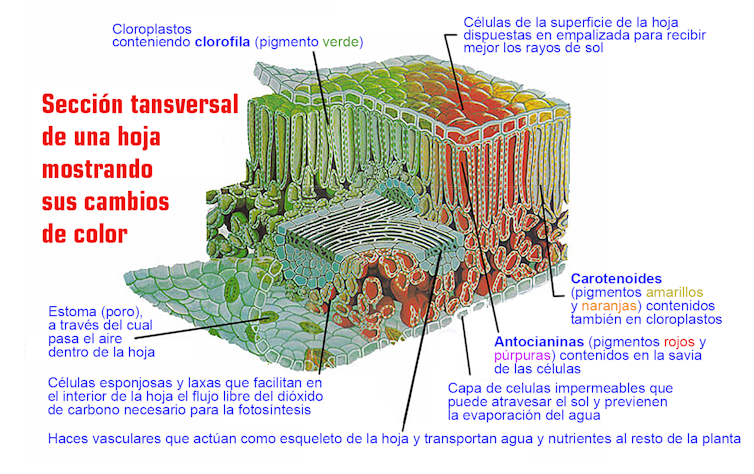 Figura 1. Los pigmentos, unas moléculas orgánicas especializadas, se encuentran en los cloroplastos celulares y en las vacuolas. Imagen:
Figura 1. Los pigmentos, unas moléculas orgánicas especializadas, se encuentran en los cloroplastos celulares y en las vacuolas. Imagen:Luis Monje
La luz es una forma de radiación electromagnética, un tipo de energía que viaja en ondas. En conjunto, todos los tipos de radiación conforman el espectro electromagnético, cuyas longitudes entre 400 y 700 nm constituyen la luz visible para el ojo humano (Figuras 2A y 2B). Cada partícula, llamada fotón, tiene una cantidad fija de energía que puede excitar un pigmento (Figura 2C).
Un pigmento excitado es inestable y tiene varias opciones disponibles para llegar a ser más estable. En las plantas, la energía de los fotones se usa para dividir moléculas de agua dentro de los cloroplastos. Además de oxígeno, en el proceso se liberan electrones e iones de hidrógeno. Estos electrones e iones se utilizan para generar energía en forma de adenosin trifosfato (ATP), que se usa en el ciclo de Calvin, cuyo objetivo es tomar CO₂ y utilizar la energía generada para transformar las moléculas de carbono en cadenas de moléculas orgánicas.
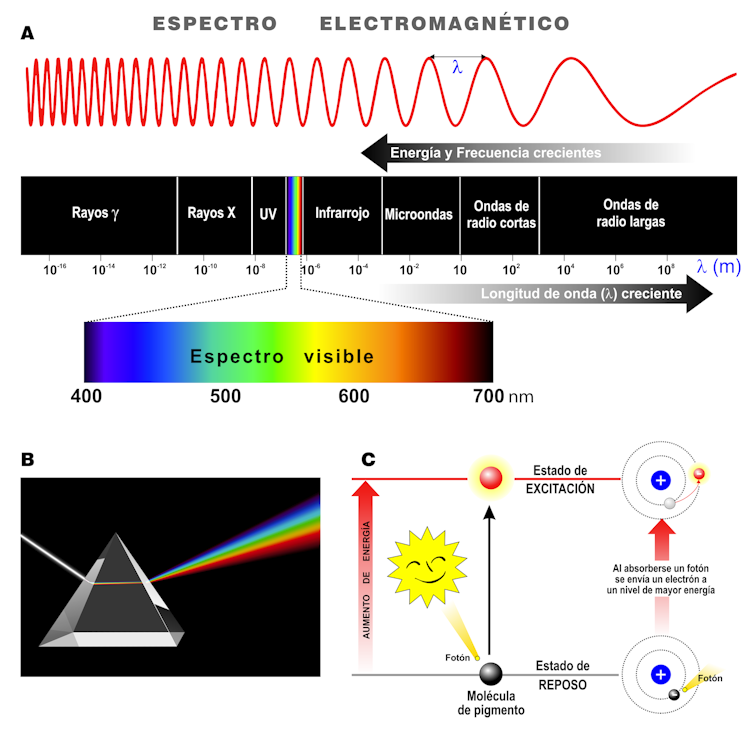 Figura 2. (A) La luz es una forma de radiación electromagnética, un tipo de energía que viaja en ondas. En conjunto, todos los tipos de radiación conforman el espectro electromagnético. (B) El espectro visible para el ojo humano es la radiación cuya longitud de onda está aproximadamente entre 400 y 700 nm. Se pueden ver los diferentes colores cuando la luz blanca atraviesa un prisma y la apreciamos como un arcoiris. (C) Solo un fotón con la cantidad justa de energía para subir un electrón entre orbitales puede excitar un pigmento. Imagen: Luis Monje
Figura 2. (A) La luz es una forma de radiación electromagnética, un tipo de energía que viaja en ondas. En conjunto, todos los tipos de radiación conforman el espectro electromagnético. (B) El espectro visible para el ojo humano es la radiación cuya longitud de onda está aproximadamente entre 400 y 700 nm. Se pueden ver los diferentes colores cuando la luz blanca atraviesa un prisma y la apreciamos como un arcoiris. (C) Solo un fotón con la cantidad justa de energía para subir un electrón entre orbitales puede excitar un pigmento. Imagen: Luis MonjeEl color de un pigmento es el resultado de la longitud de onda reflejada. El color verde de las hojas se debe a la presencia de las clorofilas, unos pigmentos que se encuentran dentro de los cloroplastos, que absorben la mayoría de las radiaciones del espectro visible, y reflejan los verdes (Figura 3). Cuando abunda en las células, como sucede durante la temporada de crecimiento de primavera e inicios de verano, el color de la clorofila domina y enmascara los colores de cualquier otro pigmento que pudiera existir en la hoja.
La clorofila tiene una función vital: captura los rayos solares y utiliza la energía resultante en la fabricación de los alimentos de la planta: azúcares simples. Durante la temporada de crecimiento, la clorofila, que se deteriora con la exposición a la luz solar, se elabora, se degrada y se reemplaza constantemente en las hojas, fabricantes incansables de nueva clorofila durante la pujante estación de crecimiento.
El ciclo vital de los caducifolios
Como la mayoría de las plantas, los ritmos circadianos de los caducifolios son sensibles al fotoperiodo, es decir, a la duración del período diario de oscuridad. A finales del verano, los días comienzan a acortarse y las noches son más largas. Como la hora de inicio de todo el proceso depende de la duración de la noche, los colores otoñales aparecen aproximadamente a la misma hora cada año en un lugar determinado, sin que importe demasiado que las temperaturas sean más frías o más cálidas de lo normal.
Cuando las noches alcanzan un valor umbral y son lo suficientemente largas, las células que se encuentran en el punto de unión del peciolo de la hoja y el tallo que la sustenta se dividen rápidamente, pero no se expanden. Se forma así una capa de abscisión de callosa, es decir, una capa impermeable de células que poco a poco va obturando el floema y, con ello, bloqueando el transporte de savia de la hoja a la rama. También bloquea el xilema y, por tanto, el flujo de minerales desde las raíces hacia las hojas.
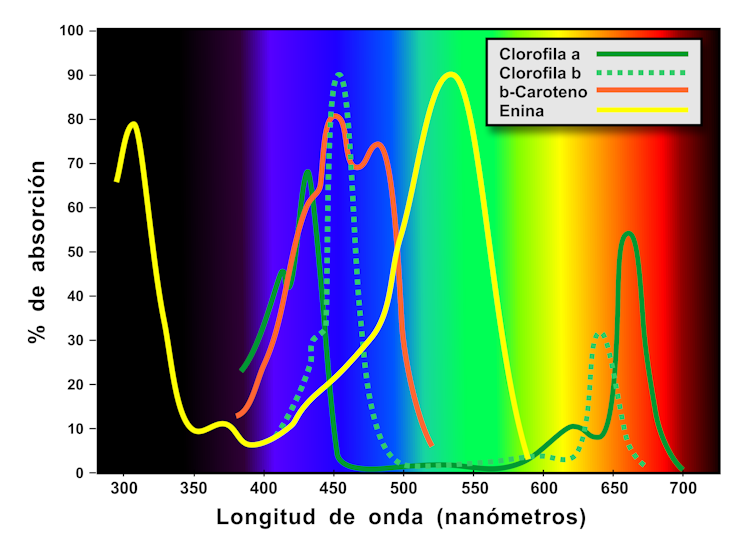 Figura 3. Superposición de espectros de las clorofilas a y b, el beta-caroteno y la enina, una antocianina típica. Mientras que las clorofilas y el beta caroteno absorben en las partes azul y amarillo/rojo del espectro visible, la enina absorbe principalmente en la parte verde del espectro, donde las clorofilas no absorben nada. Imagen: Luis Monje
Figura 3. Superposición de espectros de las clorofilas a y b, el beta-caroteno y la enina, una antocianina típica. Mientras que las clorofilas y el beta caroteno absorben en las partes azul y amarillo/rojo del espectro visible, la enina absorbe principalmente en la parte verde del espectro, donde las clorofilas no absorben nada. Imagen: Luis MonjeConforme se desarrolla esta capa, la cantidad de clorofila en la hoja comienza a disminuir. A medida que las clorofilas se degradan, se revelan los pigmentos ocultos de unos derivados oxigenados de los carotenoides, las xantofilas amarillas, y los betacarotenos naranjas (Figura 3). Estos pigmentos están presentes durante todo el año en el interior celular, pero los pigmentos rojos, las antocianinas, se sintetizan de novo una vez que se ha degradado aproximadamente la mitad de la clorofila.
Aunque existan en las hojas durante todo el año, los colores amarillo-anaranjados de los carotenoides permanecen enmascarados por la clorofila verde. A medida que se acerca el otoño y el suministro total de clorofilas va disminuyendo gradualmente, el efecto de enmascaramiento se desvanece lentamente. Cuando eso sucede, comienzan a verse las coloraciones amarillas, pardas, naranjas y muchas tonalidades intermedias que proporcionan los carotenoides.
Los carotenoides son el pigmento dominante en la coloración de aproximadamente el 15-30 % de las especies de árboles. Sus amarillos y naranjas brillantes tiñen las hojas de nogales, fresnos, arces, álamos, abedules, cerezos, plátanos de paseo y alisos, entre otros muchos.
Los rojos, los púrpuras y sus combinaciones provienen de otro grupo de pigmentos celulares, las antocianinas. Hay dos diferencias importantes entre estos pigmentos y las clorofilas y los carotenoides. La primera es que no se encuentran en los cloroplastos. Son pigmentos solubles en agua que se almacenan en las vacuolas. La segunda es que, a diferencia de los carotenoides, no existen en la hoja durante la temporada de crecimiento, sino que se producen activamente hacia el final del verano.
 Otoño en el hayedo de Urbasa, Navarra. Imagen: Luis Monje
Otoño en el hayedo de Urbasa, Navarra. Imagen: Luis MonjeCuando se acerca el otoño, las antocianinas se elaboran a partir de la savia acumulada en las células. Su síntesis de novo depende de la descomposición de los azúcares en presencia de luz intensa a medida que se reduce el nivel de fosfato en la hoja. Durante la temporada de crecimiento de verano, el nivel de fosfato es alto, porque juega un papel vital en la descomposición de los azúcares fabricados por la clorofila. En otoño, el fosfato, junto con otros nutrientes, se moviliza desde la hoja al tallo de la planta. Cuando eso sucede, el proceso de descomposición del azúcar cambia, lo que lleva a la producción de pigmentos de antocianina. Cuanto más brillante sea la luz durante este período, mayor será la producción de antocianinas y más luminoso será el color resultante.
En las regiones de clima templado, las antocianinas están presentes en aproximadamente una de cada diez especies de árboles aunque en algunos lugares hasta el 70 % de las especies de árboles pueden producir el pigmento. En los bosques otoñales tiñen a arces, robles, cornejos, cerezos y ciruelos. Estos mismos pigmentos a menudo se combinan con los colores de los carotenoides para crear los naranjas más intensos, los rojos vivos y los bronceados típicos de muchas especies de madera dura.
A medida que avanza el otoño, las células de la capa de abscisión se encallecen más y más. Como la clorofila, los otros pigmentos se degradan con la luz o cuando se congelan. Los únicos pigmentos que quedan son los taninos acumulados en las paredes celulares, que son marrones. Las conexiones entre las células se debilitan y las hojas acaban por caer.
Ha llegado el invierno y con él cae el maravilloso telón multicolor de la temporada otoñal que, en esencia, como toda la vida que nos rodea, está literalmente construida desde cero por la partícula que encumbró a Einstein: el fotón. Bastante increíble, ¿no está de acuerdo?
Sobre los autores: Manuel Peinado Lorca es catedrático de universidad en el departamento de ciencias de la vida e Investigador del Instituto Franklin de Estudios Norteamericanos y Luis Monje es biólogo y profesor de fotografía científica, ambos de la Universidad de Alcalá
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Pigmentos y fotones: la ciencia detrás de los colores otoñales del bosque se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Colores vivientes: nanoestructuras que se cultivan, no se fabrican.
- La pantalla de tu móvil solo tiene tres colores
- Los pigmentos respiratorios
En busca de biomateriales que se asemejen al tejido cerebral
Irati Diez Virto
Los biomateriales son substancias creadas para mantenerse en contacto con tejidos o fluidos biológicos. Uno de los biomateriales más habituales y conocidos son los empastes dentales. Sin embargo, el uso de estos materiales va más allá y su campo se amplía al desarrollo de implantes que, por ejemplo, sustituyan articulaciones, reparen órganos o imiten un conjunto de propiedades físicas de órganos como el cerebro. Enfrentarse al diseño de un material sintético, que contenga las propiedades de un tejido tan complejo como el cerebral, es un gran reto. Un desafío al que se enfrentan hoy día diversos grupos de investigación.
El uso de biomateriales ha ido aumentando exponencialmente desde la creación del primer biomaterial en la década de 1920, llamado Vitallium, una aleación metálica de uso odontológico. En la actualidad, existen innumerables aplicaciones para este tipo de materiales, entre ellos alrededor de 2.700 equipos médicos y unos 39.000 preparados farmacéuticos. Aunque estos materiales hayan generado un gran impacto positivo en la sanidad mundial, aún existe la necesidad de diseñar polímeros más refinados y métodos más sofisticados para caracterizar y testar estos materiales. Este es el caso de los biomateriales que pretenden imitar el tejido cerebral.
A lo largo de los años, se han llegado a diseñar varios tipos de biomateriales con esta intención. Estos tejidos sintéticos son requeridos en diversas tecnologías emergentes, como pueden ser el desarrollo de modelos de enfermedades neurológicas, la caracterización del tejido neuronal o el diseño de organoides cerebrales (versión miniaturizada y simplificada de un órgano, creado in vitro). Además, también podrían utilizarse para aplicaciones in vivo, esto es, para realizar implantes directamente en el tejido cerebral de pacientes con patologías diversas. Se cree que la utilización de biomateriales más sofisticados minimizaría la respuesta inmune de los pacientes y el rechazo al tejido. Pero para poder aplicar estos materiales exitosamente, es de vital importancia imitar las características físicas del cerebro.
 Foto: Paweł Czerwiński / Unsplash
Foto: Paweł Czerwiński / UnsplashEl mayor desafío de diseñar un tejido semejante al tejido cerebral reside en una característica física del mismo, que lo hace difícil de manipular: es muy blando. Esto se debe en parte al alto grado de hidratación de este órgano. El contenido de agua del tejido cerebral oscila entre el 73 y el 85% de la masa total, gracias a su alto contenido en proteoglicanos, moléculas que atrapan agua. También presenta muy poca cantidad de fibra de colágeno, el cual se relaciona con la rigidez de distintos órganos. Por ello, cuantificar la rigidez de este órgano es una de las tareas que está abordando la investigación en este ámbito.
Esta cuantificación se realiza mediante la medición del módulo elástico, una constante elástica que determina el grado de elasticidad (o rigidez) de un material en concreto. Hasta la fecha, no se ha podido caracterizar completamente esta medida para el tejido cerebral. Además, existen diferentes métodos experimentales para la determinación del módulo elástico y estos métodos divergen sustancialmente de un laboratorio a otro, así como las condiciones en las que se lleva a cabo dicha medición. Esta gran variedad de técnicas utilizadas genera unos resultados muy dispares entre distintos grupos de investigación, lo que hace que la comparación entre ellos sea casi imposible. Por esta razón, hasta ahora no se ha conseguido sintetizar ningún material que imite las complejas propiedades de este tejido.
Aún y así, sí existen potenciales candidatos que, aunque no son lo suficientemente sofisticados, podrían brindar grandes resultados combinándolos con otros materiales. Uno de ellos son las inyecciones de hidrogel, los cuales están siendo estudiados para el tratamiento posterior a la extirpación de glioblastoma (el tumor más común de la glia). Asimismo, este material inyectable brinda la posibilidad de administrar fármacos de una manera continuada. Aunque las propiedades viscoelásticas de estas inyecciones aún no han sido comparadas directamente con aquellas del cerebro, la mera posibilidad de que puedan ser inyectadas directamente en un paciente es extremadamente prometedora. Esto posibilitaría reemplazar los materiales rígidos y duros utilizados actualmente (Gliadel, por ejemplo) para rellenar cavidades cerebrales postoperatorias.
Por todo ello, investigaciones actuales trabajan en la caracterización de la firmeza del tejido cerebral en todas las escalas, desde la morfología visible hasta la escala nanométrica (neuronas y células glia) y bajo condiciones fisiológicas. Esta caracterización, así mismo, deberá realizarse mediante métodos y protocolos estandarizados, con el objetivo de asegurar una comparación fiable entre distintos estudios.
Únicamente cuando comprendamos en profundidad las propiedades del tejido cerebral, seremos capaces de desarrollar biomateriales que se asemejen lo suficiente a la complejidad del mismo. Esta tarea conllevará un esfuerzo y supondrá un desafío para las y los investigadores, la tecnología con la que contamos actualmente ayudará a abordar la labor.
Referencias:
Axpe, E., Orive, G., Franze, K., & Appel, E. A. (2020). Towards brain-tissue-like biomaterials. Nature Communications, 11(1), 10–13. doi: 10.1038/s41467-020-17245-x
Peppas, N. A., & Langer, R. (1994). New challenges in biomaterials. Science, 263(5154), 1715–1720. doi: 10.1126/science.8134835
Biomaterials. (2017, September). Retrieved October 26, 2020, from https://www.nibib.nih.gov/science-education/science-topics/biomaterials
Sobre la autora: Irati Diez Virto es graduada en biología por la UPV/EHU y colaboradora en la Cátedra de Cultura Científica
El artículo En busca de biomateriales que se asemejen al tejido cerebral se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Cómo ver todas las células en tejido cerebral vivo
- Películas magnetoactivas de fibroína de seda para la generación de tejido óseo
- Del mito al hecho: hemisferios, gimnasia cerebral y estilos de aprendizaje
Juan Manuel Bermúdez-García – Naukas Pro 2019: Sólidos como refrigerantes
 Foto: David Sanchez / Pixabay
Foto: David Sanchez / Pixabay
Alrededor del 20 % del consumo energético mundial se dedica a la refrigeración. El impacto de este consumo sobre el cambio climático no es pequeño, además los gases que se emplean son gases de efecto invernadero, inflamables y tóxicos. El grupo de Juan Manuel Bermúdez-García, de la Universidade da Coruña, ha desarrollado una tecnología de gases a baja presión con cero emisiones. En esta sesión de Naukas Pro 2019 expone los fundamentos de su trabajo que permitiría, por ejemplo, refrigerar edificios enteros gracias a la presión que ejercen sobre el suelo sus inquilinos al caminar. Todo empieza con el mecanismo de un botijo…
Más información sobre esta tecnología en La nueva forma de enfriar que lo cambiará todo de Deborah García Bello.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Juan Manuel Bermúdez-García – Naukas Pro 2019: Sólidos como refrigerantes se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Juan Ignacio Cirac – P4K 2019: ¿Cómo serán los ordenadores cuánticos?
- Alfredo García – Naukas Bilbao 2019: Derribando mitos sobre la energía nuclear
- Ambrosio Liceaga – Naukas P4K 2019: Nunca quisimos coches voladores
Origen y legado genético de los perros prehistóricos
Una investigación global del ADN de perros antiguos, dirigido por científicos del Instituto Francis Crick, Universidad de Oxford, Universidad de Viena y arqueólogos de más de 10 países, presenta evidencia de que había diferentes tipos de perros hace más de 11.000 años, en el período de la Edad del Hielo. En la investigación ha participado Aritza Villaluenga, del Departamento de Geografía, Prehistoria y Arqueología y del Grupo Consolidado de Investigación en Prehistoria de la Universidad del País Vasco.
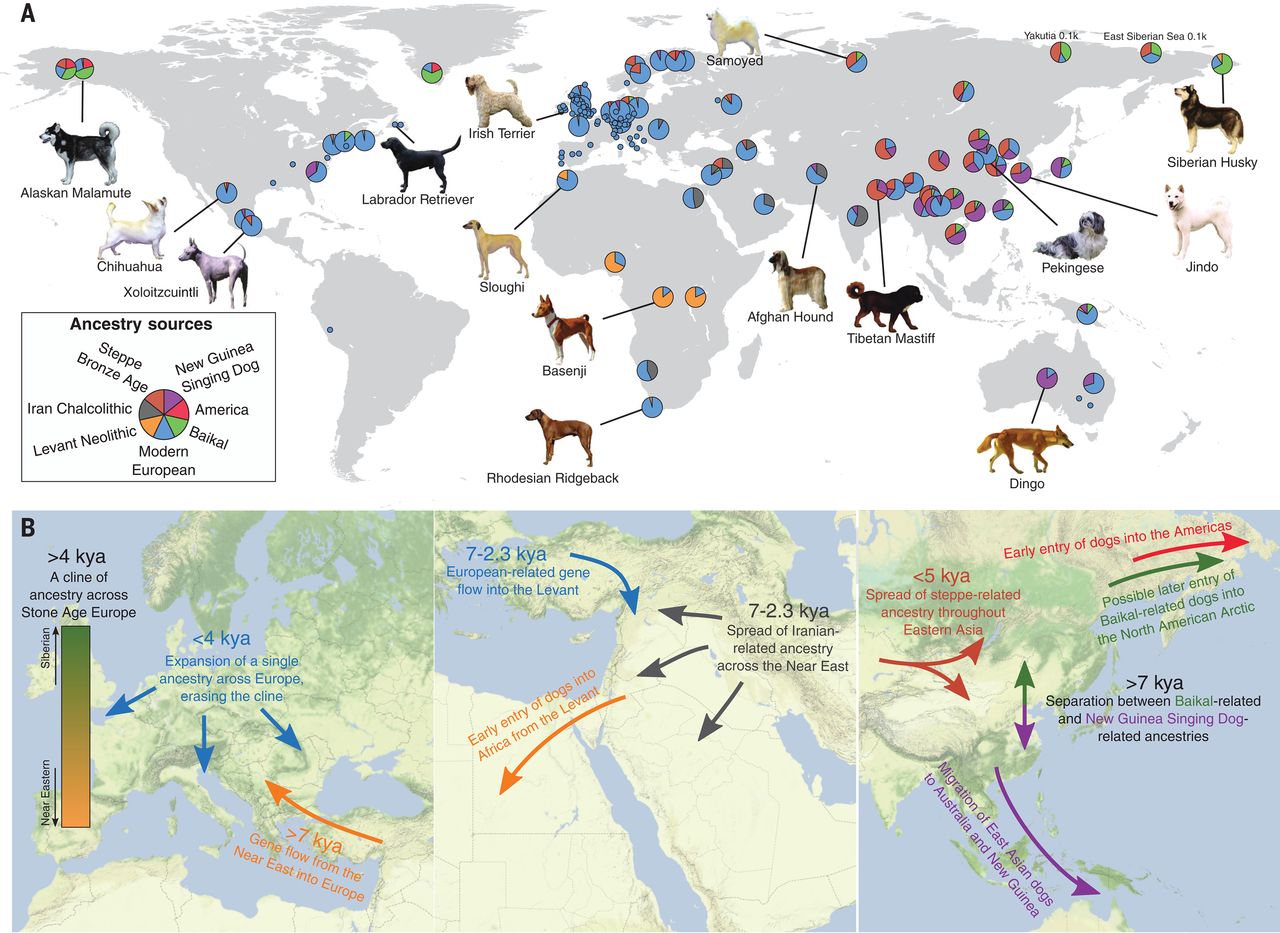
El estudio ‘Origins and Genetic legacy of Prehistoric dogs’, publicado por la revista Science, recoge el trabajo del equipo de investigación que ha secuenciado el ADN antiguo de 27 perros, algunos de los cuales vivieron hasta hace casi 11.000 años en Europa, Oriente Próximo y Siberia. Según los datos recogidos, en ese punto en la historia, justo después de la Edad del Hielo y antes de que cualquier otro animal fuera domesticado, ya existían al menos cinco tipos diferentes de perros con distintas ascendencias genéticas.
Ese hallazgo revela que la diversidad observada hoy entre perros en diferentes partes del mundo se originó cuando todos los humanos aún eran cazadores y recolectores. Según Pontus Skoglund, líder de grupo del laboratorio de Crick’s Ancient Genomics, “algunas de las variaciones que se ven entre los perros que caminan por la calle hoy en día se originaron en la Edad del Hielo. Al final de ese período, los perros ya estaban muy extendidos por todo el hemisferio norte».
El estudio de la genómica antigua implica extraer y analizar ADN del material esquelético. Proporciona una ventana al pasado, lo que permite a los investigadores descubrir cambios evolutivos que ocurrieron hace muchos miles de años.
El equipo investigador ha demostrado que, durante los últimos 10 000 años, esos primeros linajes de perros se mezclaron y se movieron para dar lugar a los perros que conocemos hoy. Por ejemplo, los primeros perros europeos eran inicialmente diversos y parecían provenir de dos poblaciones muy distintas, una relacionada con los perros de Oriente Próximo y otra con los perros siberianos. Sin embargo, en algún momento esa diversidad se perdió, ya que hoy no está presente en los perros europeos.
Como comenta Anders Bergström, investigador postdoctoral en el laboratorio de Genómica Antigua en Crick, “si miramos hacia atrás hace más de cuatro o cinco mil años, podemos ver que Europa era un lugar muy diverso en lo que respecta a los perros. Aunque los perros europeos que vemos hoy tienen una variedad extraordinaria de formas, genéticamente se derivan de un subconjunto muy estrecho de la diversidad que solía existir».
Evolución paralela
Los investigadores también compararon la evolución en la historia del perro con los cambios en la evolución humana, los estilos de vida y las migraciones. En muchos casos, se produjeron cambios comparables, ya que los humanos llevarían a sus perros con ellos mientras migraban por todo el mundo.
Pero también hay casos en los que las historias de humanos y perros no se relacionan entre sí. Por ejemplo, la pérdida de diversidad que existía en los perros en la Europa temprana fue causada por la propagación de un solo ancestro de perro que reemplazó a otras poblaciones. Ese dramático evento no se refleja en las poblaciones humanas, y queda por determinar qué causó ese cambio en la ascendencia de los perros europeos.
Para Greger Larson, director de la Red de Investigación en Paleogenómica y Bioarqueología de la Universidad de Oxford, “el perro es nuestro compañero animal más antiguo y cercano. El uso de ADN de perros antiguos nos muestra cuán atrás se remonta nuestra historia compartida y, en última instancia, nos ayudará a comprender cuándo y dónde comenzó esa relación profunda».
Por su parte, Ron Pinhasi, líder del grupo en la Universidad de Viena, afirma que “así como el ADN antiguo ha revolucionado el estudio de nuestros propios antepasados, ahora está comenzando a hacer lo mismo con los perros y otros animales domésticos. El estudio de nuestros compañeros animales agrega otra capa a nuestra comprensión de la historia humana».
Si bien este estudio proporciona nuevos conocimientos importantes sobre la historia temprana de las poblaciones de perros y sus relaciones con los humanos y entre sí, aún quedan muchas preguntas. En particular, los equipos de investigación todavía están tratando de descubrir dónde y en qué contexto cultural humano los perros fueron domesticados por primera vez.
Referencia:
Anders Bergström, Laurent Frantz, Ryan Schmidt, Erik Ersmark, Ophelie Lebrasseur, Linus Girdland-Flink, Audrey T. Lin, Jan Storå, Karl-Göran Sjögren, David Anthony, Ekaterina Antipina, Sarieh Amiri, Guy Bar-Oz, Vladimir I. Bazaliiskii, Jelena Bulatovic´, Dorcas Brown, Alberto Carmagnini, Tom Davy, Sergey Fedorov, Ivana Fiore, Deidre Fulton, Mietje Germonpré, James Haile, Evan K. Irving-Pease, Alexandra Jamieson, Luc Janssens, Irina Kirillova, Liora Kolska Horwitz, Julka Kuzmanovic-Cvetkovic, Yaroslav Kuzmin, Robert J. Losey, Daria Ložnjak Dizdar, Marjan Mashkour, Mario Novak, Vedat Onar, David Orton, Maja Pasaric´, Miljana Radivojevic´, Dragana Rajkovic´, Benjamin Roberts, Hannah Ryan, Mikhail Sablin, Fedor Shidlovskiy, Ivana Stojanovic´, Antonio Tagliacozzo, Katerina Trantalidou, Inga Ullén, Aritza Villaluenga, Paula Wapnish, Keith Dobney, Anders Götherström, Anna Linderholm, Love Dalén6, Ron Pinhasi, Greger Larson, Pontus Skoglund (2020) Origins and Genetic Legacy of Prehistoric Dogs. Science doi: 10.1126/science.aba9572
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Origen y legado genético de los perros prehistóricos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:¿En qué se parecen un trombón y un elefante?
 Foto: Geran de Klerk / Unsplash
Foto: Geran de Klerk / UnsplashParece el comienzo de un chiste. Pero no. Es la premisa de un artículo sobre la acústica de los instrumentos de viento metal publicado Joël Gilbert y Jean-Pierre Dalmont1. ¿En qué se parecen un trombón y un elefante? En su sonido, evidentemente. Y no por casualidad: la trompa del elefante se comporta, en muchos sentidos, como el tubo de uno de estos instrumentos de viento.
 Una preciosa viñeta de Laerte Coutinho
Una preciosa viñeta de Laerte CoutinhoTanto los elefantes africanos como los asiáticos viven en grupos sociales donde la comunicación vocal tiene una gran importancia. Ambas especies producen una amplia gama de señales, desde llamadas de muy baja frecuencia hasta su característico barritar, en un rango de frecuencias más agudo. Los barritos del elefante se producen por una expulsión abrupta de aire a través de su trompa. El animal hace vibrar sus cuerdas vocales de manera similar a como lo hacemos los humanos al hablar o cantar, mediante un flujo de aire procedente de los pulmones.
En otro sentido, sin embargo, el sonido de los elefantes es mucho más similar al que produce un trombón y otros instrumentos de viento metal, especialmente en su rango dinámico más forte. La cavidad interna de su sistema vocal, desde las cuerdas vocales hasta el extremo de la trompa que irradia el sonido, mide varios metros de largo (75 cm de tracto vocal más 2,5 m de tracto nasal, de acuerdo con Christian T. Herbst2), parecido al tubo del trombón, en concreto, que extendido mide alrededor de 3 m. Esto permite que se produzcan efectos no lineales en la propagación del sonido dentro de la trompa del animal (¡pequeñas ondas de choque!) el mismo fenómeno que caracteriza el timbre más brassy o metálico del trombón y que lo convierte en un excelente instrumento de larga distancia.
Hasta hace algunas décadas, se pensaba que los elefantes solo se comunicaban mediante estos barritos dentro de un entorno amplio pero relativamente limitado (estos sonidos se disipan en poco más de 1 km). Sin embargo, en los años 90, Caitlin O’Connell-Rodwell, bióloga de la Universidad de Stanford en Palo Alto, California, descubrió que estos paquidermos utilizan también infrasonidos, indetectables por el oído humano, para alcanzar distancias mucho mayores. Hoy sabemos que, gracias a sus enormes cuerdas vocales, los elefantes pueden producir vocalizaciones de muy baja frecuencia a amplitudes tan altas que hacen vibrar el suelo y viajan por su superficie a gran velocidad3, recorriendo así distancias de hasta 10 kilómetros.
Resulta aún más sorprendente el hecho de que los elefantes perciben estas señales ¡a través de sus patas! Para comprobarlo los investigadores utilizaron distintos tipos de grabaciones4: “una mezcla de llamadas de elefante, tonos sintéticos de baja frecuencia, música rock y silencio para comparar”. Las reprodujeron contra el suelo, mediante un transmisor sísmico, intentando evitar que se transmitieran también por el aire. Los elefantes reaccionaron vivamente a estas señales, especialmente a las llamadas de alerta. Como explica O’Connell-Rodwell: «las ondas sísmicas podrían viajar desde las uñas de sus pies hasta el oído a través de la conducción ósea, o a través de receptores somatosensoriales situados en el pie similares a los que se encuentran en la trompa. Creemos que puede tratarse de una combinación de ambos mecanismos».
Gracias a sus sensibles pies, los elefantes pueden enviar y recibir señales de socorro o alerta a través de distancias inconcebibles para nosotros. Y no únicamente mediante vocalizaciones. Cuando un elefante está nervioso y salta, o pisa la tierra dejando caer todo el peso de sus varias toneladas, envía información al resto de sus compañeros. Según Michael Garstang, meteorólogo de la Universidad de Virginia en Charlottesville, este curioso superpoder les serviría incluso para predecir las inclemencias del tiempo. Según un estudio publicado en el año 2014, los elefantes serían capaces de oír tormentas desde una distancia de más de 100 kilómetros5.
De manera más general, este sistema de comunicación a larga distancia les permite localizar a otros miembros de su especie, reforzar el vínculo entre grupos y mantener a los miembros de la familia en contacto, incluso si se encuentran dispersos a grandes distancias para encontrar comida y agua en tiempos de escasez. Nada mal, para un trombón con patas.
Referencias:
1Gilbert, Joël, and Jean-Pierre Dalmont. “Brassy sounds, from trombone to elephant.” Proceedings of the International Symposium on Music Acoustics, 2010.
2Herbst, Christian T., et al. “How Low Can You Go? Physical Production Mechanism of Elephant Infrasonic Vocalizations.” Science, vol. 337, 2012, pp. 595-599. doi: 10.1126/science.1219712.
3O’Connell-Rodwell, Caitlin E. “Keeping an “Ear” to the Ground: Seismic Communication in Elephants.” PHYSIOLOGY, vol. 22, 2007, pp. 287–294, doi: 10.1152/physiol.00008.2007.
4O’Connell-Rodwell, Caitlin E., et al. “Seismic properties of Asian elephant (Elephas maximus) vocalizations and locomotion.” The Journal of the Acoustical Society of America, vol. 108, no. 3066, 2000. doi:10.1121/1.1323460.
5Garstang, Michael & Davis, Robert & Leggett, Keith & Frauenfeld, Oliver & Greco, Steven & Zipser, Edward & Peterson, Michael. (2014). Response of African Elephants (Loxodonta africana) to Seasonal Changes in Rainfall. PloS one. 9. e108736. doi: 10.1371/journal.pone.0108736.
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
El artículo ¿En qué se parecen un trombón y un elefante? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Marian Rejewski, el matemático que «rompió» la Máquina Enigma
¿Cuál es la diferencia entre el número dos y la rutina?
Con esta frase comienza “Esperando al hijo”, uno de los cuentos contenidos en “La vida anticipada”, el nuevo libro de relatos del escritor Francisco Javier Guerreroi. Gracias a este cuento he (re)descubierto al matemático y criptógrafo de origen polaco Marian Rejewski quien, en 1932, «rompió» la máquina Enigma, el principal dispositivo cifrado empleado por Alemania durante la Segunda Guerra Mundial.
 Marian Rejewski. Fuente: Wikimedia Commons.
Marian Rejewski. Fuente: Wikimedia Commons.
Marian Rejewski (1905-1980) nació en Bydgoszcz (conocida también como Bromberg en alemán), ciudad situada en la partición prusiana de Polonia. En 1923, tras terminar su Gymnasium (en alemán) en Bydgoszcz, entró en la Universidad Adam Mickiewicz de Poznań para estudiar matemáticas. En 1929 obtuvo su Máster en matemáticas con una tesis sobre funciones periódicas. En esa época asistió también a un curso de criptología organizado por el Biuro Szyfrów (Oficina de Cifrado) destinado a los mejores estudiantes de matemáticas de habla alemana.
En el verano de 1930 le ofrecieron un puesto de ayudante de matemáticas en la Universidad de Poznań. Compaginaba su trabajo de profesor con un empleo a tiempo parcial para la sucursal en Poznań del Biuro Szyfrów. En aquella oficina estaban interesados en decodificar mensajes alemanes (interceptados) enviados por radio con un nuevo sistema de cifrado. Estaban codificados por una máquina Enigma, detalle que en aquellos momentos desconocían en Polonia. La sucursal de Poznań del Biuro Szyfrów cerró en el verano de 1932 y Rejewski comenzó a trabajar a tiempo completo en su sede en Varsovia. Allí se le unieron otros dos jóvenes matemáticos polacos, Jerzy Rozycki (1909-1942) y Henryk Zygalski (1908-1978). El equipo disponía de una máquina Enigma comercial que Rejewski pudo estudiar, aunque los mensajes interceptados estaban siendo enviados por máquinas Enigma militares, versiones modificadas de las primeras.
 Marian Rejewski, Henryk Zygalski y Jerzy Rozycki. Fuente: Wikimedia Commons.
Marian Rejewski, Henryk Zygalski y Jerzy Rozycki. Fuente: Wikimedia Commons.
Usando el abundante material criptográfico interceptado por los servicios de escucha del ejército polaco y sus conocimientos matemáticos, Rejewski consiguió reconstruir el cableado interno de esta máquina, el responsable de generar esas permutaciones que servían para cifrar mensajes.
Los alemanes cambiaban periódicamente el procedimiento de codificación para introducir sistemas más seguros. Tras cada modificación, Rejewski, Rozycki y Zygalski conseguían desentrañar gran parte de los mensajes Enigma que debían decodificar.
El ejército alemán invadió Polonia el 1 de septiembre de 1939, avanzando rápidamente hacia Varsovia. Rejewski y su equipo fueron evacuados a Rumania y desde allí huyeron a París, uniéndose a una unidad de decodificación conjunta franco-polaca-española en el Château de Vignolles (noreste de París) donde continuaron con su labor.
En mayo de 1940, Alemania invadió Francia. El 14 de junio las tropas alemanas entraron en París; Francia capituló el 22 de junio. Rejewski y sus colegas fueron de nuevo evacuados, esta vez a Argelia. Regresaron a Francia en septiembre de 1940, ocultando su verdadera identidad; Rejewski se hizo pasar por profesor de matemáticas de un liceo de Nantes. Trabajó en el Château des Fouzes, donde se instaló una unidad secreta de inteligencia. Tras la invasión por parte de los aliados del norte de África, las tropas alemanas ocuparon la Francia de Vichy. La unidad secreta de inteligencia del Château des Fouzes fue evacuada en noviembre de 1942. Rejewski y Zygalski (Rozycki había fallecido en un naufragio regresando de Argelia) se movieron por varias ciudades del sur de Francia, pasaron a España (donde fueron encarcelados), a Portugal y desde Gibraltar fueron trasladados a Gran Bretaña, donde llegaron a principios de agosto de 1943. Allí Rejewski se unió al ejército polaco y permaneció durante el resto de la guerra realizando labores de decodificación. Probablemente las autoridades británicas desconocían las habilidades de Rejewski; en otro caso Bletchley Park habría sido su destino adecuado.
A finales de noviembre de 1946, Rejewski fue desmovilizado y regresó a Polonia para reunirse con su familia. Investigado por su actividad durante la guerra, tras varias vicisitudes y cambios de trabajo, se jubiló en 1967, momento en el que rompió su silencio y desveló el trabajo criptológico al que se había consagrado durante la guerra. Hasta 1973 su relación con la decodificación de la máquina Enigma no fue conocida; a partir de allí los reconocimientos fueron numerosos, al menos en su país. Como suele pasar, la historia «corona» a algunos como héroes y olvida a otras y otros que, en el mejor de los casos y con mucha suerte, reciben un tributo tardío.
 Monumento a Rejewski, Rozycki y Zygalski (diseño de Grazyna Bielska-Kozakiewicz y Mariusz Krzysztof Kozakiewicz). Se trata de un prisma de base triangular regular cuyos lados están cubiertos con filas de números. En cada lado del monumento, entre los números, se esconde el nombre de uno de los descifradores de códigos.
Monumento a Rejewski, Rozycki y Zygalski (diseño de Grazyna Bielska-Kozakiewicz y Mariusz Krzysztof Kozakiewicz). Se trata de un prisma de base triangular regular cuyos lados están cubiertos con filas de números. En cada lado del monumento, entre los números, se esconde el nombre de uno de los descifradores de códigos.
«Con dos enlaces indiscutibles estaría conectado con Hitler y eso era una crueldad. Así que, le dijo muy enfadado a su amigo Henryk Zygalski al día siguiente mientras paseaban: «no debe ser cierta esa hipótesis o debe tener trampa, las matemáticas son hermosas, no despiadadas».»
Francisco Javier Guerrero, fragmento de [1]
Referencias
[1] Francisco Javier Guerrero y Lola Castillo, Esperando al hijo en La vida anticipada, Editorial Adeshoras, 2020 (páginas 35-40)
[2] John J. Robertson and F. Edmund, Marian Adam Rejewski, MacTutor History of Mathematics archive, Universidad de Saint Andrews.
[3] Marian Adam Rejewski, Wikipedia
[4] Rocío Gallardo Gómez, El ataque polaco al protocolo, Trabajo fin de Grado, Universidad de Sevilla, 2016
[5] M Rejewski, An Application of the Theory of Permutations in Breaking the Enigma Cipher, Applicationes Mathematicae 16 (4) (1980), 543-559.
[6] M Rejewski, How Polish Mathematicians Deciphered the Enigma, Annals of the History of Computing, 3 (3): 213-234
Nota:
i Ya conocíamos en el Cuaderno de Cultura Científica a Francisco Javier Guerrero. Hace casi dos años hablamos de su poemario Las razones del agua en la entrada ¡Nos encanta Fibonacci!. Comentábamos la manera en la que la sucesión de Fibonacci estructuraba el poemario y su presencia sutil y certera en algunos de sus versos.
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Marian Rejewski, el matemático que «rompió» la Máquina Enigma se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Una máquina Enigma molecular
- El enigma del número 23
- Marian Diamond: la científica que descubrió la plasticidad cerebral
Historia del Super Glue
A comienzos de los años 40 del pasado siglo, el químico Harry Wesley Coover descubrió el Super Glue por accidente. Transcurría la Segunda Guerra Mundial y Coover y su equipo trabajaban en la empresa Kodak desarrollando un plástico transparente para visores de armas de fuego. Estaba experimentando con acrilatos cuando descubrió un adhesivo súper pegajoso (cianoacrilato).
Dejaron el descubrimiento de lado hasta que en 1951 Fred Joyner, investigador del equipo de Coover, volvió a usar el mismo compuesto cuando buscaban un revestimiento resistente a la temperatura para cabinas de aviones. El investigador extendió el «pegamento» en dos lentes de un refractómetro para medir el índice de refracción y comprobó que las lentes no se despegaban y pensó que aquello podía tener una salida comercial.
Pocos años después, llegó al mercado el primer Super Glue, al que llamaron Eastman 910. Sin embargo, el pegamento no tuvo mucho éxito hasta que a finales de los años 70 descrubrieron que emanaba vapores de cianoacrilato, los cuales se adherían a la grasa de la piel y dejaban al descubierto los minúsculos surcos de las yemas de nuestros dedos.
Los vídeos de Historias de la Ciencia presentan de forma breve y amena pasajes de la nuestra historia científica y tecnológica. Los vídeos, realizados para la Cátedra de Cultura Científica de la UPV/EHU, se estrenan en el programa de ciencia Órbita Laika (@orbitalaika_tve), los lunes a las 22:00 en la 2 de RTVE.
El artículo Historia del Super Glue se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:El problema de la estructura nuclear
 Foto: Aron Visuals / Unsplash
Foto: Aron Visuals / Unsplash
El descubrimiento de la radiactividad y de la existencia de los isótopos fueron avances extraordinarios. Y, como es habitual, también plantearon nuevas preguntas sobre la estructura última de los átomos, cuestiones que involucraban al núcleo atómico.
Las reglas de desplazamiento radiactivo podían entenderse en términos del modelo del átomo de Rutherford-Bohr-Sommerfeld. Pero ese modelo ampliado lo único que decía del núcleo era que es pequeño, que tiene carga y masa, y que puede emitir partículas alfa o beta. De aquí había que deducir necesariamente que el núcleo tiene una estructura que cambia cuando ocurre un proceso radiactivo. La pregunta es inmediata: ¿Se puede desarrollar un modelo del núcleo atómico que explique los hechos de la radiactividad y la existencia de isótopos? [1]
El problema de la estructura nuclear se puede plantear como dos preguntas:
(1) ¿Cuáles son las piezas básicas (partículas) de las que está hecho el núcleo?
(2) ¿Cómo se unen estas piezas para formar el núcleo?
El intento de resolver el problema de la estructura nuclear, aunque sigue siendo una actividad de frontera en la física actual, ya ha dado lugar a muchos descubrimientos básicos y a aplicaciones prácticas a gran escala. También ha tenido importantes consecuencias económicas, sociales y políticas, que se extienden mucho más allá de la ciencia básica.
La emisión de partículas alfa y beta por los núcleos radiactivos sugería que se podría construir un modelo del núcleo comenzando con estas partículas alfa y beta como piezas básicas. Un modelo de este tipo facilitaría ver, por ejemplo, cómo se pueden emitir varias partículas, en sucesión, en una serie radioactiva. Pero no va a ser tan fácil. No todos los núcleos son radiactivos, ni todos los núcleos tienen masas que sean múltiplos de la masa de la partícula alfa. Por ejemplo, el núcleo de un átomo del elemento más ligero, el hidrógeno, con una masa atómica de una unidad (dos unidades en el caso del isótopo pesado), es demasiado ligero para contener una partícula alfa; también lo es el isótopo ligero del helio, el helio-3.
Una partícula cargada positivamente con una masa unidad parece de entrada algo mucho más racional como pieza básica. De hecho, existe una partícula así: el núcleo del isótopo más común del hidrógeno, el hidrógeno-1. A esta partícula la conocemos como protón. En el modelo de estructura atómica de Rutherford-Bohr-Sommerfeld el átomo de hidrógeno consiste en un protón con un solo electrón girando a su alrededor. Es un resultado experimental el que las masas atómicas de los nucleidos están muy cerca de números naturales; de aquí que los nucleidos se escriban usando números naturales para la masa atómica, A. Este hecho, junto con las propiedades del protón (por ejemplo, su carga positiva única) hizo que pareciera posible plantear que todos los núcleos atómicos estén compuestos de protones. ¿Podría un núcleo de masa A consistir en un número A de protones?
Notas:
[1] La respuesta a esta pregunta constituye toda una rama del conocimiento conocida como física nuclear.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo El problema de la estructura nuclear se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La estructura de la tabla periódica se deduce de la estructura de capas de los átomos
- Las reglas de desplazamiento radiactivo
- La radiactividad no es una reacción química
¿Puede la 5G interferir con los sistemas de predicción del tiempo meteorológico?
Ana García Armada
 Foto: USGS / Unsplash
Foto: USGS / UnsplashUn reciente estudio de la Universidad Rutgers, en Estados Unidos, sugiere que el despliegue de futuros servicios 5G podría afectar a la precisión de las previsiones meteorológicas.
El trabajo ha sido elaborado por el Laboratorio de Redes de Información Inalámbrica de la Escuela de Ingeniería de la citada universidad. Analicemos el estudio en profundidad para explicar cómo y porqué se puede producir esta interferencia, así como posibles soluciones.
¿De qué frecuencias estamos hablando y por qué?
El estudio se refiere a la banda de 26 gigahercios (GHz), denominada como banda n258 por el 3GPP (3rd Generation Partnership Project), un organismo que estandariza las comunicaciones móviles.
La n258 pertenece al conjunto de bandas habilitadas recientemente para su uso en comunicaciones móviles 5G. Se conocen como ondas milimétricas, aunque, siendo precisos, las milimétricas empezarían a partir de los 30 GHz, con longitudes de onda menores de 10 milímetros (de ahí el nombre de milimétricas). Otras bandas que se engloban dentro de la misma denominación son las de 28 GHz (banda n257) y 39 GHz (n260).
La Conferencia Mundial de Radiocomunicaciones (WRC) depende de la Unión Internacional de Telecomunicaciones (ITU), un organismo especializado de las Naciones Unidas para las tecnologías de la información y las comunicaciones.
En su reunión de noviembre de 2019, la WRC identificó las milimétricas, entre otras bandas de frecuencia, para su uso armonizado y global en lo que la ITU denomina International Mobile Telecommunications IMT-2020 (más conocidas como comunicaciones móviles 5G).
Explica la WRC que la adición de estas bandas de frecuencia a las que ya podían ser utilizadas para estos servicios responde a una necesidad de mayor ancho de banda. Es necesario para proporcionar comunicaciones móviles de mayor velocidad de datos a un número creciente de dispositivos, facilitar sistemas de transporte inteligentes, ciudades inteligentes, un crecimiento sostenible, mejor sanidad, agricultura y eficiencia energética.
De todas las bandas habilitadas por la ITU, la banda de 26 GHz es la elegida en Europa para el despliegue de la 5G, junto con las bandas de 700 MHz y 3,6 GHz. Una vez tomadas las decisiones a nivel global y europeo, los países europeos pueden disponer las medidas necesarias y proceder a las subastas para el uso de estas frecuencias.
¿Por qué se pueden producir interferencias?
La regulación del espectro radioeléctrico por parte de la ITU es imprescindible para asegurar que diferentes servicios de radiocomunicaciones utilizan porciones diferentes del espectro de frecuencias.
Esto nos permite disfrutar de innumerables servicios (Bluetooth, televisión, GPS, wifi, etc.) en el mismo lugar y momento, aunque todos ellos hagan uso del espectro radioeléctrico. Para que cada uno utilice una porción del mismo, el transmisor debe situar su información en la frecuencia deseada.
Aprovechando las características del espectro, estas informaciones transmitidas a la vez, pero en distinta frecuencia, se pueden separar. De esta forma, un receptor puede centrarse únicamente en una parte (o banda) del espectro, filtrando las demás (como si depuráramos agua con un filtro) de modo que las excluye y no interfieren.
Pero los filtros no son perfectos y siempre es posible que algo de información, sobre todo la que se transmita en frecuencias cercanas, pase a través del filtro y nos afecte. Este es el caso de los servicios meteorológicos de los que trata el estudio, que precisamente utilizan una frecuencia de 23,8 GHz, muy cercana al borde inferior de la banda de 26 GHz (que abarca desde 24,25 hasta 27,5 GHz).
Midiendo la radiación que reciben en esta frecuencia, los sensores meteorológicos pueden determinar la densidad de vapor de agua en la atmósfera, y a través de ellas hacer predicciones del tiempo. Es el caso de los sensores que están a bordo de satélites de la Oficina Nacional de Administración Oceánica y Atmosférica (NOAA) de Estados Unidos.
Uno podría pensar que, estando los satélites tan lejos, la fracción que reciben de la 5G que está en Tierra es insignificante (y así es). Pero, al parecer, según los autores del estudio, la radiación puede perturbar las características de las emisiones de la atmósfera, de modo que las medidas son ligeramente distintas y la precisión de los modelos de previsión del tiempo empeora.
¿Cómo evitar posibles efectos perjudiciales?
Hay esencialmente tres mecanismos para evitar que las interferencias de unos servicios puedan afectar a otros: evaluar, proteger y mejorar.
Evaluar es precisamente uno de los objetivos del estudio de Rutgers. Si conocemos mejor los efectos de las interferencias y cómo se producen, podemos evitarlos sin tener que renunciar a utilizar ninguno de los dos servicios implicados.
Una evaluación correcta nos ayuda con la protección. Esto es precisamente lo que hace la ITU. La WRC explica que, al mismo tiempo que se aprobó el uso de las bandas milimétricas para 5G, se acordaron también medidas de protección para el servicio de exploración de la Tierra a través de satélite y para sensores meteorológicos y otros similares que puedan operar en bandas adyacentes. Estas garantizan que dichos servicios permanecen sin problemas, al igual que las estaciones de radioastronomía.
Pero las medidas protectoras pueden resultar insuficientes en algunos casos. Por eso es necesario desarrollar tecnología con los siguientes objetivos:
- Modelar mejor la propagación y la interferencia.
- Evaluar el efecto de la densidad de estaciones transmisoras.
- Determinar buenas opciones de diseño de transmisores y receptores para producir y captar menos interferencia.
- Dirigir la señal fuera de la dirección que pueda afectar a las medidas de los satélites (esto se hace particularmente bien en ondas milimétricas con una tecnología denominada beamforming).
- Mejorar los sistemas de predicción meteorológica para que sean robustos a estas interferencias residuales.
Los autores del estudio de Rutgers concluyen señalando que seguirán trabajando para obtener técnicas que mitiguen el efecto de las interferencias. Los avances tecnológicos permiten un uso armonizado del espectro, que contribuye a mejorar nuestra calidad de vida, a la que sin duda contribuye también una predicción meteorológica precisa.
![]()
Sobre la autora: Ana García Armada, es catedrática det eoría de la señal y comunicaciones en la Universidad Carlos III
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo ¿Puede la 5G interferir con los sistemas de predicción del tiempo meteorológico? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El cerebro también se puede donar (y no es necesario estar sano)
- La teoría de bandas explica la conducción eléctrica
- ¿Puede la física resolver problemas en medicina?
Los perros de trineo más antiguos
 Fuente: Wikimedia Commons
Fuente: Wikimedia CommonsLos perros, como otros animales domesticados, se asociaron con los seres humanos mediante relaciones de comensalismo, seguramente. No sabemos con precisión cuándo se produjo esa asociación, pero ocurrió hace, al menos, quince mil años. Con algunos de esos perros, además, nuestros antepasados establecieron relaciones que fueron más allá del comensalismo. La caza, el pastoreo o la vigilancia, por ejemplo, son tareas para las que hemos entrenado y seleccionado variedades de perros.
Tal y como sugieren restos arqueológicos de hace unos 12500 años de antigüedad hallados en la isla de Zhokov (Mar de Siberia), grupos de cazadores recolectores habían domesticado perros para tirar de trineos. En un estudio recién publicado han comparado el genoma de un perro de hace 9500 años, procedente de ese mismo lugar, con el de un lobo siberiano de hace 33000 años, y con los de diez perros de trineo groenlandeses contemporáneos.
El perro de Zhokov está emparentado genéticamente con los perros de trineo actuales y, en mayor medida, con los de Groenlandia. Se trata de una estirpe seleccionada a través de un proceso largo, para dar respuesta a las necesidades de transporte de los pobladores de Groenlandia, desde miles de años antes, incluso, de la llegada de los inuit hace 850 años. No hay, por tanto, registros genealógicos de esta, como ocurre con las estirpes de otros perros de trineo, que son de selección mucho más reciente.
El perro de Zhokov no es antepasado directo de los modernos perros de trineo, pero sí comparte un ancestro común con ellos que vivió hace unos 12000 años. Sí se puede afirmar, sin embargo, que hace 9500 años ya había perros de trineo que se asemejaban a los actuales y que desempeñaban funciones similares. Curiosamente, ni los actuales perros groenlandeses ni los de hace 9500 años parecen haber hibridado con lobos. Es sorprendente porque es sabido que esas hibridaciones no se han dejado de producir a lo largo de la historia de la domesticación de los perros. Esos híbridos, seguramente, no ofrecen el rendimiento requerido o no se adaptan bien al trineo.
Algunas de las diferencias genéticas encontradas entre los perros groenlandeses y los de otras estirpes y latitudes se habían observado antes al comparar el genoma de mamuts y el de elefantes, por lo que se les atribuye una relación con la adaptación al frío. Otra variante genética de los perros groenlandeses está relacionada con el desempeño metabólico bajo condiciones de escasez de oxígeno; curiosamente, una variante de ese gen en humanos permite a los bajau –los llamados nómadas del mar- del sudeste asiático sumergirse en apnea durante tiempos excepcionalmente largos. En el caso de los perros no se trataría de hacer frente a condiciones de escasa concentración de oxígeno en el ambiente, sino a la alta demanda metabólica propia de esfuerzos extremos y sostenidos. También presentan variantes que les permiten alimentarse casi exclusivamente mediante dietas con muy alto contenido en grasa y bajo en carbohidratos, adaptaciones ya descritas en osos polares y seres humanos.
La continuidad en el tiempo de los perros groenlandeses no deja de resultar paradójica. Los perros de trineo actuales y la tecnología asociada proceden, en gran parte, de la cultura Thule, de hace entre 2000 y 3000 años. Los perros estuvieron a punto de desaparecer hace 850 años, cuando llegaron los inuit a Groenlandia. Pero no se extinguieron; la prueba es que hoy perduran. Así pues, aunque por Groenlandia han pasado diferentes culturas humanas, los perros de trineo groenlandeses han pervivido desde el Paleolítico, porque han formado parte esencial del modo de vida de todos esos pueblos.
Fuente: Mikkel-Holger S Sinding et al: Arctic-adapted dogs emerged at the Pleistocene-Holocene transition. Science 26 June 2020: Vol 368 (6498); 1495-1499 DOI: 10.1126/science.aaz8599
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Los perros de trineo más antiguos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:
