Cuaderno de Cultura Científica

Imagen: Siarhei Yurchanka

Aran Garcia-Leuke es doctora en física y trabajó en la universidad de Liverpool y el Lawrence Berkeley National Laboratory antes de incorporarse al DIPC como investigadora Ikerbasque. Su especialidad es la nanoelectrónica y en 20 minutos consigue hacer una presentación de este campo multidisciplinar para todos los públicos.



Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus

El artículo Aran Garcia-Leuke – Naukas Pro 2019: Intro a la nanoelectrónica se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Juan Manuel Bermúdez-García – Naukas Pro 2019: Sólidos como refrigerantes
2. Naukas Pro 2017: Amaia Zurutuza y el grafeno
3. Joaquín Sevilla – Naukas P4K 2019: Lo que esconden unos champiñones al ajillo

Fuente: Wikimedia Commons

El objetivo de las casas inteligentes es servir de ayuda a las personas que viven en ellas. Las aplicaciones para la vida diaria asistidas por el entorno pueden tener un gran impacto a nivel social, en el envejecimiento activo y en el modo de vida independiente de las personas mayores. De ahí que una de las claves de las casas inteligentes sea la deducción de la actividad humana en ellas. Para ello que se colocan diversos tipos de sensores que detectan los cambios que producen los habitantes de la casa en ese entorno (encender/apagar la luz, abrir/cerrar una puerta, etc.).

Normalmente, la información que generan estos sensores se procesa mediante técnicas de análisis de datos, y los sistemas más exitosos se basan en técnicas de aprendizaje supervisado, es decir, una persona supervisa los datos y un algoritmo aprende automáticamente el significado de todo ello. No obstante, uno de los principales problemas de las casas inteligentes es que un sistema entrenado en un entorno no es válido en otro diferente: “Los algoritmos normalmente están muy vinculados a un entorno inteligente determinado, a los tipos de sensores existentes en el entorno y a su configuración, así como a los hábitos concretos de una persona. El algoritmo aprende todo esto fácilmente, pero luego no es capaz de trasladarlo a otro entorno diferente”, explica Gorka Azkune, del grupo de investigación IXA de la UPV/EHU.

Hasta ahora los sensores se han identificado mediante números, y como consecuencia “se perdía el significado que tenían —explica el doctor Azkune—. Nosotros proponemos utilizar los nombres de los sensores en lugar de identificadores, de manera que se pueda aprovechar su significado, su semántica, para saber con qué actividad están vinculados. Así, lo que el algoritmo aprende en un entorno puede ser válido en otro entorno, aunque los sensores no sean iguales, porque su semántica es similar. Es por eso que utilizamos técnicas de procesamiento del lenguaje natural.

Se utilizan técnicas totalmente automáticas, aclara el investogador: “Al final, el propio algoritmo aprende primero de las palabras y luego de la representación que nosotros hacemos utilizando esas palabras. No hay ninguna intervención humana. Y eso es importante desde el punto de vista de la escalabilidad, pues ha quedado probado que sirve para superar el problema señalado”. De hecho, con esta nueva propuesta han conseguido resultados similares a los logrados mediante las técnica basadas en el conocimiento.

 

Referencia:

Gorka Azkune, Aitor Almeida, Eneko Agirre (2020) Cross-environment activity recognition using word embeddings for sensor and activity representation Neurocomputing doi: 10.1016/j.neucom.2020.08.044

Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa

El artículo Procesamiento lingüístico de los sensores en las casas inteligentes se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Membranas de celulosa nanoestructurada como sensores de metales
2. La confianza en las redes sociales y el uso de electrodomésticos inteligentes
3. Control adaptativo de robots para rehabilitación

Foto: Matthew Bennett / Unsplash

Salud es la ausencia de enfermedad, según una definición más bien negativa, pero Patricia Boyle, del Centro Rush para la Enfermedad de Alzheimer de Chicago, planteó la hipótesis, más positiva, de que, además, para una buena salud es importante tener algo que hacer en la vida, es decir, encontrar un sentido a la vida. Es la propuesta psicológica que da significado a las experiencias vividas e intencionalidad y objetivos que guían las conductas de las personas. La autora menciona a Viktor Frankl como autor del origen del sentido de la vida tal como ella lo entiende.

Viktor Frankl era un neurólogo y psiquiatra, nacido en Viena, que, en la Segunda Guerra Mundial, fue internado en varios campos de concentración nazis, entre ellos Auschwitz y Dachau. Sobrevivió y, en su libro El hombre en busca del sentido último, cuenta que se puede encontrar ese propósito de vida incluso en las condiciones más difíciles. Tener ese sentido de la vida es esencial para mantener la salud y el bienestar mentales. La vida tiene sentido y las metas fijadas, con el potencial de cada persona, se pueden lograr. Además, como apoya Boyle, el propósito vital también es una condición importante de la salud física y de la vitalidad.

En 2009, Patricia Boyle publicó un estudio con 1238 voluntarios con buena salud mental, una edad media de 78 años y el 73% mujeres. La toma de datos comenzó en 2004 y se prolongó durante cinco años.

En ese tiempo murieron 151 voluntarios, un 12%. El tener un propósito de vida supone un 57% menos de mortalidad en comparación con los voluntarios que, aunque declaran tener también un propósito, no se sienten muy comprometidos con él. No hay diferencias entre hombres y mujeres.

En conclusión, un sentido de vida comprometido se asocia a un riesgo de mortalidad menor por cualquier causa.

Al año siguiente, 2010, Patricia Boyle publicó los resultados de un estudio similar que relacionaba el sentido de la vida con el Alzheimer y el déficit cognitivo leve que puede ser una etapa temprana de la enfermedad. Participaron 951 voluntarios, sin diagnóstico de demencia, y son evaluados durante siete años. Tienen una edad media de 80.4 años, y el 80% son mujeres. A los siete años de seguimiento, 155, o sea, el 16% ha desarrollado Alzheimer. El análisis estadístico de las encuestas que responden indica que, quienes presentan un propósito de vida fuerte, tienen 2.4 veces menos riesgo de desarrollar la enfermedad que los que declaran un propósito de vida con escaso compromiso. También el déficit cognitivo leve aparece 1.5 veces menos en quienes tienen un propósito fuerte.

Un estudio con un enfoque más amplio es el de Joanna McHugh Power y sus colegas, de la Universidad de la Reina de Belfast, que relaciona varias actividades sociales y deportivas con la función cognitiva en personas mayores de Irlanda. Toman datos de 8163 voluntarios mayores de 50 años, con edad media de 63.5 años, el 54% son mujeres, les piden datos desde 2009, con nuevas entrevistas a los dos años, en 2011.

Las actividades sociales y deportivas ayudan al mantenimiento de la función cognitiva. Destacan los hobbies, las actividades creativas, el trabajo voluntario en ONGs, asistir a clase, ir al cine, al teatro o a conciertos.

Estamos en la era de la informática y de las redes sociales y una de las actividades que mencionaba Joanna McHugh Power podía ser internet y las redes sociales. Thomas Morton y su grupo, de la Universidad de Exeter, organizaron un estudio de los efectos del uso de internet en las personas de edad. Participaron 76 voluntarios, con 50 mujeres, una edad media de 80 años y, de ellos, 32 actúan de control. Reciben, durante tres meses, un cursillo de uso del ordenador y utilización de internet.

Los resultados muestran una mejora cognitiva en los que siguen el cursillo. Implica una mayor actividad social, más competencia y habilidad, y un refuerzo del sentido de la propia identidad. En general, mejora la salud mental y la sensación de bienestar.

Otro estudio que nos ayuda a entender cómo se consigue un buen envejecimiento se hizo en Italia. Anna Scelzo y sus colegas, del centro ASL4 de Chavarese, en el sur de la Italia rural, trabajaron con 29 voluntarios de más de 90 años. Encontraron que la longevidad excepcional se consigue con un equilibrio entre aceptación y valor para superar adversidades, siempre con una actitud positiva, y con relaciones estrechas con la familia, la religión, su tierra y un fuerte propósito de vida.

Y en un estudio en Alemania, liderado por Suzanne Wurm y su equipo, del Centro Alemán para la Edad de Berlín, trabajan con 4034 voluntarios, de 40 a 85 años, en 1996, y buscan su enfoque positivo del envejecimiento. Encuentran que los voluntarios con una imagen propia negativa hacen menos ejercicio físico que los que tienen una autoimagen positiva, todos ellos con salud comparable. Con la imagen negativa, como mucho, se intenta mantener la salud física o no se trabaja activamente para mejorarla, por ejemplo, caminando de manera regular e, incluso, aumentando el tiempo de paseo.

En España, el envejecimiento tiene éxito en las personas de edad. Cristina Dumitrache y su grupo, de la Universidad de Granada, entrevistaron a 406 voluntarios, con una edad media de casi 75 años, un rango de edad de 65 a 99 años, con el 62% de mujeres, y todos ellos viviendo en residencias.

Los resultados muestran que el 50% de la satisfacción vital de los voluntarios lo explican las relaciones sociales y la personalidad, sobre todo el optimismo, mientras que la salud y la edad, el género y la educación cuentan menos.

Pero Sara Marone y su grupo, de la Universidad de Boston, se preguntan si el propósito de vida y la salud y el bienestar mentales crean un entorno saludable para el grupo. Buscan a personas centenarias, lo que supone buena salud, menor mortalidad, riesgo reducido de enfermedades y con poca pérdida cognitiva, y averiguan qué ocurre con su descendencia. Encuentran 361 voluntarios, con edad media de 82 años, y el 64% de mujeres. Pertenecen a tres grupos: parejas de los descendientes de los que cumplieron 100 años, los propios descendientes de los centenarios, y un tercer grupo de control con personas de parecida edad.

Los resultados de las encuestas muestran que los descendientes de los centenarios tienen un propósito de vida mucho más fuerte que los voluntarios de los otros grupos. Los porcentajes indican que el propósito de vida aparece en un 30% de los descendientes de los centenarios, en un 21% de las parejas de los centenarios y en un 14% de los voluntarios control.

En conclusión, el buen propósito de vida, que presumimos tienen los centenarios, puede ayudar, en sus descendientes, a retrasar enfermedades y otros deterioros relacionados con la edad. El propósito de vida fuerte no se hereda, pero el ambiente en que crecen y se educan los descendientes ayudan a adoptarlo en la vida adulta.

Hemos visto la importancia de las relaciones sociales y, por el contrario, de la soledad. El entorno es importante y la soledad y el aislamiento social, según Julianne Holt-Lundstat y su grupo, de la Universidad Brigham Young de Provo, en Estados Unidos, y en su estudio encuentran, después de un meta-análisis de las investigaciones publicadas entre 1980 y 2014, que el aislamiento social aumenta la mortalidad por cualquier causa en un 29%, la soledad lo hace en el 26%, y vivir solo en el 32%. Pero, también, y según el análisis de una encuesta nacional hecha en Suecia, publicado por Lena Dahlberg y su equipo, del Instituto Karolinska, con más de 2500 voluntarios, y en oposición a lo que se sospecha, la soledad no aumenta con la edad en las personas mayores. Solo aparece un cierto estrés psicológico en la soledad que sigue a la pérdida del compañero pero que, en general, no implica aislamiento social.

Otro meta-análisis, publicado en 2018, por el grupo de Laura Rico Uribe, de la Universidad Autónoma de Madrid, revisa 35 artículos, con más de 770000 participantes, y llega a parecidas conclusiones: la soledad es un riesgo de mortalidad y, como dato nuevo, un riesgo mayor para los hombres que para las mujeres.

Referencias:

Boyle, P.A. et al. 2009. Purpose in life is associated with mortality among community-dwelling older persons. Psychosomatic Medicine 71: 574-579.

Boyle, P.A. et al. 2010. Effect of a purpose of life on risk of incident Alzheimer disease and mild cognitive impairment in community-dwelling older persons. Archives of General Psychiatry 67: 304-310.

Dahlberg, L. et al. 2018. Lonelier than ever? Loneliness of older people over two decades. Archives of Gerontology and Geriatrics 75: 96-103.

Dumitrache, C.G. et al. 2019. Successful aging in Spanish older adults: the role of psychosocial resources. International Psychogeriatrics 31: 181-191.

Frankl, V. 2012. El hombre en busca del sentido último: el análisis existencial y la conciencia espiritual del ser humano. Eds. Paidós. Barcelona. 240 pp.

Haupt, M. 2019. Improving images of aging. International Psychogeriatrics 31: 159-161.

Marone, S. et al. 2018. Purpose in life among centenarian offspring. Journal of Gerontology: Psychological Sciences doi: 10.1093/geronb/gby023

McHugh Power, J. et al. 2016. Mediators of the relationship between social activities and cognitive function among older Irish adults: results from the Irish longitudinal study on ageing. Aging & Mental Health doi: 10.1080/13607863.2016.1233935

Morton, T.A. et al. 2016. Activating and guiding the engagement of seniors with online social networking: Experimental findings from the AGES 2.0 Project. Journal of Aging and Health DOI: 10.1177/0898264316664440

Rico, L.A. et al. 2018. Association of loneliness with all-cause mortality: A meta-analysis. PLOS One 13: e0190033

Scelzo, A. et al. 2017. Mixed-methods quantitative-qualitative study of 29 nonagenarians and centenarians in rural Southern Italy: focus on positive psychological traits. International Psychogeriatrics 30: 31-38.

Wurm, S. et al. 2010. On the importance of a positive view on ageing for physical exercise among middle-aged and older adults: Cross-sectional and longitudinal findings. Psychology and Health 25: 25-42.

Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.

El artículo El sentido de la vida se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. La ciencia y el sentido de la vida
2. Un paseo por la ciudad
3. Los amiloides y el origen de la vida

 

«La serie de los números pares es justamente la mitad de la serie total de números. La serie de los números impares es exactamente la otra mitad. La serie de los pares y la serie de los impares son —ambas— infinitas. La serie total de los números es también infinita. ¿Será entonces doblemente infinita que la serie de los números pares y que la serie de los impares? Sería absurdo pensarlo, porque el concepto de infinito no admite ni más ni menos. ¿Entonces, las partes —la serie par y la impar—, serán iguales al todo? —Átenme ustedes esa mosca por el rabo y díganme en qué consiste lo sofístico de este argumento».

Antonio Machado, Juan de Mairena (sentencias, donaires, apuntes y recuerdos de un profesor apócrifo), 1936

Imagen: Gerd Altmann / Pixabay

 

Respondiendo a Machado, y recurriendo a la noción de cardinal de un conjunto, sí, es decir, las partes —la serie par y la impar—, son iguales al todo. De otra manera, el conjunto de los números pares y el de los impares tienen el mismo cardinal, cardinal que es el igual al de todos los enteros positivos. En efecto, es posible dar una función biyectiva entre los números naturales y los pares: basta con emparejar cada número entero positivo n con el par 2n. Un argumento similar prueba que los enteros positivos tienen el mismo cardinal que los impares (se asocia n con el impar 2n-1). Parece paradójico, ¿verdad? Pero no lo es.

Aunque si todos los enteros positivos fueran iguales, evitaríamos hablar del infinito, y Machado habría logrado esquivar este problema… Y es que, en 1988, el matemático Taje I. Ramsamujh (Florida International University) proponía en la revista Mathematical Gazette una demostración de que todos los números enteros son iguales. La reproducimos debajo. ¿Sabrías decir cuál es el error cometido en la prueba?

Fuente: T. I. Ramsamujh, 72.14 A paradox–(1) All positive integers are equal The Mathematical Gazette , Volume 72 , Issue 460 , June 1988 , pp. 113 DOI: 10.2307/3618919

 

Ramsamujh propone la siguiente demostración en su artículo:

Consideremos la siguiente proposición p(n): “Si el máximo de dos enteros positivos es n, entonces los dos enteros son iguales”. Veamos en primer lugar que p(n) es cierto para todo entero positivo. Observar que p(1) es cierto, ya que si el máximo de dos enteros positivos es 1, es obvio que ambos son iguales a 1, y por lo tanto son iguales. Supongamos ahora que p(n) es cierto y sean u y v dos enteros positivos cuyo máximo es n+1. Entonces, el máximo de u–1 y v–1 es n. Como p(n) es cierto, se sigue que u–1 = v–1. Y por lo tanto u = v, con lo que p(n+1) es cierto. Luego p(n) implica p(n+ 1) para cada entero positivo n. Por el principio de inducción matemática, se deduce que p(n) es cierto para todo entero positivo n.

Sean ahora x e y dos enteros positivos cualesquiera. Sea n el máximo de x e y. Como p(n) es cierto se sigue que x = y. acabamos de probar que dos enteros positivos cualesquiera son iguales. ¿Dónde está el error?

¿Dónde está el error? Piensa un poco…

Efectivamente, aunque u y v sean enteros positivos, u–1 y v–1 no tienen porque serlo. Si, por ejemplo, u = 1, entonces u–1 = 0, y ¡no se puede seguir argumentando como propone Ramsamujh!

Referencias:

All for One, Futility Closet, 28 agosto 2020

T.I. Ramsamujh, 72.14 A Paradox: (1) All Positive Integers Are Equal, Mathematical Gazette 72:460 [June 1988], 113

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad

El artículo Todos los números enteros positivos son iguales se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Números errores de impresión
2. El secreto de los números que no querían ser simétricos
3. Números primos gemelos, parientes y sexis (2)

John Dalton fue un prolífico científico británico. Químico, físico y matemático, nació con una alteración genética que hoy conocemos como daltonismo. A los 26 años se percató de que no distinguía los colores como lo hacía el resto y comenzó a estudiar la causa de esta afección visual. Fruto de este trabajo fue el artículo científico «Hechos extraordinarios relativos a la visión de los colores», que publicó en 1794 y donde describió esta alteración que afecta a quienes perciben los colores de forma diferente.

Los vídeos de Historias de la Ciencia presentan de forma breve y amena pasajes de la nuestra historia científica y tecnológica. Los vídeos, realizados para la Cátedra de Cultura Científica de la UPV/EHU, se estrenan en el programa de ciencia Órbita Laika (@orbitalaika_tve), los lunes a las 22:00 en la 2 de RTVE.

El artículo Historia del daltonismo se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Historia de la quinina
2. Historia del nailon
3. Historia de Nicolas Bourbaki

Imagen: Anand Kumar / Pixabay

En 1920 Rutherford sugirió que un protón dentro del núcleo podría tener un electrón ligado a él tan estrechamente como para ser, a efectos prácticos, una partícula neutra. Rutherford incluso sugirió el nombre de neutrón para esta partícula hipotética (ya que sería neutra desde el punto de vista eléctrico). La comunidad científica se puso a buscar neutrones, pero la búsqueda presentaba dos dificultades principales:

(1) No se conocían materiales naturales emisores de neutrones.
(2) Todos los métodos utilizados para detectar partículas atómicas dependían de los efectos de la carga eléctrica de estas partículas y, por lo tanto, no podían aplicarse directamente a partículas neutras.

Estas dos dificultades hicieron que hubiese que esperar doce años para que la búsqueda del neutrón tuviese éxito. La prueba definitiva llegó en 1932 como colofón de una serie de experimentos sobre reacciones nucleares realizados en diferentes países. El descubrimiento del neutrón es el primer gran ejemplo de la ciencia experimental internacional y cooperativa.

Trabajando en Alemania en 1930 Walther Bothe y Herbert Becker encontraron que cuando las muestras de boro, berilio o litio eran bombardeadas con partículas alfa emitidas por una muestra de polonio, emitían radiaciones que parecían ser del mismo tipo que los rayos gamma, ya que estos rayos no tenían carga eléctrica. El berilio era el elemento que presentaba una emisión mayor.

Observaciones posteriores en Alemania, Francia y Reino Unido apuntaban a que la radiación inducida en el berilio penetraba más lejos (atravesaba el plomo, por ejemplo) que cualquier radiación encontrada hasta ese momento. Las interacciones de esta radiación con la materia indicaban que tenía una energía de aproximadamente 10 MeV. Por tanto, la radiación era mucho más enérgica que los rayos gamma (es decir, que los fotones de alta energía) observados previamente observados. El interés en la comunidad científica se disparó, atrayendo nuevos grupos de investigadores.

Entre estos nuevos grupos se econtraban los físicos franceses Frédéric Joliot e Irène Curie [2]. El matrimonio Joliot-Curie estudió la absorción de la radiación por la parafina, un material rico en hidrógeno. En el curso de sus experimentos, los Joliot-Curie encontraron que la radiación procedente del berilio al incidir sobre la parafina expulsa una gran cantidad de núcleos de hidrógeno (protones) de la parafina. Calcularon que las energías de estos protones era de aproximadamente 5 MeV.

Utilizando los principios de conservación del momento y la energía llegaron a la conclusión de que la energía que necesitaría un rayo para transferir 5 MeV a un protón en una colisión tendría que ser del orden de 50 MeV. Pero 50 MeV es 5 veces los 10 MeV que se habían medido para la radiación del berilio. No solo eso, la cantidad de protones producidos era mucho mayor que la predicha asumiendo que la radiación consistía en fotones. Aquí había demasiadas cosas que no cuadraban.

Estas discrepancias (entre los resultados de dos conjuntos de experimentos y entre la teoría y el experimento) dejaron a la comunidad científica ante un dilema mayor. O había que concluir que los principios de conservación del momento y de la energía no se aplicaban a las colisiones entre la radiación y los protones en la parafina, o había que buscar otra modelo completamente nuevo sobre la naturaleza de la radiación.

Estos principios son tan básicos para el pensamiento científico, y habían demostrado ser tan útiles durante tanto tiempo y en una amplia gama de casos diferentes con un éxito enorme, que la comunidad científica se lanzó como loca a encontrar una alternativa para no tener que renunciar a ellos.

Notas:

[1] 1 MeV es un millón de electrón-voltios. Aquí tienes una explicación de esta unidad de energía que puede serte muy útil.

[2] Hija de Pierre y Marie Curie. Tras contraer matrimonio la pareja adoptó como apellido común Joliot-Curie.

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

El artículo El descubrimiento del neutrón (1): el gran dilema se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. El descubrimiento de Becquerel
2. El descubrimiento de la desintegración artificial
3. No solo el uranio emite rayos

Carlos Briones

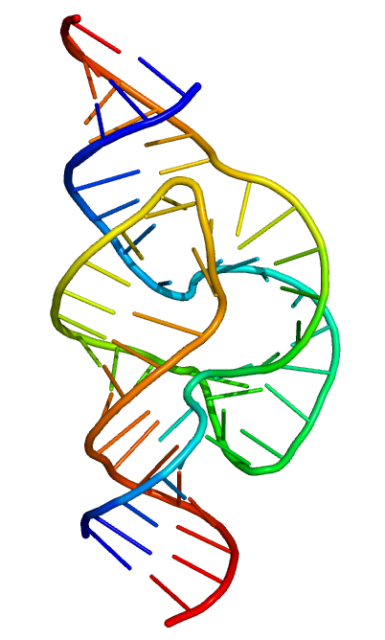
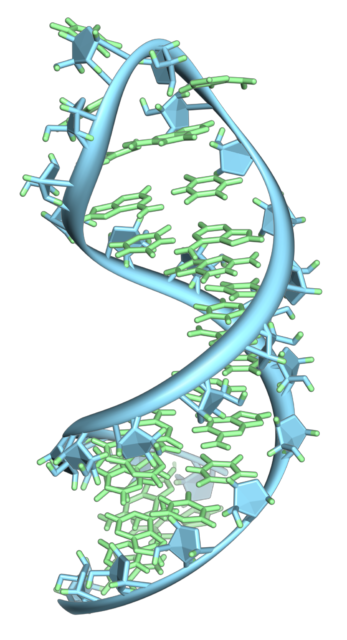Una estructura de horquilla en una molécula de ARN. Se trata de una sola cadena que se pliega sobre sí misma, no de una doble hélice como en el ADN. Esta estructura en concreto pertenece al ARN mensajero. Fuente: Vossman / Wikimedia Commons

 

La pandemia de COVID-19 ha protagonizado este año 2020 y está teniendo terribles consecuencias sanitarias, sociales y económicas en todo el mundo. Afortunadamente, durante las últimas semanas hemos comenzado a ver la luz al final del túnel gracias a la publicación de los resultados, muy positivos en cuanto a seguridad y eficacia, de los primeros candidatos a vacunas que entraron en la fase 3 de sus ensayos clínicos. Dos de ellas, las producidas por las empresas Moderna y Pfizer/BioNTech, han mostrado ya eficacias en torno al 95 %. Aunque aún falta medio año para que termine dicha fase 3 pronto comenzarán a administrarse en Estados Unidos y Europa.

Ambas vacunas están basadas en una molécula bien conocida en diferentes campos de investigación, pero que hasta ahora nunca había saltado a la opinión pública: el ARN (abreviatura de ácido ribonucleico). En concreto, utilizan un tipo llamado ARN mensajero (ARNm), con las instrucciones para que determinadas células de nuestro sistema inmune produzcan la proteína S que forma la espícula del coronavirus SARS-CoV-2, lo que desencadena una respuesta protectora en la persona que recibe la vacuna.

El ARN es una molécula que puede degradarse con facilidad, principalmente por la acción de proteínas catalíticas (o enzimas) especializadas en cortarla. Por ello, el ARN vacunal se administra incluyendo una media de 10 moléculas de ese ARNm en vesículas esféricas protectoras, formadas por lípidos (similares a los que constituyen las membranas celulares) y de tamaño nanométrico (mucho menor que nuestras células).

Foto: Daniel Schludi / Unsplash

A diferencia de otros tipos de vacunas, las basadas en ARN han de mantenerse ultracongeladas hasta casi el momento de su administración. Sin embargo, el ARN no es una molécula que se haya puesto de moda ahora, sino que lo ha estado desde hace mucho tiempo. En concreto, durante los últimos 3 800 millones de años.

El ARN, molécula central en la biología

El análisis a nivel molecular de todos los seres vivos conocidos, y en concreto la comparación de sus genomas, ha mostrado grandes similitudes entre ellos. Esto mostró, hace más de cuarenta años, que las tres grandes ramas del árbol de la vida (bacterias, arqueas y eucariotas) provienen del mismo antepasado.

A esa especie (o, tal vez, a esa comunidad de ellas) la conocemos como “último ancestro común universal” (LUCA, acrónimo formado por sus iniciales en inglés) y se estima que pudo vivir hace unos 3 700 millones de años (Ma), solo 800 millones después de que se formaran la Tierra y la Luna.

LUCA ya tenía las principales características que aparecen en toda la biología actual, y basaba su funcionamiento en tres moléculas clave: el ADN (archivo de información genética), las proteínas (moléculas catalíticas o enzimas, responsables del metabolismo, y también estructurales), y el ARN (intermediario en el flujo de información genética, que se produce en el sentido ADN→ARN→Proteínas).

El ARN es un ácido nucleico, un polímero formado por unidades o monómeros llamados ribonucleótidos. Estos pueden ser de cuatro tipos: A, C, G y U. Su estructura más estable es la cadena sencilla, en vez de la doble hélice característica del ADN.

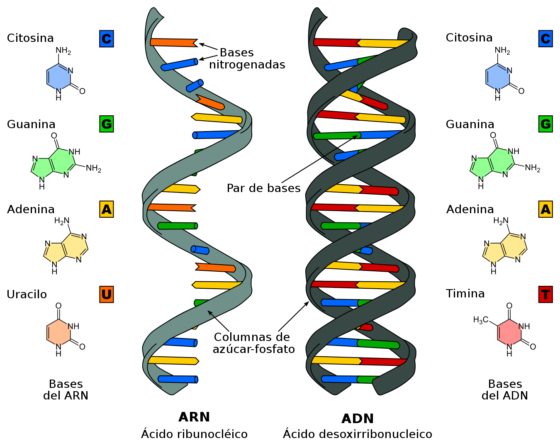Fuente: Wikimedia Commons

Sin embargo, aunque sea una cadena sencilla, cualquier molécula de ARN se pliega sobre sí misma cuando está en disolución, debido a que sus monómeros tienden a reconocerse entre ellos siguiendo las reglas A-U, G-C y G-U. Así, el ARN acaba formando estructuras más o menos complejas, lo que le permite realizar diversas funciones en las células. De hecho, el paso ARN→Proteínas está protagonizado por diferentes tipos de ARN:

• La información genética, previamente copiada (transcrita) desde el ADN, se encuentra en forma de ARNm (como el usado en las vacunas comentadas).
• Su traducción a proteínas se realiza en los ribosomas (agregados de ARN ribosomal, ARNr, y proteínas)
• En este proceso de decodificación de la información también participan los llamados ARN de transferencia (ARNt).

Además, todo el flujo de información genética está regulado por otras moléculas de ARN.

El ARN también constituye el genoma de gran número de “entidades replicativas” que no pueden considerarse auténticos seres vivos, pero que resultan fundamentales en la evolución por su continua interacción con las células a las que parasitan: muchas familias de virus (entre ellos los coronavirus), y también unos patógenos de plantas más sencillos llamados viroides.

Las dos caras de la moneda de la vida

Por lo que acabamos de comentar, el ARN es mucho más que una molécula intermediaria en el flujo de información genética. De hecho, puede servir tanto de genotipo (secuencia con información genética) como de fenotipo (molécula estructural y funcional). Es decir, el ARN es tan versátil como para poder representar las dos caras de la moneda de la vida, algo que no está al alcance del ADN (solo actúa como genotipo) ni de las proteínas (únicamente contribuyen al fenotipo).

En este sentido, un descubrimiento fundamental realizado en 1982 es que en la biología actual existen moléculas de ARN cuya estructura tridimensional les permite actuar como catalizadores, acelerando ciertas reacciones bioquímicas. Hasta entonces se pensaba que las funciones catalíticas solo podían ser realizadas por las enzimas de naturaleza proteica y, por analogía, a estos catalizadores de ARN se les llamó ribozimas. Sus descubridores recibieron el Premio Nobel de Química en 1989.

Uno de los tipos de ribozima. Fuente: Wikimedia Commons

Actualmente conocemos ocho tipos de ribozimas naturales diferentes, y otros han sido obtenidos artificialmente mediante experimentos de evolución molecular in vitro. Además, en los laboratorios también utilizamos esta tecnología para seleccionar moléculas de ARN llamadas aptámeros, que se unen a los ligandos deseados con tanta afinidad y especificidad como los anticuerpos a sus antígenos.

¿Un “mundo de ARN” en el origen de la vida?

En el campo de investigación sobre el origen de la vida, tras las ideas seminales de Charles Darwin a mediados del siglo XIX y los modelos planteados por Alexander Oparin y John Haldane en la década de 1920, las primeras aproximaciones experimentales fueron realizadas por Stanley Miller en 1953 y Joan Oró en 1959. Con ello se inauguraba un campo denominado química prebiótica, que desde entonces ha permitido obtener, a partir de compuestos químicos sencillos, los monómeros o moléculas biológicas básicas como aminoácidos, nucleótidos, azúcares y lípidos simples.

De esta forma se ha demostrado que a partir de la química existente en la Tierra primitiva, sumada a los aportes realizados por meteoritos y cometas durante la infancia de nuestro planeta, pudo formarse una sopa prebiótica (acertada metáfora que debemos a Oparin) de la que surgió la biología. Pero desde esos monómeros hasta LUCA debió recorrerse un largo camino en el que las moléculas químicas y sus interacciones se fueron haciendo cada vez más complejas, hasta llegar a formarse sistemas que combinaban los tres componentes fundamentales de los seres vivos: un compartimento basado en membranas, metabolismo para procesar la materia y la energía del entorno, y la replicación de una molécula genética.

Precisamente en esa etapa intermedia volvemos a encontrarnos con el ARN, ya que debido a su capacidad para actuar como genotipo y fenotipo se considera que pudo ser anterior a las proteínas y al ADN. Así, el modelo conocido como “mundo del ARN” plantea que entre la química prebiótica y LUCA pudieron existir protocélulas basadas en ARN (denominadas ribocitos por algunos científicos) que contenían un genoma de ARN y ribozimas como catalizadores metabólicos, cuyas funciones podrían estar moduladas por otras biomoléculas (como péptidos o diversos compuestos orgánicos) e incluso por los metales y minerales presentes en el medio.

El mundo del ARN permite resolver una paradoja que es equivalente a la del huevo y la gallina, pero en versión molecular. En efecto, si volvemos al esquema del flujo de información biológica en todas las células (ADN→ARN→Proteínas) asumimos que sin ADN no puede haber proteínas. Pero a su vez las proteínas también son necesarias para que exista el ADN, ya que la replicación de este ácido nucleico es realizada por proteínas enzimáticas. Entonces, ¿quién apareció antes, el ADN o las proteínas? Como acabamos de ver, quizá ninguna de esos dos biopolímeros sino el ARN.

Esta sugerente hipótesis aún tiene varios aspectos pendientes de resolver, pero muchos científicos consideramos al ARN como el punto de partida de la evolución darwiniana en la Tierra… o tal vez fuera de ella.

En 2021, unos 3 800 millones de años después de que el ARN protagonizara el origen de la vida, una variante de esa misma molécula va a colaborar decisivamente a la supervivencia de una especie animal que siempre se creyó superior a las demás, pero que ha sido amenazada muy seriamente por un virus también basado en ARN.

Sobre el autor: Carlos Briones es científico titular del Centro de Astrobiología (INTA-CSIC)

Este artículo fue publicado originalmente en The Conversation. Artículo original.

El artículo El ARN está de moda… desde hace 3 800 millones de años se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Los meteoritos ya no son lo que eran desde hace 466 millones de años
2. Los misterios que rodean al máximo térmico de hace 56 millones de años
3. Relaciones a distancia desde hace 16.000 años

Max Perutz recibió el premio Nobel en 1962 por su descubrimiento de la estructura de la hemoglobina, la proteína que da el color rojo a la sangre. En la imagen finalizando el primer modelo en alta resolución de la hemoglobina. Fuente: Max Perutz Labs.

Lo más probable es que al leer la palabra proteína, esta se asocie, de forma casi automática, a la carne, si se piensa en alimentos, o a la musculatura corporal, si es el organismo humano lo que se tiene en mente. Efectivamente, los músculos tienen un alto contenido en proteínas, porque son filamentos de esas moléculas las estructuras cuyo deslizamiento genera la contracción muscular.

Sin embargo, además de ser las responsables de que se contraigan los músculos y, de esa forma, trabajen, las proteínas cumplen otros cometidos esenciales en los seres vivos. Catalizan prácticamente todas las reacciones químicas que tienen lugar en los organismos; llevan oxígeno de los órganos respiratorios a los tejidos; transportan o ayudan a transportar sustancias del exterior al interior de las células, configuran arquitecturas celulares internas que cumplen funciones variadas, reciben señales del exterior de la célula y transfieren la información al interior, entre otras tareas de importancia capital.

Las proteínas están constituidas por aminoácidos, pequeñas moléculas formadas por carbono, hidrógeno, oxígeno y nitrógeno, y uno de ellos, la serina, también azufre. La inmensa mayoría de seres vivos no tiene más de veinte de estos aminoácidos. Las proteínas son cadenas, de longitud muy variable, de esas moléculas. Su estructura tridimensional depende de su composición, o sea, de los aminoácidos que las constituyen y del orden preciso en que se disponen en la cadena. Esa estructura es muy importante, porque determina su función, y muy delicada, de manera que factores ambientales como la radiación, el calor o el pH la pueden alterar impidiendo que la proteína desempeñe su función.

En la actualidad, para conocer la estructura se utilizan varios métodos. El más tradicional es la cristalografía de rayos X, basada en el análisis del patrón de difracción que se forma cuando estos se dirigen a una sustancia en estado cristalino. En esta técnica, la interacción de los rayos X con la nube de electrones del cristal genera una imagen característica, el patrón de difracción, que permite deducir la posición de los átomos y, por lo tanto, la estructura de la molécula. El problema es que este método es laborioso y no es aplicable a muchas estructuras. Más reciente es la criomicroscopía electrónica, una modalidad de microscopía que trabaja con muestras congeladas a temperaturas bajísimas, de manera que se evita la aparición de artefactos.

Pues bien, hace unos días se ha dado a conocer un avance tecnológico de gran importancia en este campo a cargo de la empresa DeepMind. Mediante inteligencia artificial, un algoritmo (denominado AlphaFold) ha sido capaz de determinar, con altísimo grado de acierto, la estructura de proteínas a partir de su secuencia de aminoácidos.

El método de AlphaFold no se basa en el conocimiento de las propiedades fisicoquímicas de las moléculas y, a partir de ese conocimiento, la deducción de sus propiedades y su forma. Lo que hace es comparar estructuras y secuencias de aminoácidos de las ciento setenta mil proteínas para las que se cuenta con el conocimiento necesario (de los doscientos millones que existen en la naturaleza); a partir de esa comparación “aprende” y predice la forma de proteínas cuya estructura se desconoce, pero de las que se sabe su secuencia.

Los creadores de AlphaFold sostienen que este desarrollo es la puerta que abrirá el paso al diseño y producción de fármacos con la forma adecuada para actuar sobre dianas específicas. Pero quizás esas pretensiones sean prematuras. El avance, no obstante, es impresionante, y marcará un antes y un después en el conocimiento de las estructuras de los seres vivos y en sus posibles aplicaciones.

Fuentes:

Michael LePage (2020): DeepMind’s AI biologist can decipher secrets of the machinery of life. New Scientist.

Robert F. Service (2020): ‘The game has changed.’ AI triumphs at solving protein structures. Science.

Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU

El artículo La forma de las proteínas mediante inteligencia artificial se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Proteínas plasmáticas
2. La búsqueda de la inteligencia artificial
3. Máquinas inteligentes (II): Inteligencia artificial y robótica

Catástrofe Ultravioleta #32 TANATOS 1

El ser humano ha desarrollado cientos de expresiones culturales para afrontar o entender la muerte. Desde los tiempos mas ancestrales: mitologías, cuentos, leyendas, luces al final del tunes, poemas, obituarios… lo único seguro en la vida es la muerte. La historia de hoy es la suma de más de dos años de entrevistas e investigación.

https://www.ivoox.com/t03e08-tanatos_md_61156819_wp_1.mp3

Puedes escucharnos en:

– Podium Podcast
– iVoox
– Spotify
– Apple Podcasts

Agradecimientos: Antonio Osuna Mascaró y Susana Monsó (ambos del Messerli Research Institute, Viena), y Javier Almunia (Loro Parque)

** Catástrofe Ultravioleta es un proyecto realizado por Javier Peláez (@Irreductible) y Antonio Martínez Ron (@aberron) con el patrocinio parcial de la Cátedra de Cultura Científica de la Universidad del País Vasco y la Fundación Euskampus. La edición, música y ambientación obra de Javi Álvarez y han sido compuestas expresamente para cada capítulo.

El artículo Catástrofe Ultravioleta #32 TANATOS 1 se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Catástrofe Ultravioleta #31 SIBERIA
2. Catástrofe Ultravioleta #04 Morgan
3. Catástrofe Ultravioleta #29 ALHAMBRA

Un estudio llevado a cabo por el grupo IBeA de la UPV/EHU ha probado que los piroclastos pueden poner en riesgo la conservación de las pinturas de Pompeya. Los iones lixiviados de estos materiales y las aguas subterráneas ricas en iones procedentes de rocas volcánicas pueden provocar la cristalización de sales en las pinturas. El flúor podría utilizarse como marcador de monitorización in situ del alcance de los daños de los murales.

Maite Maguregui realizando mediciones con herramientas portátiles en las pinturas murales de Pompeya. Fuente: IBeA / UPV/EHU

La antigua ciudad de Pompeya (al sur de Italia) quedó sepultada por material volcánico y cenizas el año 79 a.e.c., como consecuencia de la erupción del monte Vesubio. Aquel fatídico suceso ha favorecido una conservación sin precedentes del yacimiento arqueológico del entorno, debido a que los materiales piroclásticos expulsados por el Vesubio han protegido a los vestigios de las agresiones externas. Son, de hecho, unos yacimientos muy preciados tanto cultural como científicamente, en los que se entremezclan turistas y gente de ciencia.

El grupo de investigación de la UPV/EHU IBeA, adscrito al departamento de Química Analítica, lleva más de 10 años trabajando en Pompeya, en el marco del proyecto Analytica Pompeiana Universitatis Vasconicae-APUV. En 2015, la UPV/EHU y el Parque Arqueológico de Pompeya firmaron el primero de los convenios, gracias a que las metodologías y los dispositivos portátiles que utiliza el grupo de investigación permiten analizar las pinturas mediante técnicas no destructivas.

Diversos estudios llevados a cabo en la Casa de Marcus Lucretius, en la Casa Ariadne y en la Casa degli amorini dorati (casa de los cupidos dorados) han concluido que “son las sales las que provocan los mayores y más visibles daños en los murales. Al final, las sales se pueden disolver, y como consecuencia se pueden perder materiales, como pigmentos, la capa pictórica, el mortero, etc.”, señala Maite Maguregui, la investigadora principal de este estudio.

En este sentido, los investigadores han concluido que los iones lixiviados de los materiales piroclásticos y las aguas subterráneas ricas en iones procedentes de rocas volcánicas favorecen la cristalización de algunas sales. “Mientras las pinturas están bajo tierra, los piroclastos las protegen; pero una vez que son sacadas a la superficie, por efecto del aire, la humedad, etc., empiezan a formarse las sales. Por tanto, para la conservación de las pinturas murales es importante saber, en cada caso, cuál es la carga salina de los piroclastos del entorno, para poder bloquear, disminuir o prevenir las potenciales patologías. De hecho, en Pompeya hay todavía una gran parte enterrada por estudiar”, añade Maguregui.

“Cuando el volcán entró en erupción expulsó grandes cantidades de materiales, y el material piroclástico no es homogéneo en todo el entorno; pueden encontrarse numeroso estratos diferentes”, explica la investigadora. En el estudio se han realizado análisis mineralógicos de muestras tomadas en diversos puntos, y se han determinado las composiciones de los lixiviados. Por otra parte, se han realizado modelizaciones termodinámicas para predecir qué sales pueden precipitarse como consecuencia de estas lixiviaciones, así como determinar sus orígenes. Así, han concluido que las sales que da la modelización coinciden con las detectadas en las pinturas.

Las sales analizadas en los murales contienen entre otros iones el fluoruro. “Los fluoruros son iones de origen volcánico; no es uno de los elementos principales en la atmósfera. La aparición de sales de flúor indica que los materiales volcánicos y las aguas subterráneas están influyendo en la cristalización de estas sales —detalla—. Por tanto, con el flúor encontrado en un mural se puede trazar el impacto que han tenido y están teniendo los piroclastos y las aguas subterráneas en las pinturas”. El siguiente objetivo del grupo sería “hacer grandes mapeos en los murales, para ver el alcance de las sales, así como para poder determinar las pautas para el personal conservador cuando procedan a desenterrar una pintura mural”, añade.

Referencia:

Silvia Pérez-Diez, Luis Javier Fernández-Menéndez, Héctor Morillas, Alberta Martellone, Bruno De Nigris, Massimo Osanna, Nerea Bordel, Francesco Caruso, Juan Manuel Madariaga and Maite Maguregui (2020) Elucidation of the Chemical Role of the Pyroclastic Materials on the State of Conservation of Mural Paintings from Pompeii Angewandte Chemie doi: 10.1002/anie.202010497

El artículo El material volcánico que protege las pinturas de Pompeya las daña al salir a la luz se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Errores de interpretación en radiografías de pinturas
2. Un material que cambia de color en función de la polarización de la luz incidente
3. Óxido de vanadio (IV), un material para una revolución de ciencia ficción

Es un mito antiguo, algo más de un siglo, y muchas veces desmitificado. Pero ahí sigue, muy popular y extendido, y anima a seguir desmitificándolo. El mito consiste en afirmar que sólo utilizamos el 10% de nuestro cerebro. Un ejemplo actual de su popularidad es la película “Lucy”, dirigida por Luc Besson, estrenada en 2014 y protagonizada por Scarlett Johansson y Morgan Freeman. Todo estrellas y, por tanto, llegó al público, aunque parece que no gustó mucho. Su cartel anunciador proclama que “Una persona normal utiliza un 10% de su capacidad cerebral. Ella está a punto de alcanzar el 100%”. La protagonista sufre el “síndrome de Obélix” y recibe una sobredosis de una misteriosa droga que le cambia el cerebro. Con su cerebro al 100%, aprende chino en un instante, destroza a los malos y conduce coches con la mente. Algo extraordinario.

Otra muestra del alcance actual del mito del 10% nos llega desde Londres en el estudio de Marta Ferrero y su grupo. Detectan que, en 2016, el 44% de los maestros de primaria y secundaria españoles creen que usamos solo el 10% del cerebro. Y son menos de la mitad, pues hay otros países en que la creencia supera el 50% de los maestros, sobre todo en Norteamérica. En 2013, el 65% de la población de Estados Unidos creía en el mito. También en Países Bajos el 42% de los maestros aceptan el mito del 10% del cerebro, el 26% en los británicos o el 53% de los universitarios brasileños. Incluso el 6% de los neurocientíficos lo creen. También el 30% de los maestros portugueses creen en el uso del 10% del cerebro, según el estudio de Joana Rodrigues Rato y sus colegas, de la Universidad Católica de Portugal en Lisboa, con 538 voluntarios maestros desde preescolar a bachillerato.

En un estudio detallado, Sanne Dekker y su equipo, de la Universidad de Amsterdam y publicado en 2012, revelan que para el 48% y el 46% de los maestros encuestados en el Reino Unido y en los Países Bajos, es aceptable el mito del 10%. Además, el que tengan o no grandes conocimientos sobre el cerebro, pues a muchos les interesa la neurociencia, no evita la creencia en el mito. Según Dekker, tienen dificultades en distinguir ciencia y pseudociencia.

Para 2018, en una encuesta por internet en Gran Bretaña, Christian Jarrett añade que, con 220 voluntarios, de 19 a 66 años, el 40% cree que el mito del 10% es probable o definitivamente verdadero.

Un año antes, en 2017, Kelly Macdonald y sus colegas, de la Universidad de Houston, publicaron un estudio similar al de Dekker, pero con maestros de Estados Unidos. Eran 3877 voluntarios separados en tres grupos: el primero formado por el público en general, con 3045 voluntarios; el segundo con educadores, con 598 personas; y el tercero con 234 formados en neurociencia.

El 68% del primer grupo dio los neuromitos como ciertos; en el segundo grupo, el porcentaje que los aceptó fue del 56%; y en el tercer grupo, con los conocedores de neurociencias, el 47% admitió los neuromitos.

Los resultados de Macdonald son parecidos al estudio de Dekker en Gran Bretaña y los Países Bajos. La educación de los maestros en neurociencias puede reducir pero no eliminar la creencia en neuromitos, incluido el uso del 10% del cerebro. Encuentran la influencia de estas creencias en la práctica docente de los maestros.

La preparación y excelencia del maestro no influye en la aceptación de neuromitos y, se puede sospechar en su transmisión a los alumnos. Jared Horvath y su grupo, de la Universidad de Melbourne, encuestaron a 50 maestros, algunos de ellos premiados por su docencia, sobre su aceptación de neuromitos. En las respuestas, se observa que, de 15 neuromitos, solo hay dos en que se diferencian los maestros normales y los premiados por su excelencia. Y en esos dos mitos, las diferencias son pequeñas. En relación con el 10% del cerebro ambos grupos de maestros lo aceptan en parecido porcentaje.

Estos son algunos de los datos y estudios que me animan a seguir desmitificando el mito de la utilización del 10% del cerebro.

Foto: Pierre Acobas / Unsplash

El nacimiento de este mito se atribuye a una breve frase del psicólogo William James (1842-1910), de la Universidad de Harvard, en su publicación de 1907 titulada “The energies of men”. Decía que “Estamos haciendo uso de solo una pequeña parte de nuestros recursos mentales y físicos posibles”. De aquí a precisar que trataba del uso del 10% del cerebro se sigue un camino tortuoso y todavía en debate. Incluso es un concepto que se ha asociado a Albert Einstein, sin confirmación y, quizá, para justificar su poderosa inteligencia.

La neurociencia demuestra que utilizamos el 100% del cerebro para realizar tareas. El escáner del cerebro lo muestra con detalle, incluso cuando la persona está en reposo. Solo cuando hay lesiones cerebrales y graves daños hay áreas inactivas. Los daños tienen consecuencias en las capacidades mentales, vegetativas y de conducta. El escáner del cerebro, la localización de funciones ce cerebrales, el análisis de estructuras y los estudios metabólicos muestran que se utiliza con normalidad mucho más del 10% del cerebro.

Francisco Mora, de la Universidad de Granada, menciona que, desde un enfoque evolutivo, si el uso del 10% fuera cierto, la selección natural, durante millones de años, seleccionó un cerebro que pasó de pesar 450 gramos a 1500 gramos y, a la vez, dejando el 90% de ese órgano sin función e inutilizado. Con el gasto de energía que supone el cerebro, hasta el 30% del total gastado en el organismo para la especie humana, la selección natural de un órgano caro e inútil no tiene sentido.

Sin embargo, el mito perdura. Primero, porque para muchos, el mito del 10% es, sobre todo, esperanza pues se ve en términos de mejora, de que existe un gran potencial personal de que se puede llegar lejos. Se acepta que, como en la película Lucy, el aumento del uso del cerebro, más allá del 10%, permitirá aprender idiomas, tocar instrumentos musicales, mejorar en el deporte, … y mucho más.

Además, en nuestra sociedad del Primer Mundo y consumista, el mito del 10% es un buen negocio con la venta de muchos y variados métodos para pasar del 10% al 100% del cerebro como, por ejemplo, la droga de la película Lucy. Y, en tercer lugar, la creencia en el mito del 10% no supone ni perjuicio ni riesgo o daño alguno para el creyente.

Referencias:

Boyd, R. 2008. Do people only use 10 percent of their brains? Scientific American February 2.

Dekker, S. et al. 2012. Neuromyths in education: Prevalence and predictors of misconceptions among teachers. Frontiers in Psychology 3: 429.

Ferrero, M. et al. 2016. Neuromyths in education: Prevalence among Spanish teachers and an exploration of cross-cultural variation. Frontiers in Human Neuroscience 10: 496.

Horvath, J.C. et al. 2018. On the irrelevance of neuromyths to teacher effectiveness: Comparing neuro-literacy levels amongst award-winning and non-award winning teachers. Frontiers in Psychology 9: 1666.

James, W. 1907. The energies of men. The Philosophical Review 16: 1-20.

Jarrett, C. 2014. All you need to know about the 10 percent brain myth, in 60 seconds. Wired Science July 24.

Jarrett, C. 2018. Belief in brain myths and child development myths continues even among those who’ve studied psychology. BPS Research Digest March 5.

Macdonald, K. et al. 2017. Dispelling the myth: training in education or neuroscience decreases but does not eliminate beliefs in neuromyths. Frontiers in Psychology 8: 1314.

Mora, F. 2018. Mitos y verdades del cerebro. Paidós. Barcelona. 215 pp.

Rato, J.R. et al. 2013. Neuromyths in education: what is fact and what is fiction for Portuguese teachers? Educational Research 55: 441-453.

Vreeman, R.C. & A.E. Carroll. 2007. Medical myths. Bristish Medical Journal 335: 1288-1289.

Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.

El artículo Desmitificando: El 10% del cerebro se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Nuevas tecnologías para el estudio del cerebro: Desde Cajal a nuestros días
2. Desmitificando: Vacunas peligrosas
3. Desmitificando: Adopción y embarazo

 

En enero de 2014 se publicó en el periódico New York Times, en su columna de juegos y crucigramas Wordplay, un problema de ingenio bajo el título El problema de la princesa, que nosotros hemos reescrito para esta entrada del Cuaderno de Cultura Científica como El problema de la matemática excéntrica.

El problema de la matemática excéntrica: Érase una vez una matemática que vivía en un enorme castillo. El ala este del edificio, en la que ella hacía su vida, disponía de un largo pasillo con diecisiete habitaciones, cada una de las cuales tenía una puerta que daba al pasillo, para entrar y salir de la misma, así como una puerta conectando con cada habitación contigua. La matemática era un poco excéntrica y no le gustaba dormir dos noches en la misma habitación. Por este motivo, cada noche cambiaba y dormía en una habitación adyacente a la que había dormido la noche anterior, elegida al azar.

La habitante del castillo era una prestigiosa matemática con la que muchas personas querían investigar. Por este motivo, cuando alguien le proponía colaborar con ella, invitaba a esa persona a pasar treinta días en su castillo, en el ala oeste para invitados, para que pasara dos pruebas. La primera era que durante esos treinta días demostrase tener los conocimientos necesarios para investigar con ella y la otra era un entretenido reto. La excéntrica matemática, tras explicar sus manías para dormir, proponía a su invitada que cada mañana llamara a una de las diecisiete puertas, si ella abría la puerta, porque había pasado la noche en esa habitación, el reto estaría superado, si no podría intentarlo al día siguiente. Si tú fueses la persona invitada al castillo, ¿podrías desarrollar una estrategia para encontrar a la matemática antes de que pasen los treinta días?

Este problema había aparecido, en 2010, en el hilo math puzzles for dinner (rompecabezas matemáticos para la cena) de Christian Blatter para MathOverflow, que en la propia página se describen como “una página web de preguntas y respuestas para matemáticos profesionales”.

Por otra parte, el matemático ruso Alexander Shapovalov en su página web [ashap.info/], en el apartado dedicado a “problemas para divertirse y para competiciones matemáticas” afirma que el problema fue presentado por el matemático ruso V. Shorin y él mismo en la competición internacional Tournaments of Towns, que es una especie de olimpiada internacional para educación primaria que se originó en Rusia, en la edición de 1999.

Dos años después de la publicación del problema de la búsqueda de la princesa en el hilo math puzzles for dinner (rompecabezas matemáticos para la cena) de MathOverflow, los matemáticos británicos John R. Britnell y Mark Wildon hicieron público su artículo Finding a princess in a palace: A pursuit-evasion problem (Buscando una princesa en un palacio: un problema de persecución-evasión) en el analizaban matemáticamente el problema de la princesa sobre un grafo, donde las habitaciones son los vértices del grafo y las aristas son las puertas que comunican dos habitaciones.

Recordemos que un grafo está formado simplemente por puntos –llamados vértices del grafo- y líneas que unen algunos de esos puntos –llamadas aristas del grafo- (véase, por ejemplo, El problema de los tres caballeros y los tres criados, El grafo de Marion (Gray) o El juego de Sim, entre otros), y que es una estructura matemática muy sencilla, pero a la vez muy versátil.

Ilustración de la diseñadora Stefanie Posavec. Texto del artículo ¿Cómo reducir una novela a sus signos de puntuación? de Elena Sevillano para la revista Yorokobu: “un proyecto de la artista británica Stefanie Posavec que contempla una novela como un «organismo literario» y lo ‘reinterpreta’ mediante diagramas de árbol —«una estructura de planta»— y códigos de colores. Capítulos que se dividen en párrafos; párrafos que se dividen en frases; frases que se dividen en palabras. Con este método, Posavec plasmó visualmente En el camino, de Jack Kerouac. El resultado, muy bello, inspiró a Rougeux para desarrollar su Between the Words. «Quise encontrar nuevas direcciones, porque ella había explorado ya opciones muy interesantes», explica”. Imagen de la página de Stefamie Posavec.

 

Como ya se indica en el título del artículo de Britnell y Wildon, este pasatiempo pertenece a la familia de problemas de tipo persecución-evasión (como el “juego de policías y ladrones”), que son aquellos en los cuales un grupo –en este caso quien intenta resolver el rompecabezas– intenta localizar a los miembros de otro grupo –en este caso la excéntrica matemática– en un entorno cerrado –las diecisiete habitaciones comunicadas de forma lineal–.

El estudio matemático de los problemas persecución-evasión sobre grafos se remonta a la década de 1970. Por ejemplo, en el artículo Pursuit-evasion in a graph se plantea ya la cuestión general: “Supongamos que una persona está perdida y vagando por una oscura cueva. Un grupo de rescate que conoce la cueva será enviado para buscarle. ¿Cuál es el mínimo número de personas en el grupo de rescate que se necesita para encontrarle independientemente de cómo se comporte?”.

Y seguía explicando: “Existen muchas formulaciones matemáticas, no equivalentes, de este problema, dependiendo de la naturaleza de la cueva y los posibles comportamientos de la persona perdida y de las personas del grupo de rescate. […] Un ejemplo es una cueva circular, que requiere un mínimo de dos personas en el grupo de recate: la persona perdida podría moverse siempre en la parte opuesta a una única persona de rescate”.

Imagen perteneciente al interesante proyecto Cosmic Web, cuya visualización corresponde a Kim Albrecht.

Pero regresemos al problema de la matemática excéntrica y planteemos cómo resolverlo. Lo primero que hay que hacer siempre es leer bien el rompecabezas e intentar entender todos los elementos que aparecen en el mismo. Además, en problemas como este, en el cual aparecen diecisiete habitaciones conectadas en línea, lo mejor es simplificar el problema, para comprender bien en qué consiste y analizar la solución en una situación sencilla, para luego ir complicándola hasta tener la idea de la solución del problema original. Por este motivo, imaginemos que en el pasillo del castillo solo hubiese tres habitaciones en línea, como en la siguiente imagen.

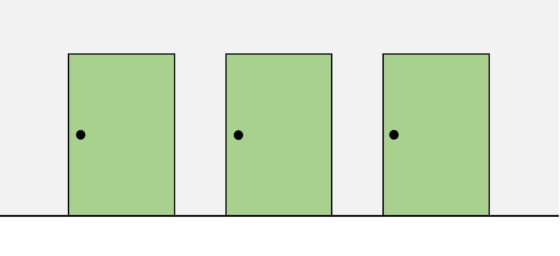
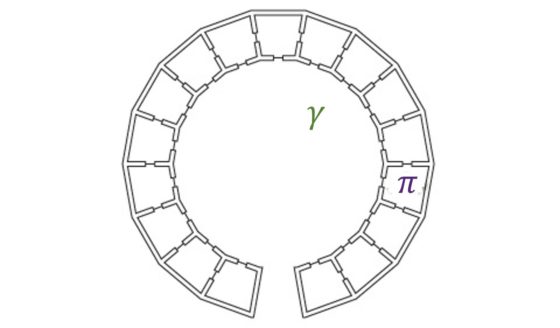
Antes de abrir ninguna puerta, la matemática puede estar en cualquier habitación, por este motivo hemos pintado de verde las puertas. ¿Qué puerta deberíamos abrir el primer día? La mejor opción es la puerta que está en el medio.

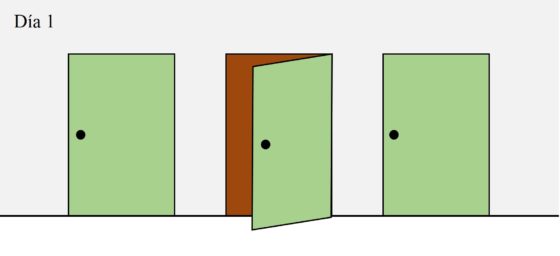
Si la matemática está en esa habitación, la hemos encontrado y se terminó. Pero si no está, entonces estará en cualquiera de las dos habitaciones, las de los extremos. Teniendo en cuenta la costumbre de la matemática de dormir cada noche en una habitación distinta, pero adyacente, la siguiente noche necesariamente dormirá en la habitación de en medio. Por lo tanto, si el segundo día abrimos la puerta de esa habitación la habremos encontrado.

En conclusión, si seguimos esta estrategia como mucho tardaremos dos días en encontrarla, resolviendo en ese plazo el reto propuesto.

¿Qué habría pasado si el primer día hubiésemos abierto una de las puertas de los extremos? Si al abrir esa puerta la habitación estuviese vacía, al día siguiente la matemática podría estar de nuevo detrás de cualquiera de las tres puertas y sería otra vez una cuestión de suerte. Abrir alguna de las puertas de los extremos no aporta ninguna certeza sobre dónde puede estar, o no estar, la matemática.

Compliquemos un poco más el problema y consideremos ahora que en el pasillo hay cuatro puertas. ¿Cuál debe ser la estrategia para encontrar a la matemática en la menor cantidad de días posibles? Ahora hemos añadido un número encima de cada puerta para identificar mejor cada una de las habitaciones.

¿Qué ocurriría si empezamos abriendo, el primer día, la puerta número 2, siguiendo la misma idea del anterior caso?

Si al abrir la puerta número 2 la matemática está ahí, entonces la hemos encontrado, aunque haya sido con un poco de suerte, ya que teníamos una probabilidad de 1 entre 4 de acertar. Pero si no hay nadie en esa habitación, al menos tenemos una pista para el siguiente día. No podrá estar en la habitación 1, puesto que para eso tendría que haber estado en la habitación 2 el día anterior, por su manía de trasladarse solo a habitaciones adyacentes.

La apertura de puertas debe estar pensada para obtener algunas certezas para el siguiente día e ir eliminando opciones. Por este motivo, el segundo día abriríamos la puerta 3.

La probabilidad de que la matemática esté tras la puerta número 3 el segundo día es de un tercio. Pero si no está en esa habitación preguntémonos qué conclusiones podemos extraer para el siguiente día. Como la habitación 2 tiene a las habitaciones 1 y 3 como adyacentes y no estaba en esas habitaciones el segundo día, entonces el tercer día no va a poder estar en la habitación 2. Lo mismo pasa con la habitación 4, que tiene a la habitación 3 como única adyacente. Por lo tanto, solo tenemos dos opciones posibles para el tercer día, habitaciones 1 y 3.

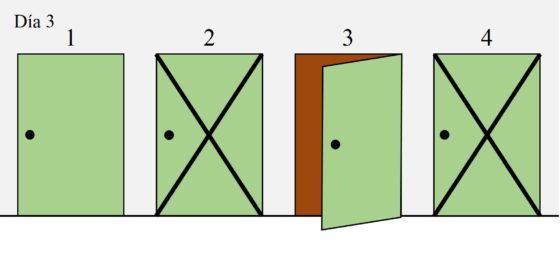
Por lo tanto, vamos a abrir la puerta 3. Si la científica no está detrás de esa puerta, al día siguiente solo podría estar en la habitación 2 y al cuarto día, como mucho, la habríamos encontrado.

Por otra parte, si el primer día empezamos abriendo las puertas 1 o 4 no obtendremos ninguna información para el día siguiente, por lo tanto, no son opciones buenas para empezar a buscar a la matemática excéntrica.

Podemos resumir nuestra estrategia para cuatro habitaciones, con las diferentes opciones, en la siguiente tabla. Cada columna es una habitación y cada fila un día. Además, las celdas verdes son las habitaciones en las que puede estar la matemática, las celdas marrones las que abrimos cada día, las celdas grises en las que no puede estar y la celda amarilla en la que va a estar finalmente, si no la hemos encontrado antes.

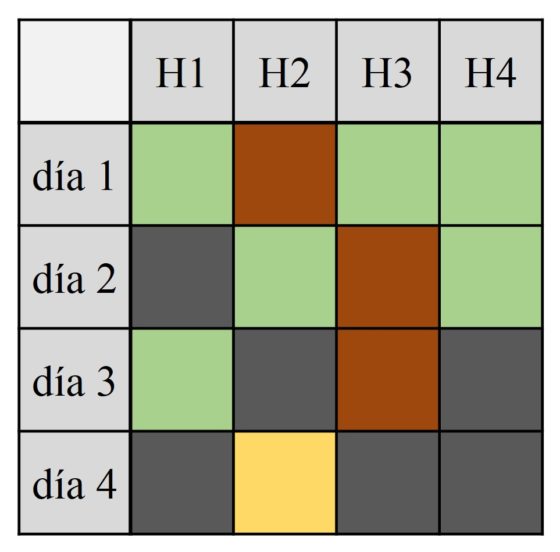
Por lo tanto, la secuencia de apertura de puertas [2, 3, 3, 2] es una estrategia ganadora para encontrar a la matemática. Así mismo, el razonamiento que hemos hecho nos dice que no podemos estar seguros de encontrarla en menos movimientos.

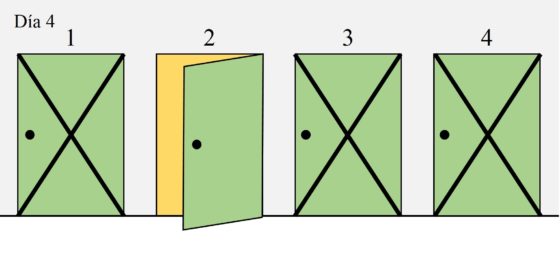
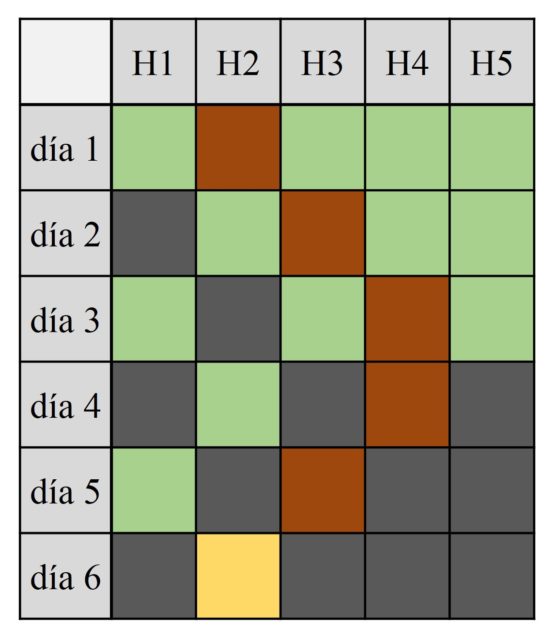
Si ahora analizamos el problema de la matemática excéntrica con cinco habitaciones, la estrategia ganadora es [2, 3, 4, 4, 3, 2] como queda explicada en la siguiente tabla. Es decir, se necesitan un mínimo de seis días para encontrar, con toda seguridad, a la persona buscada.

Si ahora volvemos al problema original, con diecisiete habitaciones, se podría dibujar una tabla similar a las anteriores y obtener que la estrategia ganadora es [2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 16, 15, 14, 13, 12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2]. Se necesitan, como mucho, treinta días para encontrar a la dueña del castillo.

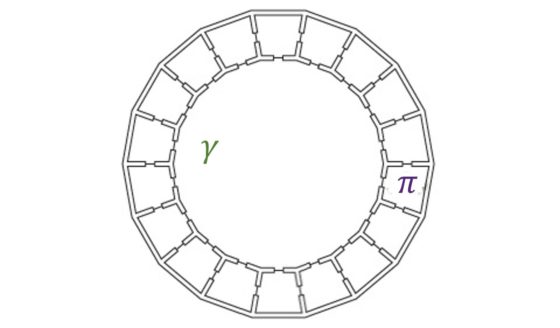
Si observamos la imagen que acompañaba al pasatiempo matemático en el New York Times nos podemos plantear claramente qué ocurriría si tuviésemos habitaciones, por ejemplo, dieciocho, distribuidas en un pasillo circular, como en la anterior imagen. Ahora no existe ninguna estrategia ganadora que nos asegure que podemos encontrar a la matemática. Podría pasar que siempre abriéramos una puerta en la que no está, incluso la que está en la posición diametralmente opuesta. En este caso todo se reduce al azar.

De hecho, nos podemos plantear si existen estrategias ganadoras dependiendo de la forma en la que están conectadas las habitaciones (matemáticamente, para diferentes grafos). Claramente, por lo comentado en el ejemplo circular, cualquier distribución/grafo que tenga ciclos, partes circulares, no va a tener estrategia ganadora. En el artículo Finding a princess in a palace: A pursuit-evasion problem (Buscando una princesa en un palacio: un problema de persecución-evasión) se mostraba el grafo más sencillo, sin partes circulares, en la cual la matemática podría no ser encontrada. Es la que mostramos en la siguiente imagen.

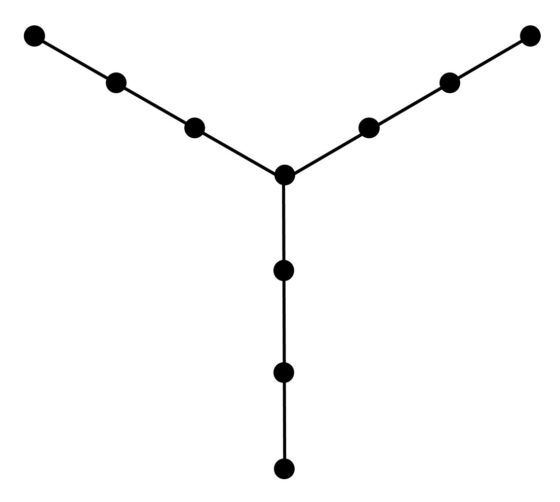
Como cada vértice se corresponde con una habitación y cada arista a una puerta entre habitaciones, la distribución de habitaciones relacionada con el anterior grafo es la que aparece en la siguiente imagen.

Un juego clásico de la familia de problemas de tipo persecución-evasión es el juego de policías y ladrones, del que ya hablaremos en alguna otra entrada del Cuaderno de Cultura Científica. Para abrir boca, vamos a terminar esta entrada con una versión sencilla de este juego.

Reglas del juego policías y ladrones:

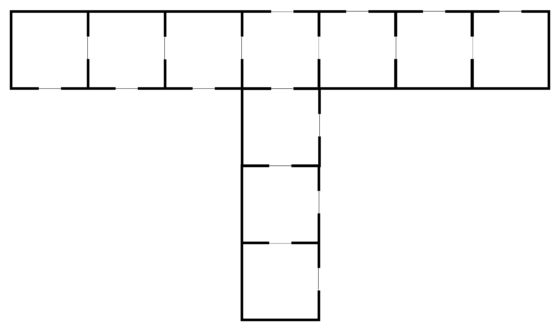
El tablero del juego consta de doce posiciones posibles –puntos negros– conectadas con líneas, como aparece en la imagen.

Es un juego para dos jugadores, el policía y el ladrón, cada uno con su ficha. La posición inicial de las fichas del policía (azul) y del ladrón (verde) es la que aparece en la imagen.

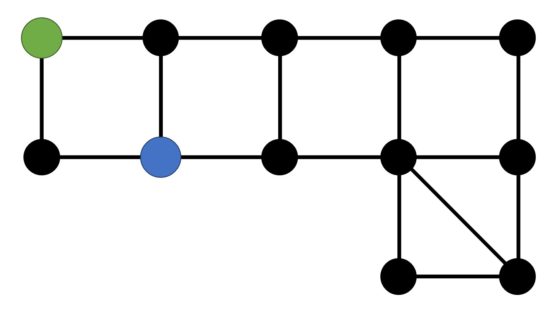
El objetivo del juego es doble. El policía debe intentar atrapar al ladrón, es decir, colocar su ficha en la posición en la que esté la ficha del ladrón; y el ladrón debe intentar no dejarse atrapar. Las reglas son las siguientes:

i) cada jugador, policía y ladrón, mueve su ficha obligatoriamente de una posición a otra que esté conectada con una línea;

ii) cada jugador, de forma alternada, realiza un solo movimiento por turno;

iii) empieza moviendo el policía.

El juego termina cuando el policía atrapa al ladrón o cuando desiste de hacerlo.

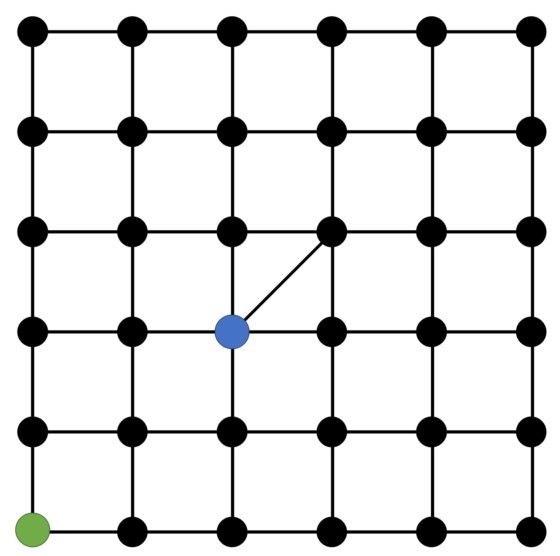
En el libro Matemáticas para divertirse de Martin Gardner se presenta este juego, pero con otro tablero y con un zorro y un ganso en lugar de un policía y un ladrón. El tablero es el de la siguiente imagen, con las posiciones iniciales que se muestran.

Bibliografía

1.- John R. Britnell, Mark Wildon, Finding a princess in a palace: A pursuit-evasion problem, The Electronic Journal of Combinatorics 20 (1), 2013.

2.- Raúl Ibáñez, Del ajedrez a los grafos, la seriedad matemática de los juegos, El mundo es matemático, RBA, 2015.

3.- T. D. Parsons, Pursuit-evasion in a graph, en Theory and Applications in Graphs, Springer-Verlag, 1978, pp. 426-441.

4.- F.V. Fomin, D.M. Thilikos, An annotated bibliography on guaranteed graph searching, Theoret. Comput. Sci. 399, pp. 236-245, 2008.

5.- Tatjana V. Abramovskaya, Fedor V. Fomin, Petr A. Golovach, Michał Pilipczuk, How to hunt an invisible rabbit on a graph, European Journal of Combinatorics 52, pp. 12-26, 2016.

6.- Mohammed Ammar, Is it possible to catch the thief? , del canal de youtube Logically yours.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica

El artículo Buscando una matemática en el castillo se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. La invención matemática
2. Buscando lagunas de números no primos
3. Buscando las soluciones del cubo de Anda

Las redes sociales son aplicaciones o herramientas que sirven para publicar, difundir y compartir contenido entre los miembros de una comunidad y propiciar la interacción y conexión entre quienes las usan. Las redes sociales son habituales en nuestro día a día, sin embargo, ¿cómo comenzaron?

En 1995 vio la luz la web SixDegrees. SixDegrees es considerada la primera red social. Esta red permitía poner en contacto a amigas y amigos, agrupándolos según el grado de relación que tuvieran, para que interactuaran a través del envío de mensajes. SixDegrees estaba basada en la teoría de los seis grados de separación del psicólogo Stanley Milgram. Esta teoría sustenta que vivamos donde vivamos estamos conectadas y conectados, entre nosotros, a través de seis pasos. SixDegrees señalaba en su presentación: “Only social network where you will meet amazing people based on your interests” (red social donde conocerás gente increíble según tus intereses). Esta descripción dejó al descubierto el nexo de unión entre quienes usamos las redes sociales, el compartir intereses comunes.

Los vídeos de Historias de la Ciencia presentan de forma breve y amena pasajes de la nuestra historia científica y tecnológica. Los vídeos, realizados para la Cátedra de Cultura Científica de la UPV/EHU, se estrenan en el programa de ciencia Órbita Laika (@orbitalaika_tve), los lunes a las 22:00 en la 2 de RTVE.

El artículo Historia de la primera red social se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Historia de la bombilla
2. Historia de la quinina
3. Historia de Nicolas Bourbaki

Cámara de niebla Wilson empleada en 1955 en el Brookhaven National Laboratory para el estudio de rayos cósmicos.

Fue posible distinguir experimentalmente entre las dos hipótesis posibles para explicar la desintegración artificial mediante el uso de un dispositivo llamado «cámara de niebla», que permite visualizar la trayectoria de cada partícula cargada. La cámara de niebla fue inventada por C.T.R. Wilson y perfeccionada por él a lo largo de los años. A partir de 1911 se convertiría en un importante instrumento científico para estudiar el comportamiento de las partículas subatómicas.

En el caso de la desintegración artificial, recordemos, las dos hipótesis eran:

(a) El núcleo del átomo bombardeado pierde un protón, que se “desprende” como resultado de una colisión con una partícula alfa especialmente rápida.

(b) La partícula alfa es “capturada” por el núcleo del átomo al que ha golpeado, formando un nuevo núcleo que, inmediatamente después, emite un protón.

Si la hipótesis (a) es válida, el protón “desprendido” sería la cuarta trayectoria en la fotografía de una desintegración en una cámara de niebla: observaríamos la de una partícula alfa antes de la colisión, la de la misma partícula alfa después de la colisión, la del núcleo que que se desplaza tras la colisión y la del protón desprendido.

En el caso de que la (b) fuese la válida, en cambio, la partícula alfa incidente debería desaparecer en la colisión, y solo se verían tres trayectorias en la fotografía: la de la partícula alfa antes de la colisión y las del núcleo desplazado tras la colisión y el protón emitido.

La cuestión se resolvió en 1925 cuando P.M.S. Blackett estudió las trayectorias producidas cuando las partículas atravesaban gas nitrógeno en una cámara de niebla. Encontró que las únicas trayectorias en las que se podía ver la desintegración artificial eran las de la partícula alfa incidente, un protón y el núcleo desplazado. La ausencia de una trayectoria correspondiente a una partícula alfa tras la colisión demostró que la partícula desaparecía por completo y que el caso (b) es la interpretación correcta de la desintegración artificial: la partícula alfa es capturada por el núcleo del átomo que golpea, formando una nuevo núcleo que luego emite un protón.

Trayectorias de partículas alfa atravesando (de izquierda a derecha) gas nitrógeno. Una de ellas ha golpeado un átomo de nitrógeno, convirtiéndolo en oxígeno y emitiendo un protón. ¿Ves las tres trayectorias? Fuente: Cassidy Physics Library

El proceso en el que una partícula es absorbida por un núcleo de nitrógeno y se emite un protón puede representarse mediante una «ecuación». La ecuación expresa el hecho de que el número de masa total es el mismo antes y después de la colisión (es decir, hay conservación del número de masa) y el hecho de que la carga total es la misma antes y después de la colisión (hay conservación de carga).

Esta reacción muestra que ha tenido lugar la transmutación de un átomo de un elemento químico en un átomo de otro elemento químico. La transmutación no se ha producido de forma espontánea, como ocurre en el caso de la radiactividad natural; se produce exponiendo átomos (núcleos) objetivo a proyectiles emitidos por un nucleido radiactivo. Es, pues, una transmutación artificial. En el artículo en el que informó sobre esta primera reacción nuclear producida artificialmente, Rutherford dijo:

Los resultados en su conjunto sugieren que, si se dispusiera de partículas alfa, o proyectiles similares, de energía aún mayor para experimentar, podríamos esperar que se descompusiera la estructura nuclear de muchos de los átomos más ligeros.[1]

El estudio posterior de las reacciones que involucran núcleos ligeros condujo al descubrimiento de una nueva partícula y a un modelo muy mejorado de la constitución del núcleo. Se han observado muchos tipos de reacciones con núcleos de todas las masas, desde los más ligeros hasta los más pesados, y las posibilidades indicadas por Rutherford han ido mucho más allá de lo que jamás podría haber imaginado en 1919.

Nota:

[1] Este llamamiento a conseguir mayores energías de «proyectiles» fue respondido no mucho después con la construcción de aceleradores de partículas.

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

El artículo La cámara de niebla se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. El descubrimiento de la desintegración artificial
2. El problema de la estructura nuclear
3. La hipótesis protón-electrón de la composición nuclear

Manuel Collado Rodríguez

Células metastáticas. Fuente: Unsplash / National Cancer Institute 

 

Hace 50 años el presidente estadounidense Richard Nixon declaró la “guerra al cáncer”. Seguía así la estela de otros exitosos programas que concentraron esfuerzos para alcanzar un objetivo que pusiera al país a la cabeza del progreso mundial. Años antes, los recursos se habían puesto para desarrollar la bomba atómica y llegar a la Luna. En el caso del cáncer, la iniciativa pretendía promover centros de investigación que reuniesen a los mejores investigadores para encontrar tratamientos contra una enfermedad que suponía una amenaza cada vez mayor para la sociedad.

Multitud de éxitos y fracasos después, asistimos ahora a un nuevo esfuerzo por impulsar la investigación biomédica contra el cáncer. Esta es la base de la iniciativa Grandes Desafíos del Cáncer, que arrancó en 2015. Su objetivo es mejorar nuestra capacidad de prevención, detección y tratamiento de la enfermedad. Para ello, busca identificar las cuestiones clave pendientes de resolver.

Un comité de sabios plantea cuáles son esas grandes preguntas que necesitan ser respondidas antes de continuar avanzando. Uno de estos grandes retos es entender y explotar en nuestro favor la senescencia celular.

¿Qué es la senescencia celular?

La división celular es el proceso que hace que una célula dé lugar a dos hijas idénticas. Esta es la base de la proliferación celular. La senescencia consiste en la incapacidad de llevar a cabo este ciclo.

Durante la senescencia, las células sufren unos cambios en su morfología y en su patrón de expresión de genes, y muestran unas secreciones extracelulares (que denominamos SASP). A este estado se llega como respuesta a daños en la integridad de la célula. Diversas agresiones celulares ponen en marcha este proceso.

La apoptosis (el proceso de suicidio celular) y la senescencia celular son los dos programas de defensa esenciales del organismo ante daños irreparables que ponen en peligro la transmisión íntegra de la información genética y la actividad correcta de las células. Si estos mecanismos fallan y permitimos que las células dañadas continúen proliferando, las células aberrantes crecerán desordenadamente hasta formar un tumor.

Por tanto, ambos son mecanismos de defensa antitumorales esenciales. Ahí tenemos una primera razón de peso para considerar que la investigación en senescencia celular es clave para entender el cáncer.

A lo largo de la vida se suceden todo tipo de agresiones a las células y, en muchas ocasiones, esto resulta en la inducción de senescencia. Esto contrasta con el hecho de que el cáncer es fundamentalmente una enfermedad del envejecimiento, mucho más frecuente en adultos y cuya incidencia aumenta claramente con la edad.

Si un organismo envejecido acumula células que han activado una respuesta de protección frente al cáncer con éxito, ¿cómo es que el cáncer se da más en personas de edad avanzada cuyos órganos y tejidos se están ya defendiendo? Una posibilidad es que la acumulación de daño con la edad termine por deshabilitar la respuesta protectora de la senescencia. Otra, inquietante, es que las células senescentes que no pueden dividirse alteren al resto hasta convertirlas en tumorales.

Así, lo que inicialmente nos protege podría volverse en nuestra contra y facilitar la enfermedad.

Las células dañadas que disparan la senescencia echan el freno para impedir su proliferación descontrolada. Además, secretan el SASP para enviar señales complejas a su entorno. Creemos que pueden estar destinadas a promover la reparación y regeneración del tejido dañado.

Así, una agresión celular es respondida mediante la parada en seco de la proliferación de la célula –ahora dañada– para impedir que pueda dividirse hasta formar un grupo de células aberrante. Además de dejar de proliferar, esas células secretan mensajes moleculares al exterior que por una parte avisan a su entorno, por otra llaman a la reparación y finalmente estimulan su propia eliminación.

Este sería el sistema cuando funciona a la perfección.

Demasiadas agresiones o un sistema ineficaz de eliminación de células dañadas puede conducir a una señalización de reparación constante y perjudicial que cause enfermedades. Este es el caso de patologías asociadas al envejecimiento como la osteoartritis, la fibrosis pulmonar y renal, el alzhéimer y el cáncer. Conocemos aspectos de esta compleja respuesta y tenemos indicios de la asociación entre acumulación de células senescentes y desarrollo de enfermedad, pero necesitamos concretar aún más cómo se desarrolla el proceso para entenderlo mejor y poder manipularlo en nuestro beneficio.

En ciencia, lo que no se ve no existe. O, al menos, se le asigna una menor importancia de la que pueda tener. En el caso de la senescencia celular, y tras décadas de estudio, carecemos de “marcadores” específicos del proceso, biomoléculas cuya aparición se asocie con la aparición de la senescencia y su evolución. Esto dificulta el trabajo en el laboratorio y su aplicación a la enfermedad humana. Debemos avanzar en este aspecto. Para ello, necesitamos emplear todos los recursos que puedan ofrecer diversas disciplinas y que, con enfoques novedosos, permitan el desarrollo de nuevas herramientas.

Fuente: Unsplash / National Cancer Institute

Cómo eliminar células senescentes

En los últimos años hemos aprendido que es posible eliminar las células senescentes. Esto no parece perjudicar al organismo y ha demostrado, de momento en animales, una capacidad asombrosa para mejorar enfermedades asociadas al envejecimiento. Todas ellas tienen como base la acumulación de células senescentes que alteran los tejidos en los que residen y se han acumulado.

Una de las aproximaciones terapéuticas más avanzada, en experimentación clínica en humanos para conocer su potencial terapéutico, son los compuestos senolíticos. Esta es la denominación genérica que reciben los compuestos capaces de inducir la muerte específica de células senescentes, dejando intactas a las células normales. Pero quizá sea poco realista plantear una terapia contra el cáncer mediante la administración de senolíticos de manera preventiva para eliminar estas células dañadas, según vayan surgiendo, para evitar su acumulación. Se requerirá mucho conocimiento para asegurarse de que una estrategia así está exenta de peligros y puede usarse sin temor a causar un perjuicio mayor que el que se quiere evitar.

Una línea de investigación más directa para explotar nuestro conocimiento de la senescencia celular en la terapia frente al cáncer consiste en intentar controlar el crecimiento tumoral. ¿Cómo? Reactivando esta respuesta protectora del organismo en las células tumorales que proliferan sin control. Dar con fármacos que induzcan este estado de incapacidad proliferativa puede evitar la progresión de los tumores. De hecho, reevaluando algunos de los fármacos antitumorales usados en la actualidad en la quimioterapia, desarrollados con el objetivo de inducir la muerte de las células tumorales, nos encontramos con que en muchas ocasiones inducen senescencia en las células tumorales.

Hasta qué punto la senescencia es nuestro aliada contra el cáncer es algo que por el momento desconocemos. Una posibilidad que manejamos es que la inducción de senescencia durante el tratamiento antitumoral pueda limitar la eficacia de la terapia. La única célula tumoral buena es la célula tumoral muerta, y dejar células tumorales zombis en el organismo puede ser beneficioso a corto plazo, pero desembocar en efectos posteriores perjudiciales. Para muchos, las células tumorales senescentes producidas por la quimioterapia suponen la base de las recaídas tan frecuentes en pacientes tras terapia. En muchas ocasiones, estas recaídas se producen por tumores que muestran unas características aún más agresivas que las originales.

Fuente:Unsplash / National Cancer Institute

La estrategia “uno-dos”

En este contexto surge la estrategia “uno-dos”. Esta pretende detener: primero, el crecimiento tumoral mediante la inducción de senescencia celular de la célula tumoral. Segundo, inducir de forma selectiva su muerte mediante la aplicación de un senolítico. Esta estrategia ha comenzado ya a ensayarse en modelos animales de cáncer y lo que hemos observado es que el efecto de la combinación de quimioterapia inductora de senescencia junto al senolítico es más eficaz que la quimioterapia sola.

Existe un aspecto positivo extra nada desdeñable en esta estrategia. Los agresivos tratamientos provocan desagradables efectos secundarios en los pacientes sometidos a quimioterapia. Al parecer, en muchos casos estos efectos secundarios derivan de la inducción de senescencia en células no tumorales que quedan dañadas. Estas pueden ser eliminadas eficazmente por los agentes senolíticos al mismo tiempo que las tumorales senescentes generadas por la quimioterapia, lo cual podría proporcionar un efecto terapéutico beneficioso con mínimos efectos secundarios.

Todos estos aspectos mencionados en el artículo son el objetivo de multitud de grupos de investigación en el mundo. Definir los objetivos prioritarios de esta investigación, plantear nuevas iniciativas para resolver las dudas y desarrollar nuevas y más eficaces intervenciones terapéuticas basadas en el uso de la senescencia celular constituyen el esfuerzo en el que se han embarcado numerosos grupos. Estos tratan de reunir fuerzas en consorcios internacionales multidisciplinares para buscar el apoyo financiero de la iniciativa Grandes Desafíos del Cáncer, que nos permita dar un gran salto hacia adelante en nuestro conocimiento y manejo del cáncer.

Sobre el autor: Manuel Collado Rodríguez, Investigador, director del laboratorio de investigación en Células Madre en Cáncer y Envejecimiento, SERGAS Servizo Galego de Saúde

Este artículo fue publicado originalmente en The Conversation. Artículo original.

El artículo La senescencia celular: el gran desafío para entender y tratar el cáncer se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Los supermicrobios amenazan con ser más letales que el cáncer
2. Nanopartículas recubiertas para el tratamiento localizado del cáncer por hipertermia magnética
3. Lo que la búsqueda de inteligencia extraterrestre nos enseña para entender la pandemia

Rosa García-Verdugo, autora

Hoy vengo a hablar de mi libro. Siempre quise decir esta frase. Y hoy, puedo por fin usarla. Y es que desde el 17 de noviembre está a la venta mi primer libro de la serie Para Curiosos de la Editorial Paidós (Grupo Planeta).

Hace ya casi dos años que mi editor, Sergi, me llamó preguntándome si me había planteado escribir un libro de ciencia, y me dio libertad total para elegir la temática. Como soy bioquímica, y desde niña tengo una fascinación total con el mundo de la genética, no lo dudé, mi libro tratará de genética. Y escribí el libro de genética que a mi me gustaría leer si no supiera nada del tema.

Un libro que empieza con un viaje por el pasado de la genética y los consabidos guisantes de Mendel y las observaciones de Darwin, pero que en vez de quedarse ahí como la mayoría de libros de texto del tema, pasa a explicar de una manera práctica –y cercana, creo– para qué sirve la genética hoy en día y que podemos esperar de ella en el futuro. Aunque este libro llevaba ya prácticamente un año escrito cuando estalló la crisis del COVID-19, no pude mantenerme al margen y por supuesto, el libro también incluye un breve capítulo dedicado a la reina de la actualidad, pero desde la perspectiva de la genética.

Son casi trescientas páginas de lectura amena, donde intento traer referencias cercanas para hacer más fácil la comprensión de conceptos, que de primeras pueden confundir hasta los expertos, además de pequeñas notas y curiosidades que poder llevar a la mesa el domingo para compartir con la familia o los amigos.

El libro se titula Genética eres tú, y es una referencia al comienzo del primer capítulo, que trata sobre el pasado de la genética. Ese capítulo comienza con una reflexión en cuanto a lo que la genética significa, no solo para los científicos, sino para todos los seres vivos, incluidos naturalmente nosotros. Y la forma en que se me ocurrió expresarlo fue adaptando un poema clásico. ¿Reconocéis la referencia?

¿Qué es genética?
Me preguntas mientras clavas en mi pupila tu pupila azul…
¿Qué es genética?
¿Y tú me lo preguntas?
Genética eres tú.

Como digo en el libro, espero que el autor, Gustavo Adolfo Bécquer, no se revuelva en su tumba al ver lo que hice con su poema, pero espero me perdone la licencia por la causa.

He pensado que para abrir boca, voy a copiar por aquí el contenido de uno de los llamados datos curiosos del libro, que por cierto ¡también tiene dibujos! y es que he podido contar con un ilustrador de lujo: Javier Pérez de Amézaga Tomás. Espero que este aperitivo os deje con las ganas de hincarle el diente al libro y que aprovechando que las fiestas se acercan y este año preveo que pasaremos mucho tiempo en casa, lo pongáis en la carta a los Reyes Magos.

Científicos colocados

Pues si os creíais que el inventor de la PCR ha sido el único científico o inventor con afición por las drogas, siento decepcionaros, porque no estaba solo. De hecho, forma parte de un grupo más que numeroso de mentes de reconocido prestigio a las que también les gusta irse «de viaje» de vez en cuando. Apuesto a que algunos de los nombres de esta lista van a sorprenderos…

Según sus preferencias por una droga en concreto:

LSD. Steve Jobs y Bill Gates tienen algo más en común que ser rivales en el mundo de la informática. Francis Crick, uno de los descubridores de la estructura tridimensional del ADN dijo que la vio en un viaje de LSD.

Cocaína. Al inventor de la bombilla incandescente Thomas Edison le iba la coca, lo mismo que al padre del psicoanálisis Sigmund Freud y a mi héroe de la infancia, que aunque sea solo un genio literario, también se merece un puesto en esta lista: el señor Sherlock Holmes.

Marihuana. Entre aquellos a los que les gustaba fumar a lo Bob Marley tenemos al biólogo evolucionista Stephen Jay Gould y al astrofísico Carl Sagan.

Combinación de diferentes sustancias. Por último, tenemos a los que les gusta mezclar drogas, como Richard Feynman (físico célebre), al que le iba la marihuana y el LSD, o el neurocientí co John C. Lilly, que consumía LSD y ketamina.Seguro que esta lista se queda corta y hay muchos otros que también se «colocan» porque, a excepción de la cocaína, las otras drogas tienen entre sus efectos el liberar la creatividad del yugo del control prefrontal y por ello es posible que hayan sido las preferidas —y una ayuda— en momentos de «eureka» para alguno de estos genios.

Ficha:

Autora: Rosa García-Verdugo

Editorial: Ediciones Paidós

Año: 2020

Colección: Para curiosos.

ISBN: 978-8449336584

Sobre la autora: Rosa García-Verdugo estudió bioquímica en Oviedo, terminando dichos estudios con un proyecto de investigación en la Universidad de Leiden (Países Bajos). Después comenzó su periplo por varios laboratorios en Madrid, Barcelona y finalmente Múnich donde en 2015 consiguió su doctorado en Neurobiología en el Instituto Max-Planck. Tras diez años dedicados a la ciencia, decide colgar la bata y ahondar en su otra pasión: la comunicación científica. Actualmente trabaja como escritora freelance y asesora de comunicación para empresas de biotecnología. Es colaboradora habitual de Mapping Ignorance.

En Editoralia personas lectoras, autoras o editoras presentan libros que por su atractivo, novedad o impacto (personal o general) pueden ser de interés o utilidad para los lectores del Cuaderno de Cultura Científica.

El artículo Genética eres tú se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Las herramientas de edición genética CRISPR y los ratones avatar
2. Sobre la predisposición genética a padecer enfermedades
3. Sobre la predisposición genética a padecer enfermedades (II)

Foto: Tiko Giorgadze / Unsplash

Una introducción a qué es y qué factores afectan al cambio climático y como abordarlos, incluyendo los aspectos socioeconómicos. Esto es lo que ofrece Elisa sainz de Murieta al presentar el trabajo que se realiza en el Basque Centre for Climate Change (BC3) en esta charla de 2019.

Elisa Sainz de Murieta es geóloga e investigadora principal del BC3 en varios proyectos H2020 relacionados con la evaluación de los costes del cambio climático y la adaptación a los efectos costeros del cambio climático en la ciudad de Dakar.



Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus

El artículo Elisa Sainz de Murieta – Naukas Pro 2019: Impactos del cambio climático se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Naukas Bilbao 2017 – José Miguel Viñas: Me río yo del cambio climático
2. Los ecosistemas acuáticos de África y el cambio climático
3. Dani y Fiti sobre el cambio climático

Un grupo internacional liderado por la doctora Banafshe Larijani, investigadora Ikerbasque adscrita al Instituto Biofisika (UPV/EHU, CSIC), ha desarrollado un nuevo método de diagnóstico que permite pronosticar con precisión qué pacientes de cáncer responderán positivamente a la inmunoterapia. Este método permitirá a los oncólogos adecuar el tratamiento a cada paciente y evitar las terapias que no vayan a tener éxito.

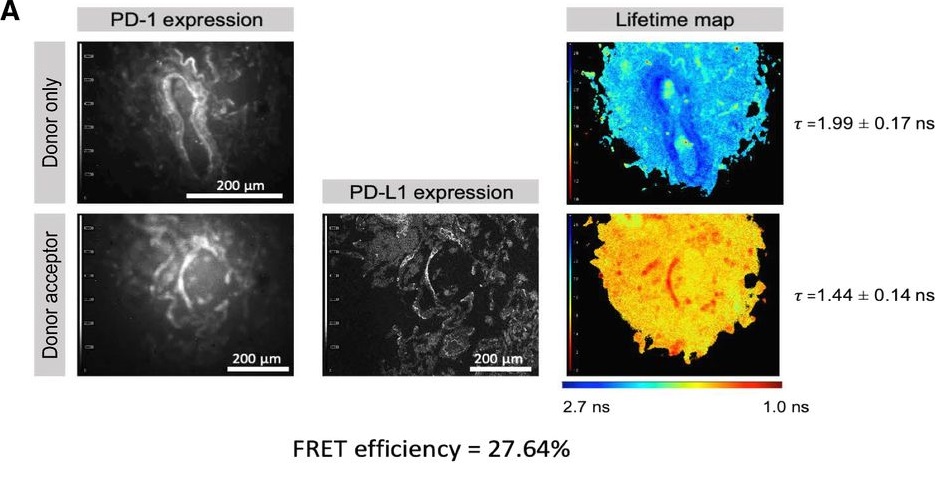
La inmunoterapia es un tipo de tratamiento del cáncer que ayuda al sistema inmunológico del paciente a combatirlo y tiene un impacto profundamente positivo en los tratamientos oncológicos, si bien no funciona en todos los casos: tiene mucho éxito en algunos pacientes, mientras que en otros tiene poco o ningún efecto. Dados los riesgos inherentes a estos procedimientos, se ha establecido una necesidad creciente de definir qué pacientes tienen más probabilidades de beneficiarse, evitando la exposición innecesaria a aquellos que no lo harán.

En el grupo liderado por la doctora Larijan, quien también es directora del Centro de Innovación Terapéutica (CTI) de la Universidad de Bath (Reino Unido), han colaborado colegas de otros centros en Euskadi (Biocruces, PIE, BCAM), europeos y la empresa FASTBASE Solutions Ltd. La nueva herramienta de pronóstico ha sido desarrollada utilizando una plataforma de microscopía avanzada que identifica las interacciones de las células inmunes con las células tumorales y también informa sobre el estado de activación de los puntos de control inmunitarios que amortiguan la respuesta antitumoral.

En una persona sana, los llamados puntos de control inmunológico regulan estrechamente la respuesta inmunitaria del cuerpo, actuando como un interruptor para prevenir enfermedades autoinmunes e inflamatorias. El equipo de la doctora Larijan ha analizado un punto de control inmunológico que consta de dos proteínas: PD-1 (presente en células inmunitarias llamadas linfocitos T) y PD-L1 (presente en otros tipos de células inmunitarias y en la superficie de muchos tipos diferentes de tumores).

Por lo general, cuando el PD-1 en la superficie de los linfocitos T se acopla con el PD-L1 en la superficie de otras células inmunes, apaga eficazmente la función inmunológica de la célula T. Y eso es lo que hacen las células tumorales: al expresar PD-L1 en su superficie, activan PD-1 en el linfocito T, con lo que desactivan su función antitumoral y permiten la supervivencia y el crecimiento del tumor. Los inhibidores empleados en la inmunoterapia funcionan interrumpiendo la interacción entre el PD-L1 en el tumor y el PD-1 en la célula T, y así restablecen la actividad antitumoral del paciente. Esta nueva herramienta determina el alcance de la interacción PD-1 / PD-L1 en una biopsia del tumor, prediciendo si es probable que la terapia con inhibidores del punto de control tenga un beneficio clínico significativo.

“Actualmente, las decisiones sobre si proceder con el tratamiento con inhibidores de puntos de control se basan simplemente en si PD-1 y PD-L1 están presentes en las biopsias, más que en su estado funcional. Sin embargo, nuestro trabajo ha demostrado que es mucho más importante saber que las dos proteínas realmente interactúan y, por lo tanto, es probable que tengan un impacto funcional en la supervivencia del tumor», indica la profesora Larijani.

Referencia:

Lissete Sánchez-Magraner, James Miles, Claire L. Baker, Christopher J. Applebee, Dae-Jin Lee, Somaia Elsheikh, Shaimaa Lashin, Katriona Withers, Andrew G. Watts, Richard Parry, Christine Edmead, Jose Ignacio Lopez, Raj Mehta, Antoine Italiano, Stephen G. Ward, Peter J. Parker and Banafshé Larijani (2020) High PD-1/PD-L1 checkpoint interaction infers tumour selection and therapeutic sensitivity to anti-PD-1/PD-L1 treatment Cancer Research  doi: 10.1158/0008-5472.CAN-20-1117

Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa

El artículo Cómo pronosticar el éxito del tratamiento del cáncer con inmunoterapia se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Inmunoterapia contra el cáncer
2. Magnetosomas para el tratamiento del cáncer
3. Nanopartículas recubiertas para el tratamiento localizado del cáncer por hipertermia magnética

Ilustración basada en una foto de Wikimedia Commons

Fue contemporáneo de Leonardo da Vinci, solo un poco mayor que Miguel Ángel y, quizás, el único creador renacentista comparable a ellos dos en cuanto a talla artística y relevancia histórica. Y, sin embargo, es probable que nunca hayas escuchado siquiera su nombre. Me refiero al compositor Josquin Desprez. Pocos músicos a lo largo de la historia han gozado de mayor prestigio entre sus contemporáneos o han ejercido una influencia más profunda y duradera sobre los que les siguieron. Desprez fue aclamado en vida como “el mejor compositores de nuestro tiempo”, el “padre de los músicos”, “el amo de todas las notas” —como se refirió a él Martín Lutero.

Josquin desarrolló su carrera en una etapa de grandes cambios musicales, que darían paso a un lenguaje musical internacional dentro de Europa. Él fue uno de los artistas que ayudó a guiar esta transición, incorporando los valores humanistas del Renacimiento en el mundo de la música. Frente a la música teórica, cerebral y erudita de la etapa anterior, sus composiciones muestran la influencia de formas populares del momento, como la frottola, un tipo de canción con una textura simple (generalmente homofónica, lo que significa que todas las voces se mueven a la vez y complementan a la principal, siguiendo el mismo ritmo), melodías fáciles de seguir, estribillos pegadizos y un texto laico generalmente alegre, desenfadado o hasta irónico. Dentro de este afán por simplificar la música y acercarla a su público, Josquin fue conocido por su don para la melodía y su capacidad de ligarla al texto para hacerlo más comprensible. Para él y otros compositores renacentistas, la música había dejado de ser una creación puramente intelectual, el resultado de complejas relaciones numéricas y mudas. La música era, ante todo, una extensión de las emociones humanas y como tal, debía imitar la entonación de los actores que con su voz eran capaces de conmover al público.

Y por qué os cuento todo esto, os preguntaréis. Pues porque tengo un problema. Tengo una canción pegadiza que me invade la cabeza cada dos por tres y que fue compuesta hace más de 500 años. La melodía es esta:

El grillo es, probablemente, la frottola más popular de Josquin Desprez. Irónica y tierna, habla de lo “buon cantore” que es el pequeño insecto y lo bien que aguanta las notas largas. Aunque también se ha especulado que Josquin podría estar refiriéndose a su amigo el cantante Carlo Grillo. Grillo formaba parte de la capilla musical del cardenal Ascanio Sforza que, al parecer, era bastante rácano a la hora de remunerar a sus músicos. Desprez podría estar al tanto de los aprietos económicos de su compañero y por ello compone esta frottola con un doble sentido, a modo de canción protesta. Léase: señor cardenal, pague usted al buen Grillo, que al contrario que muchos pájaros, él es un músico fiel y canta por amor.

El grillo è buon cantore,
Che tienne longo verso,
Dalle beve grillo canta.Ma non fa come gli altri uccelli,
Come li han cantato un poco,
Van’ de fatto in altro loco
Sempre el grillo sta pur saldo,Quando la maggior è’l caldo
Al’ hor canta sol per amore. El grillo es un buen cantante
de verso y notas largas
¡Vamos, grillo, bebe, canta!No hace como los otros pájaros.
Que cantan un poco
Y luego se van a otro sitio,
El grillo se mantiene donde está …Si el mes de mayo es cálido
él canta solo por amor.

Lo más llamativo de la canción es que la música ilustra el texto en varios momentos ¡e imita incluso el canto del simpático bicho! Nada más empezar, por ejemplo, cuando la letra que el grillo es capaz de cantar notas o versos largos (longo verso), la melodía principal se detiene obstinadamente sobre una nota exageradamente larga, mientras las voces intermedias se alternan para dibujar una especie de vaivén: el cantar rugoso del propio grillo. Más adelante, los distintos cantantes se van turnando en una textura cada vez más rápida de notas repetidas que, de nuevo, recuerda al sonido vibrante del propio grillo.

No es un ejemplo aislado, otras frottole de la época1 imitan el sonido del gato, el cisne y la grulla. Algunos se han referido a este fenómeno como música onomatopéyica o, de manera más general, figuralismo: música que “pinta” su propia letra o que imita el sonido de los eventos que habitualmente solo representa simbólicamente. Es un tipo de imitación sonora que se da también en el lenguaje. En concreto, es común que algunos nombres de animales se parezcan al sonido que hace el bicho al que representan. La propia palabra “grillo” es un buen ejemplo de ello. Grillo en castellano, cricket en inglés, kilkerra en euskera, ikhilikithi en zulu, jangkrik en indonesio, Kuriketto (クリケット) en japonés, keulikes (크리켓) en koreano, kirikiti en maorí… parece que el sonido rugoso y agudo del grillo se repite allí donde los humanos pronuncian su nombre. Y, gracias a Josquin, también allí donde lo cantan.

Nota:

1Colección impresa de frottole de Ottaviano Petrucci. El grillo figura en el tercer libro Frottole III publicado en 1505.

Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica

El artículo Un genio desconocido del Renacimiento se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. El genio cegado por su propia teoría
2. El último puzle de Bach
3. Del Tíbet a Debussy en una partitura

El héroe del río es un largometraje cómico (mudo) estrenado en 1928. Está codirigido y protagonizado por Buster Keaton que hace el papel de William, el hijo de Bill Canfield. Canfield es propietario de un barco fluvial que compite con el empresario John James King por el control del transporte de mercancías en el río Mississippi. William y Kitty (la hija de King) están enamorados, provocando el enfado de los padres de ambos.

Casi al final de la película un huracán atraviesa la ciudad. William lucha contra el viento que lo arrastra sin cesar. Tras recibir un golpe en la cabeza, desorientado, permanece en pie, aturdido delante de una casa. La fachada cae sobre él, pero una ventana providencialmente abierta lo salva de morir aplastado (la escena puede verse aproximadamente en el minuto 59:00 de la película). Parece que el actor no permitía que se le doblara en las escenas peligrosas y, en esta, asumió un enorme riesgo. ¿Realizaría algún ensayo antes de filmarla? Desde luego, el protagonista permanece inmutable durante la escena…

Seis fotogramas de la escena de la caída de la fachada. Extraídas de Steamboat Bill Jr. / Wikimedia Commons.

 

Esta secuencia se ha versionado en numerosas ocasiones, desde un episodio de la serie MacGyver hasta alguna película de Jackie Chan, pasando por Deadpan (1997) del cineasta Steve McQueen, en la que él mismo reproduce la escena protagonizada por Keaton casi 70 años antes. Durante casi 20 minutos, desde diferentes ángulos, se puede ver la fachada de una casa que cae sobre McQueen que, al igual que Keaton en 1928, no muestra ninguna reacción.

Consulto cada día la magnífica página Futility Closet que comparte historias sorprendentes sobre temas diversos, entre ellos, la matemática recreativa. En una de sus entradas, Greg Ross introduce un artículo de James Metz publicado en la revista Mathematics Teacher, en el que el autor propone diferentes y sencillos cálculos basados en esta escena de El héroe del río. Es decir, realiza un estudio matemático de la escena, fijándose en algunos de sus fotogramas.

Metz comenta en su artículo que el espacio alrededor de Keaton cuando la ventana “lo atraviesa” es realmente escaso… y tiene razón. Y propone una serie de reflexiones y cálculos para entender con precisión los detalles de la escena. Debajo reproducimos algunas de sus observaciones.

Supongamos que Keaton permanece de pie en el suelo que está situado a 5 pulgadas (1 pulgada = 2,54 centímetros) por debajo de la “bisagra” de la pared que cae. Keaton mide 5 pies y 5 pulgadas (1 pie = 30,48 centímetros; es decir, Keaton mide aproximadamente 165 centímetros). Dejando un margen de 3 pulgadas (7,62 centímetros) por encima de su cabeza, la ventana de altura h debe pasar sobre él a 5,25 pies (1 pie = 12 pulgadas) por encima de la línea de la bisagra. Viendo la escena de El héroe del río, tras la caída completa de la pared, la parte posterior de sus pies está aproximadamente a 0,5 pies (15,24 centímetros) delante de la parte inferior de la ventana. Antes de la caída, la parte inferior de la ventana está a una distancia D de la bisagra de la casa (sobre ella, por supuesto). Resumimos en un diagrama lo anteriormente expuesto:

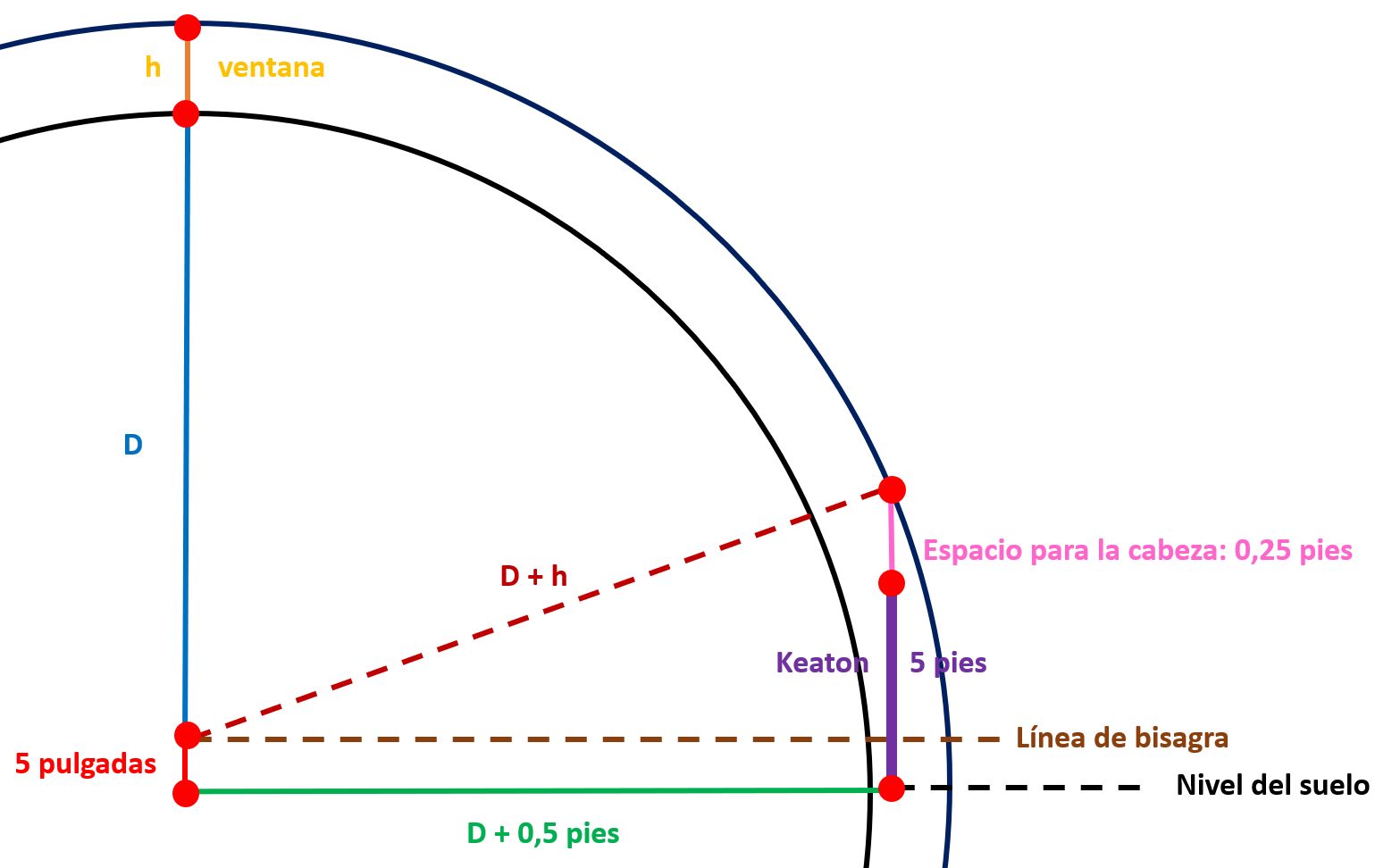Imagen 2: Esquema de la escena basada en los anteriores datos y siguiendo el esquema incluido en el artículo de Metz.

 

¿Cuál es la relación entre h y D? Se trata de una simple relación entre la hipotenusa y los catetos de un triángulo rectángulo:

(D + h)2 = (D + 0,5)2 + 5,252.

Si la anchura de los hombros de Keaton es de 1,5 pies (unos 45,72 centímetros) y los lados de la ventana pasan a 3 pulgadas (unos 7,62 centímetros) por cada lado de Keaton, ¿cuál es el ancho de la ventana? Como 3 pulgadas son 0,25 pies, la ventana tiene una anchura de 1,5 + (2 x 0,25) = 2 pies.

Observando de nuevo la escena, supongamos que la relación entre la altura y el ancho de la ventana es de 7/11. ¿Cuál es la altura h de la ventana? Como 7/11 = 2/h, despejando, es h= 22/7, es decir, unos 3 pies (unos 91,45 centímetros).

Ahora podemos calcular D usando la relación entre h y D obtenida antes. Despejando, D = 3,76 pies (unos 114,6 centímetros).

Estos son solo unos pequeños cálculos que nos ayudan a analizar la situación. ¿Serán similares a los realizados por el equipo de Keaton antes de filmar la escena? Como indica Metz en su artículo, se puede generalizar este análisis y hacerse distintas preguntas de tipo «¿qué pasaría si…?».

Referencias:

• Clearence, Futility Closet, 28 agosto 2020
• Steamboat Bill Jr. (1928), película completa, Wikimedia Commons
• James Metz, The Right Place at the Right Time, Mathematics Teacher 112:4 (2019) 247-249

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad

El artículo En el lugar correcto en el momento adecuado se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Cinco motivos por los que sin jirafas el mundo sería un lugar peor
2. Trigonometría para piratas
3. La ‘reverosis’ de Pablo