Animales urbanitas

Nos hemos acostumbrado a pensar en las ciudades como espacios reservados para los seres humanos, sus mascotas y algunas especies detritívoras. Por otro lado, nos observamos conviviendo además con animales como ratas o palomas, con larga tradición de convivencia con la nuestra. Sin embargo, la ciudad alberga una fauna mucho más rica que la que se reduce a los animales citados. Y, además, en las últimas décadas asistimos a la colonización de especies de mamíferos verdaderamente insospechadas, así como la de aves antes ajenas a nuestro entorno.
Juan Ignacio Pérez Iglesias conversó el pasado 11 de junio, en el marco del ciclo Bidebarrieta Científica, sobre los animales que conviven en las ciudades junto a nosotros y, especialmente, de las últimas especies recién llegadas a ellas en evento online titulado Animales urbanitas.
Juan Ignacio Pérez es doctor en Biología y catedrático de Fisiología en la Universidad del País Vasco (UPV/EHU), donde imparte docencia en la Facultad de Ciencia y Tecnología. Dirige la Cátedra de Cultura Científica de esta misma universidad. Es miembro de Jakiunde, la Academia de las Ciencias, las Artes y las Letras vascas, del Consejo Científico y Tecnológico de la Fundación Española para la Ciencia y Tecnología, y de los patronatos de Ikerbasque, Fundación Vasca para la Ciencia, y de la Fundación Cursos de Verano de la UPV/EHU.
Edición realizada por César ToméLópez
El artículo Animales urbanitas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Relación entre genoma y las formas graves de COVID-19
Investigadores del Área de Enfermedades Hepáticas y Gastrointestinales del Instituto de Investigación Biodonostia- OSI Donostialdea liderados por Luis Bujanda y Jesús Bañales, han participado en un estudio colaborativo internacional en el que se describe, por primera vez, que la vulnerabilidad de ciertas personas al desarrollo de formas clínicas graves en la infección por el virus SARS-CoV-2 puede estar influenciada por sus características genéticas.
 Imagen: US National Cancer Institute / Unsplash
Imagen: US National Cancer Institute / UnsplashLos investigadores han intentado responder a la pregunta de por qué algunas personas son asintomáticas o presentan cuadros leves mientras otras desarrollan cuadros de gravedad al ser infectadas por el virus SARS-CoV-2. Según explican los directores de los grupos participantes, “hemos buscando la respuesta en los genes y hemos encontrado una fuerte asociación entre ciertas variantes genéticas en los cromosomas 3 y 9 y la gravedad de la enfermedad causada por el coronavirus”.
En este estudio internacional han participado científicos de diferentes hospitales y centros del estado (Euskadi, Cataluña, Madrid y Andalucía) y de Lombardía (epicentro de la pandemia en Italia), y ha contado con la coordinación nacional de Jesús Bañales y la internacional de genetistas de Noruega y Alemania.
Tras la aprobación del proyecto por los comités éticos de las instituciones españolas e italianas participantes, se recogieron muestras de sangre de 1.610 pacientes con COVID-19 que necesitaban apoyo respiratorio (oxigeno o ventilación mecánica); de ellas 338 fueron recogidas en el Hospital Univesitario Donostia a través del Laboratoriao de Bioquímica por Adolfo Garrido y Beatriz Nafría, y con el apoyo técnico y logístico de Laura Izquierdo y el Pedro Rodrigues (Biodonostia). Se extrajo ADN de las muestras de sangre para estudiar en el laboratorio de Kiel (Alemania) cerca de 9 millones de variantes genéticas. Para ello se contó con expertos genetistas y bioinformáticos, entre ellos el Dr. Garcia-Etxebarria (responsable del Grupo de Genética Gastrointestinal del IIS Biodonostia) y el Dr. D’Amato (Investigador Ikerbasque y colaborador del mismo grupo), así como con la rápida donación económica de filántropos noruegos. Las variantes de los pacientes infectados por COVID fueron comparadas con las de 2.205 controles sanos, 950 de ellos del Grupo de Genética Gastrointestinal del IIS Biodonostia obtenidas a través del Biobanco Vasco y analizadas por medio de fondos económicos aportados por los grupos de Bujanda, Bañales y D’Amato.
Los investigadores han descubierto que variantes de dos regiones del genoma humano se asocian con un mayor riesgo de desarrollar fallo respiratorio en pacientes con infección por SARS-CoV-2. Una de ellas se localiza en el cromosoma 3 y puede afectar a la expresión de genes que favorecerían la entrada del virus, así como la generación de la “tormenta de citoquinas”. La segunda región se localiza en el cromosoma 9, en concreto en el gen que determina el grupo sanguíneo del sistema ABO. En este sentido, los datos mostraron que tener el grupo sanguíneo A se asocia con un 50% más de riesgo de necesidad de apoyo respiratorio en caso de infección por el coronavirus. Por el contrario, poseer el grupo sanguíneo O confiere un efecto protector frente al desarrollo de insuficiencia respiratoria (35% menos de riesgo).
Merece la pena resaltar también que la variante genética identificada en el cromosoma 3 era más frecuente en personas más jóvenes (media de 59 años), lo que podría explicar, al menos en parte, la gravedad de ciertos casos en este grupo de edad.
En el estudio se observó la asociación significativa de las variantes genéticas localizadas en los cromosomas 3 y 9 con la necesidad de apoyo respiratorio. Así, la frecuencia de ambas variantes genéticas en los cromosomas 3 y 9 es significativamente mayor en los pacientes que necesitaron ventilación mecánica frente a aquellos en los que únicamente se administró oxígeno, asociación que fue independiente de la edad y sexo de los pacientes. Por lo tanto, la presencia de estas variantes genéticas predispone al desarrollo de formas graves de insuficiencia respiratoria durante la infección por SARS-CoV-2.
Investigaciones previas habían indicado que factores como la edad y enfermedades crónicas como la diabetes e hipertensión, así como la obesidad, aumentan el riesgo a desarrollar casos graves de COVID-19. Sin embargo, este estudio demuestra la posibilidad de identificar personas más vulnerables al desarrollo de enfermedad grave con insuficiencia pulmonar por el coronovirus según sus características genéticas, lo que posibilita identificar grupos de riesgo que necesiten una protección especial y diseñar tratamientos personalizados.
Referencia:
The Severe Covid-19 GWAS Group (2020) Genomewide Association Study of Severe Covid-19 with Respiratory Failure The New England Journal of Medicine doi: 10.1056/NEJMoa2020283
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Relación entre genoma y las formas graves de COVID-19 se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Lado oscuro del genoma y leucemia: aspectos éticos y legales de una investigación
- Un predictor de la evolución a metástasis del melanoma
- Una nueva diana terapéutica para el neuroblastoma
La espiral maravillosa
 Ilustración: Almudena M. Castro. Vía Instagram.
Ilustración: Almudena M. Castro. Vía Instagram.Un amigo arquitecto me confesó una vez que su mayor limitación a la hora de construir viviendas es que la vida de las personas crece. Las casas, no. Por eso, los humanos tendemos a mudar la casa de cuando en cuando, para poder acoger nuevos muebles, cientos de libros, más y más recuerdos. Las caracolas no tienen esta opción. Ellas cargan de por vida con el mismo habitáculo que las vio nacer y solo con esfuerzo y saliva (baba de caracola, en este caso) consiguen ir ampliándola poco.
Lo curioso es que, en el proceso, su casa no cambia de forma. Da igual a qué distancia se mire, o bajo qué escala. La caracola siempre se parece a sí misma, con un poco más o menos de zoom. Este tipo de estructura es lo que se conoce como espiral logarítmica y obedece un patrón particularmente sencillo de crecimiento, a saber: “añade un poco más de baba, siempre en la misma dirección, mientras vas girando”. El resultado es sin duda elegante. Cada espira encaja en la anterior de acuerdo con una proporción fija. Cada fragmento de línea contiene el plan de su trazo entero, como un patinador que sólo necesitase fijar la posición de la cuchilla para dibujar la pirueta perfecta.

Jacob Bernoulli (1654-1705) llamó spira mirabilis (espiral maravillosa) a este tipo de curvas y les dedicó un tratado entero con el mismo título. Aunque las espirales logarítmicas ya habían sido descritas por Descartes, Bernoulli profundizó en su estudio y describió con gran detalle sus propiedades matemáticas. Quedó tan fascinado que pidió que grabasen una espiral maravillosa en la lápida de su tumba, acompañada por la frase latina “eadem mutato resurgo”: aunque transformado, resurjo igual. Antes de estas últimas palabras, el matemático suizo le había dedicado muchas otras a la espiral de la caracola y su característica autosemejanza. Para él, podía “ser usada como un símbolo, ya sea de fortaleza y constancia ante la adversidad, o como símbolo de la constancia del cuerpo humano, el cual después de todos sus cambios, aún después de la muerte, será restaurado a su exacta y perfecta esencia”. Jacob fue, sin duda, el mayor fan de la espiral logarítmica que ha existido jamás.
A pesar de esta especie de recursividad infinita, la longitud de una espiral logarítmica está perfectamente acotada. Gracias a la proporción fija que dicta la relación entre sus sucesivas espiras, estas forman una serie geométrica convergente. No existen las caracolas interminables. Incluso podemos calcular su longitud a partir de una simple foto de perfil, midiendo únicamente sus ángulos y su altura, como explico al final de este artículo.
Imagen: GIPHY
Por lo demás, la autosemejanza es, probablemente, la propiedad más llamativa de esta curva marina y matemática. Es la que la distingue, principalmente, de otra espiral igualmente común que hoy conocemos por el nombre de Arquímedes. El físico griego la describió extensamente en su libro Sobre las espirales del siglo III a. C. Es la figura que forman los muelles espirales, o los caminos pedregosos de los discos de vinilo. En esta espiral, las distancias entre los brazos permanecen constantes pero no se conservan las proporciones, ni la identidad a distintas escalas. Por un desdichado error, el artesano que preparó la lápida de Bernoulli grabó en ella una espiral de Arquímedes, en lugar de una logarítmica. El pobre matemático suizo, habría chillado de dolor de haber podido, después de muerto. Lo que me cuesta entender es que casi cuatro siglos después, nadie haya asaltado su sepultura para corregir semejante atropello.
¿Cómo calcular la longitud de una caracola?
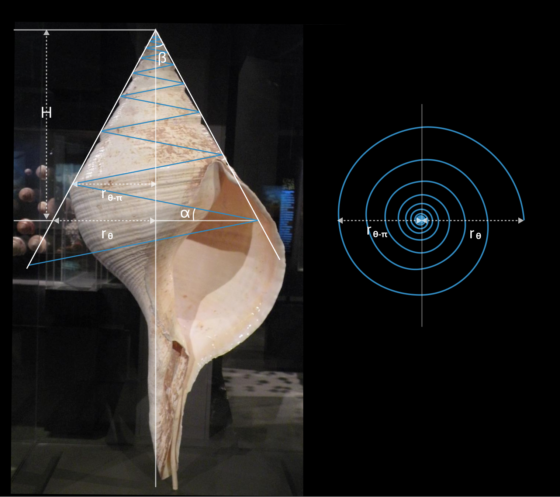
A vista de pájaro, la caracola describe una espiral plana que queda definida por la función r(θ) = ae bθ, en coordenadas polares. A partir de la fotografía y usando razones trigonométricas sencillas, como el teorema de los senos, es posible comparar la anchura de la caracola en su base y después de dar media vuelta. Esto nos permite estimar el valor de b, que caracteriza lo rápido que crecen la espiral logarítmica. Resulta que:
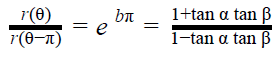
Conocido este parámetro, podemos integrar la función de la espiral para hallar su longitud en el plano, L = ae bθ/b, que no es más que el radio máximo de la espiral dividido por b. Si ahora desenroscamos imaginariamente la caracola, esta formará un canal en diagonal, de de base L y altura H. Por otra parte, el radio mayor de la espiral se relaciona con la altura mediante la relación tan α = ae bθ/H. Por lo tanto, la longitud total de la caracola vendrá dada por
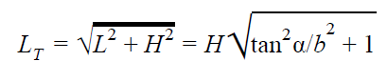
con  Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
El artículo La espiral maravillosa se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El hidrógeno en el Universo (II): El mapa espiral de la Vía Láctea
- El océano en una caracola
- Tema y variaciones
¿Saben aquel que dice … matemáticas? (I)
El humor es una actividad muy sana, así como una medicina recomendable para nuestra vida, sobre todo en momentos como el actual con la crisis del coronavirus, el confinamiento en nuestras casas de más de dos meses y un futuro incierto. Más aún, reírse de uno mismo es además un ejercicio muy saludable.
En esta entrada vamos a hablar de un tipo de humor que podríamos denominar “humor matemático”. Este tipo de humor no se define únicamente por el hecho de que se hable en los mismos de las matemáticas o de las personas que desarrollamos esta ciencia, sino que el pensamiento matemático y la propia esencia de la ciencia de Pitágoras (investigación matemática, demostraciones, razonamiento matemático, áreas de las matemáticas, conceptos matemáticos, problemas, etc) constituyen elementos fundamentales en este humor. Esto último hace que sean chistes que, en muchas ocasiones, no sean entendidos por todo el mundo.
Antes de iniciar este pequeño paseo por algunos chistes matemáticos, expliquemos el título de esta entrada del Cuaderno de Cultura Científica. Quienes tenemos una cierta edad nos acordamos de un humorista barcelonés muy conocido en las décadas de 1980 y 1990, Eugenio Jofra Ballalluy (1941-2001), de nombre artístico Eugenio y que se hizo famoso por los inicios de sus chistes “¿Saben aquel que dice/diu …?”
Por ejemplo, uno de sus chistes decía así:
Saben aquel que dice que se encuentran dos amigos y uno le diu al otro: ¿Sabes quién se ha muerto? ¿Quién? El Anselmo. Carai, ¿de qué? De cataratas. ¿Le operaron? No, le empujaron.
O este otro relacionado con las matemáticas:
Saben aquel que diu … un niño le dice a su padre: Papá, en el colegio nos han dicho que busquemos el máximo común divisor… Y el padre li diu: ¿Pero todavía no lo han encontrado? Cuando yo iba al colegio ya lo iban buscando.
 Cartel del documental Eugenio (2018), de Jordi Rovira y Xavier Baig. Imagen de la web Docs del Mes
Cartel del documental Eugenio (2018), de Jordi Rovira y Xavier Baig. Imagen de la web Docs del Mes
Para empezar con los chistes matemáticos, vamos a empezar por una serie de chistes cortos, algunos muy sencillos y otros que quizás necesiten un pequeño comentario. Empecemos con dos sobre los problemas de matemáticas, algo muy relacionado con la educación de esta materia.
¿Por qué se suicidó el libro de matemáticas? Porque tenía demasiados problemas.
…
– ¿Papá, papá, me resuelves este problema de matemáticas?
– No hijo, no estaría bien.
– Bueno, inténtalo de todas formas.
Algunos chistes tienen que ver con la estadística, jugando con el mal uso de la misma o con las malas interpretaciones.
El 33 por ciento de los accidentes mortales involucran a alguien que ha bebido. Por tanto, el 67 por ciento restante ha sido causado por alguien que no había bebido. A la vista de estos datos, está claro que la forma más segura de conducir es ir borracho.
…
La inmensa mayoría de las personas tiene un numero de piernas superior al promedio.
Ya que la mayoría de las personas tenemos dos piernas, luego basta que exista una persona con una sola pierna para que la “media” baje de 2 y la mayoría estaríamos por encima de la media. O como la ciudad del Vaticano, donde reside el papa de la iglesia católica, tiene una extensión de medio kilómetro cuadrado, se puede deducir que:
La ciudad del Vaticano tiene dos Papas por kilómetro cuadrado.
Algunos chistes tienen que ver con conceptos matemáticos, por lo que hay que conocer estos o el chiste no se entenderá. Además, la esencia de muchos de ellos es un juego de palabras con otro significado de esa expresión matemática en la vida cotidiana.
¿Qué es un niño complejo? Uno con la madre real y el padre imaginario.
El concepto de número complejo es un concepto matemático nada intuitivo, que extiende de cierta forma al de número real. Los números reales son los que manejamos en nuestra vida cotidiana. El chiste se apoya en el hecho de que un número complejo es de la forma a + bi, para a y b números reales, donde i tiene el valor de la raíz cuadrada de – 1 (aquí es donde llega la imaginación matemática, ya que, a priori, no existe la raíz cuadrada de – 1, pero se ha demostrado que es útil considerar que sí existe), como el número complejo 2 + 3i, luego todo número complejo tiene una parte real a y una parte imaginaria bi.
 Humor gráfico del artista chileno Alberto Montt relacionado con los números complejos, con la unidad imaginaria i, es decir, la raíz de – 1. Imagen de la página web de Alberto Montt, Dosis diarias
Humor gráfico del artista chileno Alberto Montt relacionado con los números complejos, con la unidad imaginaria i, es decir, la raíz de – 1. Imagen de la página web de Alberto Montt, Dosis diarias
Otro chiste dice así:
Me gustan los polinomios, pero solo hasta cierto grado.
Muchas personas recordarán los polinomios de cuando los estudiaron en el instituto, relacionados con las ecuaciones algebraicas. Un polinomio es una expresión algebraica que implica a una o varias incógnitas. Por ejemplo, la expresión 1 + x es un polinomio de grado uno, 3 – 5x + 7x2, es un polinomio de grado dos o 1 + 2x + 3x2 + 4x3 de grado tres.
Seguimos con los chistes cortos:
¿Qué es un oso polar? Un oso rectangular, después de un cambio de coordenadas.
Las coordenadas cartesianas (rectangulares) permiten determinar la posición de cada punto del plano en función de dos números que expresan la distancia del punto a los dos ejes coordenados, los cuales se cortan perpendicularmente en un punto especial, el origen. En esta imagen vemos algunos ejemplos (el signo negativo indica si se está en una parte o en otra respecto a los ejes).
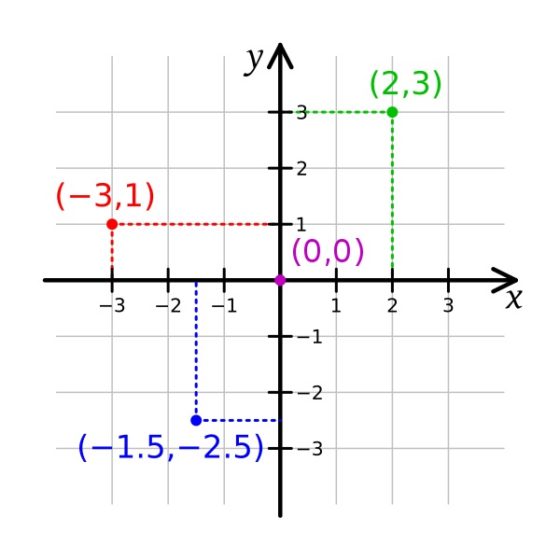 Coordenadas cartesianas o rectangulares. Imagen de K. Bolino en Wikimedia Commons
Coordenadas cartesianas o rectangulares. Imagen de K. Bolino en Wikimedia Commons
Las coordenadas polares son otro sistema para determinar la posición de los puntos del plano, también dada en función de dos valores numéricos, aunque ahora son la distancia al origen de coordenadas, el centro, y el ángulo respecto a la horizontal. En la imagen puede verse un ejemplo.
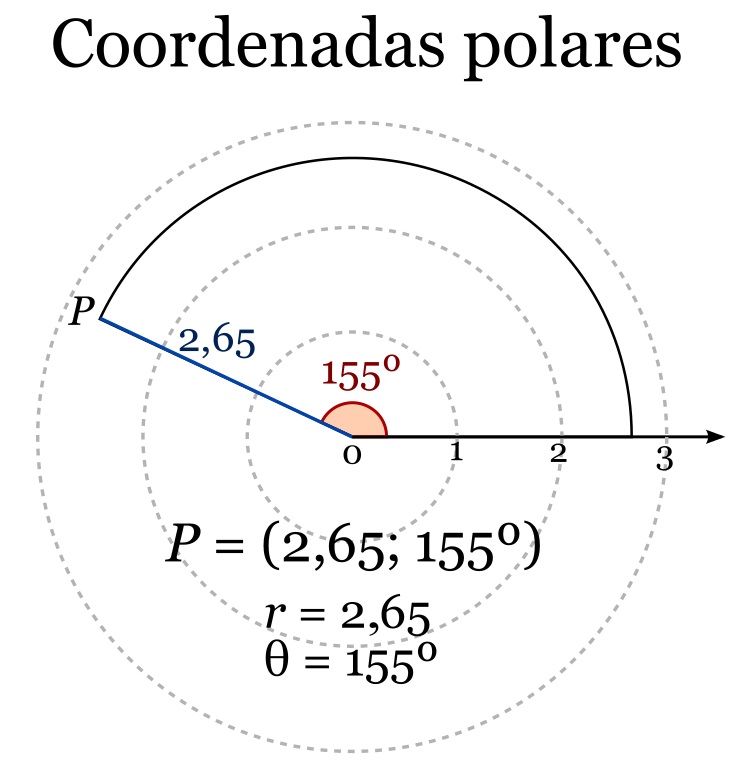 Coordenadas polares. Imagen de Drini (Pedro Sánchez) en Wikimedia Commons
Coordenadas polares. Imagen de Drini (Pedro Sánchez) en Wikimedia CommonsY se habla de cambio de coordenadas, cuando se tiene la posición en un sistema y se pasa al otro sistema, por ejemplo, de coordenadas cartesianas a polares.
Otro chiste corto sobre la ecuación algebraica de la curva llamada parábola (es la trayectoria de una pelota lanzada con un cierto grado hacia arriba y adelante) es el siguiente.
– Jesús les dice a sus discípulos:
– ¡en verdad os digo que y = x²!
– Los discípulos comentan entre sí, y dice pedro:
– Maestro, no entendemos…
– ¡Es una parábola, bruto!
Un chiste que me gusta mucho está relacionado con el hecho de que las personas que estudiamos e investigamos en matemáticas debemos ser muy precisos en nuestra ciencia. Todo tiene que estar bien demostrado y no podemos afirmar nada que no se apoye en la demostración. No hay lugar para la especulación, si luego no se sustenta con una prueba. Por ejemplo, aunque había indicios muy fuertes de que el teorema de Fermat era verdadero, no se consideró así hasta que no se demostró (puede leerse Euler y el último teorema de Fermat o el artículo Avatares literarios del último teorema de Fermat). Por supuesto que esto llevado a la vida cotidiana parece ridículo, sin embargo, es fundamental para la construcción del edificio matemático sobre el que se apoya la ciencia en general.
Una física, una ingeniera y una matemática van en un tren por Escocia. Al observar por la ventana ven una oveja negra.
– «Aja!», dice la ingeniera, «veo que las ovejas escocesas son negras».
– «Hmm…», dice la física, «querrás decir que algunas ovejas escocesas son negras».
– «No», dice la matemática, «todo lo que sabemos es que existe al menos una oveja en Escocia, y que por lo menos uno de sus lados es negro».
Este tipo de chistes, en los que queda en evidencia que los matemáticos somos precisos, exactos en nuestras conclusiones, pero que lo que hacemos no sirve para nada, es bastante habitual. Otro ejemplo:
Dos aventureros iban viajando en globo, cuando por efecto del viento se extravían y no saben dónde están. Después de unas horas ven a alguien paseando en una pradera, y deciden bajar con el globo para preguntar a esa persona por su localización.
– Hola, buenos días, nos podría decir dónde estamos.
La persona a la que han preguntado se queda pensando un rato y al final les dice:
– Están ustedes en un globo.
Entonces uno de los viajeros le dice al otro:
– Venga, vámonos, que hemos tropezado con un idiota.
– No, hombre, no es idiota, lo que pasa es que es matemático.
– Ah, ¿sí? y ¿cómo lo sabes?
– Pues muy sencillo, mira. Le hemos hecho una pregunta bien sencilla, que cualquier persona normal podría contestar inmediatamente sin problema, pero él se ha quedado un buen rato pensando la respuesta, y al final nos ha dicho algo que es absolutamente cierto, pero que ya sabíamos y que además no nos sirve para nada.
 El efecto mariposa, de la historia de humor gráfico El bueno de Cuttlas, de Capurnio, aparecida en 20 Minutos en 2005
El efecto mariposa, de la historia de humor gráfico El bueno de Cuttlas, de Capurnio, aparecida en 20 Minutos en 2005Muchos chistes están basados en la forma en que los matemáticos desarrollamos nuestras matemáticas. Los matemáticos y matemáticas vamos obteniendo nuevos resultados a partir de los que ya han sido obtenidos previamente. Construyendo nuestra ciencia sobre lo anteriormente construido. Por eso, en ocasiones un método para resolver un nuevo problema puede ser convertirlo en uno que ya está resuelto y por lo tanto aplicar el que ya está resuelto para dar por concluido el nuevo problema. Esto que en matemáticas significa simplificar las cosas y un ahorro de tiempo y esfuerzo, en la vida cotidiana puede sonar a ir dando un rodeo en lugar de ir hacia delante, y es motivo además de muchos chistes, como los siguientes.
Le preguntan a un matemático cómo freír un huevo, a lo que contesta:
– Sacaría la sartén del armario y la pondría en la cocina, echaría aceite en la sartén, después de sacar la botella de su armario, encendería el fuego, después cogería un huevo de la nevera y cuando el aceite estuviese caliente lo echaría en la sartén, con un poco de sal, y cuando estuviese hecho lo sacaría a un plato.
– ¿Y si el aceite y los huevos estuviesen ya en la encimera de la cocina?
– Entonces los guardaría de nuevo, en el armario y la nevera, y seguiría los pasos anteriores.
En muchos de los problemas que estudiamos los matemáticos, lo primero que nos preguntamos es si existe solución al problema (hay teoremas que prueban la existencia de solución), además si existe solución al problema nos preguntamos si la solución es única. Para algunos problemas no se puede decir más y aunque parezca mentira ese tipo de resultados es muy importante. Por último, aunque en los buenos casos se hace todo a la vez, se intenta diseñar métodos de resolución del problema, para obtener soluciones concretas. Por eso hay muchos chistes que nos muestran a los matemáticos como satisfechos con solo saber que la solución existe, aunque no la calculemos. Veamos un par de ejemplos, el primero comparando varios tipos de científicos.
A un grupo de personas con profesiones relacionadas con la ciencia les preguntan cuánto son 2 +2, y en función de su formación responden lo siguiente:
Ingeniería: 3,9968743
Física: 4,000000004 ± 0.00000006
Matemáticas: Espere… sólo unos minutos más … ya he probado que la solución existe y es única… pero ahora la estoy acotando…
Filosofía: ¿Qué quiere decir 2+2?
Lógica: Defina mejor 2+2 y le responderé.
Contabilidad: Cierra las puertas y ventanas y pregunta en voz baja «¿Cuánto quiere que sea el resultado?»
Informática: Consigue acceder ilegalmente a un superordenador, escribe un programa para calcularlo, y dice que la respuesta es 5, salvo por un par de errores en el programa que se corregirán pronto.
Y otro algo más sangrante aún.
Una ingeniera, una física y una matemática se quedan en un hotel a pasar la noche. La ingeniera nota que su cafetera está echando humo, así que se levanta de la cama, la desconecta, la pone en la ducha y la enfría, luego vuelve a la cama.
Un poco más tarde, la física huele humo también. Se levanta, y ve que una colilla ha caído en una papelera, y algunos papeles han prendido. Empieza a pensar «Hmm! Esto podría ser peligroso si el fuego se extendiera, las altas temperaturas podrían matar a alguien. Debería apagar este fuego. ¿Cómo puedo hacerlo? Vamos a ver… podría hacer descender la temperatura de la papelera por debajo del punto de ignición del papel, o quizás aislar el combustible del oxígeno… vaya, podría echar agua.» Así que coge la papelera, se va a la ducha, y la llena de agua. Luego se va a dormir.
La matemática se da cuenta de que su cama está ardiendo porque unas cenizas de su pipa han prendido en el colchón. Pero como ha estado viendo a sus compañeras antes, sabe que existe solución al problema del fuego, por lo que no se preocupa y se echa a dormir… mientras la cama sigue ardiendo.
 Humor gráfico del artista chileno Alberto Montt relacionado con el ábaco y con el juego de palabras “contar conmigo”. Imagen de la página web de Alberto Montt, Dosis diarias
Humor gráfico del artista chileno Alberto Montt relacionado con el ábaco y con el juego de palabras “contar conmigo”. Imagen de la página web de Alberto Montt, Dosis diariasLas personas que trabajamos dentro de las matemáticas tenemos fama de ser gente que trabajamos mucho y que además estamos absortos en nuestro mundo. Esto es la base de algunos chistes, entre ellos el siguiente.
Un médico, un abogado y un matemático están hablando de si es mejor tener esposa o amante.
Empieza a reflexionar el abogado:
– Obviamente, lo mejor es tener amante. Porque si las cosas van mal con tu esposa, el divorciarte de ella puede ser muy difícil, con un montón de problemas legales, reparto de los bienes, juicios por la custodia de los hijos o por alguna propiedad, en cambio cortar con la amante es más fácil.
El médico dice:
– No, no, está claro que lo mejor es tener una esposa, ya que el tener una mujer te da estabilidad emocional, te evita el estrés y mejora tu salud. Así puedes llevar una vida saludable y desarrollar bien tu trabajo.
El matemático dice:
– Lo mejor es tener las dos. Así mientras tu mujer piensa que estás con tu amante y esta piensa que estás con tu mujer, tú puedes hacer matemáticas.
Otro tipo de chistes tienen que ver con el hecho de que debemos definir bien el problema.
A una ingeniera, una física y una matemática les ponen como problema el construir una valla alrededor de una casa utilizando la menor cantidad posible de madera. La ingeniera va y construye una valla pequeñita. La física hace los planos de algo parecido a una valla, justo al lado de las paredes de la casa, y tan ligerito que para que no se caiga lo tiene que apoyar a la casa. Pero la matemática coge un palillo, lo rompe en tres trozos, los pone en forma de triángulo sobre una mesa fuera de la casa y dice: «Como la Tierra es topológicamente una esfera, esto está rodeando a la casa.»
Como la Tierra es como una esfera, si tenemos una valla, esta rodea las zonas a ambos lados de la misma.
 Triángulo de Penrose, de la historia de humor gráfico El bueno de Cuttlas, de Capurnio, aparecida en 20 Minutos en 2015
Triángulo de Penrose, de la historia de humor gráfico El bueno de Cuttlas, de Capurnio, aparecida en 20 Minutos en 2015
En ocasiones también el hecho de que estemos siempre trabajando con teorías y objetos abstractos es motivo para algunos chistes…
Una matemática y un físico van a una conferencia de física teórica, con teorías de Kaluza-Klein involucrando espacios de dimensión 9. El físico está hecho polvo al cabo de un rato, pero la matemática parece interesada, así que el físico le pregunta aburrido:
– Oye, ¿cómo puedes aguantar este rollo?
– Bah, es fácil, todo consiste en visualizarlo.
– Pero ¿cómo visualizar un espacio de dimensión 9?
– Visualizo un espacio de dimensión n y luego hago n igual a 9.
Hay quienes piensan que las matemáticas son muy complicadas, por lo que el cerebro de un matemático o matemática debe ser especial. En el libro Mathematical Circles Revisited» (reeditado por MAA en 2003) su autor Howard W. Eves cuenta que hace unos años en los congresos de Matemáticas se puso de moda el siguiente chiste.
Había una vez un cirujano que descubrió como quitar el cerebro de una persona y reemplazarlo por el tipo de cerebro que el paciente desease. Por supuesto diferentes tipos de cerebro costaban diferente cantidad de dinero.
Un día un paciente se le presentó al cirujano y le dijo que quería cambiar su cerebro. «Bien», dijo el cirujano, «¿Qué clase de cerebro desea usted? Los hay de diferentes precios. Por ejemplo, el cerebro de un abogado sale por 600 euros los 100 gramos, o el de un juez sale por 3.000 euros, y así otros precios».
«Oh! Pero yo no quiero esa clase de cerebros», dijo el paciente, «a mí me gustaría el cerebro de un profesor universitario».
«Veo que tiene usted un gusto exquisito y caro», le contestó el cirujano. «Ahora bien, el cerebro de un profesor de universidad de filología le costaría 600.000 euros, los 100 gramos, o el cerebro de un profesor de universidad de historia le costaría 1.200.000 euros, los 100 gramos, ¿de qué tipo de profesor de universidad desea usted el cerebro?».
«Me gustaría tener el cerebro de un profesor universitario de matemáticas», afirmó el paciente.
«Ya veo que su gusto es realmente caro», le dijo el cirujano. «Esos son los cerebros más caros de todos. Cuestan 6.000.000 euros, los 100 gramos».
«Eso es increíble» replicó el paciente. «¿Por qué cuesta tanto el cerebro de un matemático? Si el precio del cerebro de un abogado es de 600 euros por cada 100 gramos y el de un juez 3.000 euros por cada 100 gramos, ¿por qué cuesta el cerebro de un profesor universitario de matemáticas 6.000.000 euros por cada 100 gramos?».
«Oh!, creo que usted lo puede entender perfectamente» le dijo el cirujano. «Imagine la gran cantidad de matemáticos que se necesitarían para obtener 100 gramos de cerebro.»
 Galletas integrales (2008), del diseñador gráfico barcelonés Eduard Fortuny. Imagen de la página web de Eduard Fortuny, Humor tonto para gente inteligente.
Galletas integrales (2008), del diseñador gráfico barcelonés Eduard Fortuny. Imagen de la página web de Eduard Fortuny, Humor tonto para gente inteligente.Para finalizar, un chiste para quienes las matemáticas les siguen pareciendo difíciles.
Han inventado unas píldoras del conocimiento, y ávidamente los estudiantes van corriendo a la farmacia y empiezan a atiborrarse de píldoras de literatura, historia, religión… al cabo de un rato, uno de ellos le pregunta al farmacéutico:
– Oiga, ¿y no tiene ninguna para aprender matemáticas?
– Sí, espere un poquito…
El farmacéutico se mete en la trastienda, y al cabo de un rato aparece con algo que parece un melón.
– ¿Tan grande?
– Bueno, ya sabes que las matemáticas siempre fueron difíciles de tragar…
 Metro cuadrado (2009), del diseñador gráfico barcelonés Eduard Fortuny. Imagen de la página web de Eduard Fortuny, Humor tonto para gente inteligente.
Metro cuadrado (2009), del diseñador gráfico barcelonés Eduard Fortuny. Imagen de la página web de Eduard Fortuny, Humor tonto para gente inteligente.Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo ¿Saben aquel que dice … matemáticas? (I) se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La extraordinaria capacidad poética de las matemáticas
- Las dos culturas de las matemáticas: construir teorías o resolver problemas
- FUN WITH MATHS, diversión con matemáticas
Juntando semiconductores: amplificadores y memorias RAM
 Foto: Florian Olivo / Unsplash
Foto: Florian Olivo / UnsplashEl efecto neto de un transistor es amplificar (aumentar) la corriente de izquierda a derecha. Esto tiene numerosas aplicaciones, entre ellas la más simple es la amplificación de voltajes en sí misma. Otra es la creación de memorias dinámicas de acceso aleatorio.
Amplificador
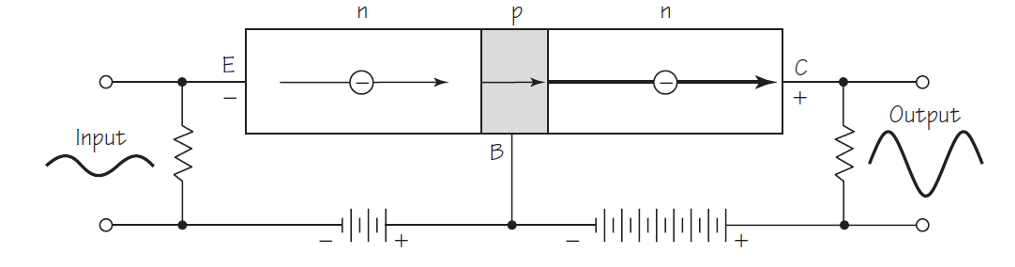 Fuente: Cassidy Physics Library
Fuente: Cassidy Physics LibrarySi colocamos una resistencia grande en un circuito que contenga un transistor, como el de la figura de arriba, podemos amplificar el voltaje entrante, ya que de acuerdo con la ley de Ohm, el voltaje es igual a la intensidad multiplicada por la resistencia. Entonces, la intensidad de una corriente que atraviesa una resistencia pequeña se corresponde con un voltaje pequeño. Pero si se hace que la misma corriente atraviese una resistencia mucho mayor, producirá un voltaje mucho mayor, es decir, el voltaje de entrada pequeño se verá amplificado para producir un voltaje de salida grande.
Por ejemplo, el voltaje amplificado puede corresponder a una porción de una onda de sonido digital, en la cual la onda analógica ha sido aproximada por una serie de voltajes únicos. Esta pequeña porción de la onda (un bit) puede ser representada por un pequeño voltaje recibido en el transistor procedente de una señal recibida por un teléfono móvil. El voltaje amplificado del transistor se puede enviar a los altavoces de los auriculares, que convierten esta señal amplificada en una vibración emitida como una onda de presión que tus oídos perciben y tu cerebro interpreta como, digamos, Rosalía cantando La llorona.
Dispositivo lógico
Un transistor puede actuar como un diodo al permitir que pase la corriente o al impedir el flujo de corriente, dependiendo del voltaje en la base. Al combinar los transistores p-n-p y n-p-n, junto con los diodos, se pueden crear varios sistemas lógicos y «puertas». Una de las aplicaciones más útiles de esto se encuentra en la creación de «memoria de acceso aleatorio dinámico» (DRAM) en ordenadores, dispositivos que almacenan datos a los que se puede acceder a voluntad en orden aleatorio. [1]
 Fuente: Cassidy Physics Library
Fuente: Cassidy Physics LibraryComo es bien sabido, la información se almacena digitalmente en los ordenadores, es decir, se almacena en forma de cadenas de números binarios formados solo por unos y ceros. Cada número binario (ya sea 1 o 0) se llama «bit» (ocho bits forman un «byte»). Por ejemplo, el número binario 10101010, que tiene ocho bits (formando un byte), es equivalente en el sistema decimal al número 170. Si escribimos el número 170 en una hoja de cálculo y la guardamos, el ordenador primero convertirá el número decimal 170 al número binario 10101010; luego asignará cada uno de los ocho bits a una sola celda dentro de la memoria dinámica de acceso aleatorio que representamos en la imagen de arriba. Cada bit corresponderá a la carga en un dispositivo llamado condensador, que, en principio, son solo dos placas que se mantienen próximas entre sí (┤├). Si el bit es 1, el condensador recibirá una pequeña carga. Si el número es 0, no recibe ninguna carga.
Si ahora le pedimos al ordenador que recupere el número 170 de la memoria, la solicitud se envía a la «línea de palabras” (word line) como un voltaje positivo, que luego se aplica a la base del transistor en cada uno de los circuitos de esa línea. Como la base ahora es positiva, la carga en el condensador puede fluir a través del transistor y hacia arriba a través de la «línea de bits» (bit line) hasta el procesador que detecta la corriente e identifica el número en esa celda como 1. Por supuesto, si no hay una carga almacenada en el condensador no habrá corriente en la línea de bits, y ese bit se identificará como 0. En la imagen de arriba vemos un esquema de las celdas de los ocho bits para el número decimal 170. Este diagrama representa solo un byte de memoria. [2]
Notas:
[1] La capacidad de estas memorias RAM es lo que te permitirá ver películas de forma fluida o jugar a videojuegos que requieran un procesamiento muy rápido de gráficos de alta calidad, como Fortnite.
[2] El ordenador en el que se ha escrito esta serie tiene 4 gigabytes de memoria RAM, esto es, 4.000.000.000 (cuatro mil millones) de bytes, o sea, esa cifra de esquemas como el de arriba.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Juntando semiconductores: amplificadores y memorias RAM se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Juntando semiconductores: contrucción y funcionamiento del transistor
- Juntando semiconductores: LEDs y rectificadores
- Juntando semiconductores: el diodo n-p
La recuperación de la vida marina en el Abra de Bilbao
 Imagen 1: vista aérea de la Ría y su desembocadura. Al fondo el puerto de Bilbao ubicado en el Abra Exterior, en tierras de Santurtzi, Zierbena y Getxo. (Fotografía: Mikel Arrazola – bajo licencia Creative Commons BY 3.0. Fuente: Wikimedia Commons)
Imagen 1: vista aérea de la Ría y su desembocadura. Al fondo el puerto de Bilbao ubicado en el Abra Exterior, en tierras de Santurtzi, Zierbena y Getxo. (Fotografía: Mikel Arrazola – bajo licencia Creative Commons BY 3.0. Fuente: Wikimedia Commons)La comarca del Gran Bilbao ha mostrado históricamente una estrecha relación con el río Nervión-Ibaizabal. Desde el siglo XIX, su cauce ha venido recibiendo grandes volúmenes de aguas residuales de origen doméstico, siderometalúrgico, minero e industrial, ante la creencia de que el medio marino podría asimilar toda esa carga contaminante. Sin embargo, las condiciones ambientales naturales del Abra de Bilbao se vieron alteradas de forma drástica.
Afortunadamente, la mayor sensibilidad y conciencia ambiental de la sociedad se tradujo en la puesta en marcha en 1984 del ‘Plan de Saneamiento Integral de la comarca del Gran Bilbao’ promovido por el Consorcio de Aguas Bilbao-Bizkaia que, junto con la paulatina transformación medioambiental de las industrias, fue produciendo una mejora paulatina de la calidad de las aguas y de la vida animal y vegetal de los fondos rocosos del Abra.
Las algas y los invertebrados que viven fijos a la roca son excelentes indicadores ecológicos para evaluar la calidad de las aguas. Debido a su naturaleza sésil (sin capacidad de movimiento) o sedentaria, acumulan los efectos de la exposición prolongada a la contaminación, dando una visión general del estado ecológico de un lugar en relación a los contaminantes y a las variables naturales existentes.
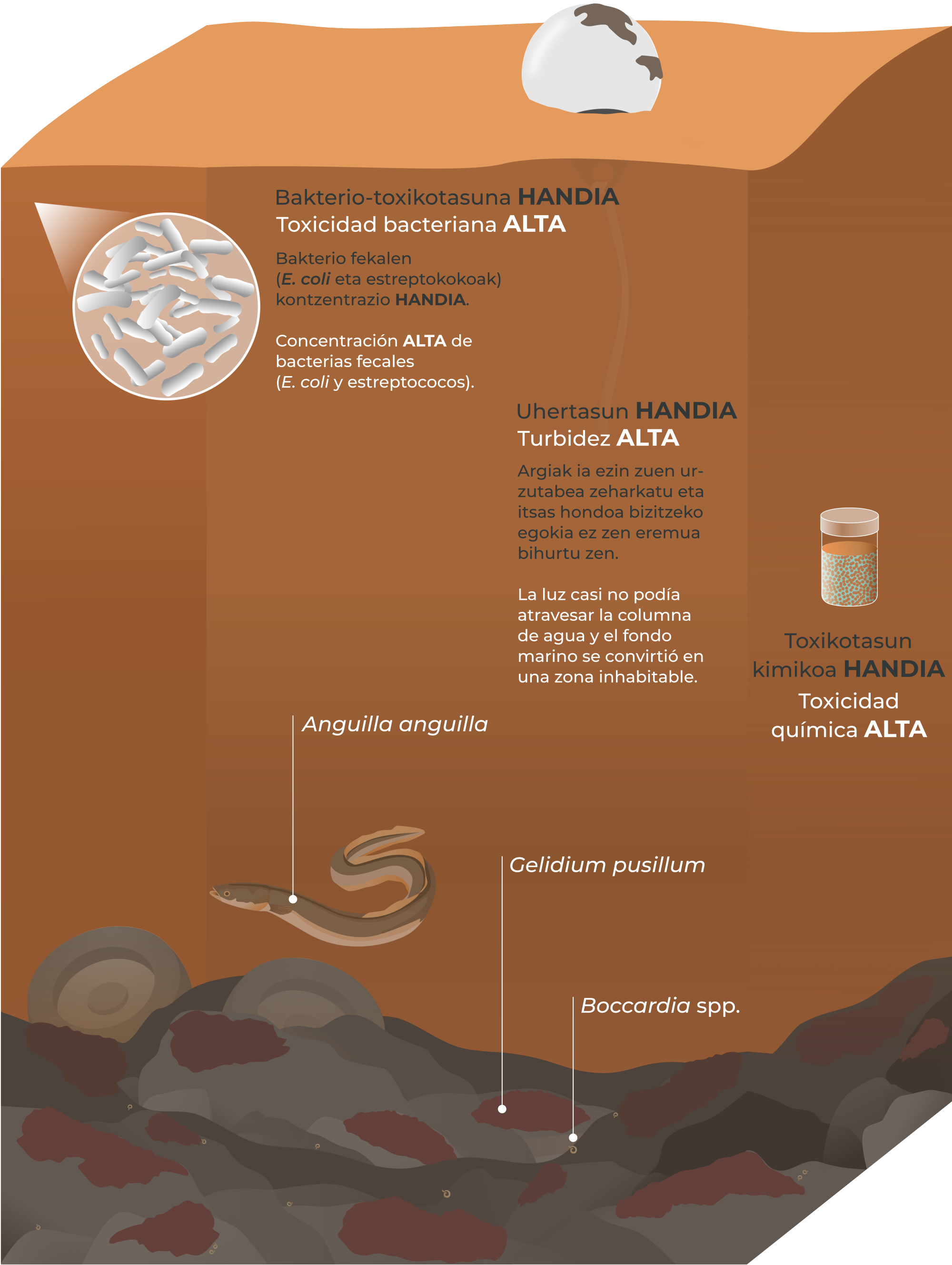 Ilustración 1: debido a la gran concentración de partículas en suspensión que había por efecto de la contaminación el agua era muy turbia y presentaba además una toxicidad química alta, la luz casi no podía atravesar la columna de agua y el fondo marino se convirtió en una zona inhabitable. (Ilustración: NorArte Studio)
Ilustración 1: debido a la gran concentración de partículas en suspensión que había por efecto de la contaminación el agua era muy turbia y presentaba además una toxicidad química alta, la luz casi no podía atravesar la columna de agua y el fondo marino se convirtió en una zona inhabitable. (Ilustración: NorArte Studio)La fuerte contaminación sufrida durante décadas en el Abra de Bilbao ocasionó la degradación ambiental de las comunidades biológicas originalmente existentes. La flora y fauna que ocupaba el lecho marino rocoso sufrió los efectos perjudiciales del aumento en la turbidez del agua, en la tasa de sedimentación y la concentración de sustancias tóxicas que junto con la menor disponibilidad de oxígeno originaron la desaparición masiva de muchas especies. En concreto, la zona intermareal rocosa (descubierta en bajamar) quedaba anegada por un fino depósito de fango y permanecía prácticamente sin vida en gran parte del Abra. Sólo las especies más tolerantes a la contaminación, como el alga roja Gelidium pusillum y gusanos del género Boccardia eran capaces de soportar unas condiciones ambientales tan adversas y estresantes.
En las campañas periódicas de muestreo llevadas a cabo por la UPV/EHU desde el año 1984 hasta la actualidad se ha podido constatar cómo la transformación industrial y la implementación gradual de los planes de saneamiento de aguas residuales han hecho posible un descenso en la contaminación, permitiendo el proceso de recuperación de la fauna y la flora desde mar abierto hacia las zonas más internas del Abra.
Han sido numerosos los cambios positivos que han favorecido el desarrollo de comunidades más maduras. La mejora en las condiciones ambientales ha facilitado el incremento de la diversidad, el aumento de la cobertura algal, el retroceso de algas morfológicamente sencillas frente al avance de especies más complejas con mayores requerimientos ambientales, el aumento de la variedad de estrategias tróficas de la fauna, y la restauración del equilibrio fauna/flora.
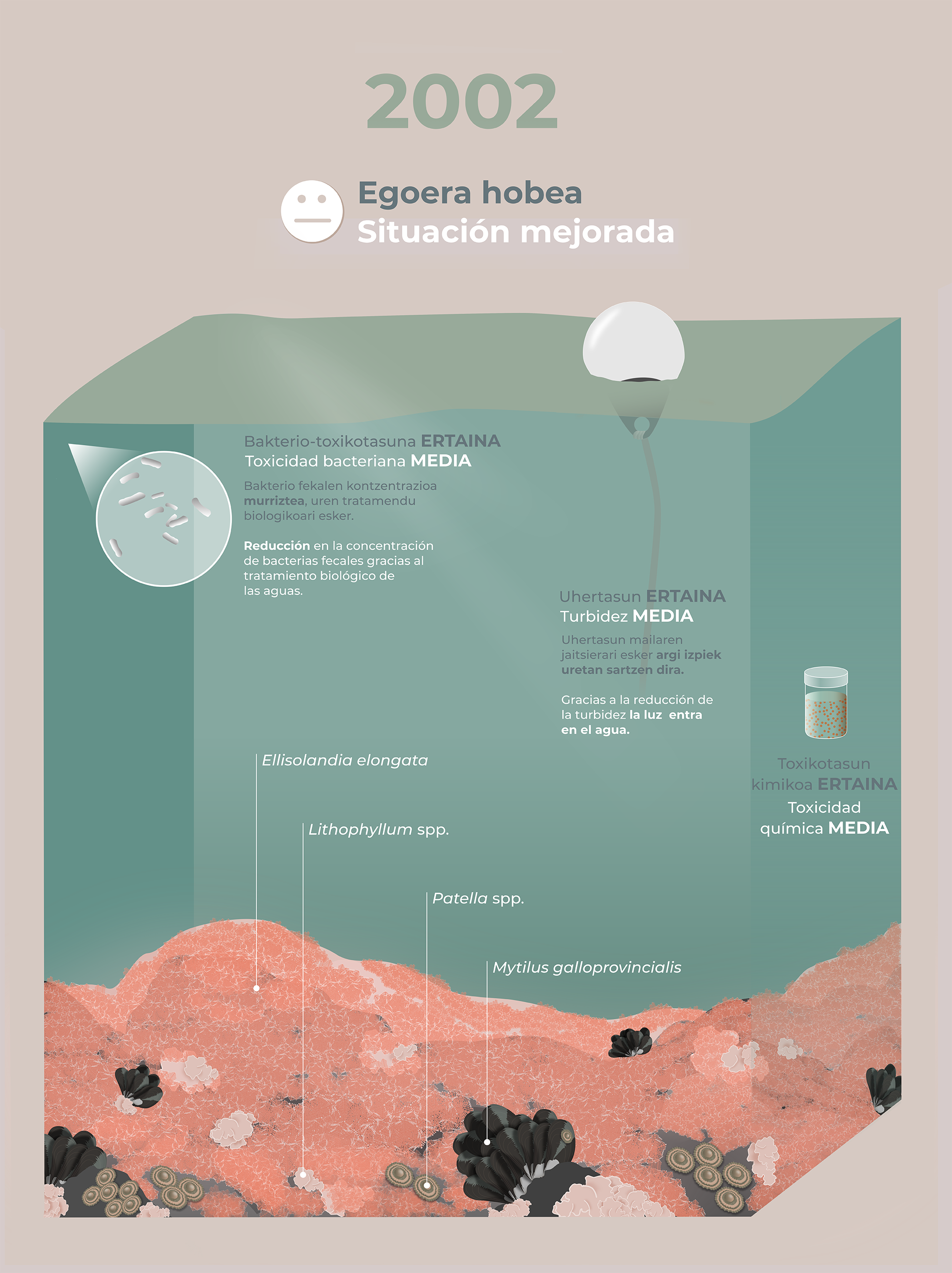 Ilustración 2: con el comienzo del tratamiento biológico y la paulatina transformación medioambiental de las industrias, mejoraron los niveles de oxígeno del agua y la concentración de bacterias fecales (y toxicidad química) disminuyó. (Ilustración: NorArte Studio)
Ilustración 2: con el comienzo del tratamiento biológico y la paulatina transformación medioambiental de las industrias, mejoraron los niveles de oxígeno del agua y la concentración de bacterias fecales (y toxicidad química) disminuyó. (Ilustración: NorArte Studio)Todos estos cambios se han sucedido de forma escalonada en el tiempo. Una primera etapa de mejora quedó identificada por el desarrollo de poblaciones de especies que de forma natural dominan los intermareales de la Costa Vasca: las algas calcáreas de color rosáceo Ellisolandia elongata y Lithophyllum incrustans. Acompañando a esta vegetación aún no muy diversa, quedaba favorecida la fauna filtradora formada por bancos amplios del mejillón Mytilus galloprovincialis, mientras que las lapas herbívoras del género Patella comenzaban a recolonizar la superficie de las rocas.
Posteriormente, el desarrollo de las mejoras ambientales permitieron el aumento de la diversidad con la entrada de especies sensibles, como las algas Bifurcaria bifurcata y Halopteris scoparia y de invertebrados típicos de costa abierta como la anémona Anemonia viridis. Además, la fauna filtradora retrocedió, favoreciendo el avance de los herbívoros y la diversidad de estrategias tróficas con la presencia de invertebrados carnívoros como el gasterópodo Ocenebra erinaceus. El desarrollo de las comunidades bentónicas (organismos que viven sobre el fondo marino) trajo además otros cambios positivos en el ecosistema, aportando recursos básicos como el de refugio, cría de alevines y alimentación para especies de peces típicas de ambientes no contaminados.
Actualmente, las comunidades continúan en fase de recuperación hacia estadíos propios de zonas limpias. A pesar de las medidas de mitigación implantadas y de los cambios favorables ya registrados, aún destaca la escasez de algas de morfología compleja y de herbívoros, entre otros aspectos.
 Ilustración 3: : en la actualidad la concentración de bacterias fecales se encuentra dentro de los niveles permitidos y la reducción de la turbidez ha facilitado que la luz llegue a mayor profundidad. Esto, junto al el descenso de la toxicidad química, ha dado paso a la presencia de ecosistemas más diversos. (Ilustración: NorArte Studio)
Ilustración 3: : en la actualidad la concentración de bacterias fecales se encuentra dentro de los niveles permitidos y la reducción de la turbidez ha facilitado que la luz llegue a mayor profundidad. Esto, junto al el descenso de la toxicidad química, ha dado paso a la presencia de ecosistemas más diversos. (Ilustración: NorArte Studio)Los programas de seguimiento llevados a cabo en el Abra han aportado una información biológica necesaria de gran valor para proponer modelos de gestión y recuperación, además de contribuir al conocimiento en la elaboración de directivas europeas para la protección del medio marino. En este sentido, el estudio continuado del proceso de recuperación del Abra posibilitará obtener información científica única y muy valiosa que permita proteger, restaurar y gestionar de forma adecuada nuestros recursos marinos.
Sobre los autores: María Bustamante, Isabel Díez, Javier Tajadura, Endika Quintano, Nahiara Muguerza, José Ignacio Saiz Salinas y José María Gorostiaga Garai son investigadores del Grupo de Investigación Bentos Marino UPV/EHU
El proyecto «Ibaizabal Itsasadarra zientziak eta teknologiak ikusita / La Ría del Nervión a vista de ciencia y tecnología» comenzó con una serie de infografías que presentan la Ría del Nervión y su entorno metropolitano vistos con los ojos de la ciencia y la tecnología. De ese proyecto han surgido una serie de vídeos y artículos con el objetivo no solo de conocer cosas interesantes sobre la ría de Bilbao y su entorno, sino también de ilustrar como la cultura científica permite alcanzar una comprensión más completa del entorno.
El artículo La recuperación de la vida marina en el Abra de Bilbao se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La recuperación de la fauna en la ría de Bilbao
- 40 años del Plan Integral de Saneamiento del Bilbao Metropolitano
- Naukas Bilbao está en marcha
El polvo del Sáhara
 Foto: Wolfgang Hasselmann / Unsplash
Foto: Wolfgang Hasselmann / UnsplashHace unos años leí que la fertilidad del suelo en las innumerables islas del Pacífico se mantenía, entre otros factores, por la llegada de polvo desde las capas altas de la atmósfera y llevado por el viento desde las estepas y desiertos del Asia Central. El polvo llega a Corea, Japón, las islas del Pacífico y, atravesando el océano y en una semana, hasta Canadá y Estados Unidos. Lo leí en el libro, muy recomendable, “Colapso. Por qué unas sociedades perduran y otras desaparecen”, de Jared Diamond.
Poco después, conocí las lluvias de barro del Levante español o la calima de Canarias. Era el polvo del Sáhara, que veremos en detalle más adelante. Ahora, volvamos al Pacífico. No es fácil calcular la cantidad de polvo que el viento transporta desde las llanuras centrales de Asia. Según Taichi Tanaka y Masaru Chiba, del Instituto de Investigación Meteorológica de Tsukuba, en Japón, las cantidades de polvo se dan en teragramos, es decir 1012 gramos, o sea, 1000000000000 gramos, un 1 seguido de 12 ceros. O, más fácil de captar, 106 toneladas o un millón de toneladas. Esta es la unidad de medida. Pues bien, Tanaka y Chiba calculan que de las llanuras de Asia salen 214 teragramos de polvo por año o, si se quiere, 214 millones de toneladas. Es una cifra siempre en debate y muy cambiante cada año, según la intensidad y dirección del viento y otras condiciones del clima.
Este polvo mantiene la fertilidad de las islas del Pacífico, como escribía Jared Diamond, pero también aumenta la productividad del propio océano. Joo-Eun Yoon y sus colegas, de la Universidad Nacional de Incheon, en Corea, lo han estudiado, en el norte del Pacífico, analizando la concentración de clorofila en el agua, una medida indirecta del crecimiento de algas microscópicas o fitoplancton. Los episodios más fuertes de viento con polvo se dan en el mes de abril, con más de la mitad del total, según datos tomados entre 1998 y 2014. Como medida del polvo en suspensión en la atmósfera utilizan su transparencia o, según la terminología técnica, su capacidad de aerosol. Todos los datos se toman de satélites preparados para tomar esas medidas.
El análisis de los resultados demuestra que la concentración de clorofila y, por tanto, la productividad en algas del Pacífico norte, crece más del 70% en los episodios de viento del oeste y polvo en suspensión.
Una consecuencia inesperada de este aumento de productividad, y de clorofila en el océano, supone la utilización de dióxido de carbono en la fotosíntesis de las algas y, en consecuencia, en la toma de carbono de la atmósfera, con disminución de gases de efecto invernadero y mitigación del cambio climático.
Pero este aumento de productividad llega lejos, como decía antes, hasta Estados Unidos y Canadá, y mantiene la fertilidad del suelo también a millones de kilómetros. El equipo de S.M. Aciego, de la Universidad de Michigan en Ann Arbor, lo ha estudiado en las montañas de la Sierra Nevada, en California.
El nutriente más importante que llega con el polvo es el fósforo, con 1.5 miligramos por gramo de polvo y, recordad, antes hablamos de teragramos o, si se quiere, millones de toneladas. El fósforo que llega a Sierra Nevada repone el perdido por erosión y por arrastre en el agua de la lluvia. Supone el 10%-20% del fósforo que llega al suelo de los bosques.
 Viento del Sahara sobre las Islas Canarias. Fuente: Earth Observatory /NASA
Viento del Sahara sobre las Islas Canarias. Fuente: Earth Observatory /NASAVolvamos a nuestro entorno más cercano, al Sáhara y su polvo. Supone, con los cálculos de Tanaka y Chiba, más del 58% del contenido en polvo de la atmósfera del planeta, con algo más de 1100 millones de toneladas al año, pero, como decía, son cifras siempre en debate y muy variables. Para acercar este polvo a nuestra geografía, repasemos la revisión de José Quereda y Jorge Olcina, de la Universidad de Alicante, sobre las lluvias de barro en la vertiente mediterránea de la Península. Siempre faltan algunos datos pues, hasta muy recientemente, las lluvias de barro eran un fenómeno que no se anotaba en los informes meteorológicos.
Son, como escriben los autores, las lluvias de barro, lluvias de tierra roja o, incluso, las lluvias de sangre de la Biblia y, no hay que olvidarlo, de los condenados de Charles Fort. Hacia el norte de la Península, y en Europa, son más raras que en el Mediterráneo, pero en absoluto desconocidas, como luego veremos.
La composición de las lluvias de barro del Levante lleva carbonatos de calcio y de magnesio. En el análisis de una lluvia de barro que cayó en Castellón en 1993, se encontró calcio, magnesio, sodio y potasio.
Como ocurría en los bosques de California, también en el Mediterráneo el polvo del Sáhara aporta nutrientes a los árboles. Por ejemplo, en el estudio que publicó Anna Ávila, de la Universitat Autònoma de Barcelona, en el macizo del Montseny, con datos desde 1983 a 1998, el polvo llevó nutrientes al suelo en el que crece el encinar. La composición del polvo prueba que proviene del Sáhara occidental y central y del Atlas de Marruecos. De los 58 episodios de lluvia de barro que están anotados en esos 15 años, el 60% del polvo llegó solo en dos, en 1985 y 1991.
El polvo aporta al encinar el 100% del fósforo, el 27% del potasio, el 45% del calcio y el 84% del magnesio que necesita como nutrientes.
No solo a las montañas, sino también a los lagos de altura como, por ejemplo y según el estudio de Anna Hervàs y su grupo, llega el polvo del Sáhara. Lo han demostrado en tres lagos de altura de los Pirineos centrales con la llegada de bacterias que, con muestreos paralelos, han encontrado que también se encuentran en las arenas del Sáhara en Mauritania. Algunas de ellas incluso son potencialmente patógenas. Y, por supuesto, también llegan nutrientes a las aguas de los lagos.
También el polvo del Sáhara llega a las islas del Mediterráneo. El grupo de Ll. Feol, de la Universitat de les Illes Balears, lo ha estudiado en las lluvias de barro en Mallorca. Fueron 253 episodios en los 22 años que van de 1982 a 2003, con gran variabilidad del número de lluvias, como es habitual, y que van de las 29 del año 1999 a solo una en 1981.
Los datos de las cantidades que se depositan sugieren a los autores que suponen un proceso sedimentario importante en las islas. Se depositan, de media, 14 gramos de polvo por metro cuadrado de suelo, pero hay picos de hasta 35 gramos por metro cuadrado. Quizá impresiona más si se traduce a 140 y 350 kilogramos de polvo por hectárea y año.
 Calima (polvo del Sáhara en la atmósfera) sobre Málaga (España). Foto: Vicente Camacho / flickr
Calima (polvo del Sáhara en la atmósfera) sobre Málaga (España). Foto: Vicente Camacho / flickrEs obvio que, además, el polvo del Sáhara contribuye a la contaminación con micropartículas en la atmósfera en la Península y en los archipiélagos. El estudio de Xavier Querol y su grupo, del Instituto de Diagnóstico Ambiental y Estudios del Agua del CSIC, en Barcelona, muestra que las concentraciones de los PM2.5 y PM 10 se multiplican hasta tres veces en episodios de polvo del Sáhara. Las PM2.5 y PM10 son pequeñas partículas sólidas, micropartículas, con un diámetro de 2.5 o 10 micrómetros, medida que es la millonésima parte de un milímetro.
Como ocurría en el norte del Pacífico con el polvo de Asia Central, también el Mediterráneo aumenta su productividad con el polvo del Sáhara. Son resultados del grupo de Mario Cabrerizo, de la Universidad de Granada, en el Mar de Alborán, con datos recogidos entre 1979 y 2016, con la conocida variabilidad en el número de episodios de cada año. Reproducen las condiciones en el laboratorio y muestran el aumento de productividad con el crecimiento de algas microscópicas o fitoplancton, tal como ocurre en el Pacífico.
Acabo con un resumen de hasta donde llega el polvo del Sáhara que, hay que recordar, supone la mayor cantidad de polvo en la atmósfera según los cálculos de Tanaka y Chiba. Los vientos que predominan en el Sáhara son del este y del sur y, por ello, el polvo llega al Atlántico cuando se mueve hacia el oeste, y hasta Europa cuando se mueve hacia el norte. A la Península llega el polvo del Sáhara con más frecuencia al centro y al sur, en verano, y con vientos del sur, según datos de 2005 a 2016, analizados por A. Russo y sus colegas de la Universidad de Lisboa.
En Europa es habitual en el Mediterráneo y llega a los Balcanes, pero en episodios menos corrientes se ha encontrado polvo del Sáhara en Escocia, Suecia, Polonia o los estados bálticos. Cuando el viento es del este, el polvo atraviesa el Atlántico y llega al Caribe y a Sudamérica, por ejemplo, a las cuencas del Amazonas y del Orinoco y, por el camino, se ha encontrado en el Mar de los Sargazos.
Incluso, con viento tormentoso de oeste sobre el Sáhara, el grupo de Jessie Creamean, de la Universidad de California en San Diego, han demostrado que el polvo del desierto atraviesa África y Asia, se une el polvo de China, atraviesa el Pacífico y llega a las montañas de California- Allí, las partículas de polvo forman núcleos de hielo que concentran agua y provocan lluvias en la costa oeste de Estados Unidos. Los autores proponen que ese polvo atmosférico ayuda a renovar los recursos de agua y a aumentar la potencia hidroeléctrica de la costa oeste de Estados Unidos.
Referencias:
Aciego, S.M: et al. 2017. Dust outpaces bedrock in nutrient supply to montane forest ecosystems. Nature Communications DOI: 10.1038/ncomms14800
Ávila, A. 1999. Las lluvias de barro y el transporte y deposición de material sahariano sobre el nordeste de la Península Ibérica. Orsis 14: 105-127.
Cabrerizo, M.J. et al. 2016. Saharan dust inputs and high UVR levels jointly alter the metabolic balance of marine oligotrophic ecosystems. Scientific Reports 6: 35892
Creamean, J.M. et al. 2013. Dust and biological aerosols from the Sahara and Asia influence precipitation in the western U.S. Science 339: 1572-1578.
Diamond, J. 2006. Colapso. Por qué unas sociedades perduran y otras desaparecen. Random House Mondadori. Barcelona. 752 pp.
Fiol, Ll.A. et al. 2005. Dust rains in Mallorca (Western Mediterranean): Their occurrence and role in some recent geological processes. Catena 63: 64-84.
Hervàs, A. et al. 2009. Viability and potential for immigration of airborne bacteria from Africa that reach high mountain lakes in Europe. Environmental Microbiology 11: 1612-1623.
Korle, L.F. et al. 2017. Downward of particle fluxes of biogenic matter and Saharan dust across the equatorial North Atlantic. Atmospheric Chemistry and Physics 17: 6023-6040.
Marinou, E. et al. 2017. Three-dimensional evolution of Saharan dust transport towards Europe based on a 9-year EARLINET-optimized CALIPSO dataset. Atmospheric Chemistry and Physics 17: 5893-5919.
Quereda Sala, J.J. & J. Olcina Cantos. 1994. Lluvias de barro en la vertiente mediterránea de la Península Ibérica. Investigaciones Geográficas 12: 7-22.
Querol, X. et al 2019. African dust and air quality over Spain: It is only dust that matters? Science of the Total Environment 686: 737-752.
Russo, A. et al. 2020. Saharan dust intrusions in the Iberian Peninsula: Predominant synoptic conditions. Science of the Total Environment doi: 10.1016/j.scitotenv.2020.137041
Tanaka, T.Y. & M. Chiba. 2006. A numerical study of the contributions of dust source regions to the global dust budget. Global and Planetary Change 52: 88-104.
Yoon, J.-E. et al. 2017. Spatial and temporal variabilities of spring Asian dust events and their impacts on chlorophyll-alpha concentrations in the western North Pacific Ocean. Geophysical Research Letters doi: 10.1002/2016GL0782124
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo El polvo del Sáhara se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Catástrofe Ultravioleta #27 VOZ 2
 Catástrofe Ultravioleta #27 VOZ 2
Catástrofe Ultravioleta #27 VOZ 2Imagina una tecnología capaz de reconstruir la voz de una persona que ya no puede hablar a partir de viejas grabaciones. En esta segunda entrega del especial de dos capítulos dedicados a la voz humana hablamos de las posibilidades que ofrecen algunos programas de reconstrucción de voz y de lo que algunas personas pueden hacer con su aparato fonador y mucha paciencia. ¡Y revelamos la verdad sobre Peláez y la coliflor!
Para donar tu voz al proyecto de Inma Hernáez: https://aholab.ehu.eus/aholab/
Escúchanos aquí:
Agradecimientos: Marco Sánchez, José Robles, Inma y Arantza Hernáez, Proyecto Revoice, Fundación Luzón, Grison, Ricardo Castella, Almudena Castro, Arthur C. Clark. “Voces invitadas”: Lorena Álvarez, Julián Mayorga, Cris Blanco y Alonso Díaz Carmona
** Catástrofe Ultravioleta es un proyecto realizado por Javier Peláez (@Irreductible) y Antonio Martínez Ron (@aberron) para Podium Podcast con el patrocinio parcial de la Cátedra de Cultura Científica de la Universidad del País Vasco y la Fundación Euskampus. La edición, música y ambientación obra de Javi Álvarez y han sido compuestas expresamente para cada capítulo.
El artículo Catástrofe Ultravioleta #27 VOZ 2 se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Catástrofe Ultravioleta #26 VOZ 1
- Preparados para una Catástrofe Ultravioleta
- Catástrofe Ultravioleta #13 LEVIATÁN
Nuevos fármacos contra las enfermedades hepatorrenales poliquísticas
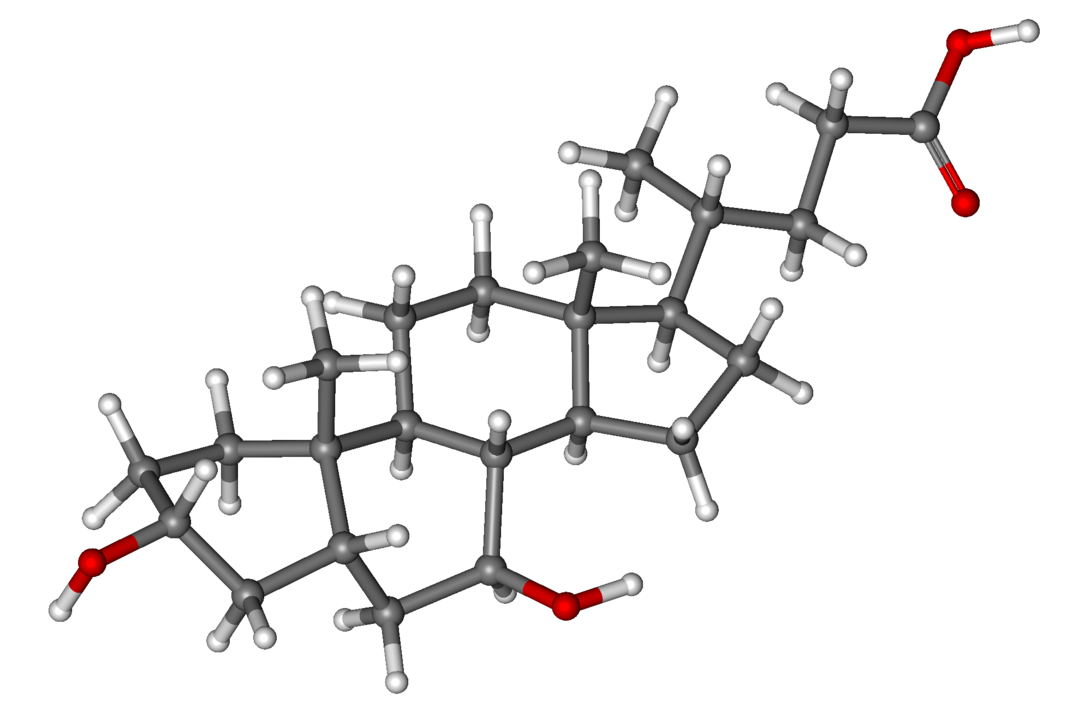 Estructura del ácido ursodeoxicólico. Se trata de un ácido producido en el hígado de algunas especies, entre ellas el oso (Ursus), donde se descubrió por primera vez.
Estructura del ácido ursodeoxicólico. Se trata de un ácido producido en el hígado de algunas especies, entre ellas el oso (Ursus), donde se descubrió por primera vez.Las enfermedades hepatorrenales poliquísticas son trastornos genéticos hereditarios caracterizados por el desarrollo progresivo de múltiples quistes sintomáticos en los riñones o el hígado, que pueden producir alteraciones en la función de dichos órganos o complicaciones relacionadas con su crecimiento. En la actualidad no existen tratamientos farmacológicos eficaces y la única opción curativa es el trasplante de dichos órganos.
Investigadores de la UPV/EHU dirigidos por el Dr. Fernando Cossío (UPV/EHU), director científico de Ikerbasque, y del grupo de Enfermedades Hepáticas del IIS Biodonostia, dirigido por el investigador Ikerbasque Dr. Jesús M. Bañales, han colaborado en el desarrollo de nuevos fármacos que han demostrado ser eficaces en la disminución del crecimiento de los quistes hepáticos y renales de modelos experimentales de dicha enfermedad, lo que puede tener gran transcendencia clínica. Este proyecto multidisciplinar liderado entre ambas instituciones vascas ha contado con la colaboración de investigadores de la Universidad de Salamanca, dirigido por el Dr. José J. G. Marín, del Instituto Idibell de Cataluña, dirigido por el Dr. Manel Esteller, y del Instituto Hormel de Minnesota (EE. UU.), encabezados por el Dr. Sergio Gradilone.
Los fármacos desarrollados se basan en la estructura del ácido ursodeoxicólico (UDCA), un ácido biliar presente en nuestro cuerpo en concentración baja y que tiene propiedades protectoras para el hígado. De hecho, su administración está indicada para el tratamiento de algunas enfermedades del hígado. Los investigadores se han basado en la estructura y propiedades de esta molécula para diseñar y sintetizar una familia de derivados químicos dirigidos a inhibir una proteína clave en la promoción del crecimiento de los quistes hepatorrenales. Los resultados publicados han demostrado que estos nuevos fármacos son capaces de bloquear el crecimiento de los quistes hepáticos y renales en un modelo animal de esta enfermedad.
Referencia:
Caballero‐Camino, F.J., Rivilla, I., Herraez, E., Briz, O., Santos‐Laso, A., Izquierdo‐Sanchez, L., Lee‐Law, P.Y., Rodrigues, P.M., Munoz‐Garrido, P., Jin, S., Peixoto, E., Richard, S., Gradilone, S.A., Perugorria, M.J., Esteller, M., Bujanda, L., Marin, J.J., Banales, J.M. and Cossio, F.P. (2020) New synthetic conjugates of ursodeoxycholic acid inhibit cystogenesis in experimental models of polycystic liver disease Hepatology doi: 10.1002/hep.31216
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Nuevos fármacos contra las enfermedades hepatorrenales poliquísticas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Un modelo teórico para acelerar el descubrimiento de nuevos fármacos
- María Trinidad Herrero, una científica contra las enfermedades neurodegenerativas #WomeninSTEM
- Avances contra la enfermedad de hígado graso no alcohólica
Las cremas solares no bastan: lo que debemos tener en cuenta para protegernos del sol
María Victoria de Gálvez
 Foto: Frank McKenna / Unsplash
Foto: Frank McKenna / UnsplashAdemás de las cremas solares, a la hora de protegernos del sol conviene tener en cuenta otros parámetros si pretendemos asegurar que la salud de la piel no se resiente en verano. A saber: sombrillas, prendas de vestir y de baño e incluso la alimentación.
Índice ultravioleta (UVI)
Para evitar las quemaduras solares, la Organización Mundial de la Salud ha establecido el llamado índice ultravioleta (UVI), que ofrece valores desde 1 (bajo) hasta 11 (muy alto). La recomendación es tomar precauciones frente a la exposición solar a partir de un valor UVI de 3.
Para conocer los datos de UVI local podemos consultar diferentes canales de información, páginas web como la de la AEMT o aplicaciones móviles como UV-DERMA, creada por la Universidad de Málaga y avalada por la Academia Española de Dermatología y Venereología (AEDV).
Además de ofrecer recomendaciones en fotoprotección, la aplicación estima el tiempo que una persona puede permanecer al sol sin quemarse en función de su fototipo y localización geográfica.
En general, conviene tener en cuenta que, aunque el uso de fotoprotectores tópicos es la medida más utilizada, lo más eficaz es evitar la exposición solar en las horas centrales del día. Es decir, entre las 12 y 16 horas, que es la franja horaria en que la irradiancia solar que alcanza la Tierra es mayor. Por otro lado, la dosis de crema importa. Estudios recientes revelan que solemos aplicar cantidades insuficientes para proteger nuestra piel de las radiaciones.
Regla de la sombra
Una forma sencilla de reconocer cuándo existe mayor riesgo de sufrir una quemadura solar es mirar nuestra propia sombra. Si resulta que supera nuestra altura, indica que los rayos del sol inciden de forma tangencial y no son peligrosos. Por el contrario, si nuestra sombra es más corta que nuestra altura se debe a que la radiación solar es más directa y tenemos más riesgo de sufrir una quemadura.
 UVILISCO. Fuente: Universidad de Málaga
UVILISCO. Fuente: Universidad de MálagaEl año pasado, en el Laboratorio de Fotobiología Dermatológica de Málaga desarrollamos un dispositivo llamado UVILISCO capaz de determinar el UVI en función de la sombra reflejada. Se trata de un dispositivo sencillo con forma de obelisco (de ahí su nombre), ideado con un fin didáctico y fácil de instalar en los patios de los colegios y centros educativos.
Con él se pretende concienciar sobre fotoprotección en la etapa escolar, ya que es en esta fase de de la vida cuando se recibe la mayor parte de radiación solar. Teniendo en cuenta que se ha demostrado que con medidas de fotoprotección el cáncer de piel fotoinducido se puede prevenir hasta en un 80%, conviene tomar medidas desde edades tempranas. UVILISCO recibió el Premio al mejor estudio clínico presentado en la Reunión Andaluza de Dermatología de la AEDV.
Ropas y tejidos
La fotoprotección mediante ropas y tejidos es de gran utilidad y asequible para todos. Está muy extendida la creencia errónea de que protegen más los tejidos claros, pero lo cierto es que ofrecen mejor fotoprotección los colores oscuros.
Conviene tener en cuenta que la humedad puede disminuir la protección de los tejidos hasta en un 30%. De ahí la importancia de no confiar en que la protección es total en casos de niños o mayores que están expuestos al sol en las playas durante tiempo prolongado con las camisetas mojadas. Por otro lado, la polución ambiental también puede reducir el nivel de fotoprotección.
En nuestro laboratorio hemos analizado diferentes tejidos utilizados habitualmente en verano. Nuestros resultados muestran que confieren fotoprotección muy alta, aunque ésta se reduce en los tejidos naturales de punto holgado, como las camisas de lino.
En el caso de sobreexposición solar por actividades recreativas, deportes al aire libre, profesiones expuestas de forma prolongada al sol (socorristas, jardineros…) es fundamental el uso de ropa fotoprotectora específica, así como gorras o sombreros de ala ancha. Especialmente en verano.
Uso de sombrillas y toldos
Para evitar las quemaduras solares en las playas, es esencial usar sombrillas y toldos. Sin caer en el error de pensar que la protección que ofrecen es total. No se trata de que la tela de la sombrilla no bloquee la radiación ultravioleta solar (que en algunos casos puede ocurrir), sino que solemos obviar la radiación solar que se refleja desde la arena, el césped o la superficie sobre la que estamos situados.
Esa radiación reflejada dependerá del coeficiente de reflexión de la superficie o albedo, que suele oscilar entre el 10% y el 20% –aunque existen superficies (como la nieve) que pueden reflejar hasta el 80% de la radiación que reciben–.
Antioxidantes
El sol tiene un alto poder oxidante, y las personas tenemos antioxidantes naturales que contrarrestan sus efectos negativos. Sin embargo, en situaciones de elevada exposición solar se genera en el organismo especies reactivas de oxígeno que, si no son neutralizadas por los antioxidantes naturales, desencadenan estrés oxidativo. Ese estrés oxidativo acelera los procesos de envejecimiento, daña el ADN celular y aumenta a largo plazo el daño cutáneo.
Para contrarrestarlo, la tendencia actual por parte de la industria farmacéutica es añadir antioxidantes a las cremas solares (y, a la inversa, añadir fotoprotectores a las cremas antienvejecimiento). Los antioxidantes también pueden administrarse de forma oral, en cápsulas o comprimidos. Si bien la protección que ofrecen frente a la quemadura solar es mínima, son un buen complemento en fotoprotección, especialmente en situaciones de sobreexposición solar y en personas con alergias solares.
Otra alternativa es consumir alimentos ricos en antioxidantes para contrarrestar los efectos oxidativos del sol. En general, las verduras y frutas frescas son ricas en antioxidantes, muchos de los cuales forman parte de los pigmentos. Por eso su consumo está especialmente indicado en época estival.
Así por ejemplo, los betacarotenos (provitamina A) aportan color a la piel y están presentes en frutas y verduras de color naranja, como el melocotón o la zanahoria. El resveratrol de la uva o el licopeno del tomate son otros ejemplos de antioxidantes naturales recomendables en épocas de alta irradiancia solar.
Sobre la autora: María Victoria de Gálvez es profesora de dermatología en la Universidad de Málaga
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Las cremas solares no bastan: lo que debemos tener en cuenta para protegernos del sol se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Estimada OCU: recuerda que NO se pueden utilizar las cremas solares del año pasado
- Tener o no tener (patas): la curiosa historia del ave del paraíso
- ¿Qué le debemos a la ciencia del Romanticismo?
Omar Gil: «Tenemos chance»
¿No será tiempo ya de reconciliar en las aulas el arte con la ciencia, para que aprender atienda nuestras necesidades afectivas y espirituales, además de nuestras necesidades intelectuales y, de esa forma, el conocimiento alimente algún tipo de sabiduría y nos ayude a reducir la fragmentación de nuestra cultura, de nuestras instituciones educativas y la de nosotros mismos? […] ¿Por qué no proponernos hacer de cada curso una obra de arte?
[…] ¿Por qué no podemos elegir ser homo discens? Aprendices. Aprendices que abrazan la diversidad de la experiencia humana y la complejidad de la naturaleza, en vez de acumular conocimientos para manipularlas. Docentes que pueden aprender junto con sus estudiantes, compartiendo con ellos las fortalezas de nuestras preguntas más que la precariedad de nuestras respuestas.
Omar Gil, Tenemos chance, Pecha Kucha Montevideo (2013)
 Omar Gil representando la obra Primos entre sí (2009). Imagen: DivulgaMAT.
Omar Gil representando la obra Primos entre sí (2009). Imagen: DivulgaMAT.Omar Gil (1965-2020) falleció el pasado 29 de mayo. No llegué a conocerlo personalmente, aunque un proyecto en marcha nos habría llevado a encontrarnos probablemente en 2021.
Omar era Licenciado en Matemáticas por la Universidad de la República (Uruguay, 1991) y Doctor en Matemáticas por la Universidad Autónoma de Madrid (1996). Realizó su tesis doctoral bajo la supervisión de Juan Luis Vázquez Suárez. Además de sus publicaciones científicas como especialista en ecuaciones en derivadas parciales, se interesó, entre otros temas, por la innovación educativa y la divulgación de las matemáticas a través de formatos artísticos.
Desde finales de 2009 intercambiamos numerosos correos compartiendo nuestro interés por la literatura, el teatro y la manera de divulgar las matemáticas a través de estas artes.
Esta correspondencia surgió gracias a su obra de teatro Primos entre sí: Omar me pidió hacer una reseña para la sección de Teatro y Matemáticas del portal DivulgaMAT. Me proporcionó el guion de la obra, así como información completa sobre la motivación y todos los materiales que acompañaban la puesta en escena. Además, Omar repasó la reseña para “limar” las posibles incorrecciones cometidas al no haber podido ver la obra en vivo.
 Portadas de sus dos libros.
Portadas de sus dos libros.
Basado en Primos entre sí, Omar publicó Matemáticamente tenemos chance en 2011, obteniendo el Premio Bartolomé Hidalgo en investigación y divulgación científica (2012) y el Premio Nacional de Literatura (2013). Y, tras este texto sobre las matemáticas en la vida cotidiana, llegaron el hermoso libro Cuentos para que Sofía no se pueda dormir (2012) y otros muchos proyectos para acercar las matemáticas a estudiantes y público en general.
Gracias, Omar, por recordarnos que «Tenemos chance», que tenemos la oportunidad de aprender matemáticas de una manera diferente. ¡Hasta siempre!
Bonus: brevísima reseña de “Primos entre sí”
Primos entre síes una obra de teatro que acerca las matemáticas, desde el juego y el humor, invitando a descubrirlas en nuestra vida cotidiana. También advierte sobre la necesidad de actualizar la visión de las matemáticas que trasmite el sistema educativo, animando a reducir la distancia entre las aulas y la creación y aplicaciones de las matemáticas.
 Cartel de la obra que contiene parte de las nociones las matemáticas tratadas: desde la numeración binaria hasta los diferentes tipos de curvaturas en superficies, pasando por la falta de conmutatividad de muchos procesos.
Cartel de la obra que contiene parte de las nociones las matemáticas tratadas: desde la numeración binaria hasta los diferentes tipos de curvaturas en superficies, pasando por la falta de conmutatividad de muchos procesos.
En la obra, Walter Berrutti (representado por el propio Omar) es un matemático uruguayo que trabaja en el exterior y visita Montevideo para dar una serie de conferencias. Se aloja en casa de su “prima”, una amiga íntima de la madre de Walter con la que el protagonista ha convivido desde la infancia como primos, como amigos y como “algo más que camaradas”.
En un tono humorístico, la acción, el juego y el discurso se unen para desmontar algunas creencias sobre la rigidez de las matemáticas. De manera socarrona a veces, se desarman algunas “verdades absolutas” que a todos nos han enseñado de pequeños: no todas las operaciones son conmutativas, no siempre la suma de los ángulos de un triángulo es de 180 grados, no siempre sucede que 1+1=2…
Walter habla, entre otras, de superficies con curvatura positiva (como la esfera), negativa (como la silla de montar) o nula (como el plano). Explica cómo al tener la esfera curvatura positiva, ningún mapa plano de la superficie terrestre puede ser exacto: algunos conservan los ángulos, otros las distancias, pero no pueden suceder ambas cosas a la vez.
Una de las nociones matemáticas tratadas en Primos entre sí son las bases de numeración. Walter recuerda que nuestro modo de contar es la base 10, la aritmética en base 11 se usa en los ISBN de los libros, la base 23 en las letras del NIF español, y finaliza hablando de la base 2, la necesaria para escuchar un CD, ver un DVD o hablar por un teléfono móvil. Precisamente los teléfonos móviles ayudan a Berrutti a enlazar con el análisis armónico, y el matemático habla sobre la transformada de Fourier de un arco iris o el análisis de frecuencias del sonido de una guitarra.
Un minidocumental sobre teoría de juegos invita a examinar las situaciones de la vida cotidiana en las que tenemos la opción de cooperar con otra persona o no hacerlo. Junto al público se explica esta situación mediante el juego que titulan El Dilema.
Finalmente, Walter introduce varios códigos detectores y correctores de errores (el de Hamming, el de Golay, la familia de códigos de Reed-Solomon, etc.) e insiste en la importancia de una buena codificación en, por ejemplo, las misiones espaciales o los discos compactos. Citando finalmente la teoría de la información de Shannon-Weaver, el matemático recuerda que todos los conceptos anteriores están basados en propiedades de los números primos…
Puede encontrarse una reseña completa en DivulgaMAT.
 Cartel de la obra en posteriores adaptaciones y representaciones. Fuente
Cartel de la obra en posteriores adaptaciones y representaciones. Fuente
Jugando aprendimos muchas cosas. Quizás las más importantes. ¿Por qué no seguimos jugando para aprender matemáticas? Haciendo malabares, magia u origami; que tienen una rica tradición matemática siempre viva. O compartiendo el movimiento de una danza, o interpretando en una pieza de teatro un personaje real, imaginario, o si se quiere todavía más abstracto.
Omar Gil, Tenemos chance, Pecha Kucha Montevideo (2013)
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo Omar Gil: «Tenemos chance» se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Los ritmos primos de Anthony Hill
- Números primos gemelos, parientes y sexis (2)
- Metros o millas… Houston, tenemos un problema!
Juantando semiconductores: contrucción y funcionamiento del transistor
 A la izquierda monocristal de silicio fabricado por el método Czochralski. A partir de este tipo de cristal se obtienen las obleas que constituirán la base de los chips. A la derecha una operaria fabrica un monocristal de silicio de este tipo, ¡en 1956! Es probable que el fotógrafo le pidiese que se subiese sus gafas de seguridad (que tiene en la frente) y se quitase los guantes térmicos, que no aparecen en la imagen. Sin estos equipos es literalmente imposible aguantar más de unos segundos en esa posición. Démonos cuenta de que está fundiendo silicio puro, con un punto de fusión de 1414 ºC. Fuente: Wikimedia Commons
A la izquierda monocristal de silicio fabricado por el método Czochralski. A partir de este tipo de cristal se obtienen las obleas que constituirán la base de los chips. A la derecha una operaria fabrica un monocristal de silicio de este tipo, ¡en 1956! Es probable que el fotógrafo le pidiese que se subiese sus gafas de seguridad (que tiene en la frente) y se quitase los guantes térmicos, que no aparecen en la imagen. Sin estos equipos es literalmente imposible aguantar más de unos segundos en esa posición. Démonos cuenta de que está fundiendo silicio puro, con un punto de fusión de 1414 ºC. Fuente: Wikimedia CommonsEs muy común hablar del transistor en general, y de los microprocesadores en particular, como la base de la microelectrónica y los ordenadores, sin entrar en más profundidades. En este texto exploramos de forma muy sencilla cómo se construye [1] un transistor comercial y cómo funciona un transistor elemental. Los enlaces remiten a las explicaciones de los conceptos empleados. Entender el funcionamiento básico no debería ser especialmente difícil y te permitirá apreciar el mundo tecnológico que te rodea a otro nivel.
Nuestra guía será la siguiente figura, donde tenemos (a) un esquema de un transistor bipolar n-p-n en el que se ha establecido una diferencia de potencial en sus extremos; y (b) un esquema simplificado de como se construye [1] de hecho este tipo de transistor por los fabricantes de microprocesadores como Intel o AMD.
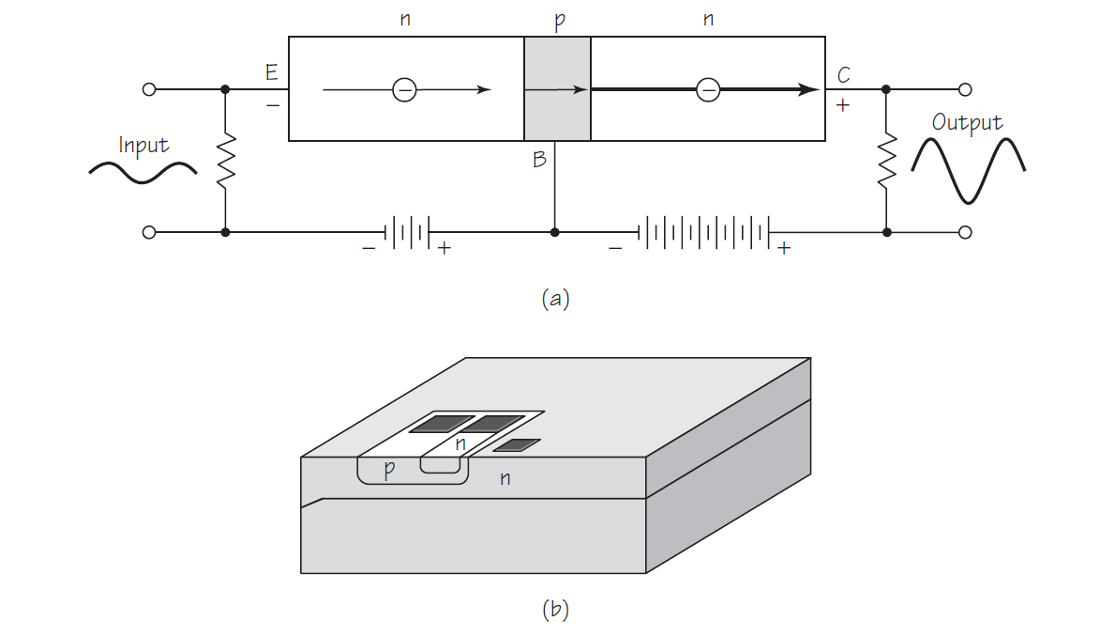 Fuente: Cassidy Physics Library
Fuente: Cassidy Physics LibrarySe coloca una capa delgada de silicio tipo n sobre un cristal muy fino (chip) de silicio tipo p muy ligeramente dopado. El silicio de tipo p, que se encuentra entre las piezas de tipo n, se denomina base. Al ser muy delgado y solo estar ligeramente dopado, la mayoría de sus electrones, que se moverán a través de él de izquierda a derecha, no serán capturados por los huecos, sin embargo, proporcionarán un campo interno para evitar cualquier flujo cuando no haya campo externo. Existe otra razón para que el chip sea muy fino: permitir que los circuitos electrónicos funcionen lo más rápido posible.
Usando ahora una emulsión fotográfica se coloca un patrón microscópico de circuito en la capa superficial del silicio de tipo n de tal manera que la capa superficial de tipo n se elimine en unos lugares y no en otros cuando se aplique una disolución ácida a toda la superficie. Esto tiene como resultado que se expone el silicio tipo p que hay debajo, de modo que se pueden hacer las conexiones eléctricas para formar el transistor n-p-n.
¿Qué hace realmente el transistor y cómo lo hace? Miremos el esquema (a) como si representara dos diodos n-p de forma consecutiva. En estos diodos si se coloca un cable con carga negativa o cero en el silicio de tipo p y un cable con carga positiva en el lado de tipo n, no hay paso de corriente. Sin embargo, si se coloca un cable positivo en la base (tipo p) y un cable negativo en el silicio tipo n a la izquierda en el esquema, las cargas fluirán desde el silicio tipo n hacia la base. Si la base es muy delgada y solo está ligeramente dopada, las cargas pasarán a través de la base hacia el silicio tipo n a la derecha. Aquí la situación se invierte. El tipo p se mantiene positivo, pero se conecta un cable positivo de voltaje aún más alto en el extremo del silicio tipo n situado a la derecha en el esquema. El propósito de esto es mantener los electrones en movimiento de izquierda a derecha. Además de los electrones de conducción que ya están en el silicio de tipo n a la derecha, están llegando nuevos electrones del silicio de tipo n y de tipo p a la izquierda. La cantidad de flujo puede ser controlada por el voltaje positivo en la base.
El efecto neto, pues, es amplificar (aumentar) la corriente de izquierda a derecha. Esto tiene numerosas aplicaciones, entre ellas la más simple es la amplificación de voltajes en sí misma. Otra es la creación de memorias dinámicas de acceso aleatorio. Las exploraremos en siguientes entregas.
Nota:
[1] Probablemente el tiempo verbal debería estar en pasado. Pero no nos debe preocupar para nuestros fines.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Juantando semiconductores: contrucción y funcionamiento del transistor se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Juntando semiconductores: historia del transistor
- Semiconductores
- Juntando semiconductores: el diodo n-p
De las minas a los puertos. Transporte tradicional del mineral
 Imagen 1: 1932, cargadero de mineral de Olabeaga en la ría de Bilbao. (Fotografía: Autoridad Portuaria de Bilbao / Fuente: Asociación Vasca de Patrimonio Industrial y Obra Pública)
Imagen 1: 1932, cargadero de mineral de Olabeaga en la ría de Bilbao. (Fotografía: Autoridad Portuaria de Bilbao / Fuente: Asociación Vasca de Patrimonio Industrial y Obra Pública)Antiguamente, los Montes de Triano y sus minas de hierro -conocidas ya en época romana- eran comunales. Los vecinos y vecinas del Valle de Somorrostro[1] combinaban las labores agrícolas y ganaderas con el trabajo en las veneras[2] y el transporte del mineral con mulas y carros de bueyes hasta los embarcaderos, donde se cargaba hacia las ferrerías. La minería era fundamental para complementar la precaria economía del caserío.
En 1864 el camino de Valle de Trápaga-Trapagaran “teñido con mena de hierro, se ve a todas horas del día concurrido por carros y por caballerías transportando este rico mineral a los embarcaderos de Galindo o a los depósitos de Ortuella.”[3]
Los principales “puertos” estaban en Ugarte, Causo y Galindo (Valle de Trápaga-Trapagaran y Sestao). Eran simples parcelas de terreno cerca de la orilla. El mineral se depositaba en el suelo, en montones, a la espera de ser embarcado. Un rentero los cuidaba, anotaba el nombre de cada propietario y de los carreteros y controlaba la calidad de la vena. En 1846 en Ugarte había 225 depósitos, que correspondían a 61 venaqueros.
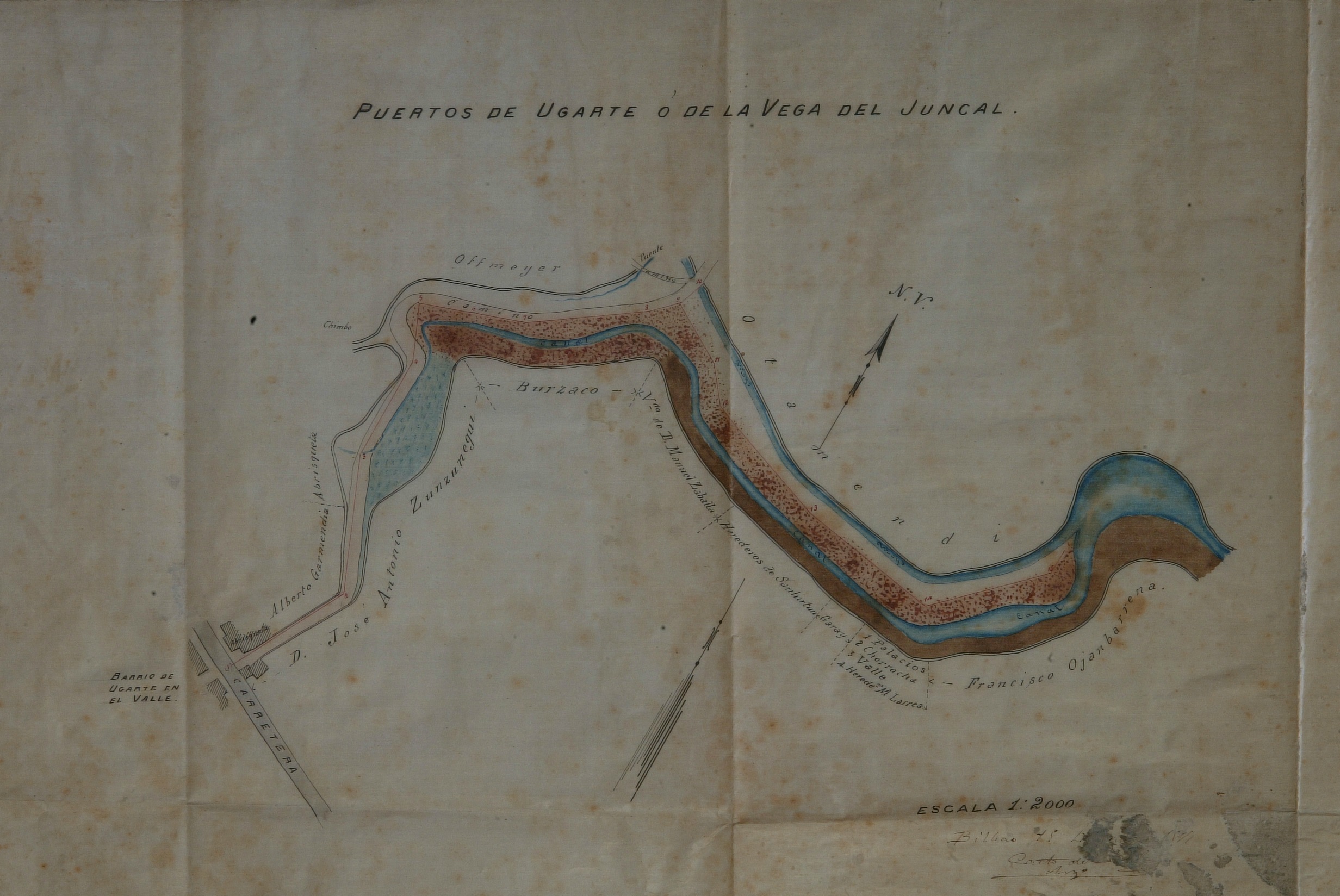 Imagen 2: plano de los puertos de Ugarte o de la vega del Juncal (1897). (Fotografía: Archivo Muncipial de Valle de Trápaga-Trapagaran)
Imagen 2: plano de los puertos de Ugarte o de la vega del Juncal (1897). (Fotografía: Archivo Muncipial de Valle de Trápaga-Trapagaran)Los ríos Galindo y Granada solo eran navegables para embarcaciones pequeñas y de escaso calado, como las gabarras. En 1826 había alrededor de 20 gabarras con 40 marineros para transportar la vena; en 1850 eran 48 gabarreros y 20 mujeres venaqueras. Cuando la marea era favorable se sacaba el mineral con la sirga hasta la Ría, desde donde se llevaba a Asua (Erandio), Sestao, Portugalete o Bilbao. De ahí se llevaba en barcos y en caballerías hacia el interior. La mayoría de las embarcaciones venaqueras (pataches y quechemarines) procedían de Plentzia y Mundaka. En 1850 había entre 200 y 300 barcos, con cerca de 1000 marineros dedicados a este comercio.
A mediados del siglo XIX se producen grandes cambios, como respuesta a la Revolución Industrial que se estaba desarrollando en Europa. En 1849 se permitió exportar el mineral al extranjero, hasta entonces prohibido por el Fuero de Bizkaia, y en 1863 se eliminaron casi todos los impuestos a la exportación, lo que supuso el empujón definitivo para la llegada de capitales extranjeros.
Las principales siderurgias europeas formaron compañías mineras, como la Orconera (inglesa) y la Franco-Belga. Así, entre 1876 y los años 30 del siglo XX se produjo la llamada gran explotación minera. Estas minas llegaron a ser las más importantes de Europa por cuatro razones fundamentales: calidad del mineral, abundancia, facilidad de extracción y cercanía del mar. La mayor parte del mineral se exportó, sobre todo a Inglaterra, y para ello se construyó una red ferroviaria que conectaba las minas con la misma Ría, donde se instalaron modernos embarcaderos que cargaban el mineral en grandes buques.
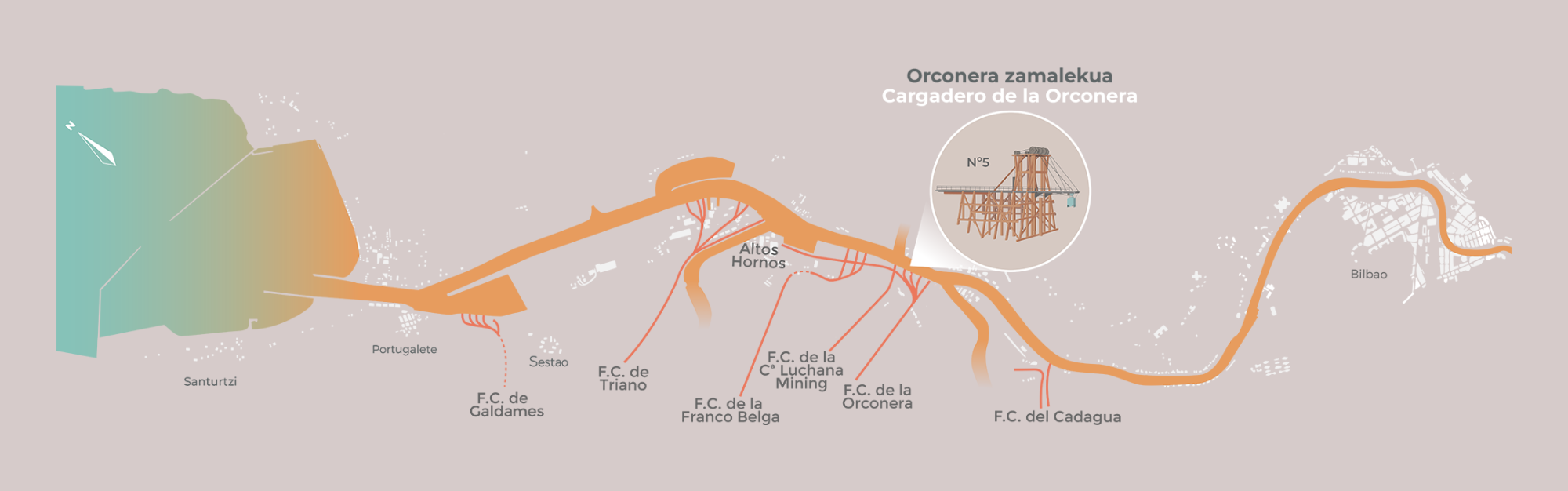 Ilustración 1: líneas de ferrocarril construidas para el transporte de mineral de hierro hasta los cargaderos ubicados a lo largo de la ría de Bilbao. (Ilustración: NorArte Studio)
Ilustración 1: líneas de ferrocarril construidas para el transporte de mineral de hierro hasta los cargaderos ubicados a lo largo de la ría de Bilbao. (Ilustración: NorArte Studio)Los ferrocarriles mineros transportaban mayor cantidad de hierro y en menor tiempo, por lo que los tradicionales puertos fluviales se fueron abandonando. Los habitantes de Valle de Trápaga-Trapagaran sabotearon las obras de construcción del ferrocarril de Triano, inaugurado en 1865, porque perjudicaba su modo de vida basado en el acarreo de mineral.
Así todo se siguió acarreando mineral, pero no hacia los puertos; todavía en 1886: “multitud de carros tirados por bueyes circulan por las carreteras y caminos de la zona minera de Somorrostro que cargan el mineral en las minas para llevarlo a los ferrocarriles”[4].
Solamente el puerto de Ugarte siguió con cierta actividad. En 1878 se había construido un canal para sacar el mineral que llegaba hasta este puerto en el tranvía aéreo de la mina Parcocha. Incluso en 1924 se dice: “El puertecito de Ugarte (donde todavía llegan gabarras) así como los al presente por los aterramientos y lavados de minerales alejados del agua, de Galindo, Causo y Salcedillo”[5]. Sin embargo, desde los años 70 del siglo XIX casi todo el mineral se cargaba en la propia Ría. La modernización de la extracción minera y de los transportes supuso el fin del modo de vida tradicional en el Valle de Somorrostro.
Notas:
[1] Valle de Somorrostro: pertenecía a Encartaciones y estaba formado por los Tres y Cuatro Concejos y la villa de Portugalete. Actualmente los Tres Concejos se corresponden con los municipios de Valle de Trápaga-Trapagaran, Santurtzi y Sestao y los Cuatro con Abanto-Zierbena, Zierbena y Muskiz.
[2] Venera: mina de la que se obtiene vena (hematites rojo de gran pureza).
[3] Delmas, JR: Guía histórico descriptiva del viajero en el Señorío de Vizcaya, en 1864. Madrid, 1944, pág. 526.
[4] Alzola, B: Informe relativo a los recursos de que la industria nacional dispone para las construcciones y armamentos navales, Madrid, 1886, pág. 10.
[5] Balparda y de las Herrerías, G: Historia crítica de Vizcaya y sus Fueros, Bilbao, 1974, T. I, pág. 487 .
Sobre el autor: Eneko Pérez Goikoetxea es historiador y miembro del equipo de educación ambiental del centro Ekoetxea Meatzaldea-Peñas Negras.
El proyecto «Ibaizabal Itsasadarra zientziak eta teknologiak ikusita / La Ría del Nervión a vista de ciencia y tecnología» comenzó con una serie de infografías que presentan la Ría del Nervión y su entorno metropolitano vistos con los ojos de la ciencia y la tecnología. De ese proyecto han surgido una serie de vídeos y artículos con el objetivo no solo de conocer cosas interesantes sobre la ría de Bilbao y su entorno, sino también de ilustrar como la cultura científica permite alcanzar una comprensión más completa del entorno.
El artículo De las minas a los puertos. Transporte tradicional del mineral se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Geología, industrialización y transporte del mineral de hierro en el entorno de la Ría de Bilbao
- Transporte eficiente de oxígeno y alimento en ingeniería de tejidos
- Un minivehículo de transporte de ruedas líquidas
Formas de moverse por la ciudad
 Foto: Free-Photos / Pixabay
Foto: Free-Photos / PixabayHan analizado miles de mapas urbanos de todo el mundo para evaluar la conectividad interior de las ciudades y cómo difiere esa conectividad entre unos países y otros. Han recurrido para ello a los mapas que recoge el proyecto de acceso libre Open Street Map. Y han cuantificado una serie de características, como son (1) el número de vías que confluyen en sus intersecciones, (2) el grado en que una única vía es necesaria para acceder a varios nodos, (3) la relación entre la distancia real que separa dos nodos y la que hay en línea recta entre ellos, y (4) el grado de sinuosidad de los trayectos entre destinos finales. Y con esas magnitudes han calculado el valor de un indicador del grado de dispersión urbana, entendida esta como ausencia de conectividad.
Han identificado, por otra parte, tres modelos urbanos de referencia. El primero es el de malla, característico de ciudades organizadas en una red de geometría rectilínea, sobre todo las que se diseñaron en América antes de que el automóvil particular alcanzase su apogeo. El segundo es el medieval, caracterizado por una disposición irregular de sus calles y con numerosas intersecciones en las que confluyen vías no perpendiculares entre sí; es propio de muchas ciudades históricas europeas. El tercero es el de “fondo de saco” (cul-de-sac); tiene muchas curvas, lazos y vías sin salida, diseños urbanos característicos de la segunda mitad del siglo XX, sobre todo en Norteamérica.
El modelo de malla se caracteriza por tener abundantes nodos o intersecciones, y por confluir un número relativamente alto de vías en esos nodos. Ese modelo tiene, en general, múltiples conexiones y muy pocas vías sin salida, al contrario que el modelo de fondo de saco. El medieval también tiene muchas intersecciones, aunque no haya muchos nodos ni sean muchas las vías que confluyen en ellos. El grado de dispersión es mínimo en el modelo en malla, algo superior en el medieval, y bastante más alto en el de fondo de saco, que tiene mínima conectividad interior.
Las ciudades con las calles mejor conectadas son las de Sudamérica, en las que abunda el modelo de malla, herencia de la colonización española. Uruguay, Paraguay y Argentina son los países con mínimos grados de dispersión. En Japón, Corea del Sur, gran parte de Europa y del Norte de África también hay niveles de conexión intraurbana relativamente altos, propios del modelo medieval. La dispersión más alta se produce en Estados Unidos, Reino Unido, Irlanda y Noruega. Hay también un grupo de países en el Sudeste y Sur de Asia con escasa conectividad urbana. En ciudades como Yakarta o Manila proliferan barrios de clase media de acceso restringido por temor al crimen, servicios públicos ineficientes y débiles regulaciones de uso del suelo. No permiten el acceso libre y, de hecho, la escasa conectividad que propician es parte de una estrategia que busca la estratificación social y el uso exclusivo de los espacios.
La estructura urbana influye en la forma en que nos desplazamos por la ciudad. Cuanto mayor es la conectividad en el interior de una ciudad, menor es el número de automóviles por hogar, y más gente opta por moverse a pie y en bicicleta. La densidad de población también afecta a esas magnitudes: hay más coches y se camina menos en las urbes de menor densidad. Por eso, estudios como este pueden ayudar a tomar decisiones que favorezcan la conectividad, y promover así los desplazamientos que permiten prescindir del vehículo particular, con lo que ello supone en términos de contaminación, salud pública y seguridad de tráfico.
Fuente: Barrington-Leigh C, Millard-Ball A (2019) A global assessment of street-network sprawl. PLoS ONE 14(11): e0223078.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Formas de moverse por la ciudad se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Alfredo García – Naukas Bilbao 2019: Derribando mitos sobre la energía nuclear
 Foto: mhollaen / Pixabay
Foto: mhollaen / PixabayAlfredo García, ingeniero con licencia de supervisor en la central nuclear de Ascó (Tarragona), es la persona tras @OperadorNuclear, el referente en la divulgación en torno a la energía nuclear en el mundo de habla hispana. Esta información, que puede parecer trivial, era secreta hasta que se hizo pública en esta charla. En ella, además, desmonta los mitos habituales sobre la energía nuclear. Como es habitual, estos mitos son más fruto de los prejuicios y el desconocimiento que de la realidad contrastada.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Alfredo García – Naukas Bilbao 2019: Derribando mitos sobre la energía nuclear se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Raúl Ibáñez – Naukas Bilbao 2019: Teorías fantásticas sobre las grafías de los números
- Naukas Bilbao 2017 – Raúl Gay: Todo sobre mi órtesis
- Francisco Villatoro – Naukas Bilbao 2019: El abrazo de la plata
Una infección vírica puede activar la aparición de diabetes tipo I
Un equipo de investigadores ha concluido que los genes no codificantes, no muy estudiados hasta la fecha, pueden ser importantes en la patogénesis de las enfermedades. Al estudiar el efecto que tiene uno de esos genes en las células productoras de insulina los investigadores han descubierto que una infección vírica puede activar ciertos procesos que podrían llevar a la célula a su destrucción.
 Foto: Myriam Zilles / Pixabay
Foto: Myriam Zilles / PixabayLa diabetes tipo I, o insulinodependiente, aparece en la juventud o la infancia. Alrededor del 10-15% de los caos de diabetes son de este tipo. Se considera un trastorno autoinmune: se produce la destrucción de las células beta propias, y estas dejan de producir insulina. “Se trata de una enfermedad autoinmune, inflamatoria y poligénica, muy compleja. Las personas que la desarrollan tienen una genética particular, pero sabemos que otra serie de factores también pueden participar en la activación de la enfermedad. Existen numerosas investigaciones que han descubierto rastros víricos en las células beta pancreáticas de personas que han desarrollado la diabetes, cosa que no se halla en personas no diabéticas. Partiendo de ese punto, hemos encontrado una interacción entre las infecciones víricas y un gen no codificante que puede incrementar el riesgo de desarrollar la enfermedad”, explica la profesora de Bioquímica y Biología Molecular de la UPV/EHU Izortze Santin Gomez.
La doctora Santin se dedica a la investigación funcional de los genes relacionados con la diabetes tipo I; concretamente, estudia “la función que cumplen estos genes en las células beta (las células productoras de insulina), para conocer el efecto que tienen en la patogénesis o desarrollo de la enfermedad”. Ha investigado la influencia de un polimorfismo que aparece en el gen Lnc13, un gen no codificante relacionado con la diabetes tipo I, en colaboración con la investigadora Ikerbasque y miembro del Departamento de Genética, Antropología Física y Fisiología Animal de la UPV/EHU Ainara Castellanos-Rubio. “Hasta ahora, se ha dado importancia sobre todo a los genes candidatos que codifican proteínas, y no se ha prestado mucha atención a otros polimorfismos que se encuentran en zonas no codificantes de proteínas, pero nosotras pensamos que estos pueden tener una gran influencia en el desarrollo de ciertas enfermedades”, comenta Santin. El grupo de investigación ha estudiado qué función cumple el gen no codificante Lnc13 en las células beta pancreáticas que han sufrido una infección vírica, y a través de qué mecanismos moleculares lo hace.
Los investigadores han llegado a una serie de conclusiones importantes: “Por un lado, cuando se da una infección vírica en las células beta, aumenta la expresión del gen Lnc13. Por otro lado, es el Lnc13 el que regula la inflamación de las células beta: la ruta metabólica que se activa cuando se incrementa el Lnc13 puede provocar que las células del sistema inmune migren a las células beta, y ese efecto está totalmente relacionado con el proceso inflamatorio que se da en la diabetes (insulitis). Hemos visto que en las personas que sufren una infección vírica, una variante (alelo) del Lnc13, que incrementa el riesgo de desarrollar la diabetes, puede provocar un proceso de inflamación desmesurada, que puede inducir la destrucción de las células beta”.
Santin explica que, por tanto, “Los polimorfismos de la zona no codificante del genoma, que hasta ahora no se han tenido en cuenta, pueden tener importantes funciones y pueden estar relacionados con la aparición de ciertas enfermedades. Por lo que es posible que a partir de ahora tengamos que comenzar a tenerlos en cuenta”. Por otro lado, en relación a la diabetes tipo I, “podemos decir que la búsqueda de cierta variante (alelo) en el estudio del genotipo del gen Lnc13 o la búsqueda de restos de infecciones víricas pueden tener un valor predictivo”, concluye.
Todo lo anterior abre las puertas a la puesta en marcha de una terapia génica: “Se puede activar la modulación de la ruta patogénica inflamatoria que hemos encontrado en nuestra investigación, jugando con la expresión de genes de la zona no codificante”.
“Está claro que la diabetes es una enfermedad compleja y poligénica —comenta Santin—; por lo tanto, no hay duda de que el gen Lnc13 no es el único factor que explica la aparición de la diabetes, pero ya es hora de entrar en el estudio de la zona no codificante del genoma, así como de incluir el Lnc13 en la ecuación que explica la genética de la enfermedad. Todavía es muy pronto para utilizarlo en el tratamiento de la diabetes, pero todo esto posibilitaría ver si jugando con la expresión del Lnc13 a nivel de células beta, podríamos detener o no el efecto patogénico provocado por las infecciones víricas”.
Referencia:
Itziar Gonzalez-Moro, Ane Olazagoitia-Garmendia, Maikel L. Colli, Nadia Cobo-Vuilleumier, Thomas S. Postler, Lorella Marselli, Piero Marchetti, Sankar Gosh, Benoit R. Gauthier, Decio L. Eizirik, Ainara Castellanos-Rubio, Izortze Santin (2020) The T1D-associated lncRNA Lnc13 modulates human pancreatic b cell inflammation by allele-specific stabilization of STAT1 mRNA PNAS doi: 10.1073/pnas.1914353117
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Una infección vírica puede activar la aparición de diabetes tipo I se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¿Qué nos puede decir un elefante del cáncer en humanos?
- Todo lo que se puede medir en un río
- Vida saludable contra la diabetes
El eco de la sangre
Bloom, a través de la puerta del bar, veía una caracola pegada a los oídos de ellos. Oía más débilmente que lo que ellos oían, cada cual para sí solo, luego cada cual para el otro, oyendo el chasquido de las olas, ruidosamente, silencioso estruendo.
[…]
El mar se creen que oyen. Cantando. Un estruendo. Es la sangre. Sopla en el oído a veces.
James Joyce, Ulises, 1922.
 Imagen de Arek Socha / Pixabay
Imagen de Arek Socha / PixabayOtro mito popular sobre las caracolas vincula su sonido al flujo sanguíneo que, supuestamente, emitiría un eco al atravesar los vasos sanguíneos de los oídos. Esta explicación se encuentra por todo internet, especialmente (e irónicamente) en webs educacionales que tienen por objetivo desmentir mitos sin fundamento científico. El mismísimo Carl Sagan cayó en este error. En su libro The Cosmic Connection, afirma: “Todo el mundo sabe que es el sonido del mar lo que se oye cuando uno se pone una caracola en la oreja. En realidad se trata del sonido amplificado de la propia sangre fluyendo”1. Si bien, a continuación se pregunta: “¿Pero es realmente cierto esto? ¿Ha sido estudiado? ¿Ha intentado alguien decodificar el mensaje de la caracola?”.
A pesar de su insistencia en la web, en la Wikipedia y hasta en el Ulises de Joyce, este mito es falso. Para comprobarlo, basta con hacer un poco de ejercicio y pegar la oreja nuevamente a la caracola. Si nuestra sangre fuese la causa de su sonido, este debería aumentar a la par que el flujo sanguíneo. Sin embargo, el ruido no cambia en absoluto.
De manera más general y según me explica el cardiólogo Julián Palacios, el flujo sanguíneo no suele producir ningún sonido, da igual lo que usemos para escucharlo. El motivo es que se trata de un flujo laminar; corre suavemente por las venas sin choques ni remolinos que puedan generar ruidos. Solo en situaciones en las que su caudal se altera, como en el caso de un estrechamiento repentino o si existen fugas de algún tipo (en un soplo cardíaco, por ejemplo) es posible escucharlo. Si alguna vez has ido al médico y te han tomado la tensión, habrás notado que a veces te colocan un estetoscopio en el antebrazo. El objetivo es poder oír los conocidos como sonidos de Korotkoff. Al ocluir con el manguito el flujo sanguíneo del brazo e ir liberándolo poco a poco, se producen turbulencias en el flujo que sí resultan audibles y permiten identificar el nivel de presión sanguínea, en base a los ciclos cardíacos. Por lo demás, la sangre es silenciosa. Y si alguna vez le da por cantar, siempre va acompañada por las marcas de su director, el pulso cardíaco: un tempo marcado por las válvulas del corazón al abrirse y cerrarse. Nada parecido a los secretos de la caracola.
Aunque resulta difícil rastrear el origen de este mito dentro de la acústica pop, a finales del siglo XIX es posible encontrarlo ya en varios textos literarios. Según Stefan Helmreich, autor de Sounding the Limits of Life, esta coincidencia en el tiempo no sería casual. Para que la idea de los ecos sanguíneos cobrase fuerza, debió de ser necesario primero concebir que la sangre podía ser escuchada. Esto solo fue posible con la invención del estetoscopio, en 1816. Cuenta la historia que René Laënnec, un médico francés demasiado pudoroso para apoyar su oído directamente contra el pecho de las damas, decidió valerse de un tubo de madera para escuchar a una distancia prudente. El artilugio no solo le ayudó a desempeñar su labor con decimonónico recato, también le permitió oír los sonidos del corazón con una claridad sin precedentes. Pronto el invento se popularizó y a lo largo del siglo XIX se fue perfeccionando.
 Estetoscopio de caracola. Fuente: D. B. Katz, US Patent 5,420,382, 30 May 1995
Estetoscopio de caracola. Fuente: D. B. Katz, US Patent 5,420,382, 30 May 1995Curiosamente, los sonidos detectados con este nuevo aparato médico se comparaban a veces con aquellos procedente de una caracola, ¡pero con el objetivo de criticarlos! Un anuncio de 1886 que promocionaba un nuevo estetoscopio binaural sugiere que un mal instrumento “recuerda al resonador de juguete de un niño, una caracola”2. El motivo podría ser el mismo que, de hecho, origina los sonidos característicos de la cavidad resonante: en un mal estetoscopio, es posible que el sonido del ambiente se cuele y sea amplificado, dificultando una correcta auscultación. Esta mala publicidad, sin embargo, no amedrentó al inventor que en 1995 patentó un estetoscopio con cabeza de gasterópodo3. En su invento, el mito termina teniendo una aplicación real y la caracola es atravesada por el eco ocasional de la sangre. Por otra parte, tampoco parece que se hayan fabricado muchos aparatos bajo su modelo.
Referencias:
1 Carl Sagan, The Cosmic Connection: An Extraterrestrial Perspective (1973): “Consider, for example, seashells. Everyone knows the “sound of the sea” to be heard when putting a seashell to one’s ear. It is really the greatly amplified sound of our own blood rushing, we are told. But is this really true? Has this been studied? Has anyone attempted to decode the message being sounded by the seashell?“
2 Advertisement for “Dr. Spencer’s Improved Binaural Stethoscope” The Practitioner: A Journal of Therapeutics and Public Health 36, no. 3 (1886).
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
El artículo El eco de la sangre se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El océano en una caracola
- Sangre de dragón
- Un simple análisis de sangre permite detectar el deterioro cognitivo tras un ictus
Un teorema en la biblioteca
Entre los años 2005 y 2011 la Real Sociedad Matemática Española y la editorial Anaya organizaron, bajo la coordinación de Antonio Pérez Sanz y mía, Raúl Ibáñez (miembros de la Comisión de Divulgación de la RSME), dos exitosos concursos literarios de narraciones escolares y relatos cortos relacionados con las matemáticas. Las narraciones escolares y los relatos cortos finalistas y ganadores de estos concursos fueron publicados por la editorial Anaya dando lugar a dos colecciones de libros bajo los nombres de Ficciones matemáticas (narraciones escolares) y Relatos matemáticos (relatos cortos).
 Portadas de los libros de la colección Relatos cortos de la editorial Anaya que recogían los relatos cortos, relacionados con las matemáticas finalistas y ganadores de los concursos literarios RSME-ANAYA
Portadas de los libros de la colección Relatos cortos de la editorial Anaya que recogían los relatos cortos, relacionados con las matemáticas finalistas y ganadores de los concursos literarios RSME-ANAYA
Esta entrada del Cuaderno de Cultura Científica toma como punto de partida la introducción que escribí para el libro Un teorema en la biblioteca, que recogía los relatos cortos del concurso RSME-ANAYA de 2007. En la misma reflexioné sobre la visión que una parte de la sociedad tiene, o tenía, de la ciencia de Pitágoras. En particular, centré mi atención en la opinión de algunas personas del mundo de la cultura y el conocimiento, ya que por una parte sus obras constituyen en alguna medida un reflejo de la sociedad en la que se desarrollan, mientras que, por otro lado, sus pensamientos y reflexiones suelen ser un referente para las demás personas.
Me gustaría iniciar este paseo por una cita del libro Los viajes de Gulliver (1726), del escritor irlandés Jonathan Swift (1667-1745):
Fui a una escuela de matemática, donde el profesor instruía a sus discípulos siguiendo un método difícilmente imaginable entre nosotros en Europa. La proposición y la demostración parecían escritas claramente en una oblea fina con tinta hecha de un colorante cefálico. Esto tenía que tragárselo el estudiante con el estómago en ayunas y no comer nada sino pan y agua durante los tres días que seguían. Al digerir la oblea, el colorante se le subía al cerebro llevándose la proposición al mismo tiempo. Pero hasta ahora el resultado ha defraudado, ya por algún error de dosis o de composición, ya por la picardía de los mozalbetes, a quienes da tanto asco esa píldora que por lo general se escabullen subrepticiamente y la expulsan por arriba antes de que pueda hacer efecto; y tampoco se les ha persuadido todavía para que guarden una abstinencia tan larga como exige la receta.
Seguro que muchos estudiantes, e incluso algunos adultos que conservan ese recuerdo negativo de su etapa escolar, desearían haber tenido una oblea como la descrita en el libro de Swift, que les hubiese permitido adquirir los conocimientos matemáticos sin necesidad de tener que estudiarlos. Aunque la visión negativa del autor de Los viajes de Gulliver tiene de las matemáticas da otra vuelta de tuerca cuando ni siquiera así los estudiantes son capaces de “tragar las matemáticas”.
 Ilustración de Gulliver con el rey y la reina de Brobdingnag de la edición francesa de 1850 de Los viajes de Gulliver. Ilustración de Willmann, Colin, & Outhwaite, al estilo de Paul Gavarni. Imagen de Wikimedia Commons
Ilustración de Gulliver con el rey y la reina de Brobdingnag de la edición francesa de 1850 de Los viajes de Gulliver. Ilustración de Willmann, Colin, & Outhwaite, al estilo de Paul Gavarni. Imagen de Wikimedia Commons
El motivo de empezar con esta cita es que la imagen negativa que muchas personas tenían, o tienen, de las matemáticas seguramente era fruto de los malos recuerdos de la etapa escolar, alimentada en gran medida por cierto miedo a enfrentarse con ellas, lo que a la larga ha podido desembocar en cierta ignorancia en materia científica y, en particular, matemática. Es más fácil criticar lo que se ignora que intentar conocerlo mejor. Aunque esto no solamente es válido para las matemáticas. Me vienen a la mente muchos otros ejemplos, pero por citar uno, existe una cierta opinión negativa en nuestra sociedad hacia el arte contemporáneo, tan necesario y a la vez tan criticado.
Aunque una parte de la culpa, no necesariamente la principal, en esa visión negativa de las matemáticas haya podido estar relacionada con la propia enseñanza de esta asignatura. Como decía el lógico norteamericano León A. Henkin (1921-2006):
Uno de los grandes errores referidos a las matemáticas que cometemos en nuestras clases, es que el profesor siempre parece saber la respuesta a cualquier problema que se plantee, lo que hace que los alumnos piensen que hay un libro en algún sitio con todas las respuestas correctas a todas las cuestiones interesantes, y que los profesores conocen esas respuestas, y que, si nos pudiéramos hacer con el libro, lo tendríamos todo establecido. Eso no se parece en nada a la verdadera naturaleza de las matemáticas.
Aunque las matemáticas son, o deberían serlo, uno de los pilares, junto con la Lengua, de la educación de los jóvenes. Como decía la escritora británica Mary Ann Cross (1819-1880), que firmaba con el conocido pseudónimo George Eliot, en referencia a la educación en general, y poniendo a las matemáticas como referente:
Se ha dicho con gran acierto que el principal objetivo de la educación es análogo al que tienen las matemáticas; es decir, no el de obtener resultados, sino el de saber obtenerlos; no el alcanzar soluciones particulares, sino métodos con los que poder alcanzar infinitas respuestas.
Pero volvamos a esa imagen negativa de la sociedad hacia las matemáticas. En España no se ha tenido un gran aprecio por esta ciencia, y así nos encontramos por ejemplo en la novela Amor y Pedagogía del escritor y filósofo bilbaíno Miguel de Unamuno (1864-1936), el siguiente diálogo,
– ¿Qué estudias ahora?
– Matemáticas.
– ¿Matemáticas? Son como el arsénico; en bien dosificada receta fortifican, administradas a todo pasto matan. Y las matemáticas combinadas con el sentido común dan un compuesto explosivo y detonante; la “supervulgarina”. ¿Matemáticas? Uno… dos… tres… todo en serie; estudia historia para aprender a ver las cosas en proceso, en flujo.
 Fotografía de Miguel de Unamuno en 1921, realizada por la Agencia de prensa Meurisse. Imagen de la Biblioteca Nacional de Francia
Fotografía de Miguel de Unamuno en 1921, realizada por la Agencia de prensa Meurisse. Imagen de la Biblioteca Nacional de Francia
También encontramos otras opiniones negativas como la del activista estadounidense por los derechos de la minoría negra norteamericana Malcom X (1925-1965), quien tenía una concepción estática de las matemáticas.
Siento tener que decir que no me gustaban las matemáticas. Muchas veces he reflexionado sobre esto. Creo que era porque en matemáticas no hay discusión posible. Si te equivocas, te equivocas y basta.
Otra opinión negativa la encontramos en el escritor alemán y premio Nobel de Literatura, Hermann Hesse (1877-1962), autor de El lobo estepario o Siddhartha, quien la muestra como un saber atemporal, como surgido de la nada.
Usted trata la historia del mundo como un matemático trabaja con las matemáticas, donde sólo existen leyes y fórmulas, sin realidad, sin bien ni mal, sin tiempo, sin ayer, sin mañana, nada excepto el eterno y presente matemático.
El filósofo confunciano japonés Sorai Ogyu (1666-1728), habla de las matemáticas como si fueran simplemente una diversión lógica con la que nos divertimos los matemáticos y que no tiene ninguna utilidad para nuestra vida cotidiana, para nuestra sociedad.
Los matemáticos se vanaglorian de sus logros exactos, pero en realidad están absortos en acrobacias mentales y no contribuyen en la sociedad.
El director de cine aragonés Luis Buñuel (1900-1983), autor de películas como Un perro andaluz, Viridiana o El discreto encanto de la burguesía, ve a las matemáticas, y la ciencia en general, como algo frío, estático, alejado de la creación y de la imaginación.
La ciencia no me interesa. Ignora el sueño, el azar, la risa, el sentimiento, la contradicción, cosas que me son preciosas.
 Cartel de la película surrealista Un perro andaluz (1929), de Luis Buñuel, con guion de Luis Bueñuel y Salvador Dalí
Cartel de la película surrealista Un perro andaluz (1929), de Luis Buñuel, con guion de Luis Bueñuel y Salvador Dalí
Como también el filósofo francés Jules de Gaultier (1858-1942).
En el punto donde se detiene la ciencia, empieza la imaginación.
Todas estas reflexiones nos muestran unas matemáticas estáticas, carentes de imaginación y creatividad, alejadas de la realidad y de los intereses de la sociedad, cuya creación es fría, mecánica y sin evolución. Esta visión es una visión fundamentada en el desconocimiento de la materia de la que escriben, y seguramente apoyada por cierta frustración. Además, continuamente, y de forma interesada, se ha tendido a enfrentar las matemáticas y la ciencia en general, con las letras, el arte y la cultura, como si fueran dos mundos diferentes, dos mundos opuestos. Por ejemplo, como nos recordaba Fernando Corbalán en su libro Matemáticas de la vida misma, el académico de la Lengua Española Francisco Rico afirmaba en 1996,
Uno de los mayores problemas de España es el insuficiente conocimiento escrito y hablado de las lenguas extranjeras. Entre otras cosas porque se enseñan mal. Del bachillerato habría que salir hablando perfectamente al menos una de ellas. La culpa es de los planes de estudios, que convierten estas asignaturas en marías. Las básicas deberían ser la lengua española y la lengua extranjera. Y la literatura, que es lo que enseña a conocer el mundo. Las asignaturas técnicas, las matemáticas, no hacen ninguna falta: cualquier calculadora u ordenador te lo da todo hecho.
Y más concretamente, la relación entre poesía y ciencia ha sido un símbolo de la opinión social y cultural del desencuentro entre las ciencias y las letras. Así, el poeta romántico inglés William Wordsworth (1770-1850), en su obra Baladas Líricas (Sobre Ciencia y Poesía) sitúa a la poesía como más importante en la vida de los seres humanos que el conocimiento científico.
El conocimiento de ambos, del poeta y del hombre de ciencia, es placer; pero el conocimiento del primero nos abre el sendero hacia una parte necesaria de nuestra existencia, de nuestra herencia natural e inalienable; el otro [la ciencia] es una adquisición personal e individual, que obtenemos lentamente y no por una simpatía habitual y directa respecto de nuestros congéneres. El hombre de ciencia busca la verdad como un benefactor desconocido y remoto, la abriga y la ama en sus soledad; el poeta, cantando una canción junto con todos los seres humanos, se regocija en la presencia de la verdad como nuestro amigo visible y compañero de todos los momentos. La poesía es el aliento y el más fino espíritu de todo conocimiento; … La poesía es el primero y último de los conocimientos; es tan inmortal como el corazón del hombre.
Otro poeta británico, Wystan Hugh Auden (1907-1973), que vivió parte de su vida en EEUU y que recibiera el Premio Pulitzer en 1948, ataca directamente al ansia de conocimiento que tiene el ser humano, que claramente está en la base de la creación tanto científica, pero también de la artística, y así nos dice en su poema Después de leer un manual de física moderna para niños.
Esta pasión de nuestra especie
por el proceso de descubrir
es un factor del que apenas se puede dudar,
pero me alegraría más
si supiera más claramente
para qué queremos el conocimiento.
Por el contrario, hay quienes como el escritor romántico alemán Johann Wolfgang von Goethe (1749-1832), autor de Fausto y Las penas del joven Werther, soñaban con reunir la ciencia y la poesía.
Se olvidó que la ciencia se originó en la poesía, no se tiene en cuenta que, después de una revolución de los tiempos, podrían reunirse de nuevo, amigablemente, en un punto más alto, para beneficio de ambas.
 Retrato del escritor Johann Wolfgang von Goethe, a la edad de 80 años, realizado por el pintor alemán Joseph Karl Stieler (1781-1858). Obra perteneciente a Neue Pinakothek. Imagen de Wikimedia Commons
Retrato del escritor Johann Wolfgang von Goethe, a la edad de 80 años, realizado por el pintor alemán Joseph Karl Stieler (1781-1858). Obra perteneciente a Neue Pinakothek. Imagen de Wikimedia Commons
Otro de los símbolos del mundo de las letras, el escritor francés Gustave Flaubert (1821-1880) también creía en que ambas visiones del mundo, la artística y la científica, eran la misma y que volverían a juntarse de nuevo.
A medida que avance, el arte será más científico, del mismo modo que la ciencia se volverá artística; los dos se reunirán en la cumbre, después de haberse separado en la base.
Y más aún, decía
La poesía es una ciencia exacta, como la geometría.
Esa visión de las matemáticas, como un conocimiento dinámico, creativo, lleno de imaginación, que busca la belleza y que se inspira en ella, es una visión más real, que muchos intelectuales han sabido reconocer en su pensamiento o en sus creaciones literarias. Veamos algunas citas en este sentido, empezando por la del matemático británico Godfrey H. Hardy (1877-1947), autor de Apología de un matemático, para quien la belleza es una parte esencial de las matemáticas.
Un matemático, al igual que un pintor o un poeta, es un creador de modelos. […] Los modelos del matemático, al igual que ocurre con los del pintor o con los del poeta, han de ser hermosos; las ideas, al igual que los colores o las palabras, deben de encajar de forma armoniosa. La belleza es el primer examen. No existe lugar eterno en el mundo de las matemáticas feas.
Para el matemático francés Henri Poincaré (1854-1912) la belleza es también un elemento fundamental en el proceso de invención matemática. El texto que recoge su conferencia La invención matemática en la Sociedad Psicológica de París en 1908 es un uno de esos textos que es aconsejable leer (recientemente se ha publicado en español por la editorial KRK, con una magnífica traducción y edición de Francisco González).
En su conferencia, Poincaré habla de la intuición como un elemento fundamental en el proceso de invención matemática, aunque esta es fruto del trabajo y el conocimiento anteriores. Además, el matemático francés habla de que “inventar es discernir, es elegir”, y en ese proceso de elección en el que la intuición es tan importante, una herramienta fundamental es la belleza, es esta la que ayuda a la mente creadora, la matemática sí, pero la científica y artista también, a realizar esa elección intuitiva, casi inconsciente.
Por ejemplo, podemos leer en la misma:
… todas las combinaciones se formarían como consecuencia del automatismo del yo subliminal, pero únicamente aquellas que fueran interesantes penetrarían en el campo de la consciencia […]. ¿Cuál es la causa de que entre mil productos de nuestra actividad inconsciente existan algunos llamados a cruzar el umbral, mientras otros se quedan atrás? ¿Es el azar el que les confiere ese privilegio? […]
… las combinaciones útiles son precisamente las más bellas, quiero decir, aquellas que resultan más atractivas para esa sensibilidad especial que todos los matemáticos conocen, pero que los profanos ignoran hasta el extremo de tomárselo casi a risa.
¿Qué ocurre entonces? Entre las muy numerosas combinaciones que el yo subliminal ha formado a ciegas, casi todas carecen de interés y utilidad, pero, por eso mismo, no tienen efecto alguno sobre la sensibilidad estética. La consciencia no la reconocería nunca. Sólo algunas son armoniosas y, por tanto, útiles y bellas al mismo tiempo, capaces de conmover a la sensibilidad especial del geómetra de la que acabo de hablar y que, una vez estimulada, atraerá sobre ella nuestra atención, y les dará así ocasión de volverse conscientes.
 Henri Poincaré, caricatura realizada por Enrique Morente, perteneciente a la exposición de la Real Sociedad Matemática Española, El rostro humano de las matemáticas. La exposición virtual pueden ver en el portal divulgamat.
Henri Poincaré, caricatura realizada por Enrique Morente, perteneciente a la exposición de la Real Sociedad Matemática Española, El rostro humano de las matemáticas. La exposición virtual pueden ver en el portal divulgamat.
La matemática rusa Sofia Kovalevskaya (1850-1891), pone el énfasis en la imaginación en el proceso creativo de las matemáticas al escribir que:
No es posible ser matemático sin llevar un poeta en el alma.
Pero también ese pensamiento llega de la mano de grandes escritores y filósofos, como el madrileño José Ortega y Gasset (1883-1955), que reconoce la participación de la imaginación en la creación matemática,
No hay modo de entender bien al hombre si no se repara en que la Matemática brota de la misma raíz que la poesía, del don imaginativo.
Una referencia clásica dentro de las matemáticas es la siguiente del escritor francés Voltaire, François-Marie Arouet (1694-1778):
Se advierte, entre los matemáticos, una imaginación asombrosa. Repetimos: existía más imaginación en la cabeza de Arquímedes que en la de Homero.
Y ya que hablamos de Voltaire, traigamos una cita más suya, aunque un poco alejada de nuestro tema de hoy: Toda secta es una bandera de error. No hay sectas en la geometría.
El poeta ruso Alexander Sergeyevich Pushkin (1799-1837) también comparó las matemáticas con la poesía.
La inspiración es necesaria en geometría, tanto como en poesía.
Y una interesante visión de las matemáticas como creadoras de belleza viene de la mano del poeta portugués Fernando Pessoa (1888-1935).
El binomio de Newton es tan bello como la Venus de Milo.
Lo que hay es poca gente que se dé cuenta de ello.
Para muchas personas es difícil entender la importancia de la imaginación en matemáticas, ya que ven, como ha quedado patente en algunas citas del principio, esta ciencia como algo estático, como un camino fijo donde solo hay que avanzar para descubrir teniendo los conocimientos técnicos adecuados, sin ninguna posibilidad de creatividad e imaginación. Sin embargo, como decía el historiador de las matemáticas W. S. Anglin:
Las matemáticas no son una marcha cautelosa a lo largo de una carretera bien despejada, sino un viaje por un desierto desconocido en el que los exploradores se pierden a menudo.
Aunque más que un vasto desierto, me gusta más la visión del matemático británico Arthur Cayley (1821-1895) en su discurso público como presidente de la British Society for the Advancement of Science, en 1883, que las mostraba como una extensión por explorar:
Es difícil dar una idea de la vasta extensión de la matemática moderna. Esta palabra «extensa» no es la correcta. Quiero decir extensa con multitud de bellos detalles. No una extensión uniforme, como un plano vacío, sin objetos, sino una parte de un bello país, visto al principio a distancia, pero que puede ser paseado y estudiado con todo detalle desde las colinas y los valles, hasta los ríos, rocas, bosques y flores. Pero, como para todas las demás cosas, así para la teoría matemática, la belleza puede ser percibida, pero no explicada.
 (c) Trinity College, University of Cambridge; Supplied by The Public Catalogue Foundation
(c) Trinity College, University of Cambridge; Supplied by The Public Catalogue FoundationPero dejemos el tema por hoy en este punto. Aun así, me gustaría finalizar esta entrada del Cuaderno de Cultura Científica con una cita de un libro que me encanta, Los Pintores Cubistas,del poeta francés Guillaume Apollinaire (1880-1918), relacionando las matemáticas con el arte, y en concreto, con el origen del cubismo.
Capítulo II: Los jóvenes pintores de las escuelas extremadas tienen como fin secreto hacer pintura pura. Es un arte plástico enteramente nuevo. Sólo está en sus comienzos y todavía no es tan abstracto como quisiera. La mayoría de los pintores nuevos están haciendo matemáticas sin saberlo o sin saberlas, pero no han abandonado todavía a la naturaleza, a la que interrogan para aprender de ella el camino de la vida.
Capítulo III: … Se ha reprochado enérgicamente a los pintores nuevos sus preocupaciones geométricas. Sin embargo, las figuras geométricas son lo esencial del dibujo. La geometría, ciencia que tiene por objeto la extensión, su medida y sus relaciones, ha sido siempre la regla misma de la pintura. Hasta ahora, las tres dimensiones de la geometría euclideana bastaban a las inquietudes que nacían del sentimiento de infinito en el alma de los grandes artistas.
Los pintores nuevos no se han planteado ser geómetras, como tampoco lo hicieron sus ancestros. Pero puede decirse que la geometría es a las artes plásticas lo que la gramática es al arte del escritor. Así pues, hoy, los sabios ya no se limitan a las tres dimensiones de la geometría euclideana. Los pintores se han visto conducidos, natural y, por así decirlo, intuitivamente, a preocuparse por las nuevas medidas posibles de la extensión que en el lenguaje de los mundillos modernos se designaban global y brevemente por el término de cuarta dimensión.
Tal y como se presenta en la mente, desde el punto de vista plástico, la cuarta dimensión estaría engendrada por las tres mediadas conocidas: configura la inmensidad del espacio eternizándose en todas las direcciones en un momento determinado. Es el espacio mismo, la dimensión del infinito; es la que dota a los objetos de plasticidad.
 Fantasía geométrica (1971), de Anatoly Fomenko. Ilustración perteneciente al libro Mathematical Impressions
Fantasía geométrica (1971), de Anatoly Fomenko. Ilustración perteneciente al libro Mathematical ImpressionsBibliografía
1.- VV. AA. (proyecto coordinado por Raúl Ibáñez y Antonio Pérez), Un teorema en la biblioteca, Colección Relatos Matemático, ANAYA-RSME, 2009.
2.- DivulgaMAT: Concursos literarios RSME-ANAYA
3.- Fernando Corbalán, Matemáticas de la vida misma, GRAO, 2007.
4.- G. H. Hardy, Apología de un matemático, Capitán Swing, 2017.
5.- Henri Poincaré, La invención matemática, edición de Francisco González, KRK, 2018.
6.- Raúl Ibáñez, Antonio Pérez (coordinadores de la edición), El rostro humano de las matemáticas, Nivola, 2008.
7.- Juan Guirado, Infinitum, eneida, 2007.
8.- Raúl Ibáñez, Cayley, el origen del álgebra moderna, Genios de las matemáticas, RBA, 2017.
9.- Anatoly T. Fomenko, Mathematical Impressions, AMS, 1990.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Un teorema en la biblioteca se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La magia del teorema de Zeckendorf
- El teorema de los cuatro colores (1): una historia que comienza en 1852
- El teorema de Marion (Walter)
Juntando semiconductores: historia del transistor
 Foto: Laura Ockel / Unsplash
Foto: Laura Ockel / UnsplashLas propiedades de los semiconductores tipo n y tipo p eran bien conocidas al final de la Segunda Guerra Mundial en 1945. Este conocimiento se debía, en no poca medida, al considerable esfuerzo de investigación que supuso el desarrollo de la electrónica en general y del radar en particular.
En 1947, tres investigadores de los Laboratorios Bell en Nueva Jersey (EE.UU.) llevaron la idea del diodo n-p un paso más allá. William Shockley, Walter Brattain y John Bardeen colocaron dos diodos de germanio de forma consecutiva, un diodo n-p al lado de un diodo p-n, compartiendo el semiconductor tipo p. Descubrieron que se podía hacer que el dispositivo permitiera el paso de la electricidad o que resistiera, es decir, que bloqueara el paso de electricidad, dependiendo de la carga aplicada a la capa central de semiconductor tipo p. Esta clase de dispositivo se denomina transistor bipolar n-p-n [1]. Un transistor bipolar p-n-p también es viable. [2]
 Una réplica del primer transistor. Fuente: Wikimedia Commons
Una réplica del primer transistor. Fuente: Wikimedia CommonsA principios de la década de 1960, a medida que los transistores basados en silicio se hacían más pequeños, fiables y baratos de fabricar, comenzaron a reemplazar los tubos de vacío más voluminosos y costosos que se usaban para amplificar voltajes, por ejemplo en sistemas de sonido estéreo, en televisores o radios [3], y como dispositivos de conmutación y gestión lógica en ordenadores. Shockley, Bardeen y Brattain recibieron el Premio Nobel en 1956 por un invento que pronto lanzaría la revolución en la electrónica computacional. [4]
La revolución en la electrónica computacional se aceleró también gracias a una guerra: la Guerra Fría. La necesidad de componentes electrónicos miniaturizados para los nuevos misiles llevó al desarrollo del circuito integrado. En 1958, Jack Kilby, de Texas Instruments, desarrolló la idea de integrar transistores y los circuitos relacionados en un solo chip de silicio.
Un año después, la Fairchild Semiconductor Corporation puso en práctica la idea desarrollando el método para integrar los elementos separados en el chip. En 1971 la recién formada Intel Corporation introdujo el primer circuito de microprocesadores integrado. Los continuos avances en el diseño de microprocesadores y las técnicas de fabricación permitieron la producción en masa de microprocesadores para ordenadores personales, teléfonos móviles, automóviles, robots industriales e incluso tostadoras, frigoríficos y muñecas «parlantes». A principios de la década de 2000, Intel y sus competidores podían colocar hasta 42 millones de transistores microscópicos en un solo chip de silicio, dos centímetros cuadrados. En 2019 el Epyc Rome de AMD contiene 39.540 millones de transistores [5].
Notas:
[1] Simplificando, y porque puede resultarte útil, el nombre de transistor viene de que puede actuar como transmisor o resistor de la corriente eléctrica.
[2] También hay otro tipo diferente de transistor, conocido como el «transistor de efecto campo», que funciona con el mismo principio general.
[3] Su efecto fue tan grande que se popularizó la sinécdoque de llamar transistor al radiorreceptor basado en transistores.
[4] Los tres se llevaban como el perro y el gato y tiró cada uno por su lado mucho antes del premio. Bardeen se fue a la Univisidad de Illinois en Urbana-Champaign para seguir con sus elucubraciones teóricas en materia condensada. Terminaría recibiendo otro premio Nobel de física por la teoría BCS de la superconductividad. Brittain siguió en Bell he hizo investigaciones aplicadas a sistemas biológicos. Y, finalmente, Shockley se mudó a la Universidad de Stanford, y desde ella sentó las bases para el desarrollo de las industrias de Silicon Valley en los alrededores de la universidad. Muchas de las compañías originales del valle (incluida Intel) fueron fundadas por personas que originalmente habían trabajado con Shockley.
 Bardeen, Shockely y Brattain. La foto tiene su aquel sabiendo lo que ocurría entre los tres. Fuente: Wikimedia Commons
Bardeen, Shockely y Brattain. La foto tiene su aquel sabiendo lo que ocurría entre los tres. Fuente: Wikimedia Commons[5] Transistores MOSFET, esto es, transistores de efecto de campo de semiconductores de óxido metálico.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Juntando semiconductores: historia del transistor se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Juntando semiconductores: el diodo n-p
- Juntando semiconductores: LEDs y rectificadores
- Semiconductores
40 años del Plan Integral de Saneamiento del Bilbao Metropolitano
 Imagen 1: la ría de Bilbao en su desembocadura en 1976. (Fotografía: El correo.com)
Imagen 1: la ría de Bilbao en su desembocadura en 1976. (Fotografía: El correo.com)En 1979, el Consorcio de Aguas Bilbao Bizkaia puso en marcha el Plan Integral de Saneamiento del Bilbao Metropolitano, el proyecto medioambiental más importante llevado a cabo en Euskadi, que ha supuesto una inversión superior a los 1.200 millones de euros.
Además de cumplir las exigencias de la Unión Europea en materia de tratamiento de las aguas residuales, el plan ha permitido la recuperación medioambiental de nuestros ríos, Ría y playas del entorno. El trabajo no ha concluido, queda todavía trabajo por hacer porque en materia de saneamiento siempre hay margen de mejora, pero estos 40 años han dejado para la historia una estampa que seguramente las personas más jóvenes ni recuerden, pero que formaba parte del ADN de nuestro Bilbao, surcado entonces por una Ría marrón, pestilente y sin posibilidad de vida animal o vegetal.
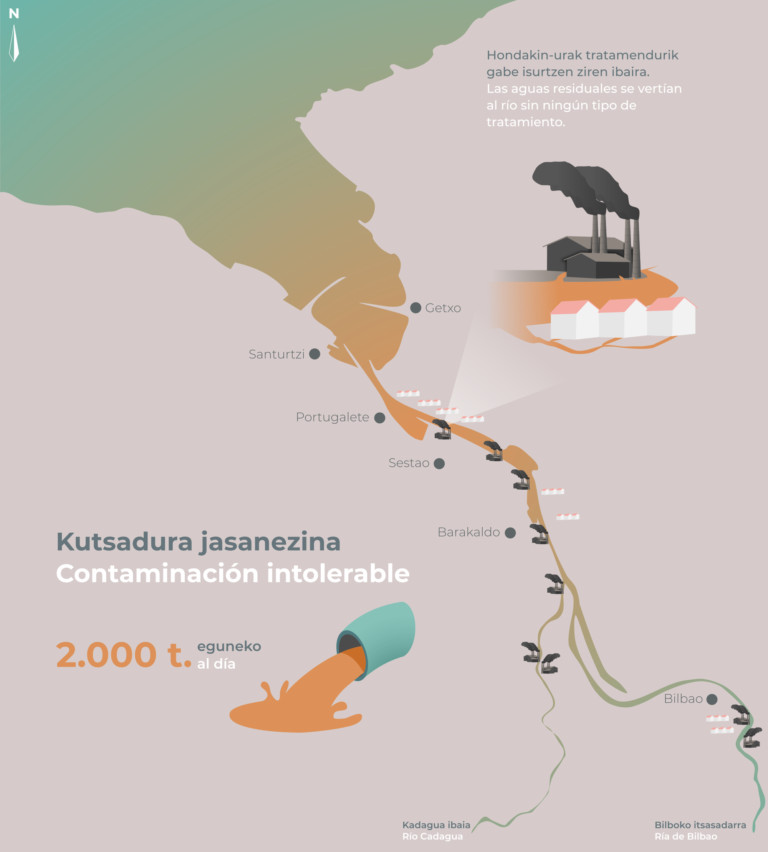 Ilustración 1: entre 1900 y 1975 la Ría se convirtió en un colector de residuos donde la vida era imposible, llegando a recibir 2.000 toneladas diarias de residuos. (Ilustración: NorArte Studio)
Ilustración 1: entre 1900 y 1975 la Ría se convirtió en un colector de residuos donde la vida era imposible, llegando a recibir 2.000 toneladas diarias de residuos. (Ilustración: NorArte Studio)El Plan Integral de Saneamiento ha transformado la imagen de la Ría y la han convertido en un nuevo espacio vertebrador de la Villa para el disfrute de toda la ciudadanía. En total, unos 280 kilómetros de colectores e interceptores recogen las aguas residuales domésticas e industriales, y varios cruces subfluviales trasladan las aguas sucias –también desde la margen derecha– hasta la Estación Depuradora de Aguas Residuales – EDAR de Galindo (Sestao), la gran obra por excelencia en saneamiento ejecutada por el Consorcio de Aguas. Desde 1990, año en que comenzó a operar la planta, se depuran al día las aguas fecales de 850.000 bizkainas y bizkainos, unos 350.000.000 litros al día. Es la depuradora principal, pero no la única, ya que las aguas se depuran en otras 31 plantas repartidas por el territorio histórico.
Pero echemos un poco la vista atrás a aquel Bilbao en blanco y negro. A mediados del siglo XIX, el entorno de la Ría inició un fuerte proceso de industrialización basado, principalmente, en la explotación y exportación del mineral de hierro y de la industria siderúrgica. De ser un pequeño puerto, la Ría de Bilbao se convirtió en uno de los principales focos industriales y comerciales, no solo del Estado, sino también de Europa.
En pocos años, la fisonomía y el paisaje del cauce sufrieron una profunda transformación. Sus márgenes se poblaron de fábricas e infraestructuras portuarias y el fuerte movimiento migratorio, propiciado por la necesidad creciente de mano de obra, provocó un rápido crecimiento poblacional del área. Entre 1900 y 1975 la población se cuadruplicó.
 Ilustración 2: características de la red de estructuras construidas para desarrollar el plan de saneamiento del Bilbao Metropolitano. (Ilustración: NorArte Studio)
Ilustración 2: características de la red de estructuras construidas para desarrollar el plan de saneamiento del Bilbao Metropolitano. (Ilustración: NorArte Studio)A la vez que se producía este desarrollo, las aguas de la Ría empezaban a mostrar una contaminación alarmante. El crecimiento urbano desordenado y la falta de conciencia medioambiental propiciaron el vertido de las aguas residuales –domésticas e industriales– directamente en el estuario, sin ningún tipo de tratamiento previo. La Ría se convirtió en un colector de residuos donde la vida era imposible.
La Ría recibía diariamente 900 toneladas de residuos sólidos procedentes, principalmente, de las explotaciones mineras, 400 toneladas de vertidos ácidos, 80 toneladas de metales, además de compuestos cianurados o compuestos nitrogenados; en definitiva, casi 2.000 toneladas diarias de residuos que la convirtieron en una cloaca sin oxígeno.
Por este motivo, uno de los principales objetivos del Plan Integral de Saneamiento fue precisamente la recuperación ambiental de la Ría de Bilbao, para lo cual se fijó un 60% de oxigenación como estándar de calidad de las aguas. Kilómetros de colectores empezaron a recoger las aguas residuales de hogares e industrias, que ya no van al cauce, sino a las plantas depuradoras, siendo la de Galindo pieza clave del sistema, el riñón que desde los años 90 depura las aguas residuales de Bizkaia. El resultado es una Ría ahora sí, viva y cada vez más apta para el desarrollo de nuevos usos deportivos y náuticos.
Paralelamente a todas estas obras hidráulicas, en 1989 comenzaron a realizarse estudios de seguimiento en el medio acuático receptor para evaluar la eficacia de las medidas adoptadas por el Plan Integral de Saneamiento, financiados por el Consorcio de Aguas y URA – Agencia Vasca del Agua. Personas expertas del centro tecnológico AZTI, en colaboración con la UPV/EHU, se encargan de llevar a cabo esta labor de vigilancia ambiental. Todos los años se realizan campañas y muestreos para evaluar el estado de la Ría y su evolución, analizando la calidad del agua, los sedimentos, la fauna y la flora.
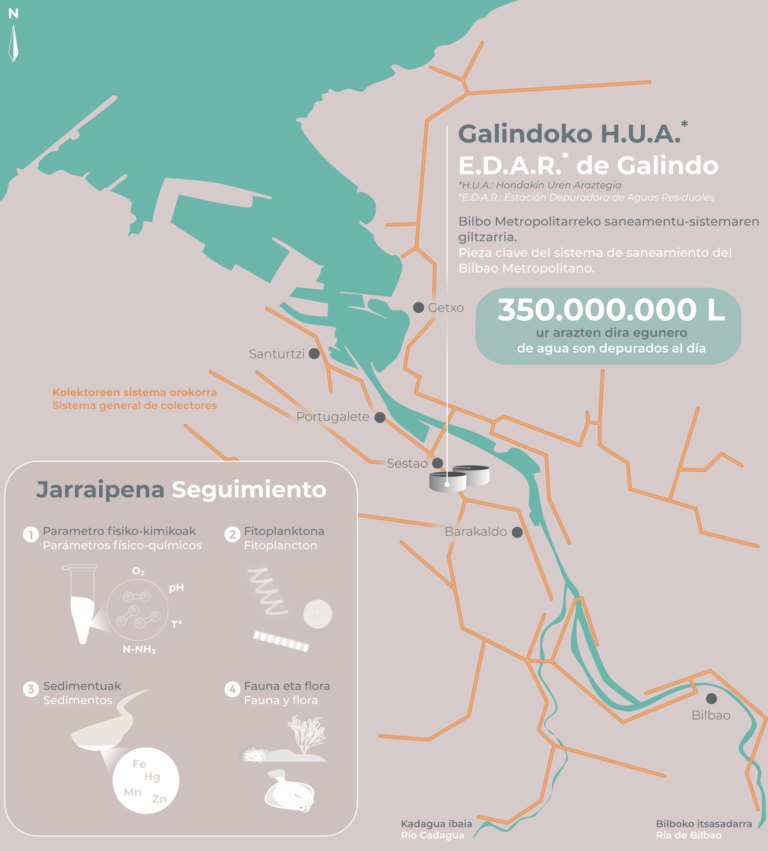 Ilustración 3: sistema de colectores para el saneamiento del Bilbao Metropolitano, a través del cual se depuran diariamente 350.000.000 litros de agua. (Ilustración: NorArte Studio)
Ilustración 3: sistema de colectores para el saneamiento del Bilbao Metropolitano, a través del cual se depuran diariamente 350.000.000 litros de agua. (Ilustración: NorArte Studio)El efecto más importante del Plan Integral de Saneamiento en la Ría ha sido la recuperación de los niveles normales de oxígeno. De valores cercanos o inferiores al 40% de saturación a comienzos de los años 90, a valores del 90% de saturación actualmente. Hoy en día no hay ninguna zona del estuario con problemas de oxigenación. Todo esto ha permitido la presencia de comunidades biológicas en todo el sistema, desde la zona interior de Bilbao hasta el Abra, con más de 60 especies de peces asentadas (lenguado, cabuxino, mojarra, platija, muble, lubina, salmonete, chicharro, anguila…), además de algas y otros organismos que viven en los sedimentos y en los sustratos rocosos.
Y esta es la historia de Cuando la vida volvió a la Ría. Ahora nos corresponde a todas y todos, conservar las masas de agua y hacer un buen uso de los sistemas de saneamiento porque son una pieza clave para asegurar la sostenibilidad del planeta, devolviendo al medio limpia el agua que utilizamos, para que siga su ciclo natural.
Sobre el autor: Pedro María Barreiro es ingeniero industrial y Gerente del Consorcio de Aguas Bilbao Bizkaia.
El proyecto «Ibaizabal Itsasadarra zientziak eta teknologiak ikusita / La Ría del Nervión a vista de ciencia y tecnología» comenzó con una serie de infografías que presentan la Ría del Nervión y su entorno metropolitano vistos con los ojos de la ciencia y la tecnología. De ese proyecto han surgido una serie de vídeos y artículos con el objetivo no solo de conocer cosas interesantes sobre la ría de Bilbao y su entorno, sino también de ilustrar como la cultura científica permite alcanzar una comprensión más completa del entorno.
El artículo 40 años del Plan Integral de Saneamiento del Bilbao Metropolitano se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La recuperación de la fauna en la ría de Bilbao
- ¿Qué esconden los sedimentos de la Ría?
- Naukas Bilbao está en marcha

