Arte & Ciencia: Química y Arte, reacciones creativas

El arte y la ciencia son dos formas de conocimiento aparentemente alejadas, en gran medida consecuencia de la especialización profesional y la educación compartimentada. Del estudio de esta impostada separación surgió el estereotipo de las dos culturas, las ciencias y las humanidades, para referirnos a esa brecha de conocimiento. La realidad es que la ciencia y el arte sí están conectadas y que ninguna forma de conocimiento es impermeable a otra. Por poner algunos ejemplos: ¿Cómo podría crearse una obra plástica sin las técnicas propiciadas por la ciencia? ¿Cómo podríamos interpretar la elección de materiales?
Estas y otras cuestiones relacionadas furon tratadas por destacados profesionales -artistas, ilustradores, filósofos y científicos- que han puesto el foco en ese difuso trazo que une la ciencia y el arte. El ciclo Ciencia & Arte se desarrolló, bajo la dirección de Deborah García Bello, a lo largo de cuatro jornadas que se celebraron los jueves días 6 y 27 de abril y 11 y 25 de mayo de 2017 en el auditorio del Museo Guggeheim Bilbao.
Esta actividad de la Cátedra de Cultura Científica de la UPV/EHU se enmarca en el programa TopARTE que conmemora el XX Aniversario del Museo Guggenheim Bilbao.

Segunda jornada. 1ª conferencia
Xavier Durán, químico y periodista científico: Química y Arte, reacciones creativas
Las primeras ilustraciones de animales y plantas, el coleccionismo de maravillas naturales, el trabajo de los artistas… A lo largo de su historia, el ser humano ha representado la naturaleza de diferentes maneras que han jugado un papel fundamental en la generación de conocimiento científico. Pero esta influencia también se ha dado en la dirección inversa, puesto que los descubrimientos científicos han servido de inspiración y han influido en el desarrollo de técnicas pictóricas y estilos artísticos, marcando el devenir de la historia del arte.
Conocimiento y representación de los fenómenos naturalesEdición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Arte & Ciencia: Química y Arte, reacciones creativas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Arte & Ciencia: Cómo descubrir secretos que esconden las obras de arte
- Arte & Ciencia: La importancia de la ciencia para la conservación del arte
- Arte & Ciencia: Conservación de obras con componentes tecnológicos
ADN basura: negacionismo y malentendidos (con cebolla) Segunda parte

En la primera parte de este artículo vimos cómo se ha construido un poderoso mito alrededor del ADN basura, un mito que lleva al negacionismo científico. Comenzábamos nuestro “épico” intento de desmontarlo explicando que la selección natural es incapaz de mantener un genoma grande totalmente funcional, y que el ADN basura no fue un parche de ignorantes sino una predicción realizada con las matemáticas de la teoría evolutiva.
ADN basura no equivale a ADN no codificante
El segundo gran malentendido es la ubicua confusión entre ADN no codificante y ADN basura. Recordemos que el ADN no codificante es aquél que no contiene información que será traducida por la célula a secuencias de proteínas. Sabemos hoy en día que alrededor del 98% del genoma humano consiste en este tipo de ADN.
Cuando la típica noticia dice “se ha encontrado algo estupendo en una región del genoma que antes se creía basura”, lo que quiere decir casi siempre es que se han encontrado algo estupendo en una región de ADN no codificante.
Pero no son lo mismo. El ADN basura no tiene utilidad, no puede tenerla por definición. El ADN no codificante puede tener diversas funciones, y esto se sabe desde hace casi medio siglo.
Se podría responder: bien, de acuerdo, pero no seamos cínicos; se trata de enfatizar que, durante mucho tiempo, los genetistas creyeron que todo el ADN no codificante era basura, sin excepción. El problema es que esa historia no es cierta. Semejante opinión nunca estuvo extendida en la comunidad científica. Los biólogos descubrieron funciones reguladoras en el ADN no codificante antes (años 60), durante (años 70) y después (80, 90…) de la consolidación del ADN basura como hipótesis. La “creencia” en el ADN basura no parece haber obstaculizado en ningún momento la investigación sobre la regulación genética. En todo momento la compatibilidad fue total.
Veamos el caso de los intrones. Son secuencias no codificantes que están en medio de genes que sí son codificantes. En nuestra especie, el típico gen con información para sintetizar una proteína está interrumpido por varios intrones, a veces larguísimos. Después de que el ADN se transcribe a ARN, las secuencias correspondientes a los intrones son cortadas y no se tienen en cuenta para fabricar la proteína.
Los intrones constituyen casi el 30% de nuestro genoma. Se descubrieron en 1977 y nadie sabía por qué existían o si contenían algo interesante. El mito dice que fueron “inmediatamente y universalmente considerados basura genómica” pero, como muestra T. Ryan Gregory, eso no fue así. Lo que abundaba era justo la opinión contraria, el “aquí tiene que haber algo”. Los científicos especularon con la utilidad oculta de los intrones desde el principio, buscaron secuencias reguladoras en su interior y realizaron interesantes experimentos para detectarlas. Si realmente hubo algunos extremistas defendiendo la inutilidad absoluta de todo el ADN de los intrones, no parece que influyeran demasiado en la opinión y en las investigaciones de sus colegas.
Hoy sabemos que, como sospechaban los genetistas de hace décadas, los intrones contienen mucha chatarra y algunas secuencias funcionales. El “gen de los ojos azules” es una variante de una secuencia reguladora que pertenece a un intrón. La variante más común está asociada con los ojos marrones y está conservada por la selección natural. La que da ojos azules cuando está en doble dosis ha sido, además, promocionada por la selección positiva durante los últimos milenios en algunas poblaciones humanas. Es solo un ejemplo de las muchas secuencias interesantes que se han encontrado formando parte del ADN no codificante… al lado de montones de ADN basura.
¿Qué es función biológica?
El tercer gran malentendido surge del Proyecto ENCODE y su concepto de función. ENCODE es, supuestamente, una enciclopedia de elementos funcionales del genoma humano pero, aquí viene el truco, ha definido “elemento funcional” a su manera..
La función biológica no es un asunto sencillo, filosóficamente hablando. Sin embargo, se suele entender que algo es funcional si tiene un efecto seleccionado. Simplificando, si una secuencia de ADN tiene un efecto que esté siendo conservado o promocionado por la selección natural, entonces es funcional. ¿Por qué usar éste y no otro criterio? Primero, porque la teoría evolutiva es la gran unificadora en la ciencia de los seres vivos (nada tiene sentido en biología si no es a la luz de la evolución) y segundo, porque otros conceptos de función no generan fácilmente hipótesis testables y por tanto científicas.
ENCODE ignora esta noción evolutiva y se saca de la manga otra completamente distinta. Para ENCODE, una secuencia de ADN es funcional si tiene “actividad bioquímica específica”. Por ejemplo, si una secuencia de ADN es transcrita, generándose una molécula de ARN, contará como funcional aunque luego ese ARN esté presente en cantidades minúsculas y se degrade sin realizar ninguna tarea dentro de la célula. Otro ejemplo: si una secuencia de ADN es reconocida por ciertas proteínas, que se adhieren a ella, también contará como funcional para ENCODE; incluso aunque tal interacción no provoque ningún tipo de efecto relevante en la célula.
El problema es que es esperable que esa “actividad bioquímica específica” también la presente el ADN basura. Por el puro azar, por las huellas o restos de su historia evolutiva, e incluso por el ruido y el caos bioquímico del interior de las células, un ADN completamente inútil puede adherirse de forma inútil a diversas moléculas, puede ser transcrito a ARN inútil o puede ser incluso, a veces, traducido a proteínas inútiles.
Toda esta actividad absurda, este derroche, este caos, no es lo que muchos tienen en mente cuando se imaginan el funcionamiento de la célula. Tanto para quien cree en una creación inteligente como para el que se imagina una selección natural todopoderosa, este escenario chapucero resulta chocante e incluso ofensivo. Pero la vida es así, y quizá no pueda ser de otra manera.
Si fabricamos secuencias totalmente aleatorias de ADN sintético también obtendremos esa “actividad bioquímica específica” que la propaganda del ENCODE ha vendido como algo inesperado y apasionante. Imaginad la siguiente inocentada: alguien crea un genoma completamente aleatorio como el que propone Sean R. Eddy y consigue colárselo al Proyecto ENCODE como si fuera un genoma real para que lo estudie. ¿Cómo serían los resultados? ¿Descubrirían un gran porcentaje de ADN con “funciones esenciales” para un organismo inexistente? ¿quizá otro gigantesco “panel de control”? La selección natural no fue el único concepto básico que desatendieron; también se les escapó el azar.
La carga de la prueba
Ya hemos visto que el ADN basura no es aquél que no sabemos para qué sirve, sino aquél que realmente no sirve para nada. Si algún buen lector sigue encontrando “arrogante” esta proposición, puede que estemos en presencia de un cuarto malentendido, que tiene que ver con la carga de la prueba.
Cierta tendencia a idealizar la naturaleza a veces nos conduce a creer que los seres vivos están optimizados a la perfección y que cualquier pequeño detalle biológico ha de ser necesario y esencial. Es fácil entonces ver el ADN basura como una bravuconada, una cuñadez, una afirmación extraordinaria que debe rechazarse, o al menos ser revisada con la misma desconfianza con la que examinaríamos una máquina de movimiento perpetuo o una demostración de percepción extrasensorial.
En realidad, la visión de los organismos como máquinas perfectas donde cada elemento es imprescindible no puede apoyarse en la teoría evolutiva y carece de base científica. Aunque resulte poco intuitivo, la ausencia de función no solo es a veces perfectamente razonable, sino que en muchos casos debe ser la hipótesis que se plantée por defecto.
Imaginemos que estudiamos una secuencia concreta, una pequeña porción del genoma específica. ¿Cómo averiguamos si es basura o no? Es imposible, podría argumentarse. Que no seamos capaces de encontrarle una función no significa que no la tenga. Quizá su utilidad se nos escape siempre, por mucho que investiguemos. En cierto experimento se extirpó una gran porción de ADN no codificante en el genoma de unos ratones. Los animales así “mutilados” se desarrollaron bien y aparentemente no presentaban diferencias con el resto. Todo apuntaba a que la porción eliminada era ADN basura. Pero ¿y si los ratones manipulados tenían una desventaja demasiado sutil? ¿Y si solo se manifestaba en el medio natural, fuera de las condiciones del laboratorio? Esos ratones, como reconocieron los propios autores, quizá tuvieran alguna anomalía no revisada. ¿Estamos ante un problema irresoluble?
No, salvo que seamos poco realistas y exijamos seguridad absoluta. Si una porción de ADN no contiene nada similar a genes ni a secuencias reguladoras conocidas, y además puedes eliminarla sin causar defectos evidentes, entonces probablemente es ADN basura. No habrá certeza total, pero tampoco una posición inamovible o dogmática. Lo que ocurre es que la carga de la prueba la tiene quien afirme, contra los indicios, que existe una función oculta en esa secuencia. Es quien debe hacer el esfuerzo de aportar evidencias.
Recordemos, además, que la selección natural debe estar actuando sobre una secuencia para que pueda hablarse propiamente de función biológica. Gracias a los avances en genómica y bioinformática, los científicos comparan masivamente genomas de muchas poblaciones y especies (¡extintas, en ocasiones!). Cada vez resulta más fácil estudiar la evolución de esa secuencia; saber su está o no conservada, si muestra señales de selección o si, por el contrario lleva millones de años cambiando a la deriva, de forma neutra.
Si algo grazna como un pato, nada como un pato, camina como un pato… no tachemos de arrogante a quien lo llama “pato”. Cuando una secuencia parece basura y evoluciona justo como corresponde al ADN basura, entonces muy probablemente es ADN basura. Ésta es la hipótesis por defecto. Quien proponga lo contrario tiene dos trabajos: probar la existencia de una función y explicar la razón de tan extraño y engañoso comportamiento evolutivo.
El test de la cebolla
El negacionismo del ADN basura viene en distintos colores y grados. La postura de algunos es confusa: claramente están incómodos pero no dejan claro exactamente por qué; quieren redefinir el concepto de alguna forma, cambiarlo de nombre o que se deje de hablar del asunto. El negacionista típico cree que el genoma es funcional en un porcentaje cercano al 100%; admite que podría haber una pizca de ADN inútil pero nunca el enorme porcentaje que suele estimarse. Esto implica rechazar (pocas veces desde el conocimiento) el desarrollo teórico que llevó a descubrir el ADN basura. Algunos sostienen que el “mal llamado” ADN basura posee, en realidad, alguna función general, universal.
El test de la cebolla es un famoso desafío para ellos planteado por T. Ryan Gregory. Si el ADN basura tiene en realidad una función universal, ¿por qué la cebolla (Allium cepa) necesita, para realizar esa función, cinco veces más ADN que un ser humano? Y, a su vez, ¿por qué unas especies cercanas de Allium, el género de la cebolla, necesitan casi 5 veces más ADN que otras?
Gregory escogió la cebolla pero es solo un ejemplo posible entre miles. Los genomas de distintos seres vivos tienen tamaños extraordinariamente diferentes que no guardan proporción con la complejidad del organismo. Una hormiga, insecto social, puede tener el doble de genoma que una abeja, otro insecto social. Las especies de salamandras tienen entre 4 y 35 veces más ADN que nosotros. Cierta ameba, no mucho más compleja que uno de nuestros miles de millones de glóbulos blancos, supera nuestro genoma en 200 veces. Un pez pulmonado tiene un genoma casi 40 veces más grande que el Homo sapiens y más de 300 veces mayor que el de un pez globo. Una planta con flor, Paris japonica, tiene un genoma más de ¡2400 veces! mayor que otra planta con flor, Genlisea aurea.
Las razones de estas descomunales y aparentemente caprichosas diferencias no se conocen aún completamente. Sin embargo, gran parte y probablemente el meollo del asunto se explica acudiendo a fenómenos biológicos bien conocidos:
Las mutaciones espontáneas duplican segmentos de ADN con una frecuencia muy alta. En las poliploidías, que muchas veces han surgido por hibridación entre especies, se multiplican los genomas (y por tanto se multiplica la gran fracción de ADN basura). Los genes así repetidos son a menudo prescindibles; dejan de ser conservados por la selección darwiniana y evolucionan hacia la degradación. Ciertas infecciones víricas y la proliferación de elementos móviles pueden incrementar el ADN drásticamente, sobre todo en periodos en los que la población se ha reducido y la selección natural es poco eficaz. Millones de estas secuencias de ADN parasitario infestan los genomas. Con el tiempo, la mayoría acaban siendo inutilizadas por mutaciones y convirtiéndose en reliquias que evolucionan a la deriva.
Las deleciones por otra parte, son mutaciones que eliminan secuencias de ADN. Ciertas especies parecen tener un sesgo interno en favor de las deleciones y esto, junto con la selección natural, ayuda a explicar por qué algunos organismos han miniaturizado el genoma durante su evolución, conservando el número habitual de genes típicos pero eliminando chatarra a mansalva.
Efectivamente, se trata de fenómenos implicados en la producción y eliminación de ADN basura. Si sostenemos que el 100% del genoma es funcional, la tremenda diversidad en el tamaño de los genomas que existe en la Tierra se convierte en un misterio científico sobrecogedor.
El test de la cebolla nos recuerda que hay una formidable variación en el mundo vivo y que no tenemos el menor indicio de que el genoma humano sea especial o radicalmente distinto al resto. Cualquier especulación salvaje sobre “paneles de control” o “millones de funciones” debe poder aplicarse también, y con todas las consecuencias, a la humilde cebolla, al murciélago, a la ameba o a la plantita carnívora. De lo contrario, estaríamos cayendo en un quinto error: el antropocentrismo.
¿Qué hay en el genoma?
Veamos, para terminar, algunos datos sobre la composición del genoma humano. Un 9% de nuestro genoma consiste en virus defectivos (estropeados, “muertos”). Alguna que otra vez, la evolución ha convertido ADN de origen vírico en una secuencia funcional, útil para el organismo, pero se trata de acontecimientos muy raros. Ese nueve por ciento procede de antiguas infecciones, son como restos en descomposición y probablemente siguen ahí porque no resultan perjudiciales.
Un impresionante 44% del genoma está hecho de transposones defectivos. Los transposones son elementos genéticos móviles descubiertos por la premio Nobel Barbara McClintock. “Saltan” en los cromosomas e insertan copias de sí mismas. Se trata casi siempre de secuencias parásitas. De nuevo, en algunas ocasiones, mutaciones surgidas en un transposón o provocadas por éste han dado lugar a funciones útiles. Ojo: solo un 0,05% de nuestros transposones pueden funcionar como tales. El resto ya no puede saltar; están “muertos” y la evolución molecular degenera sus secuencias progresivamente. Hay que decirlo otra vez: ¡son el 44% de nuestro genoma!
Los intrones (casi el 30% del genoma, como ya vimos) consisten principalmente en ADN que no está evolutivamente conservado, que carece en su mayor parte de funciones conocidas y que está plagado de transposones.
Los pseudogenes constituyen un modesto 1% del genoma del Homo sapiens (pero puede que una proporción mucho mayor en una bacteria como la Rickettsia). Una vez más se trata de secuencias cadavéricas. Antaño fueron genes codificantes clásicos, pero la selección natural los abandonó y quedaron inutilizados por las mutaciones. Desde entonces, su secuencia se desbarata acumulando cambios al azar. Un ejemplo es el gen GLO, necesario para sintetizar vitamina C, que se fastidió en el linaje de los antropoides. GLO es ahora un pseudogén sin función alguna y, como consecuencia, podemos padecer escorbuto.
Se conocen relativamente bien muchos otros elementos y tipos de secuencias en nuestro genoma. Están los genes que codifican proteínas y RNAs, las secuencias reguladoras, los telómeros, el ADN satélite… L. A. Moran tiene este post clásico sobre el asunto. En él encontraréis estimaciones conservadoras acerca de las cantidades de ADN basura y su localización.
La creencia en un genoma inexplorado y prácticamente desconocido forma parte necesaria del mito del “tesoro en el vertedero”. Este es el sexto error: el adanismo. Creer que partimos de cero, ignorar el progreso previo. Sin duda hay mucho por averiguar y las sorpresas están garantizadas, pero no debemos desdeñar la investigación acumulada. El ADN basura encaja confortablemente con todo ese conocimiento. De hecho, está bien fundido con éste; forma parte del armazón. Quien pretenda extirparlo lo tiene muy crudo, científicamente hablando. Y, sin embargo, ¡triste paradoja! su mala fama y el mito del tesoro en el vertedero durarán aún muchos años.
Este post ha sido realizado por @Paleofreak y es una colaboración de Naukas con la Cátedra de Cultura Científica de la UPV/EHU.
El artículo ADN basura: negacionismo y malentendidos (con cebolla) Segunda parte se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ADN basura: negacionismo y malentendidos (con cebolla) Primera parte
- El rombododecaedro estrellado: arte, abejas y puzzles (segunda parte)
- Llega la segunda generación de ingredientes funcionales
La ciencia y la competencia
La ciencia es un sistema de búsqueda de conocimiento, y también el depósito de saberes acumulado por este sistema. Su objetivo es esclarecer el funcionamiento del Universo, saber cómo funcionan las cosas y de qué están hechas; es una búsqueda intelectual y sistemática que intenta dejar a un lado los errores conocidos y trata de aproximarse en sucesivos ciclos a la verdad. En este sentido es inherentemente cooperativa, no competitiva: el conocimiento es de todos y los descubrimientos del otro pueden y deben enriquecer los propios. El hecho de que el final del proceso de descubrimiento científico sea la publicación así lo demuestra: el objetivo es hacer público, dar a conocer lo descubierto para que todos lo conozcan. La ciencia es, por tanto, una república cooperativa. En teoría.
Y en teoría no debería haber diferencia entre la teoría y la práctica, pero en la práctica la hay.

De izquierda a derecha: Crick, Watson, Franklin, Wilkins y Pauling. Cinco de los protagonistas de uno de los casos de competencia en ciencia más conocidos del siglo XX: el descubrimiento de la estructura del ADN. Los hechos se narran aquí.
Los humanos somos primates, y como tales intensamente sociales y muy jerárquicos; esto implica que tendemos de forma natural a competir constantemente para establecer relaciones de dominación y sumisión. Sólo por este factor la ciencia, como cualquier empeño humano, tiende a la competencia, y el triunfo máximo en ciencia es ser el primero en publicar algo: el que pasa a la historia como el descubridor. A veces las reglas de la ciencia así lo reconocen de modo explícito, como cuando el nombre de quien crea una especie biológica forma parte de su denominación taxonómica oficial: descubre y describe una nueva especie y estarás para siempre en los libros de taxonomía. Si eres el primero en desarrollar una teoría o en abrir un nuevo campo de estudio pasarás a la historia. Nadie recuerda al segundo: es el primero el que se lleva toda la gloria. Y así ha sido siempre, y seguirá siendo mientras seamos humanos.
Otro factor importante es el desarrollo de la tecnología como herramienta política. Las técnicas son hijas de la ciencia, pues consisten en aplicar el conocimiento científico para resolver problemas prácticos, y a lo largo de la historia han influido decisivamente en el poder de las naciones. Ya desde antes y desde luego sin duda desde el siglo XX está más que claro que la única forma de mantener una capacidad económica y militar importante es poseer una capacidad tecnológica y científica importante, porque la economía y la tecnología ganan guerras. Es por eso, y desgraciadamente no por amor al conocimiento, por lo que los estados subvencionan el desarrollo científico, lo cual inmediatamente introduce un factor de distorsión: el que paga no quiere regalar lo que tanto le ha costado conseguir. Hay un enfrentamiento intrínseco entre los objetivos de los estados y el alma misma de la ciencia, ya que los gobiernos quieren el secreto que es esencialmente enemigo del pensamiento científico. La coexistencia es complicada, y eso sin entrar a analizar los intereses comerciales de empresas o editoriales a la hora de controlar el acceso público a la ciencia que generan o canalizan.

Un caso de rivalidad científica que provocó portadas e hizo tambalearse a las bolsas del mundo fue el que enfrentó a los Institutos Nacionales de la Salud de Estados Unidos dirigidos por Francis Collins y a Celera Genomics Corporation dirigida por J. Craig Venter, en su afán por completar el Proyecto Genoma Humano, lo que se dio por conseguido en 2003.
La consecuencia de todo esto es que en el mundo de la ciencia real hay una competencia constante, intensa y feroz; cualquier científico que trabaje en un área de interés puede contar con seguridad con que otros científicos de otros países le están constantemente pisando los talones. La naturaleza no es de propiedad privada: los mismos genes tienen las Drosophilas o los Caenorhabditis o las Arabidopsis en China que en EE UU que en Europa, hay neutrones en cualquier departamento de física del planeta y los ceros de la función zeta de Riemann son los mismos para cualquier matemático, por lo que nadie tiene en principio ventaja: sólo el esfuerzo y el talento cuentan. Quien sea más inteligente, más eficiente y más rápido será el primero, y los demás tendrán que conformarse con ir a la cola. En teoría es la más justa de las contiendas: la naturaleza es la misma para cualquiera y sólo la capacidad determinará quién es el vencedor.
Pero en la práctica dónde estás importa, porque los recursos que se dedican a la investigación no son los mismos ni se reparten de la misma manera, por lo que algunos científicos de según qué países están en desventaja. Todos los científicos compiten a la vez que cooperan, pero algunos lo hacen con más dinero, más becarios, doctorandos y postdocs, más respaldo político, mejores perspectivas laborales y profesionales; y otros con menos. Las políticas estatales importan, porque por muy listo y talentoso que seas sin dinero, sin laboratorios, sin la posibilidad de una carrera profesional estable y sin respaldo político y cultural no se puede competir contra quien sí los tiene. Los países más ambiciosos y poderosos del mundo invierten en su ciencia porque saben que es invertir en poder para sus estados y bienestar para sus ciudadanos. Los demás invierten menos y colocan a sus científicos en posición de desventaja en una carrera en la que todos participamos, seamos conscientes o no. Esta es, también, una decisión política fundamental relacionada con la ciencia. Porque por muy cooperativamente humano que sea el conocimiento mientras seamos como somos la competencia existirá. Y en algunos países la estamos perdiendo por ceguera.
Sobre el autor: José Cervera (@Retiario) es periodista especializado en ciencia y tecnología y da clases de periodismo digital.
El artículo La ciencia y la competencia se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Un rebaño de vacas pastando como sistema complejo

La imagen de las vacas pastando en un campo ha evocado desde hace mucho tiempo una nostalgia romántica del presunto ritmo relajado de la vida rural. Sin embargo, si se analiza con cuidado, lo que parece ser un rebaño aleatoriamente disperso que come pacíficamente hierba es, de hecho, un complejo sistema de individuos en un grupo sometido a varios tipos de tensiones. Para describirlo un equipo de matemáticos y un biólogo ha construido un modelo matemático que incorpora una función de costes a la conducta dentro del rebaño para entender la dinámica de estos sistemas.
Esta investigación se encuadra dentro de lo que se llama ciencia de sistemas complejos, que busca entender no sólo los componentes individuales de un sistema dado, sino cómo estos componentes interactúan para producir un comportamiento de grupo “emergente”. Las vacas que pastan en rebaño son un ejemplo interesante de sistema complejo.
Así, una vaca individual realiza tres actividades principales a lo largo de un día normal: come, se queda quieta mientras lleva a cabo algunos procesos digestivos, y luego se echa para descansar.
Si bien este proceso parece bastante simple, convive con la búsqueda del equilibrio con la dinámica de grupo del rebaño.
Las vacas se mueven y comen en rebaño para, en principio, protegerse de los depredadores. Pero como comen a diferentes velocidades, la manada puede empezar a moverse antes de que las vacas más lentas hayan terminado de comer, lo que deja a estas vacas, habitualmente más pequeñas, frente a una difícil elección: seguir comiendo en un grupo más pequeño y menos seguro o empezar a moverse con el grupo más grande todavía con hambre. Si el conflicto entre alimentarse y mantener el ritmo del grupo se vuelve demasiado grande, puede ser ventajoso que algunos animales se dividan en subgrupos con necesidades nutricionales similares .
Los investigadores incorporaron una función de coste en su modelo para describir estas tensiones. Lo que añade complejidad matemática, pero es imprescindible para que el modelo reproduzca el comportamiento real.
Con todo, algunos resultados de la simulación son sorprendentes. De la descripción anterior uno podría creer que habría dos grupos estáticos de vacas – las comedores rápidas y las lentas – y que las vacas dentro de cada grupo llevarían a cabo sus actividades de una manera sincronizada. En lugar de eso nos encontramos que también aparecen vacas que se mueven adelante y atrás entre los dos subrebaños.
La causa principal es que este complejo sistema tiene dos ritmos en competencia. El grupo de animales grandes va más rápido y el grupo de animales pequeños va a ritmo más lento. Pero, ¿qué ocurre si eres una vaca, digamos, intermedia? La vaca podría encontrarse en el primer grupo, y después de algún tiempo, el grupo resulta ser demasiado rápido. Se va entonces al grupo más lento, pero que es demasiado lento, y termina yendo otra vez con el rápido. Pero como mientras se mueve entre los dos grupos la vaca se expone más al peligro de los depredadores, ello causa una tensión entre la necesidad de la vaca de comer y su necesidad de seguridad.
Este modelo podría aplicarse al estudio del comportamiento de rebaños en grandes extensiones, lo que sería de utilidad a ganaderos, veterinarios y gestores de parques naturales. Y, si incluimos a los rebaños de humanos, también a fuerzas del orden y agentes de protección civil.
Referencia:
Kelum Gajamannage, Erik M. Bollt, Mason A. Porter and Marian S. Dawkins (2017) Modeling the lowest-cost splitting of a herd of cows by optimizing a cost function. Chaos doi:10.1063/1.4983671
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Este texto es una colaboración del Cuaderno de Cultura Científica con N
El artículo Un rebaño de vacas pastando como sistema complejo se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Econofísica: ¿puede la economía tratarse como un sistema físico?
- Cómo diseñar un sistema para comunicarse con el otro lado de la galaxia
- #Naukas14 ¿Por qué explota una granja de vacas?
El teorema de Morcom
El cómic Le Théorème de Morcom –con guión de Benoît Peeters y dibujos de Alain Goffin– se publicó por primera vez en 1992, en Les Humanoïdes Associés. La editorial lo presenta de la siguiente manera:
Tras la muerte del famoso lógico Julius Morcom, Fred Mathison, periodista en Journal of Science, decide escribir un artículo relatando la carrera de este brillante hombre. Pronto descubre que Morcom estaba lejos de ser un matemático ordinario. Y que su trabajo sobre la “máquina universal” interesaba a más de uno… Este viaje por las sombras de los servicios secretos, durante y después de la Segunda Guerra Mundial, es una historia vibrante de suspense matemático.

Imagen 1. Portada del cómic.
¿Julius Morcom es un matemático real? Y Fred Mathison, ¿no os recuerda a alguien ese apellido? ¿Ni aun sabiendo que el tebeo trata de matemáticas y máquinas?
El nombre completo de Alan Turing era Alan Mathison Turing; de hecho, su padre se llamaba Julius Mathison Turing. Así, los nombres de los personajes –el matemático y el periodista– presentados en el resumen de la editorial se inspiran en cierto sentido en el matemático británico. Además Christopher Morcom fue el primer amor –no correspondido, aunque eran grandes amigos– de Alan Turing. Se conocieron en 1927, Morcom era un año mayor que Turing, y compartían su pasión por la ciencia y el descubrimiento. Su relación se fue fortaleciendo hasta la trágica muerte de Christopher, en 1930, debido a las complicaciones de una tuberculosis bovina.
La historia contada en este tebeo comienza el 12 de julio de 1954, en la carretera que lleva de Thornill a Strangton: un Cadillac se sale de la carretera y cae a un precipicio. Su conductor es el genial matemático Julius Morcom, que muere instantáneamente. ¿Se trata de un simple accidente de tráfico? ¿De un suicidio? ¿De un asesinato?

Imagen 2. Primeras viñetas del cómic: la muerte de Julius Morcom.
Fred Mathison, periodista de Journal of Science, se interesa por esta noticia, y comienza a indagar en el pasado del matemático: su genialidad al haber escrito con solo 24 años un artículo de lógica matemática que ponía en duda algunos conocimientos aceptados, su vida como criptógrafo durante la Segunda Guerra Mundial, y su obsesión por crear ‘máquinas inteligentes’… En una de las cartas que Morcom –su madre vive en Inglaterra, el matemático en EE. UU., esperando encontrar una mejor disposición hacia sus teorías– envía a su madre antes de morir, escribe:
Quiero volver a considerar todo a partir de cero para concebir una máquina verdaderamente inteligente, concebida a imagen de nuestro cerebro, una máquina capaz de pensar, de sentir, de reaccionar, como lo hacemos nosotros…
Enseguida, el periodista advierte que no es el único interesado en Morcom: alguien busca los apuntes que contienen sus últimos descubrimientos.
Mathison viaja a Cambridge para proseguir sus investigaciones y entrevistar a Anthony Rules, un antiguo profesor de Morcom. Rules le habla de la genialidad de su alumno, cuya tesis –On computable Numbers with an application to the ‘Entscheidungsproblem’ [Nota 1]– es una primera versión de su innovadora teoría. Y comenta, con pesar, su posterior giro hacia las máquinas inteligentes…
El periodista se reúne también con Kenneth Williams –uno de los estudiantes de Morcom–, con el que el matemático intentaba construir su máquina –una máquina real–, cuando la guerra les interrumpió.
Prosigue sus investigaciones, y cuando llega al coronel Knox, nota que los secretos militares le van a impedir conocer el trabajo de Morcom en Bletchley Park. Se entrevista con Sarah Hodges [Nota 3], asistente de Turing en el establecimiento militar. Sarah le habla de la homosexualidad del matemático, y de los problemas que esto le generaba –además de desobediencia sistemática– con las autoridades.
A partir de ese momento, asaltan la casa de Anthony Rules, la habitación en el hotel de Morcom, asesinan a Sarah… buscando documentos del genio. Pero esa búsqueda ya no tiene sentido: la madre de Morcom ha quemado los cuadernos de su hijo, repletos de cálculos, de gráficas… y de imágenes de chicos, que podían publicarse y perjudicar la imagen de Julius.
Mathison regresa a su país, marcado por los violentos acontecimientos, y decide abandonar el artículo y su trabajo en el Journal of Science, para dedicarse a escribir la verdadera historia de Julius Morcom. ¿O es la historia de Alan Turing y de la máquina ENIGMA?

Imagen 3. Alan Turing y Christopher Morcom.
Notas:
Nota 1: Entscheidungsproblem –El problema de decisión– fue un reto en lógica simbólica que consistía en encontrar un algoritmo general que decidiera si una fórmula del cálculo de primer orden es un teorema. En 1936, de manera independiente, el lógico Alonzo Church y Alan Turing demostraron que es imposible escribir tal algoritmo.
Nota 2: Bletchley Park es una instalación militar localizada en Buckinghamshire (Gran Bretaña) en la que se realizaron los trabajos de descifrado de códigos alemanes durante la Segunda Guerra Mundial.
Nota 3: Andrew Hodges es matemático, escritor y activista del movimiento de liberación gay de los años 1970. Es el autor de Alan Turing: The Enigma. Ethel Sara es el nombre de la madre de Alan Turing.
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo El teorema de Morcom se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El teorema de los cuatro colores (y 4): ¿Podemos creer la prueba de la conjetura?
- El teorema de los cuatro colores (3): Tras más de un siglo de aventura… ¿un ordenador resuelve el problema?
- El teorema de los cuatro colores (1): una historia que comienza en 1852
Evolución de los sistemas nerviosos: el tamaño encefálico
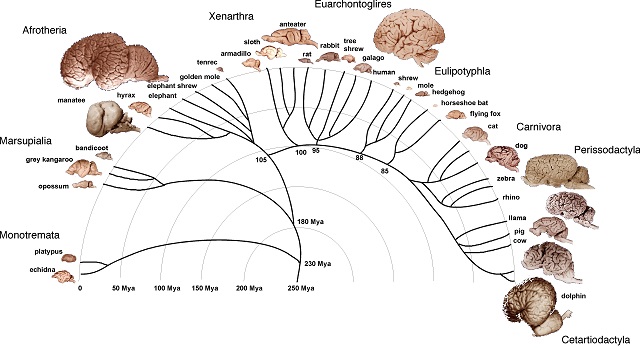
Hay sistemas nerviosos con unos pocos centenares de neuronas, como los de los nematodos, que tienen alrededor de 300. En el otro extremo están los grandes mamíferos, que llegan a tener del orden de 1011. Pero, ¡ojo! No hemos de pensar que esas diferencias marcan los extremos de una posible evolución lineal desde animales de muy sencilla configuración corporal hasta los mucho más complejos vertebrados. En el curso de la evolución ha habido divergencias que han conducido a sistemas nerviosos muy complejos siguiendo distintas trayectorias. Los cefalópodos, por ejemplo, han desarrollado sistemas nerviosos con números altísimos de neuronas: 108. Esa cifra es superior a la de muchos peces, reptiles y anfibios, como lo es la complejidad de sus circuitos y de su comportamiento.
De hecho, las diferencias numéricas suelen ir acompañadas, además, de diferencias en el grado de complejidad. En general, la circuitería nerviosa es mucho más compleja cuanto mayor es el número de neuronas que tiene un sistema. Pero de lo anterior no debe deducirse que cuantas más neuronas tiene un animal, mayor es su capacidad cognitiva necesariamente. Porque otros factores también inciden en el número de neuronas. Una ballena o un elefante puede tener el doble de neuronas que un ser humano, por la sencilla razón de que sus encéfalos son muy grandes, y no hay base para pensar que sus capacidades cognitivas son superiores a las humanas. Y al contrario, aves de encéfalos muy pequeños y con un número relativamente pequeño de neuronas, como algunos córvidos, por ejemplo, tienen capacidades cognitivas asombrosas.
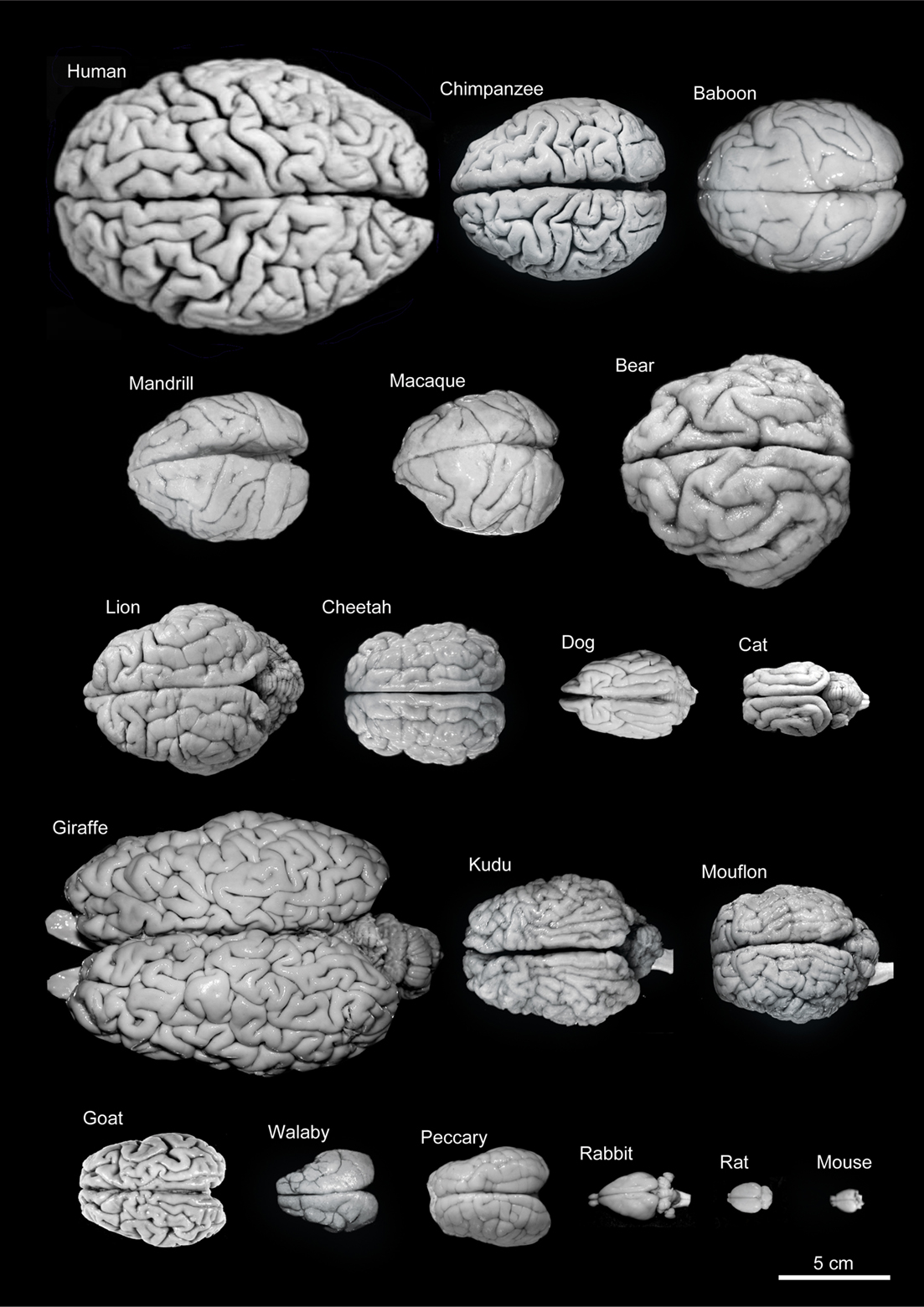
Tamaño encefálico de algunos mamíferos.
Lo anterior nos conduce a la cuestión del tamaño encefálico. En general el tamaño del encéfalo de los vertebrados es mayor cuanto mayor es el tamaño de un animal, aunque la relación no es lineal, sino potencial (del tipo B = a Wb, donde B es la masa encefálica y W la corporal), con un valor de la potencia b que es inferior a 1, lo que significa que la masa del encéfalo es una proporción menor de la masa corporal en los vertebrados de mayor tamaño.
No obstante lo anterior, hay enormes diferencias entre los tamaños encefálicos de vertebrados de similar masa corporal, de manera que un encéfalo puede ser hasta 30 veces mayor que el de otro animal del mismo tamaño. Peces, anfibios y reptiles los tienen, en general, de pequeño tamaño relativo dentro de los vertebrados, menor, incluso, que el de la mayoría de pulpos y calamares. Los encéfalos más pequeños son los de los agnatos (vertebrados sin mandíbulas) y, en estos, muy especialmente los de las lampreas. Sin embargo, los peces cartilaginosos -tiburones y rayas- los tienen de tamaño similar al de mamíferos y aves de parecidas dimensiones. Por otro lado, los anfibios tienen un tamaño encefálico inferior al de los reptiles, y dentro de aquellos, los de los anuros (ranas) son mayores que los de los urodelos (tritones). Aves y mamíferos tienen encéfalos que son del orden de diez veces mayores que los de reptiles.
En las aves los mayores tamaños encefálicos relativos son los de algunas paseriformes, como pájaros carpinteros y loros, y los menores los de algunas granívoras, como palomas y codornices. Los primates son los mamíferos con encéfalos de mayor tamaño, aunque después del humano el segundo de mayor tamaño es el de los delfines (cetáceos). Los menores son los de monotremas, marsupiales, roedores e insectívoros.
Se ha especulado mucho acerca de la base de esas diferencias. Tenemos, por un lado, la hipótesis del tejido caro. El tejido nervioso es muy caro, porque debe mantener de forma permanente los gradientes iónicos que permiten la transmisión de los impulsos nerviosos y porque ha de producir, transportar, liberar y recuperar neurotransmisores, también de forma permanente. Por eso, cuanto mayor es el encéfalo, más hay que gastar en esas costosas actividades. Por otro lado, el hígado y el tracto gastrointestinal son también órganos muy activos y caros de mantener. Se da la circunstancia de que los animales que se alimentan de productos de baja calidad nutricional tienen sistemas digestivos de mayor tamaño (disponen así de más recursos y de más tiempo para la digestión). Esas diferencias permiten explicar por qué los carnívoros tienen, normalmente, mayores encéfalos y menores sistemas digestivos que los herbívoros. Y si esa hipótesis es correcta, habría que pensar que los animales que han podido acceder a dietas de alta calidad han desarrollado encéfalos más grandes. Aunque también podría valer la interpretación en sentido opuesto: los animales de mayor tamaño encefálico disponen de mayor capacidad para encontrar alimentos de mayor calidad y se habrían especializado, por ello, en dietas carnívoras. Sea como fuere, lo cierto es que encéfalos grandes suelen asociarse a digestivos pequeños, y estos solo pueden serlo si el alimento es de alta calidad, o sea, si proporciona mucha energía y nutrientes por unidad de esfuerzo dedicado a la digestión y absorción.
Una variante de la hipótesis anterior -apropiada solo para los seres humanos- incluye la cocción de los alimentos en la ecuación, ya que cocinando los alimentos los nutrientes se hacen mucho más fácilmente digeribles, lo que amplia mucho las dietas que pueden utilizarse sin necesidad de disponer de un sistema digestivo de gran tamaño.
Y finalmente, no quiero dejar sin citar la hipótesis de Robin Dunbar, que liga el tamaño encefálico con la socialidad y, más en concreto, con los requerimientos cognitivos que impone la vida en el seno de grupos relativamente grandes de individuos. Dunbar propone que, con carácter general, las especies monógamas tienen requerimientos cognitivos superiores a las demás especies. Y encéfalos de mayor tamaño habrían evolucionado bajo esa presión selectiva, porque se supone que dentro de un mismo linaje, un mayor tamaño encefálico está asociado a mayor capacidad cognitiva. Sería, por lo tanto, un factor cualitativo, cual es el tipo de vínculo reproductivo, el responsable de las diferencias en tamaños encefálicos. Lo que habría conducido a que los primates sean los mamíferos con encéfalos de mayor tamaño relativo es que estos habrían generalizado a las relaciones sociales ciertas características de las relaciones propias del vínculo de pareja; y como consecuencia de esa generalización, el encéfalo habría alcanzado el gran tamaño relativo que tiene en este grupo. Los partidarios de esta hipótesis sostienen que el tamaño encefálico evoluciona en respuesta a las presiones selectivas que imponen las relaciones –de pareja y sociales- de los individuos de los diferentes linajes, pero que son factores dietéticos los que habrían posibilitado el cambio evolutivo. Todo demasiado especulativo.
Fuentes:
Robin I Dunbar (2009): The Social Brain Hypothesis and its Implications for Social Evolution, Annals of Human Biology 36 (5): 562-572, doi: 10.1080/03014460902960289
Lauralee Sherwood, Hillar Klandorf y Paul h. Yancey (2005): “Chapter 5: Nervous Systems”, Animal Physiology: From Genes to Organisms, Brooks/Cole, Belmont.
Georg Striedter (2005): “Chapter 4: Evolutionary Changes in Overall Brain Size”, Principles of Brain Evolution, Sinauer Associates, Massachusetts.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Evolución de los sistemas nerviosos: el tamaño encefálico se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Evolución de los sistemas nerviosos: moluscos
- Evolución de los sistemas nerviosos: anélidos y artrópodos
- Evolución de los sistemas nerviosos: cnidarios y gusanos no segmentados
Se intuye la conservación de la energía (1)

A principios del siglo XIX los avances en la ciencia, de la ingeniería y de la filosofía sugirieron nuevas ideas sobre la energía. Parecía que todas las formas de energía (incluido el calor) podían transformarse entre sí sin pérdida alguna. Por lo tanto, parecía que la cantidad total de energía en universo debía permanecer constante.
En 1800 Alessandro Volta inventó la batería eléctrica, demostrando que las reacciones químicas podían producir electricidad. Pronto se descubrió que las corrientes eléctricas podían producir calor y luz, al pasar a través de un alambre delgado. En 1820, Hans Christian Oersted descubrió que una corriente eléctrica produce efectos magnéticos. En 1831, Michael Faraday descubrió la inducción electromagnética. Cuando un imán se mueve cerca de una bobina o un alambre, se produce una corriente eléctrica en la bobina o alambre. Para algunos pensadores estos descubrimientos sugirieron que todos los fenómenos de la naturaleza estaban de alguna manera unidos. Esta idea, aunque vaga e imprecisa, terminó fructificando en forma de ley de conservación de la energía, una de las leyes más importantes en ciencia:
Los fenómenos naturales pueden implicar una transformación de la energía de una forma a otra; pero la cantidad total de energía no cambia durante la transformación.
La invención y el uso de máquinas de vapor ayudó a consolidar la ley de conservación de energía al mostrar cómo medir esos cambios de energía. Por ejemplo, Joule utilizó el trabajo realizado por pesos descendentes que hacen girar una rueda de paletas en un tanque de agua como una medida de la cantidad de energía potencial gravitacional transformada en energía térmica en el agua por su fricción con las paletas. En 1843, Joule afirmó que en tales experimentos, siempre que una cierta cantidad de energía mecánica parecía desaparecer, siempre aparecía una cantidad concreta de calor. Para él, esto era una indicación de la conservación de lo que ahora llamamos energía. Joule afirmó estar…
. . . satisfecho de que los grandes agentes de la naturaleza son por el fiat del Creador indestructibles; y que, siempre que se gasta [energía] mecánica, se obtiene siempre un equivalente exacto de calor.
Joule era básicamente un hombre práctico que tenía poco tiempo para especular sobre un posible significado filosófico más profundo de sus hallazgos. Pero otros, aunque utilizando argumentos especulativos, también estaban llegando a la conclusión de que la cantidad total de energía en el universo es constante.
En este Cuaderno hemos tratado ya en varias ocasiones el trasfondo filosófico y la historia del surgimiento de las leyes de conservación, pero ello no es óbice ni cortapisa para que en la próxima entrega de esta serie lo hagamos de nuevo centrándonos en este pilar de la ciencia que es la ley de conservación de la energía.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Se intuye la conservación de la energía (1) se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:La memoria colectiva

Fue en 2014 cuando el Gobierno Vasco aprobó la Ley 4/2014, del 27 de noviembre, de la creación del Instituto de la Memoria, la Convivencia y los Derechos Humanos. En la Exposición de motivos, esta ley especifica que
“La gestión de una memoria democrática es uno de los factores directamente vinculados a la restitución y promoción de valores como la libertad, la igualdad y la dignidad humana. La memoria es un derecho ciudadano, no una obligación. Responde a la voluntad de compartir una reflexión crítica ante los acontecimientos de nuestra historia reciente que supusieron una violación de derechos humanos sostenida y socialmente traumática.”
“La memoria es la facultad que permite mantener presente el recuerdo de lo sucedido. Se asienta en la referencia de hechos objetivos que forman parte de lo que se recuerda, pero se configura subjetivamente en cada persona. No hay dos memorias exactamente iguales. La memoria pública es, en este sentido, una construcción conflictiva, dinámica y poliédrica.”
“La misión principal de una política de memoria y convivencia no se reduce a la actualización del sufrimiento, porque el dolor no es un valor, ni debe ser considerado como un principio de autoridad memorial que sustituye a la razón.”
“…se orienta a rescatar, destacar, conmemorar y transmitir los valores y esfuerzos democráticos que en medio de graves episodios violentos, pugnaron por defender la dignidad, la igualdad, la libertad…”
“El derecho a la memoria corresponde al conjunto de la sociedad, porque la ciudadanía es depositaria y heredera natural de la historia, el recuerdo y de la memoria. El olvido impide el reconocimiento, impone una versión del pasado y genera un vacío ético.”
En el Capítulo 3.- Finalidad, y en su punto 2.-, el texto precisa que
“El instituto será un agente activo en la permanente conmemoración de los valores políticos y sociales que garanticen el conocimiento, comprensión y conciencia de la ciudadanía respecto al proceso sostenido a lo largo de décadas en defensa de la libertad y del desarrollo de la democracia en nuestro país.”
Y el 8 de marzo de 2017, hace unas semanas, se constituyó en el Parlamento Vasco la Ponencia de Memoria y Convivencia, con el objetivo de “la búsqueda de amplios consensos” en torno a las cuestiones que planteen los grupos en relación a “la memoria, la convivencia, las víctimas, la deslegitimación del terrorismo y la violencia, la política penitenciaria, la paz y los derechos humanos”.
Después de esta larga introducción quizá empezamos a comprender lo que nuestros dirigentes y, se supone, nuestro entorno social entiende por memoria colectiva, con sus objetivos e intenciones de futuro. Ahora pasemos a lo que los psicólogos experimentales empiezan a averiguar sobre la memoria colectiva.
Según estudios publicados en los últimos años, la memoria colectiva se ha convertido en objeto de estudio de la psicología experimental. Como afirman Henry Roediger III y Magdalena Abel, de la Universidad Washington de St. Louis, hasta ahora la memoria colectiva ha sido un tema importante en los estudios de humanidades pero, actualmente, se comienza a investigar desde un enfoque empírico y experimental.
Para estos autores, la memoria colectiva se construye con los sucesos compartidos por un grupo. Es una forma de memoria cuya definición concreta está en debate. Además de compartirla el grupo, debe tener una importancia básica y central en la identidad social de sus miembros.
Hay conceptos cercanos a la memoria colectiva que no tienen exactamente el mismo significado. Por ejemplo, no es lo mismo que los recuerdos colectivos. Estos son dinámicos y siguen un proceso continuo de debate sobre cómo se debe representar y recordar el pasado. La memoria colectiva, por el contrario, aunque cambia con frecuencia, es un conocimiento asentado del pasado que, además, es compartido por los miembros del grupo.
La memoria colectiva tampoco es la historia, que nos da una representación ajustada y objetiva de un pasado complejo que, siempre, incluye ambigüedades y diferentes puntos de vista y opiniones. Es, se supone, un enfoque objetivo del pasado que, además, no tiene por qué ser la memoria colectiva.
Y tampoco es, sin más, la suma de los recuerdos de los individuos del grupo. A veces, estos recuerdos tienen importancia social pero, también, muy a menudo, solo conciernen a quien recuerda. Si son compartidos por el grupo se convierten en recuerdos colectivos y, puede que, más adelante, en memoria colectiva. Así los recuerdos individuales y la historia, en último término, pueden ayudar a construir la memoria colectiva del grupo.

Este señor, Andrew Johnson, fue presidente de los Estados Unidos.
Con estos autores vamos a repasar algunos de los estudios empíricos sobre memoria colectiva que antes citaba. Para empezar, investigan el recuerdo que los estadounidenses tienen de sus presidentes. Lo preguntan en 1974, en 1991 y en 2009, y detectan que los recuerdos se mantienen. Los encuestados deben anotar los presidentes que recuerden y ordenarlos, si es posible, en el orden temporal de sus mandatos.
Hay un olvido sistemático de los presidentes alejados en más de unas décadas, un recuerdo fuerte de los últimos presidentes para cada grupo de encuestados, con su olvido posterior, y un recuerdo fuerte de los presidentes que hicieron historia como Washington y sus sucesores inmediatos, Lincoln, y los presidentes del siglo XX, cada vez más recordados puesto que están más cercanos en el tiempo e intervinieron en hechos históricamente importantes, y muy recordados todavía, como las guerras mundiales, la depresión o las guerras de Corea y Vietnam.

Imagen del ataque a Pearl Harbor
En la memoria colectiva se guardan hechos heroicos, incluso míticos, importantes para el grupo, y se minimizan o desaparecen los hechos negativos o que no confluyen con el destino aceptado para todo el grupo. Es interesante conocer qué recuerdan los estadounidenses de tres guerras en las que ha participado su país: la Guerra Civil, la Segunda Guerra Mundial y la guerra de Irak. Lo estudiaron Franklin Zaromb y su grupo, del Servicio de Educación de Princeton, con 60 voluntarios, todos hombres, la mitad de 18 a 23 años y la otra mitad, de 62 a 87 años.
Se pide a los voluntarios que hagan una lista con los diez hechos que consideran más importantes de cada guerra y que los puntúen según las emociones que les provocan. Los recuerdos importantes de la Guerra Civil y de la Segunda Guerra Mundial son parecidos para la mayoría de los encuestados. Por ejemplo, en la Segunda Guerra Mundial son Pearl Harbor, el desembarco de Normandía y las bombas atómicas sobre el Japón.
Los sucesos importantes son pocos y llegan a la memoria colectiva con relatos cortos y potentes, fáciles de aceptar y asumir. En general, las memorias colectivas se expresan como una narración con un principio, una parte media y un final. El resto de sucesos o desaparecen o se fusionan con los más recordados. Para la Segunda Guerra Mundial, el comienzo fue Pearl Harbor, la parte central con cambio de tendencia fue el desembarco de Normandía, y el final, con la victoria, fue Hiroshima y Nagasaki.
Es interesante resaltar que uno de los aspectos esenciales de una memoria colectiva es su continua reelaboración dentro de un esquema permanente y aceptado. El pasado cambia constantemente en la memoria. También se generan interpretaciones diferentes para los mismos hechos. El genocidio armenio ocurrió hace un siglo y, sin embargo, Turquía y Armenia, cada grupo con su propia memoria colectiva, siguen debatiendo sobre el suceso, su interpretación y quienes fueron los responsables y, por supuesto, sobre qué recordar e incluir en la memoria colectiva.
Otro ejemplo viene del trabajo citado de Zaromb sobre las guerras en Estados Unidos. Todos recuerdan las bombas atómicas sobre Japón pero los encuestados de más edad lo consideran un hecho heroico que contribuyó a que la guerra terminara antes y a que se salvaran miles de vidas de soldados de Estados Unidos y, en cambio, los encuestados más jóvenes lo recuerdan como una masacre con miles de japoneses muertos y como el inicio de la Guerra Fría y de la acumulación de los arsenales de armas nucleares.
También influye el silencio público sobre algunos hechos que consigue que se olviden cuando no coinciden con lo que se acepta en la memoria colectiva del grupo, como demuestran Charles Stone y William Hirst, de la Universidad de la Ciudad de Nueva York. La omisión de sucesos puede venir de la comunidad, de un líder e, incluso, del grupo al completo. Se olvida lo que, ante todo, no se quiere escuchar y, por supuesto, no se quiere recordar.

Alberto II, rey de los belgas
Stone y Hirst estudian los recuerdos de los belgas sobre los discursos de su rey en un momento político difícil, sin gobierno y con negociaciones entre los partidos sin llegar a un acuerdo. Entrevistan a 81 voluntarios y, aquellos que no escucharon el discurso del rey, recuerdan los problemas de su país y las negociaciones que están en marcha para solucionarlos, con su secuencia en el tiempo. Los que escuchan al rey recuerdan parcialmente esos problemas; en realidad, solo lo que el rey menciona, y el resto lo han olvidado.
Así, las figuras públicas pueden provocar olvidos selectivos y conformar la memoria colectiva del grupo. Pero no siempre es así y, a veces, parece funcionar de manera parcial como ocurre en el conflicto entre turcos y armenios sobre el genocidio del siglo pasado, incluso teniendo en cuenta que en Turquía está prohibido debatir y difundir este asunto.
Por tanto, la memoria colectiva, como la memoria de los individuos, solo recuerda parte de lo que ocurrió, y el resto lo olvida.
También la nostalgia, por supuesto colectiva, influye en la construcción de la memoria colectiva. El Diccionario de la Lengua define así la nostalgia:
“1.f.Penadeverseausentedelapatriaodelosdeudoso amigos.
2.f.Tristezamelancólicaoriginadaporelrecuerdodeunadichaperdida.”
El grupo de Tim Wildschut, de la Universidad de Southampton, ha demostrado que quienes sienten nostalgia colectiva, por sucesos vividos en grupo, evalúan más alto las relaciones dentro del mismo grupo que quienes sienten nostalgia individual, por hechos vividos personalmente.
Los que sienten esa nostalgia colectiva están más dispuestos a apoyar y reforzar el grupo. En resumen, Wildschut afirma que la nostalgia es importante en los sentimientos de los miembros del grupo, en sus tendencias a la acción, y, en general, en su conducta.
Como conclusiones finales podemos afirmar que la memoria colectiva es un término que refleja cómo las personas recuerdan el pasado por ser miembros de un grupo. La memoria colectiva es, siempre, un proyecto inacabado que se basa en el rescate de recuerdos individuales y en la construcción de un relato común que refuerce la identidad del grupo.
Puede estudiarse como un cuerpo de conocimiento, como el esquema que soporta a un pueblo, o como un proceso de reivindicación y cambio. La memoria colectiva probablemente impulsa la identidad del grupo y construye su discurso social y político. Y además, el estudio de cómo varios miembros del grupo recuerdan los mismos sucesos de forma diferente puede ayudar a entender los factores psicológicos que intervienen en la creación de la memoria colectiva así como su influencia en la dinámica dentro del grupo y en los conflictos internos y externos.
Referencias:
BOPV. 2014. Ley 4/2014, de 27 de noviembre, de creación del Instituto de la Memoria, la Convivencia y los Derechos Humanos. BOPV 230, nº 5141.
Roediger, III, H.L. & M. Abel. 2015. Collective memory: a new arena of cognitive study. Trends in Cognitive Sciences 19: 359-361.
Spinney, L. 2016. Our collective memory, like individual memory, is shockingly falible. British Psychological Society BPS Blog, 22 January.
Stone, C.B. & W. Hirst. 2014. (Induced) Forgetting to form a collective memory. Memory Studies 7: 314-327.
Wildschut, et al. 2014. Collective nostalgia: A group-level emotion that confers unique benefits on the group. Journal of Personality and Social Psychology doi: 10.1037/a0037760
Zaromb, F. et al. 2014. Collective memories of three wars in United States history in younger and older adults. Memory & Cognition 42: 383-399.
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo La memoria colectiva se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El deterioro de la memoria con la edad es selectivo
- Un nexo cannabinoide entre mitocondrias y memoria
- La clave de la memoria que no lo era
Posibles biomarcadores para el ictus
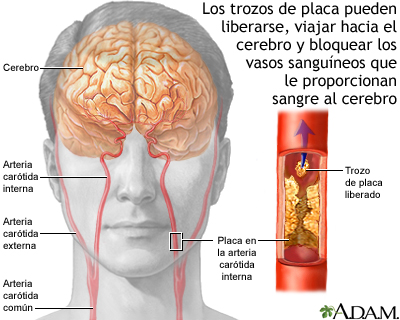
La formación de placas de ateroma o acúmulos de células y grasa mayoritariamente en los vasos principales que llevan la sangre del corazón al cerebro por el cuello, las llamadas arterias carótidas, es un factor de riesgo para desarrollar un ictus. Actualmente se desconoce el mecanismo preciso por el cual la placa se rompe dando lugar al ictus. Se sabe que las células del músculo liso (CML) presentes en la placa juegan un papel en su formación.
El grupo Neurogenomiks, vinculado al centro Achucarro Basque Centre for Neuroscience (EHUtaldea) y a la Universidad del País Vasco (UPV/EHU), en colaboración con el Hospital Universitario de Basurto acaban de publicar el resultado de un trabajo de investigación en el que han identificado, mediante un estudio de transcriptómica basado en secuenciación masiva, 67 genes y 143 isoformas reguladas diferencialmente en células CML de placas inestables (provenientes de pacientes sintomáticos) comparado con las células CML de placas estables (provenientes de pacientes asintomáticos).
Además, los análisis de enriquecimiento y de vías realizados con los datos de transcriptómicas mediante herramientas de bioestadística han demostrado que las células CML de placas instables (provenientes de pacientes sintomáticos) presentan un perfil transcriptómico de biomarcadores asociado a un fenotipo de senescencia celular y sin embargo las células CML de placas estables (provenientes de pacientes asintomáticos) presentan un perfil asociado a un fenotipo de osteogénesis.
Por tanto podemos decir que el proceso por el cual se rompe la placa de ateroma en la arteria carótida no es un proceso aleatorio sino que es una acción dirigida.
Las opciones terapéuticas existentes han mejorado pero todavía son limitantes y además hasta ahora no se han identificado parámetros analíticos, biomarcadores, que nos puedan ayudar en la práctica habitual para esta enfermedad. Por tanto, la identificación de biomarcadores con potencial en el diagnostico o pronóstico de la enfermedad cerebrovascular son de innegable interés. Los resultados de este trabajo abren las vías para el desarrollo de nuevas opciones en el diagnóstico y tratamiento que pueden mejorar el pronóstico de estos pacientes.
Referencia:
Iraide Alloza, Haize Goikuria, Juan Luis Idro, Juan Carlos Triviño, José María Fernández Velasco, Elena Elizagaray, María García-Barcina, Genoveva Montoya-Murillo, Esther Sarasola, Reyes Vega Manrique, Maria del Mar Freijo & Koen Vandenbroeck. RNAseq based transcriptomics study of SMCs from carotid atherosclerotic plaque: BMP2 and IDs proteins are crucial regulators of plaque stability. Scientific Reports 7 (2017). DOI: 10.1038/s41598-017-03687-9.
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Posibles biomarcadores para el ictus se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Biomarcadores para la detección precoz del melanoma
- Algoritmos de triaje para readmitidos en urgencias
- Una nueva diana terapéutica para el neuroblastoma
Juno, Júpiter, arte y amoniaco
Una de las ventajas que ofrece este rincón del Cuaderno de Cultura Científica es la relativa atemporalidad del arte. Un servidor puede traer prácticamente cualquier tema a colación sin preocuparse de que sea de vibrante actualidad, algo que no pueden hacer quienes divulgan sobre temas más candentes como las ondas gravitacionales o los últimos avances en medicina.
Sin embargo, recientemente ha habido una noticia de tal impacto que bien merece que le dediquemos unas líneas. Me refiero, como ya habréis deducido por el título del artículo, a las últimas imágenes que nos ha regalado el satélite Juno de la superficie de Júpiter. No tengo la menor intención de hablar de los prometedores resultados científicos que se han recibido, de eso ya se ha encargado la gente que sabe del tema. Pero sí que quería aportar un punto de vista diferente, ya que Júpiter es una enorme obra de arte con mucha química. Y, si no, contemplad la Imagen 1 para salir de toda duda.

Imagen 1. Vista de Júpiter creada por Gabriel Fiset empleando los datos de la cámara Juno. Fuente: NASA
Juno abandonó la Tierra el 5 de agosto de 2011 y casi seis años después ha llegado a su destino. Más allá de los datos gravimétricos que pueda ofrecer, lo más fascinante para quienes no sabemos resolver una ecuación diferencial son las imágenes captadas por la cámara que lleva incorporada (JunoCam). Por cierto, la NASA ha habilitado una web donde podemos obtener toda la información que deseemos y subir nuestras propias fotos del planeta. Juno ya lleva unas semanas en la órbita de Júpiter en una escena similar a la recreación artística que os enseño en la Imagen 2. Digna de una película de ciencia ficción, ¿verdad? Y, sin embargo, es a la vez una antigua leyenda griega trasladada al siglo XXI. Cuando en la NASA eligieron el nombre del satélite, no lo podrían haber hecho mejor. A continuación os explico por qué.

Imagen 2. Recreación artística de Juno orbitando alrededor de Júpiter. Fuente: NASA
Al igual que Júpiter es el más grande de todos los planetas del sistema solar, el dios homónimo era el más poderoso entre los de su especie para los romanos. Éstos, en otra demostración de pragmatismo, habían tomado sus dioses del panteón griego donde Júpiter se conocía como Zeus. Así, aunque directamente el nombre provenga del latín, el legado es más bien heleno (como diría Javier Reverte y, antes que él, Percy Bysshe Shelley: todos somos griegos). Júpiter no sólo era el rey de los cielos, también era un auténtico mujeriego y no perdía oportunidad de mancillar a cualquier mortal, ninfa o diosa que se le pusiese en el camino (de eso ya os hablé aquí). De hecho, en un “poético” acto de nomenclatura que comenzó en el siglo XVII con los satélites galileanos (Calisto, Ío, Europa y Ganimedes), las lunas de Júpiter llevan nombres de sus amantes. Algo que supuso un problema cuando, al nombrar la número treinta y tres, las amantes se agotaron. Entonces se recurrió a su progenie que, como podéis imaginar, también era abundante si tenemos en cuenta que el machote del Olimpo siempre dejaba encinta a su pareja. Y mirad por donde, mientras escribo estas líneas se anuncia el descubrimiento de dos nuevas lunas jovianas, para un total de 69. ¡A este ritmo nos vamos a quedar sin nombres mitológicos!
Volviendo a las aventuras amorosas de Júpiter, hay que decir que el dios contaba con un impedimento considerable: estaba casado. Y os podéis imaginar que a su consorte no le hacían mucha gracia sus correrías, así que siempre estaba atenta para evitar otra infidelidad y, de paso, castigar a la desdichada víctima de su marido. Efectivamente, la esposa (y hermana) se llamaba Juno. Puesto que los amoríos de Zeus son una de las representaciones más habituales en la Historia del Arte, podemos encontrar numerosas obras en las que la divina pareja es representada. Me gustaría destacar por encima de todas la que os enseño en la Imagen 3: un colosal óleo realizado por Dominique Ingres, uno de los grandes pintores franceses del XIX. Ahí podemos ver al majestuoso dios, sentado en su trono en una representación iconográfica impecable (el águila, el cetro, las nubes…). Quizás os resulte familiar por este retrato de Napoleón. A sus pies la diosa Tetis que, en contra de lo que pueda parecer, no está intentando seducir al divino ser. Simplemente implora por la vida de su hijo Aquiles en la batalla de Troya, una escena descrita en la Ilíada que Ingres tomó prestada de la obra de Homero. ¿Y dónde está Juno? Pues allí, a la izquierda, entre las nubes, vigilando la escena. 200 años antes de que un satélite con su nombre posase la mirada sobre el otro Júpiter.

Imagen 3. Júpiter y Tetis (324×260 cm) de Dominique Ingres (1811). Fuente: Wikimedia
Pero aquí no acaba el parecido entre Juno “satélite” y Juno “diosa”. Una de las aventuras más conocidas de Zeus cuenta cómo, para yacer con la sacerdotisa Ío sin que nadie se enterase, el dios tomó forma de nube (en la Imagen 4 podéis ver la interpretación que hizo Correggio). Ahora bien, Hera difícilmente se dejaba engañar y fue capaz de ver entre las nubes la fechoría de su marido. Zeus se encontró en un callejón sin salida y tuvo que transformar a Ío en ternera para salvar su vida. Como veis, no se puede elegir mejor nombre para un satélite que pretende explorar entre las nubes de un planeta gaseoso.

Imagen 4. Júpiter e Ío (164×74 cm) de Correggio (1531-32). Fuente: Wikimedia
Siguiendo con las nubes, en la primera imagen os mostraba una foto de la superficie joviana. Esas manchas que forman caprichosas formas pueden estar compuestas de amoniaco o de agua. En la imagen 5 podéis disfrutar de una vista más espectacular si cabe. Eso que contempláis es el polo sur del planeta.

Imagen 5. El polo sur de Júpiter, capturado por Juno a una distancia de 52000 km. Fuente: NASA
¿No os parece una auténtica maravilla? ¿No os recuerdan esas ondulaciones a las pinceladas de van Gogh en la noche estrellada (Imagen 6)? Si os soy sincero no soy el primero al que se le ha pasado por la cabeza.

Imagen 6. Un detalle del polo sur de Júpiter y otro de la noche estrellada de Vincent van Gogh (1889). Fuente: Wikimedia
Decíamos que el agua o el amoniaco pueden ser los principales componentes de esos cúmulos tan llamativos. Y es que, si bien Júpiter es un portento en tamaño, su composición química es extremadamente simple (hasta donde sabemos). Al igual que el Sol, está compuesto por una gran cantidad de hidrógeno y helio (los dos elementos químicos más pequeños) a la que se le suman los compuestos que ya hemos mencionado. El amoniaco (NH3), aunque un poco más complejo, es también muy simple, ya que está formado por un átomo de nitrógeno y tres de hidrógeno.
Al leer el nombre es posible que vuestra primera reacción haya sido asociarlo al producto de limpieza que tan desagradable olor desprende (hay que aclarar que la fórmula comercial es una disolución acuosa, ya que el amoniaco se encuentra en forma gaseosa a temperatura ambiente). Ahora bien, más allá de su mal olor, esta sustancia puede deparar alguna sorpresa agradable para otro de nuestros sentidos: la vista.
En la Imagen 7 os muestro un par de ejemplos. En una de las fotografías tenemos dos tubos de ensayo con disoluciones diferentes. El de la derecha contiene cobre disuelto (en forma de Cu2+) y es de una tonalidad azul clara. Si encima de ese líquido añadimos una disolución de amoniaco (que no tiene color) se forma el compuesto de la izquierda, un “complejo” de un color azul intenso. Más allá de para la formación de disoluciones de colores llamativos, el amoniaco se ha usado históricamente para la obtención de numerosos pigmentos como el verdigris e incluso juega un papel importante en la composición de alguno de ellos como el violeta de manganeso (NH4MnP2O7) que podéis ver en la otra parte de la imagen.

Imagen 7. (A) Tubos de ensayo que contienen un complejo cobre-amoniaco (izquierda) y una disolución de cobre (Cu2+). (B) Un frasco con violeta de manganeso. Fuentes: Royal Society of Chemistry y Wikimedia Commons
Y, para acabar, quería hacer una referencia sobre la etimología del amoniaco. Según parece, el nombre deriva del dios egipcio Amón cerca de cuyo templo en Libia los romanos obtenían una sal que contiene amoniaco (cloruro amónico). ¿Y sabéis qué es lo más curioso? Amón era el dios principal de los egipcios (aunque esto dependía del periodo y de la ciudad) y de ahí que los romanos lo asociaran a Júpiter. Por lo tanto, el mencionado templo estaba también dedicado a Júpiter, quien posteriormente dio el nombre a un planeta cubierto de amoniaco. Y así se cerró este particular círculo de química, astronomía y mitología.
Un último espectáculo visual
No me gustaría finalizar este artículo sin mostraros un vídeo en el que el artista Garip Ay hace una recreación de la noche estrellada sobre… ¡agua! No os lo perdáis.
Para saber más:
Daniel Torregrosa: La influencia de la mitología en la ciencia (37ª Parte): Juno en Ese Punto Azul Pálido.
Daniel Marín: Descubriendo el interior de Júpiter: primeros resultados científicos de Juno en Eureka (Naukas).
Sobre el autor: Oskar González es profesor en la facultad de Ciencia y Tecnología y en la facultad de Bellas Artes de la UPV/EHU.
El artículo Juno, Júpiter, arte y amoniaco se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Arte & Ciencia: Cómo descubrir secretos que esconden las obras de arte

El arte y la ciencia son dos formas de conocimiento aparentemente alejadas, en gran medida consecuencia de la especialización profesional y la educación compartimentada. Del estudio de esta impostada separación surgió el estereotipo de las dos culturas, las ciencias y las humanidades, para referirnos a esa brecha de conocimiento. La realidad es que la ciencia y el arte sí están conectadas y que ninguna forma de conocimiento es impermeable a otra. Por poner algunos ejemplos: ¿Cómo podría crearse una obra plástica sin las técnicas propiciadas por la ciencia? ¿Cómo podríamos interpretar la elección de materiales?
Estas y otras cuestiones relacionadas furon tratadas por destacados profesionales -artistas, ilustradores, filósofos y científicos- que han puesto el foco en ese difuso trazo que une la ciencia y el arte. El ciclo Ciencia & Arte se desarrolló, bajo la dirección de Deborah García Bello, a lo largo de cuatro jornadas que se celebraron los jueves días 6 y 27 de abril y 11 y 25 de mayo de 2017 en el auditorio del Museo Guggeheim Bilbao.
Esta actividad de la Cátedra de Cultura Científica de la UPV/EHU se enmarca en el programa TopARTE que conmemora el XX Aniversario del Museo Guggenheim Bilbao.

Primera jornada. 3ª conferencia
Oskar González Mendia, profesor en la facultad de Ciencia y Tecnología y en la facultad de Bellas Artes de la UPV/EHU: Cómo descubrir secretos que esconden las obras de arte
Las ciencias experimentales juegan un papel esencial en el análisis, tratamiento y conservación de las obras de arte. Estos procesos nos ofrecen, además, información valiosa sobre el contenido de la obra y las circunstancias en las que fue creada. Ciencia y arte tienen una relación mucho más íntima de lo que imaginamos, ya que el conocimiento científico es una herramienta imprescindible para artistas, restauradores y analistas. Les permite conocer las cualidades de los materiales para optar por unos u otros, prever cómo se degradarán los pigmentos o determinar la mejor manera para conservar una escultura.
Cómo descubrir secretos que esconden las obras de arteEdición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Arte & Ciencia: Cómo descubrir secretos que esconden las obras de arte se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Arte & Ciencia: Conservación de obras con componentes tecnológicos
- Arte & Ciencia: La importancia de la ciencia para la conservación del arte
- Ciencia, naturaleza y arte: la química y sus metáforas, por Fernando Cossío
Catástrofe Ultravioleta #17 BABEL

Catástrofe Ultravioleta #17 BABEL
La mitad de las lenguas que existen en nuestro planeta están en riesgo de desaparecer. En este capítulo de Catástrofe Ultravioleta descubriremos nuevas formas de ver el mundo a través de lenguas que estamos perdiendo.
Imagina encontrar al último hablante de la lengua mamuju en una boda en Nueva York, recuperar el lenguaje de una tribu del Amazonas gracias al loro que sobrevivió a su desaparición o registrar las últimas palabras de una lengua india de Nuevo México charlando con la última hablante viva. Cada día, lingüistas de todo el mundo luchan a contrarreloj para salvar centenares de lenguas de las que apenas quedan unos pocos hablantes. La UNESCO advierte de que más de la mitad de las 6.000 lenguas que se hablan en el planeta están en riesgo de desaparecer. ¿Quieres saber por qué es importante que no desaparezcan? Pues abre bien las orejas.
Agradecimientos: Eugenio Daria y al cabildo de La Gomera por el silbo; a Daniel Kaufman, la Endangered Language Alliance y Wikitongues por sus grabaciones; a Fernando Nava, Blanca y Miguel Gotor por sus testimonios; a Douglas, Marco, Vanderlei y Neiva por las cuñas en portugués y tupi; a Celine, Ray Jaén, Ana González y Stephen Hughes por las voces. Y, por supuesto, ¡a Alexander von Humboldt por sus palabras!
* Catástrofe Ultravioleta es un proyecto realizado por Javier Peláez (@Irreductible) y Antonio Martínez Ron (@aberron) con el apoyo de la Cátedra de Cultura Científica de la Universidad del País Vasco y la Fundación Euskampus. La edición, música y ambientación obra de Javi Álvarez y han sido compuestas expresamente para cada capítulo.
Puedes conocernos en nuestra web: Catastrofeultravioleta.com y seguirnos en el twitter Catastrofe_UV. También puedes encontrar todos los capítulos en este enlace.
El artículo Catástrofe Ultravioleta #17 BABEL se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Preparados para una Catástrofe Ultravioleta
- Catástrofe Ultravioleta #13 LEVIATÁN
- Catástrofe Ultravioleta #14 VULCANO
ADN basura: negacionismo y malentendidos (con cebolla) Primera parte

Los lectores de noticias científicas probablemente os habréis encontrado más de una vez una historia que puede resumirse así:
“Descubren algo interesante en la región del genoma que hasta hace poco se consideraba basura”
Ese algo interesante puede consistir en secuencias que determinan el desarrollo del cerebro o la forma de nuestra cara, un gen clave para la celiaquía, un trocito de ADN que determina la evolución del cáncer, otro que permitirá curar la diabetes… todo tipo de maravillas, halladas gracias a que a alguien se le ocurrió buscar en lo que sus poco espabilados colegas creían un vertedero genético.
El mito del tesoro en el vertedero
El concepto ADN basura lleva muchos años divulgándose y enseñándose como si se tratase de un error surgido directamente de la arrogancia de los científicos. Un error que ahora, gracias a nuevos hallazgos y a un cambio de mentalidad, se estaría corrigiendo.
El mito dice así: Cuando los científicos empezaron a leer el genoma humano comprobaron que solo una minúscula parte consiste en ADN codificante, es decir, en genes con información para sintetizar proteínas. El resto del ADN, ¿para qué sirve? ¿Qué hace ahí? No lo sabían. Y, como no lo sabían, decidieron que se trataba de ADN inútil. Que estaba ahí simplemente porque no hacía daño. Que era chatarra. Y así quedó establecido como ortodoxia durante un tiempo vergonzosamente largo. Hasta que, por fin, las nuevas investigaciones comprobaron que esa gran cantidad de ADN no codificante tiene papeles cruciales.
El mito tiene variantes y oscila entre dos extremos:
1.- El ADN no codificante, “antes considerado basura” contiene algunos tesoros genéticos.
2.- El mal llamado ADN basura es todo él un tesoro genético.
Es una narración atractiva. Enfrenta de un modo más o menos explícito a unos “malos”: científicos anticuados, engreídos y sin imaginación, con unos “buenos”: científicos modernos, abiertos de mente y humildes ante la magnificencia de la naturaleza. Ésta nos habría dado una lección de modestia: aquello que creíamos que era absurdo porque no comprendíamos, en realidad tendría perfecto sentido.
Incontables noticias en los periódicos, blogs, libros de divulgación y abstracts de trabajos científicos reproducen el mencionado esquema año tras año. Profesores de biología de todo el mundo, en institutos y universidades, están enseñando a sus alumnos que el ADN basura es una hipótesis fallida.
Quizá debido a la compartimentación del saber, a una no siempre buena comunicación entre expertos de distintas especialidades, y a malentendidos habituales sobre la evolución, el negacionismo del ADN basura está muy extendido entre biólogos y bioquímicos. A menudo lo expresan con argumentos que harían alzar las cejas a cualquier iniciado en biología evolutiva:
“si este ADN ha llegado hasta nuestros días es que debe tener alguna función”.
El mismísimo Francis Collins, prestigioso genetista que dirigió el Proyecto Genoma Humano y luego los Institutos Nacionales de Salud estadounidenses, se ha revelado también como un negacionista del ADN basura: “Ya no usamos más esa expresión. Fue en gran medida un caso de arrogancia eso de imaginar que podríamos prescindir de alguna parte del genoma, como si supiéramos lo bastante para afirmar que no era funcional”.
Collins es un creyente cristiano, pero no es un creacionista. Quienes rechazan la evolución desde posturas religiosas no pueden aceptar que el diseñador inteligente que supuestamente nos creó haya metido tal cantidad de morralla en nuestros núcleos celulares. Una buena proporción de los textos que atacan al ADN basura procede de las organizaciones creacionistas. ¡Lo odian! Un genoma repleto de secuencias inútiles es prueba de que los seres vivos han ido cambiando mediante procesos ciegos, inconscientes, naturales. Siempre que un equipo científico ha encontrado algo interesante en una región del genoma “anteriormente considerada basura”, los creacionistas lo han celebrado como un golpe más en la cara de Darwin.
El Proyecto ENCODE
El “meme” del ADN basura como concepto erróneo y obsoleto alcanzó su apogeo en 2012, en lo que debería ser recordado como una de las mayores catástrofes de la comunicación científica. Ese año, con gran bombo, el Consorcio del Proyecto ENCODE (Encyclopaedia of DNA Elements) publicó simultáneamente treinta trabajos sobre el genoma humano. Más del 80% de éste, según hallaron, tenía “funciones bioquímicas”.
Se gastaron unos 400 millones de dólares. Espléndidos materiales divulgativos fueron producidos al mismo tiempo que se preparaban los papers científicos. La revista Nature lanzó un portal dedicado a ENCODE. En este vídeo de dibujos animados, narrado por el comediante y activista del pensamiento crítico Tim Minchin, ENCODE aparece representado como un robot gigante que, entre otras proezas, lucha contra el cáncer. ENCODE, explica el vídeo, “es un mapa que revela que el genoma entero es una jungla de ruidosa actividad, incluso las partes que solíamos considerar chatarra; no solo los genes sino también las instrucciones que les dicen qué hacer y cuándo”.
Hubo profusión de entrevistas a los científicos que habían participado en ENCODE. Ewan Birney, uno de los líderes, afirmó que ese 80% del genoma con función se convertiría probablemente en el 100% una vez avanzaran los estudios, y añadió: “Realmente no tenemos ninguna gran porción de ADN redundante. Esta metáfora del ADN basura no es tan útil”.
Roderic Guigó, coordinador del programa Bioinformática y Genómica del Centro de Regulación Genómica, dijo: “Hemos visto que partes del genoma que considerábamos ADN basura, sin utilidad, son en realidad muy importantes. Identificamos en estas secuencias unos 4 millones de interruptores de genes, es decir, de regiones reguladoras.”
¡Cuatro millones! Varios medios publicaron que El ADN antes conocido como basura era, en realidad, un gigantesco panel de control, un sistema operativo de la célula. Los titulares fueron sensacionales:
El ADN basura, demolido (The Wall Street Journal)
El estudio Encode desacredita la teoría del “ADN basura” (The Independent)
El ADN basura es esencial para el genoma humano (ABC)
El Proyecto Encode escribe una elegía para el ADN basura (Science)
No existe el ADN basura (QUO)
Pero el ADN basura sí existe y está presente en cantidades ingentes en los genomas de la mayoría de las especies vivas. La evidencia científica a su favor es aplastante y procede de múltiples ramas de la biología. Su negacionismo es una combinación de malentendidos, exageraciones, falsa modestia, ceguera ideológica y adanismo.
¿Cómo desmontar este titánico mito construido y defendido por investigadores de incuestionable valía, las mejores revistas científicas, un multimillonario proyecto genómico internacional, profesores, periodistas, divulgadores… y, además, por si fuera poco, la estrafalaria ayuda de los creacionistas? Parece una tarea imposible. Ante tan gargantuesco y multicéfalo rival parece que solo cabe rendirse. Quizá aquí debería acabarse este artículo. Pero no; queda mucho todavía.
Muchos investigadores, por supuesto, han salido en defensa del ADN basura. Algunos de los más activos y visibles son el experto en genómica T. Ryan Gregory, el vitriólico biólogo evolutivo Dan Graur, el bioquímico Laurence A. Moran, el biólogo del desarrollo y conocido bloguero PZ Myers o el biólogo molecular y computacional Sean Eddy. Las críticas al proyecto ENCODE llegaron también a las revistas científicas en forma de diversos papers, algunos muy interesantes por su carácter divulgativo. Con la ayuda de estos científicos, comenzamos el combate dividiendo al adversario en seis malentendidos o errores principales.
El ADN basura no surge de la ignorancia
El primer malentendido en esta historia es la leyenda según la cual el ADN basura fue un parche, una solución torpe que dieron los científicos cuando descubrieron una montonera de ADN extraño y no supieron para qué servía.
En realidad, el ADN basura fue una predicción basada en los límites de la selección natural y calculada mediante las matemáticas de la genética de poblaciones. Su origen es bastante anterior al comienzo de la era genómica. Como tal predicción, se fue cumpliendo a medida que se fueron secuenciando genomas de todo tipo de especies.
La selección natural hace muchas cosas. Adapta a las poblaciones al medio, las separa y modifica hasta producir nuevas especies, estructuras, órganos, instintos… Éste es el papel constructor o creativo de la selección natural. Lo lleva a cabo con la colaboración imprescindible de las mutaciones y con la participación de otros mecanismos evolutivos. Es su aspecto peor comprendido por los no expertos y el más atacado por los “antidarwinistas”. Pero no es el que nos interesa ahora.
El que ahora toca es el papel conservador de la selección natural, mucho más intuitivo, fácil de comprender y menos polémico. La selección natural conserva las funciones biológicas y evita que los genomas degeneren fatalmente por acumulación de errores aleatorios que suceden constantemente.
Todos somos mutantes; cada uno de nosotros nace con nuevas mutaciones que, cuando afectan un gen, pueden estropearlo, deteriorando su función o anulándola por completo. Además, todos heredamos de nuestros padres un conjunto distinto de alelos (variantes de un mismo gen) estropeados que nos pueden provocar desde nada (ningún efecto detectable) hasta pequeñas molestias o desventajas, enfermedades serias o incluso la muerte prematura. Cada población de seres vivos soporta una carga mutacional que, en ocasiones, llega a resultar fatídica.
Pero, en general, los genes se mantienen buen estado. Lo que los conserva no es magia arcana; simplemente, los individuos que tienen genes menos estropeados suelen reproducirse más que aquellos que tienen los genes más estropeados. Eso hace que, en cada generación, parte de las variantes defectuosas desaparecen de las poblaciones. Sin la selección purificadora (así se llama), la información de los genomas degeneraría a lo largo de las generaciones. Los organismos nacerían cada vez menos aptos y, finalmente, la vida se extinguiría por completo.
Los límites de la selección natural
Pero la selección purificadora no es un espectro inteligente (con la cara de Charles Darwin) que detecta cualquier pequeño error en el mundo y lo elimina ipso facto. Tiene limitaciones que los especialistas conocen y calculan. La capacidad de la selección natural para limpiar los genomas depende de factores como el tamaño de las poblaciones, sus oscilaciones o su diversidad. Sin una buena formación en teoría evolutiva, tendemos a considerar que la selección es omnipotente. En general, funciona de forma mucho menos eficaz de lo que creemos.
Nuestro genoma es larguísimo. Si todo él, enterito, tuviera funciones biológicas cruciales, la selección natural tendría que haber estado protegiendo y conservando varios millones de secuencias útiles distintas. Y no puede hacerlo.
Los genetistas de poblaciones, teniendo en cuenta lo que saben sobre las tasas de mutación, los tamaños habituales de los genes, la recombinación, el censo efectivo de las poblaciones, etc., comprueban que tal hipótesis es inviable. Una selección natural tan eficaz habría requerido que cada humano tuviera una cantidad astronómica de hijos (los números, en este trabajo de Graur). Millones de hijos que luego, casi todos, a causa de pequeños defectos, tendrían que haber muerto sin descendencia. Esto habría que aplicarlo al resto de animales, plantas y microorganismos de la Tierra. No cabríamos en en el Sistema Solar.
Por tanto, en el mundo real existe un límite en el número de loci (genes en sentido amplio), que la selección natural puede conservar. En 1970 ya se había estimado que el número total de genes humanos sería como mucho de unos 30.000. Esta cantidad era asombrosamente pequeña para el pensamiento de la época. Hoy en día, sin embargo, parece muy acertada.
Susumu Ohno es citado a menudo como el padre del ADN basura (aunque la historia es más complicada). Dedujo en 1972 que esos treinta mil loci útiles incluirían tanto los genes típicos que codifican proteínas como sus posibles regiones reguladoras. El ADN esencial (útil) representaría aproximadamente el 6% de nuestro genoma. El resto, más de un 90% del genoma, no puede estar siendo conservado por la selección natural y, por tanto, carece de función. El ADN basura fue deducido mediante una teoría científica sólida, no inventado a la desesperada para tapar un misterio. Surgió del conocimiento, no a partir de la ignorancia.
(continuará en la segunda parte, donde por fin aparecerá la cebolla)
Este post ha sido realizado por @Paleofreak y es una colaboración de Naukas con la Cátedra de Cultura Científica de la UPV/EHU.
El artículo ADN basura: negacionismo y malentendidos (con cebolla) Primera parte se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El libro preferido del profesor (primera parte)
- El rombododecaedro estrellado: arte, abejas y puzzles (primera parte)
- Océanos nucleares. Cuando la basura llega antes que el ser humano
Tres historias italianas: vacunas, homeopatía, niños y derechos humanos
Mikel Mancisidor
Les voy a contar tres historias que nos llegan desde Italia. Luego reflexionaré sobre algunos aspectos que tienen que ver con los Derechos Humanos. Confío en que, como por definición todo lo relativo a los Derechos Humanos tiene vocación universal, estas ideas resulten válidas también para nuestro país o cualquier otro.
La primera historia es muy reciente y seguramente la conocen ustedes. Un niño de 7 años entró en el hospital de Urbino ya en estado de coma tras haber sufrido grandes dolores durante días. Poco después murió sin que los médicos pudieran hacer nada por salvar su vida. Sus padres habían decidido tratar la otitis que sufría el niño con homeopatía. La infección avanzó sin que la homeopatía pudiera evitarlo y afectó al cerebro hasta causarle la muerte.
También en Italia se dio un caso parecido hace unos pocos años. Luca, un niño de 4 años, ingresó ya muerto, tras 7 de días de diarreas, toses y fiebre, debido a una “neumonía intersticial y bacteriana, complicada por una infección de hongos patógenos”. Sus padres decidieron no enviar al niño a su pediatra y lo trataron en casa con homeopatía e infusiones de hinojo. Su padre, por cierto, es médico y se anuncia como homeópata y terapeuta. Los médicos que recibieron el cuerpo del niño dijeron que sufría grave desnutrición, problemas estomacales graves y costras en varias partes del cuerpo. “Al verle inmediatamente pensamos en las imágenes que se ven en la televisión cuando las grandes hambrunas africanas”, dijo ante el juez uno de los médicos. Sí, aunque resulte difícil de creer, esto sucedió en la Italia del siglo XXI, en una familia de recursos medio-altos, con padres titulados superiores y en un entorno con sobradas posibilidades de acceso a la mejor alimentación, a la mejor sanidad y a la mejor información.
Y no salimos de Italia, pero pasamos de homeopatía a los movimientos antivacunas. Una nueva ley que entrará en vigor en breve permitirá obligar a los padres a vacunar a sus hijos. En caso de que no lo hagan podrán ser sancionados con altas multas e incluso en casos extremos con la pérdida de la patria potestad. Otros países europeos cuentan con normas similares. Y es que la decisión de no vacunar a un niño puede llevar a su muerte (¿recuerdan el caso de Olot?) y además pone en peligro avances generales como la reducción de enfermedades y la progresiva erradicación de alguna de ellas.
Aclaro de entrada que no quiero hablarles aquí de homeopatía o de vacunación, puesto que poco sé de medicina y hay muchos expertos que colaboran en este Cuaderno que pueden hacerlo mucho mejor. Pero trataré de hacer algún comentario desde una perspectiva de Derechos Humanos.
Las cuestiones que queremos responder en este artículo pueden formularse así: ¿puede el estado obligar a los padres a vacunar contra su voluntad a los niños?, ¿puede el estado intervenir en caso de que los padres no estén dando a sus hijos la mejor asistencia médica disponible?, ¿se vulnera el derecho de los padres a elegir por sus hijos?, ¿tiene límites este derecho de los padres?
Estos días en redes sociales se han podido leer al respecto cosas como ésta: “la obligación de vacunar vulnera el derecho a la libertad personal, la integridad física y la intimidad personal. Debe prevalecer el derecho a no vacunarse y que tal decisión sea tomada por los padres, que en definitiva tienen la obligación de velar por la salud y educación de sus hijos.”
¿Atenta de verdad una obligación de vacunar contra esos derechos de libertad, integridad física e intimidad personal?, ¿pueden los poderes públicos entrometerse e incluso corregir esa decisión de los padres?
El Derecho Internacional de los Derechos Humanos se ha topado con asuntos de este tipo con frecuencia y su respuesta es clara. Para empezar tanto la Declaración Universal, de 1948, como el Pacto de Derechos Económicos, Sociales y Culturales, de 1996, (del cual tanto Italia como España, junto a otros 162 estados, son parte) reconoce el Derecho a la Salud en los siguientes términos: se “reconoce el derecho de toda persona al disfrute del más alto nivel posible de salud física y mental”. Llamo la atención sobre el hecho de que el derecho no es a disfrutar del nivel de salud que los padres, tutores u otros consideren mejor para un menor, sino al “más alto posible nivel posible”.
Por medio del Pacto de Derechos del Niño, de 1989, del que obviamente tanto Italia como España son parte, “los Estados Partes reconocen el derecho del niño al disfrute del más alto nivel posible de salud y a servicios para el tratamiento de las enfermedades y la rehabilitación de la salud. Los Estados Partes se esforzarán por asegurar que ningún niño sea privado de su derecho al disfrute de esos servicios sanitarios. Los Estados Partes asegurarán la plena aplicación de este derecho y, en particular, adoptarán las medidas apropiadas (…) para asegurar que todos los sectores de la sociedad, y en particular los padres y los niños, conozcan los principios básicos de la salud y la nutrición de los niños (…), tengan acceso a la educación pertinente y reciban apoyo en la aplicación de esos conocimientos”. Este Tratado es muy explícito al afirmar que “los Estados Partes adoptarán todas las medidas eficaces y apropiadas posibles para abolir las prácticas tradicionales que sean perjudiciales para la salud de los niños”.
En los conflictos que involucran a niños se aplica el conocido como principio del interés superior del niño. Se expresa así en el citado tratado: “en todas las medidas concernientes a los niños que tomen las instituciones públicas o privadas de bienestar social, los tribunales, las autoridades administrativas o legislativas, una consideración primordial será el interés superior del niño”. Además “los estados se comprometen a asegurar al niño la protección y el cuidado que sean necesarios para su bienestar, teniendo en cuenta los derechos y deberes de sus padres”. Es decir, lo primero es el derecho de los niños, su interés superior, en este caso la salud, y luego el papel de los padres, que se expresa como derecho, cierto, pero también como deber.
El Comité de Derechos del Niño “exhorta a los Estados a que sitúen el interés superior del niño en el centro de todas las decisiones que afecten a su salud y su desarrollo”. Este “interés superior del niño deberá (…) contribuir a la solución de los conflictos de intereses entre padres y trabajadores sanitarios. El Comité recalca la importancia del interés superior del niño como fundamento de todas las decisiones que se adopten con respecto al tratamiento que se dispense, niegue o suspenda a todos los niños.” (Comentario General N.º 15 del Comité de Derecho del Niño).
¿Cuál es entonces este espacio de decisión de los padres? Compare usted con lo que ya sabemos sobre el Derecho a la Educación y a libertad de elección de los padres. Se permite ciertamente que los padres elijan el tipo de educación que quieren para sus hijos: privada o pública, religiosa o laica, con más o menos deporte, arte o innovación pedagógica, con distintos tipos de equilibrio o diversidad lingüística. Pero el derecho de los padres a elegir no puede vulnerar el de los niños a acceder a una educación de calidad que incluya los contenidos mínimos que “el estado prescriba”. El derecho de elegir en educación no incluye un derecho a no educar o a educar por debajo de unos contenidos mínimos o a educar en fantasías, mitos y falsedades. Lo mismo puede predicarse en relación a la salud. Los padres podrán elegir distintos tipos de prestaciones o tratamientos médicos posibles, pero siempre que puedan ser considerados como equivalentes al “más alto nivel posible” no por cualquiera, sino tras un escrutinio profesional científicamente fundado, ajeno a mitos, tradiciones y creencias.
Al Estado le toca “adoptar todas las medidas eficaces y apropiadas posibles para abolir las prácticas tradicionales que sean perjudiciales para la salud de los niños”, como queda dicho. Y es que el estado tiene la obligación de proteger al niño frete a terceros, incluidos sus propios padres cuando corresponda. El estado, de esta forma, podría incumplir sus obligación y llegar a violar los derechos humanos del menor cuando no le protege a los “contra las violaciones del derecho a la salud por terceros”, como, por ejemplo, al no evitar “la observancia de prácticas médicas perjudiciales” (Comentario General N.º 17 del Comité de Derechos, Económicos, Sociales y Culturales – DESC).
Estos asuntos están llegando ya a los órganos de Derechos Humanos de la ONU que empiezan a examinar casos donde la ausencia de vacunación ya no se debe, como por desgracia aún sucede en ocasiones, a la pobreza, la falta de medios o la falta de voluntad del estado, sino a la negativa de los padres. Este mismo mes de Junio el Comité DESC ha tratado el asunto, por ejemplo, con Uruguay pidiéndole que asegure la vacunación de acuerdo a los criterios establecidos por el Ministerio de Salud y la Organización Mundial de la Salud.
Como vemos el derecho de los padres a elegir no es ilimitado. Puede y, en ocasiones, debe ser supervisado e incluso corregido por los poderes públicos. Esta imposición de la ley italiana, por lo tanto, no es pues una violación de ningún derecho a la integridad, intimidad o libertad, ni de padres ni de niños. Todo lo contrario: es una exigencia muy sólidamente fundada en el Derecho Internacional de los Derechos Humanos.
Sobre el autor: Mikel Mancisidor es miembro del Comité de Derechos Económicos, Sociales y Culturales de la ONU y Adjunct Professor of International Human Rights Law, Washington College of Law, American University (Washington D. C.)
El artículo Tres historias italianas: vacunas, homeopatía, niños y derechos humanos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Dudas sobre las vacunas: problemas y soluciones
- La ciencia y los objetivos del milenio (y VIII): El papel de la ciencia en la extensión de la democracia y los derechos humanos
- Homeopatía y dosis
Azúcar moreno, ¿mejor que el azúcar blanco?

Sabemos que un consumo excesivo de azúcar incrementa el riesgo de padecer enfermedades como diabetes, obesidad y, en consecuencia, cardiopatías. Estos son los principales motivos por los que la Organización Mundial de la Salud recomienda consumir un máximo de 25 g de azúcar al día.
Alcanzar esta cifra es más sencillo de lo que parece, ya que además del azúcar que añadimos al café o a las infusiones, consumimos azúcar añadido en multitud de alimentos. Para algunos, todo esto ha provocado mayor conciencia del azúcar que tomamos y hemos optado por minimizar su consumo y, en algunos casos, sustituirlo por opciones en principio más saludables. Es común que entre estas opciones se encuentre el azúcar moreno como sustituto.
Analicemos si sustituir el azúcar blanco por azúcar moreno es una buena elección.
-
Tipos de azúcar
El azúcar de cualquier tipo, sea blanco o moreno, está constituido principalmente por una sustancia denominada sacarosa. La sacarosa se extrae de dos fuentes: la remolacha azucarera o la caña de azúcar. En los climas cálidos se opta por la caña y en los climas templados por la remolacha. En el sudeste asiático, donde ya se utilizaba azúcar desde hace miles de años, se extrae de la caña; pero en España, por razones climáticas, se obtiene de la remolacha.
En la legislación podemos distinguir dos grandes grupos atendiendo a su composición: azúcar blanco y azúcar moreno. La distinción esencial se hace en función de la cantidad de sacarosa que contienen. El azúcar moreno tiene una pureza media del 85% y el blanco del 95%. Las denominaciones «azúcar natural» o «azúcar integral» no están recogidas en la legislación, sino que se trata de denominaciones coloquiales o publicitarias para denominar al azúcar moreno.
Existen otras denominaciones para el azúcar que hacen referencia a la presentación del producto, además de a su composición. Por ejemplo, el azúcar candi que está tan de moda, se presenta en forma de bloques amorfos. Se hace alargando el proceso de cristalización, añadiendo agua y prensándolo en moldes. Puede estar hecho con azúcar blanco o con azúcar moreno. En cambio, el azúcar glas, que se presenta como azúcar en polvo, de grano muy fino y de color blanco, se hace exclusivamente con azúcar blanco molido.

Azucar candi moreno
-
¿Cómo se produce el azúcar blanco?
El proceso de producción de cualquier tipo de azúcar, sea blanco, moreno, o de cualquier otra denominación, es el mismo en todas las etapas y sólo difiere ligeramente en la última. El proceso es bastante complejo, pero podemos simplificarlo.
Se lava y se trocea la caña o la remolacha y se hace un proceso análogo a una infusión en agua, de forma que se extrae un jugo dulce. Ese jugo contiene una gran cantidad de sacarosa, pero también va acompañado de otras sustancias indeseables que podrían estropearla. Estas sustancias se eliminan añadiendo otros compuestos con los que se combinan fácilmente y terminan depositándose en el fondo del jugo, por lo que se pueden extraer por decantación y filtrado. Gracias a este proceso de separación también se inhibe el crecimiento de bacterias.
Así llegamos a una disolución que es básicamente agua con sacarosa. El agua se evapora -de ahí que las fábricas de azúcar estén envueltas en grandes nubes de vapor de agua- hasta llegar a una disolución saturada. En este punto es donde la sacarosa empieza a formar cristales. Hay una pequeña parte de sacarosa que, por su contenido en agua e impurezas, no llega a cristalizar. Parte de esta sacarosa carameliza hasta volverse amarga y adquirir un color parduzco. Esta fracción es la melaza.
Esta última parte del proceso se repite hasta lograr una separación óptima entre la sacarosa cristalizada y la melaza. La melaza se emplea, entre otras cosas, para producir alcohol etílico.

Melaza
-
Cómo se produce el azúcar moreno
El azúcar moreno se produce de la misma manera que el azúcar blanco, salvo en la etapa final en la que se separa la sacarosa de la melaza. En el azúcar moreno se conserva parte de la melaza. Según la cantidad de melaza que se conserve y la forma de presentación del producto final, podemos distinguir varios tipos (mascabado, turbinado, demerara, etc.) La presencia de más o menos melaza es la responsable de las apreciables diferencias en el aroma y el sabor de los distintos tipos de azúcar moreno. Como la melaza es de color pardo, es la responsable de teñir el azúcar moreno.
Hay dos maneras de producir azúcar moreno: mezclando azúcar blanco con melaza hasta llegar a la proporción deseada, o bien no separar totalmente la sacarosa de la melaza en la última etapa de la producción. Con el modo de mezcla se controlan mejor las proporciones y se reducen costes, ya que es más sencillo fabricar varios tipos de azúcar moreno ajustando las mezclas.
No es cierto que se empleen colorantes para teñir el azúcar, ya que esto no está legalmente permitido. En todos los tipos de azúcar moreno, el color pardo se debe a la melaza. Cuando disolvemos azúcar moreno y éste pierde su color superficial revelando que el interior se asemeja al azúcar blanco, es debido a que es un azúcar moreno producido por mezcla.
-
Diferencias nutricionales entre el azúcar blanco y el azúcar moreno.
Tanto el azúcar blanco como el azúcar moreno aportan 4 kcal por gramo. Estas calorías se denominan «calorías vacías» porque aportan energía, pero no tienen valor desde el punto de vista nutricional. Ambos tipos de azúcar son, esencialmente, sacarosa con una pureza del 85% o más. El pequeño porcentaje restante, que es melaza y agua, contiene una insignificante cantidad de minerales y vitaminas.
La presencia de vitaminas y minerales que porta la melaza del azúcar moreno es lo que suele usarse como razón para sustituir un azúcar por otro. Pero, esta razón no es relevante desde el punto de vista nutricional: la cantidad de minerales o vitaminas que se encuentran en el azúcar moreno es tan baja que, para alcanzar un nivel simbólico para el organismo, habría que consumir mucho más azúcar del recomendado, así que lo que se presenta como virtud, realmente enmascara el verdadero problema: el consumo excesivo de «azúcar libre».
La Organización Mundial de la Salud recomienda no consumir más de 25 g de «azúcar libre» al día. Tanto el azúcar blanco como el azúcar moreno son «azúcar libre».
También hay que tener en cuenta que el azúcar moreno, por su contenido en melaza, que es amarga, tiene un poder edulcorante menor que el azúcar blanco, con lo que resulta tentador utilizar más cantidad para llegar al mismo dulzor. Si a esto le sumamos la errónea convicción de que es más saludable, a muchos no les temblará el pulso y utilizarán más azúcar moreno del que añadirían si se tratase de azúcar blanco.
-
Conclusiones.
No hay diferencias nutricionales relevantes entre el azúcar blanco y el azúcar moreno. Ambos son «azúcar libre» y su consumo según la Organización Mundial de la Salud ha de minimizarse.
Sustituir el azúcar blanco por azúcar moreno perpetúa el problema y, en algunos casos, lo sobredimensiona porque consumimos más, ya que tiene menor poder edulcorante y además es fácil caer en el error de creer que es un sustituto saludable. Si queremos vitaminas y minerales, no los busquemos en el azúcar.
La elección saludable y el esfuerzo que deberíamos hacer, si realmente queremos plantarle cara al problema, es endulzar cada vez menos todo lo que consumimos y comer más productos frescos y menos ultraprocesados, que son los que más azúcar añadido contienen. Si lo logramos, obtendremos una recompensa realmente valiosa: descubrir el auténtico sabor de los alimentos.
Sobre la autora: Déborah García Bello es química y divulgadora científica
El artículo Azúcar moreno, ¿mejor que el azúcar blanco? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El azúcar oculto en los alimentos
- El mejor lacón con grelos tiene su ciencia
- Las constantes de Planck y el caballo blanco de Santiago
Aislantes topológicos en sólidos amorfos
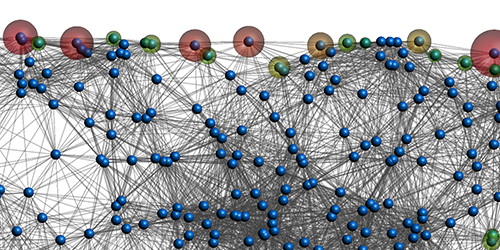
Todos sabemos que hay materiales aislantes de la electricidad y otros que la conducen: en un cable eléctrico el cobre del interior es conductor y la protección plástica exterior es aislante. Sin embargo, existen materiales que son aislantes en su conjunto pero que conducen la electricidad en su superficie, son los llamados aislantes topológicos. Esta característica se debe a unos estados cuánticos muy particulares del material en su superficie. Lo interesante del asunto es que estos estados son robustos frente a defectos y otras imperfecciones, lo que hace que estos materiales se estén investigando intensamente porque son potencialmente útiles en computación cuántica y otras aplicaciones.
Todos los aislantes topológicos conocidos son cristales, es decir estructuras tridimensionales perfectamente ordenadas. Ahora, un nuevo trabajo teórico demuestra que los materiales amorfos, los llamados vidrios, también podrían ser aislantes topológicos. Esto podría dar lugar a la búsqueda de nuevos aislantes topológicos entre en abanico muchísimo más amplio de materiales posibles.
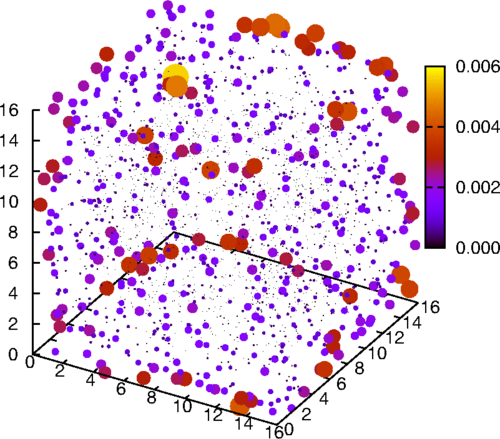
Los aislantes topológicos se caracterizan por ciertas simetrías. Por ejemplo, muchos aislantes topológicos son simétricos frente a la inversión del tiempo, lo que significa que las funciones de onda electrónicas que describen el estado no se ven alteradas por un cambio en la dirección del tiempo. Se dice que estas simetrías “protegen” los estados de la superficie, lo que significa que el sistema no puede cambiar a otro estado sin pasar por un cambio de fase. Actualmente la búsqueda de nuevos aislantes topológicos asume que las simetrías deseadas se generan en una estructura reticular ordenada, pero nada se opone a que estas simetrías aparezcan en un material no cristalino.
Los resultados, de momento una posibilidad teórica, sugieren que los aislantes topológicos podrían hacerse mediante la creación de vidrios con un fuerte acoplamiento espín-órbita o colocando al azar átomos de otros elementos en el interior de un aislante normal. De comprobarse que esto es cierto significará una pequeña revolución en el mundo de los materiales que tendrá un gran impacto en el rendimiento y el coste de los dispositivos del futuro.
Referencia:
Adhip Agarwala and Vijay B. Shenoy (2017) Topological Insulators in Amorphous Systems Physical Review Letters doi: 10.1103/PhysRevLett.118.236402
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Este texto es una colaboración del Cuaderno de Cultura Científica con Next
El artículo Aislantes topológicos en sólidos amorfos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El estaño beta es como el grafeno pero en 3D
- La fusión nuclear como fuente de neutrones eficiente
- El calor no es un fluido
Locura instantánea, un rompecabezas con cubos de colores
Locura instantánea es el nombre de un juego de ingenio de la familia de los solitarios. Es un juego que me gusta mucho, que suelo utilizar en algunas de mis charlas y que incluí en mi libro sobre las matemáticas de los juegos de ingenio, Del ajedrez a los grafos, que es el último libro de la colección El mundo es matemático (National Geographic, 2015). Mencioné este juego de pasada en mi entrada del Cuaderno de Cultura Científica, Blanche Descartes y la cuadratura del cuadrado, pero en aquella ocasión no entramos a analizarlo.

Rompecabezas “Locura instantánea”, formado por los cuatro cubos con caras de colores, junto con la caja para guardar los cubos
El rompecabezas Locura instantánea, nombre con el que fue comercializado por la empresa de juguetes Parker Brothers en 1967 y del que se vendieron más de doce millones, consta de cuatro cubos, cada una de cuyas caras está coloreada con uno de los cuatro colores del juego (en la imagen anterior, rojo, azul, verde y amarillo), siguiendo un patrón determinado, que se muestra más abajo.
El objetivo del solitario es colocar los cuatro cubos, uno encima (o a continuación) del otro, formando una torre (o un prisma rectangular de tamaño 1 x 1 x 4) de manera que cada uno de los cuatro colores aparece exactamente una vez en cada una de las cuatro caras de la torre.
En la página Sources in recreational mathematics, an annotated bibliography, el matemático estadounidense David Singmaster menciona que este juego aparece por primera vez en 1890, patentado por Frederick A. Schossow (con corazones, picas, tréboles y diamantes, en lugar de colores), con el nombre Katzenjammer (que puede traducirse como conmoción, o también, resaca), y que volvería a aparecer a lo largo del siglo XX con diferentes nombres, en los años 1940 con el nombre El gran suplicio de Tántalo, pero también Cubo 4, Cubo diabólico, Cuatro ases, rompecabezas de Symington y muchos otros.

El rompecabezas “Katzenjammer” (conmoción), patentado por Frederick A. Schossow en 1890, en cuyas caras están los cuatro palos del poker, picas, corazones, rombos y tréboles

El “locura instantánea”, fue utilizado bajo el nombre de “rompecabezas de Symington”, para hacer publicidad de los cubitos de sopa de Symington
A continuación, mostramos el esquema plano de la distribución de los colores del juego Locura instantánea (exactamente la distribución de los dados de la primera imagen), al desplegar en el plano los cuatro cubos en sus seis caras.
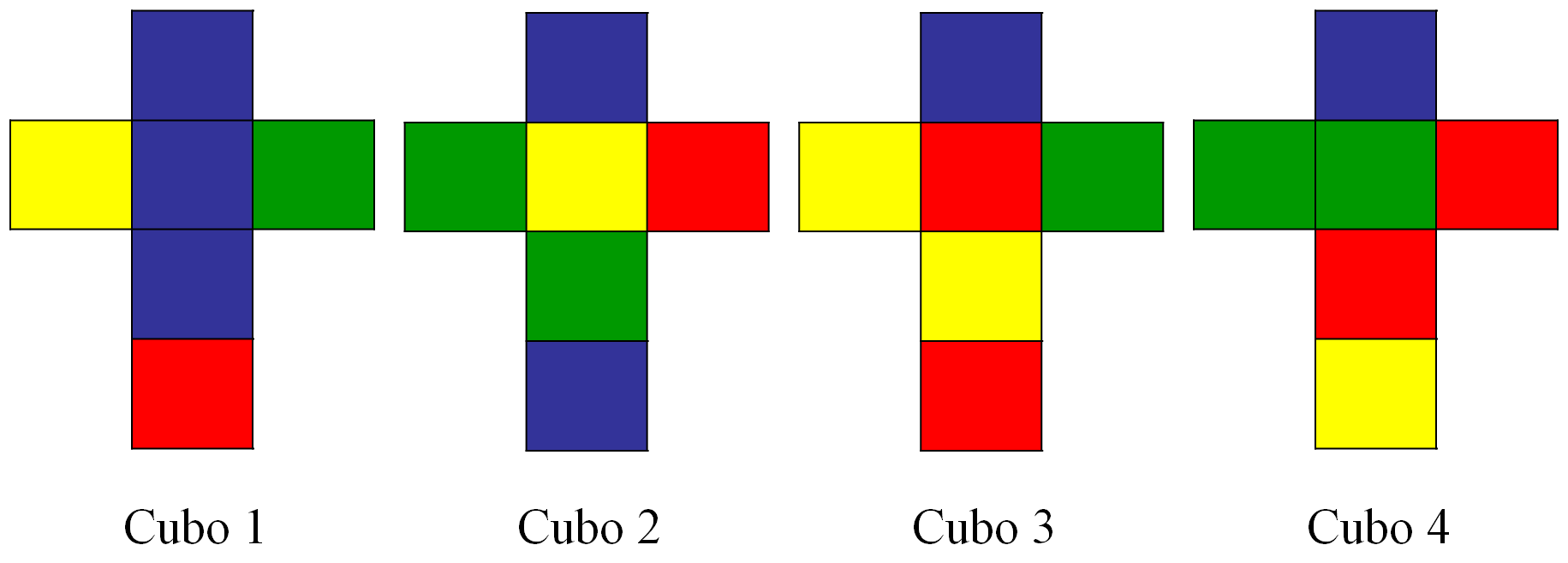
Una primera cuestión que nos podemos plantear en relación a este rompecabezas, antes de ir a lo importante que es jugar y resolver el puzzle, es la siguiente: ¿Cuál es el número de formas distintas (en relación al juego) de colocar los cuatro cubos de colores formando una torre (o una a continuación del otro)? El objetivo del juego es encontrar cual, o cuales, de ellas son una solución del rompecabezas.
Teniendo en cuenta que, de cara a su resolución, lo importante son las cuatro caras de cada cubo que van a quedar en los laterales visibles de la torre, y que es irrelevante el orden de colocación de los cubos, se puede observar que esencialmente hay tres formas distintas de colocar el primer cubo de la torre, dependiendo de cuál de las tres parejas de caras opuestas ocultemos. Y como es la primera pieza en ser colocada, da lo mismo cuál de las dos caras ocultas vaya arriba y cuál abajo.
Una vez colocado el primer cubo, hay veinticuatro formas de colocar el segundo cubo. Seis caras tiene el cubo, luego tenemos seis opciones para la cara de abajo (o equivalentemente, tenemos tres parejas de caras opuestas, pero ahora, fijada ya la posición del primer cubo, si es diferente cual de las caras va debajo), y para cada una de esas seis posiciones, puede rotarse el cubo, dando lugar a cuatro posiciones distintas, ya que hay cuatro caras laterales. Lo mismo ocurre para el tercer y cuatro cubos. En consecuencia, existen 3 x 24 x 24 x 24 = 41.472 formas distintas (desde la perspectiva del solitario) de colocar los cuatro cubos.
El método del ensayo y error, es decir, el ir probando diferentes alternativas de colocación de los cuatro cubos y ver si se ha resuelto el solitario, no parece ser muy apropiado para la resolución de este juego a la vista de las 41.472 configuraciones distintas que existen de los cubos. El recorrido por todas ellas en busca de la solución será tedioso y llevará bastante tiempo. Si utilizásemos unos 5 minutos de media para cada posición, recorrer todas llevaría 3.456 horas, más o menos, dos años y medio, dedicando cuatro horas todos los días.

“Locura instantánea” gigante realizada por el artista griego Dimitris Ioannou, para una exposición en Atenas en 2007. Los cubos están colocados en una posición que no resuelve el solitario ya que en el lado más visible hay tres caras verdes y una roja, es decir, sobran dos verdes y faltan una amarilla y una azul
Si el método de ensayo y error no parece ser el más adecuado, esto nos lleva a plantear algún otro método de resolución del juego. Para empezar podemos intentar conocer más en profundidad este solitario y extraer información útil que nos simplifique la búsqueda o nos ayude a plantear algún método de resolución.
Para empezar, veamos cuántas caras hay de cada color. Si miramos a los cuatro cubos (por ejemplo, en la imagen de los desarrollos planos) se verá que en este solitario hay 7 caras azules, 6 rojas, 5 amarillas y 6 verdes. Puesto que en la solución del rompecabezas cada color aparece una sola vez en cada lateral de la torre, serán cuatro caras de cada color, y el resto permanecerán ocultas, es decir, sabemos que van a tener que quedar ocultas 3 caras azules, 2 rojas, 1 amarilla y 2 verdes.

Versión “Cubos locos” del juego “locura instantánea”, en la cual se utilizaban números en lugar de colores
La anterior información nos da una pista de cómo podríamos intentar resolver el juego, buscando distribuciones de los cubos que oculten 3 caras azules, 2 rojas, 1 amarilla y 2 verdes.
Esta información, y el camino que nos abre, es interesante, pero se necesita complementarla con algún dato más, como por ejemplo, cuales son los pares de caras opuestas de cada cubo (que se mostrarán u ocultarán de forma conjunta, lo cual es relevante). A continuación, detallamos cuales son estos pares de caras opuestas, según su color.
Cubo 1: [azul – azul] + [azul – rojo] + [amarillo – verde]
Cubo 2: [verde – azul] + [verde – rojo] + [amarillo – azul]
Cubo 3: [amarillo – verde] + [amarillo – azul] + [rojo – rojo]
Cubo 4: [verde – rojo] + [verde – amarillo] + [rojo – azul]
Y ya tenemos una información que puede ser muy útil. Ahora, para intentar resolver el rompecabezas, se trata de elegir pares de caras opuestas de cada cubo de forma que sus colores sumen las 3 caras azules, 2 rojas, 1 amarilla y 2 verdes, que son las que deben permanecer ocultas. Es una cuestión combinatoria muy sencilla.
Por ejemplo, la combinación [azul – azul] (cubo 1), [verde – azul] (cubo 2), [rojo – rojo] (cubo 3) y [verde – amarillo] (cubo 4) resulta que, como se observa fácilmente colocando convenientemente los cubos, ya nos genera una solución, de hecho, la única.

Este es un método muy sencillo, que es el que yo utilicé para resolver el Cubo 4 cuando me enfrenté a su resolución. No es tan elegante como la solución con grafos que vamos a mostrar a continuación, ni podemos extraer información muy relevante de cara a posibles generalizaciones o rompecabezas relacionados, pero cumple una de las máximas principales de la resolución de problemas, lo primero es resolverlo. Además, nos ha permitido rápidamente no solo encontrar una solución, sino saber que es única.
Antes de abordar la resolución del juego mediante grafos, recordemos qué es un grafo etiquetado.
Grafo etiquetado: Un grafo al que le asignamos etiquetas a las aristas, o a los vértices, es un grafo etiquetado. Las etiquetas pueden ser números, colores u otras informaciones.
El rompecabezas Locura instantánea puede ser modelizado con grafos etiquetados de la siguiente forma. Los vértices del grafo son cada uno de los colores, rojo, azul, verde y amarillo. Además, para cada cubo, dos vértices van a estar unidos por una arista si esos dos colores están en caras opuestas del cubo. En nuestro caso, los grafos etiquetados (las etiquetas en los vértices son los colores) asociados a los 4 cubos son:
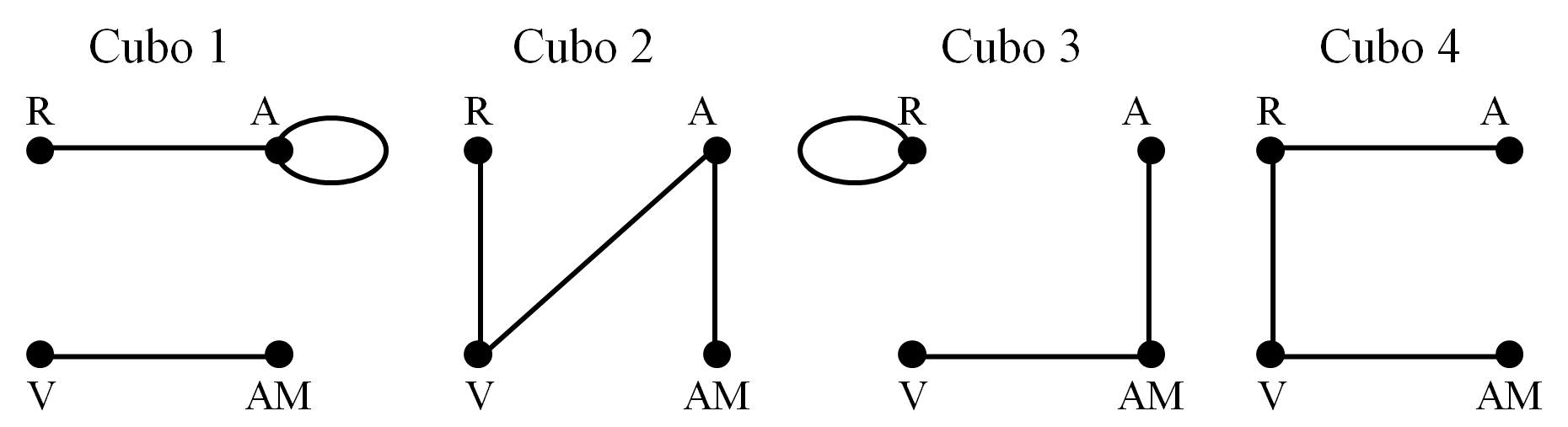
Para juntar toda esa información en un único grafo se etiquetan también las aristas con un número que se corresponde con el del cubo en el que se establece dicha arista. Así, el grafo etiquetado que modeliza El gran suplicio de Tántalo es el siguiente.

Una vez que el rompecabezas ha sido modelizado mediante este grafo, hay que utilizarlo para construir una solución, y en general, estudiar el espacio de soluciones.
Dada una solución del solitario, en particular, los cuatro colores aparecerán en la parte de delante, y también en la de detrás, de la torre. Esto se suele llamar una solución parcial, ya que no se imponen condiciones sobre los laterales de la torre. Y construir una solución parcial del Cubo diabólico es equivalente a encontrar un “subgrafo bueno” del grafo original, es decir, un subgrafo H que contiene los cuatro vértices (colores), con grado 2 (número de aristas que inciden en el vértice) con una arista etiquetada para cada uno de los números (que se corresponden con los cuatro cubos). Como cada vértice en un tal subgrafo bueno H tiene grado 2, cada color aparece exactamente dos veces, y se pueden colocar los cubos para que cada color aparezca una vez en la parte delantera y una en la de atrás.
Subgrafo bueno del grafo etiquetado asociado al rompecabezas “Locura instantánea”, con los correspondientes colores, según el subgrafo bueno, en las caras opuestas, delantera y trasera, de cada cubo
Si ahora podemos encontrar otro subgrafo bueno que no utilice las mismas aristas que el primero, es decir, en cada cubo nos va a dar otra pareja, distinta de la anterior, de caras opuestas, entonces podemos rotar cada cubo de manera que estas parejas aparezcan en las caras laterales de la torre, pero sin deshacer las caras de delante y detrás, lo que resolverá completamente el Cubo 4. Es decir, la solución de El suplicio de Tántalo se corresponde con dos soluciones parciales que encajan bien la una con la otra.
Otro subgrafo bueno, que no comparte aristas con el anterior, y la solución que se genera teniendo en cuenta la información proporcionada por los dos
Puede formularse así el resultado.
Teorema (F. de Canterblanche): El rompecabezas Locura instantánea tiene solución si, y sólo si, el grafo etiquetado asociado admite dos subgrafos buenos que no comparten aristas.
F. de Carteblanche es un seudónimo. En los años 1940, cuatro matemáticos de la Universidad de Cambridge adoptaron el seudónimo Blanche Descartes, y también el de su marido F. de Carteblanche, para publicar sobre matemáticas, pero también sobre poesía y humor matemático. Probaron algunos teoremas sobre teselaciones, publicaron sobre el coloreado de grafos, resolvieron la cuadratura del cuadrado, o descubrieron la disección de Blanche. A ellos se debe el estudio con grafos del (Gran) “suplicio de Tántalo”.
Una vez resuelto el rompecabezas, podemos ver si existen más soluciones al mismo. Calculando todos los subgrafos buenos y viendo qué parejas de subgrafos no comparten aristas obtendríamos todas las soluciones del rompecabezas. En el caso del Conmoción solo hay otro subgrafo bueno, además de los dos anteriores, y comparte aristas con ambos, luego no genera ninguna nueva solución. Es decir, la solución es única, como ya sabíamos.
Tercer subgrafo bueno del grafo asociado a los “Cuatro ases”, pero que no genera ninguna solución
Como hemos estudiado, el Locura instantánea admite una única solución, pero pueden existir otros rompecabezas con cuatro cubos de colores que no admitan soluciones o que admitan varias soluciones, como los dos mostrados en la siguiente imagen.
Estos dos solitarios con cuatro cubos de colores, uno no admite solución y el otro admite tres soluciones, como puede comprobarse analizando los grafos etiquetados asociados, sus subgrafos buenos y cuántos de ellos no comparten aristas dos a dos
Una cuestión interesante relacionada con la creación de este tipo de rompecabezas es el cálculo del número de formas distintas que hay de colorear un cubo con 4 colores (o en general, con un número k de colores), que son los cubos con los que podemos formar, a priori, rompecabezas como el Locura instantánea. Este cálculo es posible gracias al lema de Burnside, pero esa es otra historia y debe ser contada en otra ocasión.

Existen versiones del “Locura Instantánea” incluso con gatitos, como este juego de 1996 llamado “el puzzle del gato”
Bibliografía
1.- Raúl Ibáñez, Del ajedrez a los grafos, la seriedad matemática de los juegos, colección El mundo es matemático, National Geographic, 2015.
2.- David Singmaster, Sources in recreational mathematics, an annotated bibliography
3.- Página web de rompecabezas de James A. Storer
4.- Página web del artista griego Dimitris Ioannou
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Locura instantánea, un rompecabezas con cubos de colores se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El teorema de los cuatro colores (2): el error de Kempe y la clave de la prueba
- El teorema de los cuatro colores (1): una historia que comienza en 1852
- El teorema de los cuatro colores (3): Tras más de un siglo de aventura… ¿un ordenador resuelve el problema?
Evolución de los sistemas nerviosos: anélidos y artrópodos

Muchos invertebrados segmentados tienen sistemas nerviosos centrales “distribuidos”: están formados por los ganglios de cada segmento corporal. Cada ganglio se ocupa del control del segmento en el que se encuentra y además, quizás, de parte de los adyacentes. Los ganglios intercambian información a través de dos haces o troncos de axones, denominados conectivos. Esa disposición da lugar a un cordón nervioso ventral característico de anélidos y artrópodos. En el extremo anterior una o varias grandes agrupaciones de cuerpos celulares neuronales dan lugar a la formación de un cerebro. Ese cerebro recibe información de los sistemas sensoriales localizados en la cabeza y controla sus movimientos, pero los axones de varios somas neuronales del cerebro se extienden a lo largo del cordón ventral y ejercen un cierto control sobre sus ganglios; así coordina el cerebro los movimientos del conjunto del organismo.
Los anélidos fueron el primer gran grupo zoológico con un sistema nervioso central condensado de un modo significativo. En algunas especies los ganglios están fusionados. Merece la pena citar una curiosa excepción a la disposición general del sistema nervioso central en este grupo: las sanguijuelas tienen, además del cerebro anterior, un cerebro caudal, en el extremo posterior, que es de mayor tamaño que el anterior. En lo que se refiere al sistema nervioso periférico, muchos anélidos cuentan con un sistema somatogástrico muy desarrollado y en los gusanos de tierra hay además una extensa red subepidérmica de nervios finos.
Las formas de comportamiento mejor estudiadas en anélidos son las siguientes: (1) Las respuestas de huida, que son patrones de acción fijados en los que participan interneuronas y motoneuronas del sistema nervioso central con axones gigantes. (2) La regulación del latido cardiaco en los corazones tubulares de sanguijuelas, que constituyen un ejemplo de control nervioso de comportamiento rítmico. En éste participan motoneuronas del sistema periférico cuya actividad puede ser influenciada por inputs sensoriales directos o por interneuronas del sistema central que permiten ajustar el latido a las necesidades del animal. (3) Movimientos locomotores, que están bajo el control de una red del sistema central que recibe señales de receptores sensoriales periféricos (nociceptores, barorreceptores y receptores táctiles).
Los sistemas nerviosos de los artrópodos se asemejan a los de los anélidos. En las formas más primitivas consisten en una cadena de ganglios ventrales unidos por conexiones horizontales. En muchas especies, los ganglios de la cabeza y los del segmento abdominal terminal se forman por fusión de los ganglios de varios segmentos. Los artrópodos más evolucionados, como cangrejos y algunos insectos, presentan una única masa ganglionar torácica, además de la de la cabeza. Se trata de un sistema nervioso muy complejo, con numerosas neuronas y, por lo tanto, muchas conexiones sinápticas. Por ello, es capaz de desarrollar una gran variedad de comportamientos de gran complejidad.
Muchos movimientos de ajuste de la posición corporal y del movimiento de las extremidades están controlados por señales sensoriales que son sometidas a una integración considerable por parte del sistema central, aunque también hay circuitos de ámbito local.
En artrópodos hay comportamientos rítmicos motores y digestivos. Las actividades rítmicas correspondientes a la locomoción, la natación y el vuelo dependen de Generadores Centrales de Modelos formados por redes de neuronas del sistema nervioso central. En estos casos, la retroalimentación sensorial juega un papel importante. En las respuestas rítmicas de huida, como los rápidos movimientos abdominales de los cangrejos de río, participan dos neuronas gigantes motoras cuyos axones recorren toda la longitud del cuerpo y que establecen conexión sináptica mutua en el cerebro, además de otros tres pares de interneuronas con axones gigantes. El vuelo de las langostas es otra forma de comportamiento rítmico que está controlado por un Generador Central de Modelos. Se trata de un comportamiento controlado por el sistema nervioso central y dependiente de inputs sensoriales.
El sistema somatogástrico controla las actividades rítmicas implicadas en el procesamiento del alimento en el sistema digestivo. Estas actividades están reguladas por conjuntos de interneuronas y motoneuronas del ganglio somatogástrico. Su funcionamiento garantiza la correcta secuenciación de los movimientos implicados en la conducción y tratamiento mecánico del alimento.
Además de los rítmicos, los artrópodos tienen comportamientos que no lo son. Los movimientos de huida de las cucarachas constituyen el comportamiento no-rítmico mejor conocido en este filo. En él participan pares de neuronas con axones gigantes, cuyos cuerpos celulares radican en los últimos ganglios abdominales, pero cuyos axones terminan probablemente en los ganglios subesofágicos en la cabeza. Además de estos, la presencia de axones gigantes que participan en movimientos de huida está muy extendida en otros grupos de artrópodos.
Otro ejemplo de comportamiento no-rítmico es el de los movimientos de amartillamiento y salto en langostas y saltamontes. En éstos participan inputs sensoriales de diferentes tipos (visuales, auditivos y táctiles) a través del sistema nervioso central, a la vez que propioceptores y receptores cuticulares del sistema periférico. La red nerviosa implicada, en la que se producen fenómenos de inhibición cruzada, da lugar a la contracción alternativa de músculos flexores y extensores a cargo de sus correspondientes motoneuronas.
En la mayor parte de los comportamientos anteriores participan tan solo unos pocos ganglios. Sin embargo, en los artrópodos se producen comportamientos muy elaborados y se ha demostrado capacidad de aprendizaje. Todos aquellos aspectos del comportamiento que requieran una valoración del inicio, mantenimiento y duración o selección, precisan del concurso de la principal masa nerviosa del cerebro, que suele estar dividido en dos partes, el ganglio subesofágico y el superesofágico. Aunque se desconoce el funcionamiento preciso de estos órganos, se ha comprobado que el superesofágico inhibe la actividad del subesofágico, quien, a su vez, ejerce un efecto excitatorio en muchos comportamientos.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Evolución de los sistemas nerviosos: anélidos y artrópodos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Evolución de los sistemas nerviosos: cnidarios y gusanos no segmentados
- Evolución del tamaño animal
- Historia mínima de la complejidad animal
Carnot y los comienzos de la termodinámica (2)
La máquina ideal de Carnot, tan sencilla como es, explica algunos aspectos fundamentales del funcionamiento de máquinas y motores de todo tipo y permite formular un principio fundamental de la naturaleza.

Las chimeneas anchas de la derecha en realidad son torres de refrigeración. las chimeneas auténticas por las que salen los gases de la combustión del carbón de esta planta de generación eléctrica son las altas y delgadas.
Cualquier máquina que derive su energía mecánica del calor se debe enfriar para eliminar el “desperdicio” de calor a una temperatura más baja. Si hay alguna fricción u otra ineficiencia en la máquina, agregarán más calor residual y reducirá la eficiencia por debajo del límite teórico de la máquina ideal.
Sin embargo, a pesar de las ineficiencias de todas las máquinas reales, es importante saber que nada de la energía total se destruye. Lo que ocurre con la parte de la energía de entrada que llamamos residual es que no se puede emplear para hacer trabajo útil. Así, el calor residual no puede ser reciclado como energía de entrada para hacer funcionar la máquina para producir más trabajo útil y así aumentar la eficiencia del motor a base de reducir la cantidad de energía residual, porque el depósito de calor de entrada está a una temperatura más alta que el de salida, y el calor no fluye por sí mismo de frío a caliente.
La observación de Carnot, que parece tan obvia, esa de que el calor no fluye por sí solo de un cuerpo frío a uno caliente, y que la necesidad de acondicionadores de aire y refrigeradores ilustra tan bien, no es más, si se generaliza, que una forma de expresar un principio fundamental de la naturaleza: la segunda ley de la termodinámica. Esta ley es una de las más potentes que conocemos, dada su capacidad para explicar cosas: desde cómo y en qué sentido ocurren los fenómenos naturales a los límites fundamentales de la tecnología. Volveremos a ella repetidamente en esta serie.
Un ejemplo paradójico del resultado de Carnot
Si quemamos gasóil para calefacción en una caldera en el sótano de nuestro edificio, sabemos que parte del calor se pierde por la chimenea en forma de gases calientes y otra como calor perdido porque el propio quemador no puede estar aislado por completo. Con todo, los recientes avances en tecnología de calderas han dado como resultado calderas con una eficiencia nominal de hasta 0,86, o 86%.
Ahora bien, si preferimos radiadores eléctricos, nos encontramos con que es probable que la compañía de energía eléctrica todavía tenga que quemar petróleo, carbón o gas natural en una caldera, Y después conseguir que esa electricidad generada llegue a nuestra casa. Debido a que los metales se funden por encima de una cierta temperatura (por lo que la sustancia caliente no puede superar la temperatura de fusión de su contenedor) y debido a que el agua de refrigeración nunca puede bajar por debajo del punto de congelación (porque entonces sería sólida y no fluiría, lo que pone un límite inferior de temperatura a nuestra sustancia fría), el hallazgo de Carnot hace imposible que la eficiencia de la generación eléctrica supere el 60%. Dado que la caldera de la compañía de energía también pierde parte de su energía por la chimenea, y dado que existen pérdidas de electricidad en el camino desde la planta que la genera, sólo alrededor de un cuarto a un tercio de la energía que había originalmente en el combustible llega realmente a tu casa. Una eficiencia, en el mejor de los casos, del 33 %. Paradójicamente, la calefacción eléctrica es mucho menos sostenible que una caldera de gasóil si las plantas que generan energía emplean combustibles fósiles.
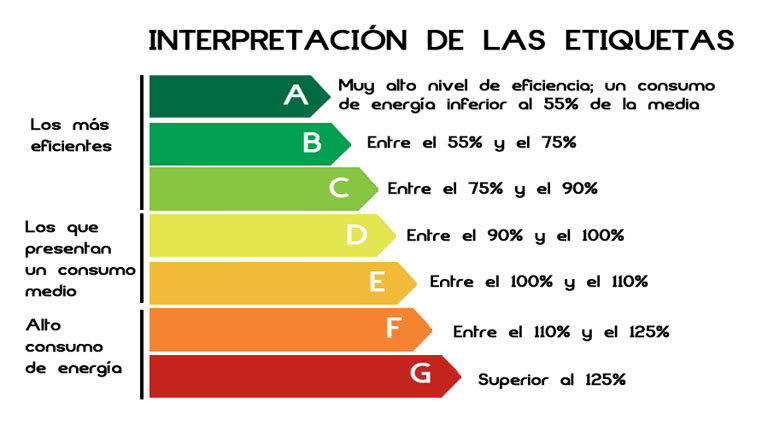
Debido a los límites encontrados por Carnot para las máquinas térmicas, a veces es importante no sólo dar la eficiencia real de una máquina térmica, sino también especificar lo cerca que está del máximo posible. Los aparatos de calefacción domésticos y muchos aparatos eléctricos de gran potencia, como frigoríficos y acondicionadores de aire, vienen ahora con una etiqueta que indica la eficiencia relativa del aparato y el potencial de ahorro anual en coste de electricidad.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Carnot y los comienzos de la termodinámica (2) se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Carnot y los comienzos de la termodinámica (1)
- Potencia y eficiencia de una máquina
- La máquina de vapor (1)
Dudas sobre las vacunas: problemas y soluciones
Ignacio López Goñi
Cada vez hay más padres que dudan de los beneficios de la vacunación. ¿Debería ser obligatoria? Los profesionales de la salud son la mejor herramienta contra los anti-vacunas.
Los programas de vacunación han contribuido a que el número de casos y de muertes por enfermedades infecciosas hayan disminuido de forma significativa en el último siglo. Las vacunas han salvado millones de vidas humas, son responsables de la erradicación de la viruela del planeta y de que la polio esté apunto de serlo. En general, las coberturas vacunales o tasas de vacunación infantil siguen creciendo a nivel mundial, lo que indica que la vacunación es una medida de salud pública ampliamente aceptada.
Sin embargo, un número cada vez más creciente de padres (*) perciben la vacunación como algo insano e innecesario. Como las vacunas se administran cuando el niño está sano, nuestro umbral del riesgo es muy bajo. Cualquier duda, aunque sea teórica, sobre la seguridad de las vacunas puede causar que los padres rechacen o retrasen la vacunación de sus hijos. Incluso algunos padres que vacunan a sus hijos suelen tener dudas y temores acerca de la vacunación. Los movimientos anti-vacunas han sido responsables de la disminución de las tasas de aceptación de las vacunas y del aumento de brotes de enfermedades infecciosas que se pueden prevenir con las vacunas. Entre los extremos de los movimientos anti-vacunas que rechazan totalmente la inmunización y los entusiastas pro-vacunas, cada vez hay más padres que dudan: padres que rechazan alguna de las vacunas pero que aceptan otras, que retrasan la vacunación de su hijo porque dudan del calendario vacunal recomendado, o que se sienten inseguros cuando vacunan a sus hijos.
En África entierran a los niños, en Europa enterramos a los ancianos
Por supuesto, la situación es diferente según el contexto y el país. En los países de altos ingresos donde los programas de vacunación están bien establecidos y en gran parte son gratuitos, las vacunas son víctimas de su propio éxito. Como gracias a las vacunas han disminuido radicalmente la frecuencia de enfermedades infecciosas, los padres no perciben el riesgo de esas enfermedades y no ven la necesidad de las vacunas: “¿para que voy a vacunar a mi hijo si ya no hay varicela?”. Se tiene más miedo a la vacuna que a la propia enfermedad. Sin embargo, en los países con ingresos medios o bajos, donde este tipo de enfermedades son todavía más frecuentes, la duda de la inmunización es menor. En países donde la mortalidad infantil es todavía muy alta debido a las enfermedades infecciosas, todavía da más miedo la enfermedad que la vacuna.
Anti-vacunas: desde Jenner hasta Twitter
Los movimientos anti-vacunas no son algo nuevo. Nada más empezar Edward Jenner, a principios de 1800, sus demostraciones de que la viruela de las vacas protegía contra la viruela humana, y a pesar de que más del 30% de los casos de viruela eran mortales, comenzaron las campañas contra la vacuna. Son famosos los dibujos satíricos publicados en 1802 en los que se ridiculizaba la vacunación de Jenner y se mostraban los bulos de sus opositores: que al vacunarte con la viruela de las vacas te salían por el cuerpo apéndices de vaca.

Caricatura publicada en 1802 en “The Punch” por James Gillray de una escena de la inoculación de la vacuna de Jenner en el Hospital de St. Pancras (Londres).
Durante el siglo XIX, en el Reino Unido primero, luego en el resto de Europa y en EE.UU. después, se crearon las primeras Ligas Anti-Vacunación y hubo varias campañas anti-vacunas que lucharon activamente contra las leyes que obligaban a la vacunación y en defensa de la libertad personal. Sin embargo, ya en pleno siglo XX, llegó la edad de oro de las vacunas en las décadas de los 50 y 60, durante las cuáles la aceptación de la inmunización fue máxima. En esos años se introdujeron las vacunas contra la poliomielitis, el sarampión, las paperas y la rubéola, con gran aceptación al comprobar cómo los casos de enfermedades y muertes se reducían de forma espectacular. En los años 70 se comenzó un gran esfuerzo internacional para expandir los programas de vacunación también a los países de bajos ingresos, con el objetivo de acabar con seis grandes asesinos: polio, difteria, tuberculosis, tosferina, sarampión y tétanos. Entonces menos del 5% de la población mundial infantil menor de un año estaba inmunizada contra estos patógenos. En los años 90 cerca del 75% de la población mundial infantil estaba vacunada contra la polio difteria, tétanos y tosferina. Sin embargo, ese periodo de aceptación entusiasta de las vacunas duraría poco tiempo.
A mediados de los 70 los movimientos anti-vacunas resurgieron con fuerza. La controversia comenzó en el Reino Unido con la vacuna contra la tosferina (pertussis en inglés, por estar causada por la bacteria Bordetella pertussis), al publicarse un trabajo que relacionada serios trastornos neurológicos en 36 niños después de haber sido vacunados con la tripe difteria-tétano-pertusis (vacuna DTP). Este trabajo tuvo una gran repercusión mediática e hizo que la cobertura vacunal en el Reino Unido bajara del 77 al 33%, con el consiguiente aumento de los casos de tosferina, algunos de ellos mortales. En EE.UU. la controversia comenzó en 1982 con la emisión de un emotivo documental periodístico “DTP: vaccination roulette” que acusaba al componente pertusis de la DTP de causar daños cerebrales severos y retraso mental. A raíz de tal escándalo se crearon grupos de presión anti-vacunas, se investigaron las empresas fabricantes de vacunas, aumentaron los precios y se redujeron las tasas de vacunación. A pesar de los estudios que se hicieron posteriormente que demostraban que no había relación alguna entre la vacuna DTP y los trastornos neurológicos, la preocupación sobre su seguridad fue un estimulo para el desarrollo de una nueva vacuna de pertusis acelular, menos reactiva y, por lo que se está viendo con el tiempo, con un menor poder protector contra la enfermedad. Quizá lo único bueno de todo aquello fue la creación del Vaccine Adverse Event Report System (VAERS), un programa nacional del CDC y la FDA para recoger, evaluar y publicar de forma transparente todo tipo de información sobre los efectos adversos que puedan ocurrir por la administración de las vacunas en EE.UU.
Unos 25 años después de la controversia sobre la vacuna DTP, el Reino Unido volvió a ser el origen de una de las mayores crisis sobre las vacunas, en esta ocasión relacionando la vacuna tripe vírica sarampión/rubeola/paperas (SRP) con el autismo. La revista The Lancet publicó en 1998 un artículo firmado por Andrew Wakefield y otros doce colegas en el que se sugería una posible asociación entre la vacuna y el autismo. Aunque en el artículo no se probaba una relación causal, las afirmaciones posteriores de Wakefield no dejaban lugar a duda de su opinión y pidió la retirada de la vacuna hasta que se hicieran más estudios. Años después se demostró que los datos de la publicación habían sido sesgados, y que Wakefiled recibió dinero para publicar estos datos contra las empresas farmacéuticas. En 2004, 10 de los 12 coautores del trabajo se retractaron de la publicación. En 2010 el Consejo General Médico inglés expulsó a Wakefield y le prohibió ejercer la medicina en el Reino Unido, y The Lancet tomó la decisión de retirar y retractarse de lo publicado en 1998. Pero habían pasado ya doce largos años. Se han evaluado y revisado más de 20.000 artículos relacionados con esta vacuna y más de 14 millones de casos de niños vacunados y no hay ningún indicio de que la vacuna SRP tenga alguna relación con el autismo infantil. A pesar de ello, la relación de las vacunas con el autismo sigue siendo una de las principales preocupaciones de muchos padres que dudan.
Como hemos comentado, en general las vacunas son mucho mejor recibidas en los países de bajos ingresos. Sin embargo, en los últimos años ha habido también algunas controversias que han hecho disminuir las coberturas vacunales y han supuesto un serio problema para las campañas mundiales de inmunización. En 1990 en Camerún se extendieron rumores de que el objetivo de las campañas de vacunación era la esterilización de las mujeres y en 2003 se boicoteó la vacuna de la polio en el norte de Nigeria también con rumores de que la vacuna era una estrategia para extender el VIH y reducir la fertilidad entre los musulmanes. A consecuencia de estos rumores, la polio resurgió en Nigeria y se extendió en 15 países africanos que ya habían sido declarados libres de la enfermedad.
Desde el año 2000, Internet ha supuesto un cambio de paradigma en la relación médico/paciente. Internet ha acelerado la velocidad de la información y ha roto barreras: la web proporciona información gratis, inmediata y disponible todo el tiempo y anónima. Internet es una oportunidad sin precedentes para los activistas anti-vacunas, para difundir su mensaje a una audiencia cada vez más amplia y reclutar nuevos miembros. Las personas que son contrarias a las vacunas, aunque sean minoría, generan una cantidad desproporcionada de contenidos anti-vacunas.
Cada mes son miles los contenidos que se vierten al ciberespacio sobre la vacunación, la inmensa mayoría subjetivos y de contenido emocional. Internet es una de las principales fuentes de información que emplean los padres para consultas sobre el tema de la vacunación. Desgraciadamente si se examinan los contenidos relacionados con la vacunación en la web o en las redes sociales sobresale la información inexacta e incorrecta. Esto hace que muchos padres pasen de dudar de las vacunas a ser resistentes a la vacunación o incluso claramente opuestos. Muy probablemente ver una web anti-vacunas aumenta los sentimientos negativos contra la inmunización, mientras que las webs pro-vacunas suelen tener un efecto mínimo.
En España no existen movimientos anti-vacunas como en EE.UU. pero el número de padres que dudan aumenta
En España no existen movimientos anti-vacunas bien organizados y beligerantes como los que hay en EE.UU. o en el Reino Unido, pero el número de padres que ponen en duda la efectividad y seguridad de las vacunas aumenta. Además, cada vez tienen más relevancia pública algunos claros anti-vacunas como Josep Pamiés o la monja Forcades, incluso sorprendentemente con la colaboración de grandes medios de comunicación y poderes públicos. También, en los últimos años se han publicado varios libros que claramente ponen en tela de juicio el valor de las vacunas: Vacunas, una reflexión crítica (Enric Costa), Los peligros de las vacunas (Xavier Uriarte), Vacunaciones sistemáticas en cuestión, ¿son realmente necesarias? (Manuel Marín Olmos), o Vacunas las justas (Miguel Jara).
La duda sobre las vacunas es ya un problema de salud pública
Los padres que mantiene una posición claramente anti-vacunas son una minoría, pero la proporción de los que dudan va en aumento. Esto es preocupante porque para el éxito de las campañas de vacunación se debe mantener una cobertura vacunal alta. Se debe conseguir que lo normal sea que un padre vacune a su hijo según el calendario que le corresponde. La vacunación es una medida individual pero que beneficia a la comunidad. A diferencia de otras intervenciones preventivas, si un padre rechaza las vacunas de su hijo no solo pone en riesgo la vida de su hijo sino también de los que le rodean, de los más débiles, otros niños, los enfermos y los ancianos. Luchar contra la oposición o la duda de las vacunas es un problema comunitario.
¿Qué impacto clínico tiene el fenómeno de los anti-vacunas? Quizá el de mayor actualidad sea el aumento de los casos de sarampión, una de las enfermedades infecciosas más contagiosas (ver El sarampión aumente en Europa, en microBIO). Las autoridades sanitarias han alertado que desde febrero de 2016 han aumentado los casos de sarampión en Europa, la mayoría en niños pequeños sin vacunar. La situación en este momento es que de los 53 países de toda la región europea solo han conseguido erradicar la enfermedad 15 países, y en 6 todavía sigue habiendo transmisión endémica. Desde enero de 2017 ya ha habido incluso algunos casos de muertes en Rumanía, Italia y Portugal. La ECDC alerta de que la probabilidad de que se extienda el sarampión a otros países es alta. Casos similares también han ocurrido en el continente americano, libre de sarampión desde el año 2002. En EE.UU. hubo tres grandes brotes en 2013 y lo mismo ocurrió en Canadá. De forma similar en los últimos años ha habido brotes de rubéola, paperas y pertusis en Polonia, Suecia, Holanda, Rumania, Bosnia EE.UU., etc. por la misma causa: personas que no habían sido vacunadas. En 2010, la OMS estimó el número de muertos por enfermedades infecciosas prevenibles por las vacunas (difteria, sarampión, tétanos, pertusis y polio) en unas 400.000. Estas muertes se podrían haber evitado con las vacunas. Es cierto, que más de la mitad ocurren en países donde los problemas de infraestructuras son responsables de la falta de vacunación, pero en otros casos es el rechazo a las vacunas la causa.
Entender las causas y el contexto del que duda
Los grupos anti-vacunas de hoy en día son en su mayoría gente de clase media (o media-alta) con estudios superiores que reclaman su derecho a una decisión informada acerca de las vacunas, prefieren soluciones “naturales”, no les gusta que les califiquen como anti-vacunas (el término “anti” es negativo) y prefieren términos neutros, como grupo pro vacunas seguras. Pero algunos de sus argumentos son los mismos que en 1800: las vacunas no son efectivas; causan enfermedades; son un negocio y se fabrican sólo para beneficio de las farmacéuticas; las vacunas contienen aditivos tóxicos peligrosos para la salud; los daños de las vacunas son ocultados por las autoridades (teorías conspiratorias); la vacunación obligatoria es contraria a la libertad y a los derechos civiles; la inmunidad natural es mucho mejor que la que inducen las vacunas; las vacunas son muchas y se dan demasiado pronto; los productos naturales y alternativos (vida “sana”, homeopatía, vitaminas) son mejores que las vacunas para prevenir las enfermedades; etc. En muchos casos se presentan datos incorrectos, hechos sacados de contexto, ambiguos o medias verdades. En muchas ocasiones apelan a las emociones y presentan historias muy duras del legitimo sufrimiento de padres que creen seriamente que sus hijos han padecidos enfermedades graves por culpa de las vacunas.
El contexto a veces no ayuda. En los últimos años ha aumentado el número de nuevas vacunas, lo que ha complicado los calendarios vacunales. El que no exista un mismo calendario vacunal en distintos países o, lo que es peor, en distintas comunidades autónomas de un mismo país genera percepciones negativas. La falta de transparencia de algunos gobiernos y empresas farmacéuticas y los errores en la forma de afrontar e informar sobre crisis sanitarias también provoca desconfianza y susceptibilidades: la crisis de las vacas locas, la pandemia de gripe aviar o el último brote de Ébola, por ejemplo. Hoy en día los pacientes quieren estar involucrados y participar en sus propias decisiones de salud.
¿Debería ser obligatoria la vacunación?
Esta es la pregunta que hace unos días lance desde mi cuenta de Twitter, y el 94% de las respuestas fue afirmativa. Es verdad que el resultado está sesgado y no es significativo: la mayoría de los seguidores de esa cuenta de Twitter son claramente pro-vacunas, pero algunos comentarios fueron muy sugerentes: “si la vacuna de la rabia es obligatoria para los perros, ¿por qué vacunar a los niños no lo es?”, “si llevar cinturón de seguridad en el coche es obligatorio, ¿por qué no las vacunas?”, “si fumar está prohibido en muchos lugares porque es malo para la salud, ¿por qué las vacunas no son obligatorias si son buenas para la salud?”, “si una persona no vacunada puede poner en riesgo la salud de mi hijo, ¿por qué no obligan a vacunarse en las guarderías?”
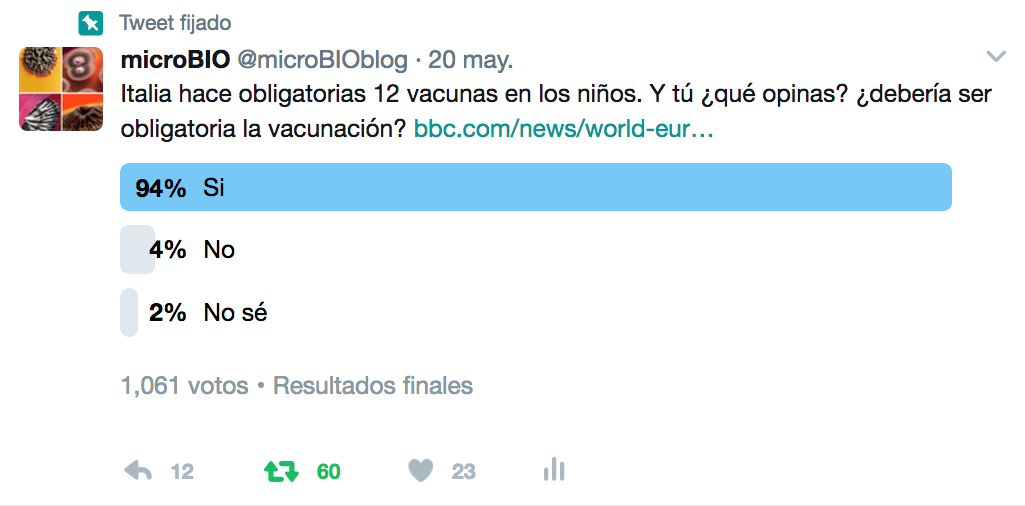
Resultado de la encuesta “¿Debería ser obligatoria la vacunación?” en Twitter.
Los recientes brotes de sarampión y de otras enfermedades evitables por las vacunas han hecho que algunos países cambien su legislación. En Italia ya es obligatoria la vacunación contra doce enfermedades infecciosas para poder matricular a tu hijo en el colegio. En Portugal no son obligatorias, pero sí gratuitas y están preparando una ley para exigir la vacunación. En Alemana, no son obligatorias, pero preparan también una ley para poder multar si no vacunas a tus hijos. En Francia son obligatorias las del tétanos, difteria y polio, y en Bélgica solo la de la polio. ¿Y en España? La vacunación es voluntaria, nuestro ordenamiento no incorpora explícitamente el deber de vacunación y nadie puede, en principio, ser obligado a vacunarse. Ahora bien, hay determinadas situaciones que permiten que los poderes públicos competentes impongan la vacunación forzosa, en caso de brotes o epidemias y de peligro para la salud pública. ¿Debería cambiarse la ley y que la vacunación fuera obligatoria?
Para controlar e incluso llegar a erradicar una enfermedad infecciosa, la OMS recomienda que la cobertura vacunal para esa enfermedad sea de al menos el 95%. Según datos oficiales, las tasas de vacunación en nuestro país en los últimos años son elevadas, superiores al 95%.

Coberturas vacunales en España desde 2006 hasta el 2015. Para más información consultar la web del MSSSI.
En España, a pesar de la no obligatoriedad, la tasa de vacunación es incluso superior a la de países en los que la vacunación es obligatoria. Por ello, el debate planteado podría ser útil si hubiera un descenso de las tasas de vacunación que pusieran en compromiso la protección del efecto rebaño y afectara a la salud pública. Adelantar cambios normativos que impusieran de forma coercitiva la vacunación, podría generar un efecto contrario al pretendido. Obligar quizá, de momento, no sea la solución.
¿Qué podemos hacer?
Para responder a los movimientos anti-vacunas o convencer a los que dudan, algunas estrategias se han basado en campañas de educación (folletos “oficiales” o similar) con información sobre la efectividad y seguridad de las vacunas. Si embargo, aunque necesaria, no parece que ésta sea la forma más efectiva. Educar a la gente tiene poco efecto o impacto en cambiar la actitud anti-vacunas. La información y educación no suelen cambiar por si solas las percepciones. Todos tenemos la tendencia de recibir mejor la información que confirma lo que pensamos y solemos rechazar lo que contradice nuestras creencias. Para muchas personas lo que convence no son los hechos, sino la credibilidad o autoridad de quién lo dice. En este sentido, la pieza fundamental para conseguir la aceptación y confianza pública de las vacunas son los profesionales de la salud (de la medicina y la enfermería). La gente cree y confía más en su médico o enfermera de lo que nos imaginamos. Muchas gente dice que la primera razón para vacunar a su hijo es la recomendación del profesional de la salud en la consulta de pediatria. Promover una buena relación con el paciente es fundamental.
Se han publicado algunas recomendaciones para estos profesiones de la salud, pero que nos pueden ayudar a todos cuando nos enfrentamos a una persona que duda: ¿cómo convencer a unos padres de que no vacunar supone un riesgo mayor?
1. Recuerda por qué nos vacunamos. Hay que explicar cómo las vacunas nos protegen de las infecciones y nos ayudan mantener la salud; reforzar la idea de que la vacunación es una norma social, porque la gente hace lo que cree que todo el mundo debe hacer. Da por hecho que va a vacunar a su hijo, ni si quiera ponlo en duda. Felicítale por vacunarlo (y concreta la fecha para la siguiente cita).
2. No intentes asustar a la gente con mensajes catastrofistas, ya que te puede salir el tiro por la culata. Explica cómo se controla de forma rigurosa la seguridad de las vacunas, algo que no se suele contar a la gente. Las vacunas son uno de los agentes farmacéuticos mejor estudiados y más seguros del mercado. Es frecuente confundir correlación con causalidad: que dos cosas ocurran al mismo tiempo no quiere decir que una sea la causa de la otra. Que el autismo se manifieste los primeros años de vida al mismo tiempo que el calendario vacunal, no demuestra que las vacunas sean la causa del autismo. Pero el sufrimiento de unos padres con un niño autista, … es tremendo.
3. Ten empatía. Evita ser despectivo. Hazte cargo de sus preocupaciones. Si tiene dudas, escucha, deja que hable, deja que acabe de hablar, reconoce el derecho que tiene para dudar y hacerse esas preguntas, sé positivo, responde de forma simple, sencilla, que se te entienda (“Hay más formaldehido en una pieza de fruta que en todas las vacunas que recibe tu niño”). Dedícale tiempo, con respeto, paciencia y confianza. Recuerda aquello de “siempre positivo, nunca negativo”.
4. La verdad es la piedra angular de la aceptación de las vacunas. Explica claramente las posibles reacciones adversas que pueda haber, que no le coja por sorpresa las reacciones locales de la vacuna. Su hijo ha ido a vacunarse estando sano, sin fiebre y las reacciones locales pueden alarmar si no se han explicado antes. La fiebre, el malestar general, un pequeño sarpullido o enrojecimiento local no significan que la vacuna no funcione sino todo lo contrario. Es señal de que la vacuna está activando las defensas. Y explica las posibles reacciones adversas graves muy raras que puede haber (menos de un caso por millón de dosis administradas). Se honesto y claro. Ningún medicamento es 100% seguro y todos tienen efectos secundarios. Reconoce los riesgos, también hay riesgo en tomar un paracetamol, pero distingue claramente las reacciones locales de los casos graves y muy raros. Hay que dar la información a medida, según las dudas y las preocupaciones de los padres.
5. Cuenta tu historia, tu propia experiencia, como profesional de la salud o como padre que vacuna a sus hijos: aquel viejo amigo del colegio que tuvo polio, o por qué tus hijos no han tenido rubéola. Y cuéntalo como una historia de ciencia. Explica que no hay nada más natural que las vacunas que inducen una inmunidad natural, al estimular a tu propio sistema inmune a producir su propia protección. Los anticuerpos que te protegen los produce tu propio cuerpo. La gente que está en riesgo es la que no hace nada.
6. Utiliza las redes sociales. Involúcrate de forma proactiva con los medios de comunicación y en las redes sociales. Proporcionarles información, comentarios independientes, ayuda a los periodistas a entender los datos. Da información, respuestas, historias, videos. Internet puede ser una herramienta muy útil para luchar contra la duda. Los algoritmos que usa Google no ayudan. Google puede darte una información sesgada. Las palabras “clave” que te sugiere y los contendidos web que te ofrece puede estar condicionados por tus propias preferencias y consultas previas. Así, Google puede contribuir a crear, mantener o aumentar tus dudas o a creer que lo que opina una minoría es mucho más frecuente que lo que realmente es. Por ejemplo, los contendidos negativos tienden a proliferar más en internet. ¿Por qué una madre que ha vacunado a su hijo y todo ha ido fenomenal y están los dos sanos y felices va a escribir su experiencia en un blog o va a dejar un comentario en Internet? Por el contario, si ha habido el menor problema, esa madre compartirá sus dudas en fórums o redes sociales y su testimonio se extenderá cómo la pólvora, generando una percepción errónea del problema. Como ya hemos dicho, los contenidos relacionados con la vacunación en la web y redes sociales son principalmente inexactos e incorrectos. Por eso, uno de los “campos de batalla” se libra en internet. Difundir mensajes en blogs, redes sociales, YouTube, … está muy bien, pero es complicado. El reto no solo es que los padres tengan acceso a la información, sino que esta se entienda y sea inteligible para cualquiera. Usa un lenguaje coloquial, muestra empatía y escucha al público.
Conclusión: En España no hay grandes movimientos anti-vacunas pero sí un aumento de padres que dudan de la seguridad y eficacia de las vacunas. De momento, las coberturas vacunales son altas y no se compromete el efecto rebaño. Por ello, imponer de forma coercitiva la vacunación, podría tener un efecto contrario al pretendido. No obstante, es necesaria una vigilancia estrecha del fenómeno anti-vacunas y su efecto en la salud pública. Los profesionales de la salud son la principal fuente de información para los padres que dudan y la forma más efectiva de convencerles de lo peligroso que es no vacunar a sus hijos.
Referencias y más información:
Las vacunas funcionan. Ignacio López-Goñi y Oihana Iturbide. 2015. Phylicom ediciones, Valencia. Colección Pequeñas Guías de Salud. ISBN: 978-84-943440-0-8
Vaccine hesitancy, vaccine refusal and the anti-vaccine movement: influence, impact and implications. Dubé, E., y col. (2015). Expert Rev Vaccines. 14(1):99-117. doi: 10.1586/14760584.2015.964212.
Identifying and addressing vaccine hesitancy. Kestenbaum, L.A., y col. (2015). Pediatr Ann. 44(4):e71-5. doi: 10.3928/00904481-20150410-07.
Promoting vaccine confidence. Smith, M.J. (2015). Infect Dis Clin North Am. 29(4):759-69. doi: 10.1016/j.idc.2015.07.004.
Vaccine hesitancy: A vade mecum v1.0. Thomson, A., y col. (2016). Vaccine. 34(17):1989-92. doi: 10.1016/j.vaccine.2015.12.049.
The impact of the web and social networks on vaccination. New challenges and opportunities offered to fight against vaccine hesitancy. Stahl, J.P., y col. (2016). Med Mal Infect. 46(3):117-22. doi: 10.1016/j.medmal.2016.02.002.
Vaccine Adverse Event Reporting System (VAERS)
El sarampión aumenta en Europa
Coberturas de vacunación en España (MSSSI)
Nota:
(*) Cuando me refiero a “padres” e “hijos” empleo los términos en plural que según el Diccionario de Lengua Española de la Real Academia significan “padre y madre de una persona” y “descendientes”, respectivamente.
Sobre el autor: Ignacio López Goñi es catedrático de microbiología de la Universidad de Navarra y autor del blog microBio.
El artículo Dudas sobre las vacunas: problemas y soluciones se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Las ideas erróneas sobre educación entre el profesorado: prevalencia, causas y soluciones
- Vacunas: El arte de salvar vidas
- Sobre la predisposición genética a padecer enfermedades

