Agrégateur de flux

Azken hamarkadetan biopolimeroek indarra hartu dute ikerketaren esparruan. Biopolimeroak, naturatik datozen polimeroak dira, beraz, berriztagarriak, biodegradagarriak, ugariak eta kostu baxukoak dira. Gainera, formatu-mota askotako materialak lor daitezke biopolimeroekin, hidrogelak esaterako.

Hidrogelak, ura eta beste fluido biologikoak xurgatu eta gordetzeko gai dira haien egitura mantenduz. Hidrogelen aplikazioak oso zabalak dira, biosentsore bezala erabili daitezke, uraren purifikaziorako edo kosmetikan eta biomedikuntzan.

Biopolimeroei eta haien aplikazioei buruz gehiago jakiteko Kizkitza González ikertzailearekin elkartu gara. Egun, Kizkitza Material Berriztagarrien Ingeniaritzan doktore-aurrekoa egiten ari da UPV/EHUn.

“Zientzialari” izeneko atal honen bitartez zientziaren oinarrizko kontzeptuak azaldu nahi ditugu euskal ikertzaileen laguntzarekin.

The post Kizkitza González: “Hidrogelak hiru dimentsioko sare polimerikoak dira” #Zientzialari (112) appeared first on Zientzia Kaiera.

La pizza puede ser una comida rica y saludable. El secreto de ambas cosas está en una buena elección de ingredientes. La parte más complicada de encontrar son las bases de pizza precocinadas o masas extendidas elaboradas con 100% harina integral. Sin embargo, en poco más de media hora podemos hacer nosotros mismos una base para pizza excepcional. El secreto de una buena masa de pizza está en la química.

Necesitamos los siguientes ingredientes para 2-4 personas: 250 g de harina integral, 3 cucharadas soperas de aceite de oliva virgen extra, 25 g de levadura de pan, 125 ml de agua (medio vaso) y una cucharadita de sal.

• ¿Por qué es mejor usar harina integral?

Por sabor y por salud.

La harina puede ser refinada o integral. La diferencia entre una y otra es la parte del grano que se usa para su elaboración. En la harina refinada se utiliza sólo el endospermo del grano, mientras que la integral incluye el cereal completo.

Los cereales tienen tres partes: la cáscara del cereal es el salvado, donde está la mayor parte de la fibra; la parte central es el endospermo, compuesto mayoritariamente por almidón; y el núcleo es el germen, donde se concentra la fracción grasa del cereal. Por eso el sabor de las harinas integrales es más intenso y complejo que el de las refinadas.

Las harinas integrales contienen todas la vitaminas y nutrientes del cereal completo, siendo especialmente interesante para nuestra salud su alto contenido en fibra. La fibra favorece el tránsito intestinal y además hace que el pan sea más saciante. No es que el integral tenga menos calorías, de hecho tiene las mismas, pero al resultar más saciante necesitaremos comer menos cantidad.

La fibra hace que el pan integral tenga menor índice glucémico, es decir, hace que metabolicemos los carbohidratos lentamente y que no aumenten repentinamente los niveles de glucosa en sangre. Por el contrario, los panes blancos tienen alto índice glucémico, lo que significa que se metabolizan muy rápido dando elevados y repentinos picos de glucosa en sangre y, en consecuencia, picos de insulina. Este es el motivo por el que el pan blanco es poco saciante y por el que las personas con diabetes limitan su consumo.

Además de la tradicional harina de trigo, se puede obtener harina de distintos cereales ricos en almidón como la espelta, el centeno, la cebada, la avena, el maíz, e incluso de leguminosas como los garbanzos o las judías, o del arroz. La harina está formada básicamente por hidratos de carbono, y en menor proporción proteínas, dependiendo del tipo de harina. El hidrato de carbono de las harinas vegetales es el almidón.

Para elaborar pan y masas de pizza se suele utilizar la harina de trigo porque ésta contiene gluten, un conjunto de proteínas, esencialmente gliadina y glutenina, que le otorgan elasticidad y consistencia a la masa. Las harinas sin gluten como las de trigo sarraceno, maíz o garbanzo, son muy difíciles de manejar. Extenderlas en forma de base de pizza es una tarea muy compleja, precisamente porque no producen masas elásticas.

• La química del amasado y del fermentado

Cuando hacemos la masa de una pizza tienen lugar varias reacciones químicas que serán las responsables de su textura, color y sabor.

Lo primero que hacemos es poner en un bol los 250 g de harina integral. A continuación desmenuzamos la levadura, añadimos la sal, el medio vaso de agua y las tres cucharadas de aceite de oliva virgen extra. Mezclamos inicialmente todos los ingredientes con ayuda de una cuchara, y a continuación amasamos a mano sobre una encimera durante 5-10 minutos. Después dejamos reposar la masa unos 30 minutos en el bol cubierto por un trapo.

Durante este proceso estarán ocurriendo una serie de reacciones químicas y bioquímicas que determinarán la textura y el sabor de la masa.

El protagonista del amasado es el gluten. La gliadina y la glutenina que componen el gluten se hidratan, captan el agua e interactúan entre sí dando lugar a la formación de un entramado reticular de gluten, que dota a la masa de elasticidad. El agua también hidrata el almidón, provoca la apertura de su estructura y la deja expuesta al ataque de las enzimas. Las enzimas también se activan al hidratarse, entre ellas las amilasas, que actúan rompiendo el almidón en hidratos de carbono simples.

La levadura (saccharomyces cerevisiae) la podemos comprar en el supermercado o en la panadería. La levadura se alimenta de los hidratos de carbono simples liberados y desprende dióxido de carbono y alcohol, responsables de la formación de burbujas. Para acelerar el proceso o crear más burbujas hay quien añade azúcar. La razón es que así la levadura tendrá más alimento con el que generar burbujas de dióxido de carbono. Aunque la textura puede mejorar en tiempo récord, nutricionalmente no es aconsejable añadir azúcar.

En el caso de no tener levadura, podemos hacer la masa con una cerveza, ya que la levadura de la cerveza es la misma que la del pan.

Hay que tener en cuenta que la sal inhibe el crecimiento de la levadura, así que añadir sal hace que el fermentado sea más lento, sin embargo, la fermentación lenta repercute positivamente en la textura final de la masa.

En el mercado tenemos otro tipo de productos que llamamos levaduras químicas que, aunque no son levaduras propiamente dichas, producen un efecto parecido sobre la masa. Se usan más en repostería para no tener que dejar fermentar la masa y poder hornearla inmediatamente. Estas levaduras químicas están compuestas esencialmente por bicarbonato sódico que en contacto con la masa y durante el horneado desprenden dióxido de carbono, responsable de las burbujas.

El aceite protege la masa de la pérdida progresiva de agua, lo que evita que se endurezca demasiado durante el horneado y una vez se enfríe.

Todas estas reacciones se producen durante el amasado y el reposo. Una vez transcurrido el tiempo de reposo, la masa habrá duplicado su volumen.

• La química del horneado.

Una vez tenemos la masa fermentada, el siguiente paso será extenderla. Si la harina tiene gluten, este proceso será bastante sencillo porque la masa será muy elástica. Podemos extenderla con las manos o con ayuda de un rodillo.

Extendemos la masa sobre una bandeja de horno cubierta con papel de horno. Este papel es un papel vegetal sulfurizado. Se ha tratado químicamente con un baño de ácido sulfúrico -de ahí el nombre- para tapar los poros de la celulosa y hacerlo impermeable y antiadherente. Este proceso también lo hace resistente a las temperaturas que manejamos en los hornos domésticos.

Sobre la masa podemos añadir los ingredientes que nos apetezcan. En este caso he utilizado tomate triturado, orégano, queso mozzarella rallado, champiñones frescos, aceitunas negras, jamón cocido extra y pimientos rojos asados.

Metemos la pizza en el horno y la dejamos a 240oC con calor arriba y abajo entre 20 y 25 minutos.

La levadura de la masa muere como consecuencia de las altas temperaturas, y el alcohol se evapora. El almidón de la harina comienza a gelatinizar, es decir, a formar una estructura diferente a la original en la que es capaz de atrapar el agua de la masa. En este proceso también interviene el gluten, que se pega al almidón creando una red que evita que las burbujas se escapen de la masa. A medida que la temperatura aumenta y la pizza continúa en el horno, empieza a dorarse. Este cambio paulatino de color es debido a la reacción química más famosa de la cocina: la reacción de Maillard entre los hidratos de carbono y las proteínas.

Todas las formas de conocimiento guardan relación entre sí, en mayor o menor medida. Preparar una pizza tiene su fundamento químico detrás. Desde el punto de vista de la salud y desde el punto de vista gastronómico. Conocerlo nos permite disfrutar más de todo el proceso. Esto es así porque el conocimiento es una forma de placer.

Sobre la autora: Déborah García Bello es química y divulgadora científica

El artículo Así es la química de una buena pizza se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. El teorema de la pizza
2. La dieta saludable es cuestión de química
3. Las reglas de una buena melodía

Ziortza Guezuraga Parkinsonen gaixotasunaren hiru fase ezberdintzeko sistema garatu dute ikerketan Kinect bideo-joko teknologia baliatuta.

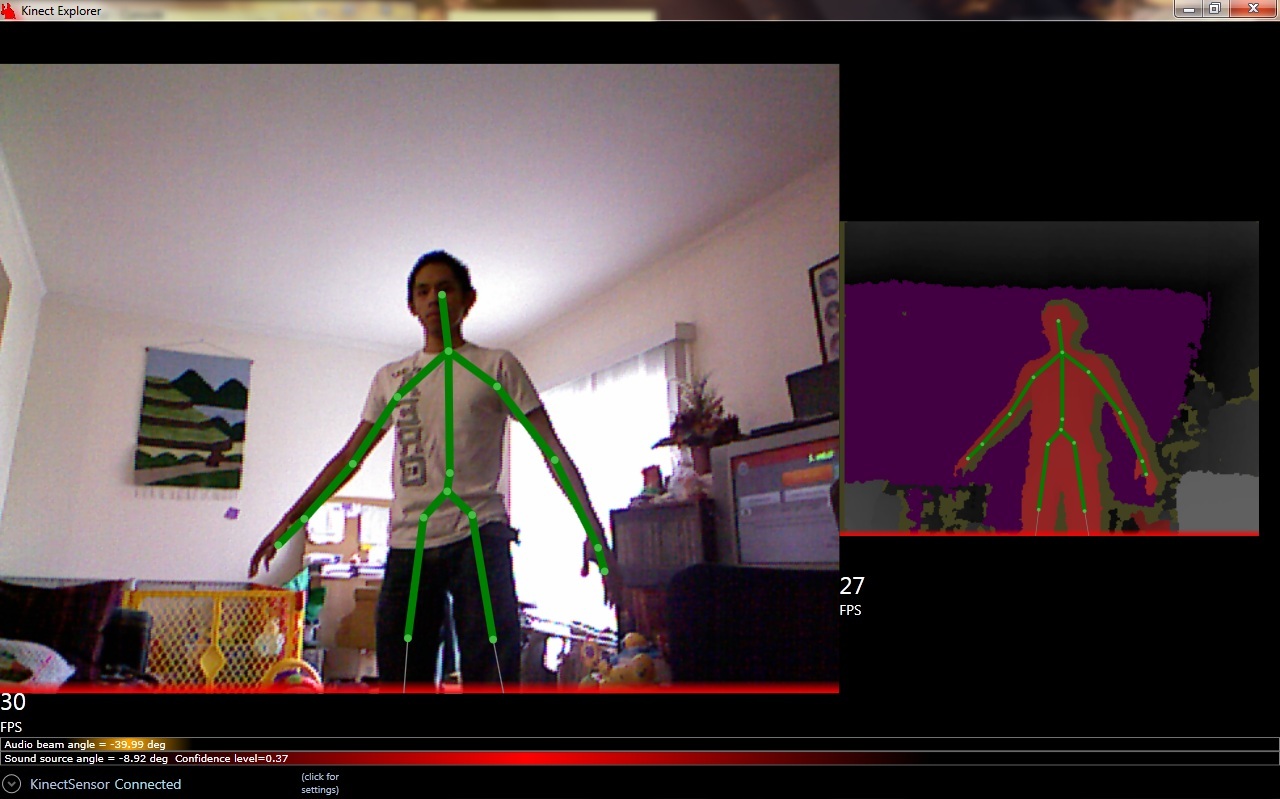
1. irudia: Kinect bideojoko teknologia baliatuta Parkinson gaixotasunaren fase ezberdinak ezagutu daitezke. (Argazkia: Sang1938)

Ibilera desgaitasunari aztertuta, parkinson gaixotasunaren faseen arabera gaixoak sailkatzeko gai da sistema. Hiru fase ezberdin daude Parkinsonen gaixotasunean ibilera gaitasunari begira:

1. Gaixotasun goiztiarrak, ezgaitasun axialik gabekoak.
2. Gaixo garatuagoak, ibileran ezgaitasunekin, baina ibilera blokeorik (FoG) gabe.
3. Gaixo garatuak, ibilera blokeoa pairatzen dutenak.

Ikerketan garatutako sistema gai da hiru faseak ezagutzeko, Kinect bideo-joko teknologia erabilita, %93,40ko doitasunarekin.

Fasea sailkatzen

Kinect erabilita garatutako sistemarekin lortutako informazioa baliatuta, parkinson gaixoen ibilera karakterizatzea izan da ikerketaren helburua. Neuroendekapenezko gaixotasuna da parkinsona eta arazo motorrak sorrarazten ditu, ibilera gaitasunean, esaterako. Hala, gaixotasunaren fase goiztiarrean pausuaren luzera laburtzea eta abiadura motela dira ibileraren ezaugarri nagusiak. Garatu ahala ibilera gaitasuna okerrera doa, ibileraren blokeoa (FoG) fasera heldu arte.

Parkinson gaixotasunaren alderdi oso ahulgarria da ibileraren blokeoa, erorketen atzean baitago, mugikortasuna gutxitu eta bizi kalitatea gutxitzeaz gain. Hori dela eta, ikerketaren helburua lokomozio aldaketak identifikatzea da, parkinsonak aurrera egin ahala modu progresiboan gertatzen direnak.

Horretarako, Kinect teknologia baliatuta, gaixo talde baten ibilera grabatu dute, parkinson faseen artean ezberdintzeko helburuarekin. 30 gaixo hartu dute parte ikerketan, neurologoek parkinson maila diagnostikaturik. Haien artean, zortzik gaixotasunaren fase goiztiarrean zeuden, hamaikak bigarren fase garatuagoan eta beste hamaikak hirugarren fasean.

Korridorean gora eta behera

4.5-5.5 metroko luzerako korridorean gora eta behera ibili dira pazienteak bi noranzkotan. Denera, 40 metro inguru ibili da paziente bakoitzak pasilloan gora-behera, norabidea aldatzeko biraketak barne. Mugimenduak batzeko bi Kinect aparailu erabili dira, bakoitzak 2.5 metro inguru grabatzen zuela. Bada leku bat non bi kamerak gainjarri egiten ziren, ibilbide osoa grabatu ahal izateko.

Kinect bakoitza ordenagailu independente batera konektatuta zegoen eta 30 frame segundoko grabatzeko gaitasuna zuen. Frame bakoitzak 25 artikulazio puntuz osatuta zegoen eta puntu bakoitzak lau balio izan ditu: 3 posizioa adierazteko eta laugarrena posizio balioa Kinectek ondorioztatutakoa den.

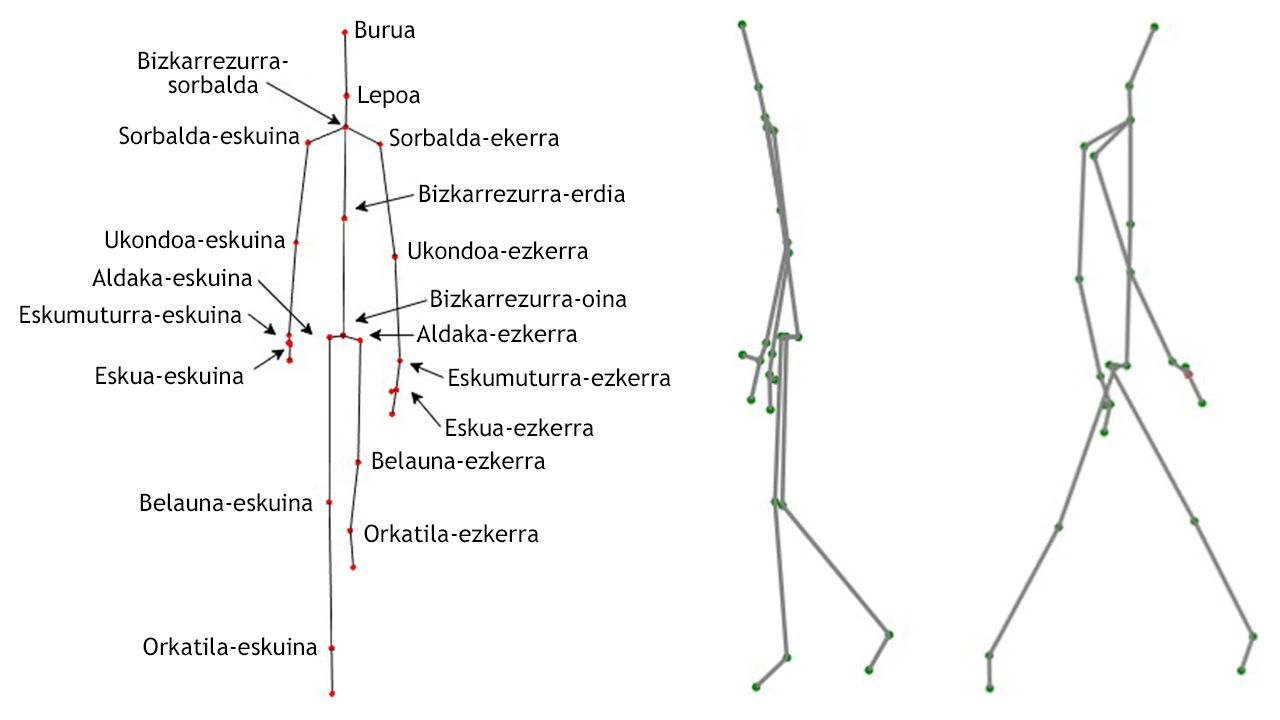
2. irudia: Kinectek ezagutzen dituen 25 artikulazio puntuetatik, 19 adierazgarrienak. (Ilustrazioa: Ziortza Guezuragak moldatua)

Sare bayestar eredua baliatu dute datuak lantzeko. Eta neurtutako datuetako batzuk bereziki adierazgarriak direla topatu dute; ezkerreko besoaren mugimendua eta posizioa, esaterako, nabarmen garrantzitsua da parkinson fasea ezagutzerakoan.

Ikerketaren ondorioen arabera, Kinect teknologian oinarritutako sistema baliagarria da ibilera desgaitasunaren larritasunari lotutako hiru fase ezberdintzeko parkinson gaixotasunari dagokionez.

Erreferentzia bibliografikoa:

Lacramioara, D., et al. , (2018). Using Kinect to classify Parkinson’s disease stages related to severity of gait impairment. BMC Bioinformatics, 10;19(1):471. DOI: 10.1186/s12859-018-2488-4.

———————————————————————–

Egileaz: Ziortza Guezuraga (@zguer) kazetaria da eta Euskampus Fundazioko Kultura Zientifikoko eta Berrikuntza Unitateko zabalkunde digitaleko teknikaria.

——————————————————————

The post Bideo-joko teknologia parkinsonaren fasea sailkatzeko appeared first on Zientzia Kaiera.

El artista futurista italiano Giacomo Balla (1871-1958) pintó una obra titulada Los números enamorados en 1924, asociando una cualidad humana, como es el enamoramiento, a los números. También en el ámbito de las matemáticas nos gusta asociar a los números, en particular, a los números naturales, cualidades humanas. Existen números amigos, sociables, novios, narcisistas, felices, tristes, hambrientos, intocables, ambiciosos, afortunados, poderosos, malvados, odiosos, prácticos o raros, pero también, con otras denominaciones curiosas, como números vampiros, parásitos, perniciosos, apocalípticos, perfectos, poligonales, cíclicos, automorfos, sublimes, abundantes, escasos o intocables.

Números enamorados (1924), del artista futurista italiano Giacomo Balla, MART, Museo d’arte moderna e contemponanea di Trento e Rovereto, Italia. Fotografía de MART

Algunas de estas familias de números deben su propiedad definitoria al comportamiento de sus divisores propios, es decir, entre los divisores no se considera al propio número. Son a estas familias de números naturales a las que vamos a dedicar la entrada de hoy de la sección Matemoción del Cuaderno de Cultura Científica.

Empecemos con unas familias de números con un origen muy antiguo. Un número se dice que es perfecto si es igual a la suma de sus divisores (propios), como ocurre con los números 6 = 1 + 2 + 3 y 28 = 1 + 2 + 4 + 7 + 14. Se los denominó perfectos porque en tiempos antiguos se dio a esta propiedad una interpretación divina. Por ejemplo, San Agustín relaciona el hecho de que Dios crease el mundo en 6 días, con la perfección de este número.

Los siguientes números perfectos, después de 6 y 28, conocidos ya desde la antigüedad, son

496 = 1 + 2 + 4 + 8 + 16 + 31 + 62 + 248

8.128 = 1 + 2 + 4 + 8 + 16 + 32 + 64 + 127 + 254 + 508 + 1.016 + 2.032 + 4.084

Se desconoce el origen exacto de los números perfectos, aunque ya eran conocidos por los matemáticos griegos. Euclides de Alejandría (aprox. 325 – 265 a.n.e.) los estudia en su obra Los Elementos, aunque antes los había estudiado Pitágoras (aprox. 570 – 495 a.n.e.), e incluso podrían haber sido conocidos por los egipcios.

Euclides demostró que para algunos números primos p, los números de la forma 2p–1 (2p – 1) son perfectos, por ejemplo, para p = 2, 3, 5, y 7, se obtienen los perfectos anteriores. Dos milenios después, el matemático suizo Leonhard Euler (1707 – 1783) demostraría que todos los números perfectos pares son de esta forma, con (2p – 1) un número primo.

El quinto número primo encontrado fue 33.550.336, para p = 13, que aparece en un manuscrito del siglo XV. El sexto y séptimo –para p = 17 y 19– fueron descubiertos por el matemático italiano Pietro Cataldi (1548 – 1626) en 1588, en concreto, 8.589.869.056 y 137.438.691.328. Y Euler, en 1772, descubrió el octavo, que es 230 (231 – 1) = 2.305.843.008.139.952.128.

Obtener números perfectos es una tarea muy difícil, luego podemos decir que “la perfección es difícil de conseguir”. Antes del siglo XX solo se conocían 9 números perfectos. El noveno fue obtenido, para p = 61, por el matemático ruso Iván Pervushin (1827 – 1900), en 1883. De hecho, en la fórmula de Euclides-Euler no basta con que p sea primo, ya que para p = 11, 211 – 1 = 2.047 = 23 x 89, no es primo, con lo cual 210 (211 – 1) no es perfecto.

Con la ayuda de los ordenadores ha sido posible calcular muchos más, pero no demasiados. Solo se conocen, hasta la fecha, 51 números perfectos. El último descubierto, en 2018, fue el correspondiente al primo p = 82.589.933.

Se desconoce si existe un número infinito o finito de números perfectos. Además, todos los números perfectos conocidos son pares, y no se sabe si existen impares. Lo que se ha conseguido demostrar es que de existir tendrían que cumplir una serie de propiedades, como tener al menos 9 divisores primos distintos o ser mayores que 101.500, entre muchas otras.

Veintiocho (modelo para una escultura pública), 1992, del artista estadounidense Jonathan Borofsky. Imagen de su página web

Ya los griegos dividieron a los números naturales que no son perfectos en dos categorías, los abundantes y los deficientes. Los números que no son perfectos pueden ser abundantes, cuando el número es menor que la suma se los divisores, como el 12 deficientes en el caso contrario, como el 14 > 1 + 2 + 7 = 10 o todos los números primos, cuyo único divisor propio es el 1. Estos conceptos, como la perfección, formaron parte de la numerología griega.

El religioso, teólogo y matemático anglosajón Alcuino de York (735 – 804) relacionaba la “segunda creación” de Dios, el diluvio universal y el Arca de Noé, con el número 8, ya que la humanidad desciende de las 8 almas que se salvaron del diluvio refugiándose en el Arca de Noé. Por lo tanto, esta es una creación imperfecta, puesto que el número 8 es deficiente, 8 > 1 + 2 + 4.

Los números llamados abundantes no son, sin embargo, tan abundantes como su nombre indica. Existen 245 números abundantes menores que 1.000, aunque solo uno de ellos impar, el número 945 = 33 x 5 x 7, los demás son pares, y solo 3 números perfectos (por supuesto, pares), el resto son deficientes. Entre los primeros 50.000 números hay 37.602 deficientes, 4 perfectos y 12.394 abundantes. Entre estos 12.394 números abundantes, solo 114 son impares.

Así como lo bello y lo excelente es raro de encontrar y se cuenta pronto, pero lo feo y lo malo siempre es prolífico, así también los números abundantes y deficientes resultan ser muchos y en desorden, y su descubrimiento no obedece a sistema alguno. Pero los perfectos, son a un tiempo escasos en número y se hallan dispuestos en un orden apropiado.

Nicómaco de Gerasa (aprox. 60 – 120 n.e.), Introducción a la Aritmética

Imagen 3 (Pie de imagen: You know my name (look up the number), acrílico sobre papel, 63 x 90 cm, del artista suizo Eugen Jost. Entre las sucesiones de números que aparecen, están los primeros números perfectos. Imagen de Plus Magazine [https://plus.maths.org/content/postcard-italy])

Entre los números abundantes, es decir, aquellos que son menores que la suma de sus divisores, se considera que son números casi perfectos aquellos tales que la suma de sus divisores es uno menos que el número. Así, el 16 es un número casi perfecto ya que 1 + 2 + 4 + 8 = 15. De hecho, todas las potencias de 2 son casi perfectas:

Los únicos números casi perfectos que se conocen son las potencias de 2, y es un problema abierto demostrar que estos son los únicos que existen.

Otra familia de números relacionada con la perfección, son los números múltiplo-perfectos o multi-perfectos, aquellos tal que la suma de sus divisores (recordemos que todo el tiempo estamos refiriéndonos a los divisores propios) no es el número, sino un múltiplo del mismo. Por ejemplo, los divisores del número 120 = 23 x 3 x 5 son 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40 y 60, cuya suma es 240 = 2 x 120. Solo se conocen 6 números multi-perfectos cuya suma sea el doble del número, 120, 672, 523.776, 459.818.240, 1.476.304.896, 51.001.180.160, y todos son pares. O, se conocen 36 cuya suma es el triple, de nuevo todos pares, de los cuales el más pequeño es 30.240.

Hardy’s Taxi, acrílico sobre lienzo, 60 x 60 cm, del artista suizo Eugen Jost. Obra perteneciente a la exposición Everything is number

Más aún, un número se dice que es ambicioso si puede llegar a ser perfecto de la siguiente forma. Dado el número se toma la suma de sus divisores, con este nuevo número se vuelve a considerar la suma de sus divisores, y se continúa así, de forma que el número es ambicioso si llega un momento que se alcanza un número perfecto, como en el caso del número 95, cuyos divisores suman 1 + 5 + 19 = 25, y los divisores de este suman 1 + 5 = 6, que es perfecto. Números no ambiciosos son el 24 o los números primos (cuyo único divisor es el 1).

Veamos que el 24 = 23 x 3 no es ambicioso. Sus divisores son 1, 2, 3, 4, 6, 8 y 12, cuya suma es 1 + 2 + 3 + 4 + 6 + 8 + 12 = 36. Ahora, los divisores de 36 = 22 x 32 son 1, 2, 3, 4, 6, 9, 12 y 18, cuya suma es 55. Ahora este número, 55 = 5 x 11, tiene solo tres divisores 1, 5 y 11, cuya suma es 17, que es primo, luego su único divisor es 1 y se estaciona la sucesión. En consecuencia, el 24 no es ambicioso. Solo se conocen 16 números ambiciosos, 25, 95, 119, 143, 417, 445, 565, 608, 650, 652, 675, 685, 783, 790, 909, 913, e incluso un número tan bajo como 276 se desconoce si es, o no, ambicioso (aunque seguramente no).

Y también relacionados con la perfección están los números sublimes, aquellos tales que tanto el número de sus divisores (incluido ahora el propio número), como la suma de los mismos son perfectos, como el 12, que tiene 6 divisores y su suma es 1 + 2 + 3 + 4 + 6 + 12 = 28, aunque solo se conoce otro número sublime más, que es el siguiente

6.086.555.670.238.378.989.670.371.734.243.169.622.657.830.773.351.885.970.528.324.860.512.791.691.264.

Números amigos (2010), del artista británico Andrew Crane

A continuación, vamos a introducir parejas de números con una fuerte conexión entre ellos, desde la perspectiva que estamos analizando en esta entrada. Empecemos por el número 284, que se puede escribir como la multiplicación de los números primos 71 y 2 de la siguiente forma 284 = 71 x 22. Por lo tanto, los divisores propios del 284 son 1, 2, 4, 71 y 142, cuya suma es

1 + 2 + 4 + 71 + 142 = 220.

Si ahora consideramos el número que nos ha salido, 220, y buscamos sus divisores, como 220 = 11 x 5 x 22, entonces estos son 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 y 110, y la suma de ellos es

1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 + 110 = 284,

precisamente el primer número. Por este motivo, se dice que los números 220 y 284 son números amigos. Es decir, dos números son amigos si la suma de los divisores (propios) del primero es igual al segundo, y viceversa.

Este par de números amigos (220, 284) ya era conocido por los pitagóricos, quienes les atribuían propiedades místicas. En general, en la antigüedad se pensaba que estos números tenían poderes místicos, y eran utilizados en textos religiosos y de magia, en particular, en relación al amor y la amistad. Los astrónomos griegos los incorporaron en sus horóscopos, talismanes y amuletos.

“Las personas expertas en los talismanes afirman que los números amigos 220 y 284 ejercen una fuerte influencia para establecer una unión o una amistad muy fuerte entre dos personas”

Ibn Jaldún (1332-1406), Muqaddima (prolegómenos), 1377

Cuenta una leyenda que había un sultán aficionado a los puzzles, que al descubrir que tenía a un matemático como prisionero, decidió plantearle la siguiente cuestión. El sultán le dijo al matemático que le planteara un reto, un problema, y que estaría libre durante el tiempo que él necesitara para resolverlo, pero una vez resuelto por el sultán, el matemático sería ejecutado.

El matemático le explicó que los números 220 y 284 son números amigos, y le planteó que buscara otro par de números amigos. El sultán no lo consiguió y el matemático murió de viejo y siendo un hombre libre.

De hecho, calcular más pares de números amigos no es una tarea sencilla. Muchos matemáticos árabes estudiaron los números amigos, entre los siglos IX y XIV, como el iraquí Thabit ibn Qurra (826 – 901) quien dio una fórmula para obtener números amigos. En particular, se obtuvieron dos nuevos pares de números amigos

(17.296, 18.416) y (9.363.584, 9.437.056).

En el siglo XVII los grandes matemáticos franceses Pierre de Fermat (1601 – 1665) y René Descartes (1596 – 1650) redescubrieron la fórmula del matemático árabe, así como los dos anteriores pares de números amigos, que es ocasiones son atribuidos a ellos. Otro gran matemático ya mencionado, Leonhard Euler, extendió la fórmula de Qurra y obtuvo 64 nuevos pares de números amigos.

Curiosamente, a todos ellos se les pasó el siguiente par de números amigos más pequeño, después de (220, 284), el par (1.184, 1.210), descubierto por el adolescente Nicolo Paganini, de 16 años, en 1866.

La tarea siguió siendo compleja y hasta 1946 solo se consiguieron descubrir 390 pares de números amigos, hasta que llegó la era de los ordenadores, y su potencia de cálculo, que, junto a nuevos algoritmos, ha permitido calcular (según la wikipedia) hasta marzo de 2019 exactamente 1.223.386.359 parejas de números amigos. Sin embargo, a día de hoy no se sabe aún si existen infinitos pares de números amigos.

Anillos hexagonales, con oro amarillo y oro rosa, con la pareja de números amigos 220 y 284, de la tienda londinense Comford Station, y la caja con la explicación de la pareja de números amigos

Otro nexo de unión entre números. Se dice que dos números son novios o casi-amigos si cada uno de ellos es igual a la suma de sus divisores menos 1, como el 48 = 1 + 3 + 5 + 15 + 25 – 1 y el 75 = 1 + 2 + 3 + 4 + 6 + 8 + 12 + 16 + 24 – 1. Las primeras parejas de números novios son (48, 75), (140, 195), (1.050, 1.925), (1.575, 1.648), (2.024, 2.295) y (5.775, 6.128). Los números de todas las parejas de novios conocidas tienen paridad opuesta, es decir, uno es par y el otro impar.

La propiedad de amistad puede generalizarse a un grupo de números, de forma que la suma de los divisores de cada uno es igual al siguiente, y la del último igual al primero, entonces se habla de números sociables. El grupo de números más pequeños que son sociables son 12.496, 14.288, 15.472, 14.536 y 14.264. Comprobémoslo:

1) 12.496 = 24 x 11 x 71, divisores: 1, 2, 4, 8, 11, 16, 22, 44, 71, 88, 142, 176, 284, 568, 781, 1.136, 1.562, 3.124 y 6.248, cuya suma es 14.288;

2) 14.288 = 24 x 19 x 47, divisores: 1, 2, 4, 8, 16, 19, 38, 47, 76, 94, 152, 188, 304, 376, 752, 893, 1.786, 3.572 y 7.144, cuya suma es 15.472;

3) 15.472 = 24 x 967, divisores: 1, 2, 4, 8, 16, 967, 1.934, 3.868 y 7.736, cuya suma es 14.536;

4) 14.536 = 23 x 23 x 79, divisores: 1, 2, 4, 8, 23, 46, 79, 92, 158, 184, 316, 632, 1.817, 3.634 y 7268, cuya suma es 14.264;

5) 14.264 = 23 x 1.783, divisores: 1, 2, 4, 8, 1.783, 3.566 y 7.132, cuya suma es 12.496.

Se conocen 5.410 grupos de números sociables (véase la lista de números sociables de David Moews), la mayoría formados por 4 números, aunque existe un grupo formado por 28 números.

También existen intocables dentro de la familia de los números naturales, son aquellos que no se pueden expresar como suma de los divisores de ningún número. El número 2 es intocable, el 3 no lo es (3 = 1 + 2, divisores del 4), el 4 tampoco (4 = 1 + 3, divisores del 9) y el 5 sí, ya que solo puede expresarse como 1 + 4, pero si el 4 es divisor del número, también lo es el 2 y la suma sería al menos 7. El siguiente intocable es el 52.

Los números intocables menores de 500 son:

2, 5, 52, 88, 96, 120, 124, 146, 162, 188, 206, 210, 216, 238, 246, 248, 262, 268, 276, 288, 290, 292, 304, 306, 322, 324, 326, 336, 342, 372, 406, 408, 426, 430, 448, 472, 474, 498.

El matemático húngaro Paul Erdös (1913-1996) demostró que existen infinitos números intocables.

“Dice Trece [la protagonista se refiere con números a los hombres que han pasado por su vida] que le ha hecho esos dos regalos –el libro [de Murakami] y lo del segundo cajón [un consolador]– para que se acuerde de él. Sin embargo, por la esencia oriental de uno y las dimensiones del otro, lo que Trece ha conseguido es que Pi, en lugar de acordarse de él, se acuerde de Dos. Por ambas razones.

Dos se ha convertido en una medida (de hecho, es un número intocable, pues no es la suma de los divisores de ningún número). No tiene tanta importancia como persona real en el presente […] sino como recuerdo y, sobre todo, como convención, como medida. Dos es la medida del sistema métrico sentimental”

Juan Pardo Vidal, La luz de la mesita de noche, Sloper, 2012

Por otra parte, un número se dice que es práctico si todos los números naturales más pequeños que él pueden ser expresados como suma de distintos divisores del número. Así, el número 12 es un número práctico ya que todos los números menores que él, desde el 1 al 11, pueden ser expresados como suma de algunos de los divisores de 12. Veámoslo: los divisores de 12 son 1, 2, 3, 4 y 6, luego 1 = 1, 2 = 2, 3 = 3, 4 = 4, 5 = 1 + 4, 6 = 2 + 4, 7 = 1 + 2 + 4, 8 = 2 + 6, 9 = 3 + 6, 10 = 4 + 6 y 11 = 1 + 4 + 6.

Los números prácticos menores que 100 son: 1, 2, 4, 6, 8, 12, 16, 18, 20, 24, 28, 30, 32, 36, 40, 42, 48, 54, 56, 60, 64, 66, 72, 78, 80, 84, 88, 90 y 96.

El concepto fue definido en 1948 por el matemático indio A. K. Srinivasan, números que en su opinión eran interesantes de estudiar por su relación con las subdivisiones del dinero, los pesos y las medidas. Aunque estos números ya fueron utilizados por el matemático italiano Fibonacci (Leonardo de Pisa, 1170 – 1240), en su obra Liber Abaci (Libro del Ábaco, 1202), en relación a las fracciones egipcias (véase la entrada de Marta Macho, Sobre fracciones egipcias).

Claramente, todas las potencias de 2 son prácticas, ya que dado 2n, se puede expresar cualquier número entre 1 y 2n – 1 como suma de potencias de 2, menores que 2n, que son sus divisores. Es solamente una cuestión de divisibilidad y el fundamento del sistema binario. Se conocen muchas propiedades de los números prácticos, como que existen infinitos, el producto de dos números prácticos es un número práctico, los números perfectos pares, luego de la forma 2p–1 (2p – 1), son prácticos, o que, salvo el 1 y el 2, todos los números prácticos son divisibles por 4 o 6, entre otras.

Instalación Forest of numbers – Bosque de números (2017), de la artista francesa Emmanuelle Moureaux. Imagen de su página web

Y no podían faltar los números raros, o extraños, que son aquellos que son abundantes, es decir, la suma de los divisores es mayor que el número, pero no se puede obtener el número exacto quitando algunos de los divisores, es decir, como suma de un subconjunto de divisores propios. Por ejemplo, el 12 es abundante, pero como 12 = 2 + 4 + 6, no es raro, y el número raro más pequeño es 70 (cuyos divisores son 1, 2, 5, 7, 10, 14, 35).

Aunque se sabe que existen infinitos números raros, estos son relativamente escasos, por ejemplo, solamente hay 7 números raros menores que 10.000, que son 70, 836, 4.030, 5.830, 7.192, 7.912 y 9.272. Todos los números raros conocidos son pares y si existe alguno impar deberá ser, por lo menos, mayor que 1021.

Cerramos este repaso a algunas tribus numéricas con los números poderosos, que son aquellos tales que, si un número primo p es divisor suyo, también lo es su cuadrado p2, como el 36, cuyos divisores primos son 2 y 3, y sus cuadrados también son divisores de 36. Curiosamente, un número m es poderoso si, y sólo si, se puede expresar como m = a2b3, para algún par de números a y b. Claramente, si un número es de la forma a2b3 es poderoso (ya que los cuadrados de los primos de la descomposición en primos de a y b claramente dividen a a2b3), pero, además, todos los números poderosos son de esta forma. Veámoslo:

Por ejemplo, para el número m = 21.600 = 25 x 33 x 52, tendríamos que b = 2 x 3 = 6 y a = 2 x 5 = 10.

Existen algunos problemas interesantes sobre los números poderosos. Como se observa fácilmente, todo número impar es resta de dos cuadrados, luego de dos números poderosos, 2 k + 1 = (k + 1)2 – k2. Lo mismo ocurre con los múltiplos de 4, ya que 4 k + 4 = (k + 2)2 – k2.

Pero, ¿qué pasaba con los números pares no divisibles por 4, podían expresarse como resta de números poderosos? El matemático e ingeniero estadounidense Solomon W. Golomb (1932 – 2016), conocido por sus trabajos sobre juegos matemáticos, observó que algunos sí podían expresarse, como 2 = 33 – 52, 10 = 133 – 37 o 18 = 192 – 73 = 35 – 152, y conjeturó que el número 6 no podía expresarse como resta de números poderosos, así como infinitos otros números pares. El matemático polaco Władysław Narkiewicz demostró que el 6 no solo podía representarse de esta forma, 6 = 5473 – 4632, sino que existían infinitas formas de hacerlo. Más aún, en 1982, el matemático estadounidense Wayne L McDaniel extendió el resultado para todos los números pares, no divisibles por 4.

Por otra parte, Paul Erdös conjeturó, y fue demostrado por el matemático británico Roger Heath-Brown, que todo número natural suficientemente grande puede expresarse como suma de tres números poderosos.

Instalación “SOHO” (2008), del artista japonés Tatsuo Miyajima. Imagen de su página web

Bibliografía

1.- Clifford A. Pickover, El prodigio de los números. Desafíos, paradojas y curiosidades matemáticas, Ma Non Troppo (ediciones Robinbook), 2002.

2.- Clifford A. Pickover, La maravilla de los números. Un viaje por los secretos de las matemáticas, sus desafíos y caprichos, Ma Non Troppo (ediciones Robinbook), 2002.

3.- Lamberto García del Cid, Números notables. El 0, el 666 y otras bestias numéricas, El mundo es matemático, RBA, 2010.

4.- Howard H. Eves, Mathematical Circles, The Mathematical Association of America (MAA), 2003.

5.- Wikipedia: Perfect number

6.- David G. Kendall, The Scale of Perfection, Journal of Applied Probability, Vol. 19, Essays in Statistical Science, pp. 125-138, 1982.

7.- Eugen Jost, A postcard from Italy, Plus Magazine, 1999

8.- Wolfram Mathworld: Multiperfect number

9.- Wolfram Mathworld: Aspiring number

10.- Wikipedia: Amicable numbers

11.- Wikipedia: Betrothed or quasi amicable numbers

12.- Wikipedia: Untouchable number

13.- Wikipedia: Practical number

14.- Página web de la artista Emmanuelle Moureaux

15.- Wikipedia: Weird number

16.- Wikipedia: Powerful number

17.- Página web del artista japonés Tatsuo Miyajima

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica

El artículo Los números enamorados se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Una conjetura sobre ciertos números en el ‘sistema Shadok’
2. El origen poético de los números de Fibonacci
3. Buscando lagunas de números no primos

Juanma Gallego Loa astean zehar nola banatzen den aztertu dute zientzialariek, eta ondorioztatu dute amarru egiterik ez dagoela: astean zehar lo egin ez duguna ezin dugu asteburuan berreskuratu.

Umeei handitan zer izan nahi duten galdetzen zaienean, ez dugu espero horietako batek “loti” izan nahi duela erantzutea. Hala balitz, seguruenera, alferrontzitzat hartuko genuke. Baina agian hori izango da klaseko ume guztien artean errealitateari gehien hurbilduko dena. Ez da txantxa. Batez bestean, bizitzaren heren bat ematen dugu lotan, baina oraindik hori zergatik egiten dugun ez dugu guztiz ulertzen. Umore puntu batekin, John Allan Hobson psikiatrak zioen loaren funtzio ezagun bakarra dela… logura sendatzea.

1. irudia: Ikertzaileek badakite loak ez diola erantzuten behar bakar bati, hainbat prozesu biologikoren multzo bati baizik. (Argazkia: Lance Anderson / Unsplash)

Aditu hori ez zen txisteak kontatzera mugatu, noski. Benetan loak funtzioren bat ote zuen argitu nahi izan zuen. Ametsei, bederen, ez zien halakorik ikusi. Hobsonek garatu zuen hipotesiaren arabera, ametsen jatorria prozesu honetan datza: enbor entzefalikoan sortzen diren seinale aleatorioei zentzu bat ematen saiatzen da garun-azala eta, horregatik, garunean bilduta dauden irudi eta esperientzien zatiekin osotasun bat gauzatzen saiatzen da. Esan beharrik ez dago, gehienetan handik hona bildutako txatal horiekin zentzuduna den ezer sortzerik ez dago, baina gizakiaren erraietan dago mundua ulertzeko eta ordenatzeko joera. Hortik abiatzen omen dira ametsak. Badirudi, beraz, antzinako gizakiek jainkoak ikusten zituzten eremuetan, edo Freuden jarraitzaileek subkontzientearen desio erreprimituak ikusi nahi dituzten ametsetan, seinale kimikoen anabasa bat ordenatzeko joera besterik ez dagoela.

Ametsei oraindik arrazoirik aurkitu ez bazaie ere, lo egiteko prozesuaren atzean dauden zioak ikertzen jarraitzen dute zientzialariek. Momentuz, adituen artean gehien zabalduta dagoen ustea da loak ez diola behar bakar bati erantzuten, eta bai, berriz, prozesu biologiko multzo bati. Besteak beste, sistema immunologikoaren eta sistema endokrinoaren funtzionamendu egokiari.

Oroimenean ere badira eraginak. Are gehiago, munduaren pertzepziorekiko ere aurkitu da harremanik. Investigación y Ciencia aldizkarian Robert Stickgold psikiatrak azaltzen du berak egindako esperimentu bat: 26 laguneko talde bat hartu zuen; horietatik erdiak ez zuen bezperan lorik egin. Guztiei hitz positiboak, negatiboak eta neutroak erakutsi zizkien, eta handik bi gauera ezustean oroimen proba egin zien. Lo gutxi egin zutenei hitzak gogoratzeko gaitasuna %40 gutxitu zitzaien, baina hitz negatiboen kasuan %20 besterik ez zen gutxitu. Adituak ondorio argia atera zuen: “Emaitza honek aukera lazgarri batera eraman gaitzake: lo egin ezean, gertakari positiboak baino, gertakari negatiboak oroituko ditugu, eguneroko bizitzaren oroimen partziala eta, seguruenena, etsigarria sortuta”.

Sistema endokrinoari dagokionez, Karine Spiegel neurozientzialariak egindako esperimentuetan ikusi da glukosa odoletik erauztea zailagoa izaten dela lo gutxi eginez gero, eta jateko gogoa handitzen dela ere (jangura eragiten duen grelina hormona gehiago baitago odolean, gosea inhibitzen duen leptina hormonaren kopuru txikiagoa dagoen bitartean). Horregatik, lo gutxi egitea pisua irabaztearekin lotu izan da sarri.

Orain beste esperimentu sorta bat gehitu zaio ikerketa lerroari. Boulder-Coloradoko Unibertsitateko (AEB) ikertzaile talde batek loaren banaketari buruzko esperimentua egin du, eta Current Biology aldizkarian argitaratu dituzte emaitzak.

Lo gutxi egin izanagatik obesitatea edo diabetesa bezalako gaitzak izateko aukerak biderkatzen direla pentsatzeko arrazoi dezente daude. Baina zenbat lo egin behar da? Oraindik ere ez dago oso garbi noraino den arriskutsua gomendatu ohi diren zortzi orduak baino gutxiago edo baino gehiago lo egitea. Bestetik, jakina da XXI. mendean mendebaldeko gizarteetan denbora lan astearen eta asteburuaren artean banatu ohi dela, eta horrek aspaldi jarri zuen mahai gainean beste galdera garrantzitsu bat: astean zehar lo egin ez dena asteburuan berreskuratzeko aukerarik al dago? Galdera horren erantzuna aurkitu nahi izan dute.

2. irudia: Lo gutxi egitean jangura handitu egiten da. Kontua ez da soilik “eskurago” dugula hozkailua: gutxiago lo eginez gero, odolean jangura arautzen duten hormonen kopurua aldatzen da. (Argazkia: Aaron Thomas / Unsplash)

Modu honetan antolatu dute esperimentua: lehenik eta behin, hiru multzotan banatu dituzte ikerketan parte hartu dituzten 36 boluntarioak. Kohorte handiak edo datu epidemiologiko andana erabiltzen duten beste hainbat ikerketarekin alderatuta, lagin txikia dela eman dezake, baina kontuan hartu behar da mota honetako esperimentuetan baldintza ahalik eta kontrolatuenak edukitzen lehenesten dela: 36 lagun hauek bi astez izan dituzte sartuta laborategi batean. Lehen taldekoek bederatzi egunetan bederatzi orduz lo egin ahal izan dute. Bigarren taldekoek bost orduz lo egin dute astean zehar, eta nahi duten adina asteburu osoan zehar. Hirugarren taldeko gizajoek, berriz, eguneko bost urte baino ezin izan dute lo egin esperimentuak iraun duen bitartean.

Gutxiago lo egiten zuten taldeetakoek mokadu gehiago hartu dituzte afariaren ondoren, eta, beraz, pisua irabazi dute. Asteburuan soilik lo asko egin dutenek gutxiago jan dute, baina astean zehar berriro gehiago jateari ekin diote, errebote efektua sortuz. Lehen talde honetan intsulinarekiko sentsibilitatea %27 gutxitu dela neurtu dute.

Intsulina beharrezkoa da elikagaietatik datozen azukreak asimilatzeko. Ezaguna da diabetesaren jatorrian dagoela hormona hau. Batzuetan, pankreak intsulina nahikoa sortzen ez duelako, eta, besteetan, organismoak ez duelako erabiltzen hormona hori modu egokian. Kasu bietan, ondorioa berdina da: glukosa ez da zeluletan sartzen, eta odolean geratzen da.

Erloju zirkadianoan ere ikusi dute eragina. Zentzu horretan, lo orduak asteburuetan berreskuratu dituztenek ondorio negatiboak izan dituzte. Egileek diote ez zutela espero ondorio hau. “Gure emaitzetatik iradoki daitekeenez, hain zabalduta dagoen joera hori ez da osasun estrategia egokia: gau eta egun lan egitea, hain zuzen, eta gero lo falta hori asteburuan konpentsatzen saiatzea”, adierazi dute.

Erreferentzia bibliografikoa:

Depner et al., Ad libitum Weekend Recovery Sleep Fails to Prevent Metabolic Dysregulation during a Repeating Pattern of Insufficient Sleep and Weekend Recovery Sleep. Current Biology 29, 1–11 March 18, 2019. DOI: https://doi.org/10.1016/j.cub.2019.01.069

———————————————————————————-

Egileaz: Juanma Gallego (@juanmagallego) zientzia kazetaria da.

———————————————————————————-

The post Astean zehar izandako lo falta ezin da konpentsatu asteburuan appeared first on Zientzia Kaiera.

Imagen: Wikimedia Commons

A principios del siglo XIX, cuando el prestigio de Newton era en gran medida el sostén de la hipótesis corpuscular de la luz, Thomas Young resucitó la hipótesis ondulatoria. En experimentos realizados entre 1802 y 1804 Young descubrió que la luz muestra el fenómeno de interferencia. La hipótesis corpuscular de la luz no puede explicar fácilmente los patrones de interferencia producidos por la luz. El famoso “experimento de doble rendija” de Young proporcionó la prueba convincente de que la luz tiene propiedades que solo se pueden explicar en términos de ondas.

El experimento de Young se puede realizar muy fácilmente. Consiste, básicamente, en dividir un solo haz de luz en dos haces para garantizar que estén en fase. Luego se permite que los haces resultantes de la división se superpongan, y los dos trenes de ondas interfieren, constructivamente en algunos lugares y destructivamente en otros. Para simplificar la interpretación del experimento, podemos suponer que se realiza con luz que tiene una única longitud de onda definida λ.

Young usó una pantalla negra con un pequeño agujero perforado para producir un haz de luz estrecho en una habitación a oscuras. En la trayectoria del haz colocó una segunda pantalla negra en la que había cortado dos rendijas estrechas, muy juntas. Tras esta pantalla colocó otra pantalla más, pero blanca. La luz que entraba por cada rendija se difractó y se extendió por el espacio más allá de la pantalla. La luz de cada rendija interfirió con la luz de la otra, y el patrón de interferencia se mostró en la pantalla blanca. Donde la interferencia era constructiva había una banda brillante en la pantalla. Donde la interferencia era destructiva, la pantalla permanecía oscura.

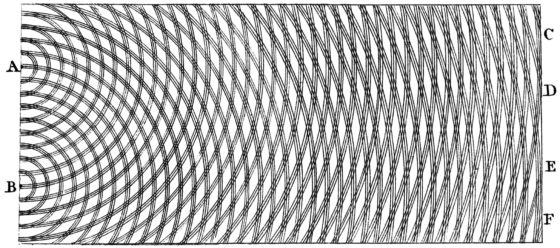Reproducción del diagrama de Thomas Young (1807) para explicar el resultado del experimento de la doble rendija (situadas en A y B) que produce mínimos en C,D,E y F, tal y como aparece en T. Young (ed. G. Peacock), 1855, Miscellaneous Works of the late Thomas Young, London: J. Murray, vol. 1. Imagen: Wikimedia Commons

Es una medida del genio de Young el que pudiese encontrar, por experimento, valores numéricos para algo tan pequeño como la longitud de onda de la luz. Él lo expresó así:

From a comparison of various experiments, it appears that the breadth of the undulations constituting the extreme red light must be supposed to be, in air, about one 36 thousandth of an inch, and those of the extreme violet about one 60 thousandth.

A partir de una comparación de varios experimentos, parece que la amplitud de las ondulaciones que constituyen la luz roja extrema debe suponerse que sea, en el aire, aproximadamente una 36-milésima de pulgada. [7·10-7 m], y las del violeta extremo alrededor de una 60-milésima [4·10-7 m].

Al anunciar su resultado, Young hizo un especial esfuerzo por evitar las críticas de los seguidores de Newton, a quien se consideraba un partidario de la hipótesis corpuscular de la luz. Señaló que el propio Newton había hecho varias afirmaciones a favor de una teoría de la luz que tenía algunos aspectos de la hipótesis ondulatoria.

Sin embargo, Young no fue tomado en serio. No fue hasta 1818, cuando el físico francés Augustin-Jean Fresnel propuso su propia hipótesis ondulatoria de base matemática, que la investigación de Young comenzó a ser reconocida como merecía.

Fresnel también tuvo que enviar su trabajo para su aprobación a un grupo de físicos comprometidos con la hipótesis corpuscular de la luz. Uno de ellos, el matemático Simeón Poisson, trató de refutar la hipótesis ondulatoria de Fresnel. Si realmente describía el comportamiento de la luz, argumentaba Poisson, debería suceder algo muy peculiar cuando se coloca un pequeño disco macizo en un haz de luz. La difracción de algunas de las ondas de luz alrededor del borde del disco redondo debería conducir a una interferencia constructiva, produciendo un punto brillante en el centro de la sombra del disco en una pantalla blanca colocada detrás del disco. La hipótesis corpuscular de la luz no permitía ideas como la difracción y la interferencia constructiva. Además, nunca se había informado de la observación de un punto brillante; incluso la idea de un punto brillante en el centro de una sombra parecía absurda. Con estos razonamientos Poisson anunció que había refutado la hipótesis ondulatoria.

Sin embargo, Dominique-François Arago, presidente del comité de la Académie des sciences que entendía del asunto, era un empirist e inmediatamente dispuso que la prueba aparentemente ridícula de Poisson se probara mediante un experimento. ¡El resultado fue que apareció un punto brillante en el centro de la sombra!

Sombra proyectada por un obstáculo de 5,8 mm de diámetro en una pantalla colocada a 183 cm detrás, cuando es iluminado por la luz del sol que pasa a través de un agujero colocado 153 cm por delante. Los colores tenues de las franjas muestran la dependencia de la longitud de onda del patrón de difracción. En el centro está el punto brillante de Poisson / Arago. Imagen: Wikimedia Commons

A partir de entonces, un número cada vez mayor de personas de ciencia valoró como importantísimos los resultados del experimento de Young de la doble rendija y el “punto brillante de Poisson”. Para 1850, con los experimentos de Foucault-Fizeau, la hipótesis ondulatoria de la luz era el consenso científico; los físicos ya habían comenzado a concentrarse en resolver las consecuencias matemáticas de este modelo y aplicarlo a las diferentes propiedades de la luz.

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

El artículo Interferencia y difracción de la luz se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Patrón de interferencia en pulsos de ondas
2. Patrón de interferencia en ondas periódicas
3. Patrones de difracción

Josu Lopez-Gazpio Musika egiteko soinuak behar dira, baina, zer da soinua? Eguneroko hizkuntzan galdera horren erantzuna nahiko argi dugun arren, agian, besterik gabe, ez gara pentsatzen jarri. Entzun ezin daitezkeen soinuak ba al daude? Nola bihurtzen da soinua musika? Zer lotura dago soinuaren -alegia, soinu desberdinen- eta musika noten artean? Bada, erantzun horiek guztiak uhinen fisikan daude eta, hortik, soinua deritzogun fenomeno fisikoan barneratuko gara. Gaur ez irakurri: entzun jarraian datorrena.

1. irudia: Soka baten bibrazioak soinua egiten du, eta sokaren bibrazio maiztasunak tonu desberdinak sortzen ditu. (Argazkia: Free-Photos – domeinu publikoko irudia. Iturria: pixabay.com)

Soinua uhin mekanikoen hedapena eragiten duen edozein fenomeno da -entzungarria zein entzunezina izan- eta hedapen hori, oro har, gorputz baten bibrazio-higidura sortzen duen fluido edo ingurune elastikoan gertatzen da. Gizakiok entzun dezakegun soinua uhinez osatzen da, airean dauden molekulen pilaketak eragiten duena. Molekulak uhin baten antzera hedatzen dira eta, belarrietako tinpanora iristen direnean hauteman dezakegun sentsazioan bihurtzen dira; izan ere, entzumen-aparatuak molekulen pilaketa guretzat ulergarria den seinale elektriko bihurtzen du. Soinuaren hedapena analogia baten bidez uler daiteke. Demagun partikulez betetako hodi bat dugula, eta partikula horiek modu uniformean banatzen direla hodian zehar. Hodiaren mutur batean, pistoi baten bidez, partikulak aurreruntz bultzatzen badira, partikulen uhin bat sortuko da. Jarraian dagoen bideoan ondo ikus daiteke fenomeno hori.

Soinuaren ezaugarriak

Soinua gerta dadin eta antzeman dezagun, hiru elementu beharrezkoak dira: soinuaren iturria izango den bibrazioa, bibrazioa hedatzea ahalbidetuko duen ingurunea eta bibrazio hori jaso eta interpretatuko duen hartzailea, esaterako, gure entzumen-aparatua. Horren ondorioz, soinu deritzon sentsazioa hautemango dugu. Soinuak hiru ezaugarri nagusi ditu –intentsitatea, tonua eta tinbrea– eta horiei esker milaka soinu desberdin bereiz daitezke -laugarren ezaugarria soinuaren iraupena da-. Intentsitatea dezibeliotan neurtzen da eta soinuaren potentzia adierazten du. 0 dB-tan entzumen-ataria finkatzen da eta hortik gora eskalan kokatzen dira soinuak. Etxeko aspiragailu baten soinua 70 dB ingurukoa litzateke eta elkarrizketa arrunt bat 40 dB ingurukoa. Bolumenarekin ez nahasteko, jakin behar da bolumena soinua sortu den lekuan bertan duen intentsitatea dela, baina, jakina, bolumen bereko soinuaren intentsitatea txikitzen doa distantziaren arabera.

Soinuaren tonuak uhin bakoitzak eskala batean duen posizioa adierazten du: horrela bereizten dira goi-soinuak eta behe-soinuak. Behe-soinuen uhinek maiztasun baxua dute eta goi-soinuen uhinek, aldiz, maiztasun altuak. Giza entzumena ez da gai edozein maiztasuneko uhinak hautemateko: 20 eta 20.000 Hz bitarteko maiztasuna dutenak soilik identifikatzeko gai da. Soinuaren hirugarren ezaugarriari dagokionez, tinbrea, tonu eta intentsitate bereko bi soinu -foku desberdinetatik igorritakoak- bereizten laguntzen duen ezaugarria da. Espektro entzungarria jarraian dagoen bideoan entzun daiteke:

Bibrazioaren maiztasunean dago musika

Entzun bezala, espektro entzungarria edo eremu tonala 20 eta 20.000 Hz tartean dago. 20.000 Hz-etik gora -alegia, 20 kHz- ultrasoinuak daude eta 20 Hz azpitik infrasoinuak. Jakina, espektro entzungarriak ez dauka etenpunturik, alegia, soinuaren tonuak edozein balio izan dezake eskala horretan. Alabaina, soinuen eskala hori taldekatuta definitzen dugu eskala jarraia erabili ordez. Horixe dira notak. Taldekatze hori egingo ez balitz, mi eta fa noten artean soinu posibleen kopuru infinitua legoke eta ezinezkoa litzateke abesti baten partitura idaztea. Eremu tonala antolatzeko, Mendebaldean espektro entzungarria hiru tonutan eta hamaika zortzidunetan banatu ohi da. Beheko tonuak -lehen lau zortzidunak, 16 Hz-tik 256 Hz-ra-, erdiko tonuak -5., 6., eta 7. zortzidunak, 256 Hz-tik 2 kHz-etara- eta goiko tonuak -azken lau zortzidunak, 2 kHz-etatik 16 kHz-etara-.

Hortaz, musika egiteko eskuragarri ditugun tonuak, alabaina, ez dira infinituak -eta ezin dute izan musikaren idazkerak praktikoa izan behar badu-. Musika egiteko eta partiturak modu ulergarrian konposatu ahal izateko, infinituak diren soinu posibleak taldekatu egin dira notak osatuz. Honela uler daiteke: maiztasun posibleak jarraiak diren arren, arrapala baten modura -edozein posiziotan egon daiteke- noten bitartez maiztasun jakin batzuk bakarrik erabiltzen dira, eskailera baten modura -eskailera-maila batean edo bestean egotea posible da, baina, ez tartean-. Noten antolakuntza hori soinu-uhinen maiztasunaren arabera egiten da, alegia, uhinak duen bibrazioaren arabera. Esaterako, do zentralak -laugarren zortziduneko do-ak, pianoaren erdigunean kokatzen dena- 261,63 Hz maiztasuna du. Horrek esan nahi du, soka batek segundoko 261,63 aldiz bibratu behar duela soinu hori egiteko. Gitarra bat nola jotzen den buruan badugu, do zentrala lortuko dugu gitarraren sokak segundoko 261,63 aldiz bibratzen badu. Jarraia dagoen bideoan ikus daiteke bibrazioaren maiztasunak nola aldatzen duen soinua. Sonua zenbat eta altuagoa izan, hura eragin duen sokak azkarrago bibratzen du.

Bibrazio maiztasunen taldekatzeari esker, partituretan soinu desberdinen kopuru mugatu –baina, erabilgarria– dago, eta haiek modu ordenatuan jotzen dira abestiak sortzeko. Alabaina, instrumentu batean nota jakin bat jotzen denean bere inguruan dagoen airearen presio aldaketa txikia gertatzen da, esfera baten gisa hedatzen dena soinu-uhina sortuz eta belarriko tinpanora iristen dean zerbait sentitzen dugu: musika.

—————————————————–
Egileaz: Josu Lopez-Gazpio (@Josu_lg) Kimikan doktorea, irakaslea eta zientzia dibulgatzailea da. Tolosaldeko Atarian Zientziaren Talaia atalean idazten du eta UEUko Kimika sailburua da.
—————————————————–

The post Musikaren zientzia (I): Soinua appeared first on Zientzia Kaiera.

UPV/EHUko Zientzia eta Teknologia Fakultatearen 50. urteurrena ospatzeko hainbat ekitaldi egingo dira Bilboko Bizkaia Aretoan.

Ezki hostotxiki (Tila cordeta Mill.) baten landaketarekin hasi ziren, 2019ko urtarrilaren 28an, UPV/EHUko Zientzia eta Teknologia Fakultatearen 50. urteurrena ospatzeko ekitaldiak. Zientziaren Oinarrien Batasunaren ikurtzat hartzen da zugaitz hau. Hasierako ekitaldi horrek, 1968ko maiatzean Bilboko Unibertsitateko Zientzia Fakultatea, gaur egun Zientzia eta Teknologia Fakultatea, sortu zeneko haziaren landaketa adierazten zuen.

Zientzia Fakultatearen lehenengo urratsak 1968/69 ikasturtean eman ziren, Deustuko zubiaren ondoan zegoen “Botica Vieja, 1″ean. 1971 urtearen amaieran egoitza oraingo kokapenera, Leioara, lekualdatu zen.

Zientzia eta Teknologia Fakultatearen titulazioen eskaintza oso bizia izan da. Natur Zientzien bost adar klasikoak eskaintzen hasi zen: Biologia, Fisika, Geologia, Kimika eta Matematika. 1994/95 eta 2000/01 ikasturteen artean, eskaintza bigarren zikloko Biokimika, Ingeniaritza Elektronikoa, Ingeniaritza Kimikoa eta Ingurugiro Zientzien lizentziaturetara zabaldu zen.

2004/2005 ikasturtetik aurrera Zientzia Fakultateak, Zientzia eta Teknologia Fakultatea izena hartu zen. Egun, bederatzi gradu eskaintzen dira, Ingeniaritza adarrean bi (Ingeniaritza Elektronikoa eta Ingeniaritza Kimikoa) eta Zientzien adarrean zazpi (Biologia, Biokimika eta Biologia Molekularra, Bioteknologia, Fisika, Geologia, Kimika eta Matematika). Fisika eta Ingeniaritza Elektronikoa gradu bikoitza eta nazioarteko hiru gradu bikoitzak ere eskaintzen dira.

Eskaintza zabal honek bilakatzen du Zientzia eta Teknologia Fakultatea gizartearen erronkei aurre egingo dien profesionalak trebatzeko Euskal Herriko erreferentzia garrantzitsuenetako bat, bai teknologia berrien garapenean, zein garapen iraunkorrean, nola ingurumenaren kontserbazioan edo biozientzien ikerketan.

Sasoi hartako egoera politikoan espero zitekeen bezala, hasierakoak zailak eta prekarioak izan ziren,. Gaur egun, irakaskuntzan, ikerketan eta garapen teknologikoan esperientzia handia duen zentroa da Fakultatea. Garatzen diren arlo desberdinetako ikerketa lerroen Shanghaiko rankingenean kokapen oso ona da horren egiaztapen argia.

Fakultate baten kalitatea ez da soilik irakasleen bikaintasunaren arabera neurtzen, hein handi batean ikasleen kalitatearen araberakoa ere bada. Gaur egun, lehen mailako ikasleak ditu. Titulazio unibertsitarioetara sartu ahal izateko sarrera nota altuenak Zientzia eta Teknologia Fakultateko titulazio batzuetan aurkitzen dira. Gradu bikoitzera sartu ahal izateko sarrera nota, UPV/EHUko altuena, adibide oso adierazlea da, lor daitekeen maximoa 14 izanik, ikasle “txarrenak” 13ko nota baino altuagoa du!

50 urte hauetan, 17.500 pertsona egresatu dira lizentziatu, ingeniari edo graduatu, eta 2.000 pertsona doktore maila lortu dute. Kopuru hauek ongi adierazten dute Zientzia eta Teknologia Fakultateak gizarteari egin dion ekarpen itzela pertsona kualifikatuei dagokionez. Gizarte arlo desberdinetan lan egiten duten profesionalak, hain zuzen, batez ere produkzio-ehunaren parte direnak, baina baita erakundeetan eta heziketa munduan lan egiten dutenak, askok erantzukizun postuetan.

Mende erdi honetan, ikerketaren bikaintasunaz eta arlo desberdinetako profesionalen prestakuntza zorrotzaren bidez, Zientzia eta Teknologia Fakultateak egin duen lana gizartearekin partekatu nahi du, Euskal Herriaren hazkunde ekonomikoan eta sozialean kolaboratu izanaren harrotasuna erakutsiz. Hartara, Biba Zientzia!, Ciencia Viva ekimena abiatu du.

Programatutako jardueretako batzuk Bilboko Bizkaia Aretoan egingo dira:

Fisikaren astea

• Martxoak 20. Baroja Aretoa.

18:30 Hitzaldia: A. Sanchez-Lavega: “¿Hay mas vida en el universo?”.

19:00 Mahai-ingurua: “Ciencia y Tecnología en el siglo XXI”.

– Cristina Oyon (SPRI taldearen Ekimen Estrategikoen arduraduna).

– Jose Maria Pitarke (CIC-Nanoguneko Zuzendari Nagusia).

– Javier García-Abajo (CSIC eta ICREAko Research Professor).

– Agustin Sanchez Lavega (UPV/EHUko Katedraduna).
Moderatzailea: Eva Caballero (Radio Euskadiko kazetaria).

• Martxoak 21. Baroja Aretoa.

18:00 Hitzaldia: Roberto Emparán (ICREA Ikerkuntza Irakaslea eta “Iluminando el lado oscuro del Universo” izeneko dibulgazioko liburu berrriaren egilea): “Reconocimiento a Stephen Hawking: de los agujeros negros a la Teoría del Todo”.

Matematikaren astea

• Martxoak 25. Oteiza Aretoa.

18:00 Mahai-ingurua: “Experiencias Matemáticas en empresa”.
*Matematikako eta Batxilergoko ikasleei eta orientatzaileei bereziki zuzenduta.

• Apirilak 2. Mitxelena Aretoa.

19:00 Ekitaldia: Judith Rivas (UPV/EHU); Nagore de las Cuevas eta Arkaitz Pascuas; Andoni Aresti Dantza Eskola eta Mungiako Udal Dantza Eskola: “Pasos de baile a ritmo de matemáticas”.

Geologiaren astea

• Apirilak 1. Oteiza Aretoa.

18:00 Hitzaldia: Irantzu Guede, UPV/EHUko Geologian doktorea, Mineralogia-Petrologia: “Geología en mitos y leyendas”.

• Apirilak 2.

Tailerrak. Chillida Aretoa.

16:00-20:00 Familientzako geologiako tailerra. Aintzane Goffard (UPV/EHUko Geologoa, Estratigrafia-Paleontologian laguntzailea) eta Irantzu Guede (UPV/EHUko Geologian doktorea, Mineralogia-Petrologia).

18:00 Hitzaldia. Oteiza Aretoa.

Humberto Astibia, UPV/EHUko katedraduna: “Los fósiles, documentos de la historia de la Vida archivados en las rocas”.

• Apirilak 3

18:00 Hitzaldia. Arriaga Aretoa.

Blanca Martínez, UPV/EHUko Geologian doktorea, Estratigrafia-Paleontologia: “Geología y música”.

• Apirilak 4

18:00 Hitzaldia. Aretoa zehazteko.

Ihintza Urain Alberdi, geologoa, 2018an egresatua: “Geologia eta ingurugiroa: Geologoaren papera energia aldaketan eta Lurraren inguruko kultura berri baten aurrean”.

• Apirilak 8. Oteiza Aretoa.

18:00 Hitzaldia: Jose María Tubía, UPV/EHUko geodinamikan katedraduna: “Riesgo geológico de los tsunamis”.

Ekitaldi nagusia.

• Apirilak 11. Mitxelena Aretoa.

18:30 Hitzaldia: Prado Martín Moruno, 2017 L’Oreal-Unesco awarded Women for Science: “La energía oscura y el destino del Universo”.

“GARGANTUA” dantza saioaren estreinaldia (“Interstellar” pelikulako GARGANTUA zulo beltzean oinarrituta). Martxel Rodriguez, dantzari profesionala eta fisikaria, “KUKAI dantza talde”-ko dantzaria.

Kimikaren astea

• Apirilak 29. Oteiza Aretoa.

18:00 Hitzaldia: Oscar González. Kimika Analitikoa Saileko irakaslea. “Artelanetan aurkitu diren gauzarik bitxienak”.

• Apirilak 30. Arriaga Aretoa.

18:00 Hitzaldia: Pascual Román, Irakasle emeritoa. Kimika Ezorganikako Katedraduna. “El sesquicentenario de la tabla periódica de los elementos químicos”.

• Maiatzak 2. Arriaga Aretoa.

18:00 Hitzaldia: Jose Luis Vilas. Kimika Makromolekular ikerketa taldeko zuzendaria. “Hidrogeles: imprimiendo salud”.

Biozientzien astea

• Maiatzak 6. Aretoa zehazteko.

18:00 Mahai-ingurua: “Zientzia, jainkoaren esistentzia, zergatik du gizakiak sinisteko beharra”.

Bestelako ekitaldiak

• Ekainak 27. Aretoa zehazteko.

19:00 “ZTF/FCTren ekarpena Euskararen Normalizazioan” Hizlariak: Pedro Miguel Etxenike, Jacinto Iturbe eta Jesusmari Txurruka.

Amaiera ekitaldia

• Uztailak 12. Mitxelena Aretoa.

The post Biba zientzia: 50 urte zientzia biziz appeared first on Zientzia Kaiera.

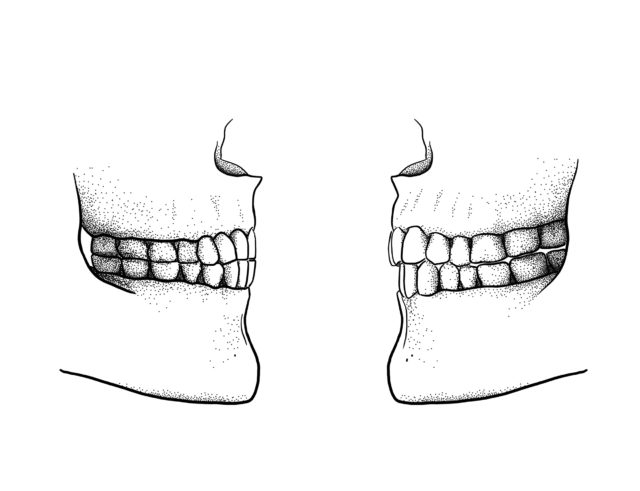Alineación dental antes y después (derecha) de los cambios en la dieta. Imagen: Scott Moisik a partir de D. E. Blasi et al (2019) Human sound systems are shaped by post-Neolithic changes in bite configuration Science doi: 10.1126/science.aav3218

Fuego, foca, foto, fofo, fumar, fieltro, feminista… Es gustoso pronunciar el sonido de la efe, ¿verdad? Quizá por eso la palabra malsonante por excelencia en inglés sea “fuck” (disculpen el exabrupto), porque a los anglosajones se les da mejor que a nadie el convertir un sonido u onomatopeya en el centro de sus palabras (“crack” es más sonoro que “crujir”, aunque tampoco está mal, y “ring” es mejor que “llamar al timbre”, ahí sí que no hay discusión).

Pero volvamos al hilo, que me pierdo. Hablábamos del sonido de la efe, y la reflexión viene a cuento de un estudio recientemente publicado en la revista Science que sugiere que si somos capaces de pronunciarlo, así como otras consonantes labiodentales (en el castellano, solo le acompañaría la pronunciación tradicional de la uve, que solo se conserva en algunas regiones), es porque hace miles de años nuestros antepasados cambiaron su alimentación, eso cambió sus mandíbulas y con eso, los sonidos que eran capaces de pronunciar, abriendo la puerta a una variedad lingüística y comunicativa no disponible anteriormente.

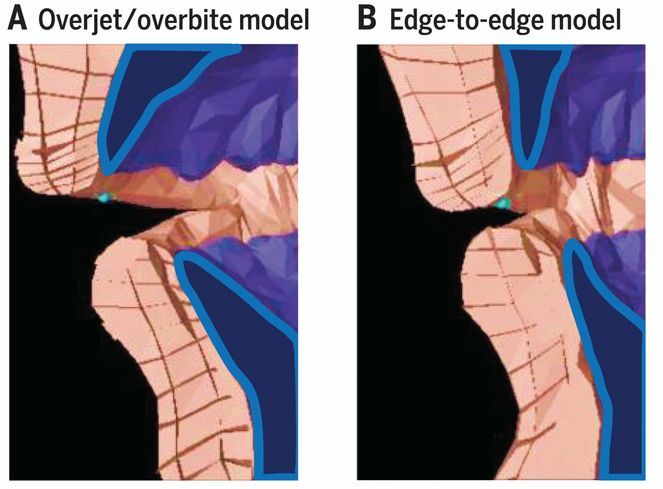Imagen: D. E. Blasi et al (2019) Human sound systems are shaped by post-Neolithic changes in bite configuration Science doi: 10.1126/science.aav3218

Comida dura, mandíbulas potentes

Vamos por partes. El estudio ha sido realizado por Balthasar Bickel, Damián Blasi y Steven Moran, del laboratorio de Lingüística de la Universidad de Zúrich, en Suiza. Su intención era poner a prueba una idea propuesta por otro lingüista, el americano Charles Hockett en 1985. Hocket escribió entonces que las lenguas habladas por los cazadores-recolectores carecían de estas consonantes labiodentales y que, al menos en parte, su dieta podía ser responsable.

Según su teoría, consumir y masticar alimentos fibrosos y duros requería de una mayor fuerza en la mandíbula y suponía un mayor desgaste de los molares, y como tal, sus mandíbulas inferiores eran mayores y los molares ocupaban más espacio en ella, empujando las demás piezas dentales hacia delante y causando una alineación entre los dientes delanteros de la mandíbula inferior y la mandíbula superior.

Esto dificultaba, dijo Hockett entonces, que los dientes de arriba tocasen el labio inferior, contacto necesario para pronunciar la gustosa efe. Para hacerse una idea, pruebe a colocar hacia delante su mandíbula inferior hasta que dientes de arriba y abajo coincidan. ¿Verdad que le resulta una postura incómoda? Eso es por la llamada sobremordida, ese espacio que la mayoría tenemos entre los dientes superiores y los inferiores cuando cerramos la mandíbula. Al introducirse la agricultura y técnicas como el molido de los cereales, la fabricación de derivados lácteos y más formas de cocinado para la carne, la postura anterior habría sido menos necesaria y esta sobremordida habría ido haciéndose cada vez más común, hasta el día de hoy.

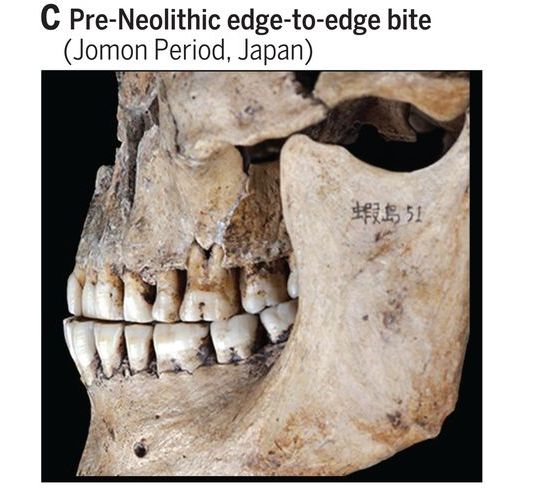Imagen: D. E. Blasi et al (2019) Human sound systems are shaped by post-Neolithic changes in bite configuration Science doi: 10.1126/science.aav3218

Un 29% menos de energía para pronunciar la F

Blasi y compañía querían poner a prueba esta idea y, esperaban a priori, demostrar que Hockett se había equivocado.

Para empezar, los investigadores utilizaron un modelo informático para calcular que con una sobremordida, producir esas consonantes labiodentales cuesta un esfuerzo un 29% inferior. Después, analizaron las lenguas del mundo y descubrieron que en las civilizaciones de cazadores y recolectores hay un 75% menos de consonantes labiodentales que en las lenguas habladas en sociedades agrícolas. Por último, estudiaron las relaciones y evoluciones lingüísticas y determinaron que las consonantes labiodentales se difunden con rapidez, de forma que esos sonidos podrían haber pasado de ser raros a ser comunes en los 8.000 años que han pasado desde la adopción de la agricultura y otros métodos de manipulación de los alimentos.

Teniendo en cuenta estas averiguaciones. Bickel sugiere que a medida que la comida más blanda se fue haciendo más habitual, más adultos fueron desarrollando sobremordidas y fueron utilizando consonantes labiodentales de forma accidental, y que por ejemplo en la antigua India, el uso de esos sonidos pudo haber sido una señal de estatus al significar un acceso a una dieta más delicada y costosa. A día de hoy hay consonantes labiodentales en el 76% de los idiomas provenientes de lenguas indoeuropeas.

“Una de las conclusiones principales es que el panorama de sonidos que tenemos hoy en día está fundamentalmente afectado por la biología de nuestro aparato fonador. No es solamente una cuestión de evolución cultural”, explicaba Bickel en una rueda de prensa.

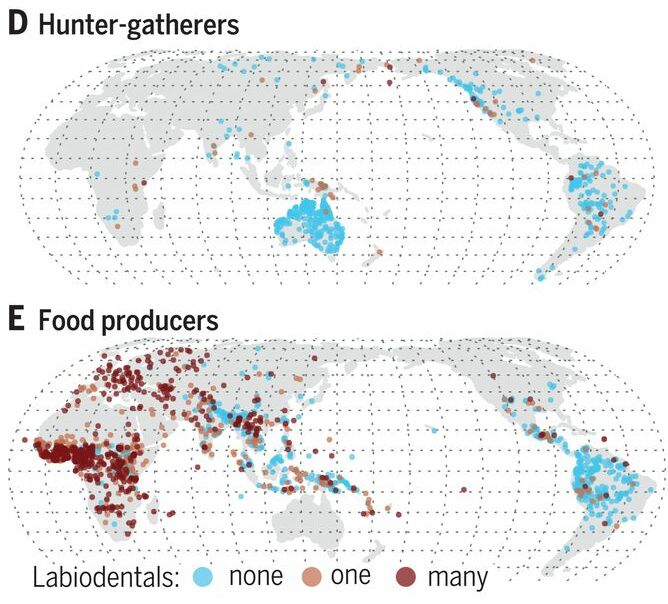Imagen: D. E. Blasi et al (2019) Human sound systems are shaped by post-Neolithic changes in bite configuration Science doi: 10.1126/science.aav3218

Si ocurrió así, no ocurrió en todas partes

Aun así, no todo el mundo ve clara la relación que Bickel y su equipo proponen entre dieta, forma de la mandíbula y sonidos del idioma. Inevitablemente, su hipótesis está basada en algunas ideas difíciles de comprobar y también en algunas contradicciones. Por ejemplo, que en la Antigua China también se comenzó a cultivar y procesar arroz de forma que fuese más sencillo de masticar y comer y en las lenguas de esa región los sonidos labiodentales son mucho menos comunes que en las lenguas europeas.

Claro que los autores no defienden que la evolución hacia la sobremordida signifique necesariamente la aparición de las consonantes labiodentales, sino que “la probabilidad de producción de esos sonidos aumenta ligeramente con el tiempo, y eso significaría que es probable que algunas lenguas los adquieran, pero no todas”, explica otro de los autores, Steven Moran, en este artículo de Smithsonian Magazine.

“¿Dónde está la causalidad, que yo la vea?”

Algunos críticos, como el paleoantropólogo Rick Potts, no terminan de aceptar la conclusión del estudio: “En mi opinión, no dan suficientes razones para aceptar que la dieta fue el motivo por el que se hicieron más comunes estos sonidos, porque no tienen en cuenta en ningún momento los componentes anatómicos de producir estos sonidos”, explica en el artículo mencionado.

Potts explica que para hacer el sonido de la efe cuando no hay sobremordida simplemente hay que retraer un poco los músculos de los lados de la mandíbula, que la hacen retroceder ligeramente. “¿Cómo podría una dieta más dura y áspera limitar esa retracción? Esa es la base para hacer esos sonidos. El estudio no demuestra de ninguna forma que una mordida en la que los dientes coinciden impida o haga energéticamente más costoso pronunciar estos sonidos”, señala.

Así que en su opinión, el estudio señala algunas correlaciones que resultan interesantes pero no llega a demostrar una causalidad probable. Es, dice, como si una investigación descubriese que culturas que habiten en el ecuador tienen preferencia por el color rojo y también que esas personas tienen en sus ojos una densidad de receptores de color menor que las personas que habitan en el Ártico, por ejemplo, y concluyesen que la falta de receptores de color es lo que las hace preferir el color rojo.

“Pero ¿cómo íbamos con eso a descartar que fuese una cuestión cultural e histórica lo que hace que los habitantes de una cultura ecuatorial tiendan a elegir el rojo, y los habitantes de culturas del polo no lo hagan?”, argumenta, señalando que el estudio no ha tenido suficientemente en cuenta la acción de la historia, la cultura y la identidad de cada grupo y cada lengua a la hora de favorecer o no los sonidos labiodentales.

Referencias:

Human sound systems are shaped by post-Neolithic changes in bite configuration – Science

Ancient switch to soft food gave us an overbite—and the ability to pronounce ‘f’s and ‘v’s – Science

The Ability to Pronounce ‘F’ and ‘V’ Sounds Might Have Evolved Along With Diet – Smithsonian Magazine

Sobre la autora: Rocío Pérez Benavente (@galatea128) es periodista

El artículo “Fuego, foca, foto…” ¿Podemos decir estas palabras gracias a la dieta de nuestros antepasados? se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. ¿Qué nos puede decir un elefante del cáncer en humanos?
2. Los vegetales de la dieta neandertal
3. Nuestros ancestros asesinos

Miren Josu Omaetxebarria, Nerea Osinalde, Jesusmari Arizmendi eta Jabi Beaskoetxea eta Kerman Aloria Masa-espektrometria (MS) orain 100 urtetik kimikarientzako ohiko teknika izan arren, azken 3 hamarkadetan baino ez da erabili proteinak analizatzeko. Edozein analito MSz analizatu nahi badugu, berau ionizatu eta gas fasera aldatu behar da.

Proteinak eta proteina zatikiak (peptidoak) bezalako makromolekulak ionizatzea eta gas fasera aldatzea elefanteak hegaz egitea hainako egitekotzat jo zen luzaroan. Ionizazio “arina” izena eman zitzaien bi ionizazio-hurbilketa garatu eta komertzializatu zirenean, baina egingarri bilakatu zen proteinen tamainako makromolekula handiak analizatzea, bai soluzio likido batean, baita egoera lehor-kristalino batean ere; bi ionizazio mota horiei electrospray ionizazioa (ESI) eta matrix assisted laser desorption ionizazioa (MALDI) deritze, hurrenez hurren. ESIn, analitoa duen soluzioari tentsio altua eragiten zaio zulodun orratz estu batetik igarotzerakoan. Kargatutako molekula-soluzioa lurrundu ahala, sortutako tantatxoen tamaina txikituz eta txikituz doa gas fasera iritsi arte pasatzen den arte. MALDIn berriz, laserra disparatzen zaio altzairuzko plater bati. Bertan, analitoa matrize batekin batera dago lehortuta. Matrizeak laserraren energia xurgatzen du eta energia hori laginari transferitzen diolarik, gas fasera aldarazten du.

Baina, zergatik proteinak? Zergatik hainbesteko jakin-mina proteinak direla eta? interesa proteinak aztertzeko? Bada bizidun ororen oinarrizko molekulak direlako. Proteinak dira gure zeluletako ataza desberdinak betetzen dituzten langile finak; besteak beste, erreakzio kimikoak katalizatu, molekulak garraiatu, eta zelulen egitura mantentzen dute, edota patogenoen aurka babesten gaituzte proteinek. Gure gorputza trilioika zelulez osatuta dago, eta zelula bakoitzak milaka proteina desberdin izan ditzake. Hain zuzen ere, zelula mota bakoitzak proteina katalogo edo sorta jakina duelako, funtzio eta ezaugarri bereziak ditu. Bizidun baten zelula guztietan dagoen gene-informazioa, hots, genoma berdin-berdina da. Geneetan dago idatzita proteina bakoitza ekoizteko informazioa. Bestela esanda, geneak proteinak egiteko errezetak dira, eta errezeta horietako bakoitzaren arabera lortzen da proteina bat edo beste bat.

Zelula batek une jakin batean duen proteina-bildumari proteoma deritzo. Genoma ez bezala, zeluletako proteoma etengabe aldatzen da; zeluletara heltzen den edozein estimulu edo erasori aurre egiteko, alegia, ingurunera egokitzeko, proteina-konbinazio desberdinak sortu, eta arituko dira elkarlanean. Horrela uler daiteke, genoma bakarra izanik, beldar bat nola bilakatu daitekeen tximeleta (1. irudia.)

1. irudia: Papilio machaon beldarra (a) eta tximeleta (b). (Iturria: Wikimedia Commons)

Zeluletako proteinek, gure antzera, euren “sare sozialak” dituztela esan dezakegu. Bakarrik baino elkarlanean betetzen dituzte beraien funtzioak. Halere, elkarrekintza horiek, gehienetan, iragankorrak izaten dira, zelularen beharren arabera sortu eta desegiten direlako. Milioika proteina-molekula izanik, gure planetan bizi garen gizaki guztien artekoa bezain konplexua da zelula bakar bateko elkarrekintza-sarea. Proteina-sare horien funtzionamenduak baldintzatuko du zelularen osasun maila eta, ondorioz, organismo osoaren osasun maila ere. Horregatik da hain garrantzitsua proteinak eta euren elkarrekintzak, alegia proteomak ikertzea eta osotasunean ulertzen saiatzea. Hori horrela izanik, gaur egungo biologiaren funtsezko erronketako bat bilakatu da proteomak kualitatiboki eta kuantitatiboki deskribatzea. Erronka horri aurre egiteko, proteomikak hartu duen gidaritza inork gutxik jartzen du zalantzatan.

Proteomikak proteomak ikertzen ditu. 1975. urtean lehenengoz Escherichia coli bakterioaren milaka proteina banatu ziren bi dimentsioko gel-elektroforesiaren bidez (2DE). Banatutako proteinak identifikatzea, hots, zeintzuk ziren zehaztea, bestelako erronka bat zen; erronka horri heltzeko ezinbestekoa izan zen alde batetik, sekuentziazio partziala egiteko tekniken garapena, Edman degradazioa esaterako. Bestetik, MS teknika bera proteinen analisirako doitzea.

Egun, MS da proteinak identifikatzeko ohiko metodoa. Proteomak osotasunean ulertzeko baina, identifikatzeaz gain, kuantifikatu egin behar dira proteinak. Hori egiteko lehen urratsak 2DE gelen irudi-analisien bidez eman ziren. Gaur egun azterketa proteomikoetarako teknika egokia izaten jarraitzen badu ere, leku txikia hartzen du masa-espektrometrian oinarritutako proteomikaren aldean (MS-based proteomics). Izan ere, proteina-lagin konplexuak analizatzeko, hots, proteinak identifikatzeko eta kuantifikatzeko, MS da aukerako metodoa gaur-gaurkoz. Izan ere, ezinbesteko teknika bilakatu da, genometan kodetuta dagoen informazioa interpretatzeko orduan.

Arestian esan bezala, ESI eta MALDI dira proteinak edota peptidoak ionizatu eta hegaz eginarazteko ohiko teknikak. MALDI-MS teknika peptido-nahastura nahiko bakunak analizatzeko erabili ohi da, baina ESI-MS sistemak (LC-MS, liquid chromatography-MS) dira lagin konplexuak analizatzeko egokienak.

Proteomak berez konplexuak izanik, LC-MS teknikak dira proteomikan gailendu direnak. Izan ere, LC-MSaren masa-zehaztasuna, sentikortasuna, bereizmena, eta abiadura dira teknikaren arrakastaren gako. Azken urteotan, LC-MS prozedura ezberdinak erabilita makina bat proteoma identifikatu, kuantifikatu eta karakterizatu dira. Proteomikaren lorpenen artean nabarmentzekoak dira 2014an argitaratutako giza proteomaren bi zirriborro, eta gaur egun Giza Proteomaren Erakundea (Human Proteome Organization, HUPO) gidatzen ari den Giza Proteomaren Proiektua (Human Proteome Project, HPP).

Baina zer da zehazki proteomikako laborategi batean egiten duguna? Edozein delarik ere eskuetan dugun lagina (biopsiaren bateko lagin bat, animalia edo landare-zelulak, bakterioak, jariakin biologikoren bat…), berau analizatzeko erabili ohi dugun lan-fluxua bottom-up proteomika izenekoa da (2. irudia). Lehenik eta behin, laginetik proteinak erauzten ditugu. Ondoren, proteinak liseritzen dituen entzima bat erabiliz, tripsina izaten da gehien bat, proteinak peptido izeneko zatikitan txikitzen ditugu. Peptido-nahasketa elektrospray ionizazioari akoplatutako alderantzizko faseko kromatografia likidoan banatuko dira. Zutabetik eluitu ahala, peptidoak ionizatu, eta masa-espektrometroan sartuko dira. Bertan, peptido-ioiak masa-karga (m/z) erlazioaren arabera banatu eta detektatuko dira. Peptido ugarienak gainontzekoetatik isolatuko dira, eta zatikatu egingo dira fragmentazio-espektroak osatzeko. Espektro horiek guztiak dira peptidoak identifikatu eta kuantifikatzeko informazioa gordetzen dutenak. Azkenik, masa-espektrometroak jasotako datu guztiak konputazio-erraminta berezien bidez analizatuko dira. Finean, jakingo dugu guk aztertutako laginean dauden proteinak zeintzuk diren, eta zein kopurutan agertzen diren.

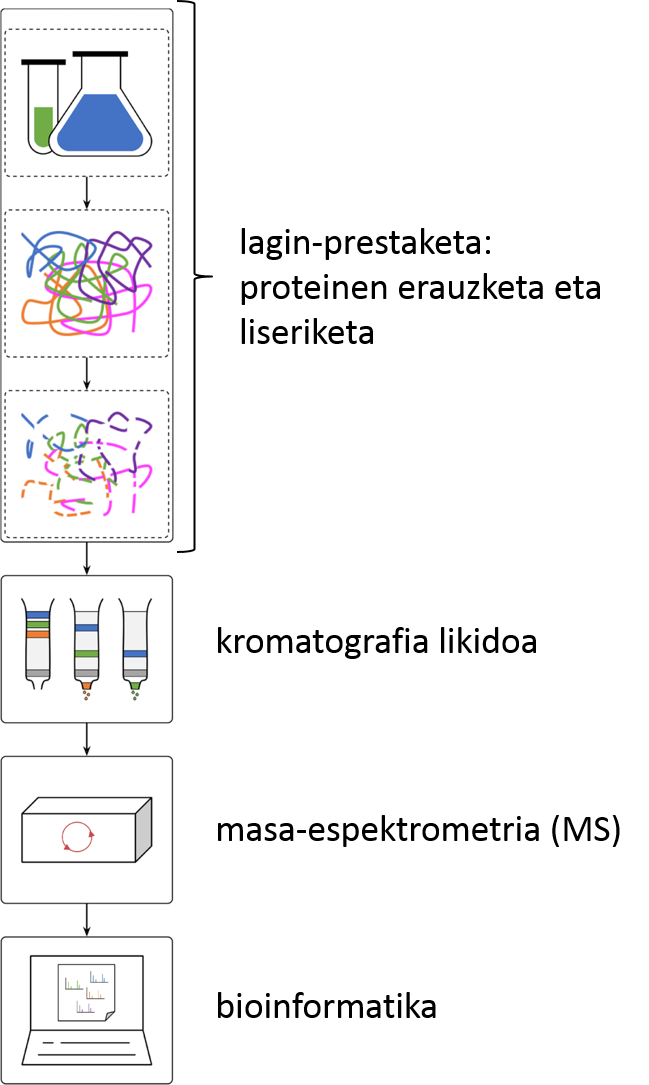
2. irudia. Bottom-up proteomika. (Ilustrazioa: Miren Josu Omaetxebarria, Nerea Osinalde, Jesusmari Arizmendi eta Jabi Beaskoetxea eta Kerman Aloria)

Azken hamarkadan, MSean oinarritutako proteomika biozientzietarako analisi-tresna nagusienetakoa bilakatu da. Izan ere, proteinak ertz askotatik ikertzea ahalbidetu digu, eta euren egiturak, aldaerak, kopuruak, itzulpen osteko eraldaketak, eta elkarrekintzak ezagutzeko bide eman digu. Horrez gain, proteomikari esker, zehaztu ahal izango dugu zeintzuk diren zenbait gaixotasunen garapenean zerikusia duten proteinak, hala nola, gaixotasunen diagnostikoa egiteko baliagarriak izango diren biomarkatzaileak. Datozen urteetan, zelulen baldintza ezberdinetako proteina katalogoak osatuz joango gara. Genomika, epigenomika, metabolomika eta eskala handian egiten diren bestelako “omikatan” lortutako emaitzekin batera, proteomikaren eskutik heldutako aurkikuntzek zelula ereduak gauzatzen lagunduko digute. Izan ere, hori da joera: diziplinarteko ezagutzak uztartuz, prozesu biologikoen konplexutasuna argitzen lagunduko diguten matematika eta estatistika-ereduak lortzea; horretan ere, proteomikak zeresana emango du.

Erreferentzia bibliografikoak:

• Fenn JB (2003) “Electrospray wings for molecular elephants (Nobel lecture)” Angew Chem Int Ed Engl. 42(33), 3871-94. DOI:10.1002/anie.200300605
• Fenn JB et al. (1989) “Electrospray ionization for mass spectrometry of large biomolecules” Science 246(4926), 64-71. DOI: 10.1126/science.2675315
• Tanaka K et al. (1988) “Protein and polymer analyses up to m/z 100 000 by laser ionization time-of-flight mass spectrometry” Rapid Communications in Mass Spectrometry 2(8), 151–153. DOI:10.1002/rcm.1290020802
• Karas M and Hillenkamp F (1988) “Laser desorption ionization of proteins with molecular masses exceeding 10,000 daltons” Anal Chem. 60(20), 2299-301. DOI: 1021/ac00171a028
• O’Farrell (1975) “High resolution two-dimensional electrophoresis of proteins” J Biol Chem 250(10), 4007-21.
• Kim MS et al. (2014) “A draft map of the human proteome” Nature 509(7502), 575-81. DOI: 10.1038/nature13302
• Wilhelm M et al. (2014) “Mass-spectrometry-based draft of the human proteome” Nature 509(7502), 582-7. DOI: 10.1038/nature13319
• HUPO: https://hupo.org/human-proteome-project

—————————————————–

Egileei buruz: Miren Josu Omaetxebarria, Nerea Osinalde, Jesusmari Arizmendi eta Jabi Beaskoetxea Biokimika eta Biologia Molekularra saileko kideak dira eta Kerman Aloria SGIker-eko teknikaria.

—————————————————–

Masa-espektrometriari buruzko artikulu-sorta

1. Masa-espektrometria (I). Neoi isotopoetatik elefante hegalariengana
2. A new hero is born: Masa-espektrometria justiziaren zerbitzura
3. Nor dago icebergaren alden ezkutuan?
4. Konposatu galduaren bila
5. Metabolomika: osotasuna, zatien baturaren aurrean
6. Esploratu gabe dauden lurraldeak kartografiatzen: masa-espektrometria bidezko irudia
7. Proteomika: Proteinak eta Masa Espektrometria eskutik helduta

The post Proteomika: Proteinak eta Masa-espektrometria eskutik helduta appeared first on Zientzia Kaiera.

50 años de ciencia viva

Los actos de conmemoración del 50 aniversario de la Facultad de Ciencia y Tecnología de la UPV/EHU comenzaron el 28 de enero de este año con la plantación de un tilo de hoja pequeña (Tila cordeta Mill.), que representa el Árbol de la Ciencia como símbolo de su unidad fundamental. El acto simbolizó la siembra de la semilla plantada en mayo de 1968, cuando se creó la Facultad de Ciencias de la Universidad de Bilbao, hoy en día Facultad de Ciencia y Tecnología.

Los primeros pasos de la Facultad de Ciencias en el curso 1968/69 se dieron junto al puente de Deusto, en “Botica Vieja, 1”. No fue hasta finales de 1971 cuando se trasladó a su emplazamiento actual en Leioa.

La Facultad de Ciencia y Tecnología ha sido una facultad viva en su oferta de titulaciones. Comenzó ofertando las cinco ramas clásicas de las Ciencias Naturales: Biología, Física, Geología, Matemáticas y Química. Entre los cursos 1994/95 y 2000/01, su oferta se amplía a las licenciaturas de segundo ciclo en Bioquímica, Ingeniería Electrónica, Ingeniería Química y Ciencias Ambientales, pasando a llamarse en el curso 2004/2005 Facultad de Ciencia y Tecnología. Hoy, oferta nueve grados, dos en la rama de Ingeniería (Ingeniería Electrónica e Ingeniería Química), y siete en la de Ciencias (Biología, Bioquímica y Biología Molecular, Biotecnología, Física, Geología, Matemáticas y Química). Se oferta también el doble grado en Física e Ingeniería Electrónica y tres dobles titulaciones internacionales de grado. Esta oferta hace de la Facultad de Ciencia y Tecnología uno de los referentes más importantes del País Vasco en la formación de profesionales capaces de jugar un papel crucial en los retos de nuestra sociedad, desde el desarrollo en nuevas tecnologías, el desarrollo sostenible, la conservación del medio ambiente o la investigación en biociencias.

Los inicios fueron precarios, como se podría esperar ante la difícil situación política de aquellos años. Hoy la facultad es un centro con gran experiencia en docencia, investigación y desarrollo tecnológico, como queda acreditado por las muy buenas posiciones en el ranking de Shanghái de distintas áreas de investigación que se desarrollan en nuestro centro.

La calidad de una facultad no se mide sólo por la excelencia del profesorado, sino también por la calidad de su alumnado: hoy cuenta con estudiantes de primer nivel. Las notas de acceso más elevadas para acceder a las titulaciones universitarias se encuentran en varias de las titulaciones de esta facultad. Un claro ejemplo es la nota de acceso superior a 13, sobre 14, para acceder al doble grado, la más alta de la UPV/EHU.

Tras 50 años de intenso trabajo, 17.500 personas han egresado en licenciatura, ingeniería o grado, y 2.000 se han doctorado. Estas cifras suponen una gran aportación de personal cualificado, profesionales que están trabajando en distintos ámbitos sociales, fundamentalmente en el tejido productivo, pero también en el institucional y el educativo, ocupando muchos de ellos puestos de responsabilidad.

Queremos compartir con la sociedad vasca el trabajo que la Facultad de Ciencia y Tecnología ha desarrollado a lo largo de medio siglo, mediante una investigación de excelencia y una formación rigurosa de profesionales en distintas áreas, mostrando así nuestro orgullo por haber colaborado en el crecimiento económico y social del País Vasco.

Biba Zientzia!, Ciencia Viva.

Todas las actividades programadas las encontrará aquí.

Las actividades programadas en el Bizkaia Aretoa de Bilbao durante los próximos 4 meses son:

Semana de la física

• 20 de marzo

Bilbao Bizkaia Aretoa (Auditorio Baroja)

18:30 Conferencia: A. Sanchez-Lavega: “¿Hay mas vida en el universo?

19:00 Mesa redonda: “Ciencia y Tecnología en el siglo XXI”

-Cristina Oyon (Responsable de Iniciativas Estratégicas del Grupo SPRI),

-Jose Maria Pitarke (Director General del CIC-Nanogune),

-Javier García-Abajo (Prof. Investigación CSIC y Research Prof. ICREA)

-Agustin Sanchez Lavega (Catedrático UPV/EHU)

Moderadora: Eva Caballero (Periodista de radio Euskadi)

• 21 de marzo

Bilbao Bizkaia Aretoa (Auditorio Baroja)

18:00 Conferencia: Roberto Emparan (Research Prof. ICREA y autor del libro de divulgación reciente “Iluminando el lado oscuro del Universo”): “Stephen Hawking: de los agujeros negros a la Teoría del Todo”

Semana de las matemáticas

• 25 de marzo

Bilbao Bizkaia Aretoa. Auditorio Oteiza

18:00 Mesa redonda: “Experiencias Matemáticas en empresa”
Dirigido a: Estudiantes de Bachillerato y de Matemáticas, Orientadores

• 2 de abril

Bilbao Bizkaia Aretoa. Auditorio Mitxelena

19:00 Evento: Judith Rivas (UPV/EHU); Nagore de las Cuevas y Arkaitz Pascuas; Andoni Aresti Dantza Eskola y Mungiako Udal Dantza Eskola : “Pasos de baile a ritmo de matemáticas”
Dirigido a: Público general

Semana de la geología

• 1 de abril

Bilbao Bizkaia Aretoa. Auditorio Oteiza

18:00 Conferencia: Irantzu Guede, doctora de la UPV/EHU en Geología, en Mineralogía Petrología: “Geología en Mitos y Leyendas”.

• 2 de abril

Bilbao Bizkaia Aretoa. Auditorio Oteiza

18:00 Conferencia: Humberto Astibia, catedrático de la UPV/EHU: “Los fósiles, documentos de la historia de la Vida archivados en las rocas”.

Taller. Auditorio Chillida

16:00-20:00 Taller de Geología para familias. Aintzane Goffard (Geologa de la UPV/EHU, ayudante en Estratigrafía-Paleontología) e Irantzu Guede (Doctora de la UPV/EHU en Geología, Mineralogía-Petrología).

• 3 de abril

Bilbao Bizkaia Aretoa. Auditorio Arriaga

18:00 Conferencia: Blanca Martínez, doctora de la UPV/EHU en Geología, en Estratigrafía-Paleontología: “Geología y música”.

• 4 de abril

Bilbao Bizkaia Aretoa (Auditorio por confirmar)

18:00 Conferencia: Ihintza Urain Alberdi, geóloga: “Geologia eta ingurugiroa: Geologoaren papera energia aldaketan eta Lurraren inguruko kultura berri baten aurrean”.

• 8 de abril

Bilbao Bizkaia Aretoa. Auditorio Oteiza

18:00 Conferencia: Jose María Tubía, catedrático de Geodinámica de la UPV/EHU: “Riesgo geológico de los tsunamis”.

Acto central

• 11 de abril

Bilbao Bizkaia Aretoa. Auditorio Mitxelena

18:30 Conferencia: Prado Martín Moruno, 2017 L’Oreal-Unesco awarded Women for Science: “La energía oscura y el destino del Universo”.

Estreno de la obra de baile “GARGANTUA” (basada en el agujero negro GARGANTUA de la película “Interstellar”). Martxel Rodriguez, físico y bailarín profesional. Miembro de “KUKAI dantza taldea”.

Semana de la química

• 29 de abril

Bilbao Bizkaia Aretoa. Auditorio Oteiza

18:00 Conferencia: Oskar González. Profesor del Departamento de Química Analítica:“Artelanetan aurkitu diren gauzarik bitxienak”

• 30 de abril

Bilbao Bizkaia Aretoa. Auditorio Arriaga

18:00 Conferencia: Pascual Román, profesor emérito. Catedrático de Química Inorgánica: “El sesquicentenario de la tabla periódica de los elementos químicos”

• 2 de mayo

Bilbao Bizkaia Aretoa. Auditorio Arriaga

18:00 Conferencia: Jose Luis Vilas, director del Grupo de Química Macromolecular. Departamento de Química Física FCT-EHU: “Hidrogeles: imprimiendo salud”

Semana de la biociencia

• 6 de mayo

Bilbao Bizkaia Aretoa (Auditorio por confirmar)

18:00 Mesa redonda: “Zientzia, jainkoaren esistentzia, zergatik du gizakiak sinisteko beharra”

Otros actos

• 27 de Junio

Bilbao Bizkaia Aretoa (auditorio por confirmar )

19:00 “ZTF/FCTren ekarpena Euskararen Normalizazioan” Conferenciantes: Pedro Miguel Etxenike, Jacinto Iturbe y Jesusmari Txurruka

Acto de clausura. 12 de julio

Bilbao Bizkaia Aretoa

Se comunicará

Sobre el autor: Fernando Plazaola Muguruza es el decano de la Facultad de Ciencia y Tecnología de la UPV/EHU

El artículo Actos por el 50 aniversario de la Facultad de Ciencia y Tecnología de la UPV/EHU se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Presentación del estudio “Percepción social de la ciencia y la tecnología en el País Vasco”
2. Geología, ver más allá de lo que pisamos
3. Geología: la clave para saber de dónde venimos y hacia dónde vamos

Imagen: Gordon Johnson / Pixabay

Una característica peculiar de los seres humanos es que, aunque nacemos con una cabeza de gran tamaño, tardamos en completar el crecimiento y desarrollo del encéfalo. A los dos años de edad alcanza el 85% de su volumen máximo, por lo que ha de seguir creciendo. Por otro lado, no todas sus áreas se desarrollan y maduran a la vez. La corteza cerebral, que es la parte más exterior, madura en último lugar. Y en ese proceso la proporción entre las denominadas materia gris y materia blanca cambia.

La materia gris corresponde a diferentes elementos: cuerpos neuronales y sus dendritas, que son prolongaciones ramificadas a través de las cuales una neurona recibe señales de otras; células de la glía, que dan soporte y protección a las anteriores; capilares sanguíneos, que proporcionan a neuronas y células gliales el oxígeno y los nutrientes que necesitan; y las conexiones entre neuronas, denominadas sinapsis. La materia gris se distribuye en la corteza del cerebro y del cerebelo, así como en numerosas estructuras de ubicación más profunda en el interior del encéfalo.

La materia blanca corresponde a los axones de las neuronas que se encuentran recubiertos por una sustancia lipídica denominada mielina. Un axón es una proyección de forma tubular que conducen señales nerviosas desde el cuerpo de una neurona hasta otras que pueden encontrarse a cierta distancia o hasta células musculares, principalmente. La vaina de mielina que recubre el axón lo aísla, y ayuda, de esa forma, a que los impulsos nerviosos se transmitan más rápida y eficazmente.

El volumen de materia gris de varias regiones de la corteza cerebral alcanza su máximo desarrollo alrededor de los 10 años de edad. Ese incremento refleja un aumento de las conexiones entre neuronas que se producen como consecuencia de la experiencia, el adiestramiento y el aprendizaje. Durante esos años, la actividad encefálica es tan intensa que llega a gastar un 60% de la energía que consume el organismo en reposo, y casi la mitad de las necesidades diarias totales de energía. Hay quienes atribuyen a ese gran consumo de energía el hecho de que el crecimiento del cuerpo durante la niñez sea lento y se prolongue en el tiempo.

A partir de los once o doce años las cosas cambian. El grosor de la materia gris de la corteza cerebral empieza a reducirse, y lo hace de forma sustancial durante la adolescencia. En algunas zonas esa reducción llega a ser del 17% hacia el final del proceso, unos 15 años después. Lo que ocurre, en parte, es que una cierta proporción de las conexiones sinápticas se “podan”, como se dice en la jerga neurocientífica. Esa poda elimina conexiones que no se usan o se usan poco y se mantienen las que más tráfico registran. A la vez aumenta la proporción de materia blanca. Eso es indicio de que los axones que conducen las señales se hacen más gruesos y que aumenta su grado de cobertura por la capa lipídica de mielina. El engrosamiento de los axones y el mayor grado de mielinización promueven una más rápida y eficaz transmisión de impulsos nerviosos y , por lo tanto, una comunicación más eficiente entre la corteza cerebral y el resto de áreas encefálicas. En definitiva: el cerebro funciona mejor.

La maduración de la corteza cerebral requiere tiempo y hace que la adolescencia sea un periodo difícil. Pero durante ese periodo la mente humana aprende a navegar en el complejo entorno social en que se desenvolverá en la edad adulta. La adolescencia puede entenderse así como el precio que paga por ese aprendizaje.

Nota:

Esta anotación es parte de una colección de tres artículos dedicados a la neuropsicología de la adolescencia. Los artículos son El desajuste adolescente, En busca de la identidad personal y este, El cerebro humano tarda en madurar.

——————-

Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU

El artículo El cerebro humano tarda en madurar se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Sistemas nerviosos: el cerebro de vertebrados
2. Daños estructurales por consumo de alcohol en el cerebro humano
3. ¿Cuántas células hay en el cuerpo humano?

Uxue Razkin

Kimika

Haragia kozinatzeko arrazoiak hauek dira: seguruagoa da, errazago mamurtzen eta digeritzen da, eta zapore hobea du. Zaporeari dagokionez, haragi gordinak badu, baina aroma eskasak ditu. Aroma eta zaporea benetan garatzeko aldaketa kimikoak gertatu behar izaten dira eta haragia ez bada berotzen uraren irakite puntutik gora, bere zaporea proteinen eta gantzen deskonposaketaren ondorioz askatutako molekulena izango da. Zer gertatzen da haragia berotzen hasten denean? Ez galdu gertatzen diren erreakzio kimikoen azalpen interesgarria Josu Lopez-Gazpioren eskutik!

Masa-espektometria teknika analitiko ahaltsua da. Hori erabiliz, lagin oso konplexuak analizatu daitezke. Gainera, zehatza, sentikorra eta bizkorra da, eta, horregatik, bereziki erabilgarria da lagin biologikoak analizatzeko. Testuan zehar, teknika batzuk azaltzen dira, hala nola, MALDI –esperimentu bakarrean ehunka biomolekula identifikatzeaz gain, molekula horiek ehunean duten kokalekua ere jakin daiteke– eta IMS teknika, oso erabilgarria dena digestio-sistemaren amaieran dagoen koloneko zelulen heltze prozesua aztertzeko, adibidez. Ezagutu gertutik aipatutako teknikak artikulu honetan.

Astronomia

Nola iritsi zen ura Lurrera? Asteroide eta kometak omen dira Lurreko uraren jatorria hoberen azaltzen dutenak. Juanma Gallegok artikulu honen bidez azaldu digu Kondrito karbonatodun izeneko meteoritoen azterketan abiatuta, asteroideek ura Lurrera ekarri zuteneko teoria berretsi dutela ikertzaileek. Karbono-konposatu asko duten meteorito horiek asteroideetan dute abiapuntu. Adituen arabera, arroka puska horiek material hidratatuak eta molekula organikoak jaso zituzten eguzki-sistema sortu zenean.

Ingurumena

Zortzi urte igaro dira hondamendi nuklearra gertatu zenetik eta oraindik nabarmenak dira ondorioak Fukushima zentralean. Oraindik ez dute eraiste-lanak abiatu oso arriskutsuak direlako; maiatzera arte ez dira hasiko. Zentralaren kanpoan, berriz, 900 tanga daude, erradioaktibitateak kutsatutako mila tona ur baino gehiagorekin. Elhuyar aldizkarian azaldu duten bezala, erradioaktibitatea kezka da oraindik ere.

Nazio Batuen Erakundeak (NBE) ingurumenari buruzko seigarren GEO txostena aurkeztu du. Bertan, klima-aldaketari aurre egiteko abiatu diren politikak aski ez direla salatu dute. Egunotan, Nairobin egiten ari diren bileretan plastikoak sortutako kutsaduran ipini dute arreta; neurri berriak adostu nahi dituzte. Aldaketa klimatikoari dagokionez, Parisen adostutakoa betetzeko, gasen isurketa %40 eta %70 artean murriztu behar da 2050erako; 2070ean ezingo delako gasik isuri. Txostenak, Berrian aipatu dutenez, beste hainbat kezka agertu ditu, hala nola airearen kutsadura, bioaniztasuna, itsasoko ekosistemak, uraren kalitatea eta lurzorua.

Genetika

Edizio genetiko heredagarriak klinikan ez erabiltzeko akordioa eskatu dute zazpi herrialdetako adituek. Horien artean aurkitzen dira, besteak beste, CRISPR edizio-teknika garatu zuten Emmanuelle Charpentier eta Feng Zhang. Oro har, adituen arabera, ez litzateke edizio genetikorik egin beharko espermatozoideetan, obuluetan eta enbrioietan, gutxienez teknika segurua dela frogatu arte.

Iberiar penintsulako azken 8.000 urteetako historia genetikoa azaltzen duen lana argitaratu dute. Hainbat aztarnategitan bildutako 271 iberiarren DNA aztertuta, zehaztu dute zer-nolakoa izan zen urte haietako migrazioek eragindako fluxu genetikoa. Elhuyar aldizkaria azaldu digu Erdialdeko Europatik etorritakoek, erromatarrek eta musulmanek utzi zutela arrasto genetikorik nabarmenena. Horretaz gain, Elhuyar aldizkarian azaldu dute, emaitzek agerian jarri dute euskaldunok penintsulako beste populazioekin ditugun desberdintasun genetikoak azken 2.000 urtekoak besterik ez direla.

Alea.eus-ek ere eman du honen berri. Ikerketa lana Iñigo Olalde gasteiztarrak gidatu du, Harvardeko Unibertsitatean lan egiten duen ikertzaileak. Harrigarriak eta esanguratsuak izan diren emaitzak jaso dituztela dio Olaldek, Brontze Aroaren hasiera aipatzen du tartean: “Kristo aurreko 2500-2000 tartean, Erdialdeko Europatik zetorren jendea iritsi zen penintsulara. Hor bi populazio bereizi ditugu: lokala eta etorri berriak”. Jarraitzen du esanez, denboran aurrera jarraitu ahala, K.a. 2.000. urtetik aurrera aldaketa gertatu zela: “Y kromosoma ia beti kanpotik datorrela ikusi dugu, eta garai horretatik lehenagoko gizonezkoek ez dute apenas oinordetzarik utzi“.

EHUko Biokimika Saileko Nerea Osinalde irakasleak kontatzen du Berrian, 2000. urtearen bueltan, DNA molekula etorkizuneko disko gogorra izan zitekeela proposatu zutela lehenengo aldiz. 2013an, esaterako, DNAn informazioa gorde zitekeela frogatzen zuen lehenengo lana argitaratu zuten. Besteak beste, Shakespeareren sonetoak eta Martin Luther Kingen Amets bat dut diskurtsoa gorde zituzten. Lau urte geroago, 215 petabyte informazio gorde zituzten DNA gramo batean. Azken datuen arabera, DNA milimetro kubiko batean 1 TB gorde daiteke. Aurrerapausoak ematen ari dira arlo honetan. Adibidez, Microsoft informatika konpainiak jada iragarri du 2020tik aurrera datu digital bereziak DNAn gordetzen hasiko dela. Gainera, duela gutxi AEBtako ikerketa talde batek DNA molekula sintetiko berri bat aurkeztu du. Hortaz, DNA etorkizuneko disko gogorra izan daitekeela uste duzue?

Emakumeak zientzian

Maria Goeppert Mayerrek 1963an irabazi zuen Fisikako Nobel saria, diziplina honetan saritu zuten bigarren emakumea izan zen –lehenengoa Marie Curie izan zen–. Bere ikerketek erakutsi zuten atomoaren nukleoa geruzez osatuta dagoela. Halaber, bere ikerketak azaldu zuen zergatik diren egonkorragoak nukleo batzuk besteak baino. Eredu hori garatzeagatik, Tipularen emakumea ezizenaz ezagutzen da Mayer fisikaria.

Medikuntza eta osasuna

Dagoeneko lau hamarkada bete ditu GIBaren kontrako borrokak. Duela gutxi izan genuen Londresko gaixoaren berri, zelula amen txertaketa antzeko teknikari esker, “erremisioan” egon da azken hamasei hilabeteotan, botika erretrobiralak kenduta ere. Badirudi ez dela kasualitatea, honen aurretik beste bat izan zelako: Berlingo gaixoa. GIB birusak kutsaturik zegoen, eta 2007an zelula amen txertaketa batekin sendatu zuten, gaur arte. Halere, zientzialariek ez dute “sendatu” aditza erabili nahi, izan ere, teknikak baditu arazoak edonorentzako tratamendu bihurtzeko. Zergatik da hain zaila birus horren aurka egitea? Berriak arrazoi batzuk eman ditu eta aditu batzuen hausnarketak bildu ditu ere.

–——————————————————————–
Asteon zientzia begi-bistan igandeetako atala da. Astean zehar sarean zientzia euskaraz jorratu duten artikuluak biltzen ditugu. Begi-bistan duguna erreparatuz, Interneteko “zientzia” antzeman, jaso eta laburbiltzea da gure helburua.

———————————————————————–

Egileaz: Uxue Razkin kazetaria da.

——————————————————————

The post Asteon zientzia begi-bistan #246 appeared first on Zientzia Kaiera.

¿Hemos intentando contactar con extraterrestres? Y si es así, ¿cómo y cuándo se ha hecho? ¿Quién lo ha hecho? Y sobre todo, ¿qué se les ha dicho en los mensajes que se han enviado? Todas las respuestas en minuto y medio.

Los vídeos de ¿Preguntas frecuentes? presentan de forma breve y amena cuestiones que, probablemente, nos hayamos planteado en alguna ocasión. Los vídeos, realizados para la Cátedra de Cultura Científica de la UPV/EHU, se estrenarán en el programa de ciencia Órbita Laika (@orbitalaika_tve), a partir del próximo 18 de marzo todos los lunes a las 22:00 en la 2 de RTVE.

Edición realizada por César Tomé López

El artículo ¿Hemos intentando contactar con extraterrestres? se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Ciencia express: los transgénicos
2. Ciencia express: el carbono-14 y los rayos cósmicos
3. Ciencia express: Cómo se formó la luna

Lan eta lan. Lanean zazpi ahalak egiten. Hitzez hitz. Eta horren ondorioz ez bazara hiltzen, depresioa ate joka izango da. José Ramón Alonsok ematen dizkigu argibideak: Karoshi, depression and work hours.

Baso-sute handiak matematika erabiliz molda daitezke. Hala ere, sutea zabaltzearen aldagai guztiak kontuan hartu behar baditugu, fluido zurrunbilotsuen fisika eta fisika estatistikoa aintzat hartu beharko dira. Hori berori egin dute BCAMeko ikertzaileek: Wildfire propagation modelling.

Gaur elektronikan erabiltzen diren metalak agortu egingo dira egunen batean, garestiak bihurtuko dira edo arloteren baten menpean izango dira. Arazo honi irtenbidea emateko ona litzateke etorkizuneko elektronikak guztiok eskuragarri izango genituzkeen material merkeak erabiltzea. Adibidez, molekula organikoak. Ondorioz, spintronikaz hitz egingo genuke eta ez elektronikaz baina, une horretara heldu orduko, hainbat pausu eman beharko dira oraindik. Momentuz DIPCko ikertzaileek pausu txiki bat eman dute: Spin in a closed-shell organic molecule stabilized on a metallic surface.

–—–

Mapping Ignorance bloga lanean diharduten ikertzaileek eta hainbat arlotako profesionalek lantzen dute. Zientziaren edozein arlotako ikerketen azken emaitzen berri ematen duen gunea da. UPV/EHUko Kultura Zientifikoko Katedraren eta Nazioarteko Bikaintasun Campusaren ekimena da eta bertan parte hartu nahi izanez gero, idatzi iezaguzu.

The post Ezjakintasunaren kartografia #253 appeared first on Zientzia Kaiera.

La Facultad de Ciencias de Bilbao comenzó su andadura en el curso 1968/69. 50 años después la Facultad de Ciencia y Tecnología de la UPV/EHU celebra dicho acontecimiento dando a conocer el impacto que la Facultad ha tenido en nuestra sociedad. Publicamos en el Cuaderno de Cultura Científica y en Zientzia Kaiera una serie de artículos que narran algunas de las contribuciones más significativas realizadas a lo largo de estas cinco décadas.

Toma de muestras de bivalvos en los manglares nicaragüenses. Foto: Ionan Marigomez / UPV/EHU

A menudo se critica a la universidad por falta de conexión con la sociedad. Se afirma que la universidad enseña conocimientos arcanos y que la investigación apenas tiene implicaciones prácticas. Este punto de vista es compartido por bastantes universitarios, por lo que algo habrá detrás del mismo. Sin embargo, un poco de perspectiva histórica muestra que hay numerosas interacciones entre la universidad y la sociedad. A título de ejemplo, vamos a analizar cuál ha sido el impacto de la Sección de Biología en la conservación de la naturaleza.

La Sección de Biología comenzó su andadura muy modestamente en la por entonces denominada Facultad de Ciencias de la Universidad de Bilbao. Esta Sección carecía de catedráticos hasta 1975 y, de los tres profesores agregados de aquel momento, ninguno pertenecía a alguna de las áreas de la biología más naturalistas, es decir, la botánica, la zoología o la ecología. Tampoco llegaban fondos para apoyar proyectos de investigación en estos ámbitos. El bum llegó en la segunda mitad de los años 80, cuando se multiplicó el número de profesores, se potenció la formación de doctores y los grupos de investigación comenzaron a recibir financiación pública para el desarrollo de sus proyectos. Los años 90 vieron la aparición de cursos de postgrado tipo máster, como por ejemplo el de “Evaluación y Recuperación Ambiental”, y el afianzamiento de colaboraciones externas de los equipos de investigación. El siglo XXI ha supuesto la puesta de largo de la investigación en muchos de esos grupos, que participan en proyectos multinacionales de indudable repercusión sobre la conservación y el manejo de los recursos naturales, llegando a alcanzar niveles de excelencia y prestigio internacionales.

En estos años, la Facultad de Ciencia y Tecnología ha formado un gran número de personas en Biología, Ciencias Ambientales y otras disciplinas ligadas con la conservación de la naturaleza. Según las estadísticas oficiales, los egresados de la la FCT incluyen más de 3850 licenciados y más de 450 graduados en Biología, a lo que se suman centenares de estudiantes de master y 475 doctores. De ellos, muchos trabajan en ámbitos relacionados con la conservación de la naturaleza. Algunos lo hacen para la administración como técnicos de medio ambiente municipales, en consorcios y mancomunidades, en las diputaciones forales, departamentos del Gobierno Vasco, parques naturales, etc. Otros muchos trabajan en empresas relacionadas con la conservación de la naturaleza, como consultoras (por ejemplo, Anbiotek o Ekolur) o en centros de I+D+I como Neiker o Azti. Otros muchos se han dedicado a la enseñanza, tanto la reglada en institutos, ikastolas, colegios y universidades, como no reglada en aulas de naturaleza, CEIDAs, etc. Finalmente, muchos egresados colaboran en asociaciones y otras entidades en pro de la conservación de la naturaleza, como grupos ecologistas, asociaciones conservacionistas o entidades de estudio e interpretación del medio ambiente como la Sociedad de Ciencias Aranzadi. Aunque es imposible de cuantificar, podemos afirmar que esta masa de gente con una formación en biología y actitudes conservacionistas ha tenido mucho que ver con la transformación que se ha registrado en la forma de entender la relación de la especie humana con el medio ambiente en el País Vasco.

Miembros de la FCT discutiendo un proyecto de restauración en el Parque Natural de Aiako Harria con técnicos de la Diputación Foral de Gipuzkoa, de Aguas del Añarbe de URA y de la Confederación Hidrográfica del Cantábrico. Fuente: Arturo Elosegi.

Por otro lado, algunos equipos de la FCT han sido muy activos en el inventariado y seguimiento de la biodiversidad de nuestro entorno. Por citar sólo algunos de ellos, el laboratorio de zoología abrió varias líneas de investigación sobre fauna fluvial y marina, sobre artrópodos del suelo o sobre moluscos terrestres. A esas líneas posteriormente se han incorporado otros grupos como el de murciélagos. Por su parte, el laboratorio de botánica abrió líneas de investigación sobre algas, musgos, plantas superiores y hongos, así como otra sobre geobotánica, que caracterizó y cartografió las principales comunidades vegetales de nuestro entorno. La información acumulada durante décadas ha sido esencial para caracterizar los lugares más biodiversos del País Vasco, para identificar sus principales factores de riesgo y, entre otras, para diseñar y optimizar la red Natura 2000.

Además de los inventarios de biodiversidad, algunos grupos han trabajado activamente en evaluar el estado de salud del medio ambiente, colaborando en poner las bases del sistema de información medioambiental del País Vasco. Por ejemplo, en los años 80, los entonces laboratorios de zoología y ecología se embarcaron en el primer gran estudio hidrobiológico de los ríos de Bizkaia, así como en la evaluación del estado medioambiental de la ría de Bilbao. El primer trabajo fue la semilla de la que derivó la red de seguimiento de los ríos del País Vasco, actualmente en manos de URA, la Agencia Vasca del Agua, mientras que el segundo comenzó una serie de estudios sobre la salud de nuestra costa. También hay que citar en este apartado al laboratorio de microbiología, que durante muchos años ha colaborado en la determinación de la calidad de las aguas de baño de la Comunidad Autónoma.

Otros grupos han centrado sus estudios en la detección y evaluación de los impactos que causa la actividad humana en la estructura y el funcionamiento de los ecosistemas. El grupo de ecología fluvial ha estudiado el impacto de las prácticas forestales, de la contaminación agrícola y urbana, de las detracciones de agua o del cambio climático en ríos vascos y de otras regiones. Lo que comenzó siendo el laboratorio de citología, por su parte, ha ido convirtiéndose en un grupo de investigación sobre ecotoxicología, que es hoy la base de la Estación Marina de Plentzia, mientras que el grupo de ecotoxicología animal y biodiversidad utiliza especies como centinelas del estado de salud de las aguas continentales. Otras líneas aplicadas han sido el estudio de suelos contaminados, que se ha abordado desde los laboratorios de zoología y fisiología vegetal, o los trabajos más agronómicos realizados en este último. Toda la información obtenida por estos grupos es utilizada por la Diputaciones Forales, por el Gobierno Vasco y por otras entidades en la planificación y gestión del territorio.

Miembros de la FCT revisando trabajos de restauración ecológica en el río Araxes (Gipuzkoa), junto con técnicos de la Diputación Foral de Gipuzkoa, de las empresas Ekolur y Basoinsa, y un científico del IGB de Berlín. Fuente: Arturo Elosegi.

Más allá de la obtención de información, algunos grupos de la Sección han colaborado estrechamente con la administración en trabajos de gestión de poblaciones, comunidades o ecosistemas. Por ejemplo, el grupo de ecología y evolución del comportamiento ha trabajado en la gestión de mamíferos amenazados, como el visón, el desmán ibérico o los murciélagos, el de ecología y gestión del pastoreo en la gestión de la ganadería en pastos de montaña, el grupo de ecofisiología vegetal en la, entre otras, recuperación de suelos degradados o contaminados, y el de ecología fluvial en proyectos de restauración de ríos. Estos trabajos no se han limitado a evaluar el efecto de prácticas de conservación realizadas por la administración, sino que han implicado a la universidad en el diseño, ejecución y seguimiento de estas prácticas, muchas de las cuales han sido pioneras a nivel estatal.

Finalmente, no podemos olvidar el papel de asesoría realizado por muchos miembros de la Sección, en su participación en los patronatos de parques naturales o de la Reserva de la Biosfera de Urdaibai, o en Naturzaintza, el consejo asesor de conservación de la naturaleza del Gobierno Vasco. Además de estas colaboraciones, es habitual que miembros de la Sección participen en reuniones para definir estrategias y planes de la administración, como la Estrategia Española de Restauración de Ríos o la Estrategia Vasca de Biodiversidad.

La Sección de Biología continúa aportando conocimiento sobre los ecosistemas de nuestro entorno, lo cual facilita la gestión de nuestros recursos naturales. Si bien hasta hace bien poco esta aportación de conocimiento residía básicamente en las áreas más naturalistas referidas arriba, hoy en día las herramientas de la biología molecular son esenciales en el estudio de la biodiversidad, lo que aumenta el número de grupos que trabajan en este campo. Por todo ello, es de esperar que la Sección de Biología de la FCT siga teniendo un papel importante en la conservación de la naturaleza en el País Vasco y en el mundo en general.

Sobre los autores: Arturo Elosegi es profesor de ecología en el Departamento de Biología Vegetal y Ecología de la Facultad de Ciencia Tecnología de la UPV/EHU. Jesús Pozo se retiró recientemente del mismo departamento.

El artículo Los biólogos de la UPV/EHU y la conservación de la naturaleza se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Una fórmula para dominarlos a todos: La conservación de la energía y la ley de la palanca
2. De las leyes de conservación (I)
3. Naturaleza, ciencia y cultura en el bicentenario de Henry David Thoreau

Uxue Razkin Wolfgang Paulik Tipularen emakumea deitu zion behin Maria Goeppert Mayerri. Harrezkero, denek hala gogoratzen dute fisikaria. Goitizenek luzaroan iraun ohi dute, batzuetan izenak baino gehiago, askotan nahi baino usuago. Kasu honetan, ezizen horren atzean azalpen zientifiko bat dago, Mayerrek egindako lanari egiten dio erreferentzia zuzen-zuzenean, bere ikerketek erakutsi baitzuten atomoaren nukleoa geruzez osatuta dagoela, tipularen antzera. Halaber, bere ikerketak azaldu zuen zergatik diren egonkorragoak nukleo batzuk besteak baino. Lan horri esker lortu zuen 1963an Fisikako Nobel saria, diziplina honetan saritu zuten bigarren emakumea hain zuzen ere –lehenengoa Marie Curie izan zen–.

Goeppert-Mayer 1906an jaio zen, Katowice-n (Polonia, lehengo Alemaniako Inperioko probintzia). Haren familia Göttingenera joan zen bizitzera, aita, Friedrich Goeppert, hiriko unibertsitateko pediatriako irakasle izendatu zutenean. Txikitatik matematikak maite zituen eta baliteke zientziarako grina haren aitak piztu izana. Izan ere, ikastera animatu zuen bere alaba hasieratik; bere heziketaz arduratuta, etxean ez gelditzeko eta zientziaren bidea hautatzeko bultzatu zuen. Horiek hola, sufragistek eraiki zuten institutu batean ikasi zuen, unibertsitatean izena emateko derrigorrezko pausoa emanez.

1. irudia: Maria Goeppert Mayer fisikaria. (Argazkia: U.S. Department of Energy / flickr)

Bada, eskola itxi zuten hain justu unibertsitatean sartzeko azterketa egin aurretik. Halere, Mayerrek bere kabuz ikasten jarraitu zuen: azterketa egin eta Göttingen Unibertsitatean onartu zuten 1924an, matematika ikasle gisa. Bertan, etorkizunean Nobel saridunak izango zirenak izan zituen irakasle, hala nola Enrico Fermi, Werner Heisenberg, Paul Dirac, eta aurretik aipatutako Wolfgang Pauli.

Lehendabiziko urtean, berriz, matematikak utzi zituen fisika ikasi nahi zuelako. Une hartan, mekanika kuantikoa indarra hartzen ari zen arloa zen; erakusleiho baten moduan funtzionatzen zuen, zientzialariek kristalera hurreratu nahi zuten, guztiz asaldatuta, zer zegoen ikusteko irrikan. Mariak kontzeptu matematikoak ezagutzen zituenez, diziplina hori ulertzeko ez zuen aparteko ahaleginik egin. Ikasketak amaitu ondoren, tesia egiteko unea iritsi eta Max Born aukeratu zuen zuzendari gisa. 1930ean doktoregoa lortu zuen fisika teorikoan.

Estatu Batuetako jarduna: nepotismoaren eta sexismoaren artean

Joseph Edward Mayerrekin ezkondu ondoren, etxez aldatu ziren, Baltimore hirira joan ziren bizitzera. Bertan, bere senarra John Jopkins Unibertsitateko Kimikako Departamentuan hasi zen lanean, Mariak, aldiz, Fisikako Departamentuan eskuratu zuen lanpostu bat, lanaldi osorik gabe eta soldatarik kobratu gabe. Unibertsitatean klaseak emateko sobera gai zen baina garaiko nepotismoak ez zion bere jarduna egiten utzi, irakasle baten emaztea baitzen.

2. irudia: Maria Goeppert Mayer (1906-1972) fisikaria, Suediako Gustavo Adolfo erregearekin, 1963. urtean Fisikako Nobel saria jaso ondorengo afarira doazela. (Argazkia: Smithsonian Institution / jabego publikoko argazkia)

Estatu Batuetan egon arren, Bornekin kontaktuan jarraitu zuen. Izan ere, 1930etik 1933ra Göttingenen igaro zituen udak harekin elkarlanean. Artikulu bat idatzi zuten bien artean fisikako entziklopedia ezagun baterako: Handbuck der Physik. Sinbiosi honek ez zuen asko iraun baina, Adolf Hitlerren igoera zela eta, Bornek bere lana galdu baitzuen judutarra izateagatik eta Eskoziara alde egin zuelako. Mayetarrak, bere aldetik, Columbiara joan ziren. Bertan, Mariari lan-eskaintza egin zioten Sarah Lawrence Eskolan zientzia irakasteko. Han aritu zen 1941etik 1945era, eta era berean, laborategi batean egiten zuen lan, uranio isotopoen bereizketan, hain zuzen. Alabaina, Harold Urey laborategiko zuzendariak bigarren mailako zereginak agintzen zizkion. Pozik egon zen baina ez zuen asko lagundu ikerketan. 1946an, Chicagora joan ziren senar-emazteak eta Mariak oso azkar lortu zuen lana Ikasketa Nuklearreko Institutuko fisika irakasle gisa. Gainera, Argonne National Laborategian –lehen Met Lab izan zena, Manhattan Proiektua garatu zuten lekua– hasi zen lanean, energia nuklearraren erabilera baketsuen garapenean.

Zenbaki magikoen dantza

Chicagora iritsi zenean, Mariak ez zeukan formakuntzarik fisika nuklearrean. Dena dela, bere lagun Fermi eta Edward Tellerren laguntzaz, arlo hori ikasten eta ikertzen hasi zen. Azken honekin, adibidez, lan egin zuen elementuen jatorria zehazteko. Gainera, haren ikerketak atomoaren nukleoa geruzez osatuta dagoela zehaztu zuen, hots, geruzetan zenbat eta asetasun handiagoa izan, nukleoa -eta, beraz, elementua- orduan eta egonkorragoa zela ikusi zuen. Horretaz gain, nukleo horiek 2, 8, 20, 28, 50, 82 edo 160 protoi edo neutroi (nukleoiak) izanda benetan egonkorrak zirela jabetu zen. Horiei zenbaki magikoak deitu zieten. Honen ondotik, nukleoaren spin-orbita teoria proposatu zuen, atomoen nukleoaren geruzen eredura iritsiz.

3. irudia: Argonne National Laborategiko fisika alorreko eraikinean Maria Goeppert Mayer fisikariaren omenez jarritako plaka. (Argazkia: Argonne National Laboratory / CC BY-NC-SA 2.0 lizentziapean)

Egindako esperimentuek fruituak eman zituen baina oso prozesu geldoa izan zen. Edonola ere, 1948an emaitzak publikatu zituen Physical Review aldizkarian. Gaia teorikoki azaltzen zuen bigarren artikulu bat bidali behar zuenean, ordea, konturatu zen ezagutzen ez zituen beste zientzialari batzuek, Hans Jensen, Otto Haxel eta Hans Suess fisikariak artean, ondorio berera iritsi zirela. Hala, bere testua geroago argitaratzeko eskatu zuen, Jensen eta bere taldeak idatzitakoarekin batera ager zedin. Baina azkenean, Mariarena urtebete geroago publikatu zuten. Horren ondotik, Jensenekin liburu bat argitaratzea erabaki zuen, geruzen egitura nuklearra deskribatuz.

1960an, Kaliforniako Unibertsitatean Fisikako katedraduna izatera iritsi zen, ordainsari baten truke lortu zuen lehenengo lanpostua izan zen. Harritzekoa da baina Mariak une hartan 54 urte zituen. Gainera, Ameriketako Estatu Batuetako Zientzien Akademia Nazionaleko eta Heidelbergeko Zientzia Akademiako kide izendatu zuten. Hori gutxi balitz bezala, hiru ohorezko titulu jaso zituen.

Aipatu dugunez, 1963an jaso zuen Fisikako Nobel saria, azkenean. Dena dela, pozak ez zuen asko iraun, 1972an bihotzekoak emanda hil baitzen. Edozein kasutan ere, Goeppert Mayerrek saria baino, egindako bidea gozatu zuen. Berak esan zuen moduan:

“saria irabaztea ez zen izan lan horixe bera egitea baino asegarriagoa”.

Iturriak:

• eldiario.es: Maria Goeppert Mayer, la última ganadora de un Nobel de Física
• Mujeres con ciencia: Maria Goeppert-Mayer: La belleza de Göttingen
• Rincón Educativo: María G. Mayer
• The Nobel Prize: Maria Goeppert Mayer

———————————————————————–

Egileaz: Uxue Razkin (@UxueRazkin) kazetaria da.

———————————————————————–

The post Maria Goeppert Mayer (1906-1972): Atomoen geruzen eredua aurkitu zuen emakumea appeared first on Zientzia Kaiera.

Imagen: Pixabay

La segunda mitad del siglo XX vio nacer la computación y el sueño de la inteligencia artificial —“la ciencia de conseguir que las máquinas hagan cosas que requerirían inteligencia si las hiciesen humanos”, en palabras de Marvin Minsky—, que hoy en día está despertando un renovado interés gracias a la rama del aprendizaje automático. Se trata de un conjunto de técnicas que se benefician de los avances tecnológicos en materia de computación de las últimas dos décadas, y se caracterizan por su capacidad de engullir enormes cantidades de datos para enfrentarse a problemas de gran complejidad. Las aplicaciones son vastas, y ya forman parte de nuestro día a día: se utilizan para detección de fraude, navegación en vehículos autónomos, sistemas de recomendación (de productos, música…), diagnóstico médico, optimización de procesos, juegos… y un largo etcétera.

En todos estos casos, decimos que la máquina aprende. Y sabemos perfectamente cómo aprende (la lógica matemática y computacional subyacente), pero ¿qué aprende exactamente? Esta pregunta, aparentemente sencilla, nos persigue en todas sus aplicaciones. Por ejemplo, ¿qué lleva a AlphaZero a considerar ventajosos los movimientos que hace y que epatan por igual a aficionados y expertos ajedrecistas? Lo cierto es que no lo sabemos. La importancia de la cuestión puede parecer relativa en decisiones no críticas como la recomendación de una película, pero resulta esencial, e incluso abre derivadas éticas, cuando hablamos de cosas como conceder o no conceder un crédito, o la reacción de un coche autónomo ante un accidente.

En realidad, el tipo de problema al que se enfrentan las técnicas de aprendizaje automático es el mismo al que se viene enfrentando la ciencia, estadística mediante, desde su nacimiento: la inferencia de patrones, de generalizaciones, a partir de datos observacionales con el objetivo de obtener predicciones. En otras palabras, dada una entrada X, ¿qué modelo o función “f” genera la salida Y=f(X)? La gran diferencia se encuentra en que tradicionalmente nos hemos enfrentado a problemas para los cuales hay una teoría matemática previa que establece la estructura de “f”. La estadística clásica es la ciencia que estudia los diferentes tipos de modelos “f” y genera las técnicas para obtener y evaluar el mejor ajuste a partir de las observaciones (x, y). Por otro lado, las técnicas de aprendizaje automático de la nueva ciencia de datos son capaces de aprender la función “f” a partir de los datos sin ningún modelo previo, sin ningún conocimiento a priori del problema. La función “f” inferida se encuentra de alguna forma codificada tras el proceso de aprendizaje, pero nos es completamente desconocida y no hay forma de extraerla: es por eso que suelen llamarse “algoritmos de caja negra”.

Así pues, la estadística clásica define modelos matemáticos en los que las relaciones entre variables son explícitas y, por tanto, son directamente interpretables. Pensemos en una simple relación lineal: cuando crece X, crece Y; por tanto, obtenemos un valor grande de Y porque X es grande. En cambio, estos algoritmos de caja negra son capaces de capturar relaciones arbitrariamente complejas y predecir con gran precisión, pero su desventaja a día de hoy es que nos las ocultan, matemáticamente hablando: no somos capaces de interpretar qué propiedades de X influyen en Y.

Por tanto, uno de los grandes retos que la inteligencia artificial tiene por delante es el de intentar obtener conocimiento a partir de la estructura que las máquinas son capaces de extraer de grandes volúmenes de datos. Quizás se logre mediante una formalización matemática de las técnicas actuales, o quizás se desarrolle una nueva estadística ahora desconocida. Sea como sea, aprender de las máquinas puede ser uno de los principales hitos del presente siglo.

Sobre el autor: Iñaki Úcar es doctor en telemática por la Universidad Carlos III de Madrid e investigador postdoctoral del UC3M-Santander Big Data Institute

El artículo Aprendiendo de las máquinas se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Máquinas inteligentes (y III): Deep blue, HAL 9000 y más allá
2. Seminario Famelab: aprendiendo a hacer monólogos
3. Máquinas inteligentes (II): Inteligencia artificial y robótica

José Antonio Fernández Masa-espektrometria teknika analitiko ahaltsu bat da, molekulak identifikatzea ahalbidetzen duena haien masatik abiatuta. Masa-espektrometria erabili ahal izateko, lagina, dagoen egoeran dagoela ere, kaltegabe transferitu eta elektrikoki kargatu behar da gas fasera. Noski, definizio horretan supersinplifikatuta daude teknikaren azpian dauden printzipio fisiko-kimikoak.

Hala ere, zenbait ondorio garrantzitsu atera daitezke bertatik: teknika honekin lagin oso konplexuak analizatu daitezke, aldez aurretik markatu gabe (hau da, detektatu nahi diren molekulak markatu behar izan gabe). Bi ezaugarri horiek izateaz gain, masa-espektrometria teknika oso zehatza, sentikorra eta bizkorra da, eta, horregatik, bereziki erabilgarria da lagin biologikoak analizatzeko. Baina molekula biologikoak kaltegabe gas-fasera transferitu ahal izateko, ionizazio-teknika bigunak garatu behar izan ziren.

Molekula termolabilak masa-espektrometro batean sartzeko gehien erabiltzen diren tekniketako bat MALDI (Matrix Assisted Laser Desoption/Ionization, 1. irudia) da. Hasteko, lagin biologikoaren zati adierazgarri bat altzairuzko plaka batean jarri eta substantzia organiko batekin (matrizea) estali behar da, matrizeak argia xurga dezan laser komertzialen igorpen eremuan (oro har ultramorean, 335-350 nm inguru). Molekula biologikoak gardenak izan ohi dira erradiazio horren aurrean, eta, horregatik, laserrak ez die eragiten. Baina matrizeak laser-erradiazioa xurgatzen du, zatikatzen da eta analitoa askatzen du gas-fasean ionizatuta.

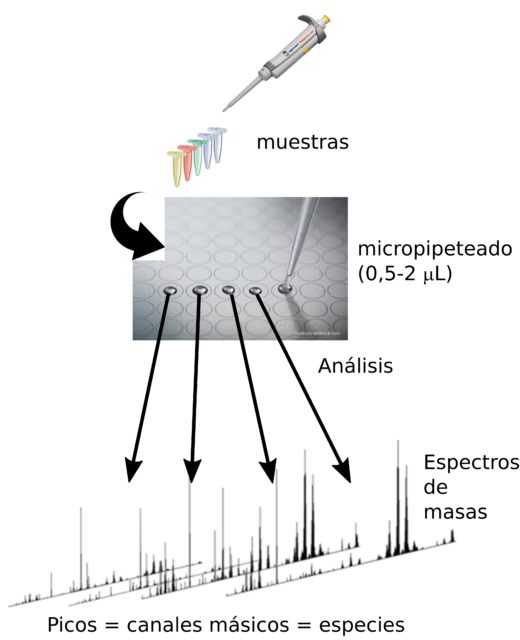
1. irudia: MALDI bidezko masa-espektometriaren eskema. (Iturria: José A. Fernández)

90ko hamarkadan, teknika finago bat garatu zen: masa-espektrometria bidezko irudia, ehunak zuzenean esploratzea ahalbidetzen duena (2. irudia). Noski, lagin solidoetan ez ezik, freskotan izoztutako ehun-ebakiduretan ere aplika daiteke zuzenean MALDI metodologia. Era horretan, molekula biologiko guztiak (detektagarriak) ehunean nola banatzen diren adierazten duten mapak lor daitezke. MALDI-IMS (MALDI-Imaging Mass Spectrometry) teknikaren bidez, esperimentu bakarrean ehunka biomolekula identifikatzeaz gain, molekula horiek ehunean duten kokalekua ere jakin daiteke (informazio espaziala), eta, horrela, aldaketak egitura histologikoekin edo banakako zelulekin erlaziona daitezke.

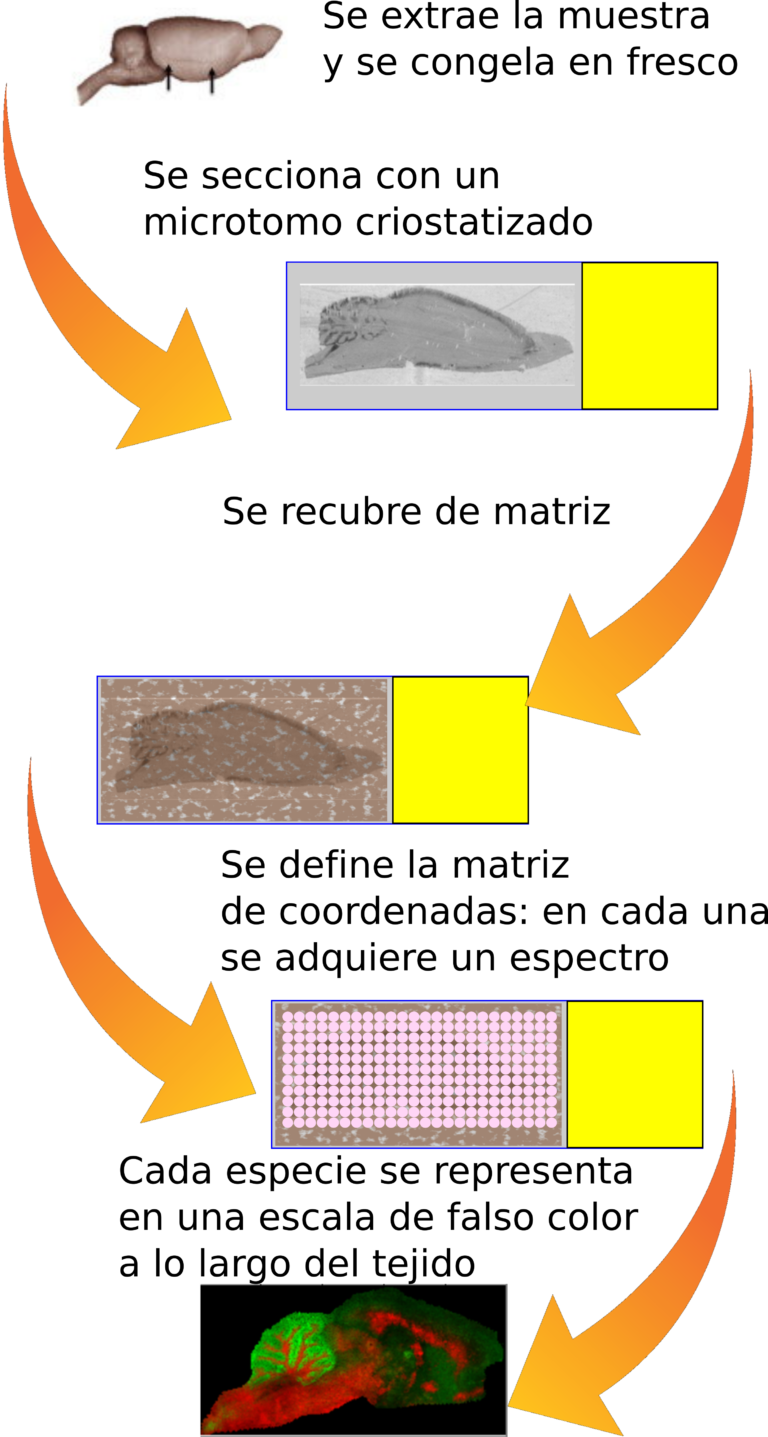
2. irudia: MALDI-IMS esperimentu baten protokoloa. (Iturria: José A. Fernández)

Koloneko zelulen azterketa

Metabolomikan, informazio espazialak garrantzi oso handia du, zelula-mota bakoitzak profil metaboliko propioa baitu eta aldatu egiten baita zelulen zikloarekin. Adibidez, IMS teknika oro erabilgarria izan da digestio-sistemaren amaieran dagoen koloneko zelulen heltze prozesua aztertzeko. Organo horren pareta (3. irudia) estalita dago kripta deritzen inbaginazioez, eta zelula epitelialen (larruazala) geruza bakar batek osatuta daude. Epitelio guztietan gertatzen den bezalaxe, kolonekoa ere higatu egiten da eta zelulak etengabe berritu behar dira. Kripten hondoan, etengabe zatitzen ari diren ama-zelulen nitxo bat dago, eta horiek hornitzen dute zelulaz kripta. Zelula berri horiek gorantz bultzatzen diete aurrekoei, eta heltzen eta zeregin espezifikoak betetzen joaten dira, azkenean kanpoaldera iritsi eta ezkatatzen diren arte.

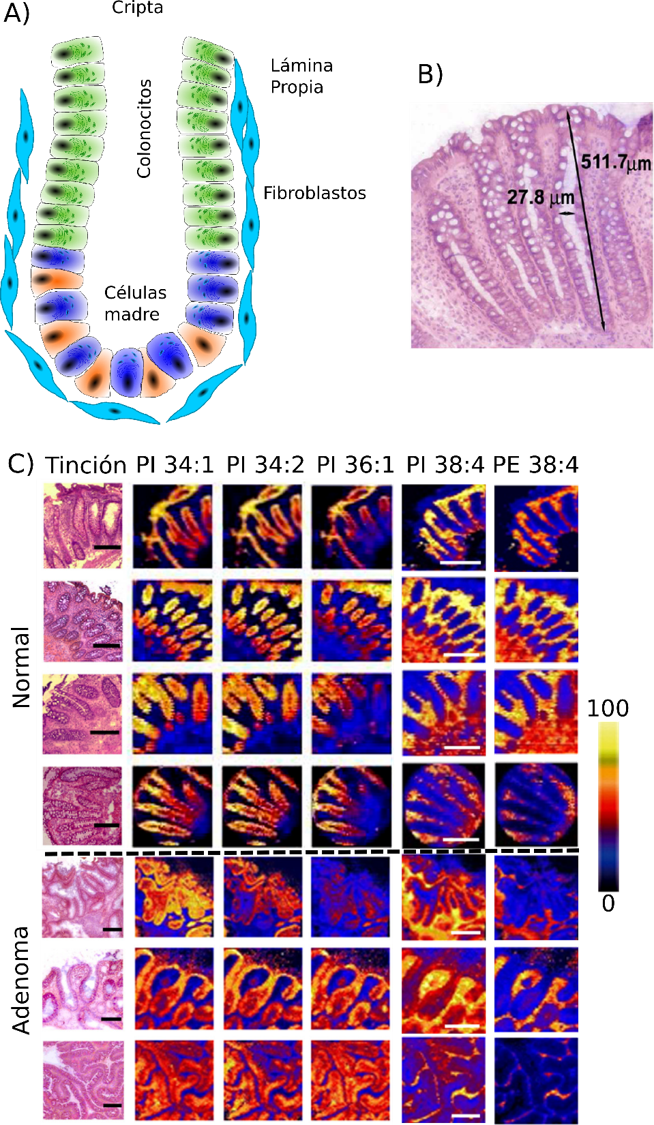
3. irudia: A) Koloneko kripta baten eskema. B) Giza kolonaren ebakidura baten irudi optikoa, non zenbait kripta ikusten diren; C) Lipido-espezie adierazgarri batzuen banaketaren irudiak giza kolon osasuntsuaren eta adenomatosoaren biopsien ebakiduretan. (Iturria: José A. Fernández)

Barceló-Coblijn doktorearen (IdisPa, Palma) taldearekin elkarlanean egin ditugun MALDI-IMS esperimentuei esker, frogatu dugu zelulak banatzeko eta heltzeko prozesu osoan profil lipidikoa edo lipidoma (zelula batean dauden lipidoen multzoa) aldatu egiten dela: kolonozitoa heltzen den neurrian, azido arakidonikoa (seinale-funtzioak dituen gantz-azidoa) duten lipido-espezieen lekuan kate motzagoko eta asegabetasun gutxiagoko gantz-azidoak jartzen dira. Laburbilduz, lipidoak zorrozki erregulatuta daudenez, profil lipidikoari erreparatuta jakin daiteke kolonozitoa kriptako zer lekutan dagoen. Are gehiago, irudien bidez jakin dezakegu lipodomako aldaketa hori konolozitoaren erdialdean eta amaieran gertatzen dela, baina kolonozitoaren nukleoaren lipidoma ez dela aldatzen heltze-prozesuan zehar.

Koloneko kriptak orri propioa deritzon ehunak inguratuta daude, zeinak euskarri ematen dien eta immunologia-sistemako zelula asko dituen, bakterioen erasoei adi beti. Gogoan izan behar dugu epitelioaren beste aldean bakterio asko daudela, elikagaiak prozesatzen eta mantenugaiak aprobetxatzen laguntzen digutenak. Bakteriak alde zuzenean dauden bitartean, onuragarriak dira. MALDI-IMS teknikari esker frogatu ahal izan genuen orri propioko zelulek eredu guztiz desberdin bati jarraitzen diotela: hanturarekin erlazionatuta dagoen azido arakidoniko asko dute, eta azido hori ugariagoa da kolonaren zati luminaletik gertu. Zelula bakoitzak lipido-konposizio propioa eta berdingabea du, eta horri esker zelulak identifika daitezke.

Ezagutza horren guztiaren aplikazio zuzen eta bistako bat da koloneko minbizia garaiz detektatzea. Zelula baten profil lipidikoa horren zorrozki erregulatuta badago, gaiztotze-prozesuak eragiten duen alterazio metabolikoak inpaktu ikaragarria izan beharko luke zelulen profil lipidikoan. Izan ere, gure emaitzek frogatzen dute koloneko ehun hondatuak alterazio morfologiko nahiz metaboliko adierazgarriak dituela. 3. irudian kolon neoplasikoari egindako biopsia bateko ebakiduraren irudi histologikoak daude. Argi ikusten da kriptek beren ohiko morfologia galdu dutela; izan ere, ama-zelulak kontrolik gabe ugaltzen ari dira eta kolonozito gehiegi sortzen dituzte, eta, gainera, kolonozitoak ez dira heltzen. Espero zitekeen moduan, kolonozito horien aztarna lipidikoa kriptaren hondoko ama-zelulen aztarna lipidikoaren berdina da, eta, ikuspuntu molekularretik, horrek frogatzen du kolonozito heldugabeak direla eta ugaltzen jarraitzen dutela bereiztera iritsi gabe. Bien bitartean, gaiztotze-prozesuak ez du eraginik orri propioko zeluletan eta ehun osasuntsuan dutenaren antzeko profil lipidikoa izaten jarraitzen dute.

Adibide honek frogatzen du garrantzitsua dela lokalizazio espaziala ahalbidetzen duten teknikak erabiltzea metaboloma, edo zehatzago esanda, lipidoma aztertzeko garaian, aldaketak maila zelularrean gertatzen baitira. Bereizmen espazialik gabe, kolonozitoetan gertatutako aldaketak gainerako zelulen lipidomaren artean barreiatuta geldituko lirateke.

Burmuinaren azterketa

MALDI-IMS teknikaren aplikazioa iraultza eragiten ari da, lipidomikaren arloan ez ezik, baita proteomikan eta arlo aplikatuagoetan ere, hala nola anatomia patologikoan. Hain zuzen ere, artikulu honetan jarri diren adibideetan lipidoen banaketa islatzen duten mapak aurkeztu diren bezalaxe, proteinak eta peptidoak ere detekta daitezke zuzenean ehunean eta dagozkion irudiak egin daitezke. Egiaz, MALDI bidez detekta daitekeen edozein molekulari aplika dakioke teknika hau eta, horrela, patologoak ehun baten histologia ikus dezake, ikuspuntu molekularretik. Ehun edo zelula mota bakoitzak profil lipidomiko/proteomiko propioa duenez, analisi estatistikorako tresnak erabil daitezke pixelak bistaratzeko aztarna molekularrean oinarrituta; horixe ikusten da 4. irudian, non arratoi baten burmuineko ebakidura sagitalean (luzetara, usaimen-erraboiletik burmuineraino) egindako MALDI-IMS esperimentuaren emaitza jaso den: pixel bakoitzaren espektroak analisi estatistikorako algoritmo baten bidez analizatu dira eta, ondoren, neurona-sare baten gainean proiektatu dira, irudian ikusten den kolore-eredua erabiliz: antzeko profil metabolikoa duten pixelek eskalan gertu dauden koloreak dituzte. Irudiak ehunaren histologia zintzoki islatzen du. Zelula mota baten metabolismoa aldatuko balitz, kolore-eredua aldatuko litzateke eta, horrela, alterazioa erraz detektatuko genuke.

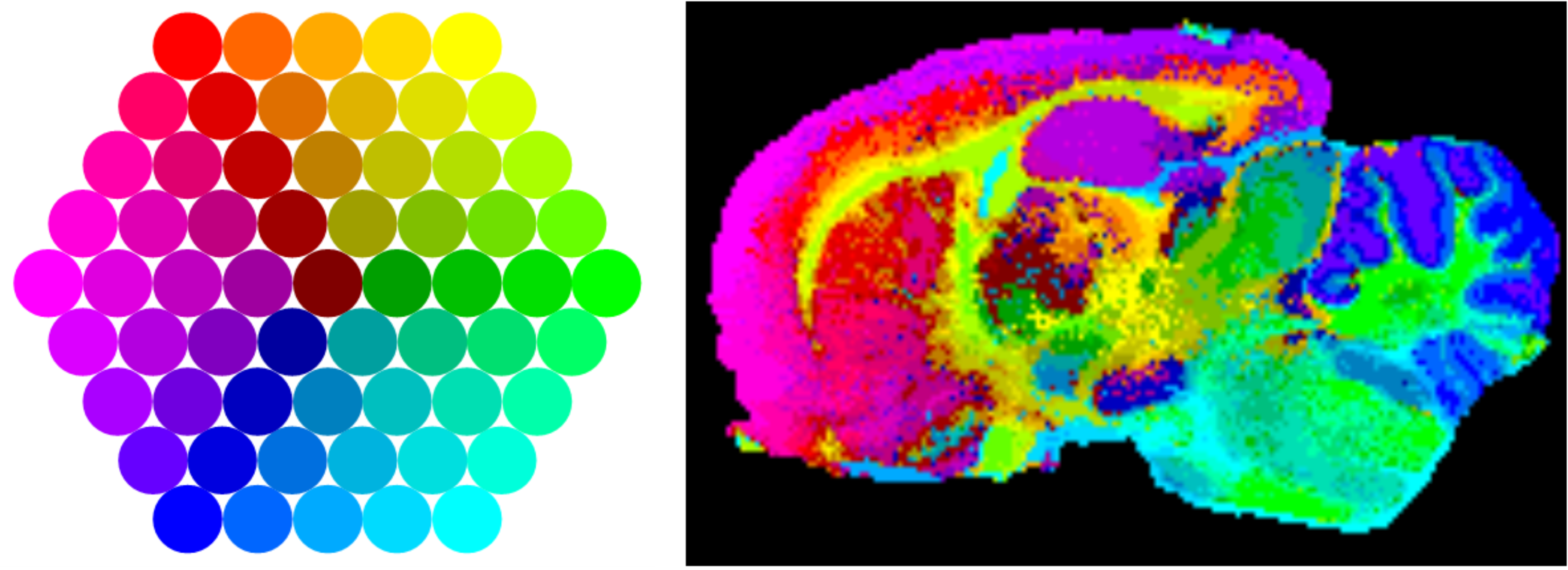
4. irudia: Arratoi baten burmuineko ebakidura sagitalaren aztarna lipidikoaren analisi estatistikoa, 100 mm-ko pixel-tamainarekin.

Laburbilduz, MALDI-IMS teknikak dimentsio gehigarri bat ematen dio lagin biologikoen analisiari: ehun bat osatzen duten metabolitoen eta proteinen lokalizazioa ehunaren baitan. Eta horrek aplikazio ugari izan ditzake etorkizunean, gaixotasun metabolikoen azterketan.

—————————————————–

Egileari buruz: José A. Fernández ikertzailea da UPV/EHUko Zientzia eta Teknologia Fakultateko Kimika Fisikoa Sailean.

—————————————————–

Masa-espektrometriari buruzko artikulu-sorta

1. Masa-espektrometria (I). Neoi isotopoetatik elefante hegalariengana
2. A new hero is born: Masa-espektrometria justiziaren zerbitzura
3. Nor dago icebergaren alden ezkutuan?
4. Konposatu galduaren bila
5. Metabolomika: osotasuna, zatien baturaren aurrean
6. Esploratu gabe dauden lurraldeak kartografiatzen: masa-espektrometria bidezko irudia

The post Esploratu gabe dauden lurraldeak kartografiatzen: masa-espektrometria bidezko irudia appeared first on Zientzia Kaiera.

Tengo un acuario en casa. Contiene doscientos peces, de los cuales el 99% son rojos. Quiero conseguir que sólo el 98% de los peces de mi pecera sean colorados, eliminando sólo algunos de este color, pero sin tener que comprar más de otras tonalidades. ¿Cuántos peces rojos debo sacar del acuario?

Imagen: Pixabay

Seguro que son pocos los que debo extraer de mi pecera. Veamos: los peces rojos representan el 99%. Por lo tanto, el 1% no son colorados, es decir, solo hay dos peces que no son rojos en el acuario. Necesito extraer algunos peces rojos para conseguir que estos dos peces lleguen a ser el 2% de los peces del acuario. Así, si dos peces no colorados deben ser el 2% del total, una sencilla regla de tres dice que deben quedar en el acuario ¡solo 98 peces rojos! Es decir, deben sacarse 100 peces rojos para que el porcentaje de peces colorados pase del 99%al 98%. Sorprendente, ¿no?

¿Y qué hago ahora con los cien peces que me sobran? Decido cambiarlos a un colega por cien kilos de patatas. Es justo, ¿no? Un pez por un kilo de patatas… Y se me plantea un nuevo problema.

Tengo 100 kilos de patatas. El 99% de su peso corresponde al agua que contienen. Quiero deshidratarlas para conseguir que contengan solo un 98% de agua. Tras hacerlo, ¿cuánto pesan las patatas? ¡Si sólo pesan 50 kilos! ¿Por qué?

Imagen: Wikimedia Commons.

Veamos: si de esos 100 kilos, 99 kilos son de agua, 1 kilo corresponde a sólido seco. Vaya, parece que estoy teniendo un “déjà vu”… esto me recuerda mucho al caso de los peces rojos. Pero centrémonos, volvamos a los tubérculos. Si tras deshidratar las patatas la parte sólida pasa a ser del 2% del total –que sigue pesando 1 kilo, porque no se ve afectada por la deshidratación– de nuevo puedo hacer una sencilla regla de tres que me dice que debe de haber solo 49 kilos de agua. Así que, efectivamente, las patatas pasan a pesar 50 kilos. Bueno, así me costará menos transportarlas.

Creo que compraré algo de queso para elaborar alguna receta y acompañar a parte de esas patatas. Me gusta el Emmental porque tiene agujeros, y –como todo el mundo sabe– a las personas que nos dedicamos a la topología nos encanta contar agujeros. Para eso se inventó la teoría de homología, ¿no? Para eso, para contar agujeros de diferentes dimensiones y así distinguir espacios no homeomorfos.

Y me ha dado por pensar en los agujeros del queso, que parece que proceden de la fermentación producida por partículas microscópicas de heno presentes en la leche. A ver:

Cuanto más queso Emmental compre, más agujeros habrá. Pero, cuantos más agujeros haya, tendré menos queso. Es decir, cuanto más queso compre… ¡tendré menos queso!

Imagen: Wikimedia Commons.

¡No me lo puedo creer! Y todo esto por culpa de cien peces rojos…

Referencias

• Marta Macho Stadler, La paradoja de los peces colorados, ZTFNews, 4 octubre 2013

• Weisstein, Eric W., Potato Paradox, MathWorld

• Paradoxe du fromage à trous, Wikipédia (consultado el 10 de marzo de 2019)

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.

El artículo Paradojas: contando peces, pesando patatas y… detectando agujeros se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Patatas ‘perfectas’ con el método ‘Edge Hotel School’
2. La topología modifica la trayectoria de los peces
3. Los peces en el río