Agrégateur de flux

Juanma Gallego Kondrito karbonatodun izeneko meteoritoen azterketan abiatuta, asteroideek ura Lurrera ekarri zuteneko teoria berretsi dute ikertzaileek. Bidean dauden espazio misioek ere uraren jatorria argitu nahi dute.

Ezinezkoa da eguzki-sistemaren jatorrietara bueltatzea, gure gertueneko planetak eta geure etxea bera den Lurra nola eratu ziren jakiteko. Baina, badugu aukera ikusteko nola eratzen ari diren eguzki-sistematik kanpoko beste hainbat sistema. Halere, nolabait, “nahi eta ezin” egoera da hori. Gero eta bereizmen hobearekin, astrofisikariak gai dira ikusteko nola sortzen diren mundu horiek, eta espektrografiak benetako “mirariak” ahalbidetzen ditu. Baina, zoritxarrez, mundu berrien fabrika horietan gertatzen diren prozesu fisiko-kimikoak atzematea ez da erraza.

1. irudia: Zientzialariek uste dute asteroideek ura ekarri zutela Lurrera, Bonbardaketa Berantiar Handia gisa ezagutzen den une batean. Irudian, NASAK egindako berreraikipen artistikoa. (Irudia: NASA)

Eguzki-sistemaren adreilu diren asteroide eta kometetan egon daiteke gakoa. Horregatik, hein handi batean, objektu horiek ikertzeko hainbat misio burutu dira; beste batzuk oraintxe bertan horretan ari dira, eta beste hainbat misio ere izango dira etorkizunean: Stardust, Rosetta, OSIRIS-Rex, Hayabusa, DART, Hera.. Japoniarrek laginak hartzeko prestatu duten Hayabusa-2k bidalitako azken bideoa ikusita, edo ESAk poesia bisuala eta zientzia uztartuz Rosettari buruz prestatutako Ambition bideo laburra ikustean hunkitzen ez den irakurleak hobe du hemendik aurrera beste irakurketaren bati heltzea.

Idealismoa alde batera utzita, ezagutza hutsa ez ezik, interes komertziala ere piztu dute arrokek, eta Planetary Resources bezalako enpresak horretan ari dira. The Expanse telesailak marraztutako mundua oso urruna eman badezake ere, duela urte gutxira arte ere zaila zirudien irudikatzea enpresa pribatuak espaziora joaten edota Israelgo startup bat Ilargirako bidea egiten.

Ezagutza soilari dagokionez, asteroide eta kometetan aurkitu nahi den erantzun nagusia da nola iritsi zen ura Lurrera. Ura sortzea ez da zaila: kopuruei dagokienez, hidrogenoa eta oxigenoa dira, hurrenenez hurren, unibertsoko lehenengo eta hirugarren postuetan dauden elementuak. Baina eguzki-sistemaren osaketa azaltzen saiatzen diren eredu gehienek oso zail ikusten dute hasierako faseetan barne planetetan ura egotea: eguzkiaren beroa dela, ur gehiena eguzki-sistemaren kanpoaldean geratu zen, izotz-lerro gisa ezagutzen den muga batetik harago, hain zuzen. Bestetik, uste da Ilargiaren sorrera planeta erraldoi baten talkari zor zaiola; talka horrek Lurrean egon zitekeen jatorrizko ur guztia eraman behar izan zuen, halabeharrez.

Asteroide eta kometak dira, beraz, Lurreko uraren jatorria hoberen azaltzen dutenak. Lehen hautagai logikoak kometak izan ziren, objektu horiek dutelako lurrunkorra den material gehien. Baina, oraingoan ere, badirudi isotopoek izango dutela azken hitza. Deuterioaren eta hidrogenoaren arteko proportzioaz ari gara. 1980ko hamarkadan ura meteoritoetatik etorri zeneko hipotesia kolokan jarri zen, orduan ikusi zelako Oort hodeiko kometetan dagoen D/H proportzioa (Deuterio/Hidrogeno) ez datorrela bat Lurreko ozeanoetan dauden proportzioekin. Rosetta misioak egiaztatu ahal izan zuen 67P/Txuriumov-Gerasimenko kometan zegoen proportzioa ere ezberdina zela (zehazki, Lurrean dagoena baino hiru handiz handiagoa da).

Horregatik, asteroideetan jarri da arreta. Bereziki gerrikoaren kanpoaldean kokatuta dauden asteroideek dute ur gehien. Pixkanaka, horien alde egiten duten probak metatzen hasiak dira. Orain aurkeztu dituzte Science Space Science Reviews aldizkarian aukera hori babesten duten proba gehiago (hemen, irekian).

2. irudia: Meteoritoak ikertuz asteroideen osaketari buruzko datuak lortzen dituzte adituek. Irudian, zientzialariak meteoritoak bilatzen, Antartidan. (Argazkia: Katherine Joy / ANSMET)

Ikertzaileek kondrito karbonatodun izeneko meteoritoetan jarri dute interesa. Karbono-konposatu asko duten meteorito horiek asteroideetan dute abiapuntu, eta adituek berretsi dute arroka puska horiek material hidratatuak eta molekula organikoak jaso zituztela eguzki-sistema sortu zenean. Hau ez da kontu berria, baina orain proba gehiago jarri dituzte mahai gainean. Ura ez ezik, kondrito karbonatodunetan biziaren sorrerarako erabilgarri izan zitezkeen molekulak iritsi zirela uste dute. Aukera hau 2016an Scientific Reports aldizkarian proposatu zuten.

Zientzialariek marraztu duten prozesuaren arabera, kondrito horiek arroken eta uraren arteko prozesuetan abiatu ziren. Garai batean, asteroideetan zegoen izotza urtu egin zen, seguruenera, 26Al isotopo erradioaktiboaren desintegrazioan sortutako beroari esker ( 26Mg-ra desintegratzean, isotopo horrek energia kopuru txikia baina etengabekoa isuri dezake, milioika urtez). Ur hori berotzean eta arrakalen artean sartzean sortu ziren kondritoen ezaugarri diren kondruloak. Ondoren, kanpoko planetetako orbitetan izandako aldaketak direla eta, kaosa sortu zen eguzki-sisteman, eta asteroide horietako asko barne planetetara bideratuak izan ziren, beraiekin batera, ura eramanez. Fase hori Bonbardaketa Berantiar Handia gisa ezagutzen dugu, eta udako gau lasai batean zeruari begira gaudela Ilargian ikusten diren kraterrak horren testigu isilak dira.

Bestetik, Lurraren osaketa kimiko berak berretsiko luke ideia hori. Espero zitekeena baino platinoaren taldeko elementu gehiago daude mantuan zein lurrazalean (teorian, siderofiloak diren elementu horiek nukleoa osatzen duten burdinarekin eta nikelarekin lurperatuak izan behar ziren Lurraren osaketaren hasierako faseetan, baina elementu horiek ere asteroideen bonbardaketa masibo horrekin iritsi zirela uste dute zientzialariek).

Dena dela, ia beti bezala, gauzak ez daude guztiz finkatuta, eta ikerketa berriak martxan dira. Gainera, gogoratu beharra dago asteroide baten eta kometa baten arteko aldea ez dela guztiz argia. Adibidez, kometa gehienak Kuiper gerrikotik edota Oort hodeitik datozen arren, orain badakigu asteroide gerrikoan ere hainbat “kometa” badirela. 133/P Elst-Pizarro da horietako bat, eta Txinak hara bidali nahi du misio bat, laginak hartu eta Lurrera ekartzeko asmoz. Unibertsoari bost axola zaio arroka horiek kometa ala asteroide ote diren, baina gizakiak, bere txikitasunean —eta bere handitasunean—, etxetzat duen Lurra nola sortu zen jakin nahi du, eta baita ere Lurrean bizia ahalbidetu duen uraren jatorria zein den. Azken finean, batez bestean, gizakiaren konposaketaren %60-70 ura besterik ez da. Nongoa zaren galdetzen dizuten hurrengoan, badakizu, lasai asko esan dezakezu belterra, zinturonianoa edo gerrikoarra zarela. Asteroide gerrikokoa, hain zuzen; Zientziak babestuko zaitu. Bertan sortu baitira zure arimaren hiru laurdenak.

Erreferentzia bibliografikoa:

Trigo-Rodriguez, J.M., Rimola, A., Tanbakouei, S. et al. (2019). Accretion of Water in Carbonaceous Chondrites: Current Evidence and Implications for the Delivery of Water to Early Earth. Space Science Reviews, 215:18. DOI: https://doi.org/10.1007/s11214-019-0583-0

———————————————————————————-

Egileaz: Juanma Gallego (@juanmagallego) zientzia kazetaria da.

———————————————————————————-

The post Izar-hautsa ez ezik, asteroide-ura ere bagara appeared first on Zientzia Kaiera.

Imagen: V Photography and Art (flickr)

¿Qué ocurre cuando la luz que viaja por un medio (por ejemplo, el aire) alcanza el límite de otro medio (por ejemplo, el vidrio)? Las respuestas a esta pregunta dependen de si se utiliza el modelo de partícula o el de onda para la luz. ¿Qué implica cada uno y cuál es mejor? ¿Cómo explican el siguiente hecho experimental (Figura 1):

Figura 1. Un haz de luz llega con un ángulo de 60º al límite entre dos medios; vemos que una parte es reflejada (también con un ángulo de 60º) y otra pasa al medio 2 con un cambio de dirección. Fuente: Wikimedia Commons

El modelo de onda ya lo hemos tratado aquí para la reflexión y aquí para la refracción. Recordemos las conclusiones principales aplicadas a la luz:

1. Un rayo de luz no es otra cosa que una línea perpendicular a las líneas de cresta de una onda. Un rayo representa la dirección en la que viaja un tren de ondas.

2. En la reflexión, el ángulo de incidencia(Θi) es igual al ángulo de reflexión (Θr), esto es, Θi = Θr

3. La refracción implica un cambio de la longitud de onda y velocidad de la onda a medida que pasa a otro medio. Cuando la velocidad disminuye, la longitud de onda disminuye y el rayo gira en una dirección hacia una línea perpendicular al límite entre los medios. Este giro hacia la perpendicular se observa, por ejemplo, cuando un rayo de luz pasa del aire al vidrio.

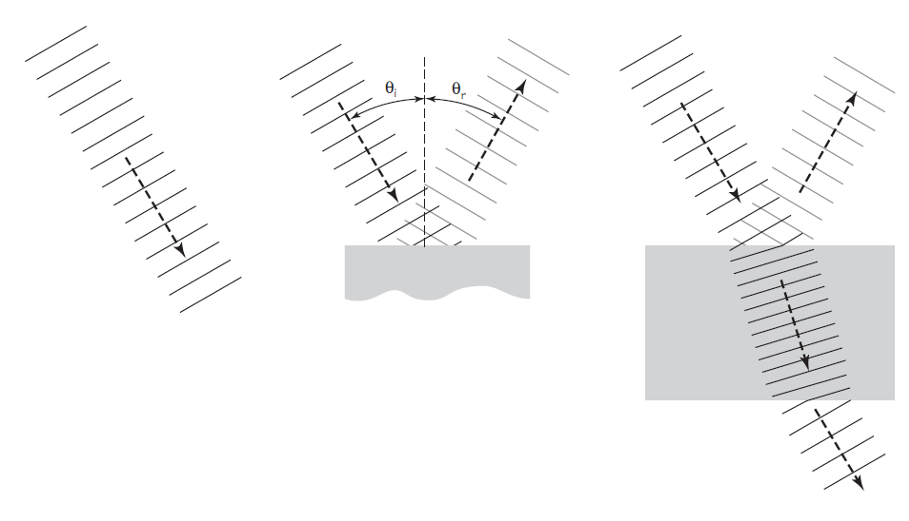Figura 2. El modelo de ondas en acción. Fuente: Cassidy Physics Library

¿Cómo explicar las mismas observaciones mediante el modelo de partículas? Primero tenemos que considerar la naturaleza de la superficie del vidrio. Aunque aparentemente homogénea, estamos en realidad ante una superficie rugosa: un microscopio lo suficientemente potente mostraría que tiene multitud de colinas y valles. Si las partículas de luz fueran similares a pequeñas bolitas de materia, al golpear una superficie tan rugosa lo que cabría esperar es que se dispersasen en todas direcciones. Por tanto, no serían reflejadas ni refractadas. Por lo tanto, hay que refinar el modelo. Newton argumentó que en realidad debe haber “algún rasgo del cuerpo que esté disperso uniformemente sobre su superficie y por el cual este actúa sobre el rayo sin contacto inmediato (some feature of the body which is evenly diffused over its surface and by which it acts upon the ray without immediate contact).

Vamos a seguir la idea de Newton, a ver a donde nos lleva. De entrada, en el caso de la reflexión, la fuerza actuante tendría que ser una que repela las partículas de luz. Pero claro, por la misma regla de tres, es necesaria una una fuerza que atraiga a las partículas de luz en lugar de repelerlas para explicar la refracción. Esto parece que se complica para el modelo de partículas. O no. Veamos

Cuando una partícula de luz se acerca a un límite con otro medio, primero tendría que superar la fuerza repelente. Si lo consiguiera, entonces encontraría una fuerza atractiva en el medio que la atraería hacia el medio. Dado que la fuerza atractiva sería un vector perpendicular a la superficie del medio, tomando como referencia la dirección del movimiento de la partícula ese vector tendría un componente en la dirección del movimiento original de la partícula, lo que implica que la velocidad de la partícula tendría que aumentar. Otra consecuencia es que, si el rayo de partículas se moviera con un ángulo oblicuo al límite, cambiaría de dirección a medida que entrase en el medio, girando hacia la línea perpendicular al límite.

De acuerdo con el modelo de partículas*, por lo tanto, podríamos afirmar lo siguiente:

1. Un rayo representa la dirección en la que se mueven las partículas.

2. En la reflexión, los ángulos de incidencia y reflexión son iguales. Esta predicción se puede derivar aplicando la ley de conservación del momento a partículas repelidas por una fuerza.

3. La refracción implica un cambio de velocidad de las partículas a medida que entran en otro medio. En concreto, cuando actúa una fuerza atractiva, la velocidad aumenta y el rayo cambia de dirección al entrar en el medio.

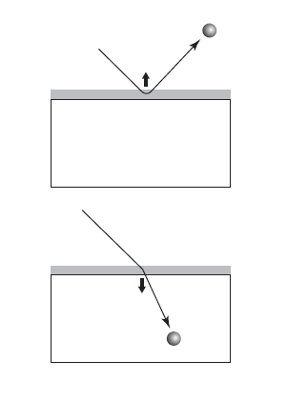Figura 3. El modelo de partículas en acción. Fuente: Cassidy Physics Library

Comparemos estas características del modelo de partículas con las características correspondientes del modelo de onda. La única diferencia está en la velocidad predicha para un rayo refractado. Observamos que un rayo se curva hacia la línea perpendicular cuando la luz pasa del aire al vidrio. El modelo de partículas predice que la luz tiene una velocidad mayor en el segundo medio. El modelo de ondas predice que la luz tiene una velocidad menor.

Podríamos pensar que no hay nada más fácil para averiguar qué modelo es el más correcto: diseñar un experimento para determinar qué predicción es correcta. Todo lo que uno tiene que hacer es medir la velocidad de la luz después de que haya entrado en el vidrio o en el agua y compararla con la velocidad de la luz en el aire. Pero no. A a finales del siglo XVII y principios del siglo XVIII, cuando Huygens argumentaba a favor del modelo de onda y Newton apoyaba el modelo de partículas, ningún experimento de este tipo era posible. La única forma disponible de medir la velocidad de la luz era la astronómica.

No sería hasta mediados del siglo XIX que Armand H.L. Fizeau y Jean B.L. Foucault conseguirían medir la velocidad de la luz en el agua. Los resultados concuerdan con las predicciones del modelo de onda: la velocidad de la luz es menor en el agua que en el aire.

Los experimentos de Foucault-Fizeau de 1850 se consideraron como el último clavo en el ataúd del modelo newtoniano de partículas para la luz, ya que, cuando se realizaron estos experimentos, buena parte de la comunidad científica ya había aceptado el modelo de onda por otras razones. Algunas de estas se derivaron del trabajo del científico inglés Thomas Young, y serán las que veamos a continuación.

Nota:

* Implícitamente en el argumento está la asunción sobre el límite del tamaño de las “partículas” de luz de Newton. Las partículas deben ser al menos tan pequeñas como las irregularidades en la superficie de un vidrio. Si fuesen mayores tendríamos el mismo efecto que una pelota de tenis rebotando en el rugoso suelo de hormigón, solo reflexión.

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

El artículo Reflexión y refracción de la luz se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Refracción de ondas
2. Aplicaciones de la reflexión de ondas: el sonar
3. Reflexión de ondas: rayos

Josu Lopez-Gazpio Haragi gordinaren kolorearen arrazoia azaldu ondoren eta muskulua haragi nola bilakatzen den ikasi ondoren, kozinatutako haragiaren sekretuak azaleratuko ditugu. Azken pausoaren kimikan sartuko gara bete-betean. Zein desberdina den harategian erositako txuleta eta platerean patata frijituekin batera jaten duguna. Aitzitik, biak produktu bera dira. Produktu bera, baina, jakia gozagarria egiteko ezinbestekoak izan diren erreakzio kimikoak eta aldaketa fisikoak gertatu ondoren lortzen dena da gustukoen duguna. Zergatik ote?

1. irudia: Kozinatutako haragiak kolore desberdinak izango ditu tenperaturaren eta kozinatze denboraren arabera. Koloreaz gainera, zapore eta usaina ere desberdina izango da. (Argazkia: Bru-nO – domeinu publikoko irudia. Iturria: pixabay.com)

Haragia kozinatuta jateko arrazoiak lau dira: seguruagoa da -kozinatzean patogenoak hiltzen dira-, errazago mamurtzen eta digeritzen da -desnaturalizatutako proteinak errazago erasotzen dituzte gure digestio-entzimek-, eta zapore hobea du. Segurtasun kontuak alde batera utzita, zaporea bera aldatzea arrazoi nahikoa da haragia kozinatzeko. Haragi gordinak zaporea du, bai, baina, aroma eskasak ditu. Haragiari egindako kalte fisikoa nahikoa da muskulu-zuntzek osagai aromatikoak askatzeko, baina, aroma eta zaporea benetan garatzeko aldaketa kimikoak gertatu behar izaten dira. Aldaketa kimikoei esker zeluletan dauden molekulak askatze dira eta birkonbinatu egiten dira konposatu berriak emateko.

Haragia ez bada berotzen uraren irakite puntutik gora, bere zaporea proteinen eta gantzen deskonposaketaren ondorioz askatutako molekulena izango da. Tenperatura ez bada 100 ºC-tik gora igotzen, ez dira lortuko haragi txigortuaren kolorea. Horrexegatik mikrouhin labean edo uretan egosiz ezin da haragi txigortuaren kolore arrea lortu. Alabaina, haragia 100 ºC-tik gora berotzen bada -frijitzean edo labean erretzean, adibidez-, gainazalean Maillard-en arretze erreakzioak gertatzen hasten dira eta haragi txigortuaren zapore eta usainak agertzen dira. Maillarden erreakzioen ondorioz nitrogenoa, oxigenoa edo sufrea duten eraztun motako molekulak sortzen dira eta horiek dira, hain zuzen ere, «haragi errearen zaporea» bezala ezagutzen duguna. Horietaz gainera, beste hainbat usain agertzen hasten dira haragian, aipatutako molekulen presentziaren kausaz. Esan behar da, bide batez, konposatu horietako batzuk toxikoak eta minbizi-sortzaileak direla, baina, kantitate oxo txikitan sortzen direla, beraz, gehiegi arduratu gabe jan daiteke barbakoan erretako haragia, neurriz egiten bada.

Kozinatutako haragiaren kolorea eta testura

Haragiaren itxura bi modutara aldatzen da kozinatzen denean. Hasiera batean zeharrargia da, uretan murgilduta dauden proteinek osatzen dituztelako zelulak. Alabaina, haragia berotzen hasten den neurrian, tenperaturaren arabera proteinak desnaturalizatzen hasten dira eta erreakzio kimikoak gertatzen dira. Erreakzio eta aldaketa horien arabera, haragiak guretzat hain gozagarriak diren usain eta zaporeak izango ditu.

2. irudia: Haragi gordinaren kolorea uniformea eta zeharrargia da. (Argazkia: gate74 – domeinu publikoko irudia. Iturria: pixabay.com)

Haragia berotzen hasten denean, 50 ºC-ko tenperaturara iristen denerako opakua bilakatzen hasten da miosina desnaturalizatzen hasten delako. Miosina proteina haritsua da, muskuluen uzkurdura ahalbidetzen duena, aktinarekin batera. Miosina desnaturalizatuak kolore zuriko pikorrak osatzen ditu eta, horren ondorioz, haragiak kolore arrosa hartzen du hasieran, berotzen hasten denean. 60 ºC-ra iristean, mioglobina desnaturalizatzen hasten da, hemikromo izena duen eta kobre kolorea duen forma osatuz. Gogoan izan mioglobina dela, hain zuzen ere, haragiaren kolore gorriaren erantzulea. Mioglobina desnaturalizatzearekin batera, haragiaren kolorea arrosa izatetik arre-grisaxka izatera pasatzen da. Mioglobinaren desnaturalizazio-tenperatura eta zuntzetako proteinena tenperatura bera denez, haragia nola eginda dagoen jakin daiteke kolore aldaketari erreparatuz. Gutxi egindako haragia eta bere zukua zukua gorria da eta ondo erretako haragiaren kasuan, aldiz, haragia arre-grisaxka da eta zukua gardena. Tarteko kasuetan, kolore arrosekoa da bai haragia eta bai zukua. Hala ere, mioglobina haragia kozinatu baino lehen desnaturalizatu bada -argiaren eraginez edo haragia izoztuta egon delako-, posible da haragiak kolore arrea izatea tenperatura baxuagoan. Honek, nolabait, sukaldariari pentsarazi diezaioke haragia ondo eginda dagoela, baina hori horrela ez izatea. Mikrobioak guztiz hil direla ziurtatzeko modu bakarra termometroa erabiltzea da haragia 70 ºC-tik gorako tenperaturan egon dela baieztatzeko.

3. irudia: Haragi kozinatuak kolore desberdinak ditu, geruzaka. Kanpoan Maillard erreakzioaren ondorioz sortutako zarakarra du, eta barruan kozinatze mailaren araberako geruza arreak, arrosak eta gorriak. (Argazkia: Global-Tyrol – domeinu publikoko irudia. Iturria: pixabay.com)

Haragiaren barnean gertatzen diren kolore aldaketez gain, zuzenean zartagiarekin kontaktuan dagoen gainazalak 100 ºC-tik gorako tenperatura hartzen duenez, Maillard erreakzioak gertatzen dira. Horiexek dira hain zuzen ere gainazaleko kolore beltz eta arreak dituzten konposatuak sortzen dituztenak, eta horiek sortzearekin batera haragi errearen zapore eta usain bereizgarriak agertzen dira. Maillarden erreakzioak erreakzio-multzo izugarria da, azukreen eta proteinen amino taldeen artean gertatzen direnak. Maillard erreakzioen ondorioz, azukreak eta aminoazidoak elkartu egiten dira eta hainbat etapa dituen prozesu kimikoan sartzen dira. Hasieran kolore marroi argiak agertzen dira eta gero konposatu ilunagoak. Azken erreakzioa, Strecker-en degradazioa deritzona, haragi errearen usainaren erantzulea da.

Erreakzio horiek guztiek eta aldaketa fisikoek haragiaren kolorea aldatzen dute, baina, baita testura ere. Haragiaren testuraren kasuan, kozinatzen denean murtxikatzea posible egiten da, elastikoagoa eta samurragoa bihurtzen delako. Haragia gehiegi egiten bada, aldiz, elastikotasun hori galdu egiten da eta berriro zurruntasuna nagusitzen da. Prozesu guzti hori zuntzen eta ehun konektiboaren proteinen desnaturalizazioaren araberakoa da. Samurtasuna lortzeko gakoetako bat 70 ºC-tan hasten da. Tenperatura horretan ehun konektiboan dagoen kolagenoa disolbatzen hasten da eta gelatina eratzen da. Hori gertatzen denean zuntzak euren artean errazago banatzen dira eta ehun konektiboa bigundu egiten da. Alabaina, horretan dago haragia ondo kozinatzearen zailtasuna. Alde batetik, zuntzen konpaktatzea murriztu behar da eta hezetasuna ez da galdu behar haragia samurra egoteko. Bestetik, ehun konektibo gogorra gelatina bigunean bihurtu behar da. Kontua da bi helburu horiek kontrajarrita daudela, alegia, gehiago berotzen bada gelatina lortzeko haragiak ur gehiegi gal dezake eta lehortu egingo da. Hortxe dago haragia ondo kozinatzearen gakoa. Oraingoan ere, kimikan erantzuna duen gakoa.

Informazio osagarria:

• Kovács, L., Csupor, D., Lente, G., Gunda, T., (2014). 100 chemical myths, misconceptions, misunderstandings, explanations. Springer, Suiza.
• McGee, Harold, (2015). La cocina y los alimentos: Enciclopedia de la ciencia y la cultura de la comida. DEBATE, Madrid.

—————————————————–
Egileaz: Josu Lopez-Gazpio (@Josu_lg) Kimikan doktorea, irakaslea eta zientzia dibulgatzailea da. Tolosaldeko Atarian Zientziaren Talaia atalean idazten du eta UEUko Kimika sailburua da.
—————————————————–

Kimika sukaldean: haragia, artikulu-sorta

1. Kimika sukaldean: haragia (I). Haragiaren kolorea
2. Kimika sukaldean: haragia (II). Muskulutik haragira
3. Kimika sukaldean: haragia (eta III). Kozinatutako haragia

The post Kimika sukaldean: haragia (eta III). Kozinatutako haragia appeared first on Zientzia Kaiera.

María Begoña Medel Bermejo

El alumnado del Grado en Creación y Diseño de la Facultad de Bellas Artes de la UPV/EHU comienza a adentrarse en el mundo del Diseño durante su tercer curso con una asignatura cuyo nombre es Diseño Gráfico.

Existe una discusión recurrente sobre la existencia o no de alguna diferencia entre el Arte y el Diseño. Desde esta asignatura, que imparto desde hace casi 30 años, suelo insistir en el hecho de que una de las características fundamentales, si no la más destacable, es la presencia de un cliente con una necesidad de comunicación. El cliente es el elemento que nos convierte en los profesionales intermediarios que resuelven un problema de comunicación, aplicando los conocimientos sobre el funcionamiento de la percepción humana en la creación de un conjunto único y original de imágenes y textos significantes que transmitirán el mensaje que se necesite.

Suele suceder que en el aula trabajamos con supuestos en los que el rol de cliente lo asume el docente o los propios alumnos, de manera rotativa. Pero, algunas veces tenemos la suerte de enfrentarnos a problemas reales para los que desarrollar soluciones de comunicación gráfica.

Durante este curso 2018-2019, de acuerdo con la Guía Docente de la asignatura Diseño Gráfico, el último proyecto que el alumnado debía desarrollar era un cartel.

Ya habíamos colaborado en otras ocasiones con otras facultades y entidades públicas en temas similares pero, nunca habíamos trabajado con la Facultad de Ciencia y Tecnología.

Tener como cliente a alguien cuyo día a día es tan diferente del nuestro era el mayor atractivo que encontré a esta posibilidad. La innovación, la creación nunca surge si trabajamos dentro de nuestra área de confort. Salir de lo común, de lo reiterativo, supone colocarse en ese lugar que resulta incómodo porque no lo conocemos, y mirar todo aquello que vamos descubriendo con ojos limpios.

Por todo lo dicho hasta ahora me puse en contacto con algunos profesores del área de Matemáticas para preguntarles si tenían algún tema en el que pudiéramos colaborar. La respuesta fue inmediata y muy positiva, necesitaban publicitar la jornada BCAM-Naukas en el día de Pi y era posible colaborar. Participar en un evento organizado por la Cátedra de Cultura Científica de la UPV/EHU, Naukas y BCAM (Basque Center for Applied Mathematics) ha sido un reto para el alumnado y la oportunidad de hacer algo que no quedara entre las paredes de la clase como un proyecto académico más, si no que consiguiera trascender y llegar al público colocando a ambas facultades y a la UPV/EHU en el punto de mira de nuestro cliente específico, el posible futuro alumnado.

Ya teníamos el tema para el proyecto de cartel de este curso.

En clase, cuando planteé el tema, hubo todo tipo de reacciones: desde el entusiasmo al temor ante lo desconocido. Pero, en general, fue bien acogido dado que la posibilidad de hacer algo real suele ser muy valorada por el alumnado.

Participaron 56 alumnas y alumnos de dos grupos, castellano y euskera, de tercer curso del grado en Creación y Diseño. Cada uno de ellos debía llevar a cabo una labor de recopilación de información sobre el tema que les permitiera llegar a concebir al menos tres conceptos totalmente diferentes que sirvieran para comunicar la celebración del día de Pi.

Cuando desarrollamos conceptos de comunicación gráfica trabajamos la creatividad desde diversos lugares para poder encontrar esa imagen que consiga atraer la atención del espectador estableciendo un vínculo emocional al conseguir descifrar el mensaje. Se trata de hacer sonreír a nuestro cerebro.

Creo que el resultado obtenido este curso permite constatar que el acercamiento al mundo de las matemáticas permite una multiplicidad de caminos. Como colofón de esta experiencia se han seleccionado dos carteles: el de Paula Castro como cartel de la jornada del 13 de marzo de 2019 y el de Jone Aldalur para comunicar la realización de talleres para escolares. Se trata de las dos primeras imágenes que aparecen a continuación junto con otros 10 carteles que fueron pre-seleccionados:

Obra de Paula Castro. Éste ha sido el cartel seleccionado como imagen general del día de Pi. La relación y conexión entre la ciencia y la profundidad del cosmos se ha realizado mediante la utilización de la imagen icónica de la luna, que representa la circunferencia, y la estela de condensación que genera el cohete en referencia al diámetro.Obra de Jone Aldalur. Se utilizó la imagen para informar sobre los talleres del día de Pi. Las pelotas con números Pi dentro del frasco tienen colores llamativos para atrapar nuestra mirada y a su vez nos remiten a los juegos de azar en los que esos números pueden decidir nuestra suerte. Obra de José Manuel García. Un contraluz crea un ambiente narrativo en el que el número Pi aparece sobre una colina desde la que surge un camino de estrellas hacia el cielo.Obra de David von Heeren. Gestos positivos realizados con las manos nos sirven para crear una pequeña adivinanza ayudados por los personajes del fondo, que nos proporcionan la pista necesaria para encontrar la clave.Obra de Jon Flores. A veces se ve más lo que no está que lo que está. Se trabaja con la elipsis repetida del elemento fundamental del cartel. Si no lo leemos en voz alta puede que no seamos capaces de descubrir el juego visual.Obra de Ainhoa Simpler. Como si fuera un juego solitario aparecen las cartas en grupos que remiten a las primeras cifras del número Pi y en cada una de ellas descubrimos la imagen de una matemática famosa.Obra de Maialen Sayans. El todo y sus partes. Los primeros números de la sucesión infinita de Pi colocados en visión frontal se convierten en un juego de transparencias que crean otra realidad.Obra de Eva Muñoz. Hasta ahora muchos matemáticos han perdido el sueño investigando el número Pi y tomando café para mantenerse despiertos. La huella del café sobre la mesa es un guiño a la circunferencia y su diámetro.Obra de Mikel Larena. Juego de transparencias con la sucesión del número Pi.Obra de Anne Fernandez. Un papel arrugado con forma esférica repleto de fórmulas matemáticas aparece en primer plano con un fondo realizado con una regla de círculos.Obra de 11 Laiene Pagazaurtundua. Metáfora visual “el árbol de la ciencia”Obra de Lukas Zelaia. Sustitución de un elemento arquitectónico por un Pi gigante que genera en el espectador nuevos puntos de vista y relaciones emocionales con la imagen mediante esta conexión inusual.

Todas ellas son imágenes muy diferentes que aportan acercamientos originales al concepto de PI desde el mundo del Diseño Gráfico.

Esperamos seguir colaborando en próximas ediciones siempre mejorando la presente y que sea de nuevo una experiencia enriquecedora para ambas facultades.

Sobre la autora: María Begoña Medel Bermejo es Doctora en Bellas Artes y profesora del Grado en Creación y Diseño BBAA/AAEE de la UPV /EHU

El artículo Un cartel para el día de pi se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Una fórmula para dominarlos a todos: La conservación de la energía y la ley de la palanca
2. Marcas de agua digitales, qué son y para qué sirven
3. El consumo de alcohol para el corazón y las dificultades de divulgar ciencia

Además de las secreciones pancreáticas, el intestino delgado también recibe secreciones procedentes del sistema biliar, que está formado por el hígado y la vesícula biliar. Nos referimos, en concreto, a la bilis y, en particular, a las sales biliares. Es este el principal asunto que trataremos en esta anotación.

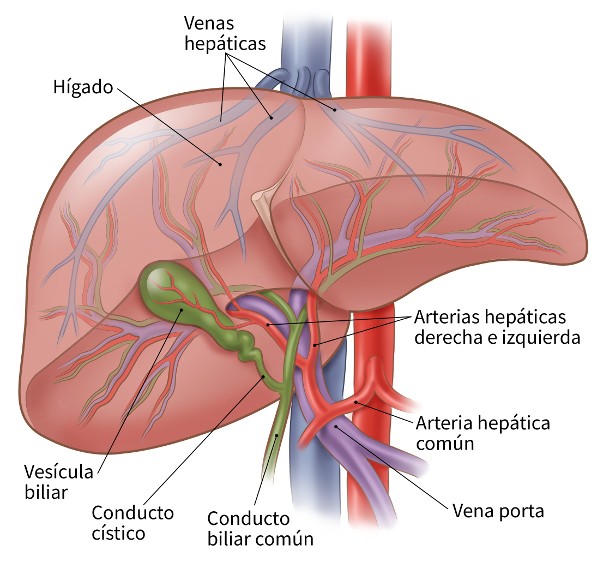Higado y vesícula biliar humanos. Imagen: cancer.org

Pero eso será algo más adelante, porque al hígado corresponden funciones adicionales de gran relevancia que queremos consignar aquí para dejar constancia de ellas. Para empezar, es el órgano que gobierna el metabolismo del conjunto del organismo; podría decirse que es el órgano metabólico maestro, su director. Se ocupa del procesamiento metabólico de proteínas, carbohidratos y lípidos, tras su absorción en el intestino, incluyendo también la gluconeogénesis (síntesis metabólica de glucosa a partir de precursores no glucídicos). Y almacena glucógeno y grasas, a la vez que otras sustancias de menor relevancia cuantitativa, como hierro, cobre y varias vitaminas.

El hígado también se ocupa de degradar productos residuales y hormonas, además de eliminar agentes tóxicos y sustancias, procedentes del exterior, sin utilidad biológica o potencialmente peligrosas (fármacos, por ejemplo). También sintetiza proteínas y lipoproteínas plasmáticas, entre las que se encuentran las que participan en la coagulación de la sangre y las que transportan fosfolípidos, colesterol y hormonas esteroideas y tiroideas.

A las tareas anteriores, hay que añadir que activa la vitamina D (tarea compartida con el riñón); elimina, mediante el concurso de sus macrófagos (células de Kupffer), bacterias y glóbulos rojos que ya han finalizado su vida útil; secreta las hormonas trombopoietina (estimula la producción de plaquetas), hepcidina (regula el metabolismo del hierro en mamíferos), IGF 1 o factor de crecimiento insulínico 1 (estimula el crecimiento); excreta el colesterol y la biliverdina y bilirrubina, que son productos derivados de la degradación de la hemoglobina; y en algunas especies de mamíferos (no en primates y conejillos de India) y de aves sintetiza ácido ascórbico (vitamina C).

Es de destacar que con la excepción de las células de Kupffer, todas las funciones aquí consignadas son realizadas por un mismo tipo celular, el hepatocito. Por lo tanto, no hay diferenciación de funciones con arreglo a tipos celulares (puesto que solo hay los dos citados), sino en virtud de los orgánulos en que se desarrolla cada una de ellas. En ellos radica la función y esta se diferencia de unos orgánulos a otros.

El hígado es un órgano muy irrigado, y el flujo sanguíneo en su interior está organizado de tal modo que cada hepatocito está en contacto con sangre venosa proveniente del tubo digestivo y sangre arterial procedente de la aorta. Los capilares procedentes del intestino se van agrupando hasta confluir en la vena porta hepática que penetra en el hígado donde se vuelve a ramificar en múltiples capilares, formando una red de (los denominados) sinusoides hepáticos. Esos sinusoides son los que permiten que la sangre procedente directamente del estómago e intestino delgado difunda a todas las células del hígado para que provean a estos de las sustancias absorbidas. La sangre sale del órgano con los productos elaborados o expulsados para su eliminación (como la urea, por ejemplo) y lo hace a través de la vena hepática, en la que confluyen los capilares que lo drenan. Además de la sangre procedente del digestivo, al hígado también le llega sangre arterial con oxígeno y otras sustancias procedentes del conjunto del organismo para su procesamiento en los hepatocitos.

El hígado se organiza en lóbulos, disposiciones hexagonales de tejido en torno a una vena central. A lo largo de los vértices exteriores de los lóbulos discurren una rama de la vena porta hepática, otra de la arteria hepática y un ducto biliar. De la vena y arteria citadas salen amplios sinusoides que se dirigen hacia la vena central. Las células de Kupffer tapizan los sinusoides, atrapan a cuantas bacterias y eritrocitos fuera de servicio se encuentran, y los eliminan. Los hepatocitos se disponen en placas de dos células cada una, de manera que todas se encuentran en contacto con los vasos sanguíneos, como hemos dicho antes. Las venas centrales de cada lóbulo convergen en la vena hepática que es la que sale del hígado y se une a la vena cava inferior.

El canalículo de la bilis discurre entre las dos células de cada placa, recibiendo secreción biliar de todas ellas. Los canalículos se dirigen hacia el exterior del lóbulo y transportan así la bilis hasta los ductos que se encuentran en los vértices de los hexágonos (lóbulos hepáticos); los ductos de cada lóbulo acaban agrupándose en el ducto hepático común, que es el que lleva la bilis al duodeno.

El hígado produce bilis de forma permanente, pero el acceso de la bilis al duodeno se encuentra controlado por el esfínter de Oddi, que solo permite su paso cuando hay quimo en el duodeno y puede, por lo tanto, ser utilizado. Cuando el esfínter se encuentra cerrado las sales biliares se acumulan en la vesícula biliar, que hace las veces de depósito. Con cada comida la bilis entra en el duodeno debido al vaciado de la vesícula y al aumento en la producción a cargo del hígado. Los seres humanos producimos entre 250 ml y 1 l de bilis cada día. El mensajero que desencadena la contracción de la vesícula y la relajación del esfínter de Oddi es la hormona CCK (la colecistoquinina que vimos en El páncreas) y que se libera por efecto de la presencia de grasa en el duodeno.

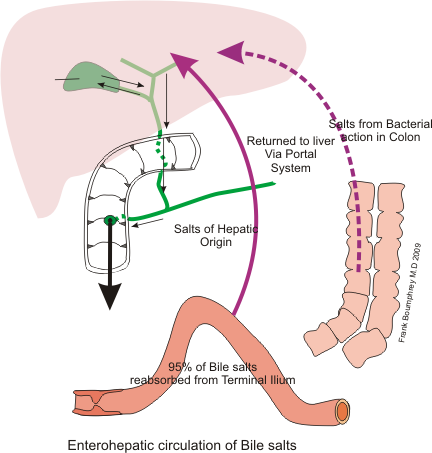Imagen: Wikimedia Commons

La bilis contiene colesterol, lecitina, sales biliares, y bilirrubina y biliverdina, y estas sustancias se encuentran en una solución ligeramente básica, similar a la producida por las células de los ductos del páncreas. Las sales biliares son derivados del colesterol y participan en la digestión y absorción de las grasas debido a su acción detergente y a la formación de micelas. Tras su intervención la digestión de lípidos, son reabsorbidas mediante transporte activo en el íleon, la zona terminal del intestino delgado. De allí, a través del sistema porta, vuelven al hígado. Se calcula que en promedio, en cada comida unas mismas sales circulan dos veces por el duodeno e intestino delgado, y que cada día se pierden con las heces un 5% de las sales biliares. Su pérdida es repuesta por los hepatocitos de manera que el total se mantiene constante.

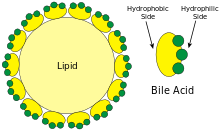Emulsificación de los lípidos por las sales biliares. Imagen: Wikimedia Commons

Las sales biliares intervienen en la digestión de las grasas favoreciendo su emulsificación. Convierten gotas grandes de lípidos en gotas de muy pequeño tamaño suspendidas en el quimo acuoso. De esa forma aumenta muchísimo la relación superficie/volumen y exponiendo una mayor superficie micelar a la acción de la lipasa pancreática, de manera que esta puede atacar las moléculas de triglicéridos. Sin la formación de emulsiones, la mayor parte de esos triglicéridos quedarían en el interior de las gotas grandes lejos del alcance enzimático.

Las sales biliares actúan como los jabones. Ambos son anfipáticos: contienen una porción hidrofóbica (un esteroide derivado del colesterol) y otra hidrofílica con carga negativa (una taurina o glicina) . Las sales se adsorben a la superficie de una gota de grasa, con una orientación acorde a su naturaleza; esto es, la porción liposoluble interactúa con la superficie de la gota lipídica, mientras que la porción cargada queda orientada hacia el exterior y disuelta en agua. Los movimientos intestinales ayudan a fragmentar esas gotas lipídicas y hacer que sean cada vez más pequeñas. En ausencia de sales biliares (detergente), las pequeñas gotas tenderían a caolescer, volviéndose a formar grandes gotas. Pero eso no ocurre porque las cargas negativas solubles en agua lo impiden; forman una especie de capa de cargas negativas que se repelen unas a otras, de manera que no llegan a entrar en contacto. Las gotas lipídicas pequeñas tienen un diámetro que varía entre 200 y 5000 nm.

Para la digestión de las grasas es esencial el concurso de la lipasa procedente del páncreas. La acción de esta enzima es efectiva porque el páncreas secreta la coenzima colipasa, también un péptido alifático, que ocupa el lugar de algunas sales biliares en la superficie de las gotas lipídicas y desde esa posición se une a la lipasa de manera que esta pueda hacer su trabajo. La enzima queda así enganchada a la superficie de las gotas, rodeada de sales biliares, pero de tal forma que puede actuar directamente sobre las moléculas lipídicas.

La absorción de lípidos en el intestino se produce gracias a la formación de micelas. Las micelas son estructuras de entre 3 y 10 nm de diámetro en las que intervienen, además de las sales biliares, el fosfolípido lecitina y el colesterol. La lecitina, como las sales biliares, es anfipática, de manera que se asocia con las sales formando agrupaciones cuya porción hidrofóbica se dispone en el interior, junto al colesterol, y la porción hidrofílica en el exterior. De esa forma, moléculas hidrofóbicas que resultan de la digestión de los lípidos (monoglicéridos, ácidos grasos libres y vitaminas liposolubles) son transportados en emulsión acuosa, gracias a la cubierta hidrofílica, hasta los enclaves del epitelio intestinal donde son absorbidos.

Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU

El artículo El hígado y la vesícula biliar se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Avances contra la enfermedad de hígado graso no alcohólica
2. Una ecuación para determinar la grasa en el hígado a partir de una resonancia
3. Proteínas plasmáticas

Teknologien aurrerapenek, antzinako gizakien bizimoduen berri izateko metodoak ekarri dizkigu. Zehazki izaki bizidunen hezurretan eta hortzetan neurtutako isotopo egonkor desberdinak ezagutzeko aukera.

Isotopo hauen bidez, antzinako gizakien elikadura eta mugikortasun ereduak eraikitzea ahalbidetzen du. Izan ere “jaten duguna gara”.

Erdi Aroko Ipar Iberiar Penintsulan kokatzen diren aztarnategietan egindako elikadura eta mugikortasun ikerketen berri izateko, Iranzu Laura Guede Geologian doktorearekin eta UPV/EHUko ikertzailearekin elkartu gara.

“Zientzialari” izeneko atal honen bitartez zientziaren oinarrizko kontzeptuak azaldu nahi ditugu euskal ikertzaileen laguntzarekin.

The post Iranzu Laura Guede: “Erdi Aroko biztanleria orokorrean, elikadurari begira orojalea zela ikusi dugu” #Zientzialari (111) appeared first on Zientzia Kaiera.

Para empezar y como ejemplo nos sirve la Comunidad Autónoma del País Vasco. El 27 de diciembre de 2016 aprobó el Consejo del Gobierno Vasco el Plan Especial de Emergencias por Riesgo de Incendios Forestales. En el texto, en la página 9, aparece un cuadro con la superficie quemada en la Comunidad entre 1985 y 2012. El máximo está en el catastrófico 1989, en el mes de diciembre, con más de 27000 hectáreas de superficie arbolada. Fue una sequía en invierno, después de una larga sequía estival, y con fuertes vientos que dificultaban la extinción de los incendios.

El siguiente año en superficie quemada fue 1985, con casi 2600 hectáreas, seguido de 2002 con 700 hectáreas y 1995 con 600 hectáreas. En 2011 fueron 140 hectáreas y en 2012, último año con datos en este Plan, fueron 175 hectáreas. En España, y según datos del Ministerio de Medio Ambiente, los años recientes con más de 400000 hectáreas quemadas fueron 1985, 1989 y 1994.

Estos son los datos para la Comunidad y para España y no hay que olvidar que a nivel del planeta, más o menos el 3% de su superficie se quema cada año. Los incendios forestales aparecen cuando las plantas colonizan la tierra, en bosques de entre 350 y 400 millones de años de antigüedad. Hay restos de carbón de incendios tan antiguos como del Silúrico, hace unos 400 millones de años.

Cada fuego es una combinación particular de frecuencia, intensidad, tamaño, estación, tipo de propagación y extensión. Pero, también es evidente que los incendios influyen, además de todo lo que significan como suceso público, en nuestra percepción del entorno, en concreto, del paisaje. Francisco Lloret y sus colegas, de la Universitat Autònoma de Barcelona, han estudiado los cambios en el paisaje en el municipio de Tivissa, en Tarragona, entre 1956 y 1993.

Tivissa. Imagen: Wikimedia Commons

Es un municipio agrícola con zonas difíciles y poco productivas que se han abandonado en los últimos años, y se han cubierto de matorrales que han homogeneizado el paisaje. Además, ha disminuido la superficie de bosques. Los autores encuentran que los incendios son más probables en áreas homogéneas con árboles, y provocan que el paisaje posterior también sea homogéneo.

Concluyen que, en las zonas con actividad humana el paisaje es más heterogéneo, por ejemplo, con distintas actividades agrícolas y modelos de explotación de la tierra, y los incendios se controlan mejor quizá por ser heterogéneas, con diferentes plantaciones que, a su vez, tienen diferente capacidad de incendiarse. Y, además, los que se aprovechan de las actividades agrícolas procuran defenderlas del fuego y no provocar incendios.

En las zonas sin actividad agrícola, muy iguales, con árboles y arbustos, los incendios se extienden con más facilidad y provocan, después y en primer término, mayor diversidad.

Es evidente que, sea a más o a menos diversidad, los incendios influyen en el paisaje y en nuestra precepción del mismo.

El incendio acercándose al complejo de Old Faithful en el Parque Nacional de Yellowstone (Estados Unidos) en 1988. Imagen: Wikimedia Commons

Sin embargo, un paisaje quemado se puede recuperar, quizá no exactamente igual al que existía antes del fuego, y puede convertirse en un área ecológicamente saludable. Fue el año 1988, en una gran sequía que, al año siguiente, en 1989, provocaría los incendios en el País Vasco, cuando ocurrió el gran incendio en Estados Unidos, en el Parque Nacional de Yellowstone, en el que ardieron más de 600000 hectáreas, algo así como Gipuzkoa, Bizkaia y gran parte de Álava. Fue uno de los mayores incendios forestales en una zona templada que aparece en la historia escrita. Daniel Donato y su grupo, del Departamento de Recursos Naturales del Estado de Washington en Olympia, nos cuentan cómo está el parque 24 años después.

Las zonas centrales del bosque, más tupidas y con más árboles, se han regenerado con fuerza y no ha influido la severidad del incendio. Las zonas más secas, con menos árboles, se han recuperado peor, en más tiempo, y, sobre todo, lo hacían con más eficacia si cerca habían quedado parcelas pequeñas sin quemar que pueden funcionar como reserva de semillas.

Una de las zonas de pino de Yellowstone que ardieron en 1988 tal y como se encontraba en 2006. El pino que sobrevivió (a la izquierda) es un Picea engelmannii, los jóvenes, Pinus contorta. Imagen: Wikimedia Commons

La regeneración culminó, en general, a los 15 años del incendio aunque, en las mejores zonas, el crecimiento ha continuado. A los 24 años, en esas zonas de bosque más maduro, el reemplazamiento de los árboles anteriores al incendio está completo. En las áreas más secas y con menos bosque, ha quedado, en muchos lugares, una estepa herbácea que necesitará varias décadas o, incluso, teniendo en cuenta el calentamiento global, nunca volverá a ser bosque.

Los resultados sobre incendios en la Península Ibérica son parecidos, tanto en Galicia, según el grupo de Otilia Reyes, de la Universidad de Santiago de Compostela, como en Cataluña, según Santiago Martín y Lluis Coll, del Centro de Ciencias Forestales de Solsona.

Son dos paisajes diferentes en dos climas distintos, en el oeste y este de la Península. En ambos casos, los incendios fueron en bosques de pinos, con el pino marítimo (Pinus pinaster), en Serres, en la costa de A Coruña y en 2014, un año antes del estudio, y pino laricio (Pinus nigra) en el centro de Cataluña y en 1998, siete años anterior al estudio.

Los resultados son parecidos y, como en Yellowstone, cuanto más potente es el bosque original, mejor se recupera. Y, también, ayuda la presencia de pequeñas parcelas no quemadas como origen de semillas para repoblar. Solo en las zonas más secas aparecen áreas con arbustos o praderas. Para la recuperación de las zonas con buen bosque original no se necesita ninguna intervención.

Como nos cuentan William Bond y John Keeley, de las universidades de El Cabo, en Sudáfrica, y de California en Los Angeles, grandes áreas del mundo arden de manera regular y, por tanto, los ecosistemas se han incendiado durante cientos de millones de años. Hay evidencias de incendios de hace 420 millones de años, desde la aparición de las plantas terrestres. Así se ha construido el paisaje que conocemos y se mantienen la estructura y la función de esos ecosistemas, muy adaptados a los incendios periódicos. Por tanto, los incendios son una fuerza evolutiva de selección natural lo que implica que los bosques que ahora conocemos se han seleccionado y aguantan y se recuperan de los incendios porque así se han formado. Y el fuego estimula la regeneración con, por ejemplo, semillas que germinan estimuladas por el calor o por sustancias químicas emitidas por la madera quemada o, también, la floración acelerada por el fuego.

Después de revisar incendios y diversidad de plantas en todo el planeta, excepto la Antártida, y desde finales del siglo XX hasta inicios de XXI, Juli Pausas y Eloi Ribeiro, del CIDE-CSIC de Montcada, en Valencia, y del ISRIC de Wageningen, en Holanda, han recopilado casi 200 millones de citas. Sus resultados demuestran que la mayor diversidad de plantas se da con la mayor productividad y, también, con la actividad de incendios. Así, el fuego explica una proporción significativa de la diversidad de las plantas. En conclusión, el fuego aumenta la heterogeneidad del paisaje y crea nuevos nichos con oportunidades para una gran variedad de especies.

Paisaje un año después de un incendio en un bosque de pinos. Imagen: Wikimedia Commons

Las plantas adaptadas al fuego han seleccionado determinadas características que les benefician en caso de incendio. En las áreas con clima mediterráneo, como la propia cuenca del Mediterráneo, California, región de El Cabo en Sudáfrica y Chile, el grupo de Philip Rundel, de la Universidad de California en Los Angeles, han revisado el número de especies vegetales adaptadas al fuego. En el Mediterráneo abundan las plantas que rebrotan después del incendio; tienen germinación estimulada por el fuego, sea por el calor, o por el humo; y florecen estimuladas por el fuego. Para estas especies, el fuego ha sido un estímulo importante para la diversificación y aparición de nuevas especies.

Como resumen final sirve la publicación de Juli Pausas y Jon Keeley, del Centro de Investigación sobre Desertificación del CSIC en Valencia y del Servicio Geológico de Estados Unidos respectivamente, cuando escriben que no solo el clima y el suelo explican la distribución de las especies animales y vegetales en el planeta, también interviene el fuego. Desde hace mucho tiempo, unos 400 millones de años, impulsando la aparición de especies nuevas adaptadas a los incendios periódicos. Sin embargo, nuestra especie ha cambiado la relación entre el fuego y los seres vivos. Primero, Homo utilizó el fuego para adaptar el entorno a sus necesidades. Pero, y en segundo lugar, lo hace con tal intensidad y extensión que cambió muchos ecosistemas y pone en peligro la sostenibilidad.

Referencias:

Archibald, S. et al. 2018. Biological and geophysical feedbacks with fire in the Earth system. Environmental Research Letters 13: 033003.

Bond, W.J. & Keeley, J.E. 2005. Fire as a global “herbivore”: the ecology and evolution of flammable ecosystems. Trends in Ecology and Evolution 20: 387-394.

Bowman, D.M.J.S. et al. 2009. Fire in the Earth system. Science 324: 481-484.

Donato, D.C. et al. 2016. Regeneration of montane forests 24 years after the 1988 Yellowstone fires: A fire-catalyzed shift in lower treelines? Ecosphere 7: e01410

Pausas, J.G. & Keeley, J.E. 2009. A burning story: The role of fire in the history of life. BioScience 59: 593-601.

Pausas, J.G. & Ribeiro. E. 2017. Fire and plant diversity at the global scale. Global Ecology and Biogeography DOI: 10.1111/geb.12596

Rundel, P.W. et al. 2018. Fire and plant diversification in Mediterranean-climate regions. Frontiers in Plant Science 9: 851.

Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.

El artículo La adaptación a los incendios forestales se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Incendios, los grafos de visibilidad y la conjetura de Collatz
2. “El bien común como adaptación” por Antonio Lafuente
3. Las aves de Prometeo

Uxue Razkin

Farmakologia

Nahasmendu bipolarra duten pertsonengan depresio-aldiak prebenitzeko litio gatzek duten eraginkortasuna aztertu dute. Tratamenduari atxikidura ona izan duten pazienteek depresio aldi gutxiago izan dituzte eta baita aldi maniako eta hipomaniako gutxiago. Arabako Unibertsitate Ospitalean egin da ikerketa eta 72 pazienteri jarraipena egin zaie hamar urtez.

Opiodeen krisia AEBek izan duten “osasun-hondamendirik handienetako eta konplexuenetako bat” dela adierazi du AEBko Elikagaien eta Sendagaien Administrazioak (FDA). Neurrien artean, aipatzen dira tratamenduari egokitutako dosi eta neurrian ematea sendagaiak, adikzioak eta gaindosiak saihesteko. Horretaz gain, botikak hartzeko modu berriak ere probatzeko asmoa du. Bestalde, gaindosiak eragindako heriotzak saihesteko, naloxona merkatuan libre saltzeko modua aztertuko du. Testuan dauden gainontzeko neurriak irakurtzeko, jo ezazue artikulura!

Medikuntza

Bigarren aldiz, hiesa zuen paziente bat sendatzea lortu dute. Hezur-muineko transplantea eginez, hiesa senda daitekeela berretsi dute. Transplantearen ondoren, ikertzaileek ez dute ikusi birusaren arrastorik eta transplantea egin ziotenetik, ez da birusik agertu, ezta botika erretrobiralak hartzeari utzita ere. Halere, ICISTEM lan-taldeko ikertzaileek esan dute zuhur jokatu eta guztiz sendatuta dagoela ziurtatzeko denbora gehiago itxoin behar dela.

Berriak ere eman ditu xehetasunak albiste honen inguruan. Kasu honetan pazientea 2003. urtetik zen GIBduna; 2012. urtean linfoma bat atzeman zioten, eta hori tratatzeko egin zioten zelula amen transplantea, 2016. urtean. Zelula horiek mutazio jakin bat zuten, GIB birusaren sarbide eragozten duena, eta itxura guztien arabera, horrek lortu du birusaren erremisioa.

Biologia

Ipurtargiak oso bitxiak dira. Gauean argi berdexka egiteko gai dira eta horrek bi helburu ditu: jakina da gorteatzeko tresna dela baina era berean, harrapakarietatik babesteko tresna ere bada: ikusgarriago egiten dira haiek jatea kaltegarria eta toxikoa izan daitekeela ohartarazteko. Argi horren atzean luziferina izeneko molekula dago. Baina zer dago zehazki lumineszentzia horren atzean? Ez galdu Josu Lopez-Gazpiok eman digun azalpen interesgarria!

Zenbait erle espeziek elikagaiak non dauden deskribatzeko darabilten “dantza” ikertu dute zientzialariek. Baina badirudi hori mito bat dela. Izan ere, erle gehienek ez dute dantzarik egiten. Hala ere, dantzarena oso kuriosoa eta liluragarria da. Portaera hori izan dute ikergai Mainzeko (Alemania) eta Lausanako (Suitza) Unibertsitateetako ikertzaileek. Proba horien bitartez saiatu dira argitzen dantzaren lengoaiak koloniaren arrakastan duen eragina. “Gure harridurarako, aurkitu dugu elikagaiak biltzerakoan erleen koloniak eraginkorragoak direla dantzaren lengoaia kendu zaienean”, azaldu du ikertzaile batek.

Meteorologia

Ikuspuntu meteorologikotik, otsaila ezohikoa izan da: ohi baino tenperatura beroagoak izan ditu eta lehorragoa izan da. Eguraldi honek eragozpenak handitu ditu: alde batetik, alergiak, baina baita suteak ere. Horretaz gain, otsaileko eta martxoaren hasierako eguraldi egonkorrak beste arazo bat eragin du: kutsadura.

Fisika

Material topologikoak ezagutu ditugu artikulu honen bidez. Berrian azaltzen digutenez, duela hamar urte pasatxo aurkitu zuten lehen material topologikoa, eta itxaropenak piztu zituen haren propietate bereziak. Zientzialariek pentsatu zuten oso material arraroak zirela. Orain, nazioarteko talde batek –bertan bi ikertzaile euskaldun ari dira lanean– materialon katalogo bat antolatu du sarean, eta tresna bat eratu du material batek halako ezaugarriak ote dituen jakiteko. Emaitza harrigarriak: materialen %27 inguruk dituzte propietate topologikoak. Topological Materials Database katalogoan azter daitezke materialak.

Adimen artifiziala

Gorka Gazkune UPV/EHUko Konputazio Zientzien eta Adimen Artifizialaren saileko irakasleak kontatzen digu honetan Elon Musk enpresari estatubatuarrak orain dela urte batzuk adimen artifiziala modu irekian garatzeko enpresa bat sortu zuela. Orain enpresa hori, OpenAI izenekoa, erreferente bilakatu da. Azken hilabete honetan, esaterako, hizkuntza-eredu zehatz eta boteretsua argitaratu dute. Baina OpenAIko ikertzaileek erabaki dute ez dutela beraien eredua jendearekin partekatuko. Badirudi eredu honek testu onak idazten dituela eta pentsatzen dute helburu gaiztoekin erabil daitekeela. Adimen artifiziala arloarekin batera beti dator etika. Ez galdu Azkuneren zutabea!

Genetika

Zer da metabolomika? teknologia omikoen baitako azken diziplinatzat hartzen da; fenotipotik gertuen dagoen diziplina da, eta, hortaz, une jakin bateko organismoaren egoera hoberen adierazten duena. Diziplina honen helburua da metaboloma osoa aztertzea, baina, genomarekin edo proteomarekin alderatuta, metaboloma definitzea ez da erraza, testuan azaltzen digutenez. Diziplina konplexu honi buruz gehiago jakiteko, jo ezazue artikulura!

–——————————————————————–
Asteon zientzia begi-bistan igandeetako atala da. Astean zehar sarean zientzia euskaraz jorratu duten artikuluak biltzen ditugu. Begi-bistan duguna erreparatuz, Interneteko “zientzia” antzeman, jaso eta laburbiltzea da gure helburua.

———————————————————————–

Egileaz: Uxue Razkin kazetaria da.

——————————————————————

The post Asteon zientzia begi-bistan #245 appeared first on Zientzia Kaiera.

Si cerrásemos los ojos para visualizar la imagen de un geólogo, probablemente imaginaríamos a una persona descubriendo fósiles y recopilando y coleccionando minerales. No obstante, esta disciplina académica cuenta con muchísimas más aplicaciones desconocidas para gran parte de la sociedad.

Con el objetivo de dar visibilidad a esos otros aspectos que también forman parte de este campo científico nacieron las jornadas divulgativas “Abre los ojos y mira lo que pisas: Geología para miopes, poetas y despistados”, que se celebraron los días 22 y 23 de noviembre de 2018 en el Bizkaia Aretoa de la UPV/EHU en Bilbao.

La iniciativa estuvo organizada por miembros de la Sección de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU, en colaboración con el Vicerrectorado del Campus de Bizkaia, el Ente Vasco de la Energía (EVE-EEE), el Departamento de Medio Ambiente, Planificación Territorial y Vivienda del Gobierno Vasco, el Geoparque mundial UNESCO de la Costa Vasca y la Cátedra de Cultura Científica de la UPV/EHU.

Los invitados, expertos en campos como la arquitectura, el turismo o el cambio climático, se encargaron de mostrar el lado más práctico y aplicado de la geología, así como de visibilizar la importancia de esta ciencia en otros ámbitos de especialización.

Asier Hilario, director científico del Geoparque de la Costa Vasca, se encarga de ahondar en la geología como recurso. Algunos de los principales destinos turísticos del mundo son pura geología, tienen millones de visitantes y aunque muchos no lo sepan, hay algo de esa geología que les interesa. Desde su experiencia, expone las principales claves y oportunidades del geoturismo para crear destinos de turismo innovadores y sostenibles que fomenten el disfrute y conocimiento de las ciencias de la Tierra.

Edición realizada por César Tomé López

El artículo ¿Existe el geoturismo? se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Geología, ver más allá de lo que pisamos
2. Patrimonio geológico: la otra mitad del ambiente
3. Geología: la clave para saber de dónde venimos y hacia dónde vamos

Ez dago xederik prozesu naturaletan. Hori da Darwinen herentzia. Jesús Zamora Bonillak garatzen du Requiem for final causes artikuluan.

Gure hesteetan bakterio jakin batzuen presentzia edo gabezia izateak, gaua eta eguna suposa dezake minbizia tratatzeko orduan. Pasquale Pellegrini ikertzaileak azaltzen du zergatia: Bacteria and cancer: the deadly mix.

Substantzia bat gainazal metaliko batean pikosegundo bat baino eskala txikiagoan adsorbatzen denean, hor gertatzen dena azaltzen duen teoriarik ez dugu izan esku artean. Orain badugu azalpena DIPCri esker: The ultrafast dynamics of adsorbates deciphered.

–—–

Mapping Ignorance bloga lanean diharduten ikertzaileek eta hainbat arlotako profesionalek lantzen dute. Zientziaren edozein arlotako ikerketen azken emaitzen berri ematen duen gunea da. UPV/EHUko Kultura Zientifikoko Katedraren eta Nazioarteko Bikaintasun Campusaren ekimena da eta bertan parte hartu nahi izanez gero, idatzi iezaguzu.

The post Ezjakintasunaren kartografia #252 appeared first on Zientzia Kaiera.

La Facultad de Ciencias de Bilbao comenzó su andadura en el curso 1968/69. 50 años después la Facultad de Ciencia y Tecnología de la UPV/EHU celebrará dicho acontecimiento dando a conocer el impacto que la Facultad ha tenido en nuestra sociedad. Durante las próximas semanas en el Cuaderno de Cultura Científica y en Zientzia Kaiera se publicarán regularmente artículos que narren algunas de las contribuciones más significativas realizadas a lo largo de estas cinco décadas. Comenzamos con la serie “Espectrometría de masas”, técnica analítica que supone el ejemplo perfecto del incesante avance de la Ciencia y la Tecnología.

La espectrometría de masas (MS) es una técnica habitual entre los químicos desde hace ya 100 años, pero no fue hasta hace 3 décadas que se empezó a utilizar como técnica de análisis de proteínas. Para analizar un analito mediante espectrometría de masas (MS) es necesario ionizar dicho analito y pasarlo a fase gaseosa. Durante mucho tiempo, la posibilidad de ionizar macromoléculas como las proteínas o fragmentos de proteínas, es decir péptidos, y pasarlos a fase gaseosa se consideraba una tarea tan posible como hacer volar a un elefante. Sin embargo, el desarrollo y comercialización de dos métodos de ionización a los que se denominó ionización “suave”, demostraron que era posible analizar macromoléculas del tamaño de las proteínas, tanto en disolución como en estado seco cristalino; éstos métodos de ionización se conocen hoy día como ionización electrospray (ESI) y ionización por desorción láser asistida por matriz, (matrix assisted laser desorption ionization) (MALDI). En ESI, se aplica un alto voltaje a la solución que contiene el analito a su paso por una fina aguja perforada. A medida que se va evaporando la solución con las moléculas cargadas, se va reduciendo el tamaño de las gotas, hasta conseguir que pasen a estado gaseoso. Por su parte, en MALDI se dispara con láser a una placa de acero en la que se ha secado el analito junto con una matriz. La matriz absorbe la energía del láser que a su vez se transfiere a la muestra, haciendo que cambie a estado gaseoso.

Pero, ¿por qué las proteínas? ¿a qué viene ese interés por analizarlas? La razón es que las proteínas son las moléculas fundamentales de todos los seres vivos. Las proteínas son las encargadas de realizar diversas tareas en nuestras células; entre otras, catalizan reacciones químicas, transportan moléculas, mantienen la estructura celular y nos protegen frente a los patógenos. Nuestro cuerpo está formado por trillones de células, y cada una de ellas cuenta con miles de proteínas diferentes. De hecho, dependiendo del catálogo o conjunto de proteínas que contenga un tipo de célula, llevará a cabo unas u otras funciones y tendrá unas u otras características. Todas las células de un ser vivo contienen la misma información genética, es decir, el genoma de todas sus células es idéntico. La información necesaria para producir cada proteína está escrita en los genes. Dicho de otro modo, los genes son las recetas que se siguen para crear las proteínas, y dependiendo de las recetas que se utilicen en cada momento, se producirán unas proteínas u otras. Se denomina proteoma a la colección de proteínas de las que dispone una célula en un momento concreto. A diferencia del genoma, el proteoma celular varía continuamente; en respuesta a cualquier estímulo que llegue a las células, o cuando deben hacer frente a cualquier ataque, es decir, con el fin de adaptarse al entorno, las células producirán diferentes proteínas que trabajarán conjuntamente. Esto explica cómo, contando ambas con el mismo genoma, una oruga se convierta en mariposa (Imagen 1).

Imagen 1. Papilio machaon oruga (a) y mariposa (b). Fuente: Wikimedia Commons.

Las proteínas, al igual que nosotros, tienen sus propias «redes sociales». Cumplen sus funciones interaccionando entre ellas más que individualmente. A pesar de ello, estas interacciones suelen ser, en la mayoría de los casos, temporales. Se crean y se destruyen según las necesidades celulares. Habiendo millones de proteínas en la células, la red de interacciones intracelulares es tan compleja como la que puede haber entre todas las personas del planeta. El funcionamiento de esa red de proteínas condicionará la salud de la célula y, en consecuencia, la de todo el organismo. Por eso es tan importante estudiar las proteínas y sus interacciones, es decir, los proteomas, e intentar interpretarlos en su conjunto. En consecuencia, uno de los retos fundamentales de la biología actual es describir los proteomas cualitativamente y cuantitativamente. Dicho objetivo parece alcanzable y pocos dudan del liderazgo que ha tomado la proteómica en este camino.

La proteómica estudia los proteomas. Fue en 1975 cuando por primera vez se separaron miles de proteínas de la bacteria Escherichia coli mediante electroforesis bidimensional en gel (2DE). Sin embargo, la identificación de dichas proteínas, concretar cuáles eran exactamente, constituía otro reto diferente. Para abordarlo, fue necesario, tanto desarrollar técnicas de secuenciación parcial, léase degradación de Edman, como ajustar la propia técnica de espectrometría de masas (MS) al análisis de proteínas. La MS es, a día de hoy, el método que se utiliza habitualmente para identificar proteínas. Para poder interpretar los proteomas en su conjunto, además de identificar las proteínas, hay que cuantificarlas. Los primeros pasos para la cuantificación de proteínas se dieron mediante el análisis de imágenes de los geles de 2DE. Si bien sigue siendo una técnica adecuada para el análisis proteómico, hoy en día ocupa un segundo lugar, muy por detrás de la proteómica basada en la espectrometría de masas (MS-based proteomics). De hecho, actualmente, la MS es el método habitual para identificar y cuantificar las proteínas en muestras proteicas complejas. Se ha convertido pues en una técnica fundamental para interpretar la información codificada en el genoma.

Tal y como se ha mencionado anteriormente, las técnicas habituales utilizadas para ionizar y evaporar proteínas y péptidos son ESI y MALDI. La técnica MALDI-MS se utiliza para analizar mezclas de péptidos relativamente simples. En cambio, los sistemas ESI-MS acoplados a la cromatografía líquida (LC-MS), son los más adecuados para el análisis de muestras complejas. Siendo los proteomas, por definición, complejos, las técnicas de LC-MS han prevalecido en la proteómica. La precisión, sensibilidad y resolución de masas, junto con su velocidad, son las claves del éxito de las técnicas de LC-MS. Durante los últimos años, se ha podido identificar, cuantificar y caracterizar un enorme número de proteomas mediante diferentes procedimientos de LC-MS. Entre los logros conseguidos a nivel de proteómica, cabe destacar dos borradores del proteoma humano publicados en 2014, y el actual Proyecto Proteoma Humano (HPP) dirigido por la Organización Mundial del Proteoma Humano (HUPO)

Pero, ¿qué es lo que hacemos exactamente en un laboratorio de proteómica? Sea cual sea la muestra recibida (muestra obtenida de una biopsia, células animales o vegetales, bacterias, secreción biológica…), habitualmente se aplica el flujo de trabajo denominado proteómica bottom-up o proteómica ascendente, de abajo hacia arriba (Imagen 2). En primer lugar, se extraen las proteínas de la muestra. A continuación, se utiliza una enzima que digiere las proteínas, habitualmente la tripsina, para trocear las proteínas en trozos pequeños denominados péptidos. Los péptidos de la mezcla se separan en la cromatografía líquida de fase inversa acoplada a la ionización por electrospray. A medida que los péptidos eluyen de la columna, se van ionizando y pasan al espectrómetro de masas. Allí, los iones de los péptido se van separando y detectando en función de su relación masa-carga (m/z). Los péptidos más abundantes se aíslan del resto, y se fragmentan, dando lugar a espectros de fragmentación. Estos espectros son los que contienen la información que permite identificar y cuantificar los péptidos. Finalmente, los datos obtenidos por el espectrómetro de masas se analizan mediante herramientas informáticas específicas. De esta manera, es posible saber qué proteínas hay en la muestra analizada y en qué cantidad.

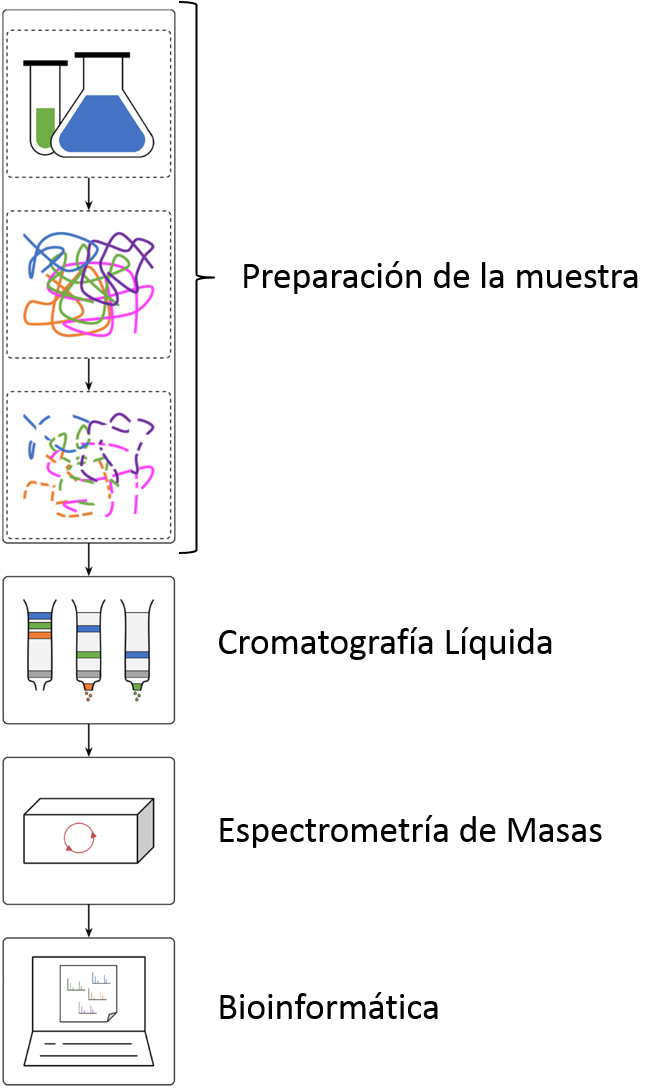Imagen 2. Proteómica bottom-up Fuente: Autores.

Durante la última década, la proteómica basada en la MS se ha convertido en una de las principales herramientas analíticas para las biociencias. Ha permitido estudiar las proteínas desde diversas vertientes, y ha facilitado el camino para conocer sus estructuras, variaciones, cantidades, modificaciones postraduccionales e interacciones. Además, gracias a la proteómica nos encontramos más cerca de identificar las proteínas implicadas en el desarrollo de diversas enfermedades y los biomarcadores necesarios para el diagnóstico de las mismas. Durante los próximos años, se irán completando los catálogos proteicos de diferentes condiciones celulares. Junto a los resultados obtenidos a partir de la genómica, epigenómica, metabolómica y otras «ómicas» a gran escala, los descubrimientos obtenidos gracias a la proteómica contribuirán a la construcción de modelos celulares. De hecho, esa es la tendencia actual: trabajar desde un punto de vista multidisciplinar con el fin de construir modelos matemáticos y estadísticos que ayuden a aclarar la complejidad de los procesos biológicos; y es precisamente ahí donde la proteómica jugará un papel relevante.

Más información

• Fenn JB (2003) “Electrospray wings for molecular elephants (Nobel lecture)” Angew Chem Int Ed Engl. 42(33), 3871-94. DOI:10.1002/anie.200300605
• Fenn JB et al. (1989) “Electrospray ionization for mass spectrometry of large biomolecules” Science 246(4926), 64-71. DOI: 10.1126/science.2675315
• Tanaka K et al. (1988) “Protein and polymer analyses up to m/z 100 000 by laser ionization time-of-flight mass spectrometry” Rapid Communications in Mass Spectrometry 2(8), 151–153. DOI:10.1002/rcm.1290020802
• Karas M and Hillenkamp F (1988) “Laser desorption ionization of proteins with molecular masses exceeding 10,000 daltons” Anal Chem. 60(20), 2299-301. DOI: 10.1021/ac00171a028
• O’Farrell (1975) “High resolution two-dimensional electrophoresis of proteins” J Biol Chem 250(10), 4007-21.
• Kim MS et al. (2014) “A draft map of the human proteome” Nature 509(7502), 575-81. DOI: 10.1038/nature13302
• Wilhelm M et al. (2014) “Mass-spectrometry-based draft of the human proteome” Nature 509(7502), 582-7. DOI: 10.1038/nature13319
• HUPO: https://hupo.org/human-proteome-project

Sobre los autores: Miren Josu Omaetxebarria, Nerea Osinalde, Jesusmari Arizmendi y Jabi Beaskoetxea, miembros del departamento de Bioquímica y Biología Molecular, y Kerman Aloria, técnico de SGIker.

El artículo Proteómica: cuando las proteínas y la espectrometría de masas van de la mano se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Cartografiando territorio inexplorado: imagen por espectrometría de masas
2. Espectrometría de masas: de un isótopo de neón a elefantes que vuelan
3. A new hero is born: La espectrometría de masas al servicio de la justicia

2019ko Emakumeen Nazioarteko Egunak gizonen eta emakumeen arteko berdintasuna aldarrikatzen du indarrez. “Erabakitzen dudana izango naiz” da 2018ko martxorako Emakundek, Emakumearen Euskal Erakundea, proposatutako leloa. Aurtengo kanpainak Garapen Iraunkorrerako Helburuen (GIH) 5. xedea hartu du gidalerro bezala:

“Emakumeen eta neskatoen aurkako edozein motatako diskriminaziori amaiera ematea ez da soilik oinarrizko giza eskubide bat, nahitaez ezinbestekoa da garapen iraunkorra bultzatzeko. Behin baino gehiagotan egiaztatu da emakumeen eta neskatoen ahalduntzeak eragin biderkatzaileak izateaz gain, mundu mailako garapena zein hazkunde ekonomikoa sustatzen laguntzen duela.”

“Lau neska gazte dira `Erabakitzen dudana izango naiz´ kanpainaren protagonistak, eta gizarteari galdetzen diote prest dagoen beraien eskubideak modu aske batean aurrera eramateko aukera bermatzeko. Neskak Historian zehar erreferenteak izan diren emakumeen irudiekin batera agertzen dira. Hala nola, Marie Curie zientzialaria, Clara Campoamor idazle eta politikoa, Frida Kahlo margolaria eta Maria Antonia Uzkudun erraketista, Txikita de Anoeta ezizenez ezagunagoa dena. Berdintasunaren bidean aurrekariak izan ziren emakumeei omenaldia egiteaz gain, beraien irudiek erreferenteak izatearen beharraz hitz egiten digute, eta beraz, hurrengo belaunaldietarako eredu bilakatu daitezen, emakumeak ikusgarri egin eta aintzat hartzeko beharraz.”

Neska-mutilentzat erreferente aparta da Skłodowska-Curie (1867-1934), nahiz eta ez izan zientzia arloko ikasketarik gazte hauen buruan dituzten hautagaien artean. Duela urtebete, Javier San Martin kazetariak Hélène Langevin-Joliot fisikaria elkarrizketatu zuen Mujeres con ciencia blogerako. Hélène Irène Joliot-Curie eta Frédéric Joliot-Curie fisikarien alaba da eta Marie Curie eta Pierre Curieren biloba.

Elkarrizketan kazetariak aipatu zion Hélène Langevin-Jolioti ikerketak denbora tarte handia eskatzen duela eta haren guraso zein aiton-amonek laborategian emango zutela bizitzaren zati handi bat. Hélène Langevin-Joliotek sutsuki erantzun zion: “Hori mitoa da. Marie Curie emakume zientzialariaren ikurra da eta hori oso garrantzitsua da baina sarritan haren figurari buruzko mitoak sortarazten ditugu. Esaterako, haren bizitza zientziarengatik sakrifikatu zuen emakumea izan zela. Ez da horrelakorik pentsatu behar ez baitzen egia. Eta, bestalde, nire gurasoek aisialdi aktiboa praktikatzen zuten. Tenisara jolasten zuten, mendi irteerak egiten zituzten…”.

Horrela da, mitoak ez dira beharrezkoak baina bai erreferentziazko emakumeak, non begiratu izateko. Horretan dihardute Mujeres con ciencia bloga eta baita Zientzia Kaierako Emakumeak Zientzian atala, erreferentziazko emakumeak bistaratzen.

2019ko martxoaren 8an, aldarrika dezagun indarrez berdintasuna oinarrian duen gizarte baten beharra: #NikErabakitzenDut.

—————————————————–

Egileez:

Marta Macho Stadler, (@MartaMachoS) UPV/EHUko Matematikako irakaslea da eta Kultura Zientifikoko Katedrak argitaratzen duen Mujeres con Ciencia blogaren editorea.

Uxune Martinez, (@UxuneM) Euskampus Fundazioko Kultura Zientifikoko eta Berrikuntza Unitateko Zabalkunde Zientifikorako arduraduna da eta Zientzia Kaiera blogeko editorea.

—————————————————–

The post Erabakitzen dudana izango naiz appeared first on Zientzia Kaiera.

Damian Ucieda Cortes. Demolition, Glasgow, Reino Unido, 2015

Uno de los cometidos más sofisticados de las ciencias es mostrar el conocimiento de forma elegante. Pensemos en las fórmulas matemáticas que describen las leyes físicas. En los modelos de moléculas y cristales. En el enunciado de hipótesis. Con qué precisión del lenguaje y con qué precisión plástica describimos cómo es lo que nos rodea. Con qué elegancia.

Para muchos, entre los que me incluyo, el paradigma de todo esto es la Tabla Periódica de los Elementos.

A lo largo de la historia se han sucedido varios intentos de ordenar los elementos químicos. Una vez tuvimos la certeza de que algunas sustancias eran elementos químicos, es decir, que estaban formadas por un solo tipo de átomos; comenzamos a ordenarlos de acuerdo con sus propiedades: peso atómico, tipo y número de elementos con los que enlaza, estado natural… Teníamos la intuición y el deseo de que los elementos que lo conforman todo, el aire, la piel, la arena, todo, respondiesen a un orden mayor, como si este orden nos hubiese venido dado.

Hubo intentos bellísimos, como el del tornillo telúrico. Para ello se construyó una hélice de papel en la que estaban ordenados por pesos atómicos los elementos químicos conocidos, enrollada sobre un cilindro vertical, y al hacer coincidir elementos químicos similares sobre la misma generatriz se apreciaba que el resto de las generatrices surgidas también mostraban relación entre los elementos químicos unidos, lo que claramente indicaba una cierta periodicidad. Era tan bonito que era una pena que no fuese cierto. El tornillo telúrico no funcionaba con todos los elementos químicos, solo servía para los más ligeros.

Hubo otro intento especialmente refinado de ordenar los elementos químicos que tenía relación con la música. Qué fabulosa la relación entre la música y la química. Al ordenar los elementos de acuerdo con su peso atómico creciente -exceptuando el hidrógeno y los gases nobles, que todavía no se conocían- el que quedaba en octavo lugar tenía unas propiedades muy similares al primero. Se le llamó ley de las octavas. Era bonito ver tal relación entre la naturaleza de los elementos químicos y la escala de las notas musicales. Lamentablemente la ley de las octavas empezaba a fallar a partir del elemento calcio. Con lo bonita que era. Una lástima.

Cuando ya se conocían 63 elementos químicos -en la actualidad conocemos 118- se ordenaron en grupos de acuerdo con sus propiedades químicas. Y dentro del grupo, se organizaron por peso atómico creciente. Quien lo hizo por primera vez, hace 150 años, tuvo la osadía de corregir algunos pesos atómicos que hacían peligrar la estética de aquella tabla. Dejó huecos para elementos que, según él, se descubrirían en el futuro. Y es que la tabla, ante todo, tenía que ser bonita, porque la realidad es bonita y tiene que responder a algún orden. Qué locura si no. Pues la tabla de los elementos químicos también.

Aquella tabla fue el origen de la actual Tabla Periódica de los Elementos. Con el tiempo, efectivamente descubrimos más elementos químicos. Rellenamos los huecos, tal y como era de esperar. Y hasta descubrimos que aquel orden no respondía a pesos atómicos crecientes, o al menos no siempre, y de ahí los cambios propuestos. Aquel orden respondía al número de protones que cada elemento químico contiene en su núcleo. Lo llamamos número atómico, pero hace 150 años no se sabía nada de esto. Era bonito, era ordenado, era elegante. Tenía que ser verdad.

En las ciencias, y en cualquier otra forma de conocimiento, la belleza es criterio de verdad. Las leyes físicas que conseguimos expresar con fórmulas matemáticas, cuanto más bellas, más ciertas. Cuanto más y mejor comprimamos su verdad en estilosos caracteres del alfabeto griego, más ciertas. Nos brindan esa sensación tan placentera de tenerlo todo bajo control. Nos hacen creer que, si está ordenado, es que lo hemos entendido.

Las ciencias describen la realidad. Lo hacen a su manera, con su lenguaje propio. El de los números, las palabras, las ilustraciones. Esa descripción nos satisface cuando es lo suficientemente elegante. Podríamos tener un conjunto de 118 elementos químicos de los que conocer absolutamente todo, de forma individual, y no haberlos ordenado jamás. Y sabríamos lo mismo, pero nos daría la impresión de que, sin orden, los datos son solo datos. No hay conocimiento sin orden.

El orden es una fantasía. Esto puede interpretarse de dos formas de fácil convivencia. Es una fantasía porque es una ilusión. La realidad es un caos y somos nosotros con nuestras leyes y nuestras tablas los que creamos la ficción de orden. Es un deseo. Y es una fantasía porque es bonito. Porque así entendemos la belleza. Por eso el orden es un deseo de belleza autocumplido.

Los grandes hitos del conocimiento, entre ellos la Tabla Periódica de los Elementos, tienen algo en común: nos hablan de nosotros. Todos ellos revelan la pasta de la que estamos hechos.

Sobre la autora: Déborah García Bello es química y divulgadora científica

El artículo El orden es una fantasía se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Los cuantificadores se aprenden en el mismo orden, sea cual sea la lengua
2. Los 880 cuadrados mágicos de orden 4 de Frénicle
3. #Naukas15 Fantasía en la divulgación: una estrella para Cervantes

María Encarnación Blanco Aurreko mendeko bigarren erdialdean iraultza handia bizi izan zen biologian. Aurrerapen teknologiko eta zientifiko handiak egin ziren (adibide ezagunena dugu DNAren helize bikoitzaren aurkikuntza), eta erredukzionismoa biologiaren arau bihurtu zen, organismo konplexuak deskonposatzen hasi baitziren haiek osatzen dituzten zatiak bakarka aztertzeko. Ondorioz, biologia molekularra asko hedatu zen. Baina, azkeneko urteetan, neurri batean esperimentala eta neurri batean filosofikoa den beste norabide-aldaketa bat ari da gertatzen biologian, sistemaren ikuspegi holistiko edo integral baterantz, osagai indibidual guztien multzoa eta haien arteko elkarrekintzak aztergai bihurtuta.

Aristotelesen esanetan, osotasuna zatien batura baino gehiago da. Aurreko mendeko ikuspegi erredukzionistaren eta gaur egungo sistemen biologiaren arteko desberdintasun horiek alderatu daitezke jakintsu itsuen eta elefantearen kondaira indiarrarekin, arazo ezezagun batetara ikuspegi indibidual edo murriztu batetik gerturatzeak berekin dakartzan mugak islatzen baititu.

1. irudia. From The Heath readers by grades liburuko ilustrazioa, D.C. Heath and Company (Boston), 1907. (Iturria: Wikimedia Commons)

Kondaira horretan, inoiz elefante bat ikusi ez duten sei jakintsu itsuk elefante baten bila joan eta ukitzea erabakitzen dute, animaliaren irudi mental bat egiteko. Lehenengoa, elefantearengana gerturatzen denean, estropezu egin eta animaliaren saihetsaren kontra erortzen da. Esperientzia horretatik ondorioztatzen du elefanteak lokatzezko pareta baten antzekoa izan behar duela. Bigarren jakintsuak elefantearen hortza ukitzen du, eta haren forma borobil eta zorrotzetik ondorioztatzen du elefanteak lantza baten antzekoa izan behar duela. Modu bertsuan, gainerako lau jakintsuek elefantearen tronpa, buztana, hanka bat eta belarri bat ukituta erabakitzen dute, hurrenez hurren, ezagutzen ez zuten animalia horrek suge, soka, zuhaitz-enbor edo abaniko baten antza izango duela. Pentsatzen dutenari buruz eztabaidatzean ez dira ados jartzen elefantearen formaren inguruan, izan ere, John Godfrey Saxe-k kondaira horri buruzko olerkian esaten duen moduan “denak neurri batean zuzen zebiltzan arren, denak oker zeuden”. Era berean, sistema biologiko konplexu guztiak behaketa partzialetan bakarrik oinarrituta ulertzen saiatzen bagara, osoak ez diren ondorioak edo ondorio okerrak atera ditzakegu.

Sistemen biologia bizkor hedatu izana teknologia omikoen ondorioa izan da neurri handi batean. Teknologia horien artean, genomika da ezagunena oraingoz, XX. mendearen amaierako eta XXI. mendearen hasierako erronka teknologiko handia Giza Genomaren Proiektua izan baita. Proiektu hori, genomaren sekuentzia osoa ezartzea helburu zuena, 2003an amaitu zen, aurreikusi baino bi urte lehenago. Horrela, zientzialarien komunitateak informazio zehatza eskuratu zuen giza geneen multzo osoaren (hots, genotipoaren) egitura, antolakuntza eta funtzioari buruz.

Genotipoa, neurri handi batean, organismo baten egoeraren arduraduna da. Baina fenotipoa, hau da, sistema biologiko baten ezaugarri fisiko guztien deskribapena (morfologia, garapena eta metabolismoa barne), ingurumen-faktoreen mende ere badago nabarmen. Metabolomika teknologia omikoen baitako azken diziplinatzat hartzen da; fenotipotik gertuen dagoen diziplina da, eta, hortaz, une jakin bateko organismoaren egoera hoberen adierazten duena.

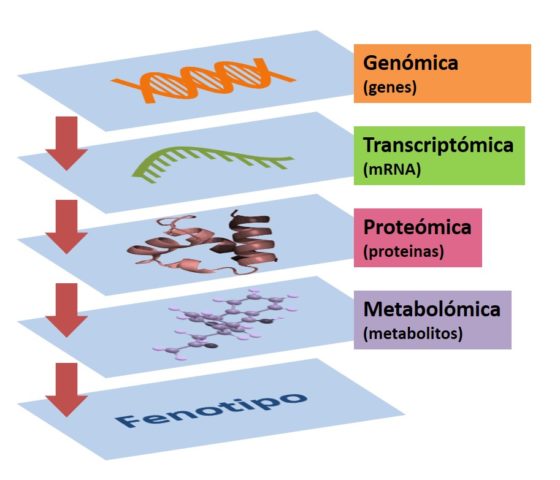
2. irudia. Jauzi omikoa: geneetatik metabolitoetara, fenotipoaren misterioak argitzen. (Iturria: M. E. Blanco)

Oraingo aroa baino 1500-2000 urte lehenago jada garrantzi handia zuen metabolitoen azterketak fluido biologikoetan, Txinako medikuntza tradizionalean zein Indian egiten zen Ayurveda-n intsektuak erabiltzen baitziren pazienteen gernuan glukosa-maila altuak detektatzeko. Metabolomikako lehen esperimentuak Nobel saria birritan jaso zuen Linus Paulingek egin zituela esan daiteke, 1971n 250 bat metabolito analizatu baitzituen hatsaren eta gernu-lurrinaren laginetan; horrela ondorioztatu zuen fluido biologiko bateko metabolito-kopuru handi batek sortutako patroi batetik abiatuta sistema biologiko konplexu baten egoerari buruzko informazioa bil daitekeela. Baina metabolomikaren boom handia 90ko hamarkadaren amaieran gertatu zen. 1999an Jeremy K. Nicholsonek metabonomika terminoa sortu zuen “sistema biziek estimulu patofisiologikoen edo genetikoen aurrean ematen duten erantzun dinamikoaren eta multiparametrikoaren neurri kuantitatiboa” deskribatzeko, hau da, informazio genetikoaren edo kanpoko aldaketa baten eraginez izaki bizidun bat zer egoeran dagoen kuantifikatzeko metabolitoen multzoaren azterketaren bidez. Harrezkero metabolomikaren erabilera esponentzialki areagotu da (2018an 4.000 aldiz baino gehiago argitaratu zen metabolomics terminoa PubMed-en) eta hainbat arlotan aplikatzen da, hala nola gaixotasunen azterketan, sendagaien garapenean, zientzia forentsean, ingurumen-analisian, nutrizioan edo toxikologian.

Metabolomika diziplina zabal eta konplexua da, eta hainbat urrats eman behar dira emaitzak interpretatu ahal izateko galdera biologikotik hasita, hau da, arazoaren planteamendutik abiatuta (adibidez, zer alde dagoen izaki osasuntsu baten eta gaixo baten artean, zer aldaketa metaboliko eragiten dituen dieta aldatzeak, zer erlazio dagoen haur baten garapenaren eta sendagai batek harengan duen eraginaren artean, edo zer eragin duen konposatu toxiko batek sistema batean, besteak beste). Lehenengo urratsa, garrantzitsuenetako bat, azterketa diseinatzea da. Tartean sartuta dauden pertsona guztiek urrats guztietan parte hartu behar dute, laginak hartzen direnetik analisi estatistikoa eta interpretazio biologikoa egiten direnera arte. Sir Ronald Aylmer Fisherek esan zuen moduan: “esperimentua egin ondoren estatistikan adituari galdetzea eta post-mortem analisi bat egiteko eskatzea gauza bera da: ziur asko esan ahalko du zergatik hil zen esperimentua”. Esperimentua egiten hasi aurretik gainerako urratsak zehaztu behar dira (lagina hartzea eta tratatzea, lagina analizatzea, datuak tratatzea eta prozesatzea), emaitzak interpretatu ahal izateko.

3. irudia: Lan-fluxua metabolomikan, galdera biologikotik emaitzen interpretaziora. (Iturria: M.E. Blanco)

Metabolomikaren helburua da metaboloma osoa aztertzea, baina, genomarekin edo proteomarekin alderatuta, metaboloma definitzea ez da erraza. Batzuetan esaten da metaboloma dela sistema biologiko batek (organismoa, organoa, ehuna, fluidoa, zelula…) sintetizatutako metabolitoen multzoa. Baina gizakion gorputzean dauden metabolitoetan, konposatu endogenoak ez ezik, jaten dugunaren edo gurekin kontaktuan dagoenaren produktuak ere badaude, hau da, metabolito exogenoak.

Metabolito endogenoak nahiz exogenoak molekula-familia oso heterogeneo bat dira, hainbat egitura, propietate fisiko-kimiko eta kontzentraziorekin. Eta heterogeneotasun hori dela eta, momentuz ezin da metaboloma osoa batera neurtu teknika bakar bat erabiliz. Horregatik, metabolomaren ahalik eta tarte zabalena hartzeko, plataforma analitiko bat baino gehiago erabili behar dira. Bereziki metabolomikaren hasieran erresonantzia magnetiko nuklearra (RMN) erabiltzen zen batez ere. Baina masa-espektrometrian (MS) oinarritutako metabolomikaren ospea areagotzen joan da denborarekin. Ebazpen handiko tresnak garatu dira, hala nola Fourieren transformatu bidezko erresonantzia ziklotronikoa (FTICR), Orbitrapa edo hegaldi-denbora (TOF), eta, gainera, detekzio mugak txikiak direnez eta analisia bizkor egiten denez, gaur egun azterketa metabolomiko gehienetan aukeratzen den teknika MSa da.

Azterketa batzuetan lagina MSan infusio zuzenez sartzen den arren (DI-MS), ohikoena da laginean aldi berean dauden milaka molekula desberdinak ionizatzeko lehiaren ondoriozko ezabaketa ionikoa eta espektroen konplexutasuna murrizten laguntzeko banaketa-teknika bat erabiltzea espektrometroan. Interesatzen zaizkigun analitoen arabera, teknika batzuk ala besteak erabiliko ditugu. Konposatu lurrunkorrak aztertzeko, MSari akoplatutako gas-kromatografia erabiltzen da (GC-MS). MSan oinarritutako metabolomikaren hasieran gehien erabiltzen zen teknika da hori, eta batez ere landareak aztertzeko erabiltzen zen, baina badu eragozpen bat: metabolito ez-lurrunkorrak analizatzeko, deribatizatu egin behar dira, eta, horretarako, tratamendu konplexu eta aspergarri bat egin behar zaio laginari. Metabolito kargatuen kasuan, elektroforesi kapilarra (CE-MS) erabili ohi da. Gaur egun, MSari akoplatutako kromatografia likidoa (LC-MS) da, zalantzarik gabe, gehien erabiltzen den teknika, eta konposatu polarrak nahiz ez-polarrak aztertzeko aukera ematen du. Ez dagoenez metaboloma osoa analizatzeko aukera ematen duen teknikarik, guztiz gomendagarria da teknika osagarriak erabiltzea.

Analisi metabolomikoetan datu asko sortzen dira, eta softwarea eta metodologia espezifikoak behar dira datu horiek guztiak tratatzeko. LC-MS sistematik hiru dimentsioko datu-set bat lortzen dugu eta sinplifikatu egin behar da harekin lan egin ahal izateko; hala, bi dimentsioko matrize bat lortu behar da, “feature” edo ezaugarri zerrenda batekin eta haien intentsitateekin. Sinplifikatu arren, ehunka laginetan milaka feature dituen matrize bat izaten jarraitzen du, eta tratamendu gehiago egin behar zaizkio (normalizazioa, eraldaketa, zentratzea, eskalatzea…), aldagai anitzeko estatistikaren bidez azter daitekeen datu-set bat lortu arte. Datuak tratatzearen helburua da aztertzen ari diren taldeen (gaixoak vs osasuntsuak, gazteak vs zaharrak, tratatuak vs ez-tratatuak…) arteko desberdintasunen zergatiak azalduko lituzketen ezaugarrien (feature) zerrenda bat lortzea, biomarkatzile gisa erabiltzeko proposatu den hipotesiari erantzuten laguntzeko.

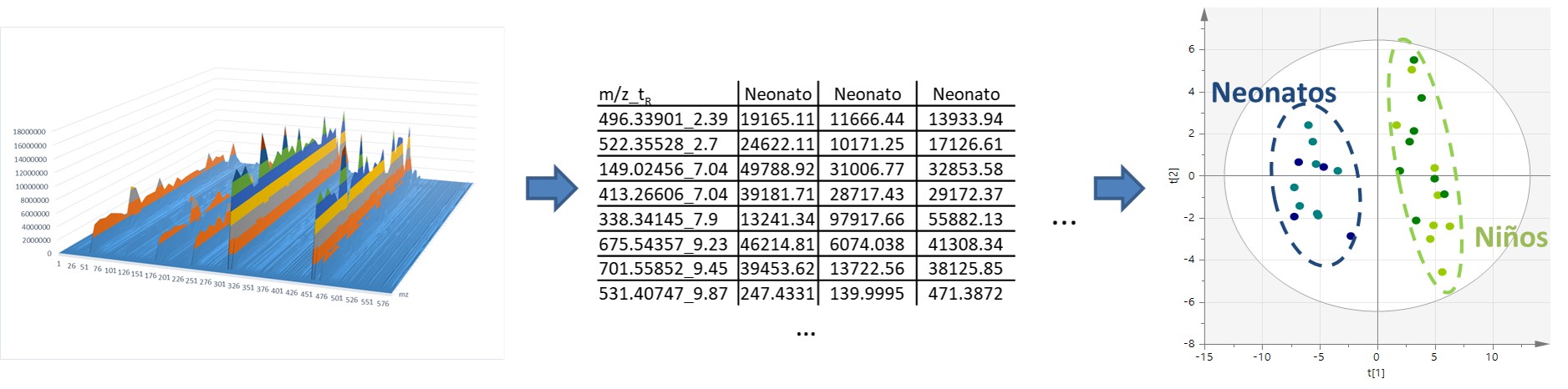
4. irudia: Datuak tratatuta, erraz interpreta daitezkeen grafikoak eta taulak lor daitezke datu konplexuetatik abiatuta. (Iturria: M.E. Blan

Emaitzen interpretazio biologikoa egin aurreko azken urratsa da aukeratutako feature edo ezaugarriak identifikatzea, LC-MS tresnak ematen digun informazioa erabilita (edukitze-denbora, masa zehatza, zatiketa-espektroa), biomarkatzaile gisa aukeratu diren metabolitoen izenak bilatzeko. Metabolito asko eta aniztasun kimiko handikoak daudenez, oraindik ere identifikazioa da LC-MSan oinarritutako metabolomikaren itogunea. Gizakion gorputzean oraindik identifikatu ez diren metabolito asko daude, zientzialarien komunitateak ahalegin handiak egiten dituen arren. Baina datu-baseetan (METLIN, Lipid Bank, KEGG, Lipid Maps edo HMDB, besteak beste) gero eta metabolito gehiago daude erregistratuta. Batzuetan, metabolito horiek identifikatze hutsarekin jada erantzuten zaio egindako galdera biologikoari, baina gehienetan ikerketa-bide berriak zabaltzen dira, arazoa konpontzeko. Adibidez, gaixo dauden gizabanakoetan ibilbide metaboliko berean kontzentrazio-aldaketak detektatzen baditugu zenbait konposatutan gizabanako osasuntsuen kontrolekin alderatuta, jakin dezakegu ibilbide hori hondatuta dagoela, eta, hortaz, zuzenago azter daiteke.

Metabolomika grafenotik eratorritako materialen toxikotasuna aztertzeko erabiltzen da, esate baterako. Grafenoa gaur egungo aurkikuntza handietako bat da: karbono-atomoen bi dimentsioko sare bat da (atomo baten lodierakoa), eta etorkizun handiko propietateak ditu besteak beste gogortasunari, malgutasunari edo eroankortasunari dagokienez. Horregatik, oso erakargarria da hainbat aplikaziotarako. Adibidez, biosentsore gisa edo sendagaien eroale gisa erabil ote daitekeen aztertzen ari da. Baina ia ezagutzen ez den konposatu bat denez, ez dakigu zer eragin izan dezakeen zelulekin kontaktuan jartzen denean. Eta kasu horretan oso erabilgarriak dira teknologia omikoak, haien bidez desberdintasunak bilatu baitaitezke konposatu horien eraginpean egon diren zelulen eta kontrol-zelulen artean, sisteman eragindako aldaketak modu ez-gidatuan aztertuta, aurretiko hipotesirik gabe.

5. irudia: Grafeno geruza bat osatzen duten karbono-atomoen egitura hexagonala. (Iturria: Wikimedia Commons)

Azterketa metabolomikoak konplexuak dira eta lan eta ahalegin handia egin behar da haiek gauzatzeko, baina oso erabilgarriak dira dagoen arazoa ia ezagutzen ez den kasuetan eta aurretiko informaziorik ez dagoenean analisi gidatu bat egin ahal izateko. Esan dugun moduan, gizakion gorputzean milaka metabolito daude, eta ia ezinezkoa izan daiteke haiek gidatuta aztertzea biomarkatzaile zehatz bat aurkitzeko helburuarekin; lastategi batean orratz bat aurkitzea bezain zaila izango litzateke, baina jakin gabe bilatzen ari garena orratz bat dela.

—————————————————–

Egileari buruz: María Encarnación Blanco UPV/EHU Zientzia eta Teknologia Fakultatean doktorea da eta gaur egun ikertzaile-lanetan dihardu Istituto Italiano di Tecnologia ikergunean. Grafenoaren konposatuek burmuinean izan dezaketen toxikotasuna aztertzeko metabolomika nola erabil daitekeen aztertzen ari da, Europako EU Graphene Flagship Project Horizon 2020 Research and Innovation Programme (Grant agreement no. 785219) egitasmoaren barruan.

—————————————————–

Masa-espektrometriari buruzko artikulu-sorta

1. Masa-espektrometria (I). Neoi isotopoetatik elefante hegalariengana
2. A new hero is born: Masa-espektrometria justiziaren zerbitzura
3. Nor dago icebergaren alden ezkutuan?
4. Konposatu galduaren bila
5. Metabolomika: osotasuna, zatien baturaren aurrean

The post Metabolomika: osotasuna, zatien baturaren aurrean appeared first on Zientzia Kaiera.

En mi anterior entrada de la sección Matemoción del Cuaderno de Cultura Científica estuvimos hablando de personas que han sido famosas en diferentes ámbitos de la sociedad y la cultura, en concreto, nos centramos en el mundo de la literatura y el cine, pero que se graduaron en matemáticas, e incluso realizaron un doctorado, Personas famosas que estudiaron matemáticas: literatura y cine. En esta entrada vamos a continuar mostrando ejemplos de otros dos ámbitos de la sociedad muy alejados el uno del otro, y a priori también del mundo de las matemáticas, como son la música y el deporte.

Efectivamente, dentro de la música también nos encontramos personas que sorprendentemente están relacionadas con las matemáticas. Uno de los más conocidos es el músico estadounidense Art Garfunkel, del famoso dúo musical Simon and Garfunkel, que fueron muy populares en la década de 1960. Algunas de sus canciones más conocidas son The sound of silence (el sonido del silencio), Mrs Robinson (Señora Robinson) o Bridge over troubled water (Puente sobre aguas turbulentas). Simon y Garfunkel empezaron a cantar juntos en 1955, bajo el nombre de Tom y Jerry (como los dibujos animados), pero fue en 1963 cuando inician el dúo Simon and Garfunkel, con el que estuvieron en activo hasta su separación en 1970, aunque se volverían a reunir para conciertos puntuales en varias ocasiones.

Fotografía de Simon and Garfunkel en un concierto en Rotterdam (Holanda) en 1982, realizada por Rob Bogaerts, de la Agencia de Fotografía ANEFO. Imagen de Wikimedia Commons

Arthur (Art) Garfunkel (Nueva York, 1941) estudió en la Universidad de Columbia. Se graduó en Historia del Arte y obtuvo el master en Matemáticas, en 1967. Empezó a realizar su tesis doctoral sobre enseñanza de las matemáticas, pero la música le desvió de ese camino. Tras la ruptura del dúo, en 1970, Garfunkel además de intentar iniciar su carrera en solitario en la música, estuvo dando clase de geometría en un instituto de secundaria en Connecticut durante dos años. Fue una pequeña laguna docente en su larga vida profesional, en la que compaginaría su trabajo como cantante, actor y poeta. En algunas entrevistas habla de ese corto período como docente de geometría, como un momento “extraño”, ya que había alcanzado un enorme éxito en el mundo de la música, con Simon and Garfunkel, y ahora enseñaba matemáticas en un instituto. Por ejemplo, comenta “Yo intentaba explicarles un problema de matemáticas y cuando les decía si tenían alguna pregunta, ellos me preguntaban cómo eran los Beatles”.

Pero vayamos a un cantante más actual, el músico inglés Jon Buckland¸ guitarrista y fundador del grupo Coldplay, conocido por álbumes como Parachutes (2000), A Rush of Blood to the Head (2002), X&Y (2005) o Viva la Vida or Death and all his Friends (2008).

Jon Buckland (Londres, 1977) estudió astronomía y matemáticas en el University College de Londres, allí conoció al otro miembro de la banda Chris Martin, quien estudiaba Cultura Antigua, se hicieron amigos y juntos montarían la banda Coldplay. Algunos títulos de la banda hacen referencia a las matemáticas, como Twisted Logic, Square One, Proof, Major Minus y 42.

Jonny Buckland, en el concerto de Coldplay en el Fuji Rock Festival (2011), en Niigata (Japan). Fotografía de Christopher Johnson, en Wikimedia Commons, originalmente en Flickr

Otro de los músicos muy conocidos relacionados con las matemáticas, aunque más con la astrofísica, es el músico británico Brian May, guitarrista y compositor de la banda de rock QUEEN. Algunas de las grandes canciones de esta mítica banda están firmadas por Brian May, como “Now I’m Here”, “We Will Rock You”, “Fat Bottomed Girls”, “Save Me”, “Flash”, “Hammer to Fall”, “Who Wants to Live Forever”, “I Want It All”, “The Show Must Go On”, “Headlong”, “Too Much Love Will Kill You” o “No-One but You (Only the Good Die Young)”.

Brian May, junto a Freddy Mercury y John Deacon, en el concierto de New Heaven de noviembre de 1977. Fotografía de Carl Lender, en Wikimedia Commons, originalmente en Flickr

Brian H. May (Londres, 1947) estudió matemáticas y física en el Imperial College de Londres, graduándose en física en 1968. Empezó su tesis doctoral en astrofísica en 1971 (realizó sus primeras observaciones del espacio, para su tesis, en el observatorio del Teide en Tenerife), pero la música se cruzó en su camino y abandonó su carrera científica. Aunque no de forma definitiva, ya que la retomaría treinta años más tarde, terminando su tesis doctoral en 2007.

Participó en varias ocasiones en el programa de televisión The Sky at Night, presentado por Sir Patrick Moore, con quien ha publicado un libro de astronomía en 2012, Bang! The complete history of the Universe.

Seguimos añadiendo personajes dentro del mundo de la música. El compositor minimalista estadounidense Philip Glass, quien ha compuesto más de 20 óperas, entre ellas La Bella y la Bestia (1994), Einstein on the Beach (1976), en la cual los números son muy importantes, solo se cantan en ella números y nombres de notas musicales, o sus óperas Galileo Galilei (2002) y Kepler (2009), un montón de bandas sonoras de películas, entre ellas Kundun (1997), de Martin Scorsese, El show de Truman (1998), de Peter Weir, Las horas (2002), de Stephen Daldry o El ilusionista (2006), de Neil Burger, así como muchos otros álbumes, por ejemplo, de composiciones para piano, entre otras. Su música se enmarca dentro del estilo de música New Age.

Philip Glass, en cuatro momentos, durante un concierto en Aarhus (Dinamarca), en 2017. Fotografía de Hreinn Gudlaugsson, en Wikimedia Commons

Con 15 años, Philip Glass (Baltimore, Maryland, 1937) empezó a estudiar matemáticas y filosofía en la Universidad de Chicago, y se graduó a los 19 años. En una entrevista sobre la ópera Einstein on the Beach a Philip Glass, quien compuso la música y el texto, y a Robert Wilson, director y productor de la ópera, este contó que cuando se conocieron le preguntó a Philip Glass como componía y este le puso un ejemplo de una fórmula matemática. Y es que las matemáticas son importantes en la obra de Philip Glass, puesto que suele utilizar estructuras matemáticas para componer algunas de ellas.

La cantante estadounidense Barbara Hendricks, soprano lírica y también cantante de jazz, que en los últimos 20 años es también conocida por su activismo por los derechos humanos, se graduó en matemáticas y en química en la Universidad de Nebraska-Lincoln. Cuando en 2009 estuvo en Bilbao, en una entrevista afirmó lo siguiente:

“Las matemáticas sirven para todo en la vida, ya que te enseñan a razonar, a resolver problemas. Pero sobre todo me han dado disciplina para mí misma, una disciplina que no es para nada opresiva, sino que me facilita ser libre”.

Fotografía, realizada por Anders Henrikson, de Barbara Hendricks en un concierto en Estocolmo (Suecia), en 2014. Imagen de Wikimedia Commons

Una opinión diferente de las matemáticas tiene la cantante británica ESKA. Nacida en Londres (1971), pero cuya familia procedía de Zimbabue, Eska Mtungwazi estudió el grado de matemáticas en la prestigiosa London School of Economics. En esa época ya empezó a adentrarse en el mundo de la música, pero la presión por tener una carreara más convencional la llevó a empezar un master en matemáticas y estadística, después en enseñanza de las matemáticas, antes de empezar a trabajar como maestra de educación primaria.

Ella les da poca importancia a sus estudios de matemáticas. En una entrevista en la Revista Yorokobu afirma:

“La educación superior no tiene por qué ser ilustradora, esa educación sirve si ayuda a la persona a seguir interesada en aprender. Yo estoy agradecida a mis padres por haberme facilitado esa educación superior, eso lo llevo conmigo, pero, claro, ¿hasta qué punto tiene esto que ver con lo que estoy haciendo ahora?”.

Portada del álbum ESKA (2015), de la cantante británica ESKA

El compositor y letrista estadounidense Stephen Sondheim, conocido y premiado, en particular, por sus contribuciones al género del musical, aunque no posee un título en matemáticas, si está muy relacionado con esta ciencia. Stephen Sondheim ha recibido un Oscar de la Academia (por la canción Sooner or Later de la película Dick Tracy, interpretada por Madonna), 8 premios Tony de teatro (por musicales como A Funny Thing Happened on the Way to the Forum, Companies, Follies, A Little Night Music o Sweeney Todd, y uno a toda su carrera), 8 premios Grammy de la academia de la música, un Pulitzer (por el drama Sunday in the Park with George), y muchos premios más.

Fotografía de Stephen Sondheim de alrededor de 1970 y cartel de la obra musical Sweeney Todd, el barbero diabólico de la calle Fleet, de la producción del National Youth Music Theatre, en el Teatro Rose de Kingston, Nueva York, en 2011. Imágenes de Wikimedia Commons

Las matemáticas, así como los problemas y juegos de ingenio, fueron su primera pasión en su juventud, antes que la música, aunque ya tocaba el piano desde niño, y la literatura.

Stephen Sondheim empezó a estudiar el grado de matemáticas en el Williams College, de Williamson, Massachusetts, pero pronto empezó a interesarse solo por la música a raíz de un curso de música del primer cuatrimestre en el que se había matriculado y abandonó las matemáticas. En una entrevista sobre esos años afirma “Yo era matemático por naturaleza, y aún lo soy, pero sabía que no quería ser matemático”. Aunque en otra entrevista afirma en relación a las matemáticas, quizás por esa parte natural matemática que llevaba dentro, “me habría encantado trabajar en el teorema de Fermat”.

Y existen muchos más ejemplos, como el trompetista estadounidense de los años 1950, Clifford Brown, quien se graduó en matemáticas en el Delaware State College y en música en el Maryland State College; el músico canadiense Dan Snaith, cuyos nombres artísticos son Caribou, Manitoba o Daphni, realizó su tesis doctoral (cuyo título era Overconvergent Siegel Modular Symbols) sobre temas de álgebra, bajo la dirección del matemático Kevin Buzzard, en el Imperial College de Londres; el guitarra y vocalista del grupo de punk californiano Angry Samoans, Greg Turner, se graduó en matemáticas Claremont Graduate University e imparte clases de matemáticas en la New Mexico Highlands University; o el cantante y compositor, Phil Alvin, de la banda de rock and roll formada en 1978 en California, The Blasters, obtuvo su grado de master en matemáticas e inteligencia artificial en la California State University, en Long Beach, y después realizó su tesis doctoral en UCLA, donde también impartió clases de matemáticas. Incluso, hubo quien empezó, pero se quedó en el camino, como la cantante Carole King, que realizó solo un año de matemáticas.

La cantante Carole King interpretando la canción “(You Make Me Feel Like) A Natural Woman” en el Madison Square Garden de Nueva York. Fotografía de Jonathan Schilling, en Wikimedia Commons

Para terminar con la música me gustaría añadir a la pionera de la música electrónica Delia Derbyshire. La música y compositora británica Ann Delia Derbyshire (1937-2001) obtuvo una beca para estudiar matemáticas en el Girton College de la Universidad de Cambridge, y finalmente se graduaría en matemáticas y música. Y salvo tres meses dando clases de matemáticas y música para el cónsul general británico en Ginebra, no volvería a tener relación con el mundo académico matemático.

Sin embargo, su relación con las matemáticas no termina ahí, ya que estas eran fundamentales para la composición de sus obras, como ella misma afirmaba en una de las pocas entrevistas que concedió. Por ejemplo, utilizó la sucesión de Fibonacci 1, 1, 2, 3, 5, 8, 13, 21, 34, … para la creación de sus composiciones (para información sobre esta sucesión pueden leerse las entradas Póngame media docena de fibonaccis o El origen poético de la sucesión de Fibonacci, entre otras).

La música y compositora Delia Derbyshire. Imagen de la página web Mujeres y música

También nos encontramos en este grupo de personas relacionadas con las matemáticas a algunos deportistas.

Empecemos con un ejemplo curioso, ya que fue una persona conocida tanto dentro del fútbol, como de las matemáticas, es el danés Harald Bohr (1887-1951), hermano del premio Nobel de Física, Niels Bohr.

Harald Bohr estudió matemáticas en la Universidad de Copenhague, donde se licenció en 1909 y obtuvo su doctorado un año más tarde. Su área de trabajo fue el Análisis Matemático. Empezó estudiando, para su tesis doctoral, la conocida serie de Dirichlet, luego en colaboración con el matemático alemán Edmund Landau obtuvo el conocido como teorema de Bohr-Landau y fundó, junto con el matemático inglés G. H. Hardy, el campo de las funciones casi periódicas. Entre 1915 y 1930 fue profesor en Universidad Tecnológica de Dinamarca y después catedrático en la Universidad de Copenhague, durante 21 años, hasta su muerte.

Fotografía de la asistencia al International Congress of Mathematicians de Zurich en 1932, entre la que se encuentra Harald Bohr (rodeado en azul). Imagen de Wikimedia Commons

Pero resulta que además de un buen matemático, fue un buen jugador de fútbol. En 1903, con dieciséis años, debutó en el club Akademisk Boldklub, del norte de Copenhague. En 1908 fue seleccionado para jugar con la selección danesa de fútbol en los Juegos Olímpicos de Londres, donde obtuvieron la medalla de plata. Volvería a jugar con la selección danesa en 1910 contra Inglaterra. Se convirtió en una celebridad como jugador de fútbol, hasta el punto de que cuando defendió su tesis doctoral dentro del público asistente a la misma había más fans de fútbol que personas del ámbito de las matemáticas.

Fotografía del equipo danés de fútbol que compitió en los Juegos Olímpicos de Londres en 1908. El matemático Harald Bohr es el segundo, empezando por la izquierda, de la fila superior. Imagen de Wikimedia Commons

El jugador inglés de fútbol Glen Johnson (Greenwich, Londres, 1984), quien jugó, entre los años 2002 y 2019, en seis clubs ingleses distintos, entre ellos el Chelsea y el Liverpool, y fue internacional en 54 partidos, entre ellos, los mundiales de Sudáfrica (2010) y Brasil (2014), empezó en 2012, en paralelo a su carrera en el fútbol, a estudiar el grado de matemáticas en la Open University, la universidad a distancia.

Fotografía del jugador inglés Glen Johnson en 2011, cuando jugaba con el Liverpool. Imagen de Badudoy en Wikimedia Commons

El exfutbolista camerunés, nacionalizado francés, Jean-Alain Boumsong (Douala, Camerún, 1979), que jugó en diferentes clubes europeos, como el francés Le Havre, el Glasgow Rangers escocés, el Newcastle United inglés, la Juventus de Turín, el Olympique de Lyon, y el Panathinaikos, así como en la selección francesa, se graduó en matemáticas por la Universidad de Le Havre.

Casi podríamos decir que también se graduó en matemáticas el mítico jugador de baloncesto de la NBA Michael Jordan (Nueva York, 1963), jugador de los Chicago Bulls, quizás el mejor jugador de baloncesto de la NBA de la historia, ya que empezó el grado de matemáticas, pero lo abandonó en su penúltimo año. Aunque sí terminó sus estudios de matemáticas el también jugador de baloncesto de la NBA David Robinson, apodado “el almirante”, que jugó durante 14 temporadas en los San Antonio Spurs. Al terminar del instituto, David Robinson ingresó en la Academia Naval de Estados Unidos, donde se graduó en matemáticas.

Fotografía de uno de los míticos mates del jugador de Baloncesto de la NBA, de los Chicago Bulls, Michael Jordan

Un jugador de baloncesto español que también es matemático es el alicantino Sergio Olmos (Elda, 1986). En un curso de verano Xpheres College, para profesionales del Baloncesto, Sergio Olmos se presentaba como “el matemático más alto del mundo” y es que este jugador de baloncesto, de 2,13 metros de altura, se graduó en matemáticas en la Universidad de Temple en Philadelphia, a donde se marchó con 17 años para continuar su carrera dentro del baloncesto. Después de los cuatro años jugando a baloncesto en la Universidad de Temple, y estudiando matemáticas, continuó su carrera de baloncesto en España, jugando en diferentes clubs, como el Valencia Basket, el Club Basquet Coruña o la Fundación Club Baloncesto Granada, en el que juega en la actualidad. Sin embargo, no abandonaría su carrera académica. Interesado por la estadística se graduó en Ciencias Económicas y Matemáticas en la británica Open University y realizó Máster de Bioestadística y Bioinformática de la Universitat de Barcelona. La empresa de bioestadística y estadística aplicada Biostatech, le incluye en su página web como uno de sus colaboradores. Y recientemente ha empezado a escribir un blog sobre matemáticas llamado Mínimos cuadrados.

El jugador de Baloncesto Sergio Olmos, hacia el año 2016, jugando en el Club Basquet Coruña

El jugador de fútbol americano John Urschel que jugó en la NFL en los Baltimore Ravens, durante tres temporadas hasta que se retiró en 2017. Por otra parte, se graduó en matemáticas en la Universidad Estatal de Pensilvania (Penn State University) en 2012, y obtuvo el grado de master en 2013. En 2014 entró como profesor adjunto en esa misma universidad, donde continúa trabajando y en 2016 empezó a realizar su tesis doctoral en el MIT (Instituto Tecnológico de Massachusetts), sobre teoría de grafos espectral, álgebra lineal numérica y machine learning (aprendizaje automático).

Su primer artículo fue “Inestabilidades en el problema de los tres cuerpos de Sol-Jupiter-Asteroide” publicado en 2013 en la revista Celestial Mechanics and Dynamical Astronomy. Ha día de hoy, ya tiene 11 artículos publicados en revistas de investigación. Tiene número de Erdös 4. Recordemos que el número de Erdös es la distancia, en co-autoría de artículos de investigación matemática entre una persona que investiga en esta ciencia y el matemático húngaro Paul Erdös (1913-1996), así él mismo tiene número de Erdös 0, alguien que ha publicado un artículo con Erdös tiene número de Erdös 1, quien ha publicado con una persona con número de Erdös 1, tiene número de Erdös 2, y así se continúa (para más información El número de Erdös-Bacon-Sabbath).

Fotografías de John Urschel, una como jugador de futbol americano en los Baltimore Ravens en 2015 (fotografía de Jeffrey Beall en Wikimedia Commons) y la otra frente a una pizarra en la Tufts University en 2018 (fotografía del propio John Urschel, en Wikimedia Commons)

Aunque no es el único jugador de fútbol americano con un grado en matemáticas. Por ejemplo, el jugador de los New York Giants y los Carolina Panthers, y en la actualidad entrenador de este último equipo, Chase Blackburn (Ohio, 1983), se graduó en matemáticas en la Universidad de Akron, en Ohio. O el jugador de las décadas de 1950 y 1960, Frank Ryan (Texas, 1936), que jugó en los equipos Los Ángeles Rams, Cleveland Browns o Washington Redskins, no solo es doctor en matemáticas por la Universidad de Rice (el título de su tesis doctoral es “A Characterization of the Set of Asymptotic Values of a Function Holomorphic in the Unit Disc”), sino que continuó su carrera como profesor e investigador en matemáticas, y tiene número de Erdös igual a 3.

Terminamos con otro deporte, como es el tenis. La tenista británica Virginia Wade, que ganó el torneo abierto de EEUU en 1968, el abierto de Australia en 1972 y el torneo de Wimbledon en 1977, estudió matemáticas y física en la Universidad de Sussex.

Fotografía de Virginia Wade jugando al tenis. Imagen de la página web de la BBC

Estos no son todos los ejemplos que existen, pero es una buena muestra.

Bibliografía

1.- Entrada en la Wikipedia sobre Art Garfunkel

2.- Página web de Art Garfunkel

3.- Entrada en la Wikipedia sobre Jon Buckland

4.- Entrada en la Wikipedia sobre Brian May

5.- Página web de Philip Glass

6.- Entrada en la Wikipedia de Philip Glass

7.- Marta Macho, Barbara Hendricks y las matemáticas, Mujeres con ciencia, 2014.

8.- Página web de ESKA

9.- Entrada en la Wikipedia de Delia Derbyshire

10.- Página web de Delia Derbyshire

11.- Entrada en la Wikipedia de Harald Bohr

12.- Entrada en la Wikipedia de Glen Johnson

13.- Entrada en la Wikipedia de Jean-Alain Boumsong

14.- Entrada en la Wikipedia de Michael Jordan

15.- Entrada en la Wikipedia de John Urschel

16.- Entrada en la Wikipedia de Sergio Olmos

17.- Entrada en la Wikipedia de Virginia Wade

18.- David Richeson, Look who majored in mathematics, blog Division by zero, 2009.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica

El artículo Personas famosas que estudiaron matemáticas: música y deporte se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Personas famosas que estudiaron matemáticas: literatura y cine
2. Con ‘n’, música ‘casi’ infinita
3. Las dos culturas de las matemáticas: construir teorías o resolver problemas

Juanma Gallego Zenbait erle espeziek elikagaiak non dauden deskribatzeko darabilten “dantza” ikertu dute zientzialariek, portaera bitxi horren atzean egon daitezkeen abantailak ezagutzeko. Atera duten ondorioa espero zutenaren kontrakoa izan da: dantzarik gabe hobeto moldatu dira.

Langile bikainak izateko ospea dute erleek, baina, beste hainbatetan bezala, hau ez da guztiz egia. Hala zioen, bederen, Jürgen Tautz zoologia katedradunak 2009an GEO aldizkarirako Horst Güntheroth-ek idatzitako artikulu batean. Erle batzuk zinez langile trebe eta arduratsuak diren arren, badira ere erlauntzetik bizpahiru aldiz baino ateratzen ez direnak. Baina, orokorrean, izugarrizko ahalegina egiten dute, eta lan hori aitortu behar zaie: 50.000 erleko kolonia batean 600 kilogramo nektar eta 30 kilogramo polen jasotzen dituzte urte bakoitzeko, eta, horretarako, 7,5 milioi ateraldi egin behar dituzte. Orotara, 20 milioi kilometro egiten dituzte, Apollo 11k ilargira egin zuen bidaia halako 26, hain zuzen.

1. irudia: Guzti-guztiak langile trebeak ez badira ere, komunean izugarrizko lana egiten dute erleek. Urte bakoitzeko, 50.000 erleko kolonia batek 20 milioi kilometro egiten ditu hegan. (Argazkia: Boris Smokrovic / Unsplash)

Wurzburgoko Unibertsitateko ikertzaile da Tautz, eta ongi ezagutzen du gaia. Unibertsitate horretan erle arrunta (Apis mellifera) ikertzeko estazio bat daukate. 70 erlauntz inguru dituzte bertan, eta mota guztietako trikimailuak erabiltzen dituzte izaki ñimiño horiek ikertzeko: kristalak, kontrolpeko baldintzetan dauden inkubazio habiak, erleei atxikitako txip elektronikoak edo infragorrian zein abiadura geldoan grabatzeko gai diren kamerak, esaterako. Beti bezala, mitoak beharrean, ezagutza eskuratzen da metodo zientifikoaren bitartez.

Guzti-guztiak langile sutsuak direnekoa ez da dagoen mito bakarra. Bigarren mitoa da erle guztiek burutzen dutela “dantza” baten antza duen mugimendua janaria non dagoen gainerako kideei azaltzeko. Baina ez da hala. Halako dantzak baliatzen dituzten hamar bat erle espezie badira, baina erle gehienek ez dute dantzarik egiten (eta 500 espezie baino gehiago dira munduan). Baina, zalantzarik ez dago, dantzarena guztiz liluragarria den portaera da. Ez soilik etologoentzat: gutxieneko kuriositatea duen edozeinentzat ere.

Mainzeko (Alemania) eta Lausanako (Suitza) Unibertsitateetako ikertzaileek ere hainbat urte eman dituzte erleekin esperimentuak egiten. Proba horien bitartez saiatu dira argitzen dantzaren lengoaiak koloniaren arrakastan duen eragina. Atera dituzten ondorioak azaltzeko ikerketa artikulu bat argitaratu dute Science Advances aldizkarian.

Bereziki, ikertzaileek argitu nahi izan dute zein den dantzak erleei ematen dien abantaila ebolutiboa —horrelakorik egotekotan—. Zientzialariek azaldutakoaren arabera, dantza horietako batzuek segundo bakar batzuk iraun badezakete ere, bost minutu arteko luzera izan dezakete. Horrelako portaera bat mantentzeko, noski, arrazoi bat egon behar da.

2. irudia: 500 erle espezie inguru daude munduan, eta, horietatik, hamar espezie inguruk baino ez dute “dantza” egiten informazioa trukatzeko. Irudian, dantzan ari den erle bat. (Argazkia:Christoph Grüter)

Esperimentuetan, erlauntz barruko baldintzak aldatu dituzte, erleak nahasi aldera, eta haiengan desorientazioa eragiteko. Besteak beste, argia kendu diete eta abaraskak posizioaz aldatu dituzte, intsektuei grabitatearen bitartez orientatzeko aukera kenduta. Baina hauek ez dira izan erleak zirikatzeko erabili dituzten amarru bakarrak. Bazka bila atera diren erleei informazioa zabaltzeko dantza egitea galarazi diete, 18 egunez. Modu horretan ziurtatu nahi dute gero ez zirela oroituko janaria zegoen lekuez.

“Gure harridurarako, aurkitu dugu elikagaiak biltzerakoan erleen koloniak eraginkorragoak direla dantzaren lengoaia kendu zaienean”, azaldu du prentsa ohar batean Mainzeko Unibertsitateko ekologo Christoph Grüter-ek. Dantzaren informazioa jaso ez duten erleak aktiboagoak direla egiaztatu dute, eta ezti gehiago sortzen dutela ere. Egoera behatzeaz gain, izan den gehikuntza kuantifikatu dute: batez bestean, dantza egiten ez duten erleek zortzi minutu gehiago eman dute janari bila, eta %29 ezti gehiago ekoiztu dute.

Aurkitu duten egoera bitxi honi azalpen bat emateko, gizakiak sorraraziko habitaten aldaketak abiapuntuan egon litezkeela proposatu dute. Esku artean duten hipotesiaren arabera, “dantzaren ohitura” ez da oraindik egokitu inguru berri horietara. Iradoki dute ere dantzaren bidez informazioa jaso ezin izan duten erleek haien kabuz atera direla, janari bila.

Ez da atera duten irakaspen bakarra. Ikusi dute ere orientaziorik gabeko dantzaren aurrean, “ikusle” diren erleek interesa galtzen dutela, eta hau etologiaren ikuspuntutik zeharo harrigarria da: nolabait, intsektu horiek dantzaren bitartez jasotzen duten informazioaren kalitatea kontuan hartzeko gai izan dira, zentzurik gabekoa zela ikusi dutenean interesa galdu dutelako. “Badirudi denbora bat pasata konturatu egiten direla zerbait gaizki dagoela”, iradoki du Grüterrek. Ikertzaileek aurreratu dute hau izango dela etorkizunean sakonkiago ikertuko duten kontua: erleak benetan informazioaren kalitatea “neurtzeko” gai ote diren.

Erreferentzia bibliografikoa:

Price, R. I’Anson, Dulex, N., Vial, N., Vincent, C., Grüter. C., (2019). Honeybees forage more successfully without the “dance language” in challenging environments. Science Advances, 5 (2): eaat0450. DOI: 10.1126/sciadv.aat0450

———————————————————————————-

Egileaz: Juanma Gallego (@juanmagallego) zientzia kazetaria da.

———————————————————————————-

The post Dantza egitea galarazi diete erleei, eta ezustekoa hartu dute appeared first on Zientzia Kaiera.

Ío con Júpiter de fondo. Fuente: NASA

Dado que podemos considerar que la luz viaja en línea recta, ¿podemos decir a qué velocidad lo hace? Galileo abordó este problema en sus Discorsi e Dimostrazioni Matematiche Intorno a Due Nuove Scienze, publicado en 1638. Señaló que las experiencias cotidianas podrían llevarnos a concluir que la luz se propaga instantáneamente. Pero que estas experiencias, cuando se analizan más de cerca, solo muestran que la luz viaja mucho más rápido que el sonido. Por ejemplo, “cuando vemos disparar una pieza de artillería a gran distancia el destello llega a nuestros ojos sin que transcurra tiempo; pero el sonido llega al oído solo después de un intervalo perceptible”.

Pero, ¿cómo sabemos realmente si la luz se movió “sin que transcurra tiempo” a menos que tengamos alguna forma precisa de medir el lapso de tiempo? Galileo continúa describiendo un experimento mediante el cual dos personas que se encontrasen en colinas distantes y usando linternas podrían medir la velocidad de la luz. Concluyó que la velocidad de la luz era probablemente finita, no infinita. Galileo, sin embargo, no estima un valor definido concreto.

Las pruebas experimentales se relacionaron con éxito por primera vez con una velocidad finita para la luz por un astrónomo danés, Ole Rømer. Las observaciones detalladas de los satélites de Júpiter habían mostrado una irregularidad inexplicable en los tiempos registrados entre los eclipses sucesivos de los satélites por el planeta. Se esperaba que un eclipse del satélite Ío ocurriera exactamente 45 s después de las 5:25 de la mañana del 9 de noviembre de 1676 (calendario juliano). En septiembre de ese año, Rømer anunció a la Academia de Ciencias de París que el eclipse observado llegaría 10 minutos tarde. El 9 de noviembre, los astrónomos del Observatorio Real de París estudiaron cuidadosamente el eclipse. Aunque escépticos, informaron que el eclipse ocurrió tarde, tal como lo había previsto Rømer.

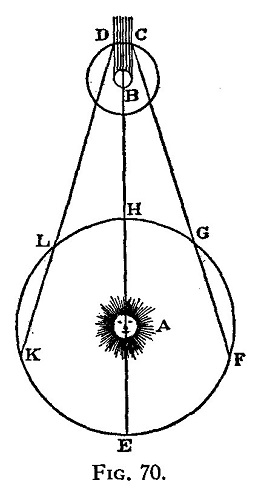Ilustración empleada por Rømer en su informe Demonstration tovchant le mouvement de la lumiere trouvé par M. Römer de l’ Academie Royale des Sciences, fechado el 7 de diciembre de 1676. A: Sol; B: Júpiter; DC: Ío

Más tarde, Rømer reveló la base teórica de su predicción a los desconcertados astrónomos en la Academia de Ciencias. Explicó que el tiempo originalmente esperado del eclipse se había calculado a partir de observaciones hechas cuando Júpiter estaba cerca de la Tierra. Pero ahora Júpiter se estaba más lejos. El retraso en el eclipse ocurrió simplemente porque la luz procedente de las inmediaciones de Júpiter, donde ocurría el eclipse, necesita un tiempo para llegar a la Tierra. Obviamente, este intervalo de tiempo debe ser mayor cuando la distancia relativa entre Júpiter y la Tierra en sus órbitas es mayor. De hecho, Rømer estimaba que la luz necesita alrededor de 22 minutos para cruzar la propia órbita de la Tierra alrededor del Sol.

Poco después, el físico holandés Christian Huygens utilizó los datos de Rømer para realizar el primer cálculo de la velocidad de la luz. Huygens combinó el valor de Rømer de 22 minutos para que la luz cruzara la órbita de la Tierra con su propia estimación del diámetro de la órbita de la Tierra. Huygens obtuvo un valor para la velocidad de la luz en el espacio que, en unidades modernas, es de aproximadamente 200.000 km/s. Esto es, aproximadamente dos tercios del valor actualmente aceptado. El error en el valor de Huygens se debió principalmente a que Rømer sobrestimó el intervalo de tiempo. Ahora sabemos que la luz solo necesita unos 16 minutos para cruzar la órbita de la Tierra.

La velocidad de la luz se ha medido de muchas maneras diferentes desde el siglo XVII. El desarrollo de dispositivos electrónicos en el siglo XX permitió mediciones muy precisas, haciendo de la velocidad de la luz una de las constantes físicas medidas con mayor precisión. Debido a la importancia del valor de la velocidad de la luz en las teorías físicas modernas*, en la actualidad su valor no se mide, sino que está definido a consecuencia de la definición de metro y es, exactamente, de 299,792,458 metros por segundo. La velocidad de la luz suele estar representada por el símbolo c.

Nota:

* Sobre esto puedes leer La velocidad de las ondas electromagnéticas y la naturaleza de la luz de la serie Electromagnetismo y El principio de constancia de la velocidad de la luz de la serie Teoría de la invariancia

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

El artículo La velocidad finita de la luz se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. El principio de constancia de la velocidad de la luz
2. La velocidad de las ondas electromagnéticas y la naturaleza de la luz
3. La relatividad del tiempo (y 3)

Josu Lopez-Gazpio Ipurtargiak koleoptero bitxiak eta liluragarriak dira. Gauean argi berdexka egiteko gai dira -gaitasun xelebrea, hasiera batean-, baina, helburu eta funtzio biologikoa duena. Orain dakigunez, gorteatzeko tresna izateaz gain harrapakarietatik babesteko tresna ere bada. Alabaina, nola liteke argia eginez harrapakariek ez ikustea? Bada, aurkakoa da ideia: ikusgarriago egiten dira haiek jatea kaltegarria eta toxikoa izan daitekeela ohartarazteko. Biolumineszentzia horren atzean luziferina izeneko molekula dago eta, hari esker lortzen dute sasien arteko gau ilunak puntutxo berdez betetzea.

1. irudia: Ipurtargiak gauean. Holandan hartutako argazkia dunen ingurunean, behe-laino eta haizerik gabeko gau sargori batean. (Argazkia: Herky – domeinu publikoko irudia. Iturria: commons.wikimedia.org

Lanpirido edo ipurtargiak kakalardo motak dira eta 2.000 espezie desberdin baino gehiago daude gure planetan. Espezie gehienek bi hegal txiki dituzte eta guztiek dute biolumineszenteak izateko gaitasuna, alegia, erreakzio kimiko baten bidez argia igortzeko gaitasuna. Ipurtargiak ez dira, jakina, luminiszenteak diren intsektu bakarrak. Hedabide honetan bertan kontatu den moduan ere, badira argi propioa duten beste zenbait espezie, onddoak kasu. Oinarrian, ipurtargiek organo luminiko izenekoak dituzte sabel azpian eta haiei esker gai dira luminiszentzia sortzen duten erreakzio kimikoak egiteko. Zein da, baina, horren helburua?

Frogatu berri denez, argiak ez dauka helburu sexuala bakarrik. Brian C. Leavell eta bere lankideek argitaratuko ikerketaren emaitzen arabera, saguzarretatik babesteko tresna ere izan daiteke. Argi distiraren bidez, harrapakariak diren saguzarrek abisua jasotzen dute: ipurtargiak ez dira elikagai atsegina -saguzarrentzat toxikoak diren substantziak dituzte eta botaka egiten dute ipurtargiak janez gero-. Hortaz, biolumineszentziak abantaila ebolutiboa da bai saguzar eta bai ipurtargientzat. Biolumineszentziaren erabilera hori frogatzeko, ikertzaileek espezieen arteko borroka gertatzeko lekua diseinatu zuten. Bertan saguzarrak, ipurtargiak, sitsak, kakalardoak eta bestelako intsektuak jarri zituzten. Ikertzaileek ikusi zutenaren arabera, ipurtargiek argiaren bidez saguzarrei ohartarazten zieten toxikoak zirela. Era berean, saguzarrek ipurtargien hegazkada kopuruarekin lotzen zuten seinale hori eta, horrela, ipurtargiak ez jaten ikasten zuten. Denborarekin, saguzarrek beste intsektuak jaten zituzten eta ez ipurtargiak.

Biolumineszentziaren oinarria

Luminiszentzia sortzen duen erreakzioak oxigenoa behar du. Horretaz gainera, beste hiru osagai ere beharrezkoak dira: luziferina molekula, luziferasa entzima eta ATPa -adenosina trifosfatoa, alegia, energia ekarpena-. Oxigenoak luziferina oxidatzen du eta luziferasak prozesuari laguntzen dio. Guzti hori gerta dadin, energia behar da eta energia hori ATP molekuletatik dator -zelulen metabolismoan ohikoa den bezala-. Luziferina oxidatzen denean argia igortzen da eta hori da, hain zuzen ere, ikusten duguna.

3. irudia: Luziferina molekula da ipurtargien bioluminiszentziaren erantzule nagusia. (Argazkia: Yikrazuul – domeinu publikoko irudia. Iturria: commons.wikimedia.org)

Erreakzioa pausoka aztertuta, lehenik eta behin luziferina adenosina trifosfatoarekin elkartzen da luziferina adenilatoa eta pirofosfatoa emanez. Hori luziferasa entziman gertatzen da; erreakzio hori gauzatzeko espezifikoa dena. Jarraian, luziferina adenilatoa oxigenoarekin elkartzen da eta adenosina monofosfatoa eta oxiluziferina -luziferina oxidatua- sortzen dira. Erreakzioaren bigarren zati horretan argia ekoizten da, 510-670 nanometroko uhin luzera duena. Horren ondorioz, kolore hori-berdexka ikusten da. Esan bezala, biolumineszentzia organismo askoren ezaugarria da, ez bakarrik intsektuena. Hain zuzen ere, sakonera handiko uretan bizi diren izakien ezaugarria ere bada. Aipatzekoa da, esaterako bonbilletan gertatzen ez den bezala, biolumineszentzia erreakzioetatik sortutako argiak ez duela beroa ekoizten, alegia, argi hotza da. Modu horretan, intsektuek ez dute alferrikako energia xahutzen luminiszentzia sortzean.

Edozein kasutan, erreakzio kimiko konplexuak daude koleoptero berezi horien argiaren atzean eta argiak zentzua ere badu. Babesteko, gorteatzeko eta identifikatzeko modua da; izan ere, bestela zertarako xahutuko dute lortzea hainbeste kosta den energia argia ekoizten? Bada, honatx galdera horren erantzunari emandako argia.

Erreferentzia bibliografikoa:

Leavell, Brian C., Rubin, Juliette R., McClure, Christopher J.W., Miner, Krystie A., Branham, Marc A., Barber, Jesse R. (2018). Fireflies thwart bat attack with multisensory warnings. Science Advances, 22 (4). DOI: 10.1126/sciadv.aat6601

Informazio osagarria:

• How and why do fireflies light up? Scientificamerican.com

—————————————————–
Egileaz: Josu Lopez-Gazpio (@Josu_lg) Kimikan doktorea, irakaslea eta zientzia dibulgatzailea da. Tolosaldeko Atarian Zientziaren Talaia atalean idazten du eta UEUko Kimika sailburua da.
—————————————————–

The post Ipurtargien argia argitzen appeared first on Zientzia Kaiera.

Escultura metálica de “Bluebelle”, una ballena azul capturada en el Atlántico sur en 1912, expuesta en la ribera del Sena durante la Cumbre del Clima de París en 2015. Fuente: Bluebird Marine Systems

Como miembro de una especie que habitualmente se cree el centro del universo, considero personalmente muy importante recibir de vez en cuando una bofetada de humildad ecológica. Una cosa que nunca falla, son las ballenas. Pensar en esos enormes mamíferos viviendo (o, bueno, sobreviviendo) en la inmensidad del océano siempre me recuerda lo insignificante que soy.

Y sin embargo, no tenía ni idea hasta hace poco de cómo las ballenas se hicieron tan grandes, ni por qué. Ni siquiera me lo había preguntado hasta que me topé con la respuesta. Por eso yo soy periodista científica, y no científica, supongo. No me hago las preguntas, pero me encanta contar las respuestas. Aquí voy con esta respuesta, por si ustedes tampoco la conocen.

¿Cuándo se hicieron enormes las ballenas?

No tenemos del todo claro cómo las ballenas se hicieron tan enormes, si les tengo que ser sincera, aunque es un debate abierto desde hace tiempo. En 2010, Graham Slater, biólogo evolucionista de la Universidad de Chicago, propuso una hipótesis según la cual los cetáceos (ballenas y delfines) se dividieron en grupos de distintos tamaños muy pronto en su evolución, hace aproximadamente 30 millones de años. En ese momento, los delfines quedaron como los más pequeños de la familia, las ballenas barbudas se convirtieron en gigantes y los zifios evolucionaron a un tamaño intermedio. Los tres grupos y sus descendientes se han mantenido más o menos estables en esos rangos de tiempo.

No todo el mundo está de acuerdo con esta teoría. Nicholas Pyenson, del Museo de Historia Natural perteneciente al Smithsonian, en Washington, decidió utilizar la enorme colección de fósiles del museo para aclarar las dudas. Tras determinar que el tamaño total de una ballena se puede inferir del tamaño de los huesos de su mandíbula, midió o obtuvo ese dato de los cráneos de 63 especies de ballena ya extinta, además de 13 especies actuales, y las fue colocando en una línea temporal que mostrase la evolución del árbol familiar de las ballenas.

Los datos obtenidos demostraban que las ballenas no aumentaron de tamaño tan pronto como Slater había sugerido en un principio, y también que no fue algo progresivo en el tiempo, sino que se habían vuelto moderadamente grandes y se habían mantenido así durante millones de años hasta hace unos 4,5 millones de años, según un estudio que publicaron después conjuntamente Pyenson, Slater y Jeremy Goldberg, de la Universidad de Stanford en Palo Alto.

En ese momento pasaron de relativamente grandes a gigantescas. La ballena azul que conocemos a día de hoy mide hasta 30 metros de largo, mientras que hace 4,5 millones de años las ballenas más grandes que existían medían solamente 10 metros.

¿Cómo fue posible?

Vale, ya sabemos cuándo. ¿Cómo pasó esto? Slater y compañía pasaron entonces a estudiar qué estaba ocurriendo en el mundo en aquel momento para que tuviese lugar este importante cambio de tamaño en las ballenas. Descubrieron que el estirón coincidió con el principio de la primera edad de hielo. En ese momento en que los glaciares se expandían, los deshielos de primavera y verano vertían enormes cantidades de nutrientes a las costas oceánicas que causaron una proliferación masiva del krill, los organismos microscópicos de los que se alimentan las ballenas.

Esto creó un nuevo patrón de alimentación: los deshielos estacionales creaban épocas de comida abundante separadas a lo largo del año, disponible para aquellos que pudiesen aprovecharla y con menos competencia debido a la desaparición de muchos otros peces y animales marinos.

Esto fue una ventaja para las ballenas: las ballenas que se alimentan cazando krill y filtrando el agua a través de sus barbas podían en este ambiente alimentarse de forma más eficiente que otros competidores. Y cuando mejor alimentadas, más grandes y rápidas eran para desplazarse de una zona de caza a otra.

¿Por qué ese tamaño gigantesco?

Quizá ahora sepamos un poco mejor, aunque todavía no de forma definitiva, cuándo y cómo las ballenas se hicieron descomunales, pero ¿por qué?

Tampoco aquí la respuesta está del todo clara. Algunos expertos postulan que pudo ser una respuesta evolutiva a los ataques de los megatiburones que poblaron los océanos hace millones de años. Pero la mayoría de las hipótesis se centran en el agua como un medio liberador: con la gravedad atenuada, los cuerpos de los mamíferos marinos, especialmente los de las ballenas, son capaces de manejar muchas más toneladas de peso. Además, es más fácil acceder a grandes territorios donde alimentarse y el menú es más variado.

Sin embargo, esta idea del océano como liberación también tiene sus detractores, y en 2018, William Gearty, de la Universidad de Stanford, propuso una explicación diferente: las ballenas y otros mamíferos marinos son tan grandes no por el alivio que el agua pone a sus limitaciones, sino porque impone otras nuevas.

A medida que entras en el agua, empiezas a perder un calor corporal que no estabas perdiendo sobre la tierra, y la forma más eficiente contrarrestar esa pérdida de temperatura es volverse más grande: a medida que crece cuerpo de un animal (de estos animales marinos concretamente cuyo cuerpo tiende a adoptar la forma de un globo), el volumen aumenta más rápido que su superficie, de forma que se genera más calor, pero se pierde menos en comparación. Claro que el volumen de un animal no puede aumentar infinitamente, ya que un cuerpo mayor también requiere más alimento, y hay un límite en la comida que un animal puede encontrar, atrapar y comer.

Según esta teoría, el tamaño de una especie se encuentra limitada por abajo por su necesidad de mantenerse caliente (demasiado pequeño y perderá demasiado calor) y por arriba por su necesidad de alimentarse (demasiado grande y no podrá comer lo suficiente). Y ese límite es mucho más estrecho en el mar que en la tierra, según el científico, que calculó que los mamíferos marinos (focas, cetáceos, manatíes…) han alcanzado de forma independiente una masa media óptima de unas 5 toneladas.

Las ballenas y las focas, en los extremos

Espera, ¿qué? ¿5 toneladas? Pero eso está muy, muy lejos de las 140 toneladas que puede pesar una ballena azul adulta, el animal más grande del mundo y con el que hemos abierto esta historia.

Sí, bueno, recordemos que se trata de una media. En el otro extremo estarían las focas, que pueden pesar, dependiendo de la especie, entre 100 y 250 kilos aproximadamente en su edad adulta. Diferencias evolutivas y de características podrían explicar como ambas especies han conseguido saltarse esos límites que propone Gearty, cada una por un lado. Las focas tienen una gruesa piel y pelo, y pasan mucho tiempo fuera del agua. Así podrían hacer frente a una pérdida de calor que en principio su pequeño tamaño facilita.

Y las ballenas azules y otras barbadas son los cazadores más eficaces del mundo y, si la explicación de Slater y sus colegas es cierta, supieron aprovechar una oportunidad que pocas especies coetáneas pudieron ver en un momento de rápidos cambios climáticos. Así han podido evolucionar y mantener esos cuerpos masivos allí donde los demás mamíferos marinos han conseguido ser grandes, pero no tanto. Gigantes de verdad, solo ellas.

Referencias:

Diversity versus disparity and the radiation of modern cetaceans – The Royal Society Publishing

Independent evolution of baleen whale gigantism linked to Plio-Pleistocene ocean dynamics – Proceedings of the Royal Society B

Why whales grew to such monster sizes – Science

Energetic tradeoffs control the size distribution of aquatic mammals – Proceedings of the National Academy of Science

Why whales got so big – The Atlantic

Sobre la autora: Rocío Pérez Benavente (@galatea128) es periodista

El artículo ¿Por qué son tan grandes las ballenas? se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. El pueblo que hablaba con las ballenas, ¿podría enseñarnos su idioma a los demás?
2. Cómo usar a las ballenas como detectores de radiación
3. Eran nuestras ballenas

Ziortza Guezuraga Nahasmendu bipolarra duten pertsonengan depresio-aldiak prebenitzeko litio gatzek duten efektibitatea aztertu dute.

1. irudia: Litio tratamenduak nahasmendu bipolarra duten pertsonengan depresioa prebenitzeko gaitasuna aztertu da.

Bizitza errealean efektu prebentiboa dute epe luzean litio gatzak erabiltzea, ikerketaren emaitzen arabera. Bizitza errealaren testuinguruan depresioa prebenitzeko litioak duen efektibotasuna aztertzea izan da helburua eta, horretarako, nahasmendu bipolarra duten 72 pazienteri jarraipena egin zaie hamar urtez.

Tratamenduari atxikidura ona izan duten pazienteek depresio aldi gutxiago izan dituzte eta baita aldi maniako eta hipomaniako gutxiago. Horretaz gain, depresio aldietan edota aldi maniako/hipomaniakoetan berriz erortzeko denbora ere motzagoa izan da atxikimendu gutxi izan duten pazienteengan.

Nahasmendu bipolarraren gaixotasun kostearen analisiaren arabera, minbizia baino kostu handiagoa izan dezake. Depresioa, aldi maniakoak, aldi hipomaniakoak eta aldi mistoak izaten dituzte nahasmendu bipolarra duten pertsonek.

Sintoma afketiboen artean, sintoma depresiboak eta mistoak dira morbositate maila altuenekin, ospitalizazio tarte luzeagoekin eta bai epe laburrean bai epe luzeaan emaitza kaskarragoekin lotuta daudenak.

Ikerketa bizitza errrealeko testuinguruan

Arabako Unibertsitate Ospitalean egin da ikerketa, psikiatria ospitaleratutako zerbitzua eta psikiatria larrialdi aretoa duen eremuko ospitale bakarra. Litio karbonatoarekin tratatutako 72 gaixo izan dira ikerketaren parte eta hamar urtez egin zaie jarraipena.

Hiru dira neurtu diren parametroak:

• Birgaixotzea. Zortzi astean behin ebaluatu dira morbilitateari begira (aldiak, ospitalizazio mota) eta alkohol eta drogen erabilerari begira.

Gaixoen %80,5 (58 gaixo) depresio aldi edo aldi mistoak izan dute gutxienez. 58 gaixoetatik 44 (%75,9) atxikimendu ona izan dute. Atxikimendu ona izan duten litioarekin tratatutako gaixoek depresio sintomekin nabarmen gertakari gutxiago izan dituzte, atxikimendu txarra izan duten gaixoekin konparatuta. Aldi maniako eta hipomaniako gutxiago ere zenbatu dira atxikimendu ona duten gaixoetan.

Birgaixotze denbora depresio edo aldi mistoan 713,07 egun izan da atxikimendu ona izan duten gaixoen kasuan eta 376,07 atxikimendu eskasekoetan. Aldi maniako edota hipomaniakoei dagokienez, 705,6 eta 462,3 egun izan dira atxikimendu ona eta kaskarra izan duten gaixoetan, hurrenez hurren.

• Atxikimendua. Tratamenduari atxikimendua ere neurtu da.

Ikertutako gaixoen %77,8 kontsideratu dira litio tratamenduari atxikiak. Alkohola neurriz gabe erabili duten edo alkoholarekiko dependentzia duten gaixoek atxikimendu maila baxuagoa izan dute alkoholik edaten ez duten edo noizean behin edaten duten gaixoekin konparaturik. Patroi bera ikusi da drogen erabilerari dagokionez.

• Kostua. Ospitaleratzearen kostuak ere izan dira kontuan.

Ospitaleratze kostuei dagokienez, atxikimendu ona izan duten pazienteen kasuan 10.349 eurokoa izan da eta 44.547 eurokoa atxikimendu txarreko gaixoen kasuan, ikerketaren 10 urteetan zehar.

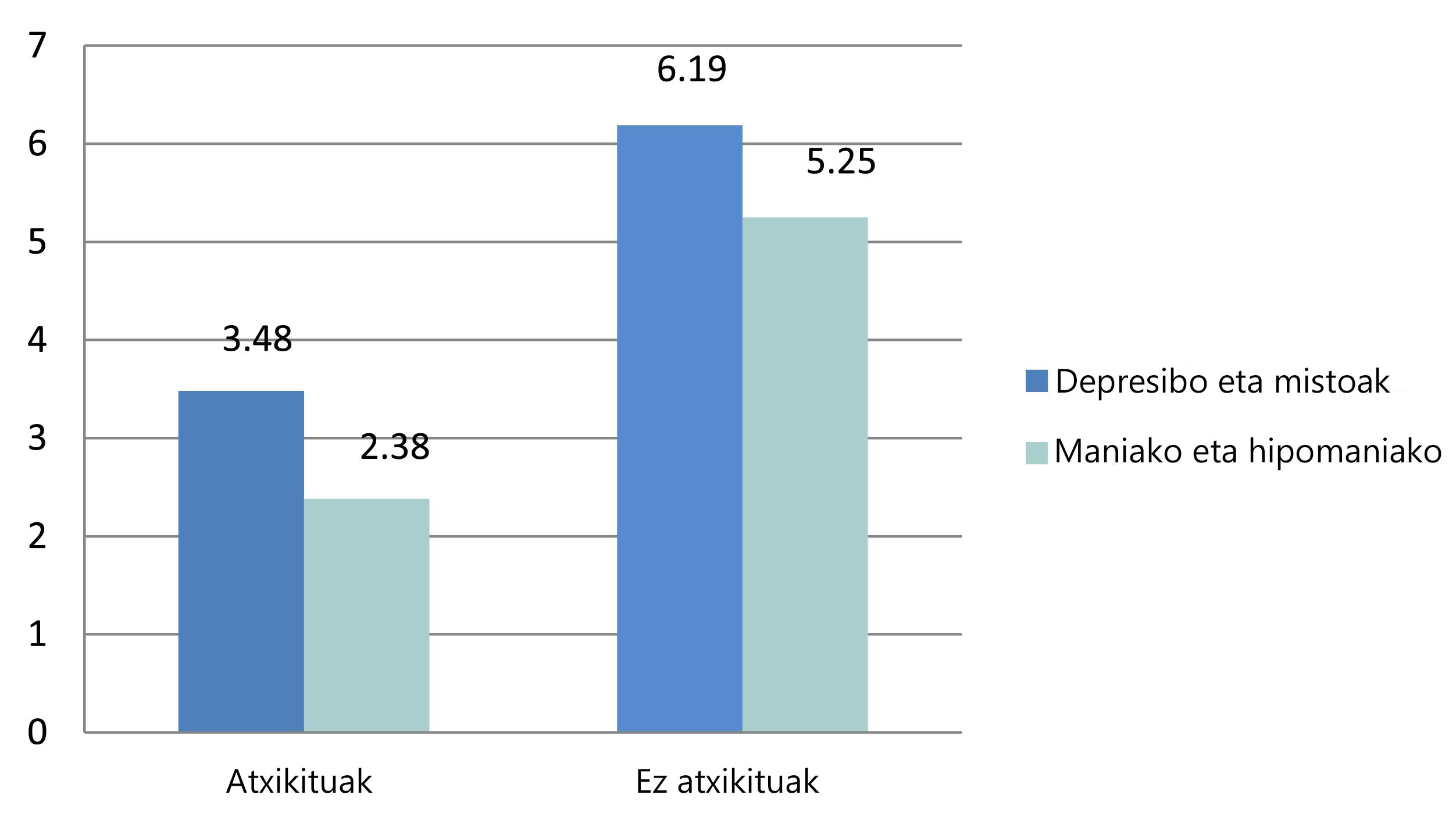
2. irudia: 10 urtean zehar aztertutako gaixoek izandako aldiak, depresibo eta mistoak, alde batetik, eta maniako eta hipomaniakoak, bestetik.

Emaitzen arabera, beraz, litioa erabilgarria da eta eraginkorra da nahasmendu bipolarrean depresio sintomak prebenitzeko bizitza errealaren testuinguruan. Gaixoek birgaixotzeak eta depresio sintomak dituzte, litio tratamenduari atxikimendu ona izanik ere, atxikimendu eskasa dutenek baino maila baxuagoan, hala ere.

Litioaren eraginkortasuna

Nahasmendu bipolarra tratatzeko botikarik garrantzitsuena. Epe luzera suizidioaren kontrako efektu prebentiboa ere badu. Aldi maniako eta maniakoetan litioak duen efektua oso ondo ikertuta dago, aldi depresiboetan eta mistoetan, baina, ebidentzia ez da hain sendoa.

Garrantzitsua da litioaren efektua bizitza errealeko testuinguruan aztertzea, nahasmendu bipolarrerako mantentze-tratamendu aukera gutxi daude eta, bereziki, depresioaren prebentziorako. Oso ikerketa gutxi daude aldi mistoetan eta depresioan litio gatzek duten efektuaren ingurukoak. Eztabaida dago depresio bipolarraren tratamendurako antidepresiboen erabilerari dagokionez, maniara aldatzeko arriskuagatik eta eraginkortasunaren inguruko kezka dela eta.

Litio gatzekin egindako tratamenduen arazo nagusietariko bat, bestelako tratamenduetan bezala, atxikimendu falta da. Tratamenduari atxikimendu faltak prebalentzia handia du nahasmendu bipolarrean, ikerketen arabera, %23,4 eta %32 artekoa. Zorroztaasun faltari, albo ondorioei eta serum litio mailaren monitoriazio beharrari egozten zaie atxikimentu falta.

Erreferentzia bibliografikoa

González-Pinto, Ana, et al., (2018). Can lithium salts prevent depressive episodes in the real world?. European Neuropsychopharmacology, 28, 12, 1351-1359. DOI: https://doi.org/10.1016/j.euroneuro.2018.09.008

———————————————————————–

Egileaz: Ziortza Guezuraga (@zguer) kazetaria da eta Euskampus Fundazioko Kultura Zientifikoko eta Berrikuntza Unitateko zabalkunde digitaleko teknikaria.

——————————————————————

The post Litio gatzak depresio-aldiak prebenitzeko appeared first on Zientzia Kaiera.