Einstein y Wolfgang Pauli
Wolfgang Pauli fue una de las figuras principales en el desarrollo de la mecánica cuántica y su trabajo le valió el premio Nobel de física en 1945. Veinte años más joven que Einstein, colaboró con él cuando ambos trabajaron en Princeton. Pauli tenía una lengua viperina y, si bien respetaba los primeros trabajos de Einstein sobre la relatividad, se mostró muy desdeñoso con sus últimas ideas.
 Einstein y Pauli en Princeton. Fuente: Wikimedia Commons
Einstein y Pauli en Princeton. Fuente: Wikimedia CommonsNacido en Viena (Austria) el 25 de abril de 1900, Pauli estuvo en contacto con la ciencia desde su más tierna infancia. De ello se encargaron su padre químico, Joseph Pauli, y un íntimo amigo de su padre, el físico Ernst Mach, cuyas ideas tanto influyeron en las primeras teorías de Einstein. En el instituto Pauli estudió la teoría de la relatividad especial de Einstein por su cuenta, a menudo escondiendo artículos en su pupitre que leía cuando las clases se volvían inaguantables. Nada más terminar el instituto, Pauli publicaría su primer artículo científico, como no podía ser de otra manera, sobre la relatividad de Einstein.
Pauli estudió física en la Universidad de Munich (Alemania), donde rápidamente su genio fue detectado y alentado por Arnold Sommerfeld. Este, conociendo de lo que era capaz su alumno de doctorado, le pidió que fuese él quien escribiese el artículo sobre la relatividad para la Encyklopaedie der mathematischen Wissenschaften (Enciclopedia de ciencias matemáticas). Dos meses después de presentar su tesis doctoral sobre la teoría cuántica de la molécula de hidrógeno ionizada, presentó el trabajo sobre la relatividad. Nada más y nada menos que 237 páginas en las que describía el estado actual de la teoría y aportaba sus propias interpretaciones. Este artículo dio a conocer a Pauli en el mundo científico. De hecho, a Sommerfeld le gustó tanto que se lo envió al propio Einstein, que alabó el genio de este joven de 21 años. Ciertamente genial, ya que el artículo de Pauli es reconocido hoy día como el catalizador del consenso de la comunidad científica sobre la relatividad.
Una vez finalizado su doctorado, pasó un año en la Universidad de Gotinga con Max Born, y a continuación investigó junto a Niels Bohr en Copenhague durante otro año. De vuelta en Alemania y mientras era profesor de la Universidad de Hamburgo, en 1924, Pauli completó la que es probablemente su contribución más famosa a la teoría cuántica: el Principio de Exclusión de Pauli. Básicamente, lo que dice el principio es que dos electrones en la órbita de un mismo átomo no pueden tener exactamente el mismo estado energético. Esta afirmación trajo como consecuencia la asignación de una nueva propiedad a los electrones, a la que él denominó espín.
Pauli también es conocido por otra contribución a la física que realizó antes de cumplir los treinta años: predijo la existencia de una partícula fundamental completamente nueva, el neutrino. No fue hasta los años sesenta que la existencia del minúsculo neutrino fue probada de forma concluyente, algo que no vería Pauli, pero que él percibió como una realidad basándose solamente en su necesidad matemática.
Un efecto menos científico también lleva el nombre de Pauli. Parece ser que tenía la facultad de influir en los experimentos, y en los aparatos necesarios para llevarlos a cabo, de la manera más extraña y siempre para mal. Las máquinas se rompían por su mera presencia. Sus amigos se referían a esto como “el efecto Pauli” y Pauli parece ser que se divertía con su reputación.
Pauli tenía fama de ser un perfeccionista. Existen numerosas referencias a él como la “conciencia de la física”, dado el interés que mostraba en ser el Pepito Grillo del trabajo de sus colegas. Es sabido que Pauli era capaz de los comentarios más mordaces y feroces acerca de la forma de hacer ciencia y de las publicaciones de otros científicos. Una de sus citas más famosas sobre un artículo es “No solo no es correcto, es que ni siquiera es incorrecto”. A Paul Ehrenfest, por ejemplo, le llegó a decir “Creo que me gustas más tú que tus artículos”.
Einstein tampoco escapó del agudo ingenio de Pauli. Si bien ambos hombres mantenían una relación cordial, Pauli se burlaba a menudo de los intereses científicos de Einstein. Pauli era uno de los muchos científicos que estaba de acuerdo con Niels Bohr en lo que se refería a la mecánica cuántica, aceptando la aproximación dada por Bohr conocida como la interpretación de Copenhague. Einstein, sin embargo, se negaba a admitir que la mecánica cuántica estuviese completa. Estaba decidido a encontrar una nueva teoría que incluyese las matemáticas de la nueva física, que Einstein tenía que admitir que hacían un magnífico trabajo previendo los resultados de los experimentos, y que también las mejorase. Einstein se refería a esta deseada teoría como teoría del campo unificado y Pauli se mofaba de este intento de unir las dos bases fundacionales de la física moderna; le gustaba repetir “Lo que Dios ha separado, el hombre nunca lo unirá”.
En 1932, Pauli escribió una revisión bastante cruel del trabajo sobre la teoría unificada de Einstein, diciendo: “La inventiva inasequible al desaliento de Einstein, así como su tenaz energía en la búsqueda de la unificación, nos han garantizado en los años recientes, en promedio, una teoría por año… Es psicológicamente interesante que durante algún tiempo la teoría en vigor es usualmente considerada por su autor como la solución definitiva”.
Tras la anexión de Austria por parte de Alemania, Pauli se mudó a Estados Unidos. Trabajó en Princeton entre 1940 y 1946, donde Einstein también tenía su oficina. A pesar del desprecio de Pauli por la teoría de la unificación de Einstein, estaba claro que ambos hombres se respetaban como colegas. Colaboraron solamente en un artículo, en 1943, sobre la teoría de la relatividad.
En enero de 1945 Einstein mandó un telegrama al comité del premio Nobel en el que decía: “Nomino a Wolfgang Pauli para el premio de física stop Sus contribuciones a teoría cuántica moderna consistente en así llamado principio de exclusión o Pauli han llegado a ser parte fundamental física cuántica moderna siendo independiente otros axiomas básicos de esa teoría stop Albert Einstein”. Wolfgang Pauli recibió el premio Nobel en la ceremonia de ese año, con 45 años, por el trabajo que hizo cuando tenía 24.
Nota:
Wolfgang Pauli no debe ser confundido con Wolfgang Paul, también ganador del Nobel de física y a quien Pauli se refería como “su parte real” (quien sepa matemáticas que entienda).
Referencia:
Einstein, A., & Pauli, W. (1943). On the Non-Existence of Regular Stationary Solutions of Relativistic Field Equations The Annals of Mathematics, 44 (2) DOI: 10.2307/1968759
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Una versión anterior de este artículo se publicó en Experientia Docet el 20 de septiembre de 2009.
El artículo Einstein y Wolfgang Pauli se ha escrito en Cuaderno de Cultura Científica.
¿Influye la luna sobre la salud de las personas? No, solo refleja cómo pueden engañarse a sí mismas
Desde tiempos remotos, numerosas culturas han creído que la luna tenía una influencia poderosa sobre los humanos, más allá de sus efectos más visibles, como las mareas. Aunque lejos quedaron las épocas en las que las sociedades adoraban a dioses relacionados con este satélite, parte del misticismo lunar sigue presente en nuestra época actual. Incluso conservamos vestigios de ellos en nuestra propia lengua. Un ejemplo de ello es la palabra «lunático», que según la Real Academia Española significa: «Que padece locura, no continua, sino por intervalos». El término proviene del latín «lunatĭcus», palabra en relación con dicho satélite que se utilizaba desde antiguo para referirse a las personas que tenían comportamientos extraños de forma errática, por culpa (supuestamente) de los ciclos lunares. De hecho, documentos de la época del famoso médico Hipócrates (400 a.e.c.) ya acusaban a la luna llena (plenilunio) de las súbitas y estrafalarias conductas de las personas.
 Imagen: Josep Monter Martinez / Pixabay
Imagen: Josep Monter Martinez / Pixabay
Dejando a un lado el estigma de la luna sobre los trastornos mentales, lo cierto es que las creencias sobre el poder de este satélite abarcan otros muchos aspectos de la salud humana y los profesionales sanitarios no están precisamente libres de ellas: varias encuestas realizadas a este colectivo indican que un porcentaje significativo de ellos cree que la luna influye sobre aspectos tan dispares como los ingresos a urgencias, la aparición de ataques de epilepsia o de infartos cardíacos, las agresiones físicas, la alteración del sueño, o el ciclo menstrual. No son una minoría: en 1995, el 43 % de los profesionales de salud mental encuestados pensaba que la luna llena alteraba el comportamiento de las personas. Esta idea sigue muy presente en los sanitarios de multitud de países, incluida España.
¿Tienen algún respaldo científico las creencias acerca del poder de la luna sobre la salud humana o es un engaño colectivo que se resiste a morir a pesar del paso de miles de años? Múltiples estudios se han realizado en las últimas décadas para aclarar el papel de este satélite en diferentes facetas sanitarias. La tónica general, sobre todo entre los estudios más rigurosos, es la misma: la luna no influye en absoluto y, si lo hace, el efecto es tan pequeño que no podemos descartar que se deba al puro azar o a las limitaciones del propio estudio (muchos poseen fallos importantes en su diseño o análisis estadístico). Es común que al intentar reproducir los resultados de algún estudio que afirma haber detectado efectos modestos de la luna sobre el cuerpo humano estos no vuelvan a mostrarse.
Esta es una panorámica general de la ciencia sobre la supuesta influencia de la luna sobre la salud:
- ¿La luna llena provoca más errores en las cirugías? Los estudios más extensos al respecto no encuentran ningún efecto de este astro. Una investigación publicada en la revista Anesthesiology no detectó ninguna diferencia significativa en más de 18.000 pacientes a los que se les realizó un bypass coronario (para asegurar la vascularización del corazón) entre 1993 y 2006. Las fases de la luna no influían en modo alguno. Otro , con datos de más de 12.000 pacientes, en el que se evaluaba el dolor tras la cirugía y los efectos adversos relacionados con el tratamiento, tampoco detectó ningún efecto lunar. Los autores concluían su artículo con «Por tanto, no hay razón para que los pacientes pospongan las cirugías o para que tengan miedo a las cirugías en una fecha concreta». Otra investigación, enfocada en los resultados de cirugías de cáncer pulmón de 2.411 pacientes, tampoco fue capaz de detectar ninguna influencia del citado satélite.
- ¿Más ingresos en urgencias en plenilunio? Las investigaciones serias lo descartan. Un estudio publicado en la revista American Journal of Emergency Medicine en 1996 no encontró ninguna diferencia entre las noches de luna llena y el resto de noches tras analizar más de 150.000 registros de visitas a urgencias.
- Quizás, ¿más visitas a urgencias o a consultas por trastornos mentales con luna llena? , numerosos estudios que, en conjunto, incluyen a decenas de miles de pacientes muestran que el ciclo lunar no tiene ningún efecto sobre ellos.
- ¿Más aparición de ataques epilépticos durante luna llena? Las al respecto lo descartan también. No se ve ningún efecto.
- ¿Sincronización del ciclo menstrual con el ciclo lunar? Tampoco. Que ambos fenómenos duren de forma similar (aunque, en realidad, la duración del ciclo menstrual varía según la mujer) no indica que se sincronicen. Un estudio que analizó el ciclo menstrual de 74 mujeres durante un año no encontró ninguna relación con las fases de la luna. Otra investigación, a partir de los datos de 1 millón y medio de mujeres que no usaban anticonceptivos hormonales y 7,5 millones de ciclos menstruales tampoco encontró sincronización alguna con la luna.
- ¿Más problemas de sueño durante las noches de luna llena? Aunque algunos estudios han observado algún , en relación con los niveles de melatonina (hormona que interviene en el sueño), otras investigaciones, más amplias y con miles de personas, no han podido observar este fenómeno.
¿Por qué, a pesar de esta aplastante evidencia científica en contra de los efectos de la luna, las creencias persisten incluso entre los profesionales sanitarios? Este fenómeno se origina a partir de un sesgo cognitivo concreto denominado «sesgo de confirmación». En esencia, cuando una persona cree en algo, de forma consciente o inconsciente tiende a prestar más atención y considerar los datos que refuerzan sus creencias, mientras que ignora o descarta los hechos que van en contra. Al final, este fenómeno distorsiona la percepción de la realidad. En medio de la vorágine de fake news en la que nos encontramos, la viñeta de Daniel Paz explica de forma muy cómica y contundente este fenómeno:
«-No, papá. Esa es una noticia falsa…
-Pero, ¿cómo va a ser falsa si dice justo lo que yo pienso?»
En el caso de la supuesta influencia de la luna sobre la salud, las personas que creen en ello se fijan especialmente si cuando hay, por ejemplo, más urgencias o más casos de visitas de psiquiatría, coincide con la luna llena en el cielo. En caso afirmativo, refuerzan sus creencias y piensan: «Debe ser la luna llena”. Todo ello a pesar de que también se dan noches, con otros ciclos lunares, en las que hay igual o más casos. Además, otro mecanismo de autoengaño es sobredimensionar el número de casos en plenilunio y llegar a pensar que son más de lo normal.
En realidad, la creencia del poder de la luna sobre el cuerpo humano nos dice mucho sobre los mecanismos psicológicos involucrados en el autoengaño y su persistencia y nada sobre sus efectos físicos reales: no hay ningún fenómeno que pudiera explicar la influencia de dicho satélite sobre la salud, más allá de su brillo por las noches. De hecho, la supuesta influencia gravitatoria de la luna llena, que ya de por sí es mínima sobre las personas, debería estar también presente con luna nueva que es cuando aparecen las mareas vivas y se suma la fuerza gravitatoria de la Luna con la de la Tierra. Más allá de este hecho físico, hay otro aún más evidente: la influencia gravitatoria de una persona que durmiera al lado de otra es mucho mayor que la de la luna. En definitiva, la física más elemental y los estudios científicos sobre diferentes aspectos de la salud humana rebaten de forma rotunda la supuesta influencia de la luna llena.
Para saber más:
Sesgos cognitivos que aquejan a la ciencia
Sobre la autora: Esther Samper (Shora) es médica, doctora en Ingeniería Tisular Cardiovascular y divulgadora científica
El artículo ¿Influye la luna sobre la salud de las personas? No, solo refleja cómo pueden engañarse a sí mismas se ha escrito en Cuaderno de Cultura Científica.
Diapasones para afinar la velocidad de la luz
 Albert A. Michelson, premio Nobel en 1907, se reincorporó a la Armada de los Estados Unidos cuando el país decidió intervenir en la Primera Guerra Mundial. Aquí fotografiado en 1918 con uniforme de capitán de corbeta (lieutenant commander). Fuente: Wikimedia Commons
Albert A. Michelson, premio Nobel en 1907, se reincorporó a la Armada de los Estados Unidos cuando el país decidió intervenir en la Primera Guerra Mundial. Aquí fotografiado en 1918 con uniforme de capitán de corbeta (lieutenant commander). Fuente: Wikimedia CommonsEn 1879, Albert A. Michelson midió la velocidad de la luz con una precisión sin precedentes. Para entonces, había cumplido 26 años, trabajaba como instructor de la Marina de los Estados Unidos, tenía muy poca formación en física y ninguna experiencia en investigación, pero su trabajo resultó revolucionario. Aquel experimento mejoró la precisión de la constante c en un orden de magnitud y sentó unas nuevas bases para hacer mediciones de alta precisión. En los siguientes años, Michelson inventó el interferómetro que hoy lleva su nombre y realizó un primer experimento para confirmar (o desmentir, más bien) la existencia del éter. En 1907 fue el primer científico norteamericano en ganar el premio Nobel de Física.
Lo más sorprendente es que los orígenes de Michelson no habían sido precisamente “prometedores” para la carrera de un científico. Cuando tenía cuatro años, su familia huyó de Polonia a California. Su padre era vendedor ambulante y se instalaron en Murphy’s Camp, “una ciudad sin ley de la fiebre del oro —según palabras de Daniel Kleppner1— que resultaba óptima para que un niño aprendiera a pelear, pero no a leer y escribir”. Cuando Albert cumplió 14 años, lo enviaron a San Francisco para estudiar secundaria. Allí, su talento científico conmovió al director del centro, que le proporcionó alojamiento y comida, además de un trabajo como ayudante en las clases de física. Gracias a él, Michelson pudo terminar el instituto y alistarse en la Academia Naval de los EE. UU., la única manera de seguir estudiando ciencias a pesar de sus pocos recursos.
Tras graduarse como marine en 1873, Michelson fue destinado a Annapolis como profesor de física y química. Fue entonces cuando su comandante le pidió que investigara la medida de la velocidad de la luz de Léon Foucault, publicada en 1862, y ante semejante reto, Michelson se vino arriba. En apenas dos años consiguió incrementar la precisión de su predecesor por diez.
¿Pero en qué consistía el experimento de Foucault que Michelson tanto se esforzó en superar? ¿Cómo se mide algo que es, en esencia, instantáneo, lo más rápido que uno pueda imaginar? Pues bien, con un muy buen cronómetro. Pero no un cronómetro común, como los que usan los entrenadores en las pistas de atletismo, sino un cronómetro hecho de espejos.
Es posible que hayas oído hablar del experimento de Foucault con anterioridad: en su montaje, la luz viaja desde una rendija hasta un primer espejo que está en movimiento (R en la figura). Allí rebota y llega a un segundo espejo esférico que está quieto (M). Regresa por donde ha venido y se vuelve a encontrar con el espejo rotatorio (R) para, finalmente, volver a su punto de origen (S). O más bien, volvería al punto de origen si el espejo rotatorio se encontrase en la misma posición que estaba cuando el rayo de luz se lo topó por primera vez. Pero la gracia de todo este montaje es que, en el camino de ida y vuelta de la luz, el espejo rotatorio ha cambiado ligeramente de posición y por eso, el rayo genera una imagen desplazada respecto a la de la rendija inicial. Midiendo este desplazamiento (2θ, en la figura), podemos calcular cuánto ha girado el espejo mientras la luz hacía su recorrido de ida y vuelta (θ). Y conociendo la velocidad angular del espejo rotatorio, sabremos cuánto tiempo ha pasado. Es el cronómetro perfecto.
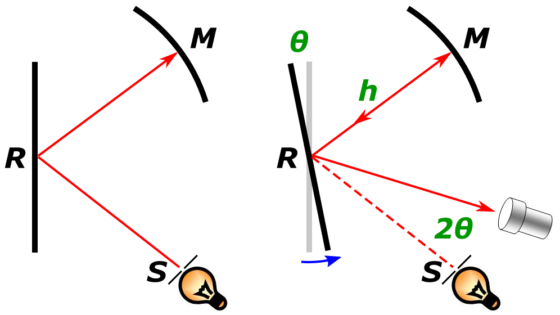
Todo este dispositivo experimental ya lo había ideado Foucault. Pero para perfeccionarlo y llevar su precisión hasta el extremo, Michelson lo repitió todo a lo grande. Para empezar, aumentó la distancia entre los espejos, hasta más de 600 metros. Pero además, necesitaba que la rotación del espejo fuese rapidísima (256 rotaciones por segundo) y, además, muy estable y muy precisa.
Una frecuencia rápida, estable y precisa, ¿os suena de algo? Dado el título de esta serie, supongo que a nadie le sorprenderá descubrir que Michelson utilizó diapasones para calibrar la velocidad de sus espejos. Parió de un sistema muy parecido, de hecho, al empleado por Lissajous para afinar el la universal. Michelson observaba los pulsos de luz de la rendija utilizando un pequeño espejo en la punta de un diapasón, que se mantenía en constante vibración gracias a una fuente electromagnética (igual que los diapasones parlantes de Helmholtz). Sincronizó la frecuencia del espejo con el diapasón ajustando la velocidad del primero hasta que la imagen se hacía estacionaria. Este diapasón se calibraba, a su vez, comparando su frecuencia con la de otro diapasón estándar, que se guardaba en una cámara aislada a una temperatura controlada. Y la frecuencia de este segundo diapasón estándar se había medido con ayuda de un cronoscopio, que permitía visualizar sus vibraciones sobre un tambor rotatorio. El cronoscopio comparaba dicha vibración con el tiempo marcado por un cronómetro, que se había calibrado tomando como referencia el tiempo de rotación de la Tierra, que se había medido desde Observatorio Naval de los EE. UU., en función de los tránsitos de las estrellas… Que ya que te pones a calibrar, pues calibras el laboratorio entero, y acabas recurriendo al movimiento de la mismísima Tierra.
Está claro que el virtuosismo experimental de Michelson y su obsesión por el detalle no conocían límites. Sus notas están llenas de detalles que lo dejan a uno alucinado (podéis leer más en el artículo de Kleppner1). Gracias a ello, obtuvo un resultado sorprendentemente ajustado, teniendo en cuenta los recursos con los que contaba: c = 299 940 ± 50 km/s, lo que constituye un error de menos del 0,05% (1 entre 2000) respecto al valor que hoy damos por bueno, c = 299 792,458 km/s.
Su logro lo convirtió en toda una celebridad en EE. UU. Y, sin embargo, no le sirvió para ganar muchos galones dentro de su oficio como militar. En 1880, consiguió permiso para ausentarse de su cargo y viajar a Europa, donde por fin podría estudiar física y matemáticas de manera rigurosa. Una vez en el viejo continente, Michelson inventó el interferómetro por el que hoy le recordamos, buscó el éter sin ningún éxito y ayudó a desmentir su existencia (el experimento Michelson-Morley, es hoy todo un hito de la física). Según cuenta Kleppner, su obsesión por medir la velocidad de la luz de manera cada vez más precisa nunca lo abandonó. El día de su muerte, el 9 de mayo de 1931, lo pilló redactando unas notas sobre cómo realizar una nueva medida. Tenía 78 años de edad.
Referencia:
1Kleppner, D. (2007). Master Michelson’s measurement. Physics Today, 60(8), 8-9. DOI: 10.1063/1.2774115
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
El artículo Diapasones para afinar la velocidad de la luz se ha escrito en Cuaderno de Cultura Científica.
Naukas Pro 2022: El lenguaje, espejo de desigualdades y mecanismo de evolución social

El lenguaje es mucho más que un simple instrumento de descripción y comunicación. A pesar de que la sociedad lo percibe como una mera herramienta de interacción social que nos ayuda a describir el mundo, a transmitir ideas y sentimientos, y a conocer las de los demás, su potencial es mucho mayor: está estrechamente ligado a nuestro pensamiento, puede modificar nuestra visión del mundo e influir en nuestra toma de decisiones.
Por ejemplo, un lenguaje sexista oculto, utilizado de forma recurrente y generalizada, puede ser una fuente inagotable de desigualdades sociales y sesgos de género. La lingüística, que lleva a cabo un estudio científico del lenguaje, es una poderosa arma de concienciación y cambio social al ser capaz de desenmascarar esas asimetrías.
Gracias a la lingüística cognitiva y a la psicolingüística podemos comprobar que el lenguaje está íntimamente relacionado con el pensamiento y con el conocimiento, y que es un potente instrumento que nos ayuda a conceptualizar la realidad y a visualizarla desde diversas perspectivas. El lenguaje no es capaz de crear la realidad, pero sí de presentarnos visiones distorsionadas y variadas de la misma.
Lorena Pérez Hernández, profesora titular de la Universidad de La Rioja y lingüista cognitiva, participó el jueves 15 de septiembre en Naukas Pro en el Palacio Euskalduna de Bilbao para analizar el papel del lenguaje como espejo de desigualdades, pero también como mecanismo de evolución social. Pérez Hernández explicó a la audiencia del Euskalduna la forma en la que la lingüística cognitiva estudia los mecanismos que subyacen al lenguaje y que están estrechamente ligados con los procesos de construcción del conocimiento.
Esta disciplina es la que nos ayuda a analizar la huella lingüística que dejan esos procesos para realizar un diagnóstico de la sociedad y desvelar las desigualdades y asimetrías sociales que en ocasiones pasan desapercibidas. Una vez obtenido ese diagnóstico podemos explorar la relación que existe entre el lenguaje, por un lado, y el pensamiento y el conocimiento por otro, y diseñar intervenciones que tengan como objetivo favorecer cambios sociales positivos.
La lingüista mencionó varias iniciativas con las que se pretende realizar un diagnóstico sobre aspectos sociales como la educación, las desigualdades, el ámbito discursivo y la comunicación política y comercial, entre otros. El objetivo de estas líneas de investigación es utilizar dichos diagnósticos para diseñar líneas de actuación que contribuyan a favorecer una evolución social positiva en términos de efectividad, sostenibilidad e igualdad.
La educación, elemento de construcción del conocimientoLos proyectos llevados a cabo hasta el momento, en colaboración con las investigadoras Iraide Ibarretxe-Antuñano (U. de Zaragoza) y Paula Pérez Sobrino (U. de La Rioja), han logrado identificar usos diferenciales del lenguaje cotidiano que se utiliza con niños y niñas, y han permitido apuntar una posible explicación a un fenómeno social concreto: la falta de interés de las pequeñas por las carreras STEM.
Además, según Pérez Hernández, estos proyectos también han puesto de relieve que las metáforas conceptuales sobre educación han comenzado a cambiar y a reflejar un nuevo concepto: la educación ha pasado de entenderse como una simple transferencia de conocimiento a concebirse como construcción del conocimiento.
Después de reiterar que el lenguaje “es mucho más que un instrumento de descripción y comunicación”, Lorena Pérez Hernández destacó que “las diferentes metáforas sobre la enseñanza condicionan en gran medida el diseño del currículum y de las intervenciones educativas”. “En este caso, el proyecto tiene como objetivo determinar si la visión de la realidad que nos transmiten esas metáforas educativas se corresponde con los resultados de aprendizaje reales”.
La lingüista explicó que su investigación tiene un doble impacto social: por un lado, pretende “servir de espejo a las desigualdades sociales y a la visión que tiene una sociedad concreta del mundo”, y por otro, busca contribuir a desarrollar intervenciones sociales positivas orientadas a los Objetivos de Desarrollo Sostenible de Naciones Unidas, temática de fondo de todas las ponencias de Naukas Pro de esta edición.
El lenguaje no es inocenteAsí, Lorena Pérez Hernández parte de la base de que “el lenguaje no es inocente” sino que está estrechamente unido al pensamiento y refleja fielmente nuestra visión del mundo. “La elección de una palabra u otra, de una estructura sintáctica u otra, etc., revelan nuestra forma de pensar y de concebir la realidad”; por eso, si analizamos el lenguaje que utilizan los hablantes de una sociedad, “podemos descubrir con un alto índice de fiabilidad cómo es esa sociedad”. “No cómo se describe a sí misma sino cómo es realmente. El lenguaje nos revela y nos delata. El análisis del lenguaje es, por lo tanto, un instrumento muy preciso de diagnóstico social”, precisó.
A continuación, constató que existe una relación íntima entre lenguaje y pensamiento, en la que el primero puede influir en el segundo. “El lenguaje no solo nos ayuda a descubrir cómo pensamos y cómo vemos el mundo, sino que también nos permite actuar sobre ese pensamiento para modificarlo” e “influir en la toma de decisiones y en las acciones de las personas de una manera compatible con los Objetivos de Desarrollo Sostenible”.
Si no ve correctamente el vídeo use este enlace.
Para saber más:
El lenguaje antes del lenguaje y normas sociales
Crónica de Roberto de la Calle / GUK
El artículo Naukas Pro 2022: El lenguaje, espejo de desigualdades y mecanismo de evolución social se ha escrito en Cuaderno de Cultura Científica.
¿Por qué moja el agua? La física de fluidos inunda nuestras vidas
Ruth Lazkoz
 Shutterstock / carlos castilla
Shutterstock / carlos castilla
“El agua moja” es una frase que se utiliza como sinónimo de obviedad. Pero ¿sabemos explicar por qué? Toca ponerse exquisitos para visitar ese y muchos otros fenómenos cotidianos usando la física de fluidos.
La física de fluidos surgió como disciplina formal en el siglo XVI para contradecir algunos planteamientos de Aristóteles. Según el filósofo, la naturaleza no aprobaba la existencia del vacío. Pero Pascal y otros abordaron la cuestión desde la perspectiva contraria. Para escudriñar la ausencia de materia había que estudiar la materia en sí.
El encargo de Pascal hecho a su cuñado de ascender a lo más alto de un volcán extinto con un par de barómetros de mercurio corroboró los experimentos sobre el peso de la atmósfera y la existencia del vacío realizados por su predecesor Torricelli. Y eso abrió una enorme compuerta del saber.
Fluidos son los gases y los líquidos, tanto el humo de una chimenea como el agua. Todos ellos son sustancias con fuerzas tan débiles entre sus partículas que no pueden recuperar su forma si la pierden.
De la pasta de dientes a la Fórmula 1Pero ¿dónde hallamos la física de fluidos en las rutinas diarias? Por ejemplo, en la manera en que se transmiten los cambios de presión entre dos puntos de un fluido. Con ello conseguimos sacar la pasta de dientes del tubo usando el mismo principio que hace funcionar la jeringa y los frenos hidráulicos.
Si nos atrevemos a generalizarlo para fluidos en movimiento encontramos, por la senda de Bernoulli, la explicación al efecto suelo de los bólidos de la Fórmula 1 –que hace que el vehículo se quede pegado al asfalto para mejorar su aerodinámica– o de cómo las marmotas enfrían sus madrigueras. De hecho, esas leyes se aplican a cualquier proceso de succión, como mamar de la teta.
Otro entorno secularmente ligado a los fluidos es la medicina. Cualquier anestesista ha de tener conocimientos sólidos de la física de líquidos y gases para manejar catéteres o sistemas de ventilación. Médicos eran también los hermanos Weber, expertos en la circulación de la sangre, cuya mágica viscosidad la hace fluir más despacio cerca de las paredes de los vasos, como mostró el también médico Pouiseille.
Es lo mismo que ocurre cuando movemos una galleta sobre la superficie de unas natillas en un cuenco. Cuanto menos líquido haya en el recipiente más fácil resultará el desplazamiento. Así es también como se comportan las placas tectónicas al desplazarse sobre el manto terrestre, una de tantas aplicaciones de la física de fluidos a la geología. Es interesante que ambas ciencias se den la mano con lo cotidiano mediante la física de fluidos. Otro nexo es la ley de Darcy para el paso de un líquido por un medio poroso, que puede ser un suelo de arena pero también el grano molido de una cafetera italiana.
Sin salirnos de la cocina, pero retornando a la viscosidad, aún nos quedan ejemplos atractivos por mencionar. Cuando el kétchup encerrado en la botella recibe un golpe certero fluye con más facilidad. El engrudo, junto con el yogur, la mayonesa y otros alimentos viscosos entra dentro de no newtonianos, así llamados por ser físicamente más complejos que aquellos con los que el gran genio se adentró en esta subdisciplina física cuando se propuso echarla a andar con su sabiduría.
Entre fogones nos resulta fácil experimentar sobre el efecto de las condiciones físicas en los fluidos en general. Queda bien patente cuando observamos que la miel fluye más fácilmente al calentarla. Esto vuelve a indicarnos cuántos flancos hay que cubrir al investigar la física de fluidos.
¿Por qué los fluidos se comportan como fluidos?No obstante, los ejemplos dados no son de excusas para esquivar el tema inicial. ¿Por qué el agua moja, el aceite mancha y la tinta tiñe? Se debe a las fuerzas de adhesión. Es decir, la afinidad entre sustancias líquidas y sólidas.
Esto se traduce en que, al poner un tejido en contacto con esos líquidos, treparían desafiando a la gravedad (fenómeno de capilaridad). Pero los líquidos son narcisistas. Sienten un tremendo apego a sí mismos: las fuerzas de cohesión. Eso genera la llamada tensión superficial, responsable de que se formen las gotas de agua y otros líquidos y mantengan su forma esférica. De ello se valen las hormigas obreras para transportar agua a su colonia.
¿Brindará conmigo para celebrar tanta ciencia? Pues entonces le invito a observar las lágrimas del vino, otra consecuencia de la tensión superficial.
Lamentablemente solo puedo cubrir la amplitud de la física de fluidos dando unas pinceladas. Al decirlo recuerdo que el hecho de que la pintura sea un fluido no newtoniano permitió inventar el gotelé. Pero no merece la pena enredarme en la nostalgia y aparcar temas de absoluta urgencia y actualidad.
La física de fluidos es fundamental para explicar un amplio abanico de fenómenos atmosféricos y oceanográficos. Y permite desmentir que el deshielo del Polo Norte eleve el nivel del mar. El argumento usa el principio de Arquímedes, el mismo que mantiene a flote los barcos de exploración de ese ámbito científico. En este contexto quiero señalar que el cambio climático hace los vuelos más susceptibles al fenómeno de la turbulencia.
Pero entonces me tentaría mucho hacerlo visual recurriendo a Humphrey Bogart. Tomaría así su imagen fumando un cigarro y liberando una columna de humo que se convierte en un festival de vueltas y revueltas.
Mejor dar un respiro a la audiencia. Y sirva la metáfora para recomendar prudencia mientras la covid-19 siga entre nosotros. Para alcanzar ese objetivo, la física de fluidos seguirá asistiendo de forma brillante a otras disciplinas y hablándonos de las gotículas y sus viajes.![]()
Sobre la autora: Ruth Lazkoz es profesora de Física Teórica en la Universidad del País Vasco / Euskal Herriko Unibertsitatea
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo ¿Por qué moja el agua? La física de fluidos inunda nuestras vidas se ha escrito en Cuaderno de Cultura Científica.
El azúcar añadido y el azúcar libre no son lo mismo pero sus efectos (perjudiciales) si lo son
Maitane González-Arceo, Saioa Gómez-Zorita y María P. Portillo
 Siempre es mucho mejor la fruta de verdad y sin azúcares añadidos. Foto: Liliana Olivares / Unsplash
Siempre es mucho mejor la fruta de verdad y sin azúcares añadidos. Foto: Liliana Olivares / UnsplashNuestra dieta incluye diferentes fuentes de azúcares o hidratos de carbono simples, que están formados por una o dos moléculas, y pueden encontrarse unidos o no a la matriz, es decir, a otros componentes del alimento. De esta forma, se clasifican en libres o no libres. El azúcar libre puede encontrarse de las siguientes maneras:
-
De manera natural como ocurre en la miel.
-
Añadido voluntariamente, tanto a nivel doméstico como industrial, con el fin de endulzar los alimentos, de modo que el producto sea más apetecible.
-
Liberado de otros componentes de los alimentos a los que se encontraba previamente unido, como la fibra. Esto ocurre, por ejemplo, al exprimir las frutas para obtener zumo.
El hecho de que esté libre (da igual que sea añadido o no) favorece que el azúcar se absorba más rápidamente que cuando está unido, ya que el cuerpo no necesita romper esas uniones entre el azúcar y la matriz del alimento previamente a la digestión y la absorción. Además, se ha observado que la ingesta de azúcares libres contribuye a incrementar la densidad calórica de la dieta. Por ejemplo, cuando se ingiere zumo de fruta exprimido se emplea mayor cantidad de fruta que cuando se ingiere entera, ya que cuando ingerimos la fruta a bocados solemos consumir una sola pieza, mientras que cuando la exprimimos se suelen emplear varias piezas para rellenar un vaso.
A diferencia del azúcar que se encuentra en los alimentos unido a la matriz, por ejemplo en la fruta y la verdura sin procesar, el azúcar libre se vincula con numerosas enfermedades metabólicas crónicas de gran prevalencia en los países occidentales como la obesidad, la dislipemia (hipercolesterolemia, hipertrigliceridemia…), la resistencia a la insulina, la diabetes mellitus tipo 2, la enfermedad de hígado graso no alcohólico y las enfermedades cardiovasculares.
Por otro lado, la ingesta de alimentos que contienen azúcar libre desplaza y, por lo tanto, reduce la ingesta de alimentos saludables como la fruta, la verdura o las legumbres. La evidencia científica no ha podido determinar cuál es la ingesta máxima de estos azúcares libres que no perjudique la salud, por lo que se debe reducir su consumo al máximo. En concreto la Organización Mundial de la Salud (OMS) recomienda limitar la ingesta de azúcares libres a menos del 5% de la ingesta calórica total.
Entonces, ¿qué alimentos se deben evitar por su alto contenido en azúcar libre?El azúcar libre está en productos como pasteles, bollería industrial y otros dulces (caseros y no caseros), bebidas azucaradas como los refrescos y zumos comerciales, postres lácteos azucarados (yogures y otras bebidas) y otros ultraprocesados. Además, también se encuentra en otros productos como la miel o los siropes o en alimentos que los contienen, tanto comprados como hechos en casa.
En el caso de los productos comerciales, se puede saber si durante su elaboración se ha añadido azúcar o no leyendo la lista de ingredientes del envase. Además, hay que tener en cuenta que los ingredientes aparecen en el listado ordenados de mayor a menor peso o cantidad. De este modo, el ingrediente que aparece en primer lugar siempre será aquel que se ha usado en mayor cantidad y los ingredientes que están al final, serán aquellos que están en menor cantidad. Por lo tanto, es importante fijarse en qué posición se encuentra el azúcar dentro del listado, ya que cuanto más atrás esté, menos azúcar tendrá el producto.
En la siguiente lista se detallan los principales nombres bajo los que puede esconderse el azúcar (libre) en los alimentos: almidón modificado, caramelo, concentrado de jugo de frutas, dextrina, dextrosa, fructosa, galactosa, glucosa, isomaltosa, jarabe (de maíz, arroz, arce, glucosa…), maltodextrina, maltosa, miel, néctar, puré de frutas, sacarosa y sirope como el de agave.
En resumen, es conveniente limitar al máximo el consumo de alimentos que contengan alto contenido de azúcar libre, añadido o no, y aumentar la ingesta de alimentos más saludables que contengan el azúcar unido a otros componentes del alimento como es el caso de las frutas y verduras. El consumo de frutas y verduras, a diferencia del consumo de alimentos con azúcar libre, no se ha asociado con ninguna enfermedad metabólica.
Sobre las autoras: Maitane González-Arceo, Saioa Gómez-Zorita y María P. Portillo pertenecen al Grupo Nutrición y Obesidad en la Facultad Farmacia de la UPV/EHU, al Centro de investigación Biomédica en red (CiberObn) y al Instituto de Investigación Sanitaria Bioaraba.
Para saber más:
El azúcar oculto en los alimentos
Azúcar y otros edulcorantes
El artículo El azúcar añadido y el azúcar libre no son lo mismo pero sus efectos (perjudiciales) si lo son se ha escrito en Cuaderno de Cultura Científica.
El rompecabezas de Sol LeWitt
En algunas entradas del Cuaderno de Cultura Científica hemos hablado de cómo las matemáticas recreativas y, en particular, algunos rompecabezas matemáticos, habían inspirado al arte, siendo utilizados como herramientas de creación artística. Por ejemplo, el conocido rompecabezas geométrico Tangram (véase la entrada El arte contemporáneo que mira al Tangram), el rompecabezas cubo soma (véase la entrada El cubo soma: diseño, arte y matemáticas), la disección de Dudeney, una disección geométrica de un triángulo equilátero cuyas piezas se pueden reordenar formando un cuadrado o viceversa (véase la entrada La disección de Dudeney, de rompecabezas matemático a creación artística) o los cuadrados latinos (véase la entrada Cuadrados latinos, matemáticas y arte abstracto). Sin embargo, en esta entrada vamos a mostrar un ejemplo de cómo el arte también puede inspirar a la matemática recreativa, en concreto, enseñaremos cómo una obra del artista conceptual y minimalista estadounidense Sol LeWitt (1928-2007) ha motivado la creación de algunos rompecabezas matemáticos.
 Bandas de color (portafolio Wadsworth) del artista estadounidense Sol LeWitt. Imagen de WikiArt
Bandas de color (portafolio Wadsworth) del artista estadounidense Sol LeWitt. Imagen de WikiArtEl artista minimalista y conceptual Sol Lewitt
Podemos relacionar al artista Sol LeWitt con dos movimientos artísticos, el minimalismo y el arte conceptual. Estos pueden ser descritos brevemente con dos lemas. La expresión que nos explica en tres palabras qué es el arte minimal es “menos es más”, atribuida al arquitecto germano-estadounidense Ludwig Mies van der Rohe (1886-1969), por ser quien la popularizó, aunque la primera vez que se publica en este sentido es de la mano del también artista estadounidense minimalista y conceptual Ad Reinhardt (1913-1967), en una entrevista en la que afirmó que “Mientras más cosas contenga, cuanto más ocupada sea la obra de arte, peor será. Más es menos. Menos es más”. Sin embargo, la frase “menos es más” se encuentra con anterioridad en la poesía, por ejemplo, en el poema Andrea del Sarto (1855) del poeta y dramaturgo británico Robert Browning (1812-1889) o en el poema Deseo de año nuevo (1774) del poeta alemán Christoph Martin Wieland (1733-1813).
Mientras que la cita que nos sirve para entender en pocas palabras qué es el arte conceptual se debe al propio Sol LeWitt, quien resumió este movimiento artístico con la frase “La idea se convierte en una máquina que hace arte”, después de afirmar que “en el arte conceptual, la idea o el concepto es el aspecto más importante de la obra. Cuando un artista utiliza una forma de arte conceptual, significa que toda la planificación y las decisiones se toman de antemano y la ejecución es un asunto superficial”.
 Estructura geométrica abierta IV (1990), del artista minimalista y conceptual Sol Lewitt, que fue expuesta en la Galería Elvira González de Madrid en 2015
Estructura geométrica abierta IV (1990), del artista minimalista y conceptual Sol Lewitt, que fue expuesta en la Galería Elvira González de Madrid en 2015Líneas rectas en cuatro direcciones y todas sus posibles combinaciones
Si observamos el trabajo de este artista conceptual y minimalista descubriremos un arte muy geométrico, en el que la combinatoria juega también un papel fundamental. Un ejemplo es la obra que nos ocupa hoy, titulada Líneas rectas en cuatro direcciones y todas sus posibles combinaciones (1975) y formada por 15 grabados. Esta obra (que podemos observar en la siguiente imagen) describe gráficamente de qué formas podemos trazar en un cuadrado grupos de segmentos rectos dentro del conjunto de cuatro tipos de líneas rectas, en horizontal, en vertical o en diagonal (ascendente o descendente), que pasan por el centro del cuadrado. La respuesta es 15, como la cantidad de grabados que compone esta obra, si excluimos la forma número 16 que sería sin ninguna línea recta, es decir, el cuadrado vacío.
 Líneas rectas en cuatro direcciones y todas sus posibles combinaciones (1975), del artista Sol Lewitt
Líneas rectas en cuatro direcciones y todas sus posibles combinaciones (1975), del artista Sol Lewitt
Aunque este no es el objetivo de esta entrada, la obra que nos ocupa está relacionada con lo que en combinatoria se llama “números combinatorios” –de cuántas formas se pueden elegir k objetos de un grupo total de n objetos– y con las partes –o subconjuntos- de un conjunto dado de n elementos.
El rompecabezas inspirado en la obra de Sol LewittCuando el matemático y divulgador estadounidense Barry Cipra vio la obra del artista Sol Lewitt, Líneas rectas en cuatro direcciones y todas sus posibles combinaciones (1975), observó que había líneas que se continuaban desde un lado a otro del cuadrado 4 x 4 que formaba la obra con los 15 + 1 (el 1 extra es el cuadrado vacío de rectas, que estaría abajo a la derecha, donde el texto) grabados juntos (imagen anterior), como la línea diagonal que parte del segundo cuadrado de la cuarta y última fila, pasando por el tercer cuadrado de la tercera fila y llegando al cuarto de la segunda fila, mientras que otras líneas no cumplían esta propiedad, como las líneas verticales del segundo y tercer cuadrados de la primera columna, que no se continúan ni hacia arriba, ni hacia abajo, hasta llegar a los lados de la obra. Entonces se le ocurrió la idea de si sería posible recolocar los 16 (15 + 1) cuadrados, sin rotar ninguno, de forma que se pudieran continuar las líneas rectas desde un lado a otro de la parte exterior de la estructura cuadrada 4 x 4 que forman los 16 cuadrados. Esta idea dio lugar al llamado rompecabezas de Sol Lewitt, que Cipra propuso por primera vez en libro What’s Happening in the Mathematical Sciences 1998-1999 / Qué está pasando en las ciencias matemáticas 1998-1999.
A continuación, vamos a describir con más detalle los elementos y las reglas del rompecabezas de Sol Lewitt, con la idea de que podáis construir vuestra propia versión física y jugar con ella.
Para empezar, debemos construir las 16 fichas del rompecabezas (por ejemplo, en cartulina, o en madera si somos más atrevidos), que son los 16 cuadrados con las diferentes opciones de representar una, dos, tres o cuatro de las líneas rectas que pasan por el centro del cuadrado, en vertical, horizontal o diagonal (ascendente o descendente). Para facilitar el desarrollo del juego –en concreto, que no se pueden girar las piezas, de forma que una línea vertical pase a horizontal, o viceversa, o que una línea diagonal en un sentido pase a una línea diagonal en el otro sentido– vamos a colorear las líneas según a la dirección de las mismas. Por ejemplo, las líneas horizontales en verde, las verticales en amarillo, las diagonales en un sentido en azul y en el otro en rojo, como se muestra en la siguiente imagen.
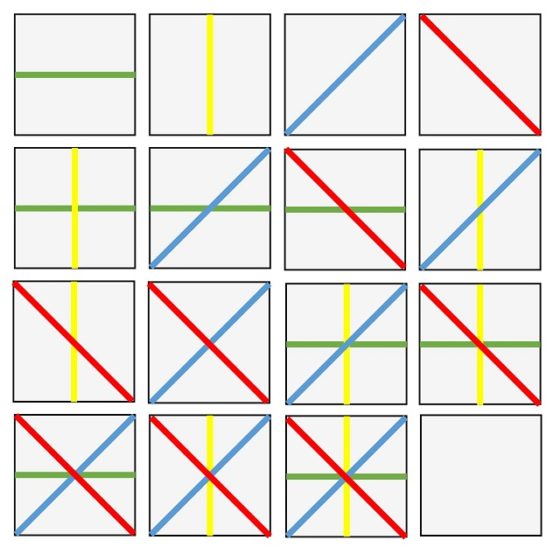 Las 16 piezas, con líneas coloreadas, del rompecabezas de Sol Lewitt
Las 16 piezas, con líneas coloreadas, del rompecabezas de Sol LewittEl rompecabezas de Sol Lewitt consiste en colocar las 16 piezas cuadrados que hemos construido formando una estructura cuadrada 4 x 4, sin rotar ninguna de las piezas, es decir, las líneas horizontales (verdes) siempre son horizontales, las verticales (amarillas) siempre verticales, las diagonales ascendentes (azules) siempre son diagonales ascendentes y las diagonales descendentes (rojas) no dejan de ser diagonales descendentes, de forma que formen líneas ininterrumpidas de un lado al otro de la estructura cuadrada 4 x 4. Así las líneas amarillas van desde la parte superior a la inferior, las verdes de la parte de la izquierda a la parte de la derecha, las azules desde el lado izquierdo al lado superior, o del lado inferior al lado derecho, y las rojas del lado superior al lado derecho, o del lado izquierdo al lado inferior.
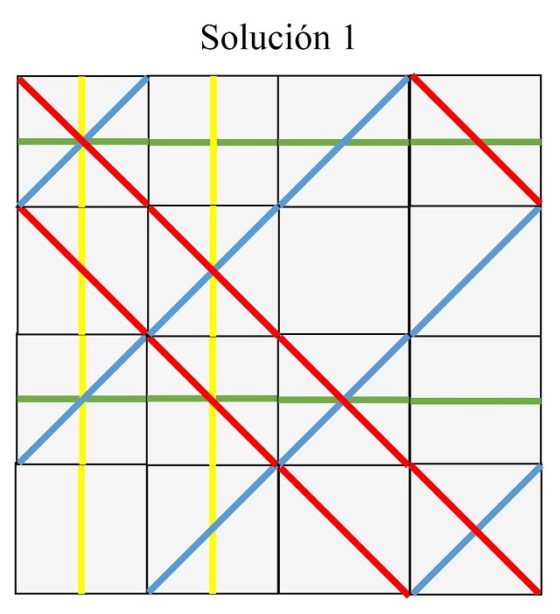
Por ejemplo, una solución del rompecabezas es la que se muestra a continuación (que llamaremos “solución 1”).
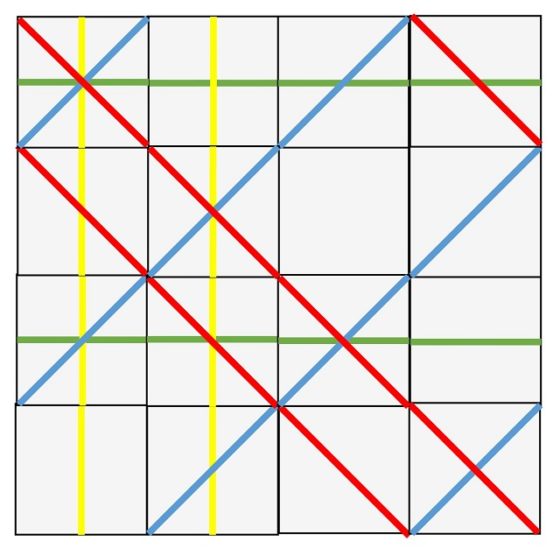 Una de las soluciones del rompecabezas de Sol Lewitt
Una de las soluciones del rompecabezas de Sol Lewitt
Como siempre que hablamos de algún rompecabezas matemático, os animamos a que primero os construyáis las dieciséis piezas geométricas y luego intentéis vosotros mismos encontrar alguna solución al rompecabezas de Sol Lewitt.
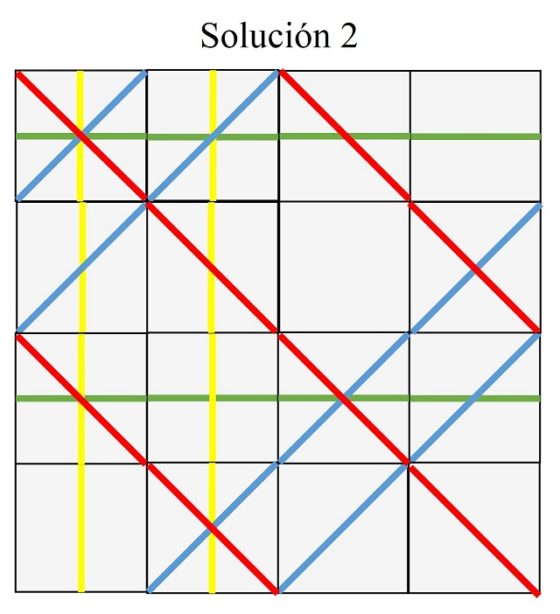
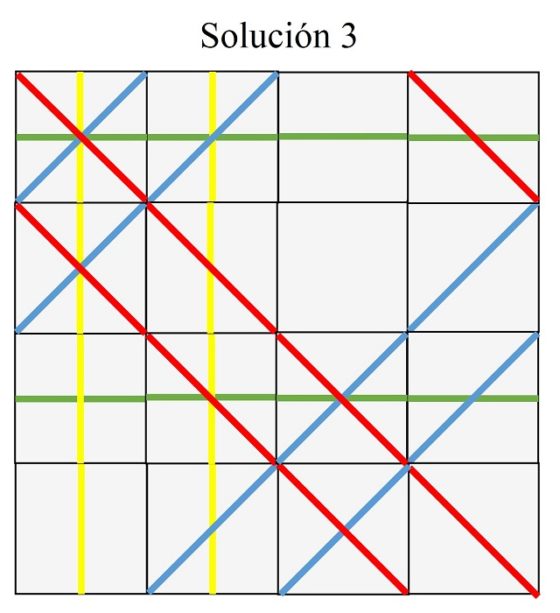
Las soluciones del rompecabezas de Sol LewittCuando el matemático Barry Cipra propuso el rompecabezas de Sol Lewitt, lo hizó sabiendo que existía alguna solución. Sin embargo, fue el matemático británico John H. Conway (1937-2020), de quien hemos hablado en la entrada Teoremas geométricos sin palabras: Conway, quien demostró que había tres soluciones “básicas” distintas (que mostramos al final de esta entrada).
Cuando decimos “básicas” queremos decir que las demás se obtienen a partir de estas a través de una serie de procesos geométricos o matemáticos, que vamos a describir a continuación. Utilizaremos la solución que hemos visto (anterior imagen) para entender mejor estos procesos.
1. Rotación de 90 grados.
Dada una solución del rompecabezas de Sol LeWitt, una rotación de 90 grados (en el sentido contrario de las agujas del reloj) nos da otra solución del rompecabezas. Tengamos en cuenta dos cuestiones. La primera es que, si realizamos una rotación de 90 grados, el conjunto de los 16 diseños combinatorios posibles con cuatro direcciones de líneas rectas –las 16 piezas del rompecabezas– se transforma de nuevo en los 16 diseños combinatorios. Es decir, seguimos teniendo todas las piezas del rompecabezas. Aunque si observamos nuestro añadido de color, las líneas horizontales ahora son amarillas, en lugar de verdes, las líneas verticales son verdes, en lugar de amarillas, las líneas diagonales ascendentes son rojas, en lugar de azules, mientras que las líneas diagonales descendentes son azules, en lugar de rojas. Pero recordemos que el color no es importante, es solo un añadido para ayudarnos a distinguir las líneas de cada dirección. Por otra parte, las líneas continuas al rotarlas siguen siendo líneas continuas, luego obtenemos una nueva solución del juego. En la siguiente imagen podemos observar la rotación de 90 grados (en el sentido contrario de las agujas del reloj) de la solución 1, que es una nueva solución.
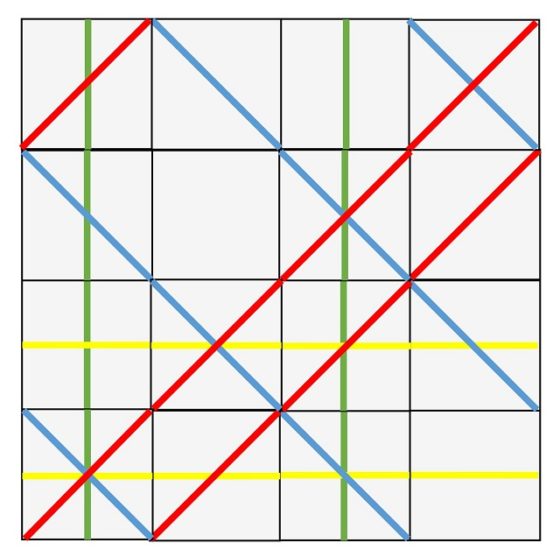 Solución del rompecabezas de Sol LeWitt que consiste en la rotación de 90 grados, en el sentido contrario de las agujas del reloj, de la solución 1
Solución del rompecabezas de Sol LeWitt que consiste en la rotación de 90 grados, en el sentido contrario de las agujas del reloj, de la solución 1
2. Reflexión.
Por otra parte, si realizamos una reflexión de una solución del rompecabezas de Sol LeWitt, es decir, si damos la vuelta a una solución, se obtiene una nueva solución. De hecho, los dos comentarios anteriores para la simetría rotacional siguen siendo válidos para las reflexiones.
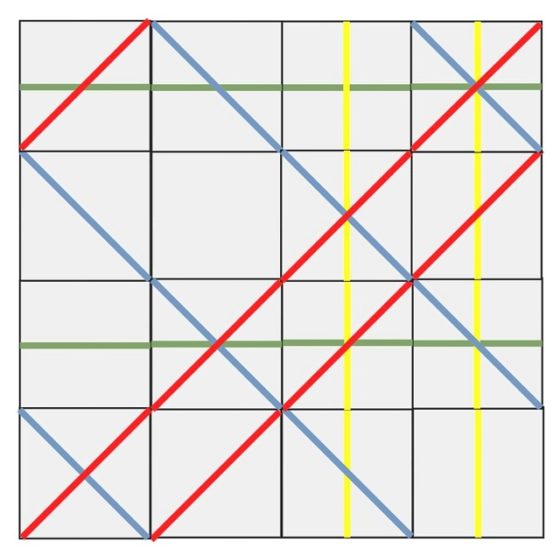 Solución del rompecabezas de Sol LeWitt que consiste en una reflexión vertical, es decir, dar la vuelta a nuestra solución de derecha a izquierda, de la solución 1
Solución del rompecabezas de Sol LeWitt que consiste en una reflexión vertical, es decir, dar la vuelta a nuestra solución de derecha a izquierda, de la solución 1
3. Simetría “toroidal”.
Partamos de nuevo de una solución del rompecabezas de Sol Lewitt, si tomamos la columna de piezas de la izquierda y la trasladamos a la parte derecha (como en la siguiente imagen se ha hecho para la solución 1) se obtiene una nueva solución.
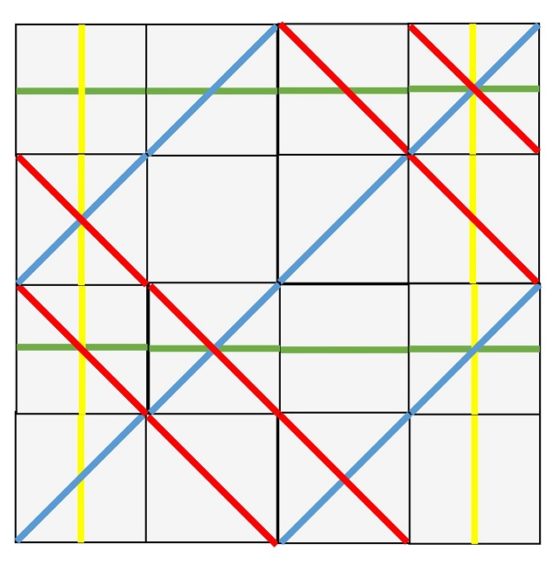 Solución del rompecabezas de Sol LeWitt que consiste en trasladar la columna de la izquierda de la solución 1 al extremo derecho
Solución del rompecabezas de Sol LeWitt que consiste en trasladar la columna de la izquierda de la solución 1 al extremo derecho
Lo mismo ocurre para las filas, si tomamos la fila de arriba de la solución y la trasladamos a la parte de abajo (como en la siguiente imagen se ha hecho para la solución 1) se obtiene también una nueva solución.
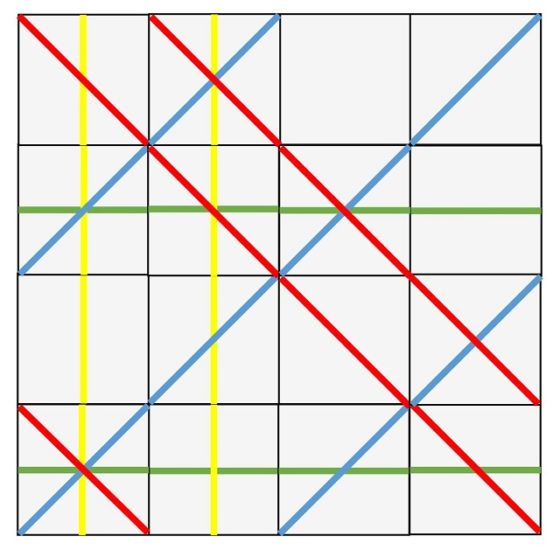 Solución del rompecabezas de Sol LeWitt que consiste en trasladar la fila de arriba de la solución 1 al extremo de abajo
Solución del rompecabezas de Sol LeWitt que consiste en trasladar la fila de arriba de la solución 1 al extremo de abajo
Pensando matemáticamente, es como si nuestra solución del rompecabezas estuviese dibujada sobre la superficie de un toro (matemático), es decir, la parte de la izquierda estuviese “pegada” a la derecha y la parte de arriba a la de abajo.
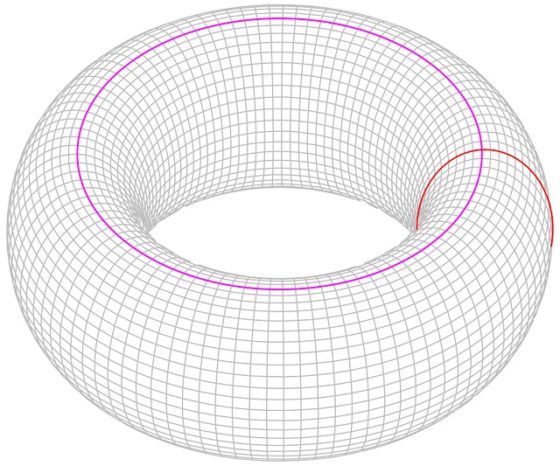 La superficie de un toro. Imagen de Wikimedia Commons, de Krishnavedala
La superficie de un toro. Imagen de Wikimedia Commons, de Krishnavedala
4. Simetría no geométrica.
Existe otro tipo de transformación, aunque no es geométrica, que convierte una solución del rompecabezas en otra distinta. Fijémonos en una cierta dirección de las líneas rectas de las dieciséis piezas que componen el juego (y la obra del artista Sol Lewitt), por ejemplo, en las líneas horizontales. Cada pieza cuadrada o tiene una línea horizontal o no la tiene, y además, la mitad de las piezas la tienen, es decir, ocho piezas, mientras que las otras ocho no la tienen. Nuestra transformación consiste en “quitar” las líneas horizontales de las piezas que las tienen y “ponerlas” en las que no las tienen. De esta forma, nuestra solución del rompecabezas da lugar a una nueva solución. En la siguiente imagen hemos realizado esta operación para la solución 1, obteniendo una nueva solución del juego.
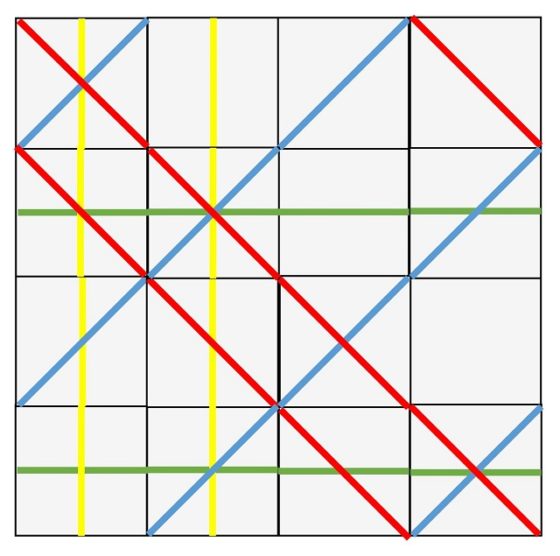 Solución del rompecabezas de Sol LeWitt que consiste en “trasladar” las líneas horizontales de las piezas que las tienen a las piezas que no las tienen en la solución 1
Solución del rompecabezas de Sol LeWitt que consiste en “trasladar” las líneas horizontales de las piezas que las tienen a las piezas que no las tienen en la solución 1
Estos son los cuatro tipos de transformaciones que llevan una solución del juego diseñado por Barry Cipra en otra distinta.
Por lo tanto, lo que demostró el matemático John H. Conway fue que existen únicamente tres soluciones, salvo transformaciones como de las vistas anteriormente, del rompecabezas de Sol Lewitt. La demostración de este resultado puede verse en el artículo de Barry Cipra titulado The Sol LeWitt Puzzle: A Problem in 16 Squares, en Puzzlers’ Tribute: A Feast for the Mind.
Las únicas tres soluciones “básicas” que existen son las siguientes.
Bibliografía:
1.- Barry Cipra, What’s Happening in the Mathematical Sciences 1998-1999, volume 4, AMS, 1999.
2.- Barry Cipra, The Sol LeWitt Puzzle: A Problem in 16 Squares, en Puzzlers’ Tribute: A Feast for the Mind (editores: D. Wolfe and T. Rodgers), A K Peters, 2002.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo El rompecabezas de Sol LeWitt se ha escrito en Cuaderno de Cultura Científica.
Einstein y Niels Bohr
Niels Bohr fue uno de los fundadores de la física del siglo XX, aunque sea recordado mayormente por haber desarrollado la conocida como interpretación de Copenhague de la mecánica cuántica. Intelectualmente a la par, Einstein y Bohr mantuvieron una estrecha amistad, llena de conversaciones animadas y debates científicos. Los dos representan los dos pilares de la física moderna, la relatividad y la mecánica cuántica.
 Einstein y Niels Bohr en Bruselas en 1930. Foto: Paul Ehrenfest / Wikimedia Commons
Einstein y Niels Bohr en Bruselas en 1930. Foto: Paul Ehrenfest / Wikimedia CommonsNiels Bohr comenzó a labrarse una reputación internacional cuando, en 1913, publicó la primera descripción del aspecto que tendría un átomo de hidrógeno cuántico viable: incluyendo un núcleo, el recientemente descubierto electrón y el concepto de estado estacionario. El modelo del átomo de Bohr se basaba en el modelo estrictamente clásico de Ernest Rutherford al que el físico danés añadió la nueva idea de que la energía no era continua, sino que venía en paquetes llamados cuantos. Este apaño de mezclar una vieja teoría con una nueva terminó no siendo la solución perfecta, pero fue el primer paso en el camino hacia la comprensión de la física atómica y representó el comienzo de un maridaje de Bohr con la física atómica que duraría toda su vida. Einstein se interesó inmediatamente por este trabajo. Solamente era seis años mayor que Bohr, y también estaba comenzando a hacerse un nombre; los dos estaban llamados a ser colegas, y cada uno siguió de cerca el trabajo del otro.
A lo largo de la siguiente década tanto Einstein como Bohr crecieron en fama y en estatura intelectual. Einstein se hizo mundialmente famoso cuando su teoría general de la relatividad fue comprobada experimentalmente en 1919, mientras que su trabajo le había proporcionado una cátedra a Bohr en la Universidad de Copenhague en 1916. En 1920 comenzaba a funcionar un centro creado para él por la Universidad, el Instituto de Física Teórica [*].
El primer encuentro entre Einstein y Bohr tuvo lugar en 1920 en Berlín. Como si se conociesen de toda la vida, hablaron de relatividad y física atómica, acerca de la creciente preocupación de Einstein de que la física cuántica estaba abandonando las leyes de la causalidad, acerca de si la luz era una onda o una partícula, acerca, en definitiva, de todo lo que estaba ocurriendo en el mundo de la física. Poco después de esta reunión ambos escribieron cartas en las que expresaban la experiencia tan formidable que había sido. Einstein a Bohr: “No a menudo en la vida un ser humano me ha causado tanta alegría por su mera presencia como tú lo has hecho”. Bohr a Einstein: “Conocerte y hablar contigo ha sido una de las mejores experiencias que nunca haya tenido”.
En 1924, Bohr propuso una teoría junto a Hendrik Anton Kramers y John Clarke Slater que capturó brevemente la imaginación de sus contemporáneos como una posible explicación a cómo interactúan la luz y la materia. La teoría BKS, como se la conoce, resultó ser incorrecta, pero es digna de mención por dos motivos. El primero es que rechazaba la existencia de partículas de luz, insistiendo en que la luz era una onda y solo una onda. En esa época, la mayor parte de la comunidad de físicos estaba de acuerdo en que la luz estaba constituida por cuantos de energía, tal y como Einstein había predicho en 1905 (efecto fotoeléctrico). Bohr sería uno de los últimos en apoyar la idea de que la luz era simultáneamente una onda y un corpúsculo (Einstein fue el primero) y es interesante hacer notar durante cuánto tiempo rechazó la teoría corpuscular de la luz.
Es llamativo que, de igual forma que Bohr fue uno de los últimos en aceptar las partículas de luz, los fotones, una vez que estuvo convencido lo hizo plenamente y sin reservas: apoyó, como converso que era, más fervientemente que nadie el concepto aparentemente absurdo de que la luz era tanto una onda como un corpúsculo, dependiendo de cómo la midieses. Este tipo de cambio de dogma intelectual es muy infrecuente, muchos científicos acabaron su carrera investigadora por no poder aceptar este tipo de cambios; Einstein sería uno de ellos. Einstein escribiría de Bohr treinta años después: “Expone sus opiniones como alguien que está siempre buscando a tientas y nunca como alguien que se cree en posesión de la verdad definitiva”. La grandeza del genio de Bohr estuvo en su increíble capacidad para mantener una mente abierta.
El segundo punto de interés de la teoría BKS es que fue la primera vez en la que Einstein y Bohr estuvieron claramente en campos opuestos. La teoría BKS abandonaba la causalidad y eso era algo que Einstein no estaba dispuesto a aceptar, lo que puso a muchos científicos frente a un dilema. Muchos de ellos respetaban tanto la inteligencia de Einstein y su liderazgo que les resultaba difícil apoyar una teoría que él rechazaba. En un mundo ideal, estos conflictos personalistas no deberían importar a la hora de determinar la corrección objetiva de una teoría, pero incluso los científicos son humanos. El hecho cierto es que tener a dos de los más grandes científicos del momento enfrentados dejó a muchos de sus colegas desubicados. Muchos se negaban a comentar qué científico pensaban que tenía razón, y los que lo hacían estaban muy incómodos con la situación. Cuando se vio forzado a tomar partido, Paul Ehrenfest, amigo íntimo de Einstein, lloró (literalmente) al declarar que pensaba que el punto de vista de Bohr era el correcto.
Los debates Bohr – EinsteinPero pronto todo el mundo tomó partido. La quinta conferencia Solvay, celebrada en octubre de 1927, ha pasado a la historia como uno de los diálogos intelectualmente más transcendentes de la historia contemporánea. Todo el mundo, incluido Einstein, veía la nueva mecánica cuántica como una herramienta matemática muy potente a la hora de predecir cómo funcionaban tanto átomos como partículas subatómicas. Pero había desacuerdos sobre las implicaciones de esa herramienta matemática. Algunos, liderados por Bohr y Werner Heisenberg, creían que la mecánica cuántica era la última palabra. Si las matemáticas decían que el futuro de átomo no era completamente preciso, entonces, simplemente, no lo era. En el otro lado estaban otros cuantos, liderados por Einstein y Erwin Schrödinger, que afirmaban que la mecánica cuántica era una maravillosa herramienta estadística, pero que en la realidad los átomos sí se comportaban con absoluta precisión y algún día, de alguna manera, los científicos desarrollarían teorías completamente nuevas que darían formalismo a esta idea.
Las discusiones ocuparon a los científicos día y noche. Uno de los participantes, Otto Stern, ofreció una narración vívida de la conferencia, describiendo como cada mañana Einstein llegaba al desayuno con una nueva contraargumentación y cada tarde aparecía Bohr con una nueva refutación. Estas discusiones han sido elevadas a la categoría de leyenda, y se las conoce como los debates Bohr-Einstein. De hecho, incluso los participantes parecían estar sobrecogidos ante lo que estaba ocurriendo en esta conferencia. En 1949 Bohr escribió un ensayo, “Discusión con Einstein sobre los problemas epistemológicos en la física atómica”, para el libro “Albert Einstein, filósofo-científico”, en el que atribuye al conjunto de los ingeniosos experimentos mentales propuestos por Einstein el haber sido el catalizador que le permitió llegar a comprender lo que ocurre en el mundo atómico.
Si bien estos debates entre Einstein y Bohr se suelen describir como batallas, Bohr mismo los recordaría como bastante agradables. En el ensayo que mencionábamos Bohr se refiere a los nuevos experimentos mentales de Einstein como “graciosos” y, Einstein en plan de burla preguntaba si “las autoridades providentes recurrían a las tiradas de dados”. En el transcurso de la conferencia las cosas se volvieron en contra de Einstein completamente. Los que antes de la conferencia habían tenido dudas, al final de la misma aceptaban la versión de Bohr de la mecánica cuántica. Esta versión llegó a ser conocida como la interpretación de Copenhague (tanto Bohr como Heisenberg eran profesores de esa universidad en el momento de celebrase la conferencia).
Einstein, sin embargo, nunca aceptó la interpretación de Copenhague, y los debates entre Einstein y Bohr continuaron durante décadas. En la sexta conferencia Solvay, celebrada en Bruselas en 1930 (y a la que corresponde la imagen, tomada por Ehrenfest), Einstein presentó un nuevo experimento mental: si una caja llena de radiación fuese dispuesta de tal manera que estuviese sobre una balanza, y que un reloj controlase que un fotón y sólo un fotón escapase de la caja en un momento concreto, se podría medir perfectamente el cambio de peso de la caja. Por tanto, y de forma simultánea, se podría medir el tiempo y la cantidad de energía de ese fotón, en abierta contradicción con el principio de incertidumbre de Heisenberg, que afirmaba que esas dos magnitudes no podían conocerse con precisión a la vez. Bohr estuvo perplejo durante unas doce horas, llegando a decir “sería el fin de la física si Einstein tuviese razón”. Pero a la mañana siguiente Bohr apareció con una refutación (además una que escoció a Einstein): teniendo en cuenta la teoría de la relatividad, al retroceder la caja debido a la emisión del fotón, el tiempo mismo del marco de referencia de la caja se vería afectado. El tiempo, después de todo, no podía medirse de forma precisa. Los dos hombres continuaron la discusión pero esa fue la última conferencia Solvay a la que asistiría Einstein, ya que en 1933 abandonaría Europa para nunca más volver.
Volverían a encontrarse en los Estados Unidos cuando Bohr visitó Princeton. Y seguían con la misma dinámica. Bohr también refutó uno de los más famosos experimentos mentales de Einstein, el argumento Einstein-Podolsky-Rosen. Bohr nunca convenció a Einstein, como no lo consiguió ningún otro físico, de que aceptara la interpretación de Copenhague.
A pesar de la Resistencia de Einstein a aceptar la interpretación de Copenhague, él consideraba que el desarrollo de la mecánica cuántica había sido una enorme logro, uno que debería incorporarse a la “teoría verdadera”, sea esta la que fuese, que tendría que desarrollarse dentro de no demasiado tiempo. Einstein también consideraba asombrosa la aportación de Bohr a la mecánica cuántica. En el ensayo que escribió en 1949 para “Albert Einstein, filósofo-científico”, Einstein afirmaría: “El que esta base tan insegura y contradictoria fuese suficiente para permitir a un hombre, con el instinto y tacto únicos de Bohr, descubrir las leyes principales de las líneas espectrales y de las capas de los electrones de los átomos, junto con su importancia para la química, me parece un milagro; y me sigue pareciendo un milagro incluso hoy”.
A pesar de una vida de disputas acerca de la mecánica cuántica, la amistad entre estos hombre se mantuvo sólida y sincera, ayudada por una tremenda admiración de la inteligencia genial del otro.
Nota:
[*] En la actualidad Instituto Niels Bohr. Se creó con fondos en su mayoría provenientes de la empresa de cervezas Carlsberg, la misma que llevaba financiando los viajes de estudios de Bohr en los últimos años. Desde 1931 hasta su muerte Bohr viviría como huésped en un palacete que fue propiedad del fundador de la empresa.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Una versión anterior de este artículo se publicó en Experientia Docet el 1 de agosto de 2010.
El artículo Einstein y Niels Bohr se ha escrito en Cuaderno de Cultura Científica.
El misterio de Fobos y Deimos
Los satélites de Marte, Fobos y Deimos, han sido -y siguen siendo- uno de los grandes misterios de la geología planetaria, en tanto que todavía no comprendemos muy bien su mecanismo de formación. Por su aspecto, muy parecido al de un asteroide común, y el espectro de la luz reflejada por la superficie, similar al de los asteroides de tipo D (asteroides muy primitivos, cuya composición estaría formada principalmente por silicatos, compuestos orgánicos e incluso por hielo de agua), se ha pensado durante décadas que podrían haber sido asteroides capturados al pasar cerca del planeta Marte.
 Fobos visto desde la Mars Reconaissance Orbiter. NASA / JPL-Caltech / University of Arizona
Fobos visto desde la Mars Reconaissance Orbiter. NASA / JPL-Caltech / University of Arizona¿Cómo podía Marte capturar unos satélites de este tamaño con su campo gravitatorio? Pues algunos científicos pensaron que esto sería posible si Fobos y Deimos hubiesen pasado a través de la atmósfera de Marte, frenándose, y esta pérdida de velocidad facilitando su entrada en órbita alrededor de Marte en vez de continuar su camino. Esta teoría, francamente, era muy difícil de asumir, ya que la atmósfera de Marte es muy tenue, no siendo suficiente para frenar los cuerpos, y sabemos por su densidad que estructuralmente cualquiera de estos dos satélites hubiera tenido muy difícil sobrevivir a este mecanismo de captura, fragmentándose y cayendo sobre el planeta debido a las enormes tensiones que hubiese sufrido en su contacto con la atmósfera.
Otro autor, Landis (2002), sugiere que en realidad los satélites de Marte no es que fuesen asteroides capturados, sino que serían los satélites de sistemas binarios de asteroides que Marte robaría con su campo gravitatorio al pasar cerca de Marte, quedándose girando alrededor del planeta rojo.
Pero estos mecanismos no convencen del todo a la comunidad científica, ya que, entre otras cosas, las órbitas de estos satélites deberían, si fueron capturados, ser bastante elípticas en comparación con lo que observamos, aunque por supuesto, los autores de estas teorías proponen mecanismos adicionales que permitirían una circularización orbital con el paso del tiempo.
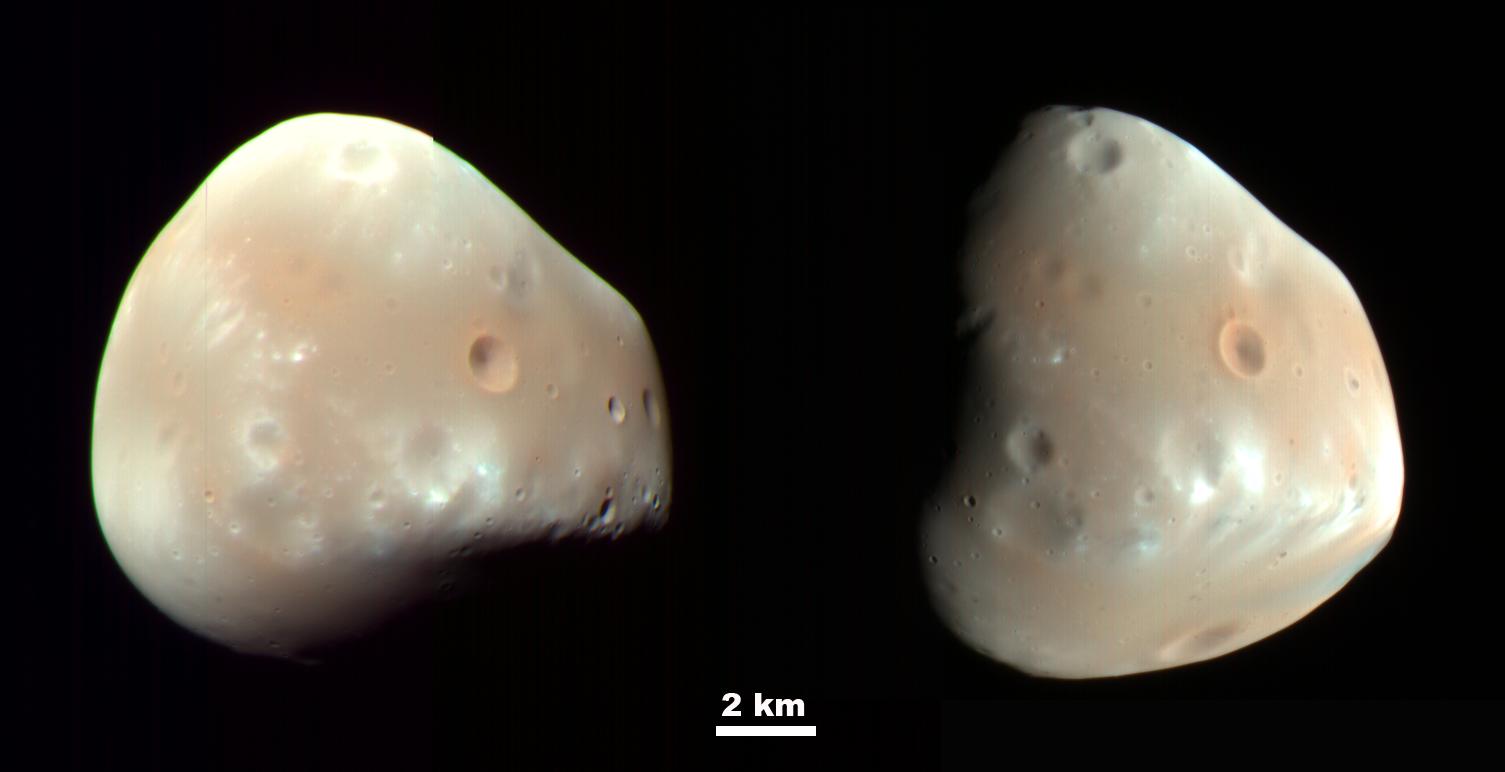 Deimos captado por la Mars Reconaissance Orbiter. NASA / JPL-Caltech / University of Arizona.
Deimos captado por la Mars Reconaissance Orbiter. NASA / JPL-Caltech / University of Arizona.La mayoría de la comunidad científica hoy día se inclina por un escenario muy similar al de la formación de nuestro satélite, la Luna: uno o varios grandes impactos contra Marte lanzarían al espacio un anillo de material rocoso que poco a poco iría coalesciendo hasta formar los satélites.
Esta teoría es muy atractiva porque sabemos que especialmente en la infancia de nuestro Sistema Solar la ocurrencia de grandes impactos era algo relativamente habitual, por lo que es un mecanismo muy posible, y los satélites formados a partir de un anillo pueden conservar una órbita más o menos circular, como la que se observa en ambos satélites de Marte.
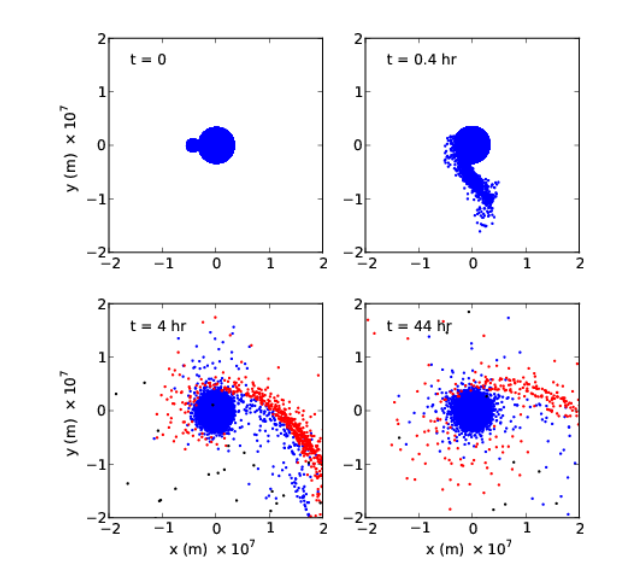 Simulación de la formación de los satélites de Marte mediante un impacto gigante, donde se aprecia la gran cantidad de materia que sale despedida como fruto de la colisión. Imagen cortesía de Citron et al. (2015).
Simulación de la formación de los satélites de Marte mediante un impacto gigante, donde se aprecia la gran cantidad de materia que sale despedida como fruto de la colisión. Imagen cortesía de Citron et al. (2015).Además, cuando observamos de cerca a Fobos y Deimos vemos su superficie completamente cubierta por cráteres de impacto, lo que nos hace pensar -pendientes de poder traer muestras que podamos datar en nuestro planeta- que son satélites formados hace mucho tiempo, por lo que su edad de formación y esa etapa violenta del Sistema Solar podrían coincidir.
Pero todavía hay al menos una teoría más y que desde hace algún tiempo rondaba la mente de algunos de los científicos: ¿Y si Fobos y Deimos en realidad fueron originalmente un solo satélite?
Esta teoría dice que Marte poseía un satélite que fue destrozado o bien por un violento impacto o bien por la gravedad de Marte al acercarse al límite de Roche, una distancia a la cual un cuerpo astronómico, al acercarse a otro, acaba desintegrándose porque la fuerza de gravedad que ejerce el cuerpo más grande es superior a la fuerza que mantiene unido y cohesionado al cuerpo más pequeño. Un ejemplo de este fenómeno lo tenemos en la fragmentación del cometa Shoemaker-Levy 9 en julio de 1992, y cuyos restos acabarían impactando contra Júpiter en 1994.
 Fragmentos del cometa Shoemaker-Levy 9 antes de su colisión con Júpiter, observados en mayo de 1994 por el telescopio espacial Hubble. NASA, ESA, and H. Weaver and E. Smith (STScI)
Fragmentos del cometa Shoemaker-Levy 9 antes de su colisión con Júpiter, observados en mayo de 1994 por el telescopio espacial Hubble. NASA, ESA, and H. Weaver and E. Smith (STScI)Este fenómeno habría ocurrido aproximadamente en un rango de fechas que oscila entre los 1000 y los 2800 millones de años (Bagheri et al. (2021)). Al fragmentarse ese satélite primigenio, se habría formado un enorme anillo rocoso alrededor de Marte, posteriormente uniéndose parte de esos trozos y formando sus dos satélites actuales, mientras que otra parte del material habría caído, probablemente, de nuevo sobre la superficie del planeta.
Pero un nuevo estudio publicado en agosto de este mismo año por Landis et al. (2022) empieza a poner en serios apuros a esta teoría: Las simulaciones demuestran que si hubiese ocurrido esto, Marte todavía tendría un sistema de anillos, algo que no observamos en la actualidad.
Pero, además, han realizado numerosas simulaciones en las que han reconstruido la evolución de las órbitas de Fobos y Deimos tal y como si se hubiesen formado a partir de un satélite anterior, observando que tenían unas probabilidades muy altas de chocar a muy alta velocidad, destruyendo ambos satélites en el impacto, de nuevo generando un sistema de anillos que hoy también sería visible.
Así que, de momento, seguimos sin saber con cierto nivel de seguridad como pudieron formarse sus satélites, aunque de momento la teoría que más aceptada se encuentra en la comunidad científica hoy día es que fueron formados a partir de uno o grandes impactos que pusieron en órbita de Marte el material suficiente para dar lugar a estos satélites, aunque todavía queda mucho tiempo para poder confirmar qué pasó realmente.
Si todo va bien, en septiembre de 2024 despegará rumbo a Marte la misión Martian Moons eXploration (MMX), que no solo se encargará de estudiar los satélites marcianos desde la distancia con sus cámaras y espectrómetros, sino que intentará tomar muestras de Fobos para su retorno a la Tierra, que está programado para el mes de julio de 2029, y con las que probablemente podamos responder a cuál fue el verdadero origen de estos satélites marcianos.
Referencias:
Landis, G. (2002). Origin of Martian Moons from Binary Asteroid Dissociation. Accedido: 12 Septiembre de 2022, de 10.48550/arXiv.0903.3434
Citron, R., Genda, H., & Ida, S. (2015). Formation of Phobos and Deimos via a Giant Impact. ArXiv. 10.48550/ARXIV.1503.05623
Bagheri, A., Khan, A., Efroimsky, M. et al. Dynamical evidence for Phobos and Deimos as remnants of a disrupted common progenitor. Nat Astron 5, 539–543 (2021). doi: 10.1038/s41550-021-01306-2
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo El misterio de Fobos y Deimos se ha escrito en Cuaderno de Cultura Científica.
La vida del metabolismo
 Foto: Paolo Bendandi / Unsplash
Foto: Paolo Bendandi / UnsplashAunque a veces percibimos el latido del corazón, por regla general no somos conscientes de lo que ocurre en nuestro interior. Lo normal es que no percibamos, por ejemplo, el trajín de las neuronas, ni el trasiego de sales y agua en los riñones. La física y química subyacentes a esos procesos son las que conforman el metabolismo basal, las que nos mantienen vivos. La energía que gastamos en ellas es el precio que, en todo momento, pagamos por estar vivos y viene a representar entre el 50% y el 70% de toda la que utilizamos.
Otros procesos físicos y químicos nos permiten desarrollar actividades tales como hablar, andar o trabajar. A la larga, también los necesitamos para vivir, aunque no en todo momento; la actividad metabólica correspondiente está vinculada a esas actividades físicas. Llamamos metabolismo de rutina, o habitual, a la suma de ambas fracciones.
En la fase fetal el metabolismo es intenso. Por un lado, los organismos de pequeño tamaño tienen, de suyo, una actividad metabólica muy alta; es un fenómeno biológico universal. Y por el otro, el feto es un organismo en crecimiento, en su interior se están formando órganos y tejidos nuevos con rapidez y esa actividad es metabólicamente cara. No obstante, si se descuenta el efecto del tamaño, la intensidad metabólica total de los más pequeños no es tan alta; estaría por debajo, incluso, de la de las personas adultas. Influye el hecho de que en el útero materno la actividad física está, muy comprensiblemente, limitada.
Después del nacimiento, ambos niveles metabólicos, el basal y el habitual, se elevan muy rápidamente hasta alcanzar valores máximos alrededor del primer año de vida. Las criaturas de esa edad tienen un metabolismo que es, descontado el antedicho efecto del tamaño, un 50% más intenso que el de los adultos. La gran producción de tejido nuevo que exige el crecimiento está en la base de ese metabolismo tan alto. Este es un aspecto importante, porque cuanto más intensa es la actividad metabólica, más alimento hay que suministrar al bebé en construcción.
A partir de los 15 meses de vida, el metabolismo desciende hasta los 20 años, para mantenerse después prácticamente constante hasta la quinta o sexta década. En torno a esta edad vuelve a iniciarse un descenso en el nivel metabólico que parece estar relacionado con el deterioro orgánico que se produce asociado al envejecimiento. Salvo durante la fase fetal, en la que el metabolismo ligado a la actividad es de menor entidad, durante el resto de la vida ambas fracciones, la correspondiente al mantenimiento vital y la asociada a la actividad física, llevan cursos bastante paralelos.
El descenso con la edad de la actividad metabólica basal ocurre, en gran medida, porque se reduce la actividad biológica de todos los órganos y, en especial, de los más activos metabólicamente, como el encéfalo y el hígado. Y el de la componente ligada a la actividad muscular, porque tras alcanzar valores máximos entre los 5 y los 10 años, desciende hasta los 18 con rapidez, se estabiliza a continuación, y vuelve a descender más lentamente a partir de los 45 años, aproximadamente.
En síntesis, el periodo vital de máxima intensidad metabólica basal es el primer año de vida, debido al fuerte crecimiento de órganos muy activos metabólicamente. El de máxima actividad física, son los años anteriores a la pubertad. La intensidad metabólica mínima se alcanza a edades avanzadas, pasados los 70, para ambas componentes del metabolismo, porque tanto la actividad de órganos y tejidos como la del sistema muscular se encuentran en declive ya desde años antes.
Fuente: Pontzer, H., Yamada, Y., Sagayama, H. et al, Daily energy expenditure through the human life course. Science 13 Aug 2021, 373 (6556): 808-812 DOI: 10.1126/science.abe5017
Para saber más:
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo La vida del metabolismo se ha escrito en Cuaderno de Cultura Científica.
CienciaClip 2020 – El eleixir de la eterna juventud

Ciencia Clip es un concurso de vídeos divulgativos de ciencia diseñados, producidos y protagonizados por estudiantes de Educación Secundaria.
El objetivo del concurso es fomentar el interés por la ciencia y la tecnología. Y ofrecer a los concursantes una oportunidad para ejercitar su creatividad y habilidades comunicativas usando herramientas que proporciona internet.
Ciencia Clip es una iniciativa de la Cátedra de Cultura Científica de la UPV/EHU y en la que colaboran Euskampus Fundazioa, Naukas, Scenio y Big Van.
Los ganadores de la edición 2022 ya están en la página web del concurso. La entrega de premios y el anuncio del vídeo ganador del premio especial se realizarán durante el evento Naukas Bilbao. En la edición de 2020 resultó ganador en la categoría de 3º y 4º de de la ESO Luis Gutiérrez, de Cáceres, con este vídeo:
Edición realizada por César Tomé López
El artículo CienciaClip 2020 – El eleixir de la eterna juventud se ha escrito en Cuaderno de Cultura Científica.
El acoso escolar se ceba en los estudiantes con altas capacidades
 Shutterstock / Ground Picture
Shutterstock / Ground PictureLa violencia entre iguales es uno de los problemas que más preocupación social suscita en los centros educativos debido a su prevalencia, su gravedad y su relación con variables de salud y de ajuste psicosocial. Numerosos estudios han puesto de manifiesto problemas de salud física, dificultades emocionales y de comportamiento, desarrollo social problemático y bajo rendimiento académico asociados a la exposición de los jóvenes a esta violencia. El acoso escolar se define como una forma de violencia en la que una o varias personas agreden a otro igual (o iguales) de forma repetida en el tiempo con intención dolosa, habiendo un desequilibrio de poder entre las partes implicadas.
Una “pandemia” escolarEl acoso escolar (y particularmente la violencia entre iguales) es un fenómeno de naturaleza “pandémica”, es decir, es una problemática que se extiende a muchos países y continentes, traspasa fronteras, supera el número de casos esperados y persiste en el tiempo.
Para constatar esta triste afirmación, remitimos al lector al informe de la UNESCO de 2018 sobre el asunto. En él se recogen datos de encuestas internacionales en más de 40 países en alumnado entre los 11 y los 17 años. Los resultados revelan que aproximadamente uno de cada tres estudiantes ha sido acosado por sus compañeros durante uno o más días en el mes previo a la encuesta.
En España, según el Informe realizado por UNICEF en 2021, encontramos que los datos de victimización por acoso escolar varían entre el 22.5 % y el 33.6 %, según los puntos de corte. De tal forma que entre 2 y 3 alumnos de cada 10 son víctimas.
Alumnos con altas capacidadesLa relación del acoso escolar y el alumnado con altas capacidades lleva en estudio casi dos décadas con resultados muy dispares: unos reportan más acoso a este colectivo, otros no perciben diferencias y unos pocos sostienen que el alumnado con altas capacidades padece menos acoso que el alumnado sin altas capacidades.
Los datos preliminares en España ya sugerían que había un problema relevante con este grupo heterogéneo de alumnos y parecían indicar que estos recibirían los envites de la violencia con mayor frecuencia.
Nuestro estudio es el más amplio en el ámbito español sobre acoso escolar y altas capacidades hasta la fecha. Han participado 449 adolescentes diagnosticados con altas capacidades de todo el territorio nacional y 950 estudiantes sin diagnóstico de altas capacidades, de 14 centros de siete comunidades autónomas (Principado de Asturias, Comunidad de Madrid, Castilla-La Mancha, Castilla y León, Comunidad Valenciana, Comunidad de Aragón y País Vasco).
Los resultados señalan que el alumnado con altas capacidades presenta una prevalencia de victimización significativamente superior: el 50,6 % está implicado en problemas de victimización, frente a un 27,6 % del alumnado sin altas capacidades.
Por el contrario, el número de agresores puros (es decir, que solo son agresores) en ambas muestras no presenta diferencias estadísticamente significativas (un 1,1 % en alumnado con altas capacidades y 2,4 % en alumnado sin altas capacidades).
Efectos y causasLa violencia afecta a todo aquel que la recibe, aunque también a quien la ejerce y a quien la observa. De tal manera que toda persona que esté relacionada con un circuito de violencia va a verse afectada por ella y los datos del estudio lo corroboran.
Ser víctima o víctima–agresiva está relacionado con altos niveles de estrés, ansiedad, depresión y una menor calidad de vida relacionada con la salud para todo tipo de alumnado. No obstante, las víctimas que presentan altas capacidades reportaron significativamente mayor estrés que las víctimas sin altas capacidades.
En el contexto social en el que nos movemos, cualquier diferencia puede hacer que las personas no mimetizadas con su entorno sean vistas como objetivo potencial de burlas, mofas, agresiones verbales o físicas, etc.
De una parte, esta mayor victimización del alumnado con altas capacidades puede deberse a su constitución como grupo minoritario, siendo este rasgo de minoría versus mayoría (población general en edad escolar) el que puede explicar parte de la propensión a ser acosados.
Distintos a los demásEsta diferencia puede darse en cualquier sentido (independientemente de si es algo positivo o no) y puede volverse un factor de riesgo para la victimización. Las diferencias pueden ser de todo tipo: físicas, como ser muy alto, bajo, obeso o delgado; presentar problemas con el habla (disfemia); llevar aparato corrector dental, gafas o implantes cocleares; pertenecer a un grupo étnico minoritario, una religión distinta a la de la mayoría o tener una orientación sexual no normativa.
Además de lo dicho, la teoría de identidad social, señala que los procesos intergrupo llevan a los individuos a comportarse de tal manera que se favorezca al propio grupo (endogrupo) y se discrimine a otros (exogrupo).
Los efectos de contraste grupal son cruciales para el desarrollo de sus normas y señales de identidad y se basan típicamente en la característica más destacada que distingue a sus miembros (paradigma mínimo dentro del grupo), lo que justifica la intimidación simplemente porque un compañero no es miembro del endogrupo, fomentando incluso la agresión.
Este efecto de distanciarse del exogrupo ha sido encontrado incluso en niños de 4 y 5 años. De esta forma puede comprenderse mejor cómo distintos grupos minoritarios sufren más victimización en comparación con el grupo mayoritario.
El respeto a la diferenciaAl menos dos de los retos clave pendientes son:
- Que los centros sean entornos seguros para todo el alumnado.
- Incluir y respetar lo diferente en el contexto escolar.
De forma general, desde la sociedad, la familia y otros ámbitos de socialización se sigue viendo lo “diferente” como negativo. Esta es la primera gran reflexión de fondo: la aceptación de las diferencias y de la diversidad es una gran asignatura pendiente.
Claves para el futuroLos alumnos con altas capacidades son diversos, también entre sí, por lo que este hecho diferencial no aceptado los hace más vulnerables. Si además, la concepción que se tiene de ellos es incorrecta o está difuminada y teñida de estereotipos, el problema se agrava. Para evitarlo, es necesario, al menos:
- Comprender correctamente qué significa presentar altas capacidades.
- Identificar adecuadamente a esta población.
- Desbancar los numerosos mitos en torno a las altas capacidades, que causan un problema cierto en esta población escolar y en sus entornos familiares.
- Abordar la atención educativa del alumnado con altas capacidades de manera adecuada y evitar, especialmente, que el docente señale al alumno o alumna con altas capacidades como diferente.

Autores: Joaquín Manuel González Cabrera, Universidad Internacional de La Rioja ; Javier Tourón, Universidad Internacional de La Rioja y Juan Manuel Machimbarrena, Universidad del País Vasco / Euskal Herriko Unibertsitatea
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo El acoso escolar se ceba en los estudiantes con altas capacidades se ha escrito en Cuaderno de Cultura Científica.
Y a ti, ¿cómo te llamamos?
Recientemente se ha descubierto un nuevo mineral cerca de Moaña, un municipio localizado en la provincia de Pontevedra, que ha recibido el nombre de ermeloita.
 Muestra del nuevo mineral ermeloita siendo analizada en los laboratorios de la Universidad de Santiago de Compostela (USC). Fuente: USC.
Muestra del nuevo mineral ermeloita siendo analizada en los laboratorios de la Universidad de Santiago de Compostela (USC). Fuente: USC.Si habéis intentado pronunciar dicho nombre en voz alta un par de veces seguidas, es probable que se os haya trabado un poco la lengua y estéis pensando ahora mismo: Pero, ¿cómo se les ha ocurrido ponerle ese nombre tan raro?
Esta pregunta nos la podríamos hacer para todos y cada uno de los minerales que conocemos hoy en día. Y es a la que voy a tratar de dar respuesta en este artículo.
Aunque no lo creáis, hay un organismo internacional que se encarga de vigilar tanto la nomenclatura como la correcta clasificación sistemática de los minerales de todo el mundo, la Commission on New Minerals, Nomenclature and Classification (CNMNC) of the International Mineralogical Association (IMA). O, en castellano, la Comisión de Nuevos Minerales, su Nomenclatura y Clasificación de la Asociación Mineralógica Internacional. Vamos, que si descubrimos un mineral desconocido por la ciencia hasta ese momento y queremos ponerle un nombre, tenemos que seguir sus reglas.
Y es entonces cuando tenemos dos caminos que podemos seguir a la hora de elegir dicho nombre. O bien lo hacemos de una manera más formal y aludimos a alguna propiedad o característica de ese nuevo mineral, tales como su composición química o su color, o nos convertimos en espíritus libres y le damos una denominación que no nos aporta ninguna información propia del mineral.
 Venas de calcita (color blanco) recristalizadas en una baldosa de la roca ornamental “Negro Markina” empleada en un soportal de Bilbao. Fuente: Blanca María Martínez
Venas de calcita (color blanco) recristalizadas en una baldosa de la roca ornamental “Negro Markina” empleada en un soportal de Bilbao. Fuente: Blanca María MartínezComo ejemplos de nombres más formales e informativos, podemos encontrarnos con la calcita, llamada así porque tiene calcio en su composición, o la magnesita, que incluye el magnesio. Y seguro que os suenan la cianita, que es de un color azul brillante, y el oropimente, que presenta un color amarillento dorado.
Pero es por la vía más informal de nomenclatura donde aparecen los nombres de minerales más curiosos e, incluso, divertidos.
Es aquí donde podemos incluir el granate. Puede que penséis que me he confundido al no ponerlo junto a la cianita y el oropimente creyendo que su nombre procede del color rojo oscuro al que conocemos, precisamente, como granate, pero es que el origen de su nombre es muy particular. El granate mineral se denomina así porque recuerda a las semillas, o granos, de la granada, la fruta del árbol conocido como granado.
 Muestra de goethita exhibida en el “Paseo Geológico de Bizkaia”, situado en el Arboretum del Campus de Leioa de la Universidad del País Vasco UPV-EHU. Fotografía de Ana Pascual (Departamento de Geología, UPV-EHU)
Muestra de goethita exhibida en el “Paseo Geológico de Bizkaia”, situado en el Arboretum del Campus de Leioa de la Universidad del País Vasco UPV-EHU. Fotografía de Ana Pascual (Departamento de Geología, UPV-EHU)Un segundo grupo de nombres hace mención o sirve como homenaje a personas famosas, no siempre relacionadas con la Geología o la Mineralogía. Como ejemplos tenemos la goethita, dedicada al filósofo alemán Johann Wolfgang von Goethe. O la livingstonita, nombrada en honor al explorador escocés David Livingstone, al que Stanley saludó con su famosa frase “el doctor Livingstone, supongo” cuando lo encontró en el corazón de África. O la smithsonita, llamada así en homenaje a James Smithson, el mineralogista inglés con cuya herencia se fundó la Institución Smithsonian.
Y hay un tercer grupo de nombres que se refieren a localidades geográficas. Entre ellos nos encontramos con la jarosita, cuya nomenclatura se refiere al Barranco Jaroso, situado en la Sierra Almagrera, provincia de Almería. También tenemos el aragonito, que hace alusión a Molina de Aragón, localidad de la provincia de Guadalajara y que se ha elegido como imagen central del logotipo del Geoparque Mundial Unesco de Molina de Aragón-Alto Tajo. O la villamaninita, que se refiere a Villamanín, villa de la provincia de León.
Pues es en este último grupo donde también podemos incluir al nuevo mineral ermeloita, ya que su nombre procede de la zona donde se ha descubierto, el Monte Ermelo.
Aquí solo os he puesto unos pocos ejemplos, pero hay miles de minerales descubiertos hasta la fecha con los que podéis pasar un buen rato buscando el origen de sus nombres. Algunos son muy, pero que muy curiosos.
Referencia:
Zaragoza Vérez, G., Rodríguez Vázquez, C. J., Fernández Cereijo, I., González del Tánago, J., Jiménez Martínez, R., Dacuña Mariño, B., Barreiro Pérez, R., Vázquez Fernández, E., Gómez Dopazo, M., and Lantes-Suárez, O. (2022). Ermeloite, IMA 2021-017a, in: CNMNC Newsletter 68, Eur. J. Mineral., 34, doi: 10.5194/ejm-34-385-2022.
Para saber más:
Introducción histórica a la mineralogía
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo Y a ti, ¿cómo te llamamos? se ha escrito en Cuaderno de Cultura Científica.
Alison Hartcourt y Ailsa Land, dos matemáticas unidas por la programación lineal
Alison Hartcourt yAilsa Land definieron en 1960 un algoritmo para resolver problemas de programación discreta. El influyente artículo en el que introdujeron este algoritmo ha tenido un enorme impacto en la literatura académica y en la resolución práctica de problemas económicos y sociales. Muchas personas desconocen que dos mujeres son las autoras de ese trabajo: ellas ocultaron deliberadamente sus nombres.
 Fuente: Jstor
Fuente: JstorAlison Hartcourt (1929)
“La estadística es números con contexto, y el contexto siempre ha sido importante para mí”.
 Alison Harcourt. Fuente: U. de Melbourne.
Alison Harcourt. Fuente: U. de Melbourne.
Alison Doignació el 24 de noviembre de 1929 en Colac (Victoria, Australia). Su madre, Louie Grant, y su padre, el médico Keith Doig, eran de ascendencia escocesa. Tenía una hermana y dos hermanos.
Tras su educación escolar, Alison se matriculó en la Universidad de Melbourne, donde obtuvo un bachillerato universitario en letras con mención en matemáticas y, posteriormente, un bachillerato universitario en ciencias con mención en física. Como muestra de sus habilidades científicas, mientras realizaba un máster para especializarse en estadística, desarrolló una técnica para la programación lineal entera.
Precisamente gracias a sus conocimientos en programación lineal, a finales de los años 1950 comenzó a trabajar en el London School of Economics (LSE). En 1960, junto a Ailsa Land, publicó un artículo histórico en la revista Econometrica en el que describía un algoritmo de optimización de ramificación y poda para resolver problemas NP-complejos. Este algoritmo tiene aplicaciones en diversos campos, que van desde la logística de transporte hasta la optimización del ángulo del haz de partículas en los tratamientos por radioterapia. Las dos investigadoras publicaron el artículo escondiendo sus nombres, tan solo con sus iniciales, para evitar que su trabajo fuera considerado “de segunda” por el hecho de ser mujeres.
En 1963, Doig regresó a Australia, siendo contratada como profesora titular de estadística en la Universidad de Melbourne.
A mediados de la década de 1960 se unió al equipo liderado por el sociólogo Ronald Henderson (1917-1994) que intentaba cuantificar el alcance de la pobreza en Australia. Este grupo desarrolló en 1973 la llamada Línea de Pobreza Henderson, el ingreso mínimo requerido para cubrir las necesidades básicas de una familia formada por dos adultos y dos niños. Las técnicas desarrolladas por el equipo de Henderson han sido utilizadas desde 1979 por el Instituto de Investigación Económica y Social Aplicada de Melbourne para actualizar regularmente el umbral de pobreza en Australia.
En 1970, Alison pidió una licencia de estudios para viajar a Suecia, donde fue coautora de dos artículos sobre química teórica junto a su marido, el químico Richard Harcourt, con el que se había casado en 1968 y con el que tuvo dos hijos.
En 1975, tras la destitución del Primer ministro de Australia, el laborista Gough Whitlam, Alison Harcourt y el estadístico Malcolm Clark notaron irregularidades en la distribución del orden de los partidos en las papeletas electorales del Senado para las elecciones federales de 1975. Lo descubrieron al observar que, en todos los estados, los partidos de la coalición ocupaban siempre una de las dos primeras posiciones.
Harcourt y Clark presentaron un informe al Comité Selecto Conjunto sobre la Reforma Electoral, dosier que en 1984 terminó en una enmienda a la Ley Electoral de la Commonwealth para introducir un nuevo método de asignación aleatoria doble a la hora de establecer las posiciones de los partidos políticos en las papeletas de votación. Este sistema todavía se usa en la actualidad. Harcourt y Clark publicaron un artículo sobre su estudio, con recomendaciones, en 1991.
Harcourt se jubiló en 1994, aunque continuó como asesora estadística durante varios años.
Entre otros muchos reconocimientos, en junio de 2019, Alison Harcourt fue nombrada Oficial de la Orden de Australia en reconocimiento a “su servicio distinguido a las matemáticas y la informática a través de la investigación pionera y el desarrollo de la programación lineal entera”.
Ailsa Horton Land (1927-2021)“Optamos por presentarlo [el artículo] solo con nuestras iniciales y apellidos de manera deliberada. Una elección que no creo que parezca apropiada hoy en día”.
 Ailsa Land. Fuente: Wikimedia Commons.
Ailsa Land. Fuente: Wikimedia Commons.
Ailsa Dicken nació el 14 de junio de 1927 en West Bromwich (Staffordshire, Inglaterra). Era la única hija de Elizabeth Greig y Harold Dicken.
Ailsa tenía un gran interés por la ciencia, pero tuvo malos resultados en la escuela primaria local por motivos de disciplina. Su familia decidió entonces enviarla a un pequeño internado mixto en Hastings durante un año. Este centro escolar tenía un enfoque especial en matemáticas, y su cincuentena de estudiantes trabajaba a su propio ritmo.
Cuando estalló la Segunda Guerra Mundial, Ailsa y su madre emigraron a Canadá para pasar una guerra más tranquila en casa de unos parientes. El padre fue llamado a filas y no pudo reunirse con ellas.
Tras tres años en Toronto, en 1943, Ailsa y su madre decidieron unirse al Cuerpo del Ejército de Mujeres Canadienses; Ailsa mintió sobre su edad para ser admitida. En 1944, las dos colaboraban en trabajos administrativos en el Cuartel General de la Defensa Nacional en Ottawa, una unidad compuesta únicamente por personal femenino que reemplazaba a los hombres enviados a Inglaterra para apoyar al ejército aliado.
Tras finalizar la guerra, en 1946, ya en Inglaterra, Ailsa ingresó en la LSE para estudiar una licenciatura en economía; como militar desmovilizada tuvo preferencia en el acceso y consiguió una beca. Durante su primer año ganó el premio Bowley por un artículo de estadística aplicada a la economía. Tras graduarse en 1950, pasó el resto de su carrera en esta institución, siendo la primera profesora de investigación operativa de Gran Bretaña.
En 1956 defendió su tesis doctoral bajo la supervisión de George Morton, con un trabajo que aplicaba técnicas de programación lineal al transporte de carbón.
Y, como hemos comentado antes, trabajó junto a Alison Doig en ese novedoso método de optimización que fue patrocinado por la empresa British Petroleum; la compañía deseaba mejorar los modelos de programación lineal existentes para las operaciones de refinería. Las dos matemáticas carecían de ordenador para realizar su tarea, pero desarrollaron un algoritmo que el personal de la empresa pudo convertir posteriormente a Fortran.
A finales de la década de 1950, Ailsa Land también trabajó con la economista Helen Makower y George Morton en una serie de problemas de programación entera, entre los cuales se encontraba el conocido problema del viajante, que es precisamente un problema NP-complejo.
Ailsa también trabajó en el desarrollo de herramientas computacionales; en 1973 publicó con Susan Powell el libro Fortran Codes for Mathematical Programming: Linear, Quadratic and Discrete.
En 1953 se casó con el especialista en sistemas de información Frank Land, también profesor de la LSE, con quien tuvo dos hijas y un hijo.
En 1994 recibió el Premio Harold Larnder de la Sociedad Canadiense de Investigación Operativa por sus aportaciones en esta área. Y, en 2019, la Sociedad de Investigación Operativa le otorgó la Medalla Beale.
El Premio Ailsa Land de la LSE se otorga cada año en su honor al estudiante más destacado en el Máster de Investigación y Análisis de Operaciones.
Alisa Land falleció el 16 de mayo de 2021, a los 93 años.
Bonus
“Sigan adelante, mujeres en matemáticas. Sigan adelante, mujeres en todas las materias STEM”.
Con este inspirador alegato de Alison Hartcourt finaliza el siguiente video producido en 2019. Sin duda, con modelos como ella y Ailsa Land, es más fácil seguir adelante.
Referencias
-
Val Silberberg, Richard and Alison Harcourt, Profile, February-March 2019, 4-5.
-
Lauren Day, ‘I’ve always loved numbers’: Meet the ground-breaking grandmother of Australian mathematics, ABC News, 8 octubre 2018.
-
Alison Harcourt, The University of Melbourne
-
Alison Hartcourt, Wikipedia
-
Ailsa H. Land, The Institute for Operations Research and the Management Sciences
-
Ailsa Land, Wikipedia
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Alison Hartcourt y Ailsa Land, dos matemáticas unidas por la programación lineal se ha escrito en Cuaderno de Cultura Científica.
Einstein y Robert Millikan
Robert Millikan fue uno de los científicos más famosos de su época. Ganó el premio Nobel de física en 1923 por la medición de la carga del electrón y por el trabajo experimental que confirmó la teoría de Einstein de que la luz estaba constituida por partículas. Irónicamente, la intención de Millikan era demostrar que la teoría era falsa, e insistió durante años en que su trabajo confirmaba simplemente que las teorías de Einstein eran valiosas herramientas matemáticas, pero solo eso, no que probase la existencia de los fotones.
 Robert Millikan y Albert Eisntein en el Instituto de Tecnología de California en 1932. Fuente: Wikimedia Commons
Robert Millikan y Albert Eisntein en el Instituto de Tecnología de California en 1932. Fuente: Wikimedia CommonsEn 1896, Millikan fue contratado por la Universidad de Chicago, y estaba todavía allí en 1905 cuando Einstein publicó un artículo en el que afirmaba que la única manera de explicar cómo la luz cede energía a los electrones es asumiendo que la luz está compuesta de partículas, de forma análoga a la corriente eléctrica. Einstein encontró que la energía de una partícula de luz es igual a su frecuencia multiplicada por una constante, h, que terminó llamándose constante de Planck. Millikan ya tenía una reputación de gran experimentador, tras haber sido capaz de medir la carga del electrón, demostrando así que los electrones eran realmente entes físicos con propiedades consistentes, y que la electricidad es un fenómeno atómico. Pero solo porque aceptase que los electrones eran partículas no significaba que creyese que la luz podía ser algo parecido. Millikan conocía muy bien los experimentos en los que se demostraba que la interacción de dos rayos de luz tenía como resultado lo que uno podía esperar si fuesen ondas. Los científicos llevaban 50 años convencidos de que la luz era una onda, y Millikan era uno de ellos. Por lo que se dispuso a demostrar que la teoría de Einstein era errónea.
El experimento de Millikan medía la energía de los electrones que eran emitidos por una placa sobre la que incidía un rayo de luz. Sin embargo, para su sorpresa, los resultados parecían confirmar la teoría de Einstein de la naturaleza corpuscular de la luz. No solo eso, el experimento permitió la determinación más precisa hasta la fecha del valor de la constante de Planck. Décadas más tarde, cuando Millikan describía su trabajo, todavía asomaba un punto de frustración: “Empleé diez años de mi vida comprobando la teoría de Einstein de 1905 y, en contra de todas mis expectativas, me vi forzado a afirmar su verificación sin ambages a pesar de lo irrazonable que era”.
Con todo, Millikan todavía no aceptaba que su experimento probase que la luz estuviese compuesta por cuantos; solo admitiría que las matemáticas de Einstein correspondían con sus experimentos. En su artículo sobre el efecto fotoeléctrico, Millikan escribió: “la ecuación fotoeléctrica de Einstein […] parece que predice exactamente en todos los casos los resultados observados […] Sin embargo, la teoría semicorpuscular [sic.] por la que Einstein llegó a su ecuación parece actualmente completamente insostenible”. Millikan también describió la teoría de Einstein sobre las partículas de luz como una “hipótesis atrevida, por no llamarla insensata”. Millikan era consciente de que sin las ecuaciones de Einstein no se podía explicar el fenómeno de la fotoelectricidad usando el punto de vista clásico sobre la luz, por lo que sabía que algo tenía que cambiar, pero la introducción arbitraria de los fotones no era, para su gusto, la respuesta. Además Millikan trabajaba con Michelson (su director de tesis), que creyó toda su vida en la existencia de un éter a través del que las ondas de luz viajaban (a pesar de que sus propios experimentos demostraban su no existencia), por lo que se reforzaban mutuamente en su creencia en la naturaleza ondulatoria de la luz como la única posible.
Mientras la comunidad científica seguía estos desarrollos, en 1919 Einstein y Millikan aparecieron mencionados juntos en la prensa popular. Ese noviembre se hizo público que las observaciones astronómicas del eclipse solar de ese año confirmaban la teoría general de la relatividad de Einstein, lo que le dio fama instantánea y motivó una serie de artículos en el The New York Times. En alguno de ellos aparecía un Einstein altanero que afirmaba que sólo doce personas en el mundo comprendían su teoría. Días después de esto hubo, como era de esperar, una reacción furibunda, y un editorial del propio periódico, del 13 de noviembre, decía: “La gente que se ha sentido un poco molesta porque se les ha dicho que no podrían entender la nueva teoría, ni siquiera si se les explicase con todo cuidado y amabilidad, sentirán alguna clase de satisfacción al saber que la solidez de la deducción de Einstein ha sido puesta en cuestión por R.A. Millikan”.
A pesar de todo, mientras Millikan continuaba negando la existencia de los fotones, su “confirmación” fue un factor que ayudó a que Einstein recibiese el premio Nobel en 1921. En 1923, Millikan recibiría él mismo el premio “por su trabajo sobre la carga elemental de la electricidad y sobre el efecto fotoeléctrico”. En su conferencia con motivo de la recepción del premio, sin embargo, Millikan volvió a mencionar que “el concepto de cuantos de luz localizados a partir del cual Einstein consiguió su ecuación debe ser considerado aún como lejos de estar establecido”.
Nunca hubo, sin embargo, animosidad personal entre los dos científicos, y se respetaban muchísimo el uno al otro. En 1921, Millikan aceptó un trabajo en lo que llegaría a llamarse Instituto de Tecnología de California (Caltech), y se dispuso a convertirlo en una institución puntera en investigación. Millikan ofreció a Einstein un puesto en el Caltech en 1923, pero el físico alemán lo rechazó. Einstein sí aceptó una invitación a visitar los Estados Unidos y Millikan actuó como su anfitrión. Finalmente (y todavía no está muy claro por qué, aunque puede que influyese el creciente antisemitismo en Alemania), en 1931 Einstein aceptó un puesto para enseñar a tiempo parcial en el Caltech.
En 1950, a los 82 años, Millikan escribió su autobiografía. Para entonces toda la comunidad científica había aceptado la existencia de los fotones, incluido Millikan. En el libro, Millikan no menciona que tardó décadas en aceptar las teorías de Einstein. Probablemente nunca sabremos si lo que Millikan contaba era realmente cómo recordaba los acontecimientos o fue la vanidad la que venció y se negó a reconocer lo que claramente había sido un error.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Una versión anterior de este artículo se publicó en Experientia Docet el 22 de nombre de 2009.
El artículo Einstein y Robert Millikan se ha escrito en Cuaderno de Cultura Científica.
¿Por qué el estómago no se digiere a sí mismo? Bueno, a veces, sí lo hace
 Imagen de Robystarm en Pixabay
Imagen de Robystarm en PixabayEl jugo gástrico es una solución extremadamente ácida. Su pH normal se encuentra entre 1,5 y 3, lo que significa que es más ácido que el vinagre y está más o menos al mismo nivel que el zumo de limón. Este pH tan bajo se debe al ácido clorhídrico (HCl) que liberan las células parietales, situadas en la pared del estómago. El HCl, más conocido como salfumán, tiene multitud aplicaciones en la vida diaria, desde productos de limpieza para el hogar hasta infinidad de usos industriales (para desatascar, desincrustar, fabricar diferentes materiales…).
Cada día, se producen en torno a 1,5-2,5 litros de jugo gástrico (compuesto principalmente por agua, HCl, enzimas digestivas y electrolitos), esencial para la digestión de los alimentos y para prevenir infecciones por diferentes agentes patógenos. ¿Cómo es posible que el estómago se libre de los efectos corrosivos del jugo gástrico, si resulta tan ácido? A grandes rasgos, intervienen cuatro elementos defensivos que protegen a este depósito muscular de ser víctima de sus propios fluidos. En primer lugar, la superficie interna del estómago está recubierta por una espesa y viscosa capa de moco alcalino gracias a la presencia de bicarbonato, Este moco actúa como una barrera tanto física como química que protege al estómago de su propio jugo y permite que en su superficie interna se dé un pH prácticamente neutro (7).
Si vamos más allá de la capa de moco, las células que recubren la superficie interna del estómago, las células epiteliales, están unidas entre sí de forma hermética a través de un complejo entramado de proteínas. Esta barrera física es muy compacta e impide el paso del jugo gástrico entre las células gástricas, lo que sería un grave problema porque provocaría la digestión del tejido más profundo del estómago.
Además de los mecanismos anteriores, las células epiteliales se renuevan constantemente a lo largo de la vida para garantizar la protección del estómago. Estas células tienen una vida media de tan solo 3-6 días, lo que implica que cada minuto que pasa se eliminan en torno a 500.000 células epiteliales que van a parar al jugo gástrico. Por último, la secreción del ácido en el estómago está regulada con suma precisión para que la acidez nunca sea excesiva en este órgano y que esta dependa, sobre todo, de la ingesta de alimentos. De ello se encargan tanto el sistema nervioso simpático y parasimpático como las hormonas gastrina, histamina, somatostatina y acetilcolina.
Por supuesto, en condiciones normales, estas cuatro medidas de protección del estómago funcionan a la perfección y no llegamos a ser conscientes de que tenemos un depósito de ácido en nuestro interior. Sin embargo, multitud de factores pueden alterar el delicado equilibrio entre los elementos protectores gástricos y el corrosivo jugo. El consumo excesivo de alcohol, la ingesta frecuente de ciertos fármacos (como los antiinflamatorios no esteroideos) o la bacteria Helicobacter pylori (que sobrevive en el medio ácido gracias a la liberación de amoníaco), entre otras muchas causas, pueden lesionar la mucosa del estómago y hacer que sufra daños por su contenido ácido. Cuando este fenómeno ocurre hablamos de úlceras pépticas: llagas que provocan un dolor sordo o ardor en la zona del estómago, que se acentúa entre comidas.
¿Qué hacemos entonces para curar las úlceras, en las que el ácido del jugo gástrico está «digiriendo» una zona del estómago? En primer lugar, lo primero es tratar la causa que ha desbaratado el delicado equilibrio en el estómago. Por ejemplo: antibióticos contra H. pylori, sustitución de medicamentos que provocan daño en la mucosa gástrica por otros que no lo hagan, abstinencia de alcohol….
Además, también hay que atenuar la liberación de HCl en el estómago, para disminuir la acidez y así dar tiempo al estómago para que se cure así mismo (por suerte, la mucosa es un portento en renovarse a sí misma). Esto lo conseguimos con los medicamentos llamados inhibidores de la bomba de protones. Entre ellos, el más popular es el omeprazol. Se conocen (mal) como «protectores gástricos», aunque en realidad lo que hacen es disminuir el ácido del estómago al bloquear los canales de las células parietales que producen el HCl.
Hoy en día, gracias a estos fármacos, el pronóstico de las úlceras es excelente. Es muy raro que una úlcera péptica evolucione y llegue a atravesar la pared del estómago, provocando la perforación de este órgano. Esto supondría una emergencia médica de gran riesgo para la vida, porque la liberación del jugo gástrico a las zonas colindantes del estómago provocaría graves daños en el cuerpo humano. Por suerte, casos así son excepcionales.
Para saber más:
El estómago (u órgano equivalente)
H. pylori crea túneles en la mucosa del estómago
Sobre la autora: Esther Samper (Shora) es médica, doctora en Ingeniería Tisular Cardiovascular y divulgadora científica
El artículo ¿Por qué el estómago no se digiere a sí mismo? Bueno, a veces, sí lo hace se ha escrito en Cuaderno de Cultura Científica.
El afinador de Eratóstenes
José Manuel González Gamarro
La historia de la música de occidente se caracteriza por una gran riqueza de textos musicales, tanto de partituras como de libros analizando sus características y propiedades. Analizando los textos se puede saber cómo era la música de hace, por ejemplo, 500 años, no solo tocando la partitura, sino leyendo sobre cómo eran los instrumentos, la manera de componer o en qué contexto se escuchaba. Huelga decir que la música de hace cientos de años era muy diferente a la que se compone en la actualidad, ha ido transformándose, tanto en su forma como en su contenido. Una de las cosas que más ha variado a lo largo de la historia es la afinación. La palabra «afinación» tiene aquí una connotación muy amplia, pues no solo se refiere a cómo se templaban los instrumentos musicales, sino a cómo se concebían las consonancias y disonancias. Esto atañe también a la manera de cantar y a la percepción del oyente de cada época, es decir, hubo sistemas de afinación (incluso se daban con simultaneidad en el tiempo) que decidían lo que sonaba bien o mal, la delgada línea entre lo prohibido y lo permitido. Hay que tener en cuenta que la forma de concebir la afinación musical también ha variado a lo largo del tiempo, desde la mera comparativa hasta la estandarización de las vibraciones por segundo que le corresponde a cada nota.
La afinación pitagóricaUna de las afinaciones más usadas y de las que más literatura ha generado es la afinación pitagórica. Más allá de las leyendas e historias que se han ido difundiendo a lo largo de los años gracias a filósofos como Boecio, a la figura de Pitágoras se le atribuyen descubrimientos musicales en relación con las matemáticas que implican el inicio de la ciencia armónica.1 Estos descubrimientos, a través supuestamente de experimentos con vasos de agua, pesos o flautas, se ejemplifican claramente en el monocordio. Este instrumento se compone de una sola cuerda y una regla numerada. Las consonancias se calculan según la parte de la cuerda que vibra. Teniendo en cuenta que la tensión de la cuerda es constante, si se divide justo a la mitad, el intervalo entre el sonido que produce la cuerda sin dividir y el sonido de la mitad de la cuerda es de una octava, es decir, la razón es 2/1. En otras palabras, si la nota de esa cuerda es, por ejemplo, un Do, al hacer vibrar solo la mitad de la cuerda volverá a sonar otro Do, pero una octava más aguda. Esto es solo un ejemplo puesto que el nombre de las notas como tal no se establecería hasta bastantes siglos después. Este intervalo de octava y esta proporción es la que se ha intentado mantener constante a lo largo de la historia y los diferentes sistemas de afinaciones. Pitágoras también definió los intervalos de quinta con la razón 3/2 (dividir la cuerda en tres partes iguales y hacer sonar dos) y el intervalo de cuarta con la razón 4/3. Según Arístides Quintiliano en su De Musica, el matemático recomendaba encarecidamente usar el monocordio para poder desechar la apreciación sensorial, es decir, decidir cuando existe consonancia mediante la apreciación intelectual, con puro cálculo numérico. Teniendo en cuenta que para sumar intervalos se multiplican sus razones y para restarlos se dividen, se pueden calcular los demás intervalos. Por ejemplo, el tono (una supuesta distancia aproximada entre Do y Re) es la diferencia entre la quinta y la cuarta y se calcula de la siguiente manera: 3/2 : 4/3 = 9/8. La diferencia entre la cuerda «al aire» y el sonido producido por la razón 9/8 es un tono.
Con el devenir de la historia, la música y los instrumentos musicales fueron ganando en complejidad. Además, para los pitagóricos las consonancias eran la cuarta, la quinta, la octava, la doble octava y la octava más la quinta. Todos los demás intervalos había que calcularlos en función de estos. Una consecuencia es la especulación matemática acorde con la musical, ya que, excepto la octava, ninguna consonancia puede dividirse en dos partes iguales, además tampoco se pueden sumar consonancias iguales para obtener otra consonancia. La suma de dos cuartas, por ejemplo, da como resultado una séptima, que no era una consonancia. El problema principal viene cuando queremos realizar una escala, es decir, una sucesión de tonos hasta llegar a la octava. Seis tonos (9/8) sucesivos sobrepasan la octava, no se llega exactamente al mismo sonido. Hay una pequeña diferencia llamada comma pitagórica. Esta diferencia son 24 cents si escogemos esta unidad logarítmica para medir intervalos. No es algo desdeñable ya que un oído fino puede apreciar una diferencia de 3 cents. Este «pequeño» desajuste ha provocado diferentes sistemas de afinación que se han ido adaptando a la transformación de la música y los cambios en la concepción de los intervalos permitidos o consonantes. Ha habido sistemas de afinación circulares, que vuelven al mismo sonido (como el nuestro de la música occidental), repartiendo ese desajuste entre las notas de la escala, así como otros sistemas irregulares. De hecho, según Murray Barbour2 ha habido más de 180 sistemas de afinación a lo largo de nuestra historia.
 Ilustración 1. Dibujo de un círculo de terceras en una escala de 31 notas. Elementa musica, Quirimus van Blakenburg, 1739. Fuente: Goldaraz Gaínza, 1998.
Ilustración 1. Dibujo de un círculo de terceras en una escala de 31 notas. Elementa musica, Quirimus van Blakenburg, 1739. Fuente: Goldaraz Gaínza, 1998.
Toda esta complejidad tiene como consecuencia la creación de diferentes escalas y de diferentes instrumentos adaptados a estas escalas. Nuestra escala tiene siete notas (Do-Re-Mi-Fa-Sol-La-Si) que si las dividimos en semitonos iguales nos da la escala cromática de doce. Este es el límite de nuestra escala occidental. Sin embargo, a lo largo de la historia, debido a estos diferentes sistemas de afinación, han existido escalas de 31 o incluso de más de 50 sonidos diferentes. Para ello también se idearon instrumentos musicales acordes a las dificultades de la afinación, como el denominado Sambuca Lincea de los músicos Fabio Colonna o Scipione Stella con seis teclados en el mismo instrumento. Todo un desafío para los músicos de hoy en día.
 Teclado de la Sambuca Lincea de F. Colonna, 1618. Fuente: Goldaraz Gaínza, 1998. El mesolabio de Eratóstenes
Teclado de la Sambuca Lincea de F. Colonna, 1618. Fuente: Goldaraz Gaínza, 1998. El mesolabio de Eratóstenes
La supuesta insistencia de Pitágoras en evitar la apreciación sensorial deja insuficiente a la aritmética a medida que transcurre el tiempo debido a que, ya no solo hay que calcular quintas o cuartas, sino tonos y partes de comma. Esto último implicaría hallar medios, tercios, cuartos, etc. de esta distancia de 24 cents mediante sus razones por lo que habría que hallar la raíz cuadrada, cúbica, cuarta, etc. de la razón 81/80, dando cantidades irracionales. Esto propició la búsqueda de otras soluciones para algunos sistemas de afinación basadas en la geometría. Una de estas soluciones es utilizar un instrumento creado por Eratóstenes de Cirene (276-194 a. C.), el mesolabio. Esta especie de ábaco se compone de tres paralelogramos rectangulares que se mueven a lo largo de unas estrías, superponiéndose unos a otros. Se usa para hallar medias y proporciones y uno de sus primeros usos fue la duplicación del volumen de un cubo, como se explica en este vídeo, pudiéndose ver su funcionamiento a partir del minuto 10:00. Aunque el cálculo pueda parecer en un principio aproximado puesto que se trata de buscar los puntos de intersección, su uso evita las complicadas operaciones matemáticas que supone hallar distancias tan pequeñas. Moviendo rectángulos con diagonales trazadas y uniendo puntos con líneas rectas en las intersecciones, se calculan dos medias proporcionales en una razón superparticular, es decir, la razón de dos números enteros consecutivos. Esto encaja como anillo al dedo en las razones usadas en la música. Es un aparato que se usa muchos años después de su invención para el cometido de la afinación. Los músicos Gioseffo Zarlino y Pedro Salinas lo usarán y dejarán constancia de ello en sus tratados.
 Dibujo del mesolabio en Dimostrationi Harmoniche, G. Zarlino, 1571.
Dibujo del mesolabio en Dimostrationi Harmoniche, G. Zarlino, 1571.
Aunque el cometido del mesolabio era encontrar dos medias, Zarlino indica que puede usarse para cualquier número de medias si se aumenta el número de paralelogramos. De hecho, este músico ilustra la división del mástil de un laúd mediante el mesolabio en el temperamento igual, doce partes iguales. También Pedro Salinas hace uso del añadido de paralelogramos para aumentar el número de medias, sin embargo, otros teóricos como el matemático Marin Mersenne sostienen que solo es posible su uso para dos medias.
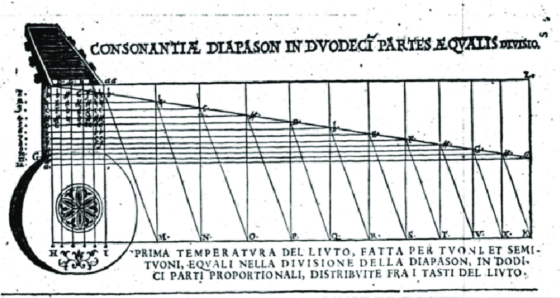 Explicación del uso del mesolabio, Sopplimenti musicali, G. Zarlino, 1588.
Explicación del uso del mesolabio, Sopplimenti musicali, G. Zarlino, 1588.Sea como fuere, Eratóstenes ideó un aparato que tuvo un uso muy prolongado en el tiempo y alejado de su primer cometido, otorgando una solución práctica a problemas que no existían en el tiempo en el que se concibió. Aunque su más conocida hazaña fue calcular la circunferencia de la Tierra, también fue capaz de inventar una especie de calculadora con un mecanismo muy sencillo y que fue muy significativo para el desarrollo de algunos sistemas de afinación de la música occidental. Este matemático que fue director de la Biblioteca de Alejandría tiene un papel primordial en la historia de esta disciplina, así como en la astronomía y la geografía, pero, aunque más discreto, también tiene un pequeño hueco en la historia de nuestra música.
Referencias:
1 Goldaraz Gaínza, J. Javier. Afinación y temperamento en la música occidental. Alianza, 1998
2 Barbour, J. M. Tuning and Temperament, a Historical Survey. Da Capo Press, 1972.
Sobre el autor: José Manuel González Gamarro es profesor de guitarra e investigador para la Asociación para el Estudio de la Guitarra del Real Conservatorio Superior de Música “Victoria Eugenia” de Granada.
El artículo El afinador de Eratóstenes se ha escrito en Cuaderno de Cultura Científica.
CienciaClip 2020 – Lo que verías al viajar a la velocidad de la luz

Ciencia Clip es un concurso de vídeos divulgativos de ciencia diseñados, producidos y protagonizados por estudiantes de Educación Secundaria.
El objetivo del concurso es fomentar el interés por la ciencia y la tecnología. Y ofrecer a los concursantes una oportunidad para ejercitar su creatividad y habilidades comunicativas usando herramientas que proporciona internet.
Ciencia Clip es una iniciativa de la Cátedra de Cultura Científica de la UPV/EHU y en la que colaboran Euskampus Fundazioa, Naukas, Scenio y Big Van.
Los ganadores de la edición 2022 ya están en la página web del concurso. La entrega premios y el anuncio del vídeo ganador del premio especial se realizarán durante el evento Naukas Bilbao. En la edición de 2020 resultó ganador en la categoría de 1º y 2º de de la ESO Javier Sirvent, de Alicante, con este vídeo:
Edición realizada por César Tomé López
El artículo CienciaClip 2020 – Lo que verías al viajar a la velocidad de la luz se ha escrito en Cuaderno de Cultura Científica.
Liberación controlada del fármaco con impresión 3D de almidones
Los métodos habituales producen medicamentos con determinados parámetros, pero en muchos casos sin satisfacer las necesidades individuales de los pacientes. De hecho, los medicamentos suelen basarse en la dosis para adultos, por lo que los pacientes pediátricos y de edad avanzada necesitan adaptarlos a las dosis adecuadas a su edad. Por otra parte, determinados pacientes o circunstancias necesitan alternativas de formas de dosificación específicas en la administración oral de los fármacos. En un extremo están los comprimidos de desintegración rápida, que se disuelven inmediatamente al colocarlos en la lengua. Pero, en el otro, está el reto de la liberación controlada del fármaco en el tiempo; sobre todo cuando el fármaco tiene un carácter hidrófobo, es decir, cuando resulta difícil que se disuelva en agua.
En esta línea, el Grupo ‘Materiales+Tecnologías’ (GMT) de la UPV/EHU desarrolla comprimidos basados en diferentes tipos de almidón mediante impresión 3D para terapias personalizadas. Han comprobado que la liberación del fármaco puede controlarse optimizando el tipo de almidón adecuado y la forma del comprimido.
 Fuente: UPV/EHU
Fuente: UPV/EHULa impresión 3D es una tecnología que consiste en la impresión de los productos capa por capa, en la que los materiales se depositan de acuerdo con el modelo digital dado por el software de diseño informático. Siguiendo una metodología rápida y sencilla y gracias a la impresión 3D, “hemos sido capaces de preparar comprimidos basados en tres tipos de almidón —dos tipos de almidón de maíz (normal y waxy) y un tipo de almidón de patata— con diferentes geometrías y cargadas con un fármaco no soluble”, indica Kizkitza González investigadora del GMT y primera autora del nuevo trabajo.
“El material que se produce hay que introducirlo en una jeringa antes de imprimirlo. Sin embargo, antes es fundamental asegurar que el material va a ser imprimible y que una vez imprimido va a mantener su forma. Para ello, hay que realizar un análisis reológico detallado”, explica la investigadora de la UPV/EHU. Los tres tipos de almidón han mostrado propiedades reológicas apropiadas, a pesar de que en el caso del almidón de patata el proceso de impresión resultó ser más laborioso debido a sus propiedades.
Asimismo, “hemos observado la importancia que tiene el origen botánico del almidón prácticamente en todas las propiedades como son la microestructura porosa, la formación de una red estable o la liberación del fármaco. En el caso del almidón de maíz normal la liberación del fármaco es instantánea y el medicamento se libera por completo en 10 minutos; en el caso del almidón de maíz waxy y el almidón de patata la liberación se da de una forma más continua, pudiendo tardar hasta 6 horas en liberarse por completo. Además, hemos podido demostrar la importancia que tiene la geometría del comprimido en la liberación del fármaco”, indica Kizkitza González.
Por último, “también se imprimieron comprimidos que combinaban diferentes tipos de almidón. En este caso, se consigue que la liberación tenga lugar en dos etapas. Por ejemplo, en el caso de una infección, en una primera etapa, con el almidón de maíz normal se podría liberar de inmediato un medicamento para paliar el dolor, y en una segunda etapa, con cualquiera de los otros dos tipos de almidón liberar un antibiótico de forma más continua”, cuenta la investigadora de la UPV/EHU.
Kizkitza González es consciente de que este trabajo es solo una primera etapa de un largo proceso, pero asegura que “los comprimidos impresos en 3D a base de almidón obtenidos mostraron propiedades prometedoras de cara a futuras aplicaciones de liberación de fármacos personalizadas”.
Referencia:
Kizkitza González, Izaskun Larraza, Garazi Berra, Arantxa Eceiza & Nagore Gabilondo (2022) 3D printing of customized all-starch tablets with combined release kinetics International Journal of Pharmaceutics doi: 10.1016/j.ijpharm.2022.121872
Para saber más:
Prótesis biocompatibles por impresión 3D
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Liberación controlada del fármaco con impresión 3D de almidones se ha escrito en Cuaderno de Cultura Científica.
Helmholtz, el físico que enseñó a los diapasones a hablar
Vivimos en el tiempo de las voces virtuales, un tiempo en el que uno casi tiene miedo de decir la palabra incorrecta, no vayan Siri, o Google, o Alexa, o Cortana a darse por aludidos. Podemos “oír” nuestro correo electrónico mientras cocinamos, escuchar libros que nunca nadie ha leído en voz alta, abrir las voces que nos esperan en nuestro buzón, o incluso preguntarle a un coche cuál es la mejor ruta a seguir. Las voces virtuales se han convertido en un lugar común, que ya casi no reparamos en ellas. Pero para poder sintetizarlas, grabarlas, transmitirlas o digitalizarlas, fue necesario entender primero cómo funciona nuestra propia voz y un físico capaz de enseñar a hablar a los diapasones.
Empecemos por lo básico: ¿dónde dirías que se forman las palabras cuando hablas? Sin pensarlo demasiado, ¿en el pecho, la boca, en la garganta quizás?
Hasta finales del siglo XVIII, esta pregunta no tenía una fácil respuesta. Muchos pensadores creían que el habla tiene su origen en las cuerdas vocales, quizás porque es lo primero que activamos y notamos vibrar al hablar. Otros argumentaban, en cambio, que la boca es lo que se mueve para pronunciar las distintas letras del lenguaje. Con el fin de aclarar esta disputa, en 1778 la Academia de Ciencias de Rusia lanzó un concurso dirigido a la comunidad científica. El premio recaería en aquella persona capaz de explicar la mecánica de las vocales humanas. Dos años más tarde, el profesor Christian Kratzenstein fue anunciado como ganador. No solo había logrado explicar por primera vez las diferencias acústicas entre los sonidos A E I O U, sino que además había fabricado una máquina capaz de producirlos artificialmente.
 Las formas de los tubos de Kratzenstein para las cinco vocales. Fuente: F. Brackhane (2015) Kempelen vs. Kratzenstein –
Las formas de los tubos de Kratzenstein para las cinco vocales. Fuente: F. Brackhane (2015) Kempelen vs. Kratzenstein –Researchers on speech synthesis in times of change, ISCA-Speech.com
El invento consistía en una serie de tubos, parecidos a los de un órgano pero con formas mucho más variopintas. Estos tubos filtraban una nota producida por una lengüeta (parecida a la de una armónica) y daban lugar a los timbres de las vocales A E I O U. Era un mecanismo sorprendentemente sencillo. Pero así es como funciona nuestra propia voz. Puedes comprobarlo en primera persona: si yo ahora te pido que cantes una “u” y a continuación una “a”, ¿qué es lo que sucede exactamente en tu garganta, y en tu cara? Aunque sostengas todo el rato la misma nota con tu voz, la forma de tu tracto vocal (tu boca, en este caso) cambia para dar lugar a distintos timbres, igual que los tubos de la máquina de Kratzenstein.
Para entender cuál era la naturaleza de estos timbres de manera precisa, fue necesario esperar un siglo más. De hecho, la misma palabra “timbre” es difícil de definir y a menudo crea confusión. El timbre es lo que distingue a dos sonidos que tienen el mismo tono y la misma intensidad. Es decir, si yo cojo un violín, una trompeta, y una guitarra, y hago que toquen la misma nota (pongamos, un la 400 Hz), con la misma intensidad y la misma duración, la cualidad sonora que me permite distinguirlos es el timbre. La diferencia entre una “a” y una “u” es una diferencia tímbrica también. Ahora bien, desde un punto de vista físico, el timbre no es nada fácil de desentrañar.
En la segunda mitad del siglo XIX, Hermann von Helmholtz se empeñó en destilar esta propiedad del sonido. El físico alemán quería entender de qué estaban hechas las vocales del lenguaje1, y por extensión, el sonido de los instrumentos musicales. Lo que descubrió es que el timbre tiene mucho que ver con la complejidad de un sonido. Todo tono está compuesto por un montón de frecuencias. Esa composición (lo que en física conocemos como su espectro), y la manera en que cambia con el tiempo, es lo que determina en gran medida eso que percibimos como “timbre”.
Para demostrarlo, al igual que Kratzenstein, Helmholtz no se contentó con presentar simplemente su explicación. Con ayuda de Rudolph Koenig, construyó una máquina capaz de sintetizar esas mismas letras a partir de sus componentes fundamentales. Constaba de un conjunto de diapasones que se mantenían en constante vibración gracias a pulsos electromagnéticos. Cada diapasón producía una frecuencia pura de una serie armónica (frecuencias proporcionadas por números enteros 1, 2, 3, 4…). Al hacerlos vibrar con distintas intensidad relativa, era posible escuchar el sonido de las vocales. ¡Los diapasones, habían aprendido hablar!
 Sintetizador de Helmholtz. Fuente: Harvard Brain Tour
Sintetizador de Helmholtz. Fuente: Harvard Brain Tour
Aquel primitivo sintetizador ayudó a comprender mejor la naturaleza del habla y los sonidos de las vocales. Pero además, al otro lado del Atlántico, los diapasones de Helmholtz inspiraron a un joven Alexander Graham Bell, que empezó a soñar con convertir la voz humana en frecuencias eléctricas, capaces de recorrer enormes distancias a través un cable de cobre2. Un siglo después, las tataranietas de aquel extraño sueño, nos ofrecen ayuda desde nuestros dispositivos móviles. Sus voces digitales nos recuerdan que nuestras palabras, en último término, también están hechas de números.
Notas y referencias:
1Hermann von Helmholtz (1863) “On the Sensations of Tone”, traducido por Alexander J. Ellis. Via: Internet Archive.
2Cuento esta historia en más detalle en Almudena Martín Castro (2022). “La Lira Desafinada de Pitágoras”. HarperCollins.
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
El artículo Helmholtz, el físico que enseñó a los diapasones a hablar se ha escrito en Cuaderno de Cultura Científica.

