Reflejando el sol
Estos días de verano con intenso calor, cada vez que me subo a mi coche, completamente negro, después de tenerlo aparcado en la calle varias horas, me acuerdo de un efecto muy poco conocido, pero realmente importante para el cambio climático. Recuerdos que también me vinieron a principios de agosto, cuando me puse pantalones cortos por primera vez este año y me percaté de que el tono de piel de mis pernas le hacía honor a mi nombre, tanto que parecían incluso despedir un brillo propio. Me estoy refiriendo al efecto albedo.
De manera resumida, el albedo se refiere a la cantidad de radiación que es capaz de reflejar una superficie con respecto al total de energía que incide sobre ella. Es una propiedad que no tiene dimensiones y su valor se expresa dentro de un rango comprendido entre 0 y 1 o en su versión porcentual entre 0 y 100%, de tal manera que las superficies que reflejan poca energía (es decir, que absorben casi toda la radiación que incide sobre ellas) tendrán un albedo muy bajo, con valores cercanos a 0, mientras que las superficies que reflejan la mayoría de la radiación que les llega tendrán valores de albedo altos, próximos a 1 o al 100%.
Albedo, en latín, blancuraAlbedo es una palabra que procede de la raíz latina albus, que significa blanco. Esto ya nos da una pista de la característica física de las superficies que principalmente determina el valor del albedo de las mismas, el color. En concreto, las superficies de colores más claros tienen un valor de albedo más alto, ya que apenas absorben la radiación que incide sobre ellas, reflejando la mayoría de esa energía, mientras que las de colores más oscuros tienen un albedo muy bajo puesto que tienen una mayor capacidad de absorción de dicha radiación.
 Valores promedio de albedo de diferentes superficies terrestres. Infografía: Johns Hopkins University
Valores promedio de albedo de diferentes superficies terrestres. Infografía: Johns Hopkins UniversityA escala planetaria, la Tierra recibe radiación directamente del Sol y, como cualquier superficie, es capaz de absorber parte de esa energía y reflejar, enviando de nuevo al espacio, la otra parte de la misma. De esta manera, el planeta tiene un valor promedio aproximado de albedo de 0.3, es decir, que refleja prácticamente el 30% de la radiación solar, absorbiendo el 70% restante.
Pero, como he dicho, esto es un promedio. Hay superficies en la Tierra de colores más oscuros, como ciertas rocas de tonalidades casi negras, frondosas masas boscosas verdes oscuras o grandes zonas oceánicas profundas de coloración azul grisácea que presentan bajos valores de albedo al absorber mayor radiación solar y, por tanto, se calientan más fácilmente. Pero otras partes de nuestro planeta tienen colores claros, incluso blancos, tales como las áreas heladas cercanas a los polos. Aquí, se refleja casi toda la radiación, por lo que el albedo es muy alto, provocando que la temperatura sea también más baja en estas zonas. Esta diferenciación en el albedo de nuestro planeta es uno de los principales mecanismos que controla la circulación atmosférica y el intercambio de calor entre las áreas ecuatoriales y las polares. Es decir, que el albedo influye directamente en el clima que tenemos en la Tierra.
Pero las actividades humanas también pueden influir en esta propiedad física de las superficies y, por tanto, provocar variaciones o alteraciones del clima a una escala temporal que nos afecta de manera directa. Una de las acciones más directas ha sido alterar el color de la nieve, que se verá reflejado en el color que tendrá el hielo acumulado en zonas de altas latitudes. Parece complicado hacer eso, pero nada más lejos de la realidad.
Desgraciadamente, ahora estamos viendo como cae ceniza de color oscuro en muchas partes de la Península Ibérica debido a los incendios forestales que azotan nuestros montes. Pues lo mismo provocamos con la quema incontrolada de carbón que tuvo lugar hace unos siglos y que todavía se mantiene en ciertas partes de nuestro planeta. Esa ceniza presente en la atmósfera es capaz de teñir la nieve de colores más oscuros que, al depositarse como capas de hielo en latitudes altas, tendrá un valor de albedo inferior al de la nieve más pura, aumentando su absorción de radiación solar y su temperatura, generando a su vez un incremento en su velocidad de fusión. Y cuando este hielo se funde, se generan masas de agua entre las capas heladas, agua que también tiene un menor albedo que el hielo blanquecino y que, nuevamente, contribuye a un aumento de su fusión. Es decir, vamos rompiendo la termorregulación atmosférica y provocamos un incremento en la velocidad de desaparición de las masas heladas polares.
 Valores de albedo a lo largo de nuestro planeta en el año 2005. Imagen: Earth Observatory / NASA
Valores de albedo a lo largo de nuestro planeta en el año 2005. Imagen: Earth Observatory / NASAComo os he comentado, el efecto albedo es uno de los factores que determinan el clima en la Tierra, pero ni mucho menos es el único. El cambio climático es un concepto muy complejo donde interfieren un montón de variables que, encima, están interrelacionadas entre sí. El problema ante el que nos enfrentamos actualmente es que, cualquier alteración provocada por la actividad humana en alguno de ellos provoca una respuesta climática que, en muchas ocasiones, no podemos prevenir, ya que no tenemos referentes o análogos en el registro geológico. Aunque a veces intentamos comparar nuestras acciones con los efectos producidos por grandes volcanes explosivos, pero tampoco podemos asegurar que la respuesta climática sea similar.
Además, ahora seguro que entendéis por qué cuando os encontráis con profesionales de la Geología en el campo generalmente llevamos gafas de sol, aunque esté nublado. No es para parecer más guay, es que las rocas de colores claros tienen un albedo alto y no queremos que el reflejo nos deslumbre mientras estamos trabajando.
Para saber más:
Ártico y Antártico se calientan a la vez
Certezas e incertidumbres sobre el cambio climático
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo Reflejando el sol se ha escrito en Cuaderno de Cultura Científica.
La sucesión de Fibonacci, el teorema de Zeckendorf y un poemario magistral
En la anotación La magia del teorema de Zeckendorf hablábamos de un truco de magia realizado con diez cartas y que se basaba en una propiedad matemática relacionada con la teoría aditiva de númerosi. Esa propiedad se conoce como el teorema de Zeckendorf, y afirma que:
Todo entero positivo se escribe, de manera única, como suma de números de Fibonacci no consecutivos. A esa escritura única se le llama la descomposición de Zeckendorf del número en cuestión.
 Teorema de Zeckendorf representado para los 89 primeros números naturales. Los colores corresponden a los números de Fibonacci 55, 34, 21, 13, 8, 5, 3, 2 y 1. Las bandas verticales de fondo tienen una anchura de 10. Fuente: Wikimedia Commons.
Teorema de Zeckendorf representado para los 89 primeros números naturales. Los colores corresponden a los números de Fibonacci 55, 34, 21, 13, 8, 5, 3, 2 y 1. Las bandas verticales de fondo tienen una anchura de 10. Fuente: Wikimedia Commons.
Este teorema lleva el nombre del matemático amateur Édouard Zeckendorf (1901-1983) e involucra a los números definidos por la sucesión de Fibonacci, serie que comienza con el 0 y el 1, y cada término se obtiene al sumar los dos anteriores: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …
Para que quede más claro, vamos a calcular la descomposición de Zeckendorf del número 100. Para ello tomamos el mayor número de Fibonacci que es menor o igual que 100, que es el 89. Se hace la diferencia 100 – 89 = 11 y se procede del mismo modo. El mayor número de Fibonacci que es menor o igual que 11 es 8; se hace la diferencia 11 – 8 = 3, que ya es un número de Fibonacci, con lo que la descomposición de Zeckendorf de 100 es: 100 = 89 + 8 + 3.
Es cierto que hay otras descomposiciones de 100 como sumas de números de Fibonacciii, pero solo la anterior consta de números de Fibonacci no consecutivos. La demostración de este teorema, tanto la existencia como la unicidad de la descomposición, puede hacerse por recurrencia.
Poesía “a la Zeckendorf”En 1979, el matemático y miembro del grupo OuLiPo (Ouvroir de Littérature Potentielle) Paul Braffort (1923-2018) rindió homenaje al teorema de Zeckendorf a través del poemario Mes hypertropes. Vingt-et-un moins un poèmes à programme (Mis hipertropos. Veintiún menos un poemas con programa).
 Portada de Mes hypertropes. Fuente: paulbraffort.net
Portada de Mes hypertropes. Fuente: paulbraffort.net
Se trata de una serie de veinte poemas cuya estructura interna se rige por este teorema matemático: el poema n tiene en cuenta los poemas correspondientes a la descomposición de Zeckendorf de ese número n. Por ejemplo, como el número 12 se escribe como 8 + 3 + 1 según el teorema de Zeckendorf, esto indica que el poema número 12 comparte algunos contenidos de los poemas 1, 3 y 8 de Mes hypertropes. Esta restricción oulipiana obliga a Braffort a construir marcos que permitan estas conexiones entre algunos de los poemas de la serie.
Los números 1, 2, 3, 5, 8 y 13 son su propia descomposición de Zeckendorf, así que Braffort relaciona estos poemas con los dos números de Fibonacci que lo generan. Por ejemplo, como 8 = 3 + 5, el poema 8 comparte contenido con el 3 y el 5. Eso significa que solo el primer poema L’explication préalable ou la raison des rimes (La explicación previa o el motivo de las rimas) no se ve influenciado por ninguno de la serie.
Tras el índice, el autor explica brevemente cómo se estructura el textoiii:
Los poemas que van a leer se han diseñado respetando el “principio de Roubaudiv” que se enuncia de este modo:
-
Solo se utilizará una estructura matemática como restricción clave de una obra literaria si se incluyen uno o varios teoremas relacionados con esta estructura.
Nuestra “estructura” es aquí la de la sucesión de Fibonacci, sucesión de números naturales donde todo elemento es la suma de los dos que le preceden: 1, 2, 3, 5, 8, 13, etc.
El teorema es el de Zeckendorf que permite representar todo entero natural como la suma de un cierto número de elementos de la sucesión de Fibonacci. Así, 9 = 8 + 1, 20 = 13 + 5 + 2, etc. Esto permite asociar a la sucesión de los veinte primeros enteros un grafo de dependencias que se reproduce a continuación.
La transferencia de la estructura matemática a la restricción literaria es de orden semántico: el contenido del poema en la posición n depende del contenido de los poemas cuyo puesto forma la representación “de Zeckendorf” de n.
Así, el poema número 20 depende del contenido de los poemas en la posición 13, 5 y 2. Observemos que una tal restricción, puramente semántica, lleva también a definir restricciones prosódicas.
Por supuesto, hemos añadido al sistema anterior algunas restricciones suplementarias que el lector descifrará sin esfuerzo.
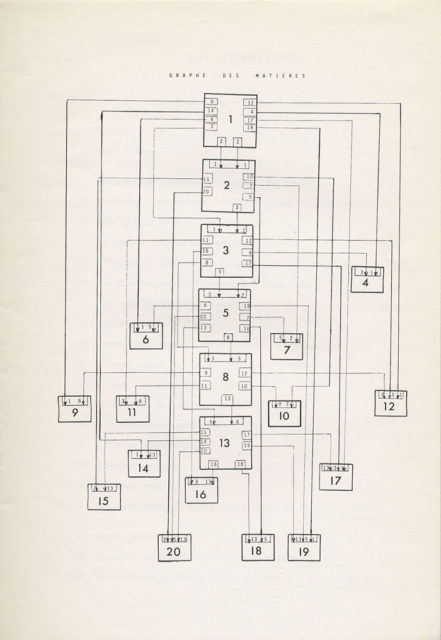 Grafo de Mes hypertropes. Fuente: paulbraffort.net
Grafo de Mes hypertropes. Fuente: paulbraffort.net
Si entendéis francés, os recomiendo la lectura de este texto. Como la mayoría de los textos escritos bajo restricción oulipiana, se descubren los detalles tras varias lecturas, mirando en cada una de ellas diferentes aspectos del contenido o de la estructura. Además, Braffort incorpora en su poemario conceptos y personajes matemáticos. Es una auténtica delicia, un juego, un reto, un rompecabezas extraordinario que enlaza las matemáticas y la literatura.
Referencias
-
Maths and poetry, Futility Closet, 11 de enero de 2015.
-
Édouard Zeckendorf (1972). Représentation des nombres naturels par une somme de nombres de Fibonacci ou de nombres de Lucas. Bull. Soc. R. Sci. Liège 41: 179-182.
-
Paul Braffort (1979).Mes hypertropes. La Bibliothèque oulipienne vol. I, no. 9, Seghers
Notas:
iLa parte de la teoría de números que estudia conjuntos de enteros y su comportamiento bajo la suma.
iiPor ejemplo, 100 = 55 + 34 + 8 + 2 + 1 o 100 = 89 + 8 + 2 + 1.
iiiTraducido por la autora.
iv Se refiere a Jacques Roubaud (1932), matemático y miembro del grupo OuLiPo.
–
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo La sucesión de Fibonacci, el teorema de Zeckendorf y un poemario magistral se ha escrito en Cuaderno de Cultura Científica.
Einstein y la belleza matemática
Einstein sometía a sus propias teorías, y a las de los demás, a un sencillo test de verosimilitud: ¿había belleza en su formulación matemática?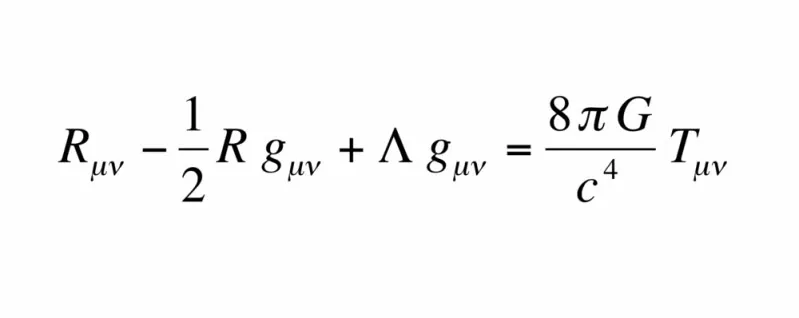
Einstein no fue el primero en examinar la veracidad de sus ecuaciones con una luz puramente subjetiva y, por tanto, acientífica. El conocido concepto de la navaja de Occam, atribuido al filósofo del siglo XIV Guillermo de Occam, afirma que, todo lo demás igual, uno debe siempre elegir la teoría más simple. Pero Einstein llevó esta idea a un grado extremo, experimentando la belleza de una ecuación precisa de una manera tan intensa como la que se puede sentir al escuchar un concierto para violín de Mozart o un aria de Puccini. No era el único, hoy día muchos científicos hablan del profundo placer que sienten ante la elegante simplicidad de mucho del trabajo de Einstein.
Cuando Einstein habló años después acerca del descubrimiento de la teoría general de la relatividad, describió un momento en el que todos sus pensamientos se fusionaron y, de repente, las fuerzas de la gravitación tuvieron sentido. Conforme escribía sus ideas en forma matemática, él sabía que era “demasiado hermoso para estar equivocado”. Aunque tendrían que pasar todavía varios años hasta que hubiese una prueba de la relatividad general externa y objetiva, la belleza de estas ecuaciones que describían el universo de forma tan sencilla era suficiente para convencer a Einstein de que había encontrado la solución correcta.
Hemos de recalcar que esto era precisamente así: la belleza matemática era suficiente para él. Cuando en 1919 Arthur Eddington suministró el prime indicio de que la teoría podía ser correcta, alguien preguntó a Einstein qué habría hecho si su teoría no hubiera pasado esta primera prueba. Burlón, Einstein respondió que lo habría sentido por Dios, “porque la teoría era correcta”.
Numerosos científicos continúan usando el rasero de belleza y simplicidad para guiar su trabajo, y muchos han descrito la belleza que percibieron la primera vez que aprendieron la teoría de la relatividad. He aquí una ecuación que explica la forma y el movimiento de todo el universo y que, incluso incorporando la constante cosmológica lambda (Λ), es lo suficientemente corta como para escribirla en la palma de la mano. Es fácil comprender por qué puede hay quien la considera tan bella como un concierto de Bach, cada nota en su sitio. Para aquellos que trabajan con matemáticas, hay un aprecio muy parecido al placer estético para las ecuaciones que explican una faceta de la naturaleza sencilla y completamente.
Sin embargo, no hay nada inherente que sugiera que algo bello sea automáticamente bueno o verdadero. Después de todo la belleza es una construcción de la mente humana y la belleza no existe fuera de ella* (nuestros lectores saben que el ser humano no es nada especial en el universo, ni siquiera en el planeta). Fue el físico Eugene Wigner el que se lamentó de la “irracional efectividad de las matemáticas”, y es demasiado fácil ver las pautas de números como que apuntan hacia algo importante cuando lo lógico es verlas como fruto de la coincidencia. Ciertamente las ecuaciones de la mecánica de Newton o las del electromagnetismo de Maxwell son bellas, pero se ha demostrado que son incompletas.
Como la fe en el Dios de las religiones abrahámicas en siglos pasados para los científicos creyentes, que fueron muchos, la fe en la belleza de las matemáticas como patrón de veracidad fue un acicate para la creatividad de Einstein, que tuvo como resultado unas magníficas aproximaciones “al pensamiento de Dios”.
Nota filosófica:
[*] La ocurrencia de que la belleza existe externamente a la mente humana y, no solo eso, sino que el conocimiento de su existencia se debe a que la has conocido antes de nacer, mientras esperabas para reencarnarte, es de un tal Platón. Para aquellos que dicen que la filosofía no es importante, baste decir que buena parte de su concepción del mundo viene dada por las idas de olla de gente que se dedicó a ella, y que la sociedad transmite inconscientemente. Si no estudias filosofía tienes muy difícil detectar estas influencias.
Este criterio de la belleza como guía puede trazarse, por tanto, hasta el siglo V a.e.c. y no deja de ser un sesgo cultural importante. Curiosamente, el filósofo de cabecera de Einstein se supone que era Spinoza, pero Spinoza ya había advertido que la belleza, como el orden, son constructos humanos sin existencia objetiva. En este sentido, en la aproximación filosófica a la física se puede argumentar que Einstein seguía más la doctrina del neoplatónico Plotino que a Spinoza, quien, a este respecto, en el Apéndice al Libro I de la Ética (1677) de Spinoza es meridianamente claro. Una ocasión más en la que se demuestra que el criterio de la justicia penal es válido: es más importante fijarte en lo que alguien hace, que en lo que dice que hace.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Una versión anterior de este artículo se publicó en Experientia Docet el 9 de mayo de 2010.
El artículo Einstein y la belleza matemática se ha escrito en Cuaderno de Cultura Científica.
¿Podría haber meditado un neandertal?
Emiliano Bruner, paleoneurólogo del Centro Nacional de Investigación sobre la Evolución Humana (CENIEH), lidera un estudio sobre la evolución de la atención en el género humano en el que se analizan las evidencias paleontológicas y arqueológicas sobre la capacidad atencional de los homínidos extintos.
 Imagen: Emiliano Bruner
Imagen: Emiliano BrunerEl estudio propone que han existido cambios evolutivos de la atención en las distintas especies del género humano, aunque solamente con Homo sapiens esta capacidad cognitiva alcanza una complejidad que revoluciona profundamente el comportamiento, la capacidad tecnológica y la estructura social de la especie.
A nivel paleoneurológico, se ha analizado el papel de la evolución de los lóbulos parietales en la atención, definida como la capacidad de mantener el proceso cognitivo centrado en un objetivo en el tiempo y en el espacio, a pesar de elementos de distracción internos y externos. A nivel arqueológico, se han evaluado las informaciones asociadas a la industria lítica y a la ecología de los homínidos extintos, considerando los comportamientos que pueden sugerir cambios evolutivos en la memoria de trabajo y en las capacidades visoespaciales.
Los lóbulos parietales, que tienen un papel fundamental en la red atencional, están también relacionados con la capacidad de imaginación visual asociada a nuestra particular habilidad de proyección en el pasado (recuerdos) y futuro (predicción). Un desajuste entre esta capacidad de proyección y la red atencional puede afectar al equilibrio entre la percepción del momento presente y las rumiaciones mentales*, principales causas de la elevada prevalencia de estrés, ansiedad y depresión en las sociedades humanas modernas.
Atención plenaLa práctica meditativa es un entrenamiento cognitivo del sistema perceptivo y atencional y, en los últimos años, ha sido ampliamente estudiada en neurociencia por sus efectos en la capacidad de dirigir y mantener la atención en el momento presente.
La forma de meditación más integrada en nuestra sociedad occidental es la llamada atención plena, quizás más conocida por el término anglosajón mindfulness. “Considerando la estrecha relación entre capacidad atencional y meditación, nos planteamos investigar, provocativamente, si los homínidos extintos hubieran sido capaces de llevar a cabo una práctica de selección y mantenimiento de los estímulos mentales», señala Bruner.
A pesar de la importancia de la atención en todos los procesos cognitivos, hasta este estudio, que ha contado con la colaboración de Roberto Colom, del Departamento de Psicología de la Universidad Autónoma de Madrid, no se había tratado esta habilidad cognitiva desde una perspectiva paleoantropológica.
Referencia:
Bruner, E. & Colom, R. (2022). Can a Neanderthal meditate? An evolutionary view of attention as a core component of general intelligence. Intelligence doi: 10.1016/j.intell.2022.101668
Para saber más:
Emiliano Bruner – Habitar un cuerpo: cognición corporal y evolución humana
La complejidad de la mente neandertal
Nota:
* El término rumiación, en psicología, es darle vueltas a un pensamiento, a una idea, o a un posible problema, de manera inconsciente y casi obsesiva, provocando cierto malestar y haciéndose realmente complicado poder parar y salir de esa situación. Fuente: IEPP
Edición realizada por César Tomé López a partir de materiales suministrados por CENIEH
El artículo ¿Podría haber meditado un neandertal? se ha escrito en Cuaderno de Cultura Científica.
¿Percibimos los colores de forma diferente según la lengua que hablamos?
Pedro Raúl Montoro Martínez
 Shutterstock / djero.adlibeshe yahoo.com
Shutterstock / djero.adlibeshe yahoo.comLa vida es una tómbola de luz y de color, como dice la canción. Cuando abrimos los ojos, aparece inmediatamente ante nosotros un mundo teñido de infinidad de colores. Pero no son una mera decoración de nuestro mundo visual: nos permiten identificar los objetos, los materiales y las sustancias de nuestro entorno. Además, facilitan la comunicación con otras personas. Podemos diferenciar un plátano maduro de otro todavía verde. O pedir en una tienda la talla cuarenta de los zapatos rojos del escaparate.
El nombre del rosaAunque el número de matices cromáticos que podemos percibir es descomunal, la función comunicativa de los colores promueve que se utilice tan solo un limitado número de vocablos referidos a ellos. Este fenómeno se conoce como categorización del color, es decir, el agrupamiento de matices en una misma categoría asociada a una palabra: verde, rojo, azul, rosa…
Es una muestra de que el mundo de los colores, como muchos otros aspectos de la percepción, puede verse afectado por influencias culturales y por nuestras experiencias de aprendizaje.
Las nieves de los esquimalesSeguro que alguna vez ha leído que los esquimales son capaces de discriminar muchos tipos diferentes de nieve gracias a que disponen de decenas de términos en su lengua (el inuit) para referirse a ese estado físico del agua. Sin embargo, se trata de un mito pseudocientífico popularizado en la primera mitad del siglo XX por el lingüista Benjamin Whorf.
Whorf era un firme defensor de que la lengua que aprendemos afecta drásticamente a la forma en la que percibimos, recordamos y pensamos el mundo, hipótesis que se denomina determinismo lingüístico.
En realidad, la lengua inuit únicamente dispone de cuatro vocablos básicos para la nieve, de cuya combinación se derivan unos cuantos más. En castellano, por ejemplo, solo tenemos un término para nieve, pero mediante la unión con otras palabras también se puede discriminar entre diferentes estados de la misma, como aguanieve, nieve polvo, nieve primavera o nieve dura. De esta forma, los esquiadores hispanohablantes no necesitan aprender la lengua inuit para poder percibir y comunicar todos estas gradaciones de la nieve.
Cómo la lengua empaqueta los colores¿Podemos descartar entonces que nuestra lengua materna influye en cómo percibimos los colores? La forma en que los empaquetamos en categorías ha sido un campo de pruebas muy activo para contrastar la hipótesis del determinismo lingüístico.
El estudio clásico de los antropólogos Brent Berlin y Paul Kay (1969) supuso una aportación muy relevante en este campo. Estos autores investigaron los vocablos para denominar colores en cien lenguas de todo el mundo y observaron que los términos cromáticos no se repartían de forma arbitraria entre los idiomas, sino siguiendo una jerarquía predecible. Si una lengua solo tiene dos vocablos de color, entonces estos son el blanco y el negro. Si tiene tres, serán el blanco, el negro y el rojo. Con cinco términos, se suman el verde y el amarillo a los anteriores. Y así sucesivamente.
En definitiva, en contra de la hipótesis de la relatividad lingüística, lo que se encuentra es un patrón universal que pivota en torno a los seis colores básicos que proponen las teorías de la percepción cromática: blanco, negro, azul, amarillo, verde y rojo.
 Los seis colores básicos: negro, verde, rojo, azul, amarillo y blanco.
Los seis colores básicos: negro, verde, rojo, azul, amarillo y blanco.Shutterstock / Lewis Tse¿Cuán azul es el azul celeste?
En castellano, al igual que en inglés, solo disponemos de un término básico para aludir a los colores azulados. Sin embargo, en lenguas como el ruso, el griego o el turco cuentan con vocablos distintos para referirse a la tonalidad clara –o celeste– y oscura. Por ejemplo, en griego, los términos son ghalazio (azul claro) y ble (azul oscuro).
 Para los griegos, los rusos y los turcos el azul celeste y el azul oscuro son colores distintos.
Para los griegos, los rusos y los turcos el azul celeste y el azul oscuro son colores distintos.Shutterstock / Vector_Up
Varios estudios han mostrado que los hablantes de estas lenguas diferencian con mayor rapidez y seguridad entre azules claros y oscuros. Además, exageran las diferencias perceptivas entre matices intermedios en comparación con hablantes de inglés o castellano, como si fueran colores más distantes para ellos.
Otros resultados similares con varias categorías cromáticas permiten concluir que el empaquetado que cada lengua realiza para darle nombre a los colores influye en la forma en que estos son percibidos y recordados por sus hablantes.
Entonces, ¿vemos como hablamos?Las investigaciones recientes demuestran que, efectivamente, existe un cierto impacto de la lengua materna sobre el procesamiento de los colores. Sin embargo, este relativismo está lejos del rotundo determinismo lingüístico que proponía Whorf.
De hecho, con un entrenamiento rápido, cualquier persona puede ampliar su vocabulario cromático y aprender con facilidad a discriminar entre matices diferentes de azul o de cualquier otro color, como varios estudios han mostrado. De la misma forma, incluso personas que no están familiarizadas con los subtipos de nieve pueden aprender a discriminarlos y a adjudicarles un nombre, como hacen los esquimales o los esquiadores.
Curiosamente, en un trabajo con hablantes de griego que habían vivido una larga temporada en Reino Unido, se encontró que eran más propensos a asemejar el ghalazio y el ble por la influencia de la lengua inglesa, que, como hemos visto, los agrupa en una sola categoría lingüística.
En definitiva, la flexibilidad de nuestro sistema perceptivo nos permite ajustarnos al entorno de manera adaptativa para seguir disfrutando de la tómbola de luz y de color.![]()
Sobre el autor: Pedro Raúl Montoro Martínez es Profesor Titular del Departamento de de Psicología Básica I de la Universidad Nacional de Educación a Distancia (España)
Este artículo fue publicado originalmente en The Conversation. Artículo original.
Para saber más:
Alucinaciones lingüísticas: los engaños de tu lengua materna
El artículo ¿Percibimos los colores de forma diferente según la lengua que hablamos? se ha escrito en Cuaderno de Cultura Científica.
Las pruebas de la educación: Marta Ferrero – ¿Jornada escolar continua o partida?

Bilbao volvió a acoger el pasado 20 de mayo de 2022 “Las pruebas de la educación”, una jornada que abordará diversas cuestiones educativas con la evidencia científica existente. Esta quinta edición está organizado por la Cátedra de Cultura Científica de la UPV/EHU y la Fundación Promaestro con la colaboración del Consejo Escolar de Euskadi, y se celebró en el Bizkaia Aretoa – UPV/EHU de la capital vizcaína.
La jornada consta de cinco ponencias de media hora de duración en la que se tratan temas como la problemática relacionada con los juegos de azar en el ámbito escolar, el impacto de la inmigración en el rendimiento del alumnado o el debate sobre la jornada escolar continua o partida, entre otras cuestiones. La dirección del seminario corrió de nuevo a cargo de Marta Ferrero profesora de la Facultad de Formación del Profesorado y Educación de la Universidad Autónoma de Madrid.
Marta Ferrero pone el foco en la nueva tendencia que apuesta por la jornada escolar continua, creciente tras la pandemia, en detrimento de la jornada partida y aporta datos e investigaciones sobre las consecuencias en términos académicos, sociales y de salud.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Las pruebas de la educación: Marta Ferrero – ¿Jornada escolar continua o partida? se ha escrito en Cuaderno de Cultura Científica.
Un tornado magnético para manipular la interfaz aire-agua
Inspirándose en materiales naturales que repelen el agua, como las hojas de loto, el estudio y desarrollo de superficies hidrofóbicas está adquiriendo un gran interés en campos como la manipulación precisa de pequeños volúmenes de fluidos. La integración de las propiedades magnéticas en los materiales hidrofóbicos favorece la manipulación remota del material al mismo tiempo que repele el agua, proporcionando nuevas perspectivas para posibles aplicaciones. En una nueva investigación, “hemos desarrollado un novedoso sistema para poder manipular la interfaz aire-agua utilizando un campo magnético externo”, señala Fernando Benito López, investigador principal del Microfluidics Cluster de la UPV/EHU.
 Imagen de la portada de la revista Langmuir
Imagen de la portada de la revista LangmuirPara ello, “hemos generado una capa de nanopartículas magnéticas hidrofóbicas capaz de flotar en la interfaz agua-aire y formar una interfaz agua-sólido-aire estable. Hemos observado que esta capa se dobla fácilmente hacia abajo por la acción de un campo magnético externo. Gracias a ello, la capa crea una estructura tipo tornado con forma cónica invertida a la que hemos bautizado como ‘Magneto Twister’ [tornado magnético]”, explica Fernando Benito López. “Esta estructura en forma de tornado se comporta como un material blando y elástico que se deforma o desaparece con el campo magnético aplicado”, añade el profesor de la UPV/EHU.
Se trata de una investigación fundamental con tres grandes aplicaciones en escenarios reales como explica Benito López: “en primer lugar, hemos utilizado el ‘Magneto Twister’ para manipular gotas de agua en un medio acuoso sin que se mezclen. Posicionamos las gotas de agua encima del cono magnético para moverlas en el medio acuoso y transportarlas a donde nos interese. Una vez que las gotas de agua estén en la zona deseada, podríamos eliminar el campo magnético para llevar a cabo una reacción química en una parte controlada de ese medio”.
Además, “el ‘tornado’ ha permitido para separar líquidos dentro de un canal de superficie abierta, lo que nos da la opción de tener reservorios independientes dentro de un canal fluídico y de almacenar reactivos que únicamente se mezclarán cuando se elimine el campo magnético externo para que una reacción química o biológica se efectúe”, explica Fernando Benito. “Sería algo similar a una válvula que se abre y se cierra para controlar el movimiento de los fluidos en dichos canales y conductos de una manera controlada en la microescala“, añade el investigador de la UPV/EHU.
Por último, “el tornado magnético se utilizó con éxito para recoger y eliminar microplásticos flotantes en la superficie del agua, simplemente moviendo el tornado hacia el microplástico para atraparlo”, señala Benito López.
Referencia:
Udara Bimendra Gunatilake, Rafael Morales, Lourdes Basabe-Desmonts eta Fernando Benito-Lopez (2022) Magneto Twister: Magneto Deformation of the Water–Air Interface by a Superhydrophobic Magnetic Nanoparticle Layer Langmuir doi: 10.1021/acs.langmuir.1c02925
Para saber más:
Formación de micelas en fase gaseosa
Nanoburbujas, un recipiente en busca de un tapón
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Un tornado magnético para manipular la interfaz aire-agua se ha escrito en Cuaderno de Cultura Científica.
Convivir con el fuego
Noches asfixiantes en zonas donde nunca lo habían sido, vientos extremadamente cálidos, intenso olor a humo, tensión en el ambiente mientras los vecinos tratan de organizarse para evitar que el fuego devore sus hogares. En el mejor de los casos, los bomberos ya están por la zona y se oyen aviones anfibios y helicópteros sobrevolando. Esta escena se está repitiendo en multitud de municipios este verano. Varias instituciones científicas hacen un llamamiento para la urgente gestión de los bosques en España.
 Efectivos de bomberos en la extinción de un incendio forestal en la carretera N120 en A Cañiza (Pontevedra) el 31 de julio. EFE/ Alberto Sxenick
Efectivos de bomberos en la extinción de un incendio forestal en la carretera N120 en A Cañiza (Pontevedra) el 31 de julio. EFE/ Alberto SxenickLos datos de la superficie quemada ya otorgan a 2022 el triste récord de ser el año en el que más hectáreas de bosque se han quemado en los últimos 30 años en España. El 31 de julio superamos las 200.000 hectáreas, una extensión mayor que la provincia de Guipúzcoa. Esta pérdida de masa forestal supone un aumento directo de las emisiones de CO2, ya que el fuego libera el carbono almacenado en plantas y suelos, perder biodiversidad y los servicios ecosistémicos de los que nos provee el bosque que van desde la obtención de madera o setas hasta la recuperación del agua y el suelo o la obtención de aire para respirar. Eso sin contar lo más importante, los dramas personales que incluyen la muerte de personas y los daños materiales además de la pérdida de esperanza de quienes viven en las zonas rurales y llevan décadas advirtiendo de lo que iba a pasar, la población de la España que han vaciado muchos años de políticas enfocadas en lo urbano.
No es momento ahora de decir “esto se venía venir” y exponer lo que se debería haber hecho, sino de remangarse y ponerse a trabajar en la gestión de los hábitats primando el conocimiento. Basar las decisiones de gestión en evidencias científicas, hacer un enfoque integrado, que atienda a la multifuncionalidad de los ecosistemas y a todos los factores de los que depende. Hay que priorizar las medidas poniendo el foco en lo más básico: Prevención, prevención y prevención. Un mantra que, por más que lo repiten las personas que viven en entornos rurales y las que se dedican a la ingeniería forestal, la biología de la conservación o el estudio de los ecosistemas, los gestores de todo el espectro político olvidan en un cajón cuando llegan las primeras lluvias y, para ahorrar, deciden que la inversión para evitar incendios se pondrá en marcha en mayo, cuando se acerque el calor. Error. Quienes viven pegados al monte saben que la labor de un operativo antiincendios va mucho más allá de apagar las llamas.
Las soluciones sostenibles a la mayoría de los problemas ambientales giran en torno a la coexistencia con el fuego, es decir, adaptarnos a su presencia anticipándonos a sus efectos más devastadores minimizando el riesgo y vulnerabilidad de los sistemas forestales. Para lograr esto hay dos líneas que se deberían trabajar paralelamente: la recuperación de la población y los trabajos del campo en las zonas donde la demografía se ha desplomado y la gestión forestal de las áreas naturales.
Tierra sin genteLos ecosistemas europeos son fruto de la interacción humana desde hace miles de años. No existen bosques que mantengan las estructuras anteriores a la aparición del ser humano. Nuestra presencia ha generado los actuales paisajes culturales donde las especies que los habitan han evolucionado y a los que se han adaptado. No se puede abordar la restauración de ecosistemas como si el ser humano no existiera u obviando que debemos convivir con el resto de especies. De hecho, uno de los mayores problemas a los que se enfrenta el medioambiente en Europa es el abandono de las zonas rurales y la sustitución de las explotaciones familiares, PYMES que son las que realmente crean empleo y tejido social en España, en favor de las de producción agroalimentaria intensiva que daña los hábitats que nos rodean y dan empleo a menos personas.
Existe un consenso claro en la comunidad científica sobre cómo el abandono agrario y la expansión y densificación del bosque en esos espacios que antes se aprovechaban a través de la actividad forestal, la agricultura y la ganadería, crean paisajes cada vez más homogéneos y vulnerables al avance del fuego. Para revertir esta situación, hay que tomar iniciativas que permitan la recuperación de paisajes donde haya un mosaico de usos: bosques, cultivos herbáceos y leñosos, pastos o matorrales. Esta estructura actúa como “cortafuegos” natural mientras se genera una renta que permita a la población que los mantiene vivir dignamente de esas actividades. Se trata de tejer alianzas entre la gestión del bosque y el resto de usos rurales y que quienes viven de la agricultura y la ganadería trabajen codo con codo con los propietarios y gestores forestales para crear territorios resilientes al fuego.
Los montes que son rentables no arden, o lo hacen con menor intensidad, y rentabilidad es sinónimo de gestión activa del territorio y de personas viviendo en él. Más allá de contar con subvenciones públicas que pueden estar justificadas por el carácter también público de muchos de los servicios que esos montes nos proporcionan, hay que crear modelos de negocio sostenibles que permitan a sus poblaciones vivir dignamente de los bienes y servicios que producen.
El papel de las administraciones pasa por poner en marcha medidas de estímulo y apoyo a la economía en zonas rurales que no se queden en las simples subvenciones, sino que busquen un efecto transformador: Mejorar la fiscalidad y agilizar la burocracia a la que se enfrentan quienes emprenden en zonas rurales; proveer de servicios sanitarios, educativos y de transporte; promover la compra pública de productos sostenibles y cuya producción se integra en el territorio (como construir con madera de nuestros bosques los edificios públicos) o dar valor a los productos que favorecen la sostenibilidad del monte e identificarlos para que los consumidores sepan que su compra apoya a economías locales que ayudan a prevenir incendios y conservar la biodiversidad; pueden ser ejemplos que trascienden las subvenciones que en muchos casos ahogan la iniciativa de las personas. Así, promover un reparto más equilibrado de la población, además de ser más sostenible, se convierte en una medida de prevención de incendios.
Estas iniciativas deben adaptarse a las particularidades de cada territorio, a su paisaje y su paisanaje. Los actores locales y su territorio no son meros receptores de las ideas científicas o de las administraciones. Implicar a quienes viven y conocen el territorio es imprescindible para mejorar nuestra protección frente al fuego porque sobre un mapa, sostiene cualquier plan de actuación, pero son las personas que viven en el territorio las que lo conocen y su participación es vital si se quiere ir más allá de un proyecto escrito. En este sentido, la Comisión Europea lleva tiempo financiando procesos de cocreación que persiguen dinámicas cruzadas entre el personal de las administraciones, científicos y la población.
Ejemplos como La red de áreas pasto-cortafuegos de Andalucía (RAPCA) o la iniciativa Ramats de Foc (rebaños de fuego), que promueven el pastoreo en zonas arboladas donde los animales actúan controlando el exceso de vegetación, muestran que ya existen iniciativas que intentan ejemplificar una gestión activa del territorio donde se implican todas las partes.
 EFE/José Luis CereijidoAyudar a extinguir, antes de que la llama prenda
EFE/José Luis CereijidoAyudar a extinguir, antes de que la llama prenda
La selvicultura, ciencia que estudia la gestión de los bosques y montes forestales, debe centrar sus objetivos en dirigir el ecosistema hacia la formación de bosques sostenibles cuyo valor paisajístico, económico y natural aumenta. Es una práctica cuyos resultados son visibles a largo plazo que necesita políticas estructurales enfocadas en la realidad de las zonas rurales y ecosistemas forestales; planificación y anticipación dotada con presupuesto y personal suficientes. Esta prevención se sustenta en el trabajo estable basado en la realidad de los montes en cada época del año. Hay que afanarse en la prevención con equipos formados por quienes viven y conocen la zona, técnicos, ingenieros y ecólogos que se encarguen de evaluar qué medidas hay que aplicar en cada lugar para que, al llegar el verano, estemos preparados.
Existen medidas centradas, principalmente, en la disminución del combustible (cantidad de biomasa) o cambios en su estructura (tamaño y disposición de la biomasa). La disminución de biomasa se logra eliminando parte de la vegetación arbustiva, sobre todo la más seca, mediante el desbroce, la retirada de las ramas y troncos muertos y las quemas prescritas. Los cambios en la estructura pasan por la elaboración de áreas cortafuegos en las que se disminuye gradualmente el combustible disponible partiendo de caminos y carreteras. Estas áreas, además de cortar el avance del fuego, permiten que los medios de extinción puedan actuar en caso de incendio.
Asimismo, la regulación de la densidad de árboles en edades tempranas y en alta densidad mediante claras o clareos son también medidas protectoras. Ante un futuro que se prevé más seco y con regímenes de precipitación irregular, conviene pensar también en áreas de monte bajo con especies herbáceas o arbustivas que necesitan menos agua para mantenerse hidratadas, una buena vacuna para evitar grandes incendios.
En las zonas con mayor riesgo es necesario fomentar la regeneración natural de especies con estructuras físicas defensivas (corcho o corteza gruesa) o estrategias de regeneración adaptadas al fuego. La mezcla de especies autóctonas es también excelente para aumentar la biodiversidad estableciendo masas forestales multifuncionales y de mayor resiliencia frente a nuevos incendios. En el caso de que prenda un fuego, un bosque mixto tiene más opciones de recuperación que uno donde solo crece una especie (monoespecífico) porque presenta mayor variedad de estrategias para adaptarse y regenerarse. Aunque, sin una correcta aplicación de clareos y claras no es necesariamente mejor desde el punto de vista de la propagación del fuego, la restauración con múltiples especies es sin duda un valor seguro.
La gestión del paisaje basada en la creación de mosaicos que combinen rodales con distinta densidad vegetal con áreas de pasto y campos de cultivo dan menos oportunidad al fuego para su propagación. En este sentido, combinar áreas boscosas en las que la intervención es mínima, con masas agroforestales y campos de labor es una buena estrategia que, de nuevo, necesita personas que vivan y convivan con la naturaleza que les rodea. El ejemplo del proyecto Mosaico, en Sierra de Gata y Las Hurdes (Extremadura), en el que se trabaja en terrenos públicos y privados con numerosas propuestas y donde más de la mitad de los emprendedores es menor de cuarenta años, demuestra que un cambio en la gestión del territorio es posible.
Todas estas medidas basadas en la gestión integral y multidisciplinar de los bosques son el principio para evitar que la llama prenda, sí, pero si aun así el fuego se produce es vital, una vez extinguido, analizar la situación para establecer una restauración adecuada.
Y después del fuego, ¿qué?Nos gustaría decir que después de un fuego la solución es sencilla: Se han quemado árboles así que plantamos más y listo, pero no lo es. No hay soluciones únicas para minimizar el impacto de los incendios forestales que son procesos complejos tanto ecológica como socialmente que requieren un análisis e interpretación de la información antes y después de cada caso. No es lo mismo un incendio sobre un suelo silíceo que sobre uno calizo y lo que sirve a los vecinos de El Courel no tiene por qué servir a los de Monfragüe.
El fuego forma parte de la dinámica natural del bosque mediterráneo, y como tal sus especies están adaptadas a esta perturbación. De hecho, los incendios forestales llegan a ser necesarios para garantizar su regeneración. Muchas especies vegetales lo necesitan para que sus semillas germinen, un proceso ecológico llamado serotinia, o aumente la brotación.
Dadas estas características particulares, los mediterráneos son ecosistemas que se suelen regenerar bien tras los incendios, de ahí que en muchos casos la mejor medida sea no hacer nada (restauración pasiva). Sin embargo, las características históricas de los incendios están cambiando, y los nuevos regímenes de incendios, mucho más virulentos, sobrepasan la capacidad de adaptación, llegando a reducir de forma permanente la biodiversidad y la funcionalidad del ecosistema.
Una correcta gestión pasa por desarrollar estrategias que busquen promover la capacidad para recuperarse o resiliencia del ecosistema y por asumir que la mejor solución posible en cada caso particular puede implicar un cambio de nuestra percepción sobre el papel del fuego en la estructuración del bosque. El proceso persigue acelerar la reparación de las funciones del sistema dañado y generalmente se extiende entre uno y tres (clima atlántico) o cinco años (clima mediterráneo), dependiendo de la intensidad del fuego y las características de la zona afectada.
La estabilización de emergencia tras el incendio comprende un conjunto de acciones a corto plazo (entre unos meses hasta un año después del incendio) dirigidas a identificar amenazas inminentes para la vida humana. Se trata de garantizar los servicios básicos para la población. Esta primera estabilización presta especial atención a reducir el riesgo asociado al deterioro del suelo y de las condiciones hidrológicas de las cuencas forestales afectadas. De hecho, toma a estas últimas como unidades de planificación e implementación de las tareas para paliar el impacto sufrido.
El suelo, la base sobre la que reconstruir todoLos efectos más obvios y llamativos de los incendios son los que afectan a los valores culturales y estéticos de los bosques y la desaparición de la vegetación y de la diversidad florística, que es también hábitat y fuente de recursos para la fauna. Algo que pasa más desapercibido son sus efectos sobre el suelo.
Los suelos son un gran reservorio de biodiversidad y el elemento esencial para la recuperación integral del ecosistema. Los habitantes de los suelos incluyen, entre otros, lombrices, ácaros, nematodos, bacterias y hongos. Estos organismos, esenciales para la recuperación de la funcionalidad y fertilidad de los suelos, son los responsables del secuestro de gran cantidad de carbono. Transforman la hojarasca en materia orgánica y nutrientes y modifican la estructura del suelo favoreciendo la infiltración de agua, factores esenciales para la supervivencia y recuperación de las plantas.
Entre estos microorganismos destacan los hongos micorrícicos, que forman simbiosis con las raíces de las plantas a las que facilitan la adquisición de agua y nutrientes a cambio de azúcares procedentes de la fotosíntesis. Los hongos micorrícicos pueden conectarse con múltiples plantas a la vez, generando unas redes miceliares a través de las que las plantas huésped intercambian recursos entre ellas. La recuperación del ecosistema edáfico procede de zonas forestales adyacentes no quemadas y de aquellos organismos resistentes que perduran a mayor profundidad en las capas minerales del suelo.
Si una vez apagado el fuego, se toman algunas medidas sencillas encaminadas a proteger el suelo de los procesos erosivos que causa la lluvia, las evidencias científicas apuntan a que, con el tiempo, el equilibrio de la comunidad original termina instaurándose.
Hacia un ecosistema funcional y resilienteTras abordar la situación del suelo, la eliminación de los árboles quemados es una medida controvertida pero necesaria en algunos casos para inducir que las especies broten con más vigor o para evitar infestaciones de insectos perforadores de los árboles supervivientes, que, además podrían extenderse a zonas no quemadas. Desde un punto de vista económico, la extracción de los pies antes de que se pudran por completo puede generar ingresos que reviertan en la recuperación del bosque.
No obstante, la extracción completa de todos los árboles podría aumentar la escorrentía o disminuir el hábitat para otras especies. Es importante estudiar cada situación para planificar en el espacio y en el tiempo las medidas más adecuadas, de hecho la restauración de ecosistemas quemados no debe hacerse mirando solo las especies que hubo en el pasado sino a las que mejor resistirán en el futuro. De nuevo, el análisis de cada caso es esencial.
La rehabilitación ofrece una interesante oportunidad para abordar un cambio de especie si se estima pertinente. Muchos incendios han permitido iniciar una nueva etapa en la trayectoria de la vegetación dominante en el ecosistema incendiado transformándolo en un bosque mixto. Si las condiciones fisiográficas del suelo, de erosión o de degradación previa así lo recomiendan.
El bosque, como sistema abierto que se autoorganiza se puede recuperar de un incendio. No esperemos tener el mismo hábitat, pero el ecosistema forestal seguirá existiendo. Sin embargo, dos incendios en el mismo lugar en un tiempo menor del necesario para su recuperación conllevarían, inevitablemente, la pérdida definitiva del ecosistema arbolado. La selvicultura y la gestión forestal son nuestra respuesta para ayudar al bosque y no nos engañemos, mientras vivamos en este planeta, somos los primeros interesados en mantener bosques y ecosistemas sanos.
Sobre las autoras:Cristina Aponte. Instituto Nacional de Investigación y Tecnología Agraria y Alimentaria (INIA-CSIC)
Andrés Bravo Oviedo. Museo Nacional de Ciencias Naturales (MNCN-CSIC)
Xiomara Cantera. Periodista del Museo Nacional de Ciencias Naturales (MNCN-CSIC)
Manuel Esteban Lucas Borja. Universidad de Castilla la Mancha
Javier Madrigal. Centro de Investigación Forestal (INIA-CSIC)
Leticia Pérez-Izquierdo. BC3, Basque Centre for Climate Change
Ana Rincón. Instituto de Ciencias Agrarias (ICA-CSIC)
Elsa Varela. Centro de Ciencia y Tecnología Forestal de Cataluña (CTFC)
Este texto apareció originalmente en SINC.
El artículo Convivir con el fuego se ha escrito en Cuaderno de Cultura Científica.
Teoremas geométricos sin palabras: Herón
Esta tercera entrega de la serie estival de demostraciones sin palabras de interesantes y hermosos resultados geométricos, que habíamos iniciado con el clásico teorema de Viviani (en la entrada Teoremas geométricos sin palabras: Viviani) y que habíamos continuado con un teorema actual, el teorema de la circunferencia de Conway (en la entrada Teoremas geométricos sin palabras: Conway), la vamos a dedicar a la clásica fórmula de Herón para el área de un triángulo.
Pero antes de adentrarnos en la fórmula de Herón, vayamos a la resolución del problema que dejamos planteado en la anterior entrada.
Un cuadrado inscrito en un triánguloEn la anterior entrada dejamos propuesto el siguiente problema sobre cuadrados que aparece recogido en el artículo A Round-Up of Square Problemas (Una recopilación de problemas con cuadrados), de los matemáticos Duane Detemple y Sonia Harold, publicado en Mathematics Magazine en 1996.
Problema (Un cuadrado inscrito en un triángulo rectángulo isósceles): Estos dos cuadrados han sido inscritos en un mismo triángulo rectángulo isósceles, pero de dos formas distintas, como se muestra en la imagen. ¿Cuál de los dos cuadrados tiene una mayor superficie?
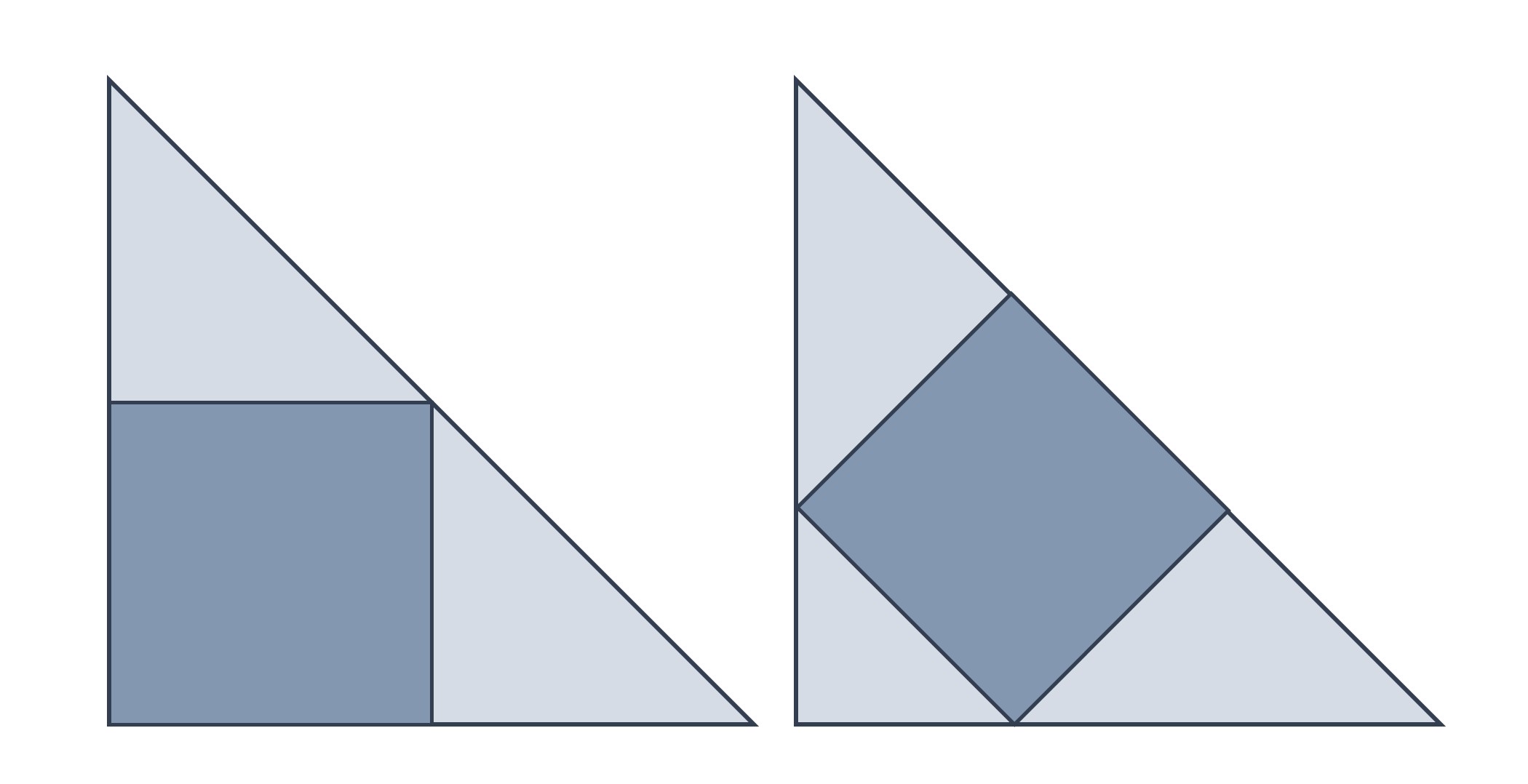
La solución a este problema es sencilla, la mayor superficie corresponde al cuadrado de la izquierda, y se puede realizar con una sencilla imagen.
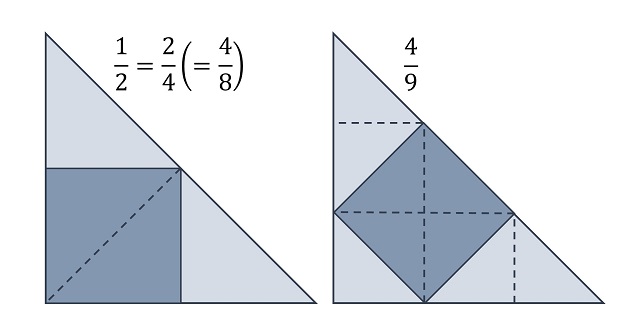
Todas las personas hemos estudiado en la escuela la sencilla fórmula para calcular el área de un triángulo, que no es otra que la mitad de la base por la altura del triángulo: Área = (base x altura) / 2.
A pesar de la sencillez de esta fórmula, podemos plantear algunas objeciones a la misma. Dado un triángulo ABC, con lados a, b y c, como el que aparece en la siguiente imagen, la primera objeción es que la información que solemos tener de este polígono es la longitud de sus lados, es decir, a, b y c, luego no es posible calcular el área directamente con esa información.
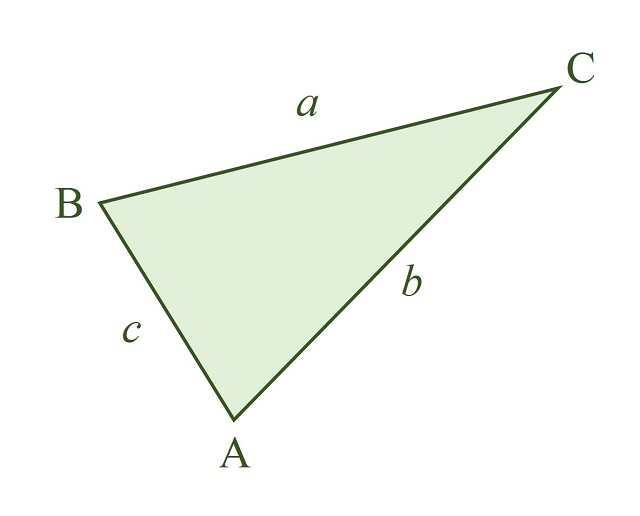
Además, dada la mencionada fórmula (base por altura dividido por dos) disponemos de tres opciones distintas para la base –obviamente, cada uno de los tres lados a, b o c– y, por lo tanto, también para la correspondiente altura. Por ejemplo, si en el anterior triángulo ABC tomamos como base el lado b, tendremos la altura h que aparece en la siguiente imagen.
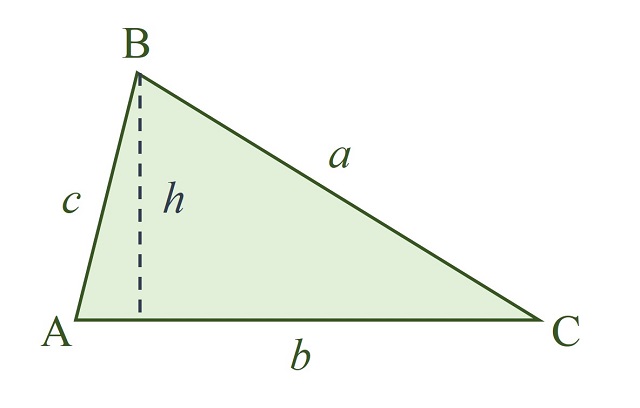
Pero no disponemos, a priori, de la información del valor de la altura h, por lo tanto, debemos de calcularlo (en la educación primaria normalmente nos daban el valor de la altura o era un triángulo rectángulo de manera que la base y la altura eran los catetos del mismo). ¿Cómo calcular la altura h, a partir de los valores de los lados a, b y c? Este es el típico problema de aplicación del teorema de Pitágoras en educación secundaria (aunque para valores concretos de los lados). Veamos cómo se solucionaría de forma genérica.
Llamamos u a una parte de la base determinada por la intersección de esta con la altura, de forma que la otra será b – u, como en la siguiente imagen.
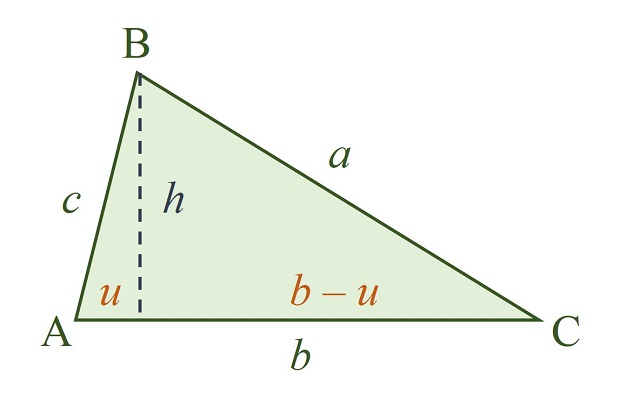
Entonces, se aplicaría el teorema de Pitágoras a los dos triángulos rectángulos determinados por la altura (h, u, c) y (h, b – u, a), obteniéndose las expresiones:
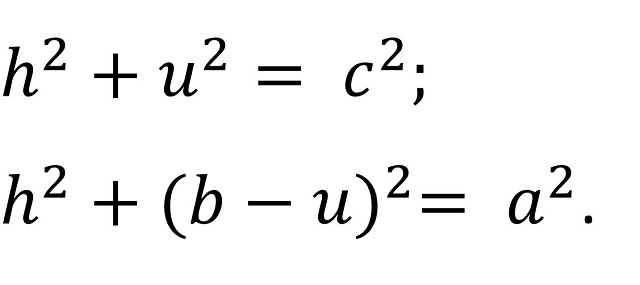
Restando ambas expresiones se tiene que a2 – c2 = b2 – 2bu y despejando u podemos obtener su valor en función de los lados a, b y c:
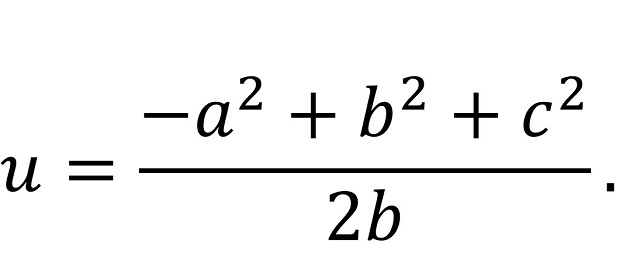
Una vez obtenido el valor de u podemos calcular h2 con la primera de las fórmulas anteriores, h2 = c2 – u2, obteniéndose la siguiente expresión (con un pequeño cálculo intermedio, que obviamos para no abusar de las fórmulas):
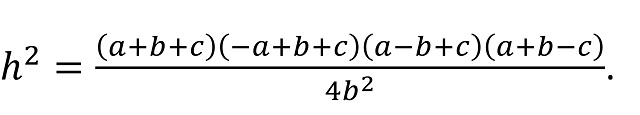
De esta forma hemos obtenido una expresión general para la altura h, si la base es b, en función de los lados a, b y c, haciendo uso del teorema de Pitágoras. Ahora, si llamamos s al semi-perímetro, es decir, s = (a + b + c) / 2, e introducimos el valor de h en la fórmula del área del triángulo, base b por altura h dividido por 2, se obtiene la expresión:
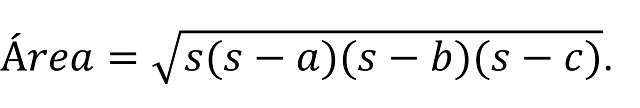
De esta forma, hemos obtenido una expresión para el área del triángulo en función, directamente, de los lados del mismo, a, b y c. Esta es la conocida como fórmula de Herón para el área del triángulo.
Así, si consideramos un triángulo de lados 13, 14 y 15, tendríamos que el semi-perímetro sería s = 21 y el área s, por la fórmula de Herón, sería la raíz cuadrada del producto de 21, 8, 7 y 6, luego de 7.056, que es 84.
La fórmula de Herón (sin palabras)La anterior fórmula del área del triángulo debe su nombre al matemático e ingeniero griego Herón de Alejandría (aprox. 10 – 70 a.n.e.), que la incluyó en su libro Metrica (alrededor de 60 a.n.e., aunque este manuscrito estuvo perdido hasta 1896). Esta fórmula podría ser conocida ya por el matemático e ingeniero griego Arquímedes de Siracusa (aprox. 287 – 212 a.n.e.), según aparece recogido en las obras del científico persa Al-Biruni (973 – después de 1.050).
Existen diferentes demostraciones de la fórmula de Herón, además de la mostrada en esta entrada haciendo uso del teorema de Pitágoras, pero nosotros, como corresponde a esta serie veraniega, vamos a mostrar la demostración que el matemático Roger B. Nelsen publicó en la revista College Mathematics Journal, en 2001, utilizando los argumentos de las demostraciones sin palabras.
Dado un triángulo ABC, las rectas que bisecan los ángulos en los vértices A, B y C (llamadas bisectrices) se intersecan en un punto P, que no es otro que el incentro I del triángulo ABC (el centro de la circunferencia inscrita en el triángulo ABC).
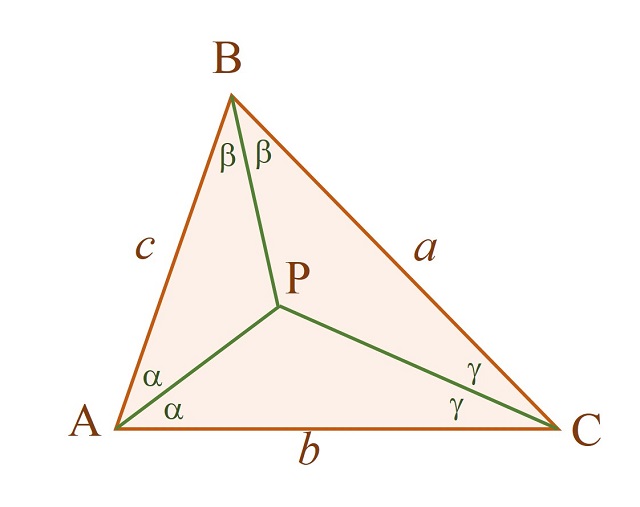
Efectivamente, si trazamos desde el punto P los tres segmentos perpendiculares a los lados a, b y c (en rojo en la siguiente imagen) se generan tres pares de triángulos semejantes (dos triángulos semejantes en cada vértice del triángulo ABC), de manera que esos tres segmentos tienen la misma longitud r, el radio de la circunferencia inscrita en el triángulo ABC. Por lo tanto, efectivamente P es el incentro I del triángulo.
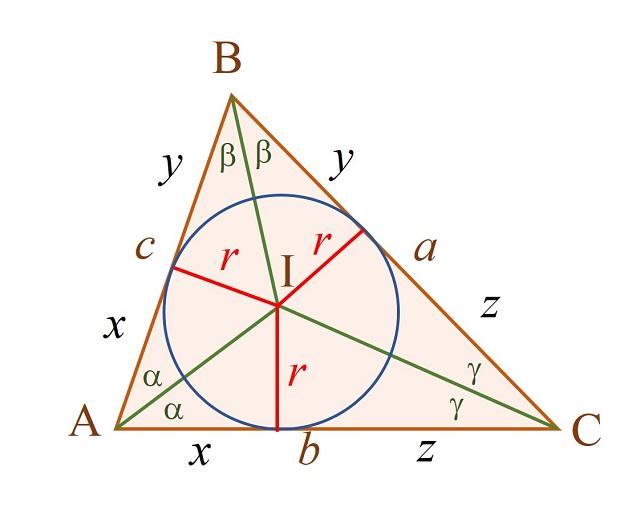
Además, llamando x, y y z como en la anterior imagen, tenemos que los lados son a = y + z, b = x + z y c = x + y, que el semi-perímetro es s = x + y + z y que entonces x = s – a, y = s – b y z = s – c.
Para demostrar la fórmula de Herón vamos a demostrar primero (sin palabras) dos pequeños resultados técnicos previos (lo que en matemáticas llamamos “lemas”).
Lema 1: El área del triángulo ABC es igual al producto del semiperímetro s y el radio r de la circunferencia inscrita en el mismo (de centro I).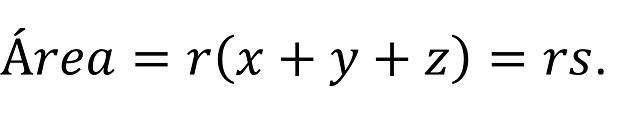
La demostración de este resultado es el siguiente diagrama, que consiste en una reordenación de los tres pares de triángulos semejantes de la imagen anterior.
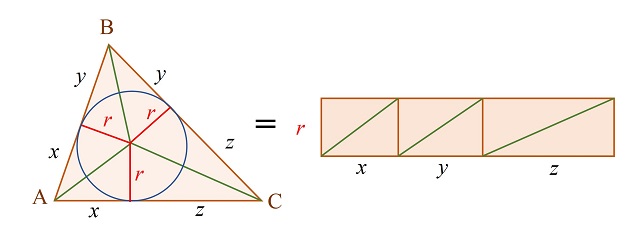
El siguiente lema es un resultado un poco técnico sobre trigonometría (podéis saltároslo si os parece muy técnico) que describe una relación entre tres ángulos alpha α, beta β y gamma γ cuya suma sea un ángulo recto, es decir, 90 grados. Por lo tanto, luego podremos aplicar este lema a los tres ángulos alpha α, beta β y gamma γ, que son la mitad de los ángulos en los vértices A, B y C del triángulo ABC, como hemos mostrado en una imagen anterior, y que suman, por tanto, 90 grados.
Lema 2: Si alpha α, beta β y gamma γ son tres ángulos positivos cuya suma es 90 grados, entonces![]()
Para demostrar (sin palabras) este segundo lema técnico vamos a construir el siguiente rectángulo, jugando un poco con la trigonometría, y a igualar el valor de la longitud de los dos lados paralelos, de la izquierda y la derecha, del rectángulo.
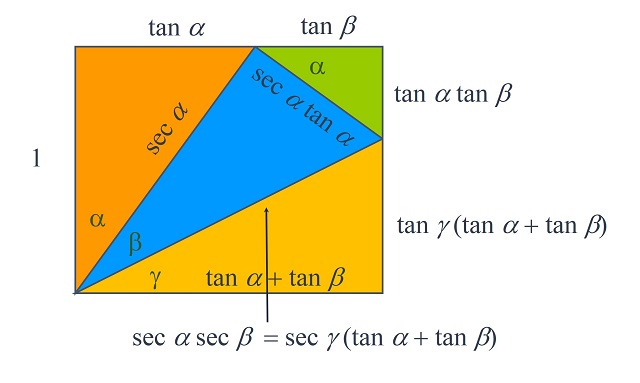
Nota: Podemos recordar algunas de las definiciones básicas de la trigonometría. Dado un ángulo alpha α se considera el triángulo rectángulo tal que alpha α es el ángulo entre uno de sus catetos y la hipotenusa, como en la siguiente imagen, entonces se definen el seno y el coseno como el cociente entre uno de los catetos y la hipotenusa, para el seno el cateto opuesto al ángulo y para el coseno el otro cateto.
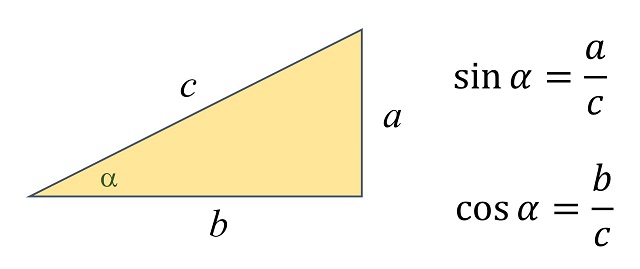
Además, se definen la tangente, la secante y la cosecante del ángulo como
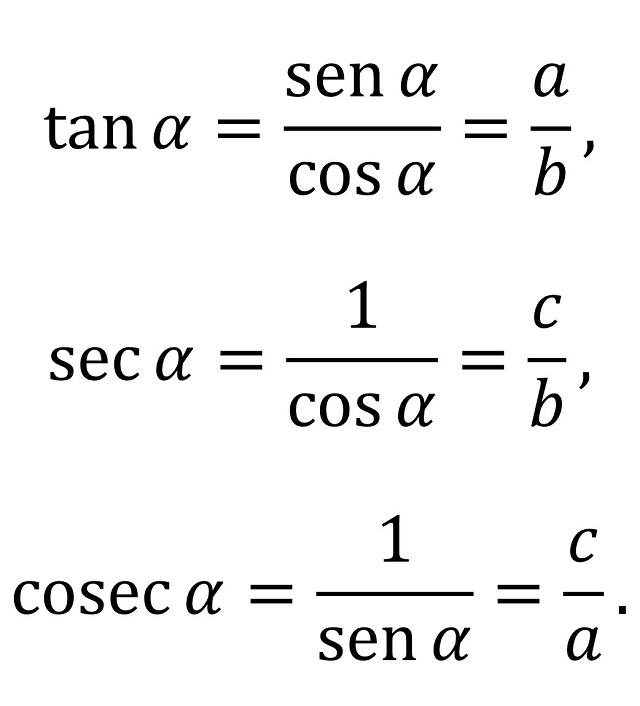
Por este motivo, si el triángulo anterior (de la definición del seno y el coseno), lo redimensionamos dividiendo sus lados por b, de forma que ese cateto tendrá una longitud de 1, queda el siguiente triángulo
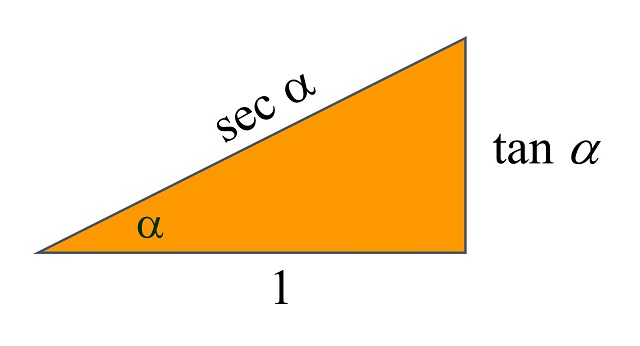
que es uno de los que aparecen en el rectángulo de la prueba visual del lema 2.
Si ahora se aplica el lema 2 al diagrama anterior en el que se descomponía el triángulo ABC en tres pares de pequeños triángulos rectángulos de ángulos alpha α, beta β y gamma γ, que recordamos en la siguiente imagen,
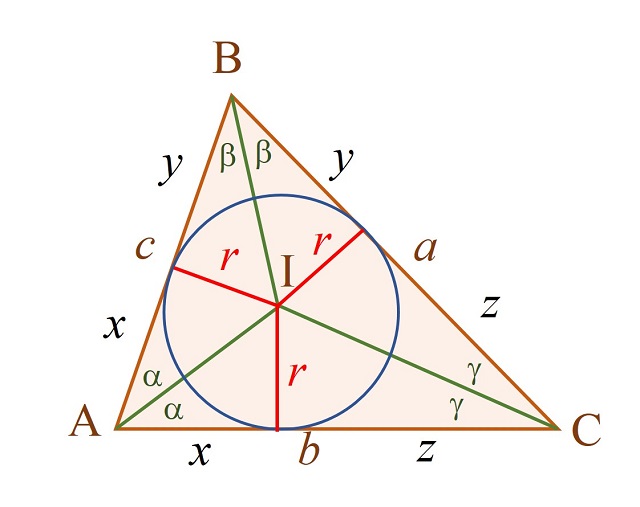
entonces se tiene que:
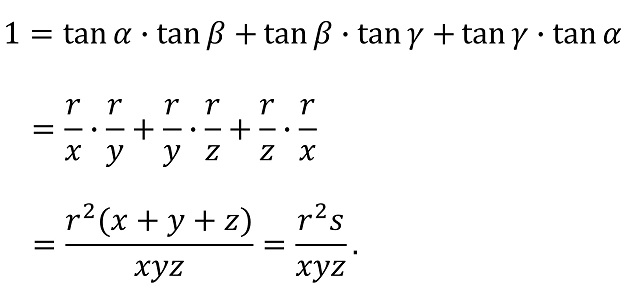
Ahora, teniendo en cuenta el lema 1 se tiene
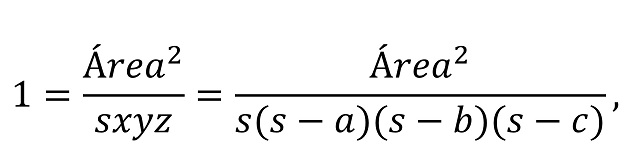
que demuestra la fórmula de Herón.
Cuadrados inscrito y circunscrito a una circunferenciaUna vez más, como viene siendo habitual en esta serie estival, vamos a terminar esta entrada con un sencillo problema que puede ser resuelto con un razonamiento visual.
Problema (Cuadrados inscrito y circunscrito a una circunferencia): ¿Cuál es la proporción de las áreas de los cuadrados inscrito y circunscrito a una misma circunferencia?
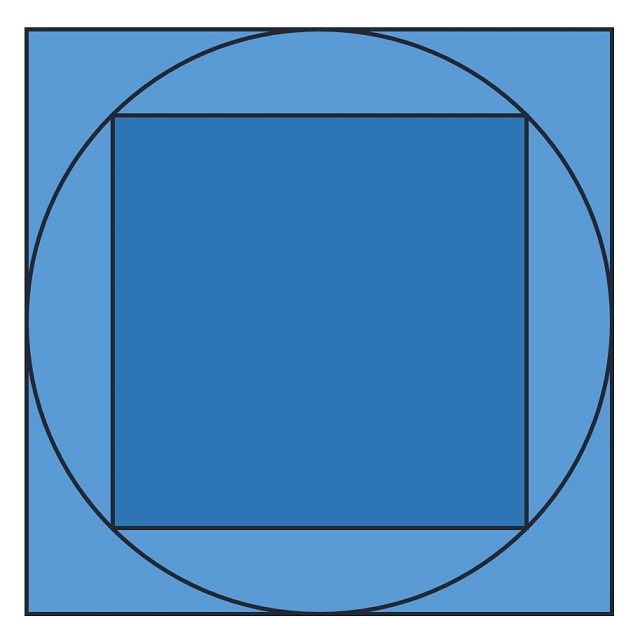
Bibliografía:
1.- Roger B. Nelsen, Proofs without Words: Exercises in Visual Thinking, Mathematical Association of America, 1997.
2.- Roger B. Nelsen, Proofs Without Words II: More Exercises in Visual Thinking, Mathematical Association of America, 2001.
3.- Claudi Alsina y Roger B. Nelsen, Charming Proofs, A Journey Into Elegant Mathematics, Mathematical Association of America, 2010.
4.- Wolfram MathWorld: Heron’s formula
5.- Roger B. Nelsen, Heron’s Formula via Proofs Without Words, College Mathematics Journal, September, 2001.
El artículo Teoremas geométricos sin palabras: Herón se ha escrito en Cuaderno de Cultura Científica.
Einstein y Max Born
El físico alemán Max Born fue, junto a Niels Bohr, Max Planck, Werner Heisenberg y Einstein* uno de los fundadores de la mecánica cuántica. Born y Einstein fueron amigos desde que se conocieron hasta la muerte de Einstein en 1955, y se mantuvieron frecuentemente en contacto a lo largo de varias décadas. Esta correspondencia es una fuente magnífica para historiadores e investigadores.
 Born en Berlín en la época de las algaradas (véase el texto). Fuente: American Institute of Physics
Born en Berlín en la época de las algaradas (véase el texto). Fuente: American Institute of PhysicsEl primer encuentro entre Einstein y Born tuvo lugar dos meses después de que Einstein abandonase su trabajo en la Oficina de Patentes en 1909. Einstein dio una célebre conferencia en una reunión científica en Salzburgo en la que afirmó que los científicos pronto demostrarían que la luz podía ser considerada tanto una onda como una partícula. El mismo Einstein había predicho que la luz estaba constituida por partículas, los cuantos de energía que terminarían llamándose fotones, pero él sabía perfectamente que la descripción ondulatoria de la luz también parecía adecuada. Siendo un pensador creativo como era, aceptó fácilmente que podía resultar que la luz fuese ambas cosas. Born se acercó a Einstein después de la charla y, muy excitado por las ideas de Einstein, discutieron esta nueva visión “cuántica” de la luz.
Lo que Einstein no podía predecir fue la dirección que sus ideas tomarían cuando cayesen en manos de otros. En los siguientes 15 años, Niels Bohr, el mismo Born y otros aceptarían completamente esta dualidad onda-corpúsculo, y llevaron la mecánica cuántica más allá, describiendo un universo que estaba gobernado por este tipo de excentricidades. Había muchas interpretaciones de cómo la luz podía ser a la vez onda y partícula; la de Born era que la luz estaba constituida por partículas pero que su movimiento estaba guiado por una onda.
Los físicos que aceptaban la mecánica cuántica veían el mundo lleno de estas rarezas; la nueva ciencia también insistía en que todas las partículas fundamentales estaban gobernadas solamente por las leyes de la probabilidad y el azar, sin más predictibilidad que la que se puede hacer al apostar a la ruleta. Esta era una visión que Einstein no podía aceptar. Escribió a Born en 1925: “[…] la mecánica cuántica es ciertamente imponente. Pero una voz interior me dice que todavía no es la verdad. La teoría explica muchas cosas, pero no nos aproxima nada al secreto del “Viejo”. Yo, en cualquier caso, estoy convencido de que Él no lanza dados”. Conforme Einstein expresaba esta opinión cada vez con más énfasis en sus intervenciones públicas, a Born le preocupaba que Einstein se estuviese alienando él mismo de la comunidad científica.
Viviendo en Berlín en la misma época, Born y Einstein tuvieron experiencias similares en Alemania. En 1918, tras terminar la Primera Guerra Mundial, los estudiantes revolucionarios de la Universidad de Berlín tomaron un edificio y retuvieron a varios empleados como rehenes. Einstein, pensando que tenía cierta influencia sobre los estudiantes, lo que era cierto, le pidió a Born que fuese con él a negociar la liberación de los rehenes. Einstein tenía la reputación de ser muy de izquierdas, cercano a los comunistas, y a los estudiantes les sorprendió que su amado profesor no les apoyase. En su autobiografía Born escribió: “Todavía puedo ver ante mí las caras atónitas de estos ansiosos jóvenes cuando el gran Einstein, que ellos creían de todo corazón que estaba de su parte, no los seguía ciegamente en su fanatismo”. Juntos los dos científicos ayudaron a conseguir una solución pacífica al conflicto, loe rehenes fueron liberados. [En la imagen Born en esta época]
Después de la Primera Guerra Mundial, el creciente nacionalismo en Alemania llevó a un antisemitismo que afectó tanto a Einstein como a Born, también judío. Ante la hostilidad de su tierra natal, Born terminaría emigrando a Escocia, mientras que Einstein se marchó a los Estados Unidos. Continuaron escribiéndose hasta la muerte de Einstein en 1955. A Born le entristecía sobremanera, sin embargo, que Einstein rechazase cada uno de los intentos que hizo para convencerle de la validez de la mecánica cuántica. Einstein discutió, y desde su punto de vista refutó, cada artículo y cada carta que Born escribió y nunca aceptó la nueva ciencia.
Nota:
[*] Quien eche de menos en este breve listado a PAM Dirac, recuérdese que Dirac, bebiendo del trabajo de los fundacionales, crea una ciencia nueva de profundas raíces matemáticas, pero él mismo no es uno de los primeros fundadores.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Una versión anterior de este artículo se publicó en Experientia Docet el 23 de agosto de 2009.
El artículo Einstein y Max Born se ha escrito en Cuaderno de Cultura Científica.
Meteoritos interestelares, muestreando otros sistemas planetarios
Un 1% de los meteoritos de mayor tamaño podrían tener un origen interestelar, lo que apunta a que son mucho más habituales de lo que se piensa. Podrían ser una ventana para estudiar otros sistemas planetarios desde la Tierra.
Para conocer mejor los planetas y otros cuerpos de nuestro Sistema Solar es fundamental no solo llegar hasta ellos, sino traer muestras a nuestro planeta que podamos estudiar con detalle en nuestros laboratorios. Esto puede parecer paradójico porque cada vez enviamos misiones más grandes, complejas y con mejor instrumentación, pero aun así siguen estando muy lejos de las capacidades analíticas de los instrumentos con los que contamos en la Tierra.
Desgraciadamente, este tipo de misiones de retorno de muestras son tremendamente caras y complejas, en las que a veces incluso se requiere de múltiples etapas -como si de una carrera de relevos fuese- para poder llegar, recoger las muestras y volver de nuevo a la Tierra. Y es que ahora mismo nos encontramos precisamente en un momento histórico de competición entre, por un lado, el equipo formado por la ESA y la NASA y, por otro, la Agencia Espacial China por ser los primeros en traer rocas de Marte a principios de la década de 2030. Sin duda no será fácil, pero será un momento histórico.
La lista de cuerpos de los que hemos traído muestras es muy escueta: La Luna, por supuesto, a través de las misiones Apolo, pero también gracias a misiones robóticas. Asteroides como Itokawa y Ryugu… y un tercero que es Bennu, y cuyo retorno está previsto para diciembre del próximo año. Incluso tenemos alrededor de un gramo de muestras de la coma del cometa 81P/Wild.
Hasta ahora nuestra principal fuente de información sobre el resto de los cuerpos del Sistema Solar han sido los meteoritos que caen sobre nuestro planeta y que fueron arrancados de aquellos por las grandes colisiones que han sufrido a lo largo de su historia y que, por suerte para nosotros, acabaron cruzándose con la Tierra, permitiéndonos conocer mejor nuestro entorno planetario.
Pero centrémonos en el título del artículo “…muestreando otros sistemas planetarios”. Puede parecer una osadía, porque si hemos hablado de que es realmente difícil el conseguir muestrear los planetas que más cerca tenemos, ¿cómo de difícil puede ser muestrear los planetas alrededor de otras estrellas?
 Imagen del cometa 2I/Borisov, tomada por el Telescopio Espacial Hubble. Cortesía de NASA, ESA, K. Meech (University of Hawaii), y D. Jewitt (UCLA).
Imagen del cometa 2I/Borisov, tomada por el Telescopio Espacial Hubble. Cortesía de NASA, ESA, K. Meech (University of Hawaii), y D. Jewitt (UCLA).En 2017 se anunciaba el descubrimiento de ‘Oumuamua, el primer objeto interestelar que atravesaba nuestro Sistema Solar del que éramos conscientes. Posteriormente, el 2I/Borisov ponía de manifiesto en 2019 que quizás este tipo de objetos provenientes de otros sistemas planetarios no eran tan raros, pero que debido a su pequeño tamaño y poca luminosidad (a veces reflejan muy poca luz por su composición superficial), eran difíciles de detectar.
Peña-Asensio et al. (2022) [3] mencionan además que quizás la mayoría de los objetos interestelares que sobreviven a su viaje por el espacio tienen que estar en una escala de metros de diámetro, ya que los cuerpos más pequeños, debido al estrés térmico y a los efectos de la radiación cósmica podrían fragmentarse, haciendo su detección imposible debido a su pequeño tamaño.
Esto supone un importante sesgo a la hora de la detección, puesto que cuanto más pequeños son, más difíciles son de detectar, pero, por otro lado, nos abre una ventana a saber que tipo de objetos tenemos que seguir buscando a la hora de plantear sistemas de búsqueda y detección, especialmente en el espectro infrarrojo donde quizás serían más fáciles de encontrar.
 Imagen compuesta de múltiples fotogramas durante el máximo de las Gemínidas en 2014 y donde se puede apreciar la traza de decenas de meteoros. Cortesía de NASA/MSFC/Danielle Moser y NASA’s Meteoroid Environment Office.
Imagen compuesta de múltiples fotogramas durante el máximo de las Gemínidas en 2014 y donde se puede apreciar la traza de decenas de meteoros. Cortesía de NASA/MSFC/Danielle Moser y NASA’s Meteoroid Environment Office.Vayamos un poco más lejos, ¿y si ya tuviésemos en nuestro planeta algún meteorito de naturaleza interestelar? También comentan Peña-Asensio et al. (2022), que es posible que algunos meteoros observados por las redes de detección en nuestro planeta pudiesen tener un origen interestelar, pero que las incertidumbres en el cálculo de los parámetros orbitales debido a la calidad y escasez de los datos no sean capaces de descubrir esta naturaleza.
En abril de este mismo año, Siraj et al. (2022) [1] publicaron un artículo en el que describen el descubrimiento del primer meteoro de origen interestelar, pero que realmente fue detectado el 1 de enero de 2014, y que tendría un tamaño aproximado de 0,5 metros de diámetro. Los restos de este objeto, según los cálculos, habrían caído en la costa de Papúa Nueva Guinea.
Estos autores además tienen bastante confianza en que hayan podido sobrevivir fragmentos de este meteoro, ya que su composición parece ser principalmente metálica, y, de hecho, proponen en otro artículo, Siraj et al. (2022) [2], el fletar una expedición oceanográfica para poder encontrar los fragmentos de este cuerpo en una superficie aproximada de 10×10 kilómetros donde se ha calculado pudieron caer.
Se recogerían, por lo tanto, las partículas ferromagnéticas encontradas en el fondo del océano mediante un sistema de imanes que atrajesen a estas partículas. Estas se analizarían para intentar descubrir cuáles pertenecerían a este cuerpo interestelar y cuáles no, ya que hay un importante flujo de micrometeoritos que caen a nuestro planeta.
En Peña-Asensio et al. (2022) [3], se mencionan también dos posibles meteoritos interestelares más, uno de 2009 y otro de 2017, lo que implicaría que al menos un 1% de los meteoritos de mayor tamaño podrían tener un origen interestelar, lo que pone de manifiesto que este tipo de objetos podrían ser mucho más habituales de lo que se pudiera pensar.
Este nuevo campo nos podría abrir una ventana de conocimiento realmente importante: Si fuésemos capaces de conocer la procedencia de los meteoros interestelares gracias a los datos de las redes de detección y además tuviésemos la oportunidad de recoger los meteoritos que hayan sobrevivido a la reentrada en la atmósfera, podríamos empezar a comparar sistemas planetarios. Y, por supuesto, los análisis podrían revelarnos si hay diferencias isotópicas importantes entre dos sistemas planetarios diferentes, o si en el fondo somos muy parecidos.
Referencias:
1. Siraj A, Loeb A. (2019) The 2019 Discovery of a Meteor of Interstellar Origin. arXiv:1904.07224v4 [astro-ph.EP]
2. Siraj A, Loeb A, Gallaudet T. (2022) An Ocean Expedition by the Galileo Project to Retrieve Fragments of the First Large Interstellar Meteor CNEOS 2014-01-08. 2022 arXiv:2208.00092v1 [astro-ph.EP]
3. Peña-Asensio E, Trigo-Rodríguez JM, Rimola A. (2022) Orbital characterization of superbolides observed from space: Dynamical association with near-Earth objects, meteoroid streams and identification of hyperbolic projectiles. Astron J. doi: 10.3847/1538-3881/ac75d2
Para saber más:
Tomanowos: el meteorito que sobrevivió a las megainundaciones y a la insensatez humana
Los meteoritos ya no son lo que eran desde hace 466 millones de años
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo Meteoritos interestelares, muestreando otros sistemas planetarios se ha escrito en Cuaderno de Cultura Científica.
Política de lobos
 Lobo ibérico (Canis lupus sygnatus) en Granada (España). Foto: Arturo de Frias Marques / Wikimedia Commons
Lobo ibérico (Canis lupus sygnatus) en Granada (España). Foto: Arturo de Frias Marques / Wikimedia Commons
Desde el mes de septiembre del año pasado el lobo ya no es especie cinegética en el territorio español. Así lo estableció una orden dictada por el Ministerio de Transición Ecológica. Ya no se pueden cazar lobos. A esa decisión se han opuesto, además de las asociaciones de ganaderos, las comunidades de Galicia, Asturias, Cantabria, y Castilla y León, en las que se encuentra el 95 % de los grandes carnívoros. Se calcula que en España hay entre 2000 y 2500 lobos distribuidos en cerca de 300 manadas.
La colisión de intereses en este asunto es clara. Están, por una parte, los movimientos conservacionistas y ecologistas, que presionan para que se implanten políticas de recuperación de espacios naturales y de las especies que en el pasado los ocupaban o cuyos efectivos se han visto muy mermados por efecto de la caza y otras actividades humanas. Y por la otra, están los ganaderos que se oponen a esas medidas y que denuncian que sus animales sufren el ataque de los lobos, por lo que la protección de estos se hace a costa de la viabilidad de sus propias haciendas. En general, los partidos ecologistas y de izquierda se oponen a la caza de lobos, mientras que los de derecha y, sobre todo, de extrema derecha, son contrarios a la protección a ultranza. Aunque hay excepciones notables.
En Estados Unidos se produjo una controversia similar cuando se decidió reintroducir el lobo en el parque de Yellowstone. Los cazadores de caribús se opusieron porque veían a los lobos como competidores, y los rancheros, por las mismas razones que los ganaderos del noroeste de la Península Ibérica. También allí las posturas están relacionadas con la ideología; son los votantes republicanos los que se muestran más en contra de las políticas conservacionistas, mientras que los demócratas son más favorables.
Con la recuperación del lobo en el centro de Europa durante los últimos años también ha empezado a haber ataques al ganado. En Alemania apenas se producían antes de 2010, pero durante la segunda década del siglo XXI, cada vez se han registrado más, hasta superar el millar en 2020, con más de 3500 cabezas muertas. Ese es el motivo por el que han investigado la relación entre los ataques de los lobos y el comportamiento electoral, y lo han hecho segmentando el espacio hasta el nivel municipal y estudiando cómo han influido en los resultados de Los Verdes (Die Grünen), el partido que más énfasis pone en las políticas conservacionistas, y de la extrema derecha, la Alternative für Deutschland (AfD), el partido que con más fuerza se opone a esas medidas.
En el estudio analizaron los resultados de las elecciones federales, territoriales y municipales desde 1990 hasta 2021. Y observaron que existe un efecto significativo de los ataques sobre el voto a la AfD, muy marcado en las elecciones a los länder y menor en las federales y municipales. Por otro lado, los ataques tuvieron un efecto negativo sobre los resultados de los Grüne, también en las elecciones territoriales, aunque no tan marcado como el beneficio que reportó a la “Alternativa”.
Los especialistas barajan dos hipótesis para explicar la vinculación entre los ataques de los lobos y el auge de la extrema derecha. Una es la amenaza económica que conllevan los ataques y que la AfD esgrime como argumento electoral. Otros interpretan la oposición a los lobos como una manifestación de resentimiento a las élites urbanas por parte de aquellos que se identifican con las formas tradicionales de vida y de explotación de recursos. Intereses, pero también valores, pesan en la balanza.
Fuente: von Hohenberg, B. C., Hager, A. (2022): Wolf attacks predict far-right voting. PNAS 119 (30) e2202224119 doi: 10.1073/pnas.2202224119
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Política de lobos se ha escrito en Cuaderno de Cultura Científica.
Las pruebas de la educación: Rocío García Carrión – Impacto de la inmigración en el rendimiento escolar

Bilbao volvió a acoger el pasado 20 de mayo de 2022 “Las pruebas de la educación”, una jornada que abordará diversas cuestiones educativas con la evidencia científica existente. Esta quinta edición está organizado por la Cátedra de Cultura Científica de la UPV/EHU y la Fundación Promaestro con la colaboración del Consejo Escolar de Euskadi, y se celebró en el Bizkaia Aretoa – UPV/EHU de la capital vizcaína.
La jornada consta de cinco ponencias de media hora de duración en la que se tratan temas como la problemática relacionada con los juegos de azar en el ámbito escolar, el impacto de la inmigración en el rendimiento del alumnado o el debate sobre la jornada escolar continua o partida, entre otras cuestiones. La dirección del seminario corrió de nuevo a cargo de Marta Ferrero profesora de la Facultad de Formación del Profesorado y Educación de la Universidad Autónoma de Madrid.
Rocío García Carrión, investigadora Ikerbasque y Ramón y Cajal en la Universidad de Deusto, nos habla sobre el impacto de la inmigración en el rendimiento escolar y analiza, desde la evidencia científica disponible, si los resultados educativos dependen o no de la proporción de alumnado inmigrante que haya en el aula.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Las pruebas de la educación: Rocío García Carrión – Impacto de la inmigración en el rendimiento escolar se ha escrito en Cuaderno de Cultura Científica.
Comportamientos ecológicos y crisis económica
Un equipo de investigación de la UPV/EHU han realizado un estudio transversal para saber si las épocas de bienestar y las crisis afectan a los factores internos (motivaciones, actitudes y eficacia percibida por el consumidor) y externos (información medioambiental y marketing) que influyen en los comportamientos ecológicos, como el activismo y la compra ecológicos.
La preocupación por el medio ambiente y por la sostenibilidad ha sido ampliamente investigada. Está probado que sigue existiendo una brecha entre las actitudes proambientales y el consumo ecológico, a pesar de que los consumidores dan cada vez más importancia al medio ambiente y que cada vez más empresas comercializan productos ecológicos. Por lo tanto, comprender los principales factores que influyen en la compra ecológica es útil para ayudar a las organizaciones a desarrollar estrategias para la producción y comercialización de productos ecológicos.
El comportamiento del consumidor de productos ecológicos es un fenómeno complejo y difícil de definir, fuertemente influenciado por variables internas del consumidor, diverso y dependiente del contexto. Los departamentos de Economía y Gestión y de Economía Financiera II de la UPV/EHU han realizado un estudio longitudinal para abordar cómo el contexto económico modera las relaciones entre el comportamiento ecológico y diversos factores, como la motivación, la actitud, la eficacia percibida por el consumidor, la información medioambiental y el marketing. Para ello, han utilizado una encuesta realizada al alumnado del Máster en Dirección Empresarial desde la Innovación y la Internacionalización de la UPV/EHU, durante épocas de crisis económica (2008-2012) y épocas de bienestar (2014-2019), que recoge sus costumbres de consumo ecológico, sus conocimientos ecológicos, sus hábitos de transporte, de reciclaje, etc.
 Foto: Priscilla Du Preez / UnsplashLas crisis económicas inciden en los comportamientos ecológicos
Foto: Priscilla Du Preez / UnsplashLas crisis económicas inciden en los comportamientos ecológicos
La profesora de la UPV/EHU María Jesús Luengo explica que “los resultados muestran una clara influencia del contexto económico, que actúa como moderador en el vínculo entre los distintos factores y el comportamiento ecológico”. La profesora destaca que “el conocimiento sobre temas ecológicos, sobre el consumo ecológico, sobre los productos ecológicos, en principio, es inferior al que creíamos, y, además, tampoco incide a la hora de tomar la decisión de hacer una compra ecológica”.
Las motivaciones, las actitudes, la eficacia percibida por el consumidor y el activismo ecológico influyen en la compra ecológica, y esa influencia es más pronunciada en épocas de crisis económica. De todos ellos el que más influye en el activismo ecológico y en la compra ecológica en tiempos de crisis es la motivación, seguido de la eficacia percibida por el consumidor: “O sea, cuando el consumidor hace esa compra ecológica, realmente le parece que está haciendo algo que es eficaz, que tiene algún tipo de repercusión; más que saber si es bueno o es malo”, explica la doctora del departamento de Economía y Gestión. Sin embargo, en tiempos de bienestar, los efectos de estos dos factores principales son similares.
“Nos ha sorprendido que ser una persona activista ecológica o sostenible, es decir, que separa la basura o que utiliza transporte público, por ejemplo, no tiene mayor relevancia a la hora de decidirse a hacer una compra ecológica o no. Es más un tema de sentir que realmente estamos haciendo algo bueno por nosotros, y por el mundo”, explica Luengo.
Dentro de las variables de marketing, el producto y el precio influyen más en el activismo ecológico que la promoción del producto y el lugar de venta en tiempos de crisis económica; mientras que el precio no tiene ningún efecto en tiempos de bienestar. “Creo que de todas las variables el precio es lo que más varía a la hora de tomar esa decisión. El precio de los productos ecológicos incide a la hora de hacer una compra ecológica en época de crisis. En épocas de bonanza económica, sin embargo, el precio apenas tiene importancia, tiene más importancia la distribución (es decir, que se nos haga más o menos cómodo llegar a estos productos), por ejemplo”, afirma.
La influencia de la información ambiental es mayor en tiempos de crisis que en tiempos de bienestar. Así pues, durante las crisis económicas la difusión de información ambiental entre los consumidores desempeña un papel importante en las actitudes medioambientales, que a su vez influyen positivamente en la compra ecológica. Sin embargo, los altos precios de los productos ecológicos afectan negativamente a la compra ecológica en tiempos de crisis, lo que podría explicar los menores niveles de compra ecológica encontrados.
Referencia:
María Jesús Luengo Valderrey, Eva Emmanuel Martínez, Rocío Rivera Revilla, Azucena Vicente Molina (2022) Ecological behaviour in times of crisis and economic well-being through a comparative longitudinal study Journal of Cleaner Production doi: 10.1016/j.jclepro.2022.131965
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Comportamientos ecológicos y crisis económica se ha escrito en Cuaderno de Cultura Científica.
Creando vocaciones geológicas con un anime
Los dibujos animados japoneses, más conocidos por estos lares como animes, se han convertido en un auténtico fenómeno de masas por todo el mundo. Aunque aquí los consideremos como un mero material de entretenimiento, en Japón buscan algo más, ya que se utilizan para mostrar a la población la historia, cultura y vida común en su país. Por eso, a diferencia de lo que podemos pensar inicialmente, no son un producto dirigido únicamente a la población infantil. Encontramos innumerables estilos y temáticas (terror, fantasía, deportes, comedia y un larguísimo etcétera) enfocados a todos los públicos objetivos que nos podemos imaginar, desde juvenil hasta adulto y desglosado por sexo y edad.
Uno de esos estilos se centra en escenas de la vida cotidiana y está dirigido a chicas adolescentes estudiantes de secundaria, por lo que las series animadas tratan temas tales como el compañerismo, la amistad, el primer romance y, sobre todo, la toma de decisiones transcendentales para estas jóvenes de cara a su futuro más inmediato. Y aquí es donde encontramos un anime titulado Koisuru Asteroid, algo que podríamos traducir como Asteroide Enamorado.
 Cartel promocional del anime Koisuru Asteroid con las jóvenes protagonistas de la serie. Imagen tomada de crunchyroll
Cartel promocional del anime Koisuru Asteroid con las jóvenes protagonistas de la serie. Imagen tomada de crunchyrollLo que hace particular a este anime, o al menos lo que ha captado mi atención, es la historia de fondo del mismo. Sin hacer muchos spoilers, la adolescente protagonista comienza los estudios de secundaria y decide apuntarse al Club de Astronomía de su instituto. Sin embargo, descubre que ese club se ha fusionado con el Club de Geología para crear el Club de Ciencias de la Tierra, así que se une a otras compañeras para hacer actividades relacionadas con esta temática fuera de su horario lectivo.
Esas actividades extraescolares son realmente interesantes y estimulantes, ya que buscan despertar la curiosidad entre las chicas y les aporta un aprendizaje colectivo basado en su propio esfuerzo e investigación. Y la serie toca muchas subdisciplinas de la Geología, mezclando varias de ellas con la propia Astronomía, mostrando la estrecha relación que existe entre dos ciencias que, a priori, parece que no tienen nada en común, pero dándonos a entender el motivo por el que el club se denomina Ciencias de la Tierra. Aunque, en realidad, deberían haberle puesto la coletilla “y del Espacio” al final. Para ello, os voy a dejar con algunos ejemplos de lo que podemos ver a lo largo de sus 12 capítulos.
En uno de los primeros capítulos quedan para pasar el día junto al lecho de un río, donde recogen diversas muestras de rocas y minerales, encargándose las más veteranas de clasificarlas y explicarles sus propiedades a las novatas. Culminando la jornada con una observación astronómica gracias a un telescopio portátil, donde discuten sobre las características geológicas y la formación de diversos planetas y satélites del Sistema Solar.
 Captura de pantalla del capítulo 2 del anime Koisuru Asteroid titulado “La Vía Láctea del cauce seco”. Imagen tomada de crunchyroll
Captura de pantalla del capítulo 2 del anime Koisuru Asteroid titulado “La Vía Láctea del cauce seco”. Imagen tomada de crunchyrollOtro día deciden ir a relajarse a unos baños termales, en donde comentan que existen diversos tipos de aguas medicinales de acuerdo a su composición y que esta depende de los materiales rocosos que atraviesa el agua caliente en su periplo subterráneo. Incluso explican que esa agua subterránea, o bien procede del agua de lluvia que se ha infiltrado por el terreno, o bien se trata de un agua que puede considerarse fósil porque lleva mucho tiempo acumulada bajo tierra.
Incluso hacen pequeños campamentos de fin de semana. En uno de ellos deciden visitar un Museo Geológico, donde piden una cita con uno de los investigadores del centro para que les ayude a identificar un fósil que encontraron en el lecho del río. El investigador no solo les clasifica el resto que encontraron las jóvenes, sino que también les enseña a leer un mapa geológico para localizar el lugar de procedencia de la roca arrastrada por el agua y les explica todo el proceso de formación del fósil desde que el organismo estaba con vida hasta la actualidad.
También participan en el típico festival cultural que organizan los centros educativos japoneses a finales del verano. Y una de las cosas que se les ocurre hacer es extraer un testigo de sondeo del patio de la escuela para analizarlo y explicarles tanto al profesorado como al resto del alumnado las características del sedimento, descubriendo que hay varias capas de fango y arcilla impermeables, lo que provoca que el jardín no drene del todo bien el agua de lluvia y acabe siempre encharcado.
Y, como colofón, una de las protagonistas decide presentarse a las Olimpiadas de Geociencias, un examen que evalúa los conocimientos en Ciencias de la Tierra de estudiantes de secundaria de todo el país, teniendo como premio ir al campeonato internacional representando a Japón. Por supuesto, las preguntas no son solo de Geología, sino que también incluye un buen número de cuestiones sobre Astronomía, mostrando, una vez más, la relación entre ambas disciplinas científicas.
Solo he puesto algunos ejemplos muy resumidos de lo que nos depara esta serie. Realmente, considero este anime como una manera fantástica de acercar la Geología al público adolescente de una manera amena y divertida, recomendando su visionado a todo el mundo, ya sean jóvenes con cierto interés por las Ciencias de la Tierra como docentes de Ciencias de la Tierra en Educación Secundaria y Bachillerato. Y, aunque pueda parecer todo ficción o simplemente cosas chulas que hacen en el lejano Oriente, en realidad también aquí tenemos muchas actividades de iniciación a las Ciencias de la Tierra pensadas para que participen adolescentes. Pueden acudir a lugares como el Museo Geominero, donde encontrarán expuesta una amplia colección de rocas, minerales y fósiles realizando una visita guiada. Asistir a las excursiones del Geolodía o solicitar una Geocharla de las ofertadas por la Sociedad Geológica de España para los centros educativos, compartiendo una mañana con profesionales de las Ciencias de la Tierra. Participar en las Olimpiadas de Geología organizadas por la Asociación Española para la Enseñanza de las Ciencias de la Tierra. O presentar sus proyectos de investigación en concursos como Ciencia en Acción o Ciencia Clip.
Después de ver esta serie y sabiendo la de opciones que existen hoy en día para que las futuras generaciones se interesen por la Geología, ojalá pudiese volver a tener dieciséis años otra vez, porque me apuntaría a todo. Así que, si sois progenitores o docentes de jóvenes con cierta inquietud por las Ciencias de la Tierra, no os cortéis en imitar a la profesora de este anime e informaros sobre todas las opciones que tenéis a vuestro alcance y de las que yo solo he nombrado unas pocas. El futuro de la Geología está en juego.
Para saber más:
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo Creando vocaciones geológicas con un anime se ha escrito en Cuaderno de Cultura Científica.
Tres problemas con el 3
Tres árboles caídos
quedaron a la orilla del sendero.
El leñador los olvidó, y conversan,
apretados de amor, como tres ciegos.
Fragmento de “Tres árboles” (1922) de Gabriela Mistral
 Composición realizada a partir de imágenes de Wikimedia Commons.
Composición realizada a partir de imágenes de Wikimedia Commons.
Hoy, 3 de agosto, proponemos tres problemas con el 3 como protagonista. ¿Sabrías encontrar la solución antes de consultarla?
Tres, eran tres…En un conjunto Aformado por cinco números enteros positivos, se pide demostrar que siempre es posible elegir tres cuya suma sea un múltiplo de 3.
Solución (ver [1])
La solución pasa por recordar la noción de aritmética modular, en particular, de las congruencias módulo 3. Cualquier número entero n es o bien múltiplo de 3, o bien congruente con 1 módulo 3 (es decir, de la forma n = 3a + 1, donde a es un número entero positivo), o bien congruente con 2 módulo 3 (es decir, de la forma n = 3a + 2, donde a es un número entero positivo).
Supongamos que, en el conjunto A, hay un número de cada tipo, es decir, uno de la forma 3a, otro del tipo 3b + 1 y otro de la forma 3c + 2 (a, b y c son enteros positivos). Entonces, la suma de los tres es: 3a + (3b + 1) + (3c + 2) = 3(a + b + c + 1), que es múltiplo de 3.
En caso contrario, es decir, si las tres posibles congruencias módulo 3 no están representadas en A, entre los cinco números dados, hay necesariamente un tipo de congruencia módulo 3 que se repite al menos tres veces. Tenemos entonces tres posibilidades:
-
Si tres de los números son múltiplos de 3 (3a, 3b y 3c), entonces su suma es 3a + 3b + 3c = 3(a + b + c), que es múltiplo de 3.
-
Si tres de los números son congruentes con 1 módulo 3 (3a + 1, 3b + 1 y 3c + 1), entonces su suma es (3a + 1) + (3b + 1) + (3c + 1) = 3(a + b + c + 1), que es múltiplo de 3.
-
Si tres de los números son congruentes con 2 módulo 3 (3a + 2, 3b + 2 y 3c + 2), entonces su suma es (3a + 2) + (3b + 2) + (3c + 2) = 3(a + b + c + 2), que es múltiplo de 3.
Tenemos tres cartas cuyos lados son blancos o negros: una de las cartas es blanca/blanca, otra negra/negra y la última blanca/negra. Las introducimos en una bolsa, que agitamos para que las cartas se muevan con facilidad. Sacamos una de las cartas al azar, la colocamos sobre la mesa y observamos que el lado visible es negro. ¿Cuál es la probabilidad de que el otro lado también sea negro?
Solución (ver [2])
Tenemos tres cartas, y por lo tanto seis caras, tres de cada color. De las tres caras de color negro, 2/3 están en la tarjeta negra/negra y 1/3 en la blanca/negra. Por lo tanto, la probabilidad de que el otro lado sea negro es de 2/3.
Un cuadrado tres por tresEn un cuadrado con 3 x 3 casillas pueden colocarse los números del 1 al 9 de manera que en ninguna columna, fila o diagonal aparezcan en orden de magnitud. Se pide demostrar que el dígito que ocupa la casilla central debe de ser impar.
Solución (ver [3])
Llamemos c al número que ocupa la casilla central, que está atravesada por una fila, una columna y dos diagonales.
 Un ejemplo de cuadrado y el problema planteado.
Un ejemplo de cuadrado y el problema planteado.
Para cumplir con el requisito impuesto en el enunciado, deben organizarse los ocho dígitos restantes de manera que ninguna de estas cuatro ternas de números (las correspondientes a la fila, la columna y las diagonales que atraviesan la casilla central) esté colocada en orden creciente o decreciente. Es decir, en cada una de estas cuatro ternas, el dígito central c debe ser el número mayor o menor de los tres.
Para conseguirlo, debe completarse cada terna que cruza la casilla central agregando dos dígitos menores o dos mayores (simultáneamente) que c.
Argumentemos ahora por reducción al absurdo. Si el dígito central c fuera par, tendríamos c – 1 números menores que c y 9 – c mayores que c. Al ser c – 1 y 9 – c números impares, se deduce que al menos una de las cuatro ternas que cruzan la diagonal debe completarse tomando un número menor y otro mayor que c, en contra de lo pedido… Así que c es necesariamente impar.
Referencias
[1] Three for Three, Futility Closet, 29 de junio de 2022
[2] The Three Cards Problem, Futility Closet, 27 de febrero de 2008
[3] Odd at Heart, Futility Closet, 20 de diciembre de 2018
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Tres problemas con el 3 se ha escrito en Cuaderno de Cultura Científica.
Einstein y Paul Ehrenfest
El físico austriaco Paul Ehrenfest fue un íntimo amigo de Einstein. Fue un hombre con una personalidad efusiva, dado a hablar entre signos de exclamación, y bastante emocional. Su disgusto fue enorme cuando Einstein se negó a aceptar ciertos aspectos de la ciencia moderna, y su pasión le llevó a la autodestrucción, acosado por sus tragedias personales.
 Foto tomada en la casa de Ehrenfest en Leiden. El niño sentado en las rodillas de Einstein es Paul (Pavlik), el mayor de los dos hijos varones de Ehrenfest y que llegaría a ser físico como su padre. Su hija Tatyana sería matemática como su madre. Fuente: Wikimedia Commons
Foto tomada en la casa de Ehrenfest en Leiden. El niño sentado en las rodillas de Einstein es Paul (Pavlik), el mayor de los dos hijos varones de Ehrenfest y que llegaría a ser físico como su padre. Su hija Tatyana sería matemática como su madre. Fuente: Wikimedia CommonsEinstein pasó menos de dos años enseñando en la universidad alemana de Praga, pero fue en esta época cuando conoció a Ehrenfest y a muchos de sus futuros colegas en la comunidad de físicos. Como joven físico Ehrenfest tuvo, como Einstein, muchas dificultades para asegurarse un puesto académico. De hecho, Ehrenfest estaba en una de las etapas de lo que sería un periplo por varias universidades europeas a la búsqueda de una posición estable cuando comenzó su amistad con Einstein.
Los dos hombres se conocieron en la estación de trenes de Praga un día de febrero. En su diario, Ehrenfest recogió sus impresiones del momento en su estilo telegráfico: “Por fin llegada a Praga, gris. Bajo [del tren]. Einstein (puro en la boca) allí, con esposa. Derechos al café… Hablamos de Viena, Zúrich, Praga…De camino al instituto primera discusión acerca de todo. Lluvia en la calle, lodo, discusión todo el rato. Instituto: salón de clases, escaleras a física teórica. Discusión constante con Einstein”.
Esas discusiones ayudaron a Einstein a formular su revolucionaria teoría general de la relatividad. Einstein y Ehrenfest, siendo ambos de lengua afilada, disfrutaron de tener alguien con quien discutir acaloradamente sobre física. Ehrenfest se hospedó con los Einstein, y, según el diario de Ehrenfest, emplearon una gran cantidad de tiempo en “discusión”. “Te. De 12-2:30. Discusión con Einstein. A la cama muy tarde”. Al día siguiente, “Empezamos a discutir inmediatamente…Tarde Einstein me habla de su artículo sobre gravitación”.
Tanto Ehrenfest como Einstein se vieron muy influenciados, y construyeron sobre las ideas, de dos viejos maestros de la física de su tiempo, el matemático francés Henri Poincaré y el físico holandés Hendrik Antoon Lorentz. La odisea de Ehrenfest por las universidades de Europa terminó con éxito cuando se le ofreció el puesto de Lorentz de catedrático de física matemática en la Universidad de Leiden en 1912.
Solo unos meses antes, Einstein había aceptado un nuevo puesto de profesor creado expresamente para él en el Politécnico de Zúrich. Einstein escribió por aquella época que se sentía aliviado por haber ya aceptado el puesto de Zúrich antes de saber de la jubilación de Lorentz, y quizás haberse visto forzado a aceptar su puesto. Pero es muy posible que Einstein estuviese intentando quedar bien: parece que Einstein y Ehrenfest eran un poquito competitivos el uno con el otro, y fue una sorpresa para la toda la comunidad científica que Ehrenfest ganase una cátedra tan prestigiosa como la de Leiden.
A pesar de estar en ciudades distintas, Einstein y Ehrenfest se escribían y veían a menudo. En 1913 Ehrenfest y su esposa, la matemática rusa Tatiana Alekséyevna Afanásieva, visitaron Zúrich y, aunque se suponía que iban a ser unas vacaciones, Ehrenfest pasó casi cada hora en discusión profunda con Einstein. Sólo una vez registró en su diario: “Un día sin Einstein”.
La rigurosa correspondencia entre Einstein y Ehrenfest da una visión desde dentro del desarrollo de la teoría general de la relatividad. Cuando Einstein se estaba preparando para remitir la teoría a la asociación científica de Alemania, escribió a Ehrenfest que su nueva teoría de la gravitación podría hacer que le internasen en un sanatorio psiquiátrico. “Espero que no tengáis uno en Leiden”, escribió, “para que os pueda visitar con seguridad”. Einstein no necesitaba preocuparse. La nueva teoría cimentó su papel como uno de los principales físicos del mundo, y poco después Ehrenfest intentó tentarle para que se uniera a él en la Universidad de Leiden. En una carta de 1919 le dice “De repente estamos todos de acuerdo en que tenemos que atarte a Leiden”, carta que cierra con esta posdata: “¡Realmente es un incordio que tú tengas algo que decir en una cuestión que nosotros estamos en mucha mejor posición para decidir que tú mismo!” Sin esperar a la respuesta de Einstein, envió otra carta: “Aquí no hay más que gente que te quiere a ti y no solo a tu corteza cerebral”.
Einstein, sin embargo, declinó la invitación, y los dos hombres continuaron con sus cartas llenas de bromas en las que discutían física teórica y, a veces, asuntos religiosos. Al igual que Einstein Ehrenfest era judío, y por eso Einstein encontró en él alguien con quien discutir no solo de física sino también de sionismo. Ehrenfest prestaba los oídos comprensivos que Einstein no encontraba en Berlín. Einstein le escribió: “Tú no me regañas por mis escarceos sionistas. Aquí hay bastante indignación, lo que, sin embargo, me es indiferente. Incluso los judíos asimilados se lamentan de mí o me reprenden”.
Pero, como dos de los principales físicos de su tiempo, Einstein y Ehrenfest no podían dejar de discutir a menudo sobre el tema más controvertido del momento: la mecánica cuántica. El campo surgió en buena medida de las propias teorías de Einstein, y Ehrenfest organizó en Leiden el primer congreso sobre mecánica cuántica durante la conmemoración de los 50 años del doctorado de Lorentz, el 11 de diciembre de 1925. Si bien ambos amigos comprendían la relatividad de manera similar, en cuestiones de mecánica cuántica estaban claramente enfrentados. Ehrenfest la admitía sin reservas; Einstein tenía muchos prejuicios. El que hubiese tenido que elegir estar en contra de las posiciones de su amigo fue muy doloroso para Ehrenfest. Emotivo como era, el asunto era capaz de llenar sus ojos de lágrimas. En vano señaló Ehrenfest a Einstein que una vez él mismo había presentado una teoría completamente nueva, la relatividad especial, y que también tuvo que convencer a los físicos veteranos de su veracidad. Einstein, ahora en el papel de veterano, rehusaba aceptar las nuevas teorías.
Tristemente, Ehrenfest no participaría en las discusiones sobre la mecánica cuántica durante mucho tiempo. Einstein y Ehrenfest parecían vivir vidas paralelas, compartiendo tragedias similares. El hijo pequeño de Einstein, Eduard, desarrolló esquizofrenia y pasó sus últimos días en una clínica. El hijo pequeño de Ehrenfest, Vassily, nació con síndrome de Down. Ante la angustia de Ehrenfest por tener que internar a su hijo en una institución, Einstein intentó consolarlo, compartiendo con él el frío razonamiento que él había aplicado a su propia tragedia: “Los individuos valiosos no deben ser sacrificados en aras de casos perdidos, ni siquiera en estas circunstancias”. Por otra parte, Einstein, plenamente consciente de la situación personal de su amigo, escribió al consejo rector de la Universidad de Leiden expresándoles su preocupación y rogándoles que disminuyesen la carga de trabajo de Ehrenfest.
A pesar de todo, Ehrenfest, el pasional, no encontraba consuelo. Escribió una carta a sus colegas en septiembre de 1933, que transcribimos íntegra:
“¡Mis queridos amigos: Bohr, Einstein, Franck, Herglotz, Joffé, Kohnstamm y Tolman!
Realmente ya no sé como llevar durante los próximos meses la carga de mi vida que se ha vuelto insoportable. No puedo soportar más que mi cátedra en Leiden se vaya por el sumidero. Debo abandonar mi posición aquí.
Quizás pueda ocurrir que pueda usar el resto de mis fuerzas en Rusia…Si, sin embargo, no se aclara pronto el que lo pueda hacer, entonces está claro que me mataré. Y, si eso ocurre alguna vez, me gustaría saber que os he escrito, con calma y sin prisas, a vosotros cuya amistad ha jugado un papel tan importante en mi vida.
…Perdonadme.”
Esta carta y otra dirigida a sus estudiantes nunca fueron enviadas. En una depresión profunda, el 25 de septiembre de 1933 Ehrenfest mató a su amadísimo hijo Vassily de un disparo en la sala de espera del médico y acto seguido se disparó a sí mismo, muriendo al instante.
En la necrológica de su amigo, Einstein escribió:
“No era sólo el mejor maestro de nuestra profesión que yo haya conocido; también estaba apasionadamente preocupado por el desarrollo y destino de los hombres, especialmente de sus estudiantes. Comprender a los demás, ganar su amistad y confianza, ayudar a cualquiera inmerso en luchas internas o externas, alentar el talento de la juventud, este era su verdadero elemento, casi más que la inmersión en problemas científicos”.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Una versión anterior de este artículo se publicó en Experientia Docet el 13 de septiembre de 2009.
El artículo Einstein y Paul Ehrenfest se ha escrito en Cuaderno de Cultura Científica.
Ideología, política y cambio climático
“Somos la primera generación en sentir el efecto del cambio climático y la última generación que puede hacer algo al respecto.”
Barack Obama, 23 septiembre 2014
“Esta muy costosa mierda del calentamiento global tiene que parar. El planeta se está congelando, registra bajas temperaturas, y nuestros científicos del calentamiento global están atrapados en el hielo.”
Donald Trump, 1 enero 2014
 Foto: William Bossen / Unsplash
Foto: William Bossen / UnsplashEs sorprendente que, mientras que el 97% de los científicos y expertos en cambio climático consideran que es un hecho demostrado provocado por la actividad humana y que el 97% de los artículos científicos publicados sobre este asunto lo apoyen, solo el 50% de los estadounidenses acepten el cambio climático, y todavía son menos los que creen que lo provoca la actividad de nuestra especie.
Una revisión diez años después y publicada en 2021, Krista Myers y su grupo, de la Universidad Estatal de Louisiana en Baton Rouge, con respuestas a una encuesta enviada a geocientíficos de Estados Unidos y Canadá, con 2780 respuestas, entre l 91% y el 100% apoyan que la causa del cambio climático es la actividad humana. Las respuestas de los 153 expertos más reconocidos y con el currículo científico más amplio es la que llega al 100%.
En España, en 2013, el 80% afirma que el cambio climático es un hecho científico, solo el 8.5% lo rechaza y el 86% acepta que es el resultado de la actividad humana. Los universitarios estudiantes de Biología e Ingeniería Química de la Universidad de Santiago de Compostela, en más de un 80%, consideran que es la actividad humana la causa del cambio climático. El estudio, firmado por Pablo Meira y Mónica Arto, se basa en entrevistas a 284 alumnos y se publicó en 2014.
En 2013, John Cook y su grupo, de la Universidad de Queensland, en Australia, revisaron 11944 artículos publicados sobre el clima entre 1991 y 2011. El 97% de los artículos que expresan una opinión sobre el cambio climático provocado por la actividad humana apoyan su existencia. Solo el 1.9% lo rechaza, y el 1.0% plantea dudas sobre que su causa sea nuestra especie. Y en encuestas a 1372 expertos en cambio climático, en 2010, el 98% acepta a nuestra especie y sus actividades como causa, según el estudio de William Anderegg y sus colegas de la Universidad de Stanford. Para John Cook, los estudios que rechazan el cambio climático provocado por la actividad humana son cada vez más escasos y su número disminuye según pasan los años.
Un par de años después, el grupo de J.S. Carlton, de la Universidad Purdue, encuestó sobre el cambio climático a 698 biofísicos de diez de las más prestigiosas universidades de Estados Unidos. Los resultados son parecidos a los del trabajo de Cook: el 93.6% afirma que el calentamiento global es un hecho, y el 91.9% apoya que su causa es la actividad humana. La conclusión de los autores del estudio es que la ciencia del cambio climático es creíble y está consolidada.
 Foto: Juan Manuel Sanchez / UnsplashNo hay sesgos científicos detectables…
Foto: Juan Manuel Sanchez / UnsplashNo hay sesgos científicos detectables…
Se puede argumentar que la publicación de artículos que apoyan el consenso sobre el cambio climático está favorecida por los editores de revistas científicas, pero la investigación de Christian Harlos y sus colegas, de la Universidad de Lund, en Suecia, demuestra que el sesgo no existe. Revisan los artículos sobre clima publicados entre 1997 y 2013 e identifican 120 textos, en revistas de gran difusión, con los resultados de 1154 experimentos. No detectan ningún sesgo, ninguna omisión de resultados sobre el cambio climático, sea a favor o en contra.
Desde la Universidad de California en Merced, Alexander Petersen y su grupo compararon la difusión de las publicaciones de 386 autores contrarios al cambio climático y de 386 expertos científicos en el mismo tema. Encontraron dos resultados diferentes en la difusión en los medios. Los contrarios al cambio climáticos tienen un 50% más de presencia que los expertos científicos. Pero en los medios de mayor difusión la diferencia de visibilidad es solo del 15. Son los nuevos medios en las redes sociales los que contribuyen a la producción y consumo de desinformación sobre el cambio climático.
Sin embargo, la desconexión entre el consenso científico y la percepción social, que se observa en Estados Unidos y en muchos otros países, se atribuye a la ideología, a aceptar la información sobre el cambio climático que no esté en contra de la ideología propia y a construir la interpretación de lo que ocurre según esa información. Lo contrario de lo que aconsejaba Sherlock Holmes cuando decía aquello de que “uno comienza a deformar los hechos para hacerlos encajar en la teoría en lugar de encajar la teoría en los hechos”.
…pero sí sesgos ideológicosLa ideología política puede tener mucha influencia no solo en la comunidad científica sino, sobre todo, en el público en general al que llegan, en muchos casos, informaciones sesgadas según el medio de comunicación que las difunda. Juan Ignacio Pérez y Joaquín Sevilla comentan como la negación de la existencia del cambio climático se vincula a la ideología conservadora. Según explican, la base ideológica se relaciona con una visión optimista del mundo, con la creencia de una naturaleza sin límites, incluso capaz de asimilar los cambios provocados por las actividades de la especie humana. Además, los efectos del cambio climático, según afirman los expertos, siempre se sitúan en el futuro, en un tiempo que nuestra especie no es muy capaz de calibrar.
Cuando Toby Bolsen y James Druckman, de las universidades Estatal de Georgia y del Noroeste, estudiaron los factores que influían en la aceptación por los ciudadanos del cambio climático y de la actividad humana como su causa, encontraron que la ideología del receptor era un factor importantes. Reúnen encuestas de 1329 voluntarios, en julio de 2014, y el análisis de sus respuestas revela que la difusión de información sobre el consenso científico sobre el cambio climático entre los ciudadanos consigue que aumente la aceptación de la actividad humana como causa, excepto para los republicanos que se consideran bien informados.
Por todo ello, Ridley Dunlap y sus colegas, de la Universidad Estatal de Oklahoma, han revisado esta polarización ideológica y, en consecuencia, política y partidaria en Estados Unidos cuando se trata el cambio climático.
Durante la década de los noventa, la brecha entre demócratas y republicanos al tratar asuntos relacionados con el medio ambiente no dejó de crecer. Hasta entonces las votaciones en el Congreso y en el Senado estaban relativamente cercanas y, a menudo, se aprobaban o rechazaban propuestas con los votos de ambos partidos. Para aprobar propuestas sobre el medio ambiente, los porcentajes de apoyo variaban entre el 30% de los republicanos y el 60% de los demócratas. Pero, a partir de esa década, los porcentajes comenzaron a separarse y, en 2015, llegaban al 5%-15% de aprobación por los republicanos y el 80%-90% en los demócratas. Son la ideología y el programa de los partidos quienes dirigen las votaciones.
Si nos centramos en el cambio climático, cerca del 80% de los demócratas aceptan el calentamiento global. Entre los republicanos, el porcentaje llega al 40%. Parecidos porcentajes, del 80% y del 40%, se obtienen en respuesta a la pregunta de si el calentamiento se debe a la actividad humana. Los resultados se invierten si se pregunta si los medios exageran los peligros del calentamiento: lo afirma el 60% de los republicanos y el 10% de los demócratas. Solo el 40% de los republicanos acepta que la mayoría de los científicos del clima han llegado al consenso respecto al cambio climático mientras que, entre los demócratas, el porcentaje llega al 80%.
Todo intento de politizar el cambio climático elimina el efecto que produce la información sobre el consenso científico. Politizar el debate disminuye la credibilidad del consenso y su aceptación se filtra a través de la ideología del receptor. Entonces cuenta más la ideología que las evidencias científicas.
Sin embargo, el estudio de Sander van der Linden y sus colegas, de la Universidad de Cambridge, con encuestas a 6301 voluntarios de Estados Unidos, muestra que resaltar el consenso científico sobre el cambio climático aumenta la aceptación del cambio climático tanto en conservadores como en liberales. Entre los conservadores sube del 60% al 80%, y entre los liberales del 80% al 90%. Para los autores, más que convencer sobre el cambio climático, lo que implica politizar el debate, lo adecuado es promover la ciencia y sus valores, destacando el consenso científico sobre el cambio climático.
Es evidente que la ideología personal influye en el debate sobre la aceptación del cambio climático. Por tanto, lo que los líderes políticos opinen o apoyen públicamente será importante en el proceso de aceptación. Lo estudiaron, en Australia, con encuestas a 1211 voluntarios, Thad Kousser y Bruce Tranter, de las universidades de California en San Diego y de Tasmania. En concreto, en las encuestas se pedía el apoyo a políticas públicas relacionadas con el cambio climático como la disminución las emisiones de dióxido de carbono o la promoción de las energías renovables. Cuando los líderes políticos discrepan, los ciudadanos reaccionan según su ideología: los conservadores se oponen y los liberales lo apoyan. Cuando los líderes están de acuerdo, los ciudadanos apoyan esas políticas y lo hacen sea cual sea su ideología.
También en Australia, Colvin y Jotzo, de la Universidad Nacional Australiana de Canberra, después de encuestar a 2033 votantes en las elecciones de 2019, detectan que la mayoría piensan que es importante para Australia disminuir las emisiones de gases con efecto invernadero. Pero la importancia que dan a las acciones para conseguirlo es mayor en los votantes de partidos políticos considerados progresistas, con un mayor nivel de educación y, también, en los más jóvenes.
 Foto: Matt Palmer / UnsplashEl efecto de la temperatura de ayer sobre la opinión de hoy
Foto: Matt Palmer / UnsplashEl efecto de la temperatura de ayer sobre la opinión de hoy
Tanto influye la ideología en las opiniones sobre el calentamiento global que Lawrence Hamilton y Mary Stampone, de la Universidad de New Hampshire en Durham, han encontrado que, después de una encuesta, y sea cual sea la temperatura de los días anteriores, casi el 80% de los demócratas acepta el cambio climático mientras que el 70% de los republicanos lo rechaza. Y los que se declaran independientes lo aceptan o lo niegan según la temperatura de los días anteriores a la encuesta: lo niegan si han estado a 6ºC bajo cero y lo aceptan si ha sido de 12ºC sobre cero.
Y no solo influye el tiempo de los días anteriores, también lo hace el de los últimos meses y años. En el estudio de Jeremiah Bohr, de la Universidad de Wisconsin, analiza el clima en 2013 y 2014 y lo compara con la aceptación del cambio climático y la ideología política según cuatro encuestas de la CBS y del New York Times.
El tiempo de los últimos cinco años amplia la percepción de los impactos del cambio climático y la polarización política en cuanto a si ha sido causado por la actividad humana o no. Esta reacción es más evidente entre los demócratas. Lo que ocurre, según el estudio de Hamilton y Stampone sobre la influencia del tiempo de los días anteriores, también se da para lo que ocurre en los años anteriores. Los demócratas se reafirman en su convicción de que la causa del cambio climático es la actividad humana si las temperaturas han sido altas, y los republicanos en su negación del cambio climático si ha hecho frío. Así, la polarización política de las creencias sobre el cambio climático crece si se dan temperaturas extremas poco habituales.
En la revisión publicada en 2017 que trata de esta relación entre ideología y medio ambiente, de Wanyum Shao, de la Universidad de Auburn, en Estados Unidos, con datos de 2012 los resultados se mantienen, con los demócratas aceptando el cambio climático y la intervención humana, y los republicanos lo niegan y, además, con la orientación más extremista del grupo Tea Party.
Incluso hay una diferencia similar entre demócratas y republicanos, en Nueva York, respecto a los desastres provocados por el clima como, por ejemplo, las inundaciones del huracán Sandy en 2012. La percepción de los demócratas de la probabilidad de sufrir inundaciones es mucho mayor que para los republicanos, con porcentajes del 70% para los primeros y casi del 50% en los segundos.
Un aspecto curioso de estas diferencias ideológicas sobre la aceptación del cambio climático lo explican Karen Douglas y Robbie Sutton, de la Universidad de Kent, en Inglaterra. Hacen una revisión que demuestra que, para muchos ciudadanos, el cambio climático no es un hecho científico sino, más bien, una creencia que, además, tiene mucho que ver con lo llamamos conspiraciones. Es típico de nuestra cultura digital y globalizada que cualquiera puede proponer que detrás de algo, de lo que sea, hay una conspiración que lo explica y justifica. En poco tiempo, miles de internautas difunden la conspiración y millones la aceptan y se la creen.
La actuación personal depende de la moralidad personalLa ideología indica lo que la persona piensa y acepta, pero su moral influye en cómo actúa según esas ideas. En la ideología se basa la conducta pero es la moralidad la que fundamenta su comportamiento, como definen Janis Dickinson y sus colegas, de la Universidad Cornell de Ithaca, al estudiar el compromiso de cada ciudadano sobre el cambio climático. Mencionan cinco ejes principales de la moralidad: compasión, justicia, honradez, autoridad y lealtad al grupo.
Trabajan con encuestas telefónicas a 1000 voluntarios hechas entre agosto y octubre de 2014. De los cinco ejes de la moral que estudian, los que mejor predicen el compromiso de cambio de vida para mitigar el cambio climático son la compasión y la justicia. Destacan estos dos ejes en los progresistas y, por ello, su aceptación de la existencia del cambio climático es mayor que en los conservadores. Estos muestran apoyo al cambio climático con honradez, autoridad y lealtad al grupo.
El contexto lo es todo en las noticias sobre cambio climáticoPero la información sobre cambio climático y sobre la ciencia, en nuestra cultura global, llega a los ciudadanos por los medios de comunicación. Los resultados de Toby Bolsen y Matthew Shapiro, de la Universidad Estatal de Georgia y del Instituto de Tecnología de Illinois en Chicago, muestran cómo influye en los lectores el marco en que se incluyen las noticias sobre el cambio climático. Esas noticias cambian si aparece el cambio climático en noticias de ciencia con el consenso científico o, por el contrario, con las incertidumbres de la ciencia. O hablar de desastres naturales y de que su número puede aumentar con el cambio climático. O de economía y afirmar que la lucha contra el cambio climático puede suponer beneficios económicos o, por el contrario, destruir industria y empleo. Y así, mencionan los autores, el marco en que se incluye la noticia o la información sobre cambio climático puede influir en su aceptación o no por los ciudadanos. Aunque, como cuentan William Anderegg y Gregory Goldsmith, de las universidades de Princeton y Oxford, y con datos del número de consultas, en Google y entre 2004 y 2014, hay picos de interés, como en 2007 y 2010, pero, en general, el interés del público se sostiene durante la década analizada.
Y, además, estamos en la era de las noticias falsas, de las fake news. Pero no solo cuenta en que marco se incluyen las noticias sobre el cambio climático, también actúan las noticias falsas que llegan a los medios. Es un debate que, como ocurre con temas muy sensibles, incita a la invención y la falsedad. Así se manipula la opinión pública para desinformar, provocar debates innecesarios, difundir verdades alternativas, como diría Donald Trump, … El editorial de Nature Communications, de 20 de abril de 2017, avisaba de lo que estaba, y está, ocurriendo y de la necesidad de que los científicos y periodistas expertos en cambio climático se comprometan a desmontar noticias falsas. Solo así llegará la ciencia del cambio climático a los ciudadanos y, además, contribuirán a que el público se eduque en ciencia y pueda tomar, cuando sea necesario, las decisiones adecuadas.
 Foto: Matt Palmer / UnsplashSe rechaza la ciencia por extensión
Foto: Matt Palmer / UnsplashSe rechaza la ciencia por extensión
Esta manera de pensar y aceptar los hechos puede llevar a rechazar no solo el cambio climático sino, además, la ciencia. Stephen Lewandowsky y Klaus Oberauer, de las universidades de Bristol, en Inglaterra, y de Zurich, en Suiza, comentan que el rechazo a los hallazgos científicos es más habitual en la derecha que en la izquierda aunque, realmente, el mecanismo de rechazo es igual en ambas ideologías. Es el procesamiento superficial de evidencias y el rechazo de toda evidencia que no encaje con las creencias de cada persona. Una buena educación e, incluso, una cultura científica suficiente no ayudan a mitigar el rechazo. Pero los autores también detectan que un conocimiento científico profundo del tema de que se trate, en este caso del cambio climático, ayuda en su aceptación. Erik Nisbet y su grupo, de la Universidad Estatal de Ohio en Columbus, añaden a esta investigación que una mentalidad abierta, sea cual sea el entorno, ayuda a cambiar de opinión y, en el caso concreto del cambio climático, a entender los costes y beneficios que supone la política gubernamental en relación con el clima.
Sobre esto de las conspiraciones y sobre el cambio climático, incluso se habla de una poderosa organización conspiratoria que recibe el nombre de Gran Conspiración del Cambio Climático, así escrito, con muchas mayúsculas. La forman científicos, periodistas y políticos que inventaron lo del calentamiento global en primer lugar y, después, asustaron con sus consecuencias. Los científicos lo hicieron para aumentar su influencia social y política y, claro está, para conseguir más fondos. También hay implicados ecologistas para promover las energías renovables. O empresarios relacionados con la energía nuclear para promover su construcción y erradicar los combustibles fósiles. Por supuesto, creer en esta conspiración es habitual entre quienes no aceptan el cambio climático y la intervención humana como su causa.
Todos, demócratas y republicanos, hablan del mismo planeta, en la misma época de la historia, y sobre el mismo tema, y nos dan una muestra exacta de cómo influyen las interpretaciones individuales basadas, está claro, en creencias que blindan las ideologías. Además, ni a demócratas ni a republicanos les gusta escuchar opiniones de otros. Jeremy Frimer y su grupo, de la Universidad de Winnipeg, en Canadá, lo han estudiado con más de 2400 voluntarios y con encuestas sobre diferentes temas. Concluyen que las personas comprometidas con su ideología están igualmente motivadas para evitar la información transversal, es decir, que no esté comprometida con ninguna ideología. Por ejemplo, la información científica. Y lo hacen porque es cansado, requiere esfuerzo y provoca frustración, y socava el sentido de la realidad compartida con quien piensa igual y con el grupo al que pertenece. No hay diferencias, concluyen, en el deseo de demócratas y republicanos de permanecer en sus respectivas burbujas ideológicas.
El efecto paísPor los analizado hasta ahora es evidente que los expertos encuentran conclusiones contradictorias. El estudio de Matthew Hornsey y su equipo, de la Universidad de Queensland, en Australia, muestra que los datos estudiados hasta 2018 provienen, en su gran mayoría, de Estados Unidos y son los que revelan la influencia de la ideología conservadora y la creencia en conspiraciones. Así se justifica el rechazo a la existencia del cambio climático. Pero el estudio de Hornsey incluye 24 países y es, precisamente, en Estados Unidos donde más influye la ideología. En el resto de los países no aparecen los mismos resultados y, como ejemplo, en España, la ideología de no aceptación del cambio climático se sitúa ligeramente a la derecha del espectro político y es tres veces menor que en Estados Unidos. Además, hay una relación menor entre el escepticismo sobre el cambio climático y la creencia en conspiraciones para promocionarlo.
La respuesta a la pregunta de quienes son responsables del cambio climático cambia según el país. El estudio de Ruxandra Malina Petrescu-Nag y sus colegas, de la Universidad Babes-Bolyai de Cluj-Napoca, en Rumania, nos sirve de ejemplo pues compara las respuestas de belgas y rumanos. Para los primeros, los responsables son todos los ciudadanos, incluso cada uno de ellos. En cambio los rumanos apuntan a las grandes compañías, los gobiernos y los consumidores en general. Además, los rumanos destacan que el cambio climático a menudo se utiliza con exageración e intención política.
Referencias:
Anderegg, W.R.L. et al. 2010. Expert credibility in climate change. Proceedings of the National Academy of Sciences USA 107: 12107-12109.
Anderegg, W.R.L. & G.R. Goldsmith. 2014. Public interest in climate change over the past decade and the effects of the “climagate” media event. Environmental Research Letters 9: 054005.
Bohr, J. 2017. Is it hot in here or is it just me? Temperature anomalies and political polarization over global warming on the American public. Climatic Change DOI: 10.1007/s10584-017-1934-z.
Bolsen, T. & J.N. Druckman. 2018. Do partisanship and politicization undermine the impact of a scientific consensus message about climate change? Processes & Intergroup Relations 21: 389-402.
Bolsen, T. & M.A. Shapiro. 2017. The US news media, polarization on climate change, and pathways to effective communication. Environmental Communication doi: 10.1080/17524032.2017.1397039.
Botzen, W.J.W. et al. 2016. Political affiliation affects adaptation to climate risks: Evidence from New York City. Climatic Change DOI: 10.1007/s10584-016-1735-9.
Carlton, J.S. et al. 2015. The climate change consensus extends beyond climate scientists. Environmental Research Letters 10: 094025.
Colvin, R.M. & F. Jotzo. 2021. Australian voters’ attitudes to climate action and their social-political determinants. PLOS One 16: e0248268.
Cook, J. et al. 2013. Quantifying the consensus on anthropogenic global warming in the scientific literature. Environmental Research Letters 8: 024024.
Dickinson, J.L. et al. 2016. Which moral foundations predict willingness to make lifestyle changes to avert climate change in USA? PLOS One 11: e163852.
Douglas, K.M. & R.M. Sutton, 2015. Climate change: Why the conspiracy theories are dangerous. Bulletin of the Atomic Scientists 71: 98-106.
Dunlap. R.E. et al. 2016. The political divide on climate change: Partisan polarization widens in the U.S. Environment. Science and Policy for Sustainable Development 58: 4-22.
Editorial. 2017. Fake news threatens a climate literate world. Nature Communications 8: 15460.
Frimer, J.A. et al. 2017. Liberals and conservatives are similarly motivated to avoid exposure to one another’s opinions. Journal of Experimental Social Psychology 72: 1-12.
Hamilton, L.C. & M.D. Stampone. 2013. Blowin’ in the wind: Short-term weather and belief in anthropogenic climate change. Weather, Climate, and Society 5: 112-119.
Harlos, C. et al. 2017. No evidence of publication bias in climate change science Climatic Change 140: 375-385.
Hornsey, M.J. et al. 2018. Relationships among conspirational beliefs, conservatism and climate scepticism across nations. Nature Climate Change 8: 614-620.
Kousser, T. & B. Tranter. 2018. The influence of political leaders on climate change attitudes. Global Environmental Change 50: 100-109.
Lewandowsky, S. & K. Oberauer. 2016. Motivated rejection of science. Current Directions in Psychological Science 25: 217-222.
Meira-Cartea, P.A. & M. Arto-Blanco. 2014. Representaciones del cambio climático en estudiantes universitarios en España: aportes para la educación y la comunicación. Educar em Revista, Curitiba, Brasil 3: 15-33.
Myers, K.F. et al. 2021. Consensus revisited: quantifying scientific agreement on climate change and climate expertise among Earth scientists 10 years later. Environmental Research Letters 16: 104030.
Nisbet, E.C. et al. 2013. Attitude change in competitive framing environments? Open-/closed-mindedness, framing effects, and climate change. Journal of Communication 63: 766-785.
Pérez, J.I. & J. Sevilla. 2022. Los males de la ciencia. Next Door Publ. Pamplona. 284 pp.
Petersen, A.M. et al. 2019. Discrepancy in scientific authority and media visibility of climate change scientists and contrarians. Nature Communications 10: 3502.
Petrescu-Mag, R.M. et al. 2022. How climate change science is reflected in people’s minds. A cross-country study on people’s perceptions of climate change. International Journal of Environmental Research and Public Health 19: 4280.
Shao, W. 2017. Weather, climate, politics, or God? Determinants of American public opinions toward global warming. Environmental Politics 26: 71-96.
van der Linden, S. et al. 2017. Scientific agreement can neutralize politicization of facts. Nature Human Behaviour doi: 10.1038/s41562-017-0259-2.
Para saber más:
Ciencia, creencias, política y matar al mensajero
«El cambio climático: ciencia, política y moral» por José Manuel Sánchez Ron
Certezas e incertidumbres sobre el cambio climático
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo Ideología, política y cambio climático se ha escrito en Cuaderno de Cultura Científica.
Cómo nos cambió la Iglesia medieval
La Iglesia Católica modificó las relaciones familiares en la Edad Media y, como consecuencia, pudo haber influido en los patrones psicológicos contemporáneos
 Ilustración: Elena Andreu
Ilustración: Elena Andreu
Jonathan F. Schulz, economista asociado a la Universidad de Harvard en el departamento de biología evolutiva humana y colegas, publicaron en noviembre de 2019 en la revista Science, un artículo que argumenta que hay una variación sustancial en los atributos psicológicos entre las culturas. Examinaron si la difusión del catolicismo en Europa generó gran parte de esta variación. En concreto, echaron la mirada atrás, a la política matrimonial y la estructura familiar que favorecía la Iglesia Occidental en la Edad Media (la rama del cristianismo que luego se convirtió en la Iglesia Católica Romana). Comprobaron, que la Iglesia tuvo el poder de desglosar las instituciones extendidas basadas en el parentesco y alentar una estructura familiar nuclear. Tanto es así, que los países con más siglos de influencia de la Iglesia (antes de 1500 de la era común) tienen hoy rasgos psicológicos característicos de las que han llamado sociedades WEIRD.
Hace algo así como una década, el antrópologo Joseph Henrich, en un artículo titulado «The weirdest people in the world” usaba la palabra “WEIRD” para describir nuestras sociedades. Además de extraño en inglés es el acrónimo de occidental, educada, industrializada, rica y democrática.
¿Pero entonces, qué rasgos tiene una persona de una sociedad WEIRD?
- Priorizan comportamientos prosociales impersonales, definidos como aquellos que benefician a un anónimo Otro; por ejemplo, ser voluntario o donante.
- Muestran altos niveles de individualismo y están insertos en intensos procesos de movilidad, cambio social y volcados en su éxito personal.
- La cultura occidental promueve formas de pensamiento más analítico y categorial, mientras que la asiática (y otras muchas) lo hace con un pensamiento más holístico y relacional.
- Se centran en las intenciones, creencias, y deseos, juzgándolas moralmente en lugar de enfatizar sus acciones. Se da importancia a la Culpa. Así en muchas sociedades No-WEIRD los castigos penales para homicidio accidental y premeditado eran las mismas mientras que en las sociedades WEIRD las penas dependen del estado mental del asesino sus intenciones y creencias.
- Son menos conformistas, menos obedientes, menos leales al grupo, y tienen menos nepotismo.
La Iglesia pudo influir en la psicología de muchas maneras y en concreto a través de los sistemas de parentesco.
La expresión “sistemas de parentesco” designa todo sistema de relaciones sociales donde se combina consanguinidad con afinidad o alianza. Es decir, de una parte intervienen elementos biológicos de filiación, término que hace referencia a los lazos de los padres con los hijos y entre hermanos, y, de otra, elementos sociales. Es decir, los lazos derivados de la relación conyugal, que son lazos de alianza que son determinados por acuerdos o conveniencias sociales.
La iglesia prohibió prácticas corrientes como la adopción, la poligamia, el divorcio, el concubinato, las segundas nupcias de los viudos, el matrimonio en el seno del parentesco y puso el acento sobre el consentimiento mutuo de los esposos en el matrimonio, su amor.i Reduciendo así la intensidad de parentesco de la sociedad.
Cuando los investigadores tuvieron que buscar datos sobre los sistemas de parentesco se basaron en el conjunto de datos del Atlas Etnográfico, elaborado a partir de observaciones de antropólogos sobre 1.291 poblaciones previas a la industrialización. Partiendo de estos datos crearon un índice de intensidad de parentesco en el que incluían la tendencia de la sociedad a contraer de matrimonios entre primos, la poligamia o a la convivencia con la familia del nuevo matrimonio. De forma adicional, tomaron los datos de prevalencia de matrimonio entre primos en el siglo XX. Así pudieron correlacionar los atributos psicológicos recopilados en variedad de pruebas, a la intensidad de parentesco de la sociedad y a los años de influencia de la Iglesia. A nivel regional, entre países y entre la primera generación de hijos de migrantes.
Concluyeron que las regiones con mayor tiempo de exposición a la Iglesia, tenían menos intensidad de parentesco y más rasgos de psicología WEIRD. Cabe preguntarse si la psicología WEIRD es solo una delgada capa que ante circunstancias adversas se rompe para desvelar a un ser humano que favorece a sus allegados por encima de todo.
Por otro lado asumir que la prosperidad occidental se debe a esta psicología es arriesgado, ya que no tiene en cuenta todos los actos inmorales no WEIRD que se han dado para que occidente haya prosperado como por ejemplo el colonialismo.
Referencias consultadas:
i Juan F. Gamella Ana María Núñez Negrillo Entre marido y mujer. Discursos eclesiásticos en las causas de dispensa de los matrimonios consanguíneos celebrados en la diócesis de Granada (1892-1963) DOI: 10.30827/Digibug.6741 https://www.ugr.es/~pwlac/G26_39Juan_Gamella-Ana_Nunez-Elisa_Carrasco.html
Schulz, J. F., Barahmi-Rad, D., Beauchamp, J., & Henrich, J. (2018, June 22). The Origins of WEIRD Psychology. https://doi.org/10.31234/osf.io/d6qhu
Jonathan F. Schulz, Duman Bahrami-Rad, Jonathan P. Beauchamp and Joseph Henrich (2019): The Church, intensive kinship, and global psychological variation. Science 366 (6466), eaau5141. DOI: 10.1126/science.aau5141.
Autora: Elena Andreu Rubert (IG: @elena_andreu_ilustra) es graduada en farmacia, e ilustradora científica. Alumna del Postgrado de Ilustración Científica de la UPV/EHU – curso 2020/21
Artículo original: Pérez Iglesias, J.I. (2020) Así nos hizo la Iglesia: Individualistas, independientes y prosociales si no es personal Cuaderno de Cultura Científica
“Ilustrando ciencia” es uno de los proyectos integrados dentro de la asignatura Comunicación Científica del Postgrado de Ilustración Científica de la Universidad del País Vasco. Tomando como referencia un artículo de divulgación, los ilustradores confeccionan una nueva versión centrada en la propia ilustración
El artículo Cómo nos cambió la Iglesia medieval se ha escrito en Cuaderno de Cultura Científica.
Las pruebas de la educación: Lucas Gortazar – El puzle de la repetición de curso

Bilbao volvió a acoger el pasado 20 de mayo de 2022 “Las pruebas de la educación”, una jornada que abordará diversas cuestiones educativas con la evidencia científica existente. Esta quinta edición está organizado por la Cátedra de Cultura Científica de la UPV/EHU y la Fundación Promaestro con la colaboración del Consejo Escolar de Euskadi, y se celebró en el Bizkaia Aretoa – UPV/EHU de la capital vizcaína.
La jornada consta de cinco ponencias de media hora de duración en la que se tratan temas como la problemática relacionada con los juegos de azar en el ámbito escolar, el impacto de la inmigración en el rendimiento del alumnado o el debate sobre la jornada escolar continua o partida, entre otras cuestiones. La dirección del seminario corrió de nuevo a cargo de Marta Ferrero profesora de la Facultad de Formación del Profesorado y Educación de la Universidad Autónoma de Madrid.
En esta charla Lucas Gortazar, director de investigación y senior fellow de Educación del Centro de Políticas Económicas de Esade además de consultor en el Departamento de Educación del Banco Mundial, aborda “el puzle de la repetición de curso”, medida “poco efectiva, cara y desigual” como se concluye tras estudiar los datos administrativos de decenas de miles de alumnos vascos de Educación Primaria y la ESO.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Las pruebas de la educación: Lucas Gortazar – El puzle de la repetición de curso se ha escrito en Cuaderno de Cultura Científica.

