El problema de los 17 caballos
 Foto: Louise Pilgaard / Unsplash
Foto: Louise Pilgaard / UnsplashEn ocasiones, cuando estoy pensando sobre qué escribir para la nueva entrada del Cuaderno de Cultura Científica, acudo a un libro que me gusta mucho, se trata del libro Famous Puzzles of Great Mathematicians (Rompecabezas famosos de grandes matemáticos), de Miodrag S. Petkovic. Hace poco revisaba algunos de los problemas de los que se habla en el libro cuando me topé con un clásico de la matemática recreativa, el problema de los 17 caballos, que también recibe otros nombres, como el problema de los 17 camellos, que es el nombre con el que yo lo conocía, o el problema de la herencia. El problema, en su forma más directa y sencilla, dice lo siguiente.
Problema de los 17 caballos: Un hombre muere y deja una herencia de diecisiete caballos que tiene que repartirse entre sus tres hijos en las proporciones 1/2 : 1/3 : 1/9 ¿Pueden los tres hermanos cumplir la voluntad de su padre?
Una rápida mirada a este problema nos dice que es un problema paradójico, o al menos problemático, puesto que 17 no se puede dividir ni por 2, ni por 3, ni por 9, luego la solución no va a ser inmediata si asumimos que los caballos no se pueden partir en trozos (por este motivo en algún texto matizan que los caballos tienen que repartirse vivos).
Este problema me recuerda a un problema chiste de una obra de teatro de los Hermanos Marx, de 1910, titulada Fun in High Skule:
Groucho: Si tuvieses 10 manzanas y quisieras repartirlas entre seis personas ¿qué harías tú?
Gummo: Haría compota de manzana.
Groucho: ¿Cuál es la forma de la Tierra?
Harpo: Pues no lo sé.
Groucho: Bien, veamos, ¿cuál es la forma de mis gemelos?
Harpo: Cuadrada.
Groucho: No los gemelos de diario, sino los que yo visto los domingos.
Harpo: Ah, redonda.
Groucho: Muy bien, ¿cuál es la forma de la Tierra?
Harpo: Cuadrada entre semana y redonda los domingos.
 Foto publicitaria, realizada por la Metro-Goldwyn-Mayer, de los Hermanos Marx en 1946
Foto publicitaria, realizada por la Metro-Goldwyn-Mayer, de los Hermanos Marx en 1946
Volviendo a la solución del problema de los 17 caballos, por una parte, tenemos la cuestión de que 17 no se puede dividir entre 2, 3 y 9, pero además si la herencia se repartiese completamente la suma de las proporciones 1/2, 1/3 y 1/9 debería ser 1, pero resulta que no es así:
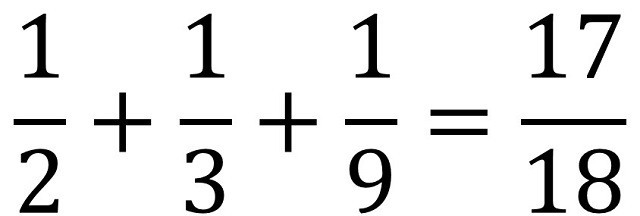
Es decir, la suma de las proporciones es menor que 1 y no se puede ejecutar toda la herencia. Por lo tanto, si nos vamos a una solución aritmética pura del problema, sin importarnos de qué estamos hablando, que es como muchas veces se resuelven los problemas matemáticos en la clase de esta signatura, tendríamos que la solución es 8,5 (17/2), 5,67 (en realidad, 17/3) y 1,89 (en realidad, 17/9) y se quedaría sin repartir el resto que es 0,94 (en realidad, 17 / 18), puesto que
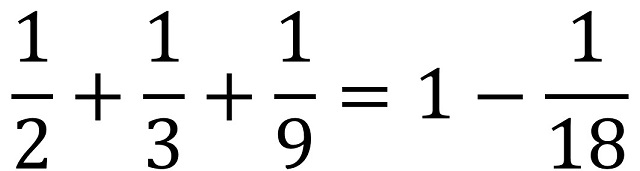
Si entendemos que la solución al problema de los 17 caballos tiene que ser siguiendo al pie de la letra las indicaciones de la herencia, que es como seguramente se entendía este problema matemático en sus orígenes, entonces tenemos dos opciones, o la solución puramente aritmética, como acabamos de describir, o pensar que es un problema imposible, en el sentido de que ni se puede dividir 17 entre 2, 3 y 9, ni la suma de esas partes, 17/2, 17/3 y 17/9 es toda la herencia, 17 caballos.
Según muchos textos, como el mencionado Famous Puzzles of Great Mathematicians, de Miodrag S. Petkovic o el texto The Penguin Dictionary of Curious and Interesting puzzles de David Wells, fue el matemático italiano Niccolo Fontana (1499 o 1500 – 1557), conocido como Tartaglia, quien sugirió la solución moderna de pedir prestado un caballo extra, así tener 18 caballos para repartir en tres partes de 9 (que es 18/2), 6 (que es 18/3) y 2 (que es 18/9) caballos, por lo que sobra 1, que se devuelve a la persona que lo había prestado.
Este problema, junto con su solución, se suele presentar como una legenda árabe, que dice lo siguiente (siguiendo la versión recogida por el matemático David Singmaster, en su libro Aventuras en las Matemáticas Recreativas, un interesante libro sobre la historia de la matemática recreativa).
Un jeque árabe murió dejando un rebaño de camellos como herencia completa para repartir entre sus tres hijos. En su testamento, especificó que el hijo mayor recibiría la mitad de la herencia; el segundo hijo, un tercio de la misma; y el tercero, una novena parte. Los hijos fueron a examinar el rebaño y descubrieron que había 17 camellos. Ahora bien, diecisiete no es divisible por dos, ni por tres, ni por nueve, y los hijos quedaron perplejos. Los camellos son valiosos y no querían cortar uno en pedazos.
Después de discutirlo, decidieron consultar al mullah Nasruddin y enviaron a buscarlo. El mullah se acercó con su camello y escuchó el dilema de los hijos del jeque. Después de reflexionar un poco, dijo que les prestaría un camello. El rebaño contaba ahora con 18 camellos y el mullah asignó la mitad de los camellos al hijo mayor, es decir, nueve camellos; luego un tercio de los camellos al segundo hijo, es decir, seis camellos; luego un noveno de los camellos al tercer hijo, es decir, dos camellos. Entonces, quedó un camello, el que les había prestado el mullah, así que este reclamó su camello y cabalgó hacia la puesta de sol.
 Imagen del problema de los 17 caballos, con el título Un legado inmanejable, perteneciente al libro Brandreth Puzzle Book (1896), que era a la vez un panfleto publicitario de las Pastillas de Brandreth y una colección de rompecabezas
Imagen del problema de los 17 caballos, con el título Un legado inmanejable, perteneciente al libro Brandreth Puzzle Book (1896), que era a la vez un panfleto publicitario de las Pastillas de Brandreth y una colección de rompecabezas
En general, podemos plantearnos el reparto de una cierta cantidad n de caballos en tres proporciones 1/a, 1/b y 1/c, donde a, b, c son números naturales distintos, tales que necesitemos el préstamo de un caballo para realizar el reparto, es decir, que se verifique la ecuación
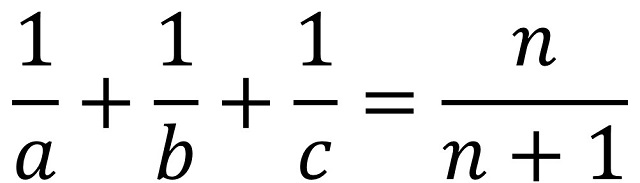
Por lo tanto, para construir todos los problemas de este tipo debemos de resolver la anterior ecuación diofántica (recordemos que las ecuaciones diofánticas son ecuaciones polinómicas de dos o más variables para las que se estudian las soluciones con números enteros, es decir, los naturales, el cero y los negativos). Existen siete soluciones (n; a, b, c) posibles, que mostramos a continuación:
(7; 2, 4, 8), (11; 2, 4, 6), (11; 2, 3, 12), (17; 2, 3, 9), (19; 2, 4, 5), (23; 2, 3, 8) y (41; 2, 3, 7),
con las cuales se pueden plantear problemas similares al problema de los 17 caballos, como así ha ocurrido con alguna de estas soluciones. Por ejemplo, Philip E. Bath en el problema El jardín del vicario de su libro Fun with Figures (Diversión con números) plantea el reparto de 7 chelines en las proporciones 1/2, 1/4 y 1/8; o S. E. Clark en el problema Los herederos y las ovejas de su libro Mental Nuts (Locuras mentales), que podéis encontrar en Internet Archive, plantea dividir una herencia de 19 ovejas en las proporciones 1/2, 1/4 y 1/5.
Si se permite que los números a, b y c no necesariamente son distintos, entonces se pueden obtener más soluciones, como (5; 2, 6, 6), (5; 3, 3, 6), (9; 2, 5, 5), (11; 3, 3, 4) o (3; 4, 4, 4).
 Portadas de los volúmenes 1 y 2 de Adventures in Recreational Mathematics, de David Singmaster
Portadas de los volúmenes 1 y 2 de Adventures in Recreational Mathematics, de David Singmaster
El matemático David Singmaster, en su libro Aventuras en las Matemáticas Recreativas, nos cuenta que este tipo de problemas son una versión moderna de algunos problemas antiguos de reparto donde las proporciones no sumaban uno. Problemas de este tipo son muy antiguos, ya aparecían en el Papiro de Rhind (escrito por el escriba Ahmes en el siglo XVI a.n.e.), que es el documento matemático más importante conservado del Antiguo Egipto.
 Fragmento del Papiro matemático de Rhind, o de Ahmes, perteneciente a la sección EA10057, British Museum
Fragmento del Papiro matemático de Rhind, o de Ahmes, perteneciente a la sección EA10057, British Museum
Terminemos esta entrada con el problema 63 del Papiro de Rhind que consiste en repartir 700 barras de pan para cuatro personas, en las proporciones 2/3 : 1/2 : 1/3 : 1/4, pero el total de las partes suma 7/4, que es mayor que 1.
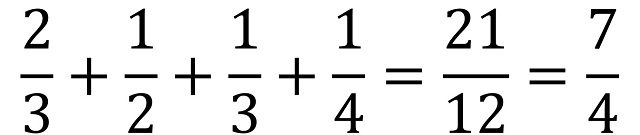
La solución al problema que se ofrece en el texto matemático egipcio es que, si 700 barras se corresponden con 7/4, entonces, la unidad es 4/7 de 700, es decir, 400 y se realiza el reparto de 2/3, 1/2, 1/3 y 1/4 de la unidad, es decir, que la cantidad de panes se reparte en 266,7 (2/3 de 400) barras de pan –o podríamos decir que 266 barras enteras y dos terceras partes de una barra-, 200 (1/2 de 400) barras, 133,3 (1/3 de 400) barras –podríamos decir que 133 barras de pan y una tercera parte de una- y 100 (1/4 de 400) barras.
Bibliografía:
1.- Miodrag S. Petrovic, Famous Puzzles of Great Mathematicians, AMS, 2009.
2.- David Wells, The Penguin Dictionary of Curious and Interesting puzzles, Penguin, 1992.
3.- Martin Gardner, Fractal Music, Hypercards and more, W. H. Freeman & Co, 1991.
4.- David Singmaster, Adventures in Recreational Mathematics (Problem Solving in Mathematics and Beyond, 21), vol. 1 y 2, World Scientific, 2021.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo El problema de los 17 caballos se ha escrito en Cuaderno de Cultura Científica.
Einstein y Johannes Stark
Johannes Stark fue un físico alemán, ganador del premio Nobel en 1919 por el descubrimiento de que en un campo eléctrico la luz se separa en líneas espectrales, fenómeno conocido en su honor como efecto Stark. Conforme comenzaba su ascenso a la fama Einstein se carteó con regularidad con Stark. En 1913 Stark modificó la ley de fotoequivalencia de Einstein, que actualmente se llama ley de Stark-Einstein o segunda ley de la fotoquímica. Tras la Primera Guerra Mundial, sin embargo, Stark abrazó fervientemente los ideales nazis, promoviendo una ciencia nueva completamente “aria” y orquestando toda una campaña de descrédito de la “judía” teoría de la relatividad de Einstein.
 Johannes Stark. Foto: nobelprize.com
Johannes Stark. Foto: nobelprize.comEn 1907, Stark, que era entonces profesor en la Technische Hochschule de Hannover, pidió a Einstein que escribiese un artículo de revisión sobre la relatividad para el Jahrbook für Radioaktivität und Elekronik (Anuario de radioactividad y electrónica). Durante esta época y en los años siguientes, Einstein y Stark mantuvieron una correspondencia bastante cordial. Solamente una excepción. Ocurrió cuando Einstein estaba viviendo en Praga y escribió un artículo sobre procesos fotoquímicos que Stark creyó que plagiaba directamente uno de sus escritos. Stark atacó a Einstein en las páginas de Annalen der Physik, a lo que Einstein respondió contundentemente en la misma revista demostrando que Stark no había entendido su trabajo.
1913 fue el annus mirabilis particular de Johannes Stark. Ese año Stark modificó una teoría sobre los fotones publicada por Einstein en 1906. La versión definitiva, conocida actualmente como ley de Stark-Einstein, o segunda ley de la fotoquímica, afirma que cada molécula implicada en una reacción fotoquímica absorbe solamente un único fotón de la radiación o luz que causa la reacción. Ese año, Stark también descubrió un efecto de la luz que ha llevado su nombre desde entonces.
Los científicos ya conocían lo que se llamaba el efecto Zeeman, en el que los campos magnéticos dividen la radiación procedente de partículas en las denominadas líneas espectrales. Estas líneas dependen de la velocidad a la que un átomo o ión dado está oscilando y pueden ser útiles a la hora de identificar exactamente qué partícula es la que está oscilando. Stark se las arregló para producir líneas espectrales similares usando un campo eléctrico en vez de uno magnético. En última instancia, el efecto Stark es más complejo a la hora de analizar la información obtenida, por lo que hoy día se prefiere usar el efecto Zeeman para el análisis de la estructura atómica.
En cualquier caso este era un trabajo que merecía un Nobel; Stark recibió el premio en 1919. En su discurso de aceptación ya aparecieron los primeros indicios de lo que más tarde serían sus posiciones políticas. El discurso comienza con la idea de que los alemanes continúan con el trabajo de los antiguos griegos de comprender la estructura atómica. A lo largo del discurso su argumentación, una y otra vez, es siempre cómo su trabajo se enmarca y contribuye a la física alemana. Las semillas del nacionalismo están enraizadas y comienzan a verse sus primeros brotes.
Tras el premio Nobel, Stark, si se me permite la expresión, pasa definitivamente al lado oscuro. No se le recuerda por sus contribuciones a la ciencia en la segunda mitad de su vida, sino por su política. Qué acontecimientos o influencias pudieron hacer que Stark se volviese contra los que hasta entonces habían sido sus colegas no están claros, pero lo cierto es que en los años veinte Stark absorbió y aceptó plenamente la retórica nazi de la gloria de la raza aria y comenzó una campaña para socavar la física moderna, lo que incluía un rencoroso ataque contra Einstein.
En 1922, cuando era profesor en la Universidad de Wurzberg, Stark escribió un libro denunciando la física moderna llamado La crisis actual en la física alemana. Afirmaba en él que materias como la relatividad eran obviamente subversiones, subversiones judías además, del pensamiento racional puro. Si bien el nazismo y su antisemitismo estaban creciendo en Alemania, todavía no eran mayoritarios y este tipo de comentarios le valió el ostracismo por parte de sus colegas. Sus afirmaciones le llevaron a tener que renunciar a su cátedra y tuvo que ganarse la vida creando una empresa de porcelana.
En 1924, Stark declaró públicamente su completa lealtad a Hitler y continuó atacando a la física “judía”, afirmando que era una ciencia que ignoraba los experimentos objetivos o la observación de los hechos. En los años 30 trabajó con Philipp Lénárd, otro premio Nobel con tendencias nacionalistas extremas que también la había tomado con Einstein, intentando crear una ciencia alemana “pura”, de forma similar a como Hitler estaba tratando de crear una raza alemana “pura”.
Stark fue nombrado presidente del Instituto Imperial de Física y Tecnología tras la llegada al poder de Hitler en 1933, cargo que ocuparía hasta 1939. En esta posición disponía de una plataforma inmejorable para la difusión de su retórica de que toda la ciencia debía dedicarse a apoyar las filosofías nazis. Afirmó que los judíos, por su evidente falta de respeto a la verdad, no eran adecuados para la física.
O lo que era peor desde su punto de vista, no se limitaban a los canales apropiados. Escribió, aparentemente con Einstein en mente, en su libro Nacionalsocialismo y Ciencia, publicado en 1934: “el celo dogmático e impulso propagandístico del científico judío le lleva a informar de sus descubrimientos no sólo en publicaciones científicas sino también en la prensa diaria o en conferencias públicas”.
En general, los ataques de Stark a la ciencia moderna no tenían una base racional: se limitaba a declarar que la relatividad era tan contraria a la experiencia diaria y al sentido común que tenía que ser errónea. Cuando Werner Heisenberg salió en defensa de Einstein, Stark lo tildó, en un artículo en el periódico oficial de la SS, Das Schwarze Korps, de “judío blanco” que debería “desaparecer” (Heisenberg se salvó usando sus contactos familiares con el Reichführer-SS Heinrich Himmler, pero esta es otra historia).
Tras la Segunda Guerra Mundial, el tribunal de desnazificación de Baviera juzgó a Stark. Einstein, viendo el panorama que se cernía sobre Alemania y el peligro real que corría su vida, la había abandonado en 1933 para no volver. Pero aún quedaban científicos para atestiguar en contra de Stark: Max von Laue, Werner Heisenberg y Arnold Sommerfeld entre ellos. Stark fue considerado “major offender” (nivel 5, el más alto de los cinco posibles niveles de colaboración con el régimen nazi, según la clasificación seguida en los tribunales constituidos en la Alemania ocupada por los Estados Unidos). Fue condenado a 4 años de trabajos forzados. La sentencia fue suspendida y Stark se retiró al campo, donde trabajó solo y aislado en su laboratorio privado hasta su muerte en 1957.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Una versión anterior de este artículo se publicó en Experientia Docet el 6 de septiembre de 2009.
El artículo Einstein y Johannes Stark se ha escrito en Cuaderno de Cultura Científica.
De casquetes polares y hielo de dióxido de carbono
Una de las cosas que quizás más sorprenden de Marte, cuando lo vemos a través de un potente telescopio o en las imágenes que nos llegan de las misiones espaciales, es la presencia de sus casquetes polares, que destacan por su color blanco, a veces inmaculado, en contraste con el color rojo de su superficie.
Nos es más llamativo todavía porque los vemos crecer y menguar con las estaciones, al igual que en nuestro planeta, aunque con un ciclo prácticamente restringido a la sublimación y a la formación de los hielos por condensación desde la atmósfera debido a las bajas temperaturas y ligera presión atmosférica.
Desde el punto de vista de la geología, el hielo es un importante agente de modelado y transporte, ya que los hielos son capaces de viajar cientos e incluso miles de kilómetros, erosionando la superficie y encajándose, formando grandes valles.
Además, las acumulaciones de hielo pueden ser estudiadas como los estratos de la roca, lo que nos aporta una valiosa información sobre el clima de un planeta a lo largo del tiempo, estudiando las burbujas de aire atrapadas y las capas de polvo, que, si me permiten la metáfora, se alternan como una inmensa tarta de chocolate y galleta.
 Un escarpe en el casquete del polo norte de Marte. Se pueden apreciar algunas de sus capas, especialmente donde se encuentran intercaladas por otras de polvo. Imagen cortesía de NASA/JPL-Caltech/UArizona.
Un escarpe en el casquete del polo norte de Marte. Se pueden apreciar algunas de sus capas, especialmente donde se encuentran intercaladas por otras de polvo. Imagen cortesía de NASA/JPL-Caltech/UArizona.Pero, además, se da la casualidad de que precisamente el hielo, junto con el viento, es uno de los agentes de modelado del relieve más activos en el planeta Marte en la actualidad, por lo que conocer la dinámica glacial del planeta es un asunto de gran interés para geólogos y climatólogos. Aunque eso sí, hoy nos centraremos solo en los casquetes de hielo, en otra ocasión hablaremos sobre los cinturones glaciales que hay en latitudes más bajas.
Hace varias décadas los científicos pensaban que estos casquetes polares estaban formados principalmente por hielo de dióxido de carbono, mientras que ahora sabemos que, probablemente, al menos en el polo sur, esa cifra esté más cerca del 1%, y que el resto sea hielo de agua, de tal manera que si se fundiese todo este hielo una importante parte de la superficie de Marte quedaría sumergida bajo las aguas.
 Casquete polar sur del planeta Marte. Se aprecia perfectamente el color blanco del hielo, así como zonas más rojizas cubiertas por el polvo. Cortesía de ESA/DLR/FU Berlin / Bill Dunford.
Casquete polar sur del planeta Marte. Se aprecia perfectamente el color blanco del hielo, así como zonas más rojizas cubiertas por el polvo. Cortesía de ESA/DLR/FU Berlin / Bill Dunford.A pesar de ese porcentaje tan bajo de dióxido de carbono, el volumen total de hielo de dióxido de carbono que alberga el casquete del polo sur es de unos 16000 kilómetros cúbicos, suficiente como para llenar el lago Superior, el lago más grande de los Grandes Lagos de Norteamérica -valga la redundancia-, de este hielo, y que en algunos lugares llega a formar capas de más de un kilómetro de potencia o espesor, mientras que el casquete en su conjunto tiene un espesor total de unos cuatro kilómetros.
Y bueno, ¿cómo conocemos estos datos? En las últimas dos décadas hemos podido hacer perfiles de la estructura de los polos marcianos gracias a dos instrumentos conocidos como MARSIS, que viaja en la sonda europea Mars Express, y SHARAD que equipa a la misión Mars Reconnaissance Orbiter, que no son más que dos radares que nos permiten «ver» con sus ondas hasta cierta profundidad, ayudándonos a estudiar las capas más someras del subsuelo marciano y cuáles son las relaciones entre estas.
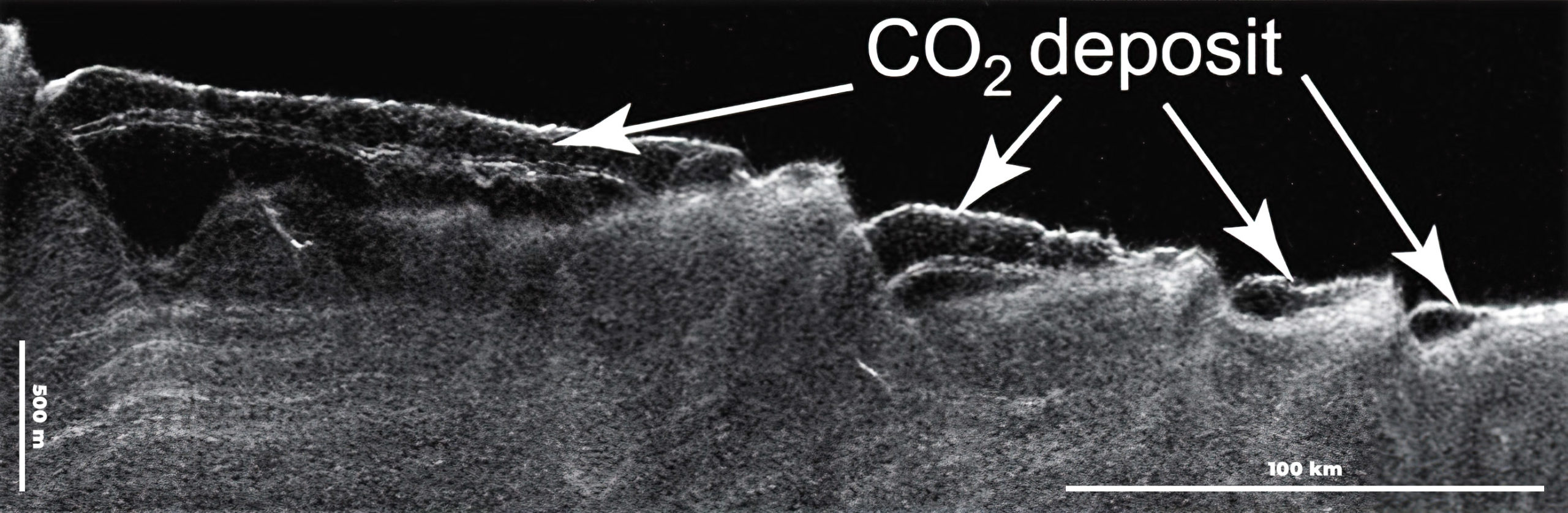 Perfil de radar tomado por el instrumento SHARAD, que se encuentra a bordo de la Mars Reconnaissance Orbiter. Se aprecian perfectamente las acumulaciones de hielos de dióxido de carbono ocupando depresiones que favorecen su depósito. Imagen cortesía de NASA/JPL-Caltech/Sapienza University of Rome/Southwest Research Institute.
Perfil de radar tomado por el instrumento SHARAD, que se encuentra a bordo de la Mars Reconnaissance Orbiter. Se aprecian perfectamente las acumulaciones de hielos de dióxido de carbono ocupando depresiones que favorecen su depósito. Imagen cortesía de NASA/JPL-Caltech/Sapienza University of Rome/Southwest Research Institute.Pero el poder ver la estructura interna de las capas de hielo nos solo no resolvió nuestras dudas, sino que nos hizo enfrentarnos a nuevas preguntas… y es que la condensación de dióxido de carbono atmosférico que da lugar a los hielos que se acumulan en los polos va depositando capas muy finas, algo parecido a nuestras escarchas invernales, relacionada además con los ciclos climáticos de Marte, que dependen en gran medida de la inclinación de su eje con respecto al Sol: cuanto menos esté inclinado, menor insolación llegará a los polos y, por lo tanto, el clima será lo suficientemente frío como para favorecer las acumulaciones de dióxido de carbono.
Aun así, en primavera y verano el aumento de las temperaturas podría provocar la sublimación de las capas de hielo más superficiales, haciendo que la acumulación de este hielo de dióxido de carbono fuese muy lenta incluso en largos periodos de tiempo. Entonces, ¿qué provoca esos grandes espesores que vemos en las capas de hielo de dióxido de carbono y la forma de las acumulaciones? Un estudio publicado el pasado mes de abril intenta resolver estas cuestiones aplicando nuestro conocimiento de los glaciares en la Tierra, adaptando los modelos que usamos hoy día para estudiar el movimiento glacial y adaptándolo a las observaciones realizadas en Marte y a sus condiciones de gravedad, tipos de hielo y clima.
Los resultados indican que los depósitos de hielo de dióxido de carbono se habrían formado por la existencia de glaciares de este compuesto, capaces de moverse por la superficie a una velocidad de unas cien veces superior a la que lo hace el hielo de agua en el planeta Marte.
 Erosión provocada por la sublimación del hielo de dióxido de carbono en el casquete polar del hemisferio sur de Marte. Imagen cortesía de NASA/JPL-Caltech/UArizona.
Erosión provocada por la sublimación del hielo de dióxido de carbono en el casquete polar del hemisferio sur de Marte. Imagen cortesía de NASA/JPL-Caltech/UArizona.Esto permite al hielo de dióxido de carbono avanzar y e ir cayendo sobre depresiones donde lentamente va acumulándose y formando estos espesores que observamos, como una enorme pero lenta cascada de hielo, al mismo tiempo evitando que en primavera y verano se sublime la mayor parte.
De hecho, muchas de las morfologías glaciares que vemos en el casquete de hielo del polo sur en realidad están formadas por los hielos de dióxido de carbono, mientras que los hielos de agua prácticamente podríamos decir que se encuentran en una situación estática en comparación con la dinámica de estos hielos.
Es cierto que este tipo de hielo nos puede parecer exótico, pero no podemos olvidar que, además del hielo de agua, en el Sistema Solar hay un tercer tipo, el de nitrógeno, que se descubrió en Plutón. Y es importante que sigamos estudiando los hielos, por su papel en el modelado del paisaje, pero también porque nos cuentan una apasionante historia de ciclos climáticos de otros planetas que quizás en algún futuro seremos capaces de descifrar.
Referencias:
Smith, I. B., Schlegel, N.-J., Larour, E., Isola, I., Buhler, P. B., Putzig, N. E., & Greve, R. (2022). Carbon dioxide ice glaciers at the south pole of Mars. Journal of Geophysical Research: Planets, 127, e2022JE007193. 10.1029/2022JE007193
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo De casquetes polares y hielo de dióxido de carbono se ha escrito en Cuaderno de Cultura Científica.
Somos simios caros
 Foto: Sasha Freemind / Unsplash
Foto: Sasha Freemind / UnsplashEs cosa sabida que los seres humanos tenemos un encéfalo comparativamente más grande que el del resto de los mamíferos, y también que el de los grandes simios -bonobos, chimpancés, gorilas y orangutanes- que son nuestros parientes evolutivos más próximos. En parte por esa razón y en parte por su elevado nivel de actividad metabólica, nuestro encéfalo resulta ser un órgano caro. Consume del orden del 20% de la energía que gastamos en condiciones de mínima actividad física.
No solo gastamos más en tejido nervioso. En poblaciones en las que no se ejerce control artificial alguno sobre la reproducción, los seres humanos tienen más crías y las tienen de mayor tamaño que las de cualquiera de los demás homínidos. También vivimos más años, bastantes más de los que cabría esperar de un mamífero de unos 60 kg de masa; para vivir más hace falta dedicar más recursos energéticos al mantenimiento y reparación de los tejidos.
Nuestro sistema digestivo, gracias al consumo de alimentos de digestión más fácil -carne y productos cocinados, principalmente- se ha reducido mucho con relación al de nuestros ancestros, y gasta por ello mucha menos energía. Además, nos desplazamos de forma más eficiente que esos otros homínidos. Pero esos factores no tienen un efecto de la entidad suficiente como para compensar las consecuencias de poseer un encéfalo cuyo gasto se ha elevado tanto, así como de los costes asociados a una mayor intensidad reproductiva y una longevidad más prolongada.
El metabolismo es el conjunto de procesos químicos que sustentan las actividades que desarrolla un ser vivo. Por tanto, el gasto metabólico total es el que resulta de agregar el correspondiente a cada una de esas actividades. Están, por un lado, aquellas cuya finalidad es el mantenimiento de los sistemas vitales; a estas corresponde un nivel de actividad metabólica que denominamos basal. Viene a ser el mínimo nivel metabólico necesario para mantenernos con vida. Tenemos, por otro lado, las implicadas en la defensa frente a patógenos, las que lleva a cabo el sistema inmunitario; cuantas más enfermedades infecciosas se sufren, más energía hay que gastar para combatirlas. Otras sirven para hacer reparaciones. Están también el crecimiento y la reproducción, actividades que comportan la producción de nuevos tejidos y que son, por ello, bastante costosas, muy especialmente para las madres. Y tenemos, por último, las que implican una cierta acción sobre el entorno, como son el desplazamiento o el trabajo.
Cuando se compara el gasto metabólico diario total de las diferentes especies de homínidos, se observa que la nuestra es la que, para un ejemplar de la misma masa (sustraída la grasa corporal), experimenta un mayor gasto de energía. Y ello se debe a que el metabolismo basal de órganos y tejidos es, en general, más elevado (encéfalo, sistema digestivo e hígado son órganos con un gasto comparativamente alto) que el de otros homínidos. Y también, aunque en una medida menor, a que somos más activos que los miembros de esas especies.
Los individuos de nuestra especie gastamos más energía que nuestros parientes evolutivos más próximos para mantenernos con vida, crecer y reproducirnos. También somos más activos, en parte para conseguir la energía que necesitamos para afrontar ese mayor gasto. Y esto explica un dato poco conocido: los seres humanos almacenan, especialmente las mujeres, mucha más grasa que los demás simios. Es lógico que así sea; al gastar tanto, conviene dotarse de reservas abundantes porque, antes o después, vendrán mal dadas y cuando eso ocurra serán necesarias para sobrevivir. Y esto explica en parte que, una vez almacenada esa grasa, sea tan difícil deshacerse de ella.
Fuente: Pontzer, H., Brown, M., Raichlen, D. et al. Metabolic acceleration and the evolution of human brain size and life history. Nature 533, 390–392 (2016).
Para saber más:
La estufa interior
Las actividades animales
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Somos simios caros se ha escrito en Cuaderno de Cultura Científica.
CienciaClip 2021 – Cristalizaciones: cómo hacer el mejor cristal

Ciencia Clip es un concurso de vídeos divulgativos de ciencia diseñados, producidos y protagonizados por estudiantes de Educación Secundaria.
El objetivo del concurso es fomentar el interés por la ciencia y la tecnología. Y ofrecer a los concursantes una oportunidad para ejercitar su creatividad y habilidades comunicativas usando herramientas que proporciona internet.
Ciencia Clip es una iniciativa de la Cátedra de Cultura Científica de la UPV/EHU y en la que colaboran Euskampus Fundazioa, Naukas, Scenio y Big Van.
Los ganadores de la edición 2022 ya están en la página web del concurso. La entrega premios y el anuncio del vídeo ganador del premio especial se realizarán durante el evento Naukas Bilbao. En la edición de 2021 resultó ganador en la categoría de 1º y 2º de Bachillerato Marina Faura, de Madrid, con este vídeo:
Edición realizada por César Tomé López
El artículo CienciaClip 2021 – Cristalizaciones: cómo hacer el mejor cristal se ha escrito en Cuaderno de Cultura Científica.
Lo que los sedimentos de hace 56 millones de años nos dicen del cambio climático
El Departamento de Geología de la UPV/EHU ha investigado sedimentos de hace 56 millones de años en la cuenca de Tremp-Graus (en el límite entre Lérida y Huesca). Del estudio se deduce que el calentamiento global de entonces tuvo tres fases en las que la distribución de las precipitaciones fue diferente. Los datos del estudio pueden servir para ajustar los modelos matemáticos utilizados para predecir los efectos del cambio climático actual.

Hace 56 millones de años se produjeron grandes emisiones de carbono a la atmósfera y a los océanos, lo que provocó un fuerte calentamiento global, denominado Máximo Térmico del Paleoceno-Eoceno, y es considerado un análogo antiguo del actual calentamiento antropogénico. “A pesar de que el origen o la causa del calentamiento de aquella época era diferente, el proceso fue muy similar al calentamiento global actual. Se sabe que el clima se calentó, pero con un cambio climático pueden darse otras alteraciones aparte del calentamiento. En concreto, hemos querido analizar cómo cambiaron entonces las condiciones hidroclimáticas en cuanto a precipitaciones”, ha señalado Aitor Payros, primer autor del estudio.
El Departamento de Geología de la UPV/EHU ha investigado los cambios aluviales e hidroclimáticos en latitudes medias registrados en la cuenca de Tremp-Graus (en el límite entre Lérida y Huesca) durante el Máximo Térmico del Paleoceno-Eoceno, y ha llegado a la conclusión de que lo que entonces ocurrió podría ser algo similar a lo que ya está sucediendo en la actualidad en el sudeste de la península ibérica. Para ello, han recopilado datos históricos de la región, y han encontrado similitudes tanto geográficas como hidroclimáticas.
Según Aitor Payros, “hemos visto que el calentamiento global modificó la distribución estacional de las precipitaciones y que además se modificó en varias fases. Al principio, las precipitaciones se concentraron en unos pocos meses, en torno al otoño; posteriormente, se distribuyeron de forma más homogénea a lo largo del año. Y, sin embargo, la última fase tendió a una mayor sequía”. En opinión de Payros, “no podemos decir que el calentamiento global provoca un aumento de las temperaturas o que las precipitaciones son más fuertes, simplemente. Las cosas no son tan simples. Se producen cambios, pero estos no se mantienen durante todo el periodo de calentamiento global. Dentro del calentamiento global pueden existir varias fases”.
Mirar al pasado para predecir el futuro“Hemos observado que al inicio de aquel calentamiento global se produjo un aumento de los contrastes estacionales en cuanto a las precipitaciones. Es decir, las precipitaciones se concentraban en torno al otoño (con frecuentes tormentas e inundaciones de gran magnitud) y en el resto de los meses se registraban periodos de sequía. Y eso es precisamente lo que está sucediendo en las últimas décadas, y en el último siglo, en el sudeste de la península ibérica: las lluvias intensas son cada vez más frecuentes en torno al otoño y al final del verano, y eso no ocurría hace 100 o 200 años”, explica Payros.
El investigador señala que no se puede saber qué es lo que ocurrirá en el futuro en el sudeste de la península ibérica, “pero si suponemos que la Tierra responde de forma similar a los mismos fenómenos o similares, podríamos pensar que en el futuro la distribución anual de las precipitaciones podría ser más homogénea en el sudeste peninsular o en otras regiones de clima similar”.
Payros reivindica el valor que puede tener el estudio de los paleoclimas: “Nosotros vemos lo que ocurrió hace millones de años. Y si aquello que ocurrió se repite una y otra vez, es decir, si la Tierra responde siempre de la misma manera a ciertos fenómenos, podemos pensar que en el futuro también seguirá funcionando de la misma manera”. Este tipo de investigaciones pueden servir para hacer previsiones de futuro: “Cuando los modelos informáticos o matemáticos utilizados para predecir el clima sean capaces de reproducir los fenómenos que tuvieron lugar durante los antiguos calentamientos globales, entonces serán capaces de prever los cambios que se producirán en el futuro. Dichos modelos informáticos y matemáticos pueden ajustarse con nuestros datos”.
Referencia:
Aitor Payros, Victoriano Pujalte, Birger Schmitz (2022) Mid-latitude alluvial and hydroclimatic changes during the Paleocene– Eocene Thermal Maximum as recorded in the Tremp-Graus Basin, Spain Sedimentary Geology doi: 10.1016/j.sedgeo.2022.106155
Para saber más:
Los misterios que rodean al máximo térmico de hace 56 millones de años
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Lo que los sedimentos de hace 56 millones de años nos dicen del cambio climático se ha escrito en Cuaderno de Cultura Científica.
El rugido de las rocas costeras
En Geología también tenemos nuestros bufones particulares. Y no me estoy refiriendo a que haya profesionales de las Ciencias de la Tierra que se dediquen con ahínco a hacer bromas para echarnos unas risas de vez en cuando, aunque generalmente tenemos buen humor y acabamos buscando la cara divertida y sarcástica de los fósiles, rocas o estructuras con las que estemos trabajando. Me estoy refiriendo a otra acepción de la palabra bufón, a una muy geológica.
 Bufón de Santiuste, Monumento Natural del litoral de la localidad de Llanes, Asturias.Fuente: turismoasturias.es (CC-by 3.0)
Bufón de Santiuste, Monumento Natural del litoral de la localidad de Llanes, Asturias.Fuente: turismoasturias.es (CC-by 3.0)Si durante este verano habéis pasado unos días de relax en alguna zona litoral, principalmente en el norte de la Península Ibérica, y os habéis lanzado a dar un buen paseo por encima de los acantilados rocosos de estas costas, es posible que os hayáis llevado algún pequeño susto cuando un chorro de aire y agua marina brotando con furia del suelo os haya cortado el camino. Pues eso es un bufón.
Como definición rápida, un bufón es una estructura geológica que se genera en acantilados costeros formados por rocas que son susceptibles de sufrir disolución por la acción del agua, tales como las rocas carbonatadas. Pero no es un proceso sencillo, ya que es necesario que la disolución producida por el agua actúe a dos niveles diferentes: tanto en la parte superficial del terreno como en el interior de las propias rocas del acantilado.
En superficie, el agua de lluvia disuelve las rocas carbonatadas formando unos conductos que se adentran hacia el interior del terreno de forma más o menos vertical, dando lugar a unas estructuras que reciben diversas denominaciones de acuerdo a su tamaño y morfología, como son las simas o las dolinas. Ya en el interior, esta agua subterránea va a circular en dirección al mar, provocando la disolución de las rocas con una orientación próxima a la horizontal, dando lugar así a unas estructuras que conocemos como galerías.
Pero el agua del mar no se va a quedar como una simple espectadora silenciosa en todo este proceso, también va a tomar parte de la magia geológica. Y esto es debido a que la acción continua del oleaje provoca la erosión del acantilado rocoso y el retroceso del litoral, pudiendo llegar a conectar alguna de esas galerías subterráneas directamente con el mar.
Ahora es cuando todas las piezas del puzle encajan, ya que tenemos una sima vertical que está conectada con una galería subterránea que, a su vez, está conectada directamente con el mar. La geología ya ha hecho su trabajo, a partir de aquí entra en juego la física de fluidos.
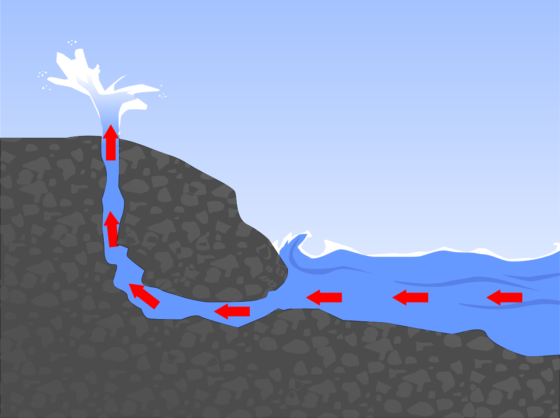 Estructura de un bufón litoral. Fuente: Wikimedia Commons
Estructura de un bufón litoral. Fuente: Wikimedia CommonsCuando se dan ciertas condiciones de oleaje, muchas veces favorecidas por la marea alta, el agua del mar puede penetrar en el interior de los acantilados a través de las galerías subterráneas. Ahí es canalizada y circula a presión por las simas verticales, llegando a salir a superficie como un chorro de espuma, aire y agua vaporizada.
Esta salida a la superficie del agua a presión genera, a su vez, un efecto sonoro muy particular, ya que parece que se produjese un tremendo resoplido o bramido. Es decir, un bufido. Y es precisamente de esta palabra de donde procede el nombre de este proceso geológico.
 Campo de bufones de Arenillas, Monumento Natural del litoral de la localidad de Llanes, Asturias. Fuente: turismoasturias.es (CC-by 3.0)
Campo de bufones de Arenillas, Monumento Natural del litoral de la localidad de Llanes, Asturias. Fuente: turismoasturias.es (CC-by 3.0)Aunque podemos encontrarnos con bufones aislados en ciertas áreas costeras, lo más habitual es que se produzcan varias estructuras más o menos agrupadas en una misma zona, dando lugar a lo que conocemos como campos de bufones. Además, los podemos encontrar de todos los tamaños que podamos imaginarnos, ya que, dependiendo de la longitud vertical y el diámetro de la sima o conducto por el que asciende el agua marina y de la presión de la misma, el chorro expulsado puede alcanzar varios metros de altura.
Esto convierte a los bufones en unas maravillas naturales con una belleza hipnótica, llegando a ser un auténtico espectáculo en momentos de temporal y mar muy picada, pero también se pueden transformar en unas estructuras peligrosas. No es recomendable acercarse mucho al litoral cuando el mar está embravecido, porque la fuerza del oleaje puede provocar que el agua expulsada por los bufones tenga la fuerza suficiente para hacer mucho daño a una persona adulta. Es mejor disfrutar del espectáculo a cierta distancia, por si acaso.
En el vídeo, Peine del Viento, en San Sebastián / Donostia. En primer término se ven y oyen 7 bufones artificiales en acción.
Para saber más:
La geodiversidad que nos rodea
El Peine del Viento de Chillida: materia, forma y lugar
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo El rugido de las rocas costeras se ha escrito en Cuaderno de Cultura Científica.
Maryna Viazovska, la matemática que empaqueta esferas
Profesora en la Cátedra de Teoría de Números en el Instituto de Matemáticas de la Escuela Politécnica Federal de Lausana (EPFL), Maryna Viazovska fue galardonada con la Medalla Fields en julio de 2022. Se premiaba su trabajo sobre el empaquetamiento de esferas: resolvió en 2016 el problema del empaquetamiento en dimensión 8 y, en colaboración con otros investigadores, en dimensión 24.
Los tiranos no pueden impedir que hagamos matemáticas. Al menos hay algo que no nos pueden quitar.
 Maryna Viazovska. Fuente: EPFL/Fred Merz.
Maryna Viazovska. Fuente: EPFL/Fred Merz.
Nacida en Kiev el 2 de diciembre de 1984, Maryna Viazovska es la mayor de tres hermanas en una familia muy cercana a la ciencia: su madre es ingeniera y su padre, químico. Casada con el físico ucraniano Daniil Evtushinsky, el matrimonio tiene un hijo y una hija.
Maryna eligió las matemáticas desde pequeña, se le daban especialmente bien en la escuela. En una de las entrevistas concedidas tras recibir la Medalla Fields, comentaba que era rápida para las matemáticas, pero no tanto para la lengua, aunque le gustaba leer, especialmente libros de ciencia ficción.
En 1998 ingresó en el Liceo de Ciencias Naturales de Kiev no. 145, una institución de enseñanza secundaria especializada en matemáticas, física y computación. Su alumnado se selecciona entre personas destacadas, como Maryna, cuyo rendimiento en matemáticas era superior a la media. Tras graduarse en 2001, ingresó en la Universidad Nacional Taras Shevchenko de Kiev para estudiar matemáticas; allí obtuvo su licenciatura en 2005. Después viajó a Alemania para cursar una maestría en la Universidad Técnica de Kaiserslautern, graduándose en 2007. En mayo de 2010 defendió su tesis de Candidato de Ciencias en el Instituto de Matemáticas de la Academia Nacional de Ciencias de Ucrania.
Después de obtener este título viajó, al Instituto Max Planck de Matemáticas en la Universidad de Bonn, donde realizó la tesis doctoral bajo la supervisión del especialista en teoría de números Don Zagier (1951). Defendida en 2013, esta memoria trataba sobre funciones modulares.
Después de un tiempo como investigadora postdoctoral en el Institut des Hautes Études Scientifiques en Francia, en 2014 Viazovska se mudó a Berlín donde trabajó en la Escuela Matemática de Berlín y la Universidad Humboldt de Berlín.
En enero de 2018 consiguió la cátedra que actualmente ocupa en la EPFL.
El problema de empaquetamiento de esferasLa conjetura de Kepler fue enunciada por Johannes Kepler (1571-1630) en su ensayo Strena seu de nive sexangula de 1611. El astrónomo comenzó a interesarse por los ordenamientos de esferas gracias a su correspondencia con el matemático y astrónomo Thomas Harriot (1560-1621). El marino Walter Raleigh (1552-1618) había planteado a Harriot el problema de encontrar la mejor manera de amontonar balas de cañón en la cubierta de sus barcos. Y Harriot se lo comentó a Kepler, quien conjeturó que la manera óptima de apilarlas era mediante un arreglo piramidal de caras centradas.
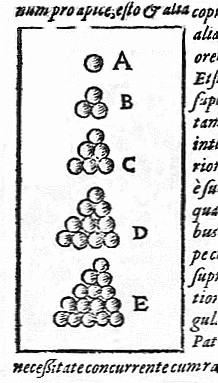 Diagrama de Strena seu de nive sexangula ilustrando la conjetura de Kepler. Fuente: Wikimedia Commons.
Diagrama de Strena seu de nive sexangula ilustrando la conjetura de Kepler. Fuente: Wikimedia Commons.
En la primavera de 2016 Maryna Viazovska anunció que había conseguido resolver un caso particular del problema de empaquetamiento de esferas, que generaliza en cualquier dimensión la conjetura de Kepler. Lo explicaba de esta manera en una entrevista concedida en 2017:
La pregunta es: ¿cuántas bolas de ocho dimensiones caben en un espacio de ocho dimensiones? Es decir, ¿con qué densidad se pueden empaquetar allí? […] En dimensión tres, este es el famoso problema de Kepler formulado ya en 1611. Se resolvió a finales del siglo XX con ayuda de computadoras. Existen innumerables maneras de colocar bolas tridimensionales, incluso con un ordenador es imposible verificar todos los casos. Pero surgió la idea de reducirlo a un cierto cálculo finito, aunque todavía muy largo y complicado. Es una historia bastante dramática. Un matemático anunció la solución, pero luego encontró muchos errores en ella. A principios de la década de 1990, otro científico de China hizo una declaración similar, pero también se encontraron muchos fallos. Y solo Tom Hales, después de pasar varios años, señaló la respuesta correcta en 1998. Se ha prestado una meticulosa atención a este trabajo, se ha revisado durante mucho tiempo, se ha revisado por pares durante cinco años, y se ha debatido si debiera considerarse como una solución matemática porque depende en gran medida de cálculos informáticos. Pero decidieron que todo era correcto. Y, recientemente, Hales también escribió una solución formal que se puede probar usando un programa de ordenador que, de hecho, está diseñado para validar tal evidencia. […] Resulta que hay una especie de atajo en el espacio de ocho dimensiones, por lo que podemos ir por un camino más fácil. En 2003, hubo novedades que indicaban que esto podía probarse. Me las arreglé para terminar este argumento de una manera lógica. Luego, trabajando con colegas, resolvimos el problema en dimensión 24.
En el artículo The sphere packing problem in dimension 8 Viazovska demostraba que el empaquetamiento óptimo de esferas de dimensión 8 era una configuración del espacio de ocho dimensiones denominada retículo E8. Su prueba involucraba una determinada función que Viazovska construía de manera explícita utilizando técnicas de teoría de números (formas modulares y casimodulares) y de análisis de Fourier.
Poco tiempo más tarde, junto a sus colaboradores habituales y el matemático Henry Cohn, resolvió el problema en dimensión 24. En este caso, esa configuración especial es el denominado retículo de Leech, que permite colocar 196 560 esferas de dimensión 24 tangentes a una esfera central. Tras el largo proceso que llevó a Viazovska a resolver el caso en dimensión 8, Cohn se dio cuenta de que la ingeniosa estrategia usada por Maryna podía utilizarse también en dimensión 24: en pocos días, este segundo caso se solucionó.
La medalla Fields llega en 2022La matemática iraní Maryam Mirzakhani (1977-2017) se convirtió en 2014 en la primera mujer en ganar la Medalla Fields, el prestigioso premio que otorga cada cuatro años la Unión Matemática Internacional (IMU) durante el Congreso Internacional de Matemáticos (ICM).
En 2018, Maryna Viazovska era una de las personas candidatas a recibirla, aunque tuvo que esperar otros cuatro años para que ese sueño se cumpliera. Es la segunda mujer que recibe este galardón; en los 86 años de existencia del premio, 62 hombres –aunque Grigori Perelman (1966) rehusó aceptarla en 2006– y dos mujeres han obtenido la Medalla Fields.
El gran mérito de Viazovska reside en haber sabido relacionar disciplinas muy distintas –el análisis de Fourier y la teoría de formas modulares– para descubrir “estructuras muy simples, naturales, profundas, cosas que nadie esperaba y que nadie más había podido encontrar”, como comentaba Henry Cohn en la laudatio que le dedicó durante el ICM para celebrar su trabajo.
La técnica descubierta por Viazovska para resolver el problema de empaquetamiento de esferas está estrechamente vinculada a las dimensiones 8 y 24. Para el resto de las dimensiones (mayores que 3) será necesario buscar nuevos métodos para encontrar esas configuraciones óptimas.
Como la propia Maryna Viazovska comenta, ella es una matemática teórica que desconoce la posible utilidad “práctica” (al margen de las matemáticas) de los objetos con los que trabaja. ¡Cuántas veces le habrán preguntado para qué sirven esas complejas estructuras que manipula!
El topólogo algebraico Jaume Aguadé escribía hace 30 años un hermoso artículo titulado Cien años de E8.; en él habla precisamente de las insólitas aplicaciones que poseen esas matemáticas que centran la investigación de Maryna Viazovska:
[…] ¿Para qué puede servir –se preguntará– empaquetar esferas de dimensión 8? Sirve para llamar por teléfono, para escuchar Mozart en un Compact Disc, para enviar un fax, para ver televisión vía satélite, para conectar, mediante un módem, con una red de ordenadores. Sirve en todos aquellos procesos en que se exija la transmisión eficiente de información digital. La teoría de la información nos enseña que los códigos de transmisión de señales son más fiables en dimensiones elevadas y el retículo de E8, con su sorprendente simetría y dada la existencia de un decodificador apropiado (Conway 1982), es un instrumento fundamental en la teoría de la codificación y transmisión de señales. […]
Referencias
-
Página personal, EPFL
-
Maryna Viazovska, The sphere packing problem in dimension 8, Ann. of Math. 185 (2017), no. 3, 991-1015
-
Henry Cohn, Abhinav Kumar, Stephen D. Miller, Danylo Radchenko and Maryna Viazovska, The sphere packing problem in dimension 24. Ann. of Math. 185 (2017), no. 3,1017-1033
-
Henry Cohn, The work of Maryna Viazovska, ICM 2022
-
Davide Castelvecchi, Ukrainian mathematician becomes second woman to win prestigious Fields Medal, Nature 607 (2022) 224-225
-
Davide Castelvecchi, ‘Mathematics is an unknown land’: meet Fields Medal winner Maryna Viazovska, Nature 607 (2022) 649
-
Thomas Lin and Erica Klarreich, In Times of Scarcity, War and Peace, a Ukrainian Finds the Magic in Math, Quanta Magazine, 5 julio 2022
-
Jaume Aguadé, Cien años de E8, La Vanguardia, 8 junio 1991
-
O’Connor, John J.; Robertson, Edmund F., Maryna Viazovska, MacTutor History of Mathematics archive, University of St Andrews
-
Francisco R. Villatoro, Medallas Fields 2022 para Maryna Viazovska, James Maynard, June Huh y Hugo Duminil-Copin, La ciencia de la mula Francis, 5 julio 2022
-
Wikipedia, Maryna Viazovska
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Maryna Viazovska, la matemática que empaqueta esferas se ha escrito en Cuaderno de Cultura Científica.
Einstein y la equivalencia masa-energía
E = mc2 es la ecuación más famosa del mundo. Dice que la energía es igual a la masa multiplicada por la velocidad de la luz al cuadrado. Pero Einstein no fue el primero en sugerir que existe una relación entre masa y energía. En 1905 los físicos ya sabían que la energía de un electrón le confería “masa electromagnética”. Así, J.J. Thomson en 1893 y Wilhem Wien en 1900 llegaron a la expresión m = (4/3) E/c2; Max Abraham (1902) y Hendrik Lorentz (1904) llegaron a expresiones similares. Einstein sí fue el primero en afirmar que esta equivalencia era una regla general, aplicable a todas las masas y no solo a casos especiales, que la energía puede “transportar” inercia, y que la masa puede “convertirse” en energía.
 A las 05:29 del 16 de julio de 1945 tenía lugar la demostración más terrorífica de la realidad de la equivalencia masa-energía: la detonación de la primera bomba atómica, nombre enclave para el Ejército de los Estados Unidos «Trinity».
A las 05:29 del 16 de julio de 1945 tenía lugar la demostración más terrorífica de la realidad de la equivalencia masa-energía: la detonación de la primera bomba atómica, nombre enclave para el Ejército de los Estados Unidos «Trinity».Einstein descubrió esta conexión a partir de un experimento mental partiendo de las ideas de la teoría especial de la relatividad. En la base de esta teoría está la afirmación de que las leyes de la física deben ser las mismas en cualquier marco de referencia, es decir, tanto si te estás moviendo como si estás quieto. Además, la teoría afirma que esas leyes son las mismas sin importar cómo sean percibidas desde cualquier otro marco de referencia. Einstein calculó que un cuerpo que emitiese luz, que es una forma de energía, al ser observado desde otro marco de referencia parecería estar perdiendo momento lineal. Mirándolo desde este marco de referencia la única explicación para esta pérdida de momento es que estuviese perdiendo masa. Dado que las leyes de la física deben ser iguales para todos los observadores (para todos los marcos de referencia) entonces, si esto es lo que está pasando en un marco de referencia, debe ser lo que está pasando en todos. Debe ser cierto que cuando un cuerpo pierde energía también está perdiendo masa, y la cantidad de masa que pierde está relacionada con la energía emitida por la expresión m = E/c2. Einstein escribió. “La masa de un cuerpo es una medida de su contenido en energía”.
De hecho E = mc2 es la versión simplificada de la ecuación completa, dado que se refiere solamente a la masa en reposo de un objeto, m0, la masa que contiene cuando está en reposo. Cuando un objeto se mueve se añaden términos adicionales y entonces la ecuación completa queda E2= (m0c2)2+ (pc)2, donde p es el momento lineal del objeto. Si el objeto está en reposo pes cero y obtenemos la versión simplificada.
Einstein descubrió la fórmula E = mc2porque las matemáticas le llevaron a ella. La ecuación de equivalencia entre masa y energía surge de forma natural del desarrollo matemático de leyes conocidas de la física. Pero Einstein sabía que su conclusión era asombrosa, y escribió una nota a su amigo Conrad Habitch. “No puedo saber si el querido Dios no se ríe de esto y me ha gastado una broma”. Además no estaba seguro si la idea podría comprobarse experimentalmente alguna vez. En el artículo en el que la daba a conocer sugería que quizás el estudio de la energía emitida durante la desintegración de las sales de radio podría ser una forma de probar su predicción.
La tecnología necesaria para medir con precisión los cambios en masa y energía simplemente no existía en 1905. La primera comprobación experimental de E = mc2no tuvo lugar hasta 1932 y se hizo por un método muy diferente. John Cockcroft y Ernest Walton eran dos físicos que trabajaban en los laboratorios Cavendish de Cambridge (Reino Unido). A principios de los años 30 del siglo pasado construyeron lo que era, en esencia, el primer acelerador de partículas y comenzaron a estudiar las colisiones entre ellas. Lanzaron protones a alta velocidad contra átomos de litio y estudiaron los resultados de la fisión: dos partículas alfa. El litio y el protón iniciales tenían más masa que las partículas alfa, pero éstas se movían mucho más rápido. Usando la última tecnología disponible, Cockcroft y Walton hicieron mediciones precisas y determinaron que la energía de las partículas alfa cuando se sumaba a su masa se correspondía con el valor de la energía más la masa del litio y protón originales. Por lo tanto, si bien la masa no se conservaba, la masa y la energía sí.
Un año después, en París (Francia) en 1933, Irène y Frédéric Joliot-Curie estudiaron el fenómeno en la dirección opuesta, cómo la energía se puede convertir en masa. Ese año, tomaron fotografías de partículas moviéndose a través de una cámara de niebla y demostraron cómo un fotón sin masa pasaba a ser partículas con masa y energía equivalentes a la cantidad de energía del fotón. La masa y la energía eran dos caras de la misma moneda.
Para saber más:
Gustave le Bon y la equivalencia masa-energía
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Una versión anterior de este artículo se publicó en Experientia Docet el 11 de julio de 2010.
El artículo Einstein y la equivalencia masa-energía se ha escrito en Cuaderno de Cultura Científica.
La evolución en mosaico de «Homo sapiens»
El estudio del genoma de nuestros parientes más cercanos, los neandertales y los denisovanos, ha abierto nuevas vías de investigación para comprender mejor nuestra historia evolutiva. Un estudio liderado por la Universidad de Barcelona ha estimado cuándo surgieron algunas de las variantes genéticas que caracterizan a nuestra especie a partir del análisis de mutaciones que son muy frecuentes en las poblaciones humanas modernas, pero no en estas otras especies de humanos arcaicos. Los resultados aportan nuevos indicios de la evolución en mosaico para nuestra especie. Además, muestran dos momentos en los que se concentran las mutaciones: uno temprano, de hace alrededor de 40.000 años, asociado al crecimiento de la población de Homo sapiens y su salida de África, y otro más antiguo, de hace más de 100.000 años, relacionado con la etapa en la que más tipos de Homo sapiens había en África.
«La comprensión de la historia profunda de nuestra especie es cada vez más completa. Aun así, es difícil determinar cuándo surgieron las variantes genéticas que nos distinguen de otras especies humanas. En este estudio hemos colocado variantes específicas de nuestra especie en una línea cronológica. Así, hemos descubierto de qué manera se concentran estas variantes en el tiempo, lo que ha reflejado eventos como el punto de divergencia del Homo sapiens respecto a otras especies humanas hace cerca de 100.000 años», explica Alejandro Andirkó, primer autor de este artículo, que ha surgido de su tesis doctoral en la UB.
 Imagen: Rob Mulally / UnsplashPredominio de variaciones relacionadas con la conducta y la anatomía facial
Imagen: Rob Mulally / UnsplashPredominio de variaciones relacionadas con la conducta y la anatomía facial
Los resultados de la investigación también muestran diferencias entre periodos evolutivos. En concreto, han constatado el predominio de variaciones genéticas relacionadas con la conducta y la estructura anatómica facial —características clave en la diferenciación de nuestra especie respecto al resto de las humanas— hace más de 300.000 años, una datación que coincide con la evidencia fósil y arqueológica disponible. «Hemos descubierto conjuntos de variantes genéticas que afectarían a la evolución de la cara y que hemos datado entre los 300.000 y los 500.000 años, justo el período anterior a la datación de los fósiles más tempranos de nuestra especie, como los descubiertos en el yacimiento arqueológico de Jebel Irhoud, en Marruecos», destaca Alejandro Andirkó.
Los investigadores también han analizado las variantes relacionadas con el cerebro, al que consideran el órgano que mejor puede ayudar a explicar las características clave del rico repertorio de comportamientos asociados con el Homo sapiens. En concreto, han datado variantes que se han relacionado con el volumen cerebral del cerebelo, el cuerpo calloso y otras estructuras en estudios médicos con humanos actuales. «Hemos descubierto que los tejidos cerebrales tienen un perfil de expresión genómica particular en distintos momentos de nuestra historia; es decir, ciertos genes relacionados con el desarrollo neuronal se expresaban más en ciertos momentos», resalta el investigador.
Reforzada la hipótesis de la evolución en mosaicoEstos resultados se complementan con una idea que es dominante en la antropología evolutiva hoy en día: que la historia de las especies humanas no es lineal, sino que distintas ramas de nuestro árbol evolutivo convivieron y muchas veces se cruzaron. «La amplitud del rango de diversidad de humanos en el pasado ha sorprendido a los antropólogos. Incluso dentro de los Homo sapiens existen fósiles, como los que he comentado antes de Jebel Irhoud, que debido a sus rasgos se llegó a pensar que pertenecían a otra especie. Por eso decimos que el ser humano ha vivido una evolución en mosaico», detalla Andirkó.
«Nuestros resultados —continúa el investigador— ofrecen una imagen de cómo cambió nuestra genética que se ajusta a esa idea, ya que no hemos encontrado evidencia de cambios evolutivos que dependieran de una mutación clave o de un puñado de ellas», subraya.
La metodología para llevar a cabo este estudio se ha basado en un método de estimación genealógica de edad de variantes (genealogical estimation of variant age) desarrollado por investigadores de la Universidad de Oxford. A partir de esta estimación, se ha aplicado una herramienta de aprendizaje automático para predecir qué genes han cambiado más en ciertos períodos y en qué tejidos estos genes pueden haber tenido un impacto mayor. En concreto, han utilizado ExPecto, una herramienta de aprendizaje profundo que usa una red convolucional —un tipo de modelo computacional— para predecir niveles de expresión de un gen y su función desde una secuencia de ADN.
«Como no existen datos sobre la expresión genómica de variantes en el pasado, esta herramienta es una aproximación a un problema que no se había podido responder hasta ahora. Aunque la predicción por aprendizaje automático es cada vez más común en el mundo clínico, que sepamos, no se había intentado usar para predecir las consecuencias de cambios genómicos a lo largo del tiempo», subraya Andirkó.
La importancia de la fase perinatal en el desarrollo del cerebro de nuestra especieEn un estudio previo, el mismo equipo de la UB, junto con el investigador Raül Gómez Buisán, también había utilizado la información genómica de los humanos arcaicos. Se trata de una investigación en la que analizaron los desiertos genómicos, regiones del genoma de nuestra especie donde no hay fragmentos genéticos de neandertales o denisovanos, y que, además, han sido sometidas a presión positiva en nuestra especie, es decir, que han acumulado más mutaciones de lo esperado por evolución neutral. Los investigadores estudiaron la expresión de genes —qué proteínas codifican para llevar a cabo diferentes funciones— hallados en estas regiones desérticas a lo largo del desarrollo del cerebro, desde fases prenatales hasta la etapa adulta, y cubriendo dieciséis estructuras cerebrales. Los resultados mostraron diferencias en la expresión génica del cerebelo, el cuerpo estriado y el tálamo. «Estos resultados ponen el foco en la relevancia de estructuras del cerebro más allá de la neocorteza, la cual ha sido tradicionalmente predominante en la investigación de la evolución del cerebro humano», explica Juan Moriano.
Además, las diferencias más notorias entre estructuras cerebrales se encontraron en las etapas prenatales. «Estas conclusiones suman nuevos indicios a la hipótesis de una trayectoria del desarrollo del cerebro específico de nuestra especie que tiene lugar en etapas perinatales —el período que comprende desde la semana 22 de gestación hasta las primeras cuatro semanas de vida neonatal—, lo que daría lugar a una forma más globular de la cabeza en los humanos modernos, en contraste con la forma más alargada en neandertales», concluye Juan Moriano.
Referencia:
Andirkó, A.; Moriano, J.; Vitriolo, A.; Kuhlwilm, M.; Testa, G., y Boeckx, C. (2022) Temporal mapping of derived high-frequency variants supports the mosaic nature of the evolution of Homo sapiens Scientific Reports doi: 10.1038/s41598-022-13589-0
Para saber más:
¿Qué factores han impulsado la evolución cognitiva en el linaje humano?
Edición realizada por César Tomé López a partir de materiales suministrados por la Universidad de Barcelona
El artículo La evolución en mosaico de «Homo sapiens» se ha escrito en Cuaderno de Cultura Científica.
Qué es y qué no es inteligencia artificial
Victor Etxebarria Ecenarro
 Detalle de «Ragazza de Trieste» de Joseph Ayerle. Muestra la imagen del rostro de la actriz Ornella Mutti tratada por una «inteligencia artificial» que ha sido entrenada para reproducir el estilo y las técnicas pictóricas que empleó Rafaello Sanzio (Rafael) (1483-1520) en su obra «La Fornarina» (1518/19). Fuente: Wikimedia Commons
Detalle de «Ragazza de Trieste» de Joseph Ayerle. Muestra la imagen del rostro de la actriz Ornella Mutti tratada por una «inteligencia artificial» que ha sido entrenada para reproducir el estilo y las técnicas pictóricas que empleó Rafaello Sanzio (Rafael) (1483-1520) en su obra «La Fornarina» (1518/19). Fuente: Wikimedia CommonsEn los últimos años el término inteligencia artificial y todo lo que tiene que ver con ello está adquiriendo un gran protagonismo y sobredimensionamiento. La expresión inteligencia artificial está siendo abusada y utilizada de forma básicamente incorrecta diariamente y en múltiples ámbitos cotidianos, desde el político al empresarial.
¿Existen realmente máquinas inteligentes, similares a las personas? Si respondemos a esta pregunta con cierto rigor, desde las bases de las ciencias fundamentales que soportan los pilares de este área –matemáticas y física–, la respuesta es que no. Y muchos científicos conjeturan y argumentan seriamente que probablemente nunca existirán.
Computar no es lo mismo que pensarPartamos de las áreas de conocimiento adyacentes a las matemáticas y la física que se expandieron desde los años 30 y 40 del siglo XX, como la ciencia de la computación, la electrónica, la automática o el propio área de inteligencia artificial. En el año 1937 vieron la luz dos publicaciones científicas de enorme importancia: la primera, Sobre los números computables, con una aplicación al Entscheidungsproblem del matemático Alan Turing, y la segunda, Análisis simbólico de relés y circuitos de conmutación, del matemático e ingeniero electrónico Claude Shannon. Estos trabajos fundaron la forma inicial de crear máquinas electrónicas capaces de computar, manejar información y manipular símbolos mediante programación algorítmica.Sin embargo, la inteligencia artificial, entendida como aquella que pretende replicar capacidades intelectuales similares a animales o personas (llamada inteligencia general o inteligencia fuerte) no se ha demostrado en absoluto. Esto es: no hay evidencia ni matemática, ni física, ni se conoce la existencia de ningún prototipo equivalente a las capacidades pensantes de un cerebro humano.
Decisión vs. elección
En 1966 el matemático y profesor de Ciencias de la Computación en el Instituto Tecnológico de Massachusetts (MIT) Joseph Weizenbaum creó en su laboratorio un programa llamado ELIZA capaz de realizar procesamiento de lenguaje natural.
Esta sencilla herramienta reconocía palabras clave en las frases del usuario para elegir una frase modelo de su base de datos con la que contestar.
ELIZA era capaz de entablar una conversación con seres humanos simulando a una psicóloga empática. Weizenbaum modeló su estilo de conversación como preguntas abiertas para animar a los pacientes a comunicarse más eficazmente con la terapeuta, y le sorprendió que su programa fuera tomado en serio por muchos usuarios.
A la vista de que gran número de admiradores consideraron el programa como verdadero precursor de las máquinas pensantes, el propio autor se vio obligado a dejar claro que consideraba esta interpretación totalmente errónea e intentó vehementemente corregir en sus intervenciones posteriores estas ideas.
Entre otros muchos escritos, Weizenbaum publicó en 1976 el libro El poder informático y la razón humana: del juicio al cálculo. Con él trataba de explicar al público en general su trabajo y sus consecuencias desde la filosofía de la ciencia, sin incluir turbadoras fórmulas matemáticas en el texto.
En el libro, el autor distingue entre las capacidades de los computadores y el razonamiento humano, y establece una distinción crucial entre decidir y elegir. Lo mismo que en la automática la decisión y control de un proceso industrial se implementa con un circuito o un computador como controlador programado de dicho proceso, Weizenbaum explica que decidir es una actividad computacional, algo que en última instancia puede programarse y, sin embargo, la elección es el producto del juicio, no del cálculo.
El papel de la mecánica cuánticaEn 1989, el físico, matemático y Premio Nobel en el año 2020 Roger Penrose publicó su influyente libro La nueva mente del emperador en el que demuestra que el pensamiento humano no es básicamente algorítmico.
A caballo entre las matemáticas, la filosofía de la ciencia y la física, el texto incorpora tanto demostraciones matemáticas como ilustradas discusiones de los famosos exámenes de inteligencia (como el test de Turing y el experimento de la habitación china). Además conjetura la posible necesidad de las leyes de la mecánica cuántica para poder explicar correctamente nuestras mentes.
La obra fue devastadora para la tradicional inteligencia artificial fuerte. Inspiró contestaciones de múltiples autores en diversas áreas de conocimiento, pero sus tesis no pudieron ser refutadas convincentemente.
Penrose avanzó aún más en sus ideas con el segundo de sus libros sobre la conciencia humana, publicado en 1994: Las sombras de la mente. En él incluye una propuesta detallada sobre cómo podrían implementarse esos procesos cuánticos en el cerebro.
Las nuevas conjeturas, en colaboración con la biología y la neurociencia médica sugeridas por Penrose, incluyen en particular el citoesqueleto de las neuronas. En concreto los microtúbulos, importantes componentes del citoesqueleto, son lugares plausibles para el procesamiento cuántico y, en última instancia, para la conciencia.
Estas ideas pueden perfectamente ser incorrectas, tal y como el propio Penrose argumenta. Muchos investigadores multidisciplinares en estos campos intentaron refutar parte de estas propuestas, pero actualmente siguen en vigor.
Sin inteligencia artificial a la vistaDesde un punto de vista global, sabemos que se han estudiado múltiples enfoques desde hace décadas para tratar de expandir la inteligencia artificial. Las redes neuronales, los sistemas expertos, la lógica fuzzy y en los últimos tiempos el deep learning y el big data han dado lugar a útiles herramientas para resolver problemas con fines específicos.
Estas herramientas pueden ser impresionantes, pero debemos tener muy claro que no nos hemos acercado al desarrollo de la inteligencia artificial general. La llamada inteligencia débil (o inteligencia estrecha) corresponde con las aplicaciones que hoy tenemos, pero las afirmaciones exageradas sobre sus éxitos, de hecho, dañan la reputación de la inteligencia artificial como ciencia.
En más de ochenta años de investigación en este área no se ha producido ninguna prueba firme de niveles humanos de inteligencia artificial general. Sabemos que los circuitos artificiales son incapaces de modelar los sistemas nerviosos incluso de los invertebrados más simples. Aún con computadores muy rápidos y con enormes bases de datos, confiar en que el razonamiento, la inteligencia y la conciencia surjan de alguna manera simplemente aumentando más y más la complejidad no parece más que un camino sin salida.
Las herramientas informáticas son muy útiles, pero aunque una máquina gane a los ajedrecistas profesionales o sea capaz de proponer un recurso legal buscando jurisprudencia en su gran base de datos, no es una máquina pensante. Es importante no banalizar, diferenciar entre herramientas tecnológicas y entes inteligentes, así como dejar a la ciencia seguir trabajando con rigor en esta apasionante materia.![]()
Sobre el autor: Victor Etxebarria Ecenarro es Catedrático de Ingeniería de Sistemas y Automática en la Universidad del País Vasco (UPV/EHU)
Este artículo fue publicado originalmente en The Conversation. Artículo original.
Para saber más:
Máquinas inteligentes (II): Inteligencia artificial y robótica
En el control de la inteligencia artificial nos jugamos el futuro
El séptimo ángel
El artículo Qué es y qué no es inteligencia artificial se ha escrito en Cuaderno de Cultura Científica.
CienciaClip 2021 – ¿Qué pasaría si el permafrost se derritiera en 24h?

Ciencia Clip es un concurso de vídeos divulgativos de ciencia diseñados, producidos y protagonizados por estudiantes de Educación Secundaria.
El objetivo del concurso es fomentar el interés por la ciencia y la tecnología. Y ofrecer a los concursantes una oportunidad para ejercitar su creatividad y habilidades comunicativas usando herramientas que proporciona internet.
Ciencia Clip es una iniciativa de la Cátedra de Cultura Científica de la UPV/EHU y en la que colaboran Euskampus Fundazioa, Naukas, Scenio y Big Van.
Los ganadores de la edición 2022 se anunciarán en la página web del concurso a principios de septiembre. La entrega premios y el anuncio del vídeo ganador del premio especial se realizarán durante el evento Naukas Bilbao. En la edición de 2021 resultó ganador en la categoría de 3º y 4º de la ESO Irene León, de Barcelona, con este vídeo:
Edición realizada por César Tomé López
El artículo CienciaClip 2021 – ¿Qué pasaría si el permafrost se derritiera en 24h? se ha escrito en Cuaderno de Cultura Científica.
Redes neuronales convolucionales para optimizar aerogeneradores
Una investigación de la Escuela de Ingeniería de Vitoria-Gasteiz de la UPV/EHU ha empleado redes neuronales convolucionales para predecir características del flujo de aire en los perfiles aerodinámicos de aerogeneradores de gran potencia, y ha demostrado que los dispositivos de control de flujo pueden ser estudiados mediante estas redes neuronales, con errores aceptables y una reducción del tiempo computacional en cuatro órdenes de magnitud.
 Detalle de una turbina eólica del parque eólico Badaia, en Álava. Fuente: Wikimedia Commons
Detalle de una turbina eólica del parque eólico Badaia, en Álava. Fuente: Wikimedia CommonsLa energía eólica se ha convertido en una importante fuente de generación de electricidad dentro de un modelo energético más limpio y sostenible. Sin embargo, es necesario mejorar el rendimiento de los aerogeneradores para poder competir con los recursos energéticos convencionales. Para contribuir esta mejora se implementan dispositivos de control de flujo en los perfiles aerodinámicos, con objeto de incrementar la eficiencia aerodinámica de los rotores de los aerogeneradores: “Así, con el mismo aerogenerador se pueden producir más megavatios, el coste del megavatio hora se reduce, y eso trasladado, por ejemplo, a una turbina eólica situada en el mar (que son enormes), resulta que el coste de implementación es ínfimo, pero la mejora aerodinámica puede rondar hasta el 8 o 10%”, explica Unai Fernández Gámiz, profesor del Departamento de Ingeniería Nuclear y Mecánica de Fluidos de la UPV/EHU.
Las simulaciones de dinámica de fluidos computacional (CFD, de su nombre en inglés) son el método más popular utilizado para analizar este tipo de dispositivos: “Se trata de un software que simula el movimiento de los fluidos, que necesita una gran capacidad computacional, es decir, computadores muy potentes y mucho tiempo de computación”, explica Fernández Gámiz.
En los últimos años, con el crecimiento de la Inteligencia Artificial, la predicción de las características del flujo mediante redes neuronales es cada vez más popular; en esta línea, el alumno de la UPV/EHU Koldo Portal Porras ha desarrollado una red neuronal convolucional (CNN, de su nombre en inglés) que determina una serie de parámetros utilizados para el control de flujo de las turbinas eólicas. Los resultados se han publicado en Scientific Reports. Estos resultados muestran que la CNN es capaz de predecir con precisión las principales características del flujo alrededor del dispositivo, con errores muy tolerables, incluidos los coeficientes aerodinámicos, tanto los valores como su tendencia.
“En comparación con las simulaciones CFD, el uso de las CNNs reduce el tiempo computacional en cuatro órdenes de magnitud”, afirma el investigador Portal Porras. “Se han conseguido resultados rápidos, casi inmediatos, con un error de entre un 5 o un 6 %, en algunos casos. Un error bastante asumible para una industria que busca fundamentalmente resultados rápidos”, añade Fernández Gámiz.
 Comparativa de los resultados obtenidos por CFD y CNN. Fuente: UPV/EHU
Comparativa de los resultados obtenidos por CFD y CNN. Fuente: UPV/EHU“Primero hemos lanzado las simulaciones en CFD con dos dispositivos de control de flujo diferentes (microtabs rotativos y Gurney flaps), y de ahí obtenemos los datos de salida, que tomamos como reales y que utilizamos para entrenar la red neuronal convolucional —explica Portal Porras—. Lo que hacemos es meter como entrada la geometría y como salida los resultados obtenidos con CFD. De esta manera la red se entrena, y después si le metemos otra geometría, con los resultados que tenía anteriores, es capaz de predecir los nuevos campos de velocidad y de presión”.
En opinión de Fernández Gámiz, Portal Porras ha conseguido “una herramienta rápida, flexible y barata. Para aplicar este tipo de redes realmente no se necesita grandes ordenadores, ni clústeres informáticos, etc. Y, además, hemos conseguido una herramienta flexible, porque es aplicable a cualquier perfil aerodinámico, a todo tipo de sistemas de dispositivos e incluso a otro tipo de geometrías”.
Portal Porras afirma que la red sirve para todo tipo de aerogeneradores, “pero los datos de entrenamiento que hemos metido eran de un perfil aerodinámico concreto. Por tanto, si metes otro perfil aerodinámico habría que hacer todo el proceso de entrenamiento, o sea, meter los datos de entrada y salida del otro aerogenerador”.
Ambos investigadores coinciden en la importancia de la inteligencia artificial: “Es un paso fundamental si queremos que nuestro entorno industrial sea competitivo. Si no entramos en temas de inteligencia artificial, no vamos a avanzar en competitividad en los mercados internacionales”.
Referencia:
Koldo Portal Porras, Unai Fernández Gámiz, Ekaitz Zulueta, Alejandro Ballesteros Coll, Asier Zulueta (2022) CNN based flow control device modelling on aerodynamic airfoils Scientific Reports doi: 10.1038/s41598-022-12157-w
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Redes neuronales convolucionales para optimizar aerogeneradores se ha escrito en Cuaderno de Cultura Científica.
Simulación experimental de una teoría gauge distinta del electromagnetismo
En la física actual, nuestra comprensión del mundo se basa en las teorías de gauge: modelos matemáticos de la física teórica que describen las interacciones entre las partículas elementales (como los electrones o los quarks) y explican de forma cuántica tres de las fuerzas fundamentales de la naturaleza: electromagnética, débil y fuerte. La cuarta, la gravedad, se describe con la teoría de la relatividad general de Einstein, que es una teoría de gauge clásica ya que aún no disponemos de otra que unifique la mecánica cuántica con la gravedad.
Las teorías gauge pueden utilizarse asimismo para explicar el comportamiento exótico de los electrones en ciertos materiales cuánticos, o los códigos de corrección de errores que necesitarán los futuros ordenadores cuánticos para funcionar de forma fiable. Por ello, estas teorías son esenciales para entender la física moderna.
Para comprenderlas mejor, una posibilidad es utilizar sistemas cuánticos. Esta estrategia recibe el nombre de simulación cuántica y constituye un tipo especial de computación cuántica. Fue propuesta por primera vez por el físico estadounidense Richard Feynman en los años 80, más de quince años después de recibir el Premio Nobel de Física por su trabajo teórico sobre las teorías de gauge.
La simulación cuántica puede entenderse como un juego de LEGO cuántico en el que los físicos experimentales dan realidad a modelos teóricos abstractos. Los construyen en el laboratorio ‘pieza cuántica a pieza cuántica’, utilizando para ello sistemas cuánticos muy bien controlados, como átomos o iones ultrafríos.
Tras montar un prototipo de este “juego” cuántico para un modelo concreto, los investigadores pueden medir con gran precisión sus propiedades en el laboratorio y utilizar sus resultados para comprender mejor la teoría que imita. Durante la última década, este tipo de simulación se ha explotado intensamente para investigar materiales cuánticos.
Sin embargo, “jugar” al LEGO cuántico con las teorías gauge es fundamentalmente más difícil, y hasta ahora sólo se había logrado investigar de ese modo la fuerza electromagnética.
Pero ahora, investigadores experimentales del Instituto de Ciencias Fotónicas (ICFO) y la Universidad Autónoma de Barcelona (UAB) han podido simular por primera vez una teoría gauge distinta del electromagnetismo, utilizando para ello átomos ultrafríos. El equipo se propuso realizar en el laboratorio una teoría gauge que se enmarca dentro de la clase de teorías de gauge topológicas, diferente de la clase de teorías gauge dinámicas a las que pertenece el electromagnetismo. Los resultados se publican en Nature.
 Representación artística de las interacciones quirales en una nube ultrafría de átomos “vestidos con luz”, la cual se comporta de forma diferente a su imagen en el espejo. Estas interacciones son la prueba irrefutable de la realización de una teoría topológica de gauge. / ICFO/Scixel
Representación artística de las interacciones quirales en una nube ultrafría de átomos “vestidos con luz”, la cual se comporta de forma diferente a su imagen en el espejo. Estas interacciones son la prueba irrefutable de la realización de una teoría topológica de gauge. / ICFO/ScixelEn el lenguaje de la teoría gauge, la fuerza electromagnética entre dos electrones surge cuando intercambian un fotón: una partícula de luz que puede propagarse también en ausencia de materia. Sin embargo, en los materiales cuánticos bidimensionales sometidos a campos magnéticos intensos, los fotones intercambiados por los electrones se comportan como si fueran extremadamente pesados y sólo pueden moverse mientras estén unidos a la materia.
Esto da a los electrones propiedades muy peculiares: sólo pueden fluir a través de los bordes del material, en una dirección que está fijada por la orientación del campo magnético, y su carga se vuelve aparentemente fraccionaria. Este comportamiento se conoce como efecto Hall cuántico fraccionario, y se describe mediante la teoría de gauge de Chern-Simons (el nombre de los matemáticos que desarrollaron uno de sus elementos clave).
El comportamiento de los electrones en el borde del material también se describe por una teoría gauge, que recibe el nombre de BF quiral, propuesta en los años 90, pero que nadie la había realizado en el laboratorio hasta que los investigadores del ICFO y la UAB la sacaron del congelador.
Mil millonésimas de grado por encima del cero absolutoPara dar realidad a esta teoría gauge topológica y simularla en su experimento, el equipo utilizó una nube de átomos enfriados a temperaturas de unas mil millonésimas de grado por encima del cero absoluto. Como especie atómica eligieron el potasio, porque uno de sus isótopos tiene dos estados que interactúan con distinta fuerza y pueden utilizarse como piezas cuánticas para construir un modelo gauge BF quiral.
A continuación, aplicaron luz láser para combinar los dos estados en uno nuevo. Esta técnica, denominada “vestir los átomos con luz”, hizo que los átomos adquirieran interacciones peculiares cuya fuerza y signo dependían de la velocidad de la nube.
Por último, crearon una guía de ondas óptica que restringía el movimiento de los átomos a una línea, y utilizaron láseres adicionales para golpear la nube de forma que se moviese a diferentes velocidades a lo largo de la guía de ondas.
En condiciones normales, al dejar evolucionar libremente los átomos en la guía de onda óptica, la nube de potasio se debería haber empezado a expandir inmediatamente. Sin embargo, la “luz de vestido” modificó completamente el comportamiento de los átomos, como los investigadores vieron al tomar imágenes de la nube en el laboratorio.
Como explica Ramón Ramos, investigador del ICFO, “en nuestro sistema, cuando los átomos se mueven hacia la derecha, sus interacciones son atractivas y anulan el comportamiento de los átomos que intentan expandirse. Así que lo que se ve en realidad es que la forma de la nube sigue siendo la misma. En términos técnicos, realizamos un solitón. Pero, si los átomos se mueven hacia la izquierda, estos átomos se expanden como un gas normal”.
El hecho de que los átomos se comporten de forma diferente al moverse en direcciones opuestas demuestra que el sistema es quiral, es decir, diferente de su imagen en el espejo. “Cuando observamos por primera vez el efecto de las interacciones quirales en nuestra nube atómica, no intentábamos simular una teoría gauge. Pero los datos eran tan bonitos e intrigantes que pensamos que necesitábamos entender mejor lo que estaba pasando. Cambiaron por completo los planes de investigación del equipo”, reconoce Leticia Tarruell, investigadora principal del estudio.
Traducir la teoría al lenguaje experimentalEl equipo entendió rápidamente que sus observaciones estaban relacionadas con un artículo teórico publicado diez años antes, que proponía utilizar un montaje casi idéntico para estudiar un tipo modificado de electromagnetismo. Sin embargo, los resultados del experimento eran diferentes de los esperados.
Como recuerda Craig Chisholm, al principio “los resultados que obteníamos no parecían coincidir en absoluto con los de la teoría. El reto era comprender en qué régimen había que estar para ver realmente el efecto correcto (el procedente del lugar adecuado) y eliminar los procedentes de lugares equivocados”.
Para el equipo experimental, el significado del electromagnetismo modificado que se mencionaba en el artículo tampoco estaba muy claro. Citaba artículos de física matemática de los años 90, que explicaban de forma mucho más detallada el modelo y lo conectaban con las teorías gauge utilizadas para describir el efecto Hall cuántico fraccionario.
Sin embargo, como dice Tarruell, “para físicos atómicos experimentales como nosotros, el contenido de esos artículos era muy difícil de entender, porque estaban escritos en un lenguaje de física matemática completamente diferente al nuestro. Era realmente frustrante saber que la respuesta a nuestras preguntas estaba ahí, ¡pero no éramos capaces de entenderla! Fue entonces cuando decidimos pedir ayuda a un físico teórico”.
Según Alessio Celi (UAB), que trabajó durante muchos años en física teórica de altas energías y gravedad antes de pasarse a la simulación cuántica, leer los artículos originales sobre teorías gauge fue relativamente fácil. Al mismo tiempo, pudo discutir con el equipo del ICFO y comprender el régimen en el que se podían realizar los experimentos y sus retos. Tras varios intentos fallidos, les propuso un modelo que explicaba adecuadamente los resultados observados en el laboratorio.
Como detalla, “el principal problema que teníamos era entrar en el marco adecuado. Una vez entendimos dónde buscar, el problema se volvió fácil de resolver”. Sorprendentemente, existía un régimen de parámetros en el que este modelo era exactamente la teoría de gauge topológica propuesta 30 años antes para describir los bordes de los materiales de Hall cuántico fraccionario.
“Creo que este proyecto nos muestra el interés de las colaboraciones interdisciplinarias. Combinar métodos experimentales de física de ultrabajas temperaturas e ideas teóricas de física de altas energías ha hecho de todos nosotros mejores físicos. Y hemos logrado la primera simulación cuántica de una teoría de gauge topológica”, concluye Tarruell.
Ahora, el equipo se prepara a explorar las nuevas líneas de investigación abiertas por este proyecto. Su objetivo es intentar extender los experimentos y la teoría de una línea a un plano, lo que les permitiría observar el efecto Hall cuántico fraccionario sin necesidad de un material cuántico. De esa forma, podrían crear de forma muy controlada cuasipartículas exóticas, llamadas anyones, que en el futuro podrían utilizarse para formas más robustas de computación cuántica.
Referencia:
Anika Frölian, Craig S. Chisholm, Elettra Neri, Cesar R. Cabrera, Ramón Ramos, Alessio Celi & Leticia Terruell (2022) Realizing a 1D topological gauge theory in an optically dressed BEC Nature doi: 10.1038/s41586-022-04943-3
Para saber más:
Einstein y el condensado de Bose-Einstein
De la simetría y su rotura (I)(II)(III)
Este texto apareció originalmente en SINC.
El artículo Simulación experimental de una teoría gauge distinta del electromagnetismo se ha escrito en Cuaderno de Cultura Científica.
Teoremas geométricos sin palabras: Snover
Con esta entrada damos por terminada la serie estival de demostraciones sin palabras de interesantes y hermosos resultados geométricos, que hemos dedicado al clásico teorema de Viviani (en la entrada Teoremas geométricos sin palabras: Viviani ), al moderno, con sabor a clásico, teorema de la circunferencia de Conway (en la entrada Teoremas geométricos sin palabras: Conway) y a la fórmula de Herón para el área de un triángulo (Teoremas geométricos sin palabras: Herón), y la vamos a dedicar, como en el caso de las anteriores entradas, a un resultado geométrico sobre triángulos, pero en este caso se trata de un sencillo resultado que no tiene nombre (aunque podríamos denominarlo “teorema de Snover”, como explicaremos más adelante), pero que me parece curioso, interesante y con una demostración sin palabras simple y elegante.
Pero antes, vayamos a la resolución del problema sobre cuadrados inscritos y circunscritos a una circunferencia que dejamos planteado en la anterior entrada.
Cuadrados inscrito y circunscrito a una circunferenciaEl problema que planteamos en la anterior entrada para ser resuelto con un razonamiento visual era el siguiente.
Problema (Cuadrados inscrito y circunscrito a una circunferencia): ¿Cuál es la proporción de las áreas de los cuadrados inscrito y circunscrito a una misma circunferencia?
La solución es bastante simple, el cuadrado inscrito tiene la mitad de área que el cuadrado circunscrito, o al revés, el área del cuadrado circunscrito es el doble que la del inscrito. Como se muestra en la siguiente imagen, la diagonal del cuadrado inscrito a la circunferencia es igual al lado del cuadrado circunscrito, lo cual es suficiente para obtener la solución al problema.
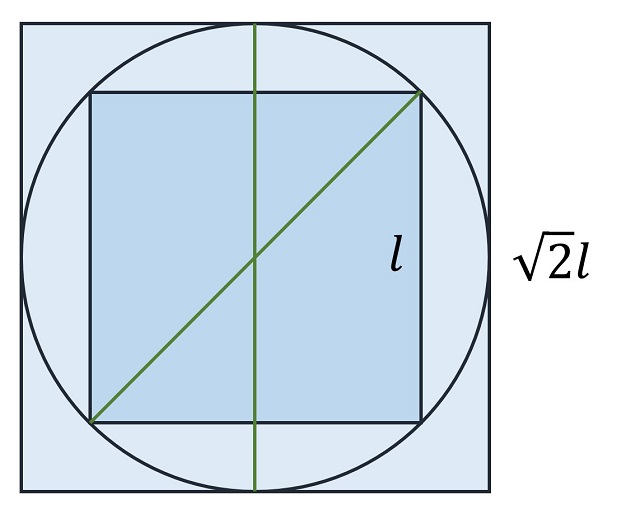
Descubrí este resultado en el segundo de los libros de la serie de demostraciones sin palabras del matemático Roger B. Nelsen: Proofs Without Words II: More Exercises in Visual Thinking (MAA, 2001). Nelsen lo presentó bajo el título “Cuatro triángulos con la misma área” y mencionó al matemático Steven L. Snover como su autor (a través de una comunicación privada), motivo por el que hemos aprovechado para denominarle, en esta entrada, teorema de Snover.
Veamos en qué consiste este resultado geométrico que bien podía haber estado incluido en la gran obra de la matemática griega, y universal, Los Elementos, del matemático griego Euclides de Alejandría (aprox. 325 – 265 a.n.e.). Se parte de un triángulo cualquiera y se trazan tres cuadrados, cada uno de ellos de lado igual a uno de los lados del triángulo y apoyado en el mismo, como se muestra en la siguiente imagen.
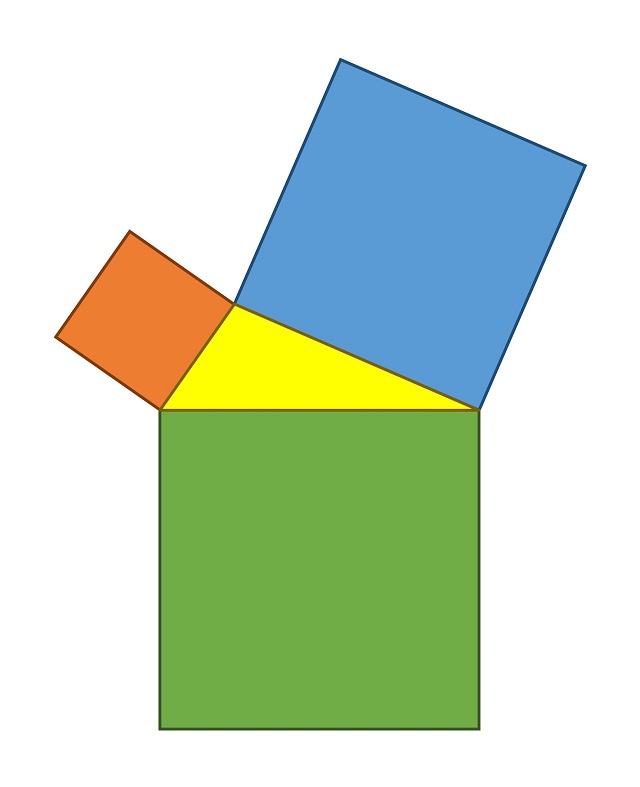
Esta primera construcción nos recuerda a la construcción del diagrama básico del teorema de Pitágoras (véanse las entradas Pitágoras sin palabras y Paseando entre árboles de Pitágoras), pero ahora partimos de un triángulo cualquiera, no necesariamente un triángulo rectángulo.
El siguiente paso consiste en trazar los tres triángulos formados por un vértice del triángulo y los vértices externos de los cuadrados construidos apoyados en dicho vértice, como se muestra en la imagen: triángulos azul, verde y marrón.
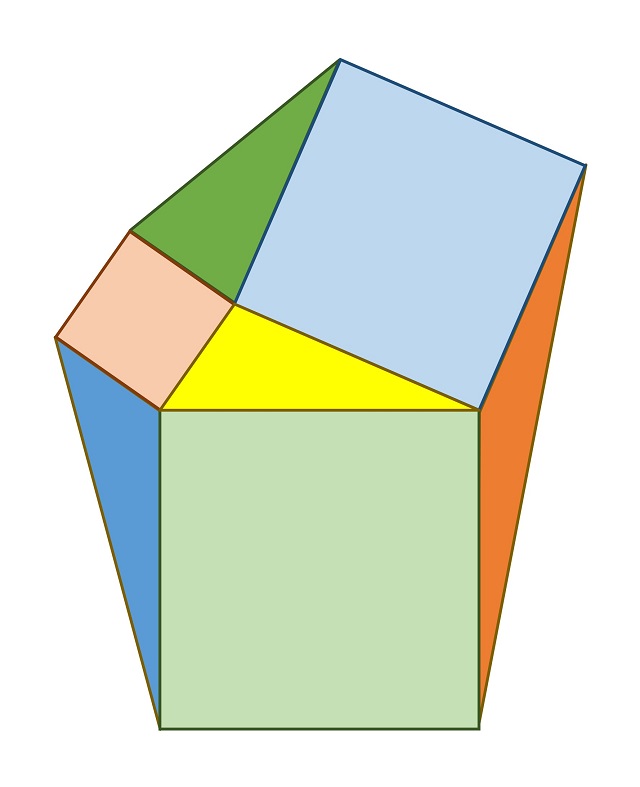
El resultado geométrico consiste en que esos tres nuevos triángulos que se han construido (azul, verde y marrón) tienen la misma área que el triángulo original (amarillo).
Teorema (de Snover): Dado un triángulo cualquiera, para cada lado del mismo se construye un cuadrado de lado igual al lado del triángulo y apoyado en el mismo. Entonces, los tres triángulos formados, cada uno de ellos, por un vértice del triángulo y los vértices externos de los cuadrados construidos apoyados en dicho vértice, tienen la misma área que el triángulo original.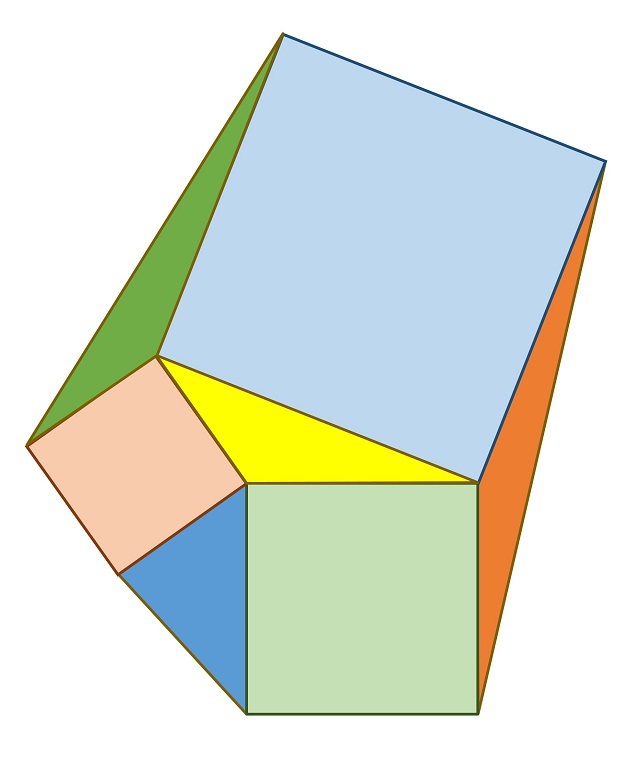
El resultado es verdadero independientemente de la forma del triángulo, ya sea equilátero (todos los lados iguales), isósceles (dos lados iguales y uno diferente), escaleno (los tres lados diferentes), acutángulo (todos los ángulos agudos, es decir, entre 0 y 90 grados), rectángulo (con un ángulo de 90 grados) u obtusángulo (con un ángulo obtuso, es decir, mayor de 90 grados). Da igual como sea el triángulo original, los tres nuevos triángulos tendrán su misma área.
Demostración sin palabrasLa demostración es muy sencilla y se basa en que cada uno de esos tres triángulos tiene la misma base y la misma altura (alguna de las tres opciones que existen para base y altura del triángulo) que el triángulo original, luego como el área de un triángulo es igual a la base por la altura dividido por dos, se concluye el resultado.
Veamos el argumento visual para el primer triángulo dibujado en esta entrada.

Espero que hayáis disfrutado de esta miniserie de cuatro entradas dedicadas a demostraciones sin palabras de interesantes y hermosos resultados geométricos sobre triángulos. Seguro que en el futuro volveremos con más hermosas demostraciones sin palabras.
Bibliografía:
1.- Roger B. Nelsen, Proofs without Words: Exercises in Visual Thinking, Mathematical Association of America, 1997.
2.- Roger B. Nelsen, Proofs Without Words II: More Exercises in Visual Thinking, Mathematical Association of America, 2001.
3.- Claudi Alsina y Roger B. Nelsen, Charming Proofs, A Journey Into Elegant Mathematics, Mathematical Association of America, 2010.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Teoremas geométricos sin palabras: Snover se ha escrito en Cuaderno de Cultura Científica.
Einstein y Hendrik Lorentz
Semanas antes de su muerte Einstein dijo que el físico holandés Hendrik Lorentz era uno de los pocos científicos que verdaderamente admiraba, y que lo consideraba como un precursor de su propio trabajo. En efecto, muchos de sus contemporáneos vieron a Lorentz casi como el cocreador de la teoría especial de la relatividad, llegando a sugerir que Lorentz y Einstein deberían haber compartido un premio Nobel por su descubrimiento. Realmente, la obra de Einstein suponía una ruptura real con la de Lorentz pero, a pesar de ello, ambos investigadores estaban estrechamente interrelacionados y eran buenos amigos. Einstein veía a Lorentz casi como a una figura paterna.
 Einstein y Hendrik Lorentz fotografiados en 1921 por Paul Ehrenfest en la puerta de su casa. Fuente: Wikimedia Commons
Einstein y Hendrik Lorentz fotografiados en 1921 por Paul Ehrenfest en la puerta de su casa. Fuente: Wikimedia CommonsLorentz se crió en Holanda, y durante sus estudios universitarios se sintió atraído por la teoría electromagnética de Maxwell. Su tesis doctoral versó sobre la reflexión y la refracción de la luz, y continuó estudiando la luz cuando se convirtió en catedrático de física matemática de la Universidad de Leiden en 1878. Su interés inicial estuvo en el éter, el medio indetectable que se suponía que empleaban las ondas de luz para viajar. Inicialmente Lorentz fue un firme creyente en la existencia del éter, llegando a rechazar por incorrectos los primeros resultados experimentales de Michelson, en los que no se encontraba la sustancia.
Pero para finales del siglo XIX, cuando el trabajo continuado de Michelson en colaboración con Morley seguía arrojando resultados negativos, Lorentz comenzó a preocuparse. Sus artículos científicos empezaron a mostrar intentos para modificar la teoría de la luz de manera que explicase los resultados del experimento de Michelson-Morley. La hipótesis que Lorentz creó proponía que a las altísimas velocidades a las que viajaba la luz, el espacio y el tiempo se contraían, compensando de esta manera el movimiento a través del éter, haciendo la longitud y el tiempo del viaje de la luz, y por tanto su velocidad, idénticos. Las ecuaciones que Lorentz creó para mostrar cómo cambiaban la longitud y el tiempo se conocen hoy día como las transformaciones de Lorentz.
Einstein admiraba el trabajo de Lorentz desde su época de estudiante y fue a través de él como Einstein se enteró de que había una crisis en la ciencia de la luz. Einstein siempre atribuyó su temprana fascinación por el electromagnetismo a la lectura de Lorentz; sin embargo, Einstein fue capaz de llevar el trabajo de Lorentz un paso más allá. En qué consistía este paso lo explicó admirablemente Lorentz en su Teoría de los electrones de 1915: “Mi principal fallo [para descubrir la teoría de la relatividad] fue aferrarme a la idea de que sólo la variable t puede ser considerada como el verdadero tiempo, y que mi tiempo local…debe ser considerado sólo como una cantidad matemática auxiliar”. En otras palabras, Lorentz incluía en sus ecuaciones dos conceptos de tiempo (uno para un observador externo y otro para el marco de referencia en el que la luz estaba viajando), pero asumía que esto era sólo un artificio matemático, no que el tiempo mismo era realmente diferente para ambos marcos de referencia. Einstein se atrevió a afirmar que las matemáticas no es que funcionasen “en principio”, sino que eran la representación precisa de lo que ocurría en realidad. El tiempo y el espacio eran de hecho diferentes para observadores diferentes. Esta idea es lo que permitió a Einstein dar el salto a la teoría especial de la relatividad, un salto que Lorentz no dio.
Lorentz, el puente entre dos paradigmasLa duda permanece sobre si Lorentz llegó a admitir completamente alguna vez la nueva teoría de Einstein. Si bien Lorentz era un innovador, un pensador adelantado a su tiempo (incluso antes de que se descubriese el electrón el ya había lanzado la hipótesis, ¡en los años 90 del siglo XIX!, de que la luz se formaba cuando oscilaba la carga eléctrica en un átomo; ganó el premio Nobel en 1902 por la formulación matemática del electrón) su pensamiento se movía en el marco de la física clásica. Se sentía cómodo en el mundo de la mecánica newtoniana, el electromagnetismo de Maxwell, y la forma en el que una causa llevaba limpiamente a un efecto de manera macroscópicamente observable. Max Born, décadas después de la muerte de Lorentz, escribió que él era de la opinión de que “Lorentz nunca se convirtió en un relativista, y sólo le regalaba la oreja a Einstein de vez en cuando para evitar discusiones”.
Lorentz también hizo públicas algunas reservas acerca de las teorías de Einstein acerca de los cuantos de luz: no estaba dispuesto a admitir que la luz estuviese constituida por partículas. Lorentz ciertamente estaba de acuerdo con que las nuevas teorías atómicas que decían que la energía no es continua, sino que viene en paquetes o cuantos como Planck había sugerido, parecían funcionar muy bien, pero no admitiría que esto pudiese aplicarse a la luz. Este “sí pero no” ilustra perfectamente la posición de Lorentz en la historia de la física, ya que se ubicó exactamente entre la física clásica y la nueva que se estaba creando. Vio la necesidad de cambio y comprendió que la nueva dinámica tenía mucho sentido, pero no podía aceptar que las extrañas ideas que acompañaban a la mecánica cuántica pudiesen ser correctas. Una posición similar a la que Einstein terminaría adoptando, pero éste aceptaría mucho más de la nueva física.
Equidistante como estaba entre la nueva y la vieja física, Lorentz fue el moderador perfecto para la primera Conferencia Solvay celebrada en 1911. Dedicada a la física atómica, la conferencia reunió a los más grandes físicos del momento para discutir los conflictos entre las teorías newtonianas y las nuevas. Lorentz mantuvo la paz admirablemente entre las distintas facciones, ya que podía ver el valor de ambos puntos de vista. En su discurso de apertura dijo: “En este estado de la cuestión se nos apareció como un maravilloso rayo de luz la bella hipótesis de los elementos [cuantos] de energía que fue expuesta primero por Planck y extendida después por Einstein…Nos ha abierto vistas maravillosas, incluso aquellos, que la consideran con cierta suspicacia, deben admitir su importancia y provecho”.
Independientemente de sus posiciones científicas, Einstein y Lorentz sentían el uno por el otro una admiración extrema. Einstein repetía a menudo que Lorentz era la persona más completa que había conocido en su vida y llegó a escribir a su amigo Johann Laub en 1909: “Le admiro [a Lorentz] como no admiro a nadie, diría que le quiero”.
Einstein respetaba tanto a Lorentz que estuvo a punto de sucederle en su puesto en Leiden cuando se retiró en 1911. Einstein, que ya había aceptado un puesto en Zúrich (un puesto que el prefería), parece que se hubiera ido a Leiden a poco que Lorentz hubiese insistido. Cuando rechazó la oferta escribió a Lorentz tras la Conferencia Solvay. “Le escribo esta carta con un corazón apesadumbrado, como alguien que ha cometido una injusticia con su padre…Si hubiese sabido que me quería [para el puesto] habría ido”.
En 1916, ese “padre” acudió para dar ánimos a un Einstein a punto de publicar su teoría general de la relatividad. Einstein había publicado primeras versiones de la teoría en 1915 y Lorentz era uno de los científicos que intentaban seguir su línea de razonamientos. Conforme la comprensión del propio Einstein aumentaba, y Lorentz comenzaba a ver exactamente lo que Einstein estaba intentando conseguir, alabó al joven investigador y le dijo que había llegado el momento de escribir la teoría completa de la forma más sencilla posible para el beneficio de toda la comunidad científica. Este parece haber sido uno de los factores importantes que llevaron a Einstein a publicar finalmente tanto el artículo en Annalen der Physik como un panfleto de cincuenta páginas que resumía y explicaba la teoría general de la relatividad.
Hendrik Lorentz murió en 1928 y Einstein, en representación de la Academia Prusiana de Ciencias, viajó a Holanda para el funeral. En su elogio dijo: “Estoy ante la tumba del hombre más noble y sabio de nuestros tiempos. Su genio lideró el camino desde el trabajo de Maxwell a los logros de la física contemporánea….Su trabajo y su ejemplo continuarán vivos como una inspiración”.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Una versión anterior de este artículo se publicó en Experientia Docet el 1 de noviembre de 2009.
El artículo Einstein y Hendrik Lorentz se ha escrito en Cuaderno de Cultura Científica.
¿Qué nos dice el dióxido de silicio sobre las erupciones en Marte?
A día de hoy sabemos todavía muy poco sobre la historia de las erupciones volcánicas en Marte y sobre qué tipos de vulcanismo se dieron cuando Marte era todavía era un planeta mucho más activo -a nivel interno- que en la actualidad.
De hecho, podríamos decir que incluso tenemos una importante incertidumbre en cuanto al grado de actividad actual del planeta y si todavía sería posible la ocurrencia de erupciones volcánicas en determinados lugares de Marte. Este es el caso de Cerberus Fossae donde, según las dataciones de Horvath et al. (2021), podría haber habido algún tipo de erupción en los últimos ~50.000 años, lo que, junto a la actividad sísmica registrada por la misión InSight en la zona (Kedar et al. (2021)), hace de este lugar un sitio muy interesante para seguir estudiando la dinámica actual del planeta rojo.
Pero, ¿Cómo fueron las erupciones del pasado? ¿Fueron erupciones explosivas y violentas o por el contrario solo hubo erupciones muy efusivas y tranquilas? ¿O quizás coexistieron ambos modelos eruptivos? Anteriormente se pensaba que si no todas, la mayoría de las erupciones en Marte habían sido con una composición basáltica y tranquilas y que las rocas ígneas -aquellas formadas por el enfriamiento del magma- era un grupo de rocas poco diverso en el planeta rojo, por lo menos las volcánicas, a diferencia de la Tierra donde si hay un gran abanico composicional fruto de distintos procesos de evolución de los magmas.
 Largas coladas de lava en Marte observadas por la Mars Odyssey. Obsérvese la longitud de estas, que no aparecen ni completas en la imagen debido a la distancia recorrida por la lava. Imagen cortesía de NASA/JPL-Caltech/ASU.
Largas coladas de lava en Marte observadas por la Mars Odyssey. Obsérvese la longitud de estas, que no aparecen ni completas en la imagen debido a la distancia recorrida por la lava. Imagen cortesía de NASA/JPL-Caltech/ASU.Pero, antes de poder resolver esta duda, tenemos que salvar ciertos obstáculos: la mayor parte de Marte la hemos observado desde su órbita y no desde su superficie, y la capa de polvo rojo ubicua que le da ese color tan característico al planeta, a veces hace palidecer las señales químicas de los distintos minerales. Si a esto le sumamos la erosión que lentamente va eliminando como si fuese una goma de borrar algunas partes de su relieve, se hace muy complicado el identificar los procesos volcánicos, especialmente los que pasaron hace mucho más tiempo.
De ahí la importancia de poder llegar a la superficie con misiones robóticas -de momento- tomar muestras, analizarlas in situ, y si es posible, devolverlas a la Tierra para que con mejores instrumentos analíticos podamos descifrar los detalles de la historia del planeta. Pero a pesar de todos los hándicaps que supone la exploración de otro planeta, a veces se hacen hallazgos en los lugares más insospechados.
Aparece tridimita, un polimorfo del dióxido de silicioY esta historia nos obliga a remontarnos al año 2015, cuando el rover Curiosity, que se encuentra en el interior del cráter Gale de Marte, toma una muestra de una roca llamada Bucksin y detecta en ella tridimita, un polimorfo del dióxido de silicio, como el cuarzo. Los polimorfos son minerales que, con una misma composición química, tienen distintas estructuras cristalinas, algo que en ocasiones responde a las condiciones donde se ha formado el propio mineral.
 El rover Curiosity se toma un selfie justo después de tomar la muestra de Bucksin, el 5 de agosto de 2015. Aunque no se ve el agujero, en la zona inferior central de la imagen se ve una mancha de color gris que destaca sobre el rojo: son los restos de la perforación de esta roca. Imagen cortesía de NASA/JPL-Caltech/MSSS.
El rover Curiosity se toma un selfie justo después de tomar la muestra de Bucksin, el 5 de agosto de 2015. Aunque no se ve el agujero, en la zona inferior central de la imagen se ve una mancha de color gris que destaca sobre el rojo: son los restos de la perforación de esta roca. Imagen cortesía de NASA/JPL-Caltech/MSSS.La tridimita se suele formar a altas temperaturas y bajas presiones, y en nuestro planeta suele estar asociada al vulcanismo explosivo, pero también podría formarse de otras maneras… como en el interior de lagos donde hay capas de agua muy ricas en sílice o incluso por fenómenos hidrotermales. Y sabemos que el interior del cráter Gale, al menos la parte inferior, representa una antigua cuenca lacustre donde con el paso del tiempo fueron acumulándose sedimentos, lo que hizo la interpretación de la tridimita fuese un verdadero reto.
Además, la tridimita podía también haber llegado fruto de la erosión de rocas de fuera del cráter y llevada hasta su interior por los ríos que desembocaban en este. El depósito de la tridimita en los sedimentos a partir de la erosión de otras rocas se pudo descartar, ya que este mineral aparecía y desaparecía bruscamente en los sedimentos analizados, y de haber sido traídos por los ríos, se esperaría una fuente más continua y con cierta gradualidad en su aparición y desaparición, no mostrando un cambio tan sumamente brusco.
También cristobalita, otro polimorfoAcompañando a la tridimita, los científicos encontraron también cristobalita, otro de los polimorfos del dióxido de silicio, que se forma a temperaturas superiores a la de la tridimita, lo que ponía a los científicos entre la espada y la pared… ¿se habrían formado estos minerales realmente a partir de la actividad volcánica?
Para poder resolver el puzle, se pusieron a analizar en que contextos geológicos de nuestro planeta y en que porcentajes aparecían estos minerales y por supuesto, junto a que otros minerales aparecían, para ver si finalmente encajaban las piezas.
Según el último estudio publicado por Payré et al. (2022), parece que la explicación más plausible requiere de erupciones volcánicas para explicar estos dos minerales: Hace unos 3.000 millones de años -aproximadamente- el magma que había en la cámara magmática, valga la redundancia, de un volcán marciano estaba cambiando su composición por un proceso que conocemos en geología como cristalización fraccional.
Este proceso hace que los magmas vayan evolucionando con el tiempo, ya que cambios en la presión y temperatura pueden hacer que unos minerales vayan formándose y segregándose del magma, provocando que la composición del magma restante vaya cambiando, porque al formarse estos minerales “retiran” los elementos que los forman.
Esto a su vez provoca que ciertos elementos puedan concentrarse en el magma, como el silicio, y que de ocurrir una erupción puede dar lugar a la formación de minerales como la tridimita y la cristobalita.
¿Y si hubo una erupción cómo llegaron estos minerales hasta el cráter? Los autores mencionan que una erupción de este tipo podría haber generado nubes de ceniza y piroclastos que se habrían desplazado grandes distancias, y que al caer se depositarían, acabando por formar parte del registro sedimentario… pero, ¿qué volcán podría haber sido el causante de esta erupción?
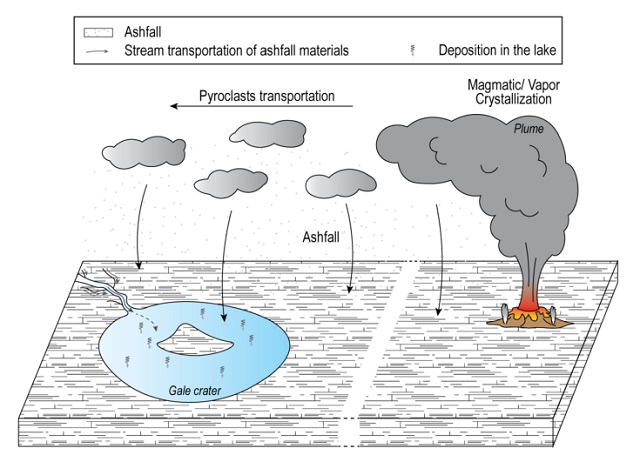 Modelo del mecanismo de transporte de la ceniza hasta el cráter Gale. Imagen cortesía de Payré et al. (2022)
Modelo del mecanismo de transporte de la ceniza hasta el cráter Gale. Imagen cortesía de Payré et al. (2022)Pues lo cierto es que es muy difícil encontrar cual habría sido el responsable, ya que no solo nos queda identificar todos los posibles volcanes marcianos -de algunos nos queda tan poco que a veces los confundimos con cráteres-, lo que junto con no poder establecer dataciones absolutas que nos permitan restringir el intervalo de edades de cada erupción, lo hace, por el momento, una labor muy difícil.
Pero sin duda, este estudio es muy interesante porque pone de manifiesto que fueron posibles otro tipo de erupciones en Marte y que fue un planeta con una mayor diversidad de procesos volcánicos de lo que cabría esperar, por lo que de nuevo se nos abre una nueva ventana para conocer mejor nuestro vecindario planetario.
Referencias:
1. Kedar S, Panning MP, Smrekar SE, et al. Analyzing Low Frequency Seismic Events at Cerberus Fossae as Long Period Volcanic Quakes. J Geophys Res Planets. 2021;126(4):1-28. doi:10.1029/2020JE006518
2. Morrisa R V., Vanimanb DT, Blakec DF, et al. Silicic volcanism on Mars evidenced by tridymite in high-SiO2 sedimentary rock at Gale crater. Proc Natl Acad Sci U S A. 2016;113(26):7071-7076. doi:10.1073/pnas.1607098113
3. Payré V, Siebach KL, Thorpe MT, Antoshechkina P, Rampe EB. Tridymite in a lacustrine mudstone in Gale Crater , Mars : Evidence for an explosive silicic eruption during the Hesperian. Earth Planet Sci Lett. 2022;594:117694. doi:10.1016/j.epsl.2022.117694
4. Horvath DG, Moitra P, Hamilton CW, Craddock RA, Andrews-Hanna JC. Evidence for geologically recent explosive volcanism in Elysium Planitia, Mars. Icarus. 2021;365:114499. doi:10.1016/j.icarus.2021.114499
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo ¿Qué nos dice el dióxido de silicio sobre las erupciones en Marte? se ha escrito en Cuaderno de Cultura Científica.
Cuentos de otro tiempo, y de este
 Ilustración de Warwick Goble para una edición de «La bella y la bestia» de 1913. Fuente: Wikimedia Commons
Ilustración de Warwick Goble para una edición de «La bella y la bestia» de 1913. Fuente: Wikimedia CommonsEs muy posible que algunos de los cuentos populares más conocidos hundan sus raíces en la prehistoria. Han llegado a esa conclusión utilizando métodos estadísticos y computacionales que, en biología, se suelen usar para reconstruir la historia evolutiva de las especies y su procedencia de otras, anteriores.
Los análisis biológicos se basan en la comparación de las secuencias genéticas de las especies –o linajes– cuya historia se desea trazar. La información genética se transmite de generación en generación pero, en ocasiones, la cadena de ADN sufre mutaciones al replicarse y surgen nuevos linajes, por ramificaciones sucesivas del original. Con la evolución y ramificación de las lenguas se hacen análisis similares, solo que, en vez de genes, lo que se transmite son palabras. Los cambios que sufren las palabras a lo largo del tiempo propician la aparición de nuevas lenguas por ramificación de aquellas de las que proceden. Las diferencias en el momento presente entre palabras que comparten origen se utilizan como criterio para reconstruir la evolución de las lenguas.
En la investigación que nos ocupa utilizaron como referencia el árbol filogenético (la “genealogía”) de las lenguas indoeuropeas y estudiaron la presencia en cincuenta de esas lenguas de los 275 “cuentos de magia” del catálogo internacional Aarne Thompson Uther, en el que se recogen más de 2000 cuentos procedentes de más de 200 sociedades. “Hansel y Gretel” y “La bella y la bestia”, por ejemplo, son dos de esos cuentos. De los 275 descartaron 199, porque era muy probable que hubiesen sido transmitidos horizontalmente, de una sociedad a otra próxima; tenían así suficiente garantía de que los 76 restantes se habían transmitido de forma vertical, de una generación a la siguiente, dentro de una misma sociedad. “Hansel y Gretel”, por ejemplo, no pasó la criba. Sí lo hizo “La bella y la bestia”.
Calcularon después la probabilidad de que cada uno de los cuentos estuviera presente en la época en que se produjeron las ramificaciones que dieron lugar a grandes subfamilias lingüísticas. Esa probabilidad depende de la presencia en las lenguas contemporáneas de las narraciones en cuestión, teniendo en cuenta también la posición de esas lenguas en el árbol filogenético. De los 76 cuentos, a catorce –“La bella y la bestia”, entre ellos– se les estimó una probabilidad igual o superior al 50% de haber existido en la lengua de la que proceden las célticas, romances, germánicas y eslavas, y pudo haber nacido hace unos 6800 años. De esos catorce, a cuatro cuentos se les calculó una probabilidad igual o superior al 50% de haber sido creados en el origen de las lenguas indoeuropeas –en la base del árbol–, hace algo más de 7000 años.
El cuento con la probabilidad más alta (87%) de haber existido en esa época tan remota es “El herrero y el diablo”, una historia cuyo eco resuena en “Fausto”. Que un cuento de hace 7000 años incluya la figura del herrero no debe extrañar. Las primeras evidencias de fundición tienen una antigüedad de unos 8000 años y proceden de Catalhöyük, Anatolia. Hay más restos de actividades de fundición de cobre durante el VI milenio a.e.c. en la misma Anatolia y en el actual Kurdistán, zonas ricas en ese mineral.
Que ciertos cuentos tengan un origen tan antiguo indica, por un lado, que dan cuenta de situaciones o circunstancias vitales que cumplen una función educativa importante en los grupos humanos que los transmiten. Por otra parte, que lo hacen de forma que explotan características de nuestra cognición que facilitan su transmisión fiel. Son historias ejemplarizantes; también son narraciones ejemplares.
Fuente: da Silva, S.G., and Tehrani, J.J. (2016). Comparative phylogenetic analyses uncover the ancient roots of Indo-European folktales. R. Soc. Open Sci. 3, 150645. doi: 10.1098/rsos.150645
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Cuentos de otro tiempo, y de este se ha escrito en Cuaderno de Cultura Científica.
CienciaClip 2021 – La ciencia detrás de la bomba atómica

Ciencia Clip es un concurso de vídeos divulgativos de ciencia diseñados, producidos y protagonizados por estudiantes de Educación Secundaria.
El objetivo del concurso es fomentar el interés por la ciencia y la tecnología. Y ofrecer a los concursantes una oportunidad para ejercitar su creatividad y habilidades comunicativas usando herramientas que proporciona internet.
Ciencia Clip es una iniciativa de la Cátedra de Cultura Científica de la UPV/EHU y en la que colaboran Euskampus Fundazioa, Naukas, Scenio y Big Van.
Los ganadores de la edición 2022 se anunciarán en la página web del concurso a principios de septiembre. La entrega premios y el anuncio del vídeo ganador del premio especial se realizarán durante el evento Naukas Bilbao. En la edición de 2021 resultó ganador en la categoría de 1º y 2º de la ESO Iván Sánchez, de Madrid, con este vídeo:
Edición realizada por César Tomé López
El artículo CienciaClip 2021 – La ciencia detrás de la bomba atómica se ha escrito en Cuaderno de Cultura Científica.
La simetría de figuras abstractas y la adquisición de la gramática en bebés
El grupo de investigación Gogo Elebiduna de la UPV/EHU está especializado en psicolingüística. Sus investigaciones se centran en cómo se adquiere, representa y organiza la facultad del lenguaje en el cerebro, y cuáles son las características universales de la representación y el procesamiento del lenguaje.
La investigadora Ikerbasque del grupo Irene de la Cruz-Pavía ha participado en un estudio en el que se ha investigado la capacidad de los bebés de 7 meses para percibir la simetría estructural en patrones visuales abstractos de tipo mosaico. Esta investigación se llevó a cabo en la Universidad de París. “Hemos examinado los patrones de mirada espontánea de casi 100 bebés ante secuencias de tipo mosaico con estructuras simétricas y asimétricas”, explica la investigadora.
Estos mosaicos estaban compuestos por baldosas cuadradas de dos categorías (A y B) que diferían en su paleta de color y su forma interna. Estas baldosas se ordenaban creando mosaicos con estructuras simétricas (p. ej. ABA, ABABA) o asimétricas (p. ej. AAB, AABBA). En el estudio se ha podido constatar que los bebés “discriminaron los mosaicos estructuralmente simétricos de los asimétricos, y que la longitud de la secuencia (3 o 5 baldosas) o el nivel de simetría no modulaban significativamente su comportamiento”. Estos resultados sugieren que los bebés detectan rápidamente la simetría estructural en patrones visuales complejos: “Los bebés de 7 meses tienen una capacidad robusta y automática de detectar que una estructura es simétrica. Esta habilidad coincide con las encontradas en estudios que hemos realizado con otros estímulos tales como la lengua de signos, o el habla, demostrando que los bebés son simplemente muy buenos en detectar estructuras y regularidades”, afirma la investigadora del Departamento de Lingüística y Estudios Vascos de la UPV/EHU.
La habilidad de los bebés para extraer estructura y reglas“La gramática de una lengua es el conjunto de estructuras y reglas de una lengua. Quiero entender hasta qué punto las habilidades de los bebés para extraer estructuras, y detectar regularidades y aprender reglas, son específicas del lenguaje o si en cambio se encuentran en otras áreas —señala la investigadora Ikerbasque—. Hemos hecho este estudio con información que es visual pero que no es lenguaje. Con estos mosaicos, hemos podido ver la habilidad que tienen los bebés para extraer estructura de distintos medios”.
Este estudio les permite entender mejor “cuáles son las habilidades fundamentales de esos bebés, que les van a permitir empezar primero con ciertas partes más accesibles de la gramática e ir poco a poco construyendo hasta tener una cosa tan compleja como es la gramática de una lengua. Lo que nosotros queremos entender es cuáles son las habilidades fundamentales que tienen los bebés para detectar estructura”.
“Tenemos muchas más preguntas que responder —concluye—. En este estudio hemos podido determinar que los bebés son capaces de detectar estructuras espontáneamente y rápidamente. Ahora queremos entender cuándo empieza esta habilidad, y entender hasta qué grado de detalle analizan esa estructura y qué aspectos de los mosaicos les permiten detectar su estructura (la forma, el color, ambos…)”.
Referencia:
Irene de la Cruz-Pavía, Gesche Westphal-Fitch, W. Tecumseh Fitch, Judit Gervain (2022) Seven-month-old infants detect symmetrical structures in multi-featured abstract visual patterns PLOS ONE DOI: 10.1371/journal.pone.0266938
Para saber más:
Cuando los bebés comienzan a combinar gesto y habla
Las habilidades matemáticas de los bebés
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo La simetría de figuras abstractas y la adquisición de la gramática en bebés se ha escrito en Cuaderno de Cultura Científica.

