Por qué se encuentran tantos dientes de espinosáuridos
Los dinosaurios espinosáuridos podían desarrollar hasta tres generaciones de dientes al mismo tiempo, una alta tasa de reemplazo que explicaría por qué se han encontrado tantas piezas de este tipo en yacimientos del Cretácico.
 Detalle de la dentadura de un fósil de Suchomimus tenerensis. Fuente: Wikimedia Commons
Detalle de la dentadura de un fósil de Suchomimus tenerensis. Fuente: Wikimedia CommonsLos científicos han reestudiado un resto fósil de mandíbula hallado en 1983 en un yacimiento del Cretácico Inferior en Igea (La Rioja, España). Se trata del fragmento de un maxilar izquierdo de dinosaurio carnívoro que preserva 8 alvéolos. En uno de estos huecos dentales han descubierto, mediante técnicas de microTAC, restos de varios dientes desarrollándose de forma simultánea.
“Hemos reconocido en un mismo alvéolo hasta tres generaciones de dientes: el diente funcional del animal; otra pieza en formación que reemplazaría al primero, y el germen del que acabaría sustituyendo a este segundo”, explica Pablo Navarro, de la Universidad de La Rioja.
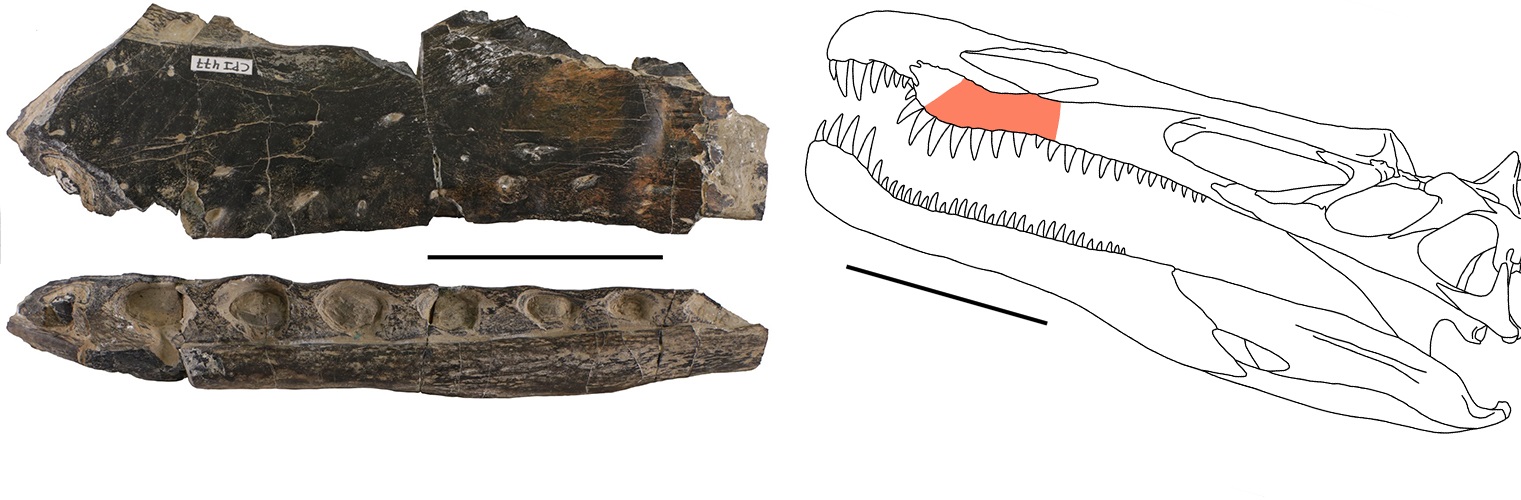 Resto fósil estudiado y ubicación en el cráneo. Escala: 5 cm. | Foto: Centro de Interpretación Paleontológica de La Rioja en Igea.
Resto fósil estudiado y ubicación en el cráneo. Escala: 5 cm. | Foto: Centro de Interpretación Paleontológica de La Rioja en Igea.Ello implica un reemplazo dental muy rápido y es, probablemente, una de las razones de que encuentren tantos dientes de espinosáuridos en la península ibérica durante el Cretácico Inferior”, añade el coautor del artículo.
Hasta ahora se sabía que algunas especies de espinosáuridos –dinosaurios carnívoros de tamaño medio/grande, que poseían un cráneo alargado y unos dientes cónicos semejantes a los de los cocodrilos- podían cambiar de dientes más rápido que otros terópodos, en apenas dos meses (se estima una tasa de reemplazo de entre 60 y 68 días); esta investigación confirma que se trata de un rasgo común a todo el grupo y aporta evidencias de cómo se producía este cambio, gracias al desarrollo de varios dientes de sustitución al mismo tiempo.
“Estos animales generaban, a lo largo de toda su vida, nuevos dientes que iban reemplazando el diente original y provocando su caída. Esto implica que un mismo animal podía generar multitud de dientes”, asegura Pablo Navarro.
 Reconstrucción artística de la cabeza de un espinosáurido. Fuente: Wikimedia Commons
Reconstrucción artística de la cabeza de un espinosáurido. Fuente: Wikimedia Commons“Estos dientes, de forma más o menos cónica y de tamaño centimétrico, eran transportados por los ríos y acumulados en zonas lacustres y, con el tiempo, quedaban fosilizados –indica el investigador-. Son uno de los restos de vertebrados más comunes en los yacimientos ibéricos del Cretácico Inferior (entre 145 y 113 millones de años)”.
Aunque no se conoce con precisión por qué cambiaban de dientes tan a menudo, se cree que esto les permitía poseer un mayor número de dientes funcionales en todo momento. Una ventaja decisiva para resistir el importante esfuerzo que les suponía sujetar a sus presas atrapándolas entre las mandíbulas.
Además de estos hallazgos, la investigación ha permitido matizar la clasificación del maxilar estudiado: los expertos no lo atribuyen, como se creía, al género Baryonix, sino a otro tipo de espinosáuridos muy cercano, un barioniquino indeterminado.
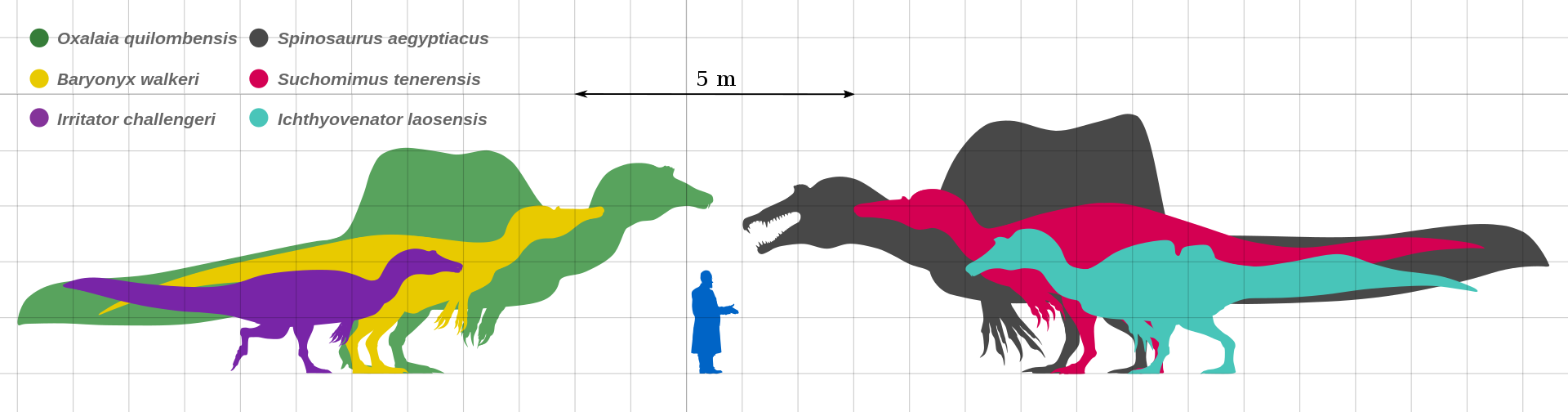 Tamaño de algunas especies de espinosáuridos. Fuente: Wikimedia Commons
Tamaño de algunas especies de espinosáuridos. Fuente: Wikimedia CommonsLos estudios paleontólogicos desarrollados hasta la fecha en Igea son relevantes por la presencia de numerosos restos óseos de espinosaurios, incluyendo esqueletos parciales pertenecientes a varios individuos. «La investigación actual permitirá mejorar nuestro conocimiento sobre la diversidad de este grupo tan particular de dinosaurios carnívoros. Es probable que al menos dos especies distintas estén representadas en los yacimientos de Igea», afirman Erik Isasmendi y Xabier Pereda-Suberbiola, paleontólogos del Departamento de Geología de la UPV/EHU, lo que convierte a esta localidad riojana en uno de los lugares destacados en el mundo en el estudio de los espinosaurios.
Referencia:
Erik Isasmendi, Pablo Navarro-Lorbés, Patxi Sáez-Benito, Luis I. Viera, Angelica Torices, Xabier Pereda-Suberbiola (2022) New contributions to the skull anatomy of spinosaurid theropods: Baryonychinae maxilla from the Early Cretaceous of Igea (La Rioja, Spain) Historical Biology doi: 10.1080/08912963.2022.2069019
Para saber más:
Veinte años de dinosaurios con plumas
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Por qué se encuentran tantos dientes de espinosáuridos se ha escrito en Cuaderno de Cultura Científica.
Los diapasones que miden nuestro tiempo
Koenig ha muerto, y sus amigos lo recordarán con cariño y respeto. Su devoción por la ciencia acústica fue única. Su vida fue la del bachiller recluso, y sus últimos años le trajeron ansiedad y privaciones porque su ciencia había perdido su valor como medio de sustento. No será olvidado pronto, pero tampoco nadie aspirará a ocupar su lugar.
W. Le Conte Steven, 19011.
Los experimentos ópticos de Lissajous permitieron visualizar por primera vez las vibraciones del sonido con una gran precisión y se convirtieron en una herramienta clave en las investigaciones acústicas de finales del siglo XIX. Sin embargo, el diapasón como instrumento de laboratorio aún presentaba una grave limitación, y es que tras golpearlo, su sonido se desvanecía muy rápidamente. Entre los científicos que intentaron sortear este inconveniente, Rudolph Koenig dio con la solución más práctica. Este luthier y físico de origen alemán ideó un mecanismo que permitía prologar la voz de lo diapasones, pero también medir con precisión su frecuencia de vibración. En el camino, y sin saberlo ni buscarlo, cambió para siempre la manera en que medimos el tiempo. Su legado aún se encuentra en el corazón de casi todos los relojes que usamos hoy en día, en forma de diapasón.
Ciertamente, Koenig no es un científico muy conocido. Durante su adolescencia, estudió física y matemáticas en Königsberg pero nunca llegó a ir a la universidad. Al terminar el instituto (o “gymnasium”, según el nombre que le daba entonces), se mudó a París para trabajar como aprendiz de un prestigioso luthier llamado Jean Baptiste Vuillaume. Fue en el taller musical, mientras aprendía a fabricar instrumentos de todo tipo, donde Koenig perfeccionó su talento para trabajar la madera y el metal.
Debió de ser entonces cuando adquirió también su pasión por la acústica. Tras siete años construyendo máquinas de hacer sonido, Koenig decidió montar su propio negocio pero, al hacerlo, le dio un giro a su carrera. Decidió dedicarse al diseño de instrumentos de laboratorio y a la investigación acústica. Sus diseños ya no servirían para generar sonidos musicales sino para estudiarlos.
Koenig alcanzó una fama legendaria como acústico y fabricante de diapasones de precisión, entre otros aparatos físicos. Colaboró estrechamente con Helmholtz, y a finales del siglo XIX, sus diseños se encontraban en todos los laboratorios acústicos del mundo. Entre ellos, había un curioso diapasón que se mantenía en constante vibración con la ayuda de un mecanismo de relojería. El conjunto era muy similar a un reloj estándar, solo que utilizaba un diapasón en el lugar que normalmente habría ocupado un péndulo, para marcar la frecuencia. Este diseño permitía además medir la frecuencia del diapasón elegido con total precisión. Bastaba con comparar el tiempo marcado por las agujas del dispositivo respecto al de un reloj bien calibrado. Fue así como Koenig comprobó que el diapasón estándar de Lissajous, ese gran aspirante a «la universal”, no producía las 435 vibraciones por segundo declaradas, sino 435,4(5)2.
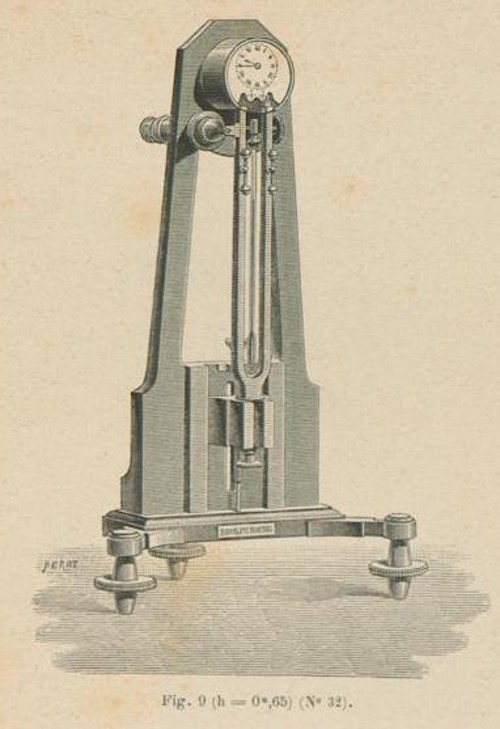 Dibujo de un reloj del catálogo Koenig de 1889 tal y como aparece en Catalogue des appareils d’acoustique. Paris: L. Landry, 1889, p. 19, Fig. 9 (No. 32). Fuente: Sound & Science: Digital Histories / Universidad Humboldt de Berlín / Instituto Max Planck de Historia de la Ciencia
Dibujo de un reloj del catálogo Koenig de 1889 tal y como aparece en Catalogue des appareils d’acoustique. Paris: L. Landry, 1889, p. 19, Fig. 9 (No. 32). Fuente: Sound & Science: Digital Histories / Universidad Humboldt de Berlín / Instituto Max Planck de Historia de la Ciencia
El reloj-diapasón de Koenig tuvo especial relevancia por otro motivo. Mientras que el mecanismo mantenía la vibración constante, la obstinada afinación del diapasón (la misma propiedad que lo convierte en una excelente herramienta para los músicos) mantenía las agujas del reloj moviéndose siempre a la misma velocidad, de manera exacta. Esto lo convertía en un fantástico aliado para medir el tiempo.
Este concepto se incorporaría a los relojes de pulsera un siglo más tarde, para producir modelos con una precisión sin precedentes. En 1960, salió a la venta el Accutron, un reloj que utilizaba un diapasón de acero de 360 hercios para marcar el tiempo. Como esta frecuencia estaba en el rango audible humano, sus usuarios podían oír un leve zumbido en fa sostenido al acercar el reloj a su oreja. Si os digo la verdad, me parece una oportunidad perdida para la poesía que no usasen un diapasón a 440 Hz, pero el hecho es que aquella innovación mejoró enormemente la precisión de los relojes. Probablemente por eso, la marca de relojes Bulova, fabricante original del Accutron, aún conserva un diapasón en su logotipo.
Con el tiempo, los procesos de fabricación fueron mejorando, así como los materiales. Cambiamos los muelles por pilas y aprendimos a dominar la electrónica. Hoy en día, en casi todos los relojes de pulsera late un diminuto diapasón en forma de horquilla. Está hecho de cuarzo y oscila a 32768 Hz. Y aunque nosotros ya no lo oímos, es posible que nuestras mascotas aún tengan muy presente su origen sonoro y musical.
 Resonador de cristal de cuarzo en forma de diapasón de un reloj «de cuarzo» moderno. Fuente: Wikimedia Commons
Resonador de cristal de cuarzo en forma de diapasón de un reloj «de cuarzo» moderno. Fuente: Wikimedia CommonsReferencias:
1Le Conte, Steven W. “Rudolph Koenig.” Science, vol. 14, no. 358, 1901, pp. 724-727. https://www.science.org/doi/10.1126/science.14.358.724.
2Feldmann, H. (1997). History of the tuning fork. I: Invention of the tuning fork, its course in music and natural sciences. Pictures from the history of otorhinolaryngology, presented by instruments from the collection of the Ingolstadt German Medical History Museum. Laryngorhinootologie, 76(2), 116–122. DOI: 10.1055/s-2007-997398
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
El artículo Los diapasones que miden nuestro tiempo se ha escrito en Cuaderno de Cultura Científica.
Teoremas geométricos sin palabras: Conway
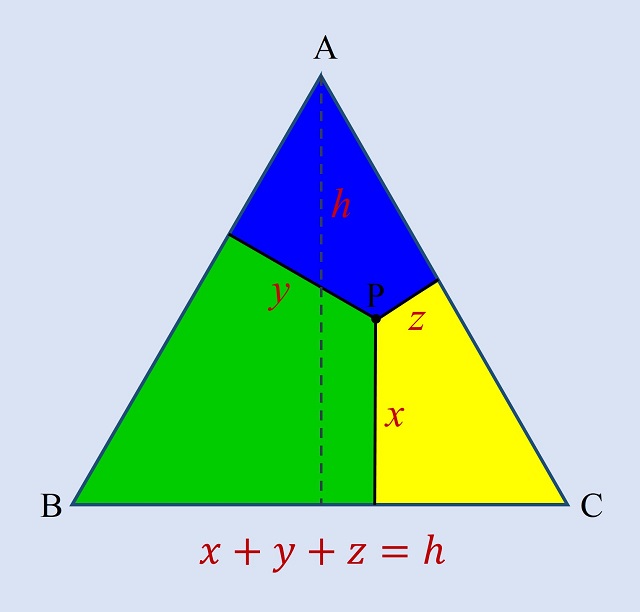
Con la anterior entrada del Cuaderno de Cultura Científica titulada Teoremas geométricos sin palabras: Viviani iniciamos una pequeña serie estival de demostraciones sin palabras de interesantes y hermosos teoremas geométricos. El teorema de la anterior entrada era un teorema clásico de la geometría del plano sobre triángulos equiláteros, el conocido teorema de Viviani. Este resultado del matemático italiano Vincenzo Viviani (1622-1703) dice que “la suma de las distancias de un punto cualquiera en el interior de un triángulo equilátero (o en alguno de sus lados) a cada uno de sus lados es igual a la altura del mismo.”
En esta entrada, vamos a pasar de un extremo al otro, de un teorema clásico, el teorema de Viviani, de hace más de 300 años, a un teorema actual, el teorema de la circunferencia de Conway. El matemático británico John Horton Conway (1937-2020), fallecido recientemente como consecuencia del covid-19, fue un prolífico e imaginativo matemático que trabajó en muchas áreas de las matemáticas, entre ellas la teoría de grupos algebraicos, las matemáticas de los juegos, la teoría de nudos, la teoría de números, la geometría o la teoría de códigos, que escribió interesantes libros, como la trilogía Winning Ways for your Mathematical Plays (Estrategias ganadoras para tus juegos matemáticos), junto a Richard K. Guy y Elwyn Berlekamp, o The Book of Numbers (El libro de los números), con Richard K. Guy, y que es conocido por temas como el autómata celular denominado el juego de la vida, los números surreales o la regla del fin del mundo, entre muchos otros.
 Fotografía del matemático británico John H. Conway realizada por Thane Plambeck en el congreso Combinatorial Game Theory (2005), celebrado en Banff International Research Station (Canada)
Fotografía del matemático británico John H. Conway realizada por Thane Plambeck en el congreso Combinatorial Game Theory (2005), celebrado en Banff International Research Station (Canada)
Pero antes de adentrarnos en el teorema de la circunferencia de Conway, vayamos a la resolución del problema que dejamos planteado en la anterior entrada y que podía resolverse con una sencilla prueba sin palabras.
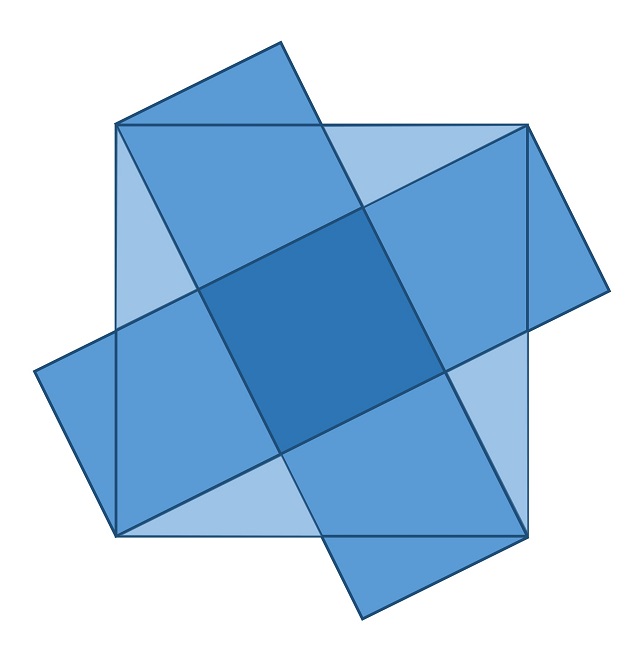
El cuadrado dentro del cuadradoEl problema, que habíamos planteado en la anterior entrada y que dejamos pendiente para todas aquellas personas que quisierais intentar resolverlo de una forma sencilla, es el siguiente.
Problema (El cuadrado dentro del cuadrado): Demuéstrese que si se trazan rectas que unen los vértices del cuadrado con los puntos medios de uno de los lados opuestos, como se muestra en la siguiente imagen, entonces el área del cuadrado central es un quinto del área del cuadrado original.
Como hemos comentado, este problema se puede resolver fácilmente de forma visual. Si nos fijamos en el siguiente dibujo, deduciremos que, como se afirma en el problema, el área del cuadrado central es igual la quinta parte del área del cuadrado grande.
El 15 de abril de 2020, con motivo de la muerte del matemático británico John H. Conway unos días antes, el 11 de abril, el matemático Matt Baker escribió en su blog Matt Baker’s Math Blog una entrada titulada Some Mathematical Gems from John Conway (Algunas joyas matemáticas de John Conway), en la que hacía un repaso personal de algunas de las contribuciones de este genial matemático. Una de esas contribuciones, que yo no conocía y que llamó mi atención, es uno de esos curiosos resultados geométricos que entraría de lleno en los objetivos de esta serie estival, puesto que es sorprendente, interesante e incluso se ha realizado una hermosa demostración sin palabras del mismo.
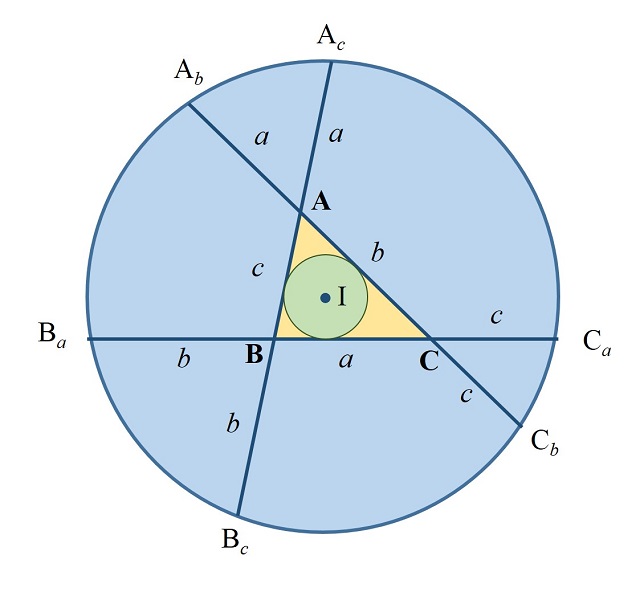
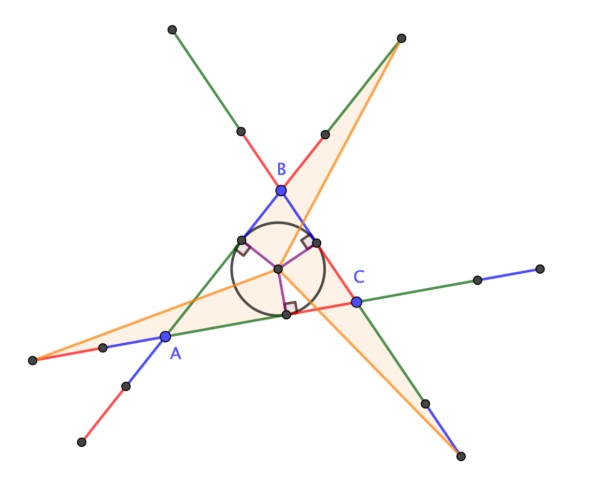
El inventor del juego de la vida descubrió la siguiente propiedad geométrica de los triángulos, en concreto, observó que, si los lados de un triángulo que se encuentran en un vértice son extendidos por una longitud igual al lado opuesto, los seis puntos finales de los seis segmentos rectos resultantes se encuentran en una misma circunferencia cuyo centro es, además, el incentro del triángulo, es decir, el centro de la circunferencia inscrita en el triángulo.
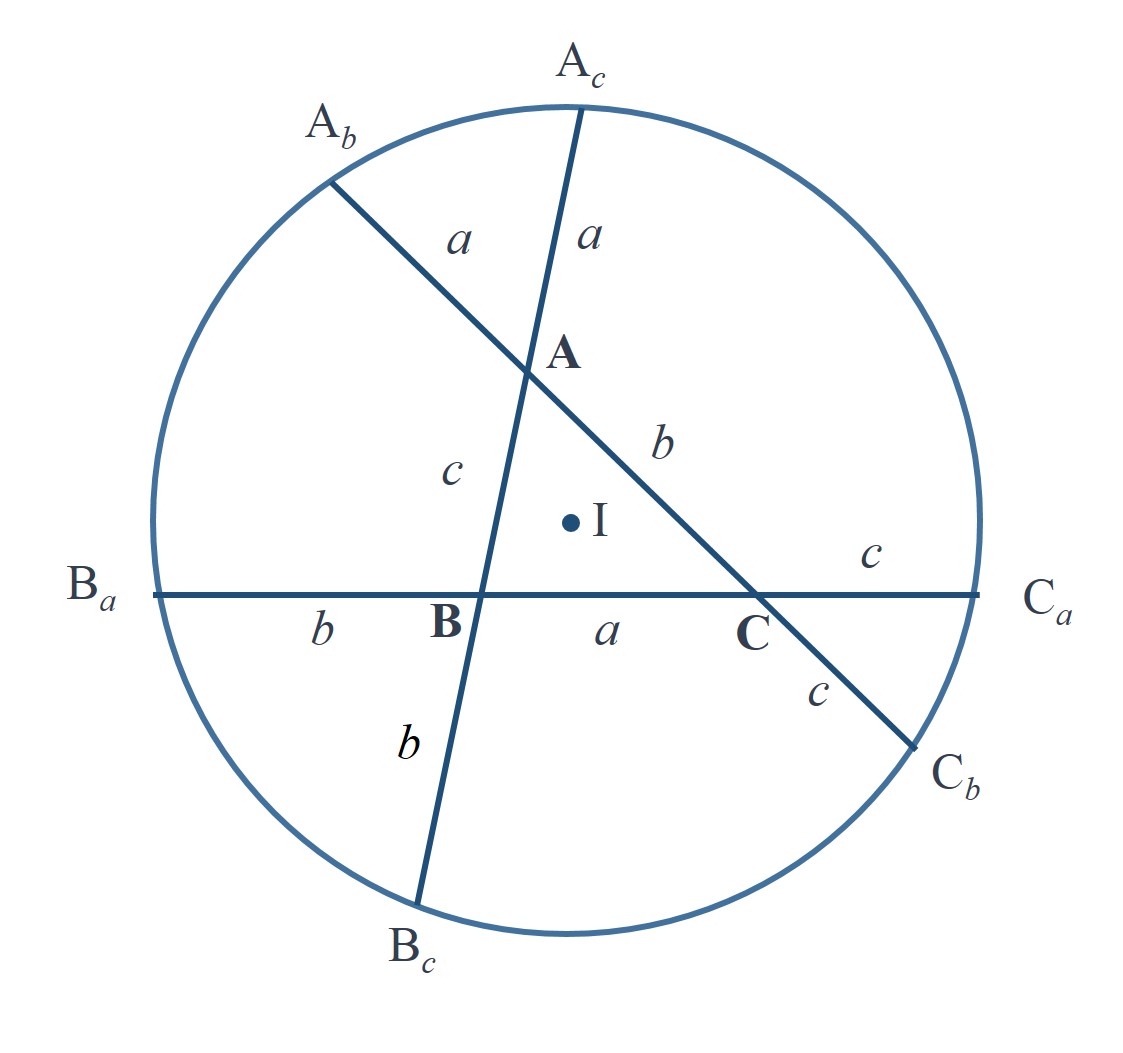
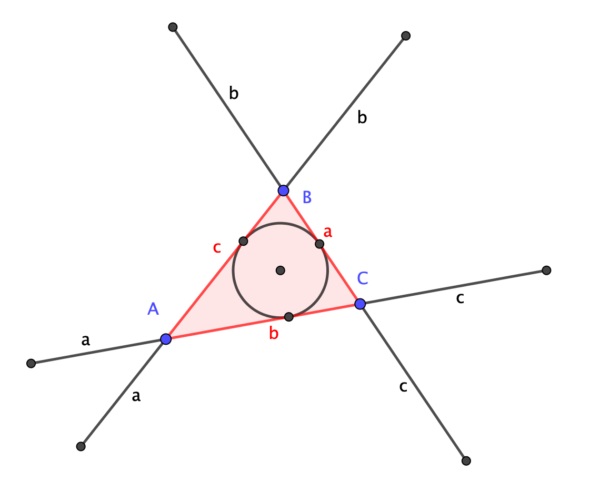
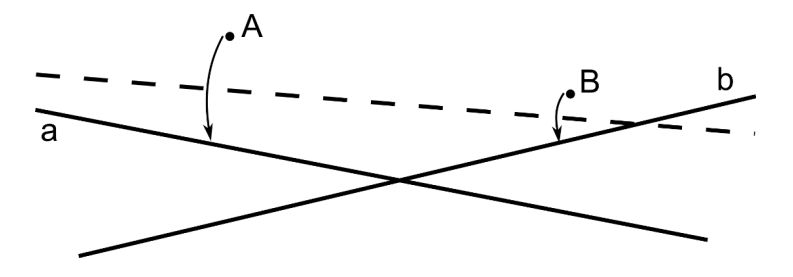
Teorema de la circunferencia de Conway: Dado un triángulo ABC, de lados a = BC, b = AC y c = AB (como se muestran en la imagen), se extienden los lados a, b y c, y se consideran los puntos Ab y Ac, que están a una distancia a en las rectas extensión de b y c, es decir, AAb = AAc = a, de igual forma se consideran los puntos Ba y Bc, que están a una distancia b en las rectas extensión de a y c, y Ca y Cb, que están a una distancia c en las rectas extensión de a y b, entonces los puntos Ab, Ac, Ba, Bc, Ca y Cb son concíclicos, es decir, están en una misma circunferencia, a la cual se denomina “circunferencia de Conway”. Más aún, el centro de la circunferencia de Conway es el incentro del triángulo ABC.
Al parecer John Conway nunca publicó nada de este resultado geométrico. Según aparece recogido en el blog de la matemática Tanya Khovanova (Tanya Khovanova’s Math Blog), el matemático tenía una camiseta del campamento de verano de matemáticas Mathcamp de 1998 en el que aparecía una ilustración de este teorema con la expresión “la circuferencia de Conway”, que vemos en la siguiente imagen. Es probable que Conway solo lo presentara de forma oral en estos campamentos o en algún evento similar.
 Fotografía de John Conway con su camiseta con el denominado teorema de la circunferencia de Conway del Mathcamp’98. Imagen de Tanya Khovanova en su blog
Fotografía de John Conway con su camiseta con el denominado teorema de la circunferencia de Conway del Mathcamp’98. Imagen de Tanya Khovanova en su blog
Sobre esta fotografía su autora comenta que “el pobre John Conway tuvo que estar de espaldas a mí hasta que descubrí la prueba del teorema y me di cuenta de qué punto debía ser el centro de la circunferencia de Conway”.
A partir del fallecimiento de Conway y la publicación del matemático Matt Baker en su blog, empezaron a publicarse diferentes demostraciones del teorema de la circunferencia de Conway, como se recoge en la página web del matemático irlandés Colm Mulcahy. Por ejemplo, la matemática estadounidense Doris Schattschneider obtuvo dos demostraciones en 2020 (abril y mayo), de la segunda de las cuales dijo que “es mucho más bonita y convincente. Una demostración que creo que Conway habría sido más propenso a realizar él mismo”, basada en un hexágono y que puede leerse en la página de Colm Mulcahy.
Sin embargo, la demostración que recogemos aquí fue obtenida por el matemático británico Alex Ryba, en mayo de 2020. Es una demostración sencilla basada en triángulos isósceles. Mostramos una ilustración con el triángulo ABC y las extensiones de longitudes a, b y c en los vértices A, B y C, con los puntos extremos Ab, Ac, Ba, Bc, Ca y Cb, que son los que hay que demostrar que están en una circunferencia de centro I, el incentro del triángulo ABC, es decir, que todos ellos equidistan del punto I.
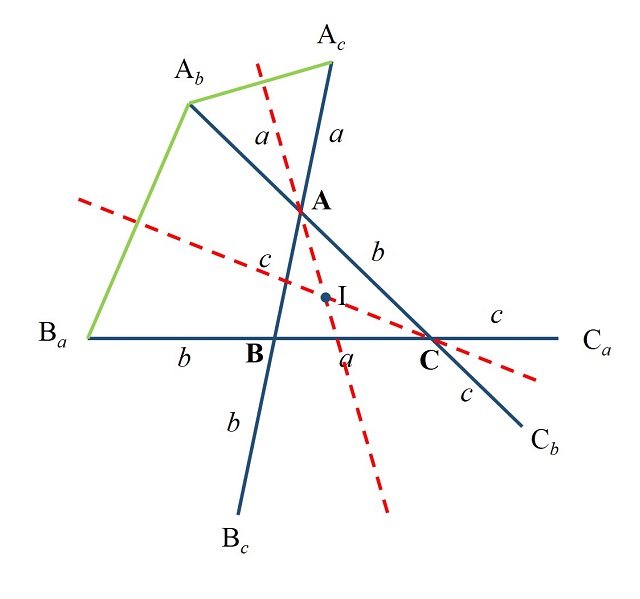
La demostración de Ryba es la siguiente: Los triángulos AbAAc y BaCAb son triángulos isósceles, con ápices (es decir, los vértices formados por los lados iguales) A y C, por lo tanto, las rectas mediatrices de las bases AbAc y BaAb (en rojo en la imagen) son además las rectas que bisecan los ángulos en los ápices A y C (llamadas bisectrices), luego son las bisectrices de los ángulos en A y C del triángulo ABC, luego se intersecan en el incentro I del triángulo ABC (esto es debido a que el incentro del triángulo es también el punto en el que se intersecan las tres bisectrices del mismo). Además, puesto que las rectas son las mediatrices de las bases AbAc y BaAb, y se cortan en I, entonces los puntos Ba, Ab y Ac equidistan de I. Argumentos similares nos determinan que los puntos Cb, Bc y Ba equidistan de I, así como Ac, Ca y Cb. Y el resultado queda probado.
Y han ido apareciendo más demostraciones del resultado, pero también se han descubierto demostraciones anteriores, como la publicada por el matemático cordobés Francisco Javier García Capitán en Forum Geometricorum, en 2013, en el artículo A Generalization of the Conway Circle. En este artículo se menciona que “esta configuración también apareció en el Problema 6 de la Olimpiada Matemática Iberoamericana de 1992”.
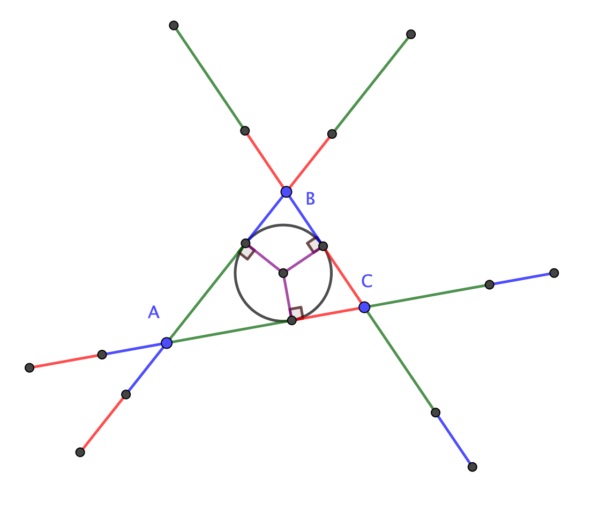
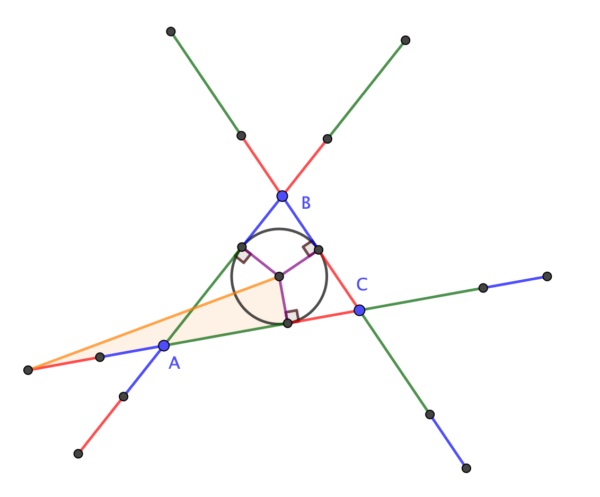
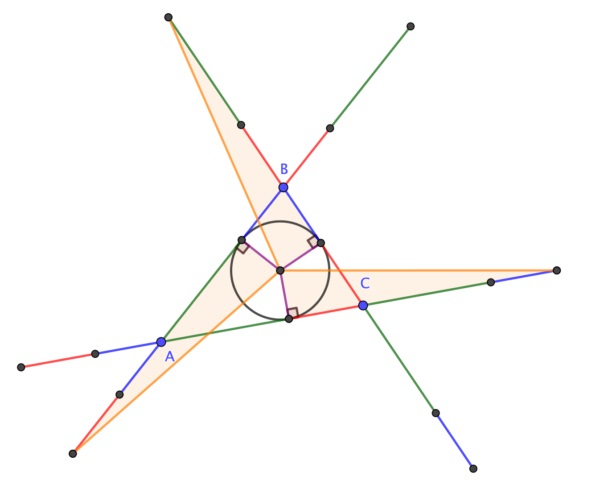
Respecto a la demostración sin palabras de este resultado geométrico, en 2020 el matemático británico Colin Beveridge, autor de libros como La biblia de las matemáticas, Guía para comprender y disfrutar el mundo de las matemáticas (Gaia, 2016) o Lo que las Matemáticas Esconden… Descubre las Matemáticas del Día a Día (Libsa, 2019), publicó en el blog The Aperiodical una hermosa demostración sin palabras del teorema de la circunferencia de Conway. Esta demostración consiste en una serie de seis imágenes que incluimos a continuación, que os dejamos para que seáis vosotros mismos quienes comprobéis que efectivamente demuestra el teorema de la circunferencia de Conway.
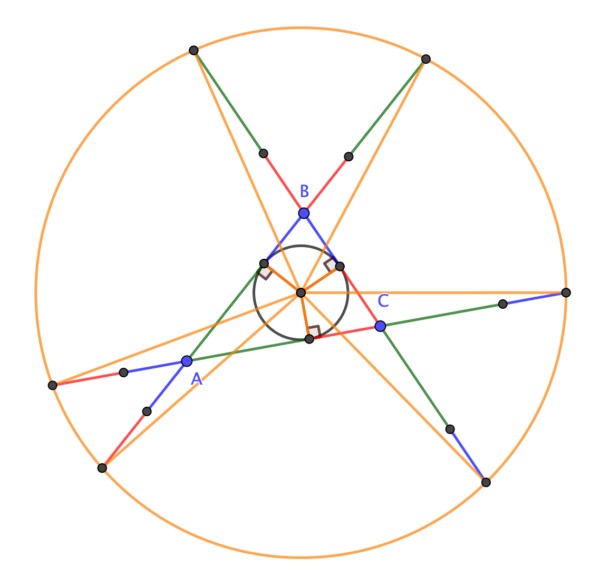
Al igual que en la anterior entrada, vamos a terminar esta con otro sencillo problema que puede ser resuelto con un razonamiento visual. Este problema, como el de la primera entrada de esta serie estival, es otro problema sobre cuadrados que aparece recogido en el artículo A Round-Up of Square Problemas (Una recopilación de problemas con cuadrados), de los matemáticos Duane Detemple y Sonia Harold, publicado en Mathematics Magazine en 1996.
Problema (Un cuadrado inscrito en un triángulo rectángulo isósceles): Estos dos cuadrados han sido inscritos en un mismo triángulo rectángulo isósceles, pero de dos formas distintas, como se muestra en la imagen. ¿Cuál de los dos cuadrados tiene una mayor superficie?
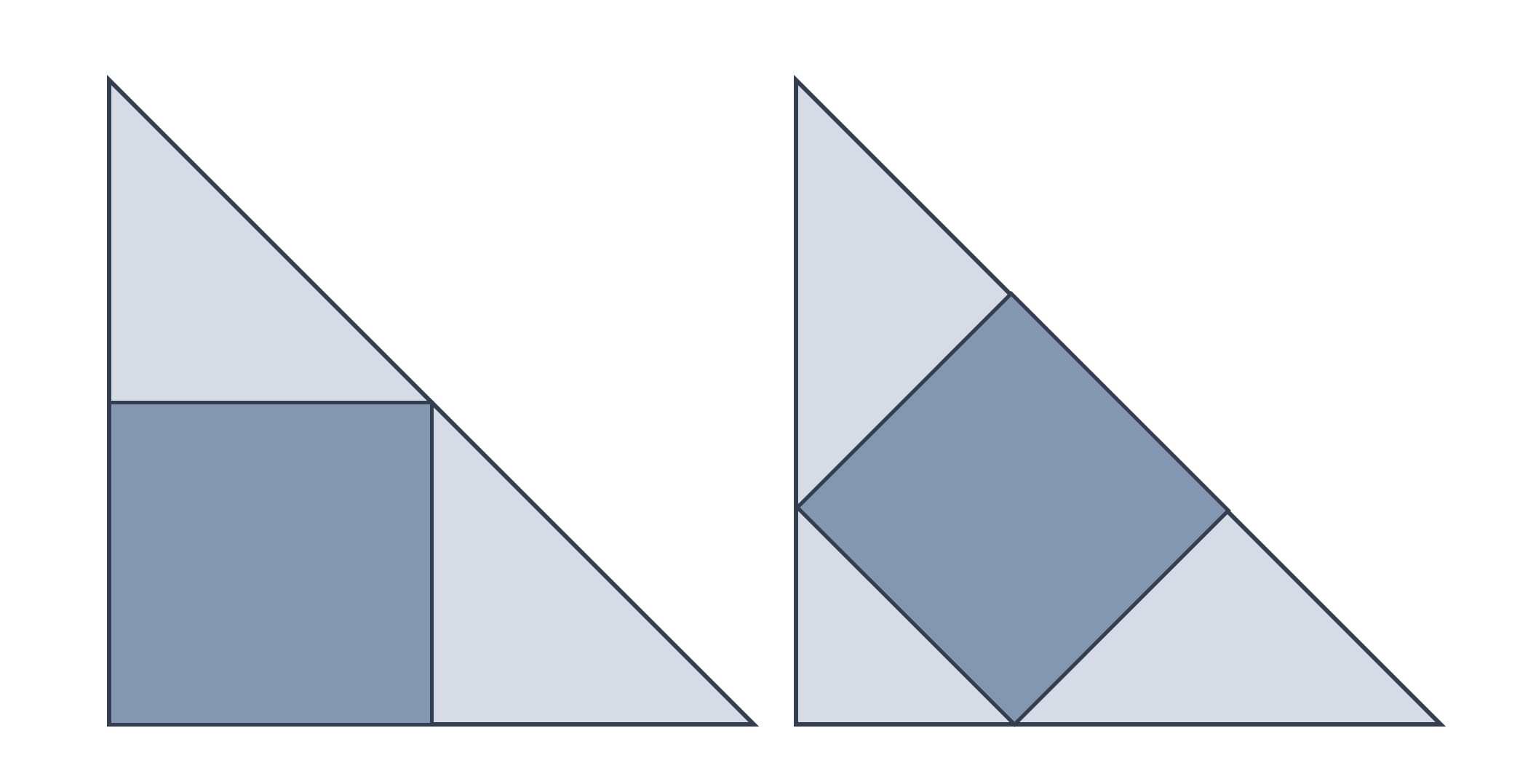
Bibliografía:
1.- Roger B. Nelsen, Proofs without Words: Exercises in Visual Thinking, Mathematical Association of America, 1997.
2.- Roger B. Nelsen, Proofs Without Words II: More Exercises in Visual Thinking, Mathematical Association of America, 2001.
3.- Claudi Alsina y Roger B. Nelsen, Charming Proofs, A Journey Into Elegant Mathematics, Mathematical Association of America, 2010.
4.- Wolfram MathWorld: Conway circle (Darij Grinberg y Eric W. Weisstein)
5.- Francisco Javier García Capitán, A Generalization of the Conway Circle, Forum Geometricorum, vol. 13, pp. 191-195, 2013.
6.- Duane Detemple y Sonia Harold, A Round-Up of Square Problemas, Mathematics Magazine 69, no. 1, pp. 15-27, 1996.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Teoremas geométricos sin palabras: Conway se ha escrito en Cuaderno de Cultura Científica.
Einstein y Georges Lemaître
El astrónomo y sacerdote jesuita Georges Lemaître fue el primero en sugerir que la totalidad del universo comenzó a partir de un solo “átomo primigenio” en algún momento en el tiempo; esta sería la primera versión de lo que ha llegado a ser la teoría actual del Big Bang*. Einstein menospreció el modelo de Lemaître, como hizo con todos los modelos en los que el universo se expandía, pero al final tuvo que admitir que Lemaître podía tener razón.
 Einstein y Lemaître tras la conferencia mencionada en el texto, en 1933. Fuente: KU Leuven
Einstein y Lemaître tras la conferencia mencionada en el texto, en 1933. Fuente: KU LeuvenTras ordenarse presbítero en 1923, Lemaître continuó sus estudios de astronomía con Arthur Eddington en la Universidad de Cambridge (Reino Unido) para después completarlos con Harlow Shapley en el Observatorio del Harvard College (EE. UU.). Para finalizar su formación académica se inscribió para el doctorado en el Instituto de Tecnología de Massachusets (MIT, por sus siglas en inglés; EE. UU.). Fue aquí donde Lemaître comenzó a pensar acerca de la historia del universo.
De hecho, Lemaître no estaba familiarizado con las ecuaciones de la relatividad de Einstein: él no creó un modelo de la historia del universo basándose en ideas sobre la estructura del universo como habían hecho Willem de Sitter o Alexander Friedmann. Lemaître se basó en la termodinámica, en concreto en la segunda ley y su concepto de entropía: todo sistema se mueve de un estado de orden a otro de desorden. Otra forma de interpretar la entropía es que toda la energía que se puede usar del sistema se pierde en el transcurso del tiempo, hasta que toda la energía termina desapareciendo. Si esto es cierto para cualquier sistema, también lo es para el universo.
El universo, por tanto, debe haber empezado en un estado de máxima energía, perdiendo energía paulatinamente hasta que finalmente muera. La conclusión lógica de la termodinámica, dijo Lemaître, era un modelo del universo en el que éste se expandiese con el tiempo: un universo que comenzó mucho más pequeño de lo que es ahora, tan pequeño que todo el universo estaba originalmente comprimido en un minúsculo átomo. Nuestro universo “estalló” a partir de esta increíblemente densa primera partícula y este universo continuaría expandiéndose, perdiendo energía y hasta llegar gradualmente a detenerse. Lemaître publicó su teoría de lo que él llamaba el “átomo primigenio” en 1927, nada más volver a Bélgica para enseñar astrofísica en la Universidad de Lovaina.
La cosmovisión de LemaîtreEn esa época, la mayoría de los científicos asumían que el universo siempre había existido tal y como es en la actualidad. Creer en un universo cambiante, es decir, creer en “un momento de creación”, parecía demasiado cercano a la religión y al misticismo. El mismo Lemaître, a pesar de su profunda cosmovisión católica, también pensaba que la ciencia y la fe no deben confundirse entre sí; según él se emplean metodologías diferentes en cada una y, al menos el propio Lemaître, nunca usó una disciplina para confirmar o negar la otra.
En cualquier caso, la familiaridad de Lemaître con la historia del génesis en la Biblia judeo-cristiana y su evidente creencia en un creador influyeron probablemente en la facilidad con la que aceptó una teoría que sugería un universo que había “empezado” en un momento dado. A diferencia de muchos de los contemporáneos de Lemaître, él creía que su teoría del átomo primigenio era una verdadera realidad física, no un simple modelo matemático, como habían dicho de Sitter y Friedmann de los suyos.
En el momento en que Lemaître publicó sus teorías por primera vez, Einstein ya había dejado bastante claras sus ideas sobre un universo en expansión. Ya había publicado sus críticas a los modelos en expansión de de Sitter y Friedmann, y su respuesta al de Lemaître no fue diferente. Einstein se vio obligado a admitir que las matemáticas parecían funcionar, pero se quejaba de que la física era “abominable”. Al igual que con la mecánica cuántica, las matemáticas parecían no poder desmentir a sus prejuicios, y Einstein despreció la idea de un universo en expansión sin más.
Como decíamos más arriba, a diferencia de de Sitter y Friedmann, Lemaître no creó un modelo solo con objetivos intelectuales. Creía que se correspondía con la realidad. Basándose en los conocimientos físicos de la época, Lemaître lanzó la hipótesis de que el átomo primigenio estaba formado por elementos radioactivos que comenzaron una reacción en cadena. La energía liberada en esta reacción en cadena habría forzado una expansión inmediata y espectacular del universo; en el proceso también habría creado vida. Lemaître era plenamente consciente de que su versión del origen del universo sería modificada a lo largo del tiempo conforme los principios de la física atómica y nuclear fuesen mejor comprendidos.
No fue hasta los años 60 que la versión moderna de la teoría del Big Bang fue aceptada y, tal y como Lemaître predijo, la teoría de lo que existía en el momento del Big Bang y por qué comenzó a expandirse era muy diferente a sus ideas originales. Lemaître fue, sin embargo, el primer científico en aceptar verdaderamente el concepto de que el universo tuvo un principio.
También Einstein, tuvo que aceptar las ideas de Lemaître. El anuncio en 1929 por parte de Edwin Hubble de que las observaciones efectivamente apuntaban hacia un universo en expansión, convenció finalmente a Einstein de que debía abandonar su noción preconcebida de un universo estático. Unos años después, en 1933, Einstein dio a Lemaître el mérito debido. En una conferencia en el Instituto Tecnológico de California en la que Lemaître describió el universo en expansión, Einstein se levantó a la conclusión, aplaudió y dijo “Esta es la explicación más hermosa y satisfactoria de la creación que haya escuchado jamás”.
Nota:
[*] Las expresiones y planteamientos que se mencionan en el texto corresponden a la visión original de Lemaître de finales de los años 20 y comienzo de los 30 del siglo pasado. La teoría actual del Big Bang es mucho más elaborada y compleja y existen conceptos, como los de tiempo o de composición, que difieren de forma radical de los expresados hace casi un siglo. Para más información sobre el modelo actual puede consultarse el enlace.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Una versión anterior de este artículo se publicó en Experientia Docet el 27 de septiembre de 2009.
El artículo Einstein y Georges Lemaître se ha escrito en Cuaderno de Cultura Científica.
¿Por qué Júpiter no tiene unos anillos tan espectaculares como Saturno?
Uno de los hechos más llamativos –al menos visualmente- de los gigantes gaseosos de nuestro Sistema Solar es que el sistema de anillos de Júpiter es mucho más tenue de lo que cabría esperar, especialmente si lo comparamos con los majestuosos anillos de Saturno. Tanto es así que fue el tercer sistema de anillos descubierto en nuestro Sistema Solar, concretamente después de los de Saturno y Urano, gracias a las observaciones realizadas por la sonda Voyager 1 en 1979 durante su visita al sistema joviano y el único que ha necesitado de una sonda espacial para su descubrimiento.
 Anillos de Júpiter observados por primera vez desde la Voyager 1. Cortesía de la NASA/JPL
Anillos de Júpiter observados por primera vez desde la Voyager 1. Cortesía de la NASA/JPLEs también destacable que, al menos en nuestro sistema planetario, todos los gigantes gaseosos tengan anillos, como si de alguna forma fuese una característica común a este tipo de planetas, algo que podremos verificar en el futuro observando los planetas extrasolares y comprobando si efectivamente se cumple esta regla.
Incluso es posible que en los últimos días hayas visto por primera vez los anillos de Júpiter gracias a las imágenes del telescopio espacial James Webb, que durante su etapa de calibración apuntó al planeta tomando un espectacular retrato en infrarrojo en el que estos son visibles, algo que llama poderosamente la atención, especialmente si comparamos esta imagen con otras similares tomadas por el Hubble, aunque en luz visible, en las que no hay rastro del anillo.
 Imagen de Júpiter en el infrarrojo tomada por el JWST. Se aprecian sutilmente los anillos y a la izquierda, la “estrella” brillante es Europa, un satélite de Júpiter. Cortesía de NASA, ESA, CSA, B. Holler y J. Stansberry (STScI)
Imagen de Júpiter en el infrarrojo tomada por el JWST. Se aprecian sutilmente los anillos y a la izquierda, la “estrella” brillante es Europa, un satélite de Júpiter. Cortesía de NASA, ESA, CSA, B. Holler y J. Stansberry (STScI)Pero vayamos al grano del asunto: ¿Por qué los anillos de Júpiter son tan diferentes a los de Saturno? Tenemos que ser conscientes que los mecanismos de formación de los anillos, así como los mecanismos que afectan a su longevidad -desconocemos con certeza si en todos los casos los sistemas de anillos son más o menos permanentes o si tienen una duración determinada por distintos factores- no se comprenden del todo y hay diferentes teorías que podrían explicarlos.
El caso es que nuevo artículo apunta a que, muy probablemente, los responsables de la escasa densidad de los anillos de Júpiter han sido sus satélites. Los científicos han realizado simulaciones físicas en las cuales la existencia de grandes satélites dificultaba la capacidad del planeta para mantener un gran sistema de anillos.
Esto nos hace pensar que Júpiter tuvo en el pasado unos anillos más densos, aunque quizás no en el sentido que lo son los de Saturno, pero la presencia de los satélites galileanos fue barriendo de sus órbitas las partículas de hielo y polvo que conformaban este sistema, ya fuese dándoles más velocidad y acabando por ser expulsadas del sistema joviano o atrayéndolas hacia los satélites, acabando sobre la superficie de estos.
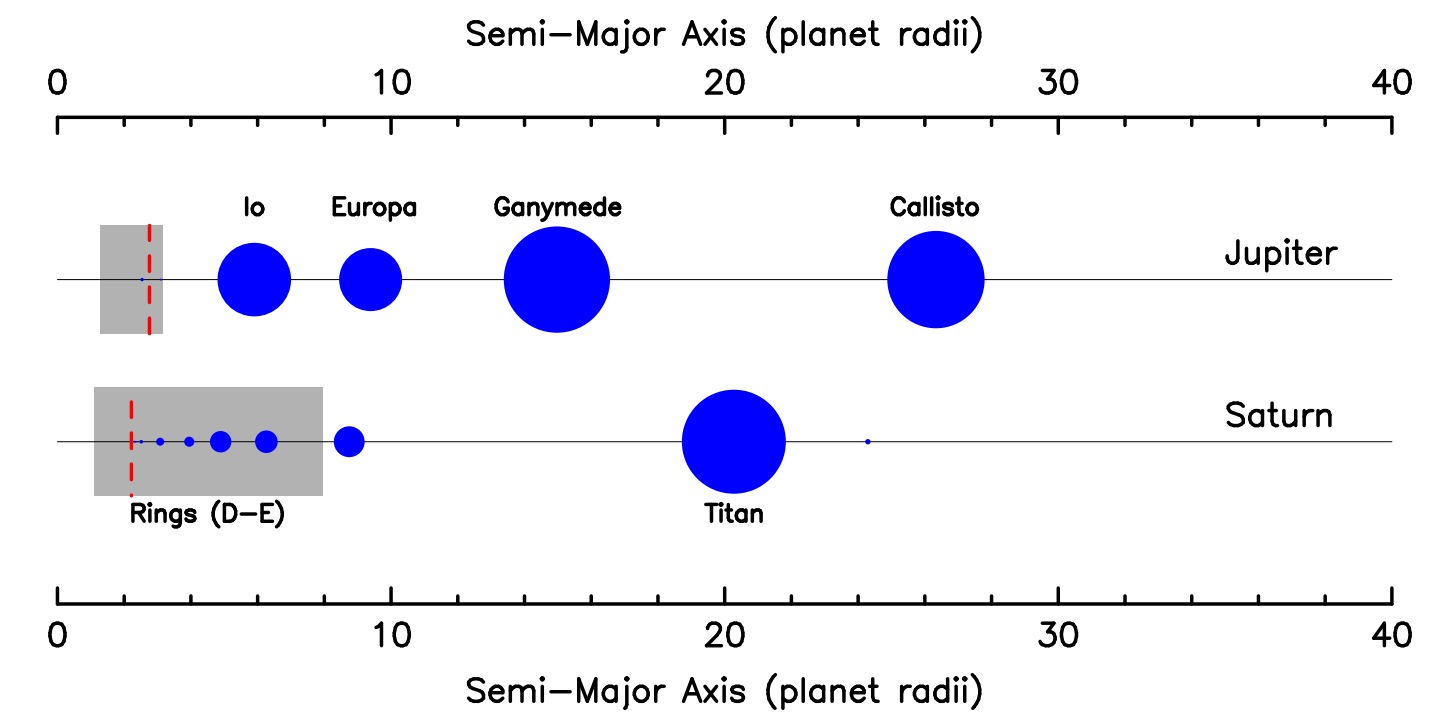 Distribución de satélites por tamaño y distancia en Júpiter y Saturno. En gris, la región donde se encuentran los anillos en cada uno de los planetas. Cortesía de Kane et al (2022)
Distribución de satélites por tamaño y distancia en Júpiter y Saturno. En gris, la región donde se encuentran los anillos en cada uno de los planetas. Cortesía de Kane et al (2022)Saturno también tiene satélites, pero el papel de los satélites en su sistema de anillos es diferente por diversos factores: el primero, la masa de los satélites en el entorno e interior del sistema de anillos es mucho menor que en el sistema joviano, que tiene muy cerca de los anillos a los satélites galileanos, y, por otro, los pequeños satélites que hay dentro de los anillos de Saturno ayudan por el efecto de la gravedad que ejercen sobre las partículas del anillo, a mantenerlos estables.
Además, estos satélites incluso pueden contribuir a mantener la densidad de partículas de los anillos, ya que los impactos que sufren estas lunas pueden lanzar partículas a la órbita de Saturno y que acaben formando parte de estos.
 El anillo E de Saturno está compuesto principalmente por partículas expulsadas de Encélado, una de las de mayor actividad geológica de nuestro Sistema Solar, contribuyendo a la longevidad del propio anillo, que va recibiendo un aporte continuo de material. Imagen cortesía de la NASA/JPL
El anillo E de Saturno está compuesto principalmente por partículas expulsadas de Encélado, una de las de mayor actividad geológica de nuestro Sistema Solar, contribuyendo a la longevidad del propio anillo, que va recibiendo un aporte continuo de material. Imagen cortesía de la NASA/JPL¿Por qué son tan interesantes los anillos desde el punto de vista de la geología? Puesto que es muy difícil conocer el interior de los gigantes gaseosos debido a sus tremendas condiciones de presión, temperatura, vientos y gravedad, la oscilación de las partículas de los anillos nos puede ayudar a descubrir la distribución de las masas en el interior de los planetas.
Pero también pueden ser un reservorio de partículas primigenias de la formación de nuestro Sistema Solar, especialmente en algunas regiones que pueden haber sufrido menos perturbaciones gravitatorias por parte de los distintos satélites, y que nos servirían para muestrear su composición.
Incluso podrían servirnos para desentrañar la historia de la evolución dinámica de los mini sistemas “planetarios” que tienen, por norma general, a su alrededor los gigantes gaseosos, abriéndonos también una ventana a estudiar las causas de la actividad interna de algunos de estos satélites.
Así que tenemos que ver los anillos como algo más que un bonito adorno planetario y maravillarnos no solo con el reflejo de su luz y sus discontinuidades, sino como una verdadera fuente de información de la que podremos aprender detalles
Bibliografía:
Kane, S. R., & Li, Z. (2022). The Dynamical Viability of an Extended Jupiter Ring System (Version 2). arXiv. doi: 10.48550/ARXIV.2207.06434
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo ¿Por qué Júpiter no tiene unos anillos tan espectaculares como Saturno? se ha escrito en Cuaderno de Cultura Científica.
Herramientas biológicas multiusos
 Ictidomys tridecemlineatus Fuente: Wikimedia Commons
Ictidomys tridecemlineatus Fuente: Wikimedia CommonsLos mamíferos que viven en nuestra latitud y más al norte han de afrontar una situación difícil si permanecen activos durante el invierno. Por un lado, deben gastar mucha energía para contrarrestar la pérdida de calor que experimentan al bajar la temperatura ambiental. Por el otro, al haber poca comida, difícilmente pueden obtener del alimento la energía que necesitan gastar para producir el calor necesario que les permita mantener su temperatura corporal constante. Han de recurrir, para ello, a metabolizar las reservas almacenadas.
Por esa razón, unos cuantos mamíferos que habitan en zonas geográficas en las que en invierno hace mucho frío y hay poca comida, hibernan. Sortean esa situación, la esquivan. No se mantienen activos durante ese periodo. Suprimen la actividad física y reducen mucho la temperatura corporal; podría decirse que “renuncian” a mantenerla elevada. De esa manera su metabolismo sufre un descenso muy fuerte, gastan así mucha menos energía. La hibernación es, en definitiva, un mecanismo de ahorro. Pero es un mecanismo que esconde misterios. Uno de ellos es la forma en que se las arreglan los animales que la practican para evitar perder masa muscular durante los meses que pasan en letargo. Cuando un animal permanece inactivo durante un periodo largo de tiempo, lo normal es que pierda masa muscular.
Los animales reciclamos proteínas de manera permanente. Continuamente las degradamos para volver a sintetizarlas a continuación; están sometidas a renovación sin pausa. Pero ese reciclaje no cursa con una eficiencia del 100%. Una pequeña parte del nitrógeno de las proteínas se pierde. Los mamíferos eliminamos ese nitrógeno en la orina mediante la molécula de urea.
Debido a la caída de la actividad metabólica, la velocidad a que se renuevan las proteínas disminuye mucho durante la hibernación, por lo que también baja mucho la cantidad de nitrógeno que se podría perder así. No obstante, a pesar de que esa gran bajada del metabolismo la minimiza, la pérdida de nitrógeno podría ser de tal magnitud que provocase una pérdida muscular considerable. Sorprendentemente, eso apenas ocurre; los pequeños mamíferos que hibernan apenas pierden musculatura. Tan es así que cuando recuperan su nivel de actividad normal a final de invierno o primavera, su masa muscular apenas ha disminuido y pueden desarrollar una vida normal.
Un hallazgo reciente ha arrojado luz sobre este misterio. En un estudio hecho con ardillas de la especie Ictidomys tridecemlineatus se ha descubierto que unas bacterias que viven en su intestino -en sus ciegos intestinales, para ser precisos- parecen tener un papel crucial en este asunto. Una parte, al menos, de la urea que resulta de la degradación de proteínas en el hígado es transportada por la sangre hasta los ciegos intestinales. Una vez allí, unas bacterias rompen las moléculas de urea y las transforman en moléculas de amonio -que es la forma disuelta del amoniaco- y de dióxido de carbono. Utilizan el amonio resultante para sintetizar aminoácidos que son absorbidos desde la luz intestinal de las ardillas a la sangre. Y de esa forma llegan a las células, donde son utilizados para sintetizar proteínas.
El proceso recuerda mucho a lo que ocurre en el sistema digestivo de los rumiantes, donde los microorganismos desempeñan, entre otras, esa misma función, recuperando el nitrógeno que se podría perder en forma de urea y utilizándolo para sintetizar sus propios aminoácidos que, tras ser absorbidos, son usados para sintetizar nuevas proteínas. Un mismo mecanismo, la conversión de la urea en aminoácidos por microorganismos simbiontes, sirve al ganado para optimizar el uso del nitrógeno y a los hibernantes para salvaguardar su masa muscular. Esos microorganismos son herramientas biológicas multiusos.
Fuente: M D Regan et al (2022): Nitrogen recycling via gut symbionts increases in ground squirrels over the hibernation season. Science 375 (6579): 460-463.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Herramientas biológicas multiusos se ha escrito en Cuaderno de Cultura Científica.
Las pruebas de la educación: Juan Francisco Navas – El juego de azar en el ámbito escolar

Bilbao volvió a acoger el pasado 20 de mayo de 2022 “Las pruebas de la educación”, una jornada que abordará diversas cuestiones educativas con la evidencia científica existente. Esta quinta edición está organizado por la Cátedra de Cultura Científica de la UPV/EHU y la Fundación Promaestro con la colaboración del Consejo Escolar de Euskadi, y se celebró en el Bizkaia Aretoa – UPV/EHU de la capital vizcaína.
La jornada consta de cinco ponencias de media hora de duración en la que se tratan temas como la problemática relacionada con los juegos de azar en el ámbito escolar, el impacto de la inmigración en el rendimiento del alumnado o el debate sobre la jornada escolar continua o partida, entre otras cuestiones. La dirección del seminario corrió de nuevo a cargo de Marta Ferrero profesora de la Facultad de Formación del Profesorado y Educación de la Universidad Autónoma de Madrid.
Para dar comienzo a la sesión, el profesor de la Universidad Complutense de Madrid Juan Francisco Navas aborda la problemática de los juegos de azar, actividad con un gran potencial adictivo, en el ámbito escolar y sobre cómo el ofrecer información al alumnado de las trampas y riesgos que conlleva esta actividad puede ser la base para que desarrollen las herramientas necesarias que les ayuden a no apostar.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Las pruebas de la educación: Juan Francisco Navas – El juego de azar en el ámbito escolar se ha escrito en Cuaderno de Cultura Científica.
Las nanopartículas para el tratamiento de la metástasis hepática dan el siguiente paso
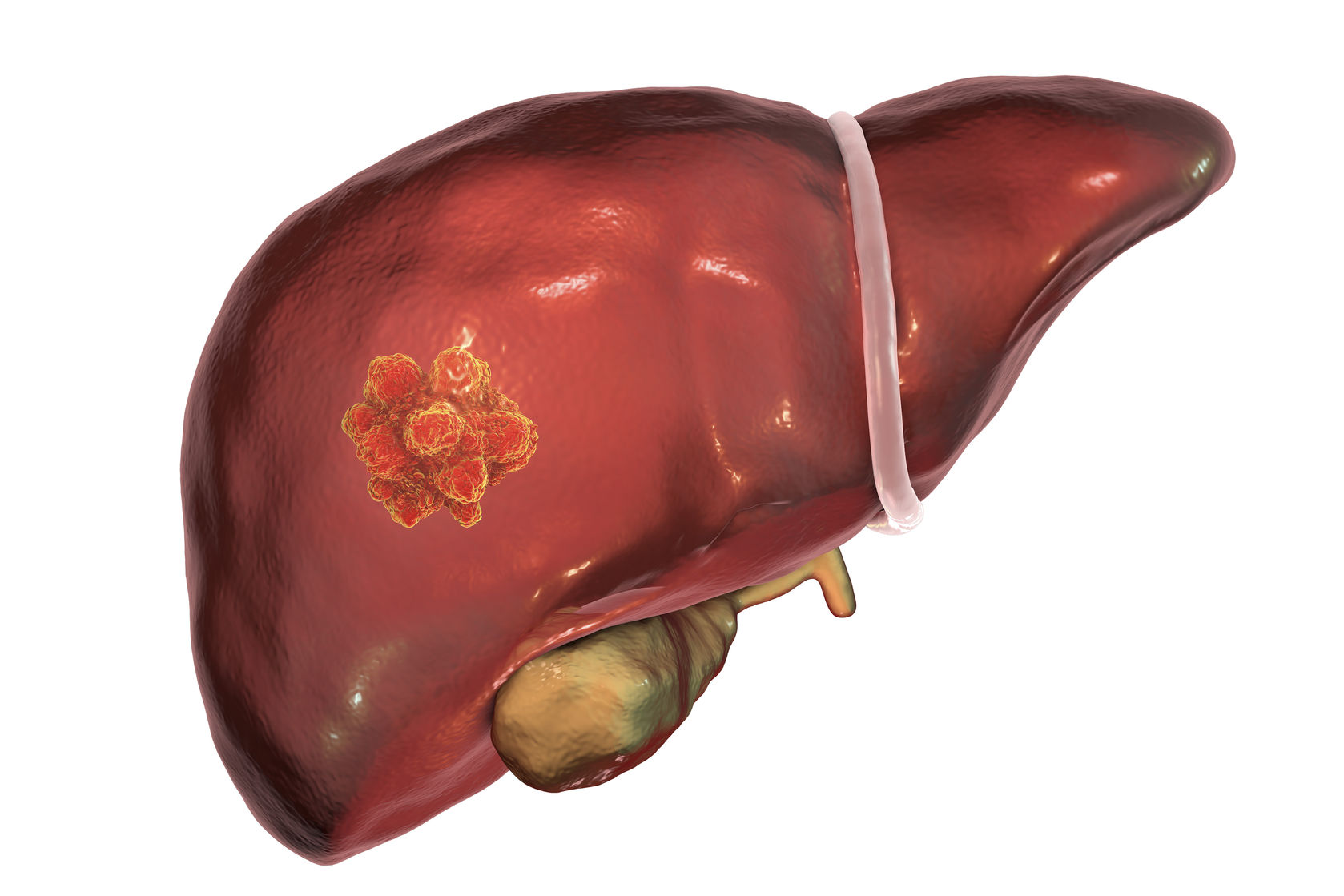 Fuente: UPV/EHU
Fuente: UPV/EHULa división de cáncer del grupo Signaling Lab de la Universidad del País Vasco, dirigida por Iker Badiola, profesor de la Facultad de Medicina y Enfermería de la UPV/EHU, en colaboración con el grupo de investigación del profesor Alejandro Sánchez de la Universidad de Santiago de Compostela, ha desarrollado una nanopartícula que ha demostrado su eficacia reduciendo la metástasis hepática en un 80% en pruebas con ratones. Al año se producen en el mundo alrededor de 1.500.000 de casos de metástasis hepática por cáncer de colon (800.000) y de cáncer de hígado (700.000).
La formulación fue presentada al programa de estudios preclínicos del Instituto Nacional del Cancer (National Cancer Institute, NCI) de los Estados Unidos, del Instituto Nacional de Salud (National Institute of Health, NIH) norteamericano, que la ha seleccionado para someterla a pruebas preclínicas en sus laboratorios homologados, tras superar un severo proceso de selección. En el programa de investigación también participa la agencia reguladora del medicamento estadounidense (Food and Drug Administration, FDA).
Un revulsivo para su desarrollo a gran escalaEsta nanopartícula ha sido patentada por la Universidad del País Vasco y recibió el premio Ernesto Vieitez otorgado por la Real Academia de las Ciencias Gallegas en 2019. La formulación ha sido transferida para su desarrollo a la empresa Nanokide Therapeutics SL, una spin-off del grupo de investigación Signaling Lab creada en 2021 en Zitek, el programa de apoyo al emprendimiento del Campus de Bizkaia de la UPV/EHU.
La empresa Nanokide Therapeutics SL trabaja en el campo de las terapias avanzadas y desarrollo formulaciones basadas en nanosistemas para el tratamiento del cáncer combinando nanoestructuras con tecnología miRNA y mRNA.
El profesor Iker Badiola, uno de los creadores de la nanopartícula y socio fundador Nanokide Therapeutics SL ha destacado la importancia del logro tanto en su vertiente científica como empresarial: «Desde el punto de vista científico ha sido avalado por una de las entidades científicas más importantes del mundo y, desde el punto de vista empresarial, se trata de un certificado de calidad que puede impulsar la proyección de Nanokide Therapeutics SL». Badiola apunta a que «la presencia de entidades como la FDA en el programa, que realizan la labor de vigilancia tecnológica, son un aval de gran valor de cara a la consecución de financiación y socios estratégicos para Nanokide Therapeutics en el desarrollo a su aplicación clínica».
Para saber más:
Nanopartículas para reducir la metástasis hepática del cáncer de colon
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Las nanopartículas para el tratamiento de la metástasis hepática dan el siguiente paso se ha escrito en Cuaderno de Cultura Científica.
¿Mar o montaña?
Esta es la pregunta que todo el mundo se hace cuando llegan estas fechas del año, ¿a dónde nos vamos de vacaciones? ¿Mar o montaña? Y muchas veces nos hemos respondido lo mismo: Ojalá fuera posible estar en los dos sitios a la vez. Pues os voy a contar un secreto. En realidad, se puede… gracias a la Geología.
Por supuesto, esto tiene truco. Es muy probable que, si habéis dado un paseo por el monte mirando hacia las rocas de vuestro alrededor, os hayáis topado con algunos fósiles de antiguos organismos marinos. Cefalópodos ya extintos, como los ammonites y belemnites, erizos de mar, corales, esponjas, bivalvos, crinoideos, trilobites y un largo etcétera pueden acompañarnos en nuestro recorrido por una montaña con más de mil metros de altura y situada a cientos de kilómetros de la playa más cercana. Así que, en estos casos, si miramos lo que nos rodea con ojos geológicos y dejamos volar un poco nuestra imaginación, nos encontraremos dando un paseo por la montaña a la vez que buceamos en un mar con varios millones de años de antigüedad.
 Detalle del fósil de un coral de hace más de 100 millones de años preservado en las rocas del monte Ranero, Karrantza (Bizkaia). El dedo se incluye como referencia para el tamaño. Imagen de Iranzu Laura Guede.
Detalle del fósil de un coral de hace más de 100 millones de años preservado en las rocas del monte Ranero, Karrantza (Bizkaia). El dedo se incluye como referencia para el tamaño. Imagen de Iranzu Laura Guede.La presencia de estos fósiles marinos en zonas tan alejadas del litoral actual ha sido objeto de debate durante milenios. Incluso, hasta no hace mucho tiempo, era una prueba irrefutable del Diluvio Universal. La única explicación posible era que el mar hubiera cubierto esas zonas tan elevadas y después descendiera el nivel del agua hasta donde lo encontramos en la actualidad.
Pero esa explicación no convencía a todo el mundo. Uno de los más reacios a creerla fue Leonardo da Vinci. Hace más de 500 años, Leonardo encontró un montón de fósiles marinos en las montañas del norte de Italia. Y lo que más le llamó la atención fue observar que muchos de los fósiles de conchas marinas conservaban juntas las dos valvas. Esto entraba en contradicción con una inundación rápida y catastrófica, porque la fuerza del agua habría separado, roto y fragmentado las valvas. Así que Leonardo le dio la vuelta a la tortilla y planteó que lo que hoy son montañas, hace mucho tiempo constituía el fondo marino y que, por algún motivo que él no podía explicar, este suelo oceánico se había elevado hasta formar las grandes cordilleras que vemos en la actualidad.
Durante los siglos posteriores, los padres de la Geología estuvieron dándole vueltas a la idea de Leonardo, hasta que a mediados del siglo XIX surgió una hipótesis que intentaba ser la explicación definitiva, la hipótesis de los geosinclinales. Se sustentaba en la base (que hoy sabemos errónea) de que la Tierra se ha ido enfriando desde su formación, lo que provoca que se vaya encogiendo de forma progresiva. Al encogerse, se debían formar grandes depresiones que actuaban como zonas de acumulación de sedimentos. Pero llegaría un momento en que se depositaría tanta cantidad de sedimento que provocaría que los márgenes de la depresión fuesen acercándose poco a poco y ese empuje de los bordes provocaría el plegamiento y ascenso vertical de los antiguos sedimentos, formando las montañas.
La hipótesis sonaba muy chula, pero tenía un pequeño problema, no podía explicar la formación de todas las cadenas montañosas. Pero la solución apareció a mediados del siglo pasado, cuando empezaron a investigarse en detalle los fondos oceánicos. Esto dio lugar a que, a finales de los años sesenta, se definiese la teoría que, por fin, puede explicar la formación de las montañas, la Tectónica de Placas.
De manera muy resumida, la capa más externa de nuestro planeta, la litosfera, es sólida y rígida y está dividida en trozos que se llaman placas tectónicas. Estos fragmentos se desplazan sobre la capa que tienen justo por debajo, la astenosfera, que es un semisólido plástico y viscoso. Para hacernos una idea, con nuestro planeta ocurre lo mismo que si ponemos una galleta (litosfera) sobre un bol con natillas (astenosfera), partimos la galleta en pedazos (placas tectónicas) y movemos el bol con movimientos continuos de muñeca (desplazamiento de las placas).
Cuando chocan entre sí dos placas tectónicas, parte de los materiales rocosos que se encuentran depositados en sus márgenes se comprimen y se apilan, engrosando la litosfera y dando lugar a una gran acumulación elevada de rocas plegadas y deformadas que denominamos cordilleras montañosas. Este es el proceso de formación de montañas y se llama orogenia (del griego “oros”, montaña, y “génesis”, origen).
 Rocas calizas, formadas en un mar tropical poco profundo hace unos 120 millones de años, que hoy encontramos en la cima del monte Untzillatx, Parque Natural de Urkiola (Bizkaia). Imagen de Iranzu Laura Guede.
Rocas calizas, formadas en un mar tropical poco profundo hace unos 120 millones de años, que hoy encontramos en la cima del monte Untzillatx, Parque Natural de Urkiola (Bizkaia). Imagen de Iranzu Laura Guede.La última gran orogenia todavía continúa en la actualidad, pero tuvo su etapa más compresiva hace entre unos 80 y 20 millones de años aproximadamente, y la conocemos como Orogenia Alpina. Como su propio nombre indica, es la que ha dado lugar a la cordillera de los Alpes, pero también a otras cadenas montañosas más cercanas, como los Pirineos o las Béticas. En nuestro caso, comenzó cuando la placa Africana chocó contra la placa Euroasiática, encontrando a la microplaca Ibérica en medio y apachurrándola de norte a sur. Así, las rocas que se habían formado a partir de los sedimentos depositados en el fondo marino millones de años antes de la colisión de las placas tectónicas, se elevaron al apilarse unos sobre otros y hoy en día se encuentran en la cima de algunos de los cinturones montañosos de mayor altura de nuestra geografía.
Gracias a la dinámica litosférica y la tectónica de placas, cuando vamos a dar un paseo por algunas de las montañas que nos encontramos en la Cordillera Cantábrica, los Pirineos o las Béticas, en realidad estamos pisando rocas formadas hace millones de años en el fondo de mares tropicales llenos de vida. Así que podemos cerrar los ojos e imaginar que estamos buceando en alguna cala de aguas transparentes de las Bahamas. Ya no tenemos que elegir entre mar o montaña, la Geología nos lo ofrece todo a la vez.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo ¿Mar o montaña? se ha escrito en Cuaderno de Cultura Científica.
Margherita Beloch Piazzolla, geómetra
Margherita Beloch Piazzolla tuvo una larga vida con la geometría como eje de estudio e investigación. Desde la matemática teórica a la aplicación de esta disciplina a la resolución de problemas cartográficos o médicos, sus aportaciones fueron notables e ingeniosas.
 Margherita Beloch Piazzolla. Fuente: Enciclopedia delle donne.
Margherita Beloch Piazzolla. Fuente: Enciclopedia delle donne.
Margherita Beloch Piazzolla nació el 12 de julio de 1879 en Frascati, en la provincia de Roma. Su madre, Bella Bailey, era estadounidense. Su padre era el historiador alemán Karl Julius Beloch. Su hermana pequeña, Dorotea, fue una compositora centrada fundamentalmente en la ópera.
Supervisada por el matemático Guido Castelnuovo (el padre de Emma Castelnuovo), Margherita se graduó en la Universidad de Roma La Sapienza en 1908, presentando una tesis sobre transformaciones birracionales en el espacio (Sulle trasformazioni birazionali nello spazio). Por su calidad, fue publicada al año siguiente en la revista Annali di Matematica Pura ed Applicata.
Comenzó a trabajar como asistente voluntaria de Castelnuovo en la Cátedra de Geometría Analítica y Proyectiva. Fue nombrada asistente de geometría descriptiva en la Universidad de Pavía en 1919. Al año siguiente ocupó el mismo cargo en la Universidad de Palermo; allí trabajó junto al especialista en geometría algebraica Michele De Franchis. En 1927 ganó una plaza de catedrática en la Universidad de Ferrara, encargándose de la enseñanza de geometría descriptiva, geometría superior, matemática complementaria y matemática superior. Permaneció en esta institución hasta su jubilación en 1955.
Margherita y la geometría algebraicaDespués de su tesis, Beloch trabajó en la clasificación de superficies algebraicas, estudiando las configuraciones de curvas racionales que se encuentran en estas superficies. Demostró un importante resultado: “Las superficies hiperelípticas de rango 2 se caracterizan por contener 16 curvas racionales”.
Realizó también algunas contribuciones a la teoría de curvas algebraicas asimétricas. Continuó trabajando en las propiedades topológicas de curvas algebraicas planas o soportadas por superficies regladas o cúbicas durante la mayor parte de su vida, escribiendo numerosos artículos sobre estos temas.
Contribuciones a la papiroflexiaEl primer libro que apunta a la papiroflexia como herramienta para construir pruebas geométricas es el famoso Geometric Exercises in Paper Folding publicado en Madrás en 1893 por el matemático T. Sundara Row. Este manual fue conocido en Europa gracias a una observación del especialista en geometría Felix Klein en su libro Vorträge über ausgewählte Fragen der Elementargeometrie (Problemas seleccionados sobre geometría elemental, 1895). En ese texto, Row afirmaba que no es posible construir la raíz cúbica de 2 utilizando la técnica del plegado de papel.
Beloch fue, además de matemática teórica, una pionera en el estudio de la papiroflexia como herramienta de construcción geométrica. En 1936 descubrió que, mediante el doblado de papel, es posible encontrar las tangentes comunes a dos parábolas, lo que permitía a su vez resolver ecuaciones cúbicas generales. Margherita adaptó el método visual de Lill, un procedimiento visual para encontrar las raíces reales de un polinomio de una variable de cualquier grado, en su construcción mediante origami. De esta manera, Beloch refutó la afirmación de Row. Publicó su hallazgo en Sul metodo del ripiegamento della carta per la risoluzione dei problemi geometrici (Periodico di Mathematiche Ser. 4, 16 (1936) 104-108), donde señalaba también la posibilidad de resolver ecuaciones de cuarto grado mediante ese método, ya que se pueden reducir a la resolución de ecuaciones de segundo y de tercer grado.
Este procedimiento se conoce hoy en día, en su honor, como el “pliegue Beloch”: dados dos puntos y dos rectas, se trata de trazar un pliegue de manera que se sitúe un punto sobre cada recta.
 Pliegue Beloch. Fuente: EMOZ.
Pliegue Beloch. Fuente: EMOZ.Contribuciones a la fotogrametría
Beloch también se interesó por la fotogrametría (la técnica que estudia la forma, las dimensiones y la posición en el espacio de un objeto usando esencialmente medidas realizadas a partir de fotografías de dicho objeto) y la aplicación de las matemáticas, en particular la geometría algebraica, a esta disciplina.
Uno de los problemas a los que se dedicó fue el de la reconstrucción cartográfica a través de fotografías aéreas.
También investigó sobre la aplicación de métodos de fotogrametría terrestre a la radiología con fines médicos. La cuestión fundamental era realizar mediciones exactas de imágenes de partes internas del cuerpo humano obtenidas mediante rayos X para proceder después a su reconstrucción fotogramétrica.
En el caso de órganos con movimientos involuntarios (como el corazón) la cuestión se complicaba a la hora de realizar los radiogramas. Para salvar este problema, Beloch construyó un equipo, el “medidor de precisión”, compuesto por dos dispositivos (de toma y de retorno), que permitía realizar dos radiografías simultáneamente, evitando que la radiación destinada a una de las placas sensibles incidiera en la otra. Además, llevaba automáticamente las imágenes radiológicas a las medidas de las distancias de los puntos del objeto fotografiado, sin necesidad de complicados dibujos o cálculos.
Presentado en 1938 en la Exposición de Invenciones «Leonardo da Vinci» de Milán, en la sección médica, fue galardonado con la Copa de Plata del Ministerio de Educación Nacional.
Margherita falleció en Roma el 28 de septiembre de 1976, a los 97 años. Una larga vida dedicada, con notable éxito, a la geometría.
Referencias
-
MassimoKofler, Margherita Beloch Piazzolla, Enciclopedia Delle Donne
-
Paola Magrone and Valerio Talamanca, Folding cubic roots: Margherita Piazzolla Beloch’s contribution to elementary geometric constructions, 16th Conference on Applied Mathematics APLIMATH 21, 2017
-
Beloch Piazzolla Margherita, Scienza a due voci dell’Università di Bologna
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Margherita Beloch Piazzolla, geómetra se ha escrito en Cuaderno de Cultura Científica.
Einstein y Philipp Lénárd
Philipp Eduard Anton von Lénárd ganó el premio Nobel de física de 1905 por sus trabajos con los rayos catódicos, pero hoy día se le recuerda más por su actividad política que por su ciencia. Se afilió al Partido Nazi en 1924 y se convirtió en un rabioso portavoz contra la “ciencia judía” en general y contra Einstein en particular. Llegó a ser asesor de Hitler y cabeza visible de la “física aria”.
 Philipp Lénárd en 1942. Foto: Bundesarchiv
Philipp Lénárd en 1942. Foto: BundesarchivLénárd comenzó su carrera estudiando los rayos catódicos, haces de electrones que viajan por un tubo de vacío en el que hay dos electrodos metálicos entre los que hay una diferencia de potencial (se llaman catódicos porque son emitidos por el electrodo negativo, el cátodo). El electrón había sido descubierto experimentalmente en 1897 por J.J. Thomson, y mucha de la investigación de Lénárd se centraba en intentar comprender la naturaleza de la electricidad. En 1899 Lénárd probó que los rayos catódicos se creaban también cuando la luz incidía sobre superficies metálicas, y pudo comprobar que la presencia de campos eléctricos y magnéticos afectaba a los rayos. No estaba nada claro cómo la luz y el metal podían producir electrones, o por qué se ralentizaban o cambiaban de dirección por la acción de distintos campos. Los mecanismos no se comprendieron hasta 1905, cuando Einstein publicó su artículo sobre el efecto fotoeléctrico: el concepto de que los cuantos de luz arrancaban electrones individuales del metal. Por tanto, los primeros trabajos de Lénárd están indisolublemente asociados al nombre de Einstein.
Al principio esto unió a los dos científicos. Einstein y Lénárd se escribieron cartas para seguir sus respectivas investigaciones en las que mostraban gran admiración el uno por el otro. En una carta Einstein llamaba a Lénárd “gran maestro” y un “genio”. Lénárd, a su vez, hizo campaña para nombrar a Einstein profesor en Heidelberg y lo describió una vez como un “pensador profundo y trascendental”. Pero su relación cambió radicalmente en cinco años.
La creciente aversión (puede que odio) hacia Einstein parece que surgió de una combinación de factores. Por un lado, Lénárd despreciaba la teoría de la relatividad de Einstein. Se aferraba a la teoría del éter, la idea de que había una sustancia física que llenaba el vacío del espacio. Einstein pensaba que la teoría del éter había sido desacreditada hacía ya bastante tiempo. De hecho la teoría de la relatividad parte de la base de que no hay éter. Einstein, además, no era tímido a la hora de expresar sus opiniones: en 1919 Lénárd dio una conferencia defendiendo el éter que Einstein describió como “infantil”.
Lénárd antiEinsteinEn 1917, Lénárd afirmó que aceptaba la teoría especial de la relatividad, pero solo una parte de la teoría general (en poco tiempo cambiaría de nuevo de opinión con respecto a la especial). Ambos físicos se enfrentaron en una serie de publicaciones: Lénárd atacando la relatividad general y Einstein defendiéndola. Estas publicaciones se volvieron cada vez más personales debido, muy probablemente, a dos razones: simples celos (Einstein se había hecho un nombre, entre otras cosas, mejorando de forma notable un trabajo comenzado por Lénárd) y antisemitismo.
Lénárd obtuvo oficialmente su carné del Partido Nacional Socialista Obrero Alemán (popularmente Partido Nazi) en 1924, mucho antes de que fuese políticamente necesario o popular, pero desde muchos años antes ya se identificaba con las posiciones antisemitas que defendía. Empezó a hablar en contra de los científicos judíos en general, y de Einstein y Max Born en particular. Sus afirmaciones eran del siguiente tenor: “el judío carece notablemente de comprensión de la verdad, a diferencia del investigador ario con su seria y cuidadosa voluntad de verdad”. Lénárd fundó un grupo llamado la Liga Antirrelatividad, que daba conferencias sobre el “fraude judío” que, según ellos, suponía la teoría de la relatividad [*].
A la conferencia impartida el 24 de agosto de 1919 por este grupo asistió el propio Einstein y se le vio riéndose silenciosamente en su asiento, a pesar de los calificativos iracundos que se le lanzaban. La aparente indiferencia era solo eso, apariencia: Einstein respondió al grupo en una carta abierta publicada en el periódico Berliner Tageblatt. La carta no fue precisamente el mejor texto de Einstein. De hecho, la carta da de él una imagen vulgar y de estar a la defensiva no solo cuando habla de su teoría, sino también cuando recurre al ad hominem al acusar a Lénárd de ser un físico teórico de segunda categoría y, por añadidura, superficial.
Que Einstein merecía el premio Nobel estaba claro, por lo menos, desde 1910. Lénárd tiene el dudoso honor de haber sido el que movió los hilos, a base de influencias, tergiversaciones, restando importancia y reclamando la falta de pruebas, para crear tal confusión que el comité Nobel no se decidió a conceder el premio hasta que las posiciones quedaron claramente definidas. Y aun así, no se atrevió a concederlo por la relatividad, sino por el efecto fotoeléctrico.
Nota:
[*] Cien años después no faltan seguidores de esta corriente que buscan errores continuamente en las ideas de Eisntein de forma anticientífica: poniendo primero el resultado, el prejuicio ideológico, y buscando formas de sostenerlo. De hecho, la inmensa mayoría de comentarios en este Cuaderno (no publicados, obviamente) a esta serie y a Teoría de la invariancia, en la que se explican los conceptos básicos de la relatividad, son de este tipo de comentaristas.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Una versión anterior de este artículo se publicó en Experientia Docet el 11 de octubre de 2009.
El artículo Einstein y Philipp Lénárd se ha escrito en Cuaderno de Cultura Científica.
Las cinco fotos del James Webb
David Barrado Navascués
 El Telescopio James Webb ha observado estrellas en su primeras y rápida etapa de formación, en la nebulosa Carina. Para una estrella individual, este período solo dura entre 50.000 y 100.000 años. Fuente: NASA, ESA, CSA y STScI
El Telescopio James Webb ha observado estrellas en su primeras y rápida etapa de formación, en la nebulosa Carina. Para una estrella individual, este período solo dura entre 50.000 y 100.000 años. Fuente: NASA, ESA, CSA y STScINASA, en colaboración con ESA y CSA, han distribuido las primeras imágenes científicas tomadas con el nuevo telescopio espacial James Webb. Un éxito de la colaboración internacional.
Son cinco imágenes y espectros de diversos objetos astrofísicos que cubren las diferentes capacidades técnicas del telescopio y de sus instrumentos. Una muestra pequeña pero magnífica de la revolución científica que se aproxima.
Una lupa cósmica que permite ver lo que hay detrásLa primera imagen, “filtrada” por el presidente de EE UU en una ceremonia muy medida, esencialmente para el público norteamericano, muestra una lente gravitacional: un cúmulo de galaxias funciona como una lente que magnifica lo que hay detrás y que de hecho permite observar otras galaxias cuando eran extremadamente jóvenes, situadas a 13 100 millones de años luz. Así, observamos miles de galaxias en una imagen tridimensional. Se podría decir que en esta imagen el tiempo se hace visible. Pura poesía hecha retrato.
 La primera imagen presentada de James Webb apunta al cúmulo masivo de galaxias J SMACS, el punto más brillante en el centro. Fuente: NASA, ESA, CSA y STScILa huella de evidencia de agua, nubes y neblina en la atmósfera de un exoplaneta
La primera imagen presentada de James Webb apunta al cúmulo masivo de galaxias J SMACS, el punto más brillante en el centro. Fuente: NASA, ESA, CSA y STScILa huella de evidencia de agua, nubes y neblina en la atmósfera de un exoplaneta
Los datos correspondientes al exoplaneta WASP-96 b, uno de los ya más de 5 000 detectados en la Vía Láctea, contienen información esencial sobre su atmósfera con unos detalles sin precedentes. Es un espectro que nos permite detectar diferentes compuestos químicos y estudiar con detalle sus propiedades. Se ha detectado vapor de agua en una atmósfera extremadamente caliente en un planeta de masa similar a la de Júpiter pero situado a una distancia muy próxima a su estrella central. Un mundo exótico, una visión extremadamente sugestiva.
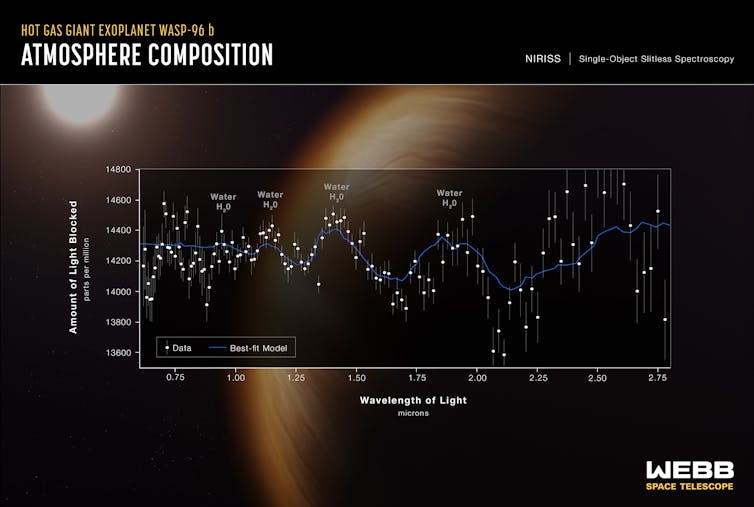 La firma distintiva del agua, junto con evidencia de nubes y neblina en el exoplaneta WASP-96 b. Fuente: NASA, ESA, CSA y STScIEl último aliento de una estrella moribunda en la nebulosa Anillo Sur
La firma distintiva del agua, junto con evidencia de nubes y neblina en el exoplaneta WASP-96 b. Fuente: NASA, ESA, CSA y STScIEl último aliento de una estrella moribunda en la nebulosa Anillo Sur
El Anillo Sur, o nebulosa de Ocho Ráfagas, es una nebulosa planetaria, una nube de gas en expansión expulsada por el astro, que rodea a una estrella moribunda. JWST ha observado el resultado de este óbito estelar: los restos de la muerte de un sistema de dos astros similares al Sol. Las nebulosas planetarias se encuentran posiblemente entre los objetos más bellos que pueden existir en el universo: los últimos suspiros al apagarse, una despedida fastuosa.
 Dos imágenes de la Nebulosa del Anillo Sur y sus dos estrellas tomadas con distintos instrumentos del James Webb. NIRCam (L) y MIRI (R). La estrella moribunda, más tenue, está expulsando gas y polvo a través del cual Webb ve con un detalle sin precedentes. Fuente: NASA, ESA, CSA y STScIEl Quinteto de Stephan: galaxias atrapadas en la música de la gravedad
Dos imágenes de la Nebulosa del Anillo Sur y sus dos estrellas tomadas con distintos instrumentos del James Webb. NIRCam (L) y MIRI (R). La estrella moribunda, más tenue, está expulsando gas y polvo a través del cual Webb ve con un detalle sin precedentes. Fuente: NASA, ESA, CSA y STScIEl Quinteto de Stephan: galaxias atrapadas en la música de la gravedad
El Quinteto de Stephan es un conjunto de galaxias que están interactuando, posiblemente uno de los espectáculos más dramáticos de universo: una danza cosmológica que sigue la música de la gravedad, un lento vals que sigue sorprendiendo por la multiplicidad de los detalles que el telescopio James Webb está revelando. Además, el instrumento MIRI permite observar las proximidades de un agujero negro, el gas que podría ser devorado por él: Saturno devorando a sus hijos a escala extragaláctica.
 Aunque se llama un ‘Quinteto de Stephan’, solo cuatro de las galaxias están realmente juntas y atrapadas en una danza cósmica. Fuente: NASA, ESA, CSA y STScIEl acantilado cósmico en el que nacen las estrellas
Aunque se llama un ‘Quinteto de Stephan’, solo cuatro de las galaxias están realmente juntas y atrapadas en una danza cósmica. Fuente: NASA, ESA, CSA y STScIEl acantilado cósmico en el que nacen las estrellas
La gran finale la proporciona la nebulosa de Carina, una inmensa nube de polvo y gas donde se están formando miles de estrellas. Las más masivas emiten una sorprendente cantidad de energía que comprime el material en sus inmediaciones, creado una inmensa ola, un tsunami que barre los que se encuentra a su paso: caos y creación en el mismo proceso.
 Este paisaje de ‘montañas’ y ‘valles’ es una joven región de formación de estrellas en la Nebulosa Carina. Capturada en luz infrarroja por el nuevo Telescopio Espacial James Webb de la NASA, esta imagen revela por primera vez áreas previamente invisibles de nacimiento de estrellas. Llamada Cosmic Cliffs, la imagen aparentemente tridimensional de Webb parece montañas escarpadas en una noche iluminada por la luna. Fuente: NASA, ESA, CSA y STScI
Este paisaje de ‘montañas’ y ‘valles’ es una joven región de formación de estrellas en la Nebulosa Carina. Capturada en luz infrarroja por el nuevo Telescopio Espacial James Webb de la NASA, esta imagen revela por primera vez áreas previamente invisibles de nacimiento de estrellas. Llamada Cosmic Cliffs, la imagen aparentemente tridimensional de Webb parece montañas escarpadas en una noche iluminada por la luna. Fuente: NASA, ESA, CSA y STScIDe este magnífico regalo que nos ha entregado el telescopio James Webb quiero destacar el espectro del planeta por la información tan detallada que nos proporciona de algo que en realidad es invisible, que queda oculto por la estrella del sistema. Solo una tecnología muy sofisticada y unas técnicas de análisis muy ingeniosas nos permiten inferir cómo es su atmósfera. Esta misma vía se usará eventualmente para observar planetas similares a la Tierra que se encuentren en sus zonas de habitabilidad. También quiero resaltar la belleza estética de la nebulosa de Carina, el drama galáctico y las respuestas que ya han dado estas imágenes a problemas que han estado presentes desde tiempos inmemoriales.
El Quinteto de Stephan, aunque también de magnífica belleza, tal vez podía haber sido mostrado aumentando la gama de colores para indicar las distintas poblaciones estelares, junto con el polvo y el gas. Aun así, maravilla la imagen por la complejidad de las interacciones que se aprecian.
El estupor del mundoEl telescopio James Webb es ya stupor mundi, el estupor del mundo. Las sorpresas no han hecho nada más que empezar.
Una vez más, y de forma espectacular, queda claro que la ciencia básica es una actividad que no solo produce conocimiento, sino también belleza y, mucho más importante, cooperación internacional. Más que nunca, y debido a los tremendos desafíos a los que la humanidad se enfrenta, ciencia, ciencia, ciencia.![]()
Sobre el autor: David Barrado Navascués es Profesor de Investigación en el área de Astrofísica en el Centro de Astrobiología (INTA-CSIC)
Para saber más:
El sucesor del Hubble: el telescopio espacial James Webb
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Las cinco fotos del James Webb se ha escrito en Cuaderno de Cultura Científica.
Redes sociales, noticias falsas y el Efecto de la Tercera Persona
Es complicado que actualmente no nos inunden los bulos y las noticias falsas en redes sociales. Es tan común que, hay cuentas, colectivos y personas dedicadas a desmentirlos. Sin embargo, ¿es necesaria esa labor?
Hago esta pregunta mientras refresco por enésima vez cualquier red social cuya aplicación tenga en el teléfono móvil. ¿Cómo me voy a tragar yo un bulo por redes sociales? Tengo suficiente criterio como para comprobar si las fuentes son fiables y la información verídica. Además, mis contactos en redes sociales también tienen criterio como para no compartir noticias falsas. En cambio, sí pienso que otra gente puede creerse bulos con facilidad.
Entonces, ¿por qué otra gente sí, pero yo no? Vamos a preguntarle a la sociología.
Las personas creen poder diferenciar la información falsa de la veraz mejor de lo que podrían otros. Esta creencia es una forma de mantener un autoconcepto positivo de uno mismo. Y es también la hipótesis del “Efecto de la Tercera Persona”.
W. Phillips Davidson propuso esta hipótesis en 1983, haciendo referencia a los medios de comunicación tradicionales. En concreto, la hipótesis dice que ‘las personas tienden a pensar que los medios influencian más a otra gente que a sí mismos’.
 El alcance de las noticias falsas en redes sociales influenciado por el Efecto de la Tercera Persona. Ilustració: Rosario García Hernández.
El alcance de las noticias falsas en redes sociales influenciado por el Efecto de la Tercera Persona. Ilustració: Rosario García Hernández.
Conociendo el Efecto de la Tercera Persona (ETP, a partir de ahora) y el funcionamiento de las redes sociales, no sería descabellado pensar que el ETP ocurre con frecuencia entre los usuarios de las RRSS. Incluso, que las RRSS se aprovechan del ETP (viralización, cámaras de eco, polarización de opiniones, etc.)
También podría plantearse que, con un mayor ETP, las personas pudieran pedir un mayor control de la difusión y publicación de información en línea. Al igual que una mayor “alfabetización digital” de los usuarios de RRSS, es decir, la toma de medidas para enseñar a las personas a ser críticas con la información.
Algunas de estas suposiciones son las que se han planteado como hipótesis en el estudio realizado por S. Mo Jang y Joon K. Kim. El estudio se hizo para observar el ETP en las noticias falsas sobre política tras las elecciones de 2016 en EEUU.
Como resultados obtuvieron que sus dos primeras hipótesis se corroboraban: el ETP ocurre respecto a las noticias falsas, tanto en la percepción individual, como de grupo. Es decir, una persona pensará que ella y los miembros de su grupo se creen menos noticias falsas que los miembros del otro grupo.
Otro resultado interesante del estudio fue que los individuos con una mayor percepción del ETP no estaban a favor del control y la regularización de las noticias falsas. Sin embargo, la mayoría de los participantes del estudio estaban a favor de la educación para el análisis crítico de la información.
Otro estudio se centra más en la existencia del ETP sobre la información en línea. En este estudio se les preguntó a los participantes quién de entre ellos, sus amigos u otras personas se verían más influenciadas por la información en un sitio web. La mayoría de los participantes se consideraban a sí mismos como los que serían menos influenciados.
De estos dos estudios podemos concluir que, como habíamos planteado antes, el ETP se da entre los usuarios de las redes sociales y otros medios digitales. Por lo que, aparte de ser conscientes del ETP y plantearnos nuestro propio sesgo, quizás deberíamos aplicar la educación para el análisis crítico de la información como una forma de controlar la propagación y el daño de los bulos y las noticias falsas.
Referencias consultadas:
Antonopoulos, N., Veglis, A., Gardikiotis, A., Kotsakis, R., & Kalliris, G. (2015). Web third-person effect in structural aspects of the information on media websites. Computers in Human Behavior doi: 10.1016/j.chb.2014.11.022
Davison, W. P. (1983). The third person effect in communication. Public Opinion Quaterly, 47 (1), 1-15. doi:10.1086/268763.
Jan S. M., Kim J. K. (2017) Third person effects of fake news: Fake news regulation and media literacy interventions Computers in Human Behavior, doi:10.1016/j.chb.2017.11.034.
Para saber más:
Sócrates y el efecto Dunning-Kruger en redes sociales
Emociones al alza, racionalidad a la baja
Correcto es lo que hace la mayoría: el principio de la prueba social
Autore: Rosario García Hernández (@swallowdraws, IG: @rosiswallow), alumne del Postgrado de Ilustración Científica de la UPV/EHU – curso 2020/21
Artículo original: Fake news: the third-person effect. Martha Villabona, Mapping Ignorance, 16 de noviembre de 2020.
“Ilustrando ciencia” es uno de los proyectos integrados dentro de la asignatura Comunicación Científica del Postgrado de Ilustración Científica de la Universidad del País Vasco. Tomando como referencia un artículo de divulgación, los ilustradores confeccionan una nueva versión centrada en la propia ilustración
El artículo Redes sociales, noticias falsas y el Efecto de la Tercera Persona se ha escrito en Cuaderno de Cultura Científica.
IV Jornada Nacional de Evolución y Neurociencias: Marcos Vázquez – Ejercicio para des-domesticarnos

¿Estamos realmente diseñados para conectar con los demás? Si es así, ¿por qué siguen existiendo los psicópatas? ¿Se pueden tratar trastornos delirantes como la paranoia desde el punto de vista de la evolución? O ¿cómo ha cambiado la atracción sexual desde la época de nuestros ‘abuelos’ homínidos hasta ahora?
A estas y otras cuestiones relativas a la evolución del comportamiento humano se trató de dar respuesta durante la IV Jornada Nacional de Evolución y Neurociencias, evento organizado por la Cátedra de Cultura Científica de la UPV/EHU y la Red de Salud Mental de Bizkaia, que tuvo lugar los días 28 y 29 de abril en el Bizkaia Aretoa – UPV/EHU de Bilbao.
Desde que en 2017 un grupo de psiquiatras de la Red de Salud Mental de Bizkaia organizara la primera edición de esta jornada, la cita se ha convertido en un punto de encuentro para profesionales de distintos ámbitos científicos como la psiquiatría, la psicología, la biología o la filosofía con un interés común: la conducta humana desde una perspectiva evolucionista y su divulgación científica en un formato accesible y ameno para todos los públicos, a la par que riguroso y actualizado.
Una de las principales funciones del encéfalo es controlar el cuerpo. Las funciones cognitivas son, evolutivamente, indisociables del movimiento. Sin embargo, los humanos las hemos intentado separar hasta domesticarnos a nosotros mismos. Marcos Vázquez nos explica cómo emplear el ejercicio para reconectar con nuestros «genes salvajes» y los beneficios que esto conlleva.
Para saber más:
IV Jornada Nacional de Evolución y Neurociencias: Fernando Valladares – Del ejercicio a la ecología y viceversa
Envejecer sanamente gracias al ejercicio físico
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo IV Jornada Nacional de Evolución y Neurociencias: Marcos Vázquez – Ejercicio para des-domesticarnos se ha escrito en Cuaderno de Cultura Científica.
El cambio climático y los colores del herrerillo
 Herrerillo común. Fuente: Wikimedia Commons
Herrerillo común. Fuente: Wikimedia CommonsUn nuevo trabajo de investigación indica que el cambio climático estaría afectando a la coloración del plumaje del herrerillo común (Cyanistes caeruleus).
El trabajo, que se ha llevado a cabo durante 15 años (2005-2019) mediante una colaboración entre científicos de la Universidad del País Vasco (UPV/EHU) y el Centre d’Ecologie Fonctionnelle et Évolutive de Montpellier (CEFE-CNRS), se centró en dos poblaciones de herrerillos del sur de Francia, una localizada en las cercanías de Montpellier y la otra en el noroeste de la isla de Córcega.
Cada año, entre 2005 y 2019, se capturaron los herrerillos reproductores de cada población. Como resultado se consiguieron más de 5.800 observaciones sobre la coloración y otras características de estas aves.
El herrerillo común se caracteriza por su llamativa coloración: posee una corona azul y el pecho es de color amarillo. Los resultados obtenidos en el estudio muestran una disminución en ambas poblaciones de la coloración azul y amarilla entre el 2005 y 2019. Esto es, a día de hoy, en estas dos poblaciones, las coronas azules y los pechos amarillos de los herrerillos son de media de colores menos intensos que en el momento en el que empezó la investigación.
“Nuestro trabajo sugiere que los cambios ambientales, y en concreto el cambio climático, podrían ser el motivo principal por el cual aves como el herrerillo están sufriendo un cambio en sus rasgos físicos, más concretamente en el brillo e intensidad de sus coloraciones”, señala David López-Idiáquez, investigador del departamento de Biología Vegetal y Ecología de la UPV/EHU.
Cambios en los patrones de emparejamiento del herrerillo“Se ha podido observar como la tendencia en ambos sexos y poblaciones es negativa en cuanto a brillo e intensidad de la coloración de las plumas, aunque en Córcega este cambio está más asociado con el clima”, explica López. “El cambio del color del plumaje parece ser resultado de la combinación entre la subida de temperatura (de 1,23ºC) y la bajada de las precipitaciones (0,64 mm), por lo que el cambio climático sería el potencial causante de esta diferencia”, apunta.
Puede parecer que solo es un cambio puramente estético, pero es justo lo contrario, ya que este cambio en el plumaje puede tener efectos en los “patrones de emparejamiento” de la especie. “En estas aves rasgos como la coloración funcionan como señales para indicar a los otros individuos la calidad del espécimen, que son decisivos, por ejemplo, a la hora de reproducirse”, precisa David López.

“Este estudio se pudo realizar gracias al seguimiento continuo de las dos poblaciones de herrerillo durante más de 15 años, lo que pone de relevancia la importancia de contar con estudios a largo plazo para comprender los efectos del cambio climático sobre los ecosistemas que nos rodean”, resalta.
Cuando se da una variación en el territorio, las poblaciones de animales tienen 4 opciones: La primera, sufrir un cambio genético; la segunda, sufrir un cambio plástico (modificación en las características físicas sin cambios genéticos); la tercera, emigrar; y, por último, desaparecer. “Es importante destacar que este cambio no es genético sino plástico, una de las formas de adaptarse a las nuevas condiciones ambientales”, revela.
Referencia:
David López-Idiáquez, Céline Teplitsky, Arnaud Grégoire, Amélie Fargevieille, María del Rey, Christophe de Franceschi, Anne Charmantier, and Claire Doutrelant (2022) Long-Term Decrease in Coloration: A Consequence of Climate Change? The American Naturalist DOI: doi: 10.1086/719655
Para saber más:
El rojo y los cambios climáticos
Los fantasmas de la evolución
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo El cambio climático y los colores del herrerillo se ha escrito en Cuaderno de Cultura Científica.
Lissajous, afinador de afinadores
El tono de un diapasón se puede ajustar con una simple lima. Si desgastas ligeramente la punta de sus brazos, la masa disminuye y el tono se vuelve más agudo. Si, por el contrario, lijas la base (el punto donde los dos brazos se unen al mango), o calientas un poco el metal, su elasticidad cambia y el tono se vuelve más grave.
John Shore, el inventor del instrumento, probablemente conocía estos principios, aunque fuese de forma puramente experimental. Un siglo después de que el trompetista presentase al mundo su nueva invención, el diapasón ya había ocupado su lugar en la historia de la música como afinador universal. Y, de la mano de su popularidad, llegó la necesidad de afinarlos con una gran precisión, de forma rápida y estandarizada.
Esto se proponía Jules Lissajous, cuando en 1854 desarrolló un nuevo método para comparar la afinación de los diapasones. Su idea era sencilla, elegante y, por qué no decirlo, de una gran belleza. Consistía en visualizar las vibraciones de los brazos del instrumento por métodos ópticos. Hasta el momento, los diapasones se habían afinado simplemente “de oído”. Cada nuevo instrumento se comparaba con uno de referencia, ya afinado, y se pulían sus brazos hasta que la frecuencia del sonido coincidiera. En cambio, Lissajous recurrió a la luz de una vela para poder detectar de manera directa cualquier mínima diferencia entre estas frecuencias.
 «Estudio óptico de los movimientos vibratorios por el método de M. Lissajous», ilustración que aparece en el libro El mundo físico: gravedad, gravitación, luz, calor, electricidad, magnetismo, etc. de A. Guillemin. Barcelona, Montaner y Simón, 1882. Fuente: Fondo Antiguo de la Universidad de Sevilla /flickr
«Estudio óptico de los movimientos vibratorios por el método de M. Lissajous», ilustración que aparece en el libro El mundo físico: gravedad, gravitación, luz, calor, electricidad, magnetismo, etc. de A. Guillemin. Barcelona, Montaner y Simón, 1882. Fuente: Fondo Antiguo de la Universidad de Sevilla /flickr
Él mismo describe su montaje en un artículo de 18571:
Primero operé con diapasones, siendo este pequeño aparato de todos los cuerpos vibrantes el más cómodo de manejar […]. Para hacer visible el movimiento vibratorio de un diapasón, fijo el extremo de una de las ramas sobre la cara convexa de un pequeño espejo plano de metal. La otra rama lleva un contrapeso, de modo que la sobrecarga es igual en las dos ramas.
Haciendo que la llama de una vela se reflejase en este pequeño espejo, Lissajous consiguió convertir el leve movimiento del diapasón en luz, en un fenómeno visible. A continuación, colocó un segundo diapasón, con su propio espejo, en dirección perpendicular al primero. Es decir, si el primer instrumento se movía en horizontal, el segundo lo hacía en vertical, y viceversa. Haciendo que la luz de la vela rebotase en cada uno de ellos de manera sucesiva, podía hacer que su movimiento se combinase para dar lugar a una única figura, hermosamente geométrica: las conocidas como figuras de Lissajous.
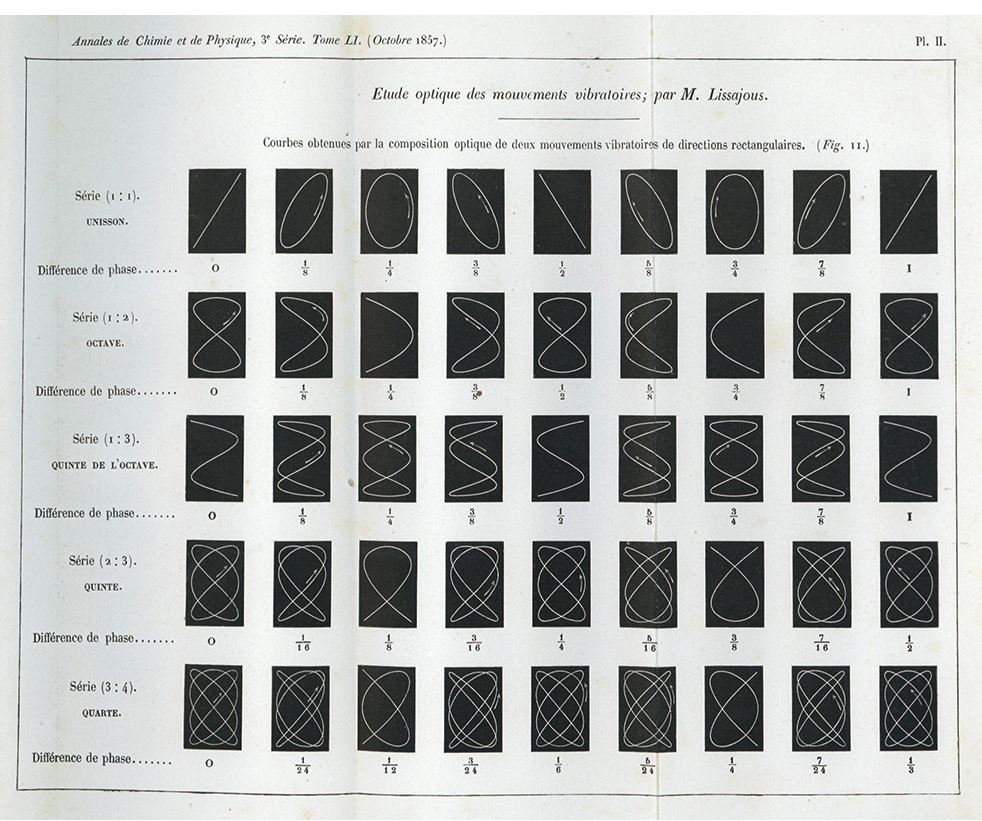 Ilustración original de «Memoria sobre el estudio óptico de los movimientos vibratorios» de M. (monsieur) Lissajous (1857). Fuente: Jeremy Norman Collection of Images – Creative Commons
Ilustración original de «Memoria sobre el estudio óptico de los movimientos vibratorios» de M. (monsieur) Lissajous (1857). Fuente: Jeremy Norman Collection of Images – Creative Commons
Recuerdo la primera vez que vi una de estas figuras en el laboratorio de la facultad de física. Usábamos un osciloscopio para sintonizar dos señales eléctricas y debíamos observar los dibujos que aparecían en la pantalla para calcular la proporción entre sus frecuencias y el posible desfase entre ellas. Era un espectáculo verlas danzar. Pero lo realmente bonito es que las figuras de Lissajous solo se cierran (y, por tanto, en apariencia, solo se quedan “quietas”) cuando las frecuencias de las dos señales coinciden a la perfección, o bien guardan una proporción armónica exacta (esto es, una proporción definida por números enteros). Si las dos ondas son iguales, dibujan un círculo. Si mantienen una proporción de 2:1, trazan algo parecido a una mariposa, cuando el ratio es 3:2, el resultado recuerda a una doble espiral2. A medida que los armónicos aumentan, el dibujo se va volviendo más complejo. Pero la condición para congelar la imagen es siempre la misma: la figura solo se cierra si las frecuencias que le dan forma encajan a la perfección. Se requiere una afinación perfecta.
En la segunda mitad del siglo XIX, el mundo de la ciencia se esforzó por crear un sistema de unidades realmente universal. Es la época en la que se fundó Oficina Internacional de Pesas y Medidas, se definieron el metro y el kilogramo, y se construyeron patrones que se han seguido usando como referencia hasta hace muy poco. También, en el mundo de la música, se intentó definir un la universal3, y para capturarlo, Lissajous fabricó un diapasón estándar cuidadosamente afinado. Vibraba a 435 Hz a una temperatura ambiente de 15 °C. Estaba llamado a convertirse en el afinador de afinadores, medidor universal de toda la música. Con su movimiento daría forma a la música que se escucharía en adelante en las salas de conciertos de todo el planeta.
O ese era el plan. Como ya vimos, su reinado duró bien poco, en realidad. Hoy en día, el estándar de afinación está fijado en 440 Hz, y ni siquiera se respeta siempre. En Europa, es común afinar a 442 Hz. Las figuras de Lissajous en cambio, tuvieron su propio legado cultural. Su forma sinuosa, bella e hipnótica a partes iguales, las ha convertido en todo un referente visual. Han aparecido en el cine, asociadas a menudo a escenarios futuristas o de ciencia ficción, marearon a los espectadores en los títulos de crédito de Vértigo, y hasta se sospecha que dan forma a un conocido logo comercial. A mí, sin embargo, me gusta recordar su origen sonoro y musical. Todas esas figuras tienen su propia armonía de dos notas asociada, y es un intervalo consonante, perfectamente afinado.
Notas y referencias:
1Lissajous, Jules A. 1857. “Mémoire sur l’Etude optique des mouvements vibratoires.” Annales de chimie et de physique 3 (51): 147-232..
2Estas relaciones de frecuencia corresponden a los intervalos musicales de octava (2:1) y quinta justa respectivamente (3:2).
3En 1858 el gobierno francés creó una comisión encargada de establecer dicho estándar. Lissajous fue miembro de este comité, que también contó con grandes compositores como Héctor Berlioz o Gioachino Rossini.
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
El artículo Lissajous, afinador de afinadores se ha escrito en Cuaderno de Cultura Científica.
Teoremas geométricos sin palabras: Viviani
Como ya hemos comentado en anteriores entradas del Cuaderno de Cultura Científica, la geometría plana está repleta de interesantes y atractivos teoremas, que suelen venir acompañados de diagramas con mucho encanto, como el teorema de Napoleón (véase la entrada Variaciones artísticas del teorema de Napoleón), el teorema de van Aubel (véase la entrada Una pequeña joya geométrica: el teorema de van Aubel), el teorema de Marion (véase la entrada El teorema de Marion (Walter)), el teorema de la bandera británica (véase la entrada El teorema de la ikurriña), el teorema de Pick (véase la entrada Calcular el área contando puntos) o el mismísimo teorema de Pitágoras (véase la entrada Pitágoras sin palabras).
 Hexágono místico de Pascal (1965), del dibujante e ilustrador infantil estadounidense Crockett Johnson (1906-1975). Esta pintura recoge el esquema del conocido teorema (del hexágono místico) de Pascal. Imagen de la página web de The National Museum of American History
Hexágono místico de Pascal (1965), del dibujante e ilustrador infantil estadounidense Crockett Johnson (1906-1975). Esta pintura recoge el esquema del conocido teorema (del hexágono místico) de Pascal. Imagen de la página web de The National Museum of American History
Estos resultados geométricos suelen tener diferentes tipos de demostraciones, en función de las técnicas utilizadas, la originalidad de las ideas contenidas, la complejidad de la misma o la extensión que ocupa. Lo más importante a la hora de demostrar un resultado matemático es obtener una demostración para el mismo, no importa lo larga, “poco elegante” o “aburrida” que nos pueda parecer, después ya podrán obtenerse demostraciones más originales, sugerentes, “hermosas”, simples o cortas. En esta búsqueda de la belleza en las demostraciones matemáticas también juegan un papel interesante las llamadas “demostraciones sin palabras”.
En 1973, el gran divulgador de las matemáticas Martin Gardner (1914-2010), se refirió a las demostraciones sin palabras como diagramas “en un vistazo” y señaló que “en muchos casos, una demostración farragosa puede ser suplida por una geométrica análoga, tan simple y bella que la veracidad de un teorema es casi vista en una ojeada”. Como comenta el matemático Roger B. Nelsen, una de las personas que más ha hecho por la difusión de las demostraciones sin palabras y autor de la serie de libros Proofs without Words (MAA), las demostraciones sin palabras no son realmente demostraciones matemáticas en sí mismas, son más bien diagramas, esquemas o dibujos que nos ayudan a comprender por qué un teorema es cierto o que encierran la idea de la verdadera demostración matemática. Son sugerentes, atractivas y todo un ejercicio de estímulo del pensamiento.
 Demostración sin palabras de que la media geométrica de dos números es menor o igual que la media aritmética, y que es igual cuando ambos números son iguales, realizada por Charles Gallant, publicada en Mathematics Magazine en 1977 y recogida en el libro Proofs without words
Demostración sin palabras de que la media geométrica de dos números es menor o igual que la media aritmética, y que es igual cuando ambos números son iguales, realizada por Charles Gallant, publicada en Mathematics Magazine en 1977 y recogida en el libro Proofs without words
Con esta entrada iniciamos una pequeña serie estival de demostraciones sin palabras de interesantes y hermosos teoremas geométricos. Esta primera entrada de la serie está dedicada a un teorema clásico de la geometría del plano sobre triángulos equiláteros, el conocido teorema de Viviani. Este resultado geométrico debe su nombre al matemático italiano Vincenzo Viviani (1622-1703), que fue discípulo de Galileo Galilei (1564-1642) y Evangelista Torricelli (1608-1647) y que muchos conocemos por la llamada curva de Viviani, que es la curva intersección de un cilindro y una esfera.
 Curva de Viviani. Imagen de “Ag2gaeh” en Wikimedia Commons
Curva de Viviani. Imagen de “Ag2gaeh” en Wikimedia Commons
Pero vayamos con el resultado geométrico anunciado, el teorema de Viviani.
Teorema de Viviani: La suma de las distancias de un punto cualquiera en el interior de un triángulo equilátero (o en alguno de sus lados) a cada uno de sus lados es igual a la altura del mismo.
Este es un resultado geométrico que es fácil de probar, sin más que utilizar que el área de un triángulo es la mitad del producto de la base por la altura: área triángulo = (base x altura ) / 2.
La demostración sería la siguiente: el triángulo equilátero ABC (de base BC y altura h) puede descomponerse como unión de los tres triángulos PBC (de base BC y altura x), PAB (de base AB y altura y) y PCA (de base CA y altura z). Tomando áreas para los cuatro triángulos,
área (ABC) = área (PBC) + área (PAB) + área (PCA),
y teniendo en cuenta que los lados del triángulo equilátero ABC son iguales AB = BC = CA (a cuya longitud llamaremos l), se tiene que
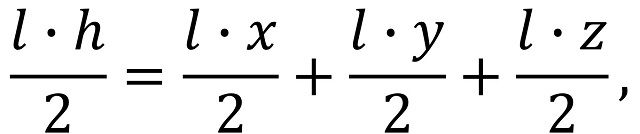
de donde se obtiene la igualdad deseada
![]()
En el libro Proofs without words, de Roger B. Nelsen, se recoge una primera demostración sin palabras del teorema de Viviani, publicada por Samuel Wolf en Mathematics Magazine, en 1989.
Expliquemos el motivo por el cual este esquema explicaría el teorema de Viviani. Para dar la explicación hemos llamado PA, PB y PC a las proyecciones (ortogonales) del punto P sobre los lados BC, CA y AB (es decir, PPA = x, PPB = z, PPC = y, de forma que el teorema establece que la altura h es igual a PPA + PPB + PPC), como se muestra en la imagen siguiente. En primer lugar, se realiza una copia desplazada A’B’C’ del triángulo equilátero ABC, de forma que el punto P quede en el lado A’C’, y denotamos por Q la proyección (ortogonal) de A’ sobre la recta RP, paralela a BC, y L a la proyección (ortogonal) de P sobre la recta A’B’.
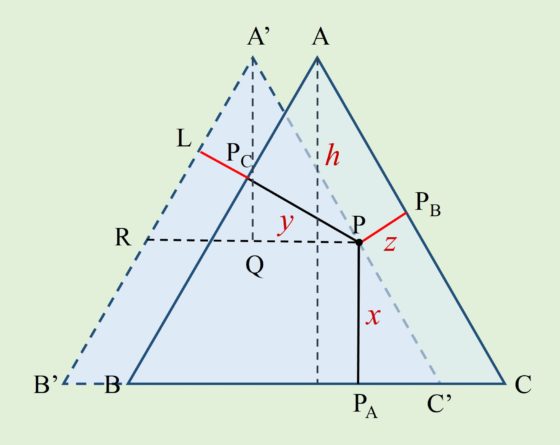
Entonces, tenemos las siguientes igualdades:
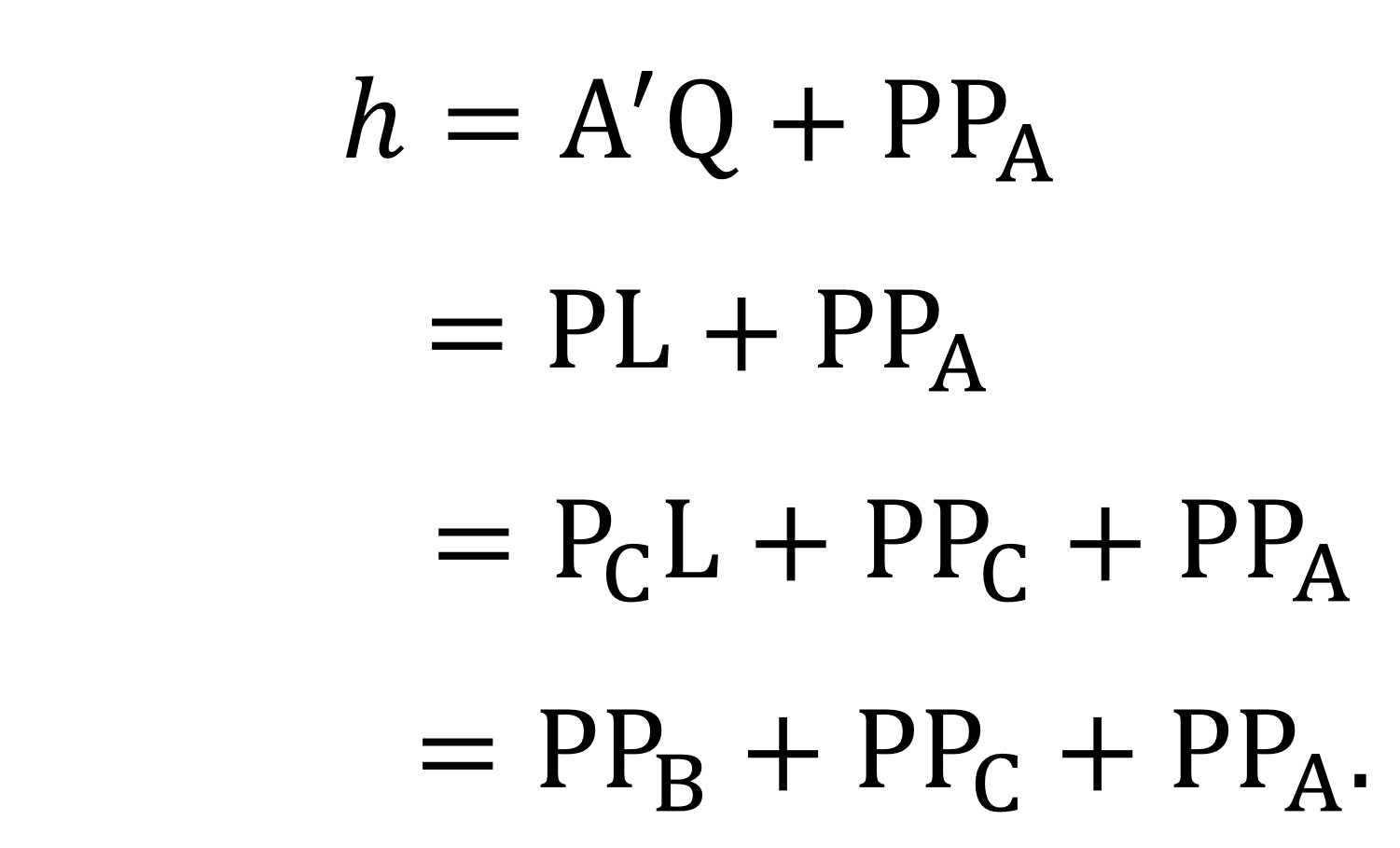
Luego el diagrama anterior es una demostración sin palabras del teorema de Viviani.
La segunda demostración sin palabras del teorema de Viviani la descubrí en el hermoso libro Charming Proofs, A Journey Into Elegant Mathematics de Claudi Alsina y Roger B. Nelsen. Es una demostración sin palabras de una gran sencillez y belleza, que publicó el matemático japonés Ken-ichiroh Kawasaki en Mathematics Magazine, en 2005.
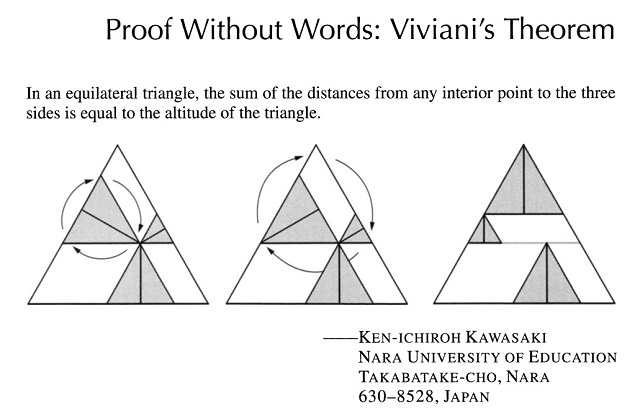
Es una hermosa demostración que se explica por sí sola.
Para terminar esta entrada estival del Cuaderno de Cultura Científica os dejo un problema que puede resolverse con una sencilla prueba sin palabras.
Problema (El cuadrado dentro del cuadrado): Demuéstrese que si se trazan rectas que unen los vértices del cuadrado con los puntos medios de uno de los lados opuestos, como se muestra en la siguiente imagen, entonces el área del cuadrado central es un quinto del área del cuadrado original.
Bibliografía:
1.- David Wells, The Penguin Dictionary of Curious and Interesting Geometry, Penguin Books, 1991.
2.- Roger B. Nelsen, Proofs without Words: Exercises in Visual Thinking, Mathematical Association of America, 1997.
3.- Roger B. Nelsen, Proofs Without Words II: More Exercises in Visual Thinking, Mathematical Association of America, 2001.
4.- Tim Doyle, Lauren Kutler, Robin Miller, Albert Schueller, Proofs Without Words and Beyond, Convergence, MAA, 2014.
5.- Claudi Alsina y Roger B. Nelsen, Charming Proofs, A Journey Into Elegant Mathematics, Mathematical Association of America, 2010.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Teoremas geométricos sin palabras: Viviani se ha escrito en Cuaderno de Cultura Científica.
Einstein y Julius Robert Oppenheimer
A Julius Robert Oppenheimer se le recuerda como al padre de la bomba atómica. Un físico brillante a la par que excelente tecnócrata, Oppenheimer organizó la parte científico-técnica del Proyecto Manhattan. Antes de eso, ya era conocido por sus trabajos en mecánica cuántica y astrofísica, aplicando las ecuaciones de Einstein a la evolución de las estrellas. Su última etapa profesional la pasó en el Instituto de Estudios Avanzados de Princeton, en un despacho justo encima del de Einstein.
 Fuente: US Govt. Defense Threat Reduction Agency
Fuente: US Govt. Defense Threat Reduction AgencyEinstein y Oppenheimer se cruzaron en multitud de ocasiones a lo largo de sus vidas, encontrándose en varias conferencias científicas, pero Oppenheimer era de una generación más joven de físicos (era 25 años menor que Einstein), una que ya fue educada después de la revolución de las teorías de la relatividad y la mecánica cuántica. Oppenheimer usó como si tal cosa ambas en su estudio del interior de las estrellas. No fue parte de los esfuerzos para descubrir las matemáticas tras las ideas como lo fue Einstein, por lo que, desde el punto de vista de Oppenheimer, Einstein era más una persona digna del mayor respeto, reconocimiento y consideración que alguien que pudiese contribuir activamente a la ciencia.
Oppenheimer nació en los Estados Unidos pero, tras estudiar en Harvard, se decidió por marcharse a Europa a completar su formación, primero a Cambridge y después a Gotinga, donde consiguió su doctorado bajo la dirección de Max Born. Regresó a Estados Unidos para ser profesor en la Universidad de California en Berkeley. Cuando comenzó la Segunda Guerra Mundial fue reclutado para dirigir el desarrollo de la bomba atómica, convirtiéndose en el director del Proyecto Manhattan. Después de la guerra, aterrizó en Princeton como director del Instituto de Estudios Avanzados, donde una guardia militar vigilaba permanentemente la caja fuerte de su despacho.
Cuando llegó de visita a Princeton en 1935, Oppenheimer, al igual que Einstein en su momento, se burló de la estirada ciudad universitaria y sus “lumbreras solipsistas brillando en una desolación separada e impotente”. Einstein, en el Instituto desde 1933, no escapó a las críticas: “Einstein está completamente chiflado”. En esa época, la comunidad de físicos se mostraba abiertamente desdeñosa con la obsesión de Einstein por encontrar una alternativa a la teoría cuántica, y Oppenheimer estaba de acuerdo. Einstein, por su parte, encontró que Oppenheimer era un “hombre de inusual capacidad con una educación amplísima”.
Oppenheimer, comunistaDurante la Segunda Guerra Mundial los dos físicos no habían tenido contacto entre sí, ya que Einstein no había formado parte del proyecto de construcción de la bomba; el F.B.I. había decidido que era un riesgo para la seguridad por sus posibles vínculos comunistas. Einstein nunca fue miembro del Partido Comunista, pero, irónicamente, Oppenheimer sí. En 2002, 35 años después de la muerte de Oppenheimer, se tuvo acceso a cartas que muestran que perteneció al Partido Comunista Americano a finales de los años 30 y hasta principios de los 40.
Su mujer también había sido abiertamente miembro del Partido Comunista y había suficientes dudas sobre Oppenheimer durante la Guerra Fría como para hacerle sujeto de los infames juicios de la caza de brujas. El senador McCarthy convocó al físico ante el comité del senado en 1954. Cuando Einstein oyó la noticia, se rió diciendo que lo único que Oppenheimer tenía que hacer era llegar a Washington, decirles a todos que eran idiotas y volverse. Obviamente, este era un consejo que no se podía seguir, y Einstein fue de los que unió su voz a la de otros científicos relevantes defendiendo la honorabilidad de Oppenheimer. A pesar del apoyo recibido, Oppenheimer perdió su autorización de seguridad de máximo nivel. De repente, no tenía permitido leer documentos sobre la bomba atómica que él mismo había redactado.
Su paso por el comité de McCarthy no afectó a su trabajo y continuó siendo director del Instituto donde, a pesar de sus continuas desavenencias en cuestiones de física moderna, Einstein y Oppenheimer mostraban el uno por el otro un profundo respeto. Diez años después de la muerte de Einstein, Oppenheimer escribió un texto en recuerdo suyo que publicaría la UNESCO en una colección de ensayos titulada “Ciencia y síntesis”. En este ensayo Oppenheimer destacaba tanto la contribución de Einstein a la ciencia como al desarrollo de la bomba y a su lucha contra ella:
“Su papel fue el de crear una revolución intelectual y descubrir más que cualquier otro científico de nuestro tiempo […] la suya fue una voz alzada con gran peso en contra de la violencia y la crueldad dondequiera que las viese y, tras la guerra, habló con profunda emoción, y yo creo que con gran influencia, acerca de la suprema violencia de estas armas atómicas”.
Para saber más:
Cómo la bomba atómica condicionó nuestra comprensión de la ciencia
La ciencia al servicio de la guerra
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Una versión anterior de este artículo se publicó en Experientia Docet el 8 de noviembre de 2009.
El artículo Einstein y Julius Robert Oppenheimer se ha escrito en Cuaderno de Cultura Científica.
La porosidad de la corteza lunar
Cuando miramos a nuestro único satélite natural, la Luna, a través de un telescopio -aunque sea uno modesto- saltan dos cosas a la vista y que son evidentes incluso con ese nivel de detalle: por un lado tenemos los mares lunares, esas grandes llanuras volcánicas de color gris oscuro que cubren una gran parte de la superficie de su cara visible y, por otro, la cantidad de cráteres de todos los tamaños que podemos ver salpicando la superficie.
 Recreación digital de la cara visible de la Luna que nos permite ver algunos de sus cráteres, especialmente cerca del límite entre el lado diurno y nocturno o terminador. También se aprecia perfectamente el contraste con los mares y como estos aparentan tener muchos menos cráteres que las zonas más claras. Cortesía del Scientific Visualization Studio de la NASA.
Recreación digital de la cara visible de la Luna que nos permite ver algunos de sus cráteres, especialmente cerca del límite entre el lado diurno y nocturno o terminador. También se aprecia perfectamente el contraste con los mares y como estos aparentan tener muchos menos cráteres que las zonas más claras. Cortesía del Scientific Visualization Studio de la NASA.Tanto es así que podemos encontrar cráteres que van desde los 2500 kilómetros de diámetro, como es la cuenca de Aitken, situada en el polo sur lunar, como cráteres de tamaño microscópico formados sobre las rocas por el continuo impacto de partículas de pequeño tamaño a lo largo de 4500 millones de años de historia.
 Cráteres a pequeña escala. En la imagen de la izquierda vemos una pequeña partícula de vidrio lunar con un cráter en su superficie y a la derecha una roca lunar, vista al microscopio electrónico, donde también se puede apreciar la marca de un pequeño impacto (el cráter tiene en torno a las 10 micras) e incluso la fracturación de la roca como consecuencia de este. Imágenes cortesía de la NASA.
Cráteres a pequeña escala. En la imagen de la izquierda vemos una pequeña partícula de vidrio lunar con un cráter en su superficie y a la derecha una roca lunar, vista al microscopio electrónico, donde también se puede apreciar la marca de un pequeño impacto (el cráter tiene en torno a las 10 micras) e incluso la fracturación de la roca como consecuencia de este. Imágenes cortesía de la NASA.En los primeros momentos de la formación de nuestro sistema planetario, especialmente entre hace 4400 y 3800 millones de años, los planetas sufrieron un elevado número de grandes impactos porque todavía existían muchos embriones planetarios que vagaban por el espacio sin llegar a formar cuerpos más grandes. Sin una órbita estable, cruzaban la trayectoria de los planetas, hasta que, poco a poco, debido a las colisiones, esta población fue reduciéndose notablemente y las colisiones se hicieron menos frecuentes.
Eso no quiere decir que hayamos dejado de recibir los impactos de otros cuerpos, solo que con el paso del tiempo la magnitud en tamaño y en cantidad de impactos, por lo general, ha ido disminuyendo gradualmente. En nuestro planeta cuesta mucho ver estas etapas tan convulsas, ya que tanto la tectónica de placas como los agentes externos (el agua, el viento o el hielo, entre otros) han conseguido borrar esa parte de nuestra historia.
Por eso la Luna es un laboratorio tan importante de cara a poder comprender mejor esas primeras etapas de formación del Sistema Solar, puesto que las ha preservado mucho mejor que la Tierra. Aunque no podemos olvidar que incluso la Luna, que nos parece un cuerpo que ha cambiado tan poco, ha seguido sufriendo tanto impactos, que han seguido alterando su superficie, como la formación de sus mares que, si bien a menor ritmo, ha continuado hasta hace unos 1500 millones de años.
 a) Porosidad actual de la corteza lunar. b) Modelo de porosidad de la corteza lunar alrededor del momento de formación de la cuenca de impacto del Polo Sur-Aitken. Se aprecia claramente como los círculos negros, que corresponden con las cuencas de impacto más antiguas, muestran una correlación importante con la porosidad observada y modelada. Cortesía de Huei et al. (2022).La porosidad de la corteza lunar
a) Porosidad actual de la corteza lunar. b) Modelo de porosidad de la corteza lunar alrededor del momento de formación de la cuenca de impacto del Polo Sur-Aitken. Se aprecia claramente como los círculos negros, que corresponden con las cuencas de impacto más antiguas, muestran una correlación importante con la porosidad observada y modelada. Cortesía de Huei et al. (2022).La porosidad de la corteza lunar
Para poder conocer mejor esta turbulenta historia de colisiones, los científicos han empezado a estudiar la porosidad de la corteza lunar, es decir, la relación entre el volumen de la roca y los huecos o espacios que ocupan los poros… ¿pero qué tienen que ver estos poros con las colisiones?
Pues parece que las grandes colisiones afectaron tanto a la corteza lunar que la convirtieron en una zona altamente porosa y que probablemente esa porosidad se extendía decenas de kilómetros hacia las profundidades de la Luna y no se limitaba a las zonas más superficiales, casi transformándola en una esponja de roca a escala planetaria, llegando a alcanzar valores de porosidad del 20%.
Anteriormente, los científicos pensaban que la porosidad observada en la Luna se había desarrollado de una manera gradual a lo largo de toda su historia, pero ahora empezamos a ver detalles que nos hacen pensar que realmente ha ocurrido de otra manera. La porosidad que observamos fue generada a partir de los impactos más grandes, que eran capaces de afectar a grandes zonas de la Luna, pero los impactos cada vez más pequeños y el propio peso de las capas superiores fue compactando de nuevo la corteza lunar y reduciendo esa porosidad.
¿Para qué puede servir este descubrimiento? Este cambio en la porosidad puede ayudarnos a reconstruir la historia de los impactos, ya que sobre la superficie lunar se superponen impactos -algunos de los cuales ya no son apreciables- y quizás la única manera de reconocer sus efectos sea a través de como han afectado a la propia estructura de la corteza.
También pone de manifiesto que, si este modelo lunar es acertado, probablemente los planetas experimentaron una gran porosidad en sus cortezas durante su “infancia” planetaria, lo que nos puede ayudar a construir modelos geodinámicos que tengan en cuento este punto partida.
E, incluso, desde el punto de vista de la astrobiología puede resultar muy interesante, ya que las fracturas pueden permitir, por un lado, que el agua llegue a mayores profundidades, generando zonas de alteración y de intercambio de sustancias que puedan ser beneficiosas para el desarrollo y sustento de la vida, pero también por crear zonas donde la vida pueda protegerse de un ambiente externo más hostil.
Finalmente, también nos puede ayudar a encontrar las zonas más antiguas de la corteza de los planetas, abriéndonos una ventana a la búsqueda de rocas donde apoyarnos para seguir estudiando el origen del Sistema Solar.
Referencias
Huang, Y.H., Soderblom, J.M., Minton, D.A. et al. (2022) Bombardment history of the Moon constrained by crustal porosity. Nat. Geosci. (2022). doi: 10.1038/s41561-022-00969-4
Para saber más:
¿Por qué las caras de la Luna son tan diferentes?
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo La porosidad de la corteza lunar se ha escrito en Cuaderno de Cultura Científica.
Q, un cuento cuántico
Javier Fernández Panadero, autor
 Fuente: Wikimedia Commons
Fuente: Wikimedia Commons
“Q era un qbit que vivía en un subespacio de las afueras”
Así comienza esta novela corta de ciencia ficción, donde acompañaremos a Q en sus aventuras por el mundo microscópico.
Como toda la ciencia ficción, la historia de Q nos lleva a un mundo extraño para hablarnos de nosotros mismos pero, por la particular naturaleza del mundo al que nos lleva, seguro que aquellos con alguna experiencia o interés en los ordenadores, la inteligencia artificial o la filosofía, la disfrutarán en más profundidad.
Pero no crean que es un texto a leer con el ceño fruncido, confiamos en que se lea con la sonrisa con que se hizo: “Es bueno que nos riamos, no sé si querría llegar a una Verdad que no incluyese el humor… o los pedos” —dice un personaje, en cierto momento.
En otras ocasiones el humor viene derivado por las particularidades del mundo de Q.
“—No es fácil mantener la coherencia cuando interaccionas con otros… ¡Ni cuando tienes hijos!” dice el padre de Q en otro momento.
“Q subió al datagrama y pidió que le pusieran cerca de la cabecera, para poder mirar el paisaje (…) En ese momento pasó el revisor contando bits. Cuando llegó al final de la cadena dijo: «CRC listo. ¡Váaaamonos!»
Aunque tampoco se trata de una sucesión de “chistes de gremio”, como reflexión no escatima la profundidad de la indagación y me atrevería a decir que esconde alguna perla de uso macroscópico.
“Pero el Sistema es el Sistema por más que cada nueva generación de qbits haya querido derrocarlo. Te mide y te cambia.”
“—Mamá, ¿aprender duele?
—Solo si te resistes.“
Q se pregunta qué es la realidad, quién es él, si hay alguna diferencia entre ser y parecer, si es la conciencia algo más que una ilusión o cómo poder acceder a todas esas respuestas con garantías… Como veis, las mismas preguntas que nos hacemos desde que nos reuníamos en torno a una hoguera, o las mismas que nos devuelve la investigación sobre la inteligencia artificial o las prospecciones filosóficas.
La multitud de referencias, bromas, easter eggs, relacionados con la física y la computación, no son imprescindibles para seguir la trama pero le dan otros niveles de lectura que podéis disfrutar
Para ayudar a quien quiera acercarse a esos otros niveles y para aprovechar y divulgar un poco sobre esas cuestiones, el autor irá colgado en su canal de Youtube una suerte de “video apéndice” en el que se desgranan estos aspectos más técnicos.
En este enlace tenéis un par de capítulos libres para que conozcáis el mundo de Q antes de sumergiros en él, valiente acto este último, de cuyas consecuencias para vuestra mente seréis los únicos responsables…
Os animamos a que nos acompañéis, en la aventura de siempre, en la única aventura… vivida por este pequeño qbit, en su curioso mundo.
 El libro se puede descargar en este enlace
El libro se puede descargar en este enlaceFicha:
Autor: Javier Fernández Panadero
Título: Q, un cuento cuántico
Año: 2022
Editorial: Autopublicado
En Editoralia personas lectoras, autoras o editoras presentan libros que por su atractivo, novedad o impacto (personal o general) pueden ser de interés o utilidad para los lectores del Cuaderno de Cultura Científica.
El artículo Q, un cuento cuántico se ha escrito en Cuaderno de Cultura Científica.

