El oído absoluto de los animales
 Foto: Ryk Naves / Unsplash
Foto: Ryk Naves / UnsplashFue una de las cosas que descubrí durante el confinamiento. En el árbol que crece frente a mi casa habita un pajarillo que ensaya su repertorio de canciones casi siempre cuando empieza a ponerse el sol. Si desconozco su especie es porque entre mis vicios no se encuentra la ornitología. Y tampoco sé si el silencio del pasado marzo le ayudó a él a alzar la voz, o a mí, a escucharlo por primera vez. Pero desde hace cosa de un año, yo lo llamo Federico y lo identifico sin fallo por su tono burlón:
—¡Mi-re-do#, mi-re-do#! —dice siempre, apoyándose en la última nota.
Lo sorprendente es que todos los días su canto es exactamente el mismo. Lo sé porque una tarde empecé a imitarle con el piano y, desde entonces, he seguido acompañándole siempre en la mayor. Nunca desafina, el tío, ni se desvía de las notas lo más mínimo. Mi re do# es exactamente su canto de guerra y lo seguirá siendo mientras pueda trinar.
Esta extraña insistencia tiene, sin embargo, una explicación bastante sencilla: Federico tiene oído absoluto. Es una habilidad que le permite identificar cada tono por su frecuencia, sin ningún tipo de referencia adicional.
Evidentemente, el pajarillo no sabe que al otro lado de la ventana hay un simio con piano que le pisa los solos usando unas teclas llamadas “mi-re-do#. Pero el hecho es que identifica estos sonidos de manera consistente y los reproduce, día tras día, sin necesidad de que nadie le ayude a afinar, ni le recuerden cómo sonaba su tonalidad habitual. La mayoría de los humanos no tenemos esta habilidad. Y no se trata solo de que no sepamos llamar a las notas que suenan por su nombre como hacía Mozart (esto requiere necesariamente algún tipo de entrenamiento musical). Tampoco solemos recordar el tono de un sonido de un día para otro. Cuando en invierno encendemos la calefacción y la caldera se pone a aullar, no sabemos si sus alaridos suenan más graves o más agudos que los del día anterior. Yo misma, que vivo rodeada de notas y partituras, tuve recurrir a mi piano para descubrir que Federico estaba afinando siempre igual.
El oído absoluto, tan excepcional entre los humanos, no es un don demasiado raro en el reino animal1. Muchas especies de aves cantoras comparten esta habilidad auditiva. También los lobos, las ratas y otros roedores, según se ha observado, reconocen a otros miembros de su propia especie por el tono de su llamada. Esto nos indica que son capaces de identificar la frecuencia fundamental de los sonidos de manera absoluta y recordarla de un día para otro.
Lo más curioso de todo es que nuestro propio encéfalo y el de otros simios muestra una representación directa de los tonos. En nuestro oído, existe un órgano encargado de separar las distintas frecuencias del sonido llamado cóclea. Está recorrida por una membrana de rigidez decreciente (la membrana basilar), que vibra de forma selectiva en distintas regiones, según lo grave o agudo que es un sonido. Las distintas frecuencias llegan a nuestro córtex auditivo, donde existe un mapa tonotópico, que se activa de manera diferente cuando suena un mi o un fa. Esta es la paradoja: podríamos adivinar qué notas está escuchando una persona con solo observar sus patrones de activación cerebral. Pero ella misma no es capaz de acceder conscientemente a esa información. Es como si hubiese olvidado cómo llegar a ella.
Esta es, precisamente, una de las hipótesis que barajan algunos antropólogos y psicólogos de la música y el lenguaje2. Su idea es que hace cientos de miles de años todos nuestros antepasados tenían oído absoluto, como Federico. La frecuencia de cada sonido era tan nítida para ellos como lo es cualquier color para nosotros en la actualidad. Sin embargo, con el paso de los siglos fuimos perdiendo esa habilidad para poder dominar otra mucho más útil en términos evolutivos: el lenguaje3. Nuestra capacidad para reconocer los contornos del habla, las emociones de la prosodia, todas las melodías que nos acompañan cada vez que nos comunicamos con otros seres humanos depende crucialmente de nuestro oído relativo, una habilidad mucho más excepcional, en términos evolutivos, que el oído absoluto.
De hecho, y según he podido averiguar, mi plumífero vecino sería incapaz de reconocer su propia melodía si yo la tocase en otro tono o si intentase imitarlo con mi propia voz, más grave que la suya. A pesar de su asombrosa musicalidad, Federico no tiene oído relativo4. Para él sería impensable reconocer un contorno melódico simplemente por las relaciones entre sus notas. Nuestro oído, en cambio, es principalmente sensible a las relaciones, las distancias, los intervalos. Este es su verdadero superpoder, la habilidad única que nos permite oír “la misma” canción aunque todas sus notas hayan cambiado.
Referencias:
1Honing, Henkjan. The Evolving Animal Orchestra. Translated by Sherry MacDonald, The MIT Press, 2019.
2Mithen, Steven. “Perfect pitch.” The Singing Neanderthals: The Origins of Music, Language, Mind and Body, Harvard University Press, 2007.
3Saffran, J. R., and Griepentrog, G. J. 2001. Absolute pitch in infant auditory learning: evidence for developmental re-organization. Developmental Psychology 37, 74–85.
4Se ha conseguido entrenar a algunas especies de aves para que reconozcan acordes en distintas tonalidades. Pero parece que el oído absoluto sigue siendo su principal referencia. Ver Hoeschele, Marisa, et al. “Searching for the Origins of Musicality across Species.” The Origins of Musicality, edited by Henkjan Honing, The MIT Press, 2018.
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
El artículo El oído absoluto de los animales se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El oído absoluto de Mozart
- El oído absoluto y las lenguas tonales
- Los animales entienden la muerte más de lo que se pensaba
Los números apocalípticos
El número de la Bestia, el 666, es un número que causa cierta pasión entre muchas personas. En el pasado ya dedicamos un par de entradas del Cuaderno de Cultura Científica a hablar del mismo: 666, el número de la Bestia (1) y 666, el número de la Bestia (2).
 El número del hombre (1977), del artista canadiense Carle Hessay (1911-1978). Imagen de la web del artista Carle Hessay
El número del hombre (1977), del artista canadiense Carle Hessay (1911-1978). Imagen de la web del artista Carle Hessay
En esta entrada vamos a introducir algunas familias de números relacionadas con el número de la Bestia, el 666. Empezaremos con una familia sencilla, que introdujo el matemático estadounidense Eric W. Weisstein, creador de la enciclopedia MathWorld, el grupo de los números bestiales, que son aquellos números que en su representación en base decimal, base 10, poseen al número de la Bestia entre sus dígitos. Serían números como 1.666, 6.661, 2.666, 6.662, 3.666, 6.663, etcétera (la sucesión A051003, de la Enciclopedia online de secuencias de números enteros).
El número bestial 1.666, que es el año del gran incendio de Londres, es uno de los números que utiliza todas las letras del sistema de numeración romano: MDCLXVI. Otro número bestial, el 2.666, nos lo encontramos como título de la novela póstuma del escritor chileno Roberto Bolaño (1953-2003).
 Portada de la edición del libro “2666” del escritor chileno Roberto Bolaño, publicado en 2004 en la colección Narrativas hispánicas de Anagrama
Portada de la edición del libro “2666” del escritor chileno Roberto Bolaño, publicado en 2004 en la colección Narrativas hispánicas de Anagrama
Otra familia de números relacionada con el número de la Bestia, son aquellos números que podríamos llamar números del apocalipsis (ojo, que en la traducción del libro La maravilla de los números, de Clifford A. Pickover se denominan “apocalípticos”, pero ese nombre es el que reciben otros números que veremos más adelante), que son aquello que poseen 666 dígitos en su representación decimal.
Por ejemplo, el siguiente número, que podemos encontrar en la página Prime Curious!,
100000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000166657
es un número del apocalipsis (porque tiene 666 dígitos), que es un número bestial (contiene al 666) y además es primo, de hecho, es el número más pequeño con estas tres propiedades a la vez.
Otro número del apocalipsis, como se nos cuenta en el mencionado libro de Pickover, es el número de Fibonacci (véanse las entradas ¡Póngame media docena de fibonaccis! o El origen poético de los números de Fibonacci) número 3.184, F3184, que es el siguiente:
116724 3740814955 4123343576 4579214184 0689747174 4343943723 6331282736 2620824523 8531296068 2327210312 2788807682 4497987607 3455971975 1986312246 9939230900 1139062569 1096510740 1965107608 1705393206 0237984793 9189700037 7475124471 3440254679 5076870699 0550322971 3343709400 9365444241 1815206857 9040410434 0056856808 1194379503 0019676693 5663379234 7218656896 1365839903 2791816735 2721163581 6503595776 8655229310 2708827224 2471094763 8211542756 8268820040 2585049861 1340877333 3220873616 4591167264 9719869891 5791355883 4313855569 5800212192 8147052087 1752067489 3636617125 3380422058 8026552914 0335814561 9514604279 4653576446 7290281171 1540760126 7725615728 6715574607 0260678592 2979179042 4885389235 8861771163.
 El número de la Bestia es 666 (1805), del pintor y poeta británico William Blake (1757-1827). Imagen del Archivo William Blake
El número de la Bestia es 666 (1805), del pintor y poeta británico William Blake (1757-1827). Imagen del Archivo William BlakePero la familia de números que quería mostraros en esta entrada son los números apocalípticos, que son aquellos números de la forma 2 elevado a un número natural, 2n, que contienen la expresión 666 entre sus dígitos. Es decir, que son números bestiales de la forma 2n. El exponente más pequeño que da lugar a un número apocalíptico es 157, ya que, si calculamos 2157, este es igual a
182.687.704.666.362.864.775.460.604.089.535.377.456.991.567.872,
que, como vemos, contiene la expresión 666.
Estos números fueron introducidos por el matemático británico Neil J. A. Sloane, creador de la Enciclopedia online de sucesiones de números enteros, y el matemático canadiense Simon Plouffe, coautor con Sloane del libro The Encyclopedia of Integer Sequences (1995). El nombre de esta sucesión de números en la Enciclopedia online de sucesiones de números enteros es A007356 y los primeros exponentes que dan lugar a números de esta familia son:
157, 192, 218, 220, 222, 224, 226, 243, 245, 247, 251, 278, 285, 286, 287, 312, 355, 361, 366, 382, 384, 390, 394, 411, 434, 443, 478, 497, 499, …
A estos números n tales que 2n es un número apocalíptico se les llama exponentes apocalípticos. En la Enciclopedia online de sucesiones de números enteros podemos ver los primeros mil exponentes apocalípticos, que incluyen los exponentes 1.968 y 1.972.
El exponente apocalíptico más pequeño que da lugar a dos secuencias de 666 es 220, ya que 2 elevado a 220 es igual a:
1.684.996.666.696.914.987.166.688.442.938.726.917.102.321.526.408.785.780.068.975.640.576.
Al principio casi no hay exponentes apocalípticos. Como hemos visto, el primero es 157, solo hay otro en esa centena 192 o doce en la siguiente {218, 220, 222, 224, 226, 243, 245, 247, 251, 278, 285, 286, 287}. Y solo hay 125 exponentes apocalípticos menores que 1.000. Sin embargo, según vamos avanzando en los números naturales, cada vez hay más exponentes apocalípticos, hasta el punto que cualquier número mayor que 29.785 es altamente probable que sea un exponente apocalíptico.
La siguiente imagen nos ilustra perfectamente lo que acabamos de comentar. En ella se representan los exponentes apocalípticos sobre la espiral de Ulam. Como ya explicamos en la entrada del Cuaderno de Cultura Científica El poema de los números primos la espiral de Ulam es una cuadrícula de números en la que se representa el número 1 en el centro y se continúan representando los demás números naturales (2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12…) en espiral alrededor del 1 (en el sentido contrario a las agujas del reloj). En el contexto de los números primos se pintaban los cuadrados con números primos de negro (u otro color), mientras que los cuadrados de los números compuestos se dejaban de blanco (o incluso se podían pintar de otro color también).
En la siguiente imagen, que contiene una cuadrícula de 120 x 120 cuadrados (es decir, 14.400 cuadrados o números) se han pintado de rojo los cuadrados de los números que son exponentes apocalípticos, mientras que quedan sin pintar los cuadrados de los números que no son exponentes apocalípticos. Por ese motivo, la parte central de la espiral de Ulam “apocalíptica” no contiene cuadrados rojos, ya que hasta el número 157 ningún número es un exponente apocalíptico. Poco a poco van apareciendo, en espiral, los cuadrados rojos y al final casi todos son rojos.
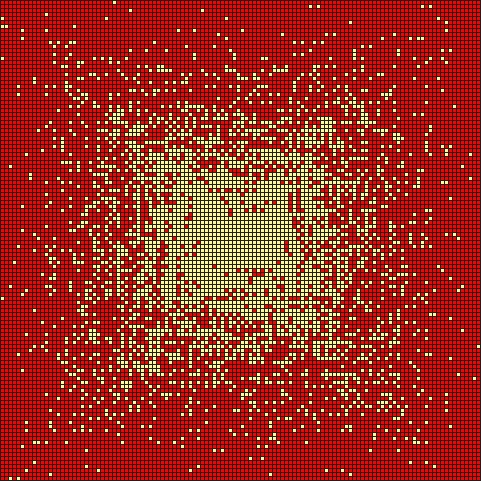 Espiral de Ulam con los exponentes apocalípticos pintados de rojo.
Espiral de Ulam con los exponentes apocalípticos pintados de rojo.
Vamos a cerrar esta entrada con dos números relacionados con el número de la Bestia y que introduce el divulgador Clifford Pickover en alguno de sus libros. El primero de ellos es el número legión (aparece en el libro Las matemáticas de Oz), que es el número de la Bestia 666 elevado al número de la Bestia 666, es decir,
666666.
Este es un número con 1.881 dígitos, que empieza con la expresión “2715417592” y termina en “0880598016”.
Y el otro, más grande aún, que aparece en el libro El prodigio de los números, es el número Leviatán, que es igual al factorial de 10 elevado al número de la Bestia, es decir,
(10666)!
Recordemos que el factorial de un número m es el número igual a la multiplicación de todos los números naturales menores, o iguales, que el mismo, es decir, m! = m x (m – 1) x (m – 2) x … x 3 x 2 x 1. Así, para los primeros números naturales sus factoriales son 1! = 1, 2! = 2, 3! = 6, 4! =24, 5! = 120, 6! = 720, 7! = 5040, y podríamos continuar.
El número leviatán es un número enorme. Para empezar, es mucho más grande que un de googol, que es 10 elevado a 100, esto es, 10100. De hecho, es más grande que 10668. Además, sus seis primeros dígitos son 134.072.
 Litografía 666 (el número de la bestia), de 1999, del artista neoexpresionista alemán A. R. Penck (1939-2017). Imagen de la página ArtPrice
Litografía 666 (el número de la bestia), de 1999, del artista neoexpresionista alemán A. R. Penck (1939-2017). Imagen de la página ArtPrice
Bibliografía
1.- Enciclopedia online de secuencias de números enteros
2.- Wolfram MathWorld: Apocalypse Number
3.- Clifford A. Pickover, La maravilla de los números, Ma Non Troppo, 2002.
4.- Numbers aplenty: apocaliptic number
5.- Clifford A. Pickover, Las matemáticas de Oz, Almuzara, 2005.
6.- Clifford A. Pickover, El prodigio de los números, Ma Non Troppo, 2002.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Los números apocalípticos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La magia de los números (el teorema de Moessner)
- El secreto de los números que no querían ser simétricos
- Los números que proporcionan alegría
Actúa localmente: huesos a partir de ARN modificado e impresoras 3D

En el mundo desarrollado la población envejece. En el mundo en desarrollo, conforme se consiguen avances económicos, sanitarios y sociales, las mujeres no tienen tantos hijos, por lo que también envejece, aunque en promedio de edad sean mucho más jóvenes. El hecho cierto es que el envejecimiento generalizado es una de las grandes macrotendencias demográficas y, por tanto, económicas para el futuro previsible.
El envejecimiento trae asociados cambios en qué se consume y cómo se consume, pero también en qué enfermedades serán cada vez más frecuentes simplemente porque lo son en las personas de mayor edad. Así, por ejemplo, los distintos tipos de cáncer o las enfermedades neurodegenerativas serán cada vez más comunes, oscureciendo estadísticamente los avances que se realizan para combatirlas. Por eso es tan importante invertir en prevención y en desarrollo de la ciencia básica y las terapias consiguientes para los tratamientos vayan por delante.
Otro tipo de patologías asociadas habitualmente al envejecimiento, menos, permítasenos el término, llamativas son las relacionadas con la degeneración ósea, como la osteoporosis. Se estima que, a nivel mundial, una de cada tres mujeres y uno de cada cinco hombres mayores de 50 años van a sufrir una fractura ósea osteoporótica. Además, aunque la mayoría de las fracturas sanarán sin complicaciones con el tratamiento apropiado, hay otros casos de deterioro de la regeneración ósea, por ejemplo, traumatismos importantes con infecciones secundarios a accidentes automovilísticos.
El hueso es el tejido más trasplantado después de la sangre por lo que la demanda de hueso para transplante solo aumentará en el futuro. Por ello, aparte de procurar regenerar el hueso existente se hace necesario tratar esas nuevas necesidades de tejido óseo.
El proyecto cmRNAbone, liderado por el AO Research Institute Davos (Suiza) pretende desarrollar una nueva terapia génica que mejore la vida de las personas con grandes lesiones traumáticas o enfermedades degenerativas óseas como la osteoporosis.
El enfoque propuesto es una combinación única de investigación genética, nano y biotecnología avanzadas, e impresión 3D: utilizando descubrimientos científicos recientes relacionados con agentes terapéuticos de ARN, el consorcio tiene como objetivo desarrollar ARN modificado químicamente (cmRNA, por sus siglas en inglés) que codifique proteínas específicas dirigidas a la neurogénesis, la vasculogénesis y la osteogénesis – tres procesos principales que influyen en la progresión de la curación. Los conjuntos de ARN producidos se combinarán con vehículos de entrega (vectores) no virales para que el suministro de ARN se incorpore en una formulación de tinta de biomaterial. El uso de una impresora 3D específicamente diseñada para el implante ayudará a demostrar las capacidades de regeneración ósea en la práctica.
Los nuevos hallazgos se aplicarán en dos estudios preclínicos simultáneos con el fin de demostrar la validez y relevancia clínica de la terapéutica diseñada en defectos óseos osteoporóticos y de tamaño crítico. Respaldado por una junta asesora clínica y científica, el consorcio dirigido por pymes garantizará una traducción fácil y rápida a la clínica una vez finalizado el proyecto. A largo plazo, los descubrimientos podrían constituir no solo un enfoque regenerativo para fracturas frágiles y defectos óseos grandes en población joven y de edad avanzada, sino también para otras enfermedades importantes que afectan a millones de pacientes.
La vasca CIDETEC Nanomedicine será la encargada de desarrollar precisamente los vectores cmRNA basados en polisacáridos, no virales, adaptados a la matriz desarrollada con el objetivo de conseguir la regeneración ósea.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Actúa localmente: huesos a partir de ARN modificado e impresoras 3D se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Actúa localmente: robots inteligentes autoadaptativos para la producción industrial
- Actúa localmente: impresión 3D de piezas aeronáuticas de titanio
- Actúa localmente: convertidores de potencia basados en carburo de silicio
¿De dónde viene el cáncer y por qué no ha desaparecido con la evolución?
Audrey Arnal, Benjamin Roche, y Frédéric Thomas
 El demonio de Tasmania es víctima de una forma particular de cáncer, transmisible de un individuo a otro. Fuente: Pixabay / pen_ash, FAL
El demonio de Tasmania es víctima de una forma particular de cáncer, transmisible de un individuo a otro. Fuente: Pixabay / pen_ash, FAL
El cáncer plantea multitud de cuestiones a los biólogos, gran parte de ellas todavía sin terminar de resolver. ¿Cómo se explican los orígenes de esta enfermedad? ¿Por qué es tan difícil de curar? ¿Por qué persiste la vulnerabilidad al cáncer en la mayoría de los organismos pluricelulares?
Los enfoques basados en la explicación de los mecanismos de esta enfermedad y las investigaciones clínicas no son suficientes frente a estos interrogantes. Debemos observar el cáncer desde una nueva perspectiva, adoptando una visión evolutiva. En otras palabras, debemos mirar el cáncer a través de los ojos de Charles Darwin, padre de la teoría de la evolución.
Desde hace unos años, el esfuerzo conjunto de biólogos evolutivos y oncólogos está fomentando reflexiones que se traducen en avances transversales beneficiosos para ambas disciplinas, a la vez que cambian nuestra comprensión de la enfermedad.
Cómo la evolución de los organismos pluricelulares prepara el terreno para el cáncer
El cáncer afecta al conjunto del reino animal pluricelular. La razón es que se trata de una enfermedad ancestral relacionada con la aparición de los metazoos (animales compuestos de varias células, en oposición a los protozoos que están constituidos por una sola célula), hace más de quinientos millones de años.
La aparición de tales organismos complejos requirió el desarrollo de altos niveles de cooperación entre la multitud de células que los componen. En efecto, esa cooperación se sostiene por comportamientos complementarios y altruistas, en particular por la apoptosis o suicidio celular (por el cual una célula activa su autodestrucción al recibir una cierta señal) y por la renuncia a la reproducción directa por parte de toda célula que no sea una célula sexual. Es decir, la evolución hacia entes pluricelulares estables se produjo por la selección de adaptaciones que, por un lado, facilitaban el funcionamiento colectivo y, por otro lado, reprimían los reflejos unicelulares ancestrales.
El cáncer representa una ruptura de esa cooperación pluricelular, seguida de la adquisición de adaptaciones que permiten que esas células «renegadas» se perfeccionen en su propio modo de vida. Dicho de otra forma, las células malignas comienzan a «hacer trampas». Pueden hacerlo pues han sufrido mutaciones genéticas (modificaciones de la secuencia de genes) o epigenéticas (modificaciones que cambian la expresión de los genes y que, además de transmisibles, son reversibles, al contrario de las mutaciones genéticas), o incluso las dos, lo que les confiere un valor selectivo más alto en comparación con las células de comportamiento cooperativo. Puede consistir, por ejemplo, en ventajas de crecimiento, de multiplicación, etc. De la misma forma, es imperativo que las células portadoras de esas modificaciones se sitúen en un microentorno favorable a su proliferación.
Si estas «rebeliones celulares» no son reprimidas de manera correcta por los sistemas de defensas del organismo (como el sistema inmunitario), la abundancia de células cancerosas puede aumentar localmente. Consecuencias: los recursos se agotan y estas células pueden iniciar entonces comportamientos individuales o colectivos de dispersión y de colonización hacia nuevos órganos, las tristemente conocidas metástasis responsables de la mayoría de los decesos debidos al cáncer.
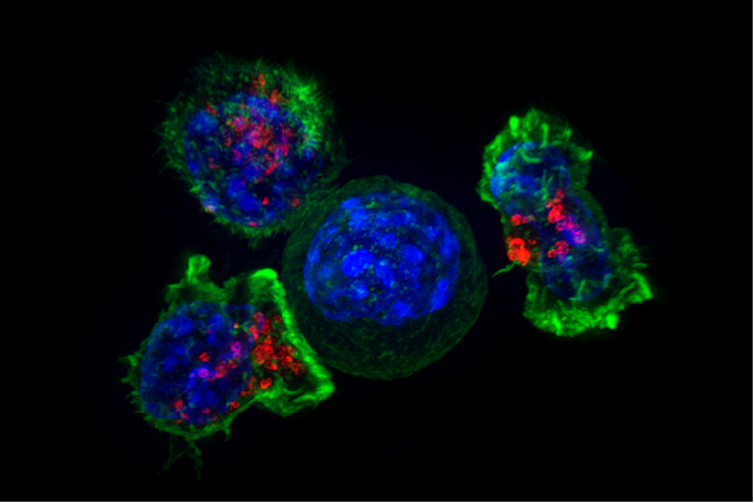 Células del sistema inmunitario (linfocitos T citotóxicos) rodean una célula cancerosa. Fuente: Alex Ritter, Jennifer Lippincott Schwartz y Gillian Griffiths, National Institutes of Health
Células del sistema inmunitario (linfocitos T citotóxicos) rodean una célula cancerosa. Fuente: Alex Ritter, Jennifer Lippincott Schwartz y Gillian Griffiths, National Institutes of HealthDe ese modo, en unos meses o años, una sola célula cancerosa puede generar un «ecosistema» complejo y estructurado, el tumor sólido (comparable a un órgano funcional), así como metástasis más o menos diseminadas por el organismo.
Un aspecto intrigante de esta enfermedad reside en el número significativo de semejanzas entre los atributos de las células cancerosas provenientes de diferentes órganos, individuos e incluso especies, lo que sugiere que los procesos que tienen lugar en cada caso son similares. Sin embargo, cada cáncer evoluciona como una nueva entidad, ya que, aparte de los cánceres transmisibles antes mencionados, los tumores desaparecen siempre junto a sus huéspedes, sin transmitir sus innovaciones genéticas ni fenotípicas.
Entonces, ¿cómo se explican esas semejanzas?
Persistencia del cáncer a lo largo del tiempo evolutivo
Desde un punto de vista evolutivo, hay dos hipótesis que pueden explicar la aparición del cáncer y la similitud de sus atributos.
La teoría del atavismo explica el cáncer como un retorno a capacidades anteriores de las células, entre las que se encuentra la liberación de un programa de supervivencia excelentemente conservado, siempre presente en toda célula eucariota y, por tanto, en todo organismo pluricelular. Se cree que la selección de este programa ancestral tuvo lugar durante el período precámbrico, que comenzó hace 4550 millones de años y terminó hace 540 millones de años. Durante este período, que vio surgir la vida sobre nuestro planeta, las condiciones medioambientales eran muy distintas de las actuales y, a menudo, desfavorables. Las fuerzas selectivas que actuaban sobre los organismos unicelulares favorecieron las adaptaciones para la proliferación celular.
Algunas de esas adaptaciones, seleccionadas a lo largo de la vida unicelular, quedaron presentes para siempre, más o menos escondidas en nuestros genomas. Cuando su expresión escapa de los mecanismos de control, comienza una lucha entre los rasgos ancestrales unicelulares y los rasgos pluricelulares actuales y es entonces cuando puede aparecer un cáncer. Es más, esta hipótesis podría explicar también por qué las células cancerosas se adaptan tan bien a los entornos ácidos y pobres en oxígeno (anóxicos), pues estas condiciones eran habituales en el Precámbrico.
La segunda hipótesis implica un proceso de selección somático –las células somáticas agrupan la totalidad de las células de un organismo a excepción de las células sexuales– que conduce a una evolución convergente, es decir, a la aparición de rasgos análogos. Esta hipótesis sugiere que la aparición de los rasgos celulares que caracterizan las células «tramposas» se somete a una fuerte selección cada vez que aparece un nuevo tumor, con independencia de cuáles sean las causas inmediatas de dichos rasgos. Estos procesos de selección somática, al tener lugar en entornos regidos en gran medida por los mismos condicionantes ecológicos (como los que reinan en el interior de los organismos pluricelulares), darían lugar a una evolución convergente.
Eso podría explicar las similitudes que observamos a través de la diversidad del cáncer. No olvidemos que solo vemos los cánceres que consiguen desarrollarse, pero no sabemos cuántos «candidatos» fracasan al no conseguir adquirir las adaptaciones necesarias en el momento adecuado.
Estas dos hipótesis no son excluyentes: la reaparición de un programa ancestral puede estar seguida de una selección somática que culmine en una evolución convergente.
Cualquiera que sea la razón del origen del cáncer, hay una pregunta que sigue sin respuesta: si esta enfermedad suele causar la muerte del huésped, ¿por qué no ha sido más eficaz la selección natural en conseguir que los organismos pluricelulares sean completamente resistentes al cáncer?
Los animales grandes no tienen más cáncer
Los mecanismos de supresión del cáncer son numerosos y complejos. Cada división celular puede provocar mutaciones somáticas que alteren los mecanismos genéticos que controlan la proliferación celular, la reparación del ADN o la apoptosis, perturbando así el control del proceso de formación del cáncer (carcinogénesis).
Si cada división celular conlleva una probabilidad dada de que se produzca una mutación cancerígena, entonces, el riesgo de desarrollar un cáncer debería ser función del número de divisiones celulares a lo largo de la vida de un organismo. Sin embargo, las especies de gran tamaño y más longevas no tienen más cáncer que aquellas pequeñas que viven menos tiempo.
En las poblaciones naturales animales, la frecuencia del cáncer varía, en general, entre un 0% y un 40 % para todas las especies estudiadas y no existe relación con la masa corporal. En los elefantes y en los ratones se observan niveles de prevalencia del cáncer bastante similares, a pesar de que los elefantes desarrollen muchas más divisiones celulares a lo largo de su vida que los ratones. Este fenómeno se conoce como «la paradoja de Peto».
La explicación de esta paradoja reside en el hecho de que las fuerzas evolutivas han seleccionado mecanismos de defensa más eficaces en los animales grandes que en los pequeños, lo que permite reducir el lastre ligado al cáncer por el aumento de tamaño. Por ejemplo, los elefantes tienen veinte copias del gen supresor de tumores TP53, mientras que los humanos solo disponemos de dos.
 La rata topo desnuda no teme al cáncer, que solo le afecta de forma anecdótica. Fuente: Meghan Murphy, Smithsonian’s National Zoo, CC BY-ND
La rata topo desnuda no teme al cáncer, que solo le afecta de forma anecdótica. Fuente: Meghan Murphy, Smithsonian’s National Zoo, CC BY-NDEncontramos excepciones notables a esta tendencia general, como es el caso de especies de pequeño tamaño con una longevidad fuera de lo normal. Estas especies tampoco desarrollan apenas cáncer. Un buen ejemplo es el de la rata topo desnuda (Heterocephalus glaber), una especie cuyos individuos viven mucho tiempo (especie longeva) y no desarrollan tumores espontáneos, con la excepción de algunos casos de cáncer detectados de forma anecdótica.
Una enfermedad que se manifiesta de forma tardía
Recordemos también que la eficacia de las defensas contra el cáncer experimenta una disminución una vez que los organismos han llevado a cabo lo esencial de su reproducción, ya que las presiones evolutivas son menores en esta etapa de la vida. Esta pérdida de eficacia, junto con la acumulación de mutaciones a lo largo del tiempo, explica que la mayor parte de los cánceres (mama, próstata, pulmón, páncreas…) aparezcan en la segunda mitad de la vida.
Una de las implicaciones evolutivas capitales es que si, desde una perspectiva darwiniana, el cáncer no es una preocupación relevante cuando se manifiesta tras la fase reproductiva, eso significa también que nuestras defensas se habrán optimizado por selección natural no para erradicar de forma sistemática los procesos oncogénicos sino para controlarlos mientras tengamos capacidad reproductora…
Al final, esas defensas low cost, cuyo objetivo es resistir frente a los tumores, se revelan más ventajosas para salvaguardar el éxito reproductor que como estrategias de erradicación sistemática, que serían sin duda mucho más costosas. El sistema inmunitario, por ejemplo, no trabaja a cambio de nada… En general, los seres vivos se rigen por soluciones de compromiso, trade-offs en inglés, que hacen que toda inversión en una función necesite de una serie de recursos y energía que ya no estarán disponibles para otras funciones. Nuestras defensas contra las enfermedades, el cáncer incluido, no quedan fuera de esta regla de funcionamiento.
Por desgracia, esas defensas low cost contra el cáncer se convierten al final en bombas con retardo… En otras palabras, ¡la lógica darwiniana no nos lleva siempre a resultados que casen con nuestras expectativas como sociedad en términos de salud!
Aunque la mayor parte de las mutaciones cancerígenas se producen en células somáticas a lo largo de la vida, hay casos raros de cáncer cuya causa se encuentra en mutaciones hereditarias en la línea germinal, la que produce las células sexuales. Esas mutaciones congénitas, a veces, son más frecuentesde lo que se esperaríadel equilibrio mutación-selección.
Esta paradoja se puede explicar por diversos procesos evolutivos. Por ejemplo, se ha sugerido que, probablemente, la selección natural no actuará sobre esas mutaciones si, una vez más, sus efectos negativos sobre la salud solo se manifiestan cuando haya terminado el período reproductivo.
Por otro lado, se podría recurrir a la teoría de la pleiotropía antagonista. Esta teoría estipula que ciertos genes tienen efectos contrarios sobre la probabilidad de supervivencia / reproducción según la edad considerada: sus efectos serían positivos al comienzo de la vida y negativos en el resto. Si el efecto positivo inicial es notable, es posible que la selección retenga esa variante genética aunque cause una enfermedad mortal más tarde.
Por ejemplo, las mujeres que presentan una mutación de los genes BRCA1 y BRCA2 tienen un riesgo significativamente más alto de desarrollar cánceres de mama o de ovario, pero esas mutaciones parecen estar relacionadas con una mayor fertilidad.
Implicaciones en materia de tratamientos
El cáncer, auténtico lastre de las poblaciones humanas, es ante todo un fenómeno regido por procesos evolutivos, desde su origen en la historia de la vida hasta su desarrollo en tiempo real en una persona enferma. La separación tradicional entre oncología y biología evolutiva, por tanto, debe desaparecer, pues limita nuestra comprensión de la complejidad de los procesos que culminan en la manifestación de la enfermedad.
Esta nueva perspectiva del cáncer podría resultar útil para el desarrollo de soluciones terapéuticas innovadoras que limiten los problemas asociados a las estrategias de tratamiento disponibles en la actualidad. Estas terapias de altas dosis, que buscan matar el máximo de células malignas, acaban provocando a menudo la proliferación de células resistentes. A la inversa, la terapia adaptativa, profundamente enraizada en la biología evolutiva, podría constituir un enfoque alternativo.
Esta estrategia consiste en disminuir la presión que conllevan las terapias de altas dosis con el fin de eliminar solo una parte de las células cancerosas sensibles. Se trata de mantener un nivel suficiente de competición entre las células cancerosas sensibles y las células cancerosas resistentes, con el fin de evitar o de limitar la proliferación sin restricciones de las resistentes.
Una problemática que no se limita al ser humano
Hasta hace poco, rara vez la oncología había adoptado los conceptos de la biología evolutiva para mejorar la comprensión de los procesos malignos. De igual forma, los ambientalistas y los biólogos evolutivos apenas se han interesado en la existencia de estos fenómenos en sus investigaciones sobre los seres vivos. Pero las cosas cambian y la consideración del cáncer –o, más bien, de los procesos oncogénicos en su conjunto– en el seno de la fauna salvaje suscita un entusiasmo creciente en el seno de la comunidad de los ambientalistas y de los biólogos evolutivos.
En efecto, a día de hoy, el cáncer se muestra con claridad como un modelo biológico pertinente para estudiar la evolución de los seres vivos, así como un fenómeno biológico de importancia para comprender diversas facetas de la ecología de las especies animales y sus consecuencias sobre el funcionamiento de los ecosistemas.
Aunque no siempre evolucionen hacia formas invasivas o metastásicas, los procesos tumorales son omnipresentes en los metazoos y hay estudios teóricos que sugieren que, probablemente, en estos últimos tengan influencia en variables fundamentales en ecología, como son los rasgos de historia de la vida, las aptitudes competitivas, la vulnerabilidad a los parásitos y a los depredadores, o incluso la capacidad de dispersarse. Esos efectos provienen tanto de consecuencias patológicas de los tumores como de los costes asociados al funcionamiento de los mecanismos de defensa de los huéspedes.
La comprensión de las consecuencias ecológicas y evolutivas de las interacciones huésped-tumor se ha vuelto también un tema de investigación de referencia en ecología y en biología evolutiva en estos últimos años.
Estos cuestionamientos científicos son todavía más pertinentes cuando la práctica totalidad de los ecosistemas del planeta, sobre todo los medios acuáticos, está contaminada hoy en día por sustancias de origen antrópico y, a menudo, mutágenicas. Por lo tanto, es primordial mejorar la comprensión de las interacciones huésped-tumor y sus efectos en cascada dentro de las comunidades, para así predecir y anticipar las consecuencias de las actividades humanas en el funcionamiento de los ecosistemas y en el mantenimiento de la biodiversidad.
Sobre los autores: Audrey Arnal es investigadora postdoctoral y Benjamin Roche director de investigación en el Institut de recherche pour le développement (IRD) ; Frédéric Thomas es director de investigación en el Centre national de la recherche scientifique (CNRS)
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo ¿De dónde viene el cáncer y por qué no ha desaparecido con la evolución? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La senescencia celular: el gran desafío para entender y tratar el cáncer
- Los supermicrobios amenazan con ser más letales que el cáncer
- La evolución nos dice que es probable que seamos la única vida inteligente del universo
La extinción de la megafauna chilena dejó a este árbol sin ayuda para dispersar sus semillas
Diego Muñoz-Concha y Andrea Loayza
 El gonfoterio (Stegomastodon platensis) fue parte de la megafauna que se extinguió en Chile a fines del Pleistoceno. Posiblemente dispersaba las semillas de queule. Ilustración: Fernán Muñoz
El gonfoterio (Stegomastodon platensis) fue parte de la megafauna que se extinguió en Chile a fines del Pleistoceno. Posiblemente dispersaba las semillas de queule. Ilustración: Fernán Muñoz
Como en una novela policial en la cual los detectives deben resolver un misterio y hallar un culpable, en las ciencias naturales los científicos también buscamos pistas, presentes y pasadas, que nos ayuden a entender lo que se observa (y lo que no) en un ecosistema. Uno de los grandes misterios ecológicos en la actualidad es la presencia de especies de plantas que producen frutos muy grandes en lugares donde ya no existen animales de gran tamaño que los consuman y puedan dispersar sus semillas. Para las plantas, la dispersión de la semilla es un proceso fundamental que permite a las especies subsistir en el tiempo y colonizar nuevos lugares.
Los frutos que son atractivos para los animales son comestibles y tienen tejidos carnosos muy nutritivos. Suelen ser de un tamaño proporcional a los principales animales que los consumen. Por eso, las plantas con frutos y semillas grandes son dispersadas por animales de gran tamaño (megafauna), ya que son los únicos capaces de tragar los frutos.
En algunos ecosistemas actuales, aún ante la presencia de plantas con frutos aparentemente adaptados para el consumo por grandes animales, no es posible encontrar fauna nativa moderna de gran tamaño que los consuma y disperse sus semillas. Estos frutos megafáunicos, observados hace décadas en ecosistemas centroamericanos, son considerados un anacronismo, y su presencia se atribuye a la desaparición de grandes bestias hace unos 10 000 años, hacia el final de la última época glacial, a fines del Pleistoceno.
Numerosas especies de plantas tienen frutos de carácter megafáunico en Sudamérica. En un estudio reciente fijamos la mirada en una escena ecológica donde participa un árbol en peligro de extinción que solo crece en una reducida extensión geográfica de la zona costera en el centro-sur de Chile.
El fruto de este árbol, llamado queule (Gomortega keule), es comestible y de gran tamaño (20 a 40 gramos). Tiene una semilla protegida por una durísima cubierta leñosa. En la época de fructificación, en otoño (abril y mayo en su zona de origen) los frutos caen al suelo y allí se pudren sin que haya animales nativos que los consuman en cantidades importantes, y menos que dispersen las semillas. Sin embargo, en Chile existen evidencias fósiles de la ocurrencia de megafauna en el Pleistoceno, como gonfoterios, équidos y cérvidos.
Lamentablemente, parece casi imposible encontrar un estómago fósil de estos animales con semillas de queule en su interior. Debemos buscar entonces otras evidencias que apunten al carácter megafáunico del fruto de queule.
 Frutos de queule en el suelo
Frutos de queule en el sueloUna observación importante corresponde al consumo de frutos de queule por parte de animales modernos de gran tamaño. Como parte de nuestro estudio, se dispusieron frutos maduros de queule en las jaulas de animales de un zoológico y también para animales domésticos en granjas locales. Algunos animales no se acercaron a los frutos, otros comieron la pulpa pero descartaron el cuesco, y algunos consumieron el fruto completo.
Esta evidencia permite asegurar que los frutos de queule son atractivos para animales de gran tamaño y que, al menos algunos de esos animales, tragan la semilla y por lo tanto pueden transportarla. Pero además es relevante conocer si la semilla mantiene su capacidad de germinar luego de pasar por la boca o el tracto digestivo del animal. Para esto realizamos experimentos de germinación con los cuescos recuperados, donde observamos germinación en todos los casos.
 Detalle de los frutos de queule
Detalle de los frutos de queule
Otra observación importante, ahora en el ambiente natural del árbol, fue la presencia de cuescos de queule en estiércol de cerdos y vacas. En algunas zonas donde persiste la especie, los habitantes locales señalan que el ganado se alimenta de los frutos de queule, lo que confirma esta observación y apoya el carácter megafáunico del fruto.
Sin embargo, puesto que no hay plántulas de queule en zonas con ganado, estos animales domésticos no están desarrollando hoy día el proceso de dispersión de semillas en forma efectiva para esta especie. Entre los animales nativos, donde existe muy poca información, solo un pequeño ciervo ha sido visto mordisqueando los frutos, pero debido a su reducido tamaño corporal (menos de 10 kilogramos), no es probable que trague la semilla.
 Cuescos de queule
Cuescos de queule
¿Debemos ayudar al queule?
Aunque parece bastante claro que el fruto megafáunico de queule representa un anacronismo, existen aún muchas interrogantes que futuras investigaciones deberán abordar para avanzar de forma efectiva en la conservación de esta especie de árbol. La escasa sobrevivencia de sus plántulas, el posible rol de dispersión de semillas por animales como roedores y por el ganado, y sobre todo los múltiples efectos de la alteración que sobre el bosque original han producido la agricultura y la silvicultura son algunas de las preguntas que deben ser respondidas.
 El ciervo más pequeño del mundo, el pudú (Pudu puda), es el único animal de ciertas proporciones que fue observado comiendo frutos de queule, aunque no es probable que pueda tragar y dispersar la semilla. Foto: Carlos Reyes y Alexis Villa, CONAF Maule.
El ciervo más pequeño del mundo, el pudú (Pudu puda), es el único animal de ciertas proporciones que fue observado comiendo frutos de queule, aunque no es probable que pueda tragar y dispersar la semilla. Foto: Carlos Reyes y Alexis Villa, CONAF Maule.La intervención con cerdos o caballos, que podrían dispersar semillas de queule, puede parecer atractiva, pero la complejidad del sistema hace difícil prever los efectos negativos que en el caso del cerdo ya se han observado en otros ecosistemas neotropicales.
Antes de pensar en la introducción de megafauna para restablecer procesos ecológicos importantes (rewilding) como la dispersión de semillas, hay que considerar experiencias recientes muy preocupantes por sus consecuencias sociales y ecológicas.
El caso de queule también puede despertar reflexiones éticas y filosóficas, pues se trata de una especie con problemas de dispersión de semillas muy posiblemente desde tiempos anteriores a los cambios planetarios que vivimos hoy, situación compartida por varias otras especies de plantas.![]()
Sobre los autores: Diego Muñoz-Concha es profesor e investigador en botánica de la Universidad Católica del Maule y Andrea Loayza es profesora asociada de la Universidad de La Serena
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo La extinción de la megafauna chilena dejó a este árbol sin ayuda para dispersar sus semillas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Árbol sagrado, árbol maldito
- Natacha Aguilar: “Necesitamos que el mar esté en equilibrio para que el planeta también lo esté”
- No todo ha sido malo este año: la ciencia nos dejó algunas buenas noticias
María Jesús del Río – Naukas Bilbao 2019: El día que el MWh alcanzó los 10.000€
 Foto: Charlotte Venema / Unsplash
Foto: Charlotte Venema / UnsplashPasó a principios de 2021 y se formó una gran polvareda que quedó en nada. Exactamente igual que en 2019. María Jesús del Río desentraña en esta charla el misterio de cómo se forma el precio de la electricidad en España. Un adelanto: como todos los precios es una cuestión de oferta y demanda y, como todos los precios, es una cuestión de las distorsiones de un mercado intervenido.
María Jesús del Río es ingeniera industrial con especialidad en electrotecnia. Atesora más de 15 años de experiencia en empresas de energías renovables, donde he desarrollado principalmente tareas de análisis de producción y seguimiento de mercados.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo María Jesús del Río – Naukas Bilbao 2019: El día que el MWh alcanzó los 10.000€ se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Ana María Zubiaga – Naukas Pro 2019: La difícil búsqueda de terapias contra el cáncer
- Naukas Bilbao 2017 – María José Calderón y Belén Valenzuela: Esta física es la leche
- Naukas Bilbao 2017 – Aberrón entrevista a María Martinón y a José Mª Bermúdez de Castro
El riesgo de división social entre vacunados y no vacunados
Ramón Ortega Lozano y Aníbal Monasterio Astobiza
 Fuente: freepik.es
Fuente: freepik.esMuchos autores (Walton, Rudinow, Hartog) han analizado la falacia de la pendiente resbaladiza como un argumento que propone que cuando se da un primer paso hacia una dirección, una serie de consecuencias inextricables conducirán, en última instancia, a un resultado desastroso. Una falacia es un argumento imperfecto, es decir, con deficiencias formales que lo convierten en irracional. En el caso de los temas que aborda la pendiente resbaladiza, los resultados siempre son negativos. Por eso suelen ser un buen caldo de cultivo para la ciencia ficción, en especial para las distopías.
Sin embargo, pese a basarse en argumentos imperfectos, la pendiente resbaladiza no impide hacer algunas críticas razonables sobre las consecuencias que podrían derivarse de intervenciones en exceso arriesgadas. María Teresa López la Vieja analiza en su libro La pendiente resbaladiza: la práctica de la argumentación moral que un uso conservador del argumento justificará el rechazo de lo nuevo, por el temor a que nos lleve hacia el desastre. Por el contrario, un uso crítico invita a mantener la prudencia ante prácticas de resultado incierto.
La vacuna y la pendiente resbaladiza
Cuando hizo acto de aparición la vacuna contra el virus SARS-CoV-2, no dejaron de pronunciarse argumentos que advertían las posibles consecuencias negativas sobre su impacto social. Muchos de ellos correspondían a la clasificación de pendiente resbaladiza, pues renunciando a la lógica formal, prevenían de un posible desastre. Uno de los principales problemas que se planteó era si la vacunación debía ser obligatoria. O si debía serlo al menos para algunos colectivos.
A partir de aquí se empezó a especular sobre la división social que podría acarrear el estar vacunado frente a los que no lo estuvieran. De hecho, una de las primeros ideas que se barajó para mostrar los peligros de esa posible desigualdad era ejemplificada con la idea de ciudadanos que podían viajar, por estar vacunados, y ciudadanos que no, por no estarlo.
¿Es posible que una falacia termine convirtiéndose en una realidad? En la actualidad, el pasaporte de vacunación parece serlo y se materializará en breve. Bajo la lógica argumentativa de la pendiente resbaladiza, la posibilidad del pasaporte de vacunación es una mala idea y representa una medida discriminatoria e iliberal, porque nos conduce en una dirección con resultados inciertos.
Pensemos en tres grupos poblacionales que pueden no vacunarse: a) aquellas personas que no pueden, porque tienen una contraindicación médica (edad, condiciones de salud y/u otros factores); b) aquellas personas que no quieren (antivacunas o por simple razón de autonomía); y c) aquellas personas que no tienen acceso a la vacuna. ¿Estas personas tendrían restringidas sus libertades de movilidad por no tener un pasaporte de vacunación? ¿Qué hacemos con estos grupos? ¿Es posible pensar en un mercado negro de pasaportes de vacunación falsificados?
Como puede verse, a veces las metáforas catastróficas que enuncian las pendientes resbaladizas pueden enunciar verdades, pese a que su argumento sea imperfecto (irracional). Incluso cuando una medida como el pasaporte de vacunación parece insuficiente para prevenir los riesgos de contagio, pues, como analizan Beriain y Rueda, ni siquiera está probado que las vacunas produzcan una inmunidad esterilizante. O lo que es lo mismo, no se ha demostrado que los vacunados no puedan contagiar o transmitir el virus.
El riesgo como fundamento de la pendiente
El concepto de riesgo es actualmente entendido como la probabilidad que existe de que tenga lugar un acontecimiento con un impacto negativo o de que un factor aumente la probabilidad de que esto ocurra. En el ámbito sanitario, el factor de riesgo son aquellas condiciones que dentro de una cadena de acontecimientos relacionados sirven para identificar causas próximas al desarrollo de una enfermedad.
Lo interesante es que esta idea de riesgo supone siempre un control social. La sociedad “saludable” tiene un comportamiento predecible y deseable, y lo que se aparta se convierte en una conducta desviada. En otras palabras, existen comportamientos que deben ser controlados para evitar riesgos.
Debido a la actual pandemia podemos ver múltiples ejemplos. Basta mencionar el uso de la mascarilla. Cuando se habla de control social, no se está haciendo referencia a unas leyes sancionadoras por no usar la mascarilla, sino a que es la misma sociedad la que vigila y controla su uso. ¿Quién vería bien, hoy en día, que una persona estornudara o tosiera sin mascarilla? Incluso aunque estuviera haciendo deporte al aire libre, su comportamiento sería censurado. O, por lo menos, no se vería con buenos ojos.
Por tanto, salud, riesgo y control social son conceptos muy unidos. Pero es importante remarcar que el peso de ese control no necesariamente proviene de un poder estatal, sino de una narrativa. Desde la antropología de la salud se ha analizado que la narración en torno al riesgo puede tener como consecuencia miedo, ansiedad y rabia. Ejemplos que también hemos visto durante la pandemia como los censurables ataques a profesionales de la salud por parte de sus vecinos.
Nuevas pendientes de vacunados y no vacunados
Dentro de la narrativa de riesgo podría ser aceptable la implementación de estos pasaportes. Como se ha mencionado arriba, la pendiente resbaladiza puede ayudarnos a generar un pensamiento crítico, para analizar con cautela los posibles desenlaces de una acción. ¿Deberíamos aventurarnos, entonces, a plantear otras pendientes a partir del pasaporte de vacunación?
Parece necesario enunciar algunas, aunque su finalidad no sea otra que la cautela, es decir, la de proponer límites que resultaría inaceptable sobrepasar frente a esa posible división social entre vacunados y no vacunados. ¿Podría comenzar a usarse un pasaporte parecido para entrar a ciertos lugares de ocio (discotecas, bares, restaurantes, cines)? ¿Podría solicitar un empleador a un candidato, previa firma de un contrato de cesión de datos privados, que muestre su certificado de inmunidad para ser contratado?
Si el virus SARS-CoV-2 se convierte en una infección respiratoria endémica, lo cual es muy probable, ¿seguirán siendo útiles los pasaportes de vacunación? ¿Los pasaportes de vacunación estarán basados en una vacuna administrada o en ciertos niveles de anticuerpos en sangre? Estas y otras muchas cuestiones se plantean de seguir la argumentación de la pendiente resbaladiza en su uso crítico-prudencial y merecen ser examinadas si no queremos acabar con una división social entre vacunados y no vacunados.![]()
Sobre los autores: Ramón Ortega Lozano es profesor de antropología de la salud y comunicación humana en la Facultad de Ciencias de la Salud San Rafael-Nebrija, Universidad Nebrija y Aníbal Monasterio Astobiza es investigador posdoctoral de la Universidad del País Vasco / Euskal Herriko Unibertsitatea
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo El riesgo de división social entre vacunados y no vacunados se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El cannabis rompe el equilibrio metabólico entre neuronas y astrocitos alterando el comportamiento social
- La secuencia de estructuras intermedias durante la división de la membrana celular
- ADN, microbiota y riesgo de celiaquía
El proyectil del camaleón
 Chamaeleo zeylanicus. Ilustración: María Lezana
Chamaeleo zeylanicus. Ilustración: María LezanaTendemos a pensar en la endotermia como la condición ideal de los animales, esa que permite la homeotermia y, por lo tanto, la llave para poder llevar una vida independiente (hasta cierto punto, entiéndase) del calor o, más frecuentemente, del frío que pueda hacer ahí fuera.
Efectivamente, el poder mantener constante la temperatura corporal tiene la ventaja de que permite que la actividad no se vea apenas condicionada por el entorno térmico. Pero también tiene una gran desventaja: sale cara. A los efectos, es como tener encendida de forma permanente una estufita interna. Quizás por esa razón son tan pocos los grupos animales cuyos miembros regulan su temperatura corporal para mantenerla constante (homeotermos). Así pues, no cabe pensar en la endotermia como “condición ideal”. De hecho, la mayoría de especies animales son poiquilotermos; esto es, permiten que su temperatura interna varíe en función de los cambios ambientales. Y a la inmensa mayoría de ellas no les va nada mal.
El efecto que ejerce la temperatura sobre la actividad animal puede ser muy importante. La velocidad de las reacciones químicas depende de la temperatura, por lo que todas las funciones basadas en reacciones químicas también dependen de la temperatura; es lo que ocurre con la contracción muscular, o con la absorción intestinal de nutrientes, por ejemplo. Por ello, las bajas temperaturas pueden limitar la capacidad de movimiento de los animales poiquilotermos, algo que puede tener consecuencias de gran trascendencia. Por ejemplo, para poder atrapar una presa hay que realizar algún tipo de movimiento, y lo mismo cabe decir cuando de lo que se trata es de huir de un depredador.
Se trata de una cuestión de tan importantes consecuencias potenciales, que muchos animales poiquilotermos han desarrollado eficaces mecanismos para neutralizar, en cierta medida al menos, la dependencia térmica de la actividad. Esto es, han conseguido que el metabolismo, así como sus niveles generales de actividad dependan de la temperatura en un grado inferior al que cabría esperar si el efecto térmico consistiese únicamente en un efecto cinético directo sobre las reacciones químicas implicadas. Gracias a esa capacidad, el nicho ecológico de las especies puede ser algo más amplio de lo que sin ella hubiera sido, y esto es más importante en los animales terrestres, porque en los medios acuáticos, y sobre todo en el mar, los cambios térmicos son de menor amplitud y, casi siempre, mucho más graduales.
Aparte de esa capacidad para mitigar la dependencia térmica que tienen numerosos animales, también hay especies que han desarrollado otras tácticas para compensar los efectos de esa “tiranía” térmica. Aquí veremos una de esas tácticas, un truco, -podría decirse-, que han desarrollado los camaleones.
Los camaleones, como todos los reptiles vivientes, son poiquilotermos, pero tienen un nicho ecológico muy amplio, máxime si los comparamos con los lagartos, a los que, por otra parte, tanto se asemejan. Los camaleones son depredadores de la modalidad “sit-and-wait”. Son de movimientos lentos, y extraordinariamente crípticos, porque se camuflan muy bien; gracias a esa capacidad sus presas potenciales no se percatan de su presencia. Y utilizan, además, un procedimiento de caza muy especial: la proyección balística de la lengua. Seguramente todos tenemos en mente imágenes de alguna proyección de la lengua de un camaleón, pues son imágenes muy habituales en documentales de televisión. La proyectan a gran velocidad; aunque su longitud puede llegar a duplicar la del cuerpo, pueden extender la lengua en 0’07 s (a una aceleración de 400 m s-2). En la lengua tienen una sustancia adhesiva y allí quedan adheridos los insectos que atrapa. Ese es, en pocas palabras, su método de caza.
Como he señalado antes, los camaleones tienen un nicho ecológico muy amplio, ya que son capaces de cazar en un intervalo amplio de temperaturas. Esa capacidad se debe a la naturaleza del movimiento de la lengua. Porque no es un movimiento muscular, sino que se debe a la extensión de los componentes elásticos de colágeno. Al parecer, la actividad muscular tiene el cometido de recoger, -podría decirse que el de enrollar y tensar-, la lengua; cuando se encuentra recogida, los componentes elásticos se encuentran contraídos y al proyectarse hacia una presa, se libera la tensión que se había generado al recogerse. En cierto modo, se asemeja al funcionamiento de una ballesta. Recoger la lengua es similar a armar la ballesta; en ambos casos hay que hacer un trabajo. Y luego, una vez que está armada, solo hay que soltarla cuando se desea. La lengua funciona, a todos los efectos, como un proyectil.
Gracias al uso de ese mecanismo, la proyección de la lengua es muy poco dependiente de la temperatura: un descenso de 10 ºC solo provoca una reducción de entre un 10% y un 20% en la velocidad y potencia con que se proyecta la lengua, cuando si ese movimiento se hubiera basado en la contracción muscular, hubiera experimentado una reducción superior al 40% para ese mismo descenso térmico. Esto es, las temperaturas bajas no reducen en exceso la velocidad de proyección, pero sí la del posterior recogimiento. Claro que para cazar insectos, la clave no está en enrollar la lengua rápidamente, sino en lanzarla después a gran velocidad.
El sistema de proyección de la lengua de los camaleones es un curioso y útil mecanismo. Gracias a él pueden vivir en zonas de temperaturas muy diversas y, además, pueden cazar desde muy temprano en la mañana en zonas frías. Y eso es algo que, por efecto del frío, les está vedado a otros reptiles. Sabíamos que su capacidad de camuflaje constituye una valiosa adaptación. Pero el mecanismo descrito en este artículo también es muy valioso, por la ventaja competitiva que comporta.
Fuente: Christopher V. Anderson & Stephen M. Deban (2010): “Balistic tongue projection in chamaleons maintains high performance at low temperature.” PNAS 107: 5495-5499.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo El proyectil del camaleón se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Un camaleón plasmónico que cambia de color en función del entorno
- A mayor tamaño menor intensidad metabólica
- Relaciones hídricas y salinas de los animales
Una fórmula descubierta por Galileo
Que se rompan las cifras,
sin poder calcular
ni el tiempo ni los besos.
Y al otro lado ya
de cómputos, de sinos,
entregarnos a ciegas
–¡exceso, qué penúltimo!–
a un gran fondo azaroso
que irresistiblemente
está
cantándonos a gritos
fúlgido de futuro:
“Eso no es nada, aún.
Buscaos bien, hay más”.
Pedro Salinas, La voz a ti debida (1933). Poema [19], versos 726-739
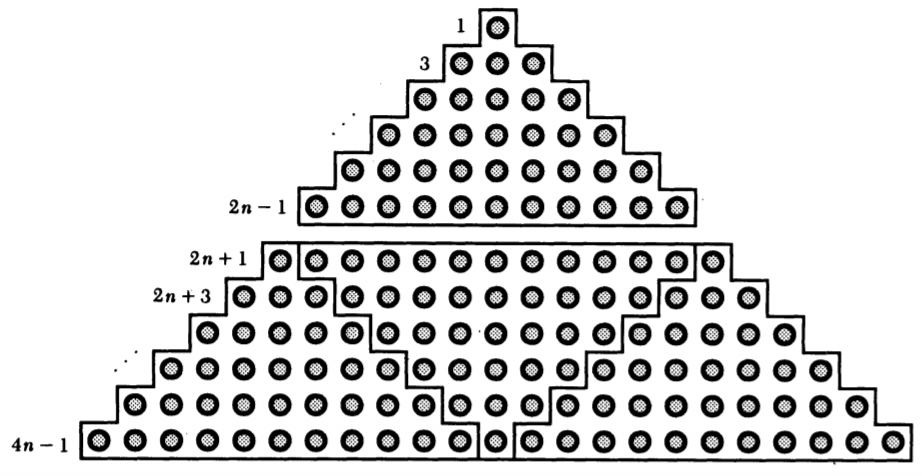 Demostración sin palabras de una fórmula descubierta por Galileo (ver [2])
Demostración sin palabras de una fórmula descubierta por Galileo (ver [2])
Este poema sobre cifras y cómputos habla de un amor sin límites. Me parece una hermosa manera de introducir una no menos bonita fórmula descubierta por Galileo en 1615:
No es difícil probar esta fórmula por inducción matemática. Propongo una sencilla demostración en dos pasos.
Veamos en primer lugar que la suma de los n primeros números impares p(n) = 1 + 3 + 5 + … + (2n-1) es n2.
Es claro que la fórmula es cierta para n=1 (1 = 12). Suponiendo que se cumple para n (es decir, p(n) = n2), veamos que es cierta para n+1. En efecto,
p(n+1) =1 + 3 + 5 + … + (2n-1) + (2n+1) = [1 + 3 + 5 + … + (2n-1)] + (2n+1) = p(n) + (2n+1).
Aplicando la hipótesis de inducción, queda que:
p(n+1) = n2 + (2n+1) = (n+1)2.
En segundo lugar, comprobemos que la suma de los siguientes n números impares q(n) = (2n+1) + (2n+3) + … + (4n-1) es 3n2.
La fórmula es cierta para n=1 (2 + 1 = 3 x 12). Suponiendo que se cumple para n (es decir, q(n) =3n2), veamos que es cierta para n+1. En efecto,
q(n+1) =(2(n+1)+1) + (2(n+1)+3) + … + (4(n+1)-1) =
(2n+3) + (2n+5) + … + (4n+3).
Observar que esta suma tiene n+1 sumandos, obtenidos al eliminar de q(n) el primer elemento (2n+1) y al añadirle los dos sumandos (4n+1) y (4n+3). Es decir,
q(n+1) = q(n) – (2n+1) + (4n+1) + (4n+3).
Aplicando la hipótesis de inducción, queda que:
q(n+1) = 3n2 – (2n+1) + (4n+1) + (4n+3) = 3n2 + 6n + 3 = 3(n+1)2.
La fórmula de Galileo es entonces cierta ya que:
p(n) / q(n) = n2 / 3n2 = 1/3.
El matemático Roger B. Nelsen es el autor del sugerente libro Proofs Without Words: Exercises in Visual Thinking (The Mathematical Association of America, 1997). En este texto propone una serie de pruebas sin palabras, es decir, demostraciones visuales, sin ninguna explicación, que ilustrarían una propiedad matemática que se desea verificar. La imagen que abre este escrito es precisamente una demostración visual de la fórmula descubierta por Galileo de la que hemos tratado en esta entrada: es la que propone Nelsen en la referencia [2].
Por cierto, la fórmula para la suma de los n primeros números impares también puede demostrarse sin palabras:
 Una prueba sin palabras para el teorema de la suma de los números impares. Fuente: Wikimedia Commons.
Una prueba sin palabras para el teorema de la suma de los números impares. Fuente: Wikimedia Commons.
El primer cuadrado formado por un bloque negro muestra que p(1) = 1. Al añadir alrededor de él una tira de 3 bloques blancos (al sumar 1 + 3) se obtiene otro cuadrado y con ello se demuestra que p(2) = 4, y así sucesivamente…
Referencias
[1] Oddity, Futility Closet, 18 marzo 2021
[2] Roger B. Nelsen, Proof without words: On a property of the sequence of odd integers (Galileo, 1615), Mathematics Magazine, Vol. 68, no. 1, 1995, pág. 41.
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Una fórmula descubierta por Galileo se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Vida de Galileo
- La mágica fórmula de Balmer
- Modelado matemático: del legado de Galileo al ambiente, la medicina y la tecnología
Actúa localmente: impresión 3D de piezas aeronáuticas de titanio
 Foto: Rafael Drück / Unsplash
Foto: Rafael Drück / Unsplash
El desarrollo de las economías emergentes lleva aparejado cambios sociales además de económicos. El surgimiento de una nueva clase media con necesidades de consumo que hasta ahora no existían es uno de los motores de las nuevas inversiones en regiones como Asia. Sin embargo, si este nuevo consumo de cientos de millones de personas fuese exactamente igual que el de las economías occidentales el perjuicio al medio ambiente y, en especial, sobre el cambio climático tendría unas consecuencias terribles. Gobiernos como el de China son conscientes de ello y por eso han adoptado medidas para que, por ejemplo, los vehículos eléctricos sean mayoritarios, si no los únicos de aquí a unos años.
Otro aspecto importante de la nueva clase media emergente es la necesidad de viajar, por los motivos que sean, a distancias o a lugares, como los archipiélagos, para los que ni el coche ni el ferrocarril son alternativas adecuadas. Si ya el actual consumo de aviación es preocupante actualmente, un incremento sustancial lo convierte en un problema global de primera magnitud. Por ello la nueva generación de aviones debe ser lo más eficiente posible. Los nuevos diseños deben reducir su huella de carbono todo lo posible hasta que los aviones eléctricos o de pila de combustible puedan ser una realidad; algo que parece muy alejado en el tiempo para la aviación comercial.
 Fuente: GE Aviation
Fuente: GE AviationA la hora de hacer un avión más eficiente en el consumo de combustible una parte importante pasa por el diseño de los motores. Existe un número que está directamente relacionado con esta eficiencia: la relación de derivación. Este número mide cuánto del aire que introduce la hélice en el habitáculo del motor pasa efectivamente por la turbina. Si el número es alto significa que de todo el aire que entra solo una pequeña parte pasa por la turbina; y al revés. Si el número es alto el motor consume menos combustible; si el número es bajo el motor es más potente. Los números altos se usan en avión comercial, los números bajos en aviones de combate; la única excepción era el Concorde, que era un avión comercial con diseño de avión de combate. Una consecuencia directa de este factor es que los motores de los aviones comerciales son voluminosos y los de los aviones de combate (o los del Concorde) del tamaño mínimo.
Si la idea es construir aviones más eficientes la consecuencia de lo anterior es evidente: hay que construir motores aún más voluminosos. Pero claro, esto choca de frente con la aerodinámica. Un motor más grande genera turbulencias indeseadas que provocan inestabilidades, ruidos y, también, mayor consumo de combustible. Este problema debe solucionarse con actuadores para controlar el flujo de aire.
Estos actuadores tienen que tener una serie de características muy concretas: deben ser de bajo peso (como todo en un avión), muy resistente mecánica y químicamente. Además es más que probable que su diseño sea cualquier cosa menos trivial.
¿De qué construir un actuador de este tipo? De acero no puede ser, porque pesaría mucho; de aluminio tampoco, porque la resistencia mecánica estaría en el límite. La respuesta ya se encontró hace tiempo: de titanio. O mejor dicho, de una aleación de titanio. Una que ha demostrado ser óptima para aplicaciones aeronáuticas es la Ti-6Al-4V, esto es, un 6 % de aluminio, un 4 % de vanadio y el 90 % restante (menos impurezas) de titanio.
 Fuente: flowcaash.eu
Fuente: flowcaash.euPero esta aleación de titanio es muy difícil de trabajar, precisamente por sus características. ¿Cómo conseguir un diseño complejo hecho de ella? Una cooperativa vasca, IK4 Lortek tiene una respuesta: por fabricación aditiva usando fusión selectiva por láser. Traducido consiste “simplemente” en diseñar la pieza tridimensional en un ordenador y este diseño pasarlo a una impresora en 3D que emplea un láser para fundir granos de la aleación de titanio, con lo que crea la pieza capa a capa (aditivamente). Este concepto foma parte de un proyecto, Flowcaash, alentado por Airbus, que pretende desarrollar diseños biomiméticos de bajo peso para integrar los actuadores de flujo en la siguiente generación de aviones, mejorando su eficiencia de combustible y aerodinámica. Todos los ensayos de las nuevas piezas se realizan en el alavés Centro de Tecnología Aeronáuticas CTA (donde se hicieron las pruebas de la sonda Exomars, por cierto).
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Actúa localmente: impresión 3D de piezas aeronáuticas de titanio se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Actúa localmente: robots inteligentes autoadaptativos para la producción industrial
- Actúa localmente: convertidores de potencia basados en carburo de silicio
- Prótesis biocompatibles por impresión 3D
Cómo conseguir lácteos más saludables cambiando la alimentación del ganado lechero
Andrés Luis Martínez Marín
 Shutterstock / Auldist
Shutterstock / AuldistLa historia del consumo de productos lácteos se remonta al Neolítico, cuando la ganadería aparece en la historia de la humanidad. A partir de ese momento, la leche se consideró el alimento por excelencia, la fuente de fortaleza y vida. La leche contiene proteínas, lactosa, grasa, minerales y otros componentes minoritarios de alto valor nutricional.
Diferentes estudios publicados en la última década indican que el consumo habitual de leche y productos lácteos (queso, mantequilla, yogur) contribuye a la prevención o repercute favorablemente en la evolución de diversas enfermedades crónicas como diabetes, cáncer y trastornos cardiovasculares. Por tanto, la leche y los productos lácteos deberían ser parte de una dieta humana equilibrada.
La grasa de la leche: un producto complejo
La grasa es el componente cuantitativa y cualitativamente más variable en la leche. No sólo es el constituyente que aporta más energía a la leche, sino que es responsable de una parte importante de sus aptitudes tecnológicas y de las propiedades organolépticas de los productos lácteos.
Cuando hablamos de grasa láctea, nos referimos generalmente a los triglicéridos porque son los compuestos mayoritarios (más del 97 % del total). Sintetizados en la glándula mamaria, están compuestos por una molécula de glicerol unida a tres moléculas de ácidos grasos.
En la grasa láctea, se han identificado más de 400 ácidos grasos diferentes, con diversas propiedades físicas, químicas y biológicas en función de su estructura química. Estos ácidos grasos pueden provenir de las siguientes fuentes:
- De los ácidos grasos presentes en los alimentos consumidos por el animal.
- De la modificación de estos mismos ácidos grasos o de la síntesis de otros nuevos por las bacterias que habitan en el rumen, la cavidad anterior del estómago de los rumiantes.
- De la síntesis en glándula mamaria.
De lo anterior se desprende que la composición de la alimentación de las hembras rumiantes repercute de forma decisiva sobre la composición de la grasa de su leche.
La grasa láctea se ha considerado un componente indeseable de la dieta desde el punto de vista de la salud porque es rica en ácidos grasos saturados de cadena media, cuyo consumo excesivo se relaciona estrechamente con el riesgo de padecer enfermedades cardiovasculares. No obstante, también es prácticamente el único aporte importante a la dieta humana de una variedad de ácidos grasos cuantitativamente menores, pero con efectos potencialmente beneficiosos sobre la salud.
Ácidos grasos exclusivos de la grasa láctea
En la dieta humana, la grasa de la leche es una fuente exclusiva, o la más importante según el caso, de ciertos ácidos grasos porque los microorganismos del rumen y la glándula mamaria son imprescindibles para su formación.
Entre ellos, la literatura científica indica que los ácidos grasos saturados de cadena corta (caproico, caprílico y, sobre todo, butírico), de cadena ramificada (isos y anteisos), de cadena lineal con número impar de carbonos y el ácido 10-hidroxiesteárico, así como los ácidos grasos insaturados transpalmitoleico, vaccénico y ruménico tienen efectos potencialmente beneficiosos para la salud humana.
Los resultados de ensayos in vitro y con modelos animales sugieren que los ácidos grasos mencionados tienen uno o varios de los siguientes efectos: inhibición de células tumorales en diversos tejidos, regulación del metabolismo corporal y la flora microbiana intestinal, así como prevención de la inflamación crónica y la diabetes.
La grasa láctea contiene además ácido α-linolénico, un ácido graso omega-3 beneficioso para la salud. Sin embargo, su cantidad es muy baja en comparación con otras fuentes dietéticas como las nueces o la semilla y el aceite de lino, por lo que su contribución relativa a la dieta humana es muy modesta.
Cómo cambiar la composición de la grasa láctea
Como las proporciones de los ácidos grasos en la grasa láctea dependen en gran medida de la alimentación de las hembras rumiantes, existe un gran interés por buscar alternativas naturales de alimentación que permitan modificar la composición de la grasa de su leche en un sentido favorable para el ser humano.
La mayoría de estudios se ha centrado en la reducción del contenido de ácidos grasos saturados de cadena media, que no son deseables, y el enriquecimiento de la grasa láctea con los ácidos ruménico y omega-3, que son beneficiosos nutricionalmente.
En algunas áreas geográficas, el clima posibilita la alimentación exclusiva o casi exclusiva de ganado lechero con pastos verdes, cuya riqueza en ácido α-linolénico permite obtener una leche con grasa de menor contenido en ácidos grasos saturados de cadena media y mayor riqueza en ácidos grasos saludables.
Sin embargo, las condiciones climáticas no permiten una producción eficiente de leche con alimentación a base de pastos en muchas regiones. En estas circunstancias, el aceite de lino, contenido en la semilla o suministrado tal cual, es una alternativa interesante para modificar la composición de la grasa láctea porque, al igual que la grasa del pasto, es muy rico en ácido α-linolénico.
Los estudios que hemos llevado a cabo en nuestro laboratorio y los de otros grupos de investigación dentro y fuera de España han demostrado que incluir aceite o semilla de lino en la alimentación de las hembras rumiantes lecheras reduce apreciablemente el contenido de ácidos grasos saturados de cadena media e incrementa los niveles de los ácidos transpalmitoleico, vaccénico, ruménico y α-linolénico en la grasa láctea. Esto se traduce en una composición mucho más favorable para la salud humana.
Una oportunidad para los ganaderos
La grasa láctea puede formar parte de una dieta humana equilibrada, siendo prácticamente el único aporte relevante a la misma de algunos ácidos grasos con efectos favorables sobre la salud.
Los ganaderos deberían interesarse en establecer sistemas diferenciados y transparentes de alimentación de sus animales que favorezcan la obtención de leche con una grasa de composición más favorable para la salud humana.
Las industrias lácteas tendrían que promover y facilitar la comercialización de la leche así obtenida, y sus productos derivados, y comunicar los efectos positivos basados en la evidencia científica a los consumidores.
Sobre el autor: Andrés Luis Martínez Marín es profesor titular de universidad en el Departamento de Producción Animal de la Universidad de Córdoba
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Cómo conseguir lácteos más saludables cambiando la alimentación del ganado lechero se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Subproductos agrícolas para mantener la calidad nutricional de los lácteos
- Conseguir ver, y quizás ayudar a entender, al SARS-CoV-2 usando electrones y mucho frío
- Cómo conseguir que la superhidrofobia dure
La música, en el electroencefalograma
 Foto: Devon Wilson / Unsplash
Foto: Devon Wilson / UnsplashEl pasado año consiguieron predecir, haciendo uso de técnicas de inteligencia artificial (IA), la estructura de las proteínas a partir de su secuencia de aminoácidos. Poco antes de acabar el año se hizo público que habían conseguido resolver la ecuación de Schrödinger mediante esas mismas técnicas. También gracias a la IA hemos sabido recientemente que los individuos de la especie Heterocephalus glaber (la rata topo desnuda) se comunican entre sí en el dialecto propio de la colonia a la que pertenecen y que esos dialectos se transmiten culturalmente. Y se acaba de dar a conocer que una inteligencia artificial ha sido capaz de identificar la pieza musical que escucha una persona, analizando los patrones de las ondas encefálicas obtenidas a partir de electroencefalogramas registrados durante la escucha de esa pieza.
La electroencefalografía (EEG) es una técnica que detecta cambios de potencial eléctrico en el cerebro a través de electrodos colocados en diferentes posiciones del cráneo. Esos cambios constituyen un reflejo de la sincronización de la actividad eléctrica de grupos de neuronas situadas en las proximidades de cada electrodo, consecuencia a su vez de los movimientos de iones a través de sus membranas. Hay versiones invasivas –denominadas electrocorticografías-, que requieren la introducción de electrodos en la corteza cerebral atravesando el cráneo, aunque la mayoría no lo son. Normalmente se utilizan para detectar cambios en la actividad eléctrica que se producen tras someter al individuo a algún estímulo o tras realizar alguna acción.
Un equipo de investigación de la Universidad Tecnológica de Delft, en los Países Bajos, colocó sendos equipos de electroencefalografía a veinte personas mientras escuchaban música con auriculares y registraron sus ondas encefálicas. Utilizaron, a tal efecto, doce piezas musicales diferentes. A los participantes se les tapaban los ojos y se les mantenía en una habitación en silencio, de manera que no hubiera ningún estímulo ambiental, aparte de la música, para que los resultados no se viesen condicionados por otras formas de información sensorial.
Los registros de cada persona eran divididos en segmentos cortos y utilizados, junto con los fragmentos musicales que les correspondían, para adiestrar a una IA, de manera que, asociando cada segmento del electroencefalograma a su correspondiente fragmento musical, fuese capaz de identificar patrones de correspondencias entre las dos secuencias de información.
A continuación, se suministraban a la IA los segmentos del EEG que no se habían utilizado en su adiestramiento, para que identificase la pieza musical a que correspondía. La IA fue capaz de identificar las piezas musicales escuchadas por cada una de las personas con un acierto del 85%. Tan interesante como ese nivel de acierto, es el hecho de que cuando a la IA se le pedía que identificase la música escuchada por una persona diferente, el grado de acierto era tan solo de un 10%.
A juicio de quienes hicieron el experimento, la razón de esa gran diferencia obedece al hecho de que la experiencia estética de cada persona al escuchar una misma pieza musical es diferente, y eso se traduce en que cada una se centra más en unos fragmentos que en otros. En otras palabras, además del procesamiento de la información contenida en cada fragmento musical, las ondas cerebrales también reflejan aspectos de la experiencia estética.
Al equipo de investigación, no obstante, lo que más interesa es identificar los elementos de la respuesta electroencefalográfica a la música que son comunes a todas las personas; esto es, aquellos que no se ven afectados por la componente hedónica. Quieren así saber más acerca del funcionamiento del encéfalo y, en última instancia, por qué nos gusta la música.
Fuente: CODS COMAD 2021, Enero 2–4, 2021, Bangalore, India.
Nota: Agradezco a Xurxo Mariño sus aclaraciones acerca de la electroencefalografía.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo La música, en el electroencefalograma se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Clara Grima – Naukas Bilbao 2019: Mathematical Rhapsody
 Espiral de Ulam. Los números primos tienden a aparecer más en unas diagonales que en otras.
Espiral de Ulam. Los números primos tienden a aparecer más en unas diagonales que en otras.Los números primos son el ADN de los números y son básicos en la criptografía de código abierto. Conocer su distribución está íntimamnete ligado con un montón de cosas estética y prácticamente interesantes. La llave para ello la tiene la hipótesis de Riemann, que está por demostrar. Clara Grima explica todo esto y más en una charla nada divertida (reto: si sonríes, pierdes).
Clara Grima es doctora en matemáticas por la Universidad de Sevilla, institución de la que es profesora titular en el departamento de Matemática Aplicada I. Divulgadora de las matemáticas, ha recibido numerosos premios en este campo.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Clara Grima – Naukas Bilbao 2019: Mathematical Rhapsody se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Naukas Bilbao 2017 – Clara Grima & Enrique F. Borja: Matemáticas, epidemias y vacunas
- Raúl Ibáñez – Naukas Bilbao 2019: Teorías fantásticas sobre las grafías de los números
- Francisco Villatoro – Naukas Bilbao 2019: El abrazo de la plata
Se busca azúcar en el espacio interestelar
 Imagen: Laxmikant Chaware / 123rf
Imagen: Laxmikant Chaware / 123rfLa presencia de carbohidratos en el medio interestelar podría estar relacionada con la aparición de la vida en la Tierra. La detección hasta la fecha de más de 200 moléculas en el espacio interestelar sugiere que las moléculas prebióticas estarían presentes en el espacio. De ahí que la detección en el espacio interestelar de un azúcar (un carbohidrato de bajo peso molecular), u otras moléculas esenciales, como aminoácidos, bases nitrogenadas o ácidos grasos vitales para todas las formas de vida conocidas, sea fundamental para poder modelar las reacciones y vías de formación de las moléculas orgánicas más complejas relacionas con la vida. “La detección de estas biomoléculas podría dar un poco de luz al proceso inicial del origen de la vida. De momento no se ha detectado ningún azúcar, solo algún precursor de los mismos”, explica Emilio J. Cocinero, investigador principal del Grupo de Espectroscopía de la UPV/EHU.
“Para buscar cualquier molécula en el espacio se recurre a la espectroscopia rotacional. Esta técnica permite determinar la estructura de una sola molécula aislada con una altísima precisión. Podría decirse que nos proporciona la huella dactilar de esa molécula. La espectroscopía rotacional es el paso previo necesario para la búsqueda de estas moléculas en el espacio interestelar —añade Cocinero—. El espacio está poblado de multitud de señales de todas las moléculas que lo componen. Por tanto resulta imposible establecer una relación señal-molécula sin una caracterización previa de cada una de las moléculas en el laboratorio. Por último, los radioastrónomos buscan esas señales, caracterizadas previamente en el laboratorio, en diferentes regiones del medio interestelar utilizando radiotelescopios”.
 D-eritrulosa. Fuente: Wikimedia Commons
D-eritrulosa. Fuente: Wikimedia CommonsLa espectroscopía rotacional es una técnica en alta resolución que requiere trabajar con muestras en fase gaseosa. “Los azúcares son sólidos, y el problema es que al calentarlos para pasarlos a fase gaseosa se forma caramelo; con lo cual no se vaporizaba el azúcar, sino que se descomponía y se transformaba en moléculas más pequeñas”, explica el investigador. Sin embargo, el grupo de investigación ha conseguido desarrollar “una técnica de vaporización que nos permite generar este azúcar en fase gaseosa evitando el proceso de descomposición. El azúcar, eritrulosa en este caso, se mezcló con un compactante, se prensó y se secó. Finalmente, esta barra sólida, se vaporizó con un láser ultrarápido ultravioleta, lo que permitió obtener moléculas de eritrulosa en fase gas”, explica. Este procedimiento es generalizable. “Hemos desarrollado una metodología experimental para poder estudiar otros azúcares”, añade el investigador perteneciente también al Instituto Biofisika (UPV/EHU, CSIC). Paralelamente esta investigación ha permitido determinar la estructura hiperprecisa de la eritrulosa.
En el laboratorio del Grupo de Espectroscopía del Departamento de Química Física de la UPV/EHU diseñan y fabrican sus propios instrumentos de alta resolución, y se centran especialmente en el estudio de azúcares. “Los azúcares llevan un retraso de unos veinte años en comparación con la detección de aminoácidos, por ejemplo; prácticamente han estado excluidos. De hecho, ya se habían detectado moléculas precursoras de los azúcares, con dos o tres unidades de carbono, en el medio interestelar. La eritrulosa sería el siguiente paso, porque tiene cuatro unidades de carbono. En los últimos años, se ha incrementado mucho la detección de moléculas en el espacio; esta detección ha crecido exponencialmente porque los niveles de detección de los radiotelescopios han mejorado notablemente. Además, sabemos que cuanto más grande la molécula es más difícil detectarla. Pero es importante ir incrementando el tamaño de las moléculas y el nivel de sensibilidad de los radiotelescopios, esto permitirá obtener más información de cómo se han podido formar esos primeros seres vivos”, afirma.
Cocinero se felicita de que han abierto una vía de colaboración con astrónomos, con los que han trabajado conjuntamente para buscar o detectar eritrulosa en el medio interestelar en tres regiones diferentes usando los nuevos datos experimentales. Por ahora la búsqueda ha dado un resultado negativo en estas tres regiones, “no se han encontrado señales de eritrulosa en el medio interestelar, pero no es de extrañar que dentro de unos años se obtenga un resultado positivo, cuando se mejoren los niveles de detección de los radiotelescopios. Estos datos servirán para realizar futuras búsquedas y posibles detecciones en otras regiones del espacio interestelar”.
Referencia:
Aran Insausti, Elena R. Alonso, Belen Tercero, José I. Santos, Camilla Calabrese, Natalja Vogt, Francisco Corzana, Jean Demaison, Jose Cernicharo, and Emilio J. Cocinero (2021) Laboratory Observation of, Astrochemical Search for, and Structure of Elusive Erythrulose in the Interstellar Medium The Journal of Physical Chemistry Letters doi: 10.1021/acs.jpclett.0c03050
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Se busca azúcar en el espacio interestelar se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El azúcar del ADN caracterizado átomo a átomo por espectrometría de microondas
- Azúcar moreno, ¿mejor que el azúcar blanco?
- ¿Azúcar moreno o azúcar milagro?
El oído absoluto de Mozart
 Wolfgang Amadeus Mozart a los 14 años, en enero de 1770. Escuela de Verona, atribuido a Giambettino Cignaroli. Fuente: Wikimedia Commons
Wolfgang Amadeus Mozart a los 14 años, en enero de 1770. Escuela de Verona, atribuido a Giambettino Cignaroli. Fuente: Wikimedia CommonsSi alguna vez has escuchado hablar del oído absoluto, probablemente lo identificarás como uno de los superpoderes musicales atribuidos al mismísimo Mozart. Desde muy joven, el célebre compositor dio muestras de su prodigioso oído. Según cierta anécdota popular, con solo siete años de edad, lo usaba para corregir a otros músicos de la corte de Salzburgo:
—Señor —le espetó una día a Andreas Schachtner— si no ha cambiado usted la afinación de su violín desde la última vez que yo lo toqué, está un cuarto de tono más grave que el mío.
Esto demuestra que el joven Wolfgang no solo debía de ser un niño bastante repelente. También era capaz de recordar sonidos exactos de un día para otro, sin ninguna referencia adicional y con una precisión superior a la que muchos adultos son capaces de discernir siquiera.
La mayoría de los mortales no tenemos esta habilidad. Escuchamos un sonido y no tenemos ni la más remota idea de qué nota es. Si alguien quiere hacer un brindis y golpea animadamente su copa, la gente no suele contestar “¡fa sostenido!”. Fue así, de hecho, como mi familia descubrió que uno de mis primos políticos tiene oído absoluto. En una cena de Navidad, empezó a responder con nombres de notas al sonido de las copas. Todos pensábamos que el pequeño Daniel —entonces era solo un niño— estaba bromeando hasta que, por pura curiosidad, se me ocurrió sacar el afinador que suelo llevar en el móvil. ¡El tío las acertaba todas!
Para los que tenemos algún entrenamiento musical, averiguar el nombre de una nota no es demasiado difícil siempre que nos indiquen otra como referencia (típicamente, la nota la). En algunos casos, esto nos puede servir para desarrollar un falso oído absoluto (o quasi-absolute pitch, como se denomina en la literatura científica). Basta con recordar una canción de manera precisa y usarla como punto de comparación para identificar el resto de los sonidos de nuestro entorno. Yo misma suelo suelo acertar bastante, gracias a un nocturno de Chopin que he tocado hasta la saciedad y tengo grabado a fuego en mi memoria musical.
Pero a Dani no le hacía falta recurrir a ninguna canción. Le bastaba con escuchar el tañido de cada copa para nombrarlo directamente. Su percepción del sonido es probablemente similar a la que cualquiera puede tener de un color o de un sabor, que no necesita más referencias para poder ser identificado. Aquella Navidad, todos nos quedamos ojipláticos. Aparte de mi primo, Mozart y cuatro gatos más, el oído absoluto es un rareza, un superpoder presente en menos de una de cada mil personas1… y también, un truco con pocos beneficios reales y algún que otro inconveniente.
En realidad, no parece que el oído absoluto de Mozart le fuese de utilidad o tuviese relación alguna con su talento musical. Aunque a lo largo de la historia esta característica se ha asociado a muchos compositores, parece deberse de una correlación más que una relación causal. Para tener oído absoluto es importante recibir un entrenamiento musical desde muy pequeño y esto es algo bastante común entre los músicos, sobre todo dentro de la tradición clásica. Dicho de otro modo, no es que el oído absoluto dé lugar a mejores músicos, sino que el entrenamiento típico de los músicos hace más probable la prevalencia de esta característica. No es que la calvicie dé lugar a monjes budistas, es que los monjes budistas, por lo que sea, se quedan sin pelo.
Más allá de amenizar las cenas de Navidad, no hay ninguna prueba de que el oído absoluto ofrezca ninguna ventaja para los músicos (o para los no músicos, ya puestos). En cambio, sí hay estudios que muestran ciertos inconvenientes, especialmente cuando interfiere con las tareas propias del oído relativo que es el verdadero héroe infravalorado de toda esta historia. Los músicos con oído absoluto pueden encontrar dificultades para reconocer ciertos intervalos, o identificar una misma melodía en distintas tonalidades2 3 4, precisamente porque el nombre de las notas (esa identidad que es tan nítida para ellos) se antepone a la relación entre los sonidos, mucho más importante para completar este tipo de tareas. Para colmo, el oído absoluto puede “desafinarse” con el tiempo, de manera que el mundo sonoro de estos músicos pasa a estar equivocado.
Mientras el oído absoluto sirve para identificar la altura de una nota aislada, algo así como las coordenadas GPS de un sonido, el oído relativo es sensible a las distancias entre sonidos, da igual dónde se encuentren, de manera que, conociendo uno, puede calcular todos los demás. El oído absoluto puede sentirse perdido si le dan una nota desafinada, o escucha una canción en el tono incorrecto, como un madrileño al que le cambian su parada de metro. El oído relativo, en cambio, se busca la vida donde sea. Es como un rastreador experto, que pasa del GPS y pijadas parecidas porque se sabe de memoria todos los mapas del mundo. El Bear Grylls de la exploración sonora. Basta con que le digan dónde está y él se solito se apaña para llegar donde haga falta.
El secreto de su éxito se basa en poder reconocer las proporciones entre frecuencias sonoras, lo que en música se conoce como intervalos. Esta es una habilidad que todos compartimos (incluidos Mozart y mi primo, claro), quizás por eso no la valoramos suficientemente. ¡Pero este es el verdadero superpoder de nuestro oído! Cada vez que imitamos o reconocemos una melodía, cada vez que leemos las emociones del habla, su prosodia, las inflexiones de la voz, estamos usando nuestro oído relativo. Esto ha llevado a algunos psicólogos a pensar que el oído absoluto no es un don, sino un vestigio: una habilidad que perdimos a lo largo de la evolución, en favor de su hermano tímido, el oído relativo. Pero esta es otra historia y será contada en otra ocasión.
Recomiendo este fantástico vídeo de Adam Neely sobre oído absoluto.
Referencias:
1Profita, Joseph, et al. 1988. “Perfect pitch”. American Journal of Medical Genetics, 29(4), 763–771. doi:10.1002/ajmg.1320290405.
2Miyazaki, K., 1992. “Perception of musical intervals by absolute pitch possessors”. Music Perception. 9, 413–426.
3Miyazaki, K., 1995. “Perception of relative pitch with different references: some absolute-pitch listeners can’t tell musical interval names”. Perception and Psychophysics. 57, 962–970.
4Kim Seung-Goo, Knösche, Thomas, R. “On the Perceptual Subprocess of Absolute Pitch”. Frontiers in Neuroscience. 2017 Oct 6;11:557. doi: 10.3389/fnins.2017.00557.
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
El artículo El oído absoluto de Mozart se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Exposiciones matemáticas en el metro de Bilbao (II)
En mi anterior entrada del Cuaderno de Cultura Científica, titulada Exposiciones matemáticas en el metro de Bilbao (I), estuvimos hablando del Día Internacional de las matemáticas, del proyecto Marzo, mes de las matemáticas, realizado en colaboración con toda la comunidad matemática española y con la colaboración de la Fundación Española para la Ciencia y la Tecnología – Ministerio de Ciencia e Innovación (FECYT), de las actividades que se están organizando dentro de este proyecto y de los excelentes e interesantes materiales que se están creando (a los cuales podéis acceder a través de la página web del proyecto), de cómo en el País Vasco (contando con el apoyo y colaboración de la Universidad del País Vasco/Euskal Herriko Unibertsitatea y el Basque Center for Applied Mathematics-BCAM, así como el Ayuntamiento de Bilbao y Metro Bilbao) se están organizando una serie de actividades, entre ellas, dos exposiciones matemáticas en el metro de Bilbao, Geometría Natural y Matemáticas para un mundo mejor, a la primera de las cuales dedicamos gran parte de la anterior entrada.
 Con motivo del Día Internacional de las Matemáticas, la rectora de la UPV/EHU, Eva Ferreira, el director de BCAM, José Antonio Lozano, y la directora de Marketing y Comunicación de Metro Bilbao, Susana Palomino, visitaron las exposiciones matemáticas organizadas en Metro Bilbao, junto a los profesores de la UPV/EHU y responsables de la organización de las exposiciones, Marta Macho, Pedro Alegría y Raúl Ibáñez.
Con motivo del Día Internacional de las Matemáticas, la rectora de la UPV/EHU, Eva Ferreira, el director de BCAM, José Antonio Lozano, y la directora de Marketing y Comunicación de Metro Bilbao, Susana Palomino, visitaron las exposiciones matemáticas organizadas en Metro Bilbao, junto a los profesores de la UPV/EHU y responsables de la organización de las exposiciones, Marta Macho, Pedro Alegría y Raúl Ibáñez.
En esta entrada hablaremos de la otra exposición expuesta en el metro de Bilbao, que finalmente titulamos Matemáticas para un mundo mejor, aunque se podría haber titulado Sabías que … las matemáticas, puesto que surge a partir de las tarjetas matemáticas Sabías que desarrolladas dentro del proyecto Marzo, mes de las matemáticas.
Por lo tanto, empecemos hablando de la actividad de las tarjetas matemáticas. Mi compañero Pedro Alegría y yo mismo, asumimos la responsabilidad de la organización de la actividad de estas tarjetas. Primero montamos una comisión para la creación de los tres tipos de tarjetas matemáticas que habíamos planteado: Matemáticas + Literatura; Pasatiempos matemáticos; y ¿Sabías que…?. En esta comisión estabamos las siguientes personas: Marithania Silvero (Andalucía), José Muñoz Santuja (Andalucía), Julio Bernués (Aragón), Ignacio García (Canarias), Diego Alonso Santamaría (Castilla y León), Claudi Alsina (Cataluña), Dolores Gómez (Galicia), Pedro Alegría (responsable, País Vasco), Raúl Ibáñez (responsable, País Vasco), Alberto Magreñán (Rioja), Lara Orcos (Rioja), Manuel de León (Madrid), Alejandro Miralles (Valencia). A todas ellas quiero agradecerles su colaboración y el magnífico trabajo que han realizado.
 Cartel del proyecto Marzo, mes de las matemáticas, diseñado por Carla Garrido
Cartel del proyecto Marzo, mes de las matemáticas, diseñado por Carla Garrido
La idea de esta actividad era la creación de una serie de materiales que podrían utilizarse como tarjetas para repartir, carteles para colocar en paredes o paneles de exposiciones, en función de las ideas que se desarrollasen en cada nodo del proyecto. Por ejemplo, en el País Vasco hemos impreso 15 tarjetas, de tamaño A5, de cada uno de los tres tipos (en castellano y euskera) para repartir en librerías, bares y comercios; hemos desarrollado la exposición Matemáticas para un mundo mejor en el metro de Bilbao, con algunas de las tarjetas del tipo ¿Sabías que…?; y vamos a realizar una exposición en la Biblioteca de Bidebarrieta (Bilbao) con algunas de las tarjetas del tipo Matemáticas + Literatura. O en Canarias se ha firmado un convenio con el Cabildo de Tenerife para mostrar las tarjetas en las pantallas del transporte público de la isla.
 Tarjeta ¿Sabías que … se puede cambiar la válvula aórtica usando matemáticas? mostrada en una de las pantallas del transporte público de Tenerife
Tarjeta ¿Sabías que … se puede cambiar la válvula aórtica usando matemáticas? mostrada en una de las pantallas del transporte público de Tenerife
En el primer tipo de tarjetas matemáticas, que decidimos denominar Matemáticas + Literatura, se trataba de incluir en cada tarjeta una cita de una novela contemporánea en la que aparecieran reflejadas, de alguna forma, las matemáticas. Por ejemplo, en la siguiente imagen se muestra la tarjeta que lleva el título Las matemáticas ¿se inventan o se descubren? cuyo texto hemos extraído de la novela La fórmula preferida del profesor, de la escritora japonesa Yoko Ogawa.
 Cara A de la tarjeta Las matemáticas ¿se inventan o se descubren?, de la novela La fórmula preferida del profesor (Yoko Ogawa), con la cita literaria. Diseño de la tarjeta de Carla Garrido.
Cara A de la tarjeta Las matemáticas ¿se inventan o se descubren?, de la novela La fórmula preferida del profesor (Yoko Ogawa), con la cita literaria. Diseño de la tarjeta de Carla Garrido.
 Cara B de la tarjeta Las matemáticas ¿se inventan o se descubren?, de la novela La fórmula preferida del profesor (Yoko Ogawa), con la cita literaria. Diseño de la tarjeta de Carla Garrido.
Cara B de la tarjeta Las matemáticas ¿se inventan o se descubren?, de la novela La fórmula preferida del profesor (Yoko Ogawa), con la cita literaria. Diseño de la tarjeta de Carla Garrido.
Incluyo, a continuación, la cita:
—¿Qué especialidad de las matemáticas investigó usted en la universidad? —le pregunté, con la intención de hablar sobre algo relacionado con las matemáticas, en señal de agradecimiento por haber atendido a mi ruego y salido a la calle.
—Es un campo que suele llamarse la reina de las matemáticas —me comentó, después de un ruidoso trago de café—. Es tan hermoso como una reina, noble y al mismo tiempo cruel como un demonio. Es fácil de explicar en pocas palabras, pues son los números enteros que todo el mundo conoce. Estaba investigando la relación de los números 1, 2, 3, 4, 5, 6…
No esperaba que el profesor utilizara una palabra como “reina”, que parecía salida de un cuento. Se oía el ruido de una pelota de tenis botando a lo lejos […].
—¿Así que está usted descubriendo esa relación?
—Efectivamente, es un descubrimiento. No es una invención. Es como excavar y sacar de debajo de la tierra teoremas que ya existían mucho antes de que naciera, sin que nadie haya detectado su existencia. Es como transcribir línea tras línea una verdad que sólo está escrita en el cuaderno de Dios. Nadie sabe dónde está ese cuaderno ni cuándo se abre.
Al decir “teoremas que ya existían…”, señaló el punto en el espacio que siempre fijaba cuando estaba “pensando”.
Otro ejemplo es la tarjeta titulada Investigación policial versus investigación matemática, de la novela Los crímenes de Oxford, del escritor argentino Guillermo Martínez.
 Cara A de la tarjeta Investigación policial versus investigación matemática, de la novela Los crímenes de Oxford (Guillermo Martínez), con la cita literaria. Diseño de la tarjeta de Carla Garrido.
Cara A de la tarjeta Investigación policial versus investigación matemática, de la novela Los crímenes de Oxford (Guillermo Martínez), con la cita literaria. Diseño de la tarjeta de Carla Garrido.
 Cara B de la tarjeta Investigación policial versus investigación matemática, de la novela Los crímenes de Oxford (Guillermo Martínez), con una breve información y una sencilla ilustración del escritor Guillermo Martínez. Diseño de la tarjeta de Carla Garrido.
Cara B de la tarjeta Investigación policial versus investigación matemática, de la novela Los crímenes de Oxford (Guillermo Martínez), con una breve información y una sencilla ilustración del escritor Guillermo Martínez. Diseño de la tarjeta de Carla Garrido.
La cita contenida en esta tarjeta es la siguiente:
Hay una diferencia entre la verdad y la parte de verdad que puede demostrarse: ése es en realidad un corolario de Tarski sobre el teorema de Gödel – dijo Seldom-. Por supuesto, los jueces, los forenses, los arqueólogos, sabían esto mucho antes que los matemáticos. Pensemos en cualquier crimen con sólo dos posibles sospechosos.
Cualquiera de ellos sabe toda la verdad que interesa: yo fui o yo no fui. Pero la justicia no puede acceder directamente a esa verdad y tiene que recorrer un penoso camino indirecto para reunir pruebas: interrogatorios, coartadas, huellas digitales… Demasiadas veces las evidencias que se encuentran no alcanzan para probar ni la culpabilidad de uno ni la inocencia del otro. En el fondo, lo que mostró Gödel en 1930 con su teorema de incompletitud es que exactamente lo mismo ocurre en la matemática. El mecanismo de corroboración de la verdad que se remonta a Aristóteles y Euclides, la orgullosa maquinaria que a partir de afirmaciones verdaderas, de primeros principios irrebatibles, avanza por pasos estrictamente lógicos hacia la tesis, lo que llamamos, en una palabra, el método axiomático, puede ser a veces tan insuficiente como los criterios precarios de aproximación de la justicia. […] Gödel mostró que aun en los niveles más elementales de la aritmética hay enunciados que no pueden ser ni demostrados ni refutados a partir de los axiomas, que están más allá del alcance de estos mecanismos formales, enunciados sobre los que ningún juez podría dictaminar su verdad o falsedad, su culpabilidad o inocencia.
Las diecinueve tarjetas pertenecientes a la clase Matemáticas + Literatura las podéis encontrar en la página del proyecto Marzo, mes de las matemáticas, en concreto aquí.
Este es un material que se puede utilizar en diferentes formatos y lugares. Como tarjetas se pueden repartir en librerías (por ejemplo, se están repartiendo en algunas librerías de Bilbao, como la Librería Cámara o la Librería Louise Michel), en bibliotecas públicas (se están repartiendo tarjetas y colocando carteles en distintas bibliotecas de España), en centros culturales o en bares; como carteles pueden colocarse en medios de transporte, ya sea en el propio medio de transporte, en las instalaciones relacionadas o en las pantallas informativas en versión digital o en centros escolares; y son ideales como pósteres para una exposición (como la exposición que estamos organizando en la Biblioteca de Bidebarrieta y otras bibliotecas de Bilbao); o para todo lo que se nos pueda ocurrir, el límite es nuestra imaginación. Más aún, ese material, como el resto de materiales que se han subido a la página del proyecto Marzo, mes de las matemáticas, está ahí para que lo podáis utilizar.
 La librería Cámara, de Bilbao, es una de las librearías que está colaborando en el reparto de tarjetas de Matemáticas + Literatura, así como de Pasatiempos matemáticos. Más aún, en su página web han añadido un apartado con el título Marzo, mes de las matemáticas, para recomendar novelas con algún contenido matemático.
La librería Cámara, de Bilbao, es una de las librearías que está colaborando en el reparto de tarjetas de Matemáticas + Literatura, así como de Pasatiempos matemáticos. Más aún, en su página web han añadido un apartado con el título Marzo, mes de las matemáticas, para recomendar novelas con algún contenido matemático.
En el segundo tipo de tarjetas matemáticas, que denominados Pasatiempos matemáticos, se trataba de incluir problemas de ingenio de diferentes dificultades. En una de las caras de la tarjeta se incluye el enunciado del pasatiempo matemático, acompañado de una ilustración, mientras que en la otra cara se incluye información relacionada con ese pasatiempo matemático. Por ejemplo, en las siguientes imágenes vemos un problema de ingenio cuyo título es Aquí hay gato encerrado.
 Cara A de la tarjeta Aquí hay gato encerrado. Diseño de la tarjeta de Carla Garrido.
Cara A de la tarjeta Aquí hay gato encerrado. Diseño de la tarjeta de Carla Garrido.
 Cara B de la tarjeta Aquí hay gato encerrado. Diseño de la tarjeta de Carla Garrido.
Cara B de la tarjeta Aquí hay gato encerrado. Diseño de la tarjeta de Carla Garrido.
El enunciado del problema Aquí hay gato encerrado, es el siguiente:
Hay 5 cajas numeradas del 1 al 5. Cada noche el gato duerme en una caja adyacente a la de la noche anterior. Cada mañana puedes abrir una caja y mirar si el gato está dentro. ¿Cuántos días necesitas para asegurarte de encontrar al gato?
Y el comentario que aparece en la otra cara es:
Este pasatiempo pertenece a la familia de problemas de tipo persecución-evasión (como el juego policías y ladrones), que son aquellos en los cuales un grupo –en este caso quien juega– intenta localizar a los miembros de otro grupo –el gato– en un entorno cerrado –las cinco cajas–. El rompecabezas fue presentado en 1999 por dos matemáticos rusos en el entorno de las olimpiadas matemáticas, aunque el estudio matemático de los problemas persecución-evasión se remonta a la década de 1970. En 2014 este pasatiempo se hizo famoso a raíz de su aparición, en una versión más general, en el periódico New York Times.
Sobre este problema en concreto escribí no hace mucho en el Cuaderno de Cultura Científica, podéis leer la entrada aquí: Buscando una matemática en el castillo.
Las diecinueve tarjetas pertenecientes a la clase Pasatiempos matemáticos las podéis encontrar en la página del proyecto Marzo, mes de las matemáticas, en concreto aquí. Además, ahí mismo podéis encontrar las soluciones a los diferentes pasatiempos.
De nuevo, este es un material que se puede utilizar en diferentes formatos y lugares. Por mencionar un par de ejemplos, en Bilbao estamos repartiéndolas en diferentes bares, librerías y comercios o en Tenerife se están mostrando en las pantallas del transporte público.
 Fotografía de una pantalla con uno de los pasatiempos matemáticos preparados para el proyecto Marzo, mes de las matemáticas, en el transporte público de La Laguna (Tenerife). Fotografía de Edith Padrón.
Fotografía de una pantalla con uno de los pasatiempos matemáticos preparados para el proyecto Marzo, mes de las matemáticas, en el transporte público de La Laguna (Tenerife). Fotografía de Edith Padrón.
El problema que aparece en esa pantalla de La Laguna es Con todas las cifras, que dice así:
Con todas las cifras, del 1 al 9, en orden creciente, intercalar los signos «+» y » –» de forma que el resultado de la operación sea 100. Por ejemplo, 1 + 2 + 3 – 4 + 5 + 6 + 78 + 9 = 100.
El tercer tipo de tarjetas es el denominado ¿Sabías que?, que recoge aplicaciones, más o menos actuales, de las matemáticas. Por ejemplo, en la siguiente imagen se incluyen las dos caras de la tarjeta ¿Sabías que … tus deportivas se diseñan utilizando matemáticas?.
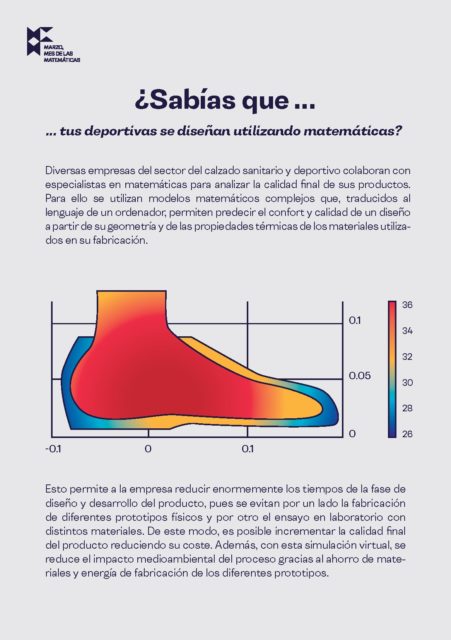 Cara A de la tarjeta ¿Sabías que … tus deportivas se diseñan utilizando matemáticas? Diseño de la tarjeta de Carla Garrido
Cara A de la tarjeta ¿Sabías que … tus deportivas se diseñan utilizando matemáticas? Diseño de la tarjeta de Carla Garrido
 Cara B de la tarjeta ¿Sabías que … tus deportivas se diseñan utilizando matemáticas? Diseño de la tarjeta de Carla Garrido.
Cara B de la tarjeta ¿Sabías que … tus deportivas se diseñan utilizando matemáticas? Diseño de la tarjeta de Carla Garrido.
El texto de esta tarjeta es el siguiente:
Diversas empresas del sector del calzado sanitario y deportivo colaboran con especialistas en matemáticas para analizar la calidad final de sus productos. Para ello se utilizan modelos matemáticos complejos que traducidos al lenguaje de un ordenador permiten predecir el confort y calidad de un diseño a partir de su geometría y de las propiedades térmicas de los materiales utilizados en su fabricación.
Esto permite a la empresa reducir enormemente los tiempos de la fase de diseño y desarrollo del producto, pues se evitan por un lado la fabricación de diferentes prototipos físicos y por otro el ensayo en laboratorio con distintos materiales. De este modo, es posible incrementar la calidad final del producto reduciendo su coste. Además, con esta simulación virtual, se reduce el impacto medioambiental del proceso gracias al ahorro de materiales y energía de fabricación de los diferentes prototipos.
El texto de esta tarjeta está basado en una investigación de los profesores J. Durany, L. Poceiro y F. Varas, de la Universidad de Vigo, a quienes agradecemos su generosidad. Además, quien quiera saber más sobre el tema puede leer este artículo.
Las dieciocho tarjetas pertenecientes a la clase ¿Sabías que…? las podéis encontrar en la página del proyecto Marzo, mes de las matemáticas, en concreto aquí. Y una vez más, este es un material que se puede utilizar en diferentes formatos y lugares. El ejemplo que traemos a esta entrada del Cuaderno de Cultura Científica son los paneles de la exposición Matemáticas para un mundo mejor, que se puede ver en el metro de Bilbao.
Finalmente, el diseño de las tarjetas matemáticas es un magnífico trabajo de la diseñadora canaria Carla Garrido.
Antes de empezar con la exposición del metro de Bilbao me gustaría dar las gracias a los profesores Jose Ignacio Royo y Alex Aginagalde por traducir al euskera los textos de las tarjetas.
 Vista parcial de la exposición Matemáticas para un mundo mejor en la estación de Moyua de Metro Bilbao. Fotografía de Marian Espinosa
Vista parcial de la exposición Matemáticas para un mundo mejor en la estación de Moyua de Metro Bilbao. Fotografía de Marian Espinosa
Empezaremos por el panel de presentación de la exposición, que fue colocada en la estación de metro Moyua del metro de Bilbao el pasado 1 de marzo, que podéis ver en la siguiente imagen.
 Panel de presentación de la exposición Matemáticas para un mundo mejor, en Metro Bilbao. Fotografía de Marian Espinosa
Panel de presentación de la exposición Matemáticas para un mundo mejor, en Metro Bilbao. Fotografía de Marian Espinosa
El texto de ese panel de presentación es el siguiente:
Esta exposición, cuyo título corresponde al lema elegido para conmemorar el Día Internacional de las Matemáticas del año 2021, ofrece un pequeño recorrido por algunas cuestiones relacionadas con aplicaciones actuales de las matemáticas al mundo que nos rodea, en áreas tan diversas como la industria, ingeniería, tecnología, sanidad, economía y deporte.
Empecemos nuestro paseo por la exposición Matemáticas para un mundo mejor, que físicamente estará en la estación de Moyua de Metro Bilbao durante el mes de marzo y en la estación de Portugalete durante el mes de abril, por el panel ¿Sabías que … se puede cambiar la válvula aórtica usando matemáticas?.
 Panel ¿Sabías que … se puede cambiar la válvula aórtica usando matemáticas?, dentro de la exposición Matemáticas para un mundo mejor, en Metro Bilbao. Fotografía de Marian Espinosa
Panel ¿Sabías que … se puede cambiar la válvula aórtica usando matemáticas?, dentro de la exposición Matemáticas para un mundo mejor, en Metro Bilbao. Fotografía de Marian Espinosa
El texto que acompaña a este panel, que es una versión reducida del texto de la correspondiente tarjeta y que está basado en una investigación de Marcos Loureiro, de la Universidade de Vigo (más información en la página web de Marcos Loureiro), es el siguiente:
La estenosis aórtica es una enfermedad que provoca un funcionamiento incorrecto de esa válvula coronaria, obligando en casos graves a su recambio. Además de la operación a corazón abierto, se puede cambiar la válvula accediendo a los órganos interiores a través de un catéter (técnica TAVI).
Gracias a técnicas de simulación numérica es posible realizar virtualmente varias TAVI a un mismo paciente. Así pueden predecirse posibles complicaciones durante la intervención, modificaciones en la válvula o las tensiones a las que estará expuesto el anillo aórtico durante el procedimiento.
Otro de los paneles de la exposición es ¿Sabías que … Suiza ganó la Copa América de vela gracias al uso de las matemáticas?, cuyo texto recoge una investigación dirigida por el matemático italiano Alfio Quarteroni (Politecnico di Milano, Italia y EPFL, Suiza) y sobre la que podéis más en la página de Alfio Quarteroni.
 Panel ¿Sabías que … Suiza ganó la Copa América de vela gracias al uso de las matemáticas?, dentro de la exposición Matemáticas para un mundo mejor, en Metro Bilbao. Fotografía de Marian Espinosa
Panel ¿Sabías que … Suiza ganó la Copa América de vela gracias al uso de las matemáticas?, dentro de la exposición Matemáticas para un mundo mejor, en Metro Bilbao. Fotografía de Marian Espinosa
El texto de este panel es el siguiente:
Hace pocos años, la manera de probar el rendimiento de un barco era exponerlo a situaciones de flujo realistas en túneles de viento. Utilizando modelos matemáticos se puede simular en un ordenador la respuesta del barco bajo distintas condiciones. Por ejemplo, se puede mejorar el diseño del yate para que navegue con la menor resistencia posible u obtener nuevas formas de velas que interactúen mejor con el aire, o crear modelos para ayudar al navegante a tomar decisiones. Estas técnicas se aplicaron al barco suizo Alinghi, que ganó la Copa América en 2003 y 2007.
Otro de los paneles es ¿Sabías que … multitud de paisajes de películas se generan por ordenador usando fractales?
 Panel ¿Sabías que … multitud de paisajes de películas se generan por ordenador usando fractales?, dentro de la exposición Matemáticas para un mundo mejor, en Metro Bilbao. Fotografía de Marian Espinosa
Panel ¿Sabías que … multitud de paisajes de películas se generan por ordenador usando fractales?, dentro de la exposición Matemáticas para un mundo mejor, en Metro Bilbao. Fotografía de Marian Espinosa
El texto de este panel es:
Los fractales son objetos matemáticos cuya estructura se repite a distintas escalas o que son extremadamente rugosos. Tienen aplicaciones en medicina, biología, geología, telecomunicaciones, economía o compresión de imágenes digitales, entre otras. Han sido utilizados incluso en el cine, como en Star Trek 2: La ira de Khan (1982) para generar un paisaje realista, en Guardianes de la galaxia, vol. 2 (2017) para crear el planeta de Ego o en Aniquilación (2018) para representar a un alienígena.
 Uno de los fotogramas de la película Aniquilación (2018) en el que se ve a la actriz Natalie Portman frente al alienígena para el que se ha utilizado en su diseño el fractal Mandelbulb
Uno de los fotogramas de la película Aniquilación (2018) en el que se ve a la actriz Natalie Portman frente al alienígena para el que se ha utilizado en su diseño el fractal Mandelbulb
Otro interesante panel de la exposición es el que corresponde al tema ¿Sabías que … escuchas música gracias a la transformación matemática de los sonidos?
 Panel ¿Sabías que … escuchas música gracias a la transformación matemática de los sonidos?, dentro de la exposición Matemáticas para un mundo mejor, en Metro Bilbao. Fotografía de Marian Espinosa
Panel ¿Sabías que … escuchas música gracias a la transformación matemática de los sonidos?, dentro de la exposición Matemáticas para un mundo mejor, en Metro Bilbao. Fotografía de Marian Espinosa
Y el texto del panel es el siguiente:
Cuando se graba digitalmente música, los sonidos se descomponen en frecuencias (notas musicales) y amplitudes (volumen). Los sonidos se transforman y almacenan como un listado de números. Esa transformación, llamada transformada de Fourier, permite distintas manipulaciones sobre la señal (el listado de números almacenados): comprimirla, filtrarla, quitar ruidos, añadir efectos, elaborar apps de reconocimiento de canciones, etc. Luego la operación inversa de la transformada permite su reproducción en cualquier dispositivo digital.
Otro panel basado en una investigación actual es ¿Sabías que … las matemáticas son fundamentales en la predicción de tsunamis?, en concreto, la investigación del grupo EDANYA de la Universidad de Málaga, a quienes agradecemos su colaboración.
 Panel ¿Sabías que … las matemáticas son fundamentales en la predicción de tsunamis?, dentro de la exposición Matemáticas para un mundo mejor, en Metro Bilbao. Fotografía de Marian Espinosa
Panel ¿Sabías que … las matemáticas son fundamentales en la predicción de tsunamis?, dentro de la exposición Matemáticas para un mundo mejor, en Metro Bilbao. Fotografía de Marian Espinosa
Cuyo texto, reducido del texto de la tarjeta correspondiente como en los demás paneles, es:
Las matemáticas son la base de los modelos usados para la simulación numérica de flujos geofísicos. A partir de datos precisos del terreno, estos modelos muestran desde la inundación que puede producir el desbordamiento de un río hasta la dinámica del mar de una zona costera. Incluso pueden predecir el tiempo de impacto de una onda de tsunami y la altura con que la ola va a alcanzar la costa. Para ello combinan algoritmos numéricos y hardware gráfico que simulan el tsunami y sus efectos en pocos minutos; así dotan a las autoridades de importantes herramientas de prevención.
E incluimos un panel más como muestra de esta exposición, el panel ¿Sabías que … los nudos pueden ayudar a curar enfermedades?
 Panel ¿Sabías que … los nudos pueden ayudar a curar enfermedades?, dentro de la exposición Matemáticas para un mundo mejor, en Metro Bilbao. Fotografía de Marian Espinosa
Panel ¿Sabías que … los nudos pueden ayudar a curar enfermedades?, dentro de la exposición Matemáticas para un mundo mejor, en Metro Bilbao. Fotografía de Marian Espinosa
Cuyo texto es el siguiente:
El ADN es la molécula que almacena nuestro código genético. Consiste en dos cadenas que se enrollan en forma de doble hélice y una serie de “peldaños” que las conectan. A veces el ADN está superenrollado, lo que hace difícil que tengan lugar ciertos procesos indispensables para la vida, aunque el organismo dispone de topoisomerasas, enzimas que manipulan y desenredan las cadenas. La teoría matemática de nudos ayuda a entender la acción de estas enzimas y a decidir cómo llevar el ADN a su estado normal.
Terminamos con la imagen que durante unos días ha estado colocada en las máquinas expendedoras de Metro Bilbao, anunciando las exposiciones.
Para terminar, una vez más, agradecer a Metro Bilbao que haya colaborado con el proyecto Marzo, mes de las matemáticas y que nos haya brindado la oportunidad de realizar estas dos exposiciones, Geometría Natural y Matemáticas para un mundo mejor, en un espacio tan especial como son las estaciones del metro.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Exposiciones matemáticas en el metro de Bilbao (II) se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Exposiciones matemáticas en el metro de Bilbao (I)
- Poesía métrica, ¿de metro?
- Más FUN WITH MATHS, diversión con matemáticas
Actúa localmente: robots inteligentes autoadaptativos para la producción industrial
 Planta de ensamblaje de Bell Aircraft Corporation en 1944. Los aviones que se ven en distintas frases de montaje corresponden a dos modelos, el Bell P-39Q-30-BE «Airacobra» y el Bell P-63A-8-BE «Kingcobra». Fuente: Wikimedia Commons.
Planta de ensamblaje de Bell Aircraft Corporation en 1944. Los aviones que se ven en distintas frases de montaje corresponden a dos modelos, el Bell P-39Q-30-BE «Airacobra» y el Bell P-63A-8-BE «Kingcobra». Fuente: Wikimedia Commons.Las personas difieren entre sí en su capacidad para comprender ideas complejas, para adaptarse eficazmente al entorno, para aprender de la experiencia, para usar diversas formas de razonamiento, para, en definitiva, superar dificultades a base de pensar. Aunque estas diferencias individuales pueden ser sustanciales, nunca son completamente consistentes: el rendimiento intelectual de una persona determinada variará con las circunstancias, con la tarea y según cómo se juzguen los resultados.
Entre las circunstancias que moldean a esta capacidad de aprender y adaptase para resolver problemas que llamamos inteligencia está la experiencia. Una experta es una persona que no solo tiene una información superior a la media en un campo concreto, sino que también es capaz de analizar información nueva más eficientemente y resolver nuevos retos más fácilmente, eso sí, en ese campo. La especialización, por tanto, aumenta la eficiencia, en general.
A comienzos del siglo XX se produjo una revolución en el uso de estas ideas que llevó a la producción en masa de productos muy sofisticados a un precio que una parte estimable de la población podía pagar: la producción en cadena. Donde antes un artesano era capaz de realizar todas las fases de fabricación de un producto, ahora cada una de las fases pasaba a ser el campo de especialización de una persona, que usaba herramientas y utensilios diseñados expresamente para esa fase de la producción. La producción en cadena, pues, requiere de la hiperespecialización en las distintas etapas, de forma que se optimice la eficiencia a la hora de resolver los problemas de esa etapa.
Esta especialización extrema lleva al problema de que el reciclaje de utensilios y capacidades de las personas se haga extremadamente complicado. Pensemos en una línea de producción de coches: cualquier cambio en la forma, dimensiones o tecnología conlleva unas inversiones enormes en utensilios; si el cambio es radical, como pasar a construir vehículos eléctricos en vez de con motores de combustión, lo mismo incluso compensa crear una fábrica entera desde cero en vez de adaptar lo que ya hay. Y no digamos nada de las personas trabajadoras: reciclar las capacidades en algo complejo y muy especializado, como las de quien ha estado 30 años operando una cuba de electrolisis de alúmina, por ejemplo, para que ahora se pueda dedicar a otra cosa con un nivel de eficiencia competitivo no es nada fácil.
En la revolución industrial que vivimos hoy la resolución de estos problemas de adaptación, tanto de las líneas de producción como de la operación de esas líneas, para fabricar los productos tecnológicamente sofisticados, pero a un precio asequible, que demanda la sociedad actual pasa por el uso de la inteligencia que no se cansa y que no tiene problemas personales asociados: la inteligencia artificial.
 Fuente: Vicomtech
Fuente: VicomtechUn ejemplo de hacia donde nos encaminamos es el proyecto ACROBA, financiado por la Unión Europea, y que ha comenzado el 1 de enero de este año. El proyecto tiene como objetivo desarrollar y demostrar la operatividad de unas nuevas plataformas robóticas inteligentes que sean capaces de adaptarse sin problemas a prácticamente cualquier circunstancia industrial. La idea es hacer frente a los cambios que demandan los consumidores de forma ágil, barata y manteniendo altos estándares de calidad
Estas nuevas plataformas industriales se basarán en el concepto de plug-and-produce (algo así como enchufa y produce), con una arquitectura modular y escalable que permitirá la conexión de sistemas robóticos con capacidades cognitivas mejoradas en entornos de producción que cambian rápidamente. En otras palabras, la plataforma ACROBA aprovechará la inteligencia artificial y los módulos cognitivos para cumplir con los requisitos de cada fabricante y mejorar la personalización productos de fabricación masiva (las casi infinitas combinaciones de las opciones de un coche de alta gama, por ejemplo), usando para ello sistemas robóticos avanzados capaces de autoadaptarse a las diferentes necesidades de producción.
Este tipo de plataforma permitirá la creación y la viabilidad de pequeñas y medianas empresas industriales, frente a las macro fábricas que requiere la producción en cadena normal. No es de extrañar, por tanto, que en el proyecto participe la vasca Vicomtech, que aporta sus conocimientos y experiencia en desarrollo de tecnologías de visión artificial e inteligencia artificial. En concreto participará en tareas cruciales en la colaboración persona-robot: extracción de características, comprensión de imágenes, descripción y reconocimiento de escenas. Tareas, todas ellas también, características de eso que llamamos inteligencia.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Actúa localmente: robots inteligentes autoadaptativos para la producción industrial se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Actúa localmente: convertidores de potencia basados en carburo de silicio
- Máquinas inteligentes (II): Inteligencia artificial y robótica
- Máquinas inteligentes (y III): Deep blue, HAL 9000 y más allá
Los invasores: Cangrejos de río
Hace unos años comenté en el Cuaderno de Cultura Científica la situación de los cangrejos de río en la Península Ibérica como especies autóctonas o invasoras. Ahora repasaré lo que sabemos y las últimas investigaciones.
Hay varias especies introducidas o invasoras y solo una, Austropotamobius pallipes o italicus que, según algunos expertos, es autóctona y para otros es una especie introducida. Y, como ven, hasta el nombre científico está en discusión.
 Procambarus clarkii. Fuente: Wikimedia Commons
Procambarus clarkii. Fuente: Wikimedia CommonsLa especie invasora más extendida y conocida es Procambarus clarkii, el cangrejo rojo o de las marismas. Su introducción buscaba el cultivo y comercialización de la especie, tal como se hace en su país de origen, en Estados Unidos. Llegó, por primera vez, a Badajoz en 1973, desde Louisiana. Eran 500 ejemplares y parece que no prosperó el cultivo. En 1974, fue introducido en las marismas del Guadalquivir, en concreto en Puebla del Río. Desde Estados Unidos enviaron 500 kilogramos, unos 40000 ejemplares, aunque solo llegaron vivos unos 100 kilogramos. Tanto de Badajoz como del Guadalquivir escaparon ejemplares y colonizaron los tramos medios y bajos de los ríos ibéricos.
En un estudio reciente de la diversidad genética de Procambarus, Lucía Acevedo y su grupo, de la Estación Biológica de Doñana, y con muestras de 28 lugares de la península, encuentran dos grupos diferentes separados en regiones geográficas distintas. Uno de los grupos es dominante en Portugal y los autores proponen que se originó a partir de los ejemplares que llegaron a Badajoz en 1973. El segundo grupo, que ocupa los ríos de España, vendría de la introducción en el Guadalquivir.
 Pacifastacus leniusculus. Fuente: Wikimedia Commons
Pacifastacus leniusculus. Fuente: Wikimedia CommonsLa segunda especie introducida es el cangrejo señal o Pacifastacus leniusculus. Llegó desde piscifactorías de Suecia aunque su origen está en Estados Unidos. Se importaron en 1974 y 1975 a criaderos de Soria y Guadalajara y, en 1976, a Cuenca y Burgos. Colonizan los tramos altos de ríos y arroyos ocupando hábitats y por su conducta los entornos preferidos del Austropotamobius. Durante varias temporadas se utilizó para repoblar los ríos de los que había desaparecido esta especie. Tanto el señal como el rojo se extendieron por los ríos peninsulares por que escaparon de los criaderos pero, también, porque fueron transportados de arroyo en arroyo por iniciativa individual de pescadores aficionados.
 Cherax destructor. Fuente: Wikimedia Commons
Cherax destructor. Fuente: Wikimedia CommonsUna tercera especie de cangrejo introducido en la península es el yabby o Cherax destructor que llegó en 1983 desde Los Angeles aunque su origen está en el suroeste de Australia. Se encuentra en pocos lugares, en Aragón y Navarra, y coloniza fondos blandos y limosos en aguas lentas como pantanos, balsas y tramos finales de grandes ríos. En Australia es una especie muy apreciada y, quizá por ello, llegó a la península.
 Cherax quadricarinatus. Fuente: Wikimedia Commons
Cherax quadricarinatus. Fuente: Wikimedia CommonsHace unas semanas se publicó el hallazgo en Asturias de otra especie del género Cherax. Andrés Arias y Antonio Torralba, de la Universidad de Oviedo, encontraron Cherax quadricarinatus en Colloto, cerca de Oviedo. Los primeros ejemplares los recogieron en 2013.
 Orconectes (ahora Faxonius) limosus. Fuente: Wikimedia Commons
Orconectes (ahora Faxonius) limosus. Fuente: Wikimedia CommonsOtra especie de cangrejo de agua dulce encontrada en la península es Orconectes (ahora Faxonius) limosus, detectada en un pantano de Girona. El muestreo se hizo en 2010 y publicaron los resultados en 2011 Lluis Benejam y su grupo, del Centro del Estudio de Biología de Conservación Terrestre y Acuática de Figueres. El origen de esta especie también es Estados Unidos.
 Austropotamobius italicus. Fuente: Wikimedia Commons
Austropotamobius italicus. Fuente: Wikimedia CommonsY la sexta especie de cangrejo de río en la península es el citado Austropotamobius pallipes o italicus que, como decía, mantiene la incógnita sobre su origen. Sería, por tanto, una especie criptogénica según la definición de James Carlton, del Colegio Williams de Williamstown, en Estados Unidos. Según su publicación de 1982, una especie criptogénica es aquella en que no se puede determinar si es autóctona, introducida o invasora.
Según algunos grupos de investigación, esta especie llegó a la península en el siglo XVI, por la intervención directa de Felipe II. Desde la paleontología o la arqueología no hay datos sobre la presencia de alguna especie de cangrejo d erío en la península. No hay que olvidar que la conservación y fosilización de sus restos no es fácil. Otra fuente de datos son los libros de gastronomía pero, hasta 1611 y en el libro de Francisco Martínez Motiño, Cocinero Mayor de Felipe II, no se mencionan los cangrejos de río.
La historia que se ha deducido sobre el origen de estos cangrejos dice que llegaron desde Milán, con un mensajero de Felipe II, hasta Alicante en 1588 y, desde el puerto, fueron transportados a Madrid, quizá a El Escorial.
A finales del siglo pasado, el Austropotamobius casi desapareció. En 1978, comenzó a extenderse por las aguas dulces de la península el hongo Aphanomyces astaci, patógeno mortal que provoca la afanomicosis en los cangrejos europeos. Los primeros casos se diagnosticaron en primavera y se identificó el Aphanomyces en Burgos y Ciudad Real. El hongo venía de Norteamérica donde tiene una presencia continua y no daña a los cangrejos locales. Llegó a Europa con la importación de los cangrejos rojo y señal, que son portadores, y extendieron la enfermedad por todo el continente.
Para evaluar si el Austropotamobius es autóctono o introducido, se analizó su diversidad genética. El estudio del ADN mitocondrial, publicado por Beatriz Matallana y su grupo, de la Universidad Complutense, con datos de 160 ejemplares de 16 lugares de ríos del norte, centro y este peninsulares, revelaron la existencia de dos grupos, uno de ellos en el norte, en el área cantábrica y el Alto Ebro, y el segundo grupo, que llamaron central, en el este y centro peninsulares.
Sin embargo, estos estudios no sirvieron para aclarar el origen de esta especie. La diversidad genética es grande, habitual en una especie autóctona, pero con una distribución en manchas discontinuas, típico de una especie introducida varias veces y, a menudo, transportada por iniciativa personal para ampliar las zonas de pesca.
El debate continua y tiene importancia práctica pues supone la concesión de tiempo y recursos para recuperar una especie dañada por la enfermedad. Pero para ello se debe considerar si es una especie autóctona y no una introducida que, en principio, se supone que perjudica a los ecosistemas del entorno. Quizá se debe reconsiderar la definición de introducida o invasora para especies como el Austropotamobius que, según algunos expertos, lleva ya cinco siglos en el entorno y es importante por su integración en la cultura y en las tradiciones del país.
Referencias:
Acevedo-Limón, L., et al. 2020. Historical, human, and environmental drivers of genetic diversity in the red swamp crayfish (Procambarus clarkii) invading the Iberian Peninsula. Freshwater Biology 65: 1460-1474.
Angulo, E. 2016. El caso de los cangrejos viajeros. Cuaderno de Cultura Científica 26 septiembre.
Arias, A. & A. Torralba-Burrial. 2021. First record of the redclaw crayfish Cherax quadricarinatus (Van Martens, 1868) on the Iberian Peninsula. Limnetica DOI: 10.23818/limn.40.03
Benejam, L. et al. 2011. First record of the spiny-cheek crayfish Orconectes limosus (Rafinesque, 1918) introduced to the Iberian Peninsula. Aquatic Invasions 6: S111-S113.
Bolea Berné, L. 1996. Primera cita de Cherax destructor (Crustacea: Decapoda: Parasticidae) en Europa. Boletín de la SEA 14: 49-51.
Carlton, J.T. 1996. Biological invasions and cryptogenic species. Ecology 77: 1653-1655.
Clavero, M. & D. Villero. 2014. Historical ecology and invasion biology: Long-term distribution changes of introduced freshwater species. BioSciences 64: 145-153.
Clavero, M. 2015. Non-native species as conservation priorities: response to Díez-León, M. et al. Conservation Biology DOI: 10.1111/cobi.12524
Clavero, M. et al. 2016. El cangrejo de río… italiano. Quercus 359: 42-52.
Clavero, M. et al 2016. Interdisciplinary to reconstruct historical introductions: solving the status of cryptogenic crayfish. Biological Reviews 91: 1036-1049.
Diéguez-Uribeondo, J. et al. 1997. The crayfish plague fungus (Aphanomyces astaci) in Spain. Bulletin Français de la Pêche et de la Pisciculture 347: 753-763.
Díez León, M. et al. 2014. Setting priorities for existing conservation needs of crayfish and mink. Conservation Biology 29: 599-601.
Galindo, F.J. et al. 2014. Cangrejo de río: la ciencia sí es aval de su carácter nativo. Quercus 342: 74-79.
García-Arberas, L. et al. 2009. The future of the indigenous freshwater crayfish Autropotamobius italicus in Basque Country streams: Is it possible to survive being an inconvenient species? Knowledge and Management of Aquatic Ecosystems DOI: 10.1051/Kmae/2010015
Gherardi, F. 2006. Crayfish invading Europe: the case study of Procambarus clarkii. Marine and Freshwater Behaviour and Physiology 39: 175-191.
Heuthonen, P. & J.V. Huner. 1999. The introduction of alien species of crayfish in Europe: A historical introduction. En “Crayfish in Europe as alien species. How to make the best of a bad situation?”, p.13-22. Ed. Por A.A. Belkema. Rotterdam.
Laurent, P.J. 1997. Introductions d’écrevisses en France et dans le monde, historique et conséquences. Bulletin Français de la Pêche et de la Pisciculture 344/345: 345-356.
Martín-Torrijos, L. et al. 2019. Mapping 15 years of crayfish plague in the Iberian Peninsula: The impact of two invasive species on the endangered native crayfish. PLOS One 14: e0219223
Matallanas, B. et al. 2016. The White-clawed crayfish in Spain – reply to Clavero and Centeno-Cuadros. Organisms Diversity & Evolution 16: 719-721.
Matallanas, B. et al. 2016. Fine-tuning of a COI PCR-RFLP assay for fast genetic characterization of Spanish white-clawed crayfish. Knowledge and Management of Aquatic Ecosystems DOI: 10.1051/kmae/2016019
Matallanas, B. et al. 2016. Update of genetic information for the white-clawed crayfish in Spain, with new insights into its population genetics and origin. Organisms Diversity & Evolution 16: 533-547.
Oficialdegui, F.J. et al. 2019. Unravelling the global invasion routes of worldwide invader, the red swamp crayfish (Procambarus clarkii). Freshwater Biology DOI: 10.1111/fwb.13312
Oficialdegui, F.J. et al. 2020. Brought more than twice: the complex introduction history of the red swamp crayfish in Europe. Knowledge and Management of Aquatic Ecosystems doi: 10.1051/kmae/2019044
Oscoz, J. et al. 2008. Nuevos datos sobre la presencia de cangrejos autóctonos en la Cuenca del Río Ebro. Gorosti 19: 4-11.
Vedia, I. & R. Miranda. 2013. Review of the state of knowledge of crayfish species in the Iberian Peninsula. Limnetica 32: 269-286.
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo Los invasores: Cangrejos de río se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:¿Cuánta ciencia hay en la música?
José Manuel González Gamarro
Cuando yo era estudiante (me refiero a edad estudiantil, porque los músicos, como muchas otras profesiones, siempre estamos estudiando) pululaba en el ambiente una cuestión: ¿eres de ciencias o de letras? En los últimos años esta cuestión ha ido perdiendo su identidad como dicotomía. Hemos podido comprobar cómo la cultura de la sociedad necesita a las humanidades tanto como a la ciencia. La cultura científica es tan importante para un doctor en historia como la cultura clásica para un doctor en biología, otra cuestión es el interés de cada uno en alejarse de su materia. Hacernos expertos en algo nunca justifica la ausencia de cultura básica en otros ámbitos ajenos a nosotros. La denominada Tercera Cultura ya fue definida por Charles Percy Snow en 1959 donde la interdisciplinariedad es la base del pensamiento. Aunque el término interdisciplinariedad pueda parecer muy moderno, a decir verdad, cuánto más hacia atrás vamos en el tiempo, más personajes ilustres encontramos que practicaban esta suerte de mezcla de conocimiento para avanzar en diferentes disciplinas. Para no alejarnos demasiado del momento presente, si nos vamos al siglo XIX tenemos un claro ejemplo interdisciplinar en Hermann von Helmholtz, que hizo aportaciones a la matemática, física acústica, filosofía, psicofísica, fisiología y teoría musical.
 Foto: Robbie Down / Unsplash
Foto: Robbie Down / UnsplashComo decía Jorge Wagensberg, la realidad misma es interdisciplinar, otra cosa es como se pactan los planes de estudio de escuelas y universidades para poder estudiarla y entenderla. En la música ocurre una analogía con respecto al planteamiento de Wagensberg, existe una frontera artificial que en los últimos años parece estar difuminándose. Si nos centramos en la música académica que se estudia en los conservatorios y universidades, podríamos deducir que la música es una disciplina perteneciente a las humanidades, a juzgar por la cantidad de estudios que existen con este enfoque. Podemos encontrar un gran volumen de investigación musical donde predominan los estudios sobre la teoría musical y su puesta en práctica, y por otro lado están los estudios de la musicología histórica, con sus diferentes ramificaciones. El predominio de la musicología histórica proviene del siglo XIX, pero ¿y antes? Hasta 1600, la musicología entendida como la ciencia que estudia la música, fue principalmente sistemática, es decir, mucho más ligada al pensamiento acústico y matemático. Esto vuelve a ser una tendencia actual. Vestir a la música únicamente de humanidades es ponerle la mitad de la ropa, negándole su inherente realidad científica.
Respondiendo a la pregunta que da título a este artículo, hay que decir que la música está repleta de ciencia, aunque eso no la convierta en una disciplina científica. Nadie negará a estas alturas el increíble cariz matemático de la música en la explicación de su teoría. Esta personalidad matemática de la música no sólo se encuentra en la analogía del código que crea su propia realidad, sino también en todos los aspectos numéricos básicos, tales como intervalos, tonalidades, compases, ritmos y en la manera de analizarla y componerla. Los más iniciados en la materia pensarán en músicas relativamente recientes, donde prima el atonalismo o el serialismo, con una técnica compositiva en base a series de elementos (ya sean notas o cualquier otro parámetro musical). Precisamente para el repertorio atonal existe una teoría de análisis desarrollada por Allen Forte1, la teoría de conjuntos de clases de alturas, donde incluso hoy en día podemos encontrar ejemplos de calculadoras específicas que nos ayudan a realizar este análisis musical. También en el análisis de la música tonal o la música pop o rock, existen teorías de análisis basadas en las matemáticas2 que provienen de Euler, que después redefinió Hugo Riemann. A partir de aquí aparecen la teoría de los vectores armónicos de Nicolas Meeùs o David Lewin y su teoría neo-riemanniana, con nuevos sistemas de representación basados en diagramas o Tonnetz.
Pero la dimensión matemática no es algo reciente en lo que se refiere a la composición musical, unos años antes de que Poisson diera a conocer su distribución de probabilidad, músicos como Kirnberger, Carl Philip Emanuel Bach, Haydn o Mozart, entre otros, ya hacían composiciones aleatorias tirando dos dados, basándose en la certeza de que no todos los números son igualmente probables. Desde Pitágoras, la teoría musical se explica desde las matemáticas, pero como vemos, esto no solo afecta a la teoría, sino a la materia prima para crear música. Más recientemente existen composiciones que hacen uso de la geometría fractal, la teoría del caos o de sistemas basados en agentes.
Sin embargo, la matemática no es la única ciencia que está en la música, también la física si pensamos en el sonido, cómo se genera a partir de vibraciones periódicas y cómo aquello que llamamos timbre es simplemente (o más bien complejamente) una diferencia de amplitud de las ondas resultantes en las que se puede descomponer cualquier sonido real. También esto es una fuente inagotable para la composición musical, ya que existen obras basadas en el timbre, es decir, en las frecuencias de los sonidos resultantes de un sonido principal. Un ejemplo paradigmático es la obra Partiels, de Gérard Grisey, basada en el espectro armónico de un sonido. Por otro lado, están los compositores de música electroacústica y la síntesis de sonido, que no es más que la creación de nuevos sonidos gracias a la informática y las funciones de forma de onda o la teoría de los cuantos acústicos de Dennis Gabor, entre otras muchas posibilidades. El estudio de la física también está presente en la historia de los diferentes sistemas de afinación de la música occidental3 y la explicación de por qué hoy en día se usa un temperamento igual (dividir una escala en 12 semitonos iguales).
La ciencia que esconde la música también la podemos encontrar en la biología, ya que existe música creada únicamente con algoritmos genéticos, que desarrollan en universidades como la de Málaga. Esta biología también la encontramos en la búsqueda del origen de la música y la evolución de los homínidos, que además podemos unir a la arqueología y su búsqueda de los primeros instrumentos musicales y formas de representar la música. Es posible hallar algo de biología en algunas teorías de análisis musical, desarrollando principios de crecimiento orgánico. En este caso habría que volver a mencionar a Hugo Riemann.
Podríamos seguir hablando de psicoacústica y entropía, análisis de la interpretación mediante espectrogramas para poder analizar lo audible pero invisible en la partitura, estudios conductuales, neuroimagen, etc. y todo esto omitiendo toda la ciencia implicada en la construcción y desarrollo histórico de los instrumentos musicales. Tampoco deberíamos olvidarnos de que la enseñanza musical se basa, o ha de basarse, en los datos que nos ofrecen investigaciones en psicología cognitiva y en la medicina especializada en el deporte o las artes escénicas. Como podemos comprobar, la dimensión científica de la música es abrumadora en cuanto dejamos la superficie de su estudio atrás.
Volviendo al principio de este artículo, aludiendo a la interdisciplinariedad, podríamos hacer un diagrama de Venn con dos grandes círculos donde estuvieran, en uno la ciencia y en el otro las humanidades. Esa área de intersección característica de estos diagramas sería la música. Si alguna vez me volvieran a preguntar si soy de ciencias o de letras, tengo clara la respuesta: soy de música.
Referencias:
1 Forte, Allen. The structure of atonal music. Vol. 304. Yale University Press, 1973.
2 Capuzzo, Guy. «Neo-Riemannian theory and the analysis of pop-rock music.» Music Theory Spectrum 26.2 (2004): 177-199.
3 Gaínza, J. Javier Goldáraz. Afinación y temperamento en la música occidental. Alianza, 1998.
Sobre el autor: José Manuel González Gamarro es profesor de guitarra e investigador para la Asociación para el Estudio de la Guitarra del Real Conservatorio Superior de Música “Victoria Eugenia” de Granada.
El artículo ¿Cuánta ciencia hay en la música? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Ciencia, arte y cultura callejera: física y música
- Música, guerra y paz
- Curso de verano “La ciencia de nuestras vidas”: Cuando la música era ciencia, por Almudena M. Castro
Javier Peláez – Naukas Bilbao 2019: Una odisea ártica
 Foto: Willian Justen de Vasconcellos / Unsplash
Foto: Willian Justen de Vasconcellos / UnsplashCuando pensamos en las expediciones más importantes de la historia, frecuentemente olvidamos la conquista del Ártico, pero durante más de cinco siglos, incontables barcos y marinos se han adentrado en sus gélidas aguas en busca de tierras desconocidas o rutas más rápidas para el comercio. Pocas de aquellas expediciones consiguieron sus objetivos; los más afortunados regresaron a casa con las manos vacías, otros se quedaron allí para siempre.
Javier Peláez es un divulgador y comunicador científico, uno de los fundadores de la plataforma Naukas.com y editor de ciencia de Yahoo! Durante más de una década ha escrito en diferentes medios de comunicación (El País, El Español, National Geographic, Voz Populi). Es coautor de los podcasts Catástrofe Ultravioleta y La Aldea Irreductible y ha colaborado en diferentes proyectos radiofónicos (Radio Nacional de España, Radio Televisión Canaria). Es ganador de tres premios Bitácoras, un premio Prisma a la mejor web de divulgación científica y un Premio Ondas al mejor programa de radio digital. Autor de «500 años de frío. La gran aventura del ártico» (Ed. Planeta, 2019).
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Javier Peláez – Naukas Bilbao 2019: Una odisea ártica se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Naukas Bilbao 2017 – Javier Fernández Panadero: Si tú supieras
- Javier Armentia – Naukas P4K 2019: La vie en rose (ciencia y sociedad de un color muy suyo)
- Isabel Moreno – Naukas Bilbao 2019: El cielo en clave de Sol

