#Naukas16 Entramos en M1
 .
.
Rosario Luque ha venido a hablar del DefCon1, ese estado de alerta militar que autoriza el uso de armas de destrucción masiva, a nivel celular y del papel que en él juegan los macrófagos.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo #Naukas16 Entramos en M1 se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Las tres conquistas del Polo Norte
 La expedición noruega de Amundsen coronando el Polo Sur
La expedición noruega de Amundsen coronando el Polo Sur
Siempre me ha resultado curioso saber que, después de miles de años de Historia, el ser humano finalmente consiguió alcanzar los cuatro puntos más extremos de nuestro planeta en apenas medio siglo. El lapso de tiempo que va de 1911 hasta 1960 fue testigo de la victoria final, y casi consecutiva, sobre los Polos, el Everest y la Fosa de las Marianas… o dicho de otra manera: el punto más alto, el más profundo, el más al norte y el más al sur de nuestro planeta.
Estos prodigiosos cincuenta años se inician con la conquista del Polo Sur por parte de la expedición noruega, liderada por Roald Amundsen, el 14 de diciembre de 1911. En mayo de 1953 el neozelandés Edmund Hillary y el sherpa Tenzing Norgay fueron los primeros seres humanos en ascender los 8848 metros de altura del Everest. En enero de 1960 el ingeniero Jacques Picard y el militar Don Walsh se posaron por primera vez en el fondo marino de la fosa de las Marianas a bordo del submarino Trieste.
Las dos últimas fechas, separadas apenas por unos años, situaban al hombre en el punto más alto y el más profundo del planeta, y si las comparamos con julio de 1969, momento en el que la humanidad consiguió poner un pie en la Luna, nos dan una idea de la extrema dificultad de las gestas alcanzadas.
 Doodle conmemorativo del 125 aniversario de la conquista del Polo Sur
Doodle conmemorativo del 125 aniversario de la conquista del Polo Sur
Hace unos días, Google nos recordaba en su portada el 125 aniversario de la conquista del Polo Sur, sin embargo si tuviese que crear uno de sus populares “doodles” y dedicarlo al Polo Norte, el asunto sería bastante más complicado. De hecho, y a raíz de esta celebración tuve en twitter un pequeño debate sobre el tema puesto que, a pesar del tiempo transcurrido, la gente no tiene aún muy claro quién fue el primer hombre que alcanzó el Polo Norte… Incluso si volvemos a acudir al célebre buscador para encontrar una respuesta nos encontraremos con una muy equivocada.
 No siempre hay que fiarse de Google
No siempre hay que fiarse de Google
La historia de la conquista del Polo Norte se ha visto envuelta en numerosos errores (y mentiras, por qué no decirlo) que condicionaron su exploración y la relegaron al olvido, simplemente porque todos pensaron que ya se había completado. Para complicarlo aún más, aparte de las consideraciones históricas, la pregunta de quién fue el primero en llegar al Polo Norte tiene sus propias connotaciones semánticas… ¿Qué se considera llegar? ¿Hay que pisar físicamente el lugar, hay que llegar de alguna manera concreta?
Dos siglos antes, cuando comenzó la exploración polar, a nadie se le hubiera ocurrido avanzar hacia el Polo… allí no había nada, y al igual que Colón, lo que buscaban los navegantes en realidad era un paso comercial, el célebre Paso del Noroeste (o del Nordeste). Poco a poco el deseo comercial se fue transformando en exploración, más tarde en pasión y finalmente en obsesión.
 ¿Peary o Cook? Hoy sabemos que ninguno.
¿Peary o Cook? Hoy sabemos que ninguno.
Obsesión como la de Robert Peary, explorador estadounidense que durante más de veinte años realizó casi una docena de intentonas, hasta que en abril de 1909 pudo gritar: ¡Al fin el Polo Norte, el premio a tres siglos, mío al fin!.
Ya sea porque mintió o porque se equivocó en sus mediciones (yo soy más partidario de la primera opción), Peary jamás llegó al Polo Norte. Pero tuvo la suerte de toparse con un adversario aún más mentiroso que él, Frederick Cook, otro aventurero que también se proclamaba como la primera persona en llegar a los 90ºN, casualmente el mismo año en que Peary regresaba de su expedición.
Ninguno de los dos lo consiguió, dejémoslo bien claro: Ni Peary, ni Cook.
Sin embargo, la fama de mentiroso de Cook (a quién unos años antes ya habían pillado falseando logros, como una fingida escalada al Denali) empujó a muchos a darle crédito a la gesta de Peary. Para auparle aún más, en noviembre Cook confesó y admitió que no había llegado, lo que aumentó aún más la apariencia de vencedor de su contrincante. Esta errónea creencia de que Robert Peary fue el primero en llegar al Polo Norte se mantuvo durante décadas, e incluso hoy en día, muchas webs aún mantienen esa información falsa en sus contenidos.
 Cook confiesa
Cook confiesa
Para lo que a nosotros nos atañe, el hecho de que a principios de siglo se diera por sentado que Peary era el gran ganador tuvo consecuencias inesperadas. La más importante fue que, al dar por finalizada la carrera hacia los 90ºN, muchos exploradores olvidaron el Polo Norte para dedicar sus esfuerzos a ganar otros objetivos. El más destacado, el propio Amundsen que, al conocerse la noticia de que el Ártico ya tenía Rey, desvió sus esfuerzos y su expedición hacia el Polo Sur.
La autoproclamación de Peary en 1909 como conquistador del Norte hizo que durante casi veinte años y, exceptuando alguna expedición danesa de exploración por Groenlandia, el Ártico apenas tuviera visitantes. Tuvimos que esperar hasta mediados de la década de los ’20 para que volviera la fiebre ártica, esta vez utilizando nuevos métodos y transportes.
En 1926, el piloto estadounidense Richard Byrd volvió a poner sobre la mesa una nueva hazaña ártica afirmando que había sobrevolado el Polo Norte subido en su fokker. Otro “bluff” que sumar al de Peary y Cook puesto que hoy sabemos con total seguridad que Byrd también mintió: Tergiversó las coordenadas en su diario y se inventó los datos para aparentar, sin mencionar su demencial historia de haber divisado desde el aire entradas a un mundo intraterrestre bajo el Polo.
 Richard Byrd… tampoco.
Richard Byrd… tampoco.
Seguimos en mayo de 1926 y a pesar de lo que todo el mundo piensa, el Polo Norte continúa virgen: Nadie lo ha alcanzado aún. Sin embargo, tan solo unos días después del vuelo en avión de Byrd, despegaba desde el archipiélago de Svalbard la primera expedición que de verdad iba a alcanzar el Polo Norte.
A bordo del dirigible Norge se embarcan dieciséis personas, encabezadas por el italiano Umberto Nobile, y… tachán… el rey del Sur, Roald Amundsen. Se sitúan sobre los 90ºN, abren la ventanilla del dirigible y lanzan tres banderas, italiana, noruega y estadounidense. Todos ellos, el 12 de mayo de 1926, se convierten, por fin, en las primeras personas en alcanzar el Polo. Admundsen además atesora el honor de ser el primero en conquistar el Polo Sur y también el Norte.
Por supuesto habrá quien considere que el sobrevuelo del Norge por parte de Nobile y Amundsen no es una conquista total puesto que, aunque no cabe duda de que fueron los primeros en llegar, en realidad, no “pisaron” el Polo Norte…
Oficialmente ya tenemos ganadores, sin embargo aún queda pendiente la cuestión semántica a la que me refería en párrafos anteriores, de quién fue el primer hombre que “pisó” el Polo Norte. Para alcanzar este honor aún tendríamos que esperar más de veinte años.
En abril de 1948, tres aviones Lisunov Li-2 soviéticos aterrizan en el Polo Norte llevando a bordo una expedición científica Sever-2, compuesta por veinticuatro personas lideradas por el explorador Alexander Kutnesov. Su misión principal era determinar mediante sonar si debajo del hielo ártico había montañas submarinas, por lo que en ningún momento supieron que eran los primeros seres humanos que pisaban el lugar más septentrional del planeta.
Es posible que también en esta ocasión haya gente que considere que llegar en avión al Polo y regresar cómodamente por aire, no merece el tratamiento de “conquista”, sobre todo si tenemos en cuenta las gestas de Hillary en el Everest o la carrera entre Scott y Amundsen en la Antártida. Dicho de otro modo: tanto el Norge como la expedición soviética alcanzaron los 90ºN mediante medios aéreos y hay quien puede pensar (no es mi caso) que estos logros son como si Hillary hubiese conquistado el Everest descendiendo en un helicóptero…
 Wally Herbert, su expedición es la única en llegar a pie al Polo Norte atravesando el mar Ártico
Wally Herbert, su expedición es la única en llegar a pie al Polo Norte atravesando el mar Ártico
Para estos “tiquismiquis” que esperan una gesta tradicional, por tierra, aún queda una tercera conquista del Polo Norte, aunque eso sí… habrá que esperar más de veinte años.
En 1969, y el año es significativo de la dureza del reto si lo comparamos con la fecha de llegada a la Luna, una expedición de tres hombres, comandada por el explorador británico Wally Herbert dará cumplida cuenta de lo que representa alcanzar el Polo Norte sin utilizar medios aéreos. Más de un año de travesía, más de un centenar de perros para los trineos y una gesta que jamás nadie ha vuelto a repetir: Alcanzar los 90ºN cruzando el océano Ártico a pie.
Estas son las tres conquistas del Polo Norte, las verdaderas.
Nobile, Amundsen, Ellsworth, Wisting a bordo del Norge fueron los primeros en llegar.
Kutnesov y sus científicos de la expedición Sever-2 fueron los primeros en pisar.
Herbert y su equipo de la British Trans-Arctic Expedition fueron los primeros en conquistar.
Este post ha sido realizado por Javier Peláez (@irreductible) y es una colaboración de Naukas con la Cátedra de Cultura Científica de la UPV/EHU.
El artículo Las tres conquistas del Polo Norte se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Sorpresas en la atmósfera del polo sur de Venus
- ¿Qué hago yo si papá viaja hacia al norte y mamá hacia el sur?
- Las tres dimensiones del sonido
#Naukas16 Exoplanetas: mundos de ciencia ficción

Los exoplanetas descubiertos superan a todo lo imaginado por los creadores de ciencia ficción. Daniel Marín nos da una vuelta por ellos.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo #Naukas16 Exoplanetas: mundos de ciencia ficción se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- #Naukas13 Naves de ciencia y no de ficción
- #NaukasKids14 Física y ciencia ficción
- #Naukas16 Cómo escribir un libro de ciencia para niños
No todo ha sido malo este año: la ciencia nos dejó algunas buenas noticias
 Donald Trump
Donald Trump
Francamente, debimos plantearnos adelantar el cambio de año cuando el 14 de enero fallecía Alan Rickman. 2016 no podía traer nada bueno. Tras ello llegó el brexit, la elección de Donald Trump, las muertes de David Bowie, Leonard Cohen, Umberto Eco, Darío Fo, Bud Spencer, Johan Cruyff, el huracán Mathew, el terremoto de Italia… Efectivamente, nada bueno.
¡Error! Aunque han pasado más desapercibidas, este año también ha traído buenas noticias, muchas de ellas por cortesía y gracia de los científicos e investigadores de todo el mundo. Si tener en cuenta lo bueno ya es una costumbre saludable de por sí, en un año que vamos a cerrar como un continuo borrón chubascoso se antoja una necesidad vital.
No están todas las que son, pero todas las que están, lo son: buenas noticias que nos ha dejado la ciencia.
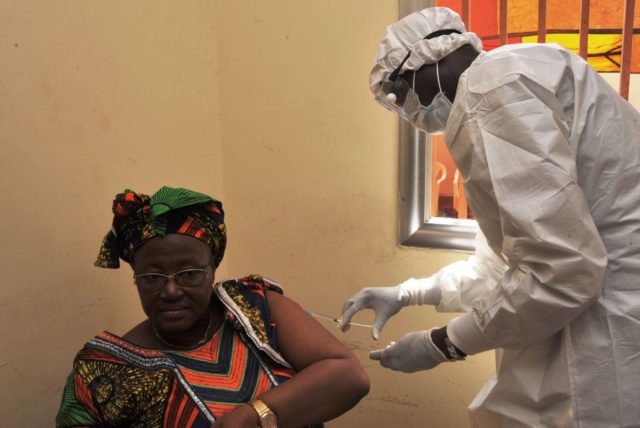 Una mujer recibe la vacuna del ébola en Conakri (Guinea). Foto: Cellou Binani – AFP
Una mujer recibe la vacuna del ébola en Conakri (Guinea). Foto: Cellou Binani – AFP
Una vacuna para el ébola
En la misma semana de Navidad llegó la que probablemente es la mejor noticia de todas: la Organización Mundial de la Salud anunciaba que la vacuna experimental sometida a la fase de ensayos clínicos en Guinea durante 2015 demostraba una eficacia del 100% para proteger a los seres humanos de la enfermedad.
La noticia llegaba tarde para todos los que fallecieron en la epidemia de ébola en África Occidental del año pasado, pero suponía una esperanzadora diferencia para la próxima vez que algo así ocurra de nuevo.
El virus del ébola se identificó por primera vez en 1976 y desde entonces ha habido brotes esporádicos de la enfermedad. El que se vivió en África entre 2013 y este 2016 ha sido el más grave de todos con más de 11.000 muertes.
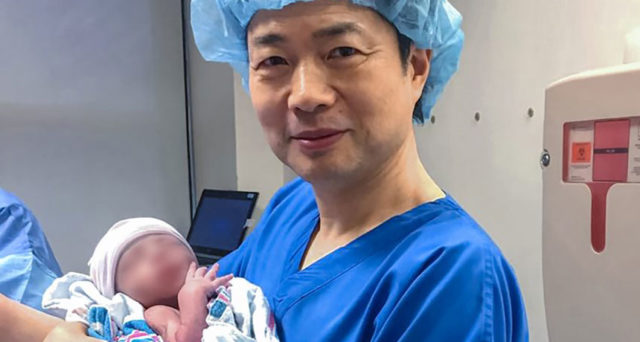 El doctor John Zhang con el niño cuyo embrión fue creado por reemplazamiento mitocondrial: óvulo (y sus mitocondrias) de una donante, núcleo del óvulo de la madre y esperma del padre.
El doctor John Zhang con el niño cuyo embrión fue creado por reemplazamiento mitocondrial: óvulo (y sus mitocondrias) de una donante, núcleo del óvulo de la madre y esperma del padre.
Un niño con tres padres
En el mes de septiembre conocíamos la noticia: cinco meses antes nacía el primer bebé con código genético de tres personas distintas. Ocurrió en Estados Unidos y el objetivo era evitar que el bebé naciese con el síndrome de Leigh, una patología genética que afecta al desarrollo del sistema nervioso.
La madre del bebé porta la carga genética responsable de este síndrome. Aunque ella no ha desarrollado la enfermedad, ésta causó la muerte de sus primeros dos hijos, así que ella y su marido buscaron la ayuda de John Zhang, especializado en la técnica de los ‘tres padres’ para evitar este tipo de enfermedades.
Hay varias formas de evitar esto. La más habitual es fertilizar el óvulo de una donante y de la madre con el esperma del padre, y antes de que ambos comiencen a dividirse se extrae el núcleo de ambos, se descarta el de la donante y se sustituye por el de la madre. En este caso, por motivos religiosos, la pareja se negó a destruir un embrión, así que el proceso fue diferente: Zhang extrajo el núcleo de un óvulo de la madre y lo introdujo en uno de la donante para ser fertilizado a posteriori.
Esto abre una nueva puerta a la manipulación de óvulos para evitar enfermedades sin afectar a embriones, un punto que causa serios dilemas éticos y morales en muchos casos.
 Impresora 3D
Impresora 3D
Un corazón en un chip
En el mes de octubre, científicos de Harvard anunciaban que habían logrado por primera vez reproducir los elementos y funcionamiento del corazón humano en un pequeño chip fabricado con una impresora 3D de forma que se pueda utilizar para investigación médica sin necesidad de utilizar modelos animales.
Se trata de un paso más en la rama de la microfluídica, que trata de fabricar pequeños chips de plástico en los que se ensayen las reacciones químicas que ocurren en cada órgano humano al entrar en contacto con distintos medicamentos o sustancias y llevar así a cabo parte de la investigación sobre enfermedades y sus curas.
Además, utilizar una impresora 3D para fabricarlos tiene ventajas añadidas, ya que el diseño se puede modificar rápidamente para adaptarse a enfermedades o alteraciones concretas de un paciente y aplicar así una investigación y medicina personalizadas.
 Nathan Copeland y su brazo robótico
Nathan Copeland y su brazo robótico
Un brazo robótico que siente
Una noche de 2004, Nathan Copeland, de 18 años, iba conduciendo bajo la lluvia cuando perdió el control de su coche y tuvo un accidente. Desde entonces, su cuerpo perdió toda sensibilidad del cuello para abajo. Hasta que este mes de octubre recuperó el sentido del tacto en un brazo.
Claro que el brazo no es suyo. Es un brazo robótico conectado con una cirugía directamente a su cerebro, de forma que recibe las señales eléctricas de forma similar a como sentimos habitualmente que algo nos roza un dedo.
No es la primera prótesis robótica que se fabrica, pero aquí la clave está en el sistema de señales bidireccionales. A Copeland se le colocó un implante neuronal y durante seis meses entrenó para aprender a dominar el dispositivo: por un lado, los electrodos recogían las señales enviadas por la zona motora del cerebro para mover el brazo robótico, mientras que por otro estimulaban eléctricamente otra región relacionada con los sentidos. para crear la sensación del tacto. Según Copeland, la sensación es prácticamente la de tener la mano y el brazo de nuevo funcionales.
 Posible presentación de los anticonceptivos masculinos
Posible presentación de los anticonceptivos masculinos
Un anticonceptivo masculino
Queda aún mucha investigación por delante, pero los primeros resultados son prometedores: en el estudio clínico de una inyección anticonceptiva masculina, los resultados demostraron una eficacia prácticamente igual a la de la píldora anticonceptiva femenina. Si bien el estudio tuvo que ser suspendido temporalmente por los efectos secundarios que sufrieron los voluntarios, se trata de un primer paso hacia un reparto equitativo del control del embarazo entre ambos miembros de una pareja.
En el estudio participaron 350 hombres con pareja estable que recibieron estas inyecciones hormonas. El efecto fue una bajada en el número de espermatozoides durante el tiempo que duró el tratamiento, recuperándose después los niveles habituales igual que ocurre con la píldora.
Sin embargo, las inyecciones presentaron efectos negativos, como acné, depresión y un incremento de la libido que causaron que el 20% de los participantes abandonase el tratamiento y por tanto el estudio se detuviese antes de lo previsto. Son aspectos que deben mejorar antes de que este anticonceptivo masculino pueda salir al mercado, pero se trata de un paso adelante en un camino que traerá una alternativa más para evitar embarazos no deseados.
 Los ratones parecen estar un paso más cerca de la inmortalidad
Los ratones parecen estar un paso más cerca de la inmortalidad
Un ratón rejuvenecido
En el futuro, el envejecimiento no será una consecuencia inevitable del paso del tiempo, sino un factor que, como cualquier enfermedad, será posible tratar y curar. Eso asegura el equipo que a finales de este año anunció que, por primera vez, había aplicado en un ratón vivo la técnica de la reprogramación celular para revertir los efectos del envejecimiento.
La reprogramación consiste en manipular las células de cualquier tejido del cuerpo (del cerebro, de un músculo, del hígado…) para revertir su especialización y convertirlas en células madre pluripotentes, con la capacidad de convertirse en cualquier otra célula. Esto, que supondría una ventaja obvia ante la necesidad de un trasplante, es de momento una técnica demasiado compleja, cuyos resultados terminan a menudo desarrollando tumores.
En el caso del ratón, la clave fue dejar la reprogramación a medias: en vez de completar el proceso, los investigadores lo aplicaron de forma parcial y lo detuvieron antes de que terminase. De esa forma las células de los tejidos seguían especializadas, pero los efectos del paso del tiempo se habían corregido. Hará falta más investigación, pero pasar de los modelos in vitro, donde se había probado la reprogramación hasta ahora, a un animal vivo es un paso adelante en el dominio de una técnica que servirá para salvar vidas y ayudarnos a luchar contra las enfermedades causadas por la vejez.
Sobre la autora: Rocío Pérez Benavente (@galatea128) es periodista en El Confidencial
El artículo No todo ha sido malo este año: la ciencia nos dejó algunas buenas noticias se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- En la ciencia todo se desarrolla vigoroso, obvio y estupendo como en un cuento de hadas
- Migraciones culturales: La costumbre de usar palillos llegó al este de China hace 500.000 años
- Fraude científico (IV). Algunas consecuencias
Un 5 % de materia oscura menos
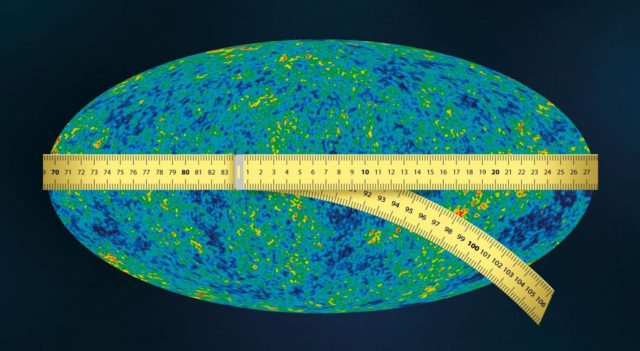
La naturaleza de la materia oscura sigue siendo uno de los grandes misterios de la ciencia. Tanto es así que hay científicos que consiguen gran eco mediático simplemente proponiendo teorías en las que la materia oscura no aparece. Pero ninguna de estas teorías termina de explicar las cosas tan bien como lo hace la materia oscura.
Mientras se dilucida de qué está compuesta, las propiedades atribuibles a la materia oscura, aparte de su masa, podrían ayudar a explicar algunas anomalías detectadas en el fondo cósmico de microondas. El telescopio Planck midió con precisión las fluctuaciones en la temperatura de éste y con estas mediciones los científicos pudieron calcular algunos parámetros cosmológicos clave.
Los valores de dos de estos parámetros, la constante de Hubble, que describe la velocidad de expansión del universo, y el asociado con el número de galaxias en cúmulos, discrepan con los obtenidos a partir de la observación de la velocidad de expansión de las galaxias y el estudio de los cúmulos. La discrepancia es significativamente mayor que los márgenes de error y los errores sistemáticos conocidos. Caben entonces dos posibilidades: o existe un error desconocido o la composición del universo en la época del fondo cósmico de microondas era diferente a la del universo posterior y que podemos observar hoy.
Una forma de explicar la discrepancia es asumir que la materia oscura se desintegra por lo que en el universo primitivo habría habido más materia oscura que ahora. Pero, ¿es esto posible?
Para resolver esta cuestión tres investigadores de la Academia Rusa de Ciencias, Igor Tkachev, Dmitry Gorbunov y Anton Chudaykin, han analizado los datos de Planck y los han comparado con un modelo basado en la hipótesis de la materia oscura que se desintegra y con el modelo estándar ΛCDM con materia oscura estable. La comparación muestra que el modelo que incluye materia oscura inestable es más consistente con los datos observacionales. Sin embargo, también encontraron que el efecto de lente gravitacional limita mucho la proporción de materia oscura que se desintegra en el modelo.
Usando datos de observaciones de varios efectos cosmológicos, los investigadores fueron capaces de dar una estimación de la concentración relativa de los componentes de la materia oscura que se desintegran, limitándola a entre un 2 y un 5 %.
En otras palabras, esto significa que en nuestro universo habría ahora hasta un 5 % de materia oscura menos de la que había 378.000 años después del Big Bang, en la llamada era de la recombinación. Lo que aún no podemos decir es ni a qué velocidad desapareció esta materia oscura, ni si sigue desintegrándose actualmente.
Referencia:
A. Chudaykin, D. Gorbunov, & I. Tkachev (2016) Dark matter component decaying after recombination: Lensing constraints with Planck data Physical Review D doi: 10.1103/PhysRevD.94.023528
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Este texto es una colaboración del Cuaderno de Cultura Científica con Next
El artículo Un 5 % de materia oscura menos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¿Y si lo que detectó LIGO fue materia oscura?
- Los supermateriales aumentan la sensibilidad 10.000 veces en los detectores de materia oscura
- Materia oscura entre nubes intergalácticas
6943, protagonista de un cuadro de Boccioni
Mientras que en las anteriores entradas del Cuaderno de Cultura Científica Matemática pop y Vi el número cinco en oro mostrábamos obras de arte en las cuales los números son los protagonistas principales de las mismas, hoy vamos a mostrar el ejemplo de un cuadro en el que un número, en concreto el 6943, es uno de los elementos destacados de la obra. Nos estamos refiriendo a Estados de ánimo, las despedidas (1911), del futurista italiano Umberto Boccioni.
 “Estados de ánimo, las despedidas” (1911), óleo sobre lienzo, de Umberto Boccioni, en el MoMA de Nueva York
“Estados de ánimo, las despedidas” (1911), óleo sobre lienzo, de Umberto Boccioni, en el MoMA de Nueva York
Nos encontramos frente a una obra que pertenece al movimiento artístico denominado futurismo. Este es un movimiento literario, artístico y social, que surge en Italia con el Manifiesto Futurista de 1909 (publicado en Le Figaro por Filippo T. Marinetti), y que junto al cubismo dan inicio a las vanguardias artísticas, que suponen el inicio del arte moderno.
Algunas de las características fundamentales del movimiento futurista son:
i) no se limita a ser un movimiento artístico, sino que es todo un movimiento cultural, e incluso social, muy relacionado con lo literario pero que también se manifestó en la arquitectura, la música o el cine;
ii) las ideas y la filosofía del movimiento se publican en manifiestos, libros y artículos;
iii) rompe, junto al cubismo, con la tradición artística anterior (como se explica, por ejemplo, en el libro La cuarta dimensión [2]), lo que se manifiesta a través de una ruptura con la perspectiva (cubismo –estática– y futurismo –dinámica–) introduciendo diferentes puntos de vista, pero también con la utilización de técnicas novedosas y revolucionarias, como el “collage” (en estos las letras, las palabras y los números se convierten en elementos importantes, tanto por su significado, como por su imagen);
iv) la característica estética fundamental del futurismo es el dinamismo y el movimiento –para lo cual utilizan magistralmente las formas y los colores–, los futuristas querían crear un nuevo arte, y una nueva sociedad, y tomaron como referencia la nueva tecnología y las máquinas, símbolos del futuro, su fuerza, su velocidad, su energía, su movimiento, aunque también creían en la guerra y en la violencia como paso hacia ese futuro.
 “Bailarina azul” (1912), óleo sobre lienzo con lentejuelas, de Gino Severini, en la Peggy Guggenheim Collection de Venecia
“Bailarina azul” (1912), óleo sobre lienzo con lentejuelas, de Gino Severini, en la Peggy Guggenheim Collection de Venecia
 “El vuelo de golondrinas” (1913), témpera sobre papel, de Giacomo Balla, en el MoMA de Nueva York
“El vuelo de golondrinas” (1913), témpera sobre papel, de Giacomo Balla, en el MoMA de Nueva York
Respecto al autor de la obra Estados de ánimo, las despedidas, Umberto Boccioni (Regio de Calabria, Italia, 1882 – Verona, Italia, 1916), fue uno de los teóricos y máximos exponentes del futurismo italiano. Publicó en 1910 junto a Carlo Carrà (1881-1966), Luigi Russolo (1885-1947), Gino Severini (1883-2003) y Giacomo Balla (1871-1958), el Manifiesto de los pintores futuristas y La pintura futurista, manifiesto técnico futurista. Estuvo fuertemente influenciado por el Cubismo, aunque hizo de la representación del movimiento su objetivo, lo que consiguió en sus pinturas con la utilización de formas y colores, como puede observarse en cuadros como Dinamismo de un ciclista (1913), o Dinamismo de un jugador de fútbol (1911).
 “Dinamismo de un jugador de fútbol” (1913), óleo sobre lienzo, de Umberto Boccioni, en el MoMA de Nueva York
“Dinamismo de un jugador de fútbol” (1913), óleo sobre lienzo, de Umberto Boccioni, en el MoMA de Nueva York
Y también en escultura, en su conocida Formas únicas de continuidad en el espacio (1913), que hoy podemos apreciar en las monedas italianas de 20 céntimos de euro. En 1913 se implicaría cada vez más en política, siendo uno de los defensores de la entrada de Italia en la Primera Guerra Mundial. Murió en el frente al caerse de su caballo.
 “Formas únicas de continuidad en el espacio” (1913), bronce, de Umberto Boccioni, en el MoMA de Nueva York
“Formas únicas de continuidad en el espacio” (1913), bronce, de Umberto Boccioni, en el MoMA de Nueva York
Pero vayamos con el cuadro que ha llamado nuestra atención por el número 6943 que está pintado casi en el medio del mismo, Estados de ánimo, las despedidas.
 “Estados de ánimo”, las despedidas (1911), óleo sobre lienzo, de Umberto Boccioni, en el MoMA de Nueva York
“Estados de ánimo”, las despedidas (1911), óleo sobre lienzo, de Umberto Boccioni, en el MoMA de Nueva York
Este es el primero de la serie de cuadros Estados de ánimo, dedicada a la salida de un tren de la estación para realizar un largo viaje. Este cuadro está centrado en las despedidas, los otros se centran en los que parten y en los que se quedan. Los futuristas no eran partidarios de la emigración como forma de resolver el problema de Italia. El cuadro está pintado con una clara influencia cubista, como puede apreciarse en el tren, las personas que están despidiéndose y el paisaje.
En la parte central del cuadro aparece destacado, con cierto protagonismo y en color amarillo oro, el número 6943. Este número no estaba en su primera versión de la obra pero al regresar de su viaje a Paris en 1911 lo añade. Como nos dice la historiadora del arte Judith Meighan [3], la locomotora 6943 fue la última de las locomotoras de la serie 6900 fabricada por la empresa italiana Breda entre los años 1900 y 1906. Por lo tanto, ese número nos remite a un año, 1906, y a lo que fue el viaje de Boccioni a París y Rusia, dejando su época de estudiante en Roma e iniciando su vida artística. Además, la locomotora 6943 fue exhibida en París como símbolo de la velocidad y de la tecnología italiana.
 Postal con la Locomotora 6943 de los Ferrocarriles del Estado Italiano, construida por la empresa italiana Breda
Postal con la Locomotora 6943 de los Ferrocarriles del Estado Italiano, construida por la empresa italiana Breda
La tipografía del número 9643 nos recuerda a la fuente Century FB Bold Condensed (que es de tipo Serif, es decir, que incluye adornos en sus extremos) y que fue diseñada por el tipógrafo estadounidense Morris Fuller Benton (1872-1948) en 1906, convirtiéndose en una de las fuentes más famosas para los titulares de periódicos y revistas norteamericanos.
 Fuente Century FB Bold Condensed
Fuente Century FB Bold Condensed
Pero no podemos terminar esta entrada del Cuaderno de Cultura Científica sin disfrutar de otro cuadro del futurista italiano Umberto Boccioni, La ciudad se levanta (1910).
 “La ciudad se levanta” (1910), óleo sobre lienzo, de Umberto Boccioni, en el MoMA de Nueva York
“La ciudad se levanta” (1910), óleo sobre lienzo, de Umberto Boccioni, en el MoMA de Nueva York
Bibliografía
1.- Raúl Ibáñez, Los números preferidos del artista, Un paseo por la geometría, Universidad del País Vasco, 2012. (www.divulgamat.net)
2.- Raúl Ibáñez, La cuarta dimensión, ¿Es nuestro universo la sombra de otro? RBA, 2010.
3.- Judith Meighan, Tragedy to triumph: Depicting migration in Italian art 1880-1920, publicado en francés en Actes de l’histoire de l’immigration, vol. 7, 2007.
4.- Enric Satué, Arte en la tipografía y tipografía en el arte, Siruela, 2007.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo 6943, protagonista de un cuadro de Boccioni se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Retrospectiva de un cuadro: El festín de los dioses
- Aritmética afectiva
- Más matemáticas para ver y tocar
#Naukas16 Dedos de zinc para el baile de San Vito
 .
.
San Vito es el santo patrón de los bailarines. Y por eso se le relaciona con una enfermedad degenerativa terrible, la de Huntington. Carmen Agustín lo explica.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo #Naukas16 Dedos de zinc para el baile de San Vito se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- #Naukas16 Cómo escribir un libro de ciencia para niños
- #Naukas16 ¿Perdemos el sentido cuando perdemos los sentidos?
- #Naukas16 Astrofotografía
Alcohol, aqua vitae
Los humanos vienen obteniendo disoluciones alcohólicas, especialmente vino y cerveza, desde épocas prehistóricas. En estas disoluciones, donde el alcohol representa entre el 4 y el 14 %, es imposible que éste arda y eso a pesar de que el etanol, el alcohol presente en el vino y la cerveza, sí arde cuando está suficientemente puro.
 .
.
Los textos del pseudo-Llull proporcionan a comienzos del siglo XIV nuevas recetas para obtener “un alcohol que puede arder”, esto es, alcohol absoluto, a diferencia de las menciones hasta entonces, que se refieren siempre a mezclas alcohol-agua. Sin embargo, se tratan de innovaciones en la técnica, no en un descubrimiento nuevo realmente. En el siglo XII, por algún motivo, todo el mundo, en Europa y China, pareció aprender a destilar alcohol a la vez. Pero quizás el conocimiento común provenía de una fuente anterior: al-Razi.
 .
.
Efectivamente, algunos textos de al-Razi parecen indicar que había conseguido separar, al menos parcialmente, la sustancia que hacía del vino una sustancia intoxicante por medio de una destilación muy simple, e identificarla como un producto diferente. La destilación, en sí, ya era un método empleado por griegos y romanos. Todo lo que vendría después serían mejoras de la técnica, algunas revolucionarias, como las de pseudo-Llull.
La separación del etanol en un estado lo suficientemente puro como para que pueda arder tuvo que esperar a la introducción de nuevas formas y materiales en los recipientes, de la refrigeración en los sitemas de enfriamiento que permiten condensar el alcohol y en el descubrimiento de que la adición de sales al recipiente de destilación consigue “extraer” el agua de la mezcla alcohol-agua.
Los primeros intentos de añadir sales en la destilación para eliminar el agua muy probablemente estaban siguiendo una noción alquímica musulmana: una esencia seca se combina con una esencia húmeda. En este caso la alquimia funcionó. Efectivamente, algunas sales absorbían suficiente agua como para conseguir que el alcohol obtenido ardiese si se le acercaba una llama.
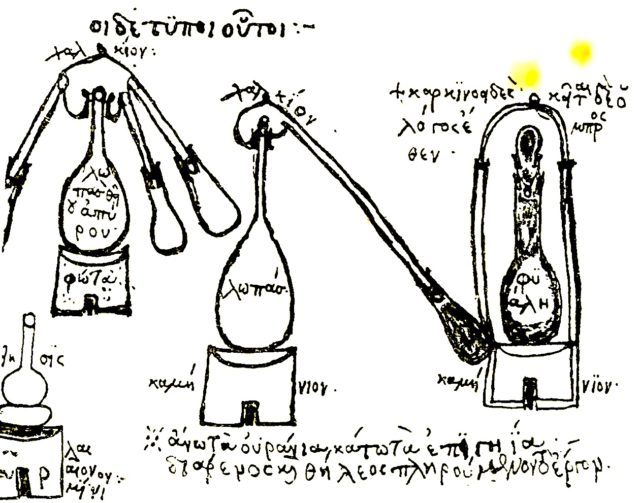 Equipo de destilación de Zósimo según un texto bizantino griego del siglo XV.
Equipo de destilación de Zósimo según un texto bizantino griego del siglo XV.
El texto europeo más antiguo en el que se menciona la preparación del alcohol es el Mappae clavicula que, realmente, es una colección de recetas que empezó a recopilarse en el siglo VII y que modificándose y ampliándose a lo largo de la Edad Media conforme era copiada y transmitida. En una de las recetas datadas en algún momento del siglo XII se lee:
“De commixtione puri et fortissimi xkok cum III qbsuf tbmkt cocta in ejus negoii vasis fit aqua quae accensa flamam incombustam servat materiam”
El químico Marcelin Berthelot, en su La chimie au Moyen Àge (La química en la Edad Media) de 1893 consiguió interpretar esta frase enigmática para muchos de una forma muy simple. Señaló que las tres palabras cifradas (en negrita en el texto) se encontraban con solo cambiar cada letra por la anterior en el alfabeto latino (romano). Así:
xkok = vini
qbsuf = parte
tbmkt = salis
Haciendo las sustituciones, el texto quedaba fácilmente entendible para un alquimista medio:
“Al mezclar un vino muy fuerte y puro con tres parte de sal, y calentando la mezcla en un recipiente adecuado para ello, el agua que se obtiene arde sin consumir el material [sobre el que se ha vertido]”
El truco del cifrado debió funcionar bien hasta el siglo XIII, porque es entonces cuando el procedimiento pasa a ser ampliamente conocido.
A partir de entonces las aplicaciones del alcohol lo convierten en una sustancia mágica, casi en la panacea. Si se aplicaba externamente ayudaba a curar heridas, secar llagas y elimar la suciedad que el agua no podía. Aplicado internamente, aliviaba el dolor y elevaba el ánimo.
En el siglo XIV Joan de Peratallada (Johannes de Rupescissa en latín, nombre por el que es más conocido) se refería al alcohol como aquae vitae (el agua de la vida) y lo prescribía como elixir tanto para el metal enfermo (con la idea de sanarlo y convertirlo en oro) como para la salud humana.
Otros practicantes del arte alquímico descubrieron que el alcohol, por su capacidad para disolver sustancias orgánicas, era un modo excelente de extraer aceites de las plantas, extractos que empezaron a investigar.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Alcohol, aqua vitae se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El alcohol de fin de semana y el ADN
- Beber alcohol produce cáncer
- Daños estructurales por consumo de alcohol en el cerebro humano
Temple por láser
El temple o templado es un tratamiento térmico superficial que se realiza a las piezas de acero, que aumenta considerablemente su dureza. El grupo de Fabricación de Alto Rendimiento de la UPV/EHU ha realizado el estudio y puesta a punto de una tecnología novedosa para llevar a cabo este proceso. Consiste en realizarlo mediante láser utilizando ópticas de barrido, lo cual lo dota de gran capacidad de adaptación a la anchura de la pieza a tratar.
 Pieza de prueba endurecida mediante láser empleando ópticas de barrido. Foto: Aitzol Lamikiz
Pieza de prueba endurecida mediante láser empleando ópticas de barrido. Foto: Aitzol Lamikiz
Mediante el temple, el acero consigue incrementar su dureza, lo cual es muy importante para las piezas de acero que requieren alta resistencia al desgaste, como los troqueles de estampación de chapa. Se realiza un proceso de calentamiento hasta unos 800-1.000 ºC, y posteriormente un rápido enfriamiento. Esto genera un cambio en la estructura del acero.
Realizar el temple utilizando un láser, al ser una fuente de calor muy localizada, permite templar solamente la superficie, dejando el núcleo de las piezas en su estado original; “de esta forma, las piezas no son tan frágiles, y al no introducir mucho calor, no se distorsiona tanto la pieza. Al final el calor lo que hace es deformar la pieza, y eso luego requiere acabarla por otros medios”, explica Aitzol Lamikiz, catedrático del departamento de Ingeniería Mecánica de la UPV/EHU y miembro del grupo de Fabricación de Alto Rendimiento que ha llevado a cabo la investigación. En la industria, se viene utilizando el proceso de temple por láser desde el año 2000. No obstante, tiene una limitación, según Lamikiz: “El láser barre una banda de anchura constante, resultando así la zona templada de anchura constante”.
Con el fin de darle mayor flexibilidad a la tecnología, este grupo de investigación de la UPV/EHU decidió evaluar la viabilidad de introducir una óptica móvil, tipo escáner, en este proceso. La óptica que utilizaron, un escáner galvanométrico, lo que hace es mover un láser muy pequeño, a gran velocidad, barriendo la superficie línea a línea. Así, se puede adaptar la anchura de templado, simplemente cambiando los parámetros en un programa. Asemejando el tratamiento del temple al proceso de pintar una pared, Lamikiz detalla que el temple por láser convencional “sería como pintar la pared con un rodillo, por lo que la anchura a la que se pinta es la de ese rodillo. Con la nueva técnica, sin embargo, cambiaríamos el rodillo por un rotulador de punta más fina”.
En la experimentación realizada, lo primero que comprobaron fue que “era posible realizar el temple mediante esa técnica. Luego fuimos viendo cómo cambia el resultado del tratamiento en función de la velocidad de movimiento del láser, la potencia utilizada, etc. Según nuestras pruebas, cuando el láser se mueve a gran velocidad, los resultados son similares a los del proceso convencional”, comenta.
Más allá de comprobar la posibilidad de utilizar esta metodología, el departamento de Ingeniería Mecánica de la UPV/EHU llevó a cabo un proyecto, denominado Hardlas, para evaluar la viabilidad del proceso, en colaboración con empresas de Euskadi y Piamonte (Italia). “El proyecto podemos decir que fue un éxito, ya que vimos que era viable, y se podía trasladar a la industria”, dice el investigador.
Aunque hayan probado la viabilidad del proceso, todavía hay pasos que faltan por dar para llegar a la industrialización. Una de las principales dificultades que han encontrado es el control del proceso: “Es muy importante conseguir que el material a tratar consiga la temperatura necesaria para que se dé el tratamiento, pero no debe superarse, porque fundiríamos el material. En nuestro proceso, al estar el láser en continuo movimiento, el control es más complejo”, explica Lamikiz. Por otro lado, las pruebas que han realizado las han llevado a cabo “en la universidad, en un equipo de laboratorio. Y para industrializar el proceso, sería importante probar con láseres más potentes, diferentes tipos de láseres, con otros materiales, etc.”, añade.
Referencia:
S. Martínez, A. Lamikiz, E. Ukar, A. Calleja, J.A. Arrizubieta, L.N. Lopez de Lacalle (2016). ‘Analysis of the regimes in the scanner-based laser hardening process’. Optics and Lasers in Engineering, 90: 72–80. DOI: 10.1016/j.optlaseng.2016.10.005.
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Temple por láser se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Caracterizando láseres de electrones libres para filmar átomos individuales
- Paneles solares orgánicos…y de colores
- La óptica se hace atómica: la lente más pequeña del mundo
Los peces en el río

Si han tenido ocasión de contemplar peces en una pecera, un estanque o, desde la orilla, en el cauce de un río, quizás haya reparado en que abren y cierran la boca de forma rítmica. Así respiran. Los movimientos de apertura y cierre de la boca, coordinados con los de los opérculos que protegen las branquias, sirven para tomar agua del exterior, hacerla pasar a través de los arcos branquiales y expulsarla después. Pero no la beben. De hecho, no tendría sentido alguno que bebiesen el agua que entra en la cavidad bucal. Es más, los peces de agua dulce han de intentar que no penetre en su cuerpo. Y como no pueden evitar que algo de agua llegue al interior, la expulsan en grandes cantidades. Veamos el porqué de todo esto.
Cuando dos disoluciones acuosas están separadas por una barrera que no permite el paso a su través de sustancias disueltas pero sí deja que pase el agua, ésta la atravesará moviéndose de donde hay mayor concentración de dichas sustancias a donde hay menor. Sus concentraciones a ambos lados de la barrera tenderán así a igualarse. Ello obedece a un fenómeno físico universal –llamado osmosis- que se manifiesta bajo diversas circunstancias.
Los peces de río viven en masas de agua de muy baja concentración salina. Por eso la llamamos agua dulce. Pero en sus fluidos corporales hay una concentración relativamente alta de sales y otras sustancias disueltas -mucho más alta que la que hay en el exterior- y han de mantenerla relativamente constante. Por ello, el agua del río tendería a entrar en el interior del pez hasta que la concentración de sustancias en sus líquidos corporales llegase a aproximarse a la exterior. Pero si eso ocurriera, el pez no sobreviviría. Por un lado, un pez no puede funcionar si la concentración de sustancias en su sangre y en sus células se reduce por debajo de cierto nivel. Y además, en ese proceso, al llenarse de agua el pez, aumentaría tanto su volumen que -en teoría al menos- podría llegar a reventar.
Los peces de agua dulce tienen una superficie corporal muy impermeable que impide la entrada de agua por esa vía. Pero no pueden ser impermeables los órganos que, por la función que desempeñan, participan en intercambios con el exterior: las branquias, que captan oxígeno y expulsan dióxido de carbono; y el sistema digestivo, que absorbe alimento. Por eso, el agua puede entrar en el organismo a través de esos órganos, y ello obliga a los peces a hacer tres cosas diferentes. Por un lado han de expulsar el agua que penetra a través de las branquias; lo hacen produciendo grandes volúmenes de orina. Por otro lado, como pierden así muchas sales –las que se escapan en la orina-, han de captar las pocas que hay en el agua y, a costa de un importante gasto de energía, transportarlas al interior; de lo contrario, los líquidos corporales acabarían teniendo una concentración similar a la del agua dulce en la que se encuentran. Y a las dos actividades anteriores han de sumar una importantísima precaución: deben evitar beber, pues sería absurdo que introdujesen así en el organismo el agua cuya entrada tratan por todos los medios de evitar.
Así pues, los peces de agua dulce –incluidos, por tanto, los de río- no beben. Tengan esto presente cuando en las celebraciones navideñas de estos días suene el popular villancico, ese que dice “mira cómo beben los peces en el río”. Eso sí, si les apetece cantar, canten. A los peces no les va a importar.
—————————————————-
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
————————————————–
Este artículo fue publicado en la sección #con_ciencia del diario Deia el 18 de diciembre de 2016.
El artículo Los peces en el río se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:#Naukas16 Las radiaciones que nunca existieron
 .
.
Lo más peligroso que hay en un laboratorio son los fantasmas. El cazafantasmas Arturo Quirantes nos lo cuenta.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo #Naukas16 Las radiaciones que nunca existieron se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- #Naukas14 Arqueología de datos
- #Naukas16 Qué pasa cuando le das un péndulo a una máquina
- #Naukas16 Si Rajoy fuese nutricionista
Veinte años de dinosaurios con plumas
 Cola de dinosaurio en ámbar. Imagen de Lida Xing et al.
Cola de dinosaurio en ámbar. Imagen de Lida Xing et al.
“Cuesta imaginar dinosaurios con plumas, pero habrá que acostumbrarse. El hallazgo es magnífico”
Este comentario de un lector tiene tan solo unos días. Se refería al reciente descubrimiento de un trozo de cola de dinosaurio no aviano (es decir, los que no son aves) cubierto de plumas y conservado tridimensionalmente en una pieza de ámbar de Birmania.
No ha sido tampoco un comentario muy repetido. Dejando a un lado las predecibles reacciones de los creacionistas, que han intentado negar el hallazgo o tergiversarlo para hacerlo encajar de alguna forma con sus creencias, parece que las personas interesadas en la ciencia se han acostumbrado ya un poco a los dinosaurios con plumas.
Y es que han pasado veinte años. Veinte años desde que se describiera el primer fósil con impresiones de algo parecido a plumaje en un pequeño dinosaurio no aviano chino. Veinte años de descubrimientos incesantes de plumas en diferentes estadios evolutivos, en especies de muy diferentes tipos, situados en muy diferentes ramas del arbusto dinosauriano. Veinte años durante los cuales los artistas, algunos rápidamente y con entusiasmo, otros despacio y a regañadientes, han ido adaptando sus representaciones de los animales extintos más famosos. Los fanáticos de los dinosaurios, mientras tanto, nos hemos dividido en pro-plumas, entusiasmados con cada nuevo hallazgo, y anti-plumas: haters con la infancia destruida por estos espantosos cambios estéticos. Según ellos, los dinosaurios con plumas “no molan” porque “parecen pollos”.
Veamos algunos de esos descubrimientos. Hagamos una selección de “dinopollos” descubiertos durante las últimas dos décadas. Pero, antes, un poco de contexto.
 Archaeopteryx, foto de 1880
Archaeopteryx, foto de 1880
En el principio solo estaba el Archaeopteryx, el “ave primigenia”. Su primer esqueleto se describió en 1863. Sus rasgos intermedios entre el típico reptil y la típica ave fueron como un enorme “¡zasca!” de la evolución a todos aquellos que la negaban. Pero Archie, el fósil transicional por excelencia, no era perfectamente intermedio en todo. Las plumas impresas en la caliza litográfica del Jurásico parecían idénticas a las plumas más complejas de las aves actuales. Y éstas son las estructuras de la piel más complejas de todos los vertebrados. Pero la teoría darwiniana explica lo complejo mediante el cambio gradual, por etapas, a partir de formas más sencillas. Si la teoría es correcta, tuvieron que haber existido animales con plumas más sencillas, en estadios evolutivos intermedios. Después de Archie pasaron más de ciento treinta años… y las protoplumas no aparecían.
Saltemos a los años 90. Había ocurrido, lógicamente, un gran progreso en paleontología, biología evolutiva, filogenia y taxonomía. El número de especies conocidas de dinosaurios era ya formidable, y también se disponía de un buen puñado de aves fósiles. Aunque no había cristalizado un consenso, muchos expertos tenían claro que el Archaeopteryx y el resto de las aves descendían de dinosaurios. Consideraban a las aves como un tipo de dinosaurio con alas, del mismo modo que los murciélagos son un tipo de mamífero. Sus estudios indicaban que los parientes más cercanos de las aves eran el Velociraptor y otros carnívoros similares.
La pequeña revolución en el conocimiento llamada Dinosaur renaissance, que había tenido lugar en las dos décadas anteriores, reconstruye a los dinosaurios como animales activos, exitosos y parecidos en conducta a las aves y los mamíferos. Este “renacimiento”se propaga hacia la cultura popular gracias a la película Parque Jurásico (1993) y a la oleada de libros, juguetes, y coleccionables que ésta genera y estimula. El furor dinosaurofílico se disparó entre niños y no tan niños. Parecía un buen momento para que comenzara el espectáculo de las plumas.
 Sinosauropteryx, foto de Sam / Olai Ose / Skjaervoy
Sinosauropteryx, foto de Sam / Olai Ose / Skjaervoy
1996. Sinosauropteryx prima. El primer espécimen fue encontrado por un granjero chino de la provincia de Liaoning. No era un pájaro como interpretaron inicialmente paleontólogos chinos, sino un diminuto carnívoro de brazos cortos, un pariente cercano del famoso Compsognathus. Sus fósiles preservaban tejidos blandos, comida (un lagarto) en el estómago y huevos listos para puesta. Cuando las fotografías llegaron al congreso de la Society of Vertebrate Paleontology en Nueva York, los paleontólogos quedaron conmocionados: el dinosaurio presentaba fibras similares a haces de pelos a lo largo del cuello, la espalda y la larguísima cola. Muy probablemente, se trataba de un plumaje de estructura primitiva.
Algunos científicos contrarios al origen dinosauriano de las aves (llamados despectivamente BAND: Birds Are Not Dinosaurs) intentaron explicar la presencia de aquellos filamentos proponiendo que eran fibras de colágeno o los restos de una cresta parecida a la una iguanas. Lo que vino después les sorprendería…
1997-1998. Protarchaeopteryx y Caudipteryx. En los fósiles de estas dos nuevas especies se habían preservado auténticas plumas, muchas y tan detalladas que no dejaban lugar a las dudas. Eran claramente plumas complejas, con su raquis (eje central) y sus barbas dispuestas lateralmente. Ambos animales poseían un abanico de estas plumas en el extremo de la cola. El Caudipteryx, además, presentaba largas plumas en la mano, plumas simétricas como las plumas primarias de las alas de las aves no voladoras. Se trataba, nuevamente dos dinosaurios no avianos procedentes de la Formación Yixian, la misma de donde procedía el Sinosauropteryx. La antigüedad era también similar: Cretácico temprano, es decir, una época posterior al Archaeopteryx. Su descubrimiento prueba que las plumas complejas estaban presentes en otros dinosaurios además de las aves.
¿Cómo reaccionaron los BAND ante el Protarchaeopteryx y el Caudipteryx? Con una genialidad (llamémoslo así). Aceptaron lo evidente: que lo que se veía en esos fósiles eran plumas. Pero dijeron que los animales eran aves y por tanto, según sus esquemas, no dinosaurios. Desgraciadamente para ellos, los análisis filogenéticos posteriores no arrojaron nunca semejante resultado.
1999. Sinornithosaurus. Liaoning siguió dándonos fósiles maravillosos. El “pájaro-saurio chino del milenio” era un dromeosáurido, carnívoro muy cercano al famoso Velociraptor, y una especie de versión en miniatura de éste. Sus fósiles presentan impresiones de plumas complejas de dos tipos que corroboran su homología con las de las aves. Este hallazgo ponía en aprietos a los fanáticos de los velocirraptores escamosos al estilo Parque Jurásico, cuyo aspecto obsoleto y ochentero se mantuvo en las secuelas de 2001 y 2015. Después del Sinosauropteryx, dibujar sin plumas a este tipo de dinosaurios carecía de sentido. Al menos desde el punto de vista del rigor científico.
1999. Beipiaosaurus. Este grandullón medía unos 2,2 metros de largo, aproximadamente el doble que los anteriores dinosaurios emplumados chinos. Y pesaba unas diez veces más. Se trata de un pariente primitivo del extraño y gigantesco Therizinosaurus. Las impresiones de la piel del Beipiaosaurus mostraron un abrigo de largas protoplumas similares a las del Sinosauropteryx, aunque mayores. Más adelante, los paleontólogos distinguieron en esta especie un tipo de fibras de apariencia aún más primitiva: gruesas, largas, huecas y sin ramificaciones. Los investigadores Richard O. Prum y Alan H. Brush habían desarrollado un convincente modelo de evolución y desarrollo de las plumas según el cual todo empieza con una “espina” hueca. Las fibras gruesas y sencillas del Beipiaosaurus se correspondían bien con ese hipotético estadio inicial.
 Psittacosaurus. Imagen de Vinther et al. 2016
Psittacosaurus. Imagen de Vinther et al. 2016
2002. Psittacosaurus. La siguiente sorpresa procedente de estos yacimientos chinos es un ejemplar de un género que ya era muy conocido: el “dinosaurio loro”. La piel está increíblemente bien preservada y es… vaya, muy escamosa. El animal estaba básicamente cubierto de pequeñas escamas poligonales y algunas placas algo más grandes y redondeadas. Pero en el dorso de la cola había algo completamente inesperado: una hilera de filamentos largos y cilíndricos, como una crin de pelos muy gruesos o de espinas muy flexibles. El Psittacosaurus era un ornitisquio y las aves surgieron en la otra rama, la de los saurisquios. Por tanto, el Psittacosaurus estaba lo más alejado evolutivamente de las aves que pueda estar un dinosaurio. La idea de que sus filamentos tuvieran algo que ver con la evolución de las plumas no convencía a los investigadores, a pesar de que su estructura encajaba con la protopluma del estadio I según la teoría de Prum y Brush. Un estudio reciente y técnicamente más avanzado ha concluido que, efectivamente, los “pelos” que adornaban la cola del dinosaurio loro eran homólogos primitivos de las plumas, coexistiendo en franca minoría con escamas.
 Microraptor. Foto de Captmondo
Microraptor. Foto de Captmondo
2003. Microraptor. Éste es un auténtico bombazo: no solo tenía plumas; tenía alas. Y no solo tenía alas; tenía ¡cuatro alas! Estamos de nuevo ante un diminuto dromeosáurido, primo del Velociraptor. Los paleontólogos chinos encontraron seis especímenes, entre ellos la joya IVPP V13352. Este esqueleto completo y articulado presenta largas plumas de vuelo asimétricas, aerodinámicas, formando la típica ala de pájaro en el brazo… y también en la pierna. El Microraptor fue reconstruido como un planeador arborícola que extendía sus cuatro extremidades formando un mismo plano. Más adelante, otros científicos cuestionaron que el animal fuera anatómicamente capaz de “despatarrarse” de aquella forma Se plantearon distintos modelos para resolver su enigmática forma de locomoción.
Pero ¿qué era este dinosaurio? ¿Una fanfarronada de la evolución que no llegó a ninguna parte mientras las aves, que ya existían, se hacían con el dominio del aire? ¿Un estadio intermedio tetráptero, como el que imaginó el naturalista William Beebe en 1915, y que también habrían atravesado los ancestros de los pájaros?
2004. Dilong. Este carnívoro de unos dos metros de largo y cubierto de estructuras precursoras de las plumas fue descrito inicialmente como tiranosauroide basal. Es decir, se interpretó como un pariente antiguo y primitivo de los tiranosaurios. Aunque ahora esa posición en el árbol evolutivo se ha revisada y no está clara, el Dilong sirvió para que nos fuéramos acostumbrando a la idea de un Tyrannosaurus rex no del todo escamoso. Realmente, los trabajos de filogenia indicaban que el rey de los dinosaurios descendía de antepasados con protoplumas.
2005. Pedopenna. Aquí tenemos un fósil consistente en un trozo de pierna, y en esa pierna puede verse una ala formada por plumas complejas. Como en el caso del Microraptor, estamos ante un posible dinosaurio tetráptero, que usaba alas tanto en brazos como en piernas para realizar un planeo o vuelo primitivo. En el el Pedopenna las plumas son más cortas y simétricas (menos aerodinámicas). Además, es más antiguo: del Jurásico. ¿Estamos ante un estadio primitivo del vuelo, o aquellas alitas traseras estaban ahí de adorno?
2006. Juravenator. Aquellos más contrariados con las dinoplumas agradecieron mucho las escamas que este pequeño carnívoro alemán presentaba en la cola y un trocito de la pata trasera. Teniendo en cuenta los avances de los años anteriores y la posición de esta especie en el árbol genealógico dinosauriano, el Juravenator debería haber estado cubierto de protoplumas. Efectivamente, dos exámenes posteriores, confirmaron la presencia de estos filamentos en la cola y otras zonas del cuerpo. Ahora sabemos que los fósiles con impresiones de escamas no excluyen en absoluto la presencia de plumas. Ojo: esto podría aplicarse aplicarse a muchos otros dinosaurios.
2007. Sinocalliopteryx. Con sus más de 2,3 metros era como una versión grande del Sinosauropteryx, aquel pequeñajo con el que iniciábamos esta lista. Este otro era un auténtico gigante en su familia: los compsognátidos. El ejemplar principal es un magnífico esqueleto casi completo y articulado, con extensas impresiones de protoplumas que permiten estudiar cómo se distribuían por todo el cuerpo: desde la cabeza hasta la punta de la cola, y ¡hasta los pies!; y con qué tamaños: eran más largas en la base de la cola, la cadera y los muslos.
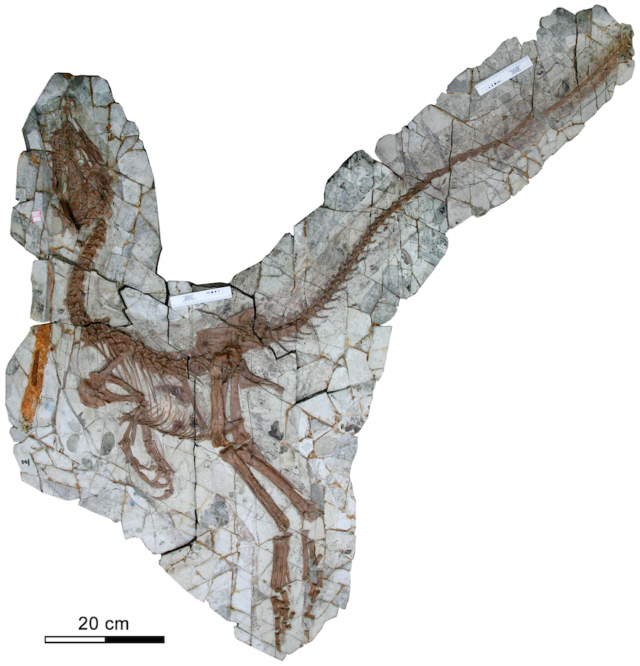 Sinocalliopteryx. Fuente: PLoS ONE
Sinocalliopteryx. Fuente: PLoS ONE
2009. Tianyulong. Otro bombazo completamente inesperado. Es un ornitisquio (recordemos: la rama de los dinosaurios en la que está el Triceratops, el Stegosaurus o el Iguanodon, pero en la que no están las aves). El fósil presenta impresiones de filamentos sencillos y bastante largos en varias zonas (bajo el cuello, en la espalda y sobre la cola). No hay ninguna razón para descartar que se trate de protoplumas del estadio I. Si tanto ornitisquios como saurisquios podían tenerlas, eso significa que, o bien evolucionaron dos veces, o bien estaban ya presentes antes de que las dos ramas se separasen, en el origen de todos los dinosaurios.
2009. Anchiornis. Del Jurásico superior y algo más antiguo que el Archaeopteryx; su nombre significa “casi pájaro”. Tenía un tamaño liliputiense: unos 34 cm de largo y un peso estimado de unos 110 gramos. Fue inicialmente clasificado como Avialae, grupo que contiene las aves y cualquier otra especie más cercana a ellas que al grupete de los velocirraptores. Otro estudio lo clasificó en el grupo del Troodon, el “dinosaurio inteligente”, famoso por el gran tamaño relativo de su encéfalo. Y un tercer trabajo llevó al Anchiornis de vuelta a Avialae. Algunos paleontólogos no tienen escrúpulos en llamarlo “bird” (ave, pájaro) aunque siempre caía fuera del propio grupo Aves.
De cualquier forma, el Anchiornis pone de manifiesto que la frontera entre dinosaurios avianos y no avianos es borrosa. Y es así como debe ser: en general, cuando dos ramas evolutivas divergen, los miembros primitivos de ambos linajes apenas se diferencian. De nuevo encontramos en esta especie plumas complejas formando superficies planas en brazos y piernas. Algo más redondeadas y cortas que en dinosaurios posteriores como el Microraptor pero, otra vez, cuatro alas.
 Sciurumimus. Imagen de Ghedoghedo
Sciurumimus. Imagen de Ghedoghedo
2011. Sciurumimus. El fósil de dinosaurio más completo de toda Europa (y seguramente el más bonito) pertenece a Otto, una cría de carnívoro jurásico de parentesco incierto. Quizá fuera un primo cercano del gran depredador Megalosaurus, o quizá un miembro primitivo del extenso grupo de los celurosaurios. Otto fue extraído de los mismos lechos de caliza que preservaron al Archaeopteryx. Su nombre científico, Sciurumimus, significa “imitador de la ardilla”. Se le llamó así por el aspecto de su cola, densamente poblada con un “pelaje” de protoplumas del estadio I.
2012 Ornithomimus. Este género norteamericano con aspecto de avestruz se conoce desde 1890; es un clásico entre los clásicos. Pero ni siquiera los dinosaurios veteranos se libran del tsunami plumífero. Gracias a Parque Jurásico se hizo famoso un pariente cercano, el Gallimimus (son aquellos herbívoros bípedos que corrían en bandada asustados por el T. rex).
Por supuesto, su piel está totalmente desnuda en la película y en las innumerables ilustraciones, esculturas y juguetes que han reproducido a esta familia de dinosaurios durante más de un siglo. El estudio de 2012 reexamina varios ejemplares de Ornithomimus y confirma la existencia de impresiones de plumas. Los autores concluyen que estaban cubiertos de plumas complejas tanto en su etapa de “polluelos” como de adultos. Estos últimos, además, tenían las plumas en el brazo dispuestas formando una ala. Siendo un animal incapaz de volar por su tamaño y proporciones, las alas probablemente servirían, como en el avestruz actual, para el cortejo. Dos años después los cines estrenaron Jurassic World . Tanto los Gallimimus generados por ordenador como los velocirraptores, en aras de una sagrada continuidad estética con las películas anteriores, vuelvieron a correr perfecta y obsoletamente desplumados.
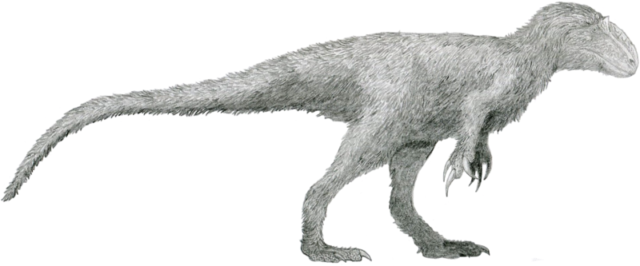 Yutyrannus, por Tomopteryx
Yutyrannus, por Tomopteryx
2012. Yutyrannus. Los yacimientos chinos de Liaoning entregaron a los científicos tres ejemplares fósiles de su depredador emplumado más formidable. Se trata de un tiranosauroide de unos nueve metros de longitud. Por comparar: el Tyrannosaurus rex, su ilustre pariente del final del Cretácico, llegaba a medir algo más de doce metros. El Yutyrannus pulveriza el récord que ostentaba el Beipiaosaurus, convirtiéndose en el dinosaurio más grande conocido cuyos fósiles presentan pruebas directas de protoplumas. Éstas tienen en los fósiles un aspecto simple, aparecen impresas en diversas zonas del cuerpo y miden hasta 20 cm de longitud. Gracias al Yutyrannus sabemos que nada impide a un carnívoro gigante llevar abrigo, y que no tiene demasiado sentido empeñarse en seguir representando desnudo a nuestro querido T. rex.
2014. Kulindadromeus. Nuestros esquemas de fueron otra vez al cuerno gracias a este dinosaurio siberiano.Hasta su descubrimento podíamos pensar que las protoplumas se habían ido complicado solo en la rama de los saurisquios, aquélla que da origen a las aves. Pero el Kulindadromeus es un ornitisquio y su piel fosilizada es una fiesta. Tiene tres tipos de escamas, incluyendo unas grandes e imbricadas que cubren la cola, y tres tipos de plumas: los clásicos filamentos simples, otros que parecen haces de fibras surgiendo de placas, y finalmente unas “cintas” más similares a plumas complejas. Si un ornitisquio primitivo como el Kulindadromeus puede presentar este nivel de complejidad, entonces debemos estar preparados para encontrar pieles emplumadas en casi cualquier otro dinosaurio, del tipo que sea. Y aceptarlo.
 Yi, por Emily Willoughby
Yi, por Emily Willoughby
2015. Yi.Terminemos con la especie más pasmosa de estas dos décadas y el dinosaurio de nombre más corto de toda la historia: el Yi qui, el dino-murciélago. Si las interpretaciones son correctas, este animalillo volaba o planeaba con unas alas completamente distintas a las de las aves y sus parientes más cercanos. Convergiendo un poco en su evolución con los murciélagos y otro poco con los pterosaurios, el Yi había logrado unas alas membranosas sustentadas por los huesos del brazo y la mano y por otro hueso nunca antes visto. En el fósil del Yi se observa una cobertura muy densa de protoplumas de complejidad intermedia. A juzgar por los huesos, sus primos Epidexipteryx y Scansoriopteryx, debían de tener unas alas similares.
Sí, los fósiles de estos otros dos géneros también presentan plumas, como tantas otros que nos hemos dejado en el tintero. Como el Changyuraptor, que es una versión gigante del Microraptor de cuatro alas. O como el Jianchangosaurus, un herbívoro de dos metros. O el Shuvuuia, un alvarezsáurido de Mongolia, o el Jinfengopteryx, un troodóntido chiquitín… Pero, en fin, habrá que acabar. En los próximos años, ¿qué otros dinosaurios se descubrirá que también tenían plumas? Haced vuestras predicciones.
Este post ha sido realizado por @Paleofreak y es una colaboración de Naukas con la Cátedra de Cultura Científica de la UPV/EHU.
El artículo Veinte años de dinosaurios con plumas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Las plumas estaban en los dinosaurios desde el principio
- ¿Se podrían recuperar los dinosaurios como en Parque Jurásico?
- El hacedor de dinosaurios
#Naukas16 El poder de las brujas

Brujas y hechiceras decían estar en contacto con fuerzas ocultas; en realidad es que sabían de botánica aplicada y les iba el teatro. Exactamente igual que Rosa Porcel.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo #Naukas16 El poder de las brujas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- #Naukas14 No me chilles que no te veo
- #Naukas15 Somos mucho más que dos
- #Naukas16 ¿Que te chupe la qué?
Qué es un dato: la longitud de un hueso
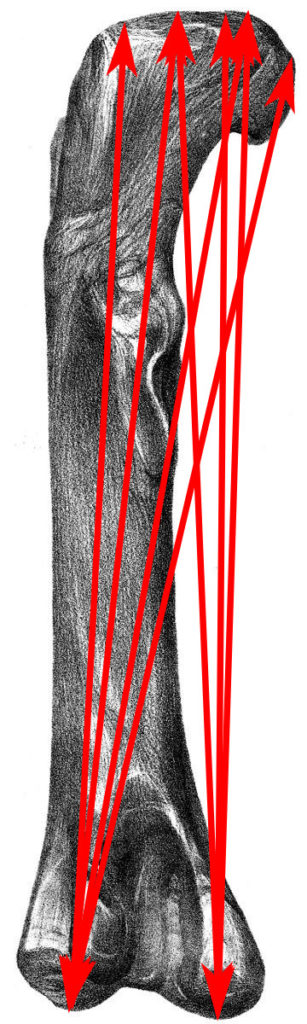 Un fémur y algunas posibilidades para determinar su longitud. Owen 1856, dominio público, modificado por Andrew Farke.
Un fémur y algunas posibilidades para determinar su longitud. Owen 1856, dominio público, modificado por Andrew Farke.
La idea de que en ciencia un dato sea una construcción teórica puede parecer absurda, o al menos contraintuitiva, pero puede ilustrarse con un ejemplo sacado en este caso de la paleontología y referido a algo que puede parecer tan objetivo y factual como es una medida de longitud. Los fósiles se miden y estas medidas se utilizan como parámetros de estudio y análisis; en muchos casos las longitudes y anchuras sirven incluso como criterio diagnóstico para separar géneros y especies. De manera que las medidas forman parte básica de las publicaciones del sector, y se dedica mucho tiempo y esfuerzo a realizarlas y registrarlas convenientemente.
Ahora bien: medir un hueso no es tan sencillo como pudiera parecer. Como cualquier elemento orgánico es muy frecuente que los huesos tengan disparidades de forma y tamaño que dependen de la vida particular del individuo concreto del que proceden. Las formas raras veces facilitan puntos terminales claros para las medidas, por lo que es muy común que algo tan aparentemente claro como una longitud pueda dar números diferentes dependiendo de dónde se coloque el calibre exactamente. Para evitarlo los científicos definen posiciones específicas, como los puntos craneométricos, para usarlos como terminales de medida y evitar ambigüedades. Pero estos puntos no son objetivos, sino que dependen de las formas concretas de los elementos anatómicos y muchas veces localizarlos es un ejercicio de juicio por parte del científico. Es decir, que los puntos terminales de medidas en teoría objetivas pueden ser bastante subjetivos.
Por si fuera poco las longitudes, anchuras y otras medidas de los elementos anatómicos son en realidad proyecciones bidimensionales de elementos tridimensionales; intentan recoger de una manera transmisible y útil lo que en realidad sirve como elemento de clasificación, que es algo tan fácil de ver y difícil de medir como es la forma. Los naturalistas son conscientes de que las relaciones entre diversos organismos se reflejan en diferencias de forma, pero resulta muy complicado objetivar esas diferencias. Los cambios que se observan a lo largo de una línea evolutiva son sencillos de ver y comprender, pero expresar esa percepción de un modo útil no es sencillo. Los intentos de analizar matemáticamente las formas a menudo resultan más sugerentes que prácticos, como cualquier estudiante de anatomía que haya quedado fascinado por ‘Sobre el Crecimiento y la Forma’ conoce de primera mano. Una cosa es comprender y muy otra medir los cambios de forma.
Yendo aún más allá las medidas y su uso como elemento de clasificación taxonómica presuponen relaciones evolutivas y que los cambios en unos y otras reflejan esas relaciones de parentesco. Al considerar cambios de tamaño o morfológicos (en términos de proporciones) como indicativos de relaciones evolutivas estamos dando por supuestos vínculos de parentesco y direcciones de evolución. El mero hecho de comparar medidas de dos seres vivos diferentes considera que sus formas son comparables y las terminales de las medidas son equivalentes. Y ni siquiera estamos entrando a considerar cuestiones estadísticas relacionadas con la intrínseca variabilidad poblacional y hasta individual de todos los seres vivos, que quizá merezca un análisis separado.
Lo que está claro es que algo tan presuntamente objetivo y científico, tan supuestamente libre de presuposiciones y condicionantes subjetivos como es medir la longitud de un elemento anatómico resulta ser un campo minado de decisiones teóricas subyacentes. Lo que podría pensarse como un dato irrefutable sobre el que construir relaciones libres de contaminación teórica es en realidad una construcción con muchos elementos subjetivos y no pocas decisiones basadas en hipótesis y teorías. Algo que conviene recordar cada vez que hagamos una medición, o creemos una hipótesis. Porque los datos más factuales y objetivos son en realidad productos de mucha teoría y no poca subjetividad.
Sobre el autor: José Cervera (@Retiario) es periodista especializado en ciencia y tecnología y da clases de periodismo digital.
El artículo Qué es un dato: la longitud de un hueso se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Relojes y cronómetros (III): el problema de la longitud
- Ciencia en primera persona: Luis Hueso
- El universo en un día: Formación del sistema solar, por Ricardo Hueso
Terraformando la Tierra

El cambio climático de origen humano es un hecho sobre el que el consenso de los científicos es prácticamente unánime. Los datos, en cualquier caso, dejan pocas opciones. La cuestión es que a la hora de hablar de cómo combatirlo parece que todo se resume en dos grandes grupos de posibilidades: por un lado emitir menos gases de efecto invernadero a la atmósfera y, por otro, desarrollar tecnologías que permitan almacenar estos mismos gases en forma sólida o líquida eliminándolos de la atmósfera. Y eso parece todo. Salvo que se piense a lo verdaderamente grande, claro, y hablemos de geoingeniería: ¿y si usamos técnicas de terraformación?
La primera vez que se habla de alterar el clima de un planeta, Venus, con la idea de terraformarlo (hacerlo habitable por seres de la Tierra) aparece en novelas de ciencia ficción de los años treinta del siglo XX. El que la ingeniería humana tiene los conocimientos necesarios para cambiar el clima de un planeta quedó patente en un artículo que Carl Sagan publicó en Science en marzo de 1961 titulado “The planet Venus”, en el que imaginaba rociar la atmósfera venusiana con algas para eliminar el dióxido de carbono y conseguir que se alcanzasen niveles de temperatura en la superficie tolerables. Esto fue antes de que se supiese que las nubes de Venus eran básicamente de ácido sulfúrico concentrado, claro.
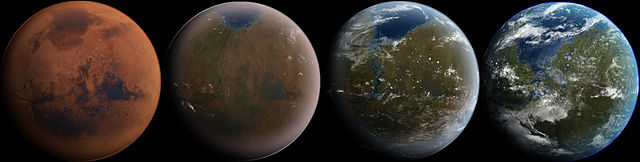 Fases de una posible terraformación de Marte. Fuente: Ittiz/Wikimedia Commons
Fases de una posible terraformación de Marte. Fuente: Ittiz/Wikimedia Commons
En 1973 Sagan volvió al tema con la publicación en Icarus de “Planetary Engineering on Mars” en el que proponía cubrir las regiones polares de materiales que absorbieran la energía incidente o de llevar plantas oscuras que creciesen en las nieves de los polos con la idea de convertir Marte en una mini-Tierra. Un estudio llevado a cabo por la NASA en 1976 llegó a la conclusión de que en Marte era posible la aplicación de una “ecosíntesis planetaria”, esto es, terraformar el planeta.
¿Y por qué no aplicar una técnica similar para revertir el cambio climático en la Tierra? Eso es lo que ha debido pensar un equipo de investigadores de la Universidad de Harvard (EE.UU.) encabezados por David W. Keith al proponer esparcir partículas de caliza o calcita (carbonato cálcico) en las capas altas de la atmósfera terrestre, a unos 20 km de altura. La calcita reflejaría y dispersaría la radiación solar incidente, con lo que se ralentizaría el calentamiento por efecto invernadero.
 Calcita en polvo con un 95 % de pureza para uso industrial. Se vende a unos 30 € la tonelada.
Calcita en polvo con un 95 % de pureza para uso industrial. Se vende a unos 30 € la tonelada.
Si bien no es la primera vez que se propone algo así (ha habido propuestas usando desde sulfatos a polvo de diamantes) el carbonato de la calcita tiene la ventaja de que neutralizaría tres ácidos presentes en la atmósfera (HNO2, HCl y HBr) que son de origen humano y forman los radicales que destruyen el ozono. En otras palabras, el uso de calcita revertiría el calentamiento global y contribuiría a reparar el agujero de la capa de ozono.
Los autores han elaborado un modelo que les permite ser muy precisos en su recomendación. El tamaño de partícula ideal es de medio micrómetro de diámetro. Habría que dispersar 5,6 millones de toneladas al año a una altura de entre 18 y 20 km, entre los 20 y los 30 º de latitud, para conseguir una dispersión homogénea. Con todo esto se conseguiría una disminución de la energía que entra al sistema de 2 W/m2, suficiente para contrarrestar los efectos del dióxido de carbono.
Aparte de que serían necesarios experimentos en altitud para confirmar que el modelo funciona en condiciones reales, experimentos a muy pequeña escala (1 kg de calcita) suficientes para comprobar cómo se dispersa la calcita y qué reacciones químicas tienen lugar realmente y a qué velocidad, los autores afirman de que es un proyecto factible incluso desde el punto de vista económico. Según sus cálculos el transporte de una tonelada de calcita costaría del orden de 1 euro y la calcita en sí es un material barato.
Más problemático parece cómo dispersar un aerosol sólido fino de forma eficaz, desde el punto de vista técnico. Pero el principal inconveniente serán los obstáculos políticos, empezando por los negacionistas del cambio climático, y de las organizaciones ecologistas (por no mencionar a los que creen en conspiraciones) para llevar a cabo un proyecto así.
Técnicamente es posible y si se diese el visto bueno ya en 2020 se podría estar ejecutando. Algo que no ocurrirá. Esperemos que no haya que recurrir a algo así de forma desesperada.
Referencia:
D.W. Keith et al (2016) Stratospheric solar geoengineering without ozone loss PNAS doi: 10.1073/pnas.1615572113
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Este texto es una colaboración del Cuaderno de Cultura Científica con Next
El artículo Terraformando la Tierra se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Así en la Tierra como en Marte: espectrógrafos y espectrómetros de masas
- Ciencia aplicada (2): El reto de simular el espacio en la Tierra
- He visto la Tierra cambiar
La traba de Pascal: geometría proyectiva y literatura
Mai quai Contii de Michèle Audin es –como la propia autora dice en su prefacio– un homenaje a la Comuna de Parísii en el que se mezcla ciencia, historia y literatura:
- ciencia porque los trece capítulos –sin contar el prefacio y el epílogo– corresponden a trece fechas de 1871, que coinciden con trece sesiones de l’Académie des sciencesiii que tenían lugar los lunes por la tarde,
- historia porque trata de un momento crucial en la historia del pueblo francés: los sesenta días de gobierno de la Comuna, detallándose lo que sucedió en el terreno revolucionario, político y cultural en París, y
- literatura porque –además de las muchas referencias literarias que pueden leerse– Michèle Audiniv escribe este texto bajo trabas oulipianas –usa pastiches, tautogramas, monovocalismos, lipogramas, etc.–, y presentando una restricción creada por ella misma, la traba de Pascal –explicada con detalle en el epílogo y en el índice– que le permite organizar los capítulos como explicaremos a continuación.
 Institut de France, lugar de reunión de l’Académie des Sciences, sito en 23 quai Conti, París
Institut de France, lugar de reunión de l’Académie des Sciences, sito en 23 quai Conti, París
Cada capítulo corresponde a un lunes, una fecha de reunión de l’Académie des Sciences. La autora narra con detalle los temas que se trataron en aquellas reuniones, tanto de tipo científico, como político o cultural. Cada fecha –cada sesión, cada capítulo– va acompañada de una figura geométrica –una elipse– con varios puntos marcados sobre ella y segmentos relacionando algunos de esos puntos. Estos nexos entre puntos van cambiando de capítulo en capítulo, al incorporar nuevos personajes o situaciones; pero aún más: cada fecha corresponde a un paso de la demostración del teorema de Pascal tal y como lo prueba la propia autora en su libro [Michèle Audin, Géométrie, Edp-Sciences, 2006, segunda edición].
El teorema de Pascalvi es un enunciado de geometría proyectiva que dice –el enunciado y la prueba son los que Michèle Audin utiliza en el texto–:
Sea C una cónica propia de imagen no vacía y sean A, B, C, D, E y F seis puntos sobre esta cónica. Sean N=(AF)∩(ED),M=(AB)∩(CD) y L=(CF)∩(EB). Entonces los puntos L, M y N están alineados.
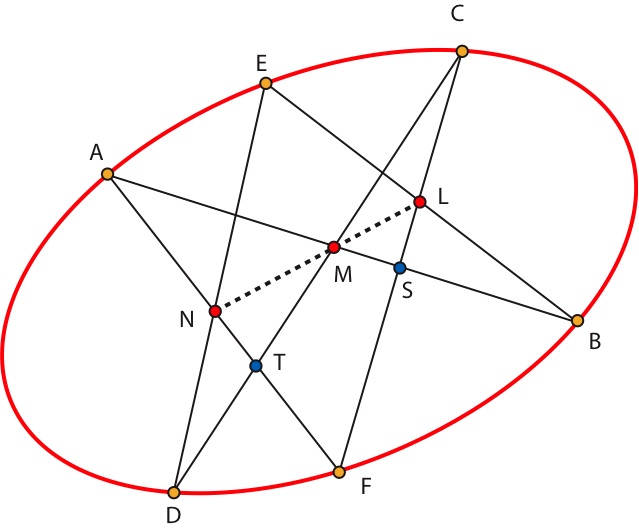 © Michèle Audin
© Michèle Audin
Demostraciónvii:
Sean S=(AB)∩(CF)yT=(CD)∩(AF). Se tiene queviii
[S,L,C,F]=[BS,BL,BC,BF]=[BA,BE,BC,BF]=[DA,DE,DC,DF]=[A,T,N,F].
Sea K=(LN)∩(AB). La perspectividad de centro K que envía CF sobre AF ,envía S sobre A, L sobre N y F sobre F. La imagen de C es entonces T. Así K ∈ CT, es decir CD. Por lo tanto K=M. CQD
Esta demostración va a ser la que estructure cada capítulo, es decir, el enunciado junto a su prueba, divididos en trece pasos, establecerán personajes y relaciones.
—oOo—
13 DE MARZO
SEA C UNA CÓNICA PROPIA DE IMAGEN NO VACÍA
(en este caso C es una elipse)
 © Michèle Audin
© Michèle Audin
Michèle Audin comienza su historia el 13 de marzo de 1871, describiendo el Mai quai Conti –sede de l’Académie des sciences– de manera exhaustiva, sin olvidarse de hablar de elipses, semicírculos, hélices, etc. La autora se pregunta sobre lo que podría estar sucediendo, sobre qué conversaciones se estarían manteniendo –el ejército prusiano acechando, posiciones políticas, etc.–, sobre lo que hicieron los académicos antes de llegar a la reunión, que calles atravesaron para llegar a la Academia desde sus casas… A través de los documentos archivados en la Academia, se puede saber quienes asistieron a cada reunión, los temas que trataron, las discusiones mantenidas, el tiempo que estuvieron reunidos, y todo tipo de detalles recogidos en las actas… hablaron de ciencia, de la situación política, de la visita de personajes del ámbito científico o literario, etc.
Este capítulo se presenta con la figura de una elipse –de la que habla también al describir el edificio, comentando que las cónicas eran muy valoradas por los arquitectos de la época–, que se irá completando durante el relato –como ya hemos comentado– añadiendo puntos y segmentos uniéndolos a medida que la narración progrese y los personajes se vayan relacionando.
Se habla, por ejemplo, del matemático Camille Jordan y su artículo Sur la résolution des équations les unes par les autres, más extenso que la media habitual de notas, pero que se publicaría de cualquier modo en el volumen 72 de los Comptes rendus de la Academia.
—oOo—
20 DE MARZO
Y SEAN A, B, C, D, E Y F SEIS PUNTOS SOBRE ESTA CÓNICA.
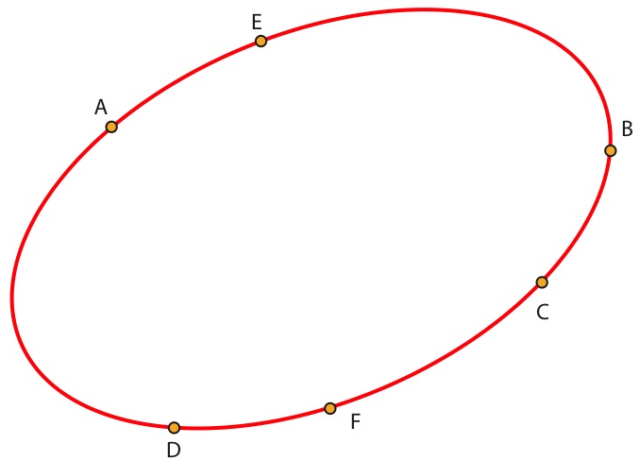 © Michèle Audin
© Michèle Audin
La autora presenta a seis de los personajes –su aspecto, sus posiciones políticas y sociales, sus vidas y algunas de sus aportaciones a la ciencia– que participaron en la reuniones durante el mes de marzo y coloca seis puntos en la elipse –que permanecerán durante toda la historia–: Charles Hermite (A), Joseph Bertrand (B), Michel Chasles (C), Charles Delaunay (D), Léonce Élie de Beaumont (E) y Hervé Faye (F). Describe de manera exhaustiva lo sucedido en la reunión, comentando en particular una visita de Victor Hugo a París para enterrar a su hijo brutalmente asesinado en las revueltas.
—oOo—
27 DE MARZO
SEAN N=(AF)∩(ED),
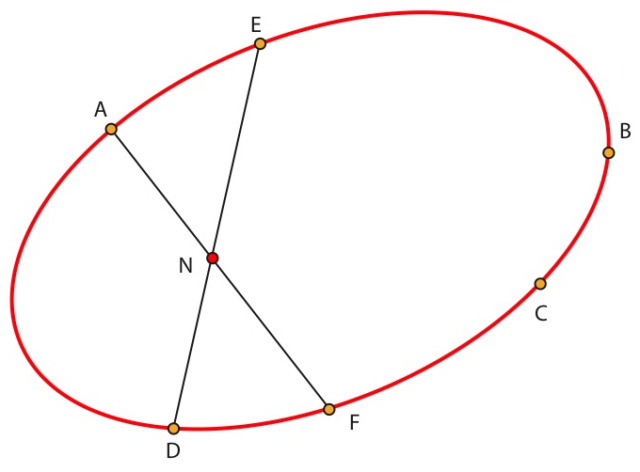 © Michèle Audin
© Michèle Audin
El astrónomo y geómetra Simon Newcomb (N) visita París para realizar observaciones y cálculos en l’Observatoire. Aunque no se sabe si encontró a Hermite (A) o Faye (F) –Hermite, el matemático principal y Faye, astrónomo– la autora comenta que probablemente ellos quisieron conocer al americano, y juega con la (A) de Hermite y la (F) de Faye a través de un divertido tautograma –este juego se repetirá en cada punto de intersección–:
Simon Newcomb, astronome américain, amateur d’algèbre, actif et aguerri, accueilli par l’Académie et accoutumé à ses alentours, affolé par l’ampleur de l’anarchie, accablé, familier de Faye, aux peu fictives facilités, fuyant frileusement la foison des fédérés faméliques, les farandoles de farouches fantassins fourbus, les fangeux et funestes faubourgs, fuyant la France.
colocando a Newcomb (N) en el punto medio del segmento que une (A) y (F).
Newcomb debía conocer a Delaunay (D) –gran especialista sobre la Luna y sus movimientos– y en vez de entregar a Léonce Élie de Beaumont (E) –el Secretario Perpetuo– el documento con sus medidas, lo llevó a la reunión del 3 de abril para terminar de redactar y completar su texto. La autora traza el segmento entre Delaunay (D) y Élie de Beaumont (E) –que como debía ser, pasa por (N)–, y dedica otro tautograma –esta vez en D y E– a Newcomb.
Hablando de la luna, se cita entre otros al astrónomo y matemático Urbain Le Verrier y al escritor Jules Verne. Y también aparecen destacados matemáticos –y alguna de sus aportaciones– como Joseph Liouville o Augustin Louis Cauchy.
—oOo—
3 DE ABRIL
M=(AB)∩(CD),
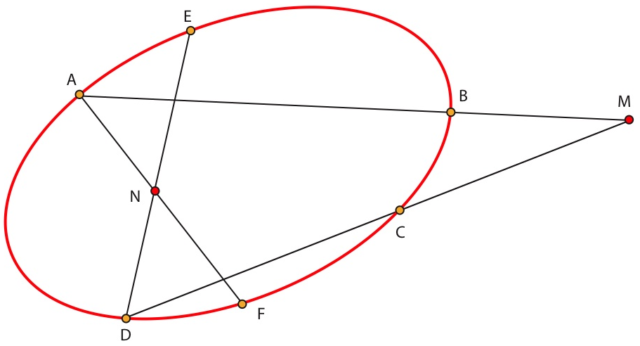 © Michèle Audin
© Michèle Audin
Un nuevo punto aparece –M, de‘moi’, la narradora– en la figura que rige el teorema de Pascal: Madame Hermite, la esposa de Charles Hermite (A) era hermana de Joseph Bertrand (B), aunque los dos científicos nunca llegaron a entenderse. Chasles –autor del Traité des coniques– y Delaunay estaban unidos por la Luna. Así. la (M) se genera a partir de la (A) y la (B), o a partir de la (C) y la (D).
La narradora –el yo, moi, que aparece–, confiesa mirar a Hermite (A) y Bertrand (B) y admirar a Chasles (C) y Delaunay (D), y lo expresa a través de un tautograma en A y en B… seguido de otro en C y D.
La autora realiza además un precioso homenaje al conocido Je me souviens de Georges Perec… con recuerdos sobre literatura, sobre derechos de las mujeres reconocidos por la Comuna, etc., transmitiendo lo vivido en París durante el mandato de la Comuna. Además, como ‘matemática y preocupada de elevar el nivel científico y cultural de sus lectores’, la narradora se permite aclarar algunos de los puntos matemáticos tratados en esta sesión de la Academia.
—oOo—
10 DE ABRIL
Y L=(CF)∩(EB).
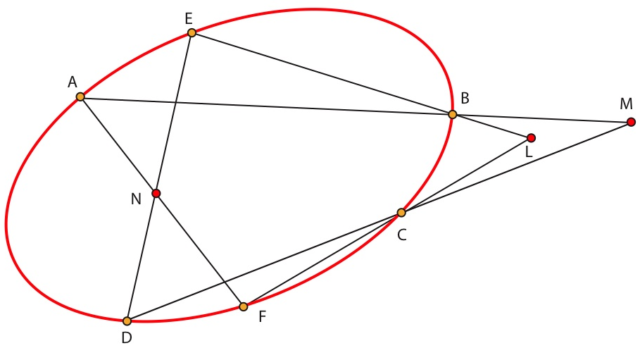 © Michèle Audin
© Michèle Audin
Aparece en la historia el periodista Prosper-Olivier Lissagaray (L), testigo de los acontecimientos y autor de Histoire de la Commune de 1871, publicado en 1896. Lissagaray no habría oído –probablemente– nunca hablar de Chasles (C) ni de Faye (F) –un tautograma en C y F le describe– pero habló en sus publicaciones de Bertrand (B) y de Élie de Beaumont (E) –otro tautograma en B y E sirve para trazar mejor a este personaje–.
Gustave Flourens es miembro de la Comuna y Lissagaray habla en particular de él y de su asesinato.
En la sesión de la Academia se habla de botánica, y Chasles continúa demostrando teoremas sobre cónicas.
—oOo—
17 DE ABRIL
ENTONCES LOS PUNTOS L, MY NESTÁN ALINEADOS.
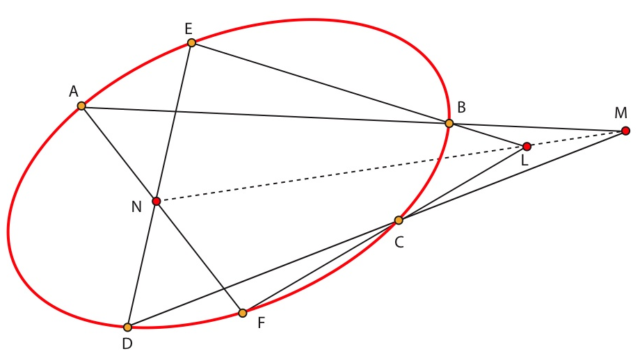 © Michèle Audin
© Michèle Audin
Con esta declaraciónix:
Qui suis-je, moi ? Qui suis-je, pour pouvoir raconter cette histoire ? Parler en même temps, presque d’une même phrase, de Prosper-Olivier Lissagaray et de Simon Newcomb ?
se traza una línea discontinua –que desaparecerá en el siguiente capítulo, ya que es el enunciado que se desea probar– entre la narradora (M), Lissagaray (L) y Newcomb (N). Un ‘tautograma’ mezclando la L con la N permite seguir la descripción del periodista y el científico.
Aparece –entre otras– una fotografía de Sofía Kovalevskaya, que habla de cómo está asistiendo a un momento histórico en París, de cómo ayuda a cuidar a los heridos y de su asistencia a las sesiones de la Academia.
—oOo—
24 DE ABRIL
SEAN S=(AB)∩(CF) Y T=(CD)∩(AF).
(comienza la demostración del teorema)
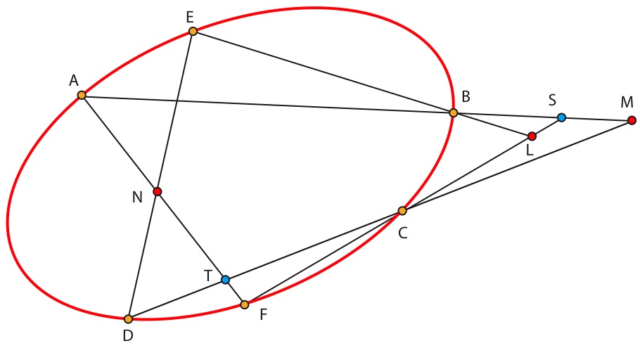 © Michèle Audin
© Michèle Audin
Desaparece la línea discontinua uniendo N, L y M –este es el comienzo de la demostración del teorema de Pascal, que dice precisamente que esa línea existe– y aparecen dos nuevos puntos: T y S.
(S) es el secretario secreto –que relata las sesiones de la Academia en elJournal Officiel de la Commune– no ha visto en esta sesión ni a Hermite (A) ni a Bertrand (B), pero si a Chasles (C) y no a Faye (F). Se trazan los segmentos entre A y B –que también pasa por M– y entre F y C –que también pasa por L–, que se cortan en S, y nuevos tautogramas en A y B y en F y C ayudan a describir al secretario.
Se habla en particular de cómo ‘gente loca’ envía demostraciones –por ejemplo del teorema de Fermat a la Academia–; así (T) representa tanto a este periodista que firma de manera anónima como a todos los que escriben a l’Académie des sciences con locas demostraciones y absurdos comentarios: T pasa por el segmento que une A y F –que pasa por N– y por el segmento que une D y C –que pasa por M–: los tautogramas en A, F, D y C ayudarán a describirlos.
… Y Chasles continúa con sus demostraciones sobre cónicas.
—oOo—
1 DE MAYO
SE TIENE QUE [S,L,C,F]=[BS,BL,BC,BF]
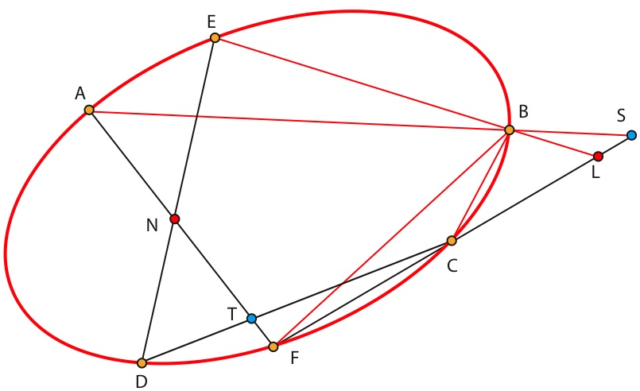 © Michèle Audin
© Michèle Audin
En la cónica desaparece M, la narradora; la de hoy es una jornada de caos, de dura batalla en la calle y de fusilamientos. Se relaciona a Bertrand (B) –que no ha acudido a la sesión de la Academia, y de diversas maneras– con el secretario secreto (S), con Lissagaray (L), con Chasles (C) y con Faye (F).
—oOo—
8 DE MAYO
=[BA,BE,BC,BF]=[DA,DE,DC,DF]
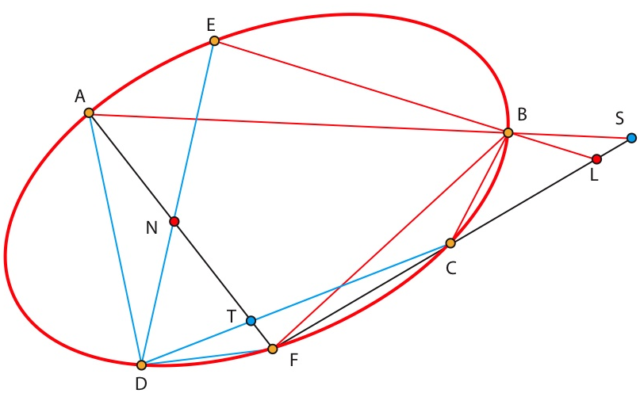 © Michèle Audin
© Michèle Audin
El 8 de mayo, Bertrand participa en la sesión de la Academia. No estaban ni Hermite (A) ni Faye (F), pero si Élie de Beaumont (E) y Chasles (C).
—oOo—
15 DE MAYO
=[A,T,N,F].
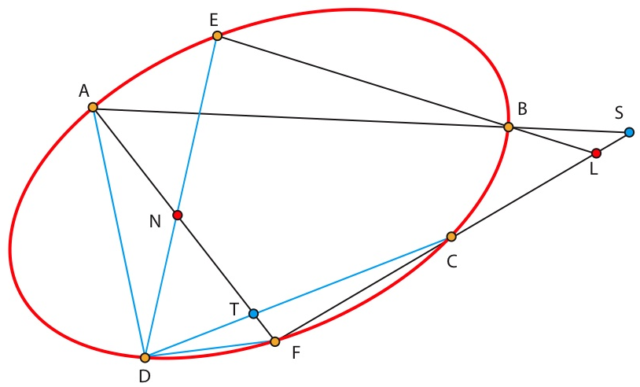 © Michèle Audin
© Michèle Audin
Es la última reunión de la Academia durante el gobierno de la Comuna, antes de la Semana Sangrienta (21 a 28 de mayo). Desaparecen las líneas entre (B) y (C) y entre (B) y (F), y las que el 8 de mayo estaban en rojo, cambian de color.
La narradora da el listado de los pocos asistentes a la reunión, entre ellos Antoine-Joseph Yvon Villarceau, conocido por una famosa construcción relacionada con el toro.
—oOo—
22 DE MAYO
SEA K=(LN)∩(AB).
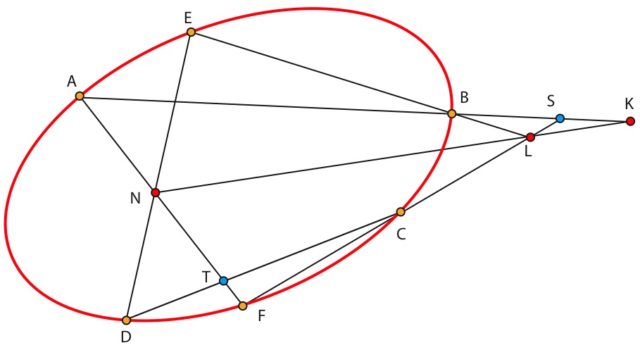 © Michèle Audin
© Michèle Audin
Aparece de nuevo a Sofía Kovalevskaya (K), que ya no está en París. Está relacionada con Newcomb (N) –ambos leen a Laplace– y con Lissagaray (L) –ella fue una de las mujeres de la Comuna–. Sofia fue también colega de Hermite (H) y de Bertrand (B), ya que tras su tesis, todo su trabajo y la demostración del teorema de Cauchy-Kovalevskaya, adquirió el estatus de matemática profesional.
—oOo—
29 DE MAYO
LA PERSPECTIVA DE CENTRO K QUE ENVÍA CF SOBRE AF ENVÍA S SOBRE A, L SOBRE N Y F SOBRE F. LA IMAGEN DE C ES ENTONCES T.
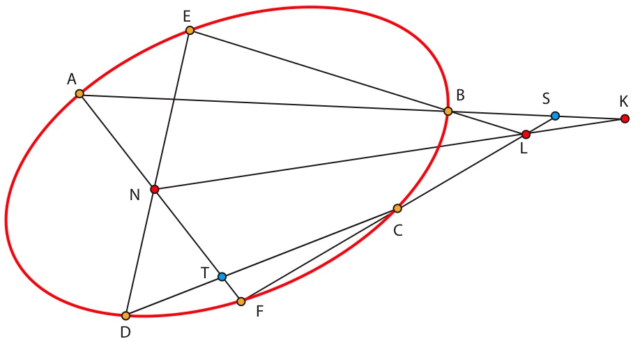 © Michèle Audin
© Michèle Audin
Como el lunes anterior, no hay reunión en la Academia. Todo ha terminado para la Comuna en París.
—oOo—
5 DE JUNIO
ASÍ K ∈ CT, ES DECIR CD. POR LO TANTO K=M.
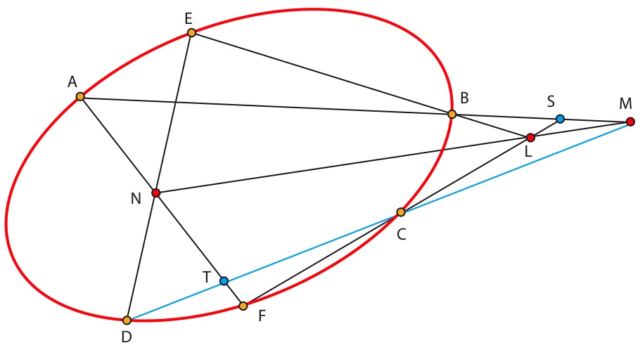 © Michèle Audin
© Michèle Audin
Tiene lugar una reunión en la Academia, en la que se habla poco de ciencia y más de la masacre cometida en París. Y se ve que (K)=(M), es decir, la narradora ha sido Sofía Kovalevskaya… el teorema-homenaje está demostrado, homenaje a las mujeres de la Comuna,… como Sofía. CQD
AGRADECIMIENTO: Quería agradecer a Michèle Audin –además de esta maravilla de texto– el haberme permitido utilizar las imágenes que acompañan a Mai Quai Conti.
Notas:
i El título es un lipograma: no se emplea la letra ‘e’, como en La Disparition de Georges Perec.
ii La Comuna de París –La Commune de Paris– fue un movimiento insurreccional que gobernó esta ciudad entre el 18 de marzo y el 28 de mayo de 1871, instaurando un proyecto político popular autogestionario. Regentó París durante 60 días promulgando, una serie de decretos revolucionarios –como la autogestión de las fábricas abandonadas por sus dueños, la creación de guarderías para los hijos de las obreras, la laicidad del Estado, la remisión de los alquileres impagados o la abolición de los intereses de las deudas–, que en su mayoría respondían a la necesidad de paliar la pobreza generalizada que había causado la guerra. La Comuna fue reprimida con extrema dureza: tras un mes de combates, el asalto final al casco urbano provocó una dura lucha en la calle–la denominada Semana Sangrienta, Semaine sanglante– del 21 al 28 de mayo; el balance final fue de unos 30.000 muertos y el sometimiento de París a la ley marcial durante cinco años. La Comuna pedía:
El reconocimiento y la consolidación de la República como única forma de gobierno compatible con los derechos del pueblo y con el libre y constante desarrollo de la sociedad. La autonomía absoluta de la Comuna, que ha de ser válida para todas las localidades de Francia y que garantice a cada municipio la inviolabilidad de sus derechos, así como a todos los franceses el pleno ejercicio de sus facultades y capacidades como seres humanos, ciudadanos y trabajadores. La autonomía de la Comuna no tendrá más límites que el derecho de autonomía igual para todas las demás comunas adheridas al pacto, cuya alianza garantizará la Unidad francesa.
Declaración de la Comuna de París al Pueblo Francés, 19 de abril de 1871
iii La Academia de Ciencias de Francia –l’Académie des sciences– es la institución que: Anima y protege el espíritu de la investigación, y contribuye al progreso de las ciencias y de sus aplicaciones. Creada en 1666, durante el reinado de Luis XIV, contó inicialmente con científicos como René Descartes, Blaise Pascal y Pierre de Fermat.
iv Perteneciente al grupo OuLiPo desde 2009.
v Os recomiendo que entréis a verlo en http://blogs.oulipo.net/ma/: el texto va acompañado de una extensa colección de documentos gráficos.
vi El teorema de Pascal –o Hexagrammum Mysticum Theorem– es un teorema de geometría proyectiva que generaliza el Teorema del hexágono de Pappus y es el dual proyectivo del Teorema de Brianchon. Fue descubierto por Blaise Pascal en 1639, cuando tenía tan solo dieciséis años.
vii Para las nociones de geometría proyectiva que aparecen, se puede consultar, por ejemplo, el libro Geometríade Carlos Ivorra Castillo, disponible gratuitamente en pdf.
viii Dados cuatro puntos distintos A, B, C y D sobre una recta, su razón doble o anarmónica [A,B,C,D] es el cociente de AC . DB entre AD . CB.
La razón doble o anarmónica de cuatro rectas concurrentes OA, OB, OC, OD es [OA,OB,OC,OD], el cociente de sen(AOC) . sen(DOB) entre sen(AOD) . sen(COB).
Se puede probar que: La razón doble de un haz de cuatro rectas es igual a la razón doble de cuatro puntos alineados en los cuales cualquier transversal que no pase por el vértice corta las cuatro líneas.
Además, si O y P son puntos sobre una cónica, [OA,OB,OC,OD]= [PA,PB,PC,PD].
ix ¿Quién soy yo? ¿Quién soy para poder contar esta historia? Hablar al mismo tiempo, casi con una misma frase, de Prosper-Olivier Lissagaray y de Simon Newcomb?
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo La traba de Pascal: geometría proyectiva y literatura se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La botella de Klein: geometría ‘palindrómica’
- Quad: pura geometría
- La geometría de los ‘cristaloides’, según Léopold Hugo
#Naukas16 ¿Que te chupe la qué?

Como es evidente por el título, Alfred López nos habla de qué hacer si te muerde una serpiente (o cualquier otro animal) venenosa.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo #Naukas16 ¿Que te chupe la qué? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- #Naukas16 Astrofotografía
- #Naukas16 Volando voy y casi no vengo porque en la gasolinera yo me entretengo
- #Naukas16 Conviviendo con robots
Llull no fue alquimista
Ramon Llull, el siervo de Dios, el beato por culto inmemorial, el misionero, el filósofo, el poeta, el místico, el teólogo, el pionero de las letras catalanas, el doctor iluminado, no fue alquimista. De hecho condenó las prácticas asociadas a la alquimia. Pero su nombre consta como autor de varios textos alquímicos que aparecieron tras su muerte. Textos que están a la altura de su genio.
Ramon nació en 1232, año arriba, año abajo, en Palma, en la recién conquistada isla de Mallorca, de padres barceloneses pertenecientes a la pequeña nobleza catalana. Criado en la corte mallorquina fue primero poeta, después estudioso y finalmente escritor en catalán, latín y árabe. Se casó y llevó la perfecta vida del cortesano, incluida la persecución y enamoramiento de doncellas, hasta que a los 30 años, inspirado por varias visiones de la crucifixión de Jesús, Llull lo dejó todo, propiedades y familia (tuvo dos hijos), y dedicó sus energías, esfuerzos y talento a la teología, las lenguas y la mística.
 Llull argumentando según Thomas le Myésier en “Electorium parvum seu breviculum” (posterior a 1321). Nótese el uso de las letras como símbolos proposicionales lógicos.
Llull argumentando según Thomas le Myésier en “Electorium parvum seu breviculum” (posterior a 1321). Nótese el uso de las letras como símbolos proposicionales lógicos.
Llull desarrolló una forma de filosofía teológica en la que relacionaba todas las formas de conocimiento y, por tanto, demostraba la presencia de Dios en el universo. Su presentación era muy original: usaba tablas muy complejas donde interrelacionaba proposiciones teológicas.
 Llull aprendiendo el árabe con su esclavo musulmán y lo que sucedió después, según Thomas le Myésier en “Electorium parvum seu breviculum” (posterior a 1321)
Llull aprendiendo el árabe con su esclavo musulmán y lo que sucedió después, según Thomas le Myésier en “Electorium parvum seu breviculum” (posterior a 1321)
También era de la convicción de que a los musulmanes, población mayoritaria en la Mallorca en la que creció, se les podía convertir usando la lógica para refutar el islam, por lo que era de la opinión de que si había que recuperar los Santos Lugares era mejor hacerlo por la predicación que militarmente (Llull nació tras la sexta cruzada y fue contemporáneo de la séptima, la octava y la novena). Como parte de su autoformación, Llull buscó los medios para aprender el árabe (para ello compró un esclavo musulmán apropiado) e intentó organizar una escuela de lenguas orientales de tal manera que los misioneros pudiesen predicar a los musulmanes en su propia lengua.
Pero todos estos esfuerzos tuvieron un éxito muy limitado. Tan limitado que Llull murió apedreado en Argelia por el mismo grupo de musulmanes a los que intentaba convertir.
Fue probablemente el misticismo de Llull (que culmina en el Llibre d’amic e amat incluido dentro del Llibre d’Evast e d’Aloma e de Blaquerna son fill publicado en Montpellier en 1283) y su lógica compleja y críptica para la inmensa mayoría los que atrajeron a los alquimistas a su órbita, y a que terminaran adoptando su nombre como el de uno de los suyos, dando comienzo de esta manera el proceso casi milagroso de la multiplicación de las personalidades de Llull.
Los textos sobre alquimia en los que aparece Llull como autor están fechados años después de su muerte (probablemente) en 1316. Si bien es posible que fuesen obra suya que no se atrevió a publicar por lo comprometido que hubiese sido dedicarse a la alquimia, no parece probable debido precisamente al enfoque tan centrado en la lógica y la palabra de Llull.
 Recetas de R. Lullius (atribuido) en el “Ymage de Vie”, finales del siglo XV. Fuente: Wellcome Library, London.
Recetas de R. Lullius (atribuido) en el “Ymage de Vie”, finales del siglo XV. Fuente: Wellcome Library, London.
Efectivamente, sea quien sea el autor, las obras alquímicas que llevan el nombre de Llull son dignas de destacar dentro de la alquimia, paradójicamente, menos mística, y sí como continuación de las muy prácticas y empíricas de al-Razi o Bacon. Todas estas obras contienen relaciones sistemáticas de la teoría y práctica de la alquimia y en ellas están llamativamente ausentes las alegorías y la oscuridad deliberada de obras posteriores.
De hecho, el autor (posiblemente Ramon de Tàrrega) es tan anacrónicamente sistemático que emplea letras del alfabeto para simbolizar los principios, las sustancias y las operaciones alquímicos, y los presenta en tablas. No solo eso, las recetas se dan como combinaciones de esas letras, incluidas recetas para unos productos que aparecen por primera vez en la literatura: ácidos minerales y un alcohol que puede arder.
Llull no será el autor, pero si lo fuese estas obras no desmerecerían en nada a su genio.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Llull no fue alquimista se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Nanopartículas para la consolidación del fuerte español de Bizerta
El patrimonio histórico-artístico, además de suponer un importante legado sociocultural es hoy en día uno de los activos más importantes en la industria relacionada con el turismo. Debido al paso del tiempo y a su exposición a diferentes procesos de deterioro, se hace necesaria su intervención para garantizar su conservación futura. “La investigación en nuevos tratamientos es hoy por hoy el ámbito más importante dentro del campo de la conservación científica, y el uso de nanopartículas, el más desarrollado”, explica Ainara Zornoza, investigadora del departamento de Física Aplicada I de la Escuela Técnica Superior de Arquitectura de la UPV/EHU, siendo esta investigación parte principal de su tesis doctoral, y autora del presente estudio dirigido por la Doctora Paula López-Arce investigadora del Museo de Ciencias Naturales (CSIC) y realizado en el Instituto de Geociencias del CSIC (CSIC-UCM).

Con el objetivo de evaluar el efecto consolidante del producto convencional más empleado en la actualidad en restauración arquitectónica y arqueológica, por un lado, y los productos más novedosos basados en nanoestructuras y nanopartículas, por otro, en una piedra muy empleada en construcciones arquitectónicas de la cuenca mediterránea, la calcarenita bioclástica, serealizó un estudio comparativo en el Fuerte Español de Bizerta (Túnez), un bastión del siglo XVI situado en la cima de una colina en Bizerta. El material pétreo muestra un alto grado de deterioro, causado por el tipo de composición mineralógica y la porosidad del material, que se ha visto afectada por la acción de la niebla salina y los inadecuados morteros usados en restauraciones anteriores”, detalla.
 .
.
Tras el diagnóstico del estado del material, procedieron a la aplicación y comparación de los productos consolidantes. Fueron cuatro los estudiados, tanto in situ como en laboratorio. El primero fue el silicato de etilo, “que es el más utilizado hoy en día, y forma una estructura reticular semejante a la del sílice en el interior de la estructura porosa del sustrato”. Otro consistió en un producto nanoestructurado, desarrollado por la Universidad de Cádiz, que, aplicado a un tipo de producto semejante al anterior, evita que este se craquele (una de las principales desventajas de ese tipo de productos). Asimismo, realizaron pruebas con dos productos basados en nanopartículas: por un lado, una dispersión acuosa de nanopartículas de sílice, que genera gel de sílice inorgánico dentro del sistema poroso, y el otro está compuesto pornanopartículas de hidróxido cálcico, que ” al exponerse al dióxido de carbono atmosférico (CO2) bajo condiciones de humedad, reacciona y se convierte en carbonato cálcico siendo el material constitutivo de las rocas carbonáticas originales”, explica la investigadora.
 .
.
Para el análisis del efecto de cada producto, midieron multitud de aspectos, como la morfología de la superficie con microscopio electrónico, en nivel de consolidación, el nivel de dureza conseguido, los cambios en el comportamiento hídrico y los cambios de color producidos. Teniendo en cuenta el conjunto de resultados, “podríamos dividir los productos en dos grupos”, comenta. En el caso del silicato de etilo y el nanoestructurado, sobre todo en el ambiente más húmedo, aumentan mucho las propiedades mecánicas, pero, sin embargo, producen una capa hidrófoba superficial y ocluye los poros. “Esto evita que el agua que llega del exterior penetre, pero, a su vez, no permite la salida del agua que llega por ascensión capilar, por lo que esa agua acumulada en el interface entre las zonas consolidadas y las zonas sin consolidar puede generar deterioros físicos, químicos y biodeterioro”, añade.
En los productos basados en nanopartículas, la mayor diferencia estriba en que lo que crean son microporos; eso no ocluye totalmente los poros, por lo que permite la salida de agua. En el caso de las nanopartículas de sílice, Zornoza especifica que “los resultados son mejores en condiciones secas, ya que se comporta como un gel que absorbe y expulsa humedad según la humedad ambiental”. Las nanoparticulas de hidróxido cálcico, por su parte, han sido las que han generado los resultados más moderados”.
A la vista de estos resultados, la investigadora destaca que la cuestión no es “establecer cuál es el mejor producto para la restauración, sino describir el comportamiento de cada uno de ellos dependiendo de las condiciones ambientales en las que se encuentre la obra y las que artificialmente se podrían generar, las características del sustrato, etc., para escoger el producto más adecuado según las necesidades específicas de cada caso y los cambios que producen los distintos productos dado que el efecto final depende de muchos factores”.
Esta investigación ha querido crear puentes entre el ámbito investigador y el de los restauradores, que hoy por hoy ” siguen estandobastante divididos: Por una parte, la comunidad científica sigue investigando, realizandopublicaciones sobre diferentes productos y sacando nuevos productos al mercado, pero, por otra parte, los conservadores-restauradores, en general, opinan que estas investigaciones no suelen ser extrapolables a aplicaciones reales y los nuevos productos no son ampliamente utilizados. Nosotros hemos intentado hacer que estas investigaciones sean reales y aplicables utilizando los productos disponibles en el mercado y realizando tratamientos lo más parecidos posibles a aplicaciones reales. Aunque es verdad que es algo muy complejo, porque estamos hablando de intervenir en patrimonio inmueble, y habiendo tantos factores que influyen en el resultado final de las intervenciones al mismo tiempo, resulta muy difícil aventurarse a cambiar la forma de trabajo e introducir nuevos productos”.
Referencias:
Zornoza-Indart, A., Lopez-Arce, P., Leal, N., Simão, J., & Zoghlami, K. (July 2016). Consolidation of a Tunisian bioclastic calcarenite: From conventional ethyl silicate products to nanostructured and nanoparticle based consolidants. Construction and Building Materials, 116, 188-202. doi: 10.1016/j.conbuildmat.2016.04.114
Zornoza-Indart, A., Lopez-Arce, P., López-Polin, L. (November 2016). Durability of traditional and new nanoparticle based consolidating products for the treatment of archaeological stone tools: Chert artifacts from Atapuerca sites (Burgos, Spain). Journal of Cultural Heritage. doi: 10.1016/j.culher.2016.10.019
Zoghlami, K., Lopez-Arce, P., and Zornoza-Indart, A. (December 2016). Differential Stone Decay of the Spanish Tower Façade in Bizerte, Tunisia. Journal of Materials in Civil Engineering. doi: 10.1061/(ASCE)MT.1943-5533.0001774
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Nanopartículas para la consolidación del fuerte español de Bizerta se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Nanopartículas de oligoquitosano para terapia génica
- Nanopartículas de hierro contra el lindano
- Nanopartículas lipídicas como vectores en terapia génica
Y el óleo se hizo cine
Desde que los hermanos Lumière crearon el primer cinematógrafo, el conocido como séptimo arte ha sufrido un sinfín de revoluciones desde el punto de vista técnico. Algunas, en tiempos realmente lejanos, como aquella que dio voz a un mudo Charles Chaplin o la que permitió apreciar en technicolor que las baldosas que pisaba Dorothy eran de color amarillo chillón. Décadas más tarde George Lucas reinventó los efectos especiales para transportarnos por una galaxia muy lejana a bordo del Halcón Milenario y su amigo Steven Spilberg se sirvió de maquetas hiperrealistas para hacernos pensar que cada vez que un vaso de agua temblase aparecería un Tiranosaurio dispuesto a devorarnos. Ya en tiempos más recientes, James Cameron explotó las posibilidades del cine en 3D y nos rodeó de unos peculiares seres azules con los que reventó los récords de recaudación. Pero, hay otra pequeña revolución en marcha, una que se fragua silenciosamente en Gdansk, esa agradable ciudad a orillas del Báltico que ya parece haber olvidado que fue el lugar donde estalló el más ignominioso capítulo de la historia de la humanidad cuando en los mapas figuraba como Ciudad libre de Danzing.
Probablemente esta revolución no cambie el modo de hacer cine. Incluso habrá quien lo vea como un paso atrás en el avance de una industria cada vez más controlada por ordenadores pero, lo cierto es que, se trata de un proyecto que justifica por partida doble que al cine se le llame arte. Hablo de Loving Vincent y sólo necesitaréis ver este tráiler de un minuto para entender a lo que me refiero:
Dorota Kobiela y el ganador de un Oscar Hugh Welchman se embarcaron hace unos seis años en un ambicioso proyecto al que hace unas semanas le daban las últimas pinceladas. No, no aprovecho que se trata de una película sobre van Gogh para hacer una metáfora fácil. Literalmente, el último fotograma de los 64000 que componen la película, fue pintado hace apenas unos días. Y es que, Loving Vincent, es una película diferente, es una película hecha en su totalidad a base de pinturas al óleo.
Como ya dijo quien cede el nombre a la película: “Solo podemos hablar a través de nuestras pinturas”. Quizás por eso, cuando Kobiela y Welchman tejieron la historia sobre la vida de van Gogh, decidieron que para que la obra se impregnase del espíritu del pintor holandés debían huir de la tecnología digital. Y no solo eso, volvieron a los orígenes del mundo de la animación y les dieron una vuelta de tuerca. Desarrollaron una nueva tecnología que les permitió implementar un peculiar proceso creativo para realizar cada uno de los aproximadamente 900 planos de los que consta el filme. Primero, se rodaron las escenas con actores y actrices reales usando la técnica croma (esa en la que se emplea un telón verde de fondo). Estas escenas se proyectaron sobre lienzos para ser transformadas en óleos por más de una centena de pintores y pintoras de todas partes del mundo que imitaban el característico estilo de van Gogh. Tras fotografiar la pintura correspondiente a un fotograma pintaban el siguiente y lo volvían a fotografiar y así, sucesivamente, hasta tener un plano con decenas de fotogramas. Una titánica tarea en la que se invierten meses para conseguir unos pocos segundos de metraje. Eso sí, una vez editada la secuencia de fotogramas se consiguen maravillas como las que habéis visto en el tráiler. Podéis entender mucho mejor el proceso creativo en este vídeo de la BBC.
![óleo //es.wikipedia.org/wiki/El_caf%C3%A9_de_noche#/media/File:Vincent_Willem_van_Gogh_076.jpg]](http://culturacientifica.com/app/uploads/2016/12/Imagen1-640x494.jpg) Imagen 1. “El café de noche” (72×92 cm) de Vincent van Gogh (1888). Fuente
Imagen 1. “El café de noche” (72×92 cm) de Vincent van Gogh (1888). Fuente
Por si imitar el estilo del pelirrojo loco no era suficiente, se han empleado más de cien de sus obras para crear los escenarios de la película. Podremos visitar el célebre Dormitorio en Arlés, ver una partida de billar en El café de noche o contemplar La noche estrellada. Igualmente, muchos rostros nos resultarán familiares ya que parecen retratos que se escapan de sus marcos para cobrar vida. En la Imagen 2 tenéis el formidable resultado de juntar la a un actor de carne y hueso (Douglas Booth) con una obra de van Gogh. Ese joven de gabardina amarilla es el protagonista, Armand Roulin, que sin darse cuenta se verá envuelto en la misteriosa muerte del pintor holandés, lo que sirve de hilo conductor de la película. Y aunque puede que Douglas Booth no sea un actor de mucho renombre, eso no significa que no vayamos a encontrar caras familiares entre el reparto como la de Saoirse Ronan (dos nominaciones al Oscar con apenas 22 años), Helen McCrort (Polly en Peaky Blinders) o Jerome Flynn (Bron en Game of Thrones).
 Imagen 2. De izquierda a derecha: Douglas Booth durante el rodaje de Loving Vincent, “Retrato de Armand Roulin” (65×54 cm) de Vincent van Gogh (1888) y resultado final del fotograma de la película Loving Vincent. Fuente: Twitter de @lovingvincent
Imagen 2. De izquierda a derecha: Douglas Booth durante el rodaje de Loving Vincent, “Retrato de Armand Roulin” (65×54 cm) de Vincent van Gogh (1888) y resultado final del fotograma de la película Loving Vincent. Fuente: Twitter de @lovingvincent
A estas alturas espero que, como yo, estés contando los días para el estreno de la película. También es posible que te estés preguntando si el autor de este artículo ha decidido retirarse del mundo científico y tiene ahora pretensiones de crítico de cine. Nada más lejos de la realidad. Pero resulta que la existencia de esta original película me sirve para hablar de algo con lo que todos y todas estamos familiarizados pero que quizás no conozcamos tan bien: la pintura al óleo.
Y es que ¿quién no ha leído “óleo sobre lienzo” en los rótulos de algún museo? Habrá incluso quien haya hecho sus pinitos con esta técnica. Pero, ¿sabemos realmente lo que es un óleo? No hay que ser catedrático en etimología para intuir que tras esa palabra se esconde una técnica pictórica vinculada, de un modo u otro, al aceite. De hecho, si consultamos el diccionario de Real Academia nos encontramos con que sorprendentemente (o no) la primera acepción no tiene conexión alguna con en el arte: “Del lat. oleum Aceite de origen vegetal, especialmente el de oliva”.
Vale, entonces algo tendrá que ver la pintura al óleo con esos líquidos indispensables en nuestras cocinas. Además, teniendo en cuenta que se usa cera de abeja o leche de vaca para aglutinar pigmentos, ¿por qué no usar aceite? Es un medio líquido, fácil de obtener y muy manejable. Entonces, ¿podría dedicarse Arguiñano a publicitar aceite de oliva virgen extra para artistas? ¿Sirve cualquier aceite para pintar un cuadro? Como muchas otras veces, la respuesta está en la química. Aunque por si acaso ya adelanto a los amantes del oro líquido que nunca les faltará este aceite, o por lo menos, no por culpa de la pintura.
Empecemos por el principio. Los aceites vegetales están formando mayoritariamente por un tipo de lípidos llamados triacilgicéridos, aunque quizás os suene más si digo triglicéridos. Exactamente, eso que junto al colesterol tanto nos preocupa al recibir los resultados de una analítica. Estos temidos compuestos están formados por una molécula de glicerol y tres ácidos grasos que se unen formando lo que se denominan ésteres (ver Imagen 3). Precisamente, será la naturaleza y la abundancia de estos ácidos grasos los que condicionen las propiedades de los diferentes aceites.
![//upload.wikimedia.org/wikipedia/commons/thumb/b/be/Fat_triglyceride_shorthand_formula.PNG/300px-Fat_triglyceride_shorthand_formula.PNG]](http://culturacientifica.com/app/uploads/2016/12/Imagen3-640x329.jpg) Imagen 3. Un triacilglícerido que contiene un ácido graso saturado (1: ácido esteárico), un ácido graso insaturado (2: ácido oleico) y un ácido graso poliinsaturado (3: ácido linolénico). Fuente: Modificado de Wikimedia Commons
Imagen 3. Un triacilglícerido que contiene un ácido graso saturado (1: ácido esteárico), un ácido graso insaturado (2: ácido oleico) y un ácido graso poliinsaturado (3: ácido linolénico). Fuente: Modificado de Wikimedia Commons
Como podéis ver en la Imagen 3, los ácidos grasos contienen una larga cadena en la que los átomos de carbonos (cada uno de los diferentes vértices) se unen entre sí (también se unen a átomos de hidrogeno aunque estos no se representan en la imagen). Pues bien, hay dos factores que tenemos que tener en cuenta a la hora de explicar las propiedades de los aceites: la longitud de estas cadenas y el número de insaturaciones. Y aquí tenemos otra palabra que relacionaréis con el mundo de la nutrición. Cuando hablamos de grasas saturadas o insaturadas lo que estamos haciendo es referirnos a como se unen los átomos de carbonos en estas cadenas. Una insaturación no es otra cosa que dos átomos de carbono que se unen mediante un doble enlace (de ahí que haya dobles líneas entre algunos puntos de las cadenas de ácidos grasos). Por ejemplo, el triglicérido de la imagen anterior tiene un ácido graso saturado en la primera posición (ácido esteárico), uno con una insaturación en la segunda (ácido oleico) y otro con tres insaturaciones en la tercera (ácido linolénico). Este detalle, que podría parecernos anecdótico, es de vital importancia para entender tanto las propiedades fisicoquímicas de los aceites como las de las grasas. De hecho, la distinción que hacemos entre estas dos substancias se debe en gran medida a los dobles enlaces. Las grasas son sólidas a temperatura ambiente porque son ricas en triacilglicéridos saturados que tienen un punto de fusión más alto. Los aceites en cambio son líquidos porque contienen un porcentaje alto de triacilglicéridos insaturados tienen un punto de fusión más bajo. Algunos aceites son ricos en grasas saturadas, pero al ser cadenas muy pequeñas siguen siendo líquidos. Aunque eso ya es harina de otro costal.
Volviendo al tema que nos ocupa, ¿cuál es la importancia de la química de los aceites en la técnica pictórica favorita del gran van Gogh? Pues evidentemente la clave está en los dobles enlaces de los ácidos grasos (si no, nos hubiésemos ahorrado esa pequeña lección de química orgánica). Resulta que estos enlaces tienen un enemigo implacable, un gas omnipresente sin la que nosotros apenas podríamos disfrutar unos segundos de Los girasoles: el oxígeno. Esta molécula ataca sin piedad a los dobles enlaces causando diferentes tipos de reacciones. Algunas pueden tener consecuencias desagradables como el enranciamiento de aceites y grasas comestibles. Otras, en cambio, son indispensables para que todavía hoy podamos observar obras como el Matrimonio Arnolfini o La Mona Lisa. Me refiero a las reacciones de polimerización a través de las cuales algunos aceites se secan y crean una capa pictórica. ¿Adivináis cuáles son esos aceites?
¡Bingo! Los que tienen ácidos grasos con muchos dobles enlaces. Se conocen como secantes y entre ellos el más importante es, sin ninguna duda, el aceite de linaza. Su gran cantidad de ácido linolénico (tres insaturaciones) y linoleico (dos insaturaciones) explica que históricamente haya sido el más empleado. En cualquier caso, existen otros aceites como el de adormidera, el de nuez o el de girasol que también pueden ser adecuados e incluso más apreciados según la aplicación que se les quiera dar. El aceite de oliva, tan estimado en la cultura mediterránea, resulta inadecuado ya que es extremadamente rico en ácido oleico (tan sólo una insaturación) y contiene muy pocas grasas poliinsaturadas.
![[Tabla 1] [Abundancia en ácidos grasos de diferentes aceites (modificado de 1)]](http://culturacientifica.com/app/uploads/2016/12/Tabla1-640x228.jpg) Tabla 1. Abundancia en ácidos grasos de diferentes aceites. Fuente: Modificado de Doerner (1998)
Tabla 1. Abundancia en ácidos grasos de diferentes aceites. Fuente: Modificado de Doerner (1998)
Veamos ahora que es lo que sucede desde que se deposita una pincelada de óleo sobre un soporte hasta que la tenemos delante de los ojos. Primero, el aceite comenzará un proceso de oxidación en el que surgirán radicales libres y se formarán peróxidos (ver Imagen 4). Este proceso dura unos pocos días y hace que el aceite gane peso debido a la absorción de oxígeno. Como los peróxidos son muy inestables, reaccionarán con los triacilglicéridos cercanos, de modo que se entrelazarán en una especie de red (polímero) que se denomina linoxina. Gracias a este proceso, que dura meses, y durante el cual el aceite pierde peso por la aparición de compuestos volátiles, se forma una capa pictórica que se adhiere al soporte. Puesto que en el camino, algunos de los triacilglicéridos que no reacciones quedarán atrapados en forma líquida dentro de la retícula, no sólo se obtendrá una película resistente sino también elástica y capaz de aguantar mejor las tensiones. En resumidas cuentas una capa ideal para el arte pictórico.
![//upload.wikimedia.org/wikipedia/commons/thumb/3/33/DryingOilDiene%27.png/800px-DryingOilDiene%27.png]](http://culturacientifica.com/app/uploads/2016/12/Imagen4.jpg) Imagen 4. Proceso esquematizado de la polimerización de los aceites secantes. La cadena del ácido graso insaturado (1) reacciona con el oxígeno para formar un peróxido (2). A su vez este peróxido reaccionará con el doble enlace de otro ácido graso formando un polímero (3). Fuente: Modificado de Wikimedia Commons
Imagen 4. Proceso esquematizado de la polimerización de los aceites secantes. La cadena del ácido graso insaturado (1) reacciona con el oxígeno para formar un peróxido (2). A su vez este peróxido reaccionará con el doble enlace de otro ácido graso formando un polímero (3). Fuente: Modificado de Wikimedia Commons
Obviamente, pese a todas sus virtudes, el óleo no es inmune al paso del tiempo y puede sufrir procesos químicos de amarilleamiento o una oxidación en mayor grado que acabe deteriorando la linoxina. Sin olvidarnos de procesos físicos por culpa de las tensiones antes mencionadas que provocan los característicos craquelados de obras antiguas (ver Imagen 5).
![//upload.wikimedia.org/wikipedia/commons/2/2e/Mona_Lisa_detail_eyes.jpg]](http://culturacientifica.com/app/uploads/2016/12/Imagen5-640x333.jpg) Imagen 5. Craquelados de La Mona Lisa de Leonardo da Vinci (ca. 1503). Fuente
Imagen 5. Craquelados de La Mona Lisa de Leonardo da Vinci (ca. 1503). Fuente
Ahora rebobinemos unas líneas. He dicho que el proceso de secado dura meses (de hecho las reacciones químicas siguen sucediendo en el óleo eternamente). ¿Significa eso que hay que esperar tanto tiempo para realizar un cuadro usando esta técnica? Afortunadamente no. Desde hace siglos se sabe que existen ciertos catalizadores, como pueden ser las sales u óxidos de plomo, cobalto y manganeso, que añadidas al aceite permiten acelerar el proceso de secado. Hoy en día se emplean catalizadores sintéticos o se realiza un tratamiento térmico al aceite que permite que el secado sea más rápido. Así, aunque desgraciadamente tendremos que esperar a bien entrado el 2017 para disfrutar Loving Vincent, esto no es debido al proceso de secado de las pinturas sino al proceso de edición posterior. En cualquier caso, espero que, llegado el momento, apreciéis que cada fotograma de la película es una pequeña obra de arte al óleo, y que tras cada pincelada de esa obra se esconde un complejo proceso químico.
Para saber más:
[1] Max Doerner (1998) Los materiales de pintura y su empleo en el arte. Editorial Reverte.
[2] Mauro Matteini y Arcangelo Moles (2004) La química de la restauración. Editorial Nerea.
Sobre el autor: Oskar González es profesor en la facultad de Ciencia y Tecnología y en la facultad de Bellas Artes de la UPV/EHU.
El artículo Y el óleo se hizo cine se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La posguerra que nos hizo
- Cine y ciencia de la mano
- #Naukas13 Astronomía en el cine, errores de película

